X что значит в алгебре: Таблица знаков (символов) в алгебре и их значения

Содержание

Таблица знаков (символов) в алгебре и их значения

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

MicroExcel.ru Математика Знаки и символы в алгебре

Ниже представлена таблица с основными математическими символами и знаками, которые используются в алгебре 7 класса и старше.


Символ / знак	Название	Значение / описание	Пример
x	переменная x	неизвестная переменная, которую нужно найти	если 2x = 6, значит x = 3
≡	эквивалентность	логическая равнозначность или эквиваленция	A ≡ B, A эквивалентно B
~	приблизительно равно	приближенное равенство (слабое)	15 ~ 14
≈	приблизительно равно	приближенное равенство	01) ≈ 0.01</nobr>» data-order=»<nobr>sin (0.01) ≈ 0.01</nobr>»>sin (0.01) ≈ 0.01
∝	пропорционально	пропорциональность величин	y ∝ x, если: y = kx, а k — константа
∞	бесконечность	отсутствие границ или количественной меры
≪	намного меньше	A намного меньше, чем B	5 ≪ 50000
≫	намного больше	A намного больше, чем B	50000 ≫ 5
( )	круглые скобки	выражение в скобках считается в первую очередь	4 ⋅ (2+3) = 20
[ ]	квадратные скобки	выражение в скобках считается в первую очередь	[(6-3)⋅(2+7)] = 27
{ }	фигурные скобки	различное применение
⌊x⌋	нижние квадратные скобки	округление числа x до нижнего целого (пол)	3⌋ = 5</nobr>» data-order=»<nobr>⌊5.3⌋ = 5</nobr>»>⌊5.3⌋ = 5
⌈x⌉	верхние квадратные скобки	округление числа x до верхнего целого (потолок)	3⌉ = 6</nobr>» data-order=»<nobr>⌈5.3⌉ = 6</nobr>»>⌈5.3⌉ = 6
x!	восклицательный знак	факториал	5! = 1⋅2⋅3⋅4⋅5 = 120
log	логарифм	log_ab Это степень, в которую нужно возвести a, чтобы получить b	log₂8=3
\| x \|	одиночная вертикальная черта	абсолютная величина (модуль)	\| -7 \| = 7
f (x)	функция с переменной x	величина x определяет значение величины f (x)	f (x) = 5x + 2
(f ∘ g)	композиция функций	е. применение одной функции к результату другой» data-order=»<nobr>(f∘ g) (x) = f (g(x)),</nobr><br>т.е. применение одной функции к результату другой»>(f∘ g) (x) = f (g(x)), т.е. применение одной функции к результату другой	f (x)=5x, g (x)=x-2 ⇒ (f ∘ g (x)) = 5 (x-2)
(a,b)	открытый интервал	(a,b) = {x \| a < x < b}	x ∈ (3,7)
[a,b]	закрытый интервал	[a,b] = {x \| a ≤ x ≤ b}	x ∈ [3,7]
∆	дельта	изменение/разница	∆t = t₂ — t₁
∆	дискриминант	Δ = b² — 4ac	y = x² + 3x — 5 Δ = 3² — 4⋅1⋅(-5) = 29
∑	сигма	сумма всех значений в выбранном диапазоне	..+x<sub>n</sub></em></span></nobr>» data-order=»<nobr><span class="math"><em>∑ x<sub>i</sub>= x<sub>1</sub>+x<sub>2</sub>+…+x<sub>n</sub></em></span></nobr>»>∑ x_i= x₁+x₂+…+x_n
∑∑	сигма	двойная сигма	png" class="stbSkipLazy alignnone size-full" width="230" height="400" data-full="https://microexcel.ru/wp-content/uploads/2020/01/formula-dvoynaya-sigma.png" />» data-order=»<img src="https://microexcel.ru/wp-content/uploads/2020/01/formula-dvoynaya-sigma.png" class="stbSkipLazy alignnone size-full" width="230" height="400" data-full="https://microexcel.ru/wp-content/uploads/2020/01/formula-dvoynaya-sigma.png" />»>
∏	заглавная буква «пи»	произведение множителей в выбранном диапазоне	.. ⋅ x<sub>n</sub></em></span></nobr>» data-order=»<nobr><span class="math"><em>∏ x<sub>i</sub>= x<sub>1</sub> ⋅ x<sub>2</sub> ⋅ … ⋅ x<sub>n</sub></em></span></nobr>»>∏ x_i= x₁ ⋅ x₂ ⋅ … ⋅ x_n
e	e (число) или число Эйлера	718281828…</nobr>» data-order=»<nobr><span class="math"><em>e</em></span> = 2.718281828…</nobr>»>e = 2.718281828…
γ	Постоянная Эйлера — Маскерони	5772156649…</nobr>» data-order=»<nobr><span class="math"><em>γ</em></span> = 0.5772156649…</nobr>»>γ = 0.5772156649…
φ	золотое сечение	golden ratio constant
π	число «пи»	141592654…</nobr><br>Это математическая константа, которая выражает отношение длины окружности к её диаметру.» data-order=»<nobr><span class="math"><em>π</em></span> = 3.141592654…</nobr><br>Это математическая константа, которая выражает отношение длины окружности к её диаметру.»>π = 3.141592654… Это математическая константа, которая выражает отношение длины окружности к её диаметру.

microexcel.ru

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

Таблица математических символов | это.

.. Что такое Таблица математических символов?

В математике повсеместно используются символы для упрощения и сокращения текста. Ниже приведён список наиболее часто встречающихся математических обозначений, соответствующие команды в TeXе, объяснения и примеры использования.

Кроме указанных символов, иногда используются их зеркальные отражения, например, обозначает то же, что и

Знаки операций или математические символы — знаки, которые символизируют определённые математические действия со своими аргументами.

Символ (Unicode)	Название	Значение	Пример
	Произношение
	Раздел математики
⇒ → ⊃	Импликация, следование	означает «если верно, то также верно». (→ может использоваться вместо ⇒ или для обозначения функции, см. ниже.) (⊃ может использоваться вместо ⇒, или для обозначения надмножества, см. ниже.).	верно, но неверно (так как также является решением).
	«влечёт» или «если…, то»
	везде
⇔	Равносильность	означает « верно тогда и только тогда, когда верно».
	«если и только если» или «равносильно»
	везде
∧	Конъюнкция	истинно тогда и только тогда, когда и оба истинны.	, если — натуральное число.
	«и»
	Математическая логика
∨	Дизъюнкция	истинно, когда хотя бы одно из условий и истинно.	, если — натуральное число.
	«или»
	Математическая логика
¬	Отрицание	истинно тогда и только тогда, когда ложно .
	«не»
	Математическая логика
∀	Квантор всеобщности	обозначает « верно для всех ».
	«Для любых», «Для всех»
	Математическая логика
∃	Квантор существования	означает «существует хотя бы один такой, что верно »	(подходит число 5)
	«существует»
	Математическая логика
=	Равенство	обозначает « и обозначают одно и то же значение».	1 + 2 = 6 − 3
	«равно»
	везде
:= :⇔	Определение	означает « по определению равен ». означает « по определению равносильно »	(Гиперболический косинус) (Исключающее или)
	«равно/равносильно по определению»
	везде
{ , }	Множество элементов	означает множество, элементами которого являются , и .	(множество натуральных чисел)
	«Множество…»
	Теория множеств
{ \| } { : }	Множество элементов, удовлетворяющих условию	означает множество всех таких, что верно .
	«Множество всех… таких, что верно…»
	Теория множеств
∅ {}	Пустое множество	и означают множество, не содержащее ни одного элемента.
	«Пустое множество»
	Теория множеств
∈ ∉	Принадлежность/непринадлежность к множеству	означает « является элементом множества » означает « не является элементом множества »
	«принадлежит», «из» «не принадлежит»
	Теория множеств
⊆ ⊂	Подмножество	означает «каждый элемент из также является элементом из ». обычно означает то же, что и . Однако некоторые авторы используют , чтобы показать строгое включение (то есть ).
	«является подмножеством», «включено в»
	Теория множеств
⊇ ⊃	Надмножество	означает «каждый элемент из также является элементом из ». обычно означает то же, что и . Однако некоторые авторы используют , чтобы показать строгое включение (то есть ).
	«является надмножеством», «включает в себя»
	Теория множеств
⊊	Собственное подмножество	означает и .
	«является собственным подмножеством», «строго включается в»
	Теория множеств
⊋	Собственное надмножество	означает и .
	«является собственным надмножеством», «строго включает в себя»
	Теория множеств
∪	Объединение	означает множество элементов, принадлежащих или (или обоим сразу).
	«Объединение … и …», «…, объединённое с …»
	Теория множеств
⋂	Пересечение	означает множество элементов, принадлежащих и , и .
	«Пересечение … и … », «…, пересечённое с …»
	Теория множеств
\	Разность множеств	означает множество элементов, принадлежащих , но не принадлежащих .
	«разность … и … », «минус», «… без …»
	Теория множеств
→	Функция	означает функцию с областью определения и областью прибытия (областью значений) .	Функция , определённая как
	«из … в»,
	везде
↦	Отображение	означает, что образом после применения функции будет .	Функцию, определённую как , можно записать так:
	«отображается в»
	везде
N или ℕ	Натуральные числа	означает множество или реже (в зависимости от ситуации).
	«Эн»
	Числа
Z или ℤ	Целые числа	означает множество
	«Зед»
	Числа
Q или ℚ	Рациональные числа	означает
	«Ку»
	Числа
R или ℝ	Вещественные числа, или действительные числа	означает множество всех пределов последовательностей из	( — комплексное число: )
	«Эр»
	Числа
C или ℂ	Комплексные числа	означает множество
	«Це»
	Числа
< >	Сравнение	обозначает, что строго меньше . означает, что строго больше .
	«меньше чем», «больше чем»
	Отношение порядка
≤ или ⩽ ≥ или ⩾	Сравнение	означает, что меньше или равен . означает, что больше или равен .
	«меньше или равно»; «больше или равно»
	Отношение порядка
≈	Приблизительное равенство	с точностью до означает, что 2,718 отличается от не больше чем на .	с точностью до .
	«приблизительно равно»
	Числа
√	Арифметический квадратный корень	означает неотрицательное действительное число, которое в квадрате даёт .
	«Корень квадратный из …»
	Числа
∞	Бесконечность	и суть элементы расширенного множества действительных чисел. Эти символы обозначают числа, меньшее/большее всех действительных чисел.
	«Плюс/минус бесконечность»
	Числа
\| \|	Модуль числа (абсолютное значение), модуль комплексного числа или мощность множества	обозначает абсолютную величину . обозначает мощность множества и равняется, если конечно, числу элементов .
	«Модуль»; «Мощность»
	Числа и Теория множеств
∑	Сумма, сумма ряда	означает «сумма , где принимает значения от 1 до », то есть .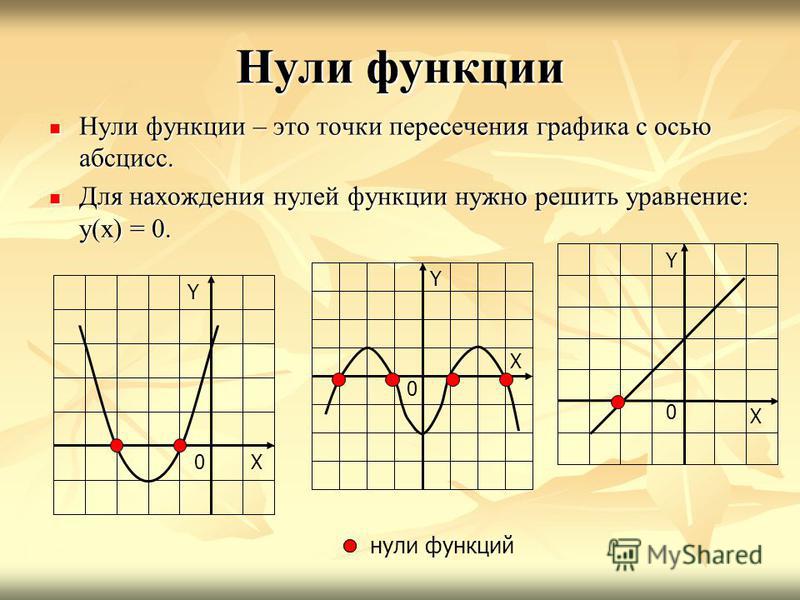 означает сумму ряда, состоящего из .
	«Сумма … по … от … до …»
	Арифметика, Математический анализ
∏	Произведение	означает «произведение для всех от 1 до », то есть
	«Произведение … по … от … до …»
	Арифметика
!	Факториал	означает «произведение всех натуральных чисел от 1 до включительно, то есть
	« факториал»
	Комбинаторика
∫	Интеграл	означает «интеграл от до функции от по переменной ».
	«Интеграл (от … до …) функции … по (или d)…»
	Математический анализ
df/dx f'(x)	Производная	или означает «(первая) производная функции от по переменной ».
	«Производная … по …»
	Математический анализ
	Производная -го порядка	или (во втором случае если — фиксированное число, то оно пишется римскими цифрами) означает «-я производная функции от по переменной ».
	«-я производная … по …»
	Математический анализ

Урок 11. многочлен p(x) и его корень. алгебраическое уравнение — Алгебра и начала математического анализа — 10 класс

Алгебра и начала математического анализа, 10 класс

Урок №11. Многочлен P(x) и его корень. Алгебраическое уравнение.

Перечень вопросов, рассматриваемых в теме

1) обобщенное понятие многочлена;

2) основные действия над многочленами;

3) определение алгебраического уравнения;

4) теорема Безу.

Глоссарий по теме

Многочлен P_n(x) = a _nx ⁿ+ a _{n – 1} x ^{n – 1} + a _{n – 2} x ^{n – 2} + . .. + a ₁ x + a ₀ , где a≠0, aₖ, k=0,1,2,3,…, aₖ,k=0,1,2,3,…,n — числа, x — переменная, называется многочленом n -ной степени .
Традиционно aₙ называется старшим коэффициентом, a₀ — свободным членом многочлена.

Стоит отметить, что каждый многочлен степени больше 2 можно разложить на множители.

Корнем многочлена Р(х) называют такое значение х, при котором многочлен обращается в нуль.

Теорема Безу. Остаток от деления многочлена Р(х) на двучлен х-а равен Р(а).

Следствие. Если число а является корнем многочлена Р(х), то многочлен

Рₙ(х)= a₀x ⁿ+ a₁ x ^{n – 1} + … + a_{n – 1} x + a_nделится без остатка на двучлен х-а.

Алгебраическое уравнение (полиномиальное уравнение) — уравнение вида P(x₁, x₂, …, x_n)=0,

где P — многочлен от переменных x₁, x₂, …, x_n, которые называются неизвестными.

Коэффициенты многочлена P обычно берутся из некоторого множества F, и тогда уравнение P(x₁, x₂, …, x_n)=0 называется алгебраическим уравнением над множеством F.

Степенью алгебраического уравнения называют степень многочлена P.

Значения переменных x₁, x₂, …, x_n, которые при подстановке в алгебраическое уравнение обращают его в тождество, называются корнями этого алгебраического уравнения.

Основная литература:

Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл. – М.: Просвещение, 2014.

Дополнительная литература:

Шабунин М.И., Ткачева М.В., Федорова Н.Е. Дидактические материалы Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл. – М.: Просвещение, 2017.

Теоретический материал для самостоятельного изучения

Общая теория многочленов многих переменных далеко выходит за рамки школьного курса.

Мы рассмотрим многочлены одной действительной переменной, да и то в простейших случаях. Рассмотрим многочлены одной переменной, приведённые к стандартному виду.

Многочлен ax + b, где a≠0, a, b — числа, x — переменная, называется многочленом первой степени.
Многочлен ax²+bx+c, где a≠0, a, b, c — числа, x — переменная, называется многочленом второй степени (квадратным трёхчленом, квадратичной функцией).
Многочлен ax³+bx²+cx+d, где a≠0, a, b, c, d — числа, x — переменная, называется многочленом третьей степени.

Вообще, многочлен P_n(x) = a _nx ⁿ+ a _{n – 1} x ^{n – 1} + a _{n – 2} x ^{n – 2} + … + a ₁ x + a ₀, где a≠0, aₖ, k=0,1,2,3,…, aₖ,k=0,1,2,3,…,n — числа, x — переменная, называется многочленом n -ной степени.
Традиционно aₙ называется старшим коэффициентом, а a₀ — свободным членом многочлена.

Стоит отметить, что каждый многочлен степени больше 2 можно разложить на множители.

Корнем многочлена Р(х) называют такое значение х, при котором многочлен обращается в нуль.

Алгебраическое уравнение (полиномиальное уравнение) — уравнение вида

P(x₁, x₂, …, x_n)=0,

где P — многочлен от переменных x₁, x₂, …, x_n, которые называются неизвестными.

Степенью алгебраического уравнения называют степень многочлена P.

Например, уравнение

является алгебраическим уравнением четвертой степени от трёх переменных (с тремя неизвестными) над множеством вещественных чисел.

Теорема Безу, невзирая на кажущуюся простоту и очевидность, является одной из базовых теорем теории многочленов. В данной теореме алгебраические характеристики многочленов (они позволяют работать с многочленами как с целыми числами) связываются с их функциональными характеристиками (которые позволяют рассматривать многочлены как функции).

Теорема Безу. Остаток от деления многочлена Р(х) на двучлен х-а равен Р(а).

Доказательство. Разделим Р(х) c остатком на (x — а).

Получим Р(х)= (x — а)·Q(х) + R; по определению остатка, многочлен r либо равен 0, либо имеет степень, меньшую степени (x — a), т.е. меньшую 1. Но степень многочлена меньше 1 только в случае, когда она равна 0, и поэтому в обоих случаях R на самом деле является числом – нулем или отличным от нуля.

Подставив теперь в равенство Р(х)= (x — а)·Q(х) + R значение x = a, мы получим Р(a)= (a — а)Q(х) + R, P(a) = R, так что действительно R = P(a).

Эту закономерность отметил и математик Безу.

Следствие. Если число а является корнем многочлена Р(х), то многочлен

Рₙ(х)= a₀x ⁿ+ a₁ x ^{n – 1} + … + a_{n – 1} x + a_nделится без остатка на двучлен х-а.

Историческая справка

Этьенн Безу — французский математик, член Парижской Академии Наук (с 1758 года), родился в Немуре 31 марта 1730 года и умер 27 сентября 1783 года. С 1763 года Безу преподавал математику в училище гардемаринов, а с 1768 года и в королевском артиллерийском корпусе.

Основные работы Этьенна Безу относятся к высшей алгебре, они посвящены созданию теории решения алгебраических уравнений.

В теории решения систем линейных уравнений он содействовал возникновению теории определителей, развивал теорию исключения неизвестных из систем уравнений высших степеней, доказал теорему (впервые сформулированную Маклореном) о том, что две кривые порядка m и n пересекаются не более чем в mn точках.

Во Франции и за её границей вплоть до 1848 года был очень популярен его шеститомный «Курс математики», написанный им в 1764-69 годах.

Безу развил метод неопределённых множителей. В элементарной алгебре его именем назван способ решения систем уравнений, основанный на этом методе.

Часть трудов Безу посвящена внешней баллистике.

Именем ученого названа одна из основных теорем алгебры.

Примеры алгебраических уравнений

алгебраическое уравнение с одним неизвестным -уравнение вида , где n- натуральное число.
Линейное уравнение от одной переменной ax+b=0, a
Квадратное уравнение ax²+bx+c=0, a.

Примеры и разбор решения заданий тренировочного модуля

Пример 1.

Разложим на множители многочлен:

Решение: )

Ответ: ))

Пример 2.

Решить уравнение: х⁴ — x³ — 6x² — x + 3 = 0.

Решение: Целые корни многочлена Р(х) = х⁴ — x³ — 6x² — x + 3 должны быть делителями свободного члена, так что это могут быть числа -1, 1, 3, -3.

Подберем корень по схеме Горнера:

	1	-1	-6	-1	3
-1	1	-2	-4	3	0

х⁴ — x³ — 6x² — x + 3= (х + 1)(х³ -2х² – 4х +3) =0

	1	-2	-4	3
-1	1	-3	-1	4
1	1	-1	-5	-2
-3	1	-5	11	-30
3	1	1	-1	0

Q(x) = х³ -2х² – 4х +3=(x- 3)(x² + x -1)=0

x² + x -1 =0

D=5

Ответ: -1; 3;

Метод интервалов — материалы для подготовки к ЕГЭ по Математике

Метод интервалов – простой способ решения дробно-рациональных неравенств. Так называются неравенства, содержащие рациональные (или дробно-рациональные) выражения, зависящие от переменной.

1. Рассмотрим, например, такое неравенство

Метод интервалов позволяет решить его за пару минут.

В левой части этого неравенства – дробно-рациональная функция. Рациональная, потому что не содержит ни корней, ни синусов, ни логарифмов – только рациональные выражения. В правой – нуль.

Метод интервалов основан на следующем свойстве дробно-рациональной функции.

Дробно-рациональная функция может менять знак только в тех точках, в которых она равна нулю или не существует.

Найдем нули функции в левой части нашего неравенства. Для этого разложим числитель на множители. (Если вы не помните, что такое нули функции и знак функции на промежутке – смотрите статью «Исследование графика функции»).

Напомним, как раскладывается на множители квадратный трехчлен, то есть выражение вида .

, где и — корни квадратного уравнения .

Получим:

Рисуем ось и расставляем точки, в которых числитель и знаменатель обращаются в нуль.

Нули знаменателя и — выколотые точки, так как в этих точках функция в левой части неравенства не определена (на нуль делить нельзя). Нули числителя и — закрашены, так как неравенство нестрогое. При и наше неравенство выполняется, так как обе его части равны нулю.

Эти точки разбивают ось на промежутков.

Определим знак дробно-рациональной функции в левой части нашего неравенства на каждом из этих промежутков. Мы помним, что дробно-рациональная функция может менять знак только в тех точках, в которых она равна нулю или не существует. Это значит, что на каждом из промежутков между точками, где числитель или знаменатель обращаются в нуль, знак выражения в левой части неравенства будет постоянным — либо «плюс», либо «минус».

И поэтому для определения знака функции на каждом таком промежутке мы берем любую точку, принадлежащую этому промежутку. Ту, которая нам удобна.
. Возьмем, например, и проверим знак выражения в левой части неравенства. Каждая из «скобок» отрицательная. Левая часть имеет знак .

Следующий промежуток: . Проверим знак при . Получаем, что левая часть поменяла знак на .

. Возьмем . При выражение положительно — следовательно, оно положительно на всем промежутке от до .

При левая часть неравенства отрицательна.

И, наконец, . Подставим и проверим знак выражения в левой части неравенства. Каждая «скобочка» положительна. Следовательно, левая часть имеет знак .

Мы нашли, на каких промежутках выражение положительно. Осталось записать ответ:

Ответ: .

Обратите внимание: знаки на промежутках чередуются. Это произошло потому, что при переходе через каждую точку ровно один из линейных множителей поменял знак, а остальные сохранили его неизменным.

Мы видим, что метод интервалов очень прост. Чтобы решить дробно-рациональное неравенство методом интервалов, приводим его к виду:

, или , или , или .

(в левой части — дробно-рациональная функция, в правой — нуль).

Затем — отмечаем на числовой прямой точки, в которых числитель или знаменатель обращаются в нуль.
Эти точки разбивают всю числовую прямую на промежутки, на каждом из которых дробно-рациональная функция сохраняет свой знак.
Остается только выяснить ее знак на каждом промежутке.
Мы делаем это, проверяя знак выражения в любой точке, принадлежащей данному промежутку. После этого — записываем ответ. Вот и всё.

Но возникает вопрос: всегда ли знаки чередуются? Нет, не всегда! Надо быть внимательным и не расставлять знаки механически и бездумно.

2. Рассмотрим еще одно неравенство.

Снова расставляем точки на оси . Точки и — выколотые, поскольку это нули знаменателя. Точка — тоже выколота, поскольку неравенство строгое.

При числитель положителен, оба множителя в знаменателе отрицательны. Это легко проверить, взяв любое число с данного промежутка, например, . Левая часть имеет знак :

При числитель положителен; первый множитель в знаменателе положителен, второй множитель отрицателен. Левая часть имеет знак :

При ситуация та же! Числитель положителен, первый множитель в знаменателе положителен, второй отрицателен. Левая часть имеет знак :

Наконец, при все множители положительны, и левая часть имеет знак :

Ответ: .

Почему нарушилось чередование знаков? Потому что при переходе через точку «ответственный» за неё множитель не изменил знак. Следовательно, не изменила знак и вся левая часть нашего неравенства.

Вывод: если линейный множитель стоит в чётной степени (например, в квадрате), то при переходе через точку знак выражения в левой части не меняется. В случае нечётной степени знак, разумеется, меняется.

3. Рассмотрим более сложный случай. От предыдущего отличается тем, что неравенство нестрогое:

Левая часть та же, что и в предыдущей задаче. Та же будет и картина знаков:

Может, и ответ будет тем же? Нет! Добавляется решение Это происходит потому, что при и левая, и правая части неравенства равны нулю — следовательно, эта точка является решением.

Ответ: .

В задаче на ЕГЭ по математике такая ситуация встречается часто. Здесь абитуриенты попадают в ловушку и теряют баллы. Будьте внимательны!

4. Что делать, если числитель или знаменатель не удается разложить на линейные множители? Рассмотрим такое неравенство:

Квадратный трехчлен на множители разложить нельзя: дискриминант отрицателен, корней нет. Но ведь это и хорошо! Это значит, что знак выражения при всех одинаков, а конкретно — положителен. Подробнее об этом можно прочитать в статье о свойствах квадратичной функции.

И теперь мы можем поделить обе части нашего неравенства на величину , положительную при всех . Придём к равносильному неравенству:

— которое легко решается методом интервалов.

Обратите внимание — мы поделили обе части неравенства на величину, о которой точно знали, что она положительна. Конечно, в общем случае не стоит умножать или делить неравенство на переменную величину, знак которой неизвестен.

5. Рассмотрим еще одно неравенство, на вид совсем простое:

Так и хочется умножить его на . Но мы уже умные, и не будем этого делать. Ведь может быть как положительным, так и отрицательным. А мы знаем, что если обе части неравенства умножить на отрицательную величину — знак неравенства меняется.

Мы поступим по другому — соберём всё в одной части и приведём к общему знаменателю. В правой части останется нуль:

И после этого — применим метод интервалов.

что это такое, как появилась, почему считают «царицей наук»?

Алгебра — это раздел математики, занимающийся символами и правилами обращения с этими символами. В элементарной алгебре эти символы (сегодня пишутся латинскими и греческими буквами) представляют величины без фиксированных значений, известные как переменные. Точно так же, как предложения описывают отношения между конкретными словами, в алгебре уравнения описывают отношения между переменными.

Полина Колесо

Возьмём следующий пример. Есть два поля общей площадью 1800 квадратных ярдов. Урожайность с каждого поля составляет ⅔ галлона зерна на квадратный ярд и ½ галлона на квадратный ярд. Первое поле дало на 500 галлонов больше, чем второе. Какова площадь каждого поля?

Распространено мнение, что такие задачи придуманы, чтобы мучить студентов, и это может быть недалеко от истины. Эта задача почти наверняка была написана, чтобы помочь учащимся понять математику, но что особенного в ней, так это то, что ей почти 4000 лет! Согласно Жаку Сезиано в «Введении в историю алгебры» , эта задача основана на вавилонской глиняной табличке около 1800 г. до н.э. Поскольку алгебра уходит своими корнями в древнюю Месопотамию, она занимает центральное место во многих достижениях науки, техники и цивилизации в целом. Язык алгебры значительно менялся на протяжении истории всех цивилизаций, унаследовавших его (включая нашу собственную).

В Тобольске восьмиклассникам предложили решить необычную задачку в рамках «профориентации». Возможно, необычный пример мог выявить будущих криминалистов!

Как решать это уравнение?

Сегодня запишем задачу так:

х + у = 1800

⅔∙х – ½∙у = 500

Буквы x и y обозначают площади полей. Первое уравнение понимается просто как «сложение двух площадей даёт общую площадь 1800 квадратных ярдов». Второе уравнение более тонкое. Поскольку x — это площадь первого поля, а урожайность первого поля составляла две трети галлона на квадратный ярд, «⅔∙x» — что означает «две трети, умноженные на x», — представляет собой общее количество произведенного зерна. по первому полю. Точно так же «½∙y» представляет собой общее количество зерна, произведенного вторым полем. Поскольку первое поле дало на 500 галлонов зерна больше, чем второе, разница (следовательно, вычитание) между зерном первого поля (⅔∙x) и зерном второго поля (½∙y) составляет (=) 500 галлонов.

Ответ таков

Конечно, сила алгебры не в кодировании утверждений о физическом мире. Учёный-компьютерщик и писатель Марк Джейсон Доминус пишет в своем блоге The Universe of Discourse: «На первом этапе вы переводите проблему в алгебру, а затем на втором этапе вы манипулируете символами почти механически, пока ответ не выскочит, как будто с помощью магии».

Здесь мы решим эту проблему, используя методы, которым их учат сегодня. И в качестве отказа от ответственности, читателю не нужно понимать каждый конкретный шаг, чтобы понять важность этой общей техники. Мы намерены сделать так, чтобы историческая значимость и тот факт, что мы можем решить проблему без каких-либо догадок, вдохновили неопытных читателей узнать об этих шагах более подробно. Вот снова первое уравнение:

х + у = 1800

Мы решаем это уравнение относительно y, вычитая x из каждой части уравнения:

у = 1800 – х

Теперь составим второе уравнение:

⅔∙х – ½∙у = 500

Поскольку мы нашли, что «1800 – x» равно y, его можно подставить во второе уравнение:

⅔∙х – ½∙(1800 – х) = 500

Затем распределите отрицательную половину (–½) по выражению «1800 – x»:

⅔∙x + (–½∙1800) + (–½∙–x) = 500

Это упрощаем:

⅔∙х – 900 + ½∙х = 500

Сложите две части x вместе и добавьте 900 к каждой части уравнения:

(7/6)∙х = 1400

Теперь разделите каждую часть уравнения на 7/6:

х = 1200

Таким образом, первое поле имеет площадь 1200 квадратных метров. Это значение можно подставить в первое уравнение для определения y:

1200 + у = 1800

Вычтите 1200 из каждой части уравнения, чтобы найти у:

у = 600

Таким образом, второе поле имеет площадь 600 квадратных ярдов.

Обратите внимание, как часто мы используем технику выполнения операции с каждой частью уравнения. Эту практику лучше всего понимать как визуализацию уравнения в виде весов с известным грузом на одной стороне и неизвестным грузом на другой. Если мы добавим или вычтем одинаковое количество грузов с каждой стороны, весы останутся сбалансированными. Точно так же весы остаются сбалансированными, если мы умножаем или делим грузы поровну.

Хотите узнать, насколько хорошо у вас развита логика? Тогда не стойте в стороне, подходите ближе и давайте решать с нами одну из лучших задач по математичке для развития логики! Справитесь?

Хотя метод сохранения баланса уравнений почти наверняка использовался всеми цивилизациями для развития алгебры, его использование для решения этой древней вавилонской задачи (как показано выше) является анахронизмом, поскольку этот метод был центральным в алгебре только последние 1200 лет.

Как алгебра стала такой, какой мы её знаем?

Полностью символическая алгебра — как показано в начале статьи — оставалась такой до научной революции. Рене Декарт (1596-1650) использовал алгебру, которую мы узнали бы и сегодня, в его публикации 1637 года «Геометрия», где впервые применил практику построения графиков алгебраических уравнений. Согласно Леонарду Млодинову в «Окне Евклида», «геометрические методы Декарта были настолько важны для его понимания, что он писал, что «вся моя физика есть не что иное, как геометрия» ».

Булева алгебра (алгебра логики)

Понятие алгебры логики
Логические функции
Булев базис (логический базис)
Аналитическое представление логических функций
Способы описания логических функций
Аксиомы алгебры логики
Теоремы алгебры логики
Законы алгебры логики

На этом уроке знакомимся с алгеброй логики (булевой алгеброй). Одним из её основателей стал английский математик Джордж Буль (1815-1864), который был из довольно бедной семьи, а в юности зарабатывал переводами сочинений древнегреческих философов. За этим занятием его и посетила мысль о том, что высказываниям можно присваивать значения 1 («истина») и 0 «ложь».

Итак, алгебра логики (булева алгебра) — это раздел математики, изучающий высказывания, рассматриваемые со стороны их логических значений (истинности или ложности) и логических операций над ними. Алгебра логики позволяет закодировать любые утверждения, истинность или ложность которых нужно доказать, а затем манипулировать ими подобно обычным числам в математике.

Создание алгебры логики в середине ХIХ века в трудах Джорджа Буля представляло собой попытку решать традиционные логические задачи алгебраическими методами.

Пусть функция от n переменных и любой из её аргументов могут принимать значения только из множества {0, 1}. Тогда эта функция называется логической, или булевой, или переключательной, или функцией алгебры логики. Описанную функцию часто называют также булевым вектором. Количество функций от n переменных равно 2 в степени n. То же самое можно сказать и иначе: число различных n-мерных булевых векторов равно 2 в степени n. А число различных функций алгебры логики от этих векторов равно уже .

Значениям переменной в булевой алгебре соответствуют состояниям элементов микросхем компьютера или любого другого электронного устройства: сигнал присутствует (логическая «1») или сигнал отсутствует (логический «0»).

На логических элементах, реализующих булевы функции, строятся логические схемы электронных устройств.

Законы булевой алгебры применяются и в программировании — при написании сложных логических условий и сложных запросов к базе данных. Один пример со скриптом на PHP приведён здесь (это статья о системе многокритериального поиска по сайту с базой данных). Ещё один пример — применение алгебры логики в создании многоуровневого меню сайта, в котором были бы открыты все пункты всех уровней, по которому пролегает путь к конечному открытому пункту меню.

Часто оказывается, что изначально построенное логическое выражение можно упростить, используя аксиомы, теоремы и законы алгебры логики.

Способам и приёмам минимизации логических функций посвящены отдельные материалы сайта — минимизация логических функций: общие сведения, минимизация логических функций: метод непосредственных преобразований и минимизация логических функций: метод Квайна.

Логические функции одной переменной

Функция	Название	Обозначение
	Константа нуля
	Повторение x
	Логическое отрицание, инверсия, «НЕ»
	Константа единицы

Переменная	Логические функции
x
0	0	0	1	1
1	0	1	0	1

Пригодится: минимизация логических функций — общие сведения
Пригодится: минимизация логических функций методом непосредственных преобразований

Нет времени вникать в решение? Можно заказать работу!

К началу страницы

Логические функции двух переменных

Функция	Название	Обозначение
	Константа нуля	или False
	Логическое умножение, конъюнкция, «И»	или или или
	Запрет по	или
	Переменная
	Запрет по	или
	Переменная
	Сложение по модулю 2, отрицание эквивалентности, исключающее «ИЛИ»	или или
	Логическое сложение, дизъюнкция, «ИЛИ»	или или или
	Функция Пирса (Вебба), «ИЛИ-НЕ»	или или
	Логическая равнозначность, эквиваленция	или или или
	Отрицание
	Правая импликация	или
	Отрицание
	Левая импликация	или
	Функция Шеффера, «И-НЕ»	или или
	Константа единицы	или True

Ниже дана таблица истинности для логических функций от двух переменных.

X1	0	0	1	1
X2	0	1	0	1
	0	0	0	0
	0	0	0	1
	0	0	1	0
	0	0	1	1
	0	1	0	0
	0	1	0	1
	0	1	1	0
	0	1	1	1
	1	0	0	0
	1	0	0	1
	1	0	1	0
	1	0	1	1
	1	1	0	0
	1	1	0	1
	1	1	1	0
	1	1	1	1

В логических схемах функции могут быть реализованы с произвольных количеством входных переменных, примеры — в материале Логические схемы и таблицы истинности.

Ответить на контрольные вопросы, а затем посмотреть ответы

Контрольный вопрос 1. Даны две переменные x1 и x2. Число различных булевых векторов и различных ФАЛ от полученных векторов равны соответственно:

8 и 16
8 и 32
4 и 8
4 и 16

Контрольный вопрос 2. Какие из функций не являются ФАЛ одной переменной (и одна, и вторая в варианте ответа):

отрицание и сложение по модулю два
эквивалентность и повторение x
отрицание и импликация
функция Шеффера и эквивалентность
запрет по x2 и отрицание

Правильные ответы на вопрос 1 и вопрос 2.

Пригодится: минимизация логических функций — общие сведения
Пригодится: минимизация логических функций методом непосредственных преобразований

Нет времени вникать в решение? Можно заказать работу!

Пройти тест по теме Математическая логика

Любую булеву функцию с произвольным количеством аргументов можно построить через подстановку элементарных функции вместо аргументов (суперпозицию). Набор простейших функций, с помощью которого можно выразить любые другие, сколь угодно сложные логические функции, называется функционально полным набором, или логическим базисом.

Инверсия (логическое отрицание, «НЕ»)


0	1
1	0

Конъюнкция (логическое умножение, «И»)


0	0	0
0	1	0
1	0	0
1	1	1

Дизъюнкция (логическое сложение, «ИЛИ»)


0	0	0
0	1	1
1	0	1
1	1	1

В булевом базисе обычно строятся логические схемы, которые реализуют сколь угодно сложные логические функции, примеры — в материале Логические схемы и таблицы истинности.

Пригодится: минимизация логических функций — общие сведения
Пригодится: минимизация логических функций методом непосредственных преобразований
Пригодится: минимизация логических функций методом Квайна

В качестве исходного описания сложных логических функций обычно используется таблица истинности, однако упрощение функций удобнее производить в аналитической форме. При аналитической записи функция алгебры логики представляется либо в виде логической суммы элементарных логических произведений (дизъюнкции элементарных конъюнкций), либо в виде логического произведения элементарных логических сумм (конъюнкции элементарных дизъюнкций). Первая форма записи имеет название дизъюнктивной нормальной формы (ДНФ), вторая — конъюнктивной нормальной формы (КНФ). В этих названиях термин «нормальная» означает отсутствие общей инверсии (отрицания) над несколькими перемнными сразу.

Дизъюнктивная нормальная форма

X1	X2	f
0	0	1
0	1	1
1	0	1
1	1	0

Конъюнктивная нормальная форма

X1	X2	f
0	0	0
0	1	0
1	0	1
1	1	0

Применяются следующие способы описания логических функций:

словесный;
табличный;
числовой;
аналитический;
координатный;
графический.

Пример табличного описания функций алгебры логики. В верхней таблице под набором подразумевается набор значений логических переменных (1 или 0), а f — это значение функции алгебры логики, заданной определённой формулой. Нижняя таблица несёт в себе более подробную информацию о наборах, поскольку в ней указаны значения переменных.

Номер набора	f
0	0
1	1
2	0
3	0
4	1
5	1
6	0
7	1

X1	X2	X3	f
0	0	0	0
0	0	1	1
0	1	0	0
0	1	1	0
1	0	0	1
1	0	1	1
1	1	0	0
1	1	1	1

Приведённые выше таблицы имеют название таблиц истинности. Такие таблицы в практике необходимо строить для любой, сколь либо сложной булевой функции. Примеры таблиц истинности для булевых функций, реализованных в логических схемах — в материале Логические схемы и таблицы истинности.

Пример числового описания логических функций

или .

Пример аналитического описания логических функций

Пример координатного описания логических функций

Карта Карно

Пример графического описания логических функций

Пригодится: минимизация логических функций — общие сведения
Пригодится: минимизация логических функций методом непосредственных преобразований
Пригодится: минимизация логических функций методом Квайна

Аксиомы конъюнкции

Аксиомы дизъюнкции

Аксиомы отрицания

если , то ; если , то .

Теоремы исключения констант

Теоремы идемпотентности (тавтологии, повторения)

для n переменных

Теорема противоречия

Теорема «исключённого третьего»

Теорема двойного отрицания (инволюции)

Ассоциативный (сочетательный) закон

Коммутативный (переместительный) закон

Дистибутивный (распределительный) закон

Законы де Моргана (законы общей инверсии или дуальности)

Закон поглощения (элиминации)

Закон склеивания (исключения)

Пригодится: минимизация логических функций — общие сведения
Пригодится: минимизация логических функций методом непосредственных преобразований
Пригодится: минимизация логических функций методом Квайна

Пройти тест по теме Математическая логика

К началу страницы

Логика высказываний

Логические схемы и таблицы истинности

Освежите свою математику: Алгебра

Подтянуть математику: Алгебра

Символы и цифры

Настоящие математики, в отличие от статистиков и инженеров, очень редко работают с числами. Они используют символы для представления не одного конкретного числа, а любого числа. Они проводят время в очень абстрактных мирах.

Иногда это может быть полезно и для остальных из нас. Мы можем узнать, что может произойти в различных ситуациях, используя символы вместо чисел.

Цифры 1, 2, 3, 4 и т. д. имеют фиксированное значение. Буквенные символы, такие как a , b , c , d и избранные x и y представляют собой переменные, которые могут принимать любые значения. Математики используют не только латинские буквы, которые мы используем в английском языке. Они также используют греческие буквы, такие как α , β , γ , δ (альфа, бета, гамма, дельта) и огромное количество специальных символов. Если какой-либо лектор использует греческую букву, которую вы не узнаете, не стесняйтесь, спросите, что это такое. Точно так же, если они используют странный символ, такой как ∝ или ⊕, спросите их, что это такое и что это значит.

В освежите свою математику , мы будем придерживаться латинских букв и знакомые символы, используемые в арифметике.

Алгебраические выражения

Это алгебраическое выражение: 4 х + 3.

Это означает «умножить переменную x на 4, а затем добавить 3». В алгебре, когда мы предшествуем переменной числом, мы умножаем. Точно так же xy означает умножение переменной x на переменную 9.0009 г а 7 xy означает умножение переменной x на переменную y и умножить все это на 7.

Правила BODMAS, упомянутые в Числах относятся и к алгебре. Например, x ² + 3(2 y + 4) означает:
1. умножить y на 2
2. добавить 4
3. квадрат х
4. умножить содержимое скобок на 3
5. добавьте количества, найденные в шагах 3 и 4.
Конечно, все это мы сможем сделать, только если заменим x и y числами.

Иногда и алгебраическое выражение содержит более одного члена, которые имеют одинаковую структуру. Например, 3 х + 4 х означает умножить х на 3, умножить х на 4, а затем добавить результаты. Всего это даст 7 x с: 3 х + 4 х = 7 х . Мы можем заменить 3 x + 4 x на 7 x . Мы называем это собиранием вместе, как термины.

Рассмотрим выражение 3 x + 2 y + 5 x + 4 y . У нас есть два члена в x и два члена в y . Мы можем собрать их вместе:

3 х + 2 у + 5 х + 4 у = (3 + 5) х + (2 + 4) у = 8 х + 6 у .

Точно так же мы можем собрать вместе термины, которые являются одной и той же степенью переменной. Рассмотрим выражение 3 x ² + 2 x + 5 x ² + 4 x . У нас есть два члена в x ² и два члена в x . Мы можем собрать их вместе:

3 х ² + 2 х + 5 х ² + 4 х = (3 + 5) х ² + (2 + 4) х = 8 х ² + 6 х .

Мы не можем собрать вместе разные силы. Мы не можем комбинировать x ² и x .

Мы могли бы упростить это еще немного, заметив, что в 8 x ² + 6 х , x присутствует в обоих терминах. Мы могли бы написать

8 х ² + 6 х = х (8 х + 6).

Мы могли бы также заметить, что члены в скобках имеют общий делитель 2, и написать

8 х ² + 6 х = х (8 х + 6) = 2 х (4 х + 3)

Захотим ли мы это сделать, будет зависеть от приложения. Иногда мы берем выражение вроде 2 x (4 x + 3) и умножаем его за скобки. Это означает, что мы умножаем каждый член в скобках на член вне его:

2 х (4 х + 3) = 2 х х 4 х + 2 х х 3 = 8 х ² + 6 х

как прежде.

Иногда у нас есть две скобки для умножения, например:

(2 х + 3)( х – 7)

Умножаем каждое слагаемое в первой скобке на каждое слагаемое во второй скобке:

(2 х + 3)( х – 7) = 2 х ² – 14 х + 3 х – 21

Затем собираем воедино подобные термы:

2 x ² – 14 x + 3 x – 21 = 2 x ² + (3 – 14) x – 21 = 2 х ² – 11 х – 21

Упражнение: алгебраические выражения

Каким будет выражение 3 х + 7, если х = 3?

Упростить 5 x ² + 7 х – 2( х ² + х ).

Проверьте ответ на упражнение по алгебраическим выражениям.

Факторы и отмена

Алгебраические выражения имеют множители, как и числа. Например, 4 x ² y имеет коэффициенты 1, 2, 4, х , 2 х , 4 х , х ² , 2 х ², 4 х ², г , 2 г , 4 г , х у , 2 х у , 4 х у , x ² y , 2 x ² y , 4 x ² 0 9 .

Мы можем использовать их, когда у нас есть одно выражение, разделенное на другое, для упрощения. Например, мы можем записать числитель и знаменатель как кратные их наименьшим множителям:

4 х ² у 2 × 2 × x × x × у 2 × x 2 x
знак равно ––––––––––––– = ––––– = –––
2 х у ² 2 × х × у × у г г

У нас две двойки сверху и одна снизу, поэтому мы можем отменить одну из 2 сверху и 2 снизу. У нас есть два x с сверху и один снизу, поэтому мы можем отменить одно из x сверху и x снизу. У нас есть один y сверху и два y снизу, поэтому мы можем исключить y сверху и один из y снизу.

Мы также можем сокращать более сложные части выражений. Например

( х ² – г ) ² ( х – 15) ( x ² – у ) × ( x ² – у ) × ( х – 15) ( х ² – у )
––––––––––––– знак равно ––––––––––––– = –––––––
( x ² – y ) ( x – 15) ² ( х ² – y ) × ( x – 15) × ( x – 15) ( х – 15)

Мы можем отменить один ( x ² – y ) и один ( x – 15) сверху и снизу.

Упражнение: множители и отмена

Упростите следующее:

25 р ³ ²
––––––
35 р р

( r – s )(2 r + s ) ²
–––––––––––
( r + s )(2 r + s )

Проверка ответа на факторы и отмена упражнения.

Вернуться к главному меню «Освежить математику».

Мартину Бланду, получившему степень магистра наук. индекс.

На домашнюю страницу Мартина Блэнда.

Эта страница поддерживается Мартином Бландом.
Последнее обновление: 16 апреля 2008 г.

Назад к началу.

Список математических символов — Простая английская Википедия, бесплатная энциклопедия

Из Простая английская Википедия, бесплатная энциклопедия

Перейти к навигацииПерейти к поиску

Следующий список содержит некоторые наиболее известные символы в математике. Обратите внимание, что эти символы могут иметь разные значения в разных контекстах.

**Эти символы чаще всего используются в линейной алгебре**
Имя	Читать как	Описание	Значение	Пример(ы)
=	равенство	равно, равно	Если x=y, x и y представляют одно и то же значение или вещь.	2+3=5
≡	определение	определяется как	Если x≡y, x определяется как другое имя y	(a+b) ² ≡a ² +2ab+b ²
≈	примерно равно	примерно равно	Если x≈y, x и y почти равны.	√2≈1,41
≠	неравенство	не равно, не равно	Если x≠y, x и y не представляют одно и то же значение или вещь.	1+1≠3
<	строгое неравенство	меньше, чем	Если x	4<5
>		больше, чем	Если x>y, x больше, чем y.	3>2
≪		намного меньше, чем	Если x≪y, то x намного меньше y.	1≪999999999
≫		намного больше, чем	Если x≫y, x намного больше, чем y.	999999999≫0,001
≤	неравенство	меньше или равно	Если x≤y, x меньше или равно y.	5≤6 и 5≤5
≥	неравенство	больше или равно	Если x≥y, x больше или равно y.	2≥1 и 2≥2
∝	пропорциональность	пропорционально	Если x∝y, то y=kx для некоторой константы k.	Если y=4x, то y∝x и x∝y
+	дополнение	плюс	x+y — это сумма x и y.	2+3=5
—	вычитание	минус	x-y — это вычитание y из x	5-3=2
×	умножение	раз	x×y — произведение x на y.	4×5=20
·	умножение	раз	x·y — произведение x на y	4·5=20
÷	отделение	разделить на	x÷y или x/y — деление x на y	20÷4=5 и 20/4=5
/	отделение	разделить на	x÷y или x/y — деление x на y	20/4=5
±	плюс-минус	плюс-минус	x±y означает как x+y, так и x-y	Уравнение 3±√9 имеет два решения: 0 и 6.
∓	минус плюс	минус или плюс	4±(3∓5) означает как 4+(3-5), так и 4-(3+5)	6∓(1±3)=2 или 4
√	квадратный корень 9{5}{к}}=1×2×3×4×5=120
!	факториал	факториал	н! произведение 1×2×3…×n	5!=1×2×3×4×5=120
⇒	материальное значение	подразумевает	A⇒B означает, что если A истинно, B также должно быть истинным, но если A ложно, B неизвестно.	x=3⇒x ² =9, но x ² =9⇒x=3 неверно, потому что x также может быть -3.
⇔	эквивалент материала	тогда и только тогда, когда	Если А истинно, то В истинно, а если А ложно, то В ложно.	х=у+1⇔х-1=у
\|…\|	абсолютное значение	абсолютное значение	\|х\| это расстояние по реальной линии (или по комплексной плоскости) между x и нулем	\|5\|=5 и \|-5\|=5
\|\|	параллельно	параллельно	Если A\|\|B, то A и B параллельны
⊥	перпендикулярно	перпендикулярно	Если A⊥B, то A перпендикулярно B
≅	конгруэнтность	соответствует	Если A≅B, то форма A конгруэнтна форме B (имеет одинаковые размеры)
ф	золотое сечение	золотое сечение	Золотое сечение — это иррациональное число, равное (1+√5)÷2 или примерно 1,6180339887.
∞	бесконечность	бесконечность	∞ — это символ, используемый для обозначения бесконечных сумм.
∈	установить членство	является элементом	a∈S означает, что a является элементом множества S	3,5∈ℝ, 1∈ℕ, 1+ i ∈ℂ
∉	установить членство	не является элементом	a∉S означает, что a не является элементом множества S	2,1∉ℕ, 1+ i ∉ℝ
{,}	Комплект кронштейнов	комплект	{a,b,c} — набор, состоящий из a, b и c	ℕ={0,1,2,3,4,5…}
ℕ	Натуральные числа	Н	ℕ обозначает набор натуральных чисел {0,1,2,3,4,5. ..} (0 может быть или не быть включенным как натуральное число)
ℤ	Целые числа	З	ℤ обозначает набор целых чисел (-3,-2,-1,0,1,2,3…)
ℚ	Рациональные числа	В	ℚ обозначает набор рациональных чисел (числа, которые можно записать в виде дроби a/b, где a∈ℤ, b∈ℕ)	8,323∈ℚ, 7∈ℚ, π∉ℚ
ℝ	Вещественные числа	Р	ℝ обозначает набор действительных чисел	π∈ℝ, 7∈ℝ, √(-1)∉ℝ
ℂ	Комплексные числа	С	ℂ обозначает набор комплексных чисел	√(-1)∈ℂ
х̄	Среднее	бар, надбар	x̄ — это среднее (среднее) x _и	, если x={1,2,3}, то x̄=2
x̄	комплексно-сопряженный	комплексное сопряжение x	Если x=a + bi, то x̄=a — bi, где i=√(-1)	х=-4 + 5,3i, х̄=-4 — 5,3i
[+\|-]	ситуативный плюс минус	Либо плюс, либо минус в зависимости от ситуации.	Если y=[+\|-]x, то x может быть положительным или отрицательным в зависимости от ситуации.	y=[+\|-]x y равно +x или -x в зависимости от сценария.

Математическая константа

Математические символы — Math Vault
Список математических символов — RapidTables

Полный список символов алгебры

Алгебра — это раздел математики, относящийся к манипулированию символами и их основным правилам. Ниже приводится подборка символов из различных разделов алгебры, включая базовую алгебру, теорию чисел, линейную алгебру и абстрактную алгебру.

Для удобства чтения эти символы разбиты по функциям и темам на таблицы и таблицы . Другие полные списки символов — с разбивкой по темам и типам — также можно найти на соответствующих страницах ниже (или на панели навигации).

Содержание

Предпочитаете версию в формате PDF?

Получите основную сводку математических символов в форме электронной книги — вместе с использованием каждого символа и кодом LaTeX.

Да. Это было бы полезно.

Константы

В алгебре константы — это символы, используемые для обозначения ключевых математических элементов и наборов. В следующих таблицах описаны наиболее распространенные из них — вместе с названием каждого символа, его использованием и примером.

(Общие общие константы см. в общих математических константах).2 + 1 = 0$ $\mathbf{0}$, $\vec{0}$ Нулевая матрица $O_{2 \times 3} = \\ \begin{pmatrix} 0 & 0 & 0 \\ 0 & 0 & 0 \end{pmatrix}$ $I$ Матрица идентичности $I_2 = \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}$ $e$ Единичный элемент группы Для всех $g \in G$ $g \circ e = e \circ g = g$.

Ключевые математические наборы

В алгебре одни наборы чисел (или другие более сложные объекты) встречаются чаще, чем другие. Эти наборы часто обозначаются некоторыми вариантами букв алфавита , многие из которых набраны жирным шрифтом на доске.

\ MathBB {P} $ \ 906393 96 9 $\mathbb{Q}_{10}$, $-1 = …999$ (как $1 + …999 = 0$). $06036 9 \mathbb{I}$

Символ Название	Пояснение	Пример
$ \ mathbb {p} $	Набор Prime Numbers	$ 127 \ in \ mathbb {P} $
		$	$ 9063	$	$	906.9063	$	$ $ 127 \ числа (начиная с $0$)	$0 \in \mathbb{N}_0$
$\mathbb{N}_1$	Набор из натуральных чисел (начиная с $1$) 906 $0 \notin \mathbb{N}_1$
$\mathbb{Z}$	Набор из целых чисел	Для всех $x, y \in \mathbb{N}$, $x-y \in \mathbb{Z}$.
$\mathbb{Z}_+$	Набор из натуральных чисел	$\mathbb{Z}_+ = \mathbb{N}_1$
$\mathbb{	Набор из рациональных чисел	$3. \overline{73} \in \mathbb{Q}$
$\mathbb{Q}_p$	Набор из p-адических чисел
$\mathbb{A}$	Набор из алгебраических чисел	$\sqrt{5} + 3 \in \mathbb{A}$
$\mathbb 2 $	$\mathbb Набор из действительных чисел	$i \notin \mathbb{R}$
$\mathbb{R}_+$	Набор из положительных действительных чисел	Для всех $x, y \in \mathbb{R}_+$, $xy \in \mathbb{R}_+$.
$\mathbb{R}_-$	Набор из отрицательных действительных чисел	Если $a, b \in \mathbb{R}_-$, то $a+b \in \mathbb{R}_-$.
$\mathbb{R}-\mathbb{Q}$	Набор из иррациональных чисел	$\log 2 \in \mathbb{R}-\mathbb{Q}$
Набор из мнимых чисел	$5i \in \mathbb{I}, 2+3i \notin \mathbb{I}$
$\mathbb{C}$	Набор из комплексных чисел	Существует число $x \in \mathbb{C}$ такое, что $x^2 + 2x + 3 = 0$. 92 + 2x +1$ $\in \mathbb{Z}[x]$

Переменные

Поскольку алгебра связана с манипулированием математическими символами, она часто использует широкий диапазон переменных как заполнители для различных объектов и количеств. В следующей таблице описаны наиболее распространенные из них, а также их соответствующее использование и примеры.

906 функций и уравненияY + 5Y \in \\ \mathbb{Z}[X, Y]$

Название символа	Используется для	Пример
$m, n, p, q$	Натуральные числа и целые числа	$m+n-2p = q$
$a, b, c$	Линейное уравнение имеет общий вид $ax+by+c = 0$.
$x, y, z$	Неизвестные в функциях и уравнениях	Если $14x + 2y = 4$, то $y = 2-7x$.
$\Delta$	Дискриминант 9{(3,5)} \frac{i + j}{2}$
$z$	Комплексные числа	$ \|z_1 z_2\| = \|z_1\| \|z_2\|$
$f(x)$, $g(x, y)$, $h(z)$	Функции	$g(f(x), 3) = h( x)$
$\mathbf{u}, \mathbf{v}, \mathbf{w}$ (или $\vec{u}, \vec{v}, \vec{w}$)	Векторы	$2\mathbf{u} + 3\mathbf{v} = 5\mathbf{w}$
$U, V, W$	Векторные пространства	$U$ — подпространство векторного пространства $V$.
$ A, B, C $	MATRICES	$ AB \ NE BA
$ $
$. mathbf{v_0}$, $3$ — собственное значение $A$.
$G, H$	Группы	Существует элемент $e \in G$ такой, что для всех $x \in G$ $x \circ e = x$.

Разделители

В математике разделители — это символы, используемые для обозначения разделения между независимыми математическими объектами. В следующей таблице представлены некоторые из наиболее распространенных разделителей в алгебре. Общие общие разделители см. в разделе Общие разделители.

Имя символа	Пояснение	Пример
\begin{bmatrix} x & y \\ w & z\end{bmatrix}$	Индикаторы векторов/матриц	$\begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} + \begin{pmatrix} 4 \\ 5 \\ 6 \end{pmatrix} = \\ \ begin{pmatrix} 5 \\ 7 \\ 9 \end{pmatrix} $
$\{ \}$	Построитель наборов	$\{ -1, 3. \overline{5}, \ pi \} \in \mathbb{R}$
$\bigg\{$	Кусочно-функциональный индикатор	$\|x\| = \begin{cases} x & x \ge 0 \\ -x & x<0 \end{cases}$
$:$, $\mid$	Маркер «такой, что»	$\mathbb{Q} =$ $\displaystyle \left\{ \frac{x}{y} \,\ middle\|\, x \in \mathbb{Z}, y \in \mathbb{N} \right\}$

Символы, связанные с функциями

В качестве основного компонента алгебры функция играет ключевую роль роль в установлении правил, касающихся манипулирования символами. В следующей таблице описаны некоторые из наиболее распространенных операторов и обозначений, связанных с функциями, а также их значение и примеры. 93$ переводит число в свой куб. $\mathrm{dom}(f)$ Домен $f$ $\mathrm{dom} (g) = \mathbb{R}_+$ $\mathrm {ran}(f)$ Диапазон $f$ Если $\mathrm{ran} (f) = \mathbb{Z}$, то $f$ является целочисленной функцией. $f(x)$ Изображение элемента $x$ под действием функции $f$ $f(g(3)) = f(5) = 7$ $f( Х)$9{+} \subseteq T$.

Операторы

В алгебре операторы можно рассматривать как особый тип функции, отображающей один или несколько математических объектов в другой, и часто получают специальные имена или обозначения из-за их повторения.

В частности, эти операторы часто связаны с числами , ключевыми функциями , линейной алгеброй и абстрактной алгеброй — подавляющее большинство из которых можно найти в таблицах ниже. Общие операторы см. в разделе Общие операторы.

Number-related Operators

$|—03 $ $ 999 \ $x$

Symbol Name	Explanation	Example
$\gcd (x,y)$	Greatest common divisor of $x$ and $y$	$\gcd (20, 15) = 5$
$\mathrm{lcm} (x, y)$	Наименьшее общее кратное чисел $x$ и $y$	$\mathrm{lcm } (x, y) = \dfrac{xy}{\gcd (x, y)}$
$x \bmod y$	Остаток от $x$ при делении на $y$	$23 \bmod 4 = 3$
$\|x\|$	Абсолютное значение от $x$	= \|5\| = 5 $
$ \ lfloor x \ rfloor $	этаж $ x	$ \ lfloor 5. 999 \ rfloor = 5 $
$ $
$ $
$ $
$ $
$ $
$ $
Для всех $x \in \mathbb{R}$ $\lceil x \rceil-1 < x \le \lceil x \rceil$. 9y $
$ \ ln x $	Натуральная логарифмическая функция	$ \ ln 10 = \ ln 2 + \ ln 5 $
$ \ \ ln 5 $
$ \ \ ln 5 $
$ \ ln 5 $
$ \ ln 5 $
$ \ ln 5 $
$ \ \ ln	$\log 1000000 = 6$
$\log_b x$	Логарифмическая функция по основанию $b$	$\log_{11} 23 = \dfrac{\ln 23}{\ln 11} $
$\sin x$, $\cos x$, $\tan x$, $\sec x$, $\csc x$, $\cot x$	6 92 \cdot 3 \cdot 5$, $\omega(60)=3$.
$\mathrm{id}_A (x)$	Тождественная функция на множестве $A$	Для всех множеств $A$ $\mathrm{id}_A$ взаимно однозначно и на.
$\mathbf{1}_A(x)$, $\chi_A(x)$	Индикаторная/характеристическая функция множества $A$	$\mathbf{1}_{\mathbb{Q }}(x) = \\ \begin{case} 1 & x \in \mathbb{Q} \\ 0 & x \notin \mathbb{Q} \end{cases}$
$\delta_{ij }$	Дельта-функция Кронекера	Для каждой единичной матрицы $I$ $I_{ij}=\delta_{ij}$.

Operators Related to Complex Numbers

Symbol Name	Explanation	Example
$\bar{z}$	Conjugate of complex number $z$	$ \overline{5 + 6i}= \\ 5-6i$
$\Re(z)$	Действительная часть комплексного числа $z$ 9{\pi i}$

Operators in Linear Algebra

Vector-related Operators

Symbol Name	Explanation	Example
$-\mathbf{v}$	Аддитивное обратное вектора $\mathbf{v}$	$\mathbf{v} + (-\mathbb{v}) = \mathbf{0}$
$k\mathbf{v}$	Скалярное произведение вектора $\mathbf{v}$ на скаляр $k$	$(-1)\mathbf{v}=-\mathbf{v}$
$\mathbf{u} + \mathbf{v}$	Сумма векторов $\mathbf{u}$ и $\mathbf{v}$	$\mathbf{u} + \mathbf{0} = \mathbf{u}$
$\mathbf{u}-\mathbf{v}$	Разница векторов $\mathbf{u}$ и $\mathbf{v}$	$(5, 7, 1)-(3, 2, 5)=$ $(2, 5, -4)$
$\mathbf{u} \cdot \mathbf{v}$	Скалярное произведение векторов $\mathbf{u}$ и $\mathbf{v}$	$(5\mathbf{u}) \cdot (7\mathbf{v}) = 35 (\mathbf{u} \cdot \mathbf{v})$
$\mathbf{u} \times \mathbf{v}$	Перемножение векторов $\mathbf{u}$ и $\mathbf{v}$	$\mathbf{v} \times \mathbf{u} =\, – ( \ mathbf{u} \times \mathbf{v} )$
$\mathbf{u} \wedge \mathbf{v}$	Произведение клиньев векторов $\mathbf{u}$ и $\mathbf {v}$	$\mathbf{u} \клин \mathbf{v} =\, – (\mathbf{v} \клин \mathbf{u})$
$\langle \mathbf{u}, \mathbf{v} \rangle$	Скалярное произведение векторов $\mathbf{u}$ и $\mathbf{v}$	В евклидовом пространстве , $\langle \mathbf{u}, \mathbf{v} \rangle = \mathbf{u} \cdot \mathbf{v}$
$\mathbf{u} \otimes \mathbf{v}$	Внешнее произведение векторов $\mathbf{u}$ и $\mathbf{v}$	$(1, 2) \otimes (3, 4) =$ $\begin{pmatrix} 1 \cdot 3 & 1 \cdot 4 \\ 2 \cdot 3 & 2 \cdot 4 \end{pmatrix}$
$\\| \mathbf{v} \\|$	Норма вектора $\mathbf{v}$	$\\| к \mathbf{v} \\| = \|к\| \\| \mathbf{v} \\|$
$\\| \mathbf{v} \\|_p$	P-норма вектора $\mathbf{v}$	$\\| \mathbf{v} \\|_1 =$ $\|v_1\|+ \cdots + \|v_n\|$
$\hat{\mathbf{v}}$	Единичный вектор в направлении вектора $ \mathbf{v}$	$\hat{\mathbf{v}} = \dfrac{\mathbf{v}}{\\| \mathbf{v} \\|}$
$\mathrm{proj}_{\mathbf{u}}\mathbf{v}$	Проекция вектора $\mathbf{v}$ на вектор $\mathbf{u}$	$ \ mathrm {proj} _ {\ mathbf {u}} \ mathbf {v} = \ dfrac {\ mathbf {v} \ cdot \ mathbf {u}} {\ mathbf {u} \ cdot \ mathbf {u}} \ , \mathbf{u}$
$\mathrm{oproj}_{\mathbf{u}} \mathbf{v}$	Ортогональная проекция вектора $\mathbf{v}$ на вектор $\ mathbf{u}$	$\mathrm{proj}_{\mathbf{u}} \mathbf{v} + \mathrm{oproj}_{\mathbf{u}} \mathbf{v} = \mathbf{v }$

Matrix-related Operators

$A 9{-1} = A$ $

Symbol Name	Explanation	Example
$-A$	Additive inverse of matrix $A$	$-A + A = O$
$kA$	Скалярное произведение матрицы $A$ на скаляр $k$	$5(3B)=(5 \cdot 3)B$
	Сумма матриц $A$ и $B$	$A + B = B+A$
$A-B$	Разность матриц $A$ и $B$	$\begin{pmatrix} 2 & 5 \\ 3 & 1 \end {pmatrix}-\begin{pmatrix} 1 и 5 \\ 2 и 4 \end{pmatrix} =$ $\begin{pmatrix} 1 & 0 \\ 1 & -3 \end{pmatrix} $
$ AB$	Произведение матриц $A$ и $B$	$(AB)_{ij} = (i\mathrm{th \ row \ of \ }A)$ $\cdot \, (j\ mathrm{th\column\of\}B)$
$\mathrm{tr}(A)$	След матрицы $A$	$\mathrm{tr}(I_n)=n$
\|A\|$, $\det (A)$	Определитель матрицы $A$	$\begin{vmatrix} 4 & 3 \\ 2 & 5 \end{vmatrix} = \\ 4 \cdot 5 -3 \cdot 2$
$\\|A\\|$	Норма матрицы $A$	$\\| А + Б \\| \le$ $\\| А \\| + \\| В \\|$
$\\| А \\|_p$ 9{\mathrm{T}})=\mathrm{rank}(A)$

Vector-space-related Operators

Symbol Name	Explanation	Example
$\ ker(f)$	Ядро линейного отображения $f$	$\mathbf{v} \in \ker(f) \iff$ $f(\mathbf{v})=\mathbf{0} $
$\mathrm{span}(S)$	Span набора векторов $S$	$\mathrm{span} \left( \{ (1, 2), (4, 5) ) \} \справа)$ 92$
$\dim(V)$	Размерность векторного пространства $V$	$\dim(W) \le \dim(V)$
$W_10 + W60$2	Сумма подпространств $W_1$ и $W_2$	Для всех $\mathbf{w_1} \in W_1$ и $\mathbf{w_2} \in W_2$ $\mathbf{w}_1+\mathbf{w }_2$ $\in W_1 + W_2$.
$W_1 \oplus W_2$	Прямая сумма подпространств $W_1$ и $W_2$	Если $W_1 + W_2 = V$ и $W_1 \cap W_2 = \{\mathbf{0}\ }$, то $W_1 \oplus W_2 = V$.
$V_1 \times V_2$	Прямое произведение векторных пространств $V_1$ и $V_2$	Если $\mathbf{v_1} \in V_1$ и $\mathbf{v}_2 \in V_2 $, затем $(\mathbf{v}_1, \mathbf{v}_2) \in V_1 \times V_2$.
$V_1 \otimes V_2$	Тензорное произведение векторных пространств $V_1$ и $V_2$	$\dim (V_1 \otimes V_2) =$ $\dim(V_1) \times \times \dim(V_2)$
$V/W$	*Факторпространство 9{\!})=\dim(V)$**

Operators in Abstract Algebra

9c ) = \{ -1, 1\}$

Symbol Name	Explanation	Example
$[a]$	Equivalence класс элемента $a$	В $\mathbb{Z}_5$, $[2] =$ $\{ 2 + 5m \mid m \in \mathbb{Z} \}$.
$\deg(p(x))$	Степень полинома $p(x)$	$\deg (p(x) q(x)) =$ $\deg(p (х)) + \deg(q(x))$
$\langle S \rangle$	Подгруппа , порожденная элементами множества $S$	Если $G=\langle S \rangle$, то $S$ является генератором $G$.
$H_1 \oplus H_2$	Direct sum of subgroups $H_1$ and $H_2$	$G = H_1 \oplus H_2$
$G_1 \times G_2$	Direct product групп $G_1$ и $G_2$	$(e_{G_1}, e_{G_2}) \in \\ G_1 \times G_2$
$ST$	Произведение групповых подмножеств $S$ и $T$	Если $S, T \subseteq G$, то $ST$ $=\{st \mid s \in S \ земля t \in T \}.$
$N \rtimes H$	Полупрямое произведение подгрупп $N$ и $H$	$G = N \rtimes H$
$G_1 \wr G_2$	Сплетение групп $G_1$ и $G_2$	$\mathbb{Z}_2 \wr \mathbb{Z}$
$G/N$	Факторгруппа группы $G$ по подгруппе $N$	$\mathbb{Z}/3\mathbb{Z} = \\ \{[0], [1], [2]\}$
$R/I$	Факторкольцо кольца $R$ по идеалу $I$	Существует естественный гомоморфизм из $R$ в $R/I$.
$\mathrm{ker}(f)$	Ядро гомоморфизма $f$	$x_1, x_2 \in \mathrm{ker}(f) \implies$ $x_1 \circ x_2 \in \mathrm{ker}(f)$
$\overline{\mathbb{F}}$	Алгебраическое замыкание поля $\mathbb{F}$	$\overline{\mathbb {R}} = \mathbb{C}$

Символы отношения

В алгебре символов отношения используются для выражения отношений между двумя математическими объектами и часто связаны с такими понятиями, как равенство, сравнение, делимость и другие отношения более высокого порядка. В следующих таблицах описаны наиболее распространенные из них, а также их использование и значение. 92 \примерно 7,4$ $x \sim y$,
$xRy$ $x$ связано с $y$ (как определено некоторым математическим соотношением) $xRy$ тогда и только тогда, когда $x+y = 2m$ для некоторого $m \in \mathbb{Z}$. $x \equiv y$ $x$ эквивалентно в $y$ $11 \equiv 23 \;\mathrm{mod}\,12$ $f(x) propto g(x)$ Функция $f$ прямо пропорциональна функции $g$ 94)} \gg 1000000$ $x \prec y$ $x$ предшествует $y$ Если $x \prec y$ и $y \prec z$, то $x \prec з$. $x \preceq y$ $x$ предшествует или равно $y$ $(u_1, u_2) \preceq (v_1,v_2)$ тогда и только тогда, когда $u_1 \le v_1$ и $u_2 \le v_2$. $x \succ y$ $x$ успехов $y$ $x \succ y \iff y \prec x$ $x \succeq y$0602 $x$ предшествует или равно $y$ $f \succeq g$ тогда и только тогда, когда $f(x) \ge g(x)$ для всех $x \in \mathbb{R}$.

Number-based Relational Symbols

Symbol Name	Explanation	Example
$m \mid n$	Integer $m$ divides integer $n$	$11 \mid 121$
$m \nmid n$	Целое число $m$ не делится на целое число $n$	$34 \nmid 90$
$m \perp n$	Целые числа $m$ и $n$ являются взаимно простыми	Если $n \pq $n \perp p$, затем $n \mid q$.

Relational Symbols in Abstract Algebra

Symbol Name	Explanation	Example
$N\vartriangleleft G$	$N$ is a normal subgroup 94$

Основной список символов см. в разделе математические символы. Списки символов, классифицированных по типам , и по предмету , см. на соответствующих страницах ниже.

Предпочитаете версию в формате PDF?

Да. Это было бы полезно.

Дополнительные ресурсы

Полное руководство по изучению высшей математики : система из 10 принципов для эффективного обучения математике, мышления и решения задач.
Ultimate LaTeX Reference Guide. Серия : четыре бесплатных электронных книги по различным подтемам вводной линейной алгебры
10 заповедей высшего математического обучения : иллюстрированное веб-руководство по 10 масштабируемым правилам для изучения высшей математики

Что такое математический термин? Определение, выражение, примеры, факты

Алгебра — это часть математики, помогающая представлять проблемы или ситуации в виде математических выражений. Например, бабушка Тима подарила ему много шоколадных батончиков. Он съел несколько, и теперь у него осталось 5. Итак, сколько конфет съел Тим?

Поставим этот вопрос с помощью алгебры:

Мы знаем, сколько конфет осталось, поэтому число 5 можно назвать константой . Константы — это числа, имеющие фиксированное числовое значение. Мы не знаем, сколько шоколадных батончиков дала ему бабушка Тима, поэтому назовем его x . Буква x представляет собой неизвестную величину и известна как переменная . Когда мы вычтем количество несъеденных батончиков из количества батончиков, которые дала ему бабушка Тима, мы узнаем, сколько он уже съел.

Что такое алгебраическое выражение?

Алгебраическое выражение состоит из неизвестных переменных, чисел и арифметических операторов.

x – 5 — простое алгебраическое выражение . Когда мы объединяем константы и переменные, связанные математическими операциями, такими как +, -, x и ÷, мы получаем алгебраическое выражение .

Рассмотрим еще несколько алгебраических выражений .

Коэффициент – это число, умноженное на переменную.Коэффициент при 5 x + 10 равен 5 и

8 – 2 x равно – 2.

Что такое термин в математике?

В алгебра алгебраическое выражение формируется из терма или группы термов вместе. Термин в математике определяется как значения, над которыми выполняются математические операции в алгебраическом выражении . Давайте разберемся на примере термина.

Оба 8x и 9 являются членами этого алгебраического выражения.

Каковы факторы термина?

Факторы термина — это числа или переменные, которые перемножаются для образования термина.

Например, коэффициенты термина 9xy равны 9, x и y.

Различные термины в алгебре

В алгебре есть два вида терминов: Подобные термины и Отличающиеся термины .

Подобные термины: Подобные термины — это термины, переменные и показатель степени которых одинаковы. Их можно упростить, объединив. Операции сложения и вычитания можно выполнять над ними вместе.

Например, 5x + 8x — это алгебраическое выражение с одинаковыми элементами.

Непохожие термины: Непохожие термины — это термины, переменные и их показатели которых отличаются друг от друга. Их нельзя упростить, объединив. Операции сложения и вычитания нельзя выполнять над ними вместе.

Например, 5x + 8y — это алгебраическое выражение с разными членами.

Давайте узнаем о «многочленах»

Многочлен состоит из двух греческих слов: слово «поли» означает «много», а «номинальный» означает «члены». Итак, мы получаем словосочетание «много терминов». Многочлены подразделяются на три различных типа в зависимости от количества членов, из которых они состоят.

Три типа многочленов:

Одночлены
Двучлены
Трехчлены

Одночлены: Он состоит только из одного члена.

Вот несколько примеров одночленов:

4x
12y
5z

900
Вот несколько примеров биномов:
4x + 27
12y -3
5z+ 2x
Трехчлен: Это многочлен, состоящий ровно из трех членов.
Here are a few examples of trinomials:
4x + 27 – 3z
12y -3 + 7z
5z+ 2x + 8y
Example 1: What are the terms, variables , и константы алгебраического выражения:
9x – 7 лет + 5 ?
Решенные примеры
Решение:
В алгебраической экспрессии, 9x -7y + 5 (дано)
. и y
Переменные — это числа, которые могут принимать различные числовые значения.
Константа — это число 5.
Константы — это числа, имеющие фиксированное числовое значение.
Пример 2: Каковы множители алгебраического выражения 3abc?
Решение:
Факторы термина — это числа или переменные, которые умножаются для образования термина.
Итак, множители 3abc равны 3, a, b и c.
Пример 3. Определите сходные и неодинаковые термины:
1215 b) 12y – 5y
Решение:
a) 4p – 7q
Это разные термины. Их переменные отличаются друг от друга.
б) 12 – 5 лет Это похожие термины. Их переменные одинаковы.
Практические задачи
3 — x
3 + x
x — 3
x + 3
Правильный ответ: x — 3
Количество воробьев, сидящих на ветвях дерева, равно x (дано). Три улетели, значит, воробьев осталось x – 3.
Таким образом, алгебраическое выражение для данного утверждения равно x – 3.
x и 9
7 и 9
7x и -9
7x и 9
Правильный ответ: 7x и 9
Термины – значения на которых математические операции происходят в алгебраическом выражении.
Членами этого алгебраического выражения являются 7x и 9.
11, y и z
y и z
11 y и z
11 и yz
Правильный ответ: 11, 9005 9z Факторы термина — это числа или переменные, которые умножаются для образования термина.
В данном алгебраическом выражении 11 y и z умножаются, чтобы получить 11yz.
Часто задаваемые вопросы
Из чего состоят члены алгебраического выражения?
Терм в алгебраическом выражении может быть:
Константа
Переменная (с коэффициентами или без них)
И константа, и переменная
Термины складываются в алгебраическое выражение. Таким образом, они известны как компоненты выражения.
Что такое многочлены?
Многочлен состоит из двух греческих слов: «поли», означающее «много», и «номинал», означающее «члены». Таким образом, получается фраза «много терминов».
Какие существуют типы многочленов?
Полиномы подразделяются на три разных типа в зависимости от количества членов, из которых они состоят. Три типа многочленов:
Мономиальный: Он состоит только из одного члена. Например, 3а.
Биномиальный: Это многочлен, состоящий ровно из двух членов. Например, 3a + 7bTrinomial: это многочлен, состоящий ровно из трех членов. Например, 3а + 7б – 5в
Что означает перевернутая буква А в математике? – Strategies for Parents
Мы обычно ассоциируем буквы латинского алфавита (A, B, C и т. д.) с английским языком. Эти буквы легко понять, в отличие от надоедливых математических Σ и π. Однако буквы могут иметь очень знакомую форму в различных дисциплинах, например, перевернутая буква А в математике (∀).
Символ ∀ может выглядеть как знакомая заглавная буква «А», написанная вверх ногами, но в математике (в частности, в исчислении предикатов) ∀ является логическим символом или универсальным квантором. Вы можете использовать его вместо «для всех». Это означает, что ∀ — это сокращенный символ, который вы будете использовать при написании доказательств, уравнений и наборов.
Хотя ∀ может показаться пугающей, понять ее так же просто, как понять азбуку. Продолжайте читать, и вы узнаете не только, что такое ∀, но и как использовать его в своей работе.
Как называется перевернутая буква А?
Перевернутая А в математике не имеет стандартного названия. Многие часто называют его «отличником». Имейте в виду, что это слово связано как с ∀, так и с ɐ, и оно использует букву как в математике, так и вне ее. Это универсальный символ количественной оценки, когда речь идет конкретно о математике/логике.
Что такое универсальный количественный анализ?
«Универсальная количественная оценка» звучит довольно пугающе, но не всегда все так, как кажется. Если мы разберем слово, вам будет легко понять его значение.
Слово «универсальный» относится к чему-то общему или применимому ко всем случаям.
В английском языке слово «квантификация» происходит от слова «количество». Кембриджское определение количественной оценки — это «акт измерения или оценки размера или количества чего-либо» (источник).
Следовательно, квантификаторы — это слова, которые мы используем для обозначения количества или количества чего-либо. Вы можете быть знакомы с этим, если вы являетесь носителем английского языка, поскольку мы понимаем слова, описывающие количества, не являющиеся конкретными — не дающие буквальное количество или точное измерение — как квантификаторы.
Эти слова включают:
Все
Немного
Многие
Некоторые
Немного
Ни один
Итак, универсальный квантификатор применим ко всем обстоятельствам. Вот почему универсальные количественные символы стоят вместо слов «для всех» и «данных любому».
Если вы хотите разбить другие понятия на части, я рекомендую вам приобрести Oxford New Essential Dictionary , доступный на Amazon. Этот словарь с более чем 100 000 статей может помочь вам с любыми вашими потребностями в обучении, будь то в школе, на работе или даже дома.
Есть несколько способов показать универсальную количественную оценку, но наиболее распространенным способом является перевернутая буква А.
Что означает перевернутая буква А?
Как было установлено ранее, ∀ — это логический символ, используемый в доказательствах, уравнениях и множествах. Символ ∀ стоит вместо слов «для всех» и «для любого» во избежание постоянного повторения (источник).
Уравнение/функция Значение
f(x) ∀ a, b, c ∈ N c (которые являются натуральными числами), потому что: a, b и c — буквы, которые стоят вместо цифр.∈ означает «является элементом» (источник).N (часто пишется как ) — это символ натуральных чисел (только строчные буквы вместо цифр стоят буквы).
r(x)=x∀x r(x) Это означает, что для всех значений x r(x) истинно.
c(x)=x+2>xC(-1)= 1+(-1)>-10>-1 (истинно)C(1)= 1+2>13>1 (истинно) C (2)= 2+2>14>1 (истинно)∀x C(x) Это означает, что для всех значений x, C(x) истинно.
Примечание: если вы хотите узнать больше о различных категориях чисел, ознакомьтесь со статьей «Что означает символ Backwards 3?»
Что такое логический символ?
Логические символы — это фигуры, представляющие логические понятия. В логике первого порядка наиболее распространенными логическими символами являются:
Квантификаторы: ∀ и ∃.
Логические связки: ∧, ∨, →, ↔ ,→ и т. д.
Знаки пунктуации: (), [] и т. д.
Переменные и индексы: a, b, c,
Символ равенства: =
Понимание символов ∀ и ∃
Мы уже установили, что ∀ показывает универсальную количественную оценку. Однако это не единственный тип количественного определения. Существует второй тип квантификации, известный как экзистенциальная квантификация. Это означает, что переменная имеет одно (или несколько) правильных значений в формуле.
В отличие от ∀, ∃ стоит вместо «существует», «есть хотя бы один» или «для некоторых».
Например, если у вас есть формула x+2<3, вы можете попытаться вычислить x, заменив ее действительными числами (как положительными, так и отрицательными):
f(x)=x+2<3
f (-1)=(-1)+2<3
f(-1)=1<3 (истинно)
f(0)=(0)+2<3
f(0)=2<3 ( верно)
f(1)=(1)+2<3
f(1)=3<3 (ложно)
f(2)=(2)+2<3
f(2)=4< 3 (ложь)
Это означает, что утверждение верно только тогда, когда x<1. Следовательно, только некоторые значения x являются правильными. Вы также можете записать это как:
∃x (f(x) x<1) (существуют только некоторые значения x, для которых f(x) истинно).
Вы также можете столкнуться с ∃! в вашей учебе. Это пример количественной оценки уникальности, когда переменная может иметь только одно значение, например, x+4=5.
Что такое логика первого порядка (кратко)?
Исчисление предикатов подпадает под рубрику, известную как логика первого порядка.
Логика первого порядка — это не просто математическое понятие. На самом деле, вы можете встретить его в философии, компьютерных науках и даже лингвистике. Логика первого порядка состоит из предикатов. Следовательно, чтобы понять логику первого порядка, нам нужно сначала понять предикаты.
Что такое предикаты?
Предикаты — это утверждения — как в английском языке, так и в математике, — которые не являются ни истинными, ни ложными. Мы можем только сделать вывод об их правильности (или неправильности) на основе заданных переменных.
Например:
X > 5 (это верно только в том случае, если x больше 5)
X — столица Соединенных Штатов (это верно только в том случае, если X — это Вашингтон, округ Колумбия)
Вы следует также понимать логику высказываний, поскольку она в некоторой степени является основой для логики предикатов.
Что такое логика предложений?
Логика предикатов сильно отличается от логики пропозиций — и пропозиций, которые являются ее частью. В логике высказываний каждое утверждение истинно или ложно, но никогда оба (источник). Например:
Стефани Майер написала Сумерки . (правда)
Солнце встает с запада. (ложь)
В математике это можно увидеть в таких утверждениях, как: логика суждений — это использование вами предикатов вместо суждений и отсутствие отношений или квантификаторов — примечание: вам нужно запомнить это слово.
Image by Jeswin Thomas via Unsplash
Сокращенная запись
Теперь, в логике первого порядка, оператор предиката делится на две части. Это полезно, поскольку помогает вам отформатировать текст в краткой и сжатой форме.
Операторы-предикаты состоят из:
Субъекта
Предиката
Субъект — это переменная, а предикат — это часть оператора, которая предоставляет информацию о субъекте.
Давайте попробуем один пример. Здесь есть ответ ∃, но он будет работать аналогично с оператором ∀:
x>5 (что означает, что x больше 5)
Мы можем показать эту формулу, используя H(x) — здесь H() представляет предикат, а x — субъект/переменную.
При письме мы используем стенографию. Без него вам пришлось бы постоянно повторять то, что вы пишете, что требует времени и через некоторое время может выглядеть неуклюже.
Итак, если вы хотите определить значения X, вам не нужно повторять:
1 больше 5 ✘ (ложь)
2 больше 5 ✘ (ложь)
3 больше 5 ✘ (ложь)
4 больше 5 ✘ (ложь)
912 чем 5 ✘ (ложь)
6 больше 5 ✓ (истина)
Скорее можно сказать:
∃x (H(x) 5
Это означает, что существуют только некоторые значения x, для которого H(x) истинно. Писать стенографически полезно, и это может помочь вам сформулировать ответ кратко.
Изображение от Гленн Карстенс-Питерс через Unsplash
Как вы печатаете перевернутые символы?
Ниже вы найдете несколько стратегий для ввода перевернутых символов, таких как перевернутая буква A.
Стратегия первая: копирование и вставка
Это самая простая стратегия для написания ∀. Все, что вам нужно, это подключение к Интернету.
Поищите в Google «универсальный символ количественной оценки». Вы должны увидеть избранный фрагмент из Википедии, который говорит:
«Традиционным символом универсального квантора является «∀», повернутая буква «А», которая означает «для всех» или «все». Соответствующий символ квантора существования — «∃», повернутая буква «Е», которая означает «существует» или «существует» (источник).
Выделите ∀ в предложении и либо нажмите ctrl+c, либо выберите его вручную, щелкнув правой кнопкой мыши. Ваш экран должен отражать показанный ниже (на ПК):
Изображение от Sona Digital Media
Перейдите к соответствующему документу и щелкните правой кнопкой мыши, чтобы вставить символ вручную. Делать это вручную, вероятно, лучше, так как это предоставляет больше возможностей.
Если вы выполняете простую вставку (ctrl+v), по умолчанию ∀, скорее всего, будет другого размера, формата и шрифта, чем то, что вы уже написали ранее.
Документы Google
Если вы используете Документы Google, вы можете исправить это, выбрав «вставить без форматирования» или Ctrl+Shift+V, что объединит букву с форматированием предыдущего текста.
Изображение от Sona Digital Media
Однако в Microsoft Word вам нужно выбрать либо «объединить форматирование», либо «сохранить только текст». Это последние два поля, которые вы увидите в разделе вставки — см. диаграмму ниже.
Изображение Sona Digital Media
Имейте в виду, что математические символы недоступны в большинстве шрифтов, поэтому шрифт может измениться на шрифт, в котором доступен символ ∀. Изменение шрифта для любых следующих слов должно быть относительно простым с помощью панели задач.
Используя эти стратегии, вы сможете вставить ∀ в любую программу путем копирования и вставки.
Стратегия вторая: вставка вручную
Существует два способа вставки символа вручную.
Если вы работаете в Word, выберите «вставить символ». После того, как вы выполните этот шаг, откроется меню. В меню измените шрифт на Cambria и подмножество на Mathematical Operators.
Изображение от Sona Digital Media
Вы также можете использовать ярлык, набрав 2200 и нажав Alt+X после этого.
Если вы используете Google Docs, выберите «Вставить специальные символы». Это приведет вас к меню, похожему на приведенное ниже.
Изображение от Sona Digital Media
Соответствуйте настройкам, которые вы видите выше — на вкладках должны быть указаны категории, символы и математика. Там вы найдете ∀ (обведено красным). Щелкните его, чтобы добавить в документ.
Вы также можете использовать строку поиска «поиск по ключевому слову (например, стрелке) или кодовой точке» и ввести «повернутый A». Или используйте функцию рисования под ним.
Вы должны быть в состоянии вставить его, используя аналогичную технику в других программах, поэтому не отчаивайтесь, если вы пишете ∀ в программе, которая не является ни Microsoft Word, ни Google Docs.
Стратегия третья: письмо вверх ногами в целом
Иногда жизнь может стать скучной, и мы вынуждены развлекаться сами. Если да, то, возможно, некоторые из вас считают, что писать вверх ногами — это отвлечься от монотонности реальной жизни. Конечно, это не имеет ничего общего с математикой, но все же может быть увлекательным!
Написание вверх ногами тоже имеет свои преимущества. Вы можете использовать его при публикации или отправке сообщений в социальных сетях или при создании паролей в социальных сетях.
Сделать это тоже просто. Посетите сайт upsidedowntext.com и напишите все, что хотите, в поле «Введите текст, слова, буквы или символы здесь:».
Предложение будет отображаться перевернутым и перевернутым, где вы можете скопировать и вставить его. Вы можете избавиться от текстовых эффектов, сняв флажки с эффектами.
Изображение от SONA Digital Media
Текст выглядит так, если вы копируете его:
˙ɹǝᴉɟᴉʇuɐnb lɐsɹǝʌᴉun ɹo loqɯʎs ɔᴉƃol ɐ s a ǝɥʇ ‘(snlnɔlɐɔ ǝʇɐɔᴉpǝɹd Uᴉ ʎ ʎ ʇ ʇ ʇ ʇ ʇ ɹɐᴉlᴉɯɐɟ ǝɥʇ ǝʞᴉl ʞool ʎɐɯ loqɯʎs A lɐɔᴉʇɐɯǝɥʇɐɯ ǝɥ┴
Примечание. Имейте в виду, что математический символ ∀ немного отличается от буквы A, перевернутой (Ɐ) сам по себе. Если вы посмотрите на различия ниже, вы увидите, что математический символ ∀ немного короче.
Изображение от Sona Digital Media
Если вы пытаетесь написать ∀, рекомендуется сначала попробовать и использовать предыдущие методы, а не полагаться на этот, как для точности, так и для вашего удобства.
Заключительные мысли
Нельзя отрицать, что ∀ играет важную роль в математике. Вот почему нам нужно знать, когда, где и как его использовать.
Итак, в следующий раз, когда вы будете работать над учебниками по математике, помните о возможностях ∀ и ∃ в экономии времени и места, независимо от того, пишете ли вы «для всех» или «для некоторых». Даже если вы забудете эти символы, скорее всего, ваши учителя этого не сделают.
Почему мы используем «X» в качестве неизвестного в математике
By
Мелисса — TodayIFoundOut. com
Комментарии (72)
В течение сотен лет x был основным символом для неизвестной величины в математических уравнениях. Так кто же начал эту практику?
Алгебра зародилась на Ближнем Востоке, во времена Золотого века средневековой исламской цивилизации (750–1258 гг. н.э.), и ее раннюю форму можно увидеть в работах Мухаммада аль-Хорезми и его книге 9 века Китаб аль- джабр валь-мукабала ( al-jabr позже трансформируется в алгебру на английском языке). Во время этого расцвета мусульманское правление и культура распространились на Пиренейский полуостров, где мавры поощряли научные исследования и математику.
Так какое это имеет отношение к букве «х» в математике? В недавнем выступлении на TED директор The Radius Foundation Терри Мур заявил, что использование «x» таким образом началось с неспособности испанских ученых перевести некоторые арабские звуки, включая букву шин (или шинь). ). По словам Мура, слово «неизвестная вещь» по-арабски — 9. 3337 al-shalan , и он много раз появлялся в ранних математических работах. (Например, вы можете увидеть, что «три неизвестных равны 15», а «неизвестное» равно 5.)
Но поскольку у испанских ученых не было соответствующего звука для «ш», они использовали звук «ск». который в классическом греческом языке записывается с помощью символа хи, X. Мур теоретизирует, как и многие другие до него, что, когда это было позже переведено на латынь, хи (X) был заменен более распространенным латинским x. Это похоже на то, как Xmas, означающее Рождество, возник из-за обычной практики религиоведов, использующих греческую букву хи (X) в качестве сокращения для «Христа».
Основная проблема с объяснением Мура заключается в том, что нет прямых документальных доказательств, подтверждающих его. Более того, люди, переводящие произведения, будут заботиться не о фонетике, а о значениях слов. Так что, было ли у них «ш» или нет, можно было бы подумать, что это не имеет значения. Несмотря на отсутствие прямых доказательств и недостатки в аргументации, она, тем не менее, остается очень популярной теорией происхождения даже среди многих ученых. (Выполните быстрый поиск в Google, и вы найдете множество докторов математических наук, повторяющих эту теорию.)
Издание Webster’s Dictionary 1909-1916 годов, среди прочих, также выдвигает подобную теорию, хотя и утверждает, что арабское слово, обозначающее «вещь» в единственном числе, «shei», было переведено в греческое «xei», а позже сокращено к х. Д-р Али Хунсари также отмечает, что греческое слово, означающее «неизвестный», xenos , также начинается с x, и условность могла просто возникнуть из аббревиатуры. Но здесь, опять же, у нас нет прямых документальных доказательств в поддержку этих теорий.
За документально подтвержденной теорией обратимся к великому философу и математику Рене Декарту (1596-1650). Вполне возможно, что Декарт не придумал практику использования «x» для неизвестного, возможно, позаимствовав его у кого-то другого, но, по крайней мере, в том, что касается дошедших до наших дней документальных свидетельств, он, кажется, является создателем практика, как отмечено в OED и феноменальной работе Флориана Каджори, История математических обозначений (1929). По крайней мере, Декарт помог популяризировать эту практику.
В частности, в своей знаменательной работе La Géométrie (1637) Декарт укрепил движение к символической записи, установив соглашение об использовании строчных букв в начале алфавита для известных величин (например, a, b и c). ) и использование тех, что в конце алфавита для неизвестных величин (например, z, y и x).
Почему? А почему x больше y, а z для неизвестных? Никто не знает. Было высказано предположение, что известность использования x для неизвестных в этой работе чаще, чем y и z, была связана с набором текста; одна история гласит, что именно печатник Декарт предложил х быть принципом, неизвестным в La Géométrie , потому что это была наименее используемая буква, и поэтому у него было больше буквенных блоков, доступных для использования. Правда это или нет, но Декарт использовал x как неизвестное по крайней мере еще в 1629 году в различных рукописях, задолго до La Géométrie . И действительно, казалось бы, он не пришел к каким-то жестким правилам относительно x, y и z, указывающих на неизвестные; в некоторых рукописях того времени он фактически использовал x, y и z для обозначения известных величин, что еще больше ставит под сомнение предполагаемые теории перевода «неизвестной вещи», перечисленные выше.
Итак, в конце концов, судя по всему, Декарт просто произвольно выбрал буквы для обозначения разных вещей в своих произведениях, как это было удобно, и так уж вышло в его знаковой работе La Géométrie, он определил конкретную переменную номенклатуру, возможно, по наитию.
Как бы то ни было, как и в случае с обозначениями Декарта для степеней (x ³ ), после публикации La Géométrie, использование x как принципа неизвестно (так же, как и более общая традиция a, b, c = известные и x, y, z = неизвестные) постепенно прижились. А остальное, как говорится, математическая история.
Если вам понравилась эта статья, вам также могут понравиться:
Откуда взялись символ амперсанда и название
Откуда взялся знак доллара
Как «XOXO» стало означать «Объятия и поцелуи»
Сделал ли Ньютон Действительно ли яблоко упало ему на голову, что вдохновило его на создание теории гравитации?
Происхождение символа хэштега
Дополнительные факты:
Знак равенства («=») был изобретен в 1557 году валлийским математиком Робертом Рекордом, которому надоело писать «равно» в своих уравнениях. Он выбрал две линии, потому что «две вещи не могут быть более равными».
Другие ранние символы, использовавшиеся для обозначения неизвестных в математике до знаковой работы Декарта, включают Бенедетто Флорентийского 1463 Trattato di praticha d’arismetrica , где он использует греческую букву rho; 1544 Arithmetic integra Майкла Стифеля, где он использует q (для количественных показателей), а также A, B, C, D и F; Номенклатура Франсуа Виета конца 16 века, в которой гласные используются как неизвестные, а согласные используются как константы, среди прочего. (Кстати, если вам интересно: что делает гласную гласной, а согласную — согласной?)
В современном английском языке x — третья наименее используемая буква, встречающаяся только примерно в 0,15% всех слов. Реже всего используются буквы q и z.
Слово «алгоритм» происходит не от кого иного, как от имени аль-Хорезми. Если вы немного исказите имя, когда произносите его, вы получите связь.
Математический объем пиццы — это пицца. Как это работает, говоришь? Если z = радиус пиццы и a = высота, то Π * радиус ² * высота = Pi * z * z * a = пицца.
Как уже упоминалось, La Géométrie была новаторской работой. В нем Декарт представил идею, которая впоследствии стала известна как декартовы координаты; это включало идеи двух перпендикулярных линий, называемых осями, называя горизонтальную x и вертикальную ось y, а также обозначая точку пересечения как начало координат. Декарту также приписывают одну из самых известных строк во всей западной мысли — Cognito ergo sum (Я мыслю, следовательно, существую)
Тем не менее, хотя Декарт известен своей идеей «Я мыслю, следовательно, я существую», он не был первым, кто выразил такую идею. Например, нечто подобное сказал Аристотель в «Никомаховой этике» : «Но если сама жизнь хороша и приятна… и если тот, кто видит, сознает, что он видит, тот, кто слышит, что он слышит, тот, кто ходит, что он ходит, и подобным образом для Во всех других видах человеческой деятельности существует способность, которая сознает свое осуществление, так что всякий раз, когда мы воспринимаем, мы сознаем, что мы воспринимаем, и всякий раз, когда мы думаем, мы сознаем, что мы думаем, и сознавать, что мы воспринимаем или думать — значит осознавать, что мы существуем…» Конечно, «я мыслю, следовательно, я существую» гораздо короче.
Мухаммад Аль-Хорезми был одним из первых директоров Дома Мудрости в Багдаде. Руководя переводами важных индийских и греческих математических и астрономических работ, Аль-Хорезми стал сторонником принятия индийской системы счисления (1-9 плюс 0) и является отцом алгебры. С публикацией The Compendious Book on Calculation by Compendious and Balancing Аль-Хорезми представил использование абстрактного анализа при решении задач (хотя и со словами, а не с символическими обозначениями). Он также ввел алгебраический метод редукции (преобразование выражения во все более простые, но эквивалентные формы), а также метод уравновешивания (выполнение одних и тех же действий с каждой частью уравнения — опять же, чтобы сделать его проще).
Программа международной оценки учащихся (PISA) оценивает компетенции 15-летних подростков в 65 странах и экономиках, в том числе по математике. В 2012 году страной/экономикой с самыми высокими показателями по математике был Шанхай-Китай, за которым следуют Сингапур, Гонконг-Китай, Китайский Тайбэй и Корея. Примечательно, что Канада заняла 13-е место, Австралия — 19-е, Ирландия — 20-е, а Великобритания — 26-е. Дети США заняли 36-е место. На самом деле, согласно PISA, успеваемость одного из наших штатов с самыми высокими баллами, Массачусетса, была настолько низкой, как будто у этих студентов было на два года меньше математического образования, чем у студентов в Шанхае, Китай. PISA также отметила, что, хотя в США на одного учащегося тратится больше, чем в большинстве стран, это не отражается на успеваемости. В 2012 году расходы на одного учащегося в США составляли 115 000 долларов, в то время как в Словацкой Республике, стране с такими же показателями, на одного учащегося тратится всего 53 000 долларов.
Однако следует отметить, что результаты PISA сильно упрощены. Например, как отмечается в отчете доктора Мартина Карнуа из Стэнфорда и Ричарда Ротштейна из Института экономической политики, американские студенты фактически показывают лучшие результаты, чем Финляндия с гораздо более высоким рейтингом, по алгебре в целом, но хуже по дробям. Кроме того, если нормализовать результаты между странами с поправкой на относительную бедность учащихся, сдающих тесты PISA, США показывают значительно лучшие результаты, занимая 6-е место по чтению и 13-е по математике, что является огромным скачком в обеих категориях. Они также отмечают в своем отчете Что на самом деле показывают международные тесты об успеваемости американских студентов? , что, когда вы делите детей на основе семейного благосостояния, фактический разрыв в производительности между странами не так уж велик, и немалая часть конечного рейтинга каждой нации основана на том, сколько бедных по сравнению со средним классом по сравнению с богатыми студенты сдают тесты. Для справки, около 40% школ, использованных PISA в выборке США, имели более 50% учащихся, имеющих право на бесплатные обеды.
Несмотря на чрезмерное упрощение результатов, PISA выявила несколько слабых мест в математических навыках американских учащихся, в том числе разработку математической модели для решения реальных задач и рассуждения с помощью геометрии. PISA отметила, что в случае успешного внедрения Common Core Standards в США это должно привести к значительному повышению производительности.
Стандарты Common Core стремятся сосредоточить математическое образование на развитии концептуального понимания ключевых математических идей, а также на овладении базовыми математическими навыками. На сегодняшний день стандарты Common Core приняты в 43 штатах. Однако важно отметить, что, хотя штаты приняли эти стандарты, каждый из них может свободно выбирать учебную программу, которую он реализует. Некоторые выбрали учебную программу, которая неузнаваема для многих родителей, которые теперь расстроены и считают это проблемой общего ядра, тогда как на самом деле общее ядро — это просто список компетенций, которые дети должны знать к концу каждого учебного года, а не как они должны изучать эти понятия. Что касается реализации, то один учебный план по математике под критикой стоит Everyday Math , разработанный Чикагским университетом. Благодаря методам, ранее недоступным для многих американских родителей (кто-нибудь использовал решетчатое умножение?), новая учебная программа заставляет некоторых рвать на себе волосы. Как сказала одна мама: «Я ненавижу Common Core… Я не могу помочь своему ребенку с домашним заданием и совершенно не понимаю новые методы». Но, опять же, эта конкретная жалоба на самом деле имеет отношение не к Common Core, а к Everyday Math .
С учетом сказанного, вот соответствующее видео (особенно с отметки 3 минуты 10 секунд) от Генри Райха в MinutePhysics Порядок операций . Если вы дочитали до этого места в этой статье, я полагаю, вы найдете это видео довольно интересным от начала до конца:
Мелисса пишет для умеренно популярного веб-сайта интересных фактов TodayIFoundOut.com . Чтобы подписаться на информационный бюллетень «Ежедневные знания» Today I Found Out, нажмите здесь или нажмите «Нравится» на Facebook здесь .
No related posts.

Таблица знаков (символов) в алгебре и их значения

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица математических символов | это.

Урок 11. многочлен p(x) и его корень. алгебраическое уравнение — Алгебра и начала математического анализа — 10 класс

Метод интервалов — материалы для подготовки к ЕГЭ по Математике

что это такое, как появилась, почему считают «царицей наук»?

Как решать это уравнение?

Ответ таков

Как алгебра стала такой, какой мы её знаем?

Булева алгебра (алгебра логики)

Логические функции одной переменной

Логические функции двух переменных

Ответить на контрольные вопросы, а затем посмотреть ответы

Освежите свою математику: Алгебра

Символы и цифры

Алгебраические выражения

Упражнение: алгебраические выражения

Факторы и отмена

Упражнение: множители и отмена

Список математических символов — Простая английская Википедия, бесплатная энциклопедия

Полный список символов алгебры

Константы

Ключевые математические наборы

Переменные

Разделители

Символы, связанные с функциями

Операторы

Number-related Operators

Operators Related to Complex Numbers

Operators in Linear Algebra

Vector-related Operators

Matrix-related Operators

Vector-space-related Operators

Operators in Abstract Algebra

Символы отношения

Number-based Relational Symbols

Relational Symbols in Abstract Algebra

Дополнительные ресурсы

Что такое математический термин? Определение, выражение, примеры, факты

Что такое алгебраическое выражение?

Что такое термин в математике?

Каковы факторы термина?

Различные термины в алгебре

Решенные примеры

Практические задачи

Часто задаваемые вопросы

Что означает перевернутая буква А в математике? – Strategies for Parents

Что такое универсальный количественный анализ?

Что означает перевернутая буква А?

Что такое логический символ?

Понимание символов ∀ и ∃

Что такое предикаты?

Что такое логика предложений?

Стратегия первая: копирование и вставка

Документы Google

Стратегия вторая: вставка вручную

Стратегия третья: письмо вверх ногами в целом

Почему мы используем «X» в качестве неизвестного в математике

Добавить комментарий Отменить ответ