ЕГЭ по информатике — Задание 2 (Мощнейший метод)
Здравствуйте, дорогие друзья! Сегодня разберём, как решать второе задание из ЕГЭ по информатике 2020.
Во втором задании ЕГЭ по информатике у нас обычно есть логическая функция, которая зависит от логических переменных. Логические переменные могут принимать только два значения: 0 (Ложь) или 1 (Истина).
С логическими переменными можно производить логические операции. При решении второго задания из ЕГЭ по информатике необходимо твёрдо знать каждую логическую операцию, и давайте рассмотрим их.
- () — операции в скобках
- ¬ — логическое отрицание
- ∧ — логическое умножение
- ∨ — логическое сложение
- ⟶ — следование
- ≡ — равнозначность
Передём к решению задач из ЕГЭ по информатике
Задача 1 (лёгкая)
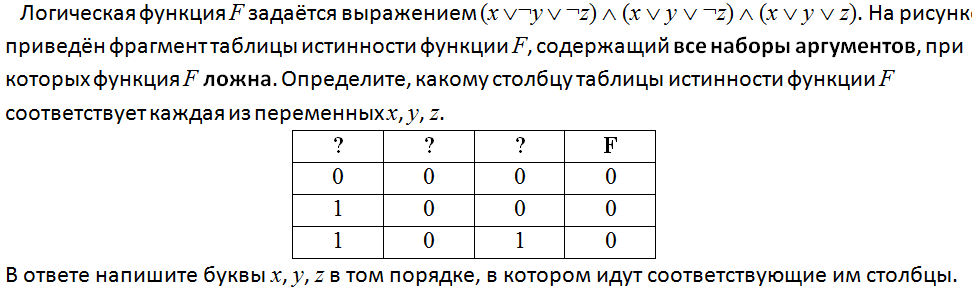
Логическая функция F задаётся выражением z ∧ ¬y ∧ (w → x).
Дан частично заполненный фрагмент, содержащий неповторяющиеся строки таблицы истинности функции F.
Определите, какому столбцу таблицы истинности соответствует каждая из переменных x, y, z, w.
В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы (сначала буква, соответствующая первому столбцу; затем буква, соответствующая второму столбцу, и т. д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно. Пример. Пусть задано выражение x → y, зависящее от двух переменных x и y, и фрагмент таблицы истинности:
Тогда первому столбцу соответствует переменная y, а второму столбцу соответствует переменная x. В ответе нужно написать: yx.
Решение:
Видим, что у функции основным действием является логическое умножение.
По таблице видно, что функция имеет значение только 1 . Логическое умножение даёт 1 (единицу) тогда, когда каждое выражение равно 1 (единице). Значит каждое выражение в нашей функции должно равняться единице.
Отсюда видно, что переменная z должна всегда быть равна 1 (единице). Это первый столбец. Отрицание y тоже должно быть 1 (единицей), тогда просто y всегда будет 0 (нулём). Это второй столбец.
Осталось определить положение
Ответ: zyxw
Задача 2 (средний уровень)
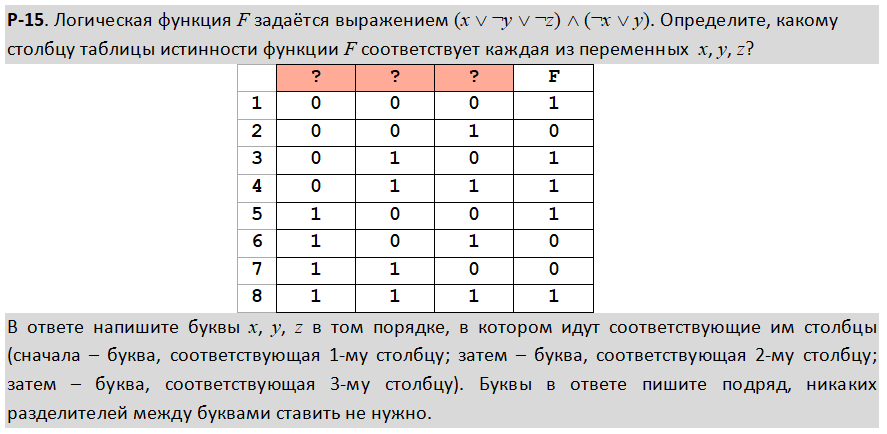
Логическая функция F задаётся выражением (x ∧ ¬y) ∨ (y ≡ z) ∨ w.
Дан частично заполненный фрагмент, содержащий неповторяющиеся строки таблицы истинности функции F.
Определите, какому столбцу таблицы истинности соответствует каждая из переменных x, y, z, w.
В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы (сначала — буква, соответствующая первому столбцу; затем — буква, соответствующая второму столбцу, и т. д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Пример. Пусть задано выражение x → y, зависящее от двух переменных x и y, и фрагмент таблицы истинности:
Тогда первому столбцу соответствует переменная y, а второму столбцу соответствует переменная x. В ответе нужно написать: yx.
Решение:
Определяем главную логическую операцию («главную скрипку»), которая соединяет разные выражения.
Видим, что это логическое сложение.
Во всех строчках таблицы функция принимает значение 0 (ноль). Значит, и каждое выражение должно принимать значение 0 (ноль).
Самым слабым звеном является переменная w, потому что она стоит одна. Переменная w должна равняться всегда 0(нулю) — этому условию может удовлетворить только третий столбец. Значит w стоит на третьем месте.
Следующим слабым звеном является равносильность. Она должна «выдавать» 0 (ноль). Равносильность «выдаёт» 0 (ноль), когда переменные разные!
Проанализируем первый и второй столбец. В третьей строчке, и там, и там, стоит 1 (единица). Значит, первый и второй столбец не могут быть одновременно y и z (или z и y).
Рассмотрим второй и четвёртый столбец. Вторая строчка содержит одинаковое значение 0 (ноль), и там, и там. Значит, второй и четвёртый столбец не могут быть одновременно y и z (или z и y).
Таким образом, y и z (или z и y) будут столбцы первый и четвёртый! И теперь можно расставить недостающие значения в этих столбцах. Расставляем, чтобы были разные значения, а второй столбец получается x.
Осталось разобраться с z и y. Обратимся к первому выражению (x ∧ ¬y) и посмотрим на третью строчку. Если в четвёртом столбце будет стоять y, то отрицание на y превратит ноль(ноль) в 1(единицу) в четвёртой строчке. Тогда окажется, что у x — 1 и ¬y — 1, и выражение (x ∧ ¬y) тоже получится 1(единицей). А у нас каждое выражение должно равняться 0(нулю). Получается y будет стоять в первом столбце, а z в четвёртом.
Тогда ответ будет равен yxwz.
Ответ: yxwz
Мощнейший метод для решения второго задания из ЕГЭ по информатике
Задача 3 (хороший уровень)
Логическая функция F задаётся выражением ((x → y ) ∧ (y → w)) ∨ (z ≡ ( x ∨ y)).
Дан частично заполненный фрагмент, содержащий неповторяющиеся строки таблицы истинности функции F. Определите, какому столбцу таблицы истинности соответствует каждая из переменных x, y, z, w.
В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы (сначала — буква, соответствующая первому столбцу; затем — буква, соответствующая второму столбцу, и т. д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Пример. Пусть задано выражение x → y, зависящее от двух переменных x и y, и фрагмент таблицы истинности:
Тогда первому столбцу соответствует переменная y, а второму столбцу соответствует переменная x. В ответе нужно написать: yx.
Решение:
«Главной скрипкой» в нашей функции является логическое сложение, потому что соединяет два выражения ((x → y ) ∧ (y → w)) и (z ≡ ( x ∨ y)).
Тогда каждое выражение должно равняться 0(нулю).
Теперь кульминация мощнейшего метода. У нас всего 4 переменных. Выпишем все комбинации для 4-х переменных. Таблица будет точно такая же, как мы писали в первом задании (её очень легко составить). Всего получается 16 комбинаций (16 = 24).
Теперь отметим зелёным плюсом те строчки, которые обращают выражение ((x → y ) ∧ (y → w)) в 0(ноль). Следующий шаг: Отметим галочкой те строчки, которые обращают в ноль второе выражение (z ≡ ( x ∨ y)) (Мы должны искать среди тех, которые уже отмечены плюсом).
При небольшой тренировке анализ подобных выражений занимает сущие секунды!
У нас получается 4 строчки, которые удовлетворяют нашей функции:
Отсюда видно, что переменная z может быть равна только 0(нулю)! Значит, она занимает третий столбец, потому что в остальных столбцах есть хотя бы одна 1(единица).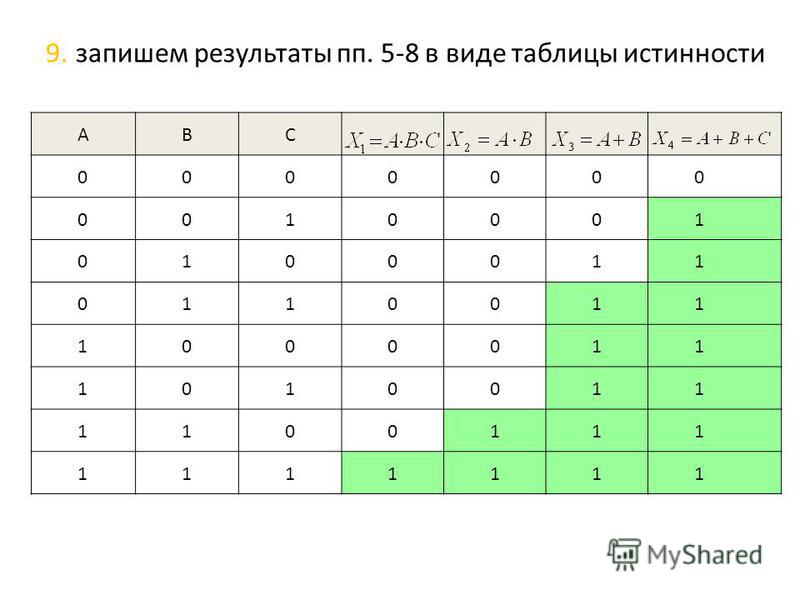
Переменная w имеет только одну 1(единицу). Значит, её ставим во второй столбец, потому что в первом и четвёртом уже по 2 единицы минимум, а третий уже занят z.
Теперь находим строчку c 1(единицей) в переменной w (Таблица данная в условии задачи) Кто в этой строчке будет иметь единицу (кроме w) — будет x! Это четвёртый столбец! Значит, x — это четвёртый столбец. Переменной y — достаётся первый столбец
Ответ: ywzx.
На этом всё! Сегодня рассмотрели теорию и основные методы для эффективного решения второго задания из ЕГЭ по информатике!
Пока!
НОУ ИНТУИТ | Лекция | Способы представления ФАЛ.
Переход от одной формы представления ФАЛ к другойАннотация: Цель лекции: познакомить студента с различными формами представления логических функций (табличным и аналитическими), а также объяснить методы перехода от одной формы представления ФАЛ к другой. Ключевые слова: таблица истинности, совершенная дизъюнктивная нормальная форма, совершенная конъюнктивная нормальная форма.
Основная форма представления функций алгебры логики – таблица истинности (ТИ), которая определяет значение функции на всех наборах переменных.
Таблицами истинности для функций одной и двух переменных являются таблицы 2.1 и 2.2 соответственно.
Помимо таблицы истинности, возможны и другие виды представления ФАЛ, наиболее распространенными из которых являются совершенная дизъюнктивная нормальная форма, описывающая все наборы переменных, на которых функция принимает значение, равное 1, и совершенная конъюнктивная нормальная форма, описывающая все наборы переменных, на которых функция принимает значение, равное 0.
Рассмотрим способы перехода от одного вида представления ФАЛ к другому.
Пример 2.1 Пусть ФАЛ задана в виде таблицы истинности (2.1).
| Номер набора | x | y | z | f(x,y,z) |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 2 | 0 | 1 | 0 | 0 |
| 3 | 0 | 1 | 1 | 1 |
| 4 | 1 | 0 | 0 | 1 |
| 5 | 1 | 0 | 1 | 1 |
| 6 | 1 | 1 | 0 | 0 |
| 7 | 1 | 1 | 1 | 1 |
intuit.ru/2010/edi»>Получить СДНФ и СКНФ этой функции.Решение
Получение СДНФ.
Для представления сокращенной записи СДНФ этой функции необходимо под знаком обобщенной дизъюнкции Σ или V перечислить через запятую номера всех наборов, на которых функция принимает значение, равное 1.:
Примечания: данный вид представления функции является сокращенной записью СДНФ, а не записью сокращенной дизъюнктивной нормальной формы.
Получение развернутой записи СДНФ включает следующие этапы.
Этап 1.
Записать дизъюнкцию k конъюнктивных термов, содержащих все переменные, от которых зависит функция, где k – количество наборов, на которых функция принимает значение, равное единице, то есть количество наборов, перечисленное в сокращенной записи СДНФ:
intuit.ru/2010/edi»>Этап 2.Записать под каждым термом двоичный эквивалент одного из наборов, на которых функция принимает значение, равное единице:
Этап 3.
Расставить знаки отрицания над теми переменными, которым в двоичном эквиваленте соответствует 0:
Полученная запись представляет собой совершенную дизъюнктивную нормальную форму для функции, заданной таблицей истинности 2.1.
Получение СКНФ.
Для представления сокращенной записи СКНФ этой функции необходимо под знаком обобщенной конъюнкции Π или Λ перечислить через запятую номера всех наборов, на которых функция принимает значение, равное 0:
Примечание: данный вид функции представляет собой сокращенную запись СКНФ, а не запись сокращенной конъюнктивной нормальной формы.
Получение развернутой записи СДНФ включает следующие этапы.
Этап 1.
Записать конъюнкцию m дизъюнктивных термов, содержащих все переменные, от которых зависит функция, где m — количество наборов, на которых функция принимает значение, равное 0, то есть количество наборов, перечисленное в сокращенной записи СКНФ:
Этап 2.
Записать под каждым термом двоичный эквивалент одного из наборов, на которых функция принимает значение, равное 0:
Этап 3.
Расставить знаки отрицания над теми переменными, которым в двоичном эквиваленте соответствует 1:
Полученная запись представляет собой совершенную конъюнктивную нормальную форму для функции, заданной таблицей истинности 2.
1.
Пример 2.2
Пусть ФАЛ задана сокращенной записью СДНФ:
Представить таблицу истинности, а также полную и сокращенную записи СКНФ этой функции.
Решение
Получение таблицы истинности
Этап 1.
Подготовить ТИ для логической функции трех переменных
| Номер набора | x | y | z | f(x,y,z) |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | |
| 1 | 0 | 0 | 1 | |
| 2 | 0 | 1 | 0 | |
| 3 | 0 | 1 | 1 | |
| 4 | 1 | 0 | 0 | |
| 5 | 1 | 0 | 1 | |
| 6 | 1 | 1 | 0 | |
| 7 | 1 | 1 | 1 |
intuit.ru/2010/edi»>Этап 2.Записать 1 в качестве значения функции в строки, соответствующие наборам, перечисленным в сокращенной записи СДНФ.
| Номер набора | x | y | z | f(x,y,z) |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 1 |
| 2 | 0 | 1 | 0 | 1 |
| 3 | 0 | 1 | 1 | |
| 4 | 1 | 0 | 0 | |
| 5 | 1 | 0 | 1 | 1 |
| 6 | 1 | 1 | 0 | |
| 7 | 1 | 1 | 1 | 1 |
intuit.ru/2010/edi»>Этап 3.Записать 0 в качестве значения функции в остальные строки таблицы.
| Номер набора | x | y | z | f(x,y,z) |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 1 |
| 2 | 0 | 1 | 0 | 1 |
| 3 | 0 | 1 | 1 | 0 |
| 4 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 1 |
| 6 | 1 | 1 | 0 | 0 |
| 7 | 1 | 1 | 1 | 1 |
intuit.ru/2010/edi»>Таблица истинности получена.Получение СКНФ.
Получение СКНФ по ТИ описано в примере 2.1.
Результатом будет:
[Решено] 1. Постройте таблицу истинности для следующего: F(x, y) =…
Получите больше от подписки*
- Доступ к более чем 100 миллионам учебных ресурсов по конкретным курсам
- Круглосуточная помощь опытных наставников по более чем 140 предметам
- Полный доступ к более чем 1 миллиону решений для учебников
*Вы можете изменить, приостановить или отменить в любое время
Вопрос задан vfb784
1. Составьте таблицу истинности для следующего: F(x, y) = x’y’ + xy’ + y(xy’)
2.
Составьте таблицу истинности для следующего:
F(x, y, z) = (y + x)(y + x’)(y’+ z)
3. Какое из следующих уравнений правильно отражает показанную ниже таблицу истинности?
A) (xy’z + x’yz’ + x’yz’ + x’y’z + x’y’z)’
B) xy’z + x’yz’ + x’yz’ + x’y’z + x’y’z
C) x’yz’ + x’yz + xy’z’ + xyz’ + xyz
D) (x’yz’ + x’yz + xy’z’ + xyz’ + xyz)’
4. Таблица истинности, показанная ниже, должна отражать функцию F(x, y, z) = (x’y’ + yz) + (xy’ + yz’), но две строки ошибочны. Определите их.
A) 1 и 2
B) 3 и 4
C) 5 и 6
D) 7 и 8
03
5. Два выражения, которые могут быть представлены одной и той же таблицей истинности, считаются логически эквивалентными.
Используйте таблицу истинности, чтобы доказать, что эти два выражения одинаковы. F1(x,y,z) = x + (yz), F2(x,y,z) = (x + y)(x + z).
Инженерия и технологии Информатика CSCI 3400
Ответ и объяснение
Решено проверенным экспертом
Рейтинг Полезно
Ответил varikutiharinadh
m ipsum dolor sit
Искинг Элит. Nam lacinia pulvinar tortor nec facilisis. Pellentesque dapibus efficitur laoreet. Nam risus ante, dapibus a molestie consequat, ultrices ac magna. Fusce dui lectus, congue vel laoreet ac, dictum vitae odio. Донец Аликет. Lorem ipsum dolor sit amet, consectetur adipiscing elit. Nam lacinia p
Разблокировать полный доступ к Course Hero
Изучите более 16 миллионов пошаговых ответов из нашей библиотеки
Подпишитесь, чтобы посмотреть ответ
Пошаговое объяснение
lestie consequat, ultrices ac magna.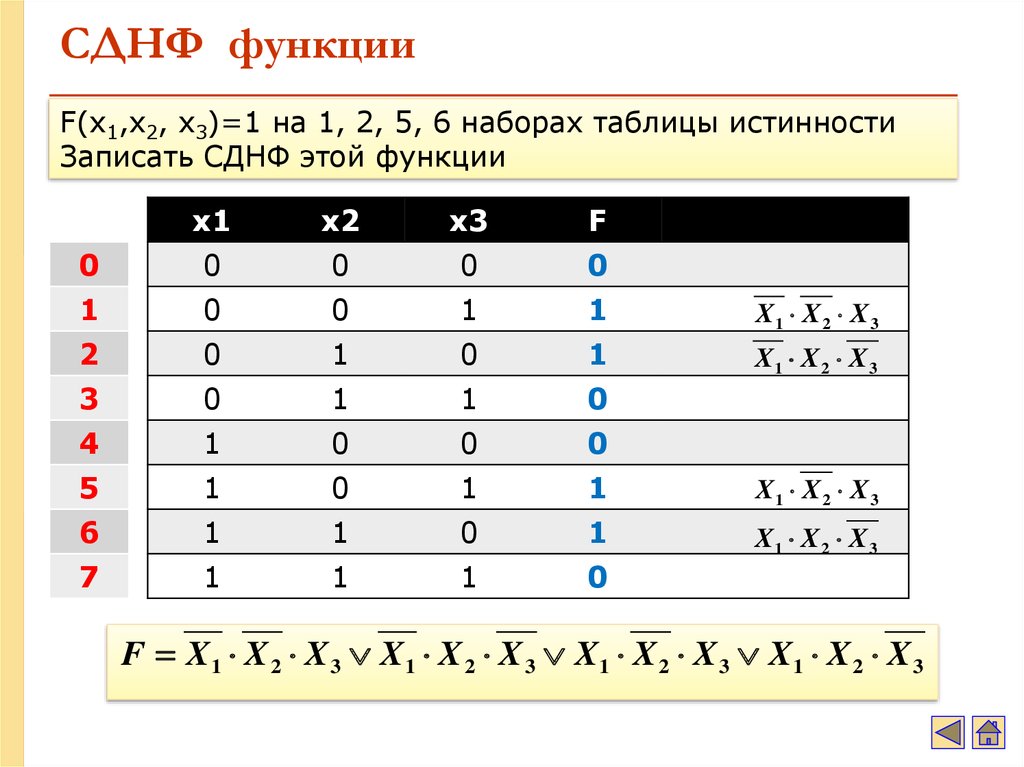
Fusce dui lectus, congue vel laoreet ac, dictum vitae odio. Донец Аликет. Lorem ipsum dolor sit amet, consectetur adipiscing elit. Nam lacinia pulvinar torto
2 Приложения
jpg
jpg
Отзывы студентов
100% (3 оценки)
Очистить форматирование
Подробное объяснение
«Спасибо!!»
Нарисуйте логическую диаграмму и таблицу истинности для
Нарисуйте логическую диаграмму и таблицу истинности для логического выражения
(X+Y)(XY’Z + XYZ + XY’Z’)
и упростите ее.
0 Счастливый Отправить ответ 286 Просмотры
Дополнительные вопросы по системе счисления и логической логике преобразования
Определите:1. Система счисления2. Десятичная система счисления3. Двоичная система счисления4. Восьмеричная система счисления5. Шестнадцатеричная система счисления6. Комплименты7. Логическая функция8. Булева алгебра9. Таблица правды10. Булев пример…
Ответы:
1.
Система счисления — Это относится к цифрам, их расположению, позиционному весу и основанию системы счисления.
2. Десятичная система счисления — Система счисления с основанием или основанием 10 известна как десятичная система счисления.
3. Двоичная система счисления — Система счисления с основанием или основанием 2 известна как двоичная система счисления.
4. Восьмеричная система счисления — Система счисления с основанием или основанием 8 известна как восьмеричная система счисления.
5. Шестнадцатеричная система счисления — Система счисления с основанием или основанием 16 известна как…
Выполните бинарные операции, как указано.1. 11111 + 100012. 111001 — 100103. 1111 x 10104. 111101/101
1.
2.
3.
4.
4
Показать графический символ, логическое выражение и таблицу истинности логических элементов И, ИЛИ, НЕ, НЕ-И, ИЛИ, X-OR, X-NOR.
Логический элемент И:
Это электронная схема, которая выдает высокий логический уровень (1), когда обе входные логические сигналы имеют высокий уровень (1), и низкий логический уровень (0), когда любой из входных логических сигналов низкий (0).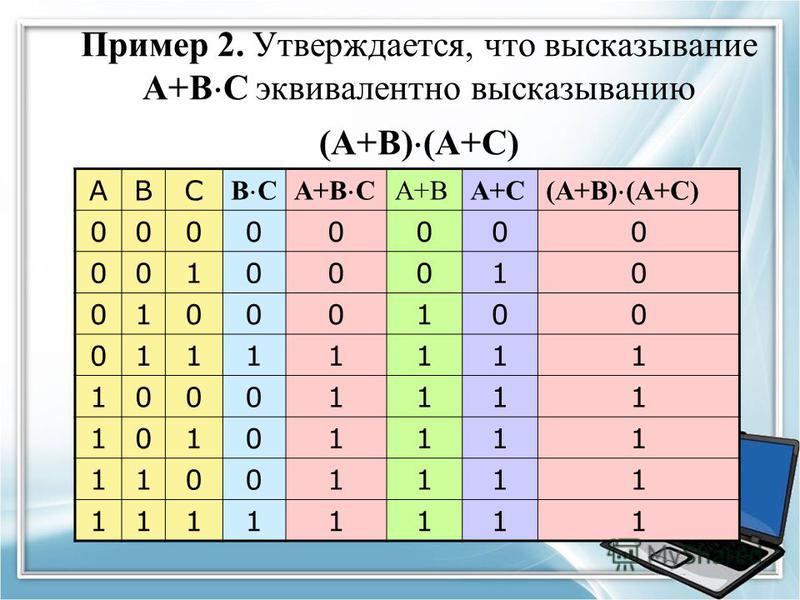
. Выход, производимый этим базовым вентилем, является продуктом его входной логики.
Алгебраическое выражение:
F=A.B
где A и B — входы, F — выход
Символ вентиля:
Таблица истинности:
| 5 | ||
| F=A.B | ||
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Диаграмма Венна:
Элемент ИЛИ:
Что такое универсальные ворота?
Элементы И-НЕ и ИЛИ-НЕ называются универсальными элементами. Это так, потому что любая цифровая схема может быть реализована с использованием любого из этих двух, то есть любой логический элемент может быть создан с использованием только вентилей НЕ-И или ИЛИ-НЕ.
Сформулируйте и докажите тождество, дополнение, коммутативность, ассоциативность, дистрибутивность и теорему Де Моргана.
Почему мы используем метод дополнения?
Перечислите все законы булевой алгебры.
Законы булевой алгебры:
1. Закон тождества: A+0=A ; A.1=A
2. Закон ограниченности: A+1=1. ; A.0=0
3. Закон идемпотента: A+A=A ; A.A=A
4. Закон дополнения: A+A’=1 ; A.A’=0
5. Коммутативный закон: A+B=B+A ; A.B=B.A
6. Распределительный закон: A+(B.C)=(A+B).(A+C) ; A.(B+C)=(A.B)+(A.C)
7. Законы поглощения: A+(A.B)=A ; A.(A+B)=A
8. Ассоциативный закон: (A+B)+C=A+(B+C) ; (А.Б).С=А.(Б.С)
9. Закон Де-Моргана: (А+В)’=А’.В’; (A.B)’=A’+B’
10. Закон инволюции: (A’)’=A
Что такое система счисления? Какие бывают системы счисления?
Для чего используется двоичная система счисления в информатике?
Что такое восьмеричная система счисления? Объясните процесс преобразования двоичного числа в восьмеричное?
Что такое шестнадцатеричная система счисления? Объясните процесс преобразования шестнадцатеричного числа в двоичное.
