Дифференциальное уравнение первого порядка в полных дифференциалах.
Определение. Пусть дифференциальное уравнение первого порядка представлено в виде
M(x,y)dx+N(x,y)dx=0,
Где M(x,y) и N(x,y) – функции двух переменных x и y. Тогда, если левая часть уравнения есть полный дифференциал некоторой функции U(x,y), т.е.
dU(x,y)=M(x,y)dx+N(x,y)dy,
то такое уравнение называется уравнением в полных дифференциалах.
Уравнение в полных дифференциалах кратко можно представить в виде
dU(x,y)=0,
а поэтому общий интеграл (решение) такого уравнения имеет вид U(x,y)=0.
Дифференциальное уравнение такого типа возникает, когда поведение системы подчинено условию сохранения некоторой величины U(энергии, массы, стоимости и т.д.).
Отметим следующий
признак, позволяющий определить является
ли рассматриваемое уравнение уравнением
в полных дифференциалах.
Путьс
dU(x,y)=M(x,y)dx+N(x,y)dy, тогда функции M(x,y) и N(x,y) должны быть для U(x,y) частными производными первого порядка, соответственно, по переменным x и y, т.е.
.
Предполагая функции M(x,y) и N(x,y) непрерывными и имеющими непрерывные частные производные, соответственно, по y и x, т.е. выполнение соотношений
,
из тождества
получаем, что для M(x,y) и N(x,y) должно выполняться условие
.
Полученное условие является не только необходимым, но и достаточным для того, чтобы уравнение M(x,y)dx+N(x,y)dy=0
Было уравнением в полных дифференциалах.
Нахождение общего решения уравнения в полных дифференциалах проводится в два этапа.
На первом этапе
функция U(x,y)
рассматривается как функция только
аргумента x,
переменная y
получает как бы фиксированное значение .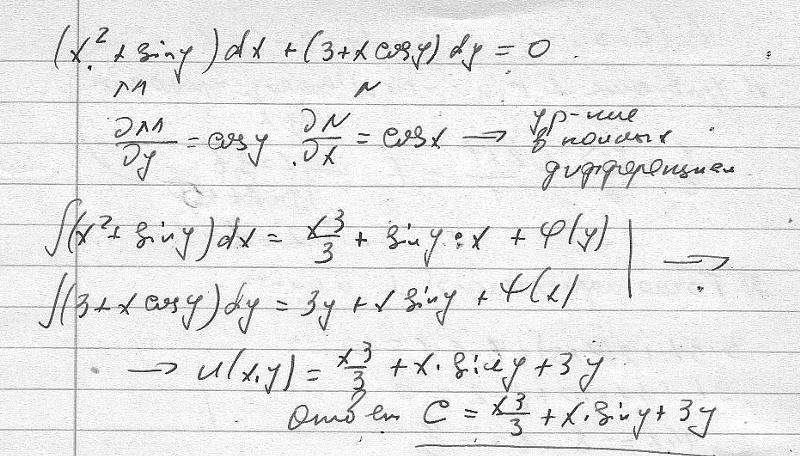
ставится в соответствие дифференциальное уравнение
.
Пусть его общее решение представляется в виде
.
Но так как решение уравнения зависит от y, то в общем решении постоянная c является функцией y, т.е. c=h(y). Следовательно, общее решение предыдущего дифференциального уравнения, снимая с y условие закрепления его значения, имеет вид
U(x,y)=g(x,y)+h(y).
На втором этапе находится вид функции h(y). Для этого обратимся к соотношению
,
в котором уже закрепляется как бы значение переменной x.
или .
Интегрируя это уравнение, находим его общее решение
.
Из , получаем окончательный вид функции U(x,y), а именно
или
.
В последнем двойном интеграле вместо можно взять функцию (т.к. ). Тогда функция U(x,y) получает вид
.
Так как общее решение исходного дифференциального уравнения записывается в виде U(x,y)=c=const, то, заменяя две постоянных на одну, получаем следующий вид общего решения уравнения
или
.
Пример 1. Дано дифференциальное уравнение
(6x2y2+6xy-1)dx+(4x3y+3x2y+2y)dy=0.В нем M(x,y)=6x2y2+6xy-1, N(x,y)=4x3y+3x2y+2y. Из и тождества ,
Следует, что данное уравнение является уравнением в полных дифференциалах. Проведем его решение в два этапа.
На первом решаем уравнение
или dU=(6x2y2+6xy-1)dx,
в котором переменная
y
считается закрепленной.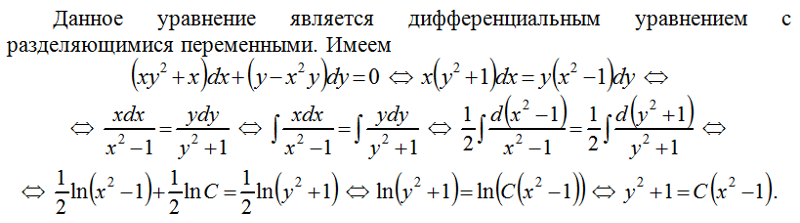 Интегрируя это
уравнение, получаем
Интегрируя это
уравнение, получаем
U(x,y)=2x3y2+3x2y-x+h(y).
На втором этапе определяем вид функции h(y), используя для этого соотношение
и дифференциальное уравнение для h и y
4x
Интегрируя последнее, получаем h=y2+c. Общий интеграл исходного уравнения тогда можно записать в виде
2x3y2+3x2y-x+y2=c.
Пример 2. Найти решение уравнения
2xsinydx+(3y2+x2cosy)dy=0.
Проверяем, является ли оно уравнением в полных дифференциалах? Для этого из M(x,y)=2xsiny, N(x,y)=3y2+x2cosy
Находим
.
Так как, очевидно, выполняется условие
,
то уравнение есть
уравнение в полных дифференциалах.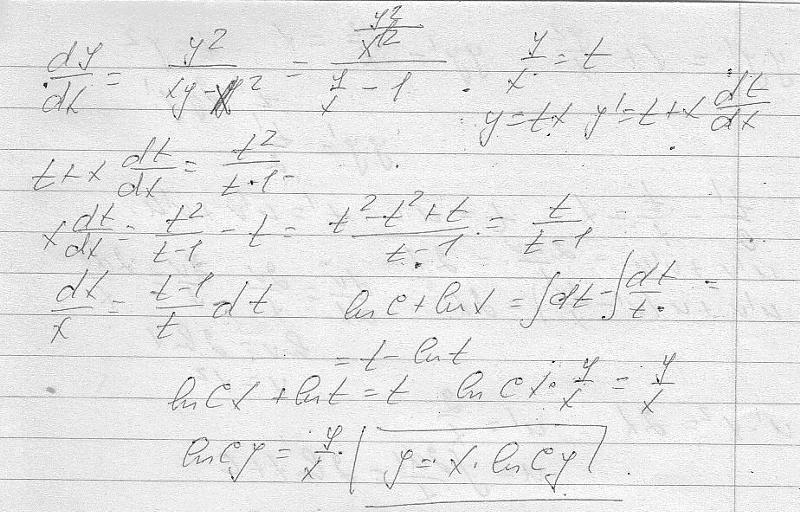
Сначала решаем уравнение
или dU=2xsinydx,
считая y постоянной. Интегрирование уравнения дает
U(x,y)=x2siny+h(y).
Затем находим функцию h(y), используя соотношения
, с одной стороны, и , с другой стороны. Соотношения приводят к дифференциальному уравнению
или .
Интегрируя последнее уравнение, получаем h=y3+c.
Тогда общий интеграл исходного дифференциального уравнения записывается в виде
X2siny+y3+c=0.
Далее рассмотрим понятие интегрирующего множителя. Ранее отмечалось, что уравнение в полных дифференциалах возникает, когда поведение системы сохраняет некоторую величину U, т.е. удовлетворяет соотношению
U(x,y)=c.
Дифференциальным аналогом его является уравнение dU(x,y)=0 или
M(x,y)dx+N(x,y)dy=0,
Где
.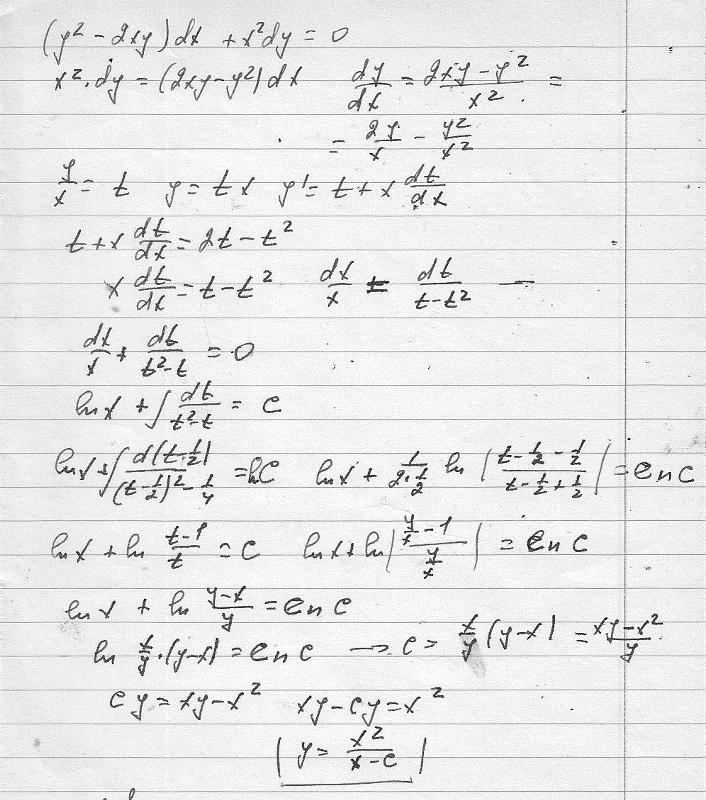
Предположим теперь, что частные производные функции U(x,y) представимы в виде
.
Тогда соотношению U(x,y)=e будет соответствовать уравнение в полных дифференциалах вида
M(x,y)g(x,y)dx+N(x,y)g(x,y)dy=0.
Если теперь данное уравнение разделить на общий множитель слагаемых g(x,y), то получим уравнение M(x,y)dx+N(x,y)dy=0.
Решение последнего уравнения эквивалентно решению предыдущего, из которого оно получено, однако оно может уже не являться уравнением в полных дифференциалах, также для него возможно будет
.
В то же время после умножения его на множитель g(x,y), оно становится уравнением в полных дифференциалах.
Определение. Функция g(x,y) называется интегрирующим множителем дифференциального уравнения
M(x,y)dx+N(x,y)dy=0,
Если после умножения
его на эту функцию оно становится
уравнением в полных дифференциалах.
Данный способ решения дифференциального уравнения называется методом интегрирующего множителя.
Найдем условие, которому должен подчиняться интегрирующий множитель g(x,y). Из предложения, что уравнение
M(x,y)g(x,y)dx+N(x,y)g(x,y)dy=0
Становится уравнением в полных дифференциалах следует выполнение условия
.
Разверернув левую и правую части этого тождества
,
заключаем, что функция g(x,y) должна являться решением уравнения
.
В общем случае решение данного уравнения вызывает затруднения. Отметим два случая, когда его решение становится проще.
Случай первый. Пусть
.
Тогда интегрирующий множитель можно искать в виде функции зависящей только от x.
Действительно,
пусть g=g(x).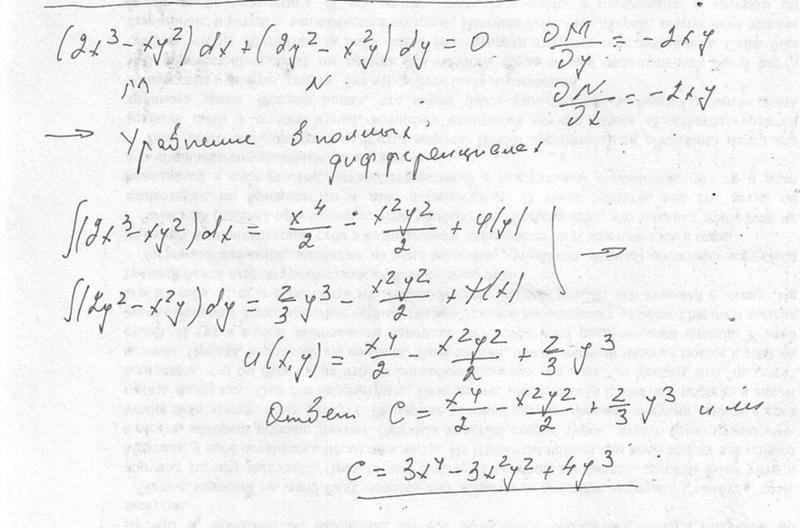 Тогда в виду
;
получаем, что искомая функция g(x)
является решением дифференциального
уравнения
Тогда в виду
;
получаем, что искомая функция g(x)
является решением дифференциального
уравнения
или ,
интегрируя которое, находим
, т.е. .
Второй слуяай относится к аналогичной ситуации, когда
.
Тогда интегрирующий множитель ищется в виде функции только от y, т.е. g=g(y).
Аналогично предыдущему, не трудно видеть, что функция g(y) является решением уравнения
и представляется в виде
.
Пример 3. Дано уравнение
(y2-3xy-2x2)dx+(xy-x2)dy=0.
Из M(x,y)=y2-3xy-2x2, N(x,y)=xy-x2, , следует , т.е. уравнение не является в полных дифференциалах.
Однако из соотношения
вытекает, что можно
найти такой интегрирующий множитель
g=g(x),
после умножения на который исходное
уравнение становится уравнением в
полных дифференциалах.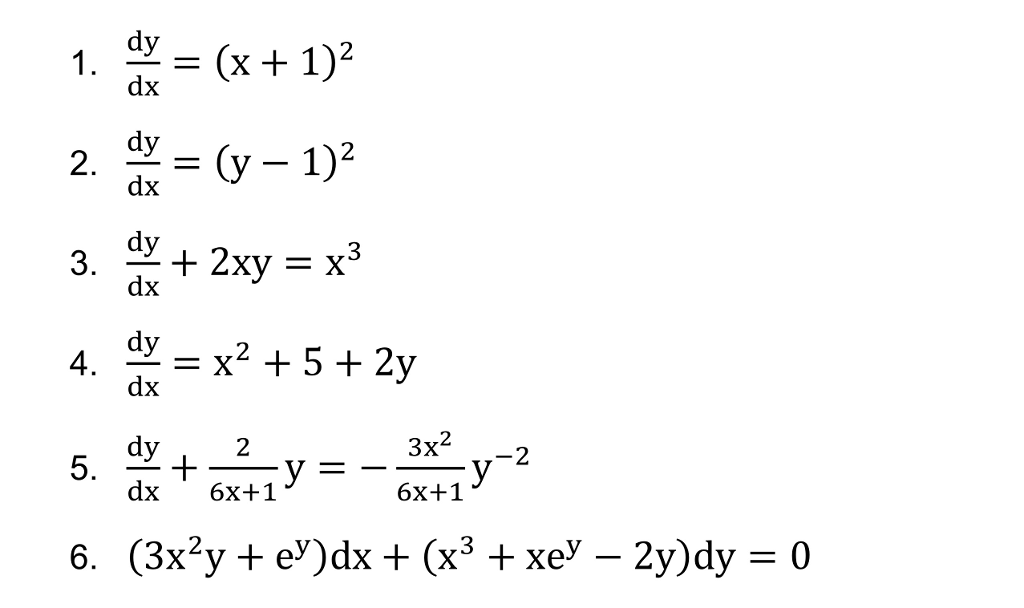
Указанный множитель находим из уравнения
,
интегрируя которое получаем , или g=xc. Так как в качестве множителя достаточно взять одну из функций, то положим c=1 и, тогда, g=x.
(xy2-3x2y-2x3)dx+(x2y-x3)dy=0,
являющееся уже уравнением в полных дифференциалах. Интегрируя его, находим
,
,
затем из U/y=x2y-x3+h/(x) и U/y=N(x,y)=x2y-x3
получаем x2y-x3+h/=x2y-x3, т.е. и,
следовательно, h=c=const. Таким образом, общее решение имеет вид
.
Пример 4. Требуется
решить уравнение
Требуется
решить уравнение
(2xy2-y)dx+(y2+x+y)dy=0.
Из M(x,y)=2xy2-y, N(x,y)=y2+x+y, следует
.
Однако из соотношения
,
вытекает, что для исходного дифференциального уравнения существует интегрирующий множитель g=g(y), с помощью которого уравнение становится уравнением в полных дифференциалах.
Интегрирующий множитель находится из уравнения
.
Интегрируя его, получаем .
Умножая исходное уравнение на множитель , приходим к уравнению
.
Это уравнение является уже уравнением в полных дифференциалах. Решаем его
,
,
затем из и ,
получаем
или .
Интегрируя последнее
уравнение, имеем
.
Таким образом, общий интеграл исходного уравнения имеет вид
.
Обыкновенные дифференциальные уравнения первого порядка
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
1. Обыкновенные дифференциальные уравнения первого порядка
{ задача Коши — геометрическая интерпретация дифференциального уравнения первого порядка — уравнения сразделенными и разделяющимися переменными — однородные дифференциальные уравнения — линейные
дифференциальные уравнения — метод Бернулли — метод Лагранжа — уравнение Бернулли — уравнения, не
разрешенные относительно производной – пример }
Задача отыскания решения дифференциального уравнения
dy
f ( x ,y )
dx
удовлетворяющего заданным начальным условиям y(x0 ) = y0 , называется
задачей Коши.
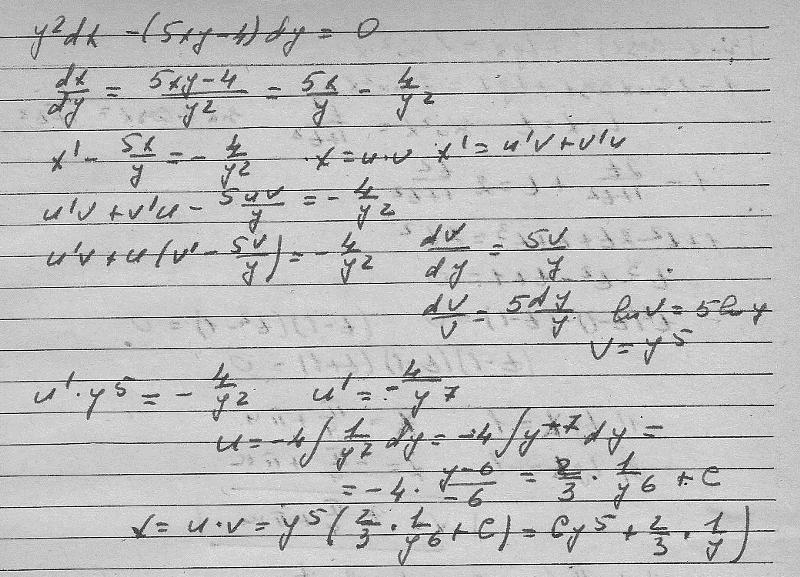
Теорема
Если функция f — правая часть
дифференциального уравнения
dy/dx = f(x,y) непрерывна в некоторой
замкнутой области D плоскости xoy и имеет в
этой области ограниченную частную
производную дf(x,y)/дy, то каждой внутренней
точке области D соответствует, и притом
единственное, решение, удовлетворяющее
Огюстен Луи Коши
(Augustin Louis Cauchy)
заданным начальным условиям.
1789 – 1857
Геометрически это означает, что через каждую точку M0 (x0,y0) области D
проходит одна и только одна интегральная кривая рассматриваемого
уравнения.
Данная теорема называется теоремой существования и единственности
решения дифференциального уравнения
y
y ( x )
M0 (x0,y0)
dy
f ( x ,y )
dx
D
x
o
y ( x )
y ( x0 ) y0
y ( x0 ) ( x0 )
d ( x )
f ( x , ( x ))
dx
@
Решить дифференциальное уравнение первого порядка, при
заданных начальных условиях
dy
xy y ( 0 ) 1
dx
y
Решение
dy
dy
xy
xdx
dx
y
2
dy
y
x
ln | y |
ln C y
2
y ( 0 ) 1 Ce 0 1
xdx
x2
Ce 2
y
M(0,1)
x2
e2
o
x
Пусть дано дифференциальное уравнение,
разрешенное относительно производной
dy/dx = f(x,y).
 Это уравнение для каждой точки
Это уравнение для каждой точкиM(x,y) определяет значение производной dy/dx,
т.е. определяет угловой коэффициент касательной
к интегральной кривой, проходящей через эту
точку. Таким образом, рассматриваемое
дифференциальное уравнение дает совокупность
направлений или, как говорят, определяет поле
направлений (поле линейных элементов).
Задача интегрирования такого уравнения, с
геометрической точки зрения, заключается в
нахождении кривых, направление
касательных к которым совпадает с
направлением поля линейных элементов в
dy
соответствующих точках.
dx
M
f ( x , y ) tg o f ( x o , y o )
Уравнением с разделенными переменными называется уравнение вида:
M ( x ) dx N ( y ) dy 0
Решение: прямое интегрирование —
M ( x ) dx N ( y ) dy
C
Уравнением с разделяющимися переменными называется уравнение вида:
M1 ( x ) N 1 ( y ) dx M2 ( x ) N 2 ( y ) dy 0
Решение: приведение к виду уравнения с разделенными переменными
путем деления обеих его частей на произведение N1 (y) M2 (x)
M1 ( x )
N2 ( y )
dx
M2 ( x )
N1 ( y ) dy C
@
Решить дифференциальное уравнение
dy
1 y2
dx
2 xy
Решение
dy
1 y2
2 ydy
dx
2
dx
2 xy
x
1 y
2 ydy
1 y2
dx
x
d(1 y2 )
dx
2
ln
|
1
y
| ln | x | ln C
2
x
1 y
1
2
Cx
x
(
1
y
) C
2
1 y
Уравнение M(x,y) dx + N(x,y) dy = 0 называется однородным
дифференциальным уравнением первого порядка, если функции M(x,y)
и N(x,y) являются однородными функциями одного и того же измерения:
M ( tx ,ty ) t n M ( x , y ), N ( tx ,ty ) t n N ( x , y )
Если уравнение может приведено к виду: dy/dx = F(x,y) = F(v) ,
где v = y/x, то оно называется однородным дифференциальным
уравнением первого порядка.

Решение: для приведения к уравнению с разделяющимися переменными
используется подстановка
v
y
y xv
x
dv
dx
F (v ) v
x
dy
dv
dv
x
v x
v F (v )
dx
dx
dx
dv
dx
dv
F (v ) v x
F ( v ) v ln | x | C
@
Решить дифференциальное ( y 2 3 x 2 ) dx 2 xydy 0 , y ( 1 ) 2
уравнение
Частное решение
Решение
y
v
dy xdv vdx
x
x 2 ( v 2 3 )dx 2 x 2v ( xdv vdx ) 0
xy 2 x 3 3
( 2 2 1 2 )1 C
C 3
2 vdv
3 dx
2 vdv
dx
0 2
3
C
( 3v 3 )dx 2v ( xdv ) 0 2
x
x
v 1
v 1
2
ln( v 2 1 ) 3 ln x ln C
Общий интеграл
( y2 x 2 )x C
Уравнение y P ( x ) y Q ( x ) , где P(x) и Q(x) — заданные непрерывные
функции, называется линейным дифференциальным уравнением первого порядка.
Если функция Q(x) = 0, то уравнение называется линейным однородным, в
противном случае — линейным неоднородным.
Метод Бернулли
Якоб Бернулли
(Jacob Bernoulli)
1654 — 1705
Применим подстановку y = u(x) v(x), где u(x) – новая неизвестная
функция, v(x) – произвольная функция, которую подчиним
некоторому условию
y ( uv ) u v u v u v u ( v P ( x ) v ) Q ( x )
dv
P ( x ) dx
v P( x ) v 0
P ( x ) dx v e
v
du P ( x ) dx
e
Q ( x ) u Q ( x ) e P ( x ) dx dx c
dx
y e P ( x ) dx ( Q ( x ) e P ( x ) dx dx c )
Метод Лагранжа решения линейного уравнения
– метод вариации произвольной постоянной
y P( x )y Q( x )
Сначала решаем однородное уравнение
y P ( x ) y 0 y Ce P ( x ) dx
Полученное решение подставляем в исходное
неоднородное дифференциальное уравнение, варьируя
(считая переменной) постоянную C .

d ( C ( x ) e P ( x ) dx )
P ( x ) dx
P ( x )C ( x )e
Q( x )
dx
C ( x ) Q( x
Жозеф Луи Лагранж
(Joseph-Louis Lagrange)
1736 — 1813
P ( x ) dx
P ( x ) dx
P ( x ) dx
C ‘e
P ( x )C ( x )e
P ( x )C ( x )e
P ( x ) dx
dC
Q( x )
e
Q( x )
dx
P ( x ) dx
)e
dx
~
C
y e P ( x ) dx ( Q ( x ) e P ( x ) dx dx C )
@
Решить дифференциальное уравнение
Метод Лагранжа
Решение
dy
2 xy
dy
2 xdx
0
2
2
dx 1 x
y
1 x
y C ( x )( 1 x 2 )
y ( x C )( 1 x 2 )
dy
2 xy
2
1
x
dx 1 x 2
dy
y
2 xdx
1 x2
y C(1 x2 )
~
dC
(1 x2 ) 1 x2 C( x ) x C
dx
y C (1 x2 ) x x3
Уравнением Бернулли называется уравнение вида:
y P( x )y Q( x )yn
При n = 0 и n = 1 – уравнение становится линейным (неоднородным или однородным)
1 dy
1
P
(
x
)
Q( x )
n
n 1
y dx
y
1
Уравнение Бернулли приводится к
z
линейному с использованием подстановки y n 1
Уравнение можно представить в виде:
Другой способ решения (Бернулли):
ищем решение в виде U(x)V(x),
на одну из функций накладываем
условие:
dv
P ( x )v 0
dx
d y 1 n
dz
1 n dy
dx
dx
y n dx
dz
( 1 n ) P ( x ) z ( 1 n )Q ( x )
dx
@
Решить дифференциальное уравнение
x
dv
x
v 0
dx
1
)
2
u
u
x
2 ln x
dx
x
x
d(u
du
u2
ln x
x 2 dx
dy
y y 2 ln x
dx
Решение
Метод Бернулли
y uv
x
dv
dx
v
x
dv
dx
1
v x v x
1 du
1
u
u2
x
xu 2
2 ln x
x dx
x
x
x
1
ln x 1 cx
u
x
1
y
ln x 1 cx
Дифференциальные уравнения, неразрешенные относительно
F ( x ,y ,
y имеют вид:
dy
) 0
dx
Если в некоторой точке M(xo,yo) уравнение F(xo,yo,p) = 0, где p = y’, имеет n
действительных корней, причем F(x,y,p) со своими первыми производными непрерывна
при x = xo, y = yo p = pi и дF / дx не обращается в ноль, то через точку M проходит n
интегральных кривых.
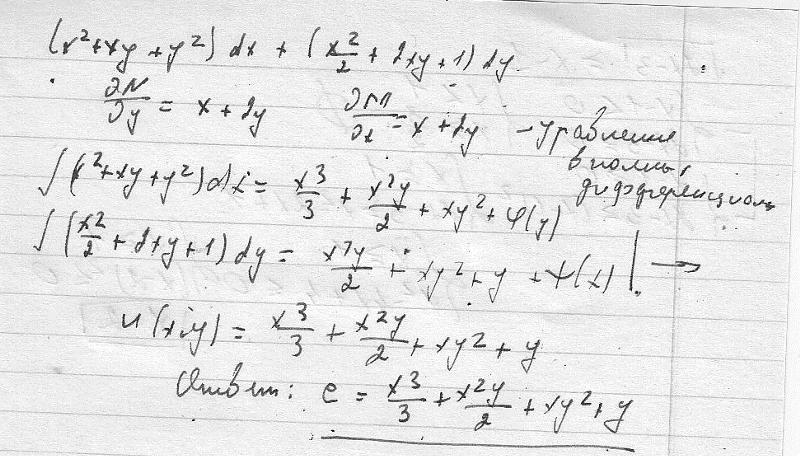
Если данное уравнение возможно разрешить относительно производной, то оно
распадается на n уравнений рассмотренного ранее вида, решив которые, получим
уравнения n семейств интегральных кривых.
Если уравнение можно представить в виде x ( y , y ) или y ( x , y ) , то
обозначая y’ = p, и рассматривая p как вспомогательную переменную, после
дифференцирования по y или x получим уравнение относительно dp/dy или dp/dx ,
разрешенные относительно производной. Искомое решение получим в
параметрической форме.
@
Решить дифференциальное уравнение
dy dy
x y
dx dx
2
Решение
dy
p
dx
x py p 2
dy
py
2 p2
2
dp 1 p
1 p2
Линейное неоднородное уравнение
dx
1
dy
p
dp
1
p ( y 2p)
p
dy
C arcsin p
y p
1 p2
x py p 2
English Русский Правила
| 1 | Найти производную — d/dx | бревно натуральное х | |
| 2 | Оценить интеграл | интеграл натурального логарифма x относительно x | |
| 3 | Найти производную — d/dx | 92)||
| 21 | Оценить интеграл | интеграл от 0 до 1 кубического корня из 1+7x относительно x | |
| 22 | Найти производную — d/dx | грех(2x) | |
| 23 | Найти производную — d/dx | 9(3x) по отношению к x||
| 41 | Оценить интеграл | интеграл от cos(2x) относительно x | |
| 42 | Найти производную — d/dx | 1/(корень квадратный из х) | |
| 43 | Оценка интеграла 9бесконечность | ||
| 45 | Найти производную — d/dx | х/2 | |
| 46 | Найти производную — d/dx | -cos(x) | |
| 47 | Найти производную — d/dx | грех(3x) | 92+1|
| 68 | Оценить интеграл | интеграл от sin(x) по x | |
| 69 | Найти производную — d/dx | угловой синус(х) | |
| 70 | Оценить предел | ограничение, когда x приближается к 0 из (sin(x))/x 92 по отношению к х | |
| 85 | Найти производную — d/dx | лог х | |
| 86 | Найти производную — d/dx | арктан(х) | |
| 87 | Найти производную — d/dx | бревно натуральное 5х92 |
Solve the differential equation dy/dx=y-x
Step-by-step Solution
1
2
3
4
5
6
7
8
9
a
b
c
d
f
g
m
n
u
v
w
x
y
z
.
(◻)
+
—
×
◻/◻
/
÷
◻ 2
◻ ◻
√◻
√
◻ √ ◻
◻ √
∞
e
π
ln
log
log ◻
lim
d/dx
D □ x
∫
∫ ◻
|◻|
θ
=
>
<
>=
<=
sin
cos
tan
cot
sec
csc
asin
acos
atan
acot
asec
acsc
sinh
cosh
tanh
coth
sech
csch
asinh
acosh
atanh
acoth 9х$
Есть другой ответ? Проверьте это здесь!
Пошаговое решение
Задача для решения:
$\frac{dy}{dx}=y-x$
Укажите метод решения
Выберите вариантЛинейное дифференциальное уравнениеТочное дифференциальное уравнениеРазделимое дифференциальное уравнениеГоднородное дифференциальное уравнениеПредложите метод или функцию 91909 91909 1
Преобразование дифференциального уравнения
$\frac{dy}{dx}-y=-x$
Узнайте, как шаг за шагом решать задачи дифференциальных уравнений онлайн.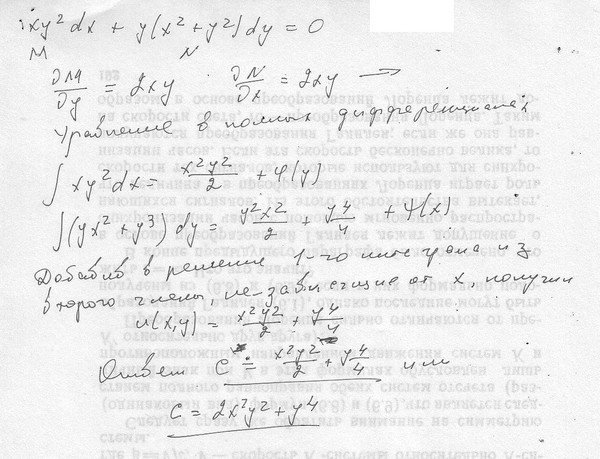
$\frac{dy}{dx}-y=-x$
Разблокируйте первые 3 шага этого решения!
Узнайте, как шаг за шагом решать задачи дифференциальных уравнений онлайн. Решите дифференциальное уравнение dy/dx=y-x. Преобразуйте дифференциальное уравнение. Мы можем определить, что дифференциальное уравнение имеет вид: \frac{dy}{dx} + P(x)\cdot y(x) = Q(x), поэтому мы можем классифицировать его как линейное дифференциальное уравнение первого порядка, где P(x)=-1 и Q(x)=-x. Чтобы решить дифференциальное уравнение, первым делом нужно найти интегрирующий множитель \mu(x). Чтобы найти \mu(x), нам сначала нужно вычислить \int P(x)dx. Таким образом, интегрирующий множитель \mu(x) равен. 9х$
Поделись этим решением
SnapXam A 2
Помощник по ответам
бета
Есть другой ответ? Проверьте это!1
2
3
4
5
6
7
8
9
a
b
c
d
f
g
m
n
u
v
w
x
y
z
.
(◻)
+
—
×
◻/◻
/
÷
◻ 2
◻ ◻
√◻
√
◻ √ ◻
◻ √
∞
e
π
ln
log
log ◻
lim
d/dx
D □ x
∫
∫ ◻
|◻|
θ
=
>
<
>=
<=
sin
cos
tan
cot
sec
csc
asin
acos
atan
acot
asec
acsc
sinh
cosh
tanh
coth
sech
csch
as inh 909ACOSH
ATANH
ACOTH
ASECH
ACSCH
Полезные советы по улучшению вашего ответа:
$ \ FRAC {DAY {DAY} {DAY} {DAY} {DAY} {DAY} {DAY} {DAY} {DAY} {DAY} {DAY} {DAY} {DAY} {DAY} {DAY} \ DAM} {DAY} \ DAM} {DY}} {DAY}} {DAY}.
