Формула площадь треугольника 5 класс: Треугольник. Площадь треугольника — урок. Математика, 5 класс.

Площадь правильного треугольника – формула полной поверхности через сторону

4.4

Средняя оценка: 4.4

Всего получено оценок: 64.

4.4

Средняя оценка: 4.4

Всего получено оценок: 64.

Правильные треугольники – это особое явление в геометрии. Все углы треугольника абсолютно точно определены значением в 60 градусов. Из-за этого, помимо обычных для треугольников способов нахождения площади, существуют и способы нахождения именно площади правильного треугольника, не характерные для других фигур. Все способы будут рассмотрены в этой статье.

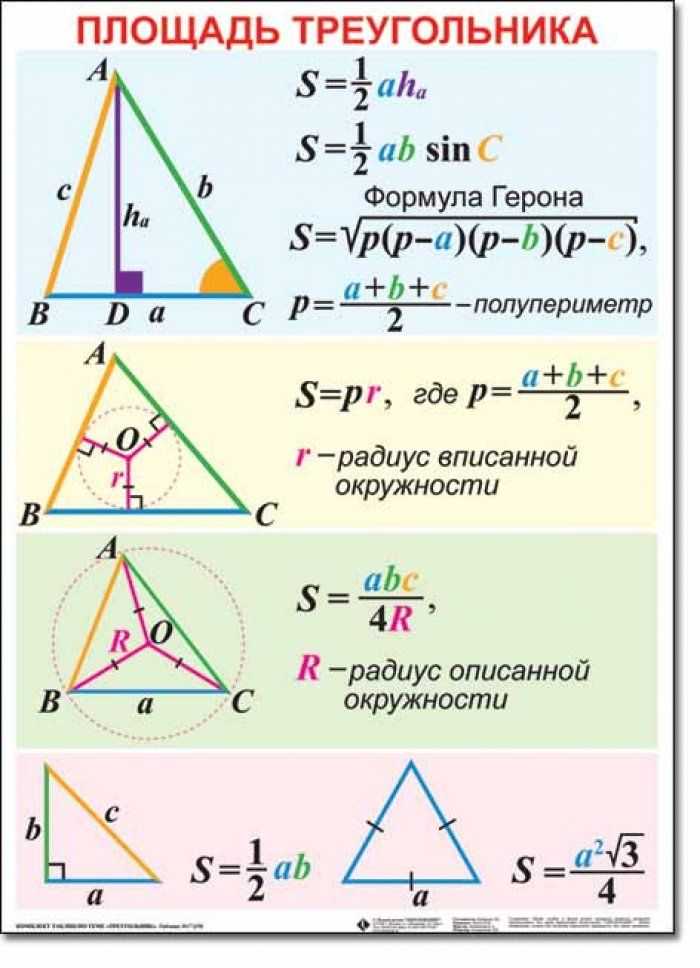
Формулы для нахождения площади треугольника.

• Первая формула площади правильного треугольника стандартна. Площадь равна половине произведения основания на высоту: $S= {1\over2}h*a$.
• Существует формула нахождения площади через сторону, которая проистекает из первой, но характерна только для правильных треугольников. В правильном треугольнике АВС проведем высоту АМ, которая будет являться так же медианой и биссектрисой.

Это свойство характерно для равнобедренных треугольников, но любой правильный треугольник и будет равнобедренным, просто любая из его сторон может считаться основанием, так как две другие стороны в любом случае будут равны.

Рис. 1. Правильный треугольник.

В результате треугольник делиться на два, равных между собой прямоугольных треугольника. Теперь найдем значение высоты, подставим его в классическую формулу площади треугольника и получим формулу для правильного треугольника.

Рис. 2. Рисунок к доказательству.

В прямоугольном треугольнике АВМ катет АМ можно выразить через синус угла АВМ. Этот угол известен и равен 60 градусам, значит, известны и значения синуса и косинуса для этого угла. Катет АМ противолежащий, значит, для его нахождения необходимо воспользоваться формулой синуса.

$$Sin(ABM)={AM\over AB}$$

С другой стороны синус 60 градусов заранее известнее и равен $$\sqrt{3} \over 2$$ . Значит можно выразить значение АМ:

$$АМ=АВ*sin(ABM)=AB* {\sqrt{3}\over 2}$$

Все стороны треугольника между собой равны, поэтому для удобства обозначим их через букву а.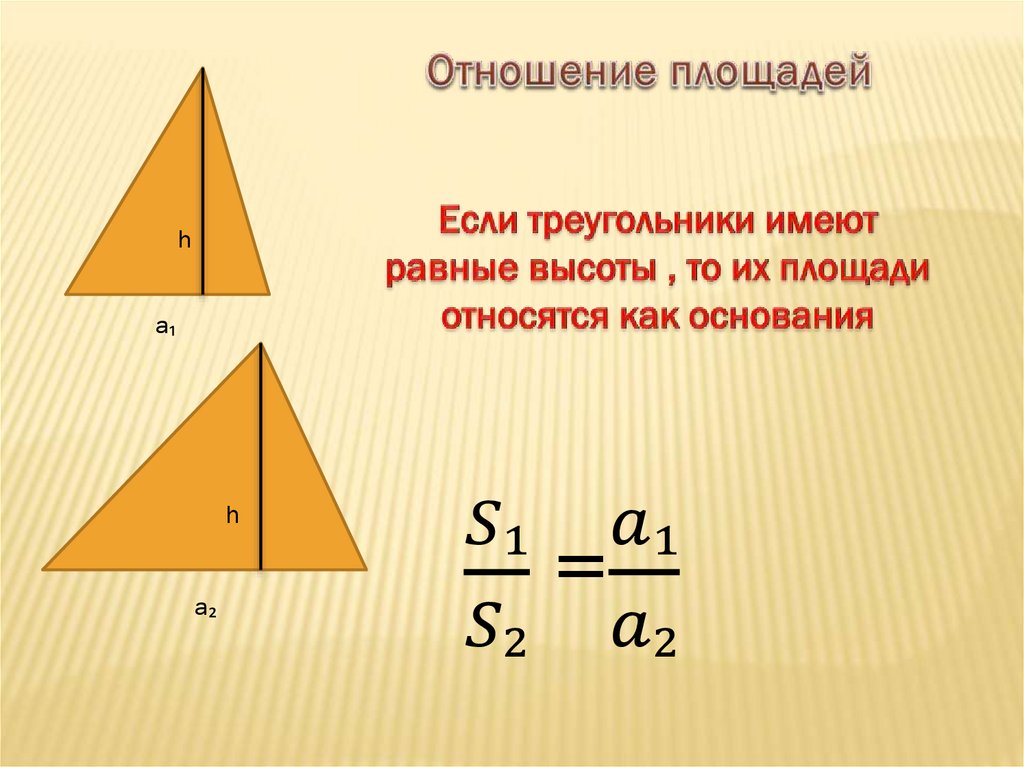

2*{\sqrt{3}\over4}$$

ВС заменили на а, так как все стороны равны между собой, а значение высоты мы находили ранее. Получившаяся формула гораздо проще классических в плане количества необходимых параметров. Для нахождения площади правильного треугольника необходимо знать только значение одной из его сторон. Это возможно за счет равенства углов в таком треугольнике.

Только в правильном треугольнике возможно нахождение площади полной поверхности через сторону.

По той же причине нельзя использовать эту формулу для равнобедренного или произвольного треугольника. Прежде чем использовать эту формулу необходимо доказать, что треугольник правильный или убедиться, что это условие прописано в исходных данных задачи.

Рис. 3. Произвольный треугольник.

Что мы узнали?

Мы узнали, как можно найти площадь правильного треугольника по стороне, разобрались как эту формулу можно просто и быстро вывести. Запомнив ход вывода можно пользоваться этим в дальнейшем, не запоминая точных значений, а просто проверяя себя, выводя формулу в черновике.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

Оценка статьи

4.4

Средняя оценка: 4.4

Всего получено оценок: 64.

---

А какая ваша оценка?

Площадь. 5 класс — презентация онлайн

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

1. Урок математики в 5классе Тема: «Площадь»  

Урок математики в 5классе
Тема: «Площадь»
Выполнила Соловьева Галина Дмитриевна,
учитель математики,
МБОУ «Перенская средняя школа»

2.

Задачи урока:• Познакомиться с понятиями «что такое площадь
фигуры»
• Повторить формулы площади прямоугольника и
квадрата
• Применение их к решению задач;
• Упражняться в нахождении площади фигур.

3. Организационный момент

Ровно встали, тихо сели,
Головами повертели.
Очень сладко потянулись
И друг другу улыбнулись.
Прозвенел сейчас звонок,
Начинаем наш урок.

4. Первую находим-вычисляем, Много формул для нее мы знаем. На второй же митинги, парады, Погулять по ней всегда мы рады.

S=ab
17.07.2019
4

5. Площадь прямоугольника

b
a
S=a·b

6. Площадь квадрата

a
a
S=
2
a
Устная проверочная работа
1
2
3
Написать
Формулу
для
вычисления
площади
прямоугольника.
Дано: прямоугольник
a = 18 см,
b = 3 см
Найти:S
Дано:
прямоугольник
S=48см2 ,
a=12 см
Найти:в
4
5
6
Написать
Формулу
для
вычисления
площади
КВАДРАТА
Дано: квадрат
a =8 см
Найти:S,P
Дано:
квадрат
S=49см2
Найти:а

8.

Ответы к устной проверочной работе1
2
3
S=ab
4
54 см2
5
4см
6
S = a2
64 см2
7 см

9. Вычислить площадь данной фигуры

Что значит измерить площадь фигуры?
Измерить площадь фигуры, значит найти число,
показывающее, сколько единичных квадратов содержится
в данной фигуре.
Вычислить площадь данной фигуры
S = 1 см2
S = 2 см2

10. Вычислить площадь нарисованной ракеты

S = 18 см2
1 см

11. Из трех данных треугольников построить квадрат.

12. Вычислить площадь каждого треугольника

8
Sкв.= 42 = 16 (см2)
Sб.треуг.= 16:2 = 8 (см2)
Sм.треуг.= 8:2 = 4 (см2)

13. Сложить из этих треугольников следующую фигуру, найти её площадь

4
S = 8+4+4 = 16 (см2)

14. Сложить из этих треугольников следующую фигуру, найти её площадь

S = 8+4+4 = 16 (см2)
4
4

15. Вывод:

• Площадь ФИГУРЫ РАВНА СУММЕ
ПЛОЩАДЕЙ ЕГО ЧАСТЕЙ
4
4
8

16.

Площадь ТРЕУГОЛЬНИКА b
a
S
ТРЕУГ
= a · b: 2
S=a·b

English     Русский Правила

Рабочие листы по площади треугольников

Изучите этот ассортимент рабочих листов по площади треугольников, чтобы повысить уровень практики учащихся от 5 класса до старшей школы. Сюда включено множество тем, таких как нахождение площади треугольника с размерами в целых числах, десятичных дробях и дробях, нахождение площади с преобразованием единиц измерения, нахождение площади трех типов треугольников и многое другое! Предлагаются два уровня: на уровне 1 представлены геометрические фигуры, а на уровне 2 сочетаются как геометрические фигуры, так и упражнения на словесный формат. Возьмите наши бесплатные рабочие листы и ускорьте практику!

Выберите единицы измерения Традиционные единицы США Метрические единицы

Площадь треугольников | Целые числа — тип 1

Используйте эту группу рабочих листов в формате PDF, чтобы найти площадь треугольников, размеры которых представлены целыми числами ≤ 20 на уровне 1 и ≥ 10 на уровне 2.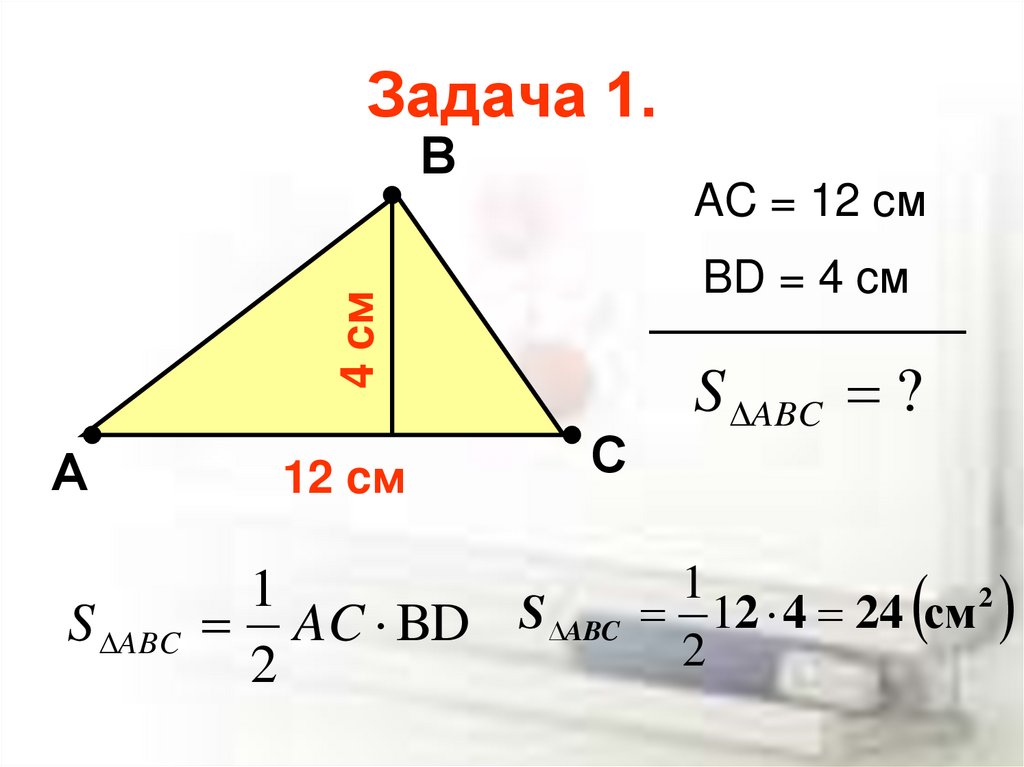 Примените формулу A = 1/2 * основание * высота; найти площадь.

Уровень 1

Уровень 2

Площадь треугольников | Целые числа — Тип 2

Этот массив печатных листов для 5-го класса по области треугольников содержит задачи в трех различных форматах с целочисленными измерениями, предлагаемыми на двух уровнях. Умножьте основание и высоту и разделите на два, чтобы рассчитать площадь.

Уровень 1

Уровень 2

Площадь треугольников | Десятичные числа

Включите этот набор рабочих листов площади треугольников с десятичными размерами. Вычислите площадь, подставив размеры основания и высоты в формулу площади треугольника.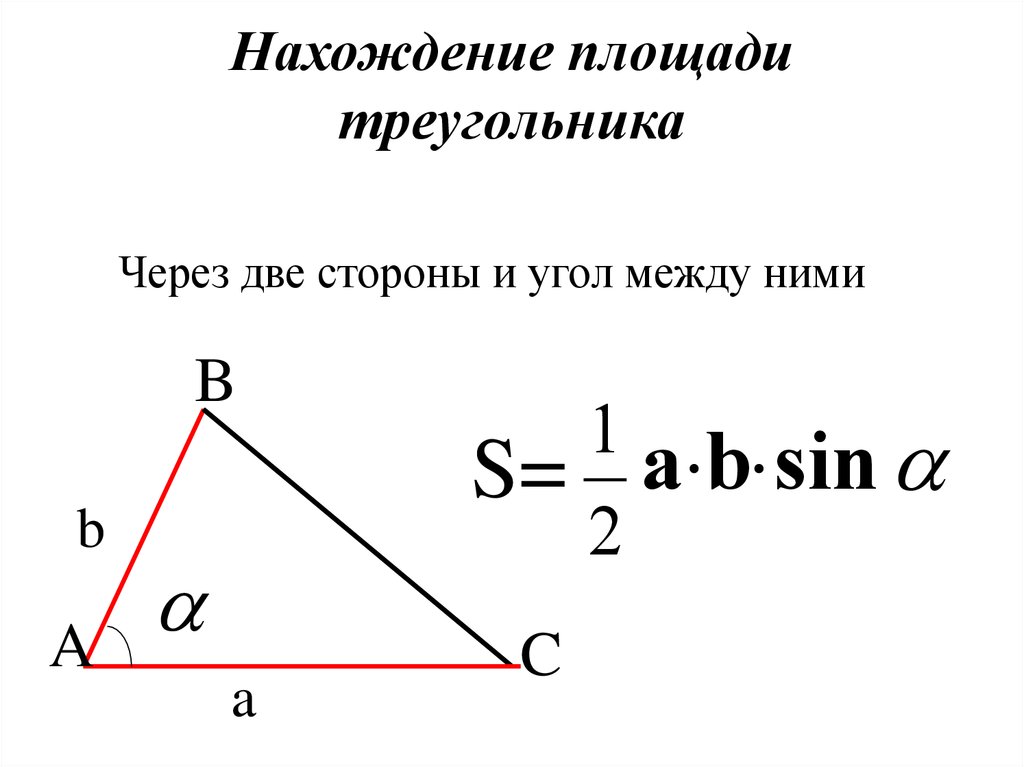

Тип 1

Тип 2

Площадь треугольников | Дроби

Перечислите площади треугольников, атрибуты которых представлены в виде дробей в этом сборнике рабочих листов PDF для 6-го класса. Каждый рабочий лист уровня 1 состоит из девяти треугольников, а уровень 2 предлагает задачи в трех форматах.

Тип 1

Тип 2

Площадь треугольников | Преобразование единиц измерения

Размеры треугольников даны в разных единицах измерения; ожидается, что учащиеся преобразуют их в указанные единицы, а затем подставят площадь в формулу треугольника, чтобы вычислить площадь.

Тип 1

Тип 2

Отсутствует база или высота | Целые числа

Переставьте площадь в формуле треугольника, сделайте неизвестное измерение предметом, замените значения площади и одного измерения, заданные целыми числами в формуле, чтобы определить отсутствующее основание или высоту.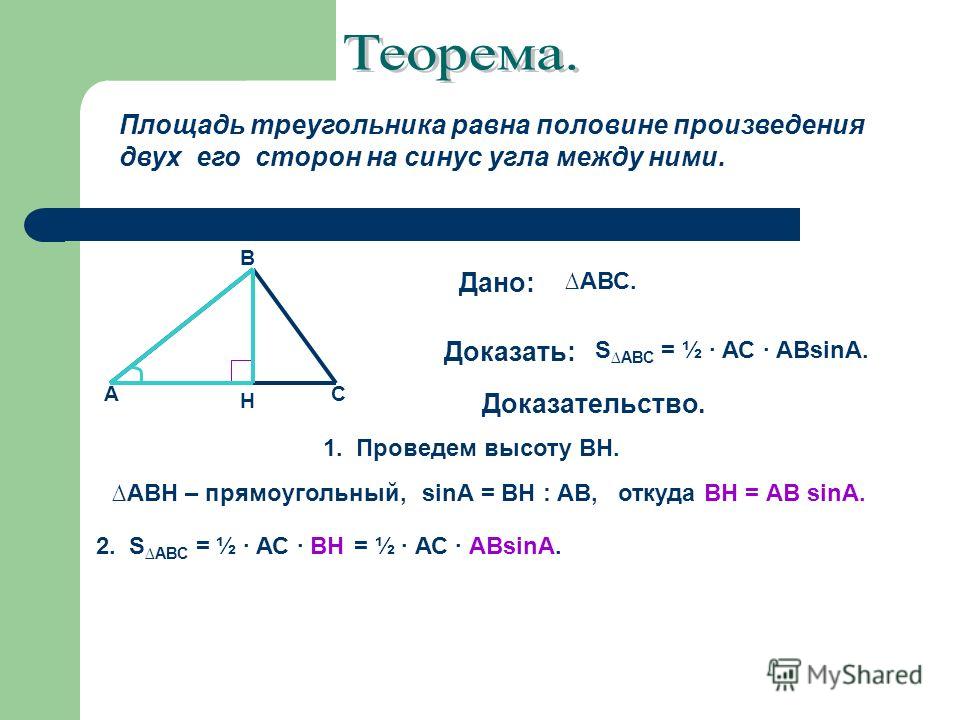

Отсутствует база или высота | Decimals

Найдите основание или высоту треугольников, используя площадь и любое из измерений, представленных в виде десятичных дробей в геометрических фигурах и в текстовом формате. Примените формулу A = 1/2 * основание * высота, чтобы найти пропущенное значение. Подходит для классов 6 и 7.

Отсутствует база или высота | Дроби

Площадь и размеры основания или высоты указываются в дробях. Измените формулу, изменив предмет на отсутствующее измерение, и рассчитайте неизвестную меру в этих печатных листах.

Отсутствует база или высота | Преобразование единиц измерения

Пройдитесь по этой стопке рабочих листов в формате PDF, в которой учащиеся 7-х и 8-х классов должны преобразовать единицы измерения, а затем подставить значения площади и высоты или основания, предлагаемые как целые и десятичные числа, для определения неизвестных размеров.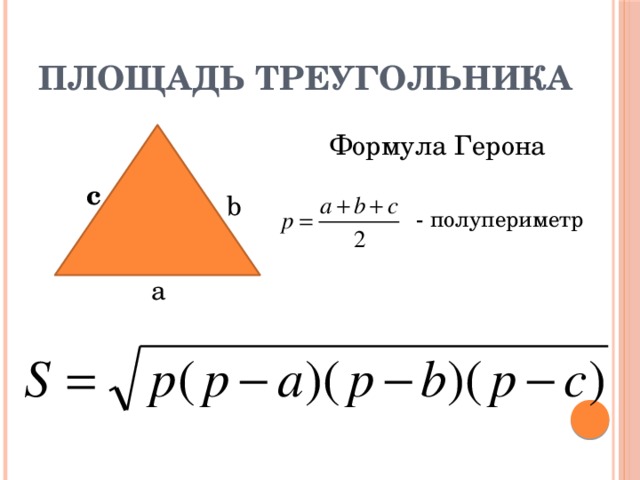

Площадь треугольников | Сложный

Каждый печатный лист здесь содержит пять сложных задач в текстовом формате; с изображением равносторонних, разносторонних и равнобедренных треугольников. Примените соответствующие формулы, подставьте размеры и вычислите площадь.

Рабочие листы площади равностороннего треугольника

Выяснение площади равностороннего треугольника не представляет труда с помощью этого набора печатных рабочих листов треугольника, содержащих меры, представленные в виде целых и десятичных чисел. Запоминание формулы A = √3/4 * a

2 , где «a» обозначает стороны, поможет вам выполнять упражнения без особых усилий.

(19 рабочих листов)

Площадь равнобедренного треугольника Рабочие листы

Если вам нужна практика в нахождении площади равнобедренного треугольника, то вам сюда.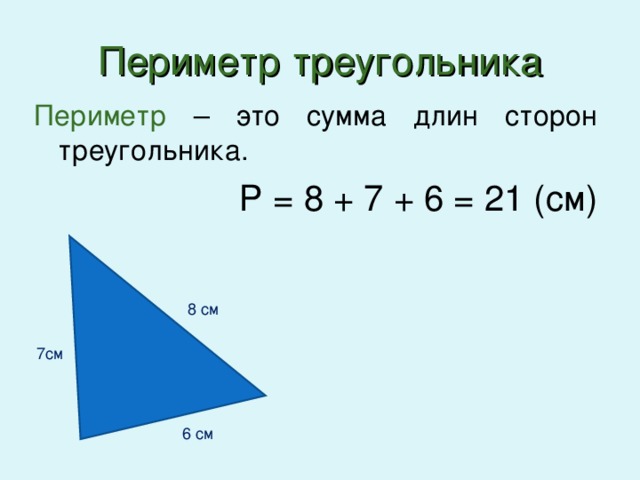 Найдите высоту треугольника по теореме Пифагора. Подставьте целое или десятичное число в формулу площади треугольника A = 1/2 * b * h и найдите площадь.

(16 листов)

Рабочие листы площади разностороннего треугольника

Переходя к разносторонним треугольникам, наши рабочие листы площади треугольника позволяют старшеклассникам попрактиковаться в вычислении площади разностороннего треугольника с помощью формулы Герона A = √ [s (s — a) ( s — b) (s — c)], где s — полупериметр. Задайте десятичные и целые размеры и найдите площадь.

(16 рабочих листов)

Связанные рабочие листы

»Площадь квадратов

»Площадь прямоугольников

» Площадь смешанных форм

»Площадь четырехугольника

» Площадь полигонов

»Площадь

Площадь рабочих листов треугольников

1. Математика>
2. Геометрия>
16.
3. Площадь >
4. Треугольники

Не позволяйте вашим амбициозным энтузиастам математики обходиться низкими оценками и, как мы часто слышим, выживать! Направляйте их к нашим ресурсам и помогите им заработать больше и преуспеть! Вспомните формулу площади умножения длины основания на высоту и последующего деления на два.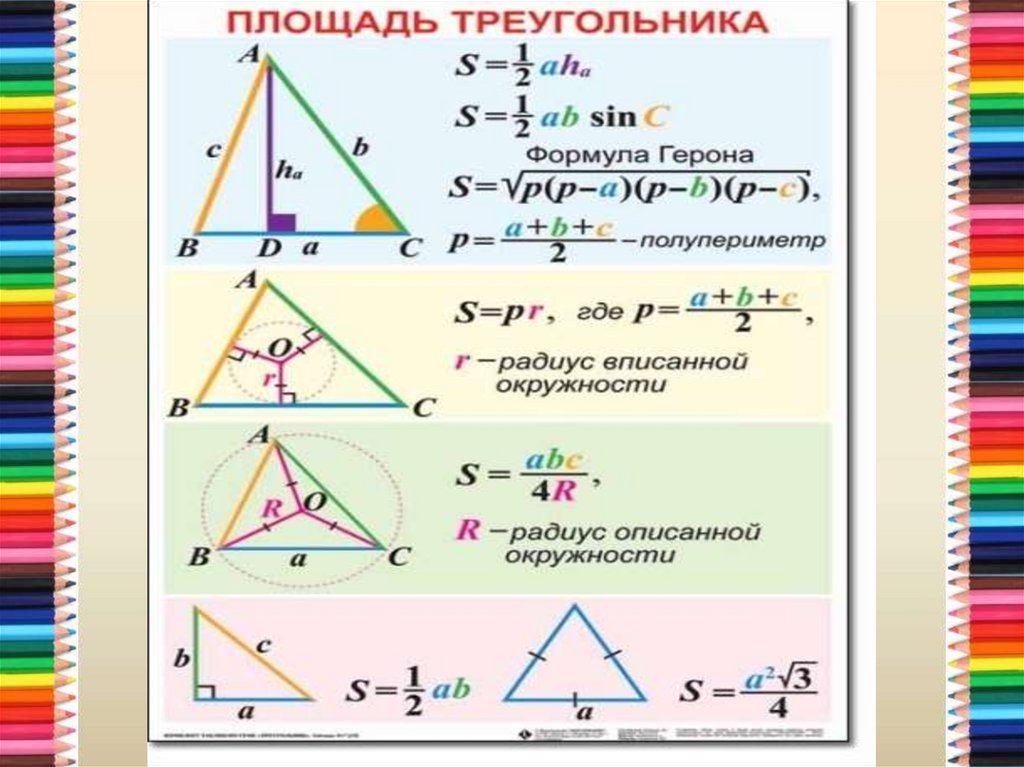 Есть идеи, в чем заключается задача? Точно треугольник! Эта коллекция бесплатных рабочих листов с областью треугольников для печати предлагает широкий спектр треугольников в виде геометрических фигур и вопросов в формате Word для практики. Задача состоит в том, чтобы подставить в формулу указанные целые, десятичные или дробные величины и вычислить площадь трехсторонней фигуры. В дополнение к этому имеются эксклюзивные упражнения по вычислению площадей различных категорий треугольников – равносторонних, равнобедренных и разносторонних треугольников. Упорное и решительное использование этих рабочих листов является ключом к получению обширных знаний о различных формулах и теоремах, связанных с нахождением площади треугольников.

Этот набор рабочих листов в формате PDF идеально подходит для учащихся от 5 до старшей школы.

CCSS: 6.G, 8.G

Выбор единиц измерения Традиционные единицы США Метрические единицы

Площадь треугольников | Целые числа – Рабочий лист №1

Пусть вас больше не смущает невозможность найти площадь геометрических фигур! Этот раздаточный материал, в котором прямоугольные треугольники и другие треугольники представлены как геометрические фигуры для расчета площади, является отличным материалом для 5-го и 6-го классов. Длина основания (b) и высота (h) указаны на рисунке. Подставляем их в формулу A = bh/2 и получаем площадь.

Площадь треугольников | Целые числа – Рабочий лист №2

Пусть в треугольниках нет ничего сложного! Этот бесплатный рабочий лист для 6-го и 7-го классов, который можно распечатать и использовать как отличный ресурс для практики и самооценки, включает в себя сочетание геометрических фигур и вопросов формата слова. Испытайте себя и вернитесь домой с такой же геометрической победой, как и прежде!

Площадь треугольников | Десятичные числа

Преданная практика и тщательная оценка лежат в основе каждой мастерской практики треугольников. Тренируйтесь с помощью этого рабочего листа в формате PDF, который отображает размеры треугольников в десятичных дробях. Половина произведения этих десятичных мер даст вам площадь. Спорим, вы вернетесь за добавкой!

Площадь треугольников | Дроби

Успех — особенно в вопросах геометрии — самый сладкий на вкус, в основе которого лежит куча строгости! Это упражнение отличается от предыдущих тем, что в нем длина основания и высота треугольников представлены в виде дробей и смешанных чисел.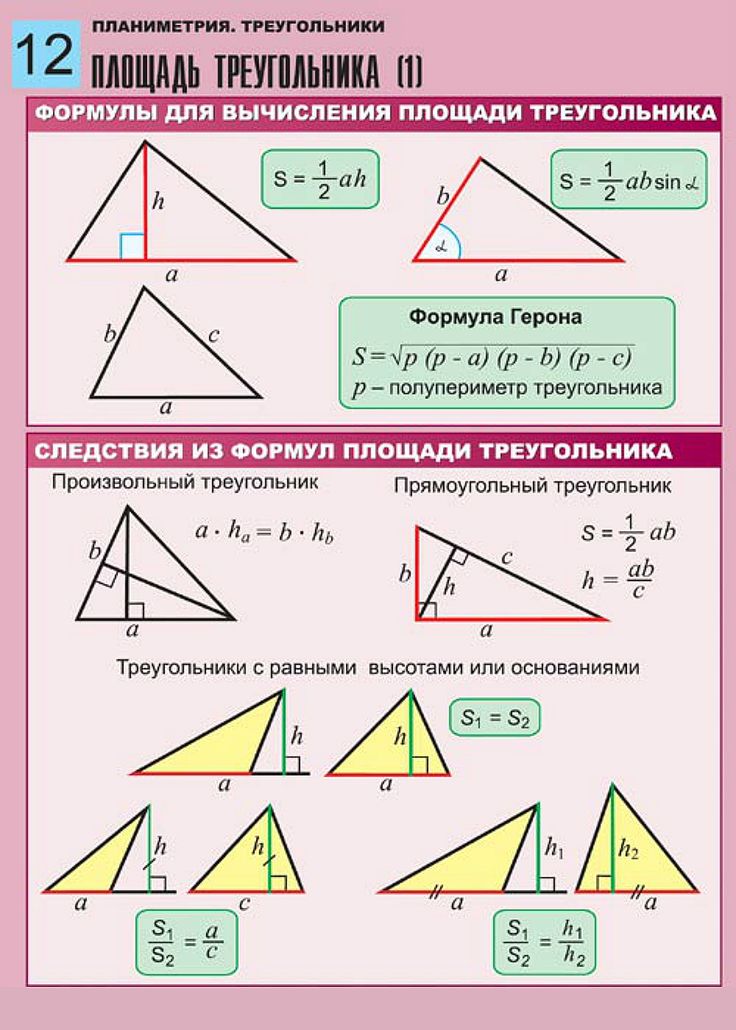 Преобразуйте смешанные числа в дроби и приступайте к нахождению площади.

Площадь равносторонних треугольников

Элитные ученики играют с треугольниками – в том числе с равносторонними, но обычные с трудом их обходят! «Равносторонний» — это латинское слово, обозначающее многоугольник с равными сторонами. Нажмите на эту ссылку, которая представляет множество трехсторонних многоугольников с конгруэнтными сторонами для практического применения. Можете ли вы вычислить их площадь, когда в вашем распоряжении есть только длина стороны? Проверьте, как!

Площадь равнобедренных треугольников

Пусть вас не смущают нюансы равнобедренного треугольника! Этот пакет рабочих листов в формате pdf для 8-го класса и старшей школы, богатый плодотворной практикой по нахождению площади треугольников с двумя конгруэнтными сторонами, очень полезен для навигации. Примените теорему Пифагора, определите высоты и рассчитайте площадь по обычной формуле.

Площадь разносторонних треугольников

Отличительная черта выдающегося математика — никогда не упускать чашку из губ! Разносторонний треугольник – это плоская фигура с тремя неравными сторонами.