Построение трехмерных графиков функций двух переменных
Вы здесь
Главная
»
Архив газеты
»
2000 год
»
№13
»
Построение трехмерных графиков функций двух переменных
Графики функций двух переменных
вида z=f(x,y), в отличие от графиков
функций y=f(x), представляют собой не
линии, а поверхности. Если график
функции y=f(x) можно легко изобразить
на плоском листе бумаги, то график
функции z=f(x,y) уже не помещается на
плоскости, а требует
пространственного представления. В
прошлых номерах «КВ» (см.
«КВ» №29, 1999
г. и №2, 2000 г.)
рассматривались способы
построения графиков функций двух
переменных, основанные на тоновой и
цветовой визуализации. Суть этих
методов состоит в том, что
значениям z ставится в соответствие
некая шкала тонов или цветовая
гамма. Иными словами, сама картинка
строится на плоскости в
координатах x и y, а третье
пространственное измерение
моделируется при помощи игры
полутонов или цветовых оттенков.
Весьма интересно, однако, было бы
увидеть не только плоское
изображение графика, но и его
пространственную реконструкцию. В
изобразительном искусстве и
черчении различные объекты
моделируются на плоскости рисунка
или чертежа в виде тех или иных
трехмерных проекций. Рассмотрим
один из возможных методов
адаптации программы тоновой
визуализации для построения
трехмерных проекций графиков
функций двух переменных. Наиболее
удобна для компьютерной реализации
так называемая фронтальная
диметрическая проекция. В ней ось X
располагается горизонтально, ось Z —
вертикально, а ось Y — под углом 45° к
горизонтальной оси X. При
фронтальном диметрическом
проецировании размеры по оси Y
необходимо делать вдвое меньшими,
чем аналогичные размеры по осям X и
Z. За основу программы возьмем код
процедуры тоновой визуализации
(«КВ» №29, 1999
г.
Иными словами, сама картинка
строится на плоскости в
координатах x и y, а третье
пространственное измерение
моделируется при помощи игры
полутонов или цветовых оттенков.
Весьма интересно, однако, было бы
увидеть не только плоское
изображение графика, но и его
пространственную реконструкцию. В
изобразительном искусстве и
черчении различные объекты
моделируются на плоскости рисунка
или чертежа в виде тех или иных
трехмерных проекций. Рассмотрим
один из возможных методов
адаптации программы тоновой
визуализации для построения
трехмерных проекций графиков
функций двух переменных. Наиболее
удобна для компьютерной реализации
так называемая фронтальная
диметрическая проекция. В ней ось X
располагается горизонтально, ось Z —
вертикально, а ось Y — под углом 45° к
горизонтальной оси X. При
фронтальном диметрическом
проецировании размеры по оси Y
необходимо делать вдвое меньшими,
чем аналогичные размеры по осям X и
Z. За основу программы возьмем код
процедуры тоновой визуализации
(«КВ» №29, 1999
г.
В результате работы программы над
лежащей тоновой тенью повиснет
легкое точечное изображение
трехмерного каркаса исследуемой
поверхности, чем-то напоминающее
натянутый прозрачный черный нейлон
(см. рисунки). В том случае, когда на
одном рисунке совмещается тоновое
изображение с «парящей» над
ним трехмерной структурой, можно
составить наиболее полное и
адекватное представление о
пространственной форме графика
функции.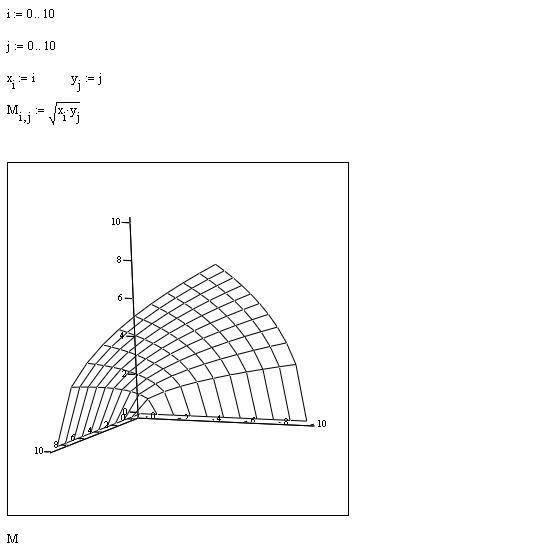
DefSng X-Z Public Function f(x As Single, y As Single) As Single f = Sin(x * y / 2) End Function Private Sub Screen_Click() Dim c As Long Dim t As Byte Dim n As Integer Dim hx As Single Dim hy As Single Dim Rz As Single Screen.Cls n = 300 m = 150 xmin = Text1(0).Text xmax = Text1(1).Text ymin = Text1(2).Text ymax = Text1(3).Text zmin = Text1(4).Text zmax = Text1(5).Text Rz = zmax — zmin hx = (xmax — xmin) / n hy = (ymax — ymin) / m y = ymin — hy / 2 For j = 300 To 450 x = xmax + hx / 2 y = y + hy For i = j To (j — 300) Step -1 x = x — hx z = f(x, y) Select Case z Case Is > zmax c = RGB(200, 200, 200) k = n Case Is < zmin c = RGB(0, 0, 0) k = 0 Case zmin To zmax t = 255 * (z — zmin) / Rz k = 300 * (z — zmin) / Rz c = RGB(t, t, t) End Select Screen.PSet (i, j), c Screen.PSet (i, j — k), RGB(0, 0, 0) Next i Next j End Sub
При помощи приведенной программы можно получить бесчисленное множество пространственных изображений различных функций. Мы уже имели возможность оценить богатство их форм и красоту, проводя опыты с тоновой визуализацией. Объемные графики весьма существенно дополняют тоновые изображения. Они в полной мере позволяют оценить неповторимую пластику нелинейных поверхностей, среди которых порой попадаются весьма изысканные и привлекательные формы, доставляющие истинное эстетическое наслаждение. Компьютерная визуализация многократно усиливает творческий потенциал геометрического мышления, стимулирует пространственное воображение, что, несомненно, способствует дальнейшему познанию загадочного и необычайно красивого мира чисел.
Визуализация графиков функций
двух переменных имеет не только
эстетическое, но и практическое
значение. Функции двух переменных
нередко выступают в качестве
математических моделей различных
процессов. После того, как эта
модель становится зримой,
анализировать ее гораздо проще.
Закономерности течения
исследуемого явления становятся
видимыми и очевидными. На графиках
отчетливо прослеживается
местоположение экстремальных
точек. А поиск минимумов или
максимумов функции, описывающей
какой-то физический или
производственный процесс, имеет
прямое отношение к решению
различного рода оптимизационных
задач.
После того, как эта
модель становится зримой,
анализировать ее гораздо проще.
Закономерности течения
исследуемого явления становятся
видимыми и очевидными. На графиках
отчетливо прослеживается
местоположение экстремальных
точек. А поиск минимумов или
максимумов функции, описывающей
какой-то физический или
производственный процесс, имеет
прямое отношение к решению
различного рода оптимизационных
задач.
Судя по письмам, при повторении
программ, приводимых в моих
статьях, у читателей нередко
возникает одна и та же ситуация,
когда вместо полной картинки в
графическом окне появляется лишь
ее микроскопическая копия. Это
вовсе не какой-то коварный глюк, а
всего лишь следствие того, что я
привык измерять экранное
пространство в пикселах, а не в
твипах. В VB же по умолчанию в
качестве экранных единиц измерения
предлагаются именно твипы. Твипы
гораздо мельче пикселов (1
логический сантиметр — 567 твипов),
поэтому итоговая картинка
получается микроскопической. Для
того, чтобы этого избежать,
необходимо поменять единицы
измерения с твипов на пикселы
(свойство ScaleMode).
Андрей КОЛЕСНИКОВ,
[email protected]
Версия для печати
Номер:
№13 за 2000 год
Рубрика:
Азбука программирования
Страховой фонд на $1 млн, ежегодный аудит и выгодные комиссии. Как создавался первый легальный криптообменник в СНГ
25 интересных Android-приложений и игр, которые вышли в 2022 году
Выглядит как флагман, а стоит дешевле. В чем секрет смартфона HONOR X9a?
Лучшие Android-приложения января
Афиша IT-мероприятий в феврале
Коттеджный посёлок «Lipki Village»: современная загородная жизнь в Беларуси
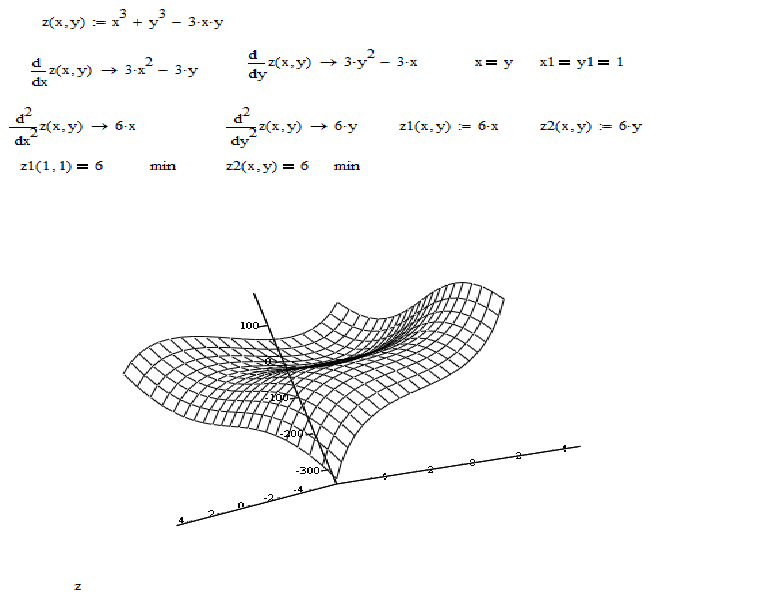
Коллекция трехмерных графиков — настоящее чудо, которое Mathcad дарит пользователю. За считанные секунды вы можете создать великолепную презентацию результатов своих расчетов. Рамки данной книги не позволяют описать технику их создания и форматирования подробно, поэтому мы ограничимся лишь вводными замечаниями и простыми примерами, которые помогут ориентироваться в дальнейшем материале. Для этого рассмотрим на простом примере функции z(x,y) и матрицы z (они заданы в листингах 1.22 и 1.23 соответственно) технику построения трехмерных графиков различных типов Чтобы создать трехмерный график, требуется нажать кнопку с изображением любого из типов трехмерных графиков на панели инструментов
Graph (График). В результате появится пустая область графика с тремя осями (рис. 1.34) и единственным местозаполнителем в нижнем левом углу. В этот местозаполнитель следует ввести либо имя
z функции z(x,y) двух переменных для быстрого построения трехмерного графика (рис. Рис. 1.34. Создание трехмерного графика Листинг 1.22. Функция для быстрого построения трехмерных
графиков Листинг 1.23. Матрица для отображения на трехмерных графиках Помимо трехмерных графиков поверхности, нажатие соответствующих кнопок на панели
Graph (График) приводит к созданию графика линий уровня (рис. 1.37), трехмерной гистограммы (рис. 1.38), трехмерного распределения точек (рис. 1.39) или векторного поля (рис. 1.40). Все эти графики представляют данные, составленные листингами 1.22 и 1.23. Рис. 1.35. Быстрое построение графика поверхности функции (продолжение листинга 1.22) Рис. 1.36. График поверхности, заданный матрицей (продолжение листинга 1. Рис. 1.37. Быстрое построение графика линий уровня (продолжение листинга 1.22) Рис. 1.38. Быстрое построение трехмерной гистограммы (продолжение листинга 1.22) Рис. 1.39. Быстрое построение графика трехмерного распределения точек (продолжение листинга 1.22) Рис. 1.40. Два графика векторных полей, заданных матрицами (продолжение листинга 1.23) Нравится Твитнуть Теги MathCad САПР Сюжеты MathCad Глава 1 Основы работы с системой Mathcad 11 9994 0 Глава 10 Работа с информационными ресурсами Mathcad 11 7006 0 Глава 2 Работа с файлами Mathcad 11 12620 0 Вы должны авторизоваться, чтобы оставлять комментарии. Вход О проекте Использование материалов Контакты Новости Статьи База знаний Радиомастер При использовании материалов данного сайта прямая и явная ссылка на сайт radiomaster.ru обязательна. 0.2542 s |
— Как построить трехмерный (XYZ) график в Excel
Задавать вопрос
спросил
Изменено 3 месяца назад
Просмотрено 5к раз
У меня есть таблица данных, но она в 2D (XY):
Х 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 Д 4 4 4 4 10 15 20 25 25 25 25 25 25 20 15 10 4 4 4 4
И полученный график будет выглядеть так:
Итак, вот моя проблема.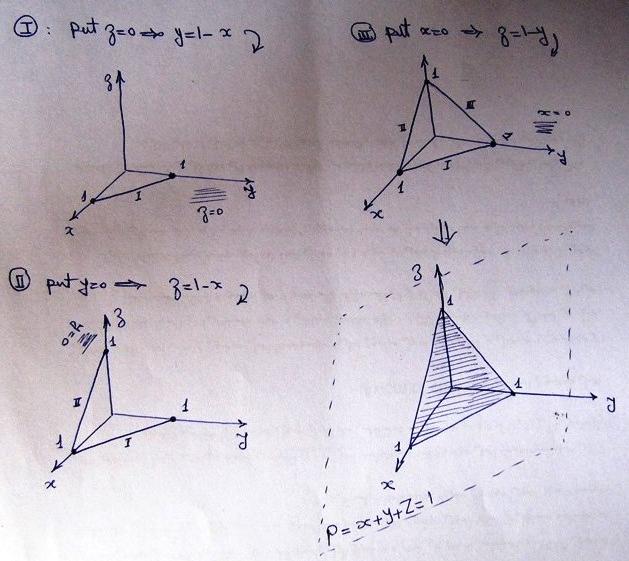 На самом деле, я хочу построить трехмерный график, который будет выглядеть точно так же, как изображение, прикрепленное выше, когда мы видим его в 2D, но для построения трехмерного графика у меня нет никаких идей о данных Z или уравнении Z, которые мне нужно учитывать. .
На самом деле, я хочу построить трехмерный график, который будет выглядеть точно так же, как изображение, прикрепленное выше, когда мы видим его в 2D, но для построения трехмерного графика у меня нет никаких идей о данных Z или уравнении Z, которые мне нужно учитывать. .
Ниже приведен пример трехмерного графика, который мне нужен:
Мне очень жаль, если мой вопрос сбивает с толку. Я очень надеюсь, что кто-то может мне помочь. Мне нужна помощь в определении уравнения Z, чтобы я мог создать трехмерный график.
После того, как трехмерный график получен, мне нужно приступить к вычислению его наклона. Вот почему мне действительно нужно знать, как построить трехмерный график на основе прикрепленного изображения.
- Microsoft-Excel
- диаграммы
- 3D
2
Это видео содержит учебник по созданию 3D-графиков в Excel.
Как только ваши данные X и Y будут правильно подготовлены (в столбце и строке соответственно), вы можете ввести данные Z в ячейки, соответствующие каждому значению X и Y.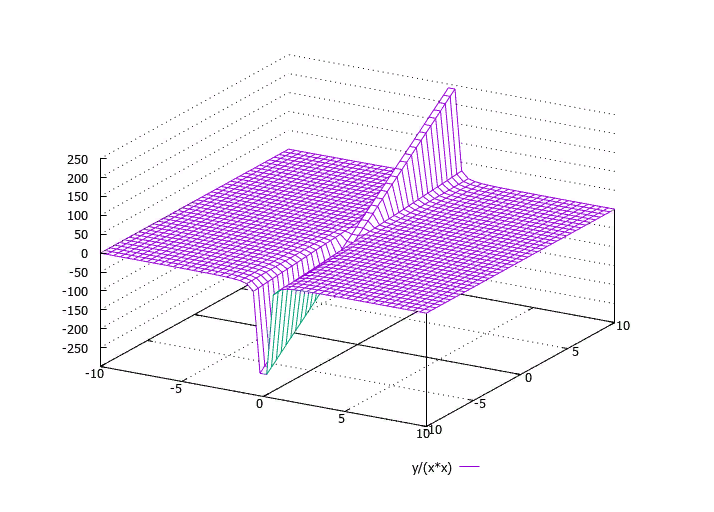 На видео это делается по формуле.
На видео это делается по формуле.
Чтобы создать график Surface , как показано в видео, нажмите Insert , Other Charts , затем один из значков под Surface .
Другие методы построения 3D-данных можно найти здесь и здесь.
2
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя адрес электронной почты и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Создать график поверхности данных высоты xyz в Python
спросил
Изменено 1 год, 1 месяц назад
Просмотрено 35 тысяч раз
Я пытаюсь создать график поверхности горы в питоне, для которого у меня есть некоторые данные xyz. Конечный результат должен выглядеть примерно так. Файл имеет следующий формат:
616000,0 90500,0 3096,712 616000,0 90525,0 3123,415 616000,0 90550,0 3158,902 616000,0 90575,0 3182,109 616000,0 90600,0 3192,991 616025.0 90500.0 3082.684 616025.0 90525.0 3116.597 616025,0 90550,0 3149,812 616025,0 90575,0 3177,607 616025,0 90600,0 3191,986
и так далее. Первый столбец представляет координату x , средний — координату y , а z — высоту, принадлежащую координате xy.
Я прочитал данные, используя pandas , а затем преобразовать столбцы в отдельные массивы x , y , z NumPy 1D. До сих пор мне удалось создать простую трехмерную точечную диаграмму с циклом для , повторяющим каждый индекс каждого одномерного массива, но это требует времени и делает вид довольно неэффективным.
Я пытался работать с scipy.interpolate.griddata и plt.plot_surface , но для данных z я всегда получаю сообщение об ошибке, что данные должны быть в 2D-массиве, но я не могу понять, почему или как это должны быть 2D данные. Я предполагаю, что, учитывая, что у меня есть данные xyz, должен быть способ просто создать из них поверхность. Есть ли простой способ?
- python
- surface
- geography
- topography
Using functions plot_trisurf and scatter from matplotlib , given X Y Z data can be plotted similar to given plot.
система импорта
импортировать CSV
импортировать numpy как np
импортировать matplotlib.pyplot как plt
из mpl_toolkits.mplot3d импортирует axes3d
# Чтение CSV-файла
csvFileName = sys.argv[1]
csvДанные = []
с open(csvFileName, 'r') как csvFile:
csvReader = csv.reader (csvFile, разделитель = ' ')
для csvRow в csvReader:
csvData.append(csvRow)
# Получить X, Y, Z
csvData = np.array(csvData)
csvData = csvData.astype(np.float)
X, Y, Z = csvData[:,0], csvData[:,1], csvData[:,2]
# График X, Y, Z
рис = plt.figure()
топор = fig.add_subplot(111, проекция='3d')
ax.plot_trisurf (X, Y, Z, цвет = «белый», edgecolors = «серый», альфа = 0,5)
ax.scatter(X, Y, Z, c='красный')
plt.show()
Здесь
- файл, содержащий
X Y Zданные, предоставленные в качестве аргумента для вышеуказанного скрипта - в
plot_trisurf, параметры, используемые для управления внешним видом. напримеральфаиспользуется для управления непрозрачностью поверхности - в
scatter,cпараметр определяет цвет точек нанесенных на поверхность
Для заданного файла данных создается следующий график
Примечание: Здесь рельеф формируется путем триангуляции заданного набора трехмерных точек. Следовательно, контуры вдоль поверхности на графике не выровнены по осям X и Y
Следовательно, контуры вдоль поверхности на графике не выровнены по осям X и Y
импортировать numpy как np
импортировать matplotlib.pyplot как plt
импортировать mpl_toolkits.mplot3d
импортировать панд как pd
df = pd.read_csv("/content/1.csv")
X = df.iloc[:, 0]
Y = df.iloc[:, 1]
Z = df.iloc[:, 2]
рис = plt.figure()
топор = fig.add_subplot(111, проекция='3d')
ax.plot_trisurf (X, Y, Z, цвет = «белый», edgecolors = «серый», альфа = 0,5)
ax.scatter(X, Y, Z, c='красный')
plt.show()
Мое выходное изображение ниже — у меня было много точек данных: введите описание изображения здесь
Есть более простой способ достичь своей цели без использования панд.
импортировать numpy как np импортировать matplotlib.pyplot как plt импортировать mpl_toolkits.mplot3d х, у = np.mgrid[-2: 2: 20j, -2: 2: 20j] z = 50 * np.sin(x + y) # тестовые данные output = plt.subplot(111, проекция = '3d') # 3D-проекция output.plot_surface (x, y, z, rstride = 2, cstride = 1, cmap = plt.

 PSet (i, j), c
Screen.PSet (i, j — k), RGB(0, 0, 0)
Next i
Next j
End Sub
PSet (i, j), c
Screen.PSet (i, j — k), RGB(0, 0, 0)
Next i
Next j
End Sub 4.7. Трехмерные графики MathCAD 12 руководство
4.7. Трехмерные графики MathCAD 12 руководство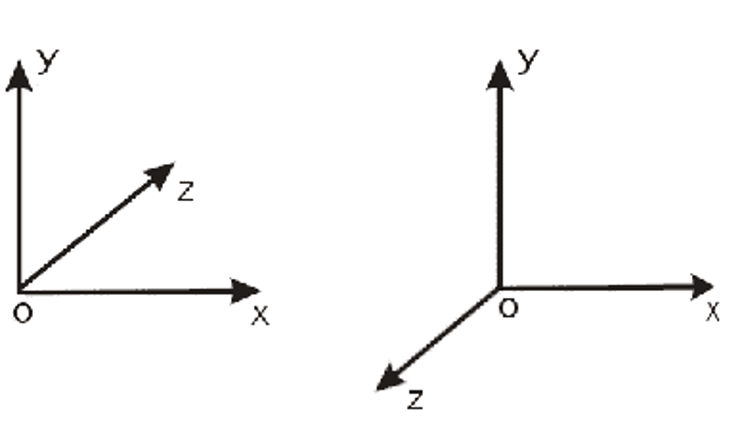 1.35), либо имя матричной переменной
z, которая задаст распределение данных zx,Y на плоскости XY (рис. 1.36). Еще раз отметим, что для получения графиков (и этих, и последующих) не требуется никакого текста, кроме соответствующего листинга и введения имени соответствующей функции или матрицы в местозаполнитель.
1.35), либо имя матричной переменной
z, которая задаст распределение данных zx,Y на плоскости XY (рис. 1.36). Еще раз отметим, что для получения графиков (и этих, и последующих) не требуется никакого текста, кроме соответствующего листинга и введения имени соответствующей функции или матрицы в местозаполнитель.