Решить дифференциальное уравнение: (x + y)(1
Решить дифференциальное уравнение:(x + y)(1 — xy)dx + (x + 2y)dy = 0.
ВХОД | РЕГИСТРАЦИЯ
Решить дифференциальное уравнение:
y’ tg y + 4x3 cos y = 2x.
Решить дифференциальное уравнение:
x(y’2 + e2y) = -2y’.
☆
Добавить в избранное
17
18
19
20
21
22
23
24
25
26
27
28
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
69
70
71
72
73
74
75
76
77
78
79
80
81
83
84
85
86
87
88
89
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
131
132
133
134
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
249
250
251
252
254
256
257
259
260
261
263
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
314
315
316
318
320
322
324
326
327
332
333
334
335
336
339
340
341
342
343
347
350
353
354
355
356
357
359
360
361
363
364
369
371
372
375
377
382
383
388
395
399
401
402
404
406
408
409
410
413
414
415
417
420
421
422
423
424
425
426
427
428
429
430
432
433
434
435
438
439
441
443
444
445
447
448
449
450
452
455
456
457
458
459
460
461
462
463
464
465
466
467
468
469
470
473
475
479
480
482
487
500
501
503
505
507
508
509
510
511
512
513
514
515
516
517
518
519
520
521
522
523
524
525
526
527
528
529
530
531
532
533
534
535
536
537
538
539
540
541
542
543
544
545
546
547
548
549
550
552
553
554
555
556
557
558
559
560
562
563
564
566
568
569
570
572
573
575
576
577
578
579
580
581
582
583
584
585
586
587
588
589
590
591
592
593
594
595
597
598
599
600
601
602
603
610
612
613
615
616
617
618
619
620
623
624
625
628
629
634
635
639
641
642
643
644
645
646
647
648
649
650
651
652
653
654
656
658
660
661
663
665
667
668
669
671
673
674
675
676
678
679
681
682
683
684
685
686
687
689
691
692
694
696
698
700
710
713
718
720
722
723
734
737
738
744
746
747
748
749
751
752
753
754
755
756
757
758
759
761
762
763
764
765
766
767
768
769
770
775
776
780
781
782
786
787
788
789
790
791
793
794
796
797
798
799
800
801
802
803
804
806
811
812
813
814
816
817
818
819
820
823
824
825
826
827
828
829
830
832
833
834
835
836
837
838
839
840
842
845
846
847
848
849
850
851
852
853
854
855
856
857
858
859
860
861
862
863
864
865
866
867
868
869
870
871
872
873
874
875
881
884
889
890
892
894
895
898
899
900
901
902
903
904
905
906
907
909
910
911
912
913
914
915
916
917
918
919
920
921
922
923
924
925
926
928
929
930
931
932
934
935
936
939
942
945
946
947
950
953955
957
961
962
964
965
966
967
970
972
973
975
976
978
979
980
981
982
986
988
990
992
993
995
996
999
1003
1005
1006
1008
1009
1010
1012
1015
1016
1018
1019
1021
1023
1027
1029
1030
1031
1033
1041
1043
1046
1047
1048
1056
1058
1059
1060
1061
1063
1064
1066
1068
1070
1071
1072
1074
1076
1078
1079
1081
1083
1084
1086
1090
1091
1092
1093
1094
1095
1096
1097
1098
1100
1102
1104
1106
1108
1109
1110
1112
1114
1116
1119
1120
1121
1123
1126
1128
1135
1141
1142
1143
1144
1145
1146
1147
1148
1150
1151
1152
1153
1154
1155
1156
1157
1158
1159
1160
1161
1162
1163
1164
1167
1168
1169
1170
1171
1172
1173
1174
1176
1179
1181
1183
1185
1186
1188
1190
1191
1192
1193
1194
1195
1196
1198
1200
1201
1202
1203
1204
1206
1209
1210
1212
1214
1216
1217
1218
1220
[c] 2022 / HelpLearn.
ru — Помощь в учебе — ГДЗ портал
Правообладателям •
Пользовательское соглашение •
Политика конфиденциальности •
Как решить dy/dx= (x+y+1) / (x-y-1)?
Исчисление
Вопрос задан 15.03.19Подписаться І 1
Подробнее
Отчет
3 ответа от опытных наставников
Лучший Новейшие Самый старыйАвтор: Лучшие новыеСамые старые
ТИМ Б. ответил 27.03.19
Репетитор
4.9 (16)
Математическая проницательность по найму
Об этом репетиторе ›
Об этом репетиторе ›
(x-y-1)dy = (x+y+1)dx или (x+y+1)dx — (x-y-1)dy = 0. Решите систему x+y+1 = 0 & x-y-1 = 0, чтобы получить (x,y) = (0,-1).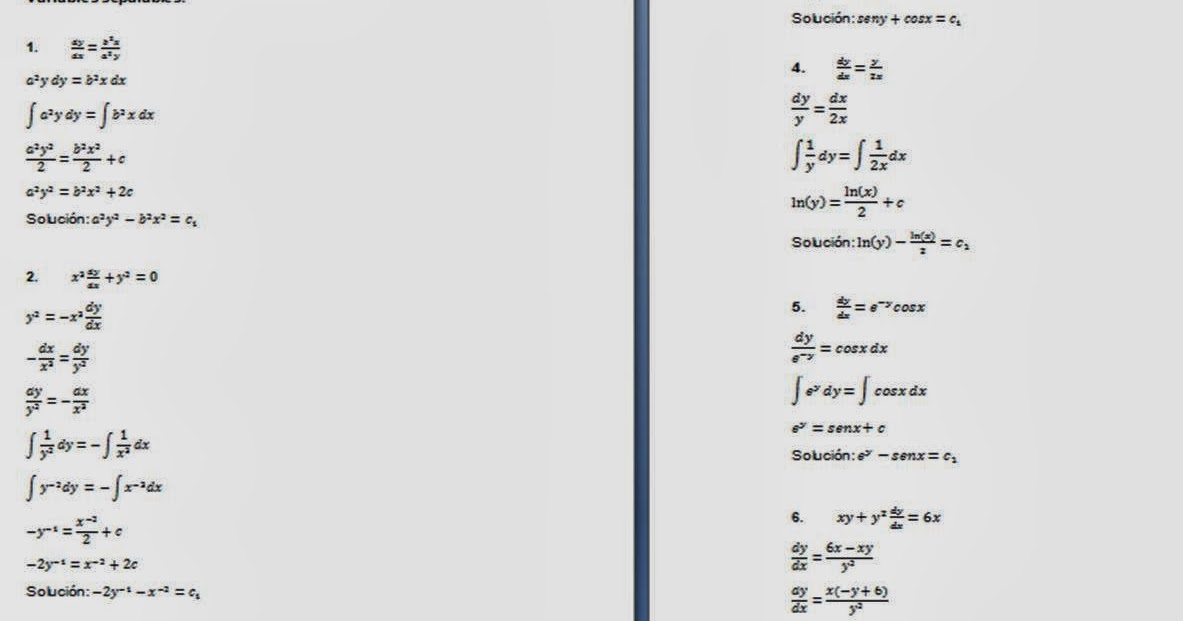
Затем используйте преобразование [y’ = vx’; dy’ = vdx’ + x’dv], чтобы получить ((x’+vx’)dx’ — (x’-vx’)(vdx’+x’dv) = 0), и умножить уравнение на (1/ x’), что дает (1+v)dx’ — (1-v)(vdx’+x’dv) = 0.
Перепишите последнее уравнение как dx’+vdx’-vdx’-x’dv+v 2 dx’+vx’dv = 0, что сводится к dx’/x’ — dv + v 2 dx’/x’ +vdv = 0. Преобразование в виде dx'(1+v 2 )/x’ + dv(v-1) = 0 или dx’/x’ = -(v-1)dv/(v 2 +1). Установите последнее уравнение как (dx’/x’) = (1/(v 2 +1) — v/(v 2 +1))dv и проинтегрировать в ln |x’| = arctan v — 0,5ln |v 2 +1| + C.
Преобразование x’ и v для получения ln |x| = arctan ((y+1)/x) — 0,5ln |((y+1) 2 /x 2 )+1|+C.
Умножьте последнее уравнение на 2 и расположите члены так, чтобы получилось 2ln |x|+ln |((y+1) 2 +x 2 )/x 2 |+C = 2arctan ((y+1) )/Икс).
Объединение натуральных логарифмов дает окончательный ответ ln ((y+1) 2 +x 2 ) — 2arctan ((y+1)/x) = C.
Голосовать за 0 голос против
Подробнее
Отчет
Том Н. ответил 27.03.19
Репетитор
4.9 (474)
Уверенное знание элементарной и высшей математики
Об этом репетиторе ›
Об этом репетиторе ›
dy/dx=(x+y+1)/(x-y-1) пусть y= v-1 тогда dy/dx= dv/dx поэтому dv/dx = (x+v)/(x-v) пусть v=xu (x) теперь dv/dx = x du/dx +u
xdu/dx + u = (x+ xu)/(x-xu) = (1+u)/(1-u), поэтому du/dx= 1 /x(-u +(u+1)/(1-u)) = 1/x(u 2 +1)/(1-u), так что du/dx((u-1)/(-u 2 -1))= 1/х. Интегрирование обеих сторон Int (du(u-1)/(-u 2 -1))= Int dx/x =log|x| + C.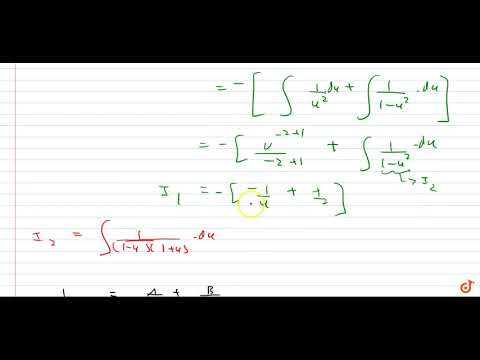
so Int -du/ (-u 2 -1) + Int udu/(-u 2 -1)
равно tan -1 u — (1/2) log|u 2 +1| а это равно log|x| + C
, поэтому u=v/x и v=y+1 подставляются в выражение, чтобы получить tan -1 (y+1)/x — (1/2)log| (y+1) 2 /x 2 +1|= log|x| + C в виде раствора
Голосовать за 0 голос против
Подробнее
Отчет
Пол М. ответил 17.03.19
Репетитор
5 (22)
Узнайте, «как» делать математику и почему «как» работает!
Об этом репетиторе ›
Об этом репетиторе ›
Сделайте замену u = y+1 так, чтобы du = dy и
du/dx=(x+u)(x-u)
Тогда
x du — u du = x dx + u dx
x du — u dx =x dx + u du
Если поделить на xy, то получится бессмысленное решение.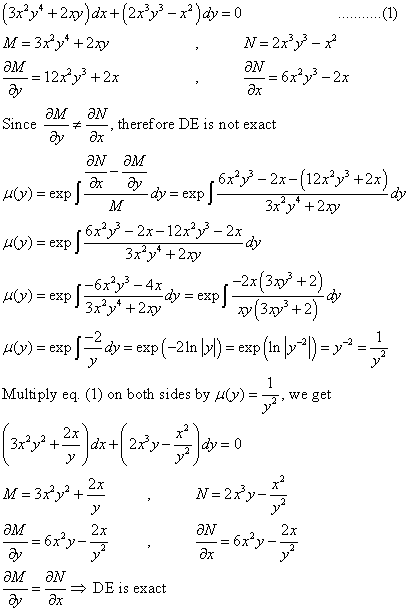
Разделите на x 2 + y 2 , чтобы получить
(x du — u dx)/(x 2 + y 2 ) = (x dx + u du)/(x 2 6 6 + y 2 )
Левая часть представляет собой производную от arctan (u/x), а правая часть представляет собой производную от (1/2)ln(x 2 + y 2 ), что делает решение
arctan[(y+1)/x] =(1/2)ln[x 2 + (y+1) 2 ] + C
Это технически правильное механическое решение; Я не уверен, что это значит!
Голосовать за 0 голос против
Подробнее
Отчет
Все еще ищете помощи? Получите правильный ответ, быстро.
Задайте вопрос бесплатно
Получите бесплатный ответ на быстрый вопрос.
Ответы на большинство вопросов в течение 4 часов.