| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктан(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 32 | 92|||
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктан(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт. )/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | тан(пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | соз(30) | |
| 47 | Найти точное значение | соз(60) | |
| 48 | Найти точное значение | ||
| 49 | Найти точное значение | соз(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | сек(60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найти точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | загар((5pi)/3) | ||
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 пи)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | угловой синус(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | КСК(45) | |
| 83 | Упростить | арктан(квадратный корень из 3) | |
| 84 | Найти точное значение | грех(135) | |
| 85 | Найти точное значение | грех(105) | |
| 86 | Найти точное значение | грех(150 градусов) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | загар((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | пи/4 | |
| 90 | Найти точное значение | грех(пи/2) | |
| 91 | Найти точное значение | сек(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | угловой синус(0) | |
| 95 | Найти точное значение | грех(120 градусов) | |
| 96 | Найти точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найти точное значение | соз(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразование градусов в радианы | 88 градусов |
4.
2 Тождества сложных углов | ТригонометрияВывод \(\cos\left(\alpha — \beta \right)\) (EMCGC)
Составные уголки
Дэнни готовится к тесту по тригонометрии и отвечает на следующий вопрос:
Вопрос:
Оцените следующее:
\(\cos\left(\text{180} ° — \text{120} ° \right)\)
Решение Дэнни:
\[\begin{массив}{rll} \cos \left( \text{180} ° — \text{120} ° \right) &= \cos \text{180} ° — \cos \text{120} ° & (\текст{строка} 1 )\\ &= -1 — \cos\left(\text{90} ° + \text{30} ° \right) & (\text{line } 2 ) \\ &= — 1 + \sin \text{30} ° & (\text{строка} 3 ) \\ &= -1 + \frac{1}{2} & (\text{line } 4 ) \\ &= -\frac{1}{2} & (\text{line } 5 ) \конец{массив}\]- Рассмотрите решение Дэнни и определите, почему оно неверно.
- Используйте калькулятор, чтобы проверить, что ответ Дэнни неверен.
{2} — 2bc \cdot \cos \hat{A}
\конец{выравнивание*}Используя формулу расстояния и правило косинуса, мы можем получить следующее тождество для составных углов:
\[\cos\left(\alpha -\beta \right) = \cos \alpha \cos\beta +\sin\alpha \sin\beta\]
Рассмотрим единичный круг \((r = 1)\) ниже. Две точки \(L\left(a;b\right)\) и \(K\left(x;y\right)\) равны показано на круге.
Мы можем выразить координаты \(L\) и \(K\) через углы \(\alpha\) и \(\beta\):
\начать{выравнивать*} \text{In } \triangle LOM, \quad \sin \beta &= \frac{b}{1} \\ \поэтому б &=\грех\бета \\ \cos\beta &=\frac{a}{1} \\ \поэтому &=\cos\бета \\ & \\ L &= \left(\cos\beta ;\sin\beta \right) \\ & \\ \text{Аналогично, } K &=\left(\cos\alpha ;\sin\alpha \right) \конец{выравнивание*} 9{2}\), у нас есть \начать{выравнивать*} 2-2 \cdot \cos\left(\alpha -\beta \right) & = 2-2\left(\cos\alpha\cos \beta +\sin\alpha \sin\beta \right) \\ 2 \cdot \cos\left(\alpha -\beta\right) & = 2\left(\cos\alpha\cos \beta +\sin\alpha \sin\beta \right) \\ \поэтому \cos\left(\alpha -\beta \right) & = \cos \alpha \cos\beta +\sin\alpha \sin\beta \end{align*}Рабочий пример 3: Вывод \(\cos \left(\alpha + \beta \right) = \cos \alpha \cos\beta — \грех\альфа \грех\бета\)
Выведите выражение для \(\cos\left(\alpha + \beta \right)\) через тригонометрические отношения \(\альфа\) и \(\бета\).
Используйте формулу составного угла для \(\cos \left(\alpha — \beta \right)\)
Мы используем формулу составного угла для \(\cos \left(\alpha — \beta \right)\) и манипулировать знаком \(\beta\) в \(\cos \left(\alpha + \beta \right)\), чтобы его можно было записать как разность двух углов:
\начать{выравнивать*} \cos (\alpha + \beta) & = \cos (\alpha — (-\beta)) \\ \text{И мы показали } \cos (\alpha — \beta )& = \cos \alpha \cos\beta +\sin\alpha \sin\beta \\ \поэтому \cos [\alpha — (- \beta )]& = \cos \alpha \cos(-\beta) +\sin\alpha \sin(-\beta) \\ \поэтому \cos (\alpha + \beta ) & = \cos \alpha \cos\beta — \sin\alpha \sin \beta \конец{выравнивание*}
Напишите окончательный ответ
\[\cos (\alpha + \beta ) = \cos \alpha \cos\beta — \sin\alpha \sin \beta\]Рабочий пример 4: Вывод \(\sin\left(\alpha — \beta\right)\) и \(\sin\left(\alpha + \бета\справа)\)
Выведите расширенные формулы для \(\sin\left(\alpha — \beta \right)\) и \(\sin\left(\alpha + \beta \right)\) через тригонометрические отношения \(\alpha\) и \(\beta\).
Используйте формулу составного угла и кофункции для расширения \(\sin\left(\alpha — \beta \справа)\)
Используя кофункции, мы знаем, что \(\sin \hat{A} = \cos ( \text{90} ° — \hat{A} )\), поэтому мы можем написать \(\sin\left(\alpha + \beta\right)\) через функцию косинуса:
\начать{выравнивать*} \sin ( \alpha — \beta ) & = \cos \left( \text{90} ° — ( \alpha — \beta ) \right) \\ & = \cos\left(\text{90} ° — \alpha + \beta\right) \\ & = \cos\left[ ( \text{90} ° — \alpha) + \beta \right] \end{align*}
Применить формулу составного угла:
\начать{выравнивать*} \cos (\alpha + \beta ) & = \cos \alpha \cos\beta — \sin\alpha \sin\beta \\ \поэтому \cos \left[ ( \text{90} ° — \alpha) + \beta \right] & = \cos ( \text{90} ° — \alpha) \cos\beta — \sin ( \text{90} ° — \alpha) \sin\beta \\ \поэтому \sin( \alpha — \beta) & = \sin \alpha \cos\beta — \cos \alpha \sin\beta \конец{выравнивание*}
Чтобы получить формулу для \(\sin ( \alpha + \beta )\), мы используем составную формулу для \(\sin ( \alpha — \beta )\) и манипулировать знаком \(\beta\):
\начать{выравнивать*} \sin (\alpha — \beta )& = \sin \alpha \cos\beta — \cos \alpha \sin\beta \\ \text{Мы можем написать } \sin ( \alpha + \beta ) & = \sin \left[ \alpha — (- \beta ) \right] \\ \поэтому \sin \left[ \alpha — (- \beta ) \right] &= \sin \alpha \cos (-\beta) — \cos \alpha \sin (-\бета) \\ \поэтому \sin ( \alpha + \beta ) & = \sin \alpha \cos\beta + \cos \alpha \sin\beta \конец{выравнивание*}
Напишите окончательные ответы
\[\sin (\alpha — \beta ) = \sin \alpha \cos\beta — \cos \alpha \sin\beta\] \[\sin (\alpha + \beta ) = \sin \alpha \cos\beta + \cos \alpha \sin\beta\]Формулы сложных углов
- \(\cos (\alpha — \beta ) = \cos \alpha \cos\beta + \sin \alpha \sin\beta\)
- \(\cos (\alpha + \beta ) = \cos \alpha \cos\beta — \sin \alpha \sin\beta\)
- \(\sin (\alpha — \beta ) = \sin \alpha \cos\beta — \cos \alpha \sin\beta\)
- \(\sin (\alpha + \beta ) = \sin\alpha \cos\beta + \cos\alpha \sin\beta\)
Примечание: мы можем использовать формулы составных углов, чтобы расширить и упростить составные углы в тригонометрии.
выражения (используя уравнения слева направо) или мы можем использовать расширенную форму для определения
тригонометрическое отношение составного угла (используя уравнения справа налево).Рабочий пример 5: формулы составного угла
Докажите, что \(\sin \text{75} °=\frac{\sqrt{2}\left(\sqrt{3}+1\right)}{4}\) без использования калькулятора.
Рассмотрим данное тождество
Мы знаем значения тригонометрических функций для специальных углов ( \(\text{30}\) °, \(\text{45}\) °, \(\text{60}\) ° и т. д.), и мы можем написать \(\text{75} ° = \text{30} ° + \text{45} °\).
Следовательно, мы можем использовать формулу составного угла для \(\sin (\alpha + \beta )\) для выражения \(\sin \text{75} °\) через известные значения тригонометрических функций.
Докажите, что левая часть тождества равна правой части
При доказательстве тождества не забывайте работать только с одной стороной тождества за раз.
\начать{выравнивать*} \text{LHS}& = \sin \text{75} ° \\ & = \sin\left( \text{45} °+ \text{30} °\right) \\ \sin \left( \text{45} °+ \text{30} °\right) & = \sin \left( \text{45} ° \right)\cos\left( \text{30} ° \right)+\cos\left( \text{45} ° \right)\sin\left( \text{30} ° \right) \\ & = \ frac {1} {\ sqrt {2}} \ cdot \ frac {\ sqrt {3}} {2} + \ frac {1} {\ sqrt {2}} \ cdot \ frac {1} {2 } \\ & = \ гидроразрыва {\ sqrt {3} + 1} {2 \ sqrt {2}} \\ & = \ frac {\ sqrt {3} + 1} {2 \ sqrt {2}} \ times \ frac {\ sqrt {2}} {\ sqrt {2}} \\ & = \ гидроразрыва {\ sqrt {2} \ влево (\ sqrt {3} + 1 \ вправо)} {4} \\ &= \текст{справа} \конец{выравнивание*}
Таким образом, мы показали, что \(\sin{75}°=\frac{\sqrt{2}\left(\sqrt{3}+1\right)}{4}\).
Рабочий пример 6: формулы составного угла
Определите значение следующего выражения без использования калькулятора:
\[\cos \text{65} ° \cos \text{35} ° + \cos \text{25} ° \cos \text{55} °\]
Используйте кофункции, чтобы упростить выражение
- Нам нужно изменить две тригонометрические функции с косинуса на синус, чтобы мы могли применить
Формула составного угла.
- Нам также нужно убедиться, что сумма (или разность) двух углов равна особому углу, поэтому что мы можем определить значение выражения без использования калькулятора. Обратите внимание, что \(\text{35} ° + \text{25} ° = \text{60} °\).
\begin{выравнивание*} &\cos \text{65} ° \cos \text{35} ° + \cos \text{25} ° \cos \text{55} ° \\ &= \cos ( \text{90} ° — \text{25} °) \cos \text{35} ° + \cos \text{25} ° \cos ( \текст{90} ° — \text{35} °) \\ &= \sin \text{25} ° \cos \text{35} ° + \cos \text{25} ° \sin \text{35} ° \конец{выравнивание*}
Применить формулу составного угла и использовать специальные углы для вычисления выражения
\начать{выравнивать*} & \sin \text{25} ° \cos \text{35} ° + \cos \text{25} ° \sin \text{35} ° \\ &= \sin ( \text{25} ° + \text{35} ° ) \\ &= \sin \text{60} ° \\ &= \ гидроразрыва {\ sqrt {3}} {2} \end{выравнивание*}Напишите окончательный ответ
\[\cos \text{65} ° \cos \text{35} ° + \cos \text{25} ° \cos \text{55} ° = \ гидроразрыва {\ sqrt {3}} {2} \]
Проверка ответов: Всегда полезно проверять ответы.
В вопросе говорилось, что мы можем
не используйте калькулятор, чтобы найти ответ, но мы можем использовать калькулятор, чтобы проверить правильность ответа:\начать{выравнивать*} \text{LHS}&= \cos \text{65} ° \cos \text{35} ° + \cos \text{25} ° \cos \text{55} ° = \текст{0,866} \ldots\\ \text{RHS}&= \frac{\sqrt{3}}{2} = \text{0,866} \ldots \\ \поэтому \text{левый} &= \text{правый} \конец{выравнивание*}
Формулы сложных углов
Учебник Упражнение 4.2
\(\tan \alpha- \tan \beta\)
\(\sin (\beta -\alpha)\)
\begin{align*} \sin (\beta -\alpha) &= \sin \beta \cos\alpha — \cos \beta \sin\alpha \\ &= \frac{-5}{13} \cdot \frac{-12}{13} — \frac{12}{13} \cdot \frac{-5}{13} \\ &= \frac{60}{169} + \frac{60}{169} \\ &= \фракция{120}{169} \end{выравнивание*}
\(\cos (\alpha + \beta)\)
\begin{align*} \cos (\alpha + \beta) &= \cos\alpha \cos \beta — \sin\alpha \sin \beta \\ &= \frac{-12}{13} \cdot \frac{12}{13} — \frac{-5}{13} \cdot \frac{-5}{13} \\ &= — \frac{144}{169} — \frac{25}{169} \\ &= — \фракция{169}{169} \\ &= -\текст{1} \end{align*}
\(\sin \text{105} °\)
\begin{align*} \sin \text{105} ° &= \sin ( \text{60} ° + \text{45} °) \\ &= \sin \text{60} ° \cos \text{45} ° + \cos \text{60} ° \sin \text{45} ° \\ &= \ frac {\ sqrt {3}} {2} \ cdot \ frac {1} {\ sqrt {2}} + \ frac {1} {2} \ cdot \ frac {1} {\ sqrt {2} } \\ &= \ гидроразрыва {\ sqrt {3} + 1} {2 \ sqrt {2}} \\ &= \ frac {\ sqrt {3} + 1} {2 \ sqrt {2}} \ times \ frac {\ sqrt {2}} {\ sqrt {2}} \\ &= \frac{\sqrt{2} \left( \sqrt{3} + 1 \right)}{4} \end{выравнивание*}
\(\cos \text{15} °\)
\begin{align*} \cos \text{15} ° &= \cos ( \text{60} ° — \text{45} °) \\ &= \cos \text{60} ° \cos \text{45} ° + \sin \text{60} ° \sin \text{45} ° \\ &= \ frac {1} {2} \ cdot \ frac {1} {\ sqrt {2}} + \ frac {\ sqrt {3}} {2} \ cdot \ frac {1} {\ sqrt {2} } \\ &= \frac{1 + \sqrt{3}}{2\sqrt{2}} \\ &= \frac{1 + \sqrt{3}}{2\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}} \\ &= \frac{\sqrt{2} \left( 1 + \sqrt{3} \right)}{4} \end{выравнивание*}
\(\sin \text{15} °\)
\begin{align*} \sin \text{15} ° &= \sin ( \text{60} ° — \text{45} °) \\ &= \sin \text{60} ° \cos \text{45} ° — \cos \text{60} ° \sin \text{45} ° \\ &= \frac{\sqrt{3}}{2} \cdot \frac{1}{\sqrt{2}} — \frac{1}{2} \cdot \frac{1}{\sqrt{2} } \\ &= \frac{\sqrt{3} — 1}{2\sqrt{2}} \\ &= \frac{\sqrt{3} — 1}{2\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}} \\ &= \frac{\sqrt{2} \left( \sqrt{3} — 1 \right)}{4} \end{выравнивание*}
\(\tan \text{15} °\)
\begin{align*} \tan \text{15} ° &= \frac{\sin \text{15} °}{\cos \text{15} °} \\ &= \frac{\sqrt{2} \left( \sqrt{3} — 1 \right)}{4} \div \frac{\sqrt{2} \left(\sqrt{3} + 1 \справа)}{4} \\ &= \frac{\sqrt{2} \left( \sqrt{3} — 1 \right)}{4} \times \frac{4}{\sqrt{2} \left( \sqrt{3} + 1 \верно)} \\ &= \frac{ \sqrt{3} — 1 }{ \sqrt{3} + 1 } \\ &= \ frac { \ sqrt {3} — 1 }{ \ sqrt {3} + 1 } \ times \ frac {\ sqrt {3} — 1} {\ sqrt {3} — 1} \\ &= \frac{ 3 — 2 \sqrt{3} + 1 }{ 2} \\ &= \frac{ 4 — 2 \sqrt{3} }{ 2} \\ &= 2 — \sqrt{3} \end{выравнивание*}
\(\cos \text{20} ° \cos \text{40} ° — \sin \text{20} ° \sin \text{40} °\)
\begin{выравнивание*} &\cos \text{20} ° \cos \text{40} ° — \sin \text{20} ° \sin \text{40} ° \\ &= \cos ( \text{20} ° + \text{40} °) \\ &= \cos\text{60} ° \\ &= \фракция{1}{2} \end{align*}
\(\sin \text{10} ° \cos \text{80} ° + \cos \text{10} ° \sin \text{80} °\)
\начать{выравнивать*} &\sin \text{10} ° \cos \text{80} ° + \cos \text{10} ° \sin \text{80} ° \\ &= \sin ( \text{10} ° + \text{80} °) \\ &= \sin\text{90} ° \\ &= \текст{1} \end{align*}
\(\cos ( \text{45} ° — x) \cos x — \sin ( \text{45} ° — x) \sin x\)
\begin{align* } &\cos ( \text{45} ° — x) \cos x — \sin ( \text{45} ° — x) \sin x \\ &= \cos (( \text{45} ° -x) + x ) \\ &= \cos\text{45} ° \\ &= \frac{1}{\sqrt{2}} \\ &= \ гидроразрыва {\ sqrt {2}} {2} \end{выравнивание*} 9{2} \text{15} ° \\ &= \cos \text{15} ° \cos \text{15} ° — \sin \text{15} ° \sin \text{15} ° \\ &= \cos ( \text{15} ° + \text{15} °) \\ &= \cos\text{30} ° \\ &= \ гидроразрыва {\ sqrt {3}} {2} \end{align*}
Докажите: \(\sin ( \text{60} ° — x) + \sin ( \text{60} ° + x) = \sqrt{3} \cos х\)
\begin{выравнивание*} \text{LHS}& = \sin ( \text{60} ° — x) + \sin ( \text{60} ° + x) \\ &= \sin \text{60} ° \cos x — \cos \text{60} ° \sin x + \sin \text{60} ° \cos x + \cos \text{60} ° \sin x \\ &= 2 \sin \text{60} ° \cos x \\ &= 2 \left( \frac{\sqrt{3}}{2} \right) \cos x \\ &= \sqrt{3} \cos x \\ &= \текст{справа} \end{выравнивание*}
Следовательно, вычислите \(\sin \text{15} ° + \sin \text{105} °\) без использования калькулятор.
Мы показали, что:
\начать{выравнивать*} \sin ( \text{60} ° — x) + \sin ( \text{60} ° + x) &= \sqrt{3} \cos x \\ \text{Если мы допустим } x &= \text{45} ° \\ \sin ( \text{60} ° — \text{45} °) + \sin ( \text{60} ° + \text{45} °) &= \sqrt{3} \cos \text{45} ° \\ \sin \text{15} ° + \sin \text{105} ° &= \sqrt{3} \cdot \frac{1}{\sqrt{2}} \\ &= \ frac {\ sqrt {3}} {\ sqrt {2}} \ cdot \ frac {\ sqrt {2}} {\ sqrt {2}} \\ &= \ гидроразрыва {\ sqrt {6}} {2} \конец{выравнивание*}
Воспользуйтесь калькулятором, чтобы проверить свой ответ.
Для \(x = \text{45} °\):
\начать{выравнивать*} \text{LHS}&= \sin \text{15} ° + \sin \text{105} ° \\ &= \text{1,2247} \ldots \\ \text{RHS} &= \text{1,2247} \ldots \\ \поэтому \text{левый} &= \text{правый} \конец{выравнивание*}
Упростите следующее без использования калькулятора:
\[\frac{\sin p \cos( \text{45} ° — p) + \cos p \sin( \text{45} ° — p)}{\cos p \cos( \text{60} ° — p) — \sin p \sin( \text{60} ° — p)}\]
\begin{выравнивание*} &\frac{\sin p \cos(\text{45} ° — p) + \cos p \sin(\text{45} ° — p)}{\cos p \cos( \text{60} ° — p) — \sin p \sin( \text{60} ° — p)} \\ &=\frac{\sin [p + ( \text{45} ° — p)]}{\cos[ p + ( \text{60} ° — p)]} \\ &= \ frac {\ sin \ text {45} ° {\ cos \ text {60} °} \\ &= \frac{1}{\sqrt{2}} \div \frac{1}{2} \\ &= \ frac {2} {\ sqrt {2}} \ times \ frac {\ sqrt {2}} {\ sqrt {2}} \\ &= \sqrt{2} \end{выравнивание*}
Докажите: \(\sin (A + B) — \sin (A -B) = 2 \cos A \sin B\)
\begin{align*} \text{LHS}& = \sin (A + B) — \sin (A -B) \\ &= \sin A \cos B + \cos A \sin B — [\sin A \cos B — \cos A \sin B] \\ &= \sin A \cos B + \cos A \sin B — \sin A \cos B + \cos A \sin B \\ &= 2 \cos A \sin B \\ &= \текст{справа} \end{align*}
Следовательно, вычислите значение \(\cos \text{75} ° \sin \text{15} °\) без с помощью калькулятора.
Мы показали, что:
\начать{выравнивать*} 2 \cos A \sin B &= \sin (A + B) — \sin (A -B) \\ \поэтому \cos A \sin B &= \frac{1}{2} \left( \sin (A + B) — \sin (A -B) \right) \\ \text{Пусть } A &= \text{75} ° \\ \text{И пусть } B &= \text{15} ° \\ \cos \text{75} ° \sin \text{75} ° &= \frac{1}{2} \left( \sin ( \text{75} ° + \text{15} °) — \sin ( \text{75} ° — \text{15} °) \right) \\ &= \frac{1}{2} \left( \sin \text{90} ° — \sin \text{60} ° \right) \\ &= \frac{1}{2} \left( 1 — \frac{\sqrt{3}}{2} \right) \\ &= \frac{2 — \sqrt{3}}{4} \конец{выравнивание*}
На приведенной ниже диаграмме точки \(P\) и \(Q\) лежат на окружности радиусом \(\text{2}\) единиц и центр в начале координат.
Докажите \(\cos (\theta — \beta) = \cos \theta \cos \beta + \sin \theta \sin \beta\).
{2} — 2bc \cdot \cos \hat{A}
\конец{выравнивание*}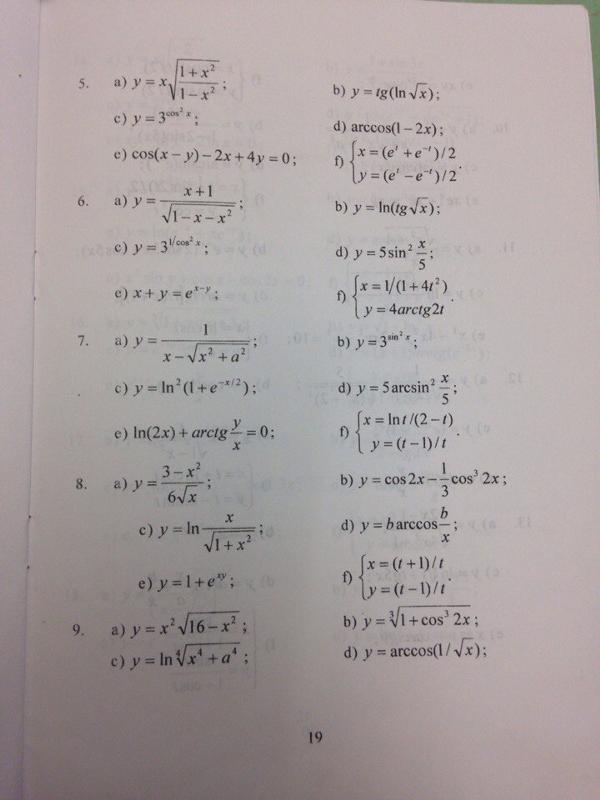
выражения (используя уравнения слева направо) или мы можем использовать расширенную форму для определения
тригонометрическое отношение составного угла (используя уравнения справа налево).
В вопросе говорилось, что мы можем
не используйте калькулятор, чтобы найти ответ, но мы можем использовать калькулятор, чтобы проверить правильность ответа:
