Лучший ответ по мнению автора
| |||||||||||||||||
Другие ответы
| ||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука
| Похожие вопросы |
В первом и втором букете 14 роз, а во втором и третем 19 роз. В каком букете больше роз в первом или
В каком букете больше роз в первом или
Длина сухопутной границы России с Китаем,Монголией и Казахстаном составляет 15293 километра.Найдите длину границы России с каждым из этих государств,если длина границы с Китаем и Монголией равна 7649
токарь с учеником изготовил 142 детали.токарь работал 12 часов изготовил 15 деталий в час.Сколько деталий изготовил ученик в час если работал 6 часов?
помогите решить задачу по геометрии:медиана bd треугольника abc разбивает его на два треугольника периметры которых равны 32 см и 36 см.найдите периметр треугольника ABC если BD=10см.
написать сочинение рассуждение ,раскрывая смысл высказывания известного русского лингвиста Валентины Даниловны Черняк:»в сложном предложении отражаются отношения ,которые говорящий усматривает
Пользуйтесь нашим приложением
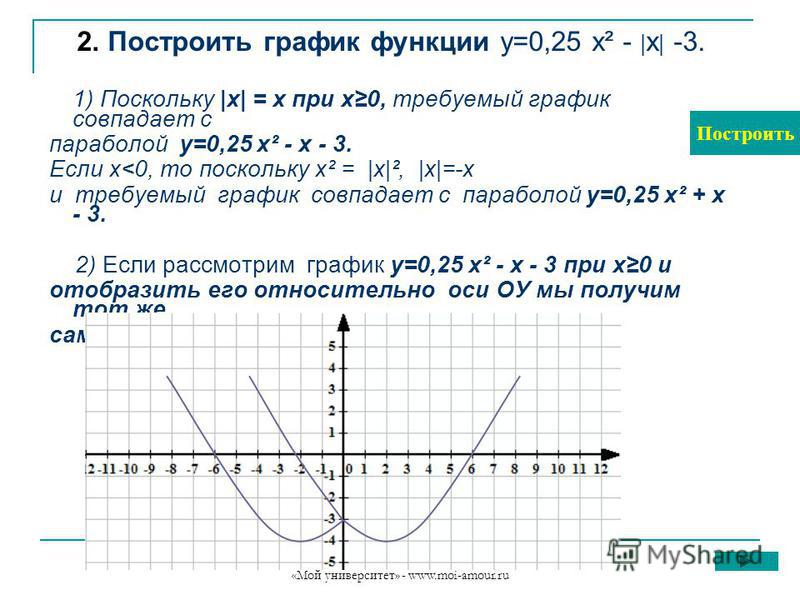
Как построить график функции y 3. Постройте график функции y=
Построение графиков функций, содержащих модули, обычно вызывает немалые затруднения у школьников. Однако, все не так плохо. Достаточно запомнить несколько алгоритмов решения таких задач, и вы сможете без труда построить график даже самой на вид сложной функции. Давайте разберемся, что же это за алгоритмы.
Однако, все не так плохо. Достаточно запомнить несколько алгоритмов решения таких задач, и вы сможете без труда построить график даже самой на вид сложной функции. Давайте разберемся, что же это за алгоритмы.
1. Построение графика функции y = |f(x)|
Заметим, что множество значений функций y = |f(x)| : y ≥ 0. Таким образом, графики таких функций всегда расположены полностью в верхней полуплоскости.
Построение графика функции y = |f(x)| состоит из следующих простых четырех этапов.
1) Построить аккуратно и внимательно график функции y = f(x).
2) Оставить без изменения все точки графика, которые находятся выше оси 0x или на ней.
3) Часть графика, которая лежит ниже оси 0x, отобразить симметрично относительно оси 0x.
Пример 1. Изобразить график функции y = |x 2 – 4x + 3|
1) Строим график функции y = x 2 – 4x + 3. Очевидно, что график данной функции – парабола. Найдем координаты всех точек пересечения параболы с осями координат и координаты вершины параболы.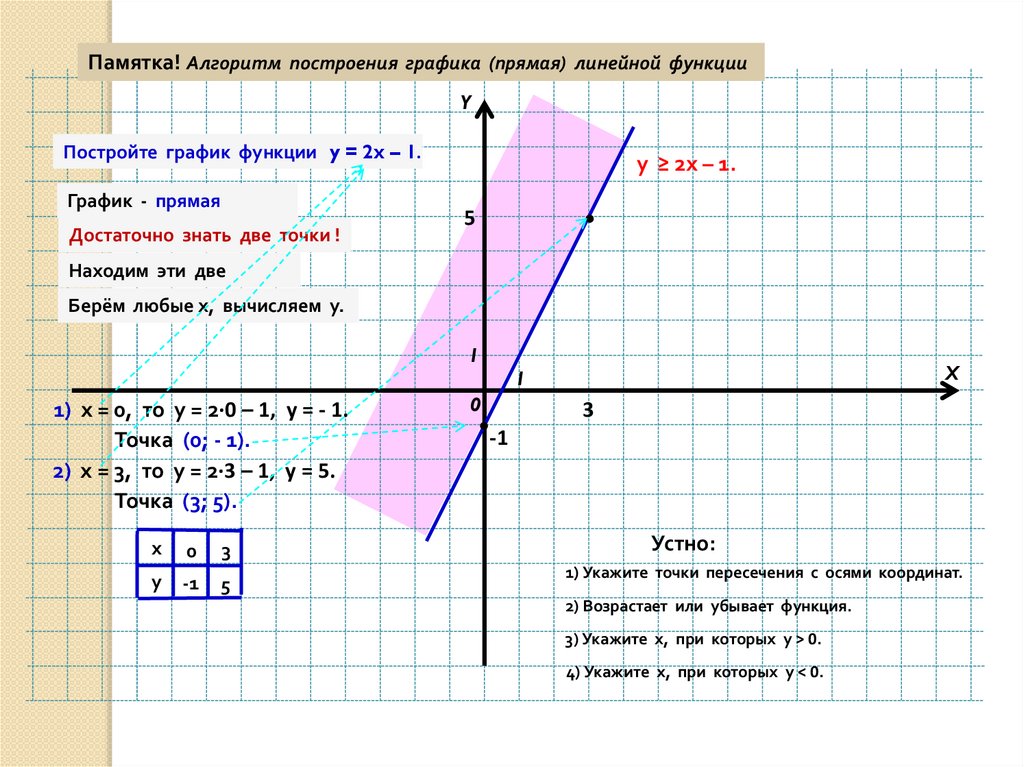
x 2 – 4x + 3 = 0.
x 1 = 3, x 2 = 1.
Следовательно, парабола пересекает ось 0x в точках (3, 0) и (1, 0).
y = 0 2 – 4 · 0 + 3 = 3.
Следовательно, парабола пересекает ось 0y в точке (0, 3).
Координаты вершины параболы:
x в = -(-4/2) = 2, y в = 2 2 – 4 · 2 + 3 = -1.
Следовательно, точка (2, -1) является вершиной данной параболы.
Рисуем параболу, используя полученные данные (рис. 1)
2) Часть графика, лежащую ниже оси 0x, отображаем симметрично относительно оси 0x.
3) Получаем график исходной функции (рис. 2 , изображен пунктиром).
2. Построение графика функции y = f(|x|)
Заметим, что функции вида y = f(|x|) являются четными:
y(-x) = f(|-x|) = f(|x|) = y(x). Значит, графики таких функций симметричны относительно оси 0y.
Построение графика функции y = f(|x|) состоит из следующей несложной цепочки действий.
1) Построить график функции y = f(x).
2) Оставить ту часть графика, для которой x ≥ 0, то есть часть графика, расположенную в правой полуплоскости.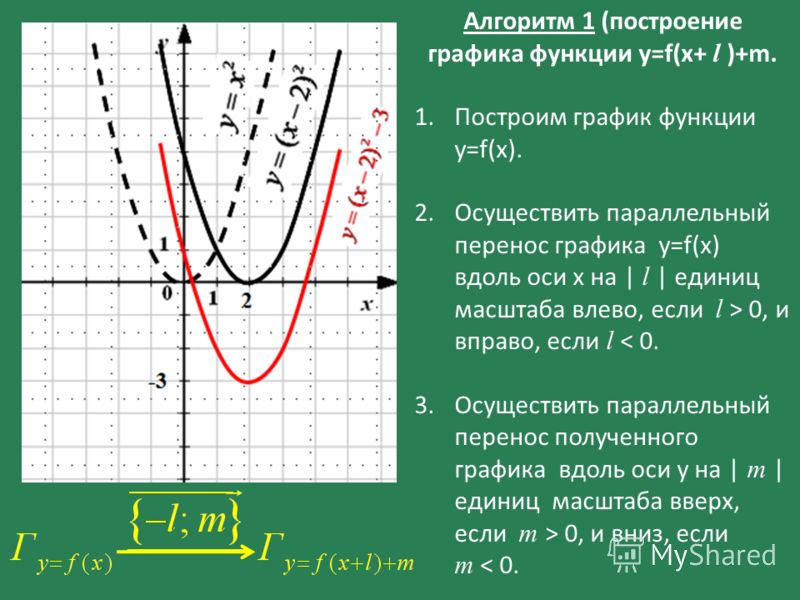
3) Отобразить указанную в пункте (2) часть графика симметрично оси 0y.
4) В качестве окончательного графика выделить объединение кривых, полученных в пунктах (2) и (3).
Пример 2. Изобразить график функции y = x 2 – 4 · |x| + 3
Так как x 2 = |x| 2 , то исходную функцию можно переписать в следующем виде: y = |x| 2 – 4 · |x| + 3. А теперь можем применять предложенный выше алгоритм.
1) Строим аккуратно и внимательно график функции y = x 2 – 4 · x + 3 (см. также рис. 1 ).
2) Оставляем ту часть графика, для которой x ≥ 0, то есть часть графика, расположенную в правой полуплоскости.
3) Отображаем правую часть графика симметрично оси 0y.
(рис. 3) .
Пример 3. Изобразить график функции y = log 2 |x|
Применяем схему, данную выше.
1) Строим график функции y = log 2 x (рис. 4) .
3. Построение графика функции y = |f(|x|)|
Заметим, что функции вида y = |f(|x|)| тоже являются четными.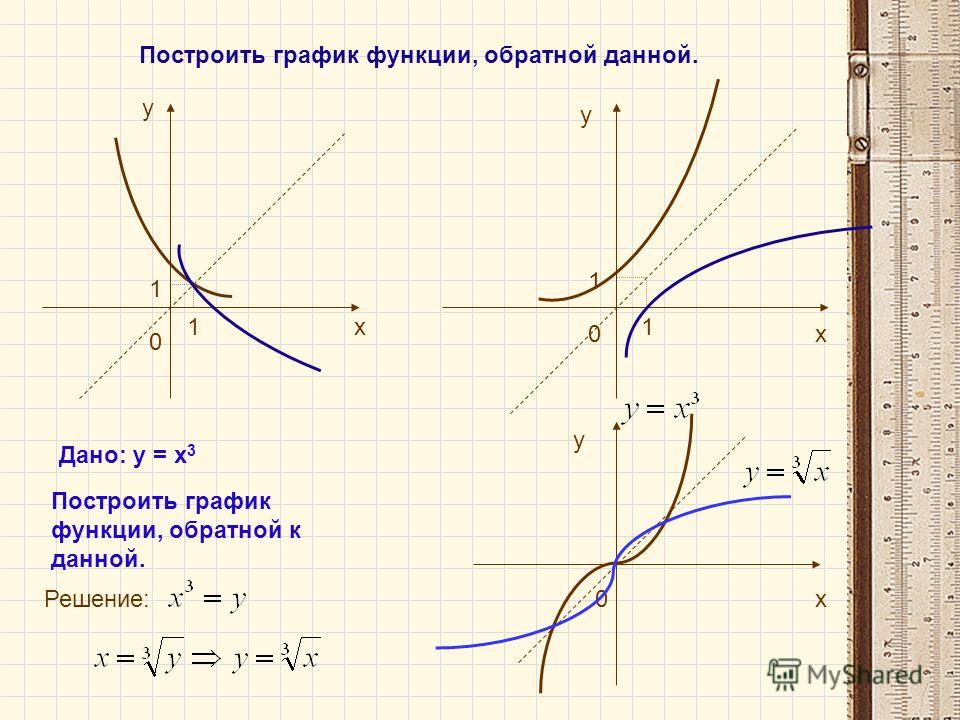 Действительно, y(-x) = y = |f(|-x|)| = y = |f(|x|)| = y(x), и поэтому, их графики симметричны относительно оси 0y. Множество значений таких функций: y ≥ 0. Значит, графики таких функций расположены полностью в верхней полуплоскости.
Действительно, y(-x) = y = |f(|-x|)| = y = |f(|x|)| = y(x), и поэтому, их графики симметричны относительно оси 0y. Множество значений таких функций: y ≥ 0. Значит, графики таких функций расположены полностью в верхней полуплоскости.
Чтобы построить график функции y = |f(|x|)|, необходимо:
1) Построить аккуратно график функции y = f(|x|).
2) Оставить без изменений ту часть графика, которая находится выше оси 0x или на ней.
3) Часть графика, расположенную ниже оси 0x, отобразить симметрично относительно оси 0x.
4) В качестве окончательного графика выделить объединение кривых, полученных в пунктах (2) и (3).
Пример 4. Изобразить график функции y = |-x 2 + 2|x| – 1|.
1) Заметим, что x 2 = |x| 2 . Значит, вместо исходной функции y = -x 2 + 2|x| – 1
можно использовать функцию y = -|x| 2 + 2|x| – 1, так как их графики совпадают.
Строим график y = -|x| 2 + 2|x| – 1. Для этого применяем алгоритм 2.
a) Строим график функции y = -x 2 + 2x – 1 (рис. 6) .
6) .
b) Оставляем ту часть графика, которая расположена в правой полуплоскости.
c) Отображаем полученную часть графика симметрично оси 0y.
d) Полученный график изображен на рисунке пунктиром (рис. 7) .
2) Выше оси 0х точек нет, точки на оси 0х оставляем без изменения.
3) Часть графика, расположенную ниже оси 0x, отображаем симметрично относительно 0x.
4) Полученный график изображен на рисунке пунктиром (рис. 8) .
Пример 5. Построить график функции y = |(2|x| – 4) / (|x| + 3)|
1) Сначала необходимо построить график функции y = (2|x| – 4) / (|x| + 3). Для этого возвращаемся к алгоритму 2.
a) Аккуратно строим график функции y = (2x – 4) / (x + 3) (рис. 9) .
Заметим, что данная функция является дробно-линейной и ее график есть гипербола. Для построения кривой сначала необходимо найти асимптоты графика. Горизонтальная – y = 2/1 (отношение коэффициентов при x в числителе и знаменателе дроби), вертикальная – x = -3.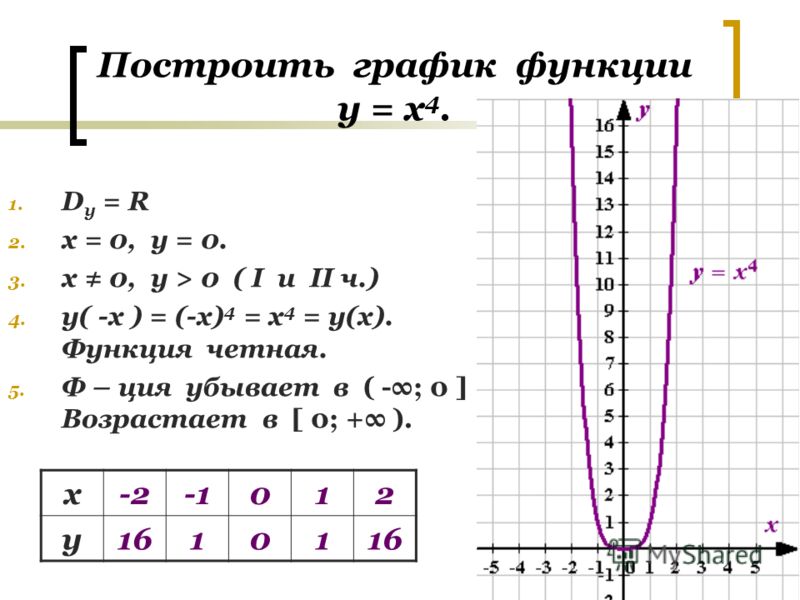
2) Ту часть графика, которая находится выше оси 0x или на ней, оставим без изменений.
3) Часть графика, расположенную ниже оси 0x, отобразим симметрично относительно 0x.
4) Окончательный график изображен на рисунке (рис. 11) .
сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Составим таблицу значений функции
Мы видим, что при (куб положительного числа положителен), а при (куб отрицательного числа отрицателен). Следовательно, график расположится на координатной плоскости в I и III четвертях. Заменим значение аргумента х противоположным значением тогда и функция примет противоположное значение; так как если , то
Значит, каждой точке графика соответствует точка того же графика, расположенная симметрично относительно начала координат.
Таким образом, начало координат является центром симметрии графика.
График функции изображён на чертеже 81. Эта линия называется кубической параболой.
В I четверти кубическая парабола (при ) «круто» поднимается
вверх (значения у «быстро» возрастают при возрастания х. см. таблицу), при малых значениях х линия «тесно» подходит к оси абсцисс (при «малых» значение у «весьма мало», см. таблицу). Левая часть кубической параболы (в III четверти) симметрична правой относительно начала координат.
Аккуратно вычерченный график может служить средством приближённого возведения чисел в куб. Так, например, положив найдём по графику
Для приближённого вычисления кубов составлены специальные таблицы.
Такая таблица имеется и в пособии В. М. Брадиса «Четырёхзначные математические таблицы».
Эта таблица содержит приближённые значения кубов чисел от 1 до 10, округлённые до 4-х значащих цифр.
Устройство таблицы кубов и правила пользования ею такие же, как и таблицы квадратов. Однако при увеличении (или уменьшении) числа в 10, 100 и т. д. раз его куб увеличивается (или уменьшается) в 1000, 1000 000 и т. д. раз. Значит, при пользовании таблицей кубов надо иметь в виду следующее правило переноса запятой:
Если в числе перенести запятую на несколько цифр, то в кубе этого числа надо перенести запятую в ту же сторону на утроенное количество цифр.
Поясним сказанное примерами:
1) Вычислить 2,2353. По таблице находим: ; прибавляем к последней цифре поправку 8 на последний знак:
2) Вычислить . Так как то находим
По таблице найдем перенеся запятую, получим
Приближённые формулы. Если в тождестве
число а мало по сравнению с единицей, то, отбросив члены с получим приближённые формулы:
По этим формулам легко найти приближённые кубы чисел, близких к единице, например: точный куб: 1,061208;
Разберем как строить график с модулем.
Найдем точки при переходе которых знак модулей меняется.
Каждое выражения, которое под модулем приравниваем к 0. У нас их два x-3 и x+3.
x-3=0 и x+3=0
x=3 и x=-3
У нас числовая прямая разделится на три интервала (-∞;-3)U(-3;3)U(3;+∞). На каждом интервале нужно определить знак под модульных выражений.
1. Это сделать очень просто, рассмотрим первый интервал (-∞;-3). Возьмем с этого отрезка любое значение, например, -4 и подставим в каждое под модульное уравнение вместо значения х.
х=-4
x-3=-4-3=-7 и x+3=-4+3=-1
У обоих выражений знаки отрицательный, значит перед знаком модуля в уравнении ставим минус, а вместо знака модуля ставим скобки и получим искомое уравнение на интервале (-∞;-3).
y=— (x-3)-(— (x+3))=-х+3+х+3=6
На интервале (-∞;-3) получился график линейной функции (прямой) у=6
2. Рассмотрим второй интервал (-3;3). Найдем как будет выглядеть уравнение графика на этом отрезке. Возьмем любое число от -3 до 3, например, 0. Подставим вместо значения х значение 0.
х=0
x-3=0-3=-3 и x+3=0+3=3
У первого выражения x-3 знак отрицательный получился, а у второго выражения x+3 положительный. Следовательно, перед выражением x-3 запишем знак минус, а перед вторым выражением знак плюс.
y=— (x-3)-(+ (x+3))=-х+3-х-3=-2x
На интервале (-3;3) получился график линейной функции (прямой) у=-2х
3.Рассмотрим третий интервал (3;+∞). Возьмем с этого отрезка любое значение, например 5, и подставим в каждое под модульное уравнение вместо значения х.
х=5
x-3=5-3=2 и x+3=5+3=8
У обоих выражений знаки получились положительными, значит перед знаком модуля в уравнении ставим плюс, а вместо знака модуля ставим скобки и получим искомое уравнение на интервале (3;+∞).
y=+ (x-3)-(+ (x+3))=х-3-х-3=-6
На интервале (3;+∞) получился график линейной функции (прямой) у=-6
4. Теперь подведем итог.Постоим график y=|x-3|-|x+3|.
На интервале (-∞;-3) строим график линейной функции (прямой) у=6.
На интервале (-3;3) строим график линейной функции (прямой) у=-2х.
Чтобы построить график у=-2х подберем несколько точек.
x=-3 y=-2*(-3)=6 получилась точка (-3;6)
x=0 y=-2*0=0 получилась точка (0;0)
x=3 y=-2*(3)=-6 получилась точка (3;-6)
На интервале (3;+∞) строим график линейной функции (прямой) у=-6.
5. Теперь проанализируем результат и ответим на вопрос задания найдем значение k, при которых прямая y=kx имеет с графиком y=|x-3|-|x+3| данной функции ровно одну общую точку.
Прямая y=kx при любом значении k всегда будет проходить через точку (0;0). Поэтому мы можем изменить только наклон данной прямой y=kx, а за наклон у нас отвечает коэффициент k.
Если k будет любое положительное число, то будет одно пересечение прямой y=kx с графиком y=|x-3|-|x+3|. Этот вариант нам подходит.
Если k будет принимать значение (-2;0), то пересечений прямой y=kx с графиком y=|x-3|-|x+3| будет три.Этот вариант нам не подходит.
Если k=-2, решений будет множество [-2;2], потому что прямая y=kx будет совпадать с графиком y=|x-3|-|x+3| на данном участке. Этот вариант нам не подходит.
Если k будет меньше -2, то прямая y=kx с графиком y=|x-3|-|x+3| будет иметь одно пересечение.Этот вариант нам подходит.
Если k=0, то пересечений прямой y=kx с графиком y=|x-3|-|x+3| также будет одно.Этот вариант нам подходит.
Ответ: при k принадлежащей интервалу (-∞;-2)U и возрастает на промежутке }
Показательная функция
- Главная
- Справочник
- Исследование функций
- Показательная функция
Основные сведения
Показательной функцией назыввается функция вида y = ax, где a > 0 и a ≠ 1.
График функции имеет следующий вид:
Рассмотрим свойства функции:
- Областью определения функции является множество всех действительных чисел R.
- Множеством значений функции являются все положительные числа, т. е. промежуток E(y): (0; +∞).
- Наименьшего и наибольшего значений функция не имеет.
- Функция не является ни нечетной, ни четной. Имеет общий вид.
- Функция непериодическая.
- График функции пересекает координатную ось Oy в точке (0; 1).
- Функция не имеет нулей.
- при a > 1 функция возрастает на всей числовой прямой; при 0 < a < 1 функция убывает на множестве R.
- Функция принимает положительные значения на всей области определения.
Примеры решения задач
Задача 1.
В одной координатной плоскости построить графики функций:
- y=2x
- y=3x
- y=5x
- y=10x
Решение.
Для начала построим график функции y=2x. Для этого найдем значения функции при x = 0, ±1, ±2, ±3.
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| y(x) | 1 | 2 | 4 | 8 |
Отметим полученные точки на координатной плоскости, соединив их плавной линией.
Большему значению аргумента х соответствует и большее значение функции у. Функция y = 2x возрастает на всей области определения D(y)=R, так как основание функции 2 > 1.
Подобным образом построим графики остальных функций.
Переменная х может принимать любое значение (D (y)=R), при этом значение у всегда будет больше нуля (E (y)=R+).
Графики всех данных функций пересекают ось Оу в точке (0; 1), так как любое число в нулевой степени равно единице; с осью Ох графики не пересекаются, так как положительное число в любой степени не может быть равным нулю.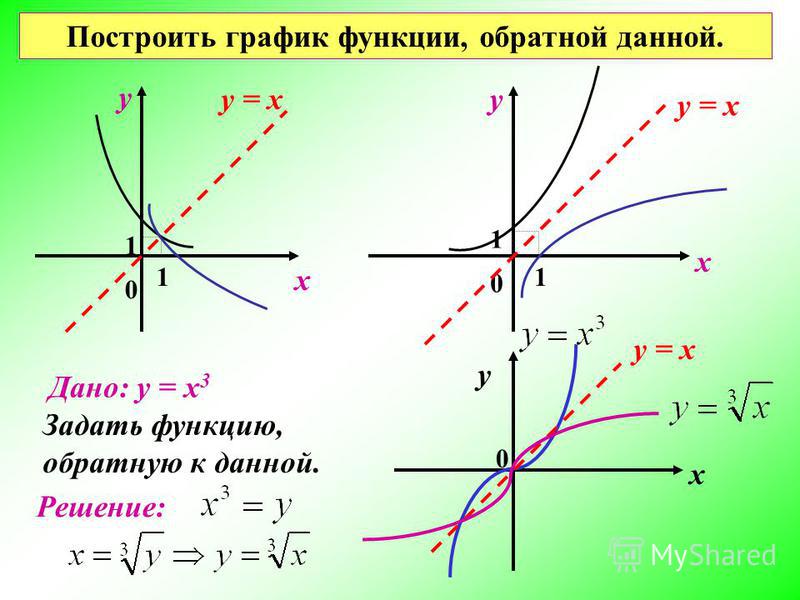 Чем больше основание a (если a>1) показательной функции y = ax, тем ближе расположена кривая к оси Оу.
Чем больше основание a (если a>1) показательной функции y = ax, тем ближе расположена кривая к оси Оу.
Все данные функции являются возрастающими, так как большему значению аргумента соответствует и большее значение функции.
Задача 2.
В одной координатной плоскости построить графики функций:
Решение.
Для начала построим график функции . Для этого найдем значения функции при x = 0, ±1, ±2, ±3.
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| y(x) | 8 | 4 | 2 | 1 |
Отметим полученные точки на координатной плоскости, соединив их плавной линией.
Большему значению аргумента х соответствует меньшее значение функции y.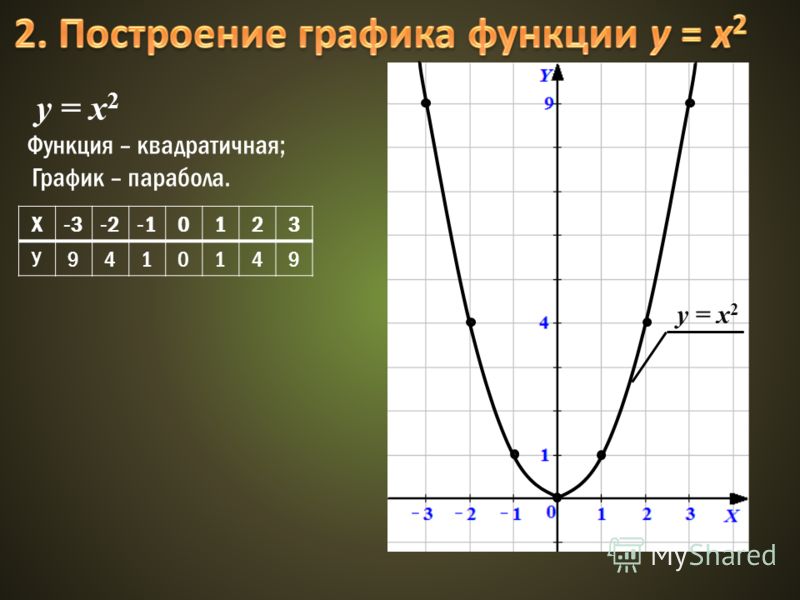 Функция убывает на всей своей области определения: D(y)=R, так как основание функции 0 < < 1.
Функция убывает на всей своей области определения: D(y)=R, так как основание функции 0 < < 1.
Подобным образом построим графики остальных функций.
Переменная х может принимать любое значение: D(y)=R, при этом область значений функции: E(y)=R+.
Графики всех данных функций пересекают ось Оу в точке (0; 1), так как любое число в нулевой степени равно единице; с осью Ох графики не пересекаются, так как положительное число в любой степени не может быть равным нулю.
Чем меньше основание а (при 0 < a < 1) показательной функции y = ax, тем ближе расположена кривая к оси Оу.
Все эти функции являются убывающими, так как большему значению аргумента соответствует меньшее значение функции.
Задание 3.
Найти область значений функции:
- y = -2x
- y = +1
- y = 3x+1 — 5
Решение.
1. y = -2x
Область значений показательной функции y = 2x – все положительные числа, т.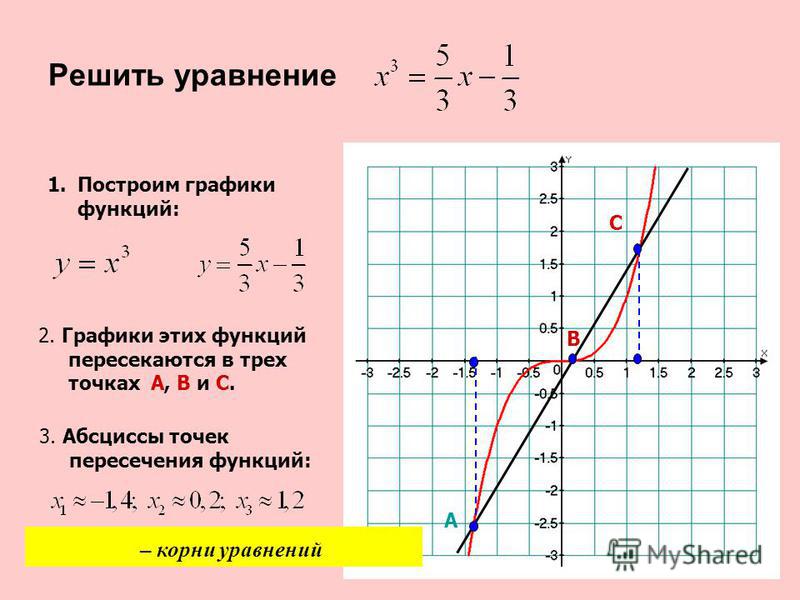 е. 0 < 2x < +∞. Значит, умножая каждую часть двойного неравенства на (-1), получаем: -∞ < 2x < 0.
е. 0 < 2x < +∞. Значит, умножая каждую часть двойного неравенства на (-1), получаем: -∞ < 2x < 0.
Ответ: E(y): (-∞; 0).
2. y = +1
0 < < +∞. Тогда, прибавляя ко всем частям двойного неравенства число 1, получаем:
0 + 1 < +1 < +∞ + 1
1 < +1 < +∞
Ответ: E(y): (1; +∞).
3. y = 3x+1 — 5.
Запишем функцию ввиде: y = 3·3x — 5, тогда:
0 < 3x < +∞
умножаем все части двойного неравенства на 3:
0·3 < 3x·3 < (+∞)·3
0 < 3x·3 < +∞
из всех частей двойного неравенства вычитаем 5:
0 — 5 < 3x·3 — 5 < +∞ — 5
-5 < 3x·3 — 5 < +∞
Ответ: E(y): (-5; +∞).
- < Назад
| «Ссылки. Встроенные функции MS Excel». Выполнив задания этой темы, вы научитесь: Выполнять операции по копированию, перемещению и автозаполнению отдельных ячеек и диапазонов.  Различать виды ссылок (абсолютная, относительная, смешанная) Определять вид ссылки, необходимой для использования в расчетах. Использовать в расчетах встроенные математические и статистические функции Excel. MS Excel содержит 320 встроенных функций. Простейший способ получения полной информации о любой из них заключается в использовании меню Справка. Для удобства функции в Excel разбиты по категориям (математические, финансовые, статистические и т.д.). Обращение к каждой функции состоит из двух частей: имени функции и аргументов в круглых скобках. Таблица. Встроенные функции Excel
* Записывается без аргументов. Таблица. Виды ссылок
Задание. 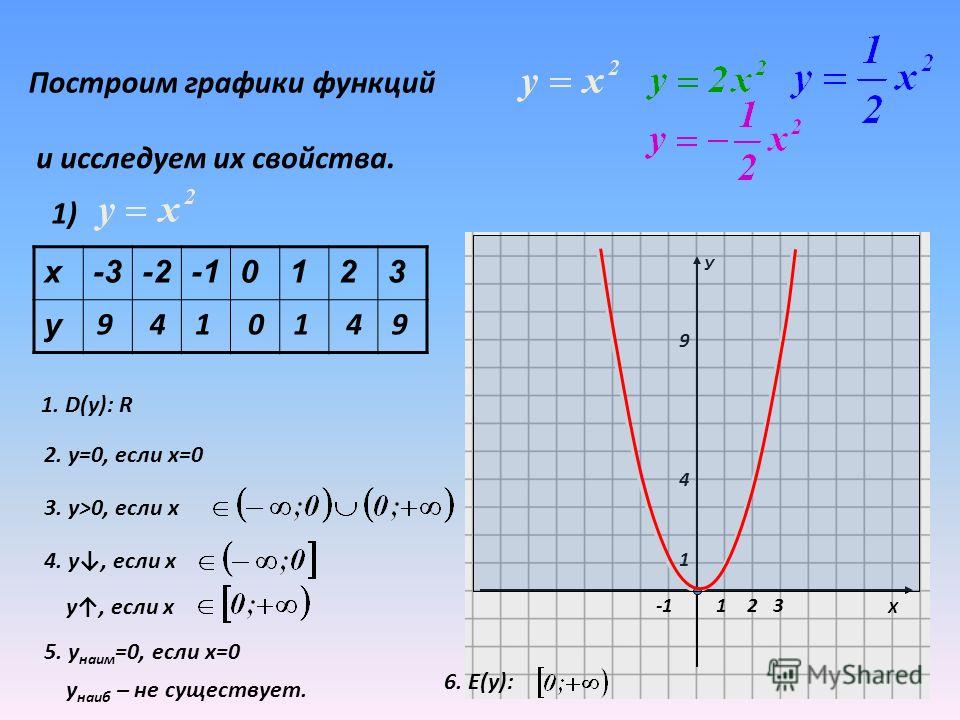 1. Заданы стоимость 1 кВт./ч. электроэнергии и показания счетчика за предыдущий и текущий месяцы. Необходимо вычислить расход электроэнергии за прошедший период и стоимость израсходованной электроэнергии. Технология работы: 1. Выровняйте текст в ячейках. Выделите ячейки А3:Е3. Главная — Формат –Формат ячейки – Выравнивание: по горизонтали – по центру, по вертикали – по центру, отображение – переносить по словам. 2. В ячейку А4 введите: Кв. 1, в ячейку А5 введите: Кв. 2. Выделите ячейки А4:А5 и с помощью маркера автозаполнения заполните нумерацию квартир по 7 включительно. 5. Заполните ячейки B4:C10 по рисунку. 6. В ячейку D4 введите формулу для нахождения расхода эл/энергии. И заполните строки ниже с помощью маркера автозаполнения. 7. В ячейку E4 введите формулу для нахождения стоимости эл/энергии =D4*$B$1. И заполните строки ниже с помощью маркера автозаполнения. Обратите внимание!
8. В ячейке А11 введите текст «Статистические данные» выделите ячейки A11:B11 и щелкните на панели инструментов кнопку «Объединить и поместить в центре». 9. В ячейках A12:A15 введите текст, указанный на рисунке. 10. Щелкнуть мышью по ячейке B12 и ввести математическую функцию СУММ, для этого необходимо щелкнуть в строке формулпо знаку fx и выбрать функцию, а также подтвердить диапазон ячеек. 11. Аналогично функции задаются и в ячейках B13:B15. 12. Расчеты вы выполняли на Листе 1, переименуйте его в Электроэнергию. Самостоятельная работа Упражнение: Рассчитайте свой возраст, начиная с текущего года и по 2030 год, используя маркер автозаполнения. Год вашего рождения является абсолютной ссылкой. Расчеты выполняйте на Листе 2. Лист 2 переименуйте в Возраст.
Практическая работа «Создание диаграмм средствами MS Excel» Выполнив задания этой темы, вы научитесь: Выполнять операции по созданию диаграмм на основе введенных в таблицу данных; Редактировать данные диаграммы, ее тип и оформление. Что собой представляет диаграмма. Диаграмма предназначена для графического представления данных. Для отображения числовых данных, введенных в ячейки таблицы, используются линии, полосы, столбцы, сектора и другие визуальные элементы. Вид диаграммы зависит от её типа. Все диаграммы, за исключением круговой, имеют две оси: горизонтальную – ось категорий и вертикальную – ось значений. При создании объёмных диаграмм добавляется третья ось – ось рядов. Часто диаграмма содержит такие элементы, как сетка, заголовки и легенда. Линии сетки являются продолжением делений, находящихся на осях, заголовки используются для пояснений отдельных элементов диаграммы и характера представленных на ней данных, легенда помогает идентифицировать ряды данных, представленные на диаграмме. Добавлять диаграммы можно двумя способами: внедрять их в текущий рабочий лист и добавлять отдельный лист диаграммы. В том случае, если интерес представляет сама диаграмма, то она размещается на отдельном листе.
После того, как диаграмма будет сформирована, в неё можно будет внести изменения. Прежде чем выполнять какие либо действия с элементами диаграммы, выделите их, щёлкнув по ним левой кнопкой мыши. После этого вызовите контекстное меню с помощью правой кнопки мыши или воспользуйтесь соответствующими кнопкамипанели инструментов Диаграмма. жүктеу/скачать 233,5 Kb. Достарыңызбен бөлісу: |
1.1: График линейного уравнения
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 37805
- Рупиндер Секон и Роберта Блум
- Колледж Де Анза
Цели обучения
В этом разделе вы научитесь:
- Рисовать линию, зная ее уравнение
- Нарисуйте линию, если вам дано ее уравнение в параметрической форме
- Начертите и найдите уравнения вертикальных и горизонтальных линий
Построение графика из этого уравнения
Уравнения, графики которых представляют собой прямые линии, называются линейными уравнениями. Ниже приведены некоторые примеры линейных уравнений:
Ниже приведены некоторые примеры линейных уравнений:
\(2 x-3 y=6, \quad 3 x=4 y-7, \quad y=2 x-5, \quad 2 y=3, \quad \text { и } \quad x-2 =0\)
Линия полностью определяется двумя точками. Следовательно, чтобы построить линейное уравнение, нам нужно найти координаты двух точек. Этого можно добиться, выбрав произвольное значение x или y, а затем найдя другую переменную.
Пример \(\PageIndex{1}\)
Нарисуйте прямую: \(y = 3x + 2\)
Решение
Нам нужно найти координаты хотя бы двух точек. Мы произвольно выбираем х = — 1, х = 0 и х = 1.
- Если x = -1, то y = 3(-1) + 2 или -1. Следовательно, (-1, -1) — точка на этой прямой.
- Если x = 0, то y = 3(0) + 2 или y = 2. Отсюда точка (0, 2).
- Если x = 1, то y = 5, и мы получаем точку (1, 5).
Ниже приведены результаты и график.
| х | -1 | 0 | 1 |
| у | -1 | 2 | 5 |
Пример \(\PageIndex{2}\)
Нарисуйте линию: \(2x + y = 4\)
Решение
Опять же, нам нужно найти координаты не менее двух точек .
Мы произвольно выбираем x = -1, x = 0 и y = 2.
- Если x = -1, то 2(-1) + y = 4, что дает y = 6. Следовательно, (-1 , 6) — точка на этой прямой.
- Если x = 0, то 2(0) + y = 4, что дает y = 4. Отсюда точка (0, 4).
- Если y = 2, то 2x + 2 = 4, что дает x = 1 и дает точку (1, 2).
В таблице ниже показаны точки, а линия представлена в виде графика.
| х | -1 | 0 | 1 |
| у | 6 | 4 | 2 |
Точки пересечения
Точки, в которых линия пересекает оси координат, называются перехватывает .
При построении линии путем нанесения двух точек часто предпочтительнее использовать точки пересечения, поскольку их легко найти.
- Чтобы найти значение абсциссы, положим y = 0
- Чтобы найти значение точки пересечения по оси y, положим x = 0.

Пример \(\PageIndex{3}\)
Найдите точки пересечения линии: \(2x — 3y = 6\) и график.
Решение
Чтобы найти точку пересечения по оси x, пусть y = 0 в уравнении и найдите x.
\[\begin{align*} 2x — 3(0) &= 6 \\[4pt] 2x — 0 &= 6 \\[4pt] 2x &= 6 \\[4pt] x &= 3 \end {align*} \nonumber \]
Таким образом, точка пересечения с x является точкой (3,0).
Чтобы найти точку пересечения с осью y, пусть x = 0 в уравнении и найдите y.
\[\begin{align*} 2(0) — 3y &= 6 \\[4pt] 0 — 3y &= 6 \\[4pt] -3y &= 6 \\[4pt] y &= -2 \end{align*} \nonumber \]
Следовательно, точкой пересечения с осью y является точка (0, -2).
Чтобы построить линию, нанесите точки пересечения по осям x (3,0) и y (0, -2) и используйте их для построения линии.
Построение графика линии из ее уравнения в параметрической форме
В высшей математике уравнения линий иногда записываются в параметрической форме. Например, \(x = 3 + 2t\), \(y = 1 + t\). Буква \(t\) называется параметром или фиктивной переменной.
Например, \(x = 3 + 2t\), \(y = 1 + t\). Буква \(t\) называется параметром или фиктивной переменной.
Параметрические линии можно изобразить в виде графика, найдя значения x и y, заменив t числовыми значениями. Постройте точки, используя их координаты (x, y), и используйте точки, чтобы нарисовать линию.
Пример \(\PageIndex{4}\)
Нарисуйте линию, заданную параметрическими уравнениями: \(x = 3 + 2t\), \(y = 1 + t\)
Решение
Пусть t = 0, 1 и 2; для каждого значения t найти соответствующие значения для x и y.
Результаты приведены в таблице ниже.
| т | х | и | Точка на линии |
|---|---|---|---|
| 0 | 3 | 1 | (3, 1) |
| 1 | 5 | 2 | (5, 2) |
| 2 | 7 | 3 | (7, 3) |
Горизонтальные и вертикальные линии
Когда уравнение линии имеет только одну переменную, результирующий график представляет собой горизонтальную или вертикальную линию.
- График прямой \(x = a\), где \(a\) — константа, представляет собой вертикальную линию, проходящую через точку \((a, 0)\). Каждая точка на этой линии имеет координату x, равную a, независимо от координаты y.
- График прямой \(y = b\), где \(b\) — константа, представляет собой горизонтальную прямую, проходящую через точку \((0, b)\). Каждая точка на этой прямой имеет координату y, равную b, независимо от координаты x.
Пример \(\PageIndex{5}\)
Нарисуйте линии: x = -2 и y = 3.
Решение
График линии x = -2 представляет собой вертикальную линию, имеющую координату x -2 независимо от значения y- координата есть. График представляет собой вертикальную линию, проходящую через точку (-2, 0).
График линии y = 3 представляет собой горизонтальную линию с координатой y, равной 3, независимо от координаты x. Следовательно, график представляет собой горизонтальную линию, проходящую через точку (0, 3).
Примечание. Большинство учащихся считают, что координаты точек всегда должны быть целыми числами. Это неверно, и в реальных жизненных ситуациях не всегда возможно. Не пугайтесь, если ваши очки включают числа, которые являются дробями или десятичными знаками.
Эта страница под названием 1.1: График линейного уравнения распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована Рупиндером Секоном и Робертой Блум с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts. ; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Рупиндер Сехон и Роберта Блум
- Лицензия
- СС BY
- Версия лицензии
- 4,0
- Показать страницу TOC
- нет
- Теги
- перехватывает
- линейное уравнение
- параметр
- источник@https://www.
 deanza.edu/faculty/bloomroberta/math21/afm3files.html.html
deanza.edu/faculty/bloomroberta/math21/afm3files.html.html
| 1 | Оценка с использованием заданного значения | квадратный корень из 50 | ||
| 2 | Оценка с использованием заданного значения | квадратный корень из 45 | ||
| 3 | Оценить | 5+5 | ||
| 4 | Оценить | 7*7 | ||
| 5 | Найти простую факторизацию | 24 | ||
| 6 | Преобразование в смешанный номер | 52/6 | ||
| 7 | Преобразование в смешанный номер | 93/8 | ||
| 8 | Преобразование в смешанный номер | 34/5 | ||
| 9 | График | у=х+1 | ||
| 10 | Оценка с использованием заданного значения | квадратный корень из 128 | ||
| 11 | Найдите площадь поверхности | сфера (3) | | |
| 12 | Оценить | 54-6÷2+6 | ||
| 13 | График | г=-2x | ||
| 14 | Оценить | 8*8 | ||
| 15 | Преобразование в десятичное число | 5/9 | ||
| 16 | Оценка с использованием заданного значения | квадратный корень из 180 | ||
| 17 | График | у=2 | ||
| 18 | Преобразование в смешанный номер | 7/8 | ||
| 19 | Оценить | 9*9 | ||
| 20 | Решите для C | С=5/9*(Ф-32) | ||
| 21 | Упростить | 1/3+1 1/12 | ||
| 22 | График | у=х+4 | ||
| 23 | График | г=-3 | ||
| 24 | График | х+у=3 | ||
| 25 | График | х=5 | ||
| 26 | Оценить | 6*6 | ||
| 27 | Оценить | 2*2 | ||
| 28 | Оценить | 4*4 | ||
| 29 | Оценить | 1/2+(2/3)÷(3/4)-(4/5*5/6) | ||
| 30 | Оценить | 1/3+13/12 | ||
| 31 | Оценить | 5*5 | ||
| 32 | Решите для d | 2д=5в(о)-вр | ||
| 33 | Преобразование в смешанный номер | 3/7 | ||
| 34 | График | г=-2 | ||
| 35 | Найдите склон | у=6 | ||
| 36 | Преобразовать в проценты | 9 | ||
| 37 | График | у=2х+2 | ||
| 38 | График | у=2х-4 | 92+5х+6=0 | |
| 41 | Преобразование в смешанный номер | 1/6 | ||
| 42 | Преобразование в десятичное число | 9% | ||
| 43 | Найти n | 12н-24=14н+28 | ||
| 44 | Оценить | 16*4 | ||
| 45 | Упростить | кубический корень из 125 | ||
| 46 | Преобразование в упрощенную дробь | 43% | ||
| 47 | График | х=1 | ||
| 48 | График | у=6 | ||
| 49 | График | г=-7 | ||
| 50 | График | у=4х+2 | ||
| 51 | Найдите склон | у=7 | ||
| 52 | График | у=3х+4 | ||
| 53 | График | у=х+5 | ||
| 54 | График | 92-9=0|||
| 58 | Оценка с использованием заданного значения | квадратный корень из 192 | ||
| 59 | Оценка с использованием заданного значения | квадратный корень из 25/36 | ||
| 60 | Найти простую факторизацию | 14 | ||
| 61 | Преобразование в смешанный номер | 7/10 | ||
| 62 | Решите для | (-5а)/2=75 | ||
| 63 | Упростить | х | ||
| 64 | Оценить | 6*4 | ||
| 65 | Оценить | 6+6 | ||
| 66 | Оценить | -3-5 | ||
| 67 | Оценить | -2-2 | ||
| 68 | Упростить | квадратный корень из 1 | ||
| 69 | Упростить | квадратный корень из 4 | ||
| 70 | Найди обратное | 1/3 | ||
| 71 | Преобразование в смешанный номер | 20.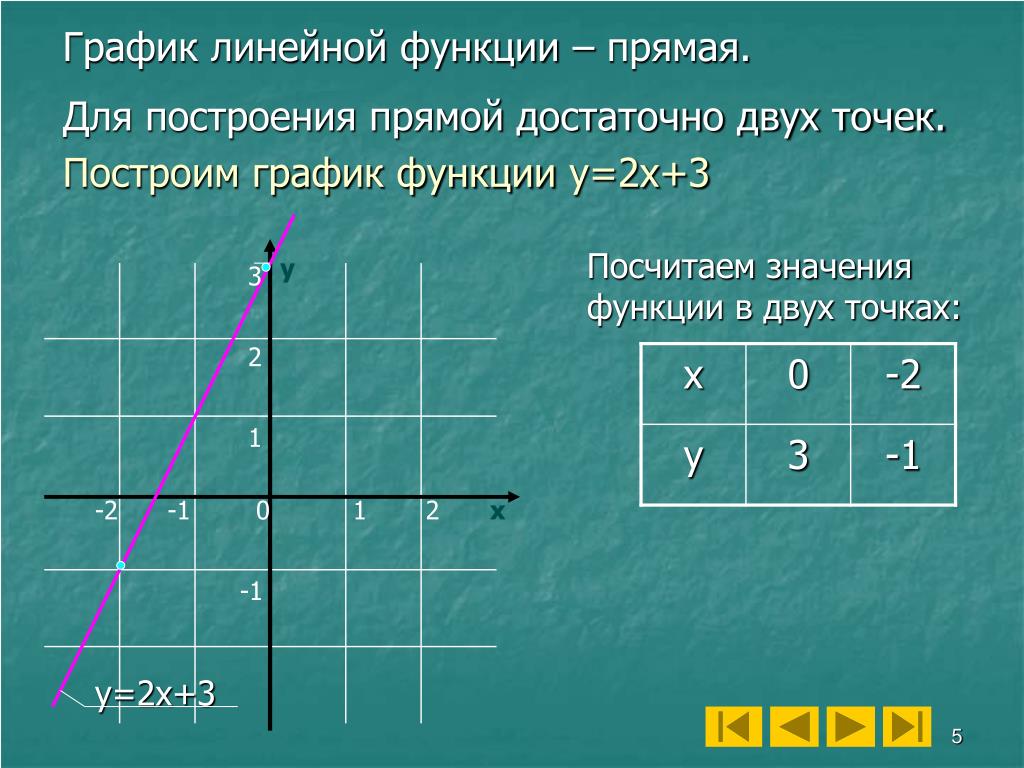 11. 11. | ||
| 72 | Преобразование в смешанный номер | 7/9 | ||
| 73 | Найти LCM | 11, 13, 5, 15, 14 | , , , , | |
| 76 | График | 3x+4y=12 | ||
| 77 | График | 3x-2y=6 | ||
| 78 | График | у=-х-2 | ||
| 79 | График | у=3х+7 | ||
| 80 | Определить, является ли многочлен | 2x+2 | ||
| 81 | График | у=2х-6 | ||
| 82 | График | у=2х-7 | ||
| 83 | График | у=2х-2 | ||
| 84 | График | у=-2х+1 | ||
| 85 | График | у=-3х+4 | ||
| 86 | График | у=-3х+2 | ||
| 87 | График | у=х-4 | ||
| 88 | Оценить | (4/3)÷(7/2) | ||
| 89 | График | 2x-3y=6 | ||
| 90 | График | х+2у=4 | ||
| 91 | График | х=7 | ||
| 92 | График | х-у=5 | ||
| 93 | Решение с использованием свойства квадратного корня 92-2x-3=0 | |||
| 95 | Найдите площадь поверхности | конус (12)(9) | | |
| 96 | Преобразование в смешанный номер | 3/10 | ||
| 97 | Преобразование в смешанный номер | 20. 07. 07. | 92)
Упорядоченные пары, построение линейного графика… Пошаговое решение математических задач
8.1 Упорядоченные пары
Такие уравнения, как d=60t, {Iota}= 0,05P, и y 3 = 2x + y 3 = отношения между парами переменных. Например, в первом уравнении, если t = 3, то d = 60 * 3 = 180. Понимая, что t — первое, а d — второе, мы можем записать пару (3, 180) для представления t = 3 и d = 180. Пара (8,180) называется упорядоченной парой. Очевидно, (180, 3) отличается от (3, 180), если t — первое число, а d — второе число.
Говорят, что (3, 180) удовлетворяет уравнению или является решением уравнения d=60t. Точно так же (100, 5) удовлетворяет {Iota} = 0,05P, где P = 100 и {Iota} = 0,05 (100) = 5 . Кроме того, (2, 7) удовлетворяет y = 2x + 3, где x = 2 и y=2*2+3=7.
В упорядоченной паре, скажем (x, y), x называется первым компонентом, а y называется вторым компонентом. Чтобы найти упорядоченные пары, удовлетворяющие такому уравнению, как y = 2x + 3, мы можем выбрать любое значение для одной переменной, а затем найти соответствующее значение для другой переменной, подставив его в уравнение. Например,
Чтобы найти упорядоченные пары, удовлетворяющие такому уравнению, как y = 2x + 3, мы можем выбрать любое значение для одной переменной, а затем найти соответствующее значение для другой переменной, подставив его в уравнение. Например,
выберите x=1, тогда y=2*1+3=5
выберите x= -2, тогда y=2(-2)+3= -1
выберите x=1/2, тогда y=2 (1/2)+3=4
Упорядоченные пары (1,5), (-2,-1) и (1/2, 4) удовлетворяют уравнению y = 2x + 3.
Присвоенная переменная к первому компоненту также называется независимой переменной, а переменная, присвоенная второму компоненту, называется зависимой переменной. Таким образом, мы связываем (x, y) с y = 2x + 3, а y «зависит» от значений, присвоенных x.
Мы также можем записать пары в виде таблиц. Выбор значений независимой переменной произволен.
d=60 т
| т | д |
| 5 | 60*5=300 |
| 10 | 60*10=600 |
| 12 | 60*12=720 |
| 15 | 60*15=900 |
{Йота}=0,5P
| P | {Йота} |
| 100 | 0,05*(100)=5 |
| 200 | 0,05(200)=10 |
| 500 | 0,05(500)=25 |
| 1000 | 0,05(1000)=50 |
y=2x+3
| x | г |
| -2 | 2(-2)+3=-1 |
| -1 | 2(-1)+3=1 |
| 0 | 2(0)+3=3 |
| 3 | 2(3)+3=9 |
Другим обозначением, обычно используемым в математике для представления зависимой переменной, является обозначение функции. Символ f(x) (читается как «f of x») используется для представления значения зависимой переменной, связанной с x. Например,
Символ f(x) (читается как «f of x») используется для представления значения зависимой переменной, связанной с x. Например,
если f(x)=2x-5
тог f(1)=2*1-5=-3
f(3)=2*3-5=1
6 33 =2*6-5=7и f(-1)=2(-1)-5=-7
(Примечание: f(x) не означает умножение f на x. f(x) — самостоятельная запись.)
Благодаря работам Рене Декарта (1596-1650) мы можем представить упорядоченные пары как точек на плоскости путем построения графика в декартовой системе координат. В этой системе две числовые линии пересекаются под прямым углом и делят плоскость на четыре квадранта. Начало, обозначенное упорядоченной парой (0, 0), является точкой пересечения. Горизонтальная числовая линия называется горизонтальной осью или осью X. Вертикальная числовая линия называется вертикальной осью или осью Y. Точки, лежащие на любой из осей, не находятся ни в одном квадранте. Они просто расположены на оси (см. рис. 8.1).
Другими словами, каждой точке соответствует одна упорядоченная пара действительных чисел, а каждой упорядоченной паре действительных чисел соответствует одна точка. Это важное соотношение является краеугольным камнем декартовой системы координат.
Это важное соотношение является краеугольным камнем декартовой системы координат.
Графики точек A(2, 1), B(-2, 3), C(-3, -2), D(l, -2) и {эпсилон}=(3, 0) показано на рисунке 8.2. (Примечание: упорядоченная пара действительных чисел и соответствующая точка на графике часто используются для обозначения друг друга. Таким образом, упорядоченная пара (2,1) и точка (2,1) взаимозаменяемы.)
Рис. 8.2
Примеры
График Наборы упорядоченных пар в примерах 1 и 2
1. {(-2,1), (0, 2) (1,3). , (2, -3)}
2. {(-1,3),(0,1),(1,-1),(2,-3),(3,-5)}
3. Если f(x)=-2x+1, найти f(-1),f(0),f(1),f(2) и f(3).
f(1)=-2(-1)+1=3
f(0)=-2(0)+1=1
f(1)=-2(1)+1=-1
f(2)=-2(2)+1=-3
f(3)=-2(3)+1=-5
8.2 Построение графика линейных уравнений
Предположим, мы хотим изобразить на графике точки, удовлетворяющие уравнению y = 2x + 3. Существует бесконечное число таких точек. точки. Мы построим график пяти, чтобы попытаться найти закономерность (см. рис. 8.3).
Существует бесконечное число таких точек. точки. Мы построим график пяти, чтобы попытаться найти закономерность (см. рис. 8.3).
Пять точек на рис. 8.3 лежат на одной прямой. На самом деле они лежат на прямой, и любая упорядоченная пара, удовлетворяющая уравнению y = 2x + 3, также будет лежать на этой прямой.
От чего зависит, будут ли точки, удовлетворяющие уравнению, лежать на прямой? Точки, удовлетворяющие любому уравнению вида
Ax+By=C
будет Лежать на прямой. Уравнение называется линейным уравнением и считается стандартной формой уравнения прямой. Мы можем записать уравнение y = 2x + 3 в стандартной форме -2x + y = 3.
| x | 2х+3=у |
| 0 | 2(0)+3=3 |
| -1 | 2(-1)+3=1 |
| 1/2 | 2(1/2)+3=4 |
| 1 | 2(1)+3=5 |
| -2 | 2(-2)+3=-1 |
(Две точки определяют линию. ) Выбор двух точек зависит от выбора любых двух значений x или любых двух значений y.
) Выбор двух точек зависит от выбора любых двух значений x или любых двух значений y.
Примеры
1. Нарисуйте график линейного уравнения x+3y = 6.
x = 0
0+3y = 6
y = 2
x = 3
3+3Y = = = = 2
x = 3
3+3Y = = 2
x = 3
3+3Y = 3Y = 3Y = 6
3y=3
y=1
На графике две точки (0, 2) и (3, 1). Возможно, вы выбрали еще два. Избегайте выбора двух точек близко друг к другу.
2. Нарисуйте график линейного уравнения 2x-5y=10
x=5
2*5-5y=10
10-5y=10
-5Y = 10
Y = 0
X = 0
2*0-5Y = 10
0-5Y = 10
Y = -2
x = -5
2 (x = -5
2 (
x = -5
2 ( -5)-5y=10-10-5y=10
-5y=20
y=-4
Отображение трех точек является хорошей идеей, просто чтобы убедиться, что график находится в правильном положении.
Хотя выбор значений для x или y может быть произвольным, принимая значение x = 0, мы найдем точку на графике, где линия пересекает ось y. Эта точка называется y-перехватом. Точка пересечения с осью X — это точка, которую можно найти, приняв y = 0. Эти две точки обычно легко найти, и они часто используются в качестве двух точек для построения графика линейного уравнения.
Примеры
Нарисуйте следующие линейные уравнения, найдя точки пересечения по осям x и
точки пересечения с y.
1. 3y+2x=6
x=0→y=2
y=0→x=3
Давайте посмотрим, как наш решатель линейных уравнений и подобные графы генерируют график линейного уравнения. Нажмите кнопку «Решить подобное», чтобы увидеть больше примеров.
Решить похожую задачуВведите свою проблему
2. 3y-2x=6
x=0→y=2
y=0→x=-3
Поскольку координата x точки пересечения с осью y всегда равна 0, мы условимся называть координату y точкой пересечения с y. В только что приведенных примерах 1 и 2 мы будем говорить, что точка пересечения с осью y равна 2, а не давать координаты (0, 2). Точно так же в примере 1 точка пересечения по оси x равна 3, а в примере 2 точка пересечения по оси x равна -3. Если линия проходит через начало координат, то точка пересечения по оси x и по оси y будет равна 0. В этом случае необходимо использовать какую-то другую точку.
В только что приведенных примерах 1 и 2 мы будем говорить, что точка пересечения с осью y равна 2, а не давать координаты (0, 2). Точно так же в примере 1 точка пересечения по оси x равна 3, а в примере 2 точка пересечения по оси x равна -3. Если линия проходит через начало координат, то точка пересечения по оси x и по оси y будет равна 0. В этом случае необходимо использовать какую-то другую точку.
Пример
График. Следующее линейное уравнение: Y — 3x = 0
Y -3X = 0
x = 0 → Y = 0
x = 2 → Y = 6
x = 2 → Y = 6
9
3. посмотрите, как наш математический решатель генерирует график этого уравнения и подобных линейных уравнений. Нажмите кнопку «Решить подобное», чтобы увидеть больше примеров.
Решить похожую задачуВведите свою задачу
8.3 Формы пересечения наклона и точки-наклона
Плотнику дали набор планов дома, требующих крыши 5:12. Что это значит для плотника? Это означает, что он должен построить крышу так, чтобы на каждые 5 дюймов подъема (расстояние по вертикали) приходилось 12 дюймов пробега (расстояние по горизонтали). То есть отношение подъема к пробегу составляет 5/12 (см. рис. 8.4.)
Что это значит для плотника? Это означает, что он должен построить крышу так, чтобы на каждые 5 дюймов подъема (расстояние по вертикали) приходилось 12 дюймов пробега (расстояние по горизонтали). То есть отношение подъема к пробегу составляет 5/12 (см. рис. 8.4.)
Рисунок 8.4
А что, если еще одна крыша будет 7:12? Стал бы плотник строить крышу так, чтобы на каждые 7 дюймов подъема приходилось 12 дюймов прогона? Конечно. Отношение подъема к бегу будет 7/12 (см. рис. 8.5). 9Рис. 8.5
Для прямой линии отношение подъема к длине называется наклоном линии.
slope=(подъем)/(набег)
График линейного уравнения y=3x-1 показан на рис. 8.6 Как вы думаете, что такое наклон линии?
Рис. 8.6
Чтобы вычислить наклон, найдите любые две точки на линии, затем найдите подъем и уклон, используя эти две точки (см. рис. 8.7а). (Коэффициент подъема
Рис. -1 y=3(-1)-1=-3-1=-4
-1 y=3(-1)-1=-3-1=-4
Теперь, используя P_1(-1, -4) и P_2(3, 8), координаты P_3 равны (3, -4 ), как показано на рисунке 8.7b. P_3 имеет те же координаты x, что и P_2, и те же координаты, что и P_1.
(Примечание. Обозначение P_1 читается как «P sub 1», а 1 называется индексом . Точно так же P_2 читается как «P sub 2», а P_3 читается как «P sub 3».)
Для линии y=3x-1,
наклон=(подъем)/(разбег)=(8-(-4))/(3-(-1))
=12/4=3
Теперь найдите наклон линии y=3x+2. Найдите две точки на линии и рассчитайте отношение, подъем/пробег
Например,
x=0 y=3*0+2=0+2=2
x=1 y=3*1+2= 3+2=5
Таким образом, P_1(0, 2), P_2(1, 5) и P_3(1, 2) показаны на рис. 8.8.
Обратите внимание, что две линии y = 3x — 1 и y = 3x + 2 имеют одинаковый наклон, равный 3. (См. рис. 8.9..) Это означает, что прямые параллельны. Все прямые с одинаковым наклоном параллельны. Все линии на рис. 8.9 имеют наклон 3 и параллельны. Рис. 8.8 Пусть P_1(x_1,y_1) и P_2(x_2, y_2) — две точки на прямой. Тогда P_3(x_2, y_1) находится под прямым углом, как показано на рисунке 8.10, и можно вычислить наклон.
Рис. 8.8 Пусть P_1(x_1,y_1) и P_2(x_2, y_2) — две точки на прямой. Тогда P_3(x_2, y_1) находится под прямым углом, как показано на рисунке 8.10, и можно вычислить наклон.
наклон=(подъем)/(бег)=(y_2-y_1)/(x_2-x_1) 92 = 6
-6+3Y_2 = 6
3Y_2 = 12
Y_2 = 4
(x_1, Y_1) = (0,2) и X_2, Y_2) = (-3,4)
. (y_2-y_1)/(x_2-x_1)=(4-2)/(-3-0)=2/(-3)=-(2/3)
2. Предположим, что порядок точек в пример 1 изменен. То есть (x_1,y_1)=(-3,4) и (x_2,y_2) = (0, 2). Будет ли это влиять на наклон?
slope=(y_2-y_1)/(x_2-x_1)=(2-4)/(0-(-3))=-2/(3)=-(2/3)
Изменение порядка точки не имеют значения при расчете наклона. И числитель, и знаменатель меняют знак, поэтому дробь имеет одинаковое значение. В примере 1 2/-3=-(2/3), а в примере 2 -2/3=-(2/3). Важной процедурой является то, что координаты должны вычитаться в одном и том же порядке как в числителе, так и в знаменатель.
В общем,
slope=(y_2-y_1)/(x_2-x_1)=(y_1-y_2)/(x_1-x_2)
Отрицательный наклон для линии 2x + 3y = 6 означает, что линия наклонена (или уклоны) вниз вправо (см. рис. 8.11). Все линии с отрицательным наклоном наклонены вниз вправо, а все линии с положительным наклоном наклонены вверх вправо.
рис. 8.11). Все линии с отрицательным наклоном наклонены вниз вправо, а все линии с положительным наклоном наклонены вверх вправо.
slope=-2/3=-(2/3)
Рис. Начните с точки (4, 5) и найдите другую точку на линии, используя наклон как (подъем)/(спуск)=3/4.
Четыре единицы вправо (бег) и три единицы вверх (подъем) от (4, 5) дадут еще одну точку на линии. Из (4, 5) вы могли переместиться на 4 единицы влево и на 3 единицы вниз или на 8 единиц вправо, а затем на 6 единиц вверх. Просто двигайтесь так, чтобы отношение подъема к бегу было 3 к 4, и вы найдете вторую точку на графике. (Для отрицательного наклона двигайтесь либо вправо, а затем вниз, либо влево, а затем вверх.)
Решите уравнение 2x+3y=6 относительно y.
2x+3y=6
3y=-2x+6
(3y)/3=(-2x+6)/3
y=(-2x)/3+6/3
y=-(2/3x)+2
Обратите внимание, что коэффициент x,-(2/3) совпадает с наклоном линии. Кроме того, для линий, обсуждавшихся ранее, y = 3x-1 и y = 3x + 2, наклон каждой линии был равен 3, что является коэффициентом x. Если линейное уравнение решается относительно y, всегда ли коэффициент при x будет наклоном? Это важный вопрос, и ответ на него можно найти в следующем обсуждении.
Если линейное уравнение решается относительно y, всегда ли коэффициент при x будет наклоном? Это важный вопрос, и ответ на него можно найти в следующем обсуждении.
Предположим, что уравнение решено относительно y и y=mx+b. Пусть (x_1,y_1) и (x_2,y_2) — две точки на прямой. (x_1!=y_1) Тогда
y_1=mx_1+b and y_2=mx_2+b
slope=(y_2-y_1)/(x_2-x_1)=((mx_2+b)-(mx_1+b)) /(x_2-x_1)
=(mx_2+b-mx_1-b)/(x_2-x_1)=(mx_2-mx_1)/(x_2-x_1)
коэффициент x =
9003, , в виде y = mx + bДля прямой y = mx + b пусть x=0. Тогда y=m*0+b=b и y = b является точкой пересечения с осью y. Поскольку m — наклон, а b — точка пересечения с осью y, мы приходим к следующему определению.
y = mx + b называется формой наклона и пересечения для уравнения прямой; m — наклон, а b — точка пересечения с осью y.
Найдите наклон (м) и точку пересечения по оси y b каждой из следующих линий, переписав уравнение в форме наклона и точки пересечения. Затем нарисуйте линию.
Затем нарисуйте линию.
1. 2x+3y = 3
3y = -2x+3
y = (-2x+3)/3
y =-(2/3x) +1
M =-(2/3 )
y-отрезок = 1.
2. x-2y=6
x = 6+2y
x-6 = 2y
(x-6)/2 = Y
1/2x-3 = Y
M = 1/2 B = -3
3 . -4x+2y = 7
2y = 4x+7
y = (4x+7)/2
y = 2x+7/2
m = 2 b = 7/2
, если а линия должна иметь определенный наклон и проходить через определенную точку, уравнение, представляющее линию, можно найти, как показано на следующем рисунке.
Предположим, что линия должна иметь наклон § и проходить через точку (1, 5). Если (x, y) представляет точку на линии, то наклон, рассчитанный с использованием (1, 5) и (x, y), должен составлять 2/3. то есть
(y-5)/(x-1)=2/3
В другой форме
y-5=2/3(x-1)
фиксированная точка (x_1,y_1) может быть представлена в виде строка
; m — наклон, а (x_1,y_1) — фиксированная точка.
Примеры
1. Найдите уравнение прямой, имеющей наклон m=3/4 и проходящей через точку (4,5).
y-y_1=m(x-x_1)
y-5=3/4(x-4) (уравнение в форме точка-наклон)
или y-5=3/4x-3
y=3/4x+2 (уравнение в форме наклона-отрезка)
или 4y=3x+8
-3x+4y=8 (уравнение в стандартной форме, Ax+By=C)
2 . Найдите уравнение прямой, проходящей через две точки (- 1, -3) и (5, -2).
m=(y_2-y_1)/(x_2-x_1)=(-2-(-3))/(5-(-1))=(-2+3)/(5+1)=1/ 6Найдите m, используя формулу для наклона .
Используя форму точка-наклон (любая точка (-1, -3 или (5, -2) даст тот же результат)
y-(-2)=1/6(x-5)
y+ 2=1/6(x-5) (уравнение в форме точка-наклон)
или y+2=1/6x-5/6
y=1/6x-17/6 (уравнение в наклон-пересечение)
или 6y=x-17
17=x-6y (уравнение в стандартной форме, Ax+By=C)
Любая из трех основных форм уравнения прямой допустима В любом случае, если ответ дан в форме, отличной от вашей, вы должны быть в состоянии признать уравнения эквивалентными. 0034
0034
Давайте посмотрим, как наш математический решатель создает графики прямых линий и посмотрим на различные наклоны линий. Нажмите кнопку «Решить подобное», чтобы увидеть больше примеров.
Решить похожую задачуВведите свою задачу
8.4 Горизонтальные и вертикальные линии
Рассмотрите уравнение y = 3. Если x = 5, чему равно y? Если х = -2, чему равно у? Если х=0, чему равно у? В каждом случае y = 3. Все точки (5, 3), (-2, 3) и (0,3) удовлетворяют условию y = 3. x может иметь любое значение, но y должен быть x. Чтобы подчеркнуть этот факт, уравнение y = 3 можно записать как 0x + y = 3 или y = 0x + 3. График уравнения y = 3 представляет собой горизонтальную линию, и каждая координата y равна 3 (см. рис. 8.12). .)
Рисунок 8.12
Каков наклон линии y = 3? Записав уравнение в форме y = 0x + 3, наклон равен 0. Кроме того, по формуле для наклона, используя (-2, 3) и (5, 3), наклон действительно равен 0:
slope = m=(y_2-y_1)/(x_2-x_1)=(3-3)/(5-(2))=0/7=0
Каковы графики уравнений y = -2 и y = 3 /2? Обе являются горизонтальными линиями с наклоном 0. На самом деле любое уравнение вида y = b (или y = 0x + b) является горизонтальной линией с наклоном 0 (см. рис. 8.13). Теперь рассмотрим уравнение x = 2. Если y = 4, чему равно x? Если у = -3, что такое х? Если у = 0, то чему равен х? В каждом случае x = 2. Все точки (2, 4), (2, -3) и (2, 0) удовлетворяют условию x = 2. y может иметь любое значение, но x должно быть равно 2. Мы можно записать x = 2 в виде 0y + x = 2 или x = 0y + 2. График уравнения x = 2 представляет собой вертикальную линию, и каждая координата x равна 2 (см. рис. 8.14).
На самом деле любое уравнение вида y = b (или y = 0x + b) является горизонтальной линией с наклоном 0 (см. рис. 8.13). Теперь рассмотрим уравнение x = 2. Если y = 4, чему равно x? Если у = -3, что такое х? Если у = 0, то чему равен х? В каждом случае x = 2. Все точки (2, 4), (2, -3) и (2, 0) удовлетворяют условию x = 2. y может иметь любое значение, но x должно быть равно 2. Мы можно записать x = 2 в виде 0y + x = 2 или x = 0y + 2. График уравнения x = 2 представляет собой вертикальную линию, и каждая координата x равна 2 (см. рис. 8.14).
Каков наклон линии x = 2? Чтобы ответить на этот вопрос, воспользуемся формулой наклона и двумя точками (2, 4) и (2, -3):
slope = m=(y_2-y_1)/(x_2-x_1)=(4-( -3))/(2-2)=7/0 undefined
Наклон не определен, потому что 0 не может быть знаменателем. Это верно для любой вертикальной линии. Графики уравнений вида x = a представляют собой вертикальные линии без наклона (или с неопределенным наклоном). Обратите внимание на то различие, что горизонтальные линии ((y = b)) имеют нулевой наклон, а вертикальные линии (x = a)) не имеют наклона. И уравнения для горизонтальных линий ((y = b)) и уравнения для вертикальных линий (x=a)) являются частными случаями общего линейного уравнения в стандартной форме Ax + By = C, обсуждаемого в разделе 8.2.
И уравнения для горизонтальных линий ((y = b)) и уравнения для вертикальных линий (x=a)) являются частными случаями общего линейного уравнения в стандартной форме Ax + By = C, обсуждаемого в разделе 8.2.
1. 2y = 5
y = 5/2
M = 0
2. x+6 = 0
x = -6
NO Slope
3. x+y = y = y = y = y = y = y = y = y = y = y = y = y = y = y = y = y = y = y = y = y = y = y = y = y = y = y = y = y = y = y = y = y = y = y = y = y = y = y = y = y = y = y = y = y = y = y = y = y = y = y = y = y = y = y = y = y = y = y = y = y = y = y. 0
y=-x
m=-1
8,5 Расстояние между двумя точками
Каково расстояние между двумя точками P_1(2, 3) и P_2(6, 3)? Каково расстояние между точками P_3 (-1, -4) и P_4 (-1, 1)? (См. рис. 8.15.)
Это верно, так как точки P_1 и P_2 лежат на одной горизонтальной линии и имеют одинаковую координату y.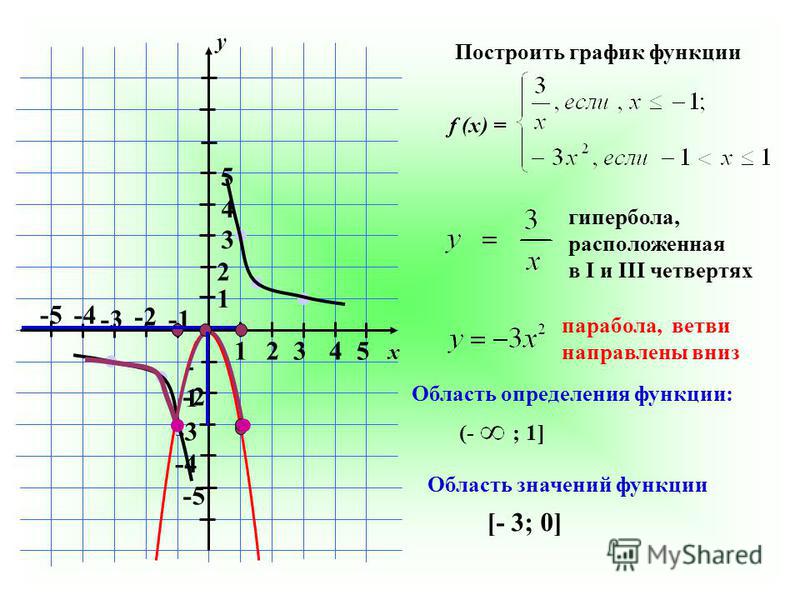 Вы нашли
Вы нашли
расстояние (от P_3 до P_4)=1-(-4)=5?
Это верно, так как точки P_3 и P_4 лежат на одной вертикальной линии и имеют одинаковую координату x.
Для расстояния от P_1 до P_2 почему бы не взять
расстояние (от P_1 до P_2) = 2-6=-4?
Причина в том, что термин расстояние означает положительное число. Как можно гарантировать положительное число после вычитания координат? Ответ состоит в том, чтобы взять абсолютное значение разности координат. Расстояние между двумя точками обозначается d.
Для P_1(x_1,y_1) и P_2(x_2,y_1) на горизонтальной линии,
для P_1 (x_1, Y_1) и P_2 (x_1, Y_2) на вертикальной линии,
Примеры
1. Найдите расстояние, D, между двумя точками (5, 7). (-3, 7). Поскольку точки лежат на горизонтальной линии (они имеют одинаковую координату y),
или
2. Найдите расстояние d между двумя точками (2, 8) и 2,-(1/2 ). Поскольку точки лежат на вертикальной линии (они имеют одинаковую x:координату),
или
Что делать, если точки не лежат на вертикальной или горизонтальной линии? Действительно, это более общий случай. Нам нужна теорема Пифагора. Сформулированная здесь теорема Пифагора будет более подробно обсуждаться в разделе 10.6.
Нам нужна теорема Пифагора. Сформулированная здесь теорема Пифагора будет более подробно обсуждаться в разделе 10.6.
Теорема Пифагора: В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов двух сторон.
Чтобы найти расстояние между двумя точками P_1(-1, 2) и P_2(5, 4), примените теорему Пифагора и вычислите длину гипотенузы, как показано на рис. 8.16. 92)
=корень(1/16+1)
=корень(1/16+16/16)
=корень(17/16)
. 2, 1), B(3,4) и C(1, -4) — равнобедренный треугольник. У равнобедренного треугольника две равные стороны.
Решение:
Длина отрезка – это расстояние между точками A и B. Обозначим это расстояние через . Таким образом, чтобы показать, что треугольник ABC равнобедренный, нам нужно показать, что = или что = . Если ни одно из этих соотношений не верно, то треугольник не имеет двух равных сторон и не является равнобедренным. 92)
= корень (9+25) = корень (34)
, так как = треугольник — это изобранные
2. 2 Линейные функции и их графики
2 Линейные функции и их графики
Цели обучения
- Изобразить линию, нанеся точки.
- Определение наклона линии.
- Определите и начертите линейную функцию, используя наклон и y — точку пересечения.
- Интерпретировать решения линейных уравнений и неравенств графически.
Обзор графических линий
Напомним, что набор всех решений линейного уравнения может быть представлен на прямоугольной координатной плоскости с помощью прямой линии, проходящей как минимум через две точки; эта линия называется ее графиком. Например, чтобы нарисовать линейное уравнение 8x+4y=12, мы сначала решим y .
8x+4y = 12 вычитание 8x с обеих сторон.4y = −8x+12 Разделите обе стороны на 4.y = −8x+124 упростить.y = −8×4+124y = −2x+3
В этой форме мы видим, что y зависит от x ; другими словами, 92 107 x 92 108 — это независимая переменная. Переменная, определяющая значения других переменных. Обычно мы думаем о x -значение упорядоченной пары ( x , y ) как о независимой переменной. а y — зависимая переменная. Переменная, значение которой определяется значением независимой переменной. Обычно мы думаем о у -значение упорядоченной пары ( x , y ) в качестве зависимой переменной. Выберите не менее двух x -значений и найдите соответствующие y -значения. Рекомендуется выбирать ноль, некоторые отрицательные числа, а также некоторые положительные числа. Здесь мы выберем пять значений x , определим соответствующие значения y , а затем сформируем репрезентативный набор упорядоченных парных решений.
Переменная, определяющая значения других переменных. Обычно мы думаем о x -значение упорядоченной пары ( x , y ) как о независимой переменной. а y — зависимая переменная. Переменная, значение которой определяется значением независимой переменной. Обычно мы думаем о у -значение упорядоченной пары ( x , y ) в качестве зависимой переменной. Выберите не менее двух x -значений и найдите соответствующие y -значения. Рекомендуется выбирать ноль, некоторые отрицательные числа, а также некоторые положительные числа. Здесь мы выберем пять значений x , определим соответствующие значения y , а затем сформируем репрезентативный набор упорядоченных парных решений.
Нанесите точки и проведите линию через точки с помощью линейки. Не забудьте добавить стрелки на обоих концах, чтобы указать, что график расширяется до бесконечности.
Полученная линия представляет все решения уравнения 8x+4y=12, которых бесконечно много. Вышеприведенный процесс описывает метод построения графика, известный как построение точек. Способ построения графика с использованием конечного числа репрезентативных упорядоченных парных решений. Этот метод будет использоваться для построения графиков более сложных функций по мере продвижения в этом курсе.
Вышеприведенный процесс описывает метод построения графика, известный как построение точек. Способ построения графика с использованием конечного числа репрезентативных упорядоченных парных решений. Этот метод будет использоваться для построения графиков более сложных функций по мере продвижения в этом курсе.
Крутизна любого уклона может быть измерена как отношение вертикального изменения к горизонтальному изменению. Например, наклон 5% можно записать как 5100, что означает, что на каждые 100 футов вперед высота увеличивается на 5 футов.
В математике мы называем наклон линии наклоном. Наклон линии измеряется как отношение изменения по вертикали к изменению по горизонтали, что часто называют «подъемом относительно пробега». Обозначается буквой м . Вертикальное изменение называется подъемом. Вертикальное изменение между любыми двумя точками на линии. а горизонтальное изменение называется пробегом. Горизонтальное изменение между любыми двумя точками на линии. Имея любые две точки (x1, y1) и (x2, y2), мы можем получить подъем и бег, вычитая соответствующие координаты.
Это приводит нас к формуле наклонаНаклон линии, проходящей через точки (x1,y1) и (x2,y2), определяется формулой m=y2−y1x2−x1.. Для любых двух точек (x1, y1) и (x2, y2), наклон задан:
наклон M = Riserun = y2 -y1x2 -x1 = ΔyΔx ← Изменение y ← Изменение в x
Греческая буквенная дельта (δ) часто используется для описания x
. изменение количества. Поэтому наклон иногда описывают с помощью обозначения ΔyΔx, которое представляет собой изменение 92 107 y 92 108, деленное на изменение х .
Пример 1
Найдите наклон линии, проходящей через (−3, −5) и (2, 1).
Решение:
Учитывая (−3, −5) и (2, 1), вычислить разность y -значений, деленную на разность x -значений. Позаботьтесь о согласованности при вычитании координат: 2−(−3)=1+52+3=65
Неважно, какую точку вы считаете первой, а какую второй. Однако, поскольку вычитание не является коммутативным, вы должны позаботиться о том, чтобы вычесть координаты первой точки из координат второй точки в том же порядке. Например, мы получим тот же результат, если применим формулу наклона с переключением точек:
Например, мы получим тот же результат, если применим формулу наклона с переключением точек:
(x1, y1) (x2, y2)(2,1) (−3,−5)
m=y2−y1x2−x1=−5−1−3−2=−6−03=65
Ответ: m=65
Убедитесь, что наклон равен 65, нарисовав линию, описанную в предыдущем примере.
Конечно, графа необязательна; Прелесть формулы наклона в том, что для любых двух точек мы можем получить наклон, используя только алгебру.
Пример 2
Найдите y -значение, для которого наклон линии, проходящей через (6,−3) и (−9,y) равно −23.
Решение:
Подставьте данную информацию в формулу наклона.
наклон (x1, y1) (x2, y2) m = −23 (6, −3) (−9, y)
m = y2 -y1x2 -x1–23 = y — ( — 3) −9- 6−23=y+3 −15
После подстановки данной информации остается только одна переменная: y . Решать.
−15(−23)=−15(−y+3 15)10=y+37=y
Ответ: y = 7
Существует четыре геометрических случая для значения наклона.
Читая график слева направо, линии с наклоном вверх имеют положительный наклон, а линии с наклоном вниз имеют отрицательный наклон. Два других случая включают горизонтальные и вертикальные линии. Напомним, что если k является вещественным числом, то мы имеем
y=kHorizontal Linex=kVertical Line
Например, если изобразить y=2, мы получим горизонтальную линию, а если изобразить x=−4, то получим вертикальную линия.
Из графиков мы можем определить две точки и рассчитать наклон, используя формулу наклона.
Обратите внимание, что точки на горизонтальной линии имеют одинаковые значения и . Следовательно, подъем равен нулю и, следовательно, наклон равен нулю. Точки на вертикальной линии имеют одинаковые значения 92 107 x 92 108. Следовательно, пробег равен нулю, что приводит к неопределенному наклону. В общем,
Линейные функции
Для любого линейного уравнения в стандартной форме Любую невертикальную линию можно записать в стандартной форме formЛюбая невертикальная линия может быть записана в виде y=mx+b, где м — уклон и (0, b ) — y -пересечение, y=mx+b. Например,
Например,
3x-4y = 8 ← Стандартная форма-4y = −3x+8y = −3x+8–4y = −3x-4+8–4y = 34x-2 ← Форма с наклоном
, где x = 0, мы видим, что y=−2 и, следовательно, (0,−2) является упорядоченным парным решением. Это точка, в которой график пересекает ось y , и называется точкой пересечения y . Точка (или точки), в которой график пересекает ось y , выражается упорядоченной парой2107 y ).. Мы можем использовать эту точку и наклон как средство для быстрого построения линии. Например, чтобы построить график y=34x−2, начните с точки пересечения y (0,−2) и отметьте наклон, чтобы найти вторую точку. Затем используйте эти точки для построения графика линии следующим образом:
Проверка вертикальной линии показывает, что этот график представляет собой функцию. Кроме того, домен и диапазон состоят из всех действительных чисел.
В общем, линейная функция Любая функция, которую можно записать в виде f(x)=mx+b, — это функция, которую можно записать в виде
f(x)=mx+bЛинейная функция
где наклон m и b представляют любые действительные числа. Поскольку y=f(x), мы можем использовать y и f(x) взаимозаменяемо, а упорядоченные парные решения на графе (x,y) можно записать в виде (x,f(x)).
Поскольку y=f(x), мы можем использовать y и f(x) взаимозаменяемо, а упорядоченные парные решения на графе (x,y) можно записать в виде (x,f(x)).
(x,y) ⇔ (x,f(x))
Мы знаем, что любой y -перехват будет иметь x -значение, равное нулю. Следовательно, y -отрезок может быть выражен как упорядоченная пара (0,f(0)). Для линейных функций
f(0)=m(0)+b=b
Следовательно, y -пересечение любой линейной функции равно (0,b). Чтобы найти x -interceptТочка (или точки), где график пересекает ось x , выраженная в виде упорядоченной пары ( x , 0), точка, где функция пересекает ось x , мы находим x , где y=0 или f(x)=0.
Пример 3
Нарисуйте график линейной функции f(x)=−53x+6 и обозначьте точку пересечения x .
Решение:
Из функции мы видим, что f(0)=6 (или b=6) и, следовательно, г — перехват (0, 6). Также мы можем видеть, что уклон m=-53=-53=подъемник. Начиная с точки пересечения и , отметьте вторую точку на 5 единиц вниз и на 3 единицы вправо. Проведите линию, проходящую через эти две точки, с помощью линейки.
Начиная с точки пересечения и , отметьте вторую точку на 5 единиц вниз и на 3 единицы вправо. Проведите линию, проходящую через эти две точки, с помощью линейки.
Чтобы определить точку пересечения x , найдите значение x , при котором функция равна нулю. Другими словами, определите 92 107 x 92 108, где f(x)=0.
f(x)=−53x+60=−53x+653x=6(35)53x=(35)6x=185=335
Следовательно, x — точка пересечения (185,0). Общее правило заключается в том, чтобы маркировать все важные точки, которые невозможно четко прочитать на графике.
Ответ:
Пример 4
Определите линейную функцию, которая определяет данный график, и найдите точку пересечения x .
Решение:
Начнем с чтения наклона по графику. В этом случае даны две точки, и мы можем видеть, что
m=riserun=−23
Кроме того, точка пересечения y равна (0, 3) и, следовательно, b=3. Мы можем подставить в уравнение любую линейную функцию.
g(x)=mx+b↓↓g(x)=−23x+3
Чтобы найти точку пересечения x , мы устанавливаем g(x)=0 и находим x .
g(x)=-23x+30=-23x+323x=3(32)23x=(32)3x=92=412
Ответ: g(x)=-23x+3; x -перехват: (92,0)
Далее рассмотрим горизонтальные и вертикальные линии. Используйте тест вертикальной линии, чтобы убедиться, что любая горизонтальная линия представляет собой функцию, а вертикальная — нет.
Для любой горизонтальной линии проверка вертикальной линии показывает, что каждые x -значение в домене соответствует ровно одному y -значению в диапазоне; это функция. С другой стороны, вертикальная линия не проходит тест на вертикальную линию; это не функция. Вертикальная линия представляет собой набор упорядоченных пар, в которых все элементы домена одинаковы. Это нарушает требование, согласно которому функции должны ассоциировать ровно один элемент в диапазоне с каждым элементом в домене. Подытожим следующим образом:
Горизонтальную линию часто называют постоянная функция . Для любого действительного числа c ,
Для любого действительного числа c ,
f(x)=cConstant Function
Пример 5
Постройте график постоянной функции g(x)=−2 и укажите область определения и диапазон.
Решение:
Здесь нам задана постоянная функция, эквивалентная y=−2. Это определяет горизонтальную линию через (0,−2).
Ответ: Домен: ℝ; диапазон: {−2}
Попробуйте! Нарисуйте график f(x)=3x−2 и обозначьте точку пересечения x .
Ответ:
(щелкните, чтобы посмотреть видео)
Линейные уравнения и неравенства: графическая интерпретация
Мы можем использовать идеи, изложенные в этом разделе, для развития геометрического понимания того, что значит решать уравнения вида f(x )=g(x), где f и g — линейные функции. Используя алгебру, мы можем решить линейное уравнение 12x+1=3 следующим образом:
12x+1=312x=2(2)12x=(2)2x=4
Решение этого уравнения x = 4. Геометрически это x -значение пересечения двух графиков f(x)=12x+1 и g(x)=3.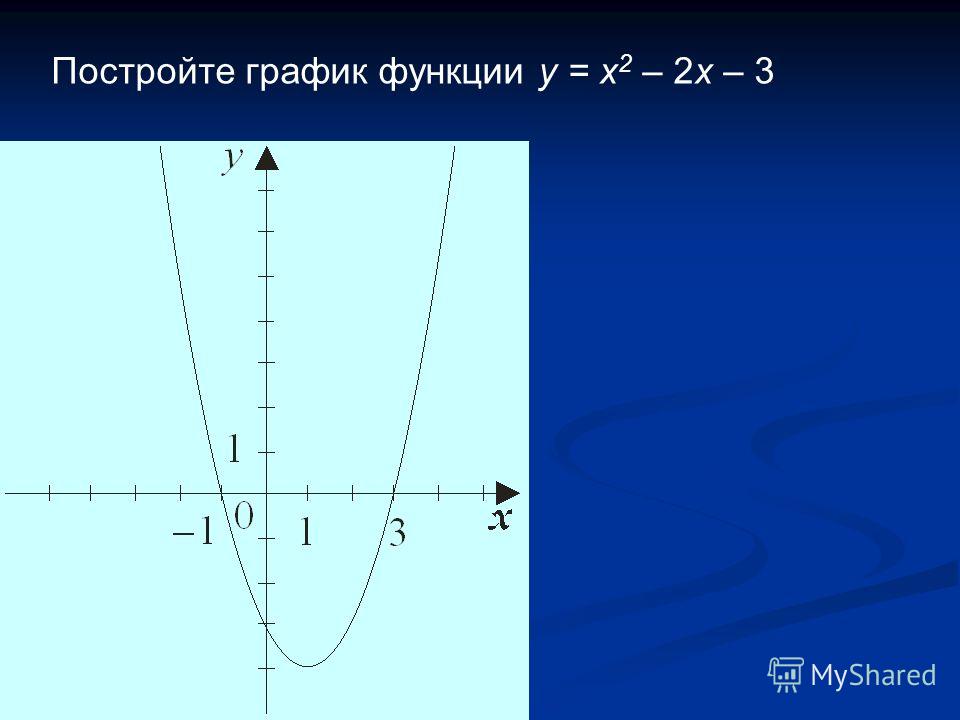 Идея состоит в том, чтобы построить графики линейных функций по обе стороны уравнения и определить, где графики совпадают.
Идея состоит в том, чтобы построить графики линейных функций по обе стороны уравнения и определить, где графики совпадают.
Пример 6
Постройте график f(x)=12x+1 и g(x)=3 на одном наборе осей и определите, где f(x)=g(x).
Решение:
Здесь f — линейная функция с наклоном 12 и y — точкой пересечения (0,1). Функция g является постоянной функцией и представляет собой горизонтальную линию. Постройте график обеих этих функций на одном наборе осей.
Из графика видно, что f(x)=g(x), где x=4. Другими словами, 12x+1=3, где x=4.
Ответ: x = 4
Мы можем немного расширить геометрическую интерпретацию для решения неравенств. Например, мы можем решить линейное неравенство 12x+1≥3, используя алгебру, следующим образом:
12x+1≥312x≥2(2)12x≥(2)2x≥4
числа больше или равные 4. Геометрически это x -значений, для которых график f(x)=12x+1 лежит над графиком g(x)=3.
Пример 7
Постройте график f(x)=12x+1 и g(x)=3 на одном наборе осей и определите, где f(x)≥g(x).
Решение:
На графике это заштриховано.
Из графика видно, что f(x)≥g(x) или 12x+1≥3, где x≥4.
Ответ: x -значения, которые решают неравенство, в интервальных обозначениях равны [4,∞).
Ключевые выводы
- Мы можем рисовать линии, нанося точки. Выберите несколько значений для x , найдите соответствующие y -значения, а затем постройте результирующие упорядоченные парные решения. Проведите линию через точки с помощью линейки, чтобы завершить график.
- Имея любые две точки на прямой, мы можем вычислить уклон алгебраически, используя формулу наклона m=riserun=y2−y1x2−x1=ΔyΔx.
- Используйте форму пересечения наклона y=mx+b, чтобы быстро нарисовать график линии. От точки пересечения и (0,b) отметьте наклон, чтобы определить вторую точку. Поскольку две точки определяют линию, проведите линию через эти две точки с помощью линейки, чтобы завершить график.

- Линейные функции имеют вид f(x)=mx+b, где наклон m и b — действительные числа. Чтобы найти точку пересечения x , если она существует, установите f(x)=0 и найдите x .
- Поскольку y=f(x), мы можем использовать y и f(x) взаимозаменяемо. Любую точку на графике функции можно выразить с помощью обозначения функции (x,f(x)).
Упражнения по теме
у=3x−6
у=2x−4
у=-5х+15
у=-3х+18
у=12х+8
у=23х+2
у=-35х+1
у=-32х+4
у=14х
г=-25x
у=10
х=-1
6х+3у=18
8x−2y=16
−2x+4y=8
-x+3y=18
12x−15y=1
16x−23y=2
х+у=0
-х+у=0
(-2,-4) и (1,-1)
(−3,0) и (3,−4)
(−52,14) и (−12,54)
(-4,-3) и (-2,-3)
(9,−5) и (9,−6)
(12,−1) и (−1,−32)
м=32; (6,10), (-4,г)
м=-13; (−6,4), (9,у)
м=-4; (−2,5), (−1,y)
м=3; (1,−2), (−2,y)
м=15; (1,у), (6,15)
м=-34; (−1,y), (−4,5)
Часть A. Построение линий по точкам
Найдите решения для пяти упорядоченных пар и постройте график.
Найдите наклон прямой, проходящей через заданные точки.
Найдите значение y , для которого наклон линии, проходящей через заданные точки, имеет заданный наклон.
По графику определить наклон.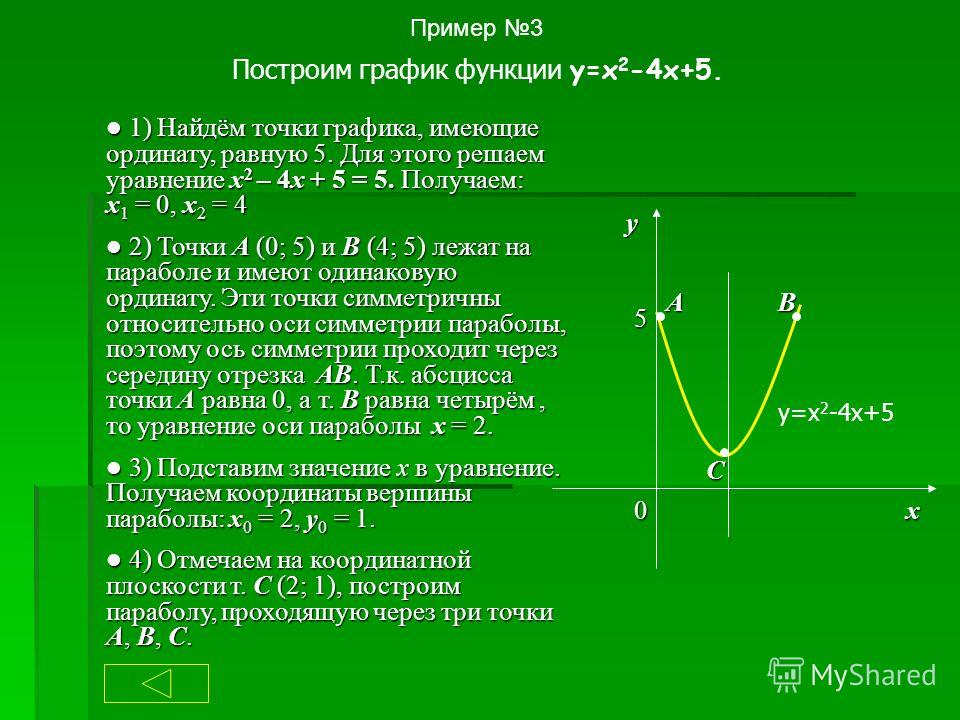
6x−3y=18
8x−2y=8
-x+12y=6
−2x−6y=8
х-2у=5
-x+3y=1
2х+3у=2
5x−4y=2
9х-4у=30
−8x+3y=28
13x+12y=−3
14x−13y=3
79x−23y=143
18x−16y=−32
−16x+29y=43
215x+16y=43
у=-14х+12
у=38х-32
у=23х+12
у=45х+1
f(x)=−5x+15
f(x)=−2x+6
f(x)=−x−2
ф(х)=х+3
f(x)=13x+2
f(x)=52x+10
f(x)=53x+2
f(x)=25x−3
f(x)=−56x+2
f(x)=−43x+3
f(x)=2x
f(x)=3
Часть B: Линейные функции
Найдите точки пересечения x и y и используйте их для построения графика следующих функций.
Нарисуйте график линейной функции и обозначьте точку пересечения размером x .
Определите линейную функцию, которая определяет данный график, и найдите точку пересечения x .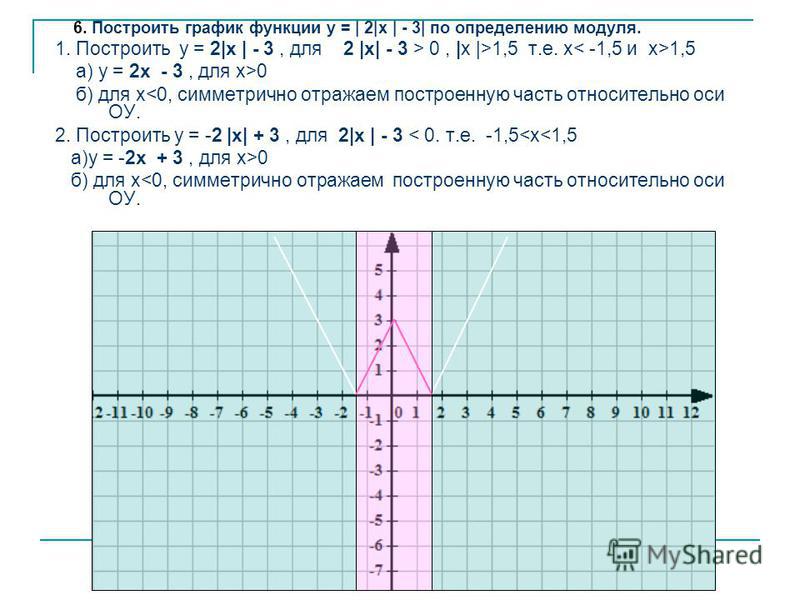
f(x)=12x−3, g(x)=1
f(x)=13x+2, g(x)=−1
f(x)=3x−2, g(x)=−5
f(x)=x+2, g(x)=−3
f(x)=−23x+4, g(x)=2
f(x)=−52x+6, g(x)=1
f(x)=3x−2, g(x)=−2x+3
f(x)=−x+6, g(x)=x+2
f(x)=-13x, g(x)=-23x+1
f(x)=23x−1, g(x)=−43x−3
f(x)=3x+7, g(x)=1
f(x)=5x−3, g(x)=2
f(x)=23x−3, g(x)=−3
f(x)=34x+2, g(x)=−1
f(x)=−x+1, g(x)=−3
f(x)=−4x+4, g(x)=8
f(x)=x−2, g(x)=−x+4
f(x)=4x−5, g(x)=x+1
f(x)=x+5, g(x)=−1
f(x)=3x−3, g(x)=6
f(x)=-45x, g(x)=-8
f(x)=-32x+6, g(x)=-3
f(x)=14x+1, g(x)=0
f(x)=35x−6, g(x)=0
f(x)=13x+2, g(x)=-13x
f(x)=32x+3, g(x)=-32x-3
Часть C: Графическая интерпретация линейных уравнений и неравенств
Постройте графики функций f и g на одном наборе осей и определите, где f(x)=g(x). Подтвердите свой ответ алгебраически.
Начертите графики функций f и g на одном наборе осей и определите, где f(x)≥g(x).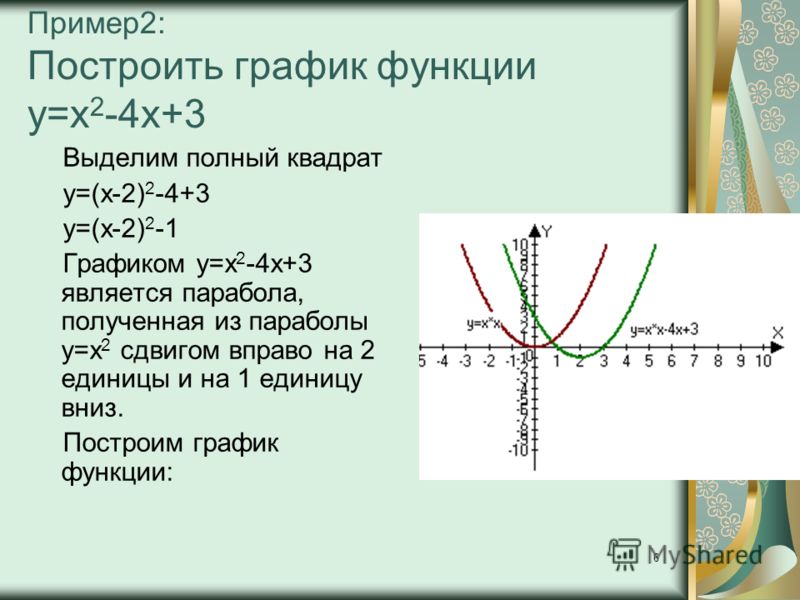 Подтвердите свой ответ алгебраически.
Подтвердите свой ответ алгебраически.
Постройте графики функций f и g на одной и той же оси и определите, где f(x)
Все ли линейные функции имеют и -пересечения? Все ли линейные функции имеют x -перехватов? Объяснять.

Может ли функция иметь более одного y -перехвата? Объяснять.
Как проверка вертикальной линии показывает, что вертикальная линия не является функцией?
Часть D: Дискуссионная доска
Ответы
1
12
Не определено
г=-5
г=1
г=-45
м=13
м=−73
м=43
м=0
f(x)=x+1; (−1,0)
f(x)=-32x; (0,0)
f(x)=-9; нет
f(x)=13x+1; (−3,0)
х=8
х=-1
х=3
х=1
х=3
[−2,∞)
[0,∞)
(-∞,4]
[3,∞)
(-∞,-6)
(10,∞)
(-∞,-4)
(-∞,-3)
Ответ может отличаться
Ответ может отличаться
Графики линейных функций | Колледж Алгебра
Результаты обучения
- График линейной функции по точкам
- График линейной функции с использованием наклона и точки пересечения с координатой Y
- График линейной функции с использованием преобразований
Ранее мы видели, что график линейной функции представляет собой прямую линию.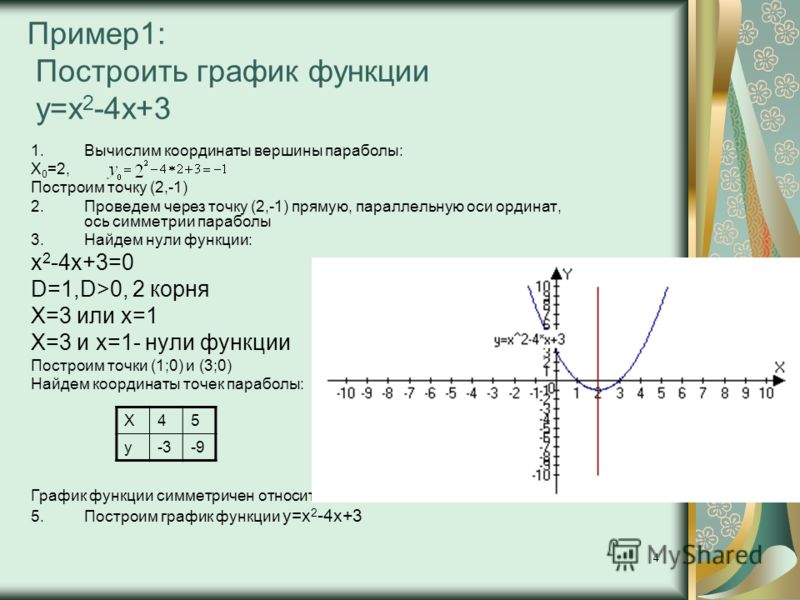 Мы также смогли увидеть точки функции, а также начальное значение на графике.
Мы также смогли увидеть точки функции, а также начальное значение на графике.
Существует три основных метода построения графиков линейных функций. Первый заключается в построении точек, а затем проведении линии через точки. Второй — с помощью г- перехват и наклон. Третий — применение преобразований к функции тождества [latex]f\left(x\right)=x[/latex].
График функции путем построения точек
Чтобы найти точки функции, мы можем выбрать входные значения, оценить функцию при этих входных значениях и вычислить выходные значения. Входные значения и соответствующие выходные значения образуют пары координат. Затем мы наносим пары координат на сетку. В общем случае мы должны оценивать функцию как минимум на двух входах, чтобы найти как минимум две точки на графике функции. Например, учитывая функцию [латекс]f\left(x\right)=2x[/latex], мы могли бы использовать входные значения 1 и 2. Вычисление функции для входного значения 1 дает выходное значение 2, которое изображается точкой (1, 2). Оценка функции для входного значения 2 дает выходное значение 4, которое представлено точкой (2, 4). Часто рекомендуется выбирать три точки, потому что, если все три точки не лежат на одной линии, мы знаем, что допустили ошибку.
Оценка функции для входного значения 2 дает выходное значение 4, которое представлено точкой (2, 4). Часто рекомендуется выбирать три точки, потому что, если все три точки не лежат на одной линии, мы знаем, что допустили ошибку.
Как: Для линейной функции построить график по точкам.
- Выберите не менее двух входных значений.
- Оценить функцию для каждого входного значения.
- Используйте полученные выходные значения для идентификации пар координат.
- Нанесите пары координат на сетку.
- Проведите линию через точки.
Пример: построение графика по точкам
График [латекс]f\left(x\right)=-\frac{2}{3}x+5[/латекс] по точкам.
Показать решение
Попробуйте
График [латекс]f\left(x\right)=-\frac{3}{4}x+6[/latex] по точкам.
Показать решение
Построение графика линейной функции с использованием точки пересечения по оси Y и наклона
Другой способ построения графика линейной функции заключается в использовании конкретных характеристик функции, а не точек на графике. Первой характеристикой является точка пересечения y-, которая является точкой, в которой входное значение равно нулю. Чтобы найти у- перехват , мы можем установить [latex]x=0[/latex] в уравнении.
Первой характеристикой является точка пересечения y-, которая является точкой, в которой входное значение равно нулю. Чтобы найти у- перехват , мы можем установить [latex]x=0[/latex] в уравнении.
Другой характеристикой линейной функции является ее наклон м , который является мерой ее крутизны. Напомним, что наклон — это скорость изменения функции. Наклон линейной функции равен отношению изменения выходов к изменению входов. Другой способ представить наклон — это разделить вертикальную разницу или подъем между любыми двумя точками на горизонтальную разницу или пробег. Наклон линейной функции будет одинаковым между любыми двумя точками. Мы столкнулись как с г- перехват и наклон в линейных функциях.
Рассмотрим следующую функцию.
[латекс]f\left(x\right)=\frac{1}{2}x+1[/latex]
Наклон равен [latex]\frac{1}{2}[/latex]. Поскольку наклон положительный, мы знаем, что график будет наклонен вверх слева направо. Точка пересечения y- представляет собой точку на графике, когда x = 0. График пересекает ось y в точке (0, 1). Теперь мы знаем наклон и точку пересечения и . Мы можем начать построение графика, нанеся точку (0, 1). Мы знаем, что наклон увеличивается по сравнению с пробегом, [латекс] м = \ гидроразрыва {\ текст {подъем}} {\ текст {прогон}} [/латекс]. В нашем примере у нас есть [latex]m=\frac{1}{2}[/latex], что означает, что подъем равен 1, а пробег равен 2. Начиная с нашего y -intercept (0, 1), мы можем подняться на 1, а затем подняться на 2 или подняться на 2, а затем подняться на 1. Мы повторяем, пока у нас не будет несколько точек, а затем мы проводим линию через точки, как показано ниже.
Точка пересечения y- представляет собой точку на графике, когда x = 0. График пересекает ось y в точке (0, 1). Теперь мы знаем наклон и точку пересечения и . Мы можем начать построение графика, нанеся точку (0, 1). Мы знаем, что наклон увеличивается по сравнению с пробегом, [латекс] м = \ гидроразрыва {\ текст {подъем}} {\ текст {прогон}} [/латекс]. В нашем примере у нас есть [latex]m=\frac{1}{2}[/latex], что означает, что подъем равен 1, а пробег равен 2. Начиная с нашего y -intercept (0, 1), мы можем подняться на 1, а затем подняться на 2 или подняться на 2, а затем подняться на 1. Мы повторяем, пока у нас не будет несколько точек, а затем мы проводим линию через точки, как показано ниже.
Общее примечание: графическое представление линейной функции график и указывает точку (0,
b ), в которой график пересекает ось y . Напомним формулу наклона:
Напомним формулу наклона:[латекс] м = \ frac {\ text {изменение на выходе (рост)}} {\ text {изменение на входе (прогон)}} = \ frac {\ Delta y} {\ Delta x} = \ frac { {y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}[/latex]
Вопросы и ответы
Все ли линейные функции имеют и -перехваты?
Да. Все линейные функции пересекают ось y и, следовательно, имеют точки пересечения с осью y. (Примечание: Вертикальная линия, параллельная оси y, не имеет точки пересечения с осью y. Имейте в виду, что вертикальная линия — это единственная линия, которая не является функцией.)
Как сделать: Учитывая уравнение для линейной функции, постройте график функции, используя точку пересечения
и и наклон.- Оцените функцию при нулевом входном значении, чтобы найти точку пересечения y-.
- Определите уклон.
- Нанесите точку пересечения y-.
- Используйте [latex]\frac{\text{rise}}{\text{run}}[/latex], чтобы определить как минимум еще две точки на линии.

- Нарисуйте линию, проходящую через точки.
Пример: построение графика с использованием точки пересечения
y- и наклонаГрафик [латекс]f\left(x\right)=-\frac{2}{3}x+5[/latex] с использованием y — перехват и наклон.
Показать решение
Попробуйте
Найдите точку на графике, который мы нарисовали в Примере: построение графика с использованием точки пересечения 92 107 и 92 108 и наклона, которая имеет отрицательное значение 92 107 x 92 108.
Показать решение
Построение графика линейной функции с использованием преобразований
Другим вариантом построения графика является использование преобразований функции тождества [латекс]f\left(x\right)=x[/latex]. Функция может быть преобразована сдвигом вверх, вниз, влево или вправо. Функцию также можно преобразовать с помощью отражения, растяжения или сжатия.
Вертикальное растяжение или сжатие
В уравнении [латекс]f\влево(х\вправо)=mx[/латекс] m действует как вертикальное растяжение или сжатие функции тождества. Когда м отрицательное значение, график также имеет вертикальное отражение. Обратите внимание, что умножение уравнения [латекс]f\left(x\right)=x[/latex] на 92 107 m 92 108 растягивает график f в 92 107 m 92 108 единиц, если 92 107 m > 1, и сжимает график f на коэффициент 92 107 м единиц, если 0 < м < 1. Это означает, что чем больше абсолютное значение м , тем круче наклон.
Когда м отрицательное значение, график также имеет вертикальное отражение. Обратите внимание, что умножение уравнения [латекс]f\left(x\right)=x[/latex] на 92 107 m 92 108 растягивает график f в 92 107 m 92 108 единиц, если 92 107 m > 1, и сжимает график f на коэффициент 92 107 м единиц, если 0 < м < 1. Это означает, что чем больше абсолютное значение м , тем круче наклон.
Вертикальные растяжения и сжатия и отражения от функции [латекс]f\left(x\right)=x[/latex].
Вертикальный сдвиг
В [latex]f\left(x\right)=mx+b[/latex] b действует как вертикальный сдвиг , перемещая график вверх и вниз, не влияя на наклон линия. Обратите внимание, что добавление значения b к уравнению [латекс]f\left(x\right)=x[/latex] сдвигает график f всего на b единиц вверх, если b положительно и | б | единицы вниз, если b отрицательное значение.
На этом графике показаны вертикальные сдвиги функции [латекс]f\влево(х\вправо)=х[/латекс].
Использование вертикального растяжения или сжатия вместе с вертикальным сдвигом — еще один способ взглянуть на определение различных типов линейных функций. Хотя это может быть не самый простой способ построения графика функции такого типа, все же важно практиковать каждый метод.
Как сделать: Имея уравнение линейной функции, используйте преобразования для построения графика линейной функции в виде [латекс]f\влево(х\вправо)=mx+b[/латекс].
- График [латекс]f\влево(х\вправо)=х[/латекс].
- Растянуть или сжать график по вертикали с коэффициентом m .
- Сдвиг графика вверх или вниз b ед.
Пример: построение графика с использованием преобразований
Построение графика [латекс]f\left(x\right)=\frac{1}{2}x — 3[/latex] с использованием преобразований.
Показать решение
Попробуйте
График [латекс]f\влево(х\вправо)=4+2x[/латекс], используя преобразования.
Показать решение
Вопросы и ответы
В примере: построение графика с использованием преобразований. Можем ли мы нарисовать график, поменяв порядок преобразований на обратный?
Нет. Порядок преобразований соответствует порядку операций. Когда функция оценивается на данном входе, соответствующий выход вычисляется в соответствии с порядком операций. Вот почему мы сначала выполнили сжатие. Например, следуя порядку операций, пусть вход будет 2.
[латекс]\begin{array}{l}f\text{(2)}=\frac{\text{1}}{\text{2}}\text{(2)}-\text{ 3}\hfill \\ =\text{1}-\text{3}\hfill \\ =-\text{2}\hfill \end{array}[/latex]
Внесите свой вклад!
У вас есть идеи по улучшению этого контента? Мы будем признательны за ваш вклад.
Улучшить эту страницуПодробнее
y = mx + b
y = mx + b это форма пересечения наклона для записи уравнения прямой линии. В уравнении «y = mx + b» «b» — это точка, в которой линия пересекает «ось y», а «m» обозначает наклон линии. Наклон или градиент линии описывает, насколько крута линия. Он может иметь как положительное, так и отрицательное значение. Когда стандартная форма линейного уравнения имеет форму Ax + By = C, где «x», «y» и «C» являются переменными, а «A», «B» являются константами, форма пересечения наклона представляет собой наиболее предпочтительный способ выражения прямой линии из-за его простоты, так как очень легко найти наклон и точку пересечения по оси y из данного уравнения.
Наклон или градиент линии описывает, насколько крута линия. Он может иметь как положительное, так и отрицательное значение. Когда стандартная форма линейного уравнения имеет форму Ax + By = C, где «x», «y» и «C» являются переменными, а «A», «B» являются константами, форма пересечения наклона представляет собой наиболее предпочтительный способ выражения прямой линии из-за его простоты, так как очень легко найти наклон и точку пересечения по оси y из данного уравнения.
| 1. | Значение y = mx + b |
| 2. | Как найти y = mx + b? |
| 3. | Написание уравнения в форме пересечения наклона |
| 4. | Решенные примеры на y mx b |
| 5. | Практические вопросы по y mx b |
| 6. | Часто задаваемые вопросы по y mx b |
Значение у = mx + b
y = mx + b – форма прямой линии, пересекающая наклон. В уравнении y = mx + b для прямой линии m называется наклоном линии, а b — точкой пересечения линии по оси y. y = mx+b, где
В уравнении y = mx + b для прямой линии m называется наклоном линии, а b — точкой пересечения линии по оси y. y = mx+b, где
y ⇒ насколько далеко вверх или вниз проходит линия,
x ⇒ как далеко проходит линия,
b ⇒ значение y при x = 0 и
34 м ⇒ насколько крута линия.Определяется как m = (разница в координатах y)/ (разница в координатах x). Обратите внимание, что разница в координатах Y обозначается как подъем или спад, а разница в координатах X обозначается как пробег.
Как найти y = mx + b?
y = mx + b — это формула, используемая для нахождения уравнения прямой линии, когда мы знаем наклон (m) и точку пересечения с осью y (b) прямой. Для определения m применим формулу, основанную на расчетах. Давайте выведем эту формулу, используя уравнение для наклона линии. Давайте рассмотрим линию, наклон которой равен «m», а точка пересечения с осью y равна «b». Пусть (x,y) — любая другая случайная точка на прямой, координаты которой неизвестны. Получаем график следующим образом.
Получаем график следующим образом.
Мы знаем, что уравнение для наклона линии в форме пересечения наклона имеет вид y = mx+b
Переписывая это, мы получаем m = (y-b) / x
Таким образом, формула для нахождения m = изменение y/ изменение x
Выведем формулу для нахождения значения наклона, если две точки \((x_{1},y_{1})\) и \((x_{2 },y_{2})\) на прямой известны. Тогда мы имеем \(y_{1} = mx_{1} + b\) и \(y_{2} = mx_{2} + b\)
Мы знаем, что наклон = изменение y/ изменение x
Подставляя значения y 1 и y 2 , мы получаем \[\begin{align}\dfrac{y_{2}-y_{1}}{x_{2}-x_{1}}& = \dfrac{(mx_{2}+b) — (mx_{1}+b)}{x_{2}-x_{1}}\\\\&=\dfrac{mx_{2}-mx_{1 }}{x_{2}-x_{1}}\\\\&= \dfrac{m(x_{2}-x_{1})}{x_{2}-x_{1}}\\\\ &=m\end{align}\]
Таким образом, мы находим, что наклон (м) рассчитывается как (изменение y)/ (изменение x)
m = (разница в координатах y)/(разница в координаты x)
Чтобы найти точку пересечения с осью y или b, подставьте значение x вместо 0 в уравнение прямой линии, которое имеет вид Ax + By + C = 0. Рассмотрим уравнение прямой линии: 3x + 5y = 10. Чтобы найти точку пересечения с осью y, замените значение «x» на 0 в уравнении и найдите «y». Подставив «x = 0» в уравнение 3x + 5y = 10, мы получим 3 (0) + 5y = 10
Рассмотрим уравнение прямой линии: 3x + 5y = 10. Чтобы найти точку пересечения с осью y, замените значение «x» на 0 в уравнении и найдите «y». Подставив «x = 0» в уравнение 3x + 5y = 10, мы получим 3 (0) + 5y = 10
⇒ 5y = 10 и, следовательно, y = 10/5 ⇒ y = 2 или ‘b’ = 2.
Написание уравнения в форме пересечения наклона
Если заданы наклон ‘m’ и точка пересечения с осью ‘b’, то уравнение прямой может быть записано в виде ‘y = mx +b’. Например, если наклон (m) для линии равен 2, а точка пересечения с осью y равна -1, то уравнение прямой линии записывается как y = 2x – 1. Значение наклона может быть положительным или отрицательным. . Как мы обсуждали в предыдущих разделах, в y = mx + b «m» представляет наклон уравнения. Чтобы найти наклон линии, учитывая ее уравнение, мы должны преобразовать его члены в форму пересечения наклона y = mx + b. Здесь «m» обозначает наклон, а «b» — точку пересечения уравнения по оси Y.
Рассмотрим уравнение 2x + 3y = 6. Требуется найти наклон и точку пересечения с осью y из уравнения, которое имеет вид Ax + By = C
Требуется найти наклон и точку пересечения с осью y из уравнения, которое имеет вид Ax + By = C
Перепишем стандартную форму уравнения линия к форме пересечения наклона y = mx + b.
2x + 3y = 6
3у = 2х + 6
y = (-2/3) x + 2
Сравнивая окончательное уравнение с y = mx + b, мы получаем, что наклон уравнения равен m = -2/3, а пересечение y уравнения равно, b = 2 или (0,2).
Важные примечания:
- Уравнение формы наклона и точки пересечения линии, наклон которой равен m, а точка пересечения по оси y равна b или (0,b) равна y = mx + b.
- Уравнение горизонтальной линии, проходящей через (a,b), имеет форму y = b.
- Уравнение вертикальной линии, проходящей через (a,b), имеет форму x = a.
- м рассчитывается по формуле подъем над пробегом или (изменение по у)/(изменение по х)
Темы, связанные с y = mx + b
Ознакомьтесь с некоторыми интересными статьями, связанными с y = mx + b.
- Формула линейного уравнения
- Уравнение прямой
- Линейные уравнения
- Линейные уравнения и полуплоскости
- Формула точки-наклона
- Двухточечная форма
Пример 1: Найдите уравнение прямой, график которой содержит точки (1,3) и (3,7)
Решение:
Требуемое уравнение прямой: y = mx + b
Используя формулу для наклона, m = изменение y / изменение x = \(\dfrac{y_{2}-y_{1}}{x_{2}-x_{1}}\) 90 152 = (7-3)/(3-1) = 4/2 ⇒ m = 2
Чтобы найти y-пересечение b, мы рассмотрим любую из координат.
Воспользуемся (1,3) и m = 2 и подставим значения в уравнение \(y_{1} = mx_{1} + b\)
3 = 2(1) + b ⇒ b = 3 — 2 = 1
Применяя m = 2 и b = 1 в уравнении прямой (y = mx + b), получаем y = 2x + 1 Таким образом, уравнение прямой имеет вид y = 2x + 1Пример 2: Найдите форму пересечения наклона линии с наклоном -2, которая проходит через точку (-1,4).

Решение :
.
Мы знаем, что форма пересечения наклона линии есть y = mx + b.
Дано, что наклон (m) = -2, а координаты, через которые проходит линия, равны (-1,4). Подставляя данные значения в уравнение формы пересечения наклона, мы получаем 4 = (-2) (-1) + b.
4 = 2 + b b = 4 — 2 = 2.
Форма пересечения наклона линии: y = — 2 x + 2,
перейти к слайдуперейти к слайду
Есть вопросы по основным математическим понятиям?
Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, почему математика стоит за нашими сертифицированными экспертами.0034
Часто задаваемые вопросы по y mx b
Что такое y = mx + b?
y = mx + b является представлением уравнения прямой линии. Это называется формой пересечения наклона. «m» относится к наклону линии, а «b» относится к «y-перехвату» линии.
Как найти наклон линии?
Для двух координат (x 1 , y 1 ) и (x 2 , y 2 ) наклон линии представляет собой отношение разности между разницей между координатами y и разностью между координатами x, также известный как подъем над пробегом.

 11.16
11.16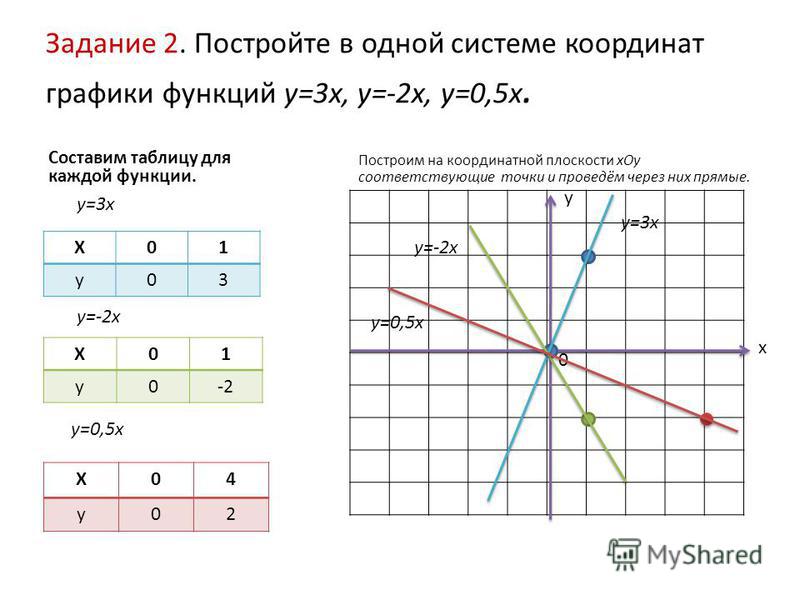 ..)
..)  ..)
..)  ..)
..)  к. установлена абсолютная ссылка.
к. установлена абсолютная ссылка.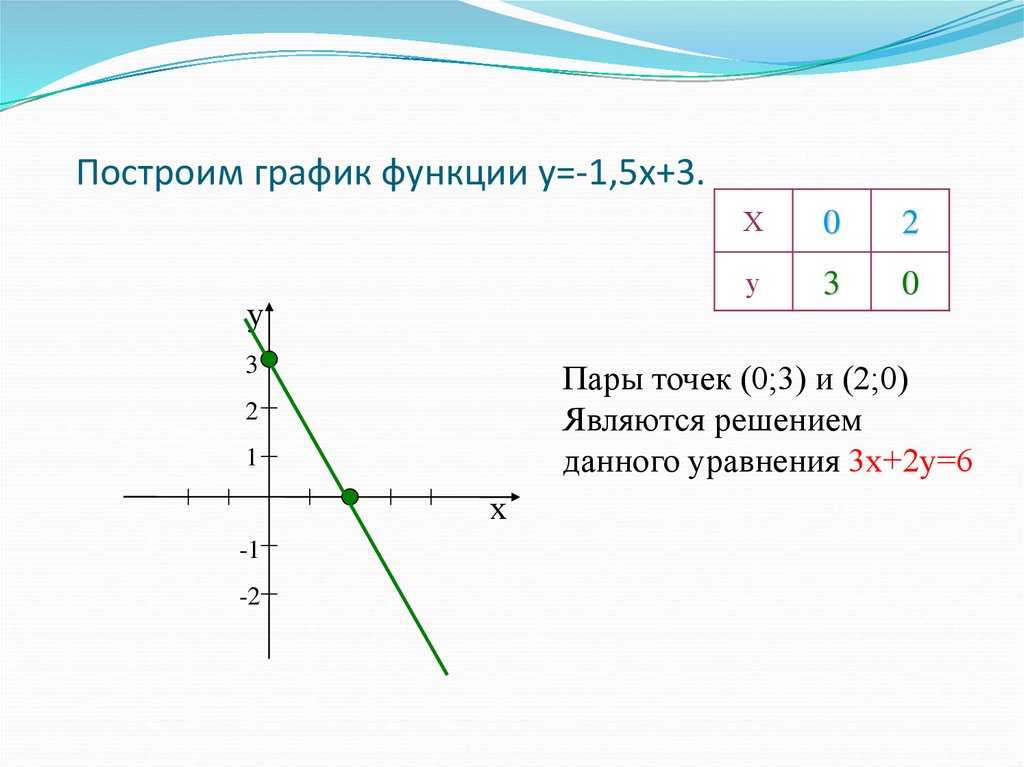
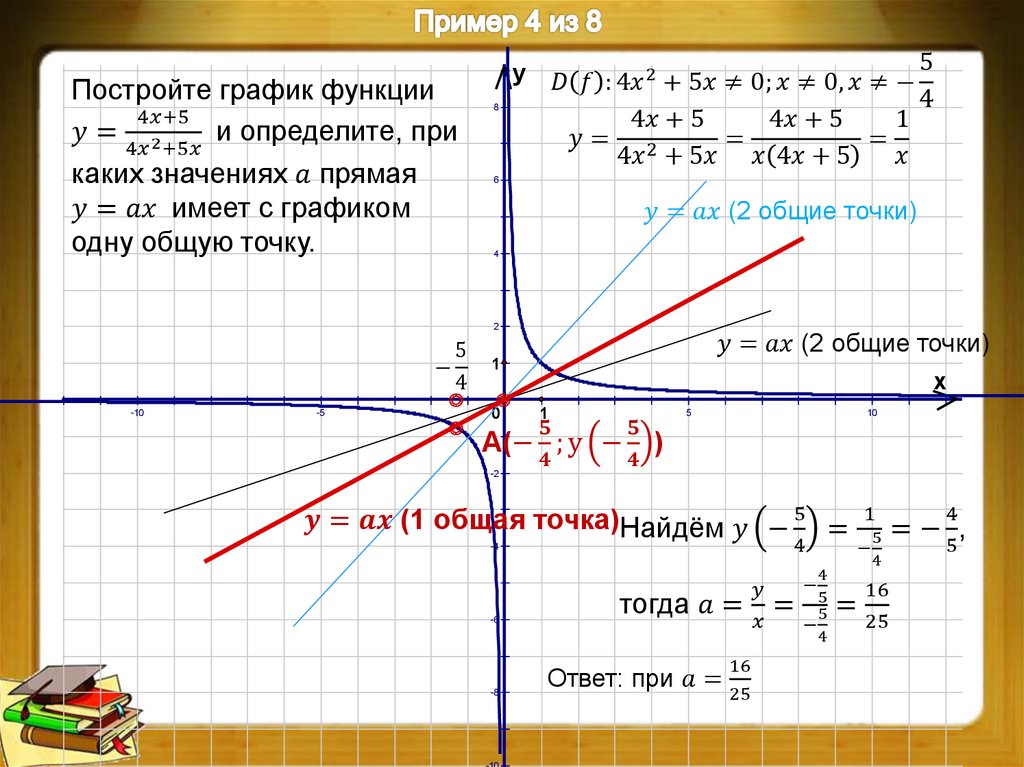 Если же нужно одновременно просматривать диаграмму и данные, на основе которых она была построена, то тогда создаётся внедрённая диаграмма.
Если же нужно одновременно просматривать диаграмму и данные, на основе которых она была построена, то тогда создаётся внедрённая диаграмма.
 deanza.edu/faculty/bloomroberta/math21/afm3files.html.html
deanza.edu/faculty/bloomroberta/math21/afm3files.html.html