y=3x-1
Сократите x-1 в числителе и знаменателе.
Алгебра 8 Мордкович (упр. 24.1
Алгебра 8 класс. Часть 2 (Задачник) УМК Мордкович (2018-2020). § 24. Функция у = ах2 + bх + с, её свойства и график. ОТВЕТЫ на упражнения 24.1 — 24.55. ГЛАВА 3. Квадратичная функция. Функция у = k/x. Нажмите на спойлер, чтобы посмотреть ответ на задание.
Вернуться в ОГЛАВЛЕНИЕ.
Задание № 24.1. Какая из следующих функций является квадратичной:
а) у = 3x2 + 5х + 6; в) у = 5х2 – 7х;
б) у = 3х – 1; г) у = 9x ?
Смотреть ответы на № 24.1
Задание № 24.2. Назовите коэффициенты a, b и с квадратичной функции:
а) у = 7х2 – 3x – 2; в) у = 8x2 – 2х;
б) y = x2/2 + 1; г) y = 2x/5 + 1/7 – 3x2/10.
Смотреть ответы на № 24.2
Задание № 24.3. Составьте квадратный трехчлен ах2 + bх + с, у которого:
а) а = 2, b = –1, с = 4; в) а = 9, b = –3, с = –1;
б) а = –1, b = 7, с = 0; г) а = 1, b = 0, с = 5.
Смотреть ответы на № 24.3
Задание № 24.4. Не выполняя построения, ответьте на вопрос, куда (вверх или вниз) направлены ветви параболы:
а) у = Зх2 – 7х + 1; в) у = –7х
б) у = —5x2 + 2x + 0,5; г) y = 6х2 + 9х + 1.
Смотреть ответы на № 24.4
Задание № 24.5. Запишите уравнение прямой, которая является осью симметрии параболы:
а) у = 2х2 – х + 1; в) у = 7х2 + 12x + 4;
б) у = –5х2 + 2х – 2; г) у = –х2 + 2x + 1.
Смотреть ответы на № 24.5
Задание № 24.6. Найдите координаты вершины параболы:
а) у = 4x2 + 8x – 1; в) у = –x2 + х – 1;
б) у = –3х2 – 6х + 2; г) у = 5x2 – 10x + 4.
Смотреть ответы на № 24.6
Задание № 24.7.
Смотреть ответы на № 24.7
Задание № 24.8.
Смотреть ответы на № 24.8
Задание № 24.9.
Смотреть ответы на № 24.9
Задание № 24.10.
Смотреть ответы на № 24.10
Задание № 24.11.
Смотреть ответы на № 24.11
Задание № 24.12.
Смотреть ответы на № 24.12
Задание № 24.13.
Смотреть ответы на № 24.13
Задание № 24.14.
Смотреть ответы на № 24.14
Задание № 24.15.
Смотреть ответы на № 24.15
Задание № 24.16.
Смотреть ответы на № 24.16
Задание № 24.17.
Смотреть ответы на № 24.17
Задание № 24.18. Постройте график функции у = х2 + 4х – 5. С помощью графика определите:
а) значение функции при х = –3; 0; 1;
б) значения аргумента, если у = –8; –5; 0;
в) наименьшее значение функции;
г) промежутки возрастания и убывания функции;
д) значения аргумента, при которых у > 0, у < 0.
Смотреть ответы на № 24.18
Задание № 24.19.
а) значение функции при х = –2; 0; 3;
б) значения аргумента, если у = –10; 6; 0;
в) наибольшее значение функции;
г) промежутки возрастания и убывания функции;
д) значения аргумента, при которых у > 0, у < 0.
Смотреть ответы на № 24.19
Задание № 24.20.
Смотреть ответы на № 24.20
Задание № 24.21.
Смотреть ответы на № 24.21
Задание № 24.22.
Смотреть ответы на № 24.22
Задание № 24.23.
Смотреть ответы на № 24.23
Задание № 24.24.
Смотреть ответы на № 24.24
Задание № 24.25.
Смотреть ответы на № 24.25
Задание № 24.26.
Смотреть ответы на № 24.26
Задание № 24.27.
Смотреть ответы на № 24.27
Задание № 24.28. а) Найдите значение коэффициента с, если известно, что график функции у = х2 + 4х + с пересекает ось ординат в точке А(0; 2).
б) Найдите значение коэффициента с, если известно, что график функции у = х2 + 4х + с пересекает ось ординат в точке В(0; 4).
Смотреть ответы на № 24.28
Задание № 24.29. а) Найдите значение коэффициента а, если известно, что график функции у = ах2 + 4х + 5 пересекает ось абсцисс в точке М(–10; 0).
б) Найдите значение коэффициента а, если известно, что график функции у = ах2 + 4х – 8 пересекает ось абсцисс в точке N(4; 0).
Смотреть ответы на № 24.29
Задание № 24.30. ) Найдите значение коэффициента b, если известно, что осью симметрии графика функции у = х2 + bх + 4 является прямая х = 1.
б) Найдите значение коэффициента b, если известно, что осью симметрии графика функции у = 2x2 + bх – 3 является прямая х = –4.
Смотреть ответы на № 24.30
Задание № 24.31. Докажите, что функция у = х2 – 4х + 5 является возрастающей на промежутке (3; 12).
Смотреть ответы на № 24.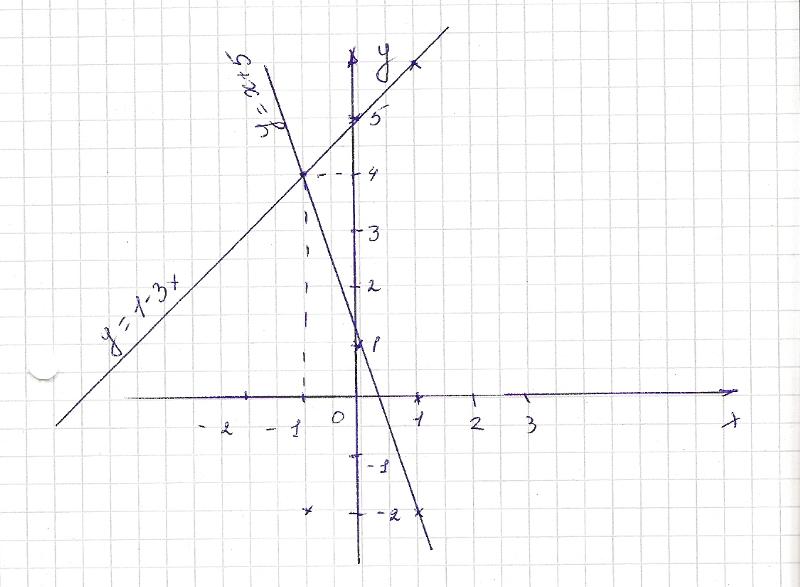 31
31
Задание № 24.32. Докажите, что функция у = х2 + 6х – 7 является убывающей на промежутке (–8; –5).
Смотреть ответы на № 24.32
Задание № 24.33.
Смотреть ответы на № 24.33
Задание № 24.34.
Смотреть ответы на № 24.34
Задание № 24.35.
Смотреть ответы на № 24.35
Задание № 24.36.
Смотреть ответы на № 24.36
Задание № 24.37.
Смотреть ответы на № 24.37
Задание № 24.38.
Смотреть ответы на № 24.38
Задание № 24.39.
Смотреть ответы на № 24.39
Задание № 24.40.
Смотреть ответы на № 24.40
Задание № 24.41.
Смотреть ответы на № 24.41
Задание № 24.42.
Смотреть ответы на № 24.42
Задание № 24.43.
Смотреть ответы на № 24.43
Задание № 24.44.
Смотреть ответы на № 24.44
Задание № 24.45.
Смотреть ответы на № 24.45
Задание № 24.46.
Смотреть ответы на № 24.46
Задание № 24.47.
Смотреть ответы на № 24.47
Задание № 24.48.
Смотреть ответы на № 24.48
Задание № 24.49.
Смотреть ответы на № 24.49
Задание № 24.50.
Смотреть ответы на № 24.50
Задание № 24.51.
Смотреть ответы на № 24.51
Задание № 24.52.
Смотреть ответы на № 24.52
Задание № 24.53.
Смотреть ответы на № 24.53
Задание № 24.54.
Смотреть ответы на № 24.54
Задание № 24.55.
Смотреть ответы на № 24.55
Вы смотрели: Алгебра 8 класс. Часть 2 (Задачник) УМК Мордкович (2018-2020). ГЛАВА 3. Квадратичная функция. Функция у = k/x. § 24. Функция у = ах2 + bх + с, её свойства и график. ОТВЕТЫ на упражнения 24.1 — 24.55. Вернуться в ОГЛАВЛЕНИЕ.
Просмотров: 72 433
3-8
x=\frac{-\left(y+4\right)±|y-2|}{-6}
Умножить 2 раза -3.
x=\frac{|y-2|-y-4}{-6}
Теперь решите уравнение x=\frac{-\left(y+4\right)±|y-2|}{ -6}, когда ± плюс. Добавьте -\left(y+4\right) к |-2+y|.
x=-\frac{|y-2|}{6}+\frac{y}{6}+\frac{2}{3}
Разделить -y-4+|-2+y| на -6.
x=\frac{-|y-2|-y-4}{-6}
Теперь решите уравнение x=\frac{-\left(y+4\right)±|y-2|} {-6}, когда ± минус. Вычесть |-2+y| от -\влево(у+4\вправо). 9{2}}{36}}
Извлеките квадратный корень из обеих частей уравнения.
x-\frac{y}{6}-\frac{2}{3}=\frac{|y-2|}{6} x-\frac{y}{6}-\frac{2} {3}=-\frac{|y-2|}{6}
Упрощение.
x=\frac{|y-2|}{6}+\frac{y}{6}+\frac{2}{3} x=-\frac{|y-2|}{6}+ \frac{y}{6}+\frac{2}{3}
Вычтите -\frac{y}{6}-\frac{2}{3} из обеих частей уравнения.
x=-\frac{|y-2|}{6}+\frac{y}{6}+\frac{2}{3}\text{, }x\neq 1 x=\frac{| y-2|}{6}+\frac{y}{6}+\frac{2}{3}\text{, }x\neq 1 9{ 2 } — 4 x — 5 = 0
Тригонометрия
4 \sin \theta \cos \theta = 2 \sin \theta
Линейное уравнение
y = 3x + 4
Арифметика 3 907
90Матрица
\left[ \begin{array} { l l } { 2 } & { 3 } \\ { 5 } & { 4 } \end{array} \right] \left[ \begin {array} { l l l } { 2 } & { 0 } & { 3 } \\ { -1 } & { 1 } & { 5 } \end{массив} \right]
Одновременное уравнение
\left.
