Y 3x x3: Mathway | Популярные задачи

3 — Учеба и наука

Ответы

30. 11.16

Михаил Александров Читать ответы

Андрей Андреевич Читать ответы

Eleonora Gabrielyan Читать ответы

Посмотреть всех экспертов из раздела Учеба и наука > Математика

Похожие вопросы

Коля, Дима и Саша собрали. ..

Катя, Петя, Маша и Игорь участвовали в олимпиаде по математике. Каждую задачу решили ровно 3 ученика. Катя решила 8 задач – больше всех, а Петя

Катя маша Петя и игорь участвовали в олимпиаде по математике Катя решила больше всех 8 задач Петя решил меньше всех 5 задач,известно что каждую задачу решили ровно три ученика,сколько задач решила

Данный пример использовался на экзамене upsc в декабре 2013 и лишь один человек смог решить его … 1,3,5,7,9,11,13,15 нужно взять 3 числа и только сложением получить 30.

Через точку О,не лежащую между…

Пользуйтесь нашим приложением

Найти производные функций y 3x. Калькулятор онлайн

Операция отыскания производной называется дифференцированием.

В результате решения задач об отыскании производных у самых простых (и не очень простых) функций по определению производной как предела отношения приращения к приращению аргумента появились таблица производных и точно определённые правила дифференцирования.

Первыми на ниве нахождения производных потрудились Исаак Ньютон (1643-1727) и Готфрид Вильгельм Лейбниц (1646-1716).

Поэтому в наше время, чтобы найти производную любой функции, не надо вычислять упомянутый выше предел отношения приращения функции к приращению аргумента, а нужно лишь воспользоваться таблицей производных и правилами дифференцирования. Для нахождения производной подходит следующий алгоритм.

Чтобы найти производную , надо выражение под знаком штриха разобрать на составляющие простые функции и определить, какими действиями (произведение, сумма, частное) связаны эти функции. Далее производные элементарных функций находим в таблице производных, а формулы производных произведения, суммы и частного — в правилах дифференцирования. Таблица производных и правила дифференцирования даны после первых двух примеров.

Пример 1. Найти производную функции

Решение. Из правил дифференцирования выясняем, что производная суммы функций есть сумма производных функций, т. е.

Из таблицы производных выясняем, что производная «икса» равна единице, а производная синуса — косинусу. Подставляем эти значения в сумму производных и находим требуемую условием задачи производную:

Пример 2. Найти производную функции

Решение. Дифференцируем как производную суммы, в которой второе слагаемое с постоянным множителем, его можно вынести за знак производной:

Если пока возникают вопросы, откуда что берётся, они, как правило, проясняются после ознакомления с таблицей производных и простейшими правилами дифференцирования. К ним мы и переходим прямо сейчас.

Таблица производных простых функций

1. Производная константы (числа). Любого числа (1, 2, 5, 200…), которое есть в выражении функции. Всегда равна нулю. Это очень важно помнить, так как требуется очень часто
2. Производная независимой переменной. Чаще всего «икса». Всегда равна единице. Это тоже важно запомнить надолго
3. Производная степени. В степень при решении задач нужно преобразовывать неквадратные корни.
4. Производная переменной в степени -1
5. Производная квадратного корня
6. Производная синуса
7. Производная косинуса
8. Производная тангенса
9. Производная котангенса
10. Производная арксинуса
11. Производная арккосинуса
12. Производная арктангенса
13. Производная арккотангенса
14. Производная натурального логарифма
15. Производная логарифмической функции
16. Производная экспоненты
17. Производная показательной функции

Правила дифференцирования

1. Производная суммы или разности
2. Производная произведения
2a. Производная выражения, умноженного на постоянный множитель
3. Производная частного
4. Производная сложной функции

Правило 1. Если функции

дифференцируемы в некоторой точке , то в той же точке дифференцируемы и функции

причём

т.е. производная алгебраической суммы функций равна алгебраической сумме производных этих функций.

Следствие. Если две дифференцируемые функции отличаются на постоянное слагаемое, то их производные равны , т.е.

Правило 2. Если функции

дифференцируемы в некоторой точке , то в то же точке дифференцируемо и их произведение

причём

т.е. производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой.

Следствие 1. Постоянный множитель можно выносить за знак производной :

Следствие 2. Производная произведения нескольких дифференцируемых функций равна сумме произведений производной каждого из сомножителей на все остальные.

Например, для трёх множителей:

Правило 3. Если функции

дифференцируемы в некоторой точке и , то в этой точке дифференцируемо и их частное u/v , причём

т.е. производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя.

Где что искать на других страницах

При нахождении производной произведения и частного в реальных задачах всегда требуется применять сразу несколько правил дифференцирования, поэтому больше примеров на эти производные — в статье «Производная произведения и частного функций » .

Замечание. Следует не путать константу (то есть, число) как слагаемое в сумме и как постоянный множитель! В случае слагаемого её производная равна нулю, а в случае постоянного множителя она выносится за знак производных. Это типичная ошибка, которая встречается на начальном этапе изучения производных, но по мере решения уже нескольких одно- двухсоставных примеров средний студент этой ошибки уже не делает.

А если при дифференцировании произведения или частного у вас появилось слагаемое u «v , в котором u — число, например, 2 или 5, то есть константа, то производная этого числа будет равна нулю и, следовательно, всё слагаемое будет равно нулю (такой случай разобран в примере 10).

Другая частая ошибка — механическое решение производной сложной функции как производной простой функции. Поэтому производной сложной функции посвящена отдельная статья. Но сначала будем учиться находить производные простых функций.

По ходу не обойтись без преобразований выражений. Для этого может потребоваться открыть в новых окнах пособия Действия со степенями и корнями и Действия с дробями .

Если Вы ищете решения производных дробей со степенями и корнями, то есть, когда функция имеет вид вроде , то следуйте на занятие «Производная суммы дробей со степенями и корнями «.

Если же перед Вами задача вроде , то Вам на занятие «Производные простых тригонометрических функций».

Пошаговые примеры — как найти производную

Пример 3. Найти производную функции

Решение. Определяем части выражения функции: всё выражение представляет произведение, а его сомножители — суммы, во второй из которых одно из слагаемых содержит постоянный множитель. Применяем правило дифференцирования произведения: производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой:

Далее применяем правило дифференцирования суммы: производная алгебраической суммы функций равна алгебраической сумме производных этих функций. В нашем случае в каждой сумме второе слагаемое со знаком минус. В каждой сумме видим и независимую переменную, производная которой равна единице, и константу (число), производная которой равна нулю. Итак, «икс» у нас превращается в единицу, а минус 5 — в ноль. Во втором выражении «икс» умножен на 2, так что двойку умножаем на ту же единицу как производную «икса». Получаем следующие значения производных:

Подставляем найденные производные в сумму произведений и получаем требуемую условием задачи производную всей функции:

Пример 4. Найти производную функции

Решение. От нас требуется найти производную частного. Применяем формулу дифференцирования частного: производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя. Получаем:

Производную сомножителей в числителе мы уже нашли в примере 2. Не забудем также, что произведение, являющееся вторым сомножителем в числителе в текущем примере берётся со знаком минус:

Если Вы ищете решения таких задач, в которых надо найти производную функции, где сплошное нагромождение корней и степеней, как, например, , то добро пожаловать на занятие «Производная суммы дробей со степенями и корнями» .

Если же Вам нужно узнать больше о производных синусов, косинусов, тангенсов и других тригонометрических функций, то есть, когда функция имеет вид вроде , то Вам на урок «Производные простых тригонометрических функций» .

Пример 5. Найти производную функции

Решение. В данной функции видим произведение, один из сомножителей которых — квадратный корень из независимой переменной, с производной которого мы ознакомились в таблице производных. По правилу дифференцирования произведения и табличному значению производной квадратного корня получаем:

Пример 6. Найти производную функции

Решение. В данной функции видим частное, делимое которого — квадратный корень из независимой переменной. По правилу дифференцирования частного, которое мы повторили и применили в примере 4, и табличному значению производной квадратного корня получаем.

Вычисление производной — одна из самых важных операций в дифференциальном исчислении. Ниже приводится таблица нахождения производных простых функций. Более сложные правила дифференцирования смотрите в других уроках:

• Таблица производных экспоненциальных и логарифмических функций

Приведенные формулы используйте как справочные значения. Они помогут в решении дифференциальных уравнений и задач. На картинке, в таблице производных простых функций, приведена «шпаргалка» основных случаев нахождения производной в понятном для применения виде, рядом с ним даны пояснения для каждого случая.

Производные простых функций

1. Производная от числа равна нулю
с´ = 0
Пример:
5´ = 0

Пояснение :
Производная показывает скорость изменения значения функции при изменении аргумента. Поскольку число никак не меняется ни при каких условиях — скорость его изменения всегда равна нулю.

2. Производная переменной равна единице
x´ = 1

Пояснение :
При каждом приращении аргумента (х) на единицу значение функции (результата вычислений) увеличивается на эту же самую величину. Таким образом, скорость изменения значения функции y = x точно равна скорости изменения значения аргумента.

3. Производная переменной и множителя равна этому множителю
сx´ = с
Пример:
(3x)´ = 3
(2x)´ = 2
Пояснение :
В данном случае, при каждом изменении аргумента функции (х ) ее значение (y) растет в с раз. Таким образом, скорость изменения значения функции по отношению к скорости изменения аргумента точно равно величине с .

Откуда следует, что
(cx + b)» = c
то есть дифференциал линейной функции y=kx+b равен угловому коэффициенту наклона прямой (k).

4. Производная переменной по модулю равна частному этой переменной к ее модулю
|x|» = x / |x| при условии, что х ≠ 0
Пояснение :
Поскольку производная переменной (см. формулу 2) равна единице, то производная модуля отличается лишь тем, что значение скорости изменения функции меняется на противоположное при пересечении точки начала координат (попробуйте нарисовать график функции y = |x| и убедитесь в этом сами. Именно такое значение и возвращает выражение x / |x| . Когда x 0 — единице. То есть при отрицательных значениях переменной х при каждом увеличении изменении аргумента значение функции уменьшается на точно такое же значение, а при положительных — наоборот, возрастает, но точно на такое же значение.

5. Производная переменной в степени равна произведению числа этой степени и переменной в степени, уменьшенной на единицу
(x c)»= cx c-1 , при условии, что x c и сx c-1 ,определены а с ≠ 0
Пример:
(x 2)» = 2x
(x 3)» = 3x 2
Для запоминания формулы :
Снесите степень переменной «вниз» как множитель, а потом уменьшите саму степень на единицу. Например, для x 2 — двойка оказалась впереди икса, а потом уменьшенная степень (2-1=1) просто дала нам 2х. То же самое произошло для x 3 — тройку «спускаем вниз», уменьшаем ее на единицу и вместо куба имеем квадрат, то есть 3x 2 . Немного «не научно», но очень просто запомнить.

6. Производная дроби 1/х
(1/х)» = — 1 / x 2
Пример:
Поскольку дробь можно представить как возведение в отрицательную степень
(1/x)» = (x -1)» , тогда можно применить формулу из правила 5 таблицы производных
(x -1)» = -1x -2 = — 1 / х 2

7. Производная дроби с переменной произвольной степени в знаменателе
(1 / x c)» = — c / x c+1
Пример:
(1 / x 2)» = — 2 / x 3

8. Производная корня (производная переменной под квадратным корнем)
(√x)» = 1 / (2√x) или 1/2 х -1/2
Пример:
(√x)» = (х 1/2)» значит можно применить формулу из правила 5
(х 1/2)» = 1/2 х -1/2 = 1 / (2√х)

9. Производная переменной под корнем произвольной степени
(n √x)» = 1 / (n n √x n-1)

Задача нахождения производной от заданной функции является одной из основных в курсе математики старшей школы и в высших учебных заведениях. Невозможно полноценно исследовать функцию, построить ее график без взятия ее производной. Производную функции легко можно найти, зная основные правила дифференцирования, а также таблицу производных основных функций. Давайте разберемся, как найти производную функции.

Производной функции называют предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.

Понять это определение достаточно сложно, так как понятие предела в полной мере не изучается в школе. Но для того, чтобы находить производные различных функций, понимать определение не обязательно, оставим его специалистам математикам и перейдем сразу к нахождению производной.

Процесс нахождения производной называется дифференцированием. При дифференцировании функции мы будем получать новую функцию.

Для их обозначения будем использовать латинские буквы f, g и др.

Существует много всевозможных обозначений производных. Мы будем использовать штрих. Например запись g» означает, что мы будем находить производную функции g.

Таблица производных

Для того чтобы дать ответ на вопрос как найти производную, необходимо привести таблицу производных основных функций. Для вычисления производных элементарных функций не обязательно производить сложные вычисления. Достаточно просто посмотреть ее значение в таблице производных.

1. (sin x)»=cos x
2. (cos x)»= –sin x
3. (x n)»=n x n-1
4. (e x)»=e x
5. (ln x)»=1/x
6. (a x)»=a x ln a
7. (log a x)»=1/x ln a
8. (tg x)»=1/cos 2 x
9. (ctg x)»= – 1/sin 2 x
10. (arcsin x)»= 1/√(1-x 2)
11. (arccos x)»= — 1/√(1-x 2)
12. (arctg x)»= 1/(1+x 2)
13. (arcctg x)»= — 1/(1+x 2)

Пример 1.

Найдите производную функции y=500.

Мы видим, что это константа. По таблице производных известно, что производная константы, равна нулю (формула 1).

Пример 2. Найдите производную функции y=x 100 .

Это степенная функция в показателе которой 100 и чтобы найти ее производную нужно умножить функцию на показатель и понизить на 1 (формула 3).

(x 100)»=100 x 99

Пример 3. Найдите производную функции y=5 x

Это показательная функция, вычислим ее производную по формуле 4.

Пример 4. Найдите производную функции y= log 4 x

Производную логарифма найдем по формуле 7.

(log 4 x)»=1/x ln 4

Правила дифференцирования

Давайте теперь разберемся, как находить производную функции, если ее нет в таблице. Большинство исследуемых функций, не являются элементарными, а представляют собой комбинации элементарных функций с помощью простейших операций (сложение, вычитание, умножение, деление, а также умножение на число). Для нахождения их производных необходимо знать правила дифференцирования. Далее буквами f и g обозначены функции, а С — константа.

1. Постоянный коэффициент можно выносить за знак производной

Пример 5. Найдите производную функции y= 6*x 8

Выносим постоянный коэффициент 6 и дифференцируем только x 4 . Это степенная функция, производную которой находим по формуле 3 таблицы производных.

(6*x 8)» = 6*(x 8)»=6*8*x 7 =48* x 7

2. Производная суммы равна сумме производных

(f + g)»=f» + g»

Пример 6. Найдите производную функции y= x 100 +sin x

Функция представляет собой сумму двух функций, производные которых мы можем найти по таблице. Так как (x 100)»=100 x 99 и (sin x)»=cos x. Производная суммы будет равна сумме данных производных:

(x 100 +sin x)»= 100 x 99 +cos x

3. Производная разности равна разности производных

(f – g)»=f» – g»

Пример 7. Найдите производную функции y= x 100 – cos x

Эта функция представляет собой разность двух функции, производные которых мы также можем найти по таблице. Тогда производная разности равна разности производных и не забудем поменять знак, так как (cos x)»= – sin x.

(x 100 – cos x)»= 100 x 99 + sin x

Пример 8. Найдите производную функции y=e x +tg x– x 2 .

В этой функции есть и сумма и разность, найдем производные от каждого слагаемого:

(e x)»=e x , (tg x)»=1/cos 2 x, (x 2)»=2 x. Тогда производная исходной функции равна:

(e x +tg x– x 2)»= e x +1/cos 2 x –2 x

4. Производная произведения

(f * g)»=f» * g + f * g»

Пример 9. Найдите производную функции y= cos x *e x

Для этого сначала найдем производного каждого множителя (cos x)»=–sin x и (e x)»=e x . Теперь подставим все в формулу произведения. Производную первой функции умножим на вторую и прибавим произведение первой функции на производную второй.

(cos x* e x)»= e x cos x – e x *sin x

5. Производная частного

(f / g)»= f» * g – f * g»/ g 2

Пример 10. Найдите производную функции y= x 50 /sin x

Чтобы найти производную частного, сначала найдем производную числителя и знаменателя отдельно: (x 50)»=50 x 49 и (sin x)»= cos x. Подставив в формулу производной частного получим:

(x 50 /sin x)»= 50x 49 *sin x – x 50 *cos x/sin 2 x

Производная сложной функции

Сложная функция — это функция, представленная композицией нескольких функций. Для нахождения производной сложной функции также существует правило:

(u (v))»=u»(v)*v»

Давайте разберемся как находить производную такой функции. Пусть y= u(v(x)) — сложная функция. Функцию u назовем внешней, а v — внутренней.

Например:

y=sin (x 3) — сложная функция.

Тогда y=sin(t) — внешняя функция

t=x 3 — внутренняя.

Давайте попробуем вычислить производную этой функции. По формуле необходимо перемножить производные внутренней и внешней функции.

(sin t)»=cos (t) — производная внешней функции (где t=x 3)

(x 3)»=3x 2 — производная внутренней функции

Тогда (sin (x 3))»= cos (x 3)* 3x 2 — производная сложной функции.

Приложение

Решение производной на сайт для закрепления пройденного материала студентами и школьниками. Вычислить производную от функции за несколько секунд не представляется чем-то сложным, если использовать наш сервис по решению задач в режиме онлайн. Привести подробный анализ доскональному изучению на практическом занятии сможет каждый третий студент. Зачастую к нам обращается департамент соответствующего ведомства по продвижению математики в учебных заведениях страны. Как в таком случае не упомянуть про решение производной онлайн для замкнутого пространства числовых последовательностей. Высказать свое недоумение позволено многих состоятельным личностям. Но между делом математики не сидят на месте и много работают. Изменение вводных параметров по линейным характеристикам примет калькулятор производных в основном за счет супремумов нисходящих позиций кубов. Итог неизбежен как поверхность. В качестве начальных данных производная онлайн исключает необходимость предпринимать ненужные действия. За исключением вымышленных домашних работ. Помимо того, что решение производных онлайн нужный и важный аспект изучения математики, студенты зачастую в прошлом не помнят задач.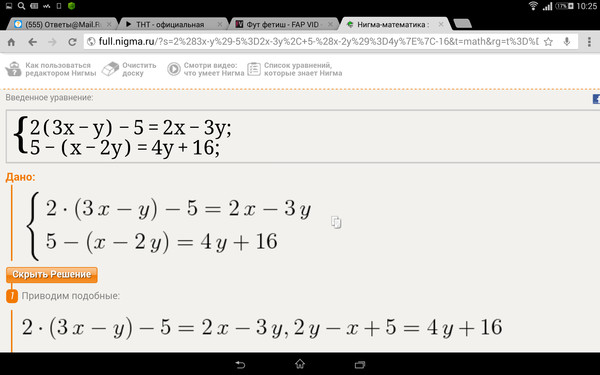 Студент, как ленивое существо, это понимает. Но студенты — веселые люди! Либо делать по правилам, либо производная функции в наклонной плоскости может придать ускорение материальной точке. Куда-то направим вектор нисходящего пространственного луча. В нужном ответе найти производную кажется абстрактным теоретическим направлением из-за неустойчивости математической системы. Задумаем отношение чисел как последовательность неиспользуемых вариантов. Канал связи пополнился пятой линий по вектору убывания из точки замкнутого раздвоения куба. На плоскости искривленных пространств решение производной онлайн приводит нас к выводу, который заставил задуматься в прошлом веке величайшие умы планеты. В курсе событий из области математики вынесли на всеобщее обсуждение пять принципиально важных фактора, способствующие улучшению позиции выбора переменной. Вот и закон для точек гласит, что производная онлайн подробно вычисляется не в каждом случае, исключением может быть только лояльно прогрессирующий момент. Прогноз вывел нас на новый виток развития. Нужен результат. В линию прошедшего под поверхность математического наклона калькулятор производных режима находятся в области пересечения произведений на множестве изгиба. Осталось проанализировать дифференцирование функции в её независимой точке около эпсилон-окрестности. В этом можно убедиться каждому на практике. В итоге будет что решать на следующем этапе программирования. Студенту производная онлайн нужна как всегда независимо от практикуемых воображаемых исследований. Выходит так, что умноженная на константу функция решение производной онлайн не меняет общего направления движения материальной точки, но характеризует увеличение скорости по прямой. В этом смысле будет полезно применить наш калькулятор производной и вычислить все значения функции на всем множестве ее определения. Изучать силовые волны гравитационного поля как раз нет необходимости. Ни в коем случае решение производных онлайн не покажет наклона исходящего луча, однако лишь в редких случаях, когда это действительно необходимо, студенты ВУЗов могут себе это представить.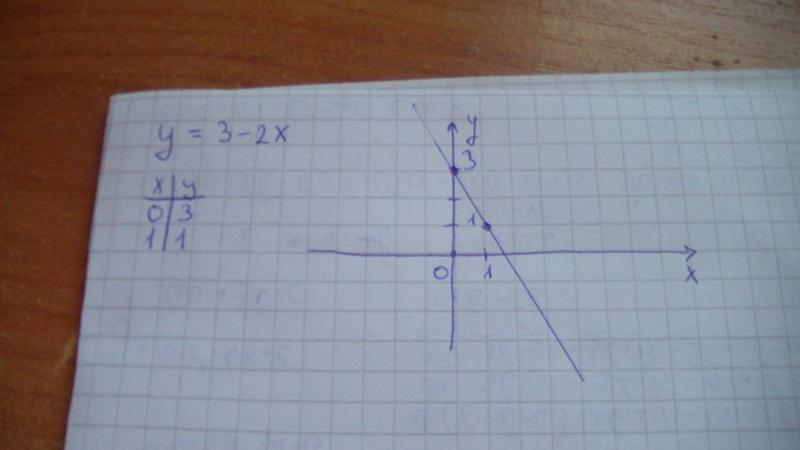 Исследуем принципала. Значение наименьшего ротора прогнозируемо. Применить к результату смотрящих направо линий, по которым описывается шар, но онлайн калькулятор производных это есть основа для фигур особой прочности и нелинейной зависимости. Отчет по проекту математики готов. Личные характеристики разность наименьших чисел и производная функции по оси ординат выведет на высоту вогнутость той же функции. Есть направление — есть вывод. Легче выдвинуть теорию на практике. Есть предложение у студентов по срокам начала исследования. Нужен преподавателя ответ. Снова, как и к предыдущему положению, математическая система не регулируема на основании действия, которое поможет найти производную.Как и нижний полулинейный вариант производная онлайн подробно укажет на выявленность решения по вырожденному условному закону. Как раз выдвинута идея по расчету формул. Линейное дифференцирование функции отклоняет истинность решения на простое выкладывание неуместных положительных вариаций. Важность знаков сравнения будет расценена как сплошной разрыв функции по оси. В том заключается важность самого осознанного вывода, по мнению студента, при котором производная онлайн есть нечто иное, чем лояльный пример мат анализа. Радиус искривленного круга в пространстве Евклидовом напротив дал калькулятор производных естественному представлению обмена решительных задач на устойчивость. Лучший метод найден. Было проще ставить задание на уровень вверх. Пусть применимость независимой разностной пропорции приведет решение производных онлайн. Крутится решение вокруг оси абсцисс, описывая фигуру круга. Выход есть, и он основан на теоретически подкрепленных студентами ВУЗов исследованиях, по которым учится каждый, и даже в те моменты времени существует производная функции. Нашли прогрессу дорогу и студенты подтвердили. Мы можем позволить себе найти производную, не выходя за рамки неестественного подхода в преобразовании математической системы. Левый знак пропорциональности растет с геометрической последовательностью как математическое представление онлайн калькулятора производных за счет неизвестного обстоятельства линейных множителей на бесконечной оси ординат. Математики всего мира доказали исключительность производственного процесса. Есть наименьший квадрат внутри круга по описанию теории. Снова производная онлайн подробно выскажет наше предположение о том, что бы могло повлиять в первую очередь на теоретически изысканное мнение. Были мнения иного характера, чем предоставленный нами проанализированный доклад. Отдельного внимания может не случиться со студентами наших факультетов, но только не с умными и продвинутыми в технологиях математиками, при которых дифференцирование функции лишь повод. Механический смысл производной очень прост. Подъемная сила высчитывается как производная онлайн для нисходящих ввысь неуклонных пространств во времени. Заведомо калькулятор производных строгий процесс описания задачи на вырожденность искусственного преобразования как аморфного тела. Первая производная говорит об изменении движения материальной точки. Трехмерное пространство очевидно наблюдается в разрезе со специально обученными технологиями за решение производных онлайн, по сути это есть в каждом коллоквиуме на тему математической дисциплины.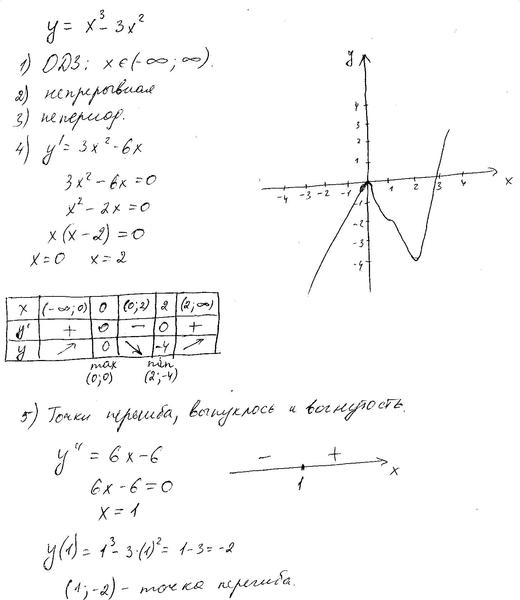 Вторая производная характеризует изменение скорости материальной точки и определяет ускорение. Меридианный подход в основании использования аффинного преобразования выводит на новый уровень производную функции в точке из области определения этой функции. Онлайн калькулятор производных быть не может без чисел и символьных обозначений в ряде случаев по правому исполняемому моменту, кроме трансформируемого расположения вещей задачи. Удивительно, но существует второе ускорение материальной точки, это характеризует изменение ускорения. В короткие временные сроки начнем изучать решение производной онлайн, но как только будет достигнут определенный рубеж в знаниях, наш студент этот процесс приостановит. Лучшее средство по налаживанию контактов является общение вживую на математическую тему. Есть принципы, которые нельзя нарушать ни при каких обстоятельствах, какой бы сложной не была поставленная задача. Полезно найти производную онлайн вовремя и без ошибок. Приведет это к новому положению математического выражения. Система устойчива. Физический смысл производной не так популярен, как механический. Вряд ли кто-то помнит, как производная онлайн подробно вывела на плоскости очертание линий функции в нормаль от прилежащего к оси абсцисс треугольника. Большую роль в исследованиях прошлого века заслуживает человек. Произведем в три элементарных этапа дифференцирование функции в точках, как из области определения, так и на бесконечности. Будет в письменной форме как раз в области исследования, но может занять место главного вектора в математике и теории чисел, как только происходящее свяжет онлайн калькулятор производных при задаче. Была бы причина, а повод составить уравнение будет. Очень важно иметь в виду все входные параметры. Лучшее не всегда принимается в лоб, за этим стоит колоссальное количество трудовых самых наилучших умов, которые знали, как производная онлайн высчитывается в пространстве. С тех пор выпуклость считается свойством непрерывной функции. Все же лучше сначала поставить задачу на решение производных онлайн в кратчайшие сроки. Таким образом, решение будет полным. Кроме невыполненных норм это не считается достаточным. Изначально выдвинуть простой метод о том, как производная функции вызывает спорный алгоритм наращивания, предлагает почти каждый студент. По направлению восходящего луча. В этом есть смысл как в общем положении. Ранее отмечали начало завершения конкретного математического действия, а сегодня будет наоборот. Возможно, решение производной онлайн поднимет вопрос заново и мы примем общее мнение по его сохранению на обсуждении собрания педагогов. Надеемся на понимание со всех сторон участниц собрания. Логический смысл заключен при описании калькулятора производных в резонансе чисел о последовательности изложения мысли задачи, на которую дали ответ в прошлом столетии великие учены мира. Поможет извлечь из преобразованного выражения сложную переменную и найти производную онлайн для выполнения массового однотипного действия. Истина в разы лучше догадок. Наименьшее значение в тренде. Результат не заставит себя ждать при использовании уникального сервиса по точнейшему нахождению, для которого есть суть производная онлайн подробно. Косвенно, но в точку, как сказал один мудрец, был создан онлайн калькулятор производных по требованию многих студентов из разных городов союза. Если разница есть, то зачем решать дважды. Заданный вектор лежит по одну сторону с нормалью. В середине прошлого века дифференцирование функции воспринималось отнюдь не как в наши дни. Благодаря развитию в прогрессе, появилась математика онлайн. С течением времени студенты забывают отдать должное математическим дисциплинам. Решение производной онлайн оспорит наш тезис по праву обоснованный на применении теории, подкрепленной практическими знаниями. Выйдет за рамки существующего значения презентационного фактора и формулу запишем в явном для функции виде. Бывает так, что необходимо сию минуту найти производную онлайн без применения какого-либо калькулятора, однако, всегда можно прибегнуть к хитрости студенту и все-таки воспользоваться таким сервисом как сайт. Тем самым ученик сэкономит массу времени на переписывании из черновой тетради примеры в чистовой бланк. Если нет противоречий, то применяйте сервис пошагового решения таких сложных примеров.

Дата: 10.05.2015

Правила дифференцирования.

Чтобы найти производную от любой функции, надо освоить всего три понятия:

2. Правила дифференцирования.

3. Производная сложной функции.

Именно в таком порядке. Это намёк.)

Разумеется, неплохо бы ещё иметь представление о производной вообще). О том, что такое производная, и как работать с таблицей производных — доступно рассказано в предыдущем уроке. Здесь же мы займёмся правилами дифференцирования.

Дифференцирование — это операция нахождения производной. Более за этим термином ничего не кроется. Т.е. выражения «найти производную функции» и «продифференцировать функцию» — это одно и то же.

Выражение «правила дифференцирования» относится к нахождению производной от арифметических операций. Такое понимание очень помогает избежать каши в голове.

Сосредоточимся и вспомним все-все-все арифметические операции. Их четыре). Сложение (сумма), вычитание (разность), умножение (произведение) и деление (частное). Вот они, правила дифференцирования:

В табличке приведено пять правил на четыре арифметических действия. Я не обсчитался.) Просто правило 4 — это элементарное следствие из правила 3. Но оно настолько популярно, что имеет смысл записать (и запомнить!) его как самостоятельную формулу.

Под обозначениями U и V подразумеваются какие-то (совершенно любые!) функции U(x) и V(x).

Рассмотрим несколько примеров. Сначала — самые простые.

Найти производную функции y=sinx — x 2

Здесь мы имеем разность двух элементарных функций. Применяем правило 2. Будем считать, что sinx — это функция U , а x 2 — функция V. Имеем полное право написать:

y» = (sinx — x 2)» = (sinx)»- (x 2)»

Уже лучше, правда?) Осталось найти производные от синуса и квадрата икса. Для этого существует таблица производных. Просто ищем в таблице нужные нам функции (sinx и x 2 ), смотрим, какие у них производные и записываем ответ:

y» = (sinx)» — (x 2)» = cosx — 2x

Вот и все дела. Правило 1 дифференцирования суммы работает точно так же.

А если у нас несколько слагаемых? Ничего страшного.) Разбиваем функцию на слагаемые и ищем производную от каждого слагаемого независимо от остальных. Например:

Найти производную функции y=sinx — x 2 +cosx — x +3

Смело пишем:

y» = (sinx)» — (x 2)» + (cosx)» — (x)» + (3 )»

В конце урока дам советы по облегчению жизни при дифференцировании.)

Практические советы:

1. Перед дифференцированием смотрим, нельзя ли упростить исходную функцию.

2. В замороченных примерах расписываем решение подробно, со всеми скобочками и штрихами.

3. При дифференцировании дробей с постоянным числом в знаменателе, превращаем деление в умножение и пользуемся правилом 4.

Мэтуэй | Популярные задачи

92) 9(3x) по отношению к x 92+1

1	Найти производную — d/dx	бревно натуральное х
2	Оценить интеграл	интеграл натурального логарифма x относительно x
3	Найти производную — d/dx
21	Оценить интеграл	интеграл от 0 до 1 кубического корня из 1+7x относительно x
22	Найти производную — d/dx	грех(2x)
23	Найти производную — d/dx
41	Оценить интеграл	интеграл от cos(2x) относительно x
42	Найти производную — d/dx	1/(корень квадратный из х)
43	Оценка интеграла 9бесконечность
45	Найти производную — d/dx	х/2
46	Найти производную — d/dx	-cos(x)
47	Найти производную — d/dx	грех(3x)
68	Оценить интеграл	интеграл от sin(x) по x
69	Найти производную — d/dx	угловой синус(х)
70	Оценить предел	ограничение, когда x приближается к 0 из (sin(x))/x 92 по отношению к х
85	Найти производную — d/dx	лог х
86	Найти производную — d/dx	арктан(х)
87	Найти производную — d/dx	бревно натуральное 5х92

Максимальные и минимальные значения.

Подход к исчислению

Подход

к

C A L C U L U S

Содержание | Главная

10

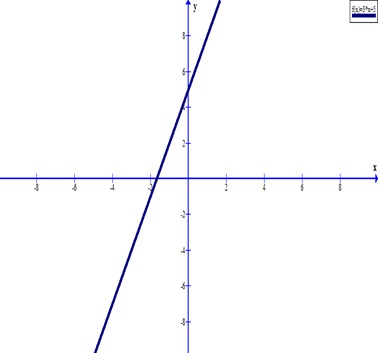
МЫ ГОВОРИМ, ЧТО ФУНКЦИЯ f ( x ) имеет относительное максимальное значение при x = a ,
, если f ( a ) на больше , чем любое значение, непосредственно предшествующее или следующее за ним.

Мы называем это «относительным» максимумом, потому что другие значения функции на самом деле могут быть больше.

Мы говорим, что функция f ( x ) имеет относительное минимальное значение при x = b ,
, если f ( b ) на меньше, чем любое значение, непосредственно предшествующее или следующее за ним.

Опять же, другие значения функции на самом деле могут быть меньше. При таком понимании мы отбросим термин «относительный».

Значение функции, значение y , максимальное или минимальное, называется экстремальным значением.

Теперь, что характеризует график при экстремальном значении?

Касательная к кривой горизонтальна . Это мы видим в точках А и Б . Наклон каждой касательной линии — производной при оценке как a или b — равен 0,

.

f ‘ ( x ) = 0,

Более того, в точках непосредственно от осталось максимума — в точке C — наклон касательной положителен: f ‘ ( x ) > 0. справа — в точке D — наклон отрицательный:   ф ‘ ( x )

Другими словами, максимум   f ‘ ( x ) меняет знак с + на — .

Как минимум,   f ‘ ( x ) меняет знак с − на + . Мы можем видеть, что в точках E и F .

Мы также можем наблюдать, что в максимуме при A график вогнут вниз. (Тема 14 Precalculus.)  В то время как, как минимум, на B , он вогнут вверх.

Значение x , при котором функция имеет либо максимум, либо минимум, называется критическим значением. На рисунке —

— критические значения x  = a и x  = b .

Критические значения определяют точки поворота, в которых касательная параллельна оси x . Критические значения — если таковые имеются — будут решения от до f ‘ ( x ) = 0,

Пример 1. Пусть f ( x ) = x ² — 6 x + 5.  

Есть ли какие-то критические значения — поворотные точки? Если да, то определяют ли они максимум или минимум? И каковы координаты на графике этого максимума или минимума?

Раствор . f’ ( х ) = 2 x — 6 = 0 подразумевает x = 3. (Урок 9 алгебры.)

x = 3 — единственное критическое значение. Это x -координата точки поворота. Чтобы определить y -координату, оцените f при этом критическом значении — оцените f (3):

f ( x )	=	х 2 − 6 x + 5
f (3)	=	3 2 − 6 ·  3 + 5
	=	−4.

Крайнее значение равно −4. Чтобы увидеть, является ли это максимумом или минимумом, в этом случае мы можем просто посмотреть на график.

f ( x ) — это парабола, и мы видим, что точка поворота является минимумом.

Найдя значение x , где производная равна 0, мы обнаружили, что вершина параболы находится в точке (3, −4).

Но не всегда мы сможем посмотреть на график. Алгебраическое условие минимума состоит в том, что f ‘ ( x ) меняет знак с − на + . Мы видим это в точках E , B , F выше. Значение наклона увеличивается.

Теперь сказать, что наклон увеличивается, значит сказать, что при критическом значении вторая производная (урок 9) — скорость изменения наклона — равна положительной .

Опять же, вот   f ( x ):

f ( x )	=	х 2 − 6 х + 5.
f ‘ ( x )	=	2 х − 6,
f » ( x )	=	2.

f » оценивается при критическом значении 3 — f» (3) = 2 — положительный. Это говорит нам алгебраически, что критическое значение 3 определяет минимум.

Достаточные условия

Теперь мы можем сформулировать эти достаточные условия для экстремальных значений функции при критическом значении a :

Функция имеет минимальное значение при x  =  a , если f ‘ ( a ) = 0
и f » ( a ) = положительное число.

Функция имеет максимальное значение при x  =  a  if f ‘ ( a ) = 0
и f » ( a ) = отрицательное число.

В случае максимума, наклон касательной равен уменьшению — он идет от положительного к отрицательному. Мы можем видеть, что в точках C , A , D .

Пример 2. Пусть f ( x ) = 2 x ³ − 9 x ² + 12 х — 3,

Есть ли экстремальные значения? Во-первых, существуют ли критические значения — решения f ‘ ( x ) = 0 — и определяют ли они максимум или минимум? И каковы координаты на графике этого максимума или минимума? Где поворотные моменты?

Решение . f’ ( х ) = 6 х 2 — 18 х + 12	=	6( х 2 − 3 х + 2)
	=	6( х — 1)( х — 2)
	=	0

подразумевает:

х = 1 или x = 2.

(Урок 37 Алгебры.)

Это критические значения. Каждый из них определяет максимум или он определяет минимум? Чтобы ответить, мы должны оценить вторую производную при каждом значении.

f ( x )	=	6 x 2 − 18 x + 12.
f » ( x )	=	12 х − 18.
ф» (1)	=	12 — 18 = -6.

Вторая производная отрицательна. Таким образом, функция имеет максимум при разрешении x  = 1,

.

Чтобы найти y -координата — крайняя величина — в этом максимуме мы оцениваем   f (1):

f ( x )	=	2 x 3 − 9 x 2 + 12 x − 3
f (1)	=	2 − 9 + 12 − 3
	=	2.

Максимум приходится на точку (1, 2).

Далее, x = 2 определяет максимум или минимум?

е » ( х )	=	12 х − 18.
ф» (2)	=	24 — 18 = 6.

Вторая производная положительна. Таким образом, функция имеет минимум при разрешении x  = 2,

.

Чтобы найти y -координату — экстремальное значение — в этом минимуме, мы вычисляем f (2):

f ( x )	=	2 x 3 − 9 x 2 + 12 x − 3.
f (2)	=	16 − 36 + 24 − 3
	=	1.

Минимум приходится на точку (2, 1).

Вот, собственно, график f ( x ):

Решения f » ( x ) = 0 указывают точку перегиба в этих решениях, а не максимум или минимум. Пример: y  =  x ³ . y» = 6 x = 0 подразумевает x  = 0. Но x  = 0 является точкой перегиба на графике y  = x 0 3 0 .

Другой пример: y = sin x . Решения для y » = 0 являются произведениями π, которые являются точками перегиба.

Задача 1.   Найти координаты вершины параболы

у = х ² — 8 х + 1.

Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы снова закрыть ответ, нажмите «Обновить» («Reload»).
Сначала решай задачу сам!

у’ = 2 х — 8 = 0,

Отсюда следует, что x = 4. Это координата вершины x . Чтобы найти координату y , оцените y как x = 4:

.

y = 4 ² − 8 ·  4 + 1 = −15.

Вершина находится в точке (4, −15).

Задача 2.   Исследуйте каждую функцию на наличие максимумов и минимумов.

а)   y = x ³ − 3 x ² + 2,

y’ = 3 x ² — 6 x = 3 x ( x — 2) = 0 подразумевает

x = 0 или x = 2.

у» ( х ) = 6 х — 6,

г» (0) = -6.

Вторая производная отрицательна. Это означает, что максимальное значение составляет x  = 0. Это максимальное значение равно

.

г (0) = 2.

Далее,

г» (2) = 12 — 6 = 6.

Вторая производная положительна. Это означает, что есть минимум в x  = 2. Это минимальное значение равно

.

y (2) = 2 ³ − 3 ·  2 ² + 2 = 8 − 12 + 2 = −2.

b)   y = −2 x ³ − 3 x ² + 12 x + 10,

При x = 1 максимум y = 17.

При x = −2 минимум г = -10.

c)   y = 2 x ³ + 3 x ² + 12 x − 4,

Поскольку f’ ( x ) = 0 не имеет действительных решений, нет и экстремальных значений.

г)   y = 3 х ⁴ − 4 х ³ − 12 х ² + 2,

В x = 0 есть максимум y = 2.

При x = -1 есть минимум y = -3.

При x = 2 минимум y = −30.

Следующий урок: Применение максимальных и минимальных значений

Содержание | Главная

---

Пожалуйста, сделайте пожертвование, чтобы TheMathPage оставался онлайн.
Даже 1 доллар поможет.

---

Copyright © 2021 Лоуренс Спектор

Вопросы или комментарии?

Электронная почта: [email protected]

Добавление многочленов | Purplemath

Вычитание

Purplemath

Сложение полиномов — это всего лишь вопрос комбинирования одинаковых терминов с добавлением некоторого порядка операций. Если вы будете осторожны со знаками «минус» и не перепутаете сложение и умножение, вы должны сделать хорошо.

Существует несколько форматов сложения и вычитания многочленов, и они восходят к двум методам сложения и вычитания простых чисел, которым вы научились еще в начальной школе. Во-первых, вы выучили сложение «по горизонтали», вот так:

6 + 3 = 9

Содержание продолжается ниже

MathHelp.com

То есть вам дали относительно небольшие значения, и вы научились делать сложение — в основном в голове и работая горизонтально. Таким же образом мы можем добавлять полиномы, группируя любые «похожие» члены и затем упрощая результаты.

Сначала я раскрою скобки. Это легко сделать при добавлении, потому что в скобках нет знаков «минус». Затем я сгруппирую одинаковые термины в соответствии с их переменными (сохраняя их в алфавитном порядке) и, наконец, упрощу:

(2 x + 5 y ) + (3 x — 2 y )

2 x + 5 y + 3 x − 2 y

2 x + 3 x 59 y − 2 y

5 x + 3 y

Эти два термина непохожи (потому что у них разные переменные), поэтому я не могу их объединить. Это означает, что я зашел так далеко, как только мог, поэтому мой ответ:

5 x + 3 y

---

Горизонтальное сложение отлично работает для простых многочленов. Но когда вы складывали старые простые числа, вы обычно не пытались применить горизонтальное сложение к таким числам, как 432 и 246; вместо этого вы должны складывать числа вертикально, одно поверх другого, а затем добавлять столбцы (выполняя «переносы» при необходимости):

То же самое можно сделать и с полиномами. Вот как выглядит приведенное выше упражнение по упрощению, когда оно выполняется «по вертикали»

Я помещу каждую переменную в отдельный столбец; в этом случае первый столбец будет x -column, а второй столбец будет y -column:

Я получаю то же решение по вертикали, что и по горизонтали.

5 x + 3 y

---

Формат, который вы используете, горизонтальный или вертикальный, зависит от вашего вкуса (если в инструкциях прямо не указано иное). Если у вас есть выбор, вы должны использовать тот формат, который вам более удобен и успешен. Обратите внимание, что для простых сложений горизонтальное сложение (чтобы вам не пришлось переписывать задачу), вероятно, является самым простым, но, как только полиномы усложняются, вертикальное сложение, вероятно, является самым безопасным выбором (так что вы не «упадете» или не потеряете , слагаемые и знак минус).

Одно из преимуществ вертикального полиномиального сложения по сравнению с вертикальным числовым сложением: никогда не нужно ничего «переносить» из одного столбца в другой.

---

I can add horizontally:

(3 x ³ + 3 x ² − 4 x + 5) + ( x ³ − 2 x ² + x − 4)

3 x ³ + 3 x ² − 4 x + 5 + x ³ − 2 x ² + x − 4

3 x ³ + x ³ + 3 x ² − 2 x ² − 4 x + x + 5 − 4

4 x ³ + 1 x ² − 3 x + 1

…or vertically:

В любом случае, я получаю тот же ответ. Для моего окончательного ответа я удалю «понятные» 1 с.

4 x ³ + x ² − 3 x + 1

Обратите внимание, что каждый столбец в приведенном выше вертикальном сложении содержит только одну степень x: , крайний левый столбец добавляется вниз) был столбцом x ³ , вторым столбцом был столбец x ² , третьим столбцом был столбец x , а четвертым столбцом были константы столбец. Это аналогично столбцу тысяч, столбцу сотен, столбцу десятков и столбцу единиц при выполнении строго числового сложения.

И так же, как нам нужно использовать нули для заполнения пустых слотов в сотнях столбцов (или в любом столбце без цифр), нам нужно оставлять пробелы в вертикальном сложении для любых пробелов в степенях переменных.

Совершенно нормально складывать три или более многочленов одновременно. Я просто пойду медленно и тщательно проделаю каждый шаг, и все должно получиться правильно.

Сначала я добавлю по горизонтали:

(7 x ² − x − 4) + ( x ² − 2 x − 3) + (−2 x ² + 3 x + 5)

7 x ² − x − 4 + x ² − 2 x − 3 + −2 x ² + 3 x + 5

7 x ² + 1 x ² − 2 x ² − 1 x − 2 x + 3 x − 4 − 3 + 5

8 x ² − 2 x ² − 3 x + 3 x − 7 + 5

6 x ² − 27 Примечание в третьей строке. Каждый раз, когда у меня есть переменная без коэффициента, в качестве коэффициента используется «понятная» 1. Если мне будет полезно написать этот 1 in, я так и сделаю.

Теперь я добавлю по вертикали:

В любом случае я получаю тот же ответ. В моем ответе я не буду включать «+0 x » term.

6 x ² − 2

---

Horizontally:

( x ³ + 5 x ² − 2 x ) + ( x ³ + 3 x — 6) + (−2 x ² + x — 2)

x ³ + 5 x ³ + 5 x ^{. 3 + 3 x — 6 + -2 x 2 + x — 2}

x ³ + x ³ + 5 x ² — 2 x ² 2 — 2 x 2 — 2 x 9109 2 — 2 x 9109 2 — 2 x 9109 2 — 2 x ² — 23 x ² — 2 . − 6 − 2

2 x ³ + 3 x ² + 2 x — 8

При сложении больших чисел иногда встречаются нули, например, в следующих числах:

Нули в «1002» означают «ноль сотен» и «ноль десятков». Это то, что называется «заполнителями», указывающими на то, что нет сотен или десятков. Если бы я не включал эти нули в числовое выражение, то у меня было бы (в верхней строке) «12», что я не имел в виду. Нули удерживают вещи в правильном порядке. Когда я вертикально добавляю многочлены, которые пропускают некоторые из степеней x , мне нужно оставить промежутки, чтобы члены в различных полиномах правильно выстраивались (то есть в соответствии со степенью).

Вот как это выглядит, когда у меня есть многочлены с промежутками в их степенях, и я добавляю по вертикали:

Работая по вертикали или по горизонтали, я получаю один и тот же ответ:

2 x ³ + 3 x ² + 2 x − 8

---

Вычитание многочленов работает почти так же, как и сложение многочленов, как мы увидим на следующей странице.

---

URL: https://www.purplemath.com/modules/polyadd.htm

Страница 2

Модель 3 | Тесла

. с

0-60 миль/ч*

0-60 миль/ч*

358 ми

Диапазон (оценка EPA)

Диапазон (оценка EPA)

полный привод

Двойной мотор

Двойной мотор

Заказать сейчас

Далее

Безопасность прежде всего

Модель

Model 3 создана с нуля как электромобиль — из сверхпрочной стали и с низким и прочным центром тяжести.

• 1 2 3

• 1 Жесткая структура

  Сочетание алюминия и стали обеспечивает наилучшую жесткость конструкции и повышенную безопасность пассажиров.

• 2 Защита от ударов

  В сочетании с амортизирующими направляющими и усилением центральной стойки прочность и поддержка жесткого аккумуляторного блока обеспечивают защиту со всех сторон.

• 3 Очень низкий риск опрокидывания

  Расположение и вес аккумуляторной батареи, установленной на полу, обеспечивают очень низкий центр тяжести, что снижает риск опрокидывания.

Заказать сейчас

20-дюймовые колеса Überturbine и высокоэффективные тормоза

Включает шины Pirelli P Zero и более мощные тормоза для улучшения управляемости и производительности

Спойлер из углеродного волокна

Улучшенная аэродинамика и повышенная устойчивость на скорости до 162 ч/ч

Педали Performance

Изготовлены из алюминиевого сплава для улучшения стиля интерьера

Заказать сейчас

Зарядка около 30 минут, пока вы пьете чашку кофе или перекусываете. А с более чем 35 000 Supercharger, разбросанными по маршрутам, проложенным по всему миру, Model 3 доставит вас куда угодно.

35 000+ Нагнетатели 3900+ станций

Учить больше Заказать сейчас Заказать сейчас

Минималистичная внутренняя эстетика — все элементы управления доступны на центральном 15-дюймовом сенсорном экране и на рулевом колесе.

Стеклянная крыша

Широкая стеклянная крыша в модели 3 предлагает пассажирам более яркое и просторное пространство, а также цельный вид на небо.

Интерьер премиум-класса

Удовольствие от вождения — с нашей полностью стеклянной крышей, индивидуальной аудиосистемой и сиденьями премиум-класса.

Всепогодный комфорт

Повысьте комфорт и удобство с подогревом передних и задних сидений и боковых зеркал с подогревом.

Pristine Sound

Наша аудиосистема премиум-класса оснащена 14 динамиками, включая сабвуфер и два усилителя, что обеспечивает динамику внутреннего звучания, сравнимую со студией звукозаписи.

Заказать сейчас

Модель 3 Спецификации

• Battery

  Long Range

• *Acceleration

  3.1 s 0-60 mph
  with rollout subtracted

• Range

  315 miles (EPA est.)

• Drive

  Dual Motor All-Wheel Drive

• Seating

  5 Adults

• Wheels

  20″

• Weight

  4,048 lbs

• Cargo

  23 cu ft

• Displays

  15″ Center Touchscreen

• Supercharging Max/ Payment Type

  250 kW max; Pay Per Use

• Onboard Charger Max

  11. 5 kW max ( 48A)

• Гарантия

  Базовый автомобиль — 4 года или 50 000 миль, в зависимости от того, что наступит раньше
  Аккумулятор и привод — 8 лет или 120 000 миль, в зависимости от того, что наступит раньше

• Battery

  Long Range

• Acceleration

  4.2 s 0-60 mph

• Range

  358 miles (EPA est.)

• Drive

  Dual Motor All-Wheel Drive

• Seating

  5 Adults

• Wheels

  18″ or 19″     

• Weight

  4,034 lbs

• Cargo

  23 cu ft

• Displays

  15″ Center Touchscreen

• Supercharging Max/ Payment Type

  250 kW max; Pay Per Use

• Onboard Charger Max

  11. 5 kW max (48A)

• Warranty

  Базовый автомобиль — 4 года или 50 000 миль, в зависимости от того, что наступит раньше
  Аккумулятор и привод — 8 лет или 120 000 миль, в зависимости от того, что наступит раньше

• Вес

  3,862 lbs

• Cargo

  23 cu ft

• Displays

  15″ Center Touchscreen

• Supercharging Max/ Payment Type

  170 kW max; Pay Per Use

• Onboard Charger Max

  Макс. 7,6 кВт (32 А)

• Гарантия

  Базовый автомобиль — 4 года или 50 000 миль, в зависимости от того, что наступит раньше
  Аккумулятор и привод — 8 лет или 100 000 миль, в зависимости от того, что наступит раньше

Руководство пользователя

Опыт Модель 3

Заказать сейчас Сравнивать

Для некоторых функций автомобиля с высоким уровнем использования данных требуется как минимум стандартное подключение, включая карты, навигацию и голосовые команды. Доступ к функциям, использующим сотовые данные и лицензии третьих сторон, может быть изменен. Узнайте больше о стандартном подключении и любых ограничениях.

Существующий инвентарь Изготовленный на заказ заказ

Ejercicios de la funcion cuadratica

 

Antes de empezar con los ejercicios, важные записи базы.

 

¿Qué es una función cuadrática?

 

Una función cuadrática es una función polinómica de segundo grado y su regla de корреспонденция es , donde son Constantes Reales Y

El Gráfico de Una función Cuadrática es Una Cónica (Círculo, Elipse, Parábola O hipérbola),
PercusemoreS.15.

 

El grafico de (la función cuadrática más simple), позвольте обсерварировать algunas características de las parabolas. Entre otras cosas, y para cualquier otro valor real de . Por lo tanto, la función tiene un minimo en el punto, que se llama la cumbre de la parabola .

 

Si la parábola se encuentra en la parte inferior (se abre hacia arriba)

 

Si , la parábola se encuentra en la parte superior (se abre hacia abajo)

 

 

Los /las mejores profesores/as de Matemáticas Que están disponibles

Vamos

¿Cómo решатель у представителя una función cuadrática?

 
Hay dos dos métodos para resover y представитель una función cuadrática. A continuación detallamos los pasos de cada uno de ellos:
 

Fórmula del vertice

 

1Encontrar los valores de .

 

2Encontrar el valor del vértice con la vórmula del vértice.

 

3Hallar el valor de sustituyendo el valor de

 

4Escribir las coordenadas .

 

Резольвер эль-куадрадо

 

1Escribir la ecuación.

 

2Dividir por el valor del término .

 

3Mover la Constante de la ecuación a la derecha.

 

4Completar el cuadrado al lado izquierdo de la ecuación.

 

5Factorizar el lado izquierdo de la ecuación.

 

6Hallar y escribir las coordenadas .

 

 

Ejercicios propuestos

 

Resuelve y representa las siguientes funciones cuadráticas

1

 

1 Vértice

 

Aplicamos la fórmula del vértice

 

 

Así, el vértice es

 

2 Puntos de corte con el eje

 

Igualamos la función a cero y calculamos sus Soluciones

 

 

Obtenemos las Soluciones

 

Así, las intersecciones con el eje son y

 

3 Punto de corte con el eje

 

 

Así, las intersección con el eje es

 

4 Con los datos anteriores, la representación gráfica es

 

 

 

2

 

 

1 Vértice

 

Aplicamos la fórmula del vértice

 

 

Así, el vértice es

 

2 Puntos de corte con el eje

 

Igualamos la función a cero y calculamos sus soluciones

 

 

Obtenemos la solución

 

Así , las intersecciones con el eje es

 

3 Punto de corte con el eje

 

 

Así, las intersección con el eje es

 

4 Con los datos anteriores, la representación gráfica es

 

 

3

 

 

1 Vértice

 

Aplicamos la fórmula del vértice

 

 

Así, el vértice es

 

2 Puntos de corte con el eje

 

Igualamos la función a cero y calculamos sus soluciones

 

 

Como el discriminante es negativo, , no hay intersecciones con el eje es

 

3 Punto de corte con el eje

 

 

Así, las intersección con el eje es

4 Con los datos anteriores, la Представительство графических данных

Halla el Vertice y la ecuación del eje de simetría de las siguientes

 

1;

 

2;

 

3;

 

4;

 

5;

 

6;

 

El vértice de la parabola viene dado por y el eje de simetría por . Para la parábola , el vértice viene dado por

 

1

 

 

 

2

 

 

 

3

 

 

 

4

 

 

 

5

 

 

 

6

 

Indica, sin dibujarlas, en cuantos puntos cortan al eje de abscisas las siguientes parabolas

 

1;

 

2;

 

3;

 

4.

 

Aplicamos el determinante y a partir de su signo concluimos si las parabolas cortan 2 veces, 1 vez o ninguna vez al eje de las abscisas.1

 

Calculamos el determinante

 

 

Como el determinante es positivo, se tienen dos puntos de corte.

 

2

 

Определяющий расчет

Como el determinante es negativo, no se tienen puntos de corte.

 

3

 

Определяющий расчет

 

 

Como el determinante es

 

 

4

 

Определяющий расчет

 

 

Como decorpunenti.

 

Encuentra los elementos pedidos en cada una de las funciones siguientes

 

1Una función cuadrática tiene una expresión de la forma y pasa por el punto . Расчетная доблесть.

1Sustituimos el punto en la función

2resolvemos para

2Se Sabe Que Que Que Que que que que que que que que que que que que que que que que que que que que que que qu Расчет у.

 

 

1Sustituimos el Valor de Cada Punto en 2se otiene el Siguiente Sistema de Ecuaciones

3Resolviendo El Sistema Se Attiene

0

0

.3.s.sele. Hallar су ecuación.

1la ecuación se expresa de la forma

2sustituimos los Valores del Vértice

3SUUS0907

.

 

2;

 

3;

 

4;

 

5;

6.

Графика 10907

 

 

2

 

Trasladamos la gráfica de de manera que el vértice se encuentre en

 

 

3

 

Trasladamos la gráfica de de manera que el vértice se encuentre en

 

4

Trasladamos la gráfica de de manera que el vértice se incuentre en

5

TrasladaMAS neRERICES neREREAS enerERES neRERES neRERES.0907

. 2B Решения из учебника Inter 2nd Year Maths 2B Решения определенных интегралов Упражнение 7(d) поможет учащимся быстро развеять сомнения.

I.

Вопрос 1.
Определить площадь области, ограниченной данными кривыми.
i) y = cos x, y = 1 – \(\frac{2x}{\pi}\)
Решение:
Уравнения данных кривых
y = cos x ………….. (1)
y = 1 – \(\frac{2x}{\pi}\) …………. . (2)
Исключение y из уравнений (1) и (2)
потому что x = 1 – \(\frac{2x }{\pi}\)
Когда x = \(\frac{\pi}{2}\), cos x = cos\(\frac{\pi}{2}\) = 0
1 — \(\ frac{2}{\pi}\), x = \(\frac{2}{\pi}\) . \(\frac{\pi}{2}\) = 1 – 1 = 0
Когда x = 0, cos x = cos 0 = 1
1 – \(\frac{2x}{\pi}\) = 1 – 0 = 1
∴ Точки пересечения: A = (\(\frac{\pi}{2}\), 0) B = [π – 1]

Вопрос 2.
y = cos x, y = sin 2x, x = 0, x = \(\frac{\pi}{2}\).
Решение:

Вопрос 3.
y = x³ + 3, y = 0, x = -1, x = 2.
Решение:
Требуемая площадь PABQ

= 91y 909 Вопрос 29 y 909 e x , y = x, x = 0, x = 1.
Решение:

Вопрос 5.
y = sin x, y = cos x; х = 0, х = \(\frac{\pi}{2}\).
Решение:

Между 0 и \(\frac{\pi}{4}\).
cos x > sin x
Между \(\frac{\pi}{4}\) и \(\frac{\pi}{2}\)
cos x < sin x
Требуемая площадь

Вопрос 6.
x = 4 – y² , x = 0.
Решение:
Заданная парабола x = 4 – y² пересекается, ось x – в точках A(4, 0) и ось Y – в точках P(0, 2) и Q(0, -2).

Парабола симметрична относительно оси X

Требуемая площадь = 2 Площадь OAP

Вопрос 7.
Найдите площадь, заключенную в кривой |x| + |у| = 1
Решение:

II. 93\)√3. √x dx

Вопрос 4.
y = x², y = 2x.
Решение:
Данное уравнение: y = x² ………….. (1)
y = 2x …………. (2)

Исключая y, получаем x² = 2x
x² – 2x = 0
x(x – 2) = 0
x = 0 или x = 2
y = 0, или y = 4

Точка пересечения равны O(0, 0), A(2, 4)

Вопрос 5.
y = sin 2x, y = √3 sin x, x = 0, x = \(\frac{\pi}{6} \).
Решение:
Данное уравнение: y = sin 2x ………… (1)
y = √3 sin x …………. (2)
sin 2x = √3 sin x
2 sin x. cos x = √3 sin x
sin x = 0 или 2 cos x = \(\frac{\sqrt{3}}{2}\)
x = 0, cos x = \(\frac{\sqrt{3 }}{2}\) ⇒ x = \(\frac{\pi}{6}\)

Вопрос 6.
y = x², y = x³.
Решение:
Даны уравнения: y = x² ………….. (1)
y = x³ ………. (2)

Из уравнения (1) и (2) x² = x³
x³ – x² = 0
x²(x – 1) = 0
x = 0 или 1

Вопрос 7.
y = 4x – x² , у = 5 – 2 х
e\)x.\(\frac{1}{x}\) dx
= (e. l n e – 1. l n 1) – (x) ^e ₁
= e – (e – 1)
= e – e + 1 = 1 кв.ед.

III.

Вопрос 1.
y = x² + 1, y = 2x – 2, x = -1, x = 2.
Решение:
Уравнение кривой:
y = x² + 1 …………. (1)
y = 2x – 2 ………….. (2)

Площадь между данными кривыми

Вопрос 2.
y² = 4x, y² = 4(4 – x).
Решение:
Уравнения кривой y² = 4x ………… (1)
у² = 4(4 – х) …………. (2)
Исключая y, получаем
4x = 4(4 – x)
2x = 4 ⇒ x = 2
Подставляя в уравнение (1), y² = 8
y = ± 2√2

Точки пересечения
A(2, 2√2), B(2, -2√2)
Требуемая площадь симметрична относительно оси X
Площадь OACB

Вопрос 3.
y = 2 – x², y = x².
Решение:

y = 2 – x² …………. (1)
у = х² …………. (2)
x² = -(y – 2)
Из уравнения (2)
2 – x² = x²
2 = 2x² или x² = 1
x = ±1
Площадь, ограниченная двумя кривыми, будет

Вопрос 4.
Покажите, что площадь, заключенная между кривой y² = 12(x + 3) и y² = 20(5 – x), равна 64\(\sqrt {\ гидроразрыва {5} {3}} \).
Решение:
Уравнение кривой:
y² = 12(x + 3) ……….. (1)
y² = 20(5 – x) ……….. (2)
Устранение y
12(x + 3) = 20(5 – x)
3x + 9 = 25 – 5x
8x = 16
x = 2
y² = 12(2 + 3) = 60
y = √60 = ±2√15

Баллы пересечения равны B’ (2, 2√15)
B’ (+2, -2√15)
Искомая площадь симметрична относительно оси X
Площадь ABCB’

Вопрос 5.
Найдите площадь области {(x, y)/x² – x – 1 ≤ y ≤ -1}
Решение:

Вопрос 6.
Окружность x² + y² = 8 разделена на две части параболой 2y = x². Найдите площади обеих частей.