Y 4 график функции: Постройте график функции y= -4

Постройте график функции y 4 3. График функции

«Натуральный логарифм» — 0,1. Натуральные логарифмы. 4. «Логарифмический дартс». 0,04. 7. 121.

«Степенная функция 9 класс» — У. Кубическая парабола. У = х3. 9 класс учитель Ладошкина И.А. У = х2. Гипербола. 0. У = хn, у = х-n где n – заданное натуральное число. Х. Показатель – четное натуральное число (2n).

«Квадратичная функция» — 1 Определение квадратичной функции 2 Свойства функции 3 Графики функции 4 Квадратичные неравенства 5 Вывод. Свойства: Неравенства: Подготовил ученик 8А класса Герлиц Андрей. План: График: -Промежутки монотонности при а > 0 при а

«Квадратичная функция и её график» — Решение.у=4x А(0,5:1) 1=1 А-принадлежит. При а=1 формула у=аx принимает вид.

«8 класс квадратичная функция» — 1) Построить вершину параболы. Построение графика квадратичной функции. x. -7. Построить график функции. Алгебра 8 класс Учитель 496 школы Бовина Т. В. -1. План построения. 2) Построить ось симметрии x=-1. y.

Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.

Сбор и использование персональной информации

Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.

От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.

Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.

Какую персональную информацию мы собираем:

• Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.

Как мы используем вашу персональную информацию:

• Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
• Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
• Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
• Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.

Раскрытие информации третьим лицам

Мы не раскрываем полученную от Вас информацию третьим лицам.

Исключения:

• В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
  3$.
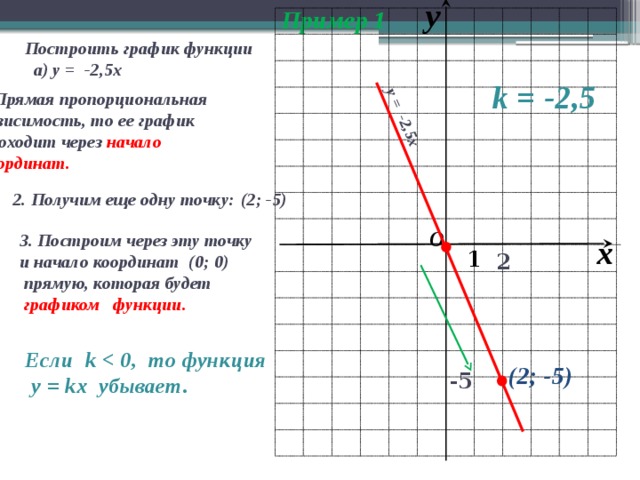
  2. Найдем точку А, координата x, которой равна 1,5. Мы видим, что координата функции находится между значениями 3 и 4 (см. рис. 2). Значит надо заказать 4 куба.

  К сожалению, не все студенты и школьники знают и любят алгебру, но готовить домашние задания, решать контрольные и сдавать экзамены приходится каждому. Особенно трудно многим даются задачи на построение графиков функций: если где-то что-то не понял, не доучил, упустил — ошибки неизбежны. Но кому же хочется получать плохие оценки?

  Не желаете пополнить когорту хвостистов и двоечников? Для этого у вас есть 2 пути: засесть за учебники и восполнить пробелы знаний либо воспользоваться виртуальным помощником — сервисом автоматического построения графиков функций по заданным условиям. С решением или без. Сегодня мы познакомим вас с несколькими из них.

  Лучшее, что есть в Desmos.com, это гибко настраиваемый интерфейс, интерактивность, возможность разносить результаты по таблицам и бесплатно хранить свои работы в базе ресурса без ограничений по времени. А недостаток — в том, что сервис не полностью переведен на русский язык.

  Grafikus.ru

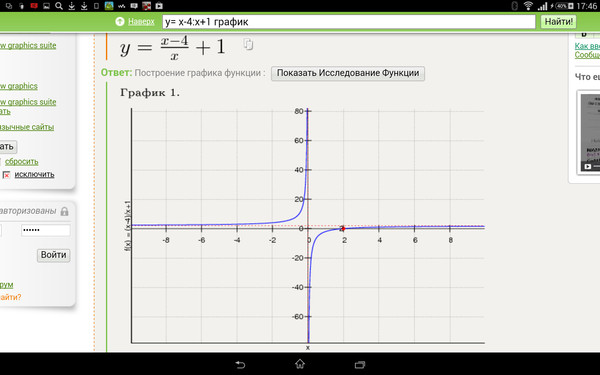
  Grafikus.ru — еще один достойный внимания русскоязычный калькулятор для построения графиков. Причем он строит их не только в двухмерном, но и в трехмерном пространстве.

  Вот неполный перечень заданий, с которыми этот сервис успешно справляется:

  • Черчение 2D-графиков простых функций: прямых, парабол, гипербол, тригонометрических, логарифмических и т. д.
  • Черчение 2D-графиков параметрических функций: окружностей, спиралей, фигур Лиссажу и прочих.
  • Черчение 2D-графиков в полярных координатах.
  • Построение 3D-поверхностей простых функций.
  • Построение 3D-поверхностей параметрических функций.

  Готовый результат открывается в отдельном окне. Пользователю доступны опции скачивания, печати и копирования ссылки на него. Для последнего придется авторизоваться на сервисе через кнопки соцсетей.

  Координатная плоскость Grafikus.ru поддерживает изменение границ осей, подписей к ним, шага сетки, а также — ширины и высоты самой плоскости и размера шрифта. 2

  y’=4*x*(x-2)*(x+2)

  у производной 3 «нуля» (когда функция обращается в ноль)
  для этого достаточно решить уравнение
  4*x*(x-2)*(x+2) =0

  откуда x1=-2, x2=0, x3=2 (это координаты абсцисс точек пересечения функции с осью абсцисс) (т.е. график пересекает точки (-2;0), (0;0), (2;0))

  Для того, чтобы определить области возрастания и убывания функции y(x) найдем знаки производной в интервалах (-беск, -2), (-2,0), (0,2) и (2,+беск):

  y'(-3)=4*(-3)*(-3-2)*(-3+2)

  y'(-3)=4*(-3)*(-5)*(-1)

  y'(-3)=-60<0, следовательно функция y(x) на интервале (-беск, -2) убывает

  y'(-1)=4*(-1)*(-1-2)*(-1+2)

  y'(-3)=4*(-1)*(-3)*(1)

  y'(-3)=12>0, следовательно функция y(x) на интервале (-2, 0) возрастает

  y'(1)=4*(1)*(1-2)*(1+2)

  y'(-3)=4*(1)*(-1)*(3)

  y'(-3)=-12<0, следовательно функция y(x) на интервале (0, 2) убывает

  y'(3)=4*(3)*(3-2)*(3+2)

  y'(-3)=4*(3)*(1)*(5)

  y'(-3)=60>0, следовательно функция y(x) на интервале (0, 2) возрастает

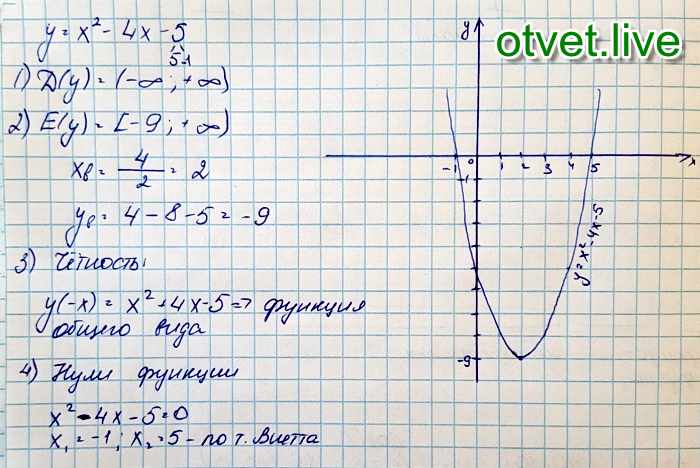
  Таким образом можно сказать, что точки функции y(x) с ординатами -2 и 2 являются минимумами функции, а точка с ординатой 0 — локальным максимумом, потому что на интервалах (-беск, -2) и (2,+беск) функция при стремлении x к -беск и к +беск, соответственно, стремится к бесконечности, т. 2+1)*(0-3)*(0+3)=-9 (т.е. график пересекает точку (0;-9))

  4) Найдем еще несколько необходимых для построения графика точек:

  y(-4)=y(4)=109, т.е. точки (-4;109) и (4;109)

  y(-1)=y(1)=-16, т.е. точки (-1;-16) и (1;16)

  Таким образом по проведенному исследованию функции y(x) можем представить форму графика функции y(x) и по опорным найденным точкам построить данный график:

  http://s2.itrash.ru/idb/c05912defb71a8ab5260270fcf09e21a/oScreen_shot_2010-05-25_at_20.21.30.jpg

  3-8 9 Оценить квадратный корень из 12 10 Оценить квадратный корень из 20 11 Оценить квадратный корень из 50 94 18
  Оценить квадратный корень из 45 19 Оценить квадратный корень из 32 20 Оценить квадратный корень из 18 92

  2.

  1. График линейного уравнения – Математика для специалистов в области общественного здравоохранения и гигиены труда

  Уравнения, графики которых представляют собой прямые линии, называются линейными уравнениями . Ниже приведены некоторые примеры линейных уравнений:

  2 x — 3 y = 6, 3 x = 4 y — 7, y = 2 x — 5, 2 Y = 3 и — 5, 2 Y = 3 и — 5, 2 Y = 3 и 0911 х — 2 = 0,

   

  Линия полностью определяется двумя точками. Следовательно, чтобы построить линейное уравнение, нам нужно найти координаты двух точек. Этого можно добиться, выбрав произвольное значение для

  x или y , а затем найдя другую переменную.

   

  Нарисуйте прямую: y = 3 x + 2

  Решение

  Нам нужно найти координаты хотя бы двух точек.

  Произвольно выбираем х = -1, х = 0 и х = 1.

  . Следовательно, (-1, -1) — точка на этой прямой.

  Если х = 0, то y = 3(0) + 2 или y = 2. Отсюда точка (0, 2).

  Если х = 1, то у = 5, и мы получаем точку (1, 5). Ниже результаты суммированы, а линия представлена ​​в виде графика.

  Х	-1	0	1
  Д	-1	2	5

   

  Нарисуйте прямую: 2

  x + y = 4

  Решение

  Опять же, нам нужно найти координаты хотя бы двух точек.

  Мы произвольно выбираем x = -1, x = 0 и y = 2.

  Если x = -1, затем 2(-1) + y = 4, что дает y = 6. Следовательно, (-1, 6) является точкой на этой прямой.

  Если x = 0, то 2(0) + y = 4, что дает y = 4. Отсюда точка (0, 4).

  Если y = 2, то 2 x + 2 = 4, что дает x = 1 и дает точку (1, 2). В таблице ниже показаны точки, а линия построена на графике.

  х	-1	0	1
  у	6	4	2

  Точки, в которых линия пересекает оси координат, называются пересечениями . При построении графика предпочтение отдается точкам пересечения, потому что их легко найти. Чтобы найти точку пересечения по оси x, положим

  y = 0, а чтобы найти точку пересечения по оси y, положим x = 0,
  .

   

  Найдите точки пересечения прямой: 2 x − 3 y = 6, и граф.

  Решение

  Чтобы найти точку пересечения x , мы принимаем y = 0 в нашем уравнении и находим x .

  Следовательно, точка пересечения x равна 3.

  Аналогичным образом, если x = 0, мы получаем точку пересечения по оси y, которая равна -2.

  Примечание: Если точка пересечения по оси x равна 3, а точка пересечения по оси y равна -2, то соответствующие точки равны (3, 0) и (0, -2) соответственно.

  В высшей математике уравнения прямых иногда записывают в параметрической форме. Например,

  x = 3 + 2 t , y = 1 + t . Буква t называется параметром или фиктивной переменной. Параметрические линии можно изобразить в виде графика, найдя значения для x и y , подставив числовые значения для t .

   

  Нарисуйте линию, заданную параметрическими уравнениями: x = 3 + 2· T , Y = 1 + T

  Решение

  LET T = 0, 1 и 2, а затем для каждого значения T Найти соответствующие значения для и111111111 гг. у .

  Результаты приведены в таблице ниже.

  т	0	1	2
  х	3	5	7
  г	1	2	3

   

  Если уравнение линии имеет только одну переменную, результирующий график представляет собой горизонтальную или вертикальную линию.

  График прямой x = a , где a — константа, представляет собой вертикальную линию, проходящую через точку ( a , 0). Каждая точка на этой линии имеет координату x a независимо от координаты y.

  График прямой y = b , где b — константа, представляет собой горизонтальную линию, проходящую через точку (0, b ). Каждая точка на этой линии имеет координату y b независимо от координаты x.

   

  Нарисуйте линии: x = -2 и y = 3.

  Решение

  График линии x = -2 представляет собой вертикальную линию с координатой x -2 нет независимо от того, что такое координата y. Следовательно, график представляет собой вертикальную линию, проходящую через (-2, 0).

  График линии y = 3 представляет собой горизонтальную линию с координатой y, равной 3, независимо от координаты x. Следовательно, график представляет собой горизонтальную линию, проходящую через (0, 3).

  No related posts.