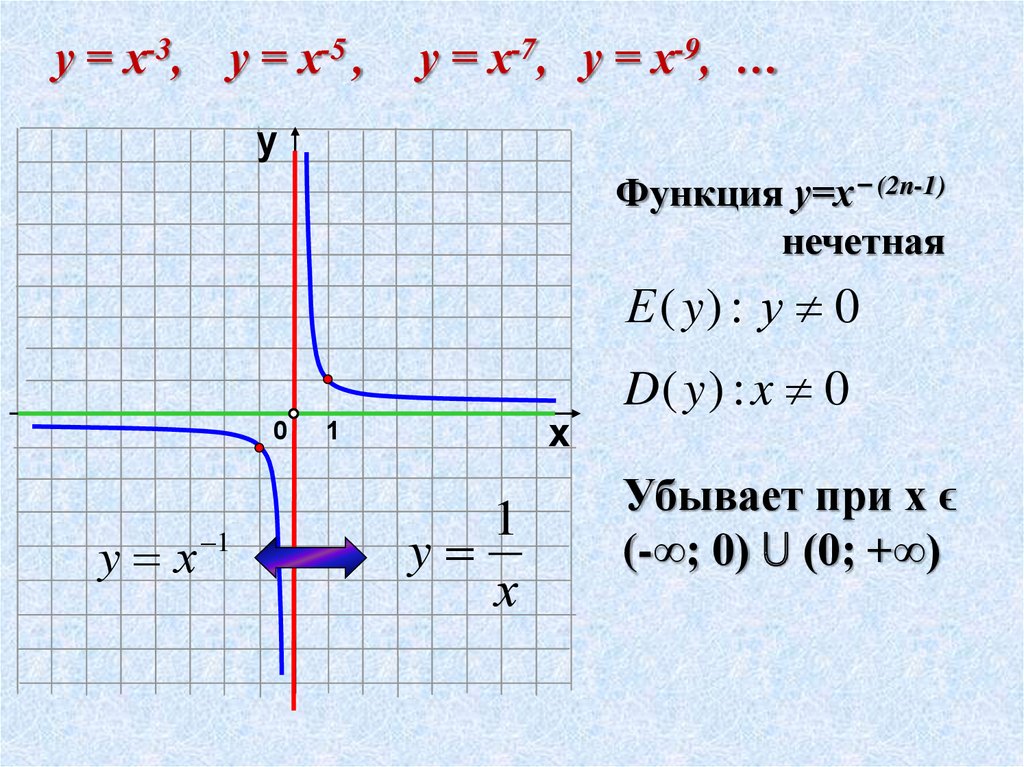
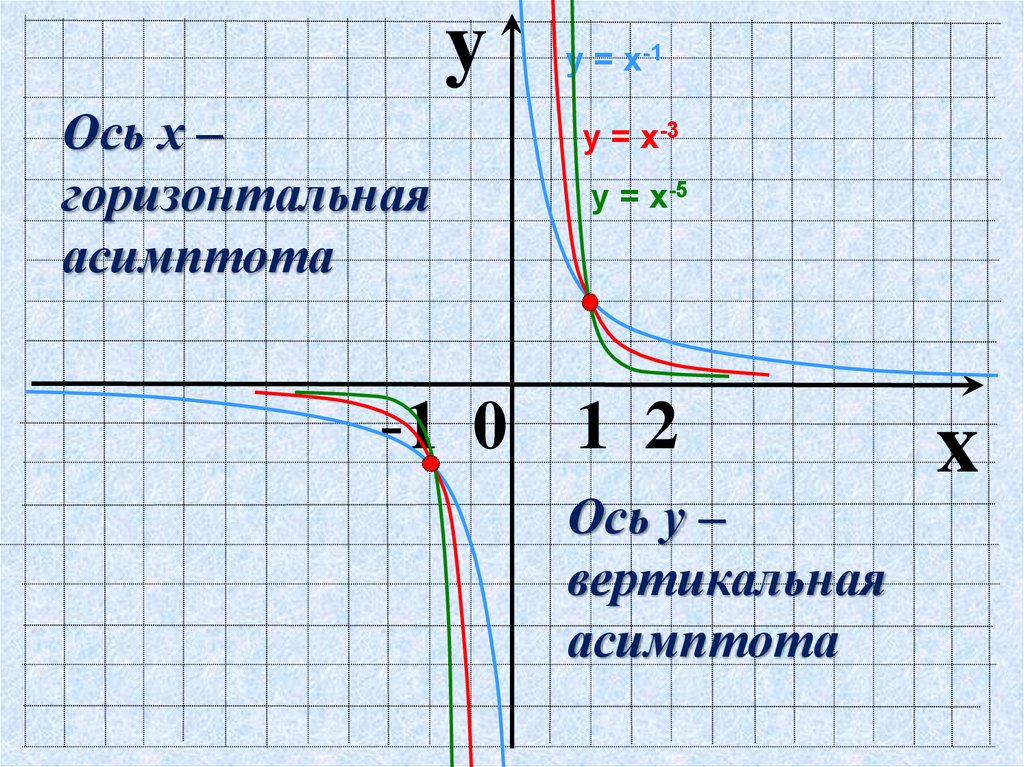
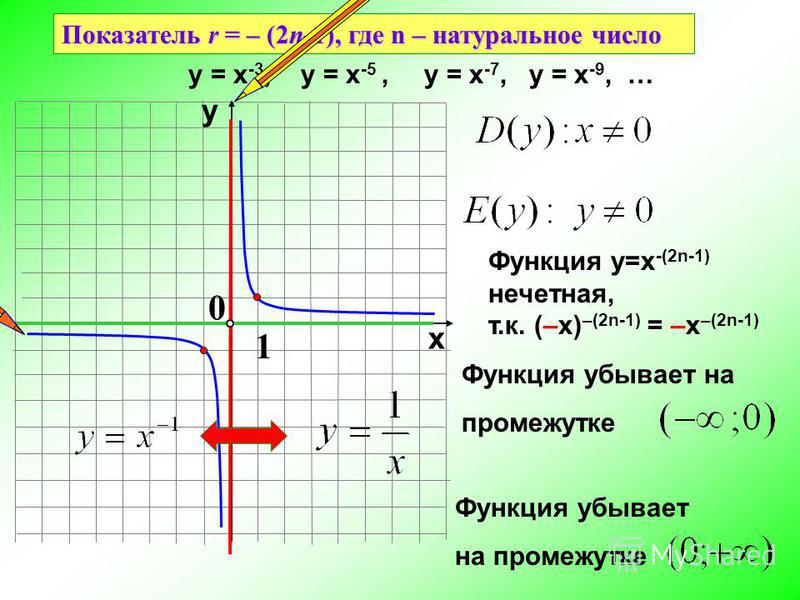
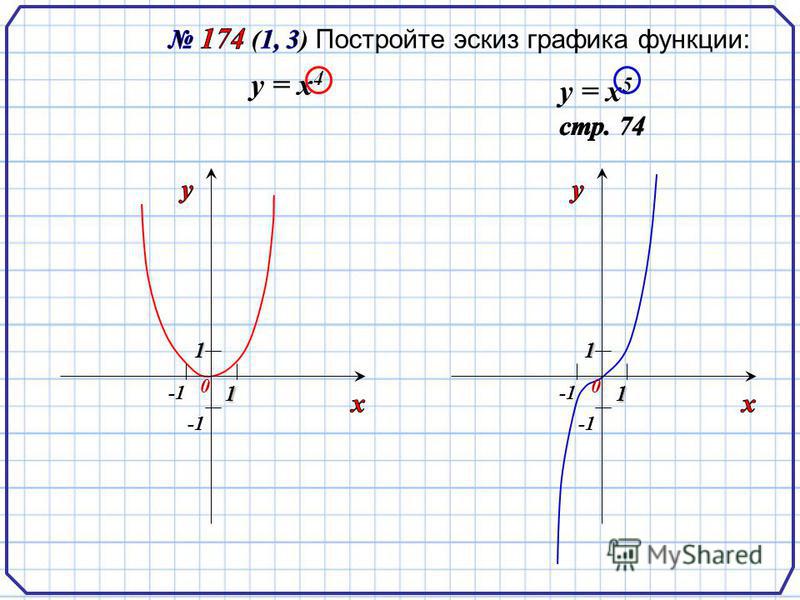
Напомним свойства и графики степенных функций с целым отрицательным показателем.
При четных n, :
Пример функции:
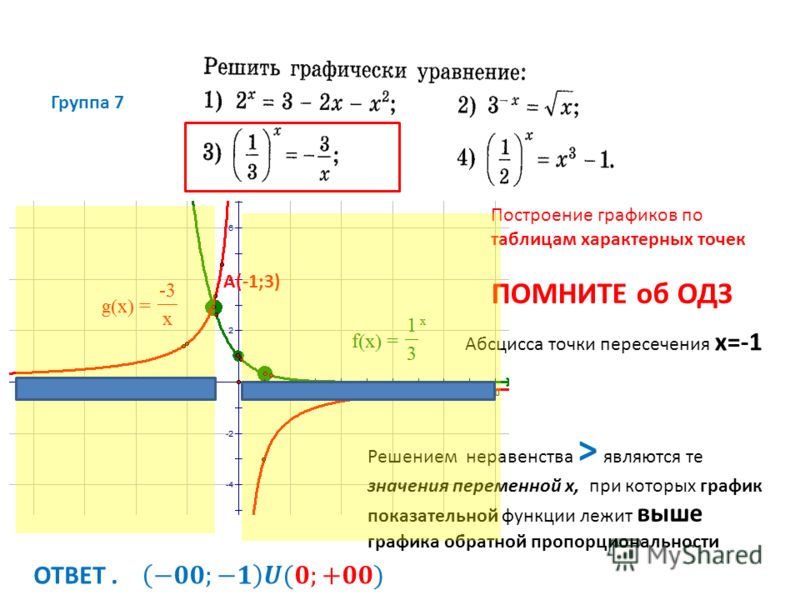
Все графики таких функций проходят через две фиксированные точки: (1;1), (-1;1). Особенность функций данного вида — их четность, графики симметричны относительно оси ОУ.
Рис. 1. График функции
При нечетных n, :
Пример функции:
Все графики таких функций проходят через две фиксированные точки: (1;1), (-1;-1). Особенность функций данного вида — их нечетность, графики симметричны относительно начала координат.
Рис. 2. График функции
Напомним основное определение.
Степенью неотрицательного числа а с рациональным положительным показателем называется число .
Степенью положительного числа а с рациональным отрицательным показателем называется число .
Для выполняется равенство:
Например: ; — выражение не существует по определению степени с отрицательным рациональным показателем; существует, т.
Перейдем к рассмотрению степенных функций с рациональным отрицательным показателем.
Например:
Для построения графика данной функции можно составить таблицу. Мы поступим иначе: сначала построим и изучим график знаменателя — он нам известен (рисунок 3).
Рис. 3. График функции
График функции знаменателя проходит через фиксированную точку (1;1). При построении графика исходной функции данная точка остается, при корень также стремится к нулю, функция стремится к бесконечности. И, наоборот, при стремлении х к бесконечности функция стремится к нулю (рисунок 4).
Рис. 4. График функции
Рассмотрим еще одну функцию из семейства изучаемых функций.
Важно, что по определению
Рассмотрим график функции, стоящей в знаменателе: , график данной функции нам известен, она возрастает на своей области определения и проходит через точку (1;1) (рисунок 5).
Рис. 5. График функции
При построении графика исходной функции точка (1;1) остается, при корень также стремится к нулю, функция стремится к бесконечности. И, наоборот, при стремлении х к бесконечности функция стремится к нулю (рисунок 6).
И, наоборот, при стремлении х к бесконечности функция стремится к нулю (рисунок 6).
Рис. 6. График функции
Рассмотренные примеры помогают понять, каким образом проходит график и каковы свойства изучаемой функции — функции с отрицательным рациональным показателем.
Графики функций данного семейства проходят через точку (1;1), функция убывает на всей области определения.
Область определения функции:
Функция не ограничена сверху, но ограничена снизу. Функция не имеет ни наибольшего, ни наименьшего значения.
Функция непрерывна, принимает все положительные значения от нуля до плюс бесконечности.
Функция выпукла вниз (рисунок 15.7)
Рис. 7. Выпуклость функции
Важно понять, что функции данного семейства ограничены снизу нулем, но наименьшего значения не имеют.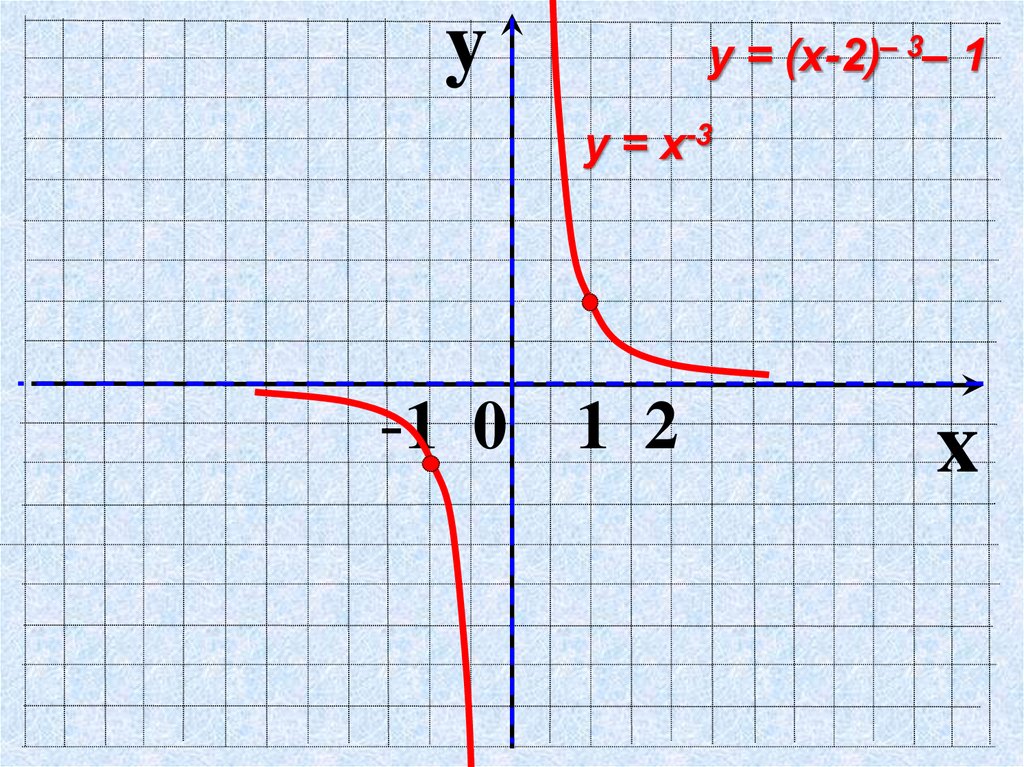 3
3
 2+n-72)=1/(n+9)
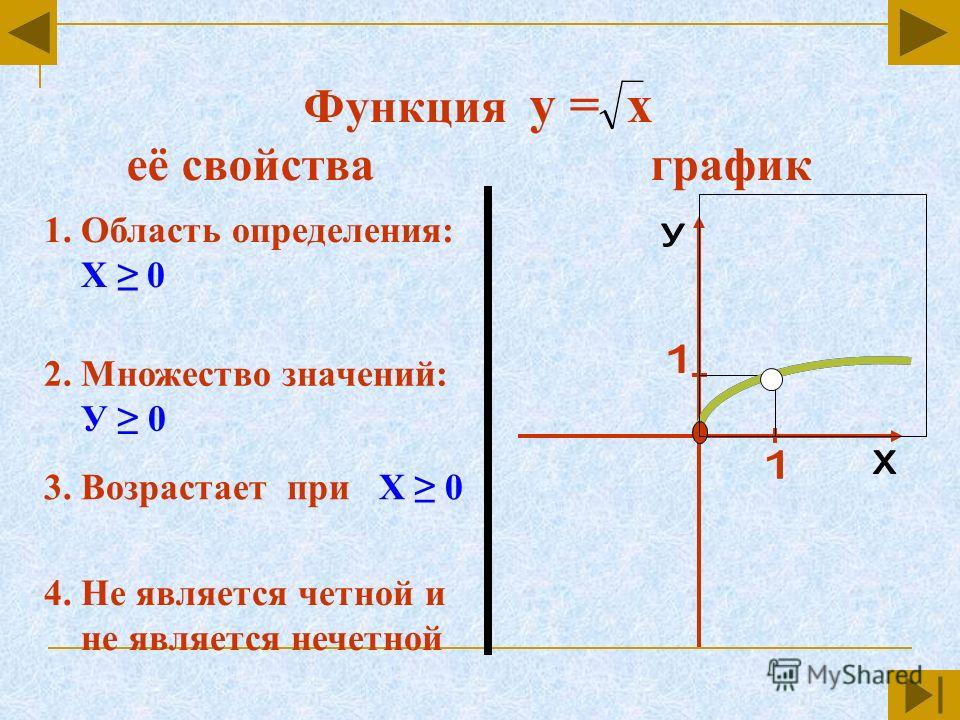
2+n-72)=1/(n+9)Свойства и график функции y=ⁿ√x (n>1, n∈N) с примерами решения
Содержание:
Зависимость, при которой каждому неотрицательному числу ставится в соответствие значение корня заданной четной степени, задает функцию
Действительно, по свойствам арифметического корня существует единственный арифметический корень четной степени из неотрицательного числа, значит, каждому неотрицательному
При функция принимает вид свойства которой рассматривались в 8-м классе.
Для любого действительного числа существует единственный корень нечетной степени (по свойствам корня нечетной степени).
Рассмотрим свойства функции для четных и нечетных показателей корня.
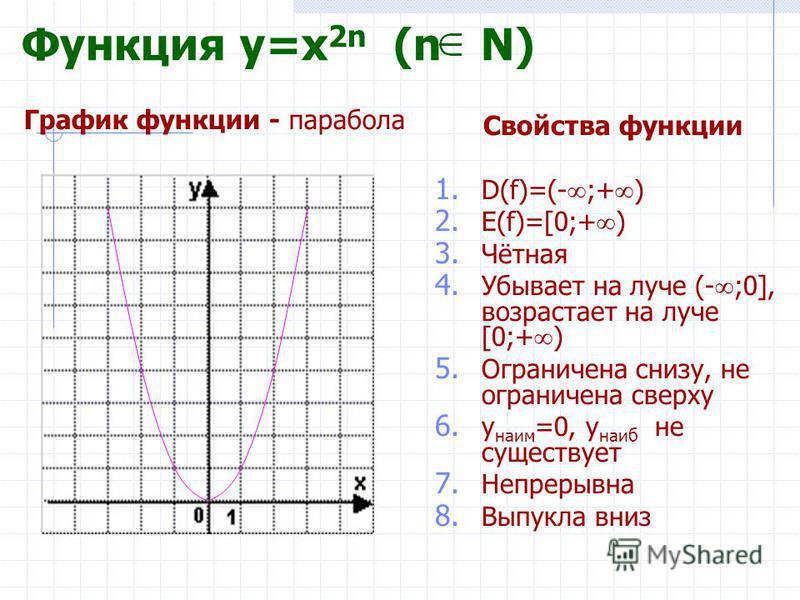
Функция y=2k√x, где K∈NФункция
1. Область определения функции. По свойству арифметического корня
2. Множество значений функции. Наибольшее и наименьшее значения функции. По определению арифметического корня из числа: и По свойству степени с натуральным показателем для любого существует значение т. е. множеством значений функции является множество неотрицательных чисел:
Наибольшее и наименьшее значения функции. По определению арифметического корня из числа: и По свойству степени с натуральным показателем для любого существует значение т. е. множеством значений функции является множество неотрицательных чисел:
При функция принимает наименьшее значение Наибольшего значения у функции не существует.
3. Нули функции. Так как при то значение является единственным нулем функции.
4. Промежутки знакопостоянства функции, при всех
5. Промежутки монотонности функции. Функция возрастает на всей области определения.
Действительно, если В противном случае
или Противоречие доказывает утверждение.
6.Четность (нечетность) функции. Так как область определения функции не симметрична относительно начала координат, то функция не является четной и не является нечетной.
7. График функции. Графики функций при изображены на рисунке 120.
Функция
1. Область определения функции. По свойству корня нечетной степени
2. Множество значений функции. Наибольшее и наименьшее значения функции. По определению корня По свойству степени с натуральным показателем для любого существует Таким образом, множеством значений функции является множество всех действительных чисел:
Наибольшего и наименьшего значений у функции не существует.
3. Нули функции. Так как при то значение является единственным нулем функции.
4. Промежутки знакопостоянства функции, если если
5. Промежутки монотонности функции. Функция возрастает на всей области определения.
Если В противном случае или Противоречие доказывает утверждение.
6. Четность (нечетность) функции. Так как область определения функции симметрична относительно начала координат и то функция является нечетной.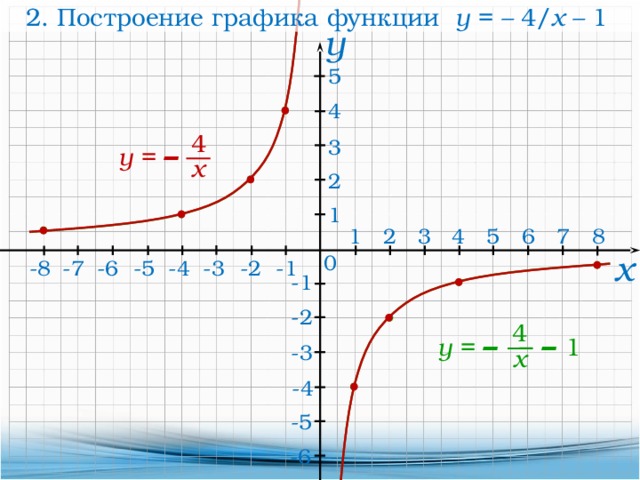 Ее график симметричен относительно начала координат.
Ее график симметричен относительно начала координат.
7. График функции. Графики функций при изображены на рисунке 121.
Примеры заданий и их решенияПример №1Найдите область определения функции:
Решение:
а) Так как область определения корня четной степени есть множество неотрицательных чисел, то подкоренное выражение должно быть неотрицательным. Решим неравенство получим
б) Так как область определения корня нечетной степени есть множество всех действительных чисел, то подкоренное выражение может принимать любые значения при
Пример №2Найдите множество значений функции:
Решение:
а) Множеством значений функции является промежуток По свойству неравенств: значит,
б)Множеством значений функции является множество всех действительных чисел Значит, и множеством значений функции является множество всех действительных чисел, т. е.
е.
Определите наименьшее значение функции
Решение:
Так как функция для четных имеет наименьшее значение, равное нулю, при Следовательно, наименьшее значение данной функции равно 7 и достигается при
Пример №4Найдите нули функции:
Решение:
а) Так как значение корня степени равно нулю, если его подкоренное выражение равно нулю, то решим уравнение Его корни являются нулями функции
б) Так как значение корня степени равно нулю, если его подкоренное выражение равно нулю, то решим уравнение Его корни являются нулями функции
- Заказать решение задач по высшей математике
Какие значения принимает функция на указанных промежутках:
Решение:
а) Так как для то принимает положительные значения для
б)Так как то функция не определена для отрицательных значений из промежутка
в)Так как то функция принимает неотрицательные значения для
г)Так как то функция принимает неотрицательные значения для
Пример №6Расположите числа в порядке возрастания.
Решение:
Запишем числа в виде корней с одинаковыми показателями:
Поскольку функция возрастает на промежутке то значит,
Пример №7Какой (четной или нечетной) является функция:
Решение:
а) Функция является нечетной, так как при нечетном есть нечетная функция.
б) Функция ни четная, ни нечетная, так как при четном не является четной и не является нечетной функцией.
в) Так как область определения функции есть множество всех действительных чисел и то функция четная.
г) Так как область определения функции есть множество всех действительных чисел и то функция четная.
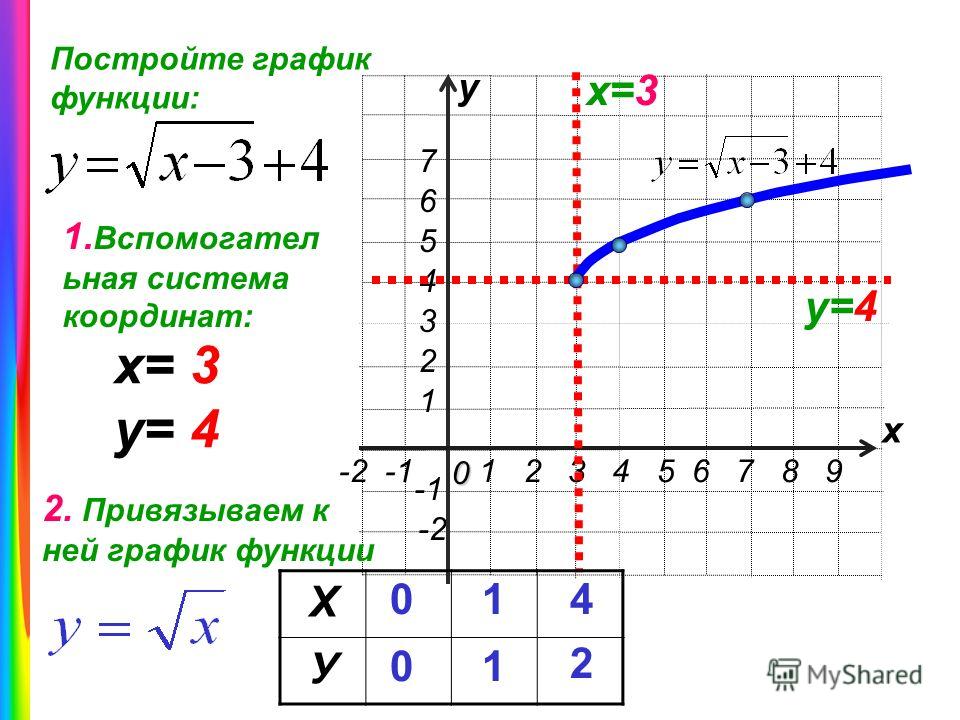
Пример №8Постройте график функции:
Решение:
а) График функции получается из графика функции сдвигом на 2 единицы вверх вдоль оси ординат (рис. 122).
б) График функции получается из графика функции сдвигом на 2 единицы влево вдоль оси абсцисс (см. рис. 122).
рис. 122).
Постройте график функции:
Решение:
а) График функции получается из графика функции сдвигом на 2 единицы вниз вдоль оси ординат ( рис. 123)
б) График функции получается из графика функции сдвигом на 2 единицы вправо вдоль оси абсцисс (см. рис. 123)
График функции е в степени 1 х. Функции и их графики
«Натуральный логарифм» — 0,1. Натуральные логарифмы. 4. «Логарифмический дартс». 0,04. 7. 121.
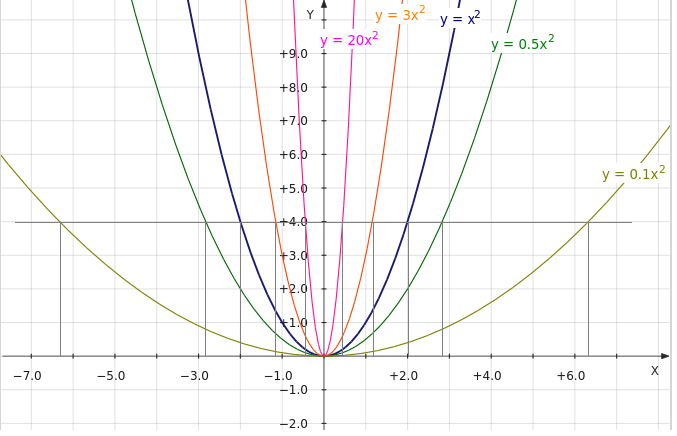
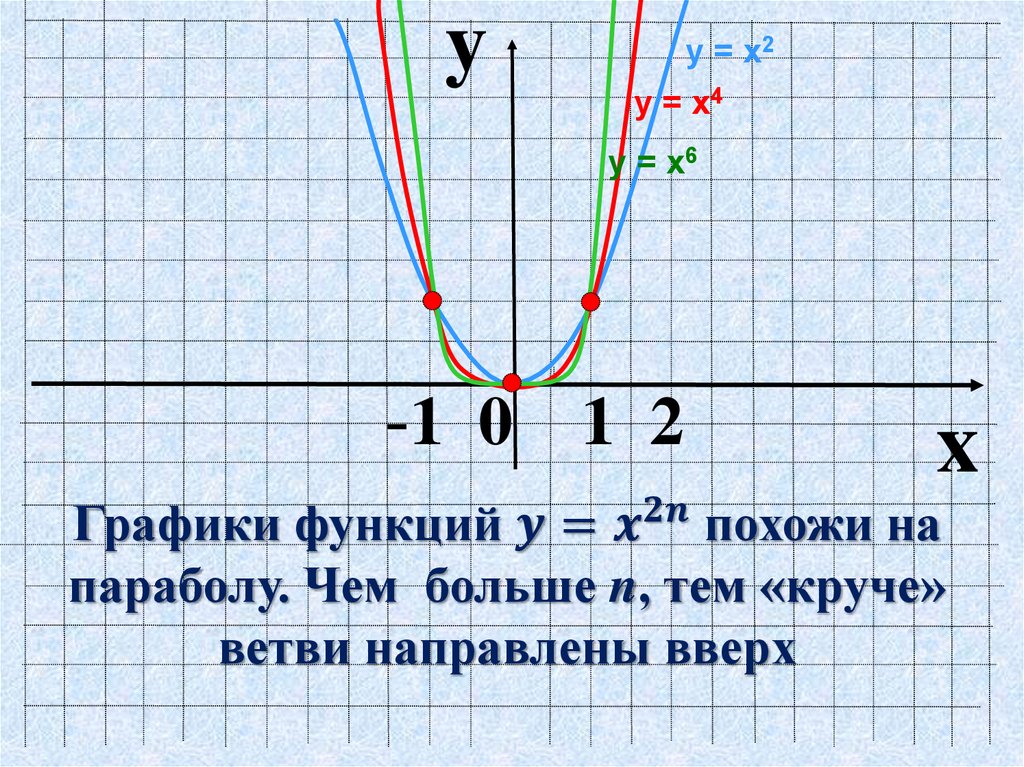
«Степенная функция 9 класс» — У. Кубическая парабола. У = х3. 9 класс учитель Ладошкина И.А. У = х2. Гипербола. 0. У = хn, у = х-n где n – заданное натуральное число. Х. Показатель – четное натуральное число (2n).
«Квадратичная функция» — 1 Определение квадратичной функции 2 Свойства функции 3 Графики функции 4 Квадратичные неравенства 5 Вывод. Свойства: Неравенства: Подготовил ученик 8А класса Герлиц Андрей. План: График: -Промежутки монотонности при а > 0 при а
«Квадратичная функция и её график» — Решение.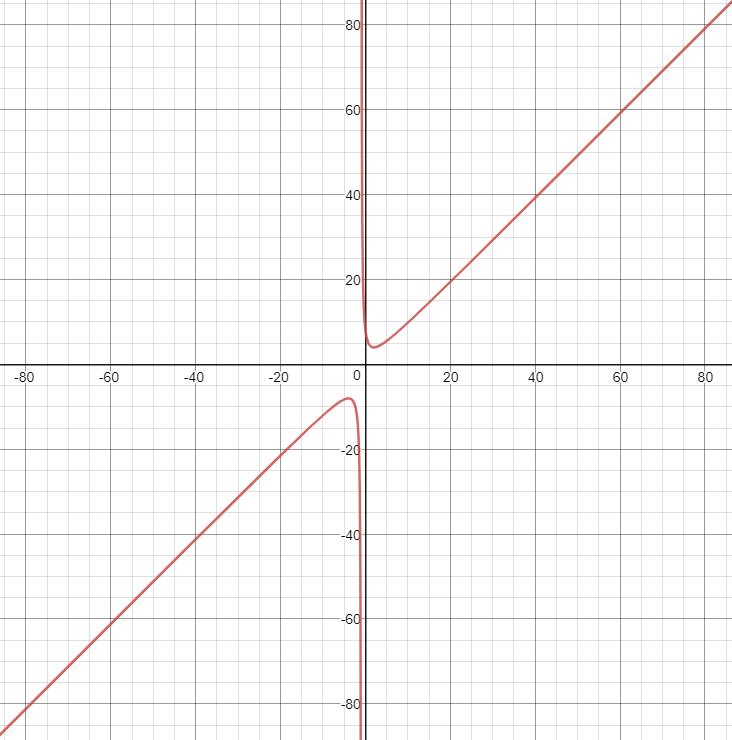 у=4x А(0,5:1) 1=1 А-принадлежит. При а=1 формула у=аx принимает вид.
у=4x А(0,5:1) 1=1 А-принадлежит. При а=1 формула у=аx принимает вид.
«8 класс квадратичная функция» — 1) Построить вершину параболы. Построение графика квадратичной функции. x. -7. Построить график функции. Алгебра 8 класс Учитель 496 школы Бовина Т. В. -1. План построения. 2) Построить ось симметрии x=-1. y.
Выберем на плоскости прямоугольную систему координат и будем откладывать на оси абсцисс значения аргумента х , а на оси ординат — значения функции у = f (х) .
Графиком функции y = f(x) называется множество всех точек, у которых абсциссы принадлежат области определения функции, а ординаты равны соответствующим значениям функции.
Другими словами, график функции y = f (х) — это множество всех точек плоскости, координаты х, у которых удовлетворяют соотношению y = f(x) .
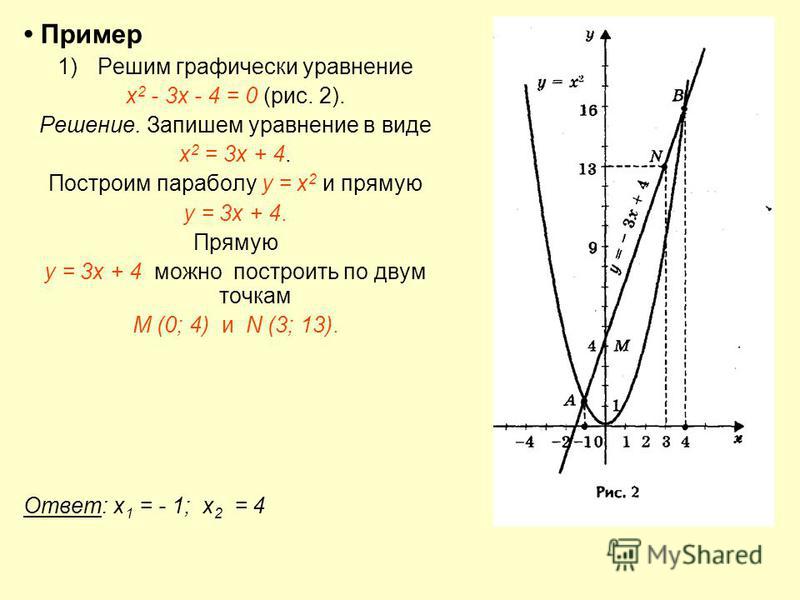
На рис. 45 и 46 приведены графики функций у = 2х + 1 и у = х 2 — 2х .
Строго говоря, следует различать график функции (точное математическое определение которого было дано выше) и начерченную кривую, которая всегда дает лишь более или менее точный эскиз графика (да и то, как правило, не всего графика, а лишь его части, расположенного в конечной части плоскости).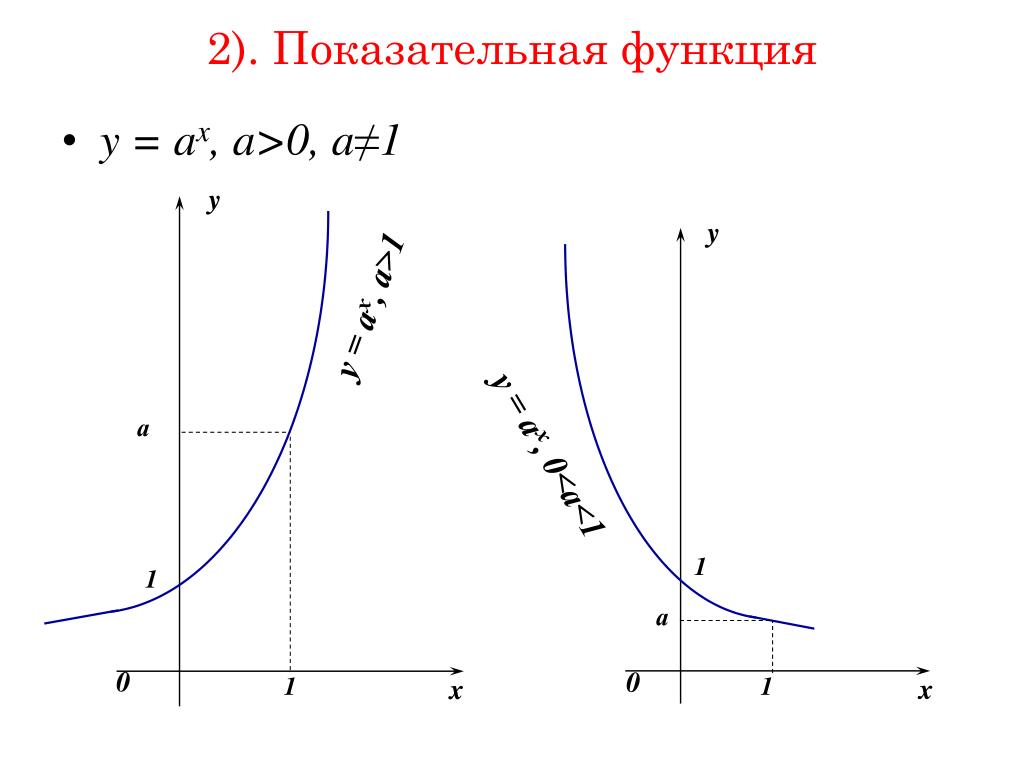 В дальнейшем, однако, мы обычно будем говорить «график», а не «эскиз графика».
В дальнейшем, однако, мы обычно будем говорить «график», а не «эскиз графика».
С помощью графика можно находить значение функции в точке. Именно, если точка х = а принадлежит области определения функции y = f(x) , то для нахождения числа f(а) (т. е. значения функции в точке х = а ) следует поступить так. Нужно через точку с абсциссой х = а провести прямую, параллельную оси ординат; эта прямая пересечет график функции y = f(x) в одной точке; ордината этой точки и будет, в силу определения графика, равна f(а) (рис. 47).
Например, для функции f(х) = х 2 — 2x с помощью графика (рис. 46) находим f(-1) = 3, f(0) = 0, f(1) = -l, f(2) = 0 и т. д.
График функции наглядно иллюстрирует поведение и свойства функции. Например, из рассмотрения рис. 46 ясно, что функция у = х 2 — 2х принимает положительные значения при х и при х > 2 , отрицательные — при 0 наименьшее значение функция у = х 2 — 2х принимает при х = 1 .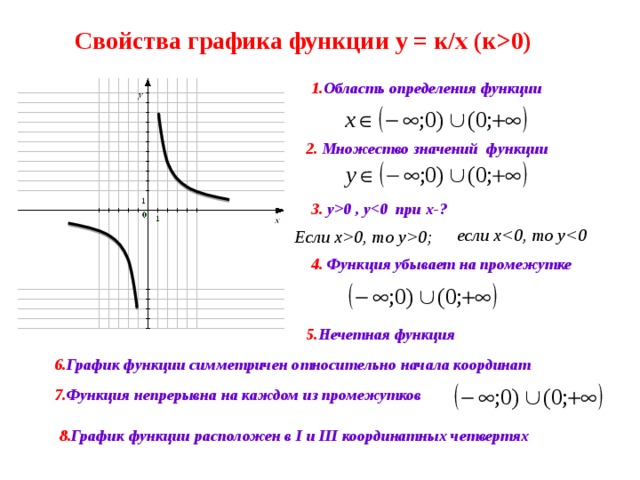
Для построения графика функции f(x) нужно найти все точки плоскости, координаты х , у которых удовлетворяют уравнению y = f(x) . В большинстве случаев это сделать невозможно, так как таких точек бесконечно много. Поэтому график функции изображают приблизительно — с большей или меньшей точностью. Самым простым является метод построения графика по нескольким точкам. Он состоит в том, что аргументу х придают конечное число значений — скажем, х 1 , х 2 , x 3 ,…, х k и составляют таблицу, в которую входят выбранные значения функции.
Таблица выглядит следующим образом:
Составив такую таблицу, мы можем наметить несколько точек графика функции y = f(x) . Затем, соединяя эти точки плавной линией, мы и получаем приблизительный вид графика функции y = f(x).
Следует, однако, заметить, что метод построения графика по нескольким точкам очень ненадежен. В самом деле поведение графика между намеченными точками и поведение его вне отрезка между крайними из взятых точек остается неизвестным.
Пример 1 . Для построения графика функции y = f(x) некто составил таблицу значений аргумента и функции:
Соответствующие пять точек показаны на рис. 48.
На основании расположения этих точек он сделал вывод, что график функции представляет собой прямую (показанную на рис. 48 пунктиром). Можно ли считать этот вывод надежным? Если нет дополнительных соображений, подтверждающих этот вывод, его вряд ли можно считать надежным. надежным.
Для обоснования своего утверждения рассмотрим функцию
.
Вычисления показывают, что значения этой функции в точках -2, -1, 0, 1, 2 как раз описываются приведенной выше таблицей. Однако график этой функции вовсе не является прямой линией (он показан на рис. 49). Другим примером может служить функция y = x + l + sinπx; ее значения тоже описываются приведенной выше таблицей.
Эти примеры показывают, что в «чистом» виде метод построения графика по нескольким точкам ненадежен. Поэтому для построения графика заданной функции,как правило, поступают следующим образом. Сначала изучают свойства данной функции, с помощью которых можно построить эскиз графика. Затем, вычисляя значения функции в нескольких точках (выбор которых зависит от установленных свойств функции), находят соответствующие точки графика. И, наконец, через построенные точки проводят кривую, используя свойства данной функции.
Сначала изучают свойства данной функции, с помощью которых можно построить эскиз графика. Затем, вычисляя значения функции в нескольких точках (выбор которых зависит от установленных свойств функции), находят соответствующие точки графика. И, наконец, через построенные точки проводят кривую, используя свойства данной функции.
Некоторые (наиболее простые и часто используемые) свойства функций, применяемые для нахождения эскиза графика, мы рассмотрим позже, а сейчас разберем некоторые часто применяемые способы построения графиков.
График функции у = |f(x)|.
Нередко приходится строить график функции y = |f(x) |, где f(х) — заданная функция. Напомним, как это делается. По определению абсолютной величины числа можно написать
Это значит, что график функции y =|f(x)| можно получить из графика, функции y = f(x) следующим образом: все точки графика функции у = f(х) , у которых ординаты неотрицательны, следует оставить без изменения; далее, вместо точек графика функции y = f(x) , имеющих отрицательные координаты, следует построить соответствующие точки графика функции у = -f(x) (т. е. часть графика функции
е. часть графика функции
y = f(x) , которая лежит ниже оси х, следует симметрично отразить относительно оси х ).
Пример 2. Построить график функции у = |х|.
Берем график функции у = х
(рис. 50, а) и часть этого графика при х (лежащую под осью х ) симметрично отражаем относительно оси х . В результате мы и получаем график функции у = |х| (рис. 50, б).Пример 3 . Построить график функции y = |x 2 — 2x|.
Сначала построим график функции y = x 2 — 2x. График этой функции — парабола, ветви которой направлены вверх, вершина параболы имеет координаты (1; -1), ее график пересекает ось абсцисс в точках 0 и 2. На промежутке (0; 2) фукция принимает отрицательные значения, поэтому именно эту часть графика симметрично отразим относительно оси абсцисс. На рисунке 51 построен график функции у = |х 2 -2х| , исходя из графика функции у = х 2 — 2x
График функции y = f(x) + g(x)
Рассмотрим задачу построения графика функции y = f(x) + g(x).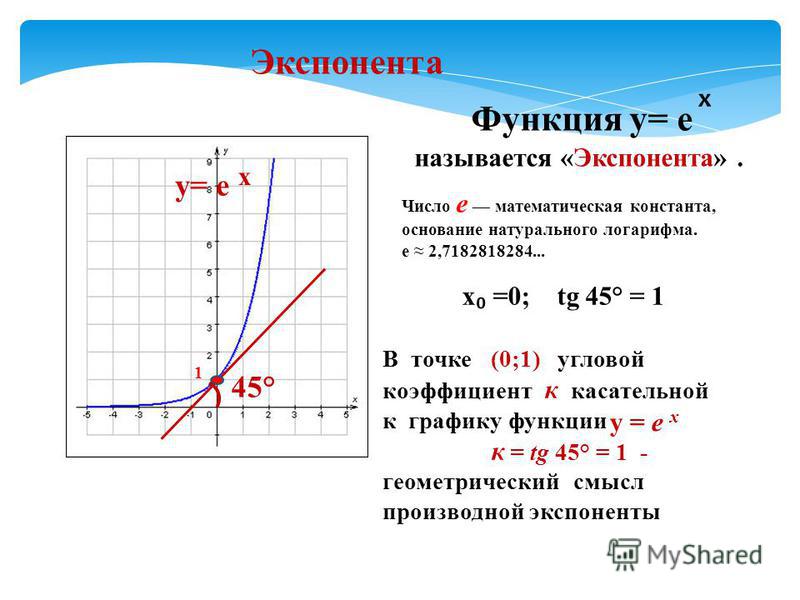 если заданы графики функций y = f(x) и y = g(x)
если заданы графики функций y = f(x) и y = g(x)
Заметим, что областью определения функции y = |f(x) + g(х)| является множество всех тех значений х, для которых определены обе функции y = f{x) и у = g(х), т. е. эта область определения представляет собой пересечение областей определения, функций f{x) и g{x).
Пусть точки (х 0 , y 1 ) и (х 0 , у 2 ) соответственно принадлежат графикам функций y = f{x) и y = g(х) , т. е. y 1 = f(x 0), y 2 = g(х 0). Тогда точка (x0;. y1 + y2) принадлежит графику функции у = f(х) + g(х) (ибо f(х 0) + g(x 0 ) = y1 +y2 ),. причем любая точка графика функции y = f(x) + g(x) может быть получена таким образом. Следовательно, график функции у = f(х) + g(x) можно получить из графиков функций y = f(x) . и y = g(х) заменой каждой точки (х n , у 1) графика функции y = f(x) точкой (х n , y 1 + y 2), где у 2 = g(x n ), т.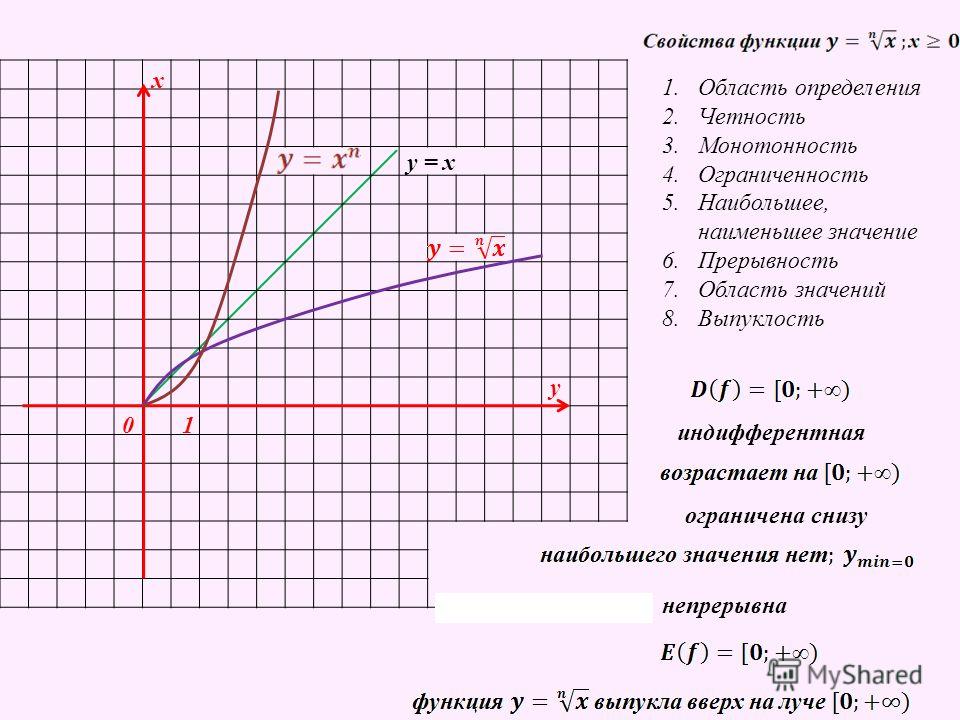
Такой метод построения графика функции y = f(x) + g(х ) называется сложением графиков функций y = f(x) и y = g(x)
Пример 4 . На рисунке методом сложения графиков построен график функции
y = x + sinx .
При построении графика функции y = x + sinx мы полагали, что f(x) = x, а g(x) = sinx. Для построения графика функции выберем точки с aбциссами -1,5π, -, -0,5, 0, 0,5,, 1,5, 2. Значения f(x) = x, g(x) = sinx, y = x + sinx вычислим в выбранных точках и результаты поместим в таблице.
Построение графиков функций, содержащих модули, обычно вызывает немалые затруднения у школьников. Однако, все не так плохо. Достаточно запомнить несколько алгоритмов решения таких задач, и вы сможете без труда построить график даже самой на вид сложной функции.
1. Построение графика функции y = |f(x)|
Заметим, что множество значений функций y = |f(x)| : y ≥ 0. Таким образом, графики таких функций всегда расположены полностью в верхней полуплоскости.
Построение графика функции y = |f(x)| состоит из следующих простых четырех этапов.
1) Построить аккуратно и внимательно график функции y = f(x).
2) Оставить без изменения все точки графика, которые находятся выше оси 0x или на ней.
3) Часть графика, которая лежит ниже оси 0x, отобразить симметрично относительно оси 0x.
Пример 1. Изобразить график функции y = |x 2 – 4x + 3|
1) Строим график функции y = x 2 – 4x + 3. Очевидно, что график данной функции – парабола. Найдем координаты всех точек пересечения параболы с осями координат и координаты вершины параболы.
x 2 – 4x + 3 = 0.
x 1 = 3, x 2 = 1.
Следовательно, парабола пересекает ось 0x в точках (3, 0) и (1, 0).
y = 0 2 – 4 · 0 + 3 = 3.
Следовательно, парабола пересекает ось 0y в точке (0, 3).
Координаты вершины параболы:
x в = -(-4/2) = 2, y в = 2 2 – 4 · 2 + 3 = -1.
Следовательно, точка (2, -1) является вершиной данной параболы.
Рисуем параболу, используя полученные данные (рис. 1)
2) Часть графика, лежащую ниже оси 0x, отображаем симметрично относительно оси 0x.
3) Получаем график исходной функции (рис. 2 , изображен пунктиром).
2. Построение графика функции y = f(|x|)
Заметим, что функции вида y = f(|x|) являются четными:
y(-x) = f(|-x|) = f(|x|) = y(x). Значит, графики таких функций симметричны относительно оси 0y.
Построение графика функции y = f(|x|) состоит из следующей несложной цепочки действий.
1) Построить график функции y = f(x).
2) Оставить ту часть графика, для которой x ≥ 0, то есть часть графика, расположенную в правой полуплоскости.
3) Отобразить указанную в пункте (2) часть графика симметрично оси 0y.
4) В качестве окончательного графика выделить объединение кривых, полученных в пунктах (2) и (3).
Пример 2. Изобразить график функции y = x 2 – 4 · |x| + 3
Так как x 2 = |x| 2 , то исходную функцию можно переписать в следующем виде: y = |x| 2 – 4 · |x| + 3. А теперь можем применять предложенный выше алгоритм.
1) Строим аккуратно и внимательно график функции y = x 2 – 4 · x + 3 (см. также рис. 1 ).
2) Оставляем ту часть графика, для которой x ≥ 0, то есть часть графика, расположенную в правой полуплоскости.
3) Отображаем правую часть графика симметрично оси 0y.
(рис. 3) .
Пример 3. Изобразить график функции y = log 2 |x|
Применяем схему, данную выше.
1) Строим график функции y = log 2 x (рис. 4) .
3. Построение графика функции y = |f(|x|)|
Заметим, что функции вида y = |f(|x|)| тоже являются четными. Действительно, y(-x) = y = |f(|-x|)| = y = |f(|x|)| = y(x), и поэтому, их графики симметричны относительно оси 0y. Множество значений таких функций: y ≥ 0. Значит, графики таких функций расположены полностью в верхней полуплоскости.
Множество значений таких функций: y ≥ 0. Значит, графики таких функций расположены полностью в верхней полуплоскости.
Чтобы построить график функции y = |f(|x|)|, необходимо:
1) Построить аккуратно график функции y = f(|x|).
2) Оставить без изменений ту часть графика, которая находится выше оси 0x или на ней.
3) Часть графика, расположенную ниже оси 0x, отобразить симметрично относительно оси 0x.
4) В качестве окончательного графика выделить объединение кривых, полученных в пунктах (2) и (3).
Пример 4. Изобразить график функции y = |-x 2 + 2|x| – 1|.
1) Заметим, что x 2 = |x| 2 . Значит, вместо исходной функции y = -x 2 + 2|x| – 1
можно использовать функцию y = -|x| 2 + 2|x| – 1, так как их графики совпадают.
Строим график y = -|x| 2 + 2|x| – 1. Для этого применяем алгоритм 2.
a) Строим график функции y = -x 2 + 2x – 1 (рис. 6) .
b) Оставляем ту часть графика, которая расположена в правой полуплоскости.
c) Отображаем полученную часть графика симметрично оси 0y.
d) Полученный график изображен на рисунке пунктиром (рис. 7) .
2) Выше оси 0х точек нет, точки на оси 0х оставляем без изменения.
3) Часть графика, расположенную ниже оси 0x, отображаем симметрично относительно 0x.
4) Полученный график изображен на рисунке пунктиром (рис. 8) .
Пример 5. Построить график функции y = |(2|x| – 4) / (|x| + 3)|
1) Сначала необходимо построить график функции y = (2|x| – 4) / (|x| + 3). Для этого возвращаемся к алгоритму 2.
a) Аккуратно строим график функции y = (2x – 4) / (x + 3) (рис. 9) .
Заметим, что данная функция является дробно-линейной и ее график есть гипербола. Для построения кривой сначала необходимо найти асимптоты графика. Горизонтальная – y = 2/1 (отношение коэффициентов при x в числителе и знаменателе дроби), вертикальная – x = -3.
2) Ту часть графика, которая находится выше оси 0x или на ней, оставим без изменений.
3) Часть графика, расположенную ниже оси 0x, отобразим симметрично относительно 0x.
4) Окончательный график изображен на рисунке (рис. 11) .
сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
График функции 2 в степени модуль х. График функции
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.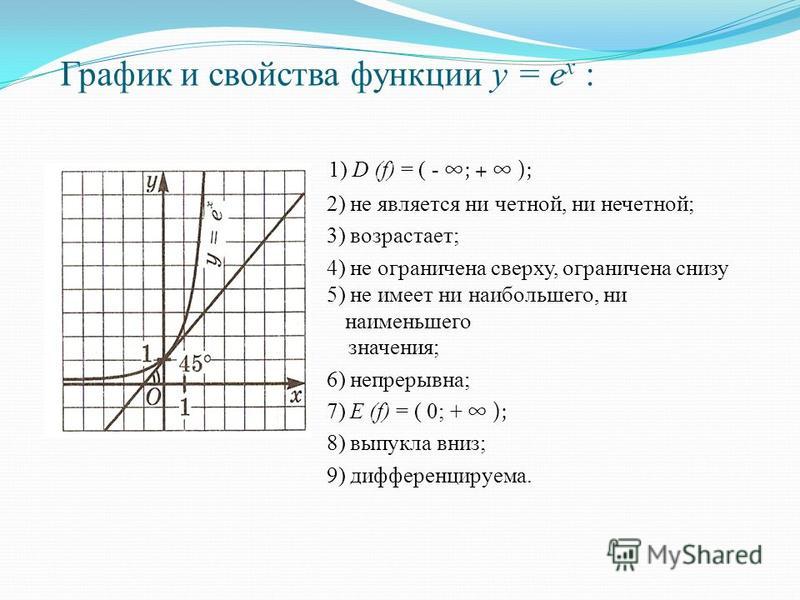
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.

Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения. 3$.
3$.
2. Найдем точку А, координата x, которой равна 1,5. Мы видим, что координата функции находится между значениями 3 и 4 (см. рис. 2). Значит надо заказать 4 куба.
Построение графиков функций, содержащих модули, обычно вызывает немалые затруднения у школьников. Однако, все не так плохо. Достаточно запомнить несколько алгоритмов решения таких задач, и вы сможете без труда построить график даже самой на вид сложной функции. Давайте разберемся, что же это за алгоритмы.
1. Построение графика функции y = |f(x)|
Заметим, что множество значений функций y = |f(x)| : y ≥ 0. Таким образом, графики таких функций всегда расположены полностью в верхней полуплоскости.
Построение графика функции y = |f(x)| состоит из следующих простых четырех этапов.
1) Построить аккуратно и внимательно график функции y = f(x).
2) Оставить без изменения все точки графика, которые находятся выше оси 0x или на ней.
3) Часть графика, которая лежит ниже оси 0x, отобразить симметрично относительно оси 0x.
Пример 1. Изобразить график функции y = |x 2 – 4x + 3|
1) Строим график функции y = x 2 – 4x + 3. Очевидно, что график данной функции – парабола. Найдем координаты всех точек пересечения параболы с осями координат и координаты вершины параболы.
x 2 – 4x + 3 = 0.
x 1 = 3, x 2 = 1.
Следовательно, парабола пересекает ось 0x в точках (3, 0) и (1, 0).
y = 0 2 – 4 · 0 + 3 = 3.
Следовательно, парабола пересекает ось 0y в точке (0, 3).
Координаты вершины параболы:
x в = -(-4/2) = 2, y в = 2 2 – 4 · 2 + 3 = -1.
Следовательно, точка (2, -1) является вершиной данной параболы.
Рисуем параболу, используя полученные данные (рис. 1)
2) Часть графика, лежащую ниже оси 0x, отображаем симметрично относительно оси 0x.
3) Получаем график исходной функции (рис. 2 , изображен пунктиром).
2. Построение графика функции y = f(|x|)
Заметим, что функции вида y = f(|x|) являются четными:
y(-x) = f(|-x|) = f(|x|) = y(x). Значит, графики таких функций симметричны относительно оси 0y.
Значит, графики таких функций симметричны относительно оси 0y.
Построение графика функции y = f(|x|) состоит из следующей несложной цепочки действий.
1) Построить график функции y = f(x).
2) Оставить ту часть графика, для которой x ≥ 0, то есть часть графика, расположенную в правой полуплоскости.
3) Отобразить указанную в пункте (2) часть графика симметрично оси 0y.
4) В качестве окончательного графика выделить объединение кривых, полученных в пунктах (2) и (3).
Пример 2. Изобразить график функции y = x 2 – 4 · |x| + 3
Так как x 2 = |x| 2 , то исходную функцию можно переписать в следующем виде: y = |x| 2 – 4 · |x| + 3. А теперь можем применять предложенный выше алгоритм.
1) Строим аккуратно и внимательно график функции y = x 2 – 4 · x + 3 (см. также рис. 1 ).
2) Оставляем ту часть графика, для которой x ≥ 0, то есть часть графика, расположенную в правой полуплоскости.
3) Отображаем правую часть графика симметрично оси 0y.
(рис. 3) .
Пример 3. Изобразить график функции y = log 2 |x|
Применяем схему, данную выше.
1) Строим график функции y = log 2 x (рис. 4) .
3. Построение графика функции y = |f(|x|)|
Заметим, что функции вида y = |f(|x|)| тоже являются четными. Действительно, y(-x) = y = |f(|-x|)| = y = |f(|x|)| = y(x), и поэтому, их графики симметричны относительно оси 0y. Множество значений таких функций: y ≥ 0. Значит, графики таких функций расположены полностью в верхней полуплоскости.
Чтобы построить график функции y = |f(|x|)|, необходимо:
1) Построить аккуратно график функции y = f(|x|).
2) Оставить без изменений ту часть графика, которая находится выше оси 0x или на ней.
3) Часть графика, расположенную ниже оси 0x, отобразить симметрично относительно оси 0x.
4) В качестве окончательного графика выделить объединение кривых, полученных в пунктах (2) и (3).
Пример 4. Изобразить график функции y = |-x 2 + 2|x| – 1|.
1) Заметим, что x 2 = |x| 2 . Значит, вместо исходной функции y = -x 2 + 2|x| – 1
можно использовать функцию y = -|x| 2 + 2|x| – 1, так как их графики совпадают.
Строим график y = -|x| 2 + 2|x| – 1. Для этого применяем алгоритм 2.
a) Строим график функции y = -x 2 + 2x – 1 (рис. 6) .
b) Оставляем ту часть графика, которая расположена в правой полуплоскости.
c) Отображаем полученную часть графика симметрично оси 0y.
d) Полученный график изображен на рисунке пунктиром (рис. 7) .
2) Выше оси 0х точек нет, точки на оси 0х оставляем без изменения.
3) Часть графика, расположенную ниже оси 0x, отображаем симметрично относительно 0x.
4) Полученный график изображен на рисунке пунктиром (рис. 8) .
Пример 5. Построить график функции y = |(2|x| – 4) / (|x| + 3)|
1) Сначала необходимо построить график функции y = (2|x| – 4) / (|x| + 3). Для этого возвращаемся к алгоритму 2.
a) Аккуратно строим график функции y = (2x – 4) / (x + 3) (рис. 9) .
Заметим, что данная функция является дробно-линейной и ее график есть гипербола. Для построения кривой сначала необходимо найти асимптоты графика. Горизонтальная – y = 2/1 (отношение коэффициентов при x в числителе и знаменателе дроби), вертикальная – x = -3.
2) Ту часть графика, которая находится выше оси 0x или на ней, оставим без изменений.
3) Часть графика, расположенную ниже оси 0x, отобразим симметрично относительно 0x.
4) Окончательный график изображен на рисунке (рис. 11) .
сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
3-8 PDF ЭКСПОНЕНЦИАЛЬНЫЙ РОСТ И ЗАПАД В этом разделе мы рассмотрим различные приложения, моделируемые экспоненциальными функциями.  Экспоненциальные функции моделируют многие научные явления. Некоторые приложения экспоненциальных функций включают рост населения, сложные проценты и радиоактивный распад. Радиоактивный распад используется для датирования древних предметов, найденных на археологических раскопках. Экспоненциальные функции моделируют многие научные явления. Некоторые приложения экспоненциальных функций включают рост населения, сложные проценты и радиоактивный распад. Радиоактивный распад используется для датирования древних предметов, найденных на археологических раскопках.Экспоненциальные функции Рассмотрим каждую из следующих функций.
Показательная функция — это функция, имеющая общий вид y = ab x , a ≠ 0, b — положительное действительное число, а b ≠ 1.  В экспоненциальной функции 909 основание b — константа. Показатель степени x — это независимая переменная, где областью определения является набор действительных чисел. В экспоненциальной функции 909 основание b — константа. Показатель степени x — это независимая переменная, где областью определения является набор действительных чисел. Существует два типа экспоненциальных функций: экспоненциальный рост и экспоненциальный спад .
Например, :
Экспоненциальные функции (03:50) Стоп! Перейдите к вопросам 1–5 по этому разделу, затем вернитесь, чтобы перейти к следующему разделу.Графики экспоненциальных функций Как и в случае с другими функциями, для построения графика экспоненциальной функции можно использовать упорядоченные пары.
В первом примере будет показан график экспоненциального роста , поскольку основание больше 1. ( b = 2)
Графики показательных функций, показывающие рост , имеют следующие характеристики:
Экспоненциальный рост — деление клеток (02:33)
В следующем примере показан график экспоненциального убывания , поскольку основанием является число от 0 до 1. ( b = 1/2)
Графики экспоненциальных функций, показывающие рост , имеют следующие характеристики:
Множитель a в y = ab x может растянуть или сжать граф родительского графа y = b x . 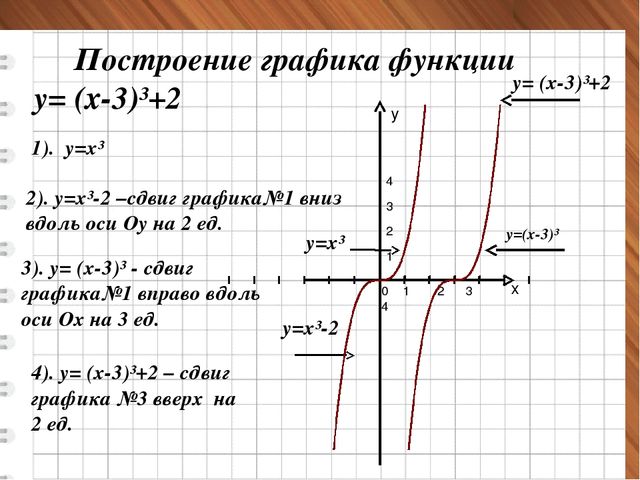 Если a < 0, график будет отражаться по оси x . Если a < 0, график будет отражаться по оси x .Графики y = 2 x (синего цвета) и y = 3(2) х (красным цветом) показаны ниже. Каждый и -значение y = 3(2) x в 3 раза превышает соответствующее y значение родительской функции y = 2 x . График родительской функции y = 2 x растянут в 3 раза. Обратите внимание на y — точка пересечения y = 3(2) x равно 3. Домен функции — действительные числа, а диапазон — все положительные числа.
Теперь давайте рассмотрим характеристики экспоненциальных графиков. Что такое домен у = 4 х ? Настоящие числа. «Нажмите здесь», чтобы проверить ответ. *Домен ВСЕХ экспоненциальных функций — действительные числа. Каков диапазон y = 3 x ? Диапазон равен г > 0. «Нажмите здесь», чтобы проверить ответ. Что такое y — точка пересечения y = 2 x ? y -перехват равен 1. «Нажмите здесь», чтобы проверить ответ. Что такое y -пересечение y = ? Точка пересечения и равна 1/3. «Нажмите здесь», чтобы проверить ответ. Каков диапазон y = ? Диапазон и «Нажмите здесь», чтобы проверить ответ. *Диапазон состоит из отрицательных чисел, поскольку отрицательный знак заставлял график отражаться по оси x . 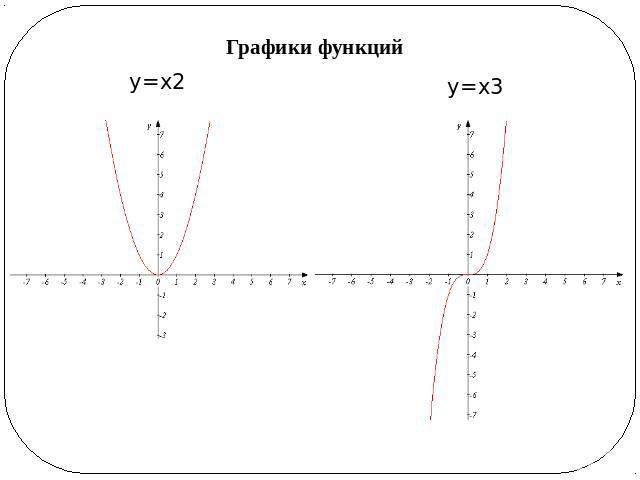 Стоп! Перейдите к вопросам № 6–13 по этому разделу, затем вернитесь, чтобы перейти к следующему разделу.Применение экспоненциального роста и затухания Для решения задач экспоненциального роста и затухания применяйте правила, приведенные в таблице.
Когда количество увеличивается на фиксированный процент через равные промежутки времени, закономерность может быть представлена следующей функцией.
Теперь давайте посмотрим, как эти правила применяются к некоторым обычным приложениям роста и распада в реальном мире.
Deriving the Equation for Annual Compound Interest (02:19) Using a Graphing Calculator to Calculate Annual Compound Interest (02:38)
В следующем примере демонстрируется экспоненциальный рост, когда исходная сумма неоднократно умножается на положительное число, называемое коэффициентом роста. Коэффициент роста определяется путем добавления 100% и скорости роста. Если сумма удваивается, это означает, что 100% прибавляются к 100%, поэтому множитель становится равным 200% или 2. Если сумма утроена, то множитель будет 300% или 3.
Если популяция кроликов утроится по каждые 6 месяцев, сколько будет в этом районе через три года? 21 870 [ y = 30(3) 6 ] «Нажмите здесь», чтобы проверить ответ.
Какой тип начисления наиболее выгоден? Компаундирование ежедневно «Нажмите здесь», чтобы проверить ответ. Стоп! Перейдите к вопросам № 14–30 по этому разделу, затем вернитесь, чтобы перейти к следующему разделу. |
6.5 Экспоненциальные функции | Функции
6.
 5 Экспоненциальные функции (EMA4V) 9{Икс}\).
5 Экспоненциальные функции (EMA4V) 9{Икс}\).\(-\текст{2}\) | \(-\текст{1}\) | \(\текст{0}\) | \(\текст{1}\) | 9{х}\)9{х}\) | 9{х}\) |
В какой точке эти графики пересекаются?
Объясните, почему они не обрезают ось \(х\).

Укажите домен и диапазон \(h(x)\).
При увеличении \(x\) увеличивается или уменьшается \(h(x)\)?
Какой из этих графиков увеличивается медленнее всего? 9{x}\) и \(k>1\), тем больше значение \(k\), тем круче кривая графика. Правда или ЛОЖЬ?
Заполните следующую таблицу для каждой функции и начертите графики та же система координат: \(F(x)={\left(\dfrac{1}{2}\right)}^{x}\), \(G(x)={\left(\dfrac{1}{3}\right)}^{x}\), \(H(x)={\left(\dfrac{1}{5}\right)}^{x}\)
\(-\текст{2}\) | \(-\текст{1}\) | \(\текст{0}\) | \(\текст{1}\) | 9{х}\)9{х}\) | 9{х}\) |
Укажите точку пересечения \(y\) для каждой функции.

Опишите связь между графиками \(f(x)\) и \(F(x)\).
Опишите связь между графиками \(g(x)\) и \(G(x)\).
Укажите домен и диапазон \(H(x)\).
9{x}\) и \(k>1\), больше значение \(k\), тем круче кривая график. Правда или ложь?
Правда или ложь?Приведите уравнение асимптоты для функций.
Подставьте значения в уравнения
\(-\текст{2}\) | \(-\текст{1}\) | \(\текст{0}\) | \(\текст{1}\) 9{х}\) | \(\ гидроразрыва{1}{4}\) | \(\ гидроразрыва{1}{2}\) | \(\текст{1}\) | \(\текст{2}\) 9{х}\) | \(\ гидроразрыва{1}{9}\) | \(\frac{1}{3}\) | \(\текст{1}\) | \(\текст{3}\) 9{х}\) | \(\ гидроразрыва{1}{25}\) | \(\frac{1}{5}\) | \(\текст{1}\) | \(\текст{5}\) | \(\текст{25}\) |
\(-\текст{2}\) | \(-\текст{1}\) | \(\текст{0}\) | \(\текст{1}\) | \(\текст{2}\) | 9{х}\)\(\текст{4}\) | \(\текст{2}\) | \(\текст{1}\) | \(\ гидроразрыва{1}{2}\) | 9{х}\)\(\текст{9}\) | \(\текст{3}\) | \(\текст{1}\) | \(\ гидроразрыва{1}{3}\) | 9{х}\)\(\текст{25}\) | \(\текст{5}\) | \(\текст{1}\) | \(\ гидроразрыва{1}{5}\) | \(\ гидроразрыва{1}{25}\) |
Нанесите точки и соедините их плавной кривой
Заметим, что все графики проходят через точку \((0;1)\).
 Любое число с показателем степени \(\text{0}\) равно
\(\текст 1}\).
Любое число с показателем степени \(\text{0}\) равно
\(\текст 1}\).Графики не пересекают ось \(x\), потому что вы никогда не сможете получить \(\text{0}\), возведя любое ненулевое число в степень любого другого числа.
Домен: \(\left\{x:x\in \mathbb{R}\right\}\)
Диапазон: \(\left\{y:y\in \mathbb{R}, y>0\right\}\)
По мере увеличения \(x\) увеличивается \(h(x)\).
 9{0}=1 \qquad z \ne 0\).
9{0}=1 \qquad z \ne 0\).\(F(x)\) есть отражение \(f(x)\) относительно оси \(y\).
\(G(x)\) есть отражение \(g(x)\) относительно оси \(y\).
Домен: \(\left\{x:x\in \mathbb{R}\right\}\)
Диапазон: \(\left\{y:y\in \mathbb{R}, y>0\right\}\)
9{x}+q\) (EMA4X)CAPS заявляет, что исследует только влияние \(a\) и \(q\) на экспоненциальную график.
 Однако учащимся также важно видеть, что \(b\) имеет
различное влияние на график в зависимости от того, \(b > 1\) или \(0
Однако учащимся также важно видеть, что \(b\) имеет
различное влияние на график в зависимости от того, \(b > 1\) или \(0 По этой причине эффект \(b\) включен в исследование, так что учащиеся можно увидеть, что происходит, когда \(b > 1\) и когда \(0
Также обратите внимание, что приведенный выше рабочий пример дополнительно усиливает влияние \(b\) на экспоненциальный график.
Эффекты \(a\), \(q\) и \(b\) на экспоненциальном графике.
На том же наборе осей постройте следующие графики (\(a=1\), \(q=0\) и \(b\) изменения):
9{х}\)
\(-\текст{2}\) | \(-\текст{1}\) | \(\текст{0}\) | \(\текст{1}\) | 9{х}\)||||||
| 9{х}\) | |||||||||
| 9{х}\) | |||||||||
| 9{х}\) |
Используйте свои результаты, чтобы вывести эффект \(b\).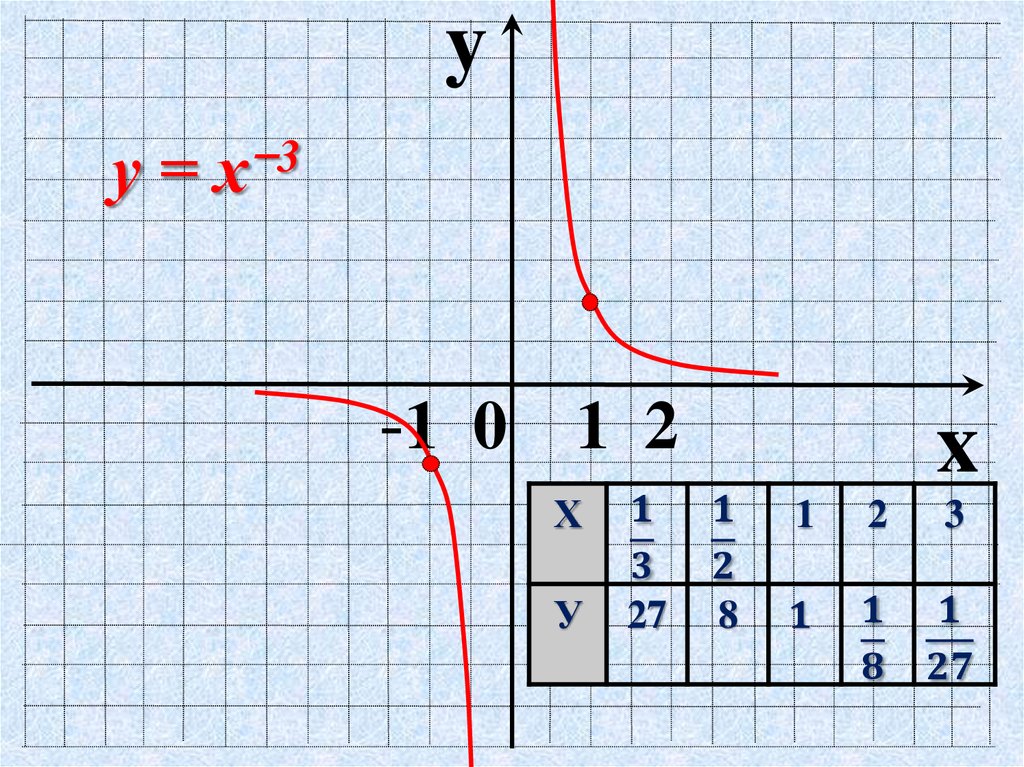 9{х}+2\)
9{х}+2\)
\(-\текст{2}\) | \(-\текст{1}\) | \(\текст{0}\) | \(\текст{1}\) | 9{х}-2\)||||||
| 9{х}-1\) | |||||||||
| 9{х}\) | |||||||||
| 9{х}+1\) | |||||||||
| 9{х}+2\) |
Используйте полученные результаты, чтобы определить эффект \(q\).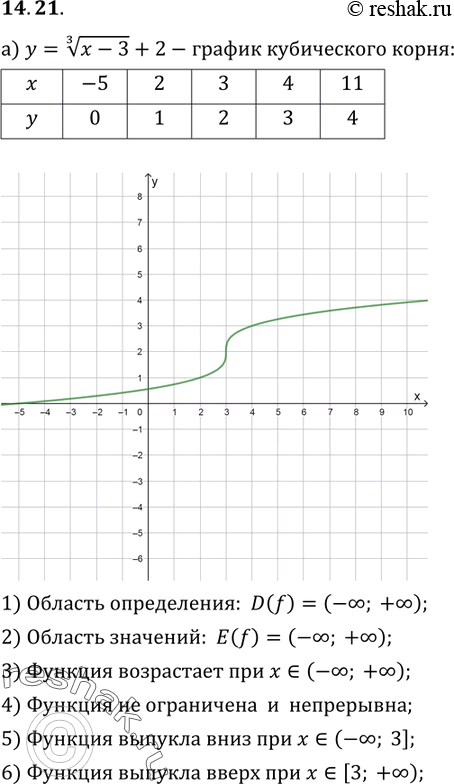 9{х}\)
9{х}\)
\(-\текст{2}\) | \(-\текст{1}\) | \(\текст{0}\) | \(\текст{1}\) | 9{х}\)||||||
| 9{х}\) | |||||||||
| 9{х}\) | |||||||||
| 9{х}\) |
Используйте свои результаты, чтобы вывести эффект \(a\).
Эффект \(q\)
Эффект \(q\) называется вертикальным сдвигом, потому что все точки перемещаются на одинаковое расстояние в том же направлении (скользит весь график вверх или вниз).
Для \(q>0\) график смещается вертикально вверх на \(q\) единиц.
Для \(q<0\) график смещается вертикально вниз на \(q\) единиц.
Горизонтальная асимптота смещена на \(q\) единиц и представляет собой прямую \(y=q\).
Эффект \(а\)
Знак \(a\) определяет, изгибается ли график вверх или вниз.
Для \(0 Для \(a>0\) график изгибается вниз. Для \(a<0\) график изгибается вверх. Он отражает график о
горизонтальная асимптота.
Он отражает график о
горизонтальная асимптота.
Для \(b > 1\):
Для \(a>0\) график изгибается вверх.
Для \(a<0\) график изгибается вниз. Он отражает график о горизонтальная асимптота.
\(б>1\) | \(а<0\) | \(а>0\) |
\(д>0\) | ||
\(д<0\) |
Влияние \(a\) и \(q\) на экспоненциальный график, когда \(b > 1\).
\(0 | \(а<0\) | \(а>0\) |
\(д>0\) | ||
\(д<0\) | 9{x}+1& > 1 \конец{выравнивание*} |

 ) f ( x ) = 0,83 x будет представлять экспоненциальное затухание, поскольку 0 < b 9), оцените 4 x для x = 0,5.
) f ( x ) = 0,83 x будет представлять экспоненциальное затухание, поскольку 0 < b 9), оцените 4 x для x = 0,5.
 В этом разделе мы рассмотрим графики, демонстрирующие экспоненциальный рост и экспоненциальное затухание.
В этом разделе мы рассмотрим графики, демонстрирующие экспоненциальный рост и экспоненциальное затухание.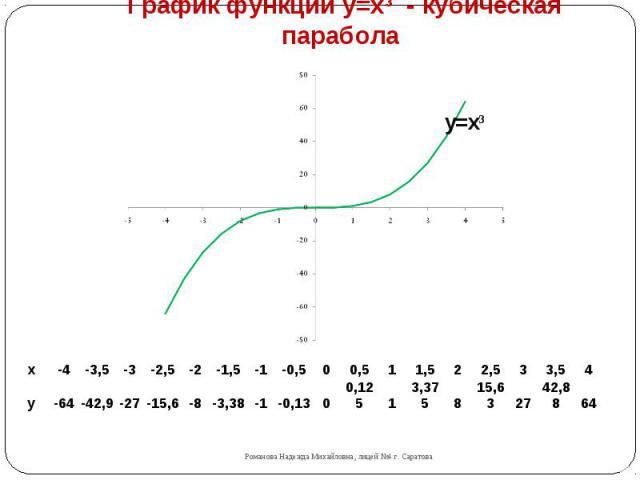
 )
)
 г — перехват. Весь диапазон состоит из положительных чисел, поэтому y > 0.
г — перехват. Весь диапазон состоит из положительных чисел, поэтому y > 0. 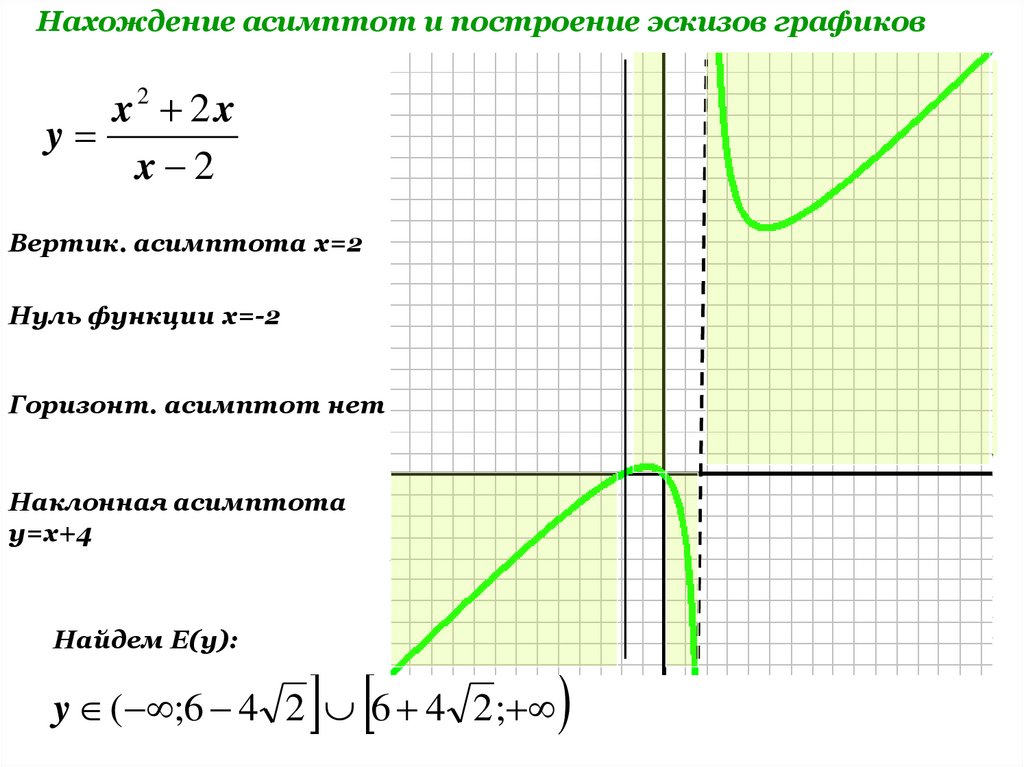

 Правда или ложь?
Правда или ложь?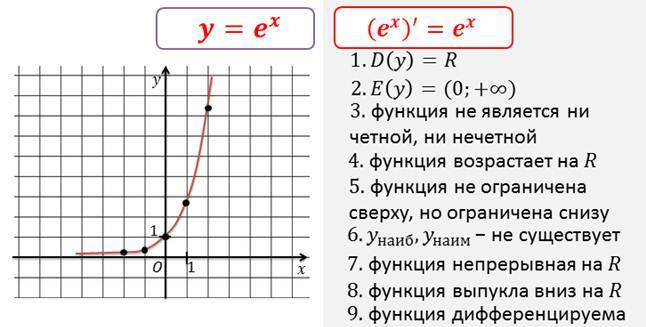 Любое число с показателем степени \(\text{0}\) равно
\(\текст 1}\).
Любое число с показателем степени \(\text{0}\) равно
\(\текст 1}\).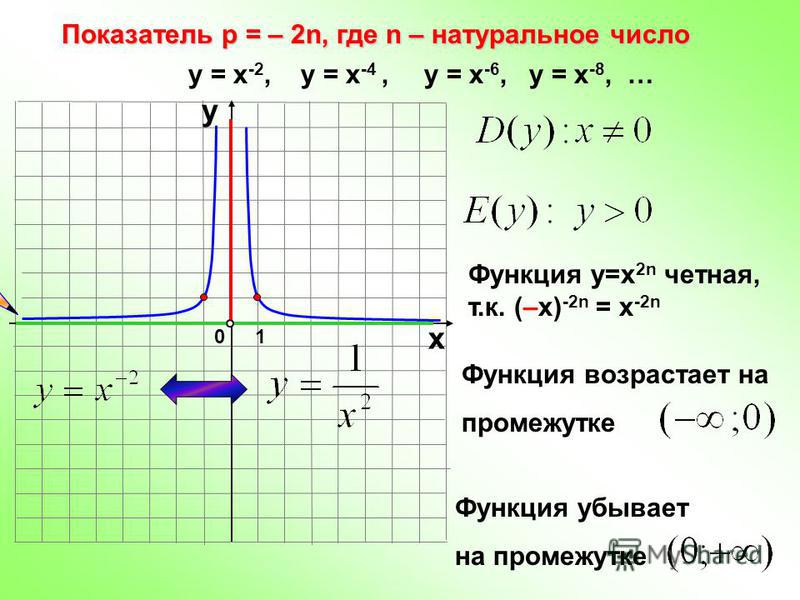 9{0}=1 \qquad z \ne 0\).
9{0}=1 \qquad z \ne 0\). Однако учащимся также важно видеть, что \(b\) имеет
различное влияние на график в зависимости от того, \(b > 1\) или \(0
Однако учащимся также важно видеть, что \(b\) имеет
различное влияние на график в зависимости от того, \(b > 1\) или \(0  {0}+q \\
& = а(1)+q \\
& = а + д
\конец{выравнивание*}
9{x}+q\), нам нужно определить
четыре характеристики:
{0}+q \\
& = а(1)+q \\
& = а + д
\конец{выравнивание*}
9{x}+q\), нам нужно определить
четыре характеристики: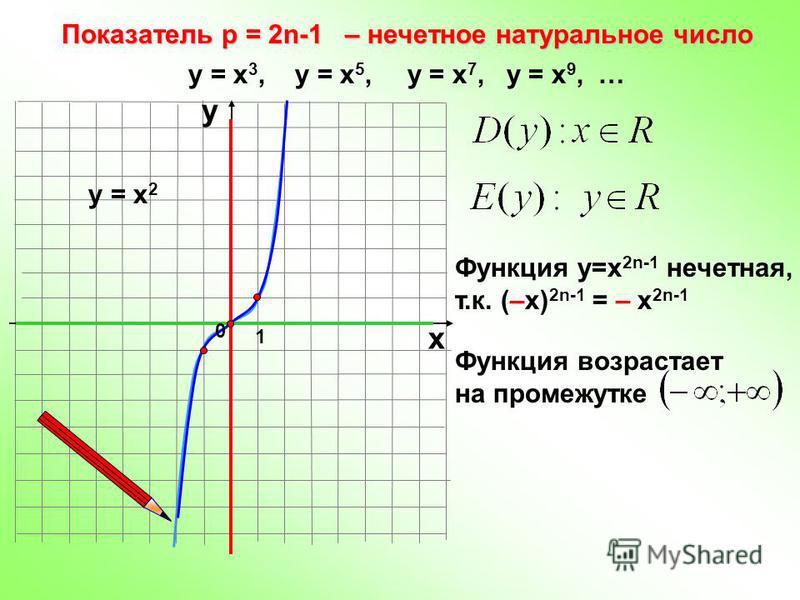 {0}+2 \\
& = 3+2 \\
& = 5
\конец{выравнивание*}
9{х}& = -\фракция{2}{3}
\конец{выравнивание*}
{0}+2 \\
& = 3+2 \\
& = 5
\конец{выравнивание*}
9{х}& = -\фракция{2}{3}
\конец{выравнивание*} {0}+6 \\
& = 4
\конец{выравнивание*}
9{Икс} \\
\поэтому х& = 1
\конец{выравнивание*}
{0}+6 \\
& = 4
\конец{выравнивание*}
9{Икс} \\
\поэтому х& = 1
\конец{выравнивание*} {(0)} +
\текст 1} \\
& = \left( -\frac{2}{3} \right). (\текст{1}) +
\текст 1} \\
& = (-\текст{0,66666…}) + \текст{1} \\
& = \текст{0,33}
\конец{выравнивание*}
{(0)} +
\текст 1} \\
& = \left( -\frac{2}{3} \right). (\текст{1}) +
\текст 1} \\
& = (-\текст{0,66666…}) + \текст{1} \\
& = \текст{0,33}
\конец{выравнивание*} {x}
\конец{выравнивание*}
91 & = \текст{3}
\конец{выравнивание*}
{x}
\конец{выравнивание*}
91 & = \текст{3}
\конец{выравнивание*} {x} + q\). дается одно очко
на кривой: 9{\ влево (-3 \ вправо)} \\
-\текст{0,125} & = а (\текст{0,125}) \\
-1 & = а
\конец{выравнивание*}
{x} + q\). дается одно очко
на кривой: 9{\ влево (-3 \ вправо)} \\
-\текст{0,125} & = а (\текст{0,125}) \\
-1 & = а
\конец{выравнивание*}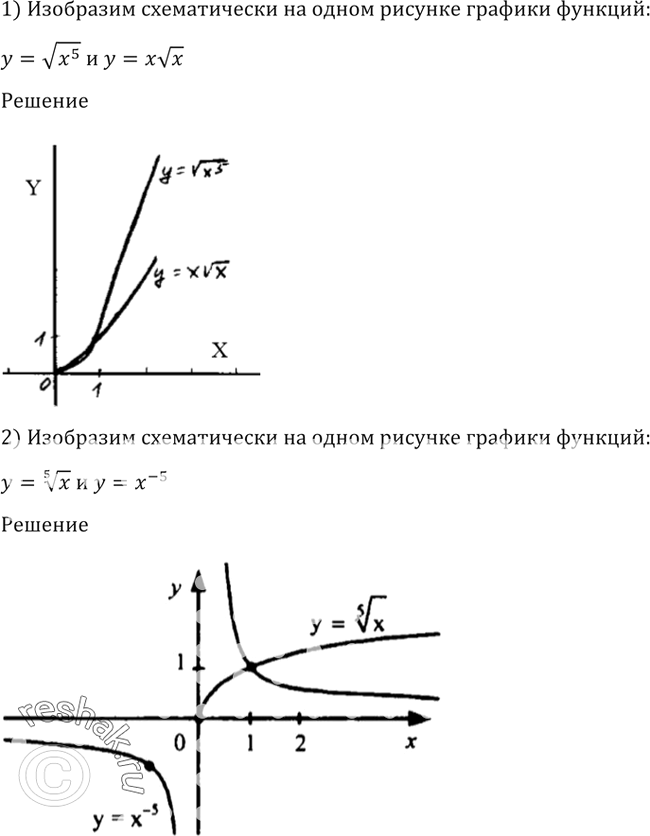 {х} \\
х &= 1
\конец{выравнивание*}
9{x}\):
{х} \\
х &= 1
\конец{выравнивание*}
9{x}\): 0 = 1
\конец{выравнивание*}
9{х}-3\)
0 = 1
\конец{выравнивание*}
9{х}-3\) Повторяем 8 раз. Чтобы найти вероятность того, что каждый раз, когда мы получаем зеленый шар, нам нужно использовать следующее распределение: биномиальное с числом попыток 8 и вероятностью успеха 0,2 биномиальное с числом попыток 25 и вероятностью успеха 0,5 биномиальное с числом попыток 5 и вероятность успеха 0,2 биномиальная с числом испытаний 8 и вероятностью успеха 0,8 биномиальная с числом испытаний 8 и вероятностью успеха 1/3 Распределение Пуассона со средним 5 Распределение Пуассона со средним 8 биномиальное с числом испытаний 25 и вероятностью успеха 0,27. Среднее количество домов с 3 и более спальнями, продаваемых Acme Reality, составляет 14 домов в неделю. Чтобы найти вероятность того, что ровно 3 таких дома будут проданы завтра, нам нужно использовать следующее распределение: Распределение Пуассона со средним 2 Распределение Пуассона со средним 14 Распределение Пуассона со средним 7 с числом испытаний 2 и вероятностью успеха 2/7 Биномиальное с числом испытаний 7 и вероятностью успеха 1/7Стандартное нормальное распределение8.
Повторяем 8 раз. Чтобы найти вероятность того, что каждый раз, когда мы получаем зеленый шар, нам нужно использовать следующее распределение: биномиальное с числом попыток 8 и вероятностью успеха 0,2 биномиальное с числом попыток 25 и вероятностью успеха 0,5 биномиальное с числом попыток 5 и вероятность успеха 0,2 биномиальная с числом испытаний 8 и вероятностью успеха 0,8 биномиальная с числом испытаний 8 и вероятностью успеха 1/3 Распределение Пуассона со средним 5 Распределение Пуассона со средним 8 биномиальное с числом испытаний 25 и вероятностью успеха 0,27. Среднее количество домов с 3 и более спальнями, продаваемых Acme Reality, составляет 14 домов в неделю. Чтобы найти вероятность того, что ровно 3 таких дома будут проданы завтра, нам нужно использовать следующее распределение: Распределение Пуассона со средним 2 Распределение Пуассона со средним 14 Распределение Пуассона со средним 7 с числом испытаний 2 и вероятностью успеха 2/7 Биномиальное с числом испытаний 7 и вероятностью успеха 1/7Стандартное нормальное распределение8.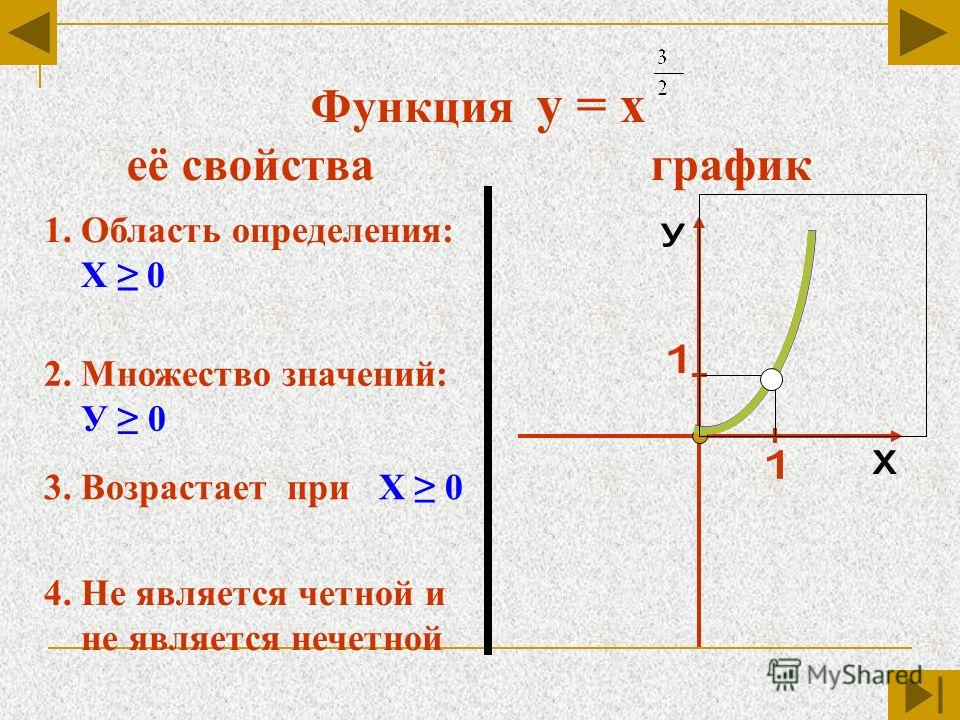 Случайная величина X принимает значения 1,2,3,…,8,9, и 10, каждое с одинаковой вероятностью, а именно с вероятностью 0,1. Найдите вероятность того, что X получит не менее 3,9. Случайная величина X принимает значения 1,2,3,…,8,9,10, каждое с одинаковой вероятностью, а именно с вероятностью 0,1. Найдите вероятность того, что X получит не более 4,10. Карта вытягивается с заменой из обычной колоды карт 16 раз. Пусть случайная величина X представляет собой количество треф среди выбранных 16 карт (в каждой колоде 13 треф; в колоде 52 карты). Найдите дисперсию X,11. Срок службы инструмента, изготовленного машиной, имеет нормальное распределение со средним значением 12 месяцев и стандартным отклонением 2 месяца. Найдите вероятность того, что инструмент, изготовленный на этом станке, прослужит менее 7 месяцев. Округлите до тысячных.12. Срок службы инструмента, изготовленного машиной, имеет нормальное распределение со средним значением 12 месяцев и стандартным отклонением 2 месяца. Найдите вероятность того, что инструмент, изготовленный этой машиной, прослужит от 7 до 12 месяцев.
Случайная величина X принимает значения 1,2,3,…,8,9, и 10, каждое с одинаковой вероятностью, а именно с вероятностью 0,1. Найдите вероятность того, что X получит не менее 3,9. Случайная величина X принимает значения 1,2,3,…,8,9,10, каждое с одинаковой вероятностью, а именно с вероятностью 0,1. Найдите вероятность того, что X получит не более 4,10. Карта вытягивается с заменой из обычной колоды карт 16 раз. Пусть случайная величина X представляет собой количество треф среди выбранных 16 карт (в каждой колоде 13 треф; в колоде 52 карты). Найдите дисперсию X,11. Срок службы инструмента, изготовленного машиной, имеет нормальное распределение со средним значением 12 месяцев и стандартным отклонением 2 месяца. Найдите вероятность того, что инструмент, изготовленный на этом станке, прослужит менее 7 месяцев. Округлите до тысячных.12. Срок службы инструмента, изготовленного машиной, имеет нормальное распределение со средним значением 12 месяцев и стандартным отклонением 2 месяца. Найдите вероятность того, что инструмент, изготовленный этой машиной, прослужит от 7 до 12 месяцев.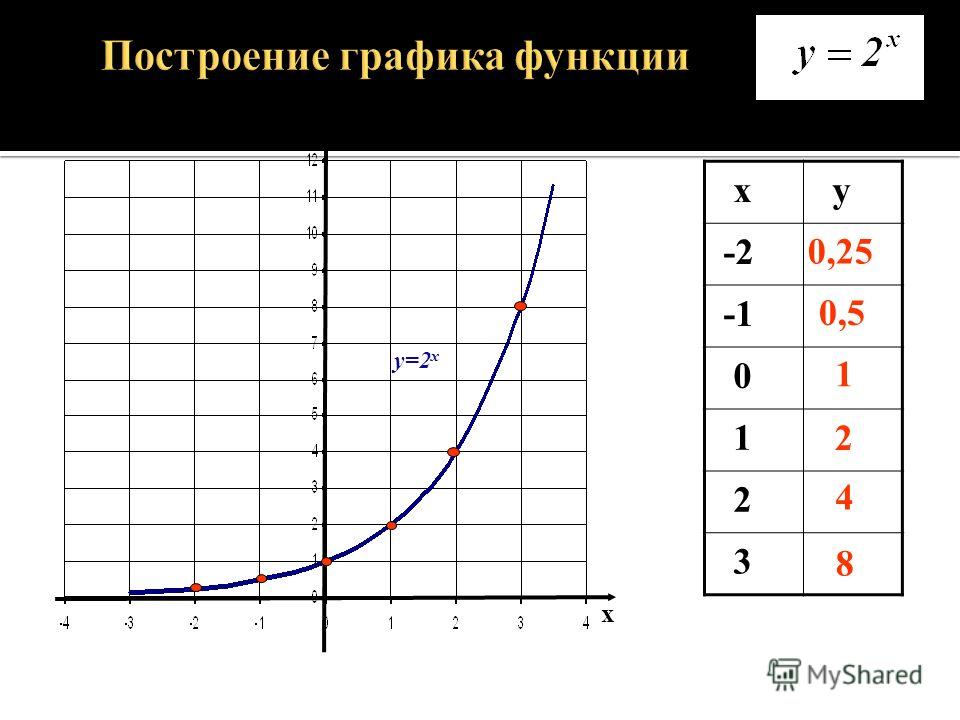 Округлить до тысячных.13. Срок службы инструмента, изготовленного машиной, имеет нормальное распределение со средним значением 12 месяцев и стандартным отклонением 2 месяца. Найдите длину инструмента, который отделяет дно 83,398% хватит? Округлить до сотых.14. Срок службы инструмента, изготовленного машиной, имеет нормальное распределение со средним значением 12 месяцев и стандартным отклонением 2 месяца. Какова вероятность того, что среднее количество месяцев, в течение которых прослужат эти 100 инструментов, больше 12,2 месяцев? Округлить до тысячных.15. Игральную кость бросают 360 раз. Если вы хотите использовать нормальное приближение, чтобы найти вероятность того, что число 4 выпало не менее 100 раз, какое среднее значение нормального распределения вы бы использовали в этом случае. 16. Игральную кость бросают 180 раз. Если вы хотите использовать нормальное приближение, чтобы найти вероятность того, что число 4 выпало не менее 20 раз, какое стандартное отклонение нормального распределения вы бы использовали в этом случае17.
Округлить до тысячных.13. Срок службы инструмента, изготовленного машиной, имеет нормальное распределение со средним значением 12 месяцев и стандартным отклонением 2 месяца. Найдите длину инструмента, который отделяет дно 83,398% хватит? Округлить до сотых.14. Срок службы инструмента, изготовленного машиной, имеет нормальное распределение со средним значением 12 месяцев и стандартным отклонением 2 месяца. Какова вероятность того, что среднее количество месяцев, в течение которых прослужат эти 100 инструментов, больше 12,2 месяцев? Округлить до тысячных.15. Игральную кость бросают 360 раз. Если вы хотите использовать нормальное приближение, чтобы найти вероятность того, что число 4 выпало не менее 100 раз, какое среднее значение нормального распределения вы бы использовали в этом случае. 16. Игральную кость бросают 180 раз. Если вы хотите использовать нормальное приближение, чтобы найти вероятность того, что число 4 выпало не менее 20 раз, какое стандартное отклонение нормального распределения вы бы использовали в этом случае17. Игральную кость бросают 360 раз. Допустим, вы хотите использовать нормальное приближение, чтобы найти вероятность того, что число 4 выпало менее 100 раз. Вам нужно найти вероятность того, что X<100. Объясните, как бы вы использовали поправку на непрерывность в этом случае.18. Игральную кость бросают 360 раз. Допустим, вы хотите использовать нормальное приближение, чтобы найти вероятность того, что число 4 выпало ровно 100 раз. Вам нужно найти вероятность того, что X=100. Объясните, как бы вы использовали поправку на непрерывность в этом случае.19. Как называется теорема, утверждающая, что выборочное распределение выборочного среднего приблизительно нормально, когда выборка большая?20. Определите, имеют ли следующие случайные величины биномиальное распределение: А) Из класса статистики (с заменой) из 400 учеников выбираются десять учеников. Пусть X будет числом учеников, сдавших класс. Б) Жребий бросают три раза. Пусть X будет суммой трех полученных чисел. C) Монета подбрасывается до тех пор, пока не выпадет решка.
Игральную кость бросают 360 раз. Допустим, вы хотите использовать нормальное приближение, чтобы найти вероятность того, что число 4 выпало менее 100 раз. Вам нужно найти вероятность того, что X<100. Объясните, как бы вы использовали поправку на непрерывность в этом случае.18. Игральную кость бросают 360 раз. Допустим, вы хотите использовать нормальное приближение, чтобы найти вероятность того, что число 4 выпало ровно 100 раз. Вам нужно найти вероятность того, что X=100. Объясните, как бы вы использовали поправку на непрерывность в этом случае.19. Как называется теорема, утверждающая, что выборочное распределение выборочного среднего приблизительно нормально, когда выборка большая?20. Определите, имеют ли следующие случайные величины биномиальное распределение: А) Из класса статистики (с заменой) из 400 учеников выбираются десять учеников. Пусть X будет числом учеников, сдавших класс. Б) Жребий бросают три раза. Пусть X будет суммой трех полученных чисел. C) Монета подбрасывается до тех пор, пока не выпадет решка.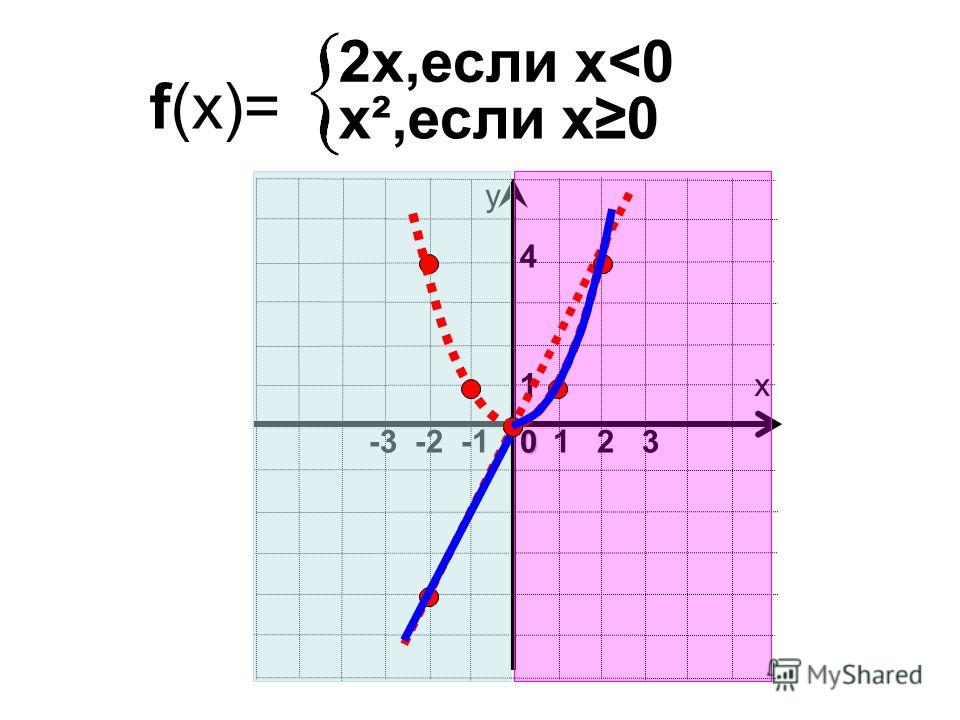 Пусть X — число бросков. Только А — биномиальное распределение, только В — биномиальное распределение, только С — биномиальное распределение, только А и В — биномиальное распределение, только А и С — биномиальное распределение, только В и С — биномиальное распределение, все А, В и C являются биномиальными распределениями, ни одно из них не является биномиальным
Пусть X — число бросков. Только А — биномиальное распределение, только В — биномиальное распределение, только С — биномиальное распределение, только А и В — биномиальное распределение, только А и С — биномиальное распределение, только В и С — биномиальное распределение, все А, В и C являются биномиальными распределениями, ни одно из них не является биномиальным 5 x + 1)
5 x + 1)  Что происходит, когда x идет влево?
Что происходит, когда x идет влево? В нашем предыдущем примере с вашим младшим братом ваше лицо было бы асимптотой.
В нашем предыдущем примере с вашим младшим братом ваше лицо было бы асимптотой.
 Ничего страшного, еще могут написать или отправить открытку.Если мы найдем пару точек, то увидим именно это:
Ничего страшного, еще могут написать или отправить открытку.Если мы найдем пару точек, то увидим именно это: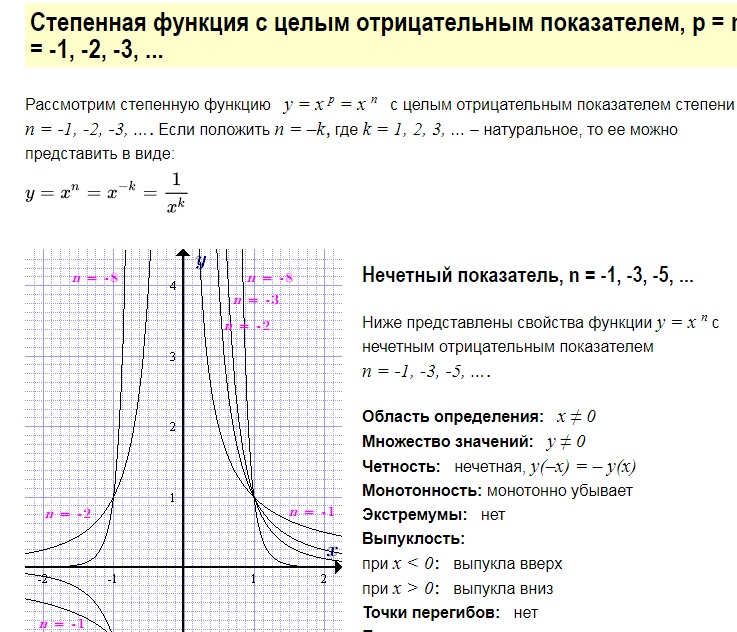
 ..и распознать его как экспоненциальный график с отрицательным показателем степени. Поскольку это сэкономит вам время, а время — деньги, способность распознавать экспоненциальный график приносит вам деньги. Или что-то вроде того.
..и распознать его как экспоненциальный график с отрицательным показателем степени. Поскольку это сэкономит вам время, а время — деньги, способность распознавать экспоненциальный график приносит вам деньги. Или что-то вроде того.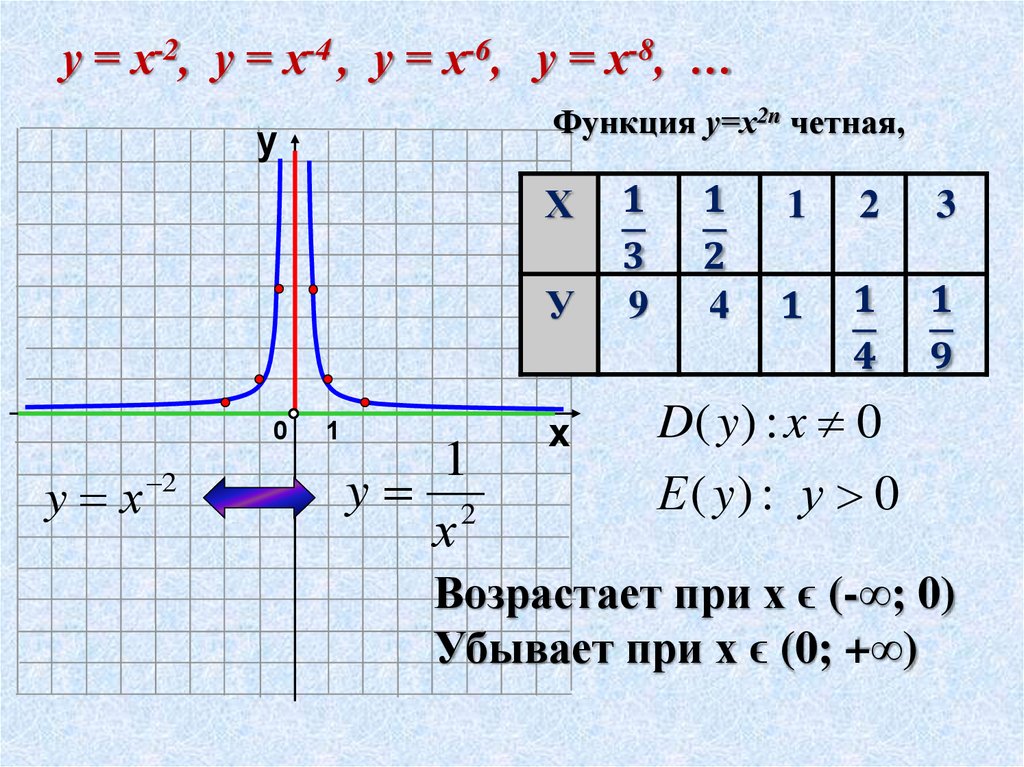 Однако
когда трансцендентные и алгебраические функции смешиваются в уравнении, графическом или числовом
методы иногда являются единственным способом найти решение.
Однако
когда трансцендентные и алгебраические функции смешиваются в уравнении, графическом или числовом
методы иногда являются единственным способом найти решение.
 Исчисление — это алгебра с понятием предела. Люди всегда
есть этот страх исчисления, что я не могу понять. Сам расчет несложный. Причина
люди не преуспевают в вычислениях не из-за вычислений, а потому что они плохие
по алгебре.
Исчисление — это алгебра с понятием предела. Люди всегда
есть этот страх исчисления, что я не могу понять. Сам расчет несложный. Причина
люди не преуспевают в вычислениях не из-за вычислений, а потому что они плохие
по алгебре.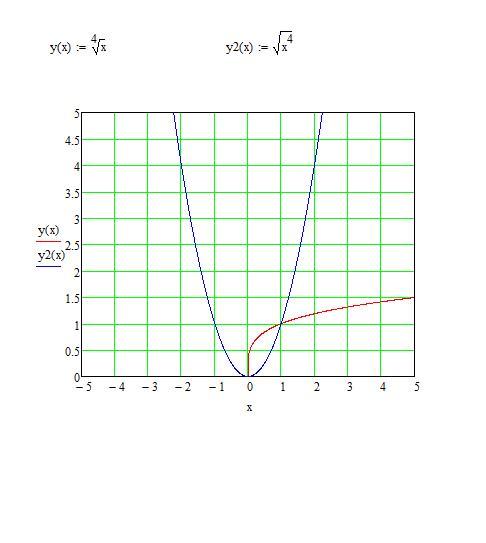
 Формула
Показанная мной выше формула немного отличается от формулы в книге, но согласуется
с формулой, которую вы будете использовать, если пойдете
к конечной математике (Math 160). В конечной математике есть
целую главу о финансах и соответствующих формулах.
Формула
Показанная мной выше формула немного отличается от формулы в книге, но согласуется
с формулой, которую вы будете использовать, если пойдете
к конечной математике (Math 160). В конечной математике есть
целую главу о финансах и соответствующих формулах.