Y 4 x 2 и y x 2: Вычислить площадь фигуры, ограниченной линиями: y=4-x^2; y=x^2-2x

{2}-4ac}}{2a}.

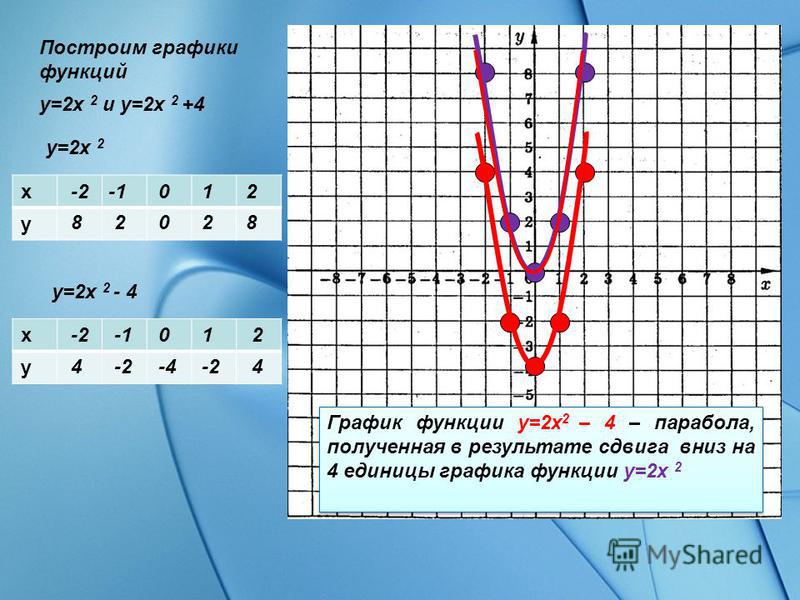
x=\frac{-\left(-4\right)±\sqrt{16-4\times 4\left(1-y\right)}}{2\times 4}

Возведите -4 в квадрат.

x=\frac{-\left(-4\right)±\sqrt{16-16\left(1-y\right)}}{2\times 4}

Умножьте -4 на 4.

x=\frac{-\left(-4\right)±\sqrt{16+16y-16}}{2\times 4}

Умножьте -16 на 1-y.

x=\frac{-\left(-4\right)±\sqrt{16y}}{2\times 4}

Прибавьте 16 к -16+16y.

x=\frac{-\left(-4\right)±4\sqrt{y}}{2\times 4}

Извлеките квадратный корень из 16y.

x=\frac{4±4\sqrt{y}}{2\times 4}

Число, противоположное -4, равно 4.

x=\frac{4±4\sqrt{y}}{8}

Умножьте 2 на 4.

x=\frac{4\sqrt{y}+4}{8}

Решите уравнение x=\frac{4±4\sqrt{y}}{8} при условии, что ± — плюс. Прибавьте 4 к 4\sqrt{y}.

x=\frac{\sqrt{y}+1}{2}

Разделите 4+4\sqrt{y} на 8.

x=\frac{-4\sqrt{y}+4}{8}

Решите уравнение x=\frac{4±4\sqrt{y}}{8} при условии, что ± — минус. Вычтите 4\sqrt{y} из 4.

x=\frac{-\sqrt{y}+1}{2}

Разделите 4-4\sqrt{y} на 8.

{2}+2 x-3}

3-8 9 Оценить квадратный корень из 12 10 Оценить квадратный корень из 20 11 Оценить квадратный корень из 50 94 18 Оценить квадратный корень из 45 19 Оценить квадратный корень из 32 20 Оценить квадратный корень из 18 92

Найти площадь области, ограниченной параболой y = 4×2, касательной к этой параболе в точке (4, 64) и оси x.

Исчисление

Мохаммад Н.

спросил 05.12.20

Найдите площадь области, ограниченной параболой y  = 4 x ² , касательной к этой параболе в точке (4, 64) и оси x .

Подписаться І 1

Подробнее

Отчет

2 ответа от опытных наставников

Лучший Новейшие Самый старый

Автор: ЛучшиеНовыеСамыеСтарые

Уильям В. ответил 05.12.20

Репетитор

5,0 (839)

Опытный репетитор и инженер на пенсии

Смотрите таких репетиторов

Смотрите таких репетиторов

Площадь под y = 4x ² = ₀ ∫ ⁴ (4x ² ) dx = (4/3)x ³ оценивается между 0 и 4 (4/03) 1 = (4/03) 6 3 ) — 4/3(0 ³ ) = 256/3

Наклон касательной можно найти, взяв производную:

y’ = 8x и y'(4) = 8(4) = 32 поэтому уравнение касательной в точке (4, 64) с использованием формы точки и наклона линии имеет вид: y — 64 = 32(x — 4) или y = 32x -64. Когда у = 0, х = 2,

Площадь под касательной равна ₂ ∫ ⁴ (32x — 64) dx = 16x ² — 64x вычислено между 2 и 4 = 16(4 ² ) — 64(4) — (16 2 ² ) — 64(2)) = 256 — 256 — 64 + 128 = 64

Площадь между кривой и касательной = 256/3 — 64 = 256/3 — 196/3 = 64/3

Голосовать за 1 Понизить

Подробнее

Отчет

Том К. ответил 05.12.20

Репетитор

4.9 (94)

Знающий и дружелюбный репетитор по математике и статистике

Об этом репетиторе ›

Об этом репетиторе ›

Тангенс y = 4x ² в точке (4,64) имеет наклон 8x =8*4 = 32.

Таким образом, y =mx+b дает 64 =32(4) +b, поэтому b=-64

Тогда 0 = 32x -64, поэтому x = 2.