Y 5 2x график: Построить график функции: y=5-2x Дам 50 баллов

Решить x-3y=6,2x+y=5 | Microsoft Math Solver

x=3

y=-1

Викторина

Simultaneous Equation

5 задач, подобных этой:

x — 3 y = 6,2 x + y = 5

Подобные задачи из результатов поиска в Интернете

Поделиться

Скопировано в буфер обмена

x-3y=6,2x+y=5

Чтобы решить два уравнения методом подстановки, сначала решите одно из уравнений для одной из переменных. Затем подставьте результат для этой переменной в другое уравнение.

x-3y=6

Выберите один из уравнений и решите его для x, изолируя x в левой части знака равенства.

x=3y+6

Прибавьте 3y к обеим частям уравнения.

2\left(3y+6\right)+y=5

Подставьте 6+3y вместо x в другом уравнении 2x+y=5.

6y+12+y=5

Умножьте 2 на 6+3y.

7y+12=5

Прибавьте 6y к y.

7y=-7

Вычтите 12 из обеих частей уравнения.

y=-1

Разделите обе части на 7.

x=3\left(-1\right)+6

Подставьте -1 вместо y в x=3y+6. Так как получившееся уравнение содержит только одну переменную, вы можете напрямую найти решение для x.

x=-3+6

Умножьте 3 на -1.

x=3

Прибавьте 6 к -3.

x=3,y=-1

Система решена.

x-3y=6,2x+y=5

Приведите уравнения к стандартному виду, а затем решите систему уравнений с помощью матриц.

\left(\begin{matrix}1&-3\\2&1\end{matrix}\right)\left(\begin{matrix}x\\y\end{matrix}\right)=\left(\begin{matrix}6\\5\end{matrix}\right)

Запишите уравнения в матричном виде.

inverse(\left(\begin{matrix}1&-3\\2&1\end{matrix}\right))\left(\begin{matrix}1&-3\\2&1\end{matrix}\right)\left(\begin{matrix}x\\y\end{matrix}\right)=inverse(\left(\begin{matrix}1&-3\\2&1\end{matrix}\right))\left(\begin{matrix}6\\5\end{matrix}\right)

Левое произведение с матрицей, обратной \left(\begin{matrix}1&-3\\2&1\end{matrix}\right).

\left(\begin{matrix}1&0\\0&1\end{matrix}\right)\left(\begin{matrix}x\\y\end{matrix}\right)=inverse(\left(\begin{matrix}1&-3\\2&1\end{matrix}\right))\left(\begin{matrix}6\\5\end{matrix}\right)

Произведение матрицы на обратную ей является единичной матрицей.

\left(\begin{matrix}x\\y\end{matrix}\right)=inverse(\left(\begin{matrix}1&-3\\2&1\end{matrix}\right))\left(\begin{matrix}6\\5\end{matrix}\right)

Перемножение матриц слева от знака равенства.

\left(\begin{matrix}x\\y\end{matrix}\right)=\left(\begin{matrix}\frac{1}{1-\left(-3\times 2\right)}&-\frac{-3}{1-\left(-3\times 2\right)}\\-\frac{2}{1-\left(-3\times 2\right)}&\frac{1}{1-\left(-3\times 2\right)}\end{matrix}\right)\left(\begin{matrix}6\\5\end{matrix}\right)

Для матрицы \left(\begin{matrix}a&b\\c&d\end{matrix}\right) с размерностью 2\times 2 обратная матрица имеет вид \left(\begin{matrix}\frac{d}{ad-bc}&\frac{-b}{ad-bc}\\\frac{-c}{ad-bc}&\frac{a}{ad-bc}\end{matrix}\right), поэтому матричное уравнение можно переписать в виде задачи умножения матриц.

\left(\begin{matrix}x\\y\end{matrix}\right)=\left(\begin{matrix}\frac{1}{7}&\frac{3}{7}\\-\frac{2}{7}&\frac{1}{7}\end{matrix}\right)\left(\begin{matrix}6\\5\end{matrix}\right)

Выполните арифметические операции.

\left(\begin{matrix}x\\y\end{matrix}\right)=\left(\begin{matrix}\frac{1}{7}\times 6+\frac{3}{7}\times 5\\-\frac{2}{7}\times 6+\frac{1}{7}\times 5\end{matrix}\right)

Перемножьте матрицы.

\left(\begin{matrix}x\\y\end{matrix}\right)=\left(\begin{matrix}3\\-1\end{matrix}\right)

Выполните арифметические операции.

x=3,y=-1

Извлеките элементы матрицы x и y.

x-3y=6,2x+y=5

Для решения методом исключения коэффициенты одной из переменных должны быть одинаковыми в обоих уравнениях, чтобы переменная сократилась при вычитании одного уравнения из другого.

2x+2\left(-3\right)y=2\times 6,2x+y=5

Чтобы сделать x и 2x равными, умножьте все члены в обеих частях первого уравнения на 2 и все члены в обеих частях второго уравнения на 1.

2x-6y=12,2x+y=5

Упростите.

2x-2x-6y-y=12-5

Вычтите 2x+y=5 из 2x-6y=12 путем вычитания подобных членов в обеих частях уравнения.

-6y-y=12-5

Прибавьте 2x к -2x. Члены 2x и -2x сокращаются, после чего в уравнении остается только одна переменная, и его можно решить.

-7y=12-5

Прибавьте -6y к -y.

-7y=7

Прибавьте 12 к -5.

y=-1

Разделите обе части на -7.

2x-1=5

Подставьте -1 вместо y в 2x+y=5. Так как получившееся уравнение содержит только одну переменную, вы можете напрямую найти решение для x.

2x=6

Прибавьте 1 к обеим частям уравнения.

x=3

Разделите обе части на 2.

x=3,y=-1

Система решена.

Выяснить, согласуются ли x y 5 2x 2y 10 несовместимы…

Перейти к

• Пара линейных уравнений с двумя переменными — упражнение 3.1
• Пара линейных уравнений с двумя переменными — упражнение 3.2
• Пара линейных уравнений с двумя переменными — упражнение 3.3
• Пара линейных уравнений с двумя переменными — упражнение 3. 4
• Пара линейных уравнений с двумя переменными — упражнение 3.5
• Пара линейных уравнений с двумя переменными — упражнение 3.6
• Пара линейных уравнений с двумя переменными — упражнение 3.7

• Вещественные числа
• Полиномы
• Пара линейных уравнений с двумя переменными
• Квадратные уравнения
• Арифметические прогрессии
• Треугольники
• Координатная геометрия
• Введение в тригонометрию
• Некоторые приложения тригонометрии
• Круги
• Конструкции
• Области, связанные с кругами
• Площади поверхности и объемы
• Статистика
• Вероятность

Главная > Решения НЦЭРТ Класс 10 Математика >

Глава 3. Пара линейных уравнений с двумя переменными > Пара линейных уравнений с двумя переменными — упражнение 3.2 > Вопрос 10

Вопрос 10 Пара линейных уравнений с двумя переменными — Упражнение 3.2

Выясните, согласуются ли x + y = 5, 2x + 2y = 10 или нет?

Ответ:

, x + y = 5 и 2x + 2y = 10

(A ₁ /A ₂ ) = 1/2

(B ₁ /B ₂ 63

(B ₁ /B ₂ 63 ) = 1/2

(с ₁ /с ₂ ) = 1/2

Поскольку (а ₁ /а ₂ ) = (b _{1 90 066 /b 2 9 9 9 c 1 /c 2 )}

∴Уравнения совпадают и имеют бесконечное число возможных решений.

Итак, уравнения согласованы.

Для x + y = 5 или x = 5 – y

Для 2x + 2y = 10 или x = (10-2y)/2

Итак, уравнения представлены на графиках следующим образом:

Связанные вопросы

Сравнив отношения (a1/a2), (b1/b2), (c1/c2), найдите, (3/2)x+(5/3)y = 7; 9х – 10у = 1. ..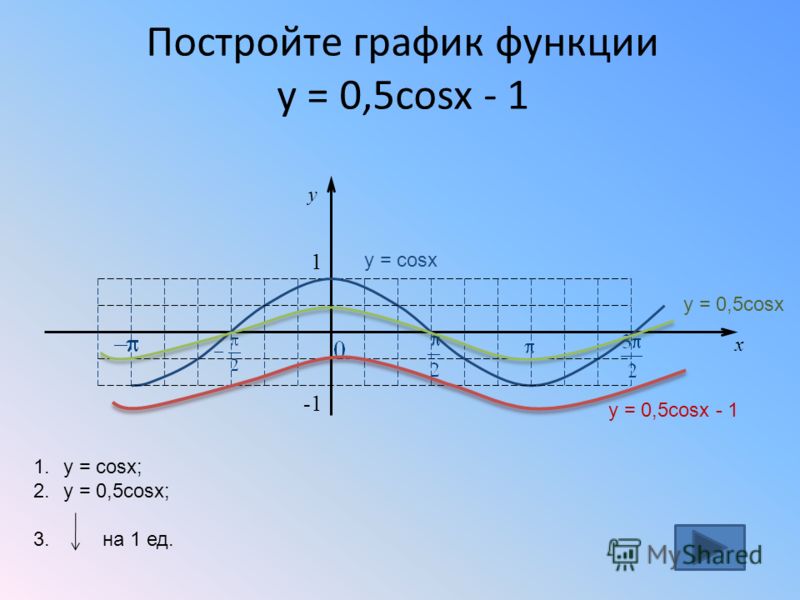

**10 учеников X класса приняли участие в викторине по математике. Если девушек на 4 больше, чем…

**5 карандашей и 7 ручек вместе стоят 50, тогда как 7 карандашей и 5 ручек вместе стоят 46. Найдите цену…

**При сравнении соотношений a₁/a₂ , b₁/b₂ , c ₁/…

** При сравнении отношений a1/a2, b1/b2, c1/c2 для 9x + 3y + 12 = 0 и 18x + 6y + 24 = 0 может быть…

Сравнив отношения (a1/a2), (b1/b2), (c1/c2), найдите, является ли 2x – 3y = 8; 4х – 6у = 9 ст…

Фейсбук WhatsApp

Копировать ссылку

Было ли это полезно?

Упражнения

Пара линейных уравнений с двумя переменными — Упражнение 3. 1

Пара линейных уравнений с двумя переменными — Упражнение 3.2

Пара линейных уравнений с двумя переменными — Упражнение 3.3

Пара линейных уравнений — Упражнение с двумя переменными 3.4

Пара линейных уравнений с двумя переменными — Упражнение 3.5

Пара линейных уравнений с двумя переменными — Упражнение 3.6

Пара линейных уравнений с двумя переменными — Упражнение 3.7

Главы

Реальные числа

Полиномиалы ​​

Пара линейных уравнений в двух переменных

Квадратичные уравнения

Арифметические прогрессии

. Построения

Площади, относящиеся к кругам

Площади и объемы поверхностей

Статистика

Вероятность

Courses

Quick Links

Terms & Policies

Terms & Policies

2022 © Quality Tutorials Pvt Ltd All rights reserved

Graphs of Equations

 

Graphs of Equations

 

Using a coordinate Система с горизонтальной осью, обозначенной буквой x, и вертикальной осью, обозначенной буквой y, позволяет строить графики уравнений, содержащих буквы x и y.

Иногда мы называем координату x входом уравнения, а координату y выходом уравнения. Начертить уравнение означает нанести на график все точки (x, y), для которых уравнение верно.

  

Пример 15.   Для уравнения y = 5 — 2x найдите y, если x равно 2.

 

Ответ:

Замена x на число 2 дает результат y = 5 — 2(2) или   у = 1 . Другими словами, точка (2,1) находится на графике уравнения y = 5 — 2x.

 

Пример 16.   Для уравнения 5x — 2y = 40 найдите y, если x = 10. — 40 = 2 года или г = 5 . Другими словами, точка (10,5) находится на графике уравнения 5x — 2y = 40.

 

Заменив значение x и значение y упорядоченной пары в уравнении, мы можем определить, является ли точка

удовлетворяет уравнению. Чтобы удовлетворить уравнению, нужно найти решение уравнения. Если значения x и y точки являются решением уравнения, то точка находится на графике уравнения.

 

Пример 17.   Для 3x + 2y = 12 определить, соответствует ли точка (2,3) удовлетворяет уравнению.

 

Ответ:

Замена x на 2 и y на 3 дает 3(2) + 2(3) = 12.  Упрощение дает 6 + 6 = 12. Так как верно 12 = 12, то точка (2,3) удовлетворяет уравнению 3x + 2y = 12 и находится на графике уравнения.

 

Пример 18.   Для 3x + 2y = 12 определите, удовлетворяет ли точка (1,-3) уравнению.

 

Ответ:

Замена x на 1 и y на -3 дает 3(1) + 2(-3) = 12.   Упрощение дает 3 — 6 = 12. Поскольку -3 ≠ 12, точка (1, -3) не удовлетворяют уравнению. Следовательно, точка (1,-3) не находится на графике уравнения.

 

Пример 19.   Для определить, удовлетворяет ли точка (5,10) уравнению.

 

 

Ответ:

Замена x на 5 и y на 10 дает . Упрощение дает , , . Поскольку 5 = 5 верно, точка (5,10) удовлетворяет уравнению.

 

 

Графическое изображение уравнения 9. 0062

A) Выберите несколько значений x

B) Используйте эти значения x и уравнение, чтобы найти значения Y

C) Постройте точки, которые вы нашли

D) Нарисовать линию через линию через точки на графике

 

В некоторых случаях может быть удобнее сначала выбрать некоторые значения y.

В этом курсе все уравнения, которые мы нарисуем, будут прямыми линиями. Однако не все графики представляют собой прямые линии. Например, график y = x

2 имеет U-образную форму и называется параболой.

 

Две точки, которые удобно использовать для построения графика, — точки пересечения линии. Пересечение y находится путем замены x на 0 и нахождения y. Пересечение x находится путем замены y на 0 и нахождения x. Точка пересечения оси Y — это точка на оси Y, где линия пересекается, а точка пересечения X — точка на оси X, где пересекается линия.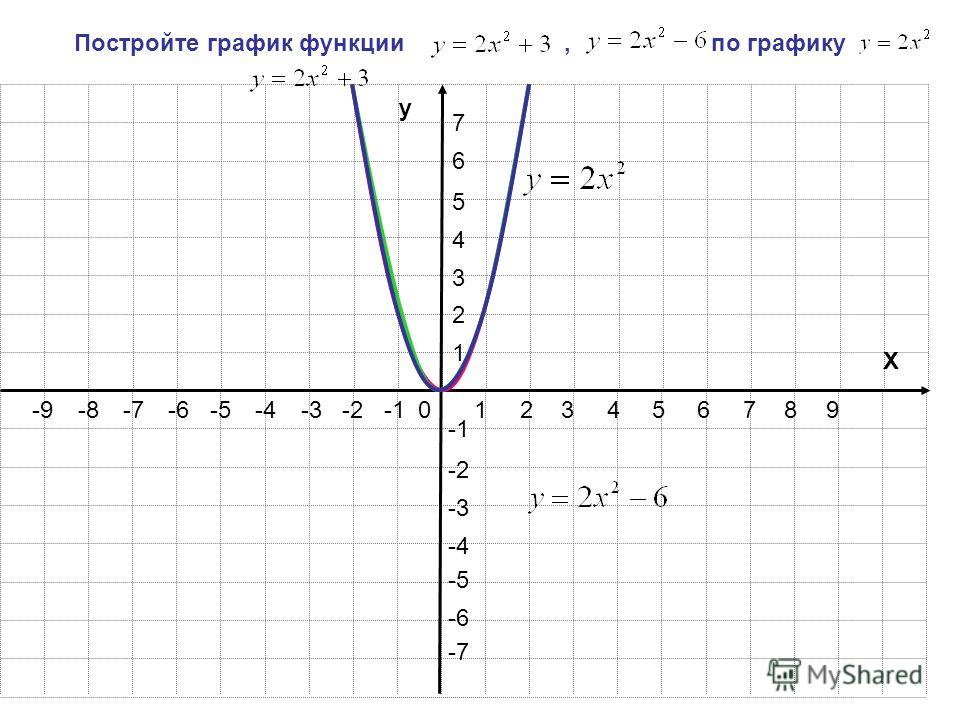

  

Пример 20.   Найдите точки пересечения прямой 3x + 8y = 48,

 

Ответ:

Замена x на 0 дает 3(0) + 8y = 48.   Итак, y = 6, а точка пересечения с осью y является точкой (0,6). Замена y на 0 дает 3x + 8(0) = 48. Таким образом, x = 16, а точка пересечения с x — это точка (16,0).

 

Пример 21.   Изобразите уравнение y = 3x — 4 на осях ниже.

 

Ответ:

Замена x на 0 в уравнении дает y = -4. Замена x на 2 дает y = 2. Замена x на 3 дает y = 5. Таким образом, мы должны изобразить соответствующие точки (0,-4), (2,2) и (3,5), а затем нарисовать линию через них. Значения x должны быть выбраны разумно, чтобы результирующие точки не находились за пределами области, охватываемой вашими координатными осями. Три точки и линия, проходящая через них, показаны ниже: 9Пример 22. Постройте уравнение y = x.

 

Ответ:

Это означает изобразить на графике каждую точку, у которой координата y имеет то же значение, что и ее координата x. Такой график будет состоять из таких точек, как (-3,-3), (0,0), (1,1), (4,4) и всех других точек, где координата y равна координате x . График показан ниже:

 

 

Пример 23.   Нарисуйте уравнение y = 2x — 1.

 

Ответ:

Это означает графическое отображение тех точек, координата y которых на 1 меньше, чем удвоенная координата x. Несколько точек на этом графике будут (0,-1), (3,5), (100,199) и так далее. График показан ниже:

 

 

Пример 24.   Нарисуйте уравнение .

.

 

 

Ответ:

Это означает нанести на график те точки, координата y которых на 1 больше, чем две трети координаты x. Хорошей идеей было бы нанести точку, где x = 0 и y = 1, а затем точки, значения x которых кратны трем. Например, когда х = 3, у = 3; когда х = -3, у = -1; когда x = 6, y = 5. Нанесите точки (0,1), (3,3), (-3,-1) и (6,5). График показан ниже:

Пример 25.

No related posts.