ОглавлениеВВЕДЕНИЕЧасть первая.  Глава I. ДЕЙСТВИТЕЛЬНЫЕ И КОМПЛЕКСНЫЕ ЧИСЛА 2. Простые и составные числа. Признаки делимости. 3. Наибольший общий делитель и наименьшее общее кратное. 4. Целые числа. Рациональные числа. 5. Десятичные дроби. Представление рациональных чисел десятичными дробями. 6. Иррациональные числа. Действительные числа. 7. Действия с приближенными числами. 8. Числовая ось. Координаты точки на плоскости. § 2. Степени и корни 9. Степени с натуральными показателями. 10. Степени с целыми показателями. 11. Корни. 12. Степени с рациональными показателями. Степени с действительными показателями. 13. Алгоритм извлечения квадратного корня. § 3. Комплексные числа 14. Основные понятия и определения. 15. Рациональные действия с комплексными числами. 16. Геометрическое изображение комплексных чисел. Тригонометрическая форма комплексного числа. 17. Действия с комплексными числами, заданными в тригонометрической форме. 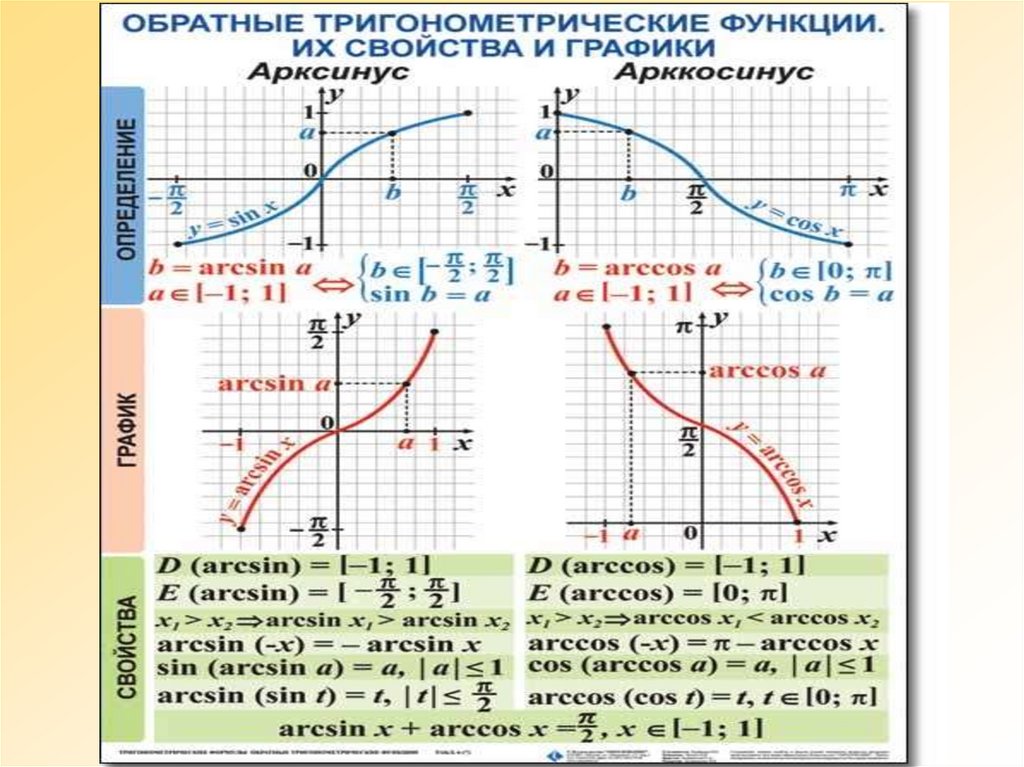 Формула Муавра. Формула Муавра.18. Извлечение корня из комплексного числа. Глава II. ТОЖДЕСТВЕННЫЕ ПРЕОБРАЗОВАНИЯ 19. Алгебраические выражения. Одночлены и многочлены. 20. Формулы сокращенного умножения. 21. Бином Ньютона. 22. Разложение многочлена на множители. 23. Дробные алгебраические выражения. § 2. Иррациональные алгебраические выражения 24. Радикалы из алгебраических выражений. 25. Освобождение от иррациональности в знаменателе дроби. Глава III. ЛОГАРИФМЫ 26. Определение и свойства логарифмов. 27. Логарифмы по различным основаниям. Модуль перехода. § 2. Десятичные логарифмы 28. Характеристика и мантисса десятичного логарифма. 29. Применение десятичных логарифмов к вычислениям. Глава IV. ФУНКЦИИ И ГРАФИКИ 30. Величина. Числовые множества. 31. Определение функции. 33. Элементарное исследование поведения функции. 34. Сложная функция. 35. Обратная функция. 36.  n. n.41. Обратная пропорциональная зависимость. Степенная функция с рациональным показателем степени. 42. Показательная функция. 43. Логарифмическая функция. § 3. Преобразование графиков 44. Параллельный сдвиг графика. 45. График квадратного трех члена. 46. График дробно-линейной функции. 47. Преобразование симметрии. Сжатие и растяжение графика. 48. Построение графиков функций. 49. Сложение графиков. § 4. Некоторые сведения о рациональных функциях 50. Целые и дробные рациональные функции. Деление многочленов. 51. Схема Горнера. Теорема Безу. 52. Нули многочлена. Разложение многочлена на множители. Глава V. УРАВНЕНИЯ 53. Уравнение. Корни уравнения. 54. Равносильные уравнения. 55. Системы уравнений. 56. Графическое решение уравнений. §. 2. Алгебраические уравнения с одной неизвестной 57. Число и кратность корней. 58. Уравнения первой степени (линейные уравнения). 59. Уравнения второй степени (квадратные уравнения). 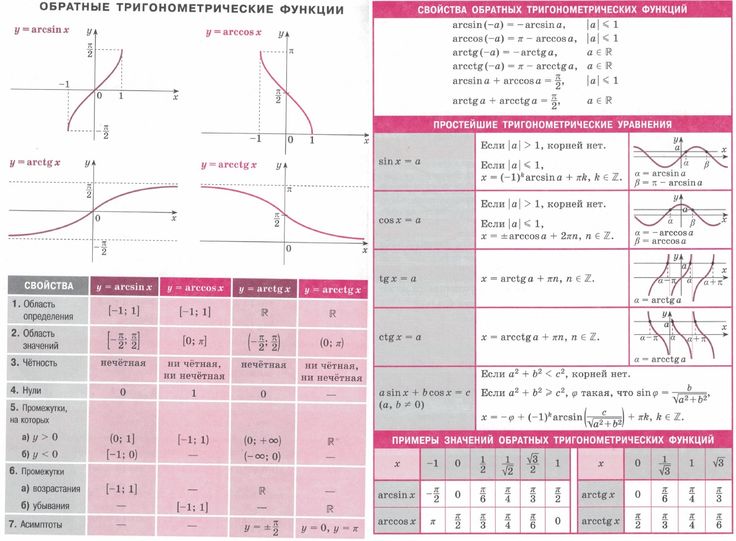 60. Формулы Виета. Разложение квадратного трехчлена на множители. 61. Исследование квадратного уравнения. 62. Уравнения высших степеней. Целые корни. 63. Двучленные уравнения. 64. Уравнения, сводящиеся к квадратным. 65. Возвратные уравнения. § 3. Системы алгебраических уравнений 66. Линейные системы. 67. Определители второго порядка. Исследование линейных систем двух уравнений с двумя неизвестными. 68. Системы, состоящие из уравнения второй степени и линейного уравнения. 69. Примеры систем двух уравнений второй степени. Системы уравнений высших степеней. 70. Иррациональные уравнения. 71. Показательные уравнения. 72. Логарифмические уравнения. 73. Разные уравнения. Системы уравнений. Глава VI. НЕРАВЕНСТВА 74. Свойства неравенств. Действия над неравенствами. 75. Алгебраические неравенства. § 2. Решение неравенств 76. Множество решений неравенства.  Равносильные неравенства. Равносильные неравенства.77. Графическое решение неравенств. 79. Квадратные неравенства. 80. Неравенства высших степеней. Неравенства, содержащие дробные рациональные функции от х. 81. Иррациональные, показательные и логарифмические неравенства. 82. Неравенства с двумя неизвестными. Глава VII. ПОСЛЕДОВАТЕЛЬНОСТИ 83. Числовая последовательность. 84. Предел числовой последовательности. 85. Бесконечно малые. Правила предельного перехода. § 2. Арифметическая прогрессия 86. Арифметическая прогрессия. Формула общего члена. 87. Свойства арифметической прогрессии. 88. Формула для суммы n членов арифметической прогрессии. § 3. Геометрическая прогрессия 89. Геометрическая прогрессия. Формула общего члена. 90. Свойства геометрической прогрессии. 91. Формулы для суммы n членов геометрической прогрессии. 92. Бесконечно убывающая геометрическая прогрессия. Глава VIII. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ УГЛА (ДУГИ) 93. Вектор, проекция вектора. 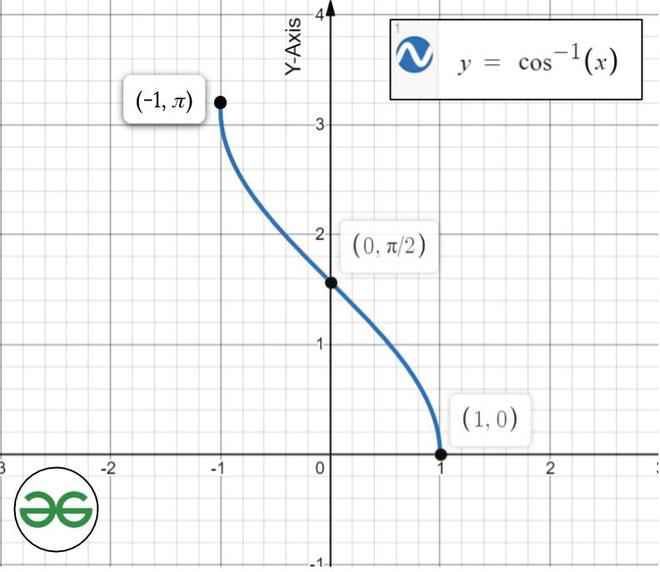 94. Положительные углы и дуги, меньшие 360°. 95. Углы и дуги, большие 360°. 96. Отрицательные углы. Сложение и вычитание углов. § 2. Тригонометрические функции произвольного угла 97. Определение основных тригонометрических функций. 98. Изменение основных тригонометрических функций при изменении угла от 0 до 2pi. 99. Основные тригонометрические тождества. 100. Вычисление значений тригонометрических функций по значению одной из них. 101. Значения тригонометрических функций некоторых углов. § 4. Четность, нечетность и периодичность тригонометрических функций 102. Четность и нечетность. 103. Понятие периодической функции. 104. Периодичность тригонометрических функций. § 5. Формулы приведения 105. Зависимость между тригонометрическими функциями дополнительных углов. 106. Формулы приведения. Глава IX. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ ЧИСЛОВОГО АРГУМЕНТА И ИХ ГРАФИКИ § 1. 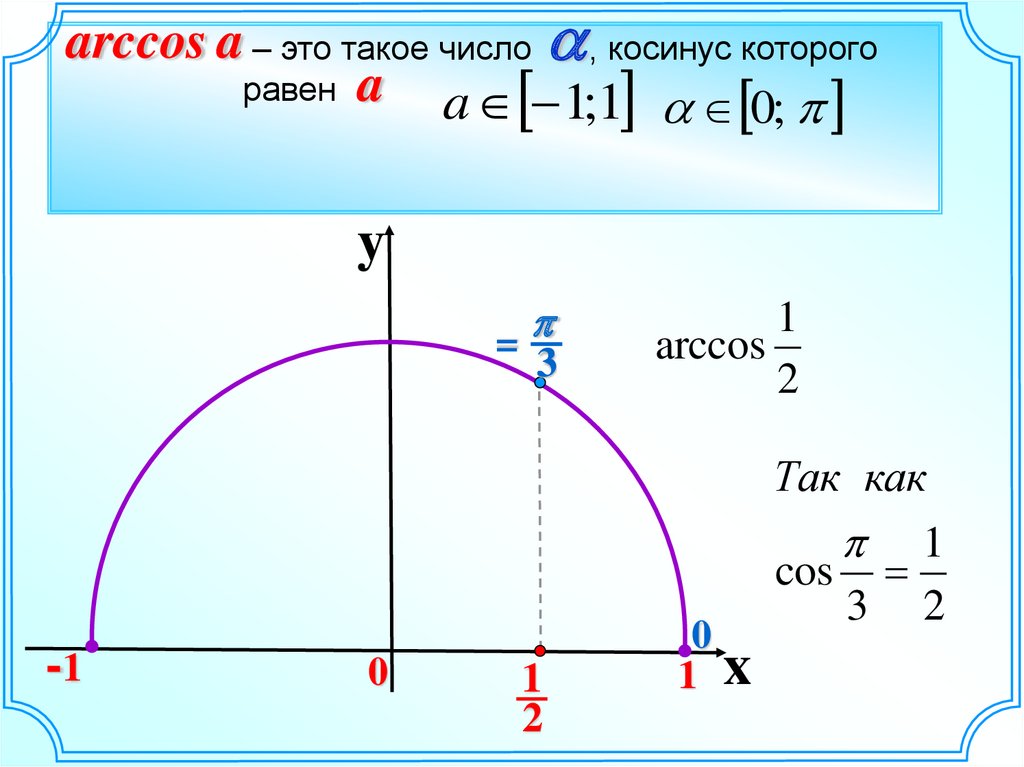 Тригонометрические функции числового аргумента Тригонометрические функции числового аргумента108. Области определения и области изменения значений тригонометрических функций. 109. Некоторые неравенства и их следствия. § 2. Графики тригонометрических функций 110. Первоначальные сведения о таблицах тригонометрических функций. 111. Основные графики. 112. Примеры построения графиков некоторых других тригонометрических функций. 113. Дальнейшие примеры построения графиков функций. Глава X. ПРЕОБРАЗОВАНИЕ ТРИГОНОМЕТРИЧЕСКИХ ВЫРАЖЕНИЙ 114. Расстояние между двумя точками на плоскости. 115. Косинус суммы и разности двух аргументов. 116. Синус суммы и разности двух аргументов. 117. Тангенс суммы и разности двух аргументов. 118. О формулах сложения для нескольких аргументов. § 2. Формулы для двойного и половинного аргумента. Выражение sin na и cos na через степени sin a и cos a 119. Тригонометрические функции двойного аргумента. 120. Выражение sin na и cos na через степени sin a и cos a при натуральном числе n. 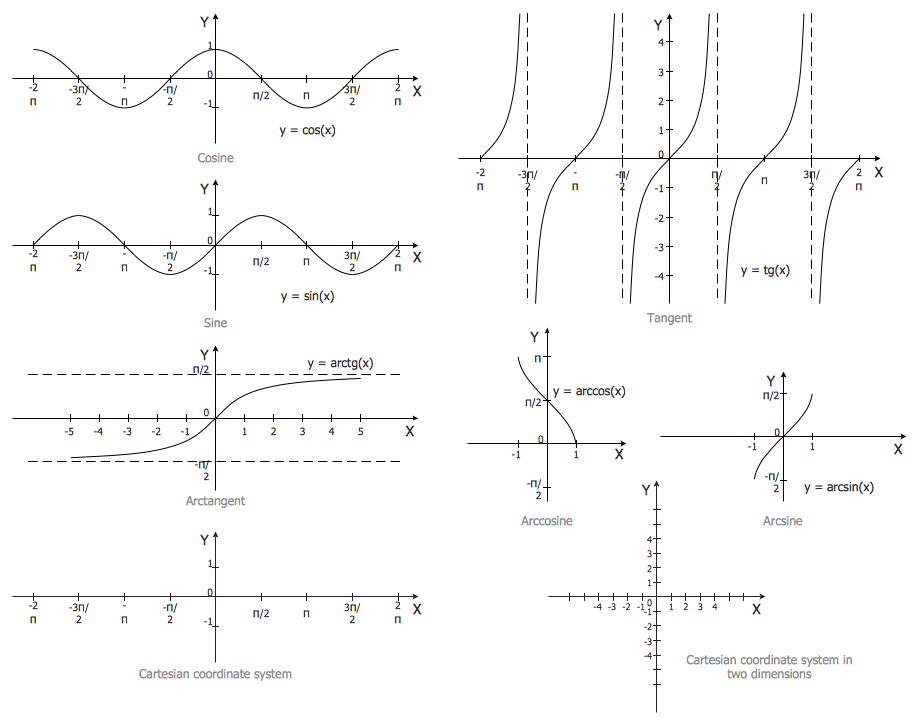 121. Тригонометрические функции половинного аргумента. 122. Выражение основных тригонометрических функций аргумента а через tg(a/2). § 3. Преобразование в сумму выражений вида sina•cosb, cosa•cosb и sinа•sinb § 4. Преобразование в произведение сумм вида § 5. Преобразование некоторых выражений в произведения с помощью введения вспомогательного аргумента 127. Преобразование в произведение выражения a•sina + b•cosa. 128. Преобразование в произведение выражений a•sina+b и a•cosa+b 129. Преобразование в произведение выражения a•tga+b. Глава XI. ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ И ИХ ГРАФИКИ 130. Функция у = arcsin x (арксинус). 131. Функция y = arccos x (арккосинус). 132. Функция y = arctg x (арктангенс). 133. Функция y = arcctg x (арккотангенс). 134. Пример. § 2. Операции над обратными тригонометрическими функциями 135. Тригонометрические операции. 136. Операции сложения (вычитания). § 3. Обратные тригонометрические операции над тригонометрическими функциями 137.  Функция у = arcsin (sin x). Функция у = arcsin (sin x).138. Функция y = arctg (tg x). Глава XII. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА 139. Уравнение sin х = а. 140. Уравнение cos х = a. 141. Уравнение tg x = a. 142. Уравнение ctg x = a. 143. Некоторые дополнения. § 2. Способ приведения к одной функции одного и того же аргумента 145. Некоторые типы уравнений, приводящихся к уравнениям относительно функции одного аргумента. 146. Способ разложения на множители. 147. Решение рациональных тригонометрических уравнений с помощью универсальной тригонометрической подстановки tg(x/2) = t. § 3. Некоторые частные приемы решения тригонометрических уравнений и систем 148. Введение вспомогательного аргумента. 149. Преобразование произведения в сумму или разность. 150. Переход к функциям удвоенного аргумента. 151. Решение уравнения типа… § 4. Решение тригонометрических неравенств 154. Простейшие тригонометрические неравенства.  155. Примеры тригонометрических неравенств, сводящихся к простейшим. Часть вторая. ГЕОМЕТРИЯ 156. Точка. Прямая. Луч. Отрезок. 157. Плоскость. Фигуры и тела. 160. Равенство фигур. Движение. 161. Равенство тел. § 2. Измерение геометрических величин 162. Сложение отрезков. Длина отрезка. 163. Общая мера двух отрезков. 164. Сравнительная длина отрезков и ломаных. 165. Измерение углов. 166. Радианная мера угла. 167. Измерение площадей. 168. Площадь прямоугольника. Объем прямоугольного параллелепипеда. Глава XIV. ПЕРПЕНДИКУЛЯРНЫЕ И ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ. ЗАДАЧИ НА ПОСТРОЕНИЕ 169. Перпендикуляр и наклонные. 170. Свойство перпендикуляра, проведенного к отрезку в его середине. 171. Параллельные прямые. 172. Углы, образованные двумя параллельными прямыми и секущей. 173. Углы с параллельными или перпендикулярными сторонами. § 2. Геометрические места точек. Окружность 174. Геометрическое место точек. 175. Свойство биссектрисы угла.  176. Окружность. 177. Взаимное расположение прямой и окружности. Касательная и секущая. 178. Хорда и диаметр. Сектор и сегмент. 179. Взаимное расположение двух окружностей. § 3. Основные задачи на построение 181. Деление отрезка пополам. Построение перпендикуляров. 182. Построение углов. 183. Другие задачи на построение. Глава XV. ТРЕУГОЛЬНИКИ, ЧЕТЫРЕХУГОЛЬНИКИ 184. Стороны и углы треугольника. 185. Биссектрисы треугольника. Вписанная окружность. 186. Оси симметрии сторон треугольника. Описанная окружность. 187. Медианы и выcоты треугольника. 188. Равенство треугольников. 189. Построение треугольников. 190. Равнобедренные треугольники. 191. Прямоугольные треугольники. § 2. Параллелограммы 192. Четырехугольники. 193. Параллелограмм и его свойства. 194. Прямоугольник. § 3. Трапеция 196. Трапеция. 197. Средняя линия треугольника. 198. Средняя линия трапеции. 199. Деление отрезка на равные части. 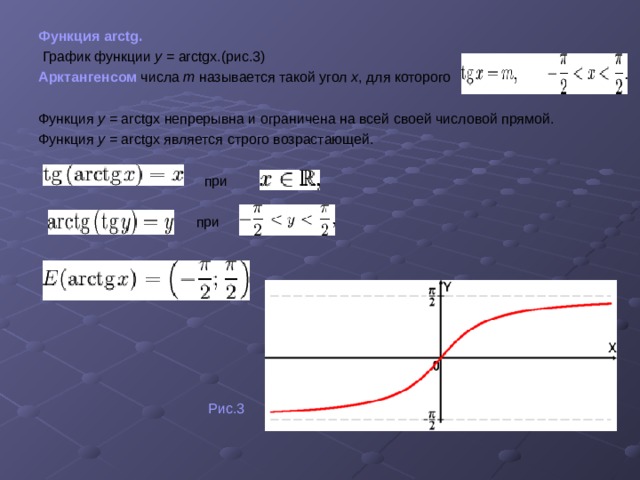 § 4. Площади треугольников и четырехугольников 200. Площадь параллелограмма. 201. Площадь треугольника. 202. Площадь трапеции. Глава XVI. ПОДОБИЕ ГЕОМЕТРИЧЕСКИХ ФИГУР 203. Пропорциональные отрезки. 204. Свойства биссектрис внутреннего и внешнего углов треугольника. § 2. Подобное преобразование фигур (гомотетия) 205. Определение гомотетичных фигур. 206. Свойства преобразования подобия. § 3. Общее подобное соответствие фигур 207. Подобные фигуры. 208. Периметры и площади подобных треугольников. 209. Применение подобия к решению задач на построение. Глава XVII. МЕТРИЧЕСКИЕ СООТНОШЕНИЯ В ТРЕУГОЛЬНИКЕ И КРУГЕ 210. Углы с вершиной на окружности. 211. Углы с вершиной внутри и вне круга. 212. Угол, под которым виден данный отрезок. 213. Четырехугольники, вписанные в окружность. 214. Пропорциональные отрезки в круге. 215. Задачи на построение. § 2. Метрические соотношения в треугольнике 216. Пропорциональные отрезки в прямоугольном треугольнике.  Теорема Пифагора. Теорема Пифагора.218. Теорема синусов. Формула Герона. 217. Квадрат стороны, лежащей против острого или тупого утла и треугольнике. Теорема косинусов. 218. Теорема синусов. Формула Герона. 219. Радиусы вписанной и описанной окружностей. § 3. Решение треугольников 220. Таблицы функций. 221. Решение треугольников. Сводка основных формул. 222. Решение прямоугольных треугольников. 223. Решение косоугольных треугольников. Глава XVIII. ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ. ДЛИНА окружности И ПЛОЩАДЬ КРУГА 224. Выпуклые многоугольники. 225. Правильные многоугольники. 226. Соотношения между стороной, радиусом и апофемой. 227. Периметр и площадь правильного n-угольника. 228. Удвоение числа сторон правильного многоугольника. § 2. Длина окружности. Площадь круга и его частей 229. Длина окружности. 230. Площадь круга и его частей. Глава XIX. ПРЯМЫЕ И ПЛОСКОСТИ В ПРОСТРАНСТВЕ 231. Взаимное расположение двух прямых в пространстве. 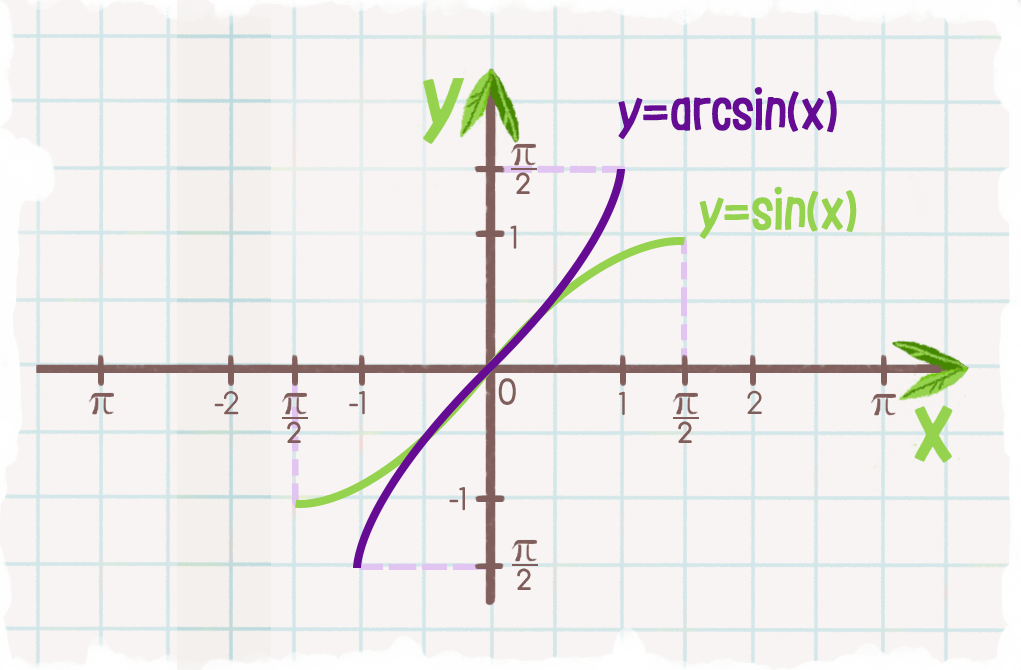 232. Взаимное расположение прямой линии и плоскости. 233. Взаимное расположение двух плоскостей. 234. Свойства параллельных прямых и плоскостей. 235. Построения в стереометрии. § 2. Перпендикулярность прямых и плоскостей 236. Перпендикуляр к плоскости. 237. Перпендикуляр и наклонные. 238. Угол между прямой и плоскостью. 239. Связь между перпендикулярностью и параллельностью прямых и плоскостей. 240. Общий перпендикуляр двух скрещивающихся прямых. § 3. Двугранные и многогранные углы 241. Двугранный угол. 242. Взаимно перпендикулярные плоскости. 243. Трехгранные углы. 244. Многогранные углы. § 4. Многогранники 245. Многогранники. 246. Правильные многогранники. Глава XX. МНОГОГРАННИКИ И КРУГЛЫЕ ТЕЛА 247. Цилиндры и призмы. 248. Параллелепипеды. 249. Объемы призм и цилиндров. 250. Площадь боковой поверхности призмы. 251. Площадь поверхности цилиндра. § 2. Пирамида. Конус 252. Свойства пирамиды и конуса. 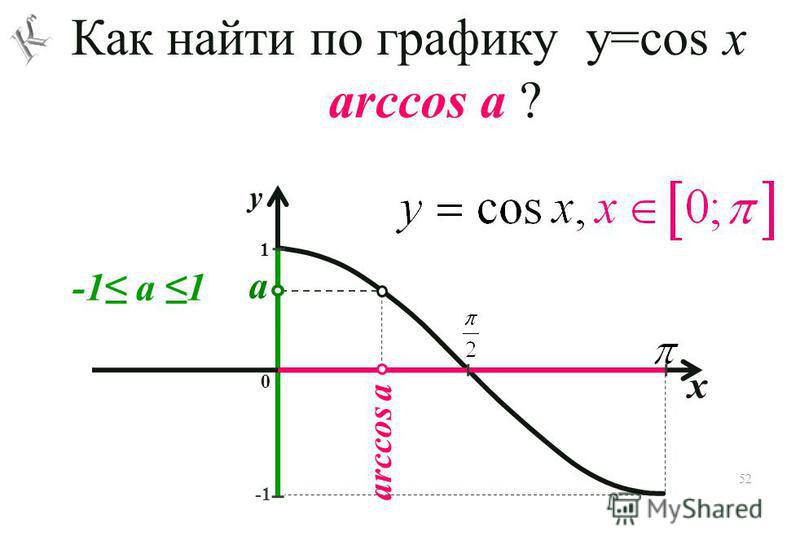 253. Объем пирамиды и конуса. 254. Площадь боковой поверхности правильной пирамиды и конуса. 255. Усеченный конус и усеченная пирамида. § 3. Шаровая поверхность. Шар 256. Шар и шаровая поверхность. 257. Объем шара и его частей. 258. Площадь поверхности шара и ее частей. 259. Понятие телесного угла. Ответы к упражнениям Приложения |
Математика: Справ. материалы
Математика: Справ. материалы
ОглавлениеСЛОВО К УЧАЩИМСЯГЛАВА I. ЧИСЛА § 1. Натуральные числа 2. Арифметические действия над натуральными числами. 3. Деление с остатком. 4. Признаки делимости. 5. Разложение натурального числа на простые множители. 6. Наибольший общий делитель нескольких натуральных чисел. 7. Наименьшее общее кратное нескольких натуральных чисел. 8. Употребление букв в алгебре. Переменные. § 2. Рациональные числа 10. Равенство дробей. Основное свойство дроби. Сокращение дробей. 11. Приведение дробей к общему знаменателю. 12. Арифметические действия над обыкновенными дробями. 13. Десятичные дроби. 14. Арифметические действия над десятичными дробями. 15. Проценты. 16. Обращение обыкновенной дроби в бесконечную десятичную периодическую дробь. 17. Обращение бесконечной десятичной периодической дроби в обыкновенную дробь. 18. Координатная прямая. 19. Множество рациональных чисел.  § 3. Действительные числа 21. Действительные числа. Числовая прямая. 22 Обозначения некоторых числовых множеств. 23. Сравнение действительных чисел. 25. Числовые промежутки. 26. Модуль действительного числа. 27. Формула расстояния между двумя точками координатной прямой. 28. Правила действий над действительными числами. 29. Свойства арифметических действий над действительными числами. 30. Пропорции. 31. Целая часть числа. Дробная часть числа. 32. Степень с натуральным показателем. 33. Степень с нулевым показателем. Степень с отрицательным целым показателем. 34. Стандартный вид положительного действительного числа. 35. Определение арифметического корня. 36. Корень нечетной степени из отрицательного числа. 37. Степень с дробным показателем. 38. Свойства степеней с рациональными показателями. 39. Приближенные значения чисел. Абсолютная и относительная погрешности. 40. Десятичные приближения действительного числа по недостатку и по избытку.  3. 3.112. Построение графика функции y = f(x-m)+n 113. График квадратичной функции. 114. Способы построения графика квадратичной функции 115. Построение графика функции y = f(kx). 116. Сжатие и растяжение графиков тригонометрических функций. 117. График гармонического колебания ГЛАВА IV. ТРАНСЦЕНДЕНТНЫЕ ВЫРАЖЕНИЯ § 12. Преобразование выражений, содержащих переменную под знаком логарифма 119. Определение логарифма положительного числа по данному основанию. 120. Свойства логарифмов. 121. Переход к новому основанию логарифма. 122. Логарифмирование и потенцирование. 123. Десятичный логарифм. Характеристика и мантисса десятичного логарифма. § 13. Формулы тригонометрии и их использование для преобразования тригонометрических выражений 125. Формулы сложения и вычитания аргументов. 126. Формулы приведения. 127. Соотношения между тригонометрическими функциями одного и того же аргумента. 128. Формулы двойного угла. 129. Формулы понижения степени. 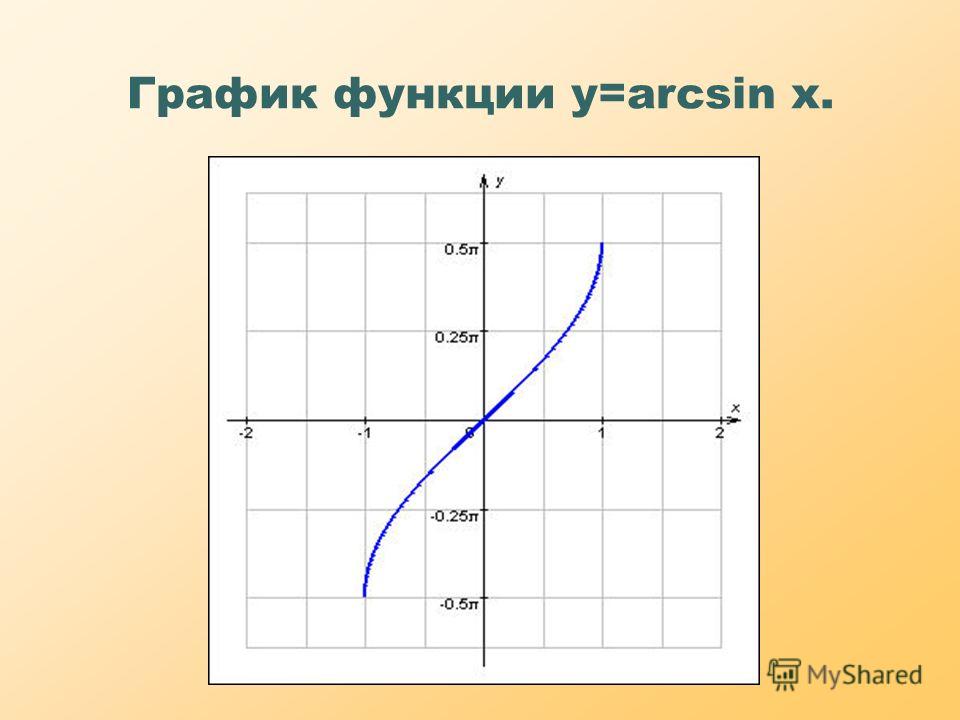 130. Преобразование суммы тригонометрических функций в произведение. 131. Преобразование произведения тригонометрических функций в сумму. 132. Преобразование выражения a cos t + b sin t к виду A sin (t + a). 133. Примеры преобразований выражений, содержащих обратные тригонометрические функции. ГЛАВА V. УРАВНЕНИЯ И СИСТЕМЫ УРАВНЕНИЙ § 14. Уравнения с одной переменной 135. Равносильность уравнений. 136. Линейные уравнения. 137. Квадратные уравнения. 138. Неполные квадратные уравнения. 139. Теорема Виета. 140. Системы и совокупности уравнений. 141. Уравнения, содержащие переменную под знаком модуля. 142. Понятие следствия уравнения. Посторонние корни. 143. Уравнения с переменной в знаменателе. 144. Область определения уравнения. 145. Рациональные уравнения. 146. Решение уравнения p(x) = 0 методом разложения его левой части на множители. 147. Решение уравнений методом введения новой переменной. 148. Биквадратные уравнения. 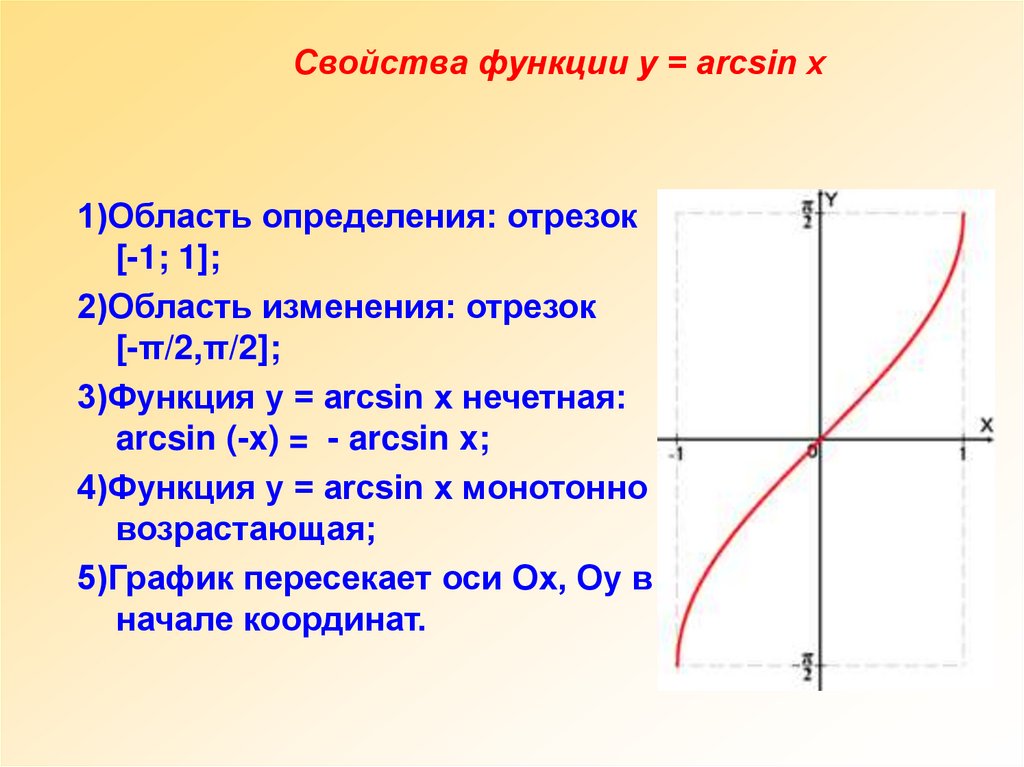 149. Решение задач с помощью составления уравнений. 150. Иррациональные уравнения. 151. Показательные уравнения. 152. Логарифмические уравнения. 153. Примеры решения показательно-логарифмических уравнений. 154. Простейшие тригонометрические уравнения. 155. Методы решения тригонометрических уравнений. 156. Универсальная подстановка (для тригонометрических уравнений). 157. Метод введения вспомогательного аргумента (для тригонометрических уравнений). 158. Графическое решение уравнений. 159. Уравнения с параметром. § 15. Уравнения с двумя переменными 161. График уравнения с двумя переменными. 162. Линейное уравнение с двумя переменными и его график. § 16. Системы уравнений 164. Решение систем двух уравнений с двумя переменными методом подстановки. 165. Решение систем двух уравнений с двумя переменными методом сложения. 167. Графическое решение систем двух уравнений с двумя переменными. 168. Исследование системы двух линейных уравнений с двумя переменными.  169. Решение систем двух уравнений с двумя переменными методами умножения и деления. 170. Системы показательных и логарифмических уравнений. 171. Системы тригонометрических уравнений с двумя переменными. 172. Системы трех уравнений с тремя переменными. 173. Решение задач с помощью составления систем уравнений. Глава VI. НЕРАВЕНСТВА § 17. Решение неравенств с переменной 175. Графическое решение неравенств с одной переменной. 176. Линейные неравенства с одной переменной. 177. Системы неравенств с одной переменной. 178. Совокупность неравенств с одной переменной. 179. Дробно-линейные неравенства. 180. Неравенства второй степени. 181. Графическое решение неравенств второй степени. 182. Неравенства с модулями. 183. Решение рациональных неравенств методом промежутков. 184. Показательные неравенства. 185. Логарифмические неравенства. 186. Иррациональные неравенства. 187. Решение тригонометрических неравенств. 188. 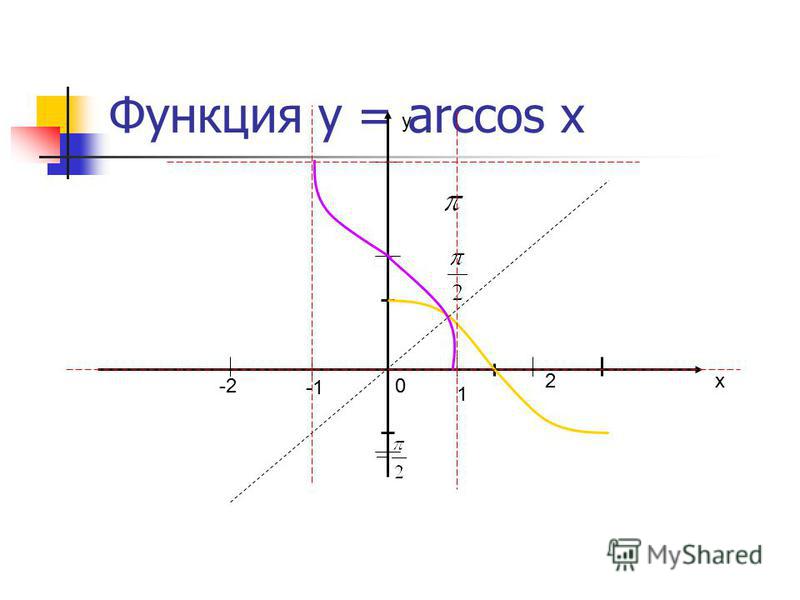 Неравенства и системы неравенств с двумя переменными. Неравенства и системы неравенств с двумя переменными.§ 18. Доказательство неравенств 190. Синтетический метод доказательства неравенств. 191. Доказательство неравенств методом от противного. 192. Использование неравенств при решении уравнений. ГЛАВА VII. ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОГО АНАЛИЗА § 19. Числовые последовательности 194. Способы задания последовательности. 195. Возрастание и убывание последовательности. 196. Определение арифметической прогрессии. 197. Свойства арифметической прогрессии 198. Определение геометрической прогрессии. 199. Свойства геометрической прогрессии. 200. Понятие о пределе последовательности. 201. Вычисление пределов последовательностей. 202. Сумма бесконечной геометрической прогрессии при |q| § 20. Предел функции 204. Вычисление пределов функции при х->оо. 205. Предел функции в точке. Непрерывные функции. 206. Вертикальная асимптота. 207. Вычисление пределов функций в точке. § 21. 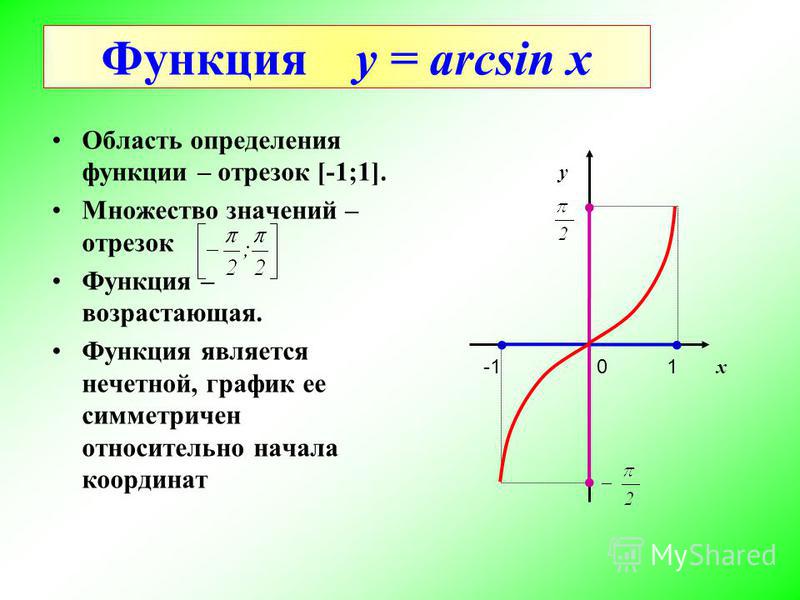 Производная и ее применения Производная и ее применения209. Определение производной. 210. Формулы дифференцирования. Таблица производных. 211. Дифференцирование суммы, произведения, частного. 212. Сложная функция и ее дифференцирование. 213. Физический смысл производной. 214. Вторая производная и ее физический смысл. 215. Касательная к графику функции. 216. Применение производной к исследованию функций на монотонность. 217. Применение производной к исследованию функций на экстремум. 218. Отыскание наибольшего и наименьшего значений непрерывной функции на отрезке. 219. Отыскание наибольшего или наименьшего значения непрерывной функции на незамкнутом промежутке. 220. Задачи на отыскание наибольших или наименьших значений величин. 221. Применение производной для доказательства тождеств. 222. Применение производной для доказательства неравенств. 223. Общая схема построения графика функции. § 22. Первообразная и интеграл 225. Таблица первообразных. 226.  Правила вычисления первообразных. Правила вычисления первообразных.227. Интеграл. 228. Связь между интегралов и первообразной (формула Ньютона—Лейбница). 229. Правила вычисления интегралов. 230. Использование интеграла для вычисления площадей плоских фигур. ГЕОМЕТРИЯ. ГЛАВА I. ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ НА ПЛОСКОСТИ 2. Точка. Прямая. 3. Определения. Аксиомы. Теоремы. § 2. Основные свойства простейших геометрических фигур 5. Луч. 6. Окружность. Круг. 7. Полуплоскость. 8. Угол. Градусная мера угла. 9. Смежные и вертикальные углы. 10. Центральные и вписанные углы. 11. Параллельные прямые. 12. Признаки параллельности прямых. 13. Перпендикулярные прямые. 14. Касательная к окружности. 15. Треугольники. 16. Равенство треугольников. 17. Равнобедренный треугольник. 18. Сумма углов треугольника. 19. Прямоугольный треугольник. Теорема Пифагора. 20. Окружности, вписанные в треугольник и описанные около треугольника. § 3. Геометрические построения на плоскости 22. 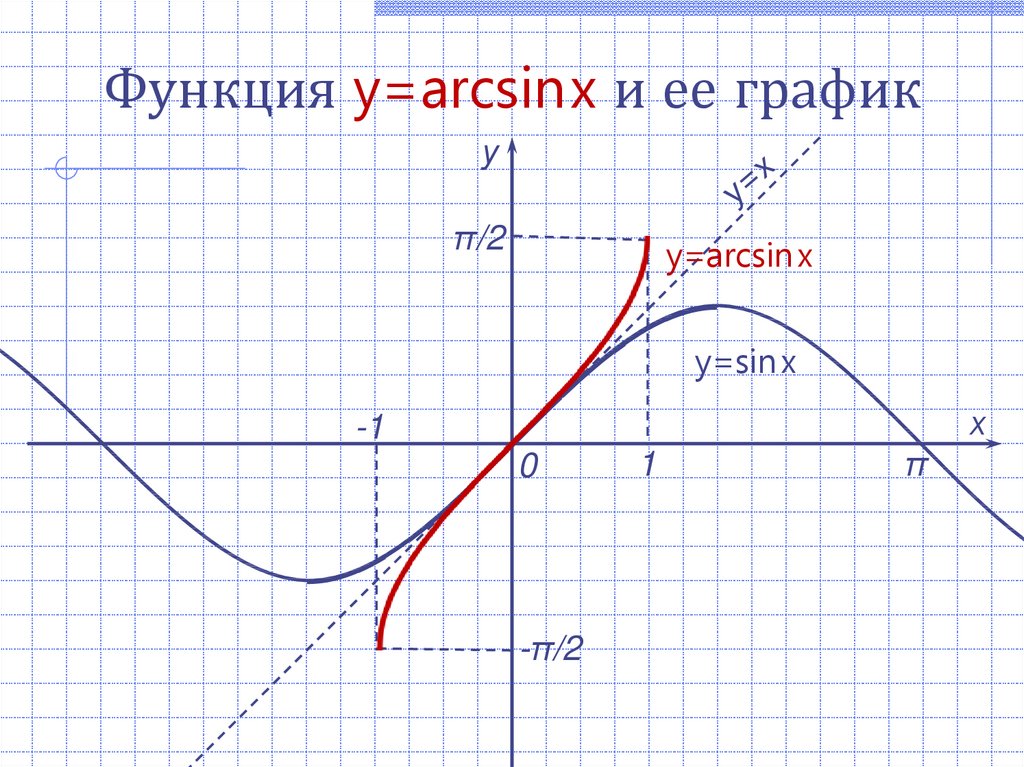 Простейшие задачи на построение. Простейшие задачи на построение.23. Геометрическое место точек на плоскости. § 4. Четырехугольники 25. Параллелограмм. 26. Прямоугольник. Ромб. Квадрат. 27. Трапеция. § 5. Многоугольники 29. Выпуклые многоугольники. 30. Правильные многоугольники. 31. Длина окружности. § 6. Решение треугольников 33. Соотношения между сторонами и углами в прямоугольном треугольнике. 34. Теорема косинусов. Теорема синусов. 35. Решение треугольников. § 7. Площади плоских фигур 37. Площади многоугольников. 38. Площади подобных фигур. 39. Площадь круга. ГЛАВА II. Прямые и плоскости в пространстве § 9. Параллельность прямых и плоскостей 42. Параллельность прямой и плоскости. 43. Параллельные плоскости. § 10. Перпендикулярность прямых и плоскостей 45. Перпендикуляр и наклонная к плоскости. 46. Перпендикулярность плоскостей. ГЛАВА III. ТЕЛА В ПРОСТРАНСТВЕ § 11. Многогранники 48. Многогранные углы. Многогранники.  49. Призма. Параллелепипед. Куб. 50. Пираприда. 51. Правильные многогранники. § 12. Тела вращения 53. Конус. 54. Шар. § 13. Изображение пространственных фигур на плоскости 56. Ортогональное проектирование. 57. Геометрическое место точек в пространстве. § 14. Объемы тел 59. Объем параллелепипеда, призмы и пирамиды. 60. Объем цилиндра и конуса. 61. Общая формула объемов тел вращения. § 15. Площади поверхностей тел 63. Понятие площади поверхности. 64. Площади поверхностей тел вращения. ГЛАВА IV. ДЕКАРТОВЫ КООРДИНАТЫ § 16. Координаты на плоскости и в пространстве 66. Координаты середины отрезка. § 17. Уравнения фигур на плоскости 68. Пересечение двух окружностей. 69. Уравнение прямой. 70. Пересечение прямой и окружности. § 18. Уравнения фигур в пространстве 72. Уравнение сферы. 73. Взаимное расположение сферы и плоскости. 74. Пересечение двух сфер. ГЛАВА V. РЕОБРАЗОВАНИЯ ФИГУР 76. 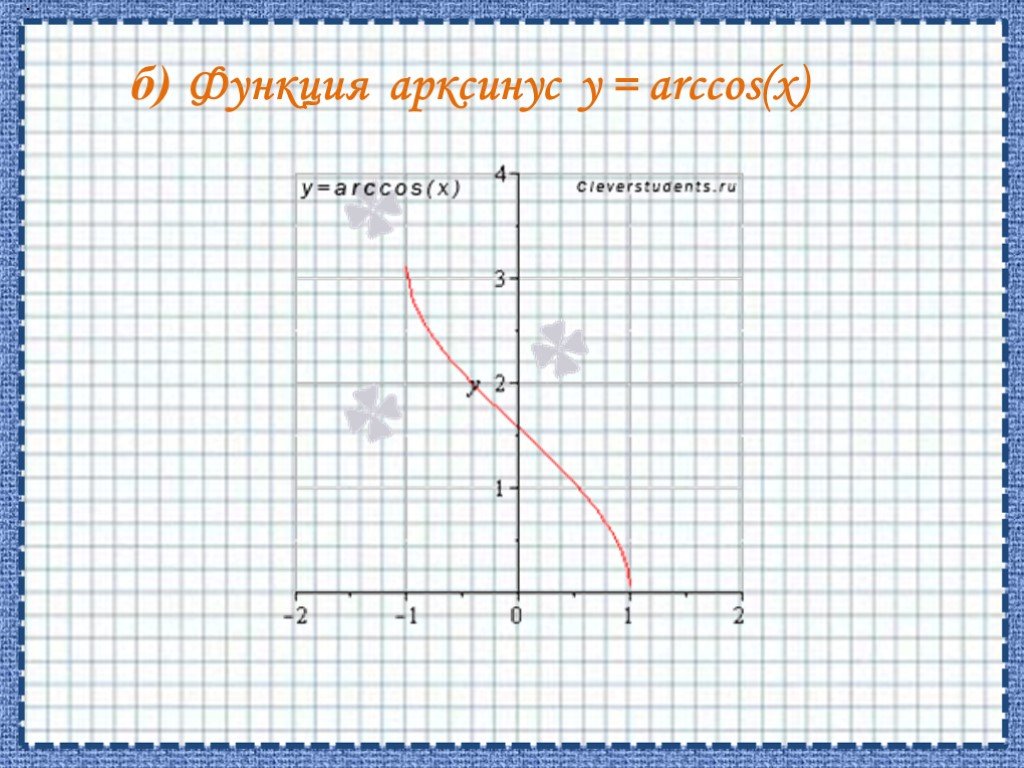 Понятие движения. Понятие движения.§ 20. Подобие фигур 78. Подобные фигуры. ГЛАВА VI. ВЕКТОРЫ 80. Понятие вектора. 81. Координаты вектора. § 22. Операции над векторами 83. Умножение вектора на число. Коллинеарные векторы. 84. Скалярное произведение векторов. ПРИЛОЖЕНИЯ ГЕОМЕТРИЯ |
APC Обратные тригонометрические функции
Мотивирующие вопросы
Может ли периодическая функция, не прошедшая тест горизонтальной линии, иметь обратную функцию?
Для ограниченных функций косинуса, синуса и тангенса, как определить соответствующие функции арккосинуса, арксинуса и арктангенса?
Каковы ключевые свойства функций арккосинуса, арксинуса и арктангенса?
Тригонометрические функции \(f(t) = \sin(t)\text{,}\) \(g(t) = \cos(t)\text{,}\) и \(h(t) = \tan(t)\) являются периодическими, поэтому каждая из них не проходит проверку горизонтальной прямой, и, таким образом, эти функции в своих полных областях определения не имеют обратных функций.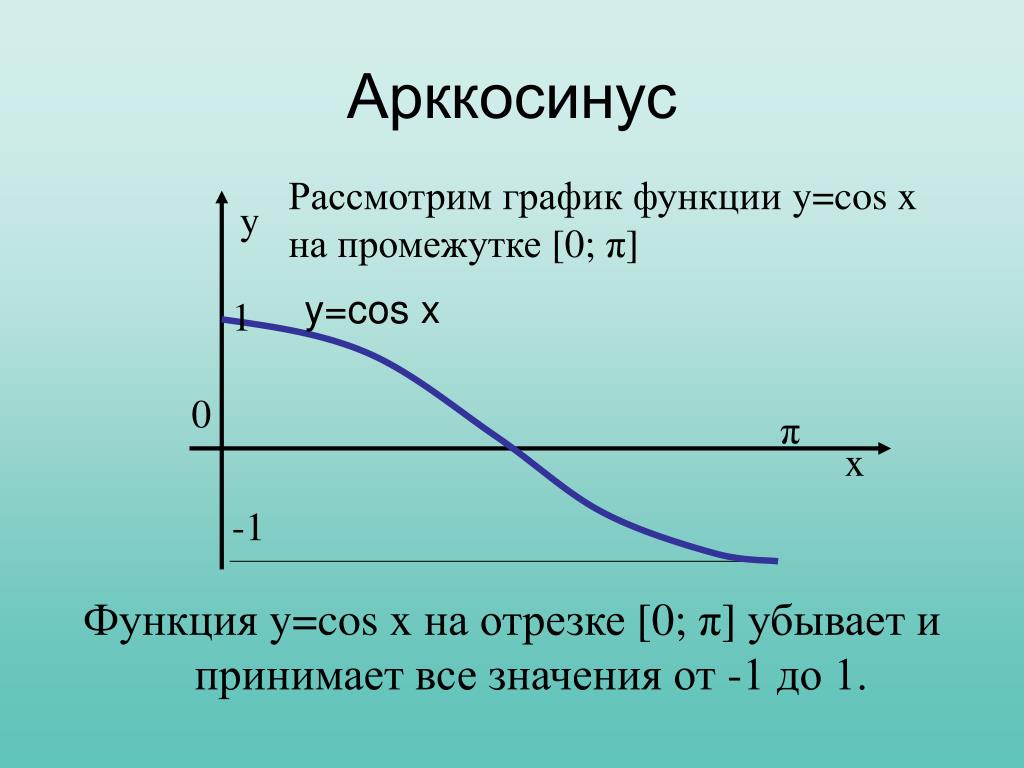 В то же время разумно думать об изменении перспективы и углов обзора как о результатах в определенных ограниченных настройках. Например, мы можем сказать, что оба 9{-1}\влево(\frac{\sqrt{3}}{2}\вправо)
\end{уравнение*}
В то же время разумно думать об изменении перспективы и углов обзора как о результатах в определенных ограниченных настройках. Например, мы можем сказать, что оба 9{-1}\влево(\frac{\sqrt{3}}{2}\вправо)
\end{уравнение*}
в зависимости от контекста, в котором мы рассматриваем соотношение между углом и длиной стороны.
Также важно понять, почему важен вопрос нахождения угла по известному значению тригонометрической функции. Предположим, что мы знаем следующую информацию о прямоугольном треугольнике: один катет имеет длину \(2,5\text{,}\), а гипотенуза имеет длину \(4\text{.}\). Если мы допустим \(\theta\) равным угол, противоположный стороне длины \(2,5\text{,}\), отсюда следует, что \(\sin(\theta) = \frac{2,5}{4}\text{.}\) Естественно, мы хотим использовать обратная функция синуса для решения самого последнего уравнения для \(\theta\text{.}\) Но функция синуса не имеет обратной функции, так как же мы можем решить эту ситуацию?
В то время как исходные тригонометрические функции \(f(t) = \sin(t)\text{,}\) \(g(t) = \cos(t)\text{,}\) и \(h(t ) = \tan(t)\) не имеют обратных функций, оказывается, что мы можем рассматривать их ограниченные версии, у которых есть соответствующие обратные функции. Таким образом, мы исследуем, как мы можем иначе думать о тригонометрических функциях, чтобы мы могли осмысленно обсуждать обратные функции.
Таким образом, мы исследуем, как мы можем иначе думать о тригонометрических функциях, чтобы мы могли осмысленно обсуждать обратные функции.
Предварительный просмотр 4.3.1.
Рассмотрим график функции стандартного косинуса на рисунке 4.3.1 вместе с выделенной частью графика на \([0,\pi]\text{.}\)
Рисунок 4.3.1. Функция косинуса на \([-\frac{5\pi}{2},\frac{5\pi}{2}]\) с выделенной частью на \([0,\pi]\).Пусть \(g\) будет функцией, область определения которой равна \(0 \le t \le \pi\) и чьи выходы определяются правилом \(g(t) = \cos(t)\text{.} \) Хорошо заметьте : \(g\) определяется в терминах функции косинуса, но, поскольку он имеет другую область определения, это , а не функция косинуса.
Каков домен \(g\text{?}\)
9{-1}(-1)\text{.}\) Используйте правильные обозначения для маркировки результатов.
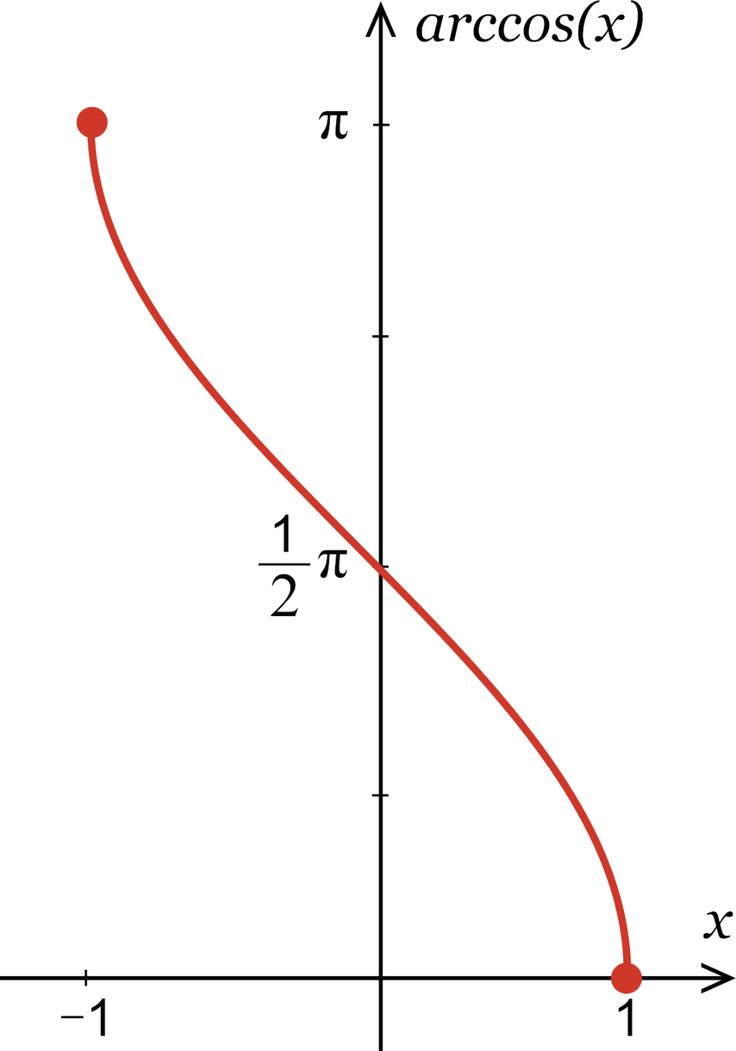
Подраздел 4.3.1 Функция арккосинуса
Для функции косинуса, ограниченной областью определения \([0,\pi]\), которую мы рассматривали в предварительном задании 4.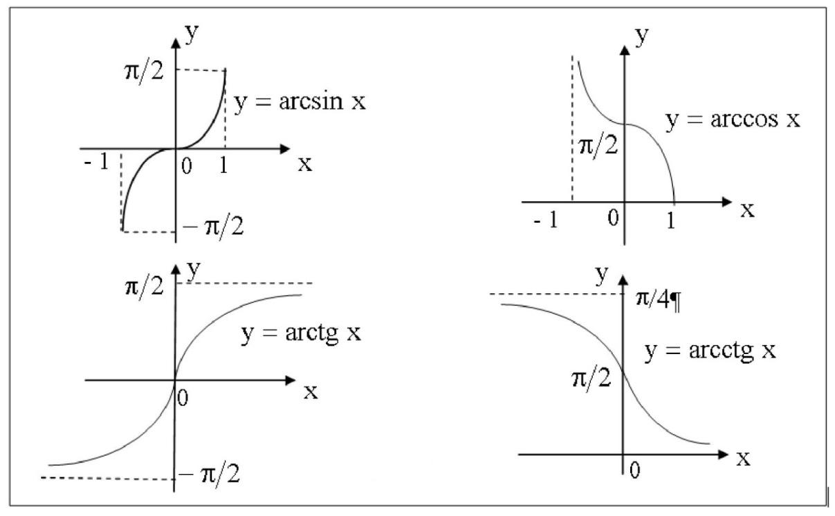 3.1, функция строго убывает в своей области определения и, таким образом, проходит тест горизонтальной линии. Следовательно, эта ограниченная версия функции косинуса имеет обратную функцию; мы будем называть эту обратную функцию функцией арккосинуса .
3.1, функция строго убывает в своей области определения и, таким образом, проходит тест горизонтальной линии. Следовательно, эта ограниченная версия функции косинуса имеет обратную функцию; мы будем называть эту обратную функцию функцией арккосинуса .
Определение 4.3.2.
Пусть \(y = g(t) = \cos(t)\) определено в области \([0,\pi]\text{,}\) и наблюдается \(g : [0,\pi] \to [-1,1]\text{.}\) Для любого действительного числа \(y\), которое удовлетворяет \(-1 \le y \le 1\text{,}\) арккосинусу \(y \) , обозначаемый
\begin{уравнение*} \арккос(у) \end{уравнение*}
— это угол \(t\), удовлетворяющий \(0 \le t \le \pi\) такой, что \(\cos(t) = y\text{.}\)
Обратите внимание, что выход арккосинуса функция — угол. Кроме того, напомним, что в контексте единичного круга угол, измеренный в радианах, и соответствующая длина дуги вдоль единичного круга численно равны. Вот почему мы используем «арк» в «арккосинусе»: при заданном значении \(-1 \le y \le 1\text{,}\) функция арккосинуса дает соответствующие дуга (измеренная против часовой стрелки от \((1,0)\)) такая, что косинус этой дуги равен \(y\text{.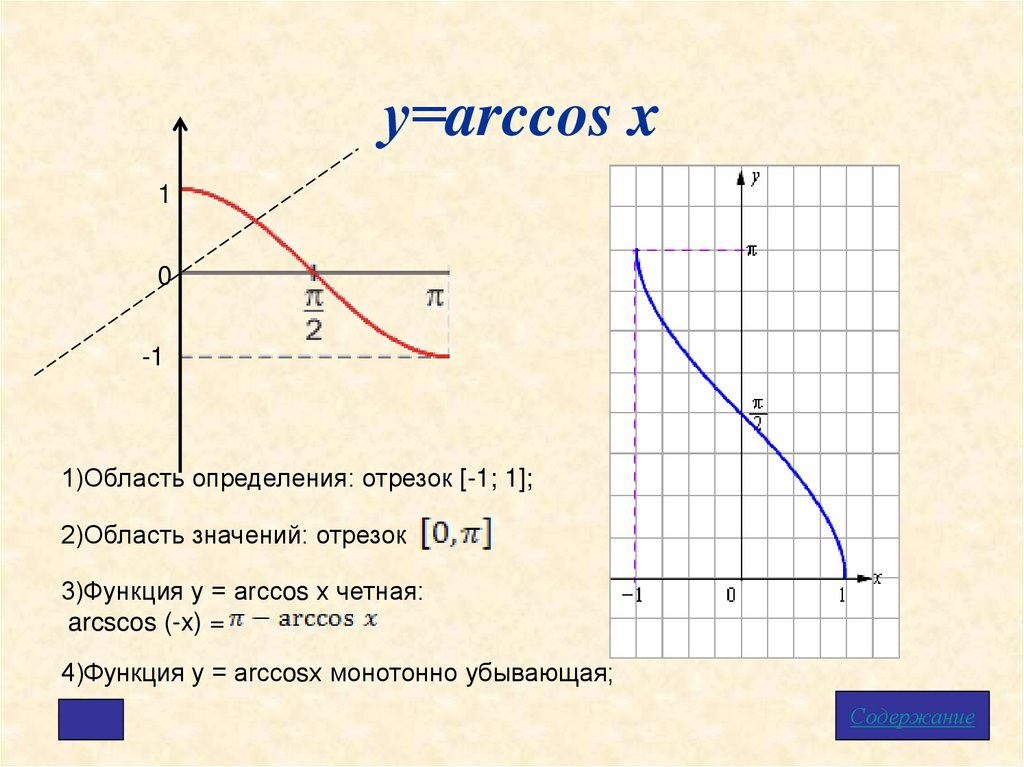 {-1}(y)\) говорят одно и то же для функции и ее обратной в общем случае 9t\) и \(t = \ln(y)\) говорят об одном и том же), функция арккосинуса позволяет нам делать то же самое для определенных углов и выходных значений косинуса. Например, сказать \(\cos(\frac{\pi}{2}) = 0\) — это то же самое, что написать \(\frac{\pi}{2} = \arccos(0)\text{,} \), который гласит: «\(\frac{\pi}{2}\) — это угол, косинус которого равен \(0\)». Действительно, эти отношения отражены на графике выше, где мы видим, что любая точка \((a,b)\), лежащая на графике \(y = \cos(t)\), соответствует точке \(( b,a)\), лежащий на графике \(y = \arccos(t)\text{.}\)
{-1}(y)\) говорят одно и то же для функции и ее обратной в общем случае 9t\) и \(t = \ln(y)\) говорят об одном и том же), функция арккосинуса позволяет нам делать то же самое для определенных углов и выходных значений косинуса. Например, сказать \(\cos(\frac{\pi}{2}) = 0\) — это то же самое, что написать \(\frac{\pi}{2} = \arccos(0)\text{,} \), который гласит: «\(\frac{\pi}{2}\) — это угол, косинус которого равен \(0\)». Действительно, эти отношения отражены на графике выше, где мы видим, что любая точка \((a,b)\), лежащая на графике \(y = \cos(t)\), соответствует точке \(( b,a)\), лежащий на графике \(y = \arccos(t)\text{.}\)
Мероприятие 4.3.2.
Используйте специальные точки на единичной окружности (см., например, рисунок 2.3.1), чтобы определить точные значения каждого из следующих числовых выражений. Сделайте это без использования вычислительного устройства.
\(\displaystyle \arccos(\frac{1}{2})\)
\(\displaystyle \arccos(\frac{\sqrt{2}}{2})\)
\(\displaystyle \arccos(\frac{\sqrt{3}}{2})\)
\(\displaystyle \arccos(-\frac{1}{2})\)
\(\displaystyle \arccos(-\frac{\sqrt{2}}{2})\)
\(\displaystyle \arccos(-\frac{\sqrt{3}}{2})\)
\(\displaystyle \arccos(-1)\)
\(\displaystyle \arccos(0)\)
\(\displaystyle \cos(\arccos(-\frac{1}{2}))\)
\(\displaystyle \arccos(\cos(\frac{7\pi}{6}))\)
Подраздел 4.
 3.2 Функция арксинуса
3.2 Функция арксинусаАналогичным образом мы можем разработать обратную функцию для ограниченной версии функции синуса. Как и в случае с функцией косинуса, нам нужно выбрать интервал, на котором функция синуса всегда увеличивается или всегда уменьшается, чтобы функция прошла тест горизонтальной линии. Стандартным выбором является область \([-\frac{\pi}{2}, \frac{\pi}{2}]\), в которой \(f(t) = \sin(t)\) возрастает и достигает всех значений в диапазоне функции синуса. Таким образом, мы рассматриваем \(f(t) = \sin(t)\), так что \(f : [-\frac{\pi}{2}, \frac{\pi}{2}] \to [- 1,1]\) и, следовательно, определить соответствующую функцию арксинуса.
Определение 4.3.3.
Пусть \(y = f(t) = \sin(t)\) определено в области \([-\frac{\pi}{2},\frac{\pi}{2}]\text{ ,}\) и наблюдаем \(f : [-\frac{\pi}{2},\frac{\pi}{2}] \to [-1,1]\text{.}\) Для любого реального число \(y\), которое удовлетворяет \(-1 \le y \le 1\text{,}\) арксинусу \(y\) , обозначаемому
\begin{уравнение*} \arcsin(y) \end{уравнение*}
— это угол \(t\), удовлетворяющий неравенству \(-\frac{\pi}{2} \le t \le \frac{\pi}{2}\) такой, что \(\sin(t) = y\ текст{. }\)
}\)
Мероприятие 4.3.3.
Целью этого упражнения является понимание основных свойств функции арксинуса способом, аналогичным нашему обсуждению функции арккосинуса в подразделе 4.3.1.
Используя определение 4.3.3, каковы область определения и диапазон функции арксинуса?
Точно определить следующие значения: \(\arcsin(-1)\text{,}\) \(\arcsin(-\frac{\sqrt{2}}{2})\text{,}\) \ (\ arcsin(0)\text{,}\) \(\ arcsin(\frac{1}{2})\text{,}\) и \(\ arcsin(\frac{\sqrt{3}}{ 2})\текст{.}\)
На осях, показанных на рисунке 4.3.4, нарисуйте аккуратный график ограниченной синусоидальной функции на интервале \([-\frac{\pi}{2},\frac{\pi}{2}]\) вдоль с соответствующей обратной функцией арксинуса. Отметьте не менее трех точек на каждой кривой так, чтобы каждая точка на графике синусоиды соответствовала точке на графике арксинуса. Кроме того, нарисуйте линию \(y = t\), чтобы продемонстрировать, как графики являются отражением друг друга через эту линию.
Рисунок 4.3.4. Оси для построения ограниченной синусоидальной функции и ее обратной функции арксинуса.
Верно или неверно: \(\arcsin(\sin(5\pi)) = 5\pi\text{.}\) Напишите полное предложение, объясняющее ваши рассуждения.
Подраздел 4.3.3 Функция арктангенса
Наконец, мы разрабатываем обратную функцию для ограниченной версии функции тангенса. Выберем область \((-\frac{\pi}{2}, \frac{\pi}{2})\), на которой \(h(t) = \tan(t)\) возрастает и достигает все значения в диапазоне функции тангенса.
Определение 4.3.5.
Пусть \(y = h(t) = \tan(t)\) определено в области \((-\frac{\pi}{2},\frac{\pi}{2})\text{ ,}\) и наблюдаем \(h : (-\frac{\pi}{2},\frac{\pi}{2}) \to (-\infty,\infty)\text{.}\) Для любое действительное число \(y\text{,}\) арктангенс \(y\) , обозначаемый
\begin{уравнение*} \арктан(у) \end{уравнение*}
— это угол \(t\), удовлетворяющий условию \(-\frac{\pi}{2} \lt t \lt \lt \frac{\pi}{2}\), такой, что \(\tan(t) = y\ текст{. }\)
}\)
Мероприятие 4.3.4.
Целью этого упражнения является понимание основных свойств функции арктангенса.
Используя определение 4.3.5, каковы область определения и диапазон функции арктангенса?
Точно определить следующие значения: \(\arctan(-\sqrt{3})\text{,}\) \(\arctan(-1)\text{,}\) \(\arctan(0)\ текст{,}\) и \(\arctan(\frac{1}{\sqrt{3}})\text{.}\)
График ограниченной функции тангенса на интервале \((-\frac{\pi}{2},\frac{\pi}{2})\) представлен на рисунке 4.3.6. Нарисуйте соответствующую обратную функцию, функцию арктангенса, на тех же осях. Отметьте не менее трех точек на каждой кривой так, чтобы каждая точка на графике касательной соответствовала точке на графике арктангенса. Кроме того, нарисуйте линию \(y = t\), чтобы продемонстрировать, как графики являются отражением друг друга через эту линию.
Рисунок 4.3.6. Оси для построения ограниченной функции тангенса и ее обратной функции арктангенса.Закончите следующее предложение: «поскольку \(t\) неограниченно возрастает, \(\arctan(t)\) \(\ldots\)».

Подраздел 4.3.4 Резюме
Любая функция, не прошедшая тест горизонтальной линии, не может иметь обратную функцию. Однако для периодической функции, которая не проходит тест горизонтальной прямой, если мы ограничим область определения функции интервалом, равным длине одного периода функции, мы затем определим связанную функцию, которая на самом деле имеет обратная функция. Это позволяет нам развивать функции, обратные ограниченным функциям косинуса, синуса и тангенса.
Мы решили определить ограниченные функции косинуса, синуса и тангенса в соответствующих областях \([0,\pi]\text{,}\) \([-\frac{\pi}{2}, \frac{ \pi}{2}]\text{,}\) и \((-\frac{\pi}{2}, \frac{\pi}{2})\text{.}\) на каждом таком интервале , ограниченная функция является строго убывающей (косинус) или строго возрастающей (синус и тангенс) и, следовательно, имеет обратную функцию. Каждая функция ограниченного синуса и косинуса имеет диапазон \([-1,1]\text{,}\), а диапазон ограниченного тангенса представляет собой набор всех действительных чисел.
 Таким образом, мы определяем обратную функцию каждого следующим образом:
Таким образом, мы определяем обратную функцию каждого следующим образом:Для любого \(y\), такого что \(-1 \le y \le 1\text{,}\), арккосинус \(y\) (обозначается \(\arccos(y)\)) равен угол \(t\) в интервале \([0,\pi]\) такой, что \(\cos(t) = y\text{.}\) косинус равен \(y\text{.}\)
Для любого \(y\), такого что \(-1 \le y \le 1\text{,}\) арксинус \(y\) (обозначается \(\arcsin(y)\)) равен угол \(t\) в интервале \([-\frac{\pi}{2}, \frac{\pi}{2}]\) такой, что \(\sin(t) = y\text{. }\) То есть \(t\) — это угол, синус которого равен \(y\text{.}\)
Для любого действительного числа \(y\text{,}\) арктангенс \(y\) (обозначается \(\arctan(y)\)) представляет собой угол \(t\) в интервале \(( -\frac{\pi}{2}, \frac{\pi}{2})\) такие, что \(\tan(t) = y\text{.}\) угол, тангенс которого равен \(y\text{.}\)
Чтобы обсудить свойства трех обратных тригонометрических функций, мы разместим их на тех же осях, что и соответствующие им ограниченные тригонометрические функции.
 Когда мы это делаем, мы используем \(t\) в качестве входной переменной для обеих функций одновременно, чтобы мы могли нанести их на одни и те же координатные оси. 9{-1}(t) = \arctan(t)\) (выделено темно-синим цветом).
Когда мы это делаем, мы используем \(t\) в качестве входной переменной для обеих функций одновременно, чтобы мы могли нанести их на одни и те же координатные оси. 9{-1}(t) = \arctan(t)\) (выделено темно-синим цветом).
Упражнения 4.3.5 Упражнения
1.
Не используя калькулятор, найдите все решения \(\displaystyle \cos(\theta) = \frac{\sqrt{3}}{2}\) в интервале \(0 \leq \theta \leq 2\pi \text{.}\) Если есть несколько ответов, введите их в виде списка, разделенного запятыми. Ваши ответы должны быть точными значениями (данными в виде дробей, а не десятичных приближений).
\(\тета\) =
2.
Не используя калькулятор, найдите все решения \(\displaystyle \sin(\theta) = \frac{\sqrt{2}}{2}\) в интервале \(0 \leq \theta \leq 2\pi \text{.}\) Если есть несколько ответов, введите их в виде списка, разделенного запятыми. Ваши ответы должны быть точными значениями (данными в виде дробей, а не десятичных приближений).
\(\тета\) =
3.
Не используя калькулятор, найдите все решения \(\displaystyle \tan(\theta) = 1\) в интервале \(0 \leq \theta \leq 2\pi\text{.}\) Если больше чем один ответ, введите свои ответы в виде списка, разделенного запятыми. Ваши ответы должны быть точными значениями (данными в виде дробей, а не десятичных приближений).
\(\тета\) =
4.
Точно решите приведенные ниже уравнения. Дайте ответы в радианах и найдите все возможные значения \(t\) в интервале \(0 \leq t \leq 2 \pi\text{.}\) Если имеется более одного ответа, введите свои решения в список, разделенный запятыми.
(a) \(\displaystyle \sin{(t)} = \frac{\sqrt{3}}{2}\), когда \(t =\)
(b) \(\displaystyle \cos{ (t)} = \frac{\sqrt{2}}{2}\), когда \(t =\)
(c) \(\displaystyle \tan{(t)} = -\sqrt{3}\ ) когда \(t =\)
5.
Используйте специальные точки на единичной окружности (см., например, рисунок 2.3.1), чтобы определить точные значения каждого из следующих числовых выражений.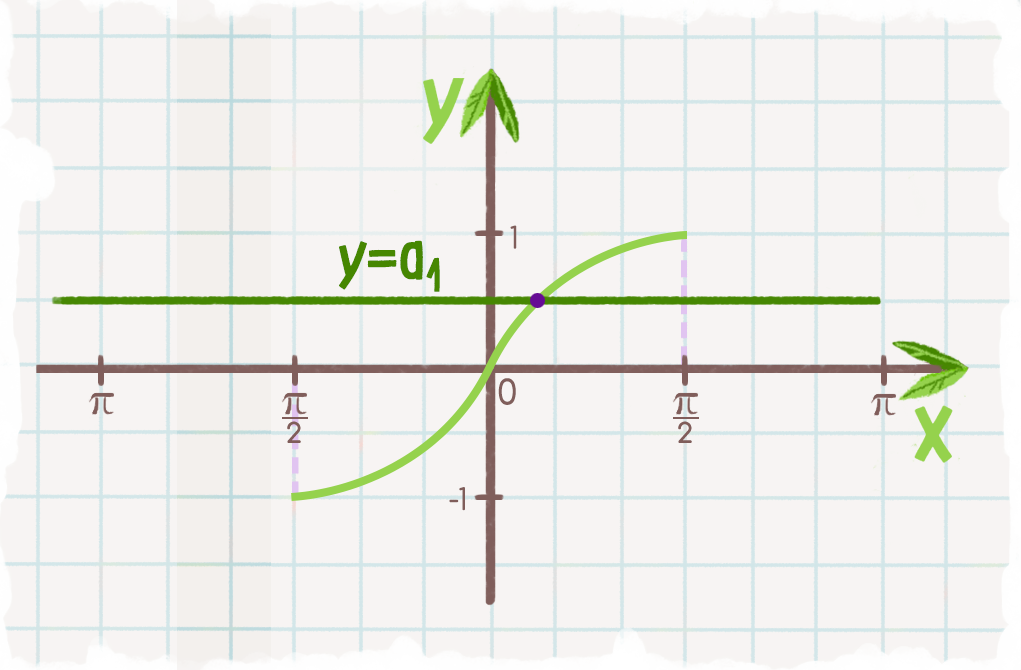 Сделайте это без использования вычислительного устройства.
Сделайте это без использования вычислительного устройства.
\(\displaystyle \arcsin(\frac{1}{2})\)
\(\displaystyle \arctan(-1)\)
\(\displaystyle \arcsin(-\frac{\sqrt{3}}{2})\)
\(\displaystyle \arctan(-\frac{1}{\sqrt{3}})\)
\(\displaystyle \arccos(\sin(\frac{\pi}{3}))\)
\(\displaystyle \cos(\arcsin(-\frac{\sqrt{3}}{2}))\)
\(\displaystyle \tan(\arcsin(-\frac{\sqrt{2}}{2}))\)
\(\displaystyle \arctan(\sin(\frac{\pi}{2}))\)
\(\displaystyle \sin(\arcsin(-\frac{1}{2}))\)
\(\displaystyle \arctan(\tan(\frac{7\pi}{4}))\)
6.
Для каждого из следующих утверждений определите, является ли утверждение истинным или ложным. Если это так, напишите одно предложение, чтобы обосновать свои рассуждения. Если ложно, приведите пример значения, показывающего, что утверждение не выполняется.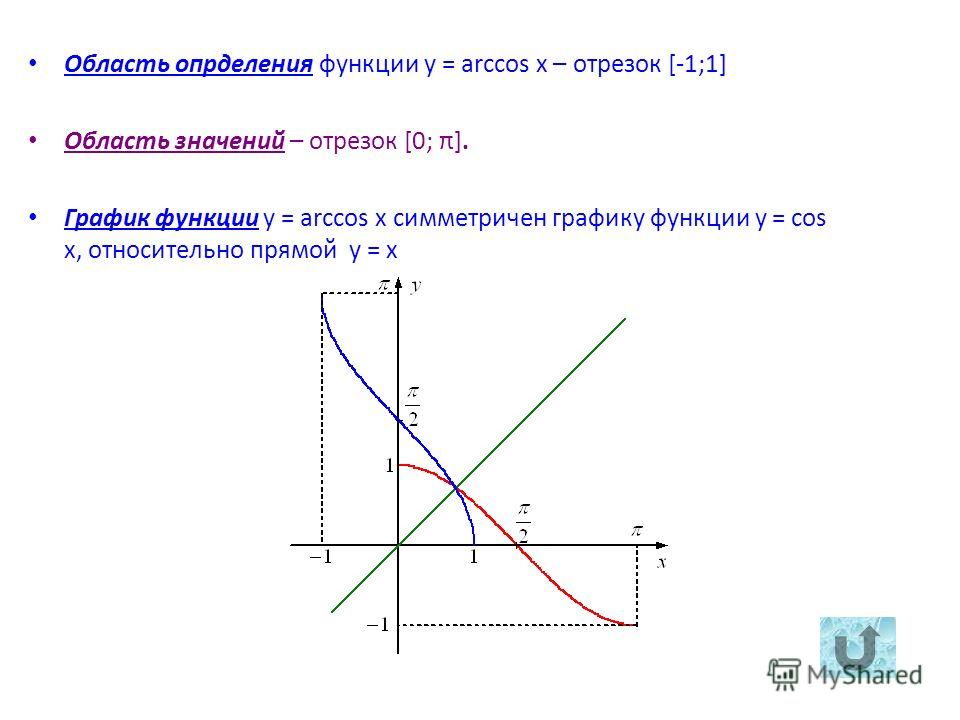
Для любого \(y\), такого что \(-1 \le y \le 1\text{,}\) \(\sin(\arcsin(y)) = y\text{.}\)
Для любого действительного числа \(t\text{,}\) \(\arcsin(\sin(t)) = t\text{.}\)
Для любого действительного числа \(t\text{,}\) \(\arccos(\cos(t)) = t\text{.}\)
Для любого \(y\), такого что \(-1 \le y \le 1\text{,}\) \(\cos(\arccos(y)) = y\text{.}\)
Для любого действительного числа \(y\text{,}\) \(\tan(\arctan(y)) = y\text{.}\)
Для любого действительного числа \(t\text{,}\) \(\arctan(\tan(t)) = t\text{.}\)
7.
Рассмотрим составную функцию \(h(x) = \cos(\arcsin(x))\text{.}\) Эту функцию имеет смысл рассмотреть, поскольку функция арксинуса дает угол, при котором функция косинуса может затем быть оценены. В следующих вопросах мы исследуем, как выразить \(h\) вообще без использования тригонометрических функций.
Каков домен \(h\text{?}\) Диапазон \(h\text{?}\)
Поскольку функция арксинуса дает угол, допустим, что \(\theta = \arcsin(x)\text{,}\), так что \(\theta\) — это угол, синус которого равен \(x\text{.
Рисунок 4.3.10. Прямоугольный треугольник, соответствующий углу \(\theta = \arcsin(x)\text{.}\)Рисунок 4.3.11. Прямоугольный треугольник, соответствующий углу \(\alpha = \arctan(x)\text{.}\) }\) По определению, мы можем изобразить \(\theta\) как угол в прямоугольном треугольнике с гипотенузой \(1\) и вертикальным катетом длины \(x\text{,}\), как показано на рисунке 4.3. .10. Используйте теорему Пифагора, чтобы определить длину горизонтального участка как функцию \(x\text{.}\)
}\) По определению, мы можем изобразить \(\theta\) как угол в прямоугольном треугольнике с гипотенузой \(1\) и вертикальным катетом длины \(x\text{,}\), как показано на рисунке 4.3. .10. Используйте теорему Пифагора, чтобы определить длину горизонтального участка как функцию \(x\text{.}\)Каково значение \(\cos(\theta)\) как функции \(x\text{?}\) Что мы показали относительно \(h(x) = \cos(\arcsin(x) ))\текст{?}\)
Как насчет функции \(p(x) = \cos(\arctan(x))\text{?}\) Как вы можете рассуждать аналогичным образом, чтобы записать \(p\) таким образом, чтобы не было никаких тригонометрические функции вообще? (Подсказка: пусть \(\alpha = \arctan(x)\) и рассмотрим прямоугольный треугольник на рисунке 4.3.11.)
Функция Arccos(x)
Arccos(x), cos -1 (x), функция арккосинуса.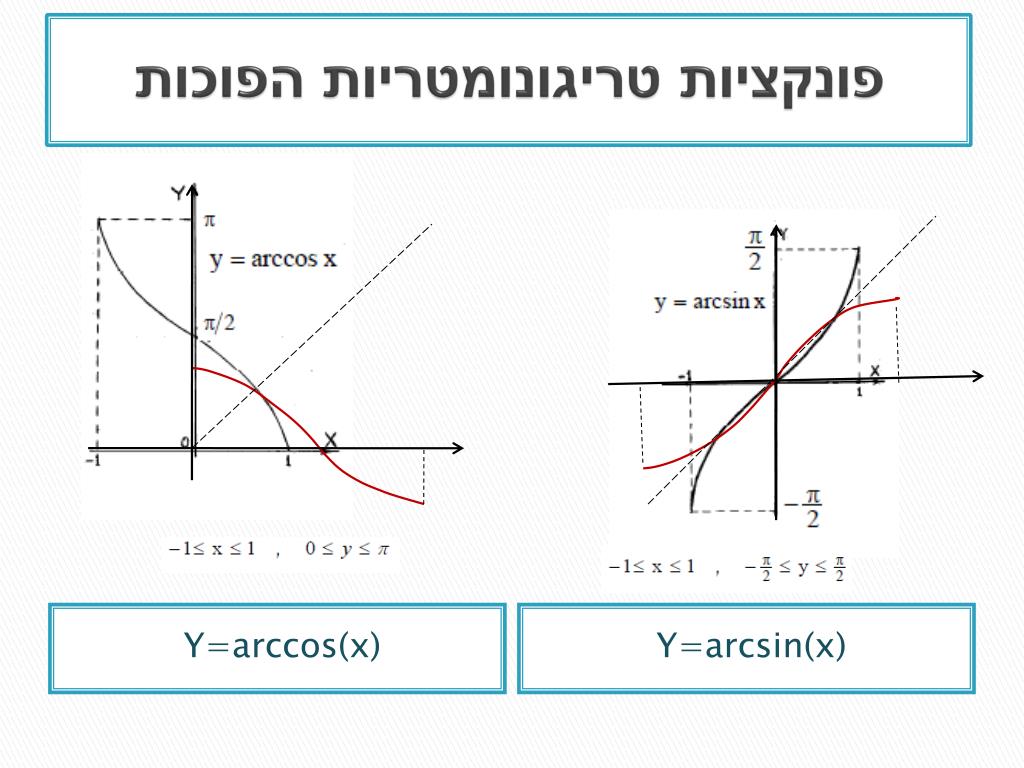
- Определение Arccos
- График арккос
- Правила Arccos
- Стол Arccos
Определение Arccos
Арккосинус x определяется как функция арккосинуса x, когда -1≤x≤1.
Когда косинус y равен x:
COS Y = x
Тогда арккозин x равен обратной косинусной функции x, которая равна Y:
Arccos x = COS -1 x = Y
6666. Здесь cos -1 x означает арккосинус, а не косинус в степени -1.
Рекламные объявления
Например:
arccos 1 = cos -1 1 = 0 рад = 0°
График arccos
Arccos rules
| Rule name | Rule |
| Cosine of arccosine | cos( arccos x ) = x |
| Arccosine of cosine | arccos( cos x ) = x + 2kπ, когда k∈ℤ (k целое) |
| Arccos отрицательного аргумента | arccos(-x) = π — arccos x = 180° — arccos x |
| Дополнительные углы | |
| Arccos sum | arccos( α ) + arccos( β ) = arccos( αβ — √(1- α 2 )(1- β 2 ) ) |
| Arccos difference | arccos( α ) — arccos( β ) = arccos( αβ + √(1- α 2 )(1- β 2 ) ) |
| Arccos sin of x | 5)π» data-order=»arccos( sin <em>x</em> ) = -<em>x</em> — (2<em>k</em>+0.5)π»> arccos( sin x ) = — x — (2 K +0,5) π |
| Синус из арккозина | COS (Arcsin x ) = SIN (ARCCOS x ) = a 2 |
| Tangent of arccosine | net/wp-content/uploads/2018/09/tangent-of-arccosine.png" />» data-order=»<img src="https://allcalculators.net/wp-content/uploads/2018/09/tangent-of-arccosine.png" />»> |
| Derivative of arccosine | |
| Indefinite integral of arccosine | ∫ arccos x dx = x arccos x — √1- x 2 + C |

.gif)


 Таким образом, мы определяем обратную функцию каждого следующим образом:
Таким образом, мы определяем обратную функцию каждого следующим образом: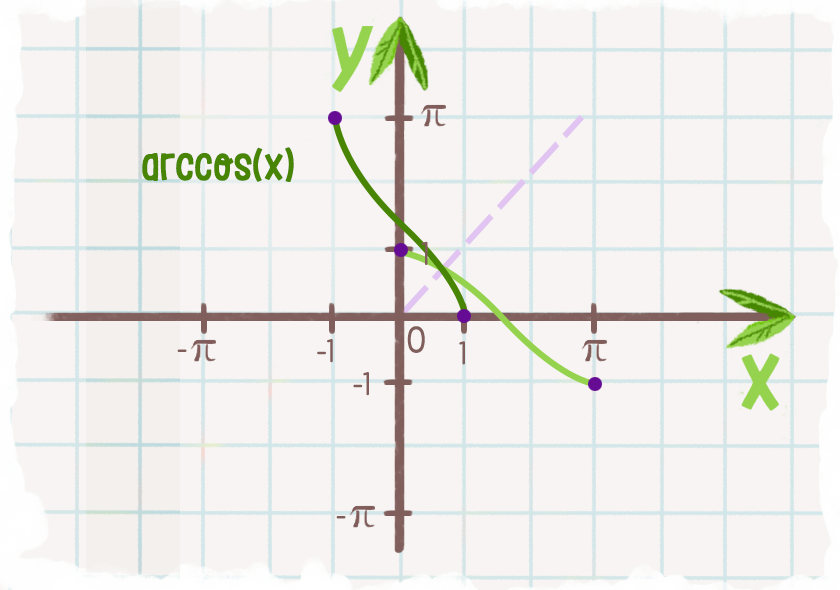 Когда мы это делаем, мы используем \(t\) в качестве входной переменной для обеих функций одновременно, чтобы мы могли нанести их на одни и те же координатные оси. 9{-1}(t) = \arctan(t)\) (выделено темно-синим цветом).
Когда мы это делаем, мы используем \(t\) в качестве входной переменной для обеих функций одновременно, чтобы мы могли нанести их на одни и те же координатные оси. 9{-1}(t) = \arctan(t)\) (выделено темно-синим цветом).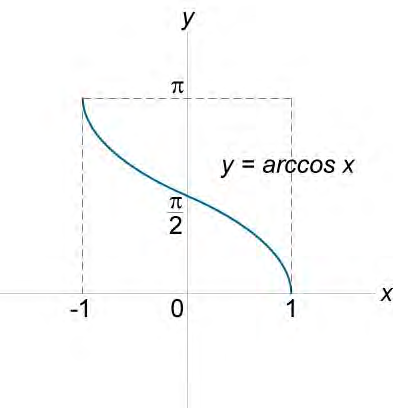 }\) По определению, мы можем изобразить \(\theta\) как угол в прямоугольном треугольнике с гипотенузой \(1\) и вертикальным катетом длины \(x\text{,}\), как показано на рисунке 4.3. .10. Используйте теорему Пифагора, чтобы определить длину горизонтального участка как функцию \(x\text{.}\)
}\) По определению, мы можем изобразить \(\theta\) как угол в прямоугольном треугольнике с гипотенузой \(1\) и вертикальным катетом длины \(x\text{,}\), как показано на рисунке 4.3. .10. Используйте теорему Пифагора, чтобы определить длину горизонтального участка как функцию \(x\text{.}\)