| 1 | Найти производную — d/dx | бревно натуральное х | |
| 2 | Оценить интеграл | интеграл натурального логарифма x относительно x | |
| 3 | Найти производную — d/dx | 92)||
| 21 | Оценить интеграл | интеграл от 0 до 1 кубического корня из 1+7x относительно x | |
| 22 | Найти производную — d/dx | грех(2x) | |
| 23 | Найти производную — d/dx | 9(3x) по отношению к x||
| 41 | Оценить интеграл | интеграл от cos(2x) относительно x | |
| 42 | Найти производную — d/dx | 1/(корень квадратный из х) | |
| 43 | Оценка интеграла 9бесконечность | ||
| 45 | Найти производную — d/dx | х/2 | |
| 46 | Найти производную — d/dx | -cos(x) | |
| 47 | Найти производную — d/dx | грех(3x) | 92+1|
| 68 | Оценить интеграл | интеграл от sin(x) по x | |
| 69 | Найти производную — d/dx | угловой синус(х) | |
| 70 | Оценить предел | ограничение, когда x приближается к 0 из (sin(x))/x 92 по отношению к х | |
| 85 | Найти производную — d/dx | лог х | |
| 86 | Найти производную — d/dx | арктан(х) | |
| 87 | Найти производную — d/dx | бревно натуральное 5х92 |
Идентификаторы базовой функции обратного запуска
Идентификаторы базовой функции обратного запуска
Мы используем MathJax
Основные обратные тригонометрические тождества бывают нескольких видов.
сорта. К ним относятся реципрокные, симметричные и
кофункциональные тождества.
Теорема об обратных взаимных тождествах
Следующие тождества верны для всех значений, для которых они определено:
| $\arcsin x=\operatorname{ arccsc}_1 \dfrac{1}{x} = \left\{ \begin{массив}{ll} \operatorname{ arccsc}_2 \dfrac{1}{x} & \text{if } 0 |
| $\arccos x=\operatorname{ arcsec}_1 \dfrac{1}{x} = \left\{ \begin{массив}{ll} \operatorname{arcsec}_2 \dfrac{1}{x} & \text{if } 0 |
| $\arctan x=\operatorname{ arccot}_2 \dfrac{1}{x} = \left\{ \begin{массив}{ll} \operatorname{arccot}_1 \dfrac{1}{x} & \text{if } x>0 \\ \pi+\operatorname{ arccot}_1 \dfrac{1}{x} & \text{if } x |
| $\operatorname{ arccot}_1 x = \left\{ \begin{массив}{ll} \arctan \dfrac{1}{x} & \text{if} x> 0 \\ -\pi+\arctan \dfrac{1}{x} & \text{if } x |
| $\operatorname{ arccot}_2 x = \arctan\dfrac{1}{x}$ |
| $\operatorname{ arcsec}_1 x = \arccos\dfrac{1}{x}$ |
$\operatorname{ arcsec}_2 x = \left\{
\begin{массив}{ll}
\arccos \dfrac{1}{x} & \text{if } x\ge 1 \\
2\pi-\arccos\dfrac{1}{x} & \text{if} x \le -1
\end{массив} \right. $ |
| $\operatorname{ arccsc}_1 x = \arcsin\dfrac{1}{x}$ |
| $\operatorname{ arccsc}_2 x = \left\{ \begin{массив}{ll} \arcsin \dfrac{1}{x} & \text{if} x\ge 1 \\ -\pi-\arcsin \dfrac{1}{x} & \text{if } x \le -1 \end{массив} \right.$ |
Доказательство: Доказательство первого равенство использует обратный триггер определения и обратное Личности Теорема. Прежде всего отметим, что диапазоны функция обратного синуса и функция первого обратного косеканса почти идентичны, то действуйте следующим образом:
Доказательства остальных тождеств аналогичны, но необходимо соблюдать крайнюю осторожность с интервалами домена и диапазона на какие определения действительны.♦
Теорема об обратном симметричном тождестве
Следующие тождества верны для всех значений, для которых они определены:
| $\arcsin(-x)=-\arcsinx$ |
| $\arccos(-x)=\pi-\arccos x$ |
| $\arctan(-x)=-\arctan x$ |
| $\operatorname{ arccot}_1 (-x)=\pi-\operatorname{ arccot}_1 x$ |
| $\operatorname{ arccot}_2 (-x)=-\operatorname{ arccot}_2 x$ |
| $\operatorname{ arcsec}_1 (-x)=\pi-\operatorname{ arcsec}_1 x$ |
$\operatorname{ arcsec}_2 (-x)=\left\{
\begin{массив}{ll}
\pi+\operatorname{ arcsec}_2 x & \text{if } x\ge 1 \\
-\pi+\operatorname{ arcsec}_2 x & \text{if } x\le 1
\end{массив} \right. $ |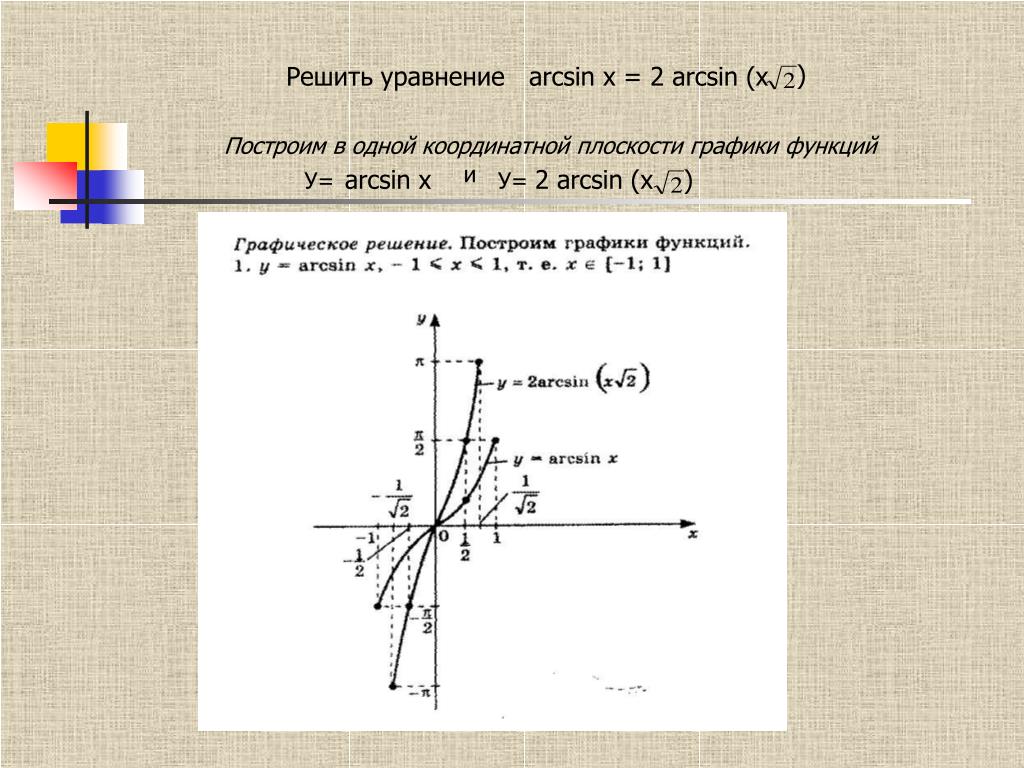
| $\operatorname{ arccsc}_1 (-x)=-\operatorname{ arccsc}_1 x$ |
| $\operatorname{ arccsc}_2 (-x)=\left\{ \begin{массив}{ll} -\pi+\operatorname{ arccsc}_2 x & \text{if } x\ge 1 \\ \pi+\operatorname{ arccsc}_2 x & \text{if } x\le 1 \end{массив} \right.$ |
Доказательство: Доказательство первого идентичность включает в себя симметричное тождество для функции синуса.
\начать{выравнивать} y &= \arcsin(-x) \\ -х &= \sin у \\ х &= -\sin у \\ х &= \sin(-y) \\ -y &= \arcsin x \\ y &= -\arcsin x \\ \arcsin(-x) &= -\arcsinx \end{выравнивание}Теорема тождеств обратных кофункций
Следующие тождества верны для всех значений, для которых они определены:
| $\arcsin x + \arccos x = \dfrac{\pi}{2}$ |
| $\arctan x + \operatorname{ arccot}_1 x = \dfrac{\pi}{2}$ |
| $\arctan x + \operatorname{ arccot}_2 x = \left\{ \begin{массив}{ll} \dfrac{\pi}{2} & \text{if} x\ge 0 \\ -\dfrac{\pi}{2} & \text{if} x |
| $\operatorname{ arcsec}_1 x+ \operatorname{ arccsc}_1 x=\dfrac{\pi}{2}$ |
| $\operatorname{ arcsec}_2 x+ \operatorname{ arccsc}_2 x=\dfrac{\pi}{2}$ |
Доказательство: Доказательство теоремы об обратных тождествах кофункций использует теорему о кофункциях.