cos x, функция косинус х,
Дата публикации: .
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой.
Скачать:Функция y=cos(x) (PPTX)
Что будем изучать:
1. Определение.
2. График функции.
3. Свойства функции Y=cos(X).
4. Примеры.
Определение функции косинуса у=cos(x)
Ребята, мы уже познакомились с функцией Y=sin(X).
Давайте вспомним одну из формул привидения: sin(X + π/2) = cos(X).
Благодаря этой формуле, мы можем утверждать, что функции sin(X + π/2) и cos(X) тождественны, и их графики функций совпадают.
График функции sin(X + π/2) получается из графика функции sin(X) параллельным переносом на π/2 единиц влево. Это и будет график функции Y=cos(X).
График функции Y=cos(X) так же называют синусоидой.
Свойства функции cos(x)
- Запишем свойства нашей функции:
- Область определения – множество действительных чисел.
- Функция четная. Давайте вспомним определение четной функции. Функция называется четной, если выполняется равенство y(-x)=y(x). Как мы помним из формул привидения: cos(-x)=-cos(x), определение выполнилось, тогда косинус – четная функция.
- Функция Y=cos(X) убывает на отрезке [0; π] и возрастает на отрезке [π; 2π]. В этом мы можем убедиться на графике нашей функции.
- Функция Y=cos(X) ограничена снизу и сверху. Данное свойство следует из того, что
-1 ≤ cos(X) ≤ 1 - Наименьшее значение функции равно -1 (при х = π + 2πk). Наибольшее значение функции равно 1 (при х = 2πk).
- Функция Y=cos(X) является непрерывной функцией. Посмотрим на график и убедимся, что у нашей функции нет разрывов, это и означает непрерывность.
- Область значений отрезок [- 1; 1]. Это также хорошо видно из графика.
- Функция Y=cos(X) — периодическая функция.
 Посмотрим опять на график и увидим, что функция принимает одни и те же значения через некоторые промежутки.
Посмотрим опять на график и увидим, что функция принимает одни и те же значения через некоторые промежутки.
Примеры с функцией cos(x)
1. Решить уравнение cos(X)=(x — 2π)2 + 1
Решение: Построим 2 графика функции: y=cos(x) и y=(x — 2π)2 + 1 (см. рисунок).
y=(x — 2π)2 + 1 — это парабола, смещенная вправо на 2π и вверх на 1. Наши графики пересекаются в одной точке А(2π;1), это и есть ответ: x = 2π.
2. Построить график функции Y=cos(X) при х ≤ 0 и Y=sin(X) при x ≥ 0
Решение: Чтобы построить требуемый график, давайте построим два графика функции по «кусочкам». Первый кусочек: y=cos(x) при х ≤ 0. Второй кусочек: y=sin(x)
при x ≥ 0. Изобразим оба «кусочка» на одном
графике.
3. Найти наибольшее и наименьшее значение функции Y=cos(X) на отрезке [π; 7π/4]
Решение: Построим график функции и рассмотрим наш отрезок [π; 7π/4]. На графике видно, что наибольшие и наименьшие значения достигаются на концах отрезка: в точках π и 7π/4 соответственно.
Ответ: cos(π) = -1 – наименьшее значение, cos(7π/4) = наибольшее значение.
4. Построить график функции y=cos(π/3 — x) + 1
Решение: cos(-x)= cos(x), тогда искомый график получится путем переноса графика функции y=cos(x) на π/3 единиц вправо и 1 единицу вверх.
Задачи для самостоятельного решения
1)Решить уравнение: cos(x)= x – π/2.
2) Решить уравнение: cos(x)= — (x – π)2 — 1.
3) Построить график функции y=cos(π/4 + x) — 2.
4) Построить график функции y=cos(-2π/3 + x) + 1.
5) Найти наибольшее и наименьшее значение функции y=cos(x) на отрезке [0; 5π/3].
6) Найти наибольшее и наименьшее значение функции y=cos(x) на отрезке [- π/6; 5π/4].
График функции у cos х 2. Графики тригонометрических функций кратных углов
«Графики функций и их свойства» — y = ctg x. 4) Ограниченность функции. 3) Нечётная функция. (График функции симметричен относительно начала координат). y = tg x. 7) Функция непрерывна на любом интервале вида (?k; ? + ?k).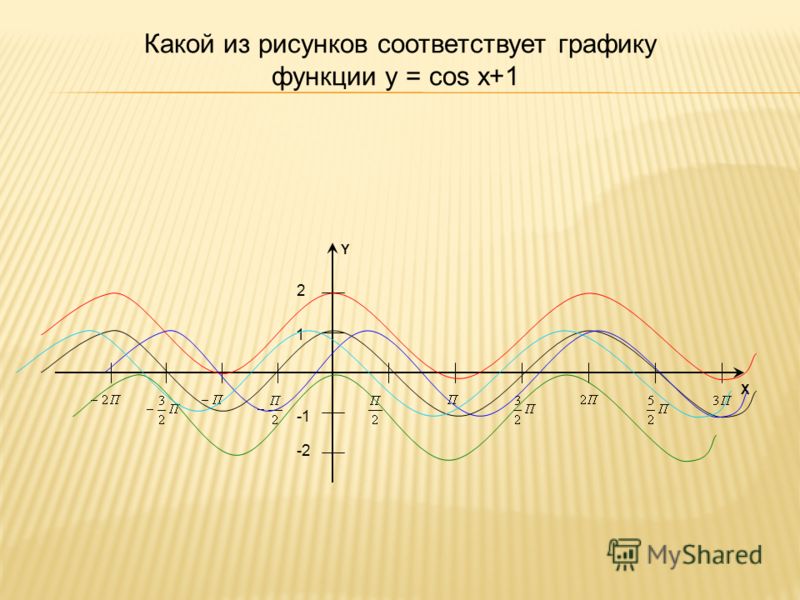
«График функции Y X» — Шаблон параболы у = х2. Чтобы увидеть графики, щелкни мышкой. Пример 2. Построим график функции y = x2 + 1, опираясь на график функции y=x2 (щелчок мышкой). Пример 3. Докажем, что графиком функции у = х2 + 6х + 8 является парабола, и построим график. График функции y=(x — m)2 является параболой с вершиной в точке (m; 0).
«Математика графики» — Как можно строить графики? Наиболее естественно функциональные зависимости отражаются с помощью графиков. Интересное применение: рисунки,… Зачем мы изучаем графики? Графики элементарных функций. Что вы можете нарисовать с помощью графиков? Рассматриваем применение графиков в учебных предметах: математике, физике,…
«Построение графиков с помощью производной» — Обобщение. Построить эскиз графика функции. Найти асимптоты графика функции. График производной функции.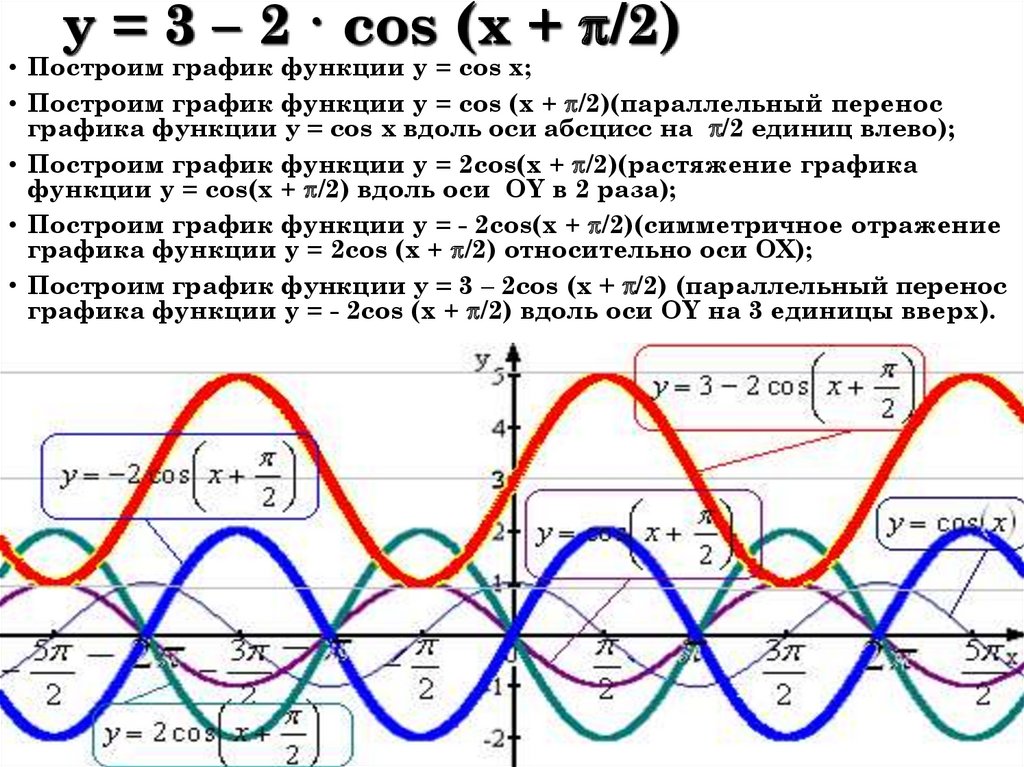 Дополнительное задание. Исследовать функцию. Назвать промежутки убывания функции. Самостоятельная работа учащихся. Расширить знания. Урок закрепления изученного материала. Оцените свои умения. Точки максимума функции.
Дополнительное задание. Исследовать функцию. Назвать промежутки убывания функции. Самостоятельная работа учащихся. Расширить знания. Урок закрепления изученного материала. Оцените свои умения. Точки максимума функции.
«Графики с модулем» — Отобрази «нижнюю» часть в верхнюю полуплоскость. Модуль действительного числа. Свойства функции y = |x|. |x|. Числа. Алгоритм построения графика функции. Алгоритм построения. Функция y= lхl. Свойства. Самостоятельная работа. Нули функции. Советы великих. Решение самостоятельной работы.
«Уравнение касательной» — Уравнение касательной. Уравнение нормали. Если,то и кривые пересекаются под прямым углом. Условия параллельности и перпендикулярности двух прямых. Угол между графиками функций. Уравнение касательной к графику функции в точке. Пусть функция дифференцируема в точке. Пусть прямые заданы уравнениями и.
Всего в теме 25 презентаций
Теперь мы рассмотрим вопрос о том, как строить графики тригонометрических функций кратных углов ωx , где ω — некоторое положительное число.
Для построения графика функции у = sin ωx сравним эту функцию с уже изученной нами функцией у = sin x . Предположим, что при х = x 0 функция у = sin х принимает значение, равное у 0 . Тогда
у 0 = sin x 0 .
Преобразуем это соотношение следующим образом:
Следовательно, функция у = sin ωx
Например, график функции у = sin 2х получается путем «сжатия» синусоиды у = sin x вдвое вдоль оси абсцисс.
График функции у = sin x / 2 получается путем «растяжения» синусоиды у = sin х в два раза (или «сжатия» в 1 / 2 раза) вдоль оси х.
Поскольку функция у = sin ωx повторяет свои значения в ω раз чаще, чем функция
у = sin x , то период ее в ω раз меньше периода функции у = sin x . Например, период функции у = sin 2х равен 2π / 2 = π , а период функции у = sin x / 2 равен π
/ x / 2 = 4π .
Интересно провести исследование поведения функции у = sin аx на примере анимации, которую очень просто можно создать в программе Maple :
Аналогично строятся графики и других тригонометрических функций кратных углов. На рисунке представлен график функции у = cos 2х , который получается путем «сжатия» косинусоиды у = cos х в два раза вдоль оси абсцисс.
График функции у = cos x / 2 получается путем «растяжения» косинусоиды у = cos х вдвое вдоль оси х.
На рисунке вы видите график функции у = tg 2x , полученный «сжатием» тангенсоиды у = tg x вдвое вдоль оси абсцисс.
График функции
И, наконец, анимация, выполненная программой Maple:
Упражнения
1. Построить графики данных функций и указать координаты точек пересечения этих графиков с осями координат. Определить периоды данных функций.
а). y = sin 4x / 3 г). y = tg 5x / 6 ж). y = cos 2x / 3
б). у= cos 5x / 3 д). у = ctg 5x / 3 з). у= ctg x / 3
в). y = tg 4x / 3 е). у = sin 2x / 3
2. Определить периоды функций у = sin (πх) и у = tg ( πх / 2 ).
3. Приведите два примера функции, которые принимают все значения от -1 до +1 (включая эти два числа) и изменяются периодически с периодом 10.
4 *. Приведите два примера функций, которые принимают все значения от 0 до 1 (включая эти два числа) и изменяются периодически с периодом π / 2 .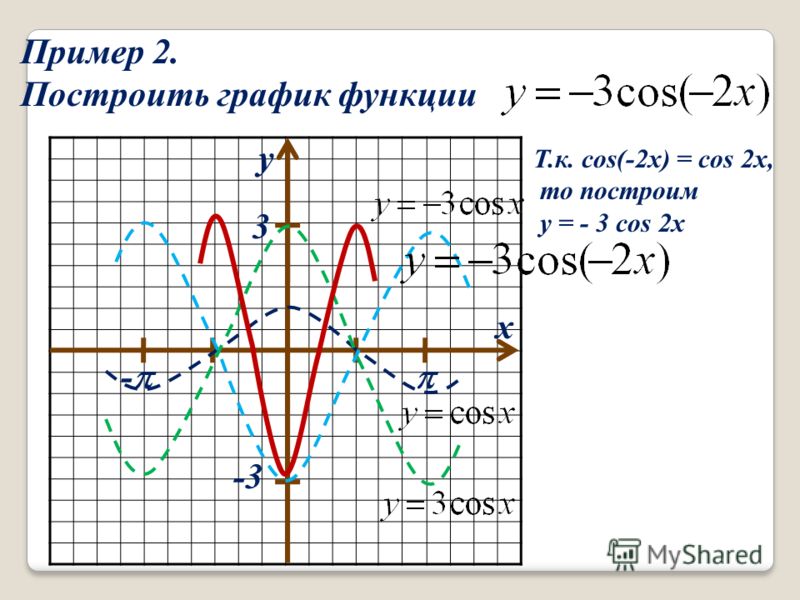
5. Приведите два примера функций, которые принимают все действительные значения и изменяются периодически с периодом 1.
6 *. Приведите два примера функций, которые принимают все отрицательные значения и нуль, но не принимают положительные значения и изменяются периодически с периодом 5.
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой.
Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 10 класса
Алгебраические задачи с параметрами, 9–11 классы
Программная среда «1С: Математический конструктор 6.1»
Что будем изучать:
1. Определение.
2. График функции.
3. Свойства функции Y=cos(X).
Определение функции косинуса у=cos(x)
Ребята, мы уже познакомились с функцией Y=sin(X).
Давайте вспомним одну из формул привидения : sin(X + π/2) = cos(X).
Благодаря этой формуле, мы можем утверждать, что функции sin(X + π/2) и cos(X) тождественны, и их графики функций совпадают.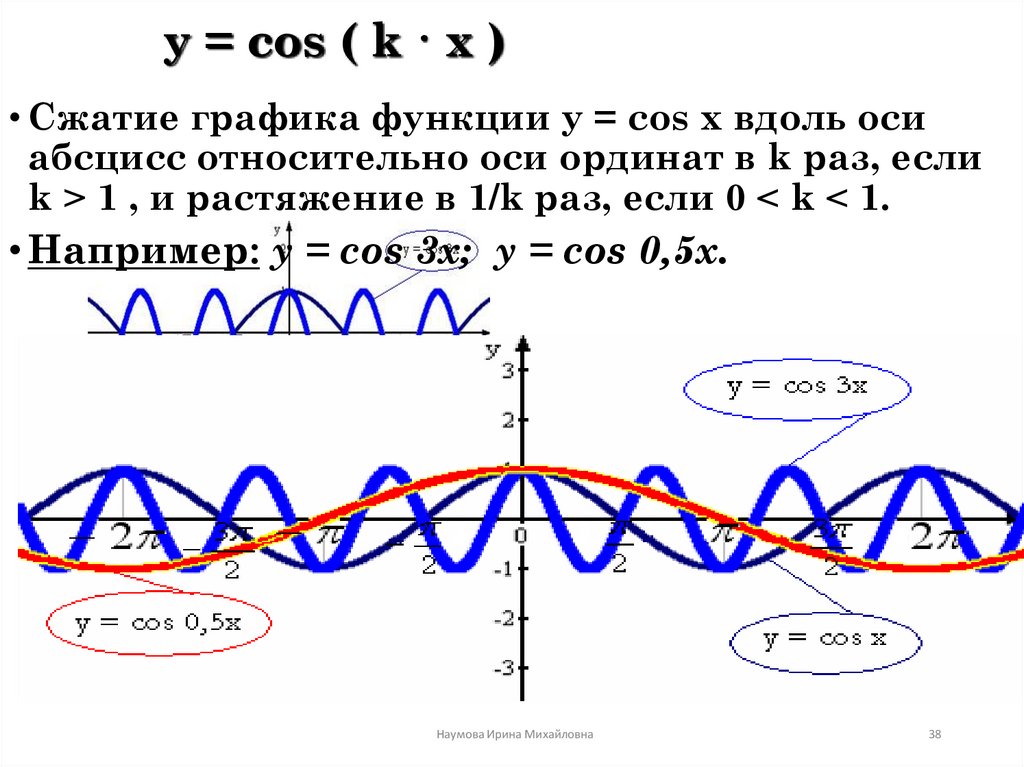
График функции sin(X + π/2) получается из графика функции sin(X) параллельным переносом на π/2 единиц влево. Это и будет график функции Y=cos(X).
График функции Y=cos(X) так же называют синусоидой.
Свойства функции cos(x)
- Запишем свойства нашей функции:
- Область определения – множество действительных чисел.
- Функция четная. Давайте вспомним определение четной функции. Функция называется четной, если выполняется равенство y(-x)=y(x). Как мы помним из формул привидения: cos(-x)=-cos(x), определение выполнилось, тогда косинус – четная функция.
- Функция Y=cos(X) убывает на отрезке и возрастает на отрезке [π; 2π]. В этом мы можем убедиться на графике нашей функции.
- Функция Y=cos(X) ограничена снизу и сверху. Данное свойство следует из того, что
-1 ≤ cos(X) ≤ 1 - Наименьшее значение функции равно -1 (при х = π + 2πk). Наибольшее значение функции равно 1 (при х = 2πk).
- Функция Y=cos(X) является непрерывной функцией. Посмотрим на график и убедимся, что у нашей функции нет разрывов, это и означает непрерывность.

- Область значений отрезок [- 1; 1]. Это также хорошо видно из графика.
- Функция Y=cos(X) — периодическая функция. Посмотрим опять на график и увидим, что функция принимает одни и те же значения через некоторые промежутки.
Примеры с функцией cos(x)
1. Решить уравнение cos(X)=(x — 2π) 2 + 1
Решение: Построим 2 графика функции: y=cos(x) и y=(x — 2π) 2 + 1 (см. рисунок).
y=(x — 2π) 2 + 1 — это парабола, смещенная вправо на 2π и вверх на 1. Наши графики пересекаются в одной точке А(2π;1), это и есть ответ: x = 2π.
2. Построить график функции Y=cos(X) при х ≤ 0 и Y=sin(X) при x ≥ 0
Решение: Чтобы построить требуемый график, давайте построим два графика функции по «кусочкам». Первый кусочек: y=cos(x) при х ≤ 0. Второй кусочек: y=sin(x)
при x ≥ 0. Изобразим оба «кусочка» на одном
графике.
3. Найти наибольшее и наименьшее значение функции Y=cos(X) на отрезке [π; 7π/4]
Решение: Построим график функции и рассмотрим наш отрезок [π; 7π/4]. На графике видно, что наибольшие и наименьшие значения достигаются на концах отрезка: в точках π и 7π/4 соответственно.
На графике видно, что наибольшие и наименьшие значения достигаются на концах отрезка: в точках π и 7π/4 соответственно.
Ответ: cos(π) = -1 – наименьшее значение, cos(7π/4) = наибольшее значение.
4. Построить график функции y=cos(π/3 — x) + 1
Решение: cos(-x)= cos(x), тогда искомый график получится путем переноса графика функции y=cos(x) на π/3 единиц вправо и 1 единицу вверх.
Задачи для самостоятельного решения
1)Решить уравнение: cos(x)= x – π/2.
2) Решить уравнение: cos(x)= — (x – π) 2 — 1.
3) Построить график функции y=cos(π/4 + x) — 2.
4) Построить график функции y=cos(-2π/3 + x) + 1.
5) Найти наибольшее и наименьшее значение функции
y=cos(x) на отрезке .
6) Найти наибольшее и наименьшее значение функции
y=cos(x) на отрезке [- π/6; 5π/4].
Определить точку (точки) пересечения графиков y=cosx и y=cos2x на интервале xE [0,2pi]
Тригонометрия предварительного исчисления
Аадил В.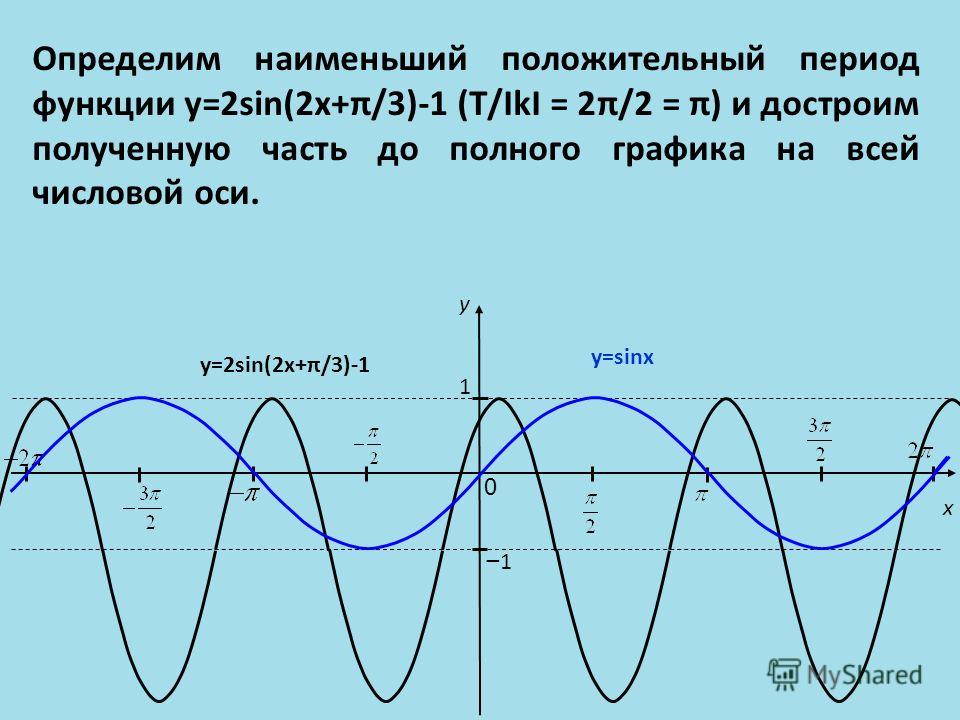
Подписаться І 1
Подробнее
Отчет
2 ответа от опытных наставников
Лучший Новейшие Самый старыйАвтор: Лучшие новыеСамые старые
Осман А. ответил 19.12.21
Репетитор
5 (34)
Профессор инженерной математики – тригонометрия и геометрия
Смотрите таких репетиторов
Смотрите таких репетиторов
Определить точку (точки) пересечения графиков y = cos x и y = cos 2x на интервале xE [0, 2π]
Подробное решение:
y = cos x и y = cos 2x [0, 2π]
В точке интерсекции.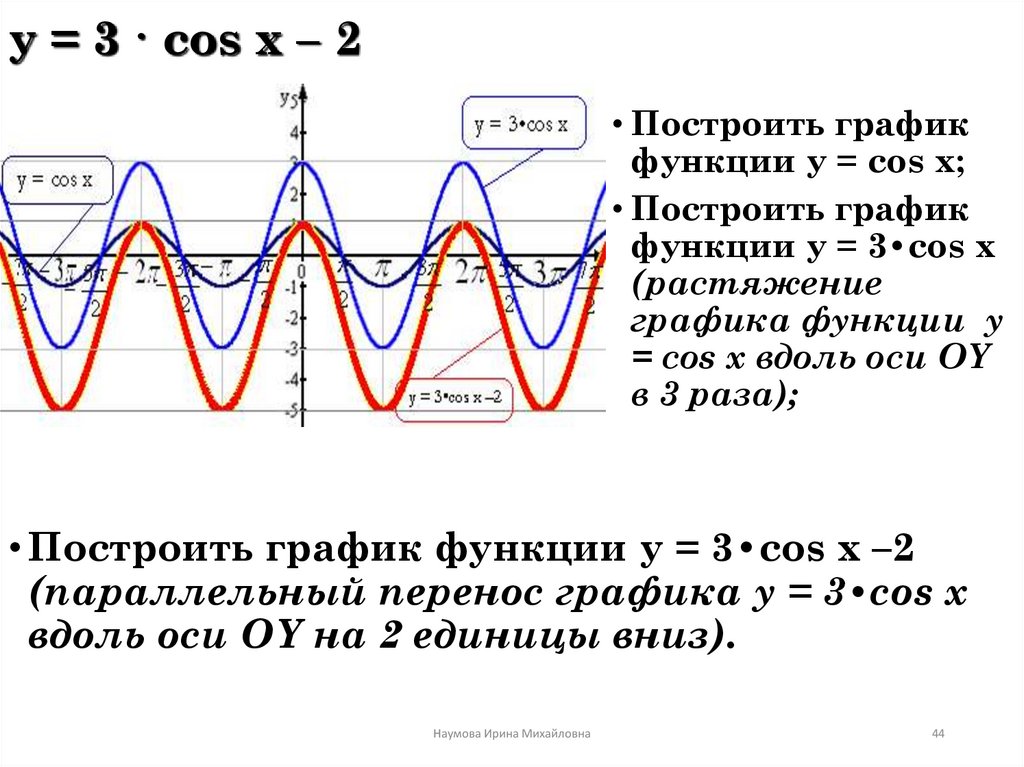 cos 2x = cos x ==> 2 cos 2 x – 1 = cos x==>2 cos 2 x – cos x – 1 = 0==>(cos x – 1)(2 cos x + 1) = 0 ==>
cos 2x = cos x ==> 2 cos 2 x – 1 = cos x==>2 cos 2 x – cos x – 1 = 0==>(cos x – 1)(2 cos x + 1) = 0 ==>
cos x – 1 = 0 ==> cos x = 1 ==> x = cos -1 1 ==> x = 0
2 cos x + 1 = 0 ==> 2 cos x = – 1 ==> cos x = – 1/2 (Q2 и Q3)
Квадрант 2: cos x = –1 /2 ==> x = cos -1 (–1/2) ==> x = π – π/3 ==> x = 2π/3
Квадрант 3: cos x = –1/2 ==> x = cos -1 (–1/2) ==> x = π + π/3 ==> x = 4π/3
Следовательно, точки пересечения находятся в точке: x = { 0 , 2π/3 , 4π/3 }
Голосовать за 0 голос против
Подробнее
Отчет
Марк М.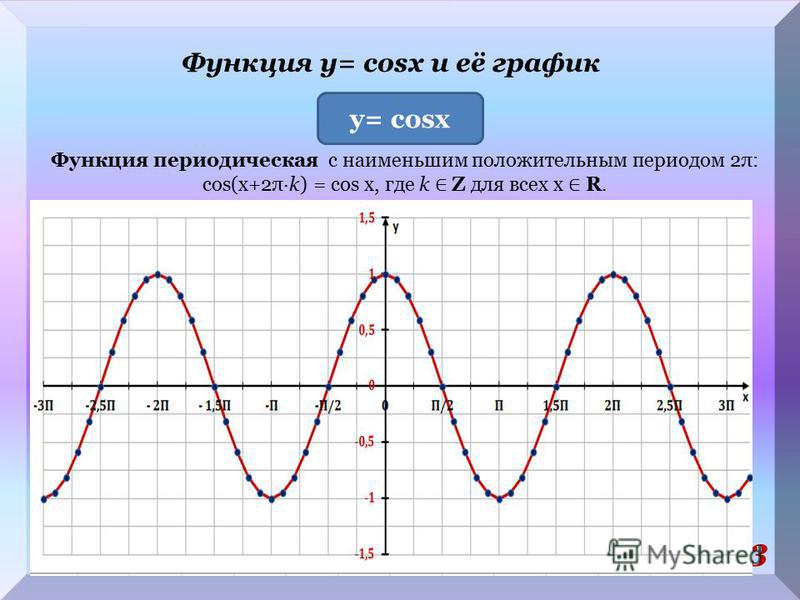 ответил 17.12.21
ответил 17.12.21
Репетитор
5,0 (248)
Учитель математики — высококвалифицированный специалист NCLB
Об этом репетиторе ›
Об этом репетиторе ›
cos x = cos 2 x
0 = cos 2 x — cos x
Коэффициент и использование правила нулевого продукта.
Голосовать за 0 голос против
Подробнее
Отчет
Все еще ищете помощи? Получите правильный ответ, быстро.
Задайте вопрос бесплатно
Получите бесплатный ответ на быстрый вопрос.
Ответы на большинство вопросов в течение 4 часов.
ИЛИ
Найдите онлайн-репетитора сейчас
Выберите эксперта и встретьтесь онлайн.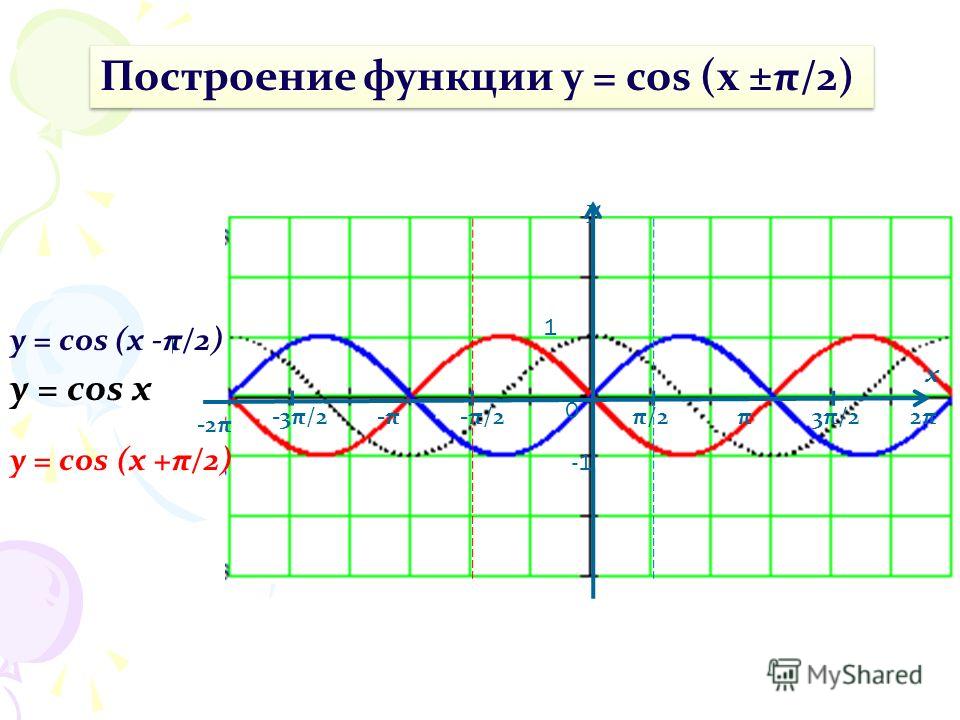 Никаких пакетов или подписок, платите только за то время, которое вам нужно.
Никаких пакетов или подписок, платите только за то время, которое вам нужно.
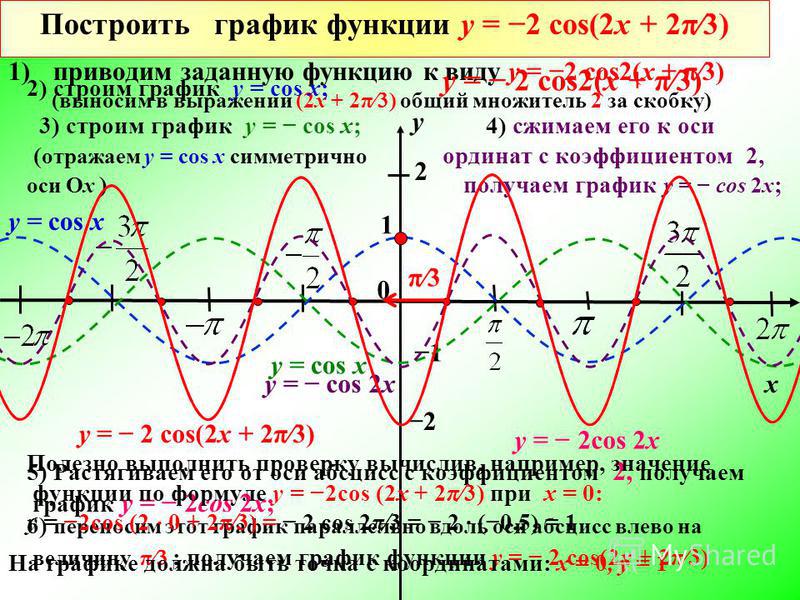
тригонометрия — Как нарисовать $y=2\cos\,2x+3\sin\,2x$ , $x$ для $[-\pi,\pi]$.
спросил
Изменено 10 лет, 6 месяцев назад
Просмотрено 1к раз
$\begingroup$
Используйте добавление ординаты, чтобы нарисовать график $y=2\cos\,2x+3\sin\,2x$ , $x$ для $[-\pi,\pi]$.
Я знаю, что на графике будет три линии, из примера видно, что
$x=0$, $x=\frac{\pi}{4}$, $x=\frac{\pi}{2 }$ и что-то в этом роде, я понятия не имею, как это сделать. Не могли бы вы объяснить пошагово, чтобы я мог ответить на другие вопросы.
Ответ выглядит так.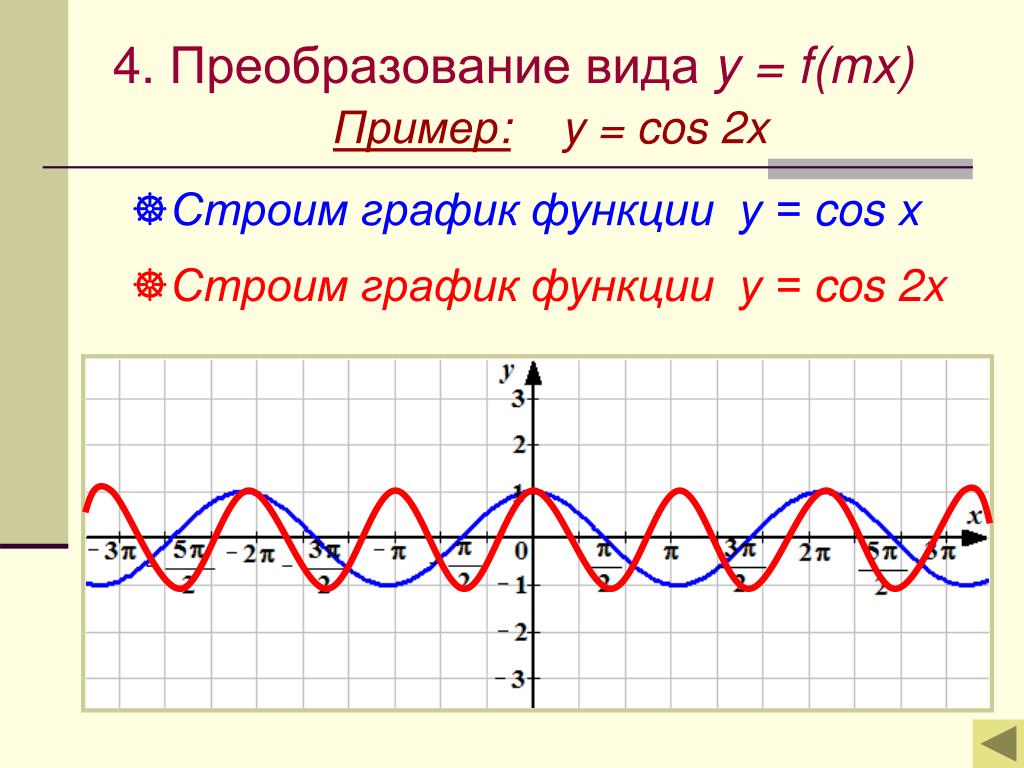 Спасибо.!
Спасибо.!
- тригонометрия
$\endgroup$
8
$\begingroup$
Вы, наверное, знаете график $y=\cos(\theta)$ и $y=\sin(\theta)$ на $[-2\pi,2\pi]$.
График $y=\cos(2\theta)$ на $[-\pi,\pi]$ получается из графика $y=\cos(\theta)$ на $[-2\pi ,2\pi]$, выполнив горизонтальное сжатие в $2$ (мы делаем замену с $y=f(x)$ на $y=f(2x)$).
Аналогично, график $y=\sin(2\theta)$ на $[-\pi,\pi]$ является результатом сжатия по горизонтали в 2 раза графика $y=\sin(\ theta)$ на $[-2\pi,2\pi]$.
График $y=2\cos(2\theta)$ получается из графика $y=\cos(2\theta)$ путем вертикального растяжения с коэффициентом $2$. График $y=3\sin(2\theta)$ получается из графика $y=\sin(2\theta)$ путем вертикального растяжения в $3$.
Когда у вас есть графики $y=2\cos(2\theta)$ и $y=3\sin(2\theta)$ (полученные с помощью простых геометрических операций, описанных выше), вы получаете график
$$y= 2\cos(2\тета) + 3\sin(2\тета)$$
«прибавлением ординаты».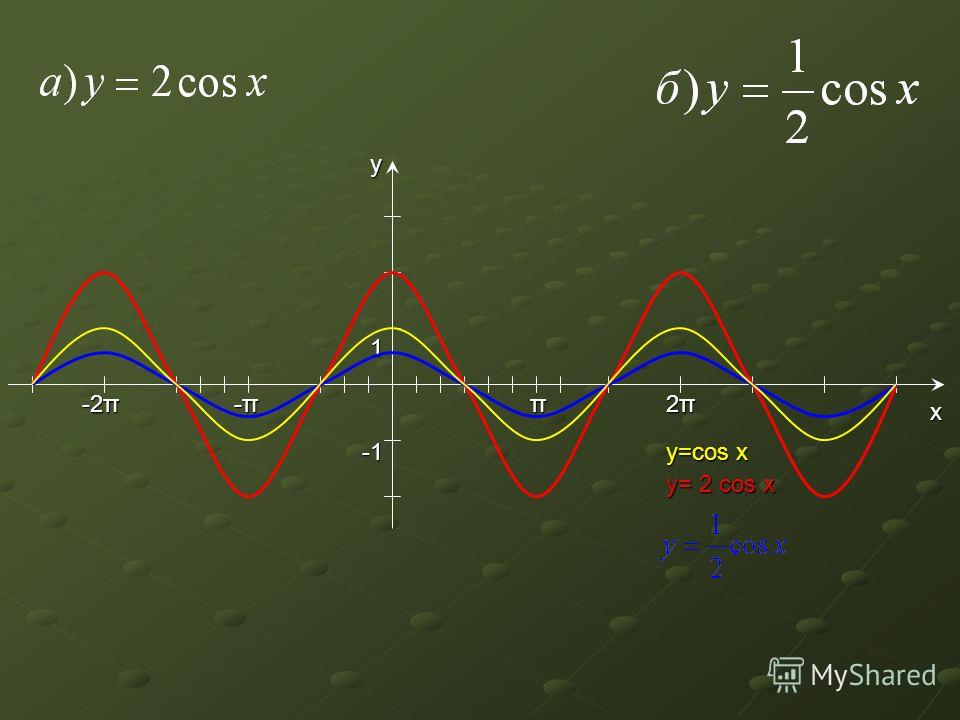 Вы хотите представить, что вы строите график $y=3\sin(2\theta)$ «поверх» графика $y=2\cos(2\theta)$, так что в итоге вы складываете значения. Делая это, вы можете получить довольно разумное геометрическое приближение.
Вы хотите представить, что вы строите график $y=3\sin(2\theta)$ «поверх» графика $y=2\cos(2\theta)$, так что в итоге вы складываете значения. Делая это, вы можете получить довольно разумное геометрическое приближение.
$\endgroup$
5
$\begingroup$
Я предполагаю, что вы имели в виду $\theta \in [-\pi,\pi]$, а не $x$.
Вы могли заметить, что $y = \sqrt{13} (\frac{2}{\sqrt{13}} \cos 2 \theta+\frac{3}{\sqrt{13}} \sin 2 \theta) $. Пусть $\alpha$ — такой угол, что $\sin(\alpha) = \frac{2}{\sqrt{13}}$ и $\cos(\alpha) = \frac{3}{\sqrt{ 13}}$ (нужно убедиться, что такой угол существует). Тогда формулы сумм-произведений для $\sin, \cos$ дают: 9{\circ}$, после этого построение графика функции должно быть простым.
$\endgroup$
$\begingroup$
Вот так.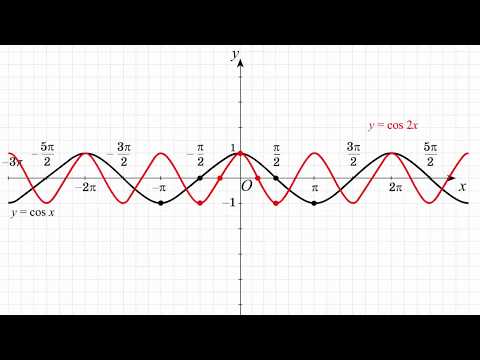

 Посмотрим опять на график и увидим, что функция принимает одни и те же значения через некоторые промежутки.
Посмотрим опять на график и увидим, что функция принимает одни и те же значения через некоторые промежутки.