урок алгебры в 8 классе «Стандартный вид числа»
Тема урока :
СТАНДАРТНЫЙ ВИД ЧИСЛА
Цели урока:
Познавательная:
1. Ознакомить учащихся с записью чисел в стандартном виде и полученные значения использовать при решении задач. Установить межпредметные связи.
2.Показать способы записи больших и малых чисел.
3.Формировать умение синтезировать и обобщать полученные знания.
4.Показать значимость темы при изучении смежных дисциплин.
5.Развивать у учащихся познавательный интерес к предмету.
Развивающая:
развивать у учащихся мышление, речь, память, умение выделить главное, продолжить развитие умения анализировать.
Воспитательная:
воспитывать общую культуру, активность, самостоятельность, умение общаться, патриотизм.
Тип урока:
урок
объяснения и первичного закрепления новых знаний.
Оборудование:
маршрутный лист,
техническое оснащение урока – компьютеры,
компьютерная презентация в Microsoft PowerPoint.
Методы обучения:
по источнику приобретённых знаний – словесные, практические, наглядные;
по уровню познавательной активности – проблемный, частично-поисковый.
Форма урока: урок-практикум.
«Дорогу осилит идущий…!»
ХОД УРОКА:
I. Организация начала урока
Здравствуйте! Проверьте, пожалуйста, свою готовность к уроку.
А теперь обратимся к эпиграфу нашего урока «Дорогу осилит идущий…!»
Что означают эти слова?
Каждый из вас получит маршрутный лист, в котором будет фиксировать свою работу и в конце урока оценит её
( раздаются маршрутные листы)
Слайд №1
Витамины,минералы,продукты.
(Задание № 1 на МЛ)
Правильные ответы записаны на обратной стороне доски.
Самопроверка. Слайд №2-3
Набираем баллы.
II Сообщение темы и цели урока
Слайд №4
–
Прежде чем приступить к изучению новой темы, выполните задания на первой
странице маршрутного листа (проверка на экране). Если вы правильно выполнили
задания, то вы должны получить слово – СТАНДАРТ.
Что такое стандарт? Где вы встречались с этим словом? Что оно означает?
(Самое первое задание на МЛ- таблица)
Слайд №5
Стандарт (от англ. – standard) Образец, эталон, модель, с которым сопоставляются,
сравниваются подобные объекты, процессы. (Универсальный энциклопедический
словарь). Т.е., когда говорят о стандарте, людям легче представить о чем идет
речь. А мы сегодня будем говорить о стандартном виде числа. Итак, это тема
сегодняшнего урока.
Слайд № 6
II. Актуализация
знаний учащихся.
Актуализация
знаний учащихся.
Подготовка к активной учебно-познавательной деятельности на основном этапе урока
В окружающем нас мире мы сталкиваемся с очень большими и очень маленькими числами. Мы уже с вами знаем, как записывать большие и маленькие числа с помощью степени числа.
IV.Усвоение новых знаний
Слайды № 7-8
– Удобно ли
записывать числа в таком виде? Почему? (Занимают много места, тратится много
времени, сложно запоминать.)
– Как вы считаете, какой выход нашли из этой ситуации? (Записывать числа
с помощью степеней.)
(Задание № 3 на МЛ)
Использование понятия степени делает запись выражения более краткой и компактной.
Особенно часто степени используются при записи больших чисел. Такие числа записывают с помощью степени с основанием 10. Например:
10-1 = 0,1
100 = 1
101 = 10
102 = 100
103 = 1000
!!!Показатель
степени с основанием 10 показывает, сколько нулей надо записать после цифры 1.
Например, радиус земного шара, приблизительно равный 6,37 млн. м, записывают в виде 6,37 • 106 м.
Степень 106 равна 1 000 000 поэтому:
6,37 • 106 м = 6 370 000 м
Кроме этого, запись чисел с помощью степени используется для записи натуральных чисел в виде суммы разрядных слагаемых.
4 835 = 4 • 1000 +
8 • 100 + 3 • 10 + 5 = 4 • 10
!!!Каждое
число, бóльшее 10, можно записать в стандартном виде:
a • 10n, где 1 ≤ a ≤ 10 и n — натуральное число.
Такая запись называется стандартным видом числа.
Слайд №9
Запишите массу
Земли, используя степень числа. 598 • 1025 г. Теперь запишите массу
атома водорода. 17 • 10–20 г. А можно ли по другому записать
эти числа, используя степени? Попробуйте! 59,8 • 1026 , 5,98 •
1027; 0, 598 • 1028; 5980 • 1024.
17 • 10–20; 1,7 • 10–19; 0,17 • 10–18; 170 •
10–21;
– Все результаты
правильные. Но можно ли говорить о стандартной записи? Как быть? (Договориться
о единой записи чисел.)
Но можно ли говорить о стандартной записи? Как быть? (Договориться
о единой записи чисел.)
– Попробуйте обсудить с соседом, какая же запись должна быть единой,
стандартной?
– Каким же должен быть множитель перед степенью числа 10, чтобы было удобно и
ЗАПОМНИТЬ число и представить его?
– Откройте, пожалуйста, слайд №10
И учебники п 11 стр.104 ,найдите определение стандартного вида числа и запишите его в маршрутные листы.
– Стандартным видом числа называется запись вида а • 10n,
где 1 < а < 10, n – целое. n – называют порядком числа.
–
В стандартном виде можно записать любое положительное число!!!
Почему? (По определению. Т.к. первый множитель число, принадлежащее промежутку
от [1 до 10) (положительный) и второй множитель – число 10 в какой либо степени
(тоже положительный), то при умножении двух положительных чисел получится
только положительное число.)
Слайд № 11
–
Итак, как же записать массу Земли в стандартном виде? (5,98 • 1027)
– Назовите порядок числа.
Слайд № 12
– А масса атома водорода? (1,7•10–19. Порядок – 19.)
V.Первичное закрепление знаний
Слайд № 13-19
( Задание №4 на МЛ)
Число | n | Число | n | Число | n |
1,392 • 109 м – диаметр Солнца | 9 | 5 • 10–8 кг – масса крыла мухи | –8 | 5 • 10–3 км/ч – скорость улитки | –3 |
1, 03 • 10–7 м – диаметр вируса гриппа | –7 | 5,5• 107 кг – масса Останкинской телебашни | 7 | 4,5 ______ км/ч – скорость человека | 0 |
Если n > 0, то > 10,
если n < 0, то < 1 (Если порядок положительный, то число больше 10, если –
отрицательный – число меньше 1, а если равен нулю, то число находится в
промежутке от 1 до 10)
– Как вы думаете, что можно сказать о числе, зная его порядок? (Насколько
большим или маленьким является число. Чем больше порядок числа, тем больше само
число. Большой по модулю отрицательный порядок говорит о том, что число
маленькое.)
Чем больше порядок числа, тем больше само
число. Большой по модулю отрицательный порядок говорит о том, что число
маленькое.)
Проверка задания слайд № 20
VI.Закрепление знаний
Слайд № 21
(Задание № 5 на МЛ)
определение стандартного вида числа:
Чтобы записать число в стандартном виде – если один из множителей уменьшается, то второй увеличивается и, наоборот, – если первый множитель увеличивается, то второй уменьшается.
Слайд № 22
( Задание №6 на МЛ)
Вам нужно записать предложенные в левой части числа в стандартном виде
Самопроверка. Получилось слово НАНО
– Приставка «нано» в переводе с греческого означает «карлик». Вам знакомо это слово? Где вы с ним встречались?
(Нанотехнологии.)
Сообщение учащихся.
Дома вам нужно было прочитать сказку Лескова «ЛЕВША».Если вы внимательно ее читали,то можете вспомнить
первого
человека, который занимался нанотехнологиями, т. е. очень маленькими размерами.
е. очень маленькими размерами.
Сообщение учащихся.
Слайд № 23
Это Левша. Он подковал блоху, сделанную англичанами, чтобы доказать, «что на
Руси умельцы имеются, да получше чем везде».
VII.Обобщение и систематизация
слайд № 24
В астрономии для определения расстояний используют такую единицу измерения
как астрономическая единица длины (а.е.) – среднее расстояние от Земли до Солнца
равное 150 млн.км. Выбери из предложенных вариантов запись 1 а.е. в стандартном виде.
Самопроверка слайд № 24
Переходим на слайд № 25
(Задание № 7 на МЛ)
Это задание,которое вам необходимо выполнить самостоятельно, сделав запись на слайде презентации.
На этом же слайде вы делаете надпись выполнивших данную работу
Для ознакомления
Слайд № 26
–
В древнерусском счете 107 называли – «ворон», а 10
– Вы узнали, что такое стандартный вид числа и научились записывать число в стандартном виде. Как вы думаете, стандартный вид числа нужен только для того, чтобы сократить (упростить) запись чисел?
(Используя свойства степени числа удобно выполнять действия с большими и маленькими числами.)
– Совершенно верно. Решим несколько примеров. Решите два любые из примеров.
(Задание № 8 на МЛ)
– Какие свойства вы применяли при выполнении действий?
(Свойства степени; переместительное и сочетательные свойства.)
– Если выполняются действия с числами в стандартном виде, обязательно ответ
получится в стандартном виде?
(Нет)
– Как его представить в стандартном виде?
(Перенести запятую и изменить порядок.)
VIII.Контроль и самопроверка знаний
Графический диктант
(Задание № 9 на МЛ)
Ответьте на вопросы («да» – галочка, «нет» – палочка)
Число 3 • 105 записано в стандартном виде (+)
Число 0,81 • 106 записано в стандартном виде (–)
7,45 • 10–5 записано в стандартном виде (+)
Число 50 записано в стандарном виде (–)
Верно ли высказывание: «Чем больше порядок числа, тем больше само число?» (+)
Если порядок числа отрицательный, то и само число отрицательно? (–)
Если перемножить два числа в стандартном виде, то ответ будет числом в стандартном виде? (–)
В
стандартном виде можно записать любое число. (+)
(+)
Самопроверка слайд № 27
IX. Подведение итогов урока. Компетенции.
– Итак, подведем итог урока.
– С каким новым понятием вы познакомились?
– Как записать число в стандартном виде?
– Какие условия нужно поставить на каждый множитель?
– Можно ли представить в стандартном виде отрицательное число?
– Число 0?
– Почему?
– Для чего нужна стандартная запись числа?
– Где применяется стандартный вид числа?
– Какие числа или постоянные, записанные в стандартном виде из различных наук
вы знаете?
– Почему поставлены такие условия на множители, т.е. почему можно представить
только положительные числа (вспомните, что выражают такими числами)?
(Различные величины и единицы измерения, а они могут быть только положительными.)
Выставление
оценки по итогам работы на уроке (маршрутный лист).
Продолжите мое предложение
Мне бы пригодилась запись числа в стандартном виде, если бы я был…..
X. Информация о домашнем задании и инструктаж по его выполнению
По учебнику
Изучить п 11выучить правила,
Решить №№
На 6 баллов №№ 497,501
На 9 баллов №№ 502,504,515
На 12 баллов №№515,518,519
МАРШРУТНЫЙ ЛИСТ
ученика(цы) 8класса
______________________________________
тема урока:
2. Упростите запись числа, используя степень:
5 980 000 000 000 000 000 000 000 000 = 1 б
0,000 000 000 000 000 000 0017 =
3. Назовите порядок числа
число | n | число | n | число | n |
1,392∙109 |
| 5 ∙ 10-8 |
| 5 ∙ 10 -3 |
|
1, 03 ∙ 10-7 |
| 5,5∙ 107 |
| 4,5 |
|
6 б
4.
1,392∙109 = |
1, 03 ∙ 10-7 = |
5 ∙ 10-8 = |
5,5∙ 107 = |
5 ∙ 10 -3 = |
4,5 ∙ 10 0 = |
6 б
5. Сделайте вывод, сравнив порядки чисел:
Если n > _____, то число α _________
3 б
Если n __ _____, то число _________α _________
Если n __ _____, то число _________α _________
6. Выберите букву, соответствующую записи числа в стандартном виде:
270 | 27 ∙ 101 | П |
0,00088 | 0,88 ∙ 10-3 | К |
2,7 ∙ 102 | Н | 8,8 ∙ 104 | Т | ||
0,27 ∙ 103 | А | 8,8 ∙ 10-4 | Н | ||
35600000 | 3,56 ∙ 107 | А |
53,67 | 53,67 ∙ 101 | А |
3,56 ∙ 10 -7 | И | 0,5367 ∙ 10-2 | Е | ||
35,6 ∙ 106 | Т | 5,367 ∙ 101 | О |
4 б
_________ — 10 ___ (греч. —
____________)
—
____________)
7. Молекулы- мельчайшие частицы вещества.Так в 1 грамме молекулы воды 6 б
содержится
3,7·1022 молекул (т.е 37 000 000 000 000 000 000 000 ).
Вычисли, используя калькулятор, массу одной молекулы воды и ответ запиши
в стандартном виде.
8. Выполните действия с числами в стандартном виде и запишите ответ
в стандартном виде:
(2 ∙ 103) ∙ ( 1,5 ∙ 105) =
|
1 б |
(9 ∙ 107) : ( 3 ∙ 10-3) =
|
1 б |
(1,5 ∙ 10-3) ∙ ( 9 ∙ 105) =
|
2 б |
(2,4 ∙ 10-3) : (8 ∙ 105) =
|
2 б |
(8,1 ∙ 1019) ∙ ( 3 ∙ 1021) =
|
2 б |
(3,6 ∙ 103) : (5 ∙ 10-5) =
|
2 б |
(7,5 ∙ 10-3) + ( 1,23 ∙ 10-3) =
|
3 б |
(4,5 ∙ 107) – ( 4,05 ∙ 107) =
|
3 б |
9. Графический диктант:
Графический диктант:
8 б
Всего баллов:
52-54 баллов и более – «12»
42 – 51 баллов – «9»
25 – 41 баллов – «6»
Менее 25 баллов – «2»
Оценка за урок ________________________________________________________
которое начиналось словами :
Мне бы пригодилась запись числа в стандартном виде, если бы я был…..
Задание № 1
1. Выполнить действия:
3,5·103·3,0·102
2,1·10-5·2,2·103
2,25·104: (1,5·10-2)
3,3·10-3:3,0·10-4
1,14·109:(1,9·10-2)
6,0·10-5·(1,2·10-3)
2. Выразить в километрах:
Выразить в километрах:
3,45·103м
2,5·109м
3,8·10-3см
в метрах:
2,5·103км
3,25·10-2км
6,25·106см
в граммах:
3,1·10-2кг
4,42·103кг
Задание № 2
1. Порядок натурального числа равен 3. Десятичная запись этого числа содержит … цифр.
2. Сторона прямоугольника м. и м.
Найди периметр прямоугольника.
3. Десятичная запись некоторого натурального числа содержит 6 цифр. Найди порядок этого числа.
4. Сторона прямоугольника м. и м. Найди периметр прямоугольника.
Тест 1
1. В астрономии для определения расстояний используют такую единицу измерения как астрономическая единица длины (а.е.) – среднее расстояние от Земли до Солнца равное
150 млн.км. Выбери из предложенных вариантов запись 1 а.е. в стандартном виде.
А.
150·109 м
Б. 150·106 м
В. 15·1010 м
Г.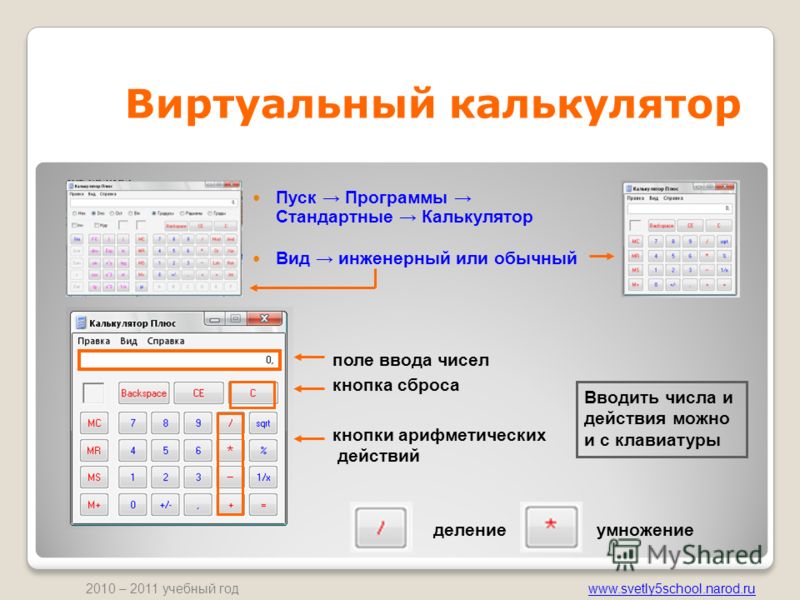 1,5·1011 м
1,5·1011 м
Д. 1,5·1012 м
Е. 0,15·1012 м
2. Световой год – это расстояние, которое свет со скоростью 300 000 км/с, проходит за 1 год ( учти, что в 1 году — 365 суток, в 1 сутках – 24 часа, в 1 часе – 3600 с). Используя калькулятор, рассчитай данное расстояние в метрах и результат представь в стандартном виде.
А.
946·1013 м
Б. 9,46·1015 м
В. 9,46·1013 м
Г. 9,46·1017 м
Д. среди предложенных ответов правильного нет
3. Молекулы- мельчайшие частицы вещества. Так в 1 грамме молекулы воды содержится 3,7·1022 молекул (т.е 37 000 000 000 000 000 000 000 ). Вычисли, используя калькулятор, массу одной молекулы воды () и ответ запиши в стандартном виде.
А.
2,7·10-26 кг
Б. 2,7·10-23 кг
В. 27·10-27 кг
Г. 0,27·10-25 кг
Д. среди предложенных ответов нет правильного.
4.
Установи соответствие между единицами измерения физических величин.
Калькулятор на Python 3 с графическим интерфейсом — как написать код программы
Многие программисты стараются изучать языки программирования с помощью написания достаточно простых программ. Один из вариантов – написание калькулятора. Конечно, можно посчитать в отладчике Python или запустив консоль. Но гораздо лучше написать на python свой калькулятор с графическим интерфейсом.
Считаем в консоле
Чтобы посчитать математические выражения можно запустить консоль. Запустить python. После этого набираем математические выражения и получаем ответ. Для этого даже не надо уметь программировать.
Делаем простой калькулятор
Лучше всего закреплять свои знания по программированию с помощью написания простых программ. Таких приложений можно придумать много – календарь, программа для хранения заметок, получение прогноза погоды.
Можно написать программу, которая делает скриншоты и сохраняет полученные изображения в папку. В любом случае, надо выбрать какое-нибудь не сложное задание, чтобы не закопаться в нем. Потом его можно будет расширить и сделать по-настоящему полезное приложение.
Потом его можно будет расширить и сделать по-настоящему полезное приложение.
В нашем случае мы разберем, как создать простой графический калькулятор на Python 3. Для реализации графического интерфейса воспользуемся стандартным пакетом Tkinter. Он входит в состав Python 3. Соответственно, если у вас установлен Python, то дополнительно не надо ничего устанавливать.
В первых строках файла calculator.py подключаем библиотечные функции:
- Tkinter для графического интерфейса;
- Decimal для вычислений с большей точность, так как точности float не достаточно.
Импорт библиотек и исходные данные
Создаем окно приложения — объект Tk с заголовком Calculator. Во вложенном кортеже buttons будут храниться обозначения для кнопок. В список stack будем добавлять введенные числа и операции, которые надо совершить. activeStr предназначен для хранения набираемого числа.
from tkinter import * from decimal import * root = Tk() root.title('Calculator') buttons = (('7', '8', '9', '/', '4'), ('4', '5', '6', '*', '4'), ('1', '2', '3', '-', '4'), ('0', '.', '=', '+', '4') ) activeStr = '' stack = []
Вычисление результата
Функция calculate получает из списка stack операнды и операцию которую над ними надо произвести. Результат отображается в надписи label. Получать из списка строки будем с помощью метода pop.
def calculate():
global stack
global label
result = 0
operand2 = Decimal(stack.pop())
operation = stack.pop()
operand1 = Decimal(stack.pop())
if operation == '+':
result = operand1 + operand2
if operation == '-':
result = operand1 - operand2
if operation == '/':
result = operand1 / operand2
if operation == '*':
result = operand1 * operand2
label. configure(text=str(result))
configure(text=str(result))Обработка нажатия
В функции click выполняется обработка нажатой клавиши. В качестве ее аргумента передается текст, отображаемый на кнопке, которую нажали. Хотелось бы хранить вводимое значение прямо в надписи, а не создавать для этого отдельную переменную. Но так не получается из-за алгоритма работы. После того как посчитан результат, он записывается в надписи. При попытке после этого начать вводить новое число, оно бы дописывало прежний результат.
В списке с операторами и командами для калькулятора не обязательно их будет 3. Но при обработке с помощью метода pop, будут рассматриваться 3 последних введенных значения. А после проведения расчета список очистится. Далее в него добавляется полученный результат, на случай если пользователь нажмет на калькуляторе клавишу операции сразу, а не будет вводить новое число.
def click(text):
global activeStr
global stack
if text == 'CE':
stack. clear()
activeStr = ''
label.configure(text='0')
elif '0' <= text <= '9':
activeStr += text
label.configure(text=activeStr)
elif text == '.':
if activeStr.find('.') == -1:
activeStr += text
label.configure(text=activeStr)
else:
if len(stack) >= 2:
stack.append(label['text'])
calculate()
stack.clear()
stack.append(label['text'])
activeStr = ''
if text != '=':
stack.append(text)
else:
if text != '=':
stack.append(label['text'])
stack.append(text)
activeStr = ''
label.configure(text='0')
clear()
activeStr = ''
label.configure(text='0')
elif '0' <= text <= '9':
activeStr += text
label.configure(text=activeStr)
elif text == '.':
if activeStr.find('.') == -1:
activeStr += text
label.configure(text=activeStr)
else:
if len(stack) >= 2:
stack.append(label['text'])
calculate()
stack.clear()
stack.append(label['text'])
activeStr = ''
if text != '=':
stack.append(text)
else:
if text != '=':
stack.append(label['text'])
stack.append(text)
activeStr = ''
label.configure(text='0')Внешний вид
Теперь займемся оформлением внешнего вида калькулятора и зададим обработку нажатия кнопок. Создаем надпись для вывода набираемых значений и результатов. В цикле создаем кнопки. Расположение кнопок и надписи осуществляется в табличном виде с помощью упаковщика grid. И в завершении запускаем цикл обработки событий mainloop.
Создаем надпись для вывода набираемых значений и результатов. В цикле создаем кнопки. Расположение кнопок и надписи осуществляется в табличном виде с помощью упаковщика grid. И в завершении запускаем цикл обработки событий mainloop.
label = Label(root, text='0', width=35)
label.grid(row=0, column=0, columnspan=4, sticky="nsew")
button = Button(root, text='CE', command=lambda text='CE': click(text))
button.grid(row=1, column=3, sticky="nsew")
for row in range(4):
for col in range(4):
button = Button(root, text=buttons[row][col],
command=lambda row=row, col=col: click(buttons[row][col]))
button.grid(row=row + 2, column=col, sticky="nsew")
root.grid_rowconfigure(6, weight=1)
root.grid_columnconfigure(4, weight=1)
root.mainloop()У надписи выставлена ширина 35, для того, чтобы оформление кнопок подстраивалось под надпись. И в результате кнопки при этом значении лучше выглядят.
Для того, чтобы кнопки правильно работали, пришлось для каждой из кнопок создать свою функцию с помощью lambda.
По аналогии приведенного кода python калькулятора можно сдель, допустим, календарь. Для этого надо будет запрашивать текущую дату у операционной системы. Открывать нужный месяц, рассчитывать какие числа выпадут на понедельники, какой год високосный. Сделать возможность менять год и месяцы.
Калькулятор стандартной формы
Базовый калькулятор
Калькулятор стандартной формы
введите число для преобразования в стандартную форму
Операнд 1
Ответ:
Поделитесь этой ссылкой для ответа: help
Вставьте эту ссылку в электронное письмо, текст или социальные сети.
Получить виджет для этого калькулятора
© Calculator Soup
Поделитесь этим калькулятором и страницей
Калькулятор Использование
Найдите стандартную форму положительного или отрицательного числа с помощью калькулятора стандартной формы. Преобразование числового формата в стандартную форму в виде десятичной дроби, умноженной на степень 10.
Что такое стандартная форма
Стандартная форма — это способ написания числа, чтобы его было легче читать. Он часто используется для очень больших или очень маленьких чисел. Стандартная форма похожа на научную нотацию и обычно используется в науке и технике.
Число записывается в стандартной форме, когда оно представлено как десятичное число, умноженное на 10.
В качестве примера рассмотрим скорость света, которая движется со скоростью около 671 000 000 миль в час. В стандартной форме это число эквивалентно 6,71 x 10 9 . {б} \]
{б} \]
Где
- a — это число, абсолютное значение которого представляет собой десятичное число, большее или равное 1 и меньшее 10: \[ 1 \le \left\lvert a \right\rvert \lt 10 \]
- b — целое число и степень 10, необходимая для того, чтобы произведение умножения в стандартной форме равнялось исходному числу .
Как преобразовать число в стандартную форму
Стандартная форма номера: a x 10 b где a — число, 1 ≤ | и | < 10. b — степень числа 10, необходимая для того, чтобы стандартная форма была математически эквивалентна исходному числу.
- Перемещайте десятичную точку в вашем номере, пока не останется только одна ненулевая цифра слева от десятичной точки. Полученное десятичное число равно a .
- Подсчитайте, на сколько знаков вы передвинули десятичную точку.
 Это число b .
Это число b .- Если вы переместите десятичную запятую влево b будет положительным.
- Если вы переместите десятичную дробь вправо b будет отрицательным.
- Если вам не нужно было перемещать десятичную дробь b = 0 .
- Напишите свой номер научной записи как a x 10 b и читать как « a умножить на 10 в степени b «.
- Удалять конечные 0, только если они стоят слева от десятичной точки.
Пример: преобразование 459 608 в стандартную форму
- Переместите запятую на 5 знаков влево, чтобы получить 4,59608
- а = 4,59608
- Мы переместили десятичную дробь влево, так что b положительно
- б = 5
- Число 459 608, преобразованное в стандартную форму, равно 4,59608 x 10 5
Пример: преобразование 0,000380 в стандартную форму
- Переместите десятичную дробь на 4 знака вправо и удалите ведущие нули, чтобы получить 3,80
- а = 3,80
- Мы переместили десятичную дробь вправо, так что b будет отрицательным
- б = -4
- Число 0,000380, преобразованное в стандартную форму, равно 3,80 x 10 -4
- Обратите внимание, что мы не удаляем завершающий 0, потому что изначально он был справа от десятичной дроби и, следовательно, является значащей цифрой.

Дополнительные ресурсы
См. Калькулятор научной нотации для сложения, вычитания, умножения и деления чисел в научной нотации или E-нотации.
Для округления значащих цифр используйте Калькулятор значимых цифр.
Если вам нужен научный калькулятор, см. наши ресурсы на научные калькуляторы.
Подписаться на калькуляторSoup:
Калькулятор стандартных форм (конвертер): Расчет стандартных обозначений.
Калькулятор стандартной формы
Калькулятор стандартной формы используется для преобразования чисел в стандартную форму путем подстановки десятичного значения в число. Он преобразует длинное число в легко читаемую стандартную форму.
Это калькулятор стандартной формы, который берет число от пользователя и преобразует его в стандартную форму.
В этом содержании мы объясним, что такое стандартная форма, как использовать наш калькулятор стандартной формы, а также как рассчитать стандартную форму.
Как использовать калькулятор стандартной формы?
Чтобы использовать этот калькулятор стандартных обозначений , , выполните следующие действия:
- Введите число в данное поле ввода.
- Нажмите кнопку Вычислить , чтобы увидеть результат.
- Вы можете сбросить значения с помощью Сброс
Этот калькулятор уравнений стандартной формы мгновенно покажет вам преобразованную стандартную форму данного числа. Вы также можете использовать наш калькулятор научных обозначений и преобразователь научных обозначений для расчета научных обозначений.
Что такое стандартная форма?
Если вам интересно, что такое стандартная форма в математике , вы в правильном месте.
Стандартная форма используется для облегчения чтения очень больших или очень маленьких чисел. Стандартная форма числа — это любое число от 1,0 до 10,0, умноженное на степень 10. Например, 1,2× 10 2
Стандартная форма числа — это любое число от 1,0 до 10,0, умноженное на степень 10. Например, 1,2× 10 2
Для демонстрации стандартной формы взгляните на следующие примеры:
Число: 85500000000000
Стандартная форма: 8,55 × 10 13
Номер: 0,000458912
Стандартная форма: 4,58 × 10 -4
Как писать в стандартной форме?
Вы можете использовать наш калькулятор преобразования в стандартную форму, чтобы вычислить стандартную форму любого числа. Однако мы объясним, как можно преобразовать число в стандартную форму вручную. Чтобы преобразовать число в стандартную форму, выполните следующие действия:
- Запишите число.
- Определите десятичную точку в числе. Если в заданном числе нет десятичной точки, то считается, что оно находится справа от числа после последней цифры.
- После определения десятичной точки переместите десятичную запятую к первой ненулевой цифре в числе.

4. Подсчитайте общее количество цифр, на которые вы переместили десятичную точку. Умножьте число на 10 и возведите степень 10 на общее количество перемещенных десятичных цифр. Если десятичная дробь перемещается справа налево, степень будет положительной, а если десятичная дробь перемещается слева направо, степень будет отрицательной.
Пример:
Преобразовать 0,0009 в стандартную форму.
Решение:
Следуйте инструкциям, чтобы найти стандартную форму данного числа.
Шаг 1 : Запишите число.
0,0009
Шаг 2 : Определите десятичную точку в числе. Вы можете видеть, что десятичная точка лежит после 4 цифр с левой стороны.
Шаг 3 : После определения десятичной точки переместите десятичную запятую на первая ненулевая цифра в номере.
Оно станет 9.

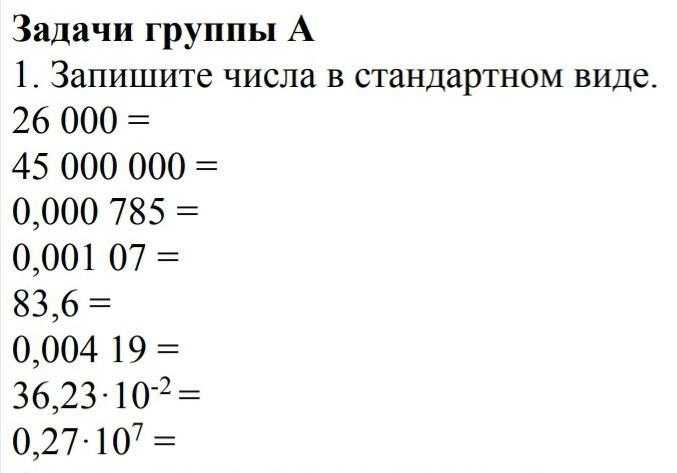 title('Calculator')
buttons = (('7', '8', '9', '/', '4'),
('4', '5', '6', '*', '4'),
('1', '2', '3', '-', '4'),
('0', '.', '=', '+', '4')
)
activeStr = ''
stack = []
title('Calculator')
buttons = (('7', '8', '9', '/', '4'),
('4', '5', '6', '*', '4'),
('1', '2', '3', '-', '4'),
('0', '.', '=', '+', '4')
)
activeStr = ''
stack = [] configure(text=str(result))
configure(text=str(result)) clear()
activeStr = ''
label.configure(text='0')
elif '0' <= text <= '9':
activeStr += text
label.configure(text=activeStr)
elif text == '.':
if activeStr.find('.') == -1:
activeStr += text
label.configure(text=activeStr)
else:
if len(stack) >= 2:
stack.append(label['text'])
calculate()
stack.clear()
stack.append(label['text'])
activeStr = ''
if text != '=':
stack.append(text)
else:
if text != '=':
stack.append(label['text'])
stack.append(text)
activeStr = ''
label.configure(text='0')
clear()
activeStr = ''
label.configure(text='0')
elif '0' <= text <= '9':
activeStr += text
label.configure(text=activeStr)
elif text == '.':
if activeStr.find('.') == -1:
activeStr += text
label.configure(text=activeStr)
else:
if len(stack) >= 2:
stack.append(label['text'])
calculate()
stack.clear()
stack.append(label['text'])
activeStr = ''
if text != '=':
stack.append(text)
else:
if text != '=':
stack.append(label['text'])
stack.append(text)
activeStr = ''
label.configure(text='0') Это число b .
Это число b .
