10 класс. Алгебра. Тригонометрические функции. Функции у=sinx, y=cosx, их свойства, графики, типовые задачи. — Функция y=cosx, ее основные свойства, график и типовые задачи.
Комментарии преподавателяФункция y=cost, её свойства, график и типовые задачи
На прошлом уроке мы построили график функции, осуществив сдвиг кривой на влево, и рассмотрели свойства функции Сейчас мы детализируем эти свойства и применим их к решению важнейших типовых задач.
Рассмотрим поведение функции и отметим важнейшие точки на промежутке
В координатной плоскости (рис. 1).
На числовой окружности (рис. 2).
Сформулируем основные особенности функции при
1. Функция монотонно убывает от до
2. Функция принимает все значения из отрезка
3. Каждое свое значение функция принимает при единственном значении аргумента (следует из монотонности функции).
Задача 1. Найти пределы изменения функции на данном отрезке.
1)
Рис. 3.
На заданном отрезке функция монотонно убывает, значит, наименьшее значение принимает на правом конце.
Ответ:
2)
Рис. 4.
Функция монотонно убывает.
Ответ:
3)
Рис. 5.
На данном промежутке функция немонотонна.
Ответ:
Монотонность функции означает, что не только каждому значению аргумента соответствует единственное значение функции, но и обратное – каждое значение функции достигается при единственном значении аргумента.
Например:
Если единственное решение на промежутке
Если
Сколько решений имеет уравнение на промежутке Одно, также в силу монотонности.
Задача 2. Найти все значения параметра при каждом из которых уравнение имеет хотя бы одно решение:
1)
2)
Решение:
1) Построим график функции (рис.
6).
Уравнение имеет хотя бы одно решение при
В данном случае множество значений параметра совпадает со множеством значений функции.
Ответ:
2) Решим другим способом, используя область значений функции
Ответ:
Задача 3. Решить уравнение
Решение:
Построим в одних координатных осях графики функций (рис. 7).
Графики имеют только одну общую точку
Решим уравнение еще одним способом.
Ответ:
Задача 4. Найти число корней уравнения
Решение (рис. 8).
На промежутке функция монотонно возрастает, функция монотонно убывает. Это значит, что на данном промежутке графики имеют только одну общую точку.
На промежутке функция убывает, функция возрастает, значит, и на этом промежутке графики также имеют только одну общую точку.
Ответ: Два корня.
Мы рассмотрели и детализировали свойства функции и использовали их при решении задач.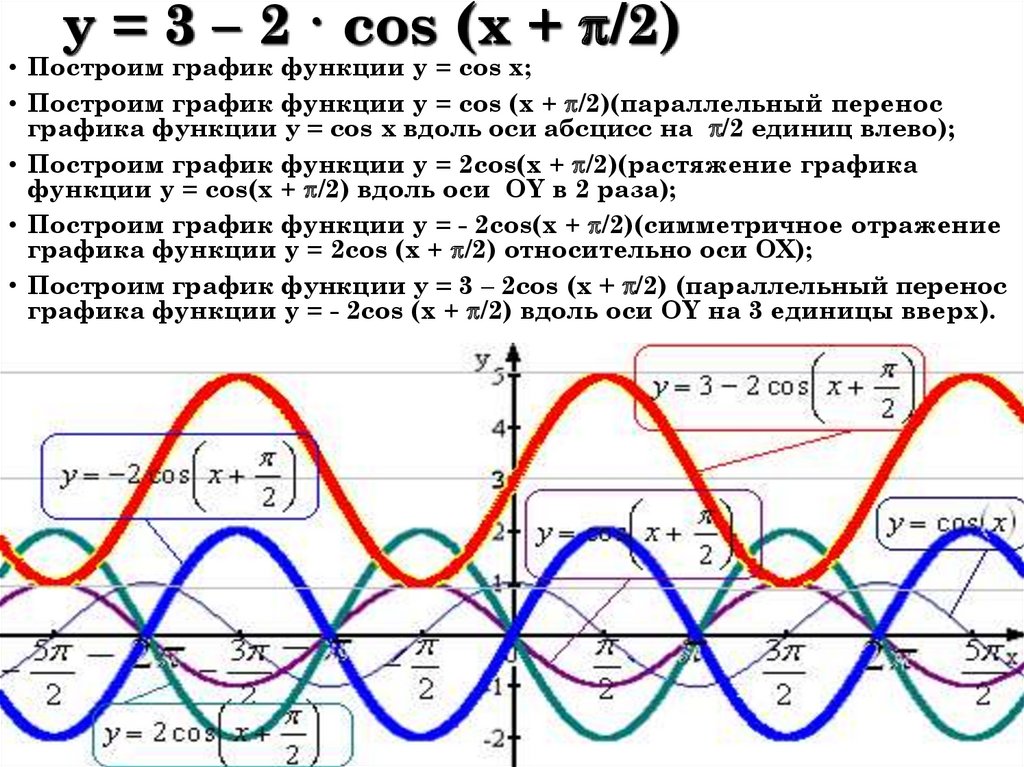
В дальнейшем рассмотренные свойства будут неоднократно использоваться.
ИСТОЧНИК
http://interneturok.ru/ru/school/algebra/10-klass/trigonometricheskie-funkcii/funktsiya-y-cos-t-eyo-svoystva-grafik-i-tipovye-zadachi
http://www.youtube.com/watch?v=RAib0ZZBTEg
http://www.youtube.com/watch?v=BTcC6Gw3T1U
http://11book.ru/images/shcoolbook_ru/10/10_a_mord_baz.pdf
http://vklasse.org/10-klass/reshebniki/algebra/ag-mordkovich-2009-zadachnik/glava-2-trigonometricheskie-funktsii/11-funktsiya-ucos-x-ee-svojstva-i-grafik/13
http://www.yaklass.ru/p/algebra/10-klass/trigonometricheskie-funktcii-10781/svoistva-funktcii-y-cosx-i-ee-grafik-10783/re-25f9a2dd-12ec-4034-b283-f0a0973c4f52
http://rpp.nashaucheba.ru/pars_docs/refs/47/46657/img7.jpg
Повторяем и систематизируем школьный курс алгебры и начал анализа
Повторяем и систематизируем школьный курс алгебры и начал анализа
ОглавлениеПРЕДИСЛОВИЕГЛАВА I. § 1. НАТУРАЛЬНЫЕ ЧИСЛА И ДЕЙСТВИЯ НАД НИМИ § 2. СЛОЖЕНИЕ И ЗАКОНЫ СЛОЖЕНИЯ § 4. УМНОЖЕНИЕ И ЗАКОНЫ УМНОЖЕНИЯ § 5. ДЕЛЕНИЕ § 6. ПРИЗНАКИ ДЕЛИМОСТИ ЧИСЕЛ § 7. ПОНЯТИЕ МНОЖЕСТВА § 8. ОПЕРАЦИИ НАД МНОЖЕСТВАМИ § 9. ВЗАИМНО ОДНОЗНАЧНОЕ СООТВЕТСТВИЕ § 10. ПРОСТЫЕ И СОСТАВНЫЕ ЧИСЛА § 11. НАИБОЛЬШИЙ ОБЩИЙ ДЕЛИТЕЛЬ § 12. НАИМЕНЬШЕЕ ОБЩЕЕ КРАТНОЕ Контрольные вопросы ГЛАВА II § 1. ОБЫКНОВЕННЫЕ ДРОБИ § 2.  ПРАВИЛЬНЫЕ И НЕПРАВИЛЬНЫЕ ДРОБИ§ 3. ОСНОВНОЕ СВОЙСТВО ДРОБИ § 4. СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДРОБЕЙ § 5. УМНОЖЕНИЕ ДРОБЕЙ § 6. ДЕЛЕНИЕ ДРОБЕЙ § 7. ДЕСЯТИЧНЫЕ ДРОБИ § 8. ОБРАЩЕНИЕ ДЕСЯТИЧНОЙ ДРОБИ В ОБЫКНОВЕННУЮ И ОБЫКНОВЕННОЙ В ДЕСЯТИЧНУЮ. ПЕРИОДИЧЕСКИЕ ДРОБИ § 9. ОТНОШЕНИЕ. ПРОПОРЦИЯ § 10. СВОЙСТВА ПРОПОРЦИИ § 11. ПРОЦЕНТ. ОСНОВНЫЕ ЗАДАЧИ НА ПРОЦЕНТЫ § 12. ДЕЛЕНИЕ ЧИСЛА НА ЧАСТИ, ПРЯМО И ОБРАТНО ПРОПОРЦИОНАЛЬНЫЕ ДАННЫМ ЧИСЛАМ Контрольные вопросы ГЛАВА III § 1. КООРДИНАТНАЯ ПРЯМАЯ § 2. МНОЖЕСТВО ЦЕЛЫХ ЧИСЕЛ § 3. МНОЖЕСТВО РАЦИОНАЛЬНЫХ ЧИСЕЛ § 4. МОДУЛЬ ЧИСЛА § 5. СРАВНЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ § 6. СЛОЖЕНИЕ И ВЫЧИТАНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ § 7. УМНОЖЕНИЕ И ДЕЛЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ § 8. ВОЗВЕДЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ В СТЕПЕНЬ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ Контрольные вопросы ГЛАВА IV § 1. СВОЙСТВА СТЕПЕНИ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ § 2. ЧИСЛОВЫЕ ВЫРАЖЕНИЯ § 3. ВЫРАЖЕНИЯ С ПЕРЕМЕННЫМИ § 4. ТОЖДЕСТВЕННО РАВНЫЕ ВЫРАЖЕНИЯ § 5.  ОДНОЧЛЕНЫ§ 6. МНОГОЧЛЕНЫ § 7. ПРЕОБРАЗОВАНИЕ СУММЫ И РАЗНОСТИ МНОГОЧЛЕНОВ § 8. УМНОЖЕНИЕ МНОГОЧЛЕНА НА ОДНОЧЛЕН И МНОГОЧЛЕНА НА МНОГОЧЛЕН § 9. РАЗЛОЖЕНИЕ МНОГОЧЛЕНА НА МНОЖИТЕЛИ СПОСОБОМ ВЫНЕСЕНИЯ ОБЩЕГО МНОЖИТЕЛЯ ЗА СКОБКИ § 10. РАЗЛОЖЕНИЕ МНОГОЧЛЕНА НА МНОЖИТЕЛИ СПОСОБОМ ГРУППИРОВКИ § 11. ФОРМУЛЫ СОКРАЩЕННОГО УМНОЖЕНИЯ Контрольные вопросы ГЛАВА V § 2. ЦЕЛЫЕ И ДРОБНЫЕ ВЫРАЖЕНИЯ § 3. ТОЖДЕСТВЕННОЕ ПРЕОБРАЗОВАНИЕ СУММЫ И РАЗНОСТИ ДВУХ ДРОБЕЙ § 4. ТОЖДЕСТВЕННОЕ ПРЕОБРАЗОВАНИЕ ПРОИЗВЕДЕНИЯ И ЧАСТНОГО ДВУХ ДРОБЕЙ § 5. СТЕПЕНЬ ДРОБИ Контрольные вопросы ГЛАВА VI § 1. ПОНЯТИЕ ОБ ИРРАЦИОНАЛЬНОМ ЧИСЛЕ § 2. РАЗВИТИЕ ПОНЯТИЯ О ЧИСЛЕ. МНОЖЕСТВО ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ § 3. КОРЕНЬ СТЕПЕНИ ИЗ ДЕЙСТВИТЕЛЬНОГО ЧИСЛА § 4. АЛГОРИТМ ИЗВЛЕЧЕНИЯ КВАДРАТНОГО КОРНЯ ИЗ ЧИСЛА § 5. АРИФМЕТИЧЕСКИЕ ДЕЙСТВИЯ С ДЕЙСТВИТЕЛЬНЫМИ ЧИСЛАМИ § 6. ПРЕОБРАЗОВАНИЯ АРИФМЕТИЧЕСКИХ КОРНЕЙ § 7. СТЕПЕНЬ С ЦЕЛЫМ И ДРОБНЫМ ПОКАЗАТЕЛЕМ Контрольные вопросы ГЛАВА VII § 1.  УРАВНЕНИЯ С ОДНОЙ ПЕРЕМЕННОЙ§ 2. ПОНЯТИЕ О РАВНОСИЛЬНОСТИ УРАВНЕНИЙ § 3. СВОЙСТВА ЧИСЛОВЫХ РАВЕНСТВ И ТЕОРЕМЫ О РАВНОСИЛЬНОСТИ УРАВНЕНИЙ § 4. ЛИНЕЙНОЕ УРАВНЕНИЕ С ОДНОЙ ПЕРЕМЕННОЙ, СОДЕРЖАЩЕЕ ПАРАМЕТР Контрольные вопросы ГЛАВА VIII § 1. ПОНЯТИЕ ФУНКЦИИ § 2. СПОСОБЫ ЗАДАНИЯ ФУНКЦИИ § 3. МОНОТОННОСТЬ ФУНКЦИИ § 4. ЧЕТНЫЕ И НЕЧЕТНЫЕ ФУНКЦИИ СПРАВОЧНЫЙ МАТЕРИАЛ § 5. ПЕРИОДИЧЕСКИЕ ФУНКЦИИ § 6. ПРОМЕЖУТКИ ЗНАКОПОСТОЯНСТВА И КОРНИ ФУНКЦИИ Контрольные вопросы ГЛАВА IX § 1. ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ ГРАФИКОВ ФУНКЦИЙ § 2. ЛИНЕЙНАЯ ФУНКЦИЯ И ЕЕ ГРАФИК § 3. КВАДРАТИЧНАЯ ФУНКЦИЯ И ЕЕ ГРАФИК § 4. ФУНКЦИЯ y=k/x И ЕЕ ГРАФИК § 5. ДРОБНО-ЛИНЕЙНАЯ ФУНКЦИЯ И ЕЕ ГРАФИК Контрольные вопросы ГЛАВА X § 1. КВАДРАТНЫЕ УРАВНЕНИЯ § 2. ТЕОРЕМА ВИЕТА § 3. ГРАФИЧЕСКИЙ СПОСОБ РЕШЕНИЯ КВАДРАТНЫХ УРАВНЕНИЙ § 4. УРАВНЕНИЕ СО МНОГИМИ ПЕРЕМЕННЫМИ § 5. СИСТЕМЫ УРАВНЕНИЙ Контрольные вопросы ГЛАВА XI § 1. НЕРАВЕНСТВА § 2.  ОСНОВНЫЕ СВОЙСТВА НЕРАВЕНСТВ§ 3. ДЕЙСТВИЯ С НЕРАВЕНСТВАМИ § 4. ДОКАЗАТЕЛЬСТВА НЕРАВЕНСТВ § 5. НЕРАВЕНСТВА, СОДЕРЖАЩИЕ ПЕРЕМЕННУЮ Контрольные вопросы ГЛАВА XII § 1. СИСТЕМЫ И СОВОКУПНОСТИ НЕРАВЕНСТВ § 2. НЕРАВЕНСТВА И СИСТЕМЫ НЕРАВЕНСТВ С ДВУМЯ ПЕРЕМЕННЫМИ § 3. РЕШЕНИЕ НЕРАВЕНСТВ, СОДЕРЖАЩИХ ПЕРЕМЕННУЮ ПОД ЗНАКОМ МОДУЛЯ § 4. РЕШЕНИЕ РАЦИОНАЛЬНЫХ НЕРАВЕНСТВ МЕТОДОМ ПРОМЕЖУТКОВ Контрольные вопросы ГЛАВА XIII § 1. ЧИСЛОВАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ § 2. АРИФМЕТИЧЕСКАЯ ПРОГРЕССИЯ § 3. ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИЯ § 4. СУММА БЕСКОНЕЧНОЙ ГЕОМЕТРИЧЕСКОЙ ПРОГРЕССИИ ПРИ |q|Контрольные вопросы ГЛАВА XIV § 1. ГРАДУСНОЕ ИЗМЕРЕНИЕ УГЛОВЫХ ВЕЛИЧИН § 2. РАДИАННОЕ ИЗМЕРЕНИЕ УГЛОВЫХ ВЕЛИЧИН § 3. СИНУС И КОСИНУС ЧИСЛОВОГО АРГУМЕНТА § 4. ТАНГЕНС И КОТАНГЕНС ЧИСЛОВОГО АРГУМЕНТА. СЕКАНС И КОСЕКАНС ЧИСЛА а § 5. ОСНОВНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ТОЖДЕСТВА § 6. ДОПОЛНИТЕЛЬНЫЕ СВОЙСТВА ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ Контрольные вопросы ГЛАВА XV § 1.  ФОРМУЛЫ ПРИВЕДЕНИЯ§ 2. ФОРМУЛЫ СЛОЖЕНИЯ § 3. ФОРМУЛЫ ДВОЙНОГО УГЛА СПРАВОЧНЫЙ МАТЕРИАЛ § 4. ПРЕОБРАЗОВАНИЕ ПРОИЗВЕДЕНИЯ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ В СУММУ § 5. ФОРМУЛЫ СУММЫ И РАЗНОСТИ ОДНОИМЕННЫХ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ § 6. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ ПОЛОВИННОГО АРГУМЕНТА § 7. ВЫРАЖЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ ЧЕРЕЗ ТАНГЕНС ПОЛОВИННОГО АРГУМЕНТА Контрольные вопросы ГЛАВА XVI § 1. СВОЙСТВА ФУНКЦИИ y = sin(x) И ЕЕ ГРАФИК § 2. СВОЙСТВА ФУНКЦИ И у = cos(x) И ЕЕ ГРАФИК § 3. СВОЙСТВА ФУНКЦИ И у=tg(x) И ЕЕ ГРАФИК § 4. СВОЙСТВА ФУНКЦИ И y=ctg(x) И ЕЕ ГРАФИК § 5. НАХОЖДЕНИЕ ПЕРИОДОВ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ Контрольные вопросы ГЛАВА XVII § 1. АРКСИНУС И АРККОСИНУС § 2. АРКТАНГЕНС И АРККОТАНГЕНС Контрольные вопросы ГЛАВА XVIII § 1. РЕШЕНИЕ УРАВНЕНИЙ ВИДА cos(x)=а § 2. РЕШЕНИЕ УРАВНЕНИЙ ВИДА sin(x)=a § 3. РЕШЕНИЕ УРАВНЕНИЙ ВИДА tg(х)=а § 4. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ, ПРИВОДИМЫХ К КВАДРАТНОМУ  РЕШЕНИЕ ОДНОРОДНЫХ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ§ 6. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ, РЕШАЕМЫЕ С ПОМОЩЬЮ ФОРМУЛ СЛОЖЕНИЯ, ПОНИЖЕНИЯ СТЕПЕНИ § 7. РЕШЕНИЕ СИСТЕМ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ Контрольные вопросы ГЛАВА XIX § 1. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ВИДА sin(х) > а, sin(х) § 2. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ВИДА cos(x) > a, cos(x) § 3. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ВИДА tg(х) > a, tg(х) § 4. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ГЛАВА XX § 1. ПРИРАЩЕНИЕ АРГУМЕНТА И ПРИРАЩЕНИЕ ФУНКЦИИ § 2. ПРЕДЕЛ ФУНКЦИИ § 3. НЕПРЕРЫВНОСТЬ ФУНКЦИИ § 4. ОПРЕДЕЛЕНИЕ ПРОИЗВОДНОЙ § 5. ПРОИЗВОДНАЯ СУММЫ, ПРОИЗВЕДЕНИЯ, ЧАСТНОГО § 6. ПРОИЗВОДНАЯ СТЕПЕННОЙ И СЛОЖНОЙ ФУНКЦИИ § 7. ПРОИЗВОДНЫЕ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ Контрольные вопросы ГЛАВА XXI § 1. ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ К НАХОЖДЕНИЮ ПРОМЕЖУТКОВ МОНОТОННОСТИ ФУНКЦИИ § 2. КРИТИЧЕСКИЕ ТОЧКИ ФУНКЦИИ, ЕЕ МАКСИМУМЫ И МИНИМУМЫ § 3. ОБЩАЯ СХЕМА ИССЛЕДОВАНИЯ ФУНКЦИИ § 4.  ЗАДАЧИ НА НАХОЖДЕНИЕ НАИМЕНЬШЕГО И НАИБОЛЬШЕГО ЗНАЧЕНИЯ ФУНКЦИИКонтрольные вопросы ГЛАВА XXII § 1. ФОРМУЛЫ ПРИБЛИЖЕННЫХ ВЫЧИСЛЕНИЙ СПРАВОЧНЫЙ МАТЕРИАЛ § 2. КАСАТЕЛЬНАЯ К ГРАФИКУ ФУНКЦИИ § 3. СКОРОСТЬ И УСКОРЕНИЕ В ДАННЫЙ МОМЕНТ ВРЕМЕНИ § 4. ГРАФИКИ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ Контрольные вопросы ГЛАВА XXIII § 1. ПОТЕРЯННЫЕ И ПОСТОРОННИЕ КОРНИ ПРИ РЕШЕНИИ УРАВНЕНИЙ (НА ПРИМЕРАХ) § 2. ПОСТОРОННИЕ КОРНИ ИРРАЦИОНАЛЬНОГО УРАВНЕНИЯ (НА ПРИМЕРАХ) § 3. РЕШЕНИЕ ИРРАЦИОНАЛЬНЫХ УРАВНЕНИЙ § 4. РЕШЕНИЕ ИРРАЦИОНАЛЬНЫХ НЕРАВЕНСТВ СПРАВОЧНЫЙ МАТЕРИАЛ Контрольные вопросы ГЛАВА XXIV § 1. ПОКАЗАТЕЛЬНАЯ ФУНКЦИЯ, ЕЕ СВОЙСТВА И ГРАФИК § 2. ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ § 3. ПОКАЗАТЕЛЬНЫЕ НЕРАВЕНСТВА § 4. СИСТЕМЫ ПОКАЗАТЕЛЬНЫХ УРАВНЕНИЙ И НЕРАВЕНСТВ ГЛАВА XXV § 1. ОБРАТНАЯ ФУНКЦИЯ § 2. ПОНЯТИЕ ЛОГАРИФМА § 3. СВОЙСТВА ЛОГАРИФМОВ § 4. ЛОГАРИФМИЧЕСКАЯ ФУНКЦИЯ, ЕЕ СВОЙСТВА И ГРАФИК § 5. ТЕОРЕМЫ О ЛОГАРИФМЕ ПРОИЗВЕДЕНИЯ, ЧАСТНОГО И СТЕПЕНИ. 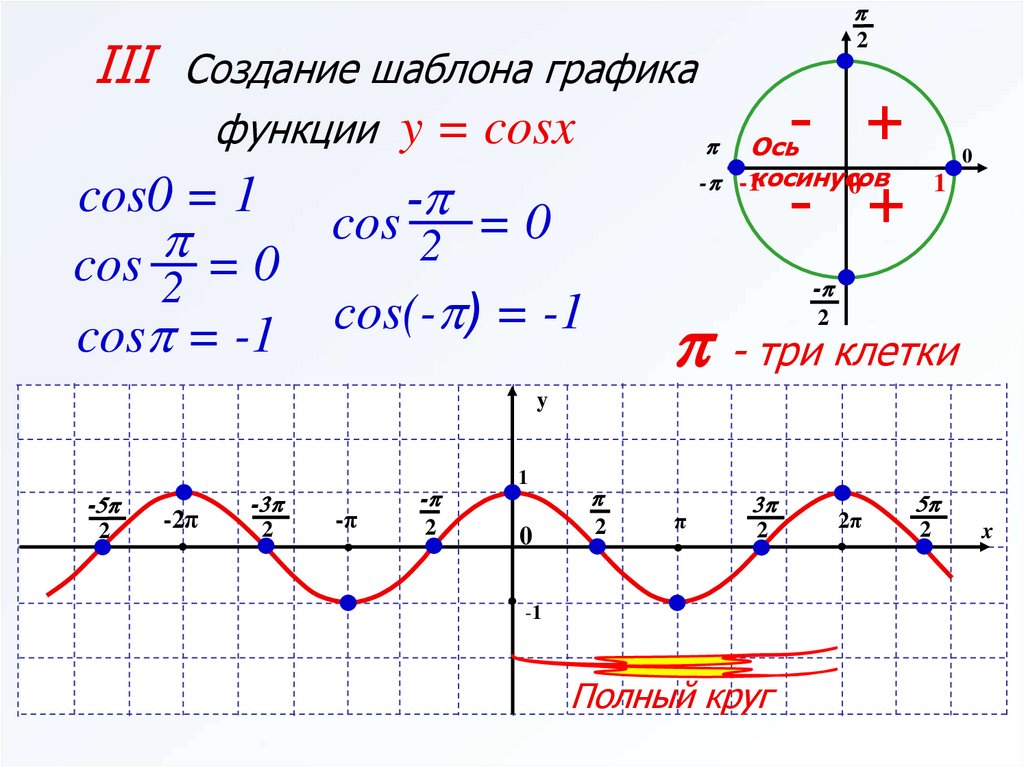 ФОРМУЛА ПЕРЕХОДА К НОВОМУ ОСНОВАНИЮ§ 6. ДЕСЯТИЧНЫЕ ЛОГАРИФМЫ И ИХ СВОЙСТВА § 7. ЛОГАРИФМИРОВАНИЕ И ПОТЕНЦИРОВАНИЕ Контрольные вопросы ГЛАВА XXVI § 1. ЛОГАРИФМИЧЕСКИЕ УРАВНЕНИЯ § 2. ЛОГАРИФМИЧЕСКИЕ НЕРАВЕНСТВА § 3. СИСТЕМЫ ЛОГАРИФМИЧЕСКИХ УРАВНЕНИЙ И НЕРАВЕНСТВ § 4. ПРОИЗВОДНЫЕ ЛОГАРИФМИЧЕСКОЙ И ПОКАЗАТЕЛЬНОЙ ФУНКЦИЙ. ЧИСЛО e Контрольные вопросы ГЛАВА XXVII § 1. ПОНЯТИЕ ПЕРВООБРАЗНОЙ ФУНКЦИИ § 2. ОСНОВНОЕ СВОЙСТВО ПЕРВООБРАЗНОЙ ФУНКЦИИ § 3. ТРИ ПРАВИЛА НАХОЖДЕНИЯ ПЕРВООБРАЗНЫХ § 4. КРИВОЛИНЕЙНАЯ ТРАПЕЦИЯ И ЕЕ ПЛОЩАДЬ Контрольные вопросы ГЛАВА XXVIII § 1. ФОРМУЛА НЬЮТОНА—ЛЕЙБНИЦА § 2. ОСНОВНЫЕ ПРАВИЛА ИНТЕГРИРОВАНИЯ § 3. ВЫЧИСЛЕНИЕ ПЛОЩАДЕЙ С ПОМОЩЬЮ ИНТЕГРАЛА § 4. МЕХАНИЧЕСКИЕ И ФИЗИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА ПРИЛОЖЕНИЕ Введение 1. Задачи на движение 2. Задачи на совместную работу 3. Задачи на планирование 4. Задачи на зависимость между компонентами арифметических действий 5.  Задачи на проценты6. Задачи на смеси (сплавы) 7. Задачи на разбавление |
С. Повторяем и систематизируем школьный курс алгебры и начал анализа.—М.: Просвещение, 1990.— 416 с.
Периодические и симметричные функции
Длина окружности единичного круга C = 2π r = 2π(1) = 2π. Следовательно, если точка P проходит по единичной окружности на расстоянии 2π, она оказывается там же, где и началась. Другими словами, для любого заданного значения q при добавлении или вычитании 2π координаты точки
Рисунок 1
Периодические котерминальные углы.
Отсюда следует, что
Если k является целым числом,
Функции, обладающие этим свойством, называются периодическими функциями . Функция f является периодической, если существует положительное действительное число q такое, что f ( x + q ) = f ( x ) для всех 903 x 900 в области x 900.
ф . Наименьшее возможное значение для q , для которых это верно, называется периодом f .
Пример 1: Если sin y = y = (3/5)/10, то каково значение каждого из следующих: sin( y + 8π), sin( y + 6π ), ( y + 210π)?
Все три имеют одинаковое значение, потому что функция синуса является периодической и имеет период 2π.
Изучение периодических свойств круговых функций приводит к решению многих реальных проблем. Эти проблемы включают движение планет, звуковые волны, генерацию электрического тока, волны землетрясений и приливы.
Пример 2: График на рисунке 2 представляет функцию f с периодом 4. Как будет выглядеть график для интервала −10 ⩽ x ⩽ 10?
Рисунок 2
Чертеж для примера 2.
Этот график охватывает интервал в 4 единицы. Поскольку период равен 4, этот график представляет один полный цикл функции.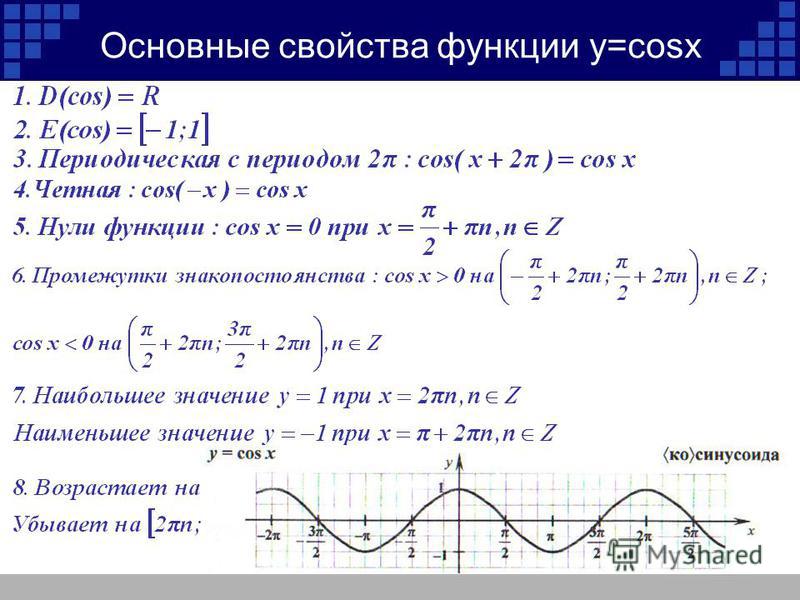
Поэтому просто скопируйте сегмент графика слева и справа (рис. 3 ).
Рисунок 3
Чертеж для примера 2.
Внешний вид графика функции и свойства этой функции очень тесно связаны. Из рисунка 4 видно, что
Косинус известен как четная функция , а синус известен как нечетная функция . Вообще говоря,
для каждого значения x в области g . Некоторые функции нечетные, некоторые четные, а некоторые нечетные и нечетные.
Если функция четная , то график функции будет симметричен оси y . Альтернативно, для каждой точки на графике точка (− x , − y ) также будет на графике.
Если функция нечетная , то график функции будет симметричен относительно начала координат. В качестве альтернативы, для каждой точки ( x , y ) на графике точка (− x , − y ) также будет на графике.
Пример 3: Постройте график нескольких функций и укажите их периоды (рис. 5).
Рисунок 5
Чертежи для примера 3.
Пример 4 : Постройте график нескольких нечетных функций и укажите их периоды (рис. 6).
Рисунок 6
Результаты, например 4.
Пример 5: Является ли функция f(x) = 2 x 3 + x четной, нечетной или ни одной?
Поскольку f(−x) = − f(x) , функция нечетная.
Пример 6: Является функцией f(x) = sin x – cos x четное, нечетное или ни то, ни другое?
функция не является ни четной, ни нечетной. Примечание. Сумма нечетной функции и четной функции не является ни четной, ни нечетной.
Пример 7: Является ли функция f ( x ) = x sin x cos x четной, нечетной или ни одной?
Поскольку f (− x ) = f ( x ), функция четная.
Калькулятор косинуса | cos(x)
Калькулятор косинуса
cos(x):
Результат:
| 0 |
Что такое cos?
Косинус (или косинус) — тригонометрическая функция. В прямоугольном треугольнике cos угла x определяется как отношение стороны, прилежащей к углу, к его гипотенузе.
$$cos\, x = {соседний \по гипотенузе}$$
Рассмотрим прямоугольный треугольник ниже.
В этом треугольнике прямой угол лежит в точке B. Мы хотим найти косинус x. Сторона, примыкающая к углу х, равна ВС, а гипотенуза — АС. Следовательно,
$$cos\, x\, =\, {соседний \над гипотенузой} \,=\,{BC\над AC}$$
Свойства функции косинуса
Ниже приведены некоторые свойства функции cos.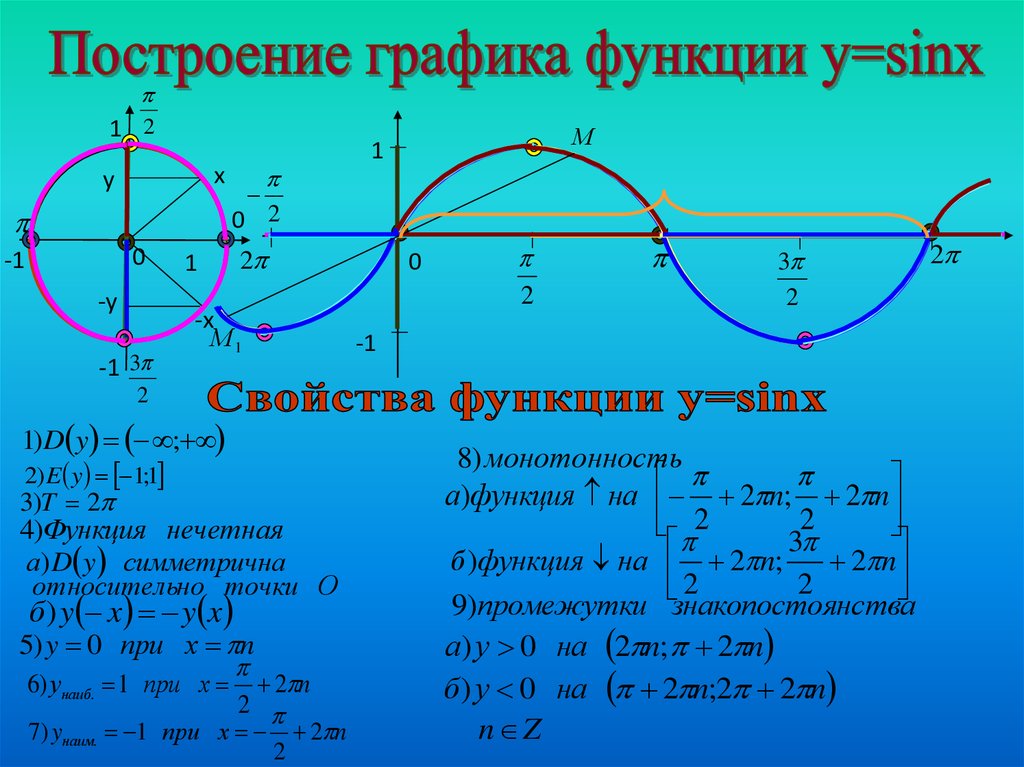
Угол — Обозначается переменной x или θ, это параметр, для которого рассчитывается значение cos.
Домен — значения угла x, для которых мы можем вычислить cos(x). Это значение изменяется от -инфинитива до +инфинитива.
Диапазон – Значения, между которыми лежит cos(x) любого угла x. Это значение равно -1≤ cos(x) ≤1.
Период – Горизонтальная длина одного полного цикла функции cos. Период для cos(x) составляет 2π радиан или 360⁰.
Ниже приведен график функции косинуса.
Как и функция sin, функция cos также является периодической по своей природе с периодом 2π радиан (или 360⁰). Это означает, что график повторяется каждые 2π радиан. На приведенном выше графике ось x обозначает угол, а ось y обозначает cos этого угла.
Из графика видно, что cos(x) начинается с +1, затем падает до -1. Оттуда снова идет вверх. Он достигает значения +1 при 2π радианах и -1 при π радианах.
Единственная разница между синусом и графиком cos заключается в том, что график синуса начинается с 0 при 0⁰, тогда как график cos имеет значение +1 при 0⁰.
Значения cos(x)
Ниже приведены некоторые часто используемые значения cos(x).
| Угол x в градусах | Угол x в радианах | кос(х) |
|---|---|---|
| 0 | 0 | 0 |
| 30 | $$π\over6$$ | $$√3\over2$$ |
| 45 | $$π\over4$$ | $$1\over√2$$ |
| 60 | $$π\over3$$ | $$1\over2$$ |
| 90 | $$π\over2$$ | 0 |
| 120 | $$2π\over3$$ | $$-1\over2$$ |
| 135 | $$3π\over4$$ | $$-1\over√2$$ |
| 150 | $$5π\over6$$ | $$-√3\over2$$ |
| 180 | № | -1 |
| 270 | $$3π\over2$$ | 0 |
| 360 | 2π | 1 |
Значение cos(x) может быть положительным или отрицательным, в зависимости от того, где находится угол x в четырех квадрантах.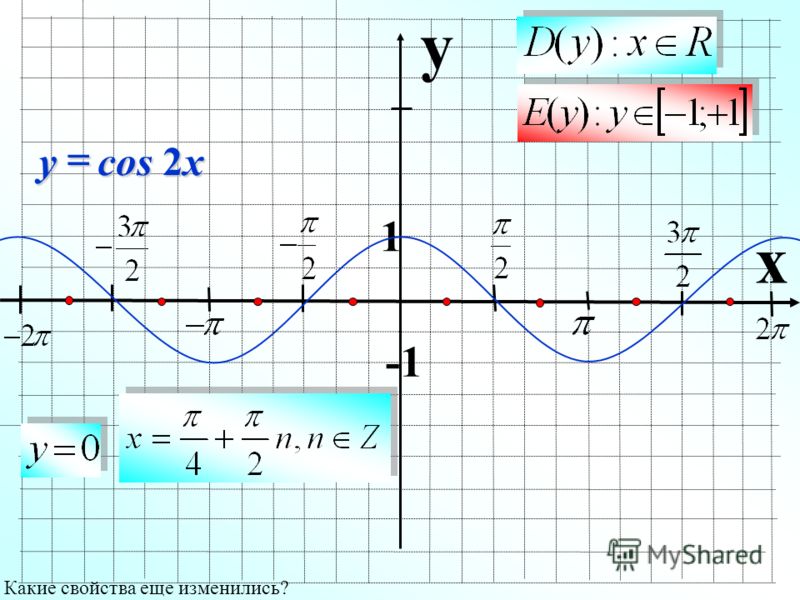
Например, cos 45⁰ положительный, а cos 135⁰ отрицательный. Это было проиллюстрировано ниже.
| Квадрант | x в градусах | х в радианах | Знак функции cos | Диапазон значений cos |
|---|---|---|---|---|
| 1 | от 0⁰ до 90⁰ | $$0\, до\, {π\over2}$$ | + | 0 |
| 2 | от 90⁰ до 180⁰ | $${π\over2}\, до\, π$$ | — | -1 |
| 3 | от 180⁰ до 270⁰ | $$π\, to\, {3π\over2}$$ | — | -1 |
| 4 | от 270⁰ до 360⁰ | $${3π\over2}\, до\, 2π$$ | + | 0 |
Если угол x не лежит в пределах от 0⁰ до 360⁰ (или от 0 до 2π радиан), его можно выразить как кратное, сумму или разность одного из указанных выше углов, а затем определить его значение cos. 98\over8!} — …$$
Чем больше членов, тем точнее аппроксимация.
Области применения
Тригонометрические функции, такие как функция синуса и косинуса, используются для описания простого гармонического движения, поскольку колебательное движение объекта представляет собой графики этих двух тригонометрических функций.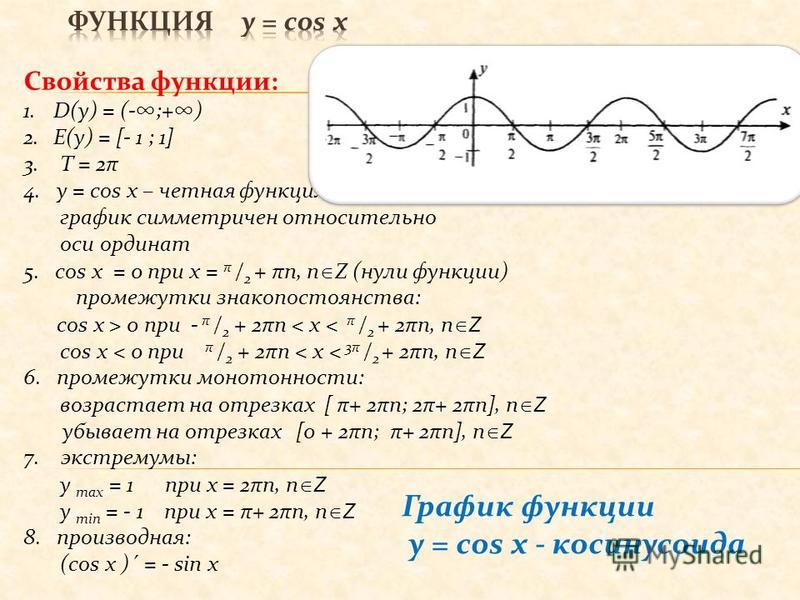
Когда объект совершает простое гармоническое движение, расстояние, пройденное объектом, выражается с помощью функций sin или cos. Функция cos и формулы, включающие ее, также часто используются для решения тригонометрических задач или доказательства тригонометрических тождеств.
В этом разделе мы рассмотрим несколько примеров задач, связанных с использованием функции cos.
Ответ: Эту проблему можно визуализировать следующим образом.
Лестница обозначена AC, длина 25 футов. Стена обозначается AB. Нам нужно найти расстояние между стеной и основанием лестницы, которое равно ВС.
Используя формулу cos, мы можем вычислить, как далеко стена находится от основания лестницы.
Следовательно, BC ≈ 17,68 фута.
Лестница находится почти в 17,68 футах от стены.