| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | sin(45 град. ) ) |
|
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) ) |
|
| 17 | Найти точное значение | sec(30 град. ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | ||
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень 3) | |
| 24 | Найти точное значение | csc(60 град.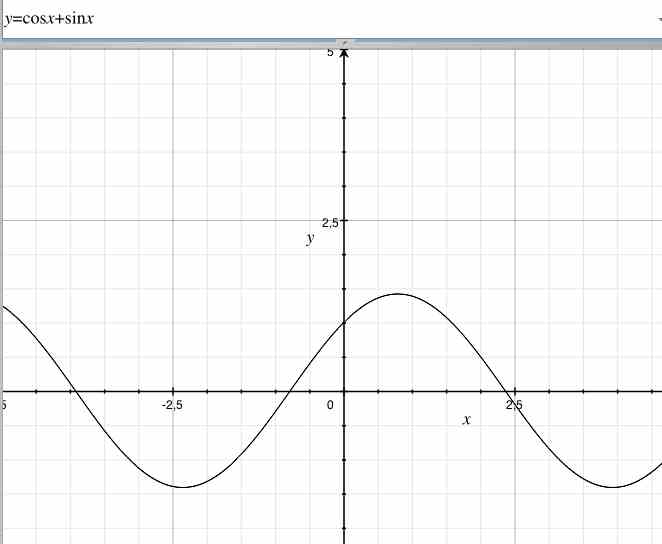 ) ) |
|
| 25 | Найти точное значение | sec(45 град. ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) ) |
|
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град.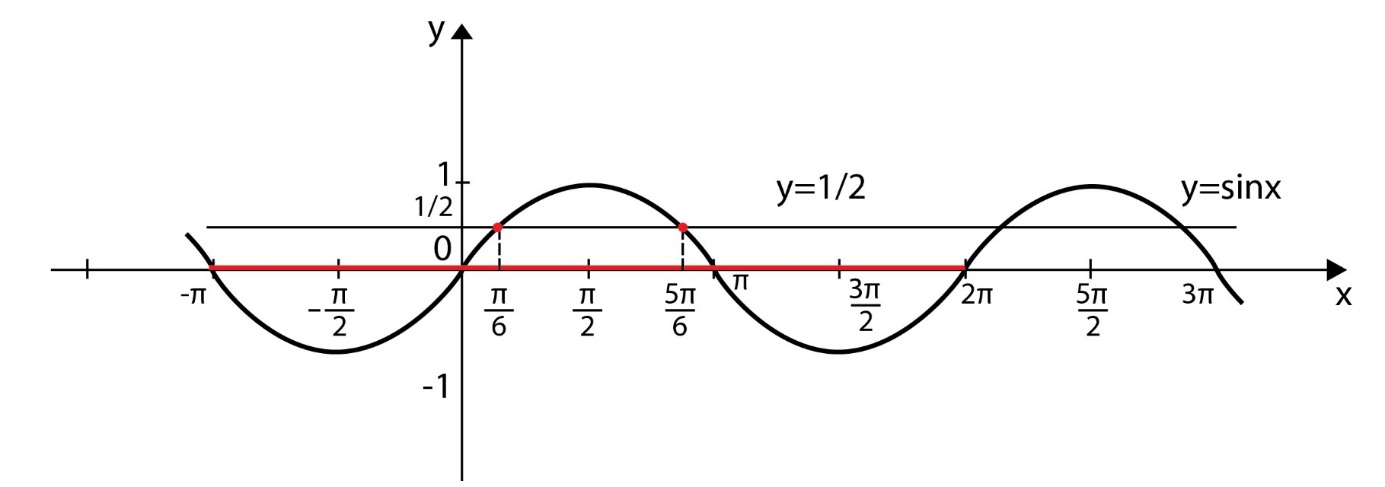 ) ) |
|
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) ) |
|
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) ) |
|
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) ) |
|
| 77 | Найти точное значение | arctan(-( квадратный корень 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) ) |
|
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град. ) ) |
|
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
y корень sinx найти область определения функции
Вы искали y корень sinx найти область определения функции? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное
решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и найти область определения функции y 1 корень sinx, не
исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.
Например, «y корень sinx найти область определения функции».
Подробное
решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и найти область определения функции y 1 корень sinx, не
исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.
Например, «y корень sinx найти область определения функции».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как y корень sinx найти область определения функции,найти область определения функции y 1 корень sinx,найти область определения функции y корень sinx. На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и y корень sinx найти область определения функции. Просто введите задачу в окошко и нажмите
«решить» здесь (например, найти область определения функции y корень sinx).
На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и y корень sinx найти область определения функции. Просто введите задачу в окошко и нажмите
«решить» здесь (например, найти область определения функции y корень sinx).
Где можно решить любую задачу по математике, а так же y корень sinx найти область определения функции Онлайн?
Решить задачу y корень sinx найти область определения функции вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
y sin x корень
Вы искали y sin x корень? На нашем сайте вы можете получить ответ на любой математический вопрос здесь.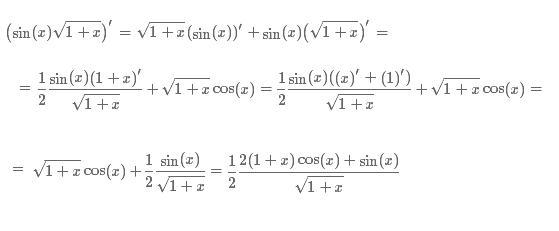 Подробное
решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и y sin корень x найти область определения функции, не
исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.
Например, «y sin x корень».
Подробное
решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и y sin корень x найти область определения функции, не
исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.
Например, «y sin x корень».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как y sin x корень,y sin корень x найти область определения функции,y sin корень из x,y корень sin x,y корень sin корень x область определения,найти область определения функции y sin корень x,найти область определения функции y корень sin x.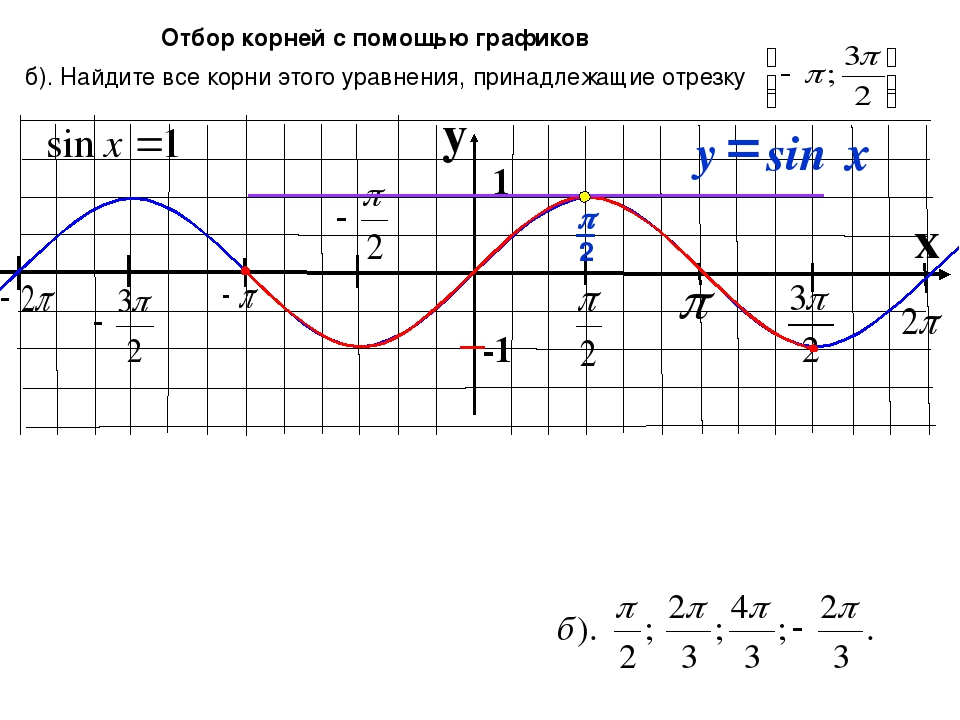 На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и y sin x корень. Просто введите задачу в окошко и нажмите
«решить» здесь (например, y sin корень из x).
На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и y sin x корень. Просто введите задачу в окошко и нажмите
«решить» здесь (например, y sin корень из x).
Где можно решить любую задачу по математике, а так же y sin x корень Онлайн?
Решить задачу y sin x корень вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Область допустимых значений — ОДЗ (ЕГЭ — 2021)
Давай разберем пример, наглядно показывающий, что такое ОДЗ:
Решим уравнение \( \displaystyle \sqrt{2x+3}=x\). {2}}-2{x}-3=0\).
{2}}-2{x}-3=0\).
Теперь решаем квадратное уравнение. Я воспользуюсь теоремой Виета (если забыл, что это такое, – посмотри тему «Квадратные уравнения»).
Получаем корни:
\( \displaystyle \left[ \begin{array}{l}x=3\\x=-1\end{array} \right.\)
Вроде все? А давай-ка теперь сделаем проверку – подставим полученные значения в начальное уравнение:
\( \displaystyle x=3:\text{ }\sqrt{2\cdot 3+3}=3\text{ }\Leftrightarrow \text{ }\sqrt{9}=3\) – все верно.
\( \displaystyle x=-1:\text{ }\sqrt{2\cdot \left( -1 \right)+3}=-1\text{ }\Leftrightarrow \text{ }\sqrt{1}=-1\) – неверно! А все почему?
Да потому, что мы не учли ОДЗ!
По определению квадратный корень из любого числа не может быть отрицательным.
Значит, глядя на уравнение \( \displaystyle \sqrt{2x+3}=x\) мы должны сразу же написать:
\( \displaystyle \left\{ \begin{array}{l}x\ge 0;\\2x+3\ge 0.\end{array} \right.\)
Если помнишь тему «Иррациональные уравнения», ты сразу скажешь, что второе условие в этой системе писать необязательно. {2}}\), а значит – автоматически неотрицательно.
{2}}\), а значит – автоматически неотрицательно.
Итак, с помощью этих рассуждений приходим к такой области допустимых значений:
\( \displaystyle x\ge 0\).
Тогда сразу становится ясно, что корень \( \displaystyle x=-1\) не подходит. И остается единственный ответ \( \displaystyle x=3\).
Всего мы изучаем несколько разных функций, для которых важна ОДЗ. Вот они со своими ОДЗ в удобной табличке:
Тригонометрические функции
Область определения и множество значений тригонометрических функций
Каждому действительному числу x соответствует единственная точка единичной окружности, получаемая поворотом точки (1;0) на угол x радиан. Для этого угла определены sin x и cos x. Тем самым каждому действительному числу x поставлены в соответствие числа sin x и cos x, т.е. на множестве R всех действительных чисел определены функции
y = sin x и y = cos x Таким образом, областью определения функций y = sin x и y = cos x является множество R всех действительных чисел.
Чтобы найти множество значений функции y = sin x, нужно выяснить, какие значения может принимать y при различных значениях x, т.е. установить, для каких значений y есть такие значения x, при которых sin x = y. Известно, что уравнение sin x = a имеет корни, если |a| ≤ 1, и не имеет корней, если |a| > 1. Следовательно, множеством значений функции y = sin x является отрезок -1 ≤ y ≤ 1. Аналогично множеством значений функции y = cos x также является отрезок -1 ≤ y ≤ 1.
Функция y = tg x определяется формулой y = tg x = sin x/cos x. Эта функция определена при тех значениях x, для которых cos x ≠ 0 Известно, что cos x = 0 при x = π/2 + πn, n Є Z.
Следовательно, областью определения функции y = tg x является множество чисел x ≠ π/2 + πn, n Є Z.
Так как уравнение tg x = a имеет корни при любом действительном значении a, то множеством значений функции y = tg x является множество R всех действительных чисел.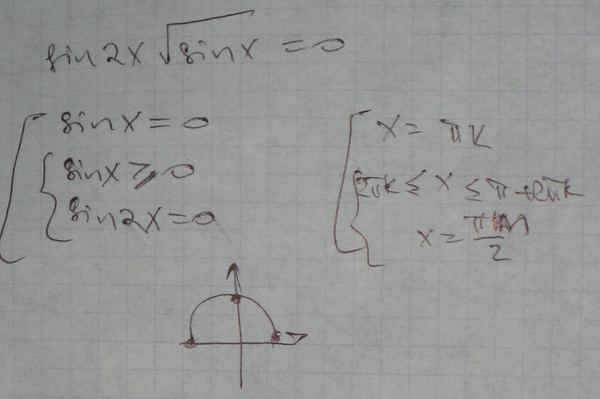
Функции y = sin x, y = cos x, y = tg x называют тригонометрическими функциями.
Четность, нечетность, периодичность тригонометрических функций
Известно, что для любого значение x верны равенства
sin (-x) = -sin x, cos (-x) = cos x Следовательно, y = sin x — нечетная функция, а y = cos x — чётная функция. Так как для любого значения x из области определения функции y = tg x верно равенство tg (-x) = -tg x, то y = tg x — нечетная функция.Известно, что для любого значения x верны равенства
sin (x + 2π) = sin x, cos (x + 2π) = cos x. Из этих равенств следует, что значения синуса и косинуса периодически повторяются при изменении аргумента на 2π. Такие функции называются периодическими с периодом 2π. Функция f (x) называется периодической, если существует такое число T ≠ 0, что для любого x из области определения этой функции выполняется равенство f (x — T) = f (x) = f (x + T).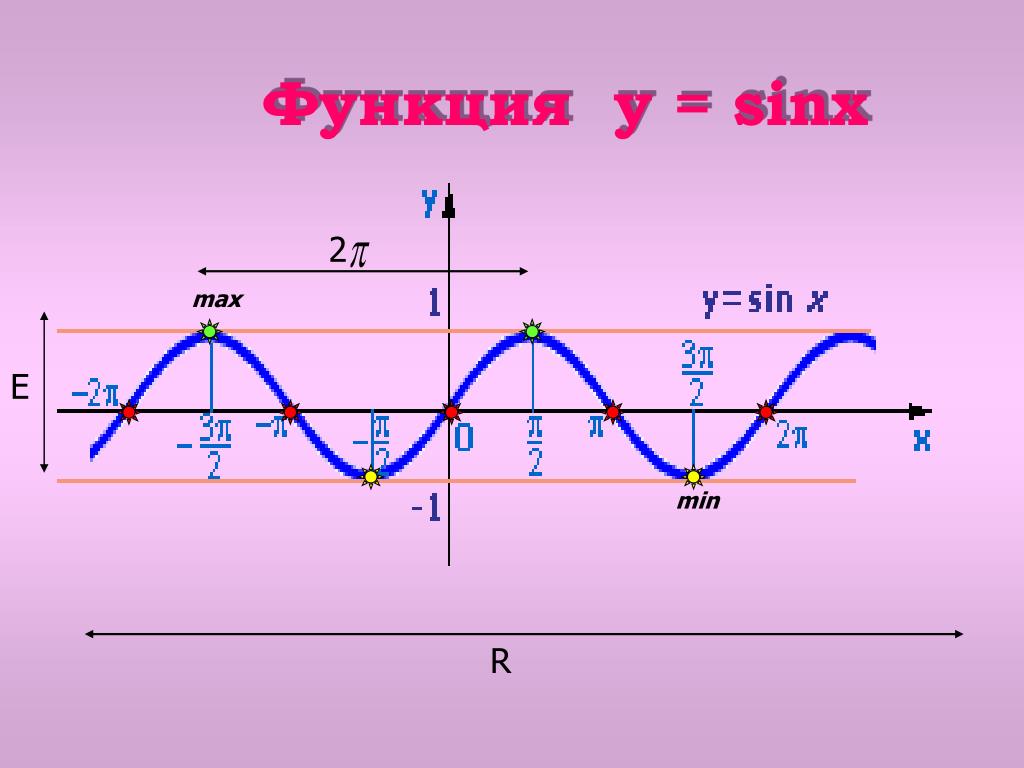 Число T называется периодом функции f (x).
Из этого определения следует, что если x принадлежит области определения функции f (x), то числа x + T, x — T и вообще числа x + Tn, n Є Z, также принадлежат области определения этой периодической функции и f (x + Tn) = f (x), n Є Z
Число T называется периодом функции f (x).
Из этого определения следует, что если x принадлежит области определения функции f (x), то числа x + T, x — T и вообще числа x + Tn, n Є Z, также принадлежат области определения этой периодической функции и f (x + Tn) = f (x), n Є Z
Число 2π является наименьшим положительным периодом функции y = cos x, также и для функции y = sin x. π — наименьший положительный период функции tg x.
Другие заметки по алгебре и геометрии
| Функция | Описание | Пример ввода | Результат ввода |
|---|---|---|---|
| pi | Число \(\pi\) | pi | $$ \pi $$ |
| e | Число \(e\) | e | $$ e $$ |
| e^x | Степень числа \(e\) | e^(2x) | $$ e^{2x} $$ |
| exp(x) | Степень числа \(e\) | exp(1/3) | $$ \sqrt[3]{e} $$ |
| |x| abs(x) |
Модуль (абсолютное значение) числа \(x\) | |x-1| abs(cos(x)) |
\( |x-1| \) \( |\cos(x)| \) |
| sin(x) | Синус | sin(x-1) | $$ sin(x-1) $$ |
| cos(x) | Косинус | 1/(cos(x))^2 | $$ \frac{1}{cos^2(x)} $$ |
| tg(x) | Тангенс | x*tg(x) | $$ x \cdot tg(x) $$ |
| ctg(x) | Котангенс | 3ctg(1/x) | $$ 3 ctg \left( \frac{1}{x} \right) $$ |
| arcsin(x) | Арксинус | arcsin(x) | $$ arcsin(x) $$ |
| arccos(x) | Арккосинус | arccos(x) | $$ arccos(x) $$ |
| arctg(x) | Арктангенс | arctg(x) | $$ arctg(x) $$ |
| arcctg(x) | Арккотангенс | arcctg(x) | $$ arcctg(x) $$ |
| sqrt(x) | Квадратный корень | sqrt(1/x) | $$ \sqrt{\frac{1}{x}} $$ |
| root(n,x) | Корень степени n root(2,x) эквивалентно sqrt(x) |
root(4,exp(x)) | $$ \sqrt[4]{ e^{x} } $$ |
| x^(1/n) | Корень степени n x^(1/2) эквивалентно sqrt(x) |
(cos(x))^(1/3) | $$ \sqrt[\Large 3 \normalsize]{cos(x)} $$ |
| ln(x) log(x) log(e,x) |
Натуральный логарифм (основание — число e) |
1/ln(3-x) | $$ \frac{1}{ln(3-x)} $$ |
| log(10,x) | Десятичный логарифм числа x | log(10,x^2+x) | $$ log_{10}(x^2+x) $$ |
| log(a,x) | Логарифм x по основанию a | log(3,cos(x)) | $$ log_3(cos(x)) $$ |
| sh(x) | Гиперболический синус | sh(x-1) | $$ sh(x-1) $$ |
| ch(x) | Гиперболический косинус | ch(x) | $$ ch(x) $$ |
| th(x) | Гиперболический тангенс | th(x) | $$ th(x) $$ |
| cth(x) | Гиперболический котангенс | cth(x) | $$ cth(x) $$ |
| Вывод | Перевод, пояснение | ||
| Solve for x over the real numbers | Решить относительно х в действительных числах (бывают ещё комплексные) | ||
| Multiply both sides by … | Умножаем обе части на … | ||
| Equate exponents of … on both sides | Приравниваем степени … в обоих частях (с обоих сторон) | ||
| Simplify and substitute … | Упрощаем и делаем подстановку … | ||
| Bring … together using the commom denominator … | Приводим … к общему знаменателю … | ||
| The left hand side factors into a product with two terms | Левая часть разбивается на множители как два многочлена | ||
| Split into two equations | Разделяем на два уравнения | ||
| Take the square root of both sides | Извлекаем квадратный корень из обоих частей | ||
Subtract .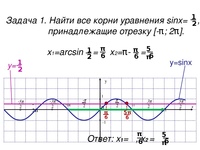 {-x}} \) {-x}} \) | |||
| \(coth(x)\) | Гиперболический котангенс. У нас пишут \(cth(x) = \frac{1}{th(x)} \) |
Простейшие тригонометрические уравнения
Простейшими тригонометрическими уравнениями называют уравнения
Cos (x) = a, sin (x) = a, tg (x) = a, ctg (x) =a
Уравнение cos (x) = a
Объяснение и обоснование
- Корни уравнения cosx = а. При | a | > 1 уравнение не имеет корней, поскольку | cosx | < 1 для любого x (прямая y = а при а > 1 или при а < -1 не пересекает график функцииy = cosx).
Пусть | а | < 1. Тогда прямая у = а пересекает график функции
у = cos х. На промежутке [0; п] функция y = cos x убывает от 1 до -1. Но убывающая функция принимает каждое свое значение только в одной точке ее области определения, поэтому уравнение cos x = а имеет на этом промежутке только один корень, который по определению арккосинуса равен: x1 = arccos а (и для этого корня cos x = а).
Косинус — четная функция, поэтому на промежутке [-п; 0] уравнение cos x = а также имеет только один корень — число, противоположное x1, то есть
x2 = -arccos а.
Таким образом, на промежутке [-п; п] (длиной 2п) уравнение cos x = а при | а | < 1 имеет только корни x = ±arccos а.
Функция y = cos x периодическая с периодом 2п, поэтому все остальные корни отличаются от найденных на 2пп (n € Z). Получаем следующую формулу корней уравнения cos x = а при
| а | < 1:
x = ±arccos а + 2пп, n £ Z.
- Частные случаи решения уравнения cosx = а.
Полезно помнить специальные записи корней уравнения cos x = а при
а = 0, а = -1, а = 1, которые можно легко получить, используя как ориентир единичную окружность.
Поскольку косинус равен абсциссе соответствующей точки единичной окружности, получаем, что cos x = 0 тогда и только тогда, когда соответствующей точкой единичной окружности является точка A или точка B.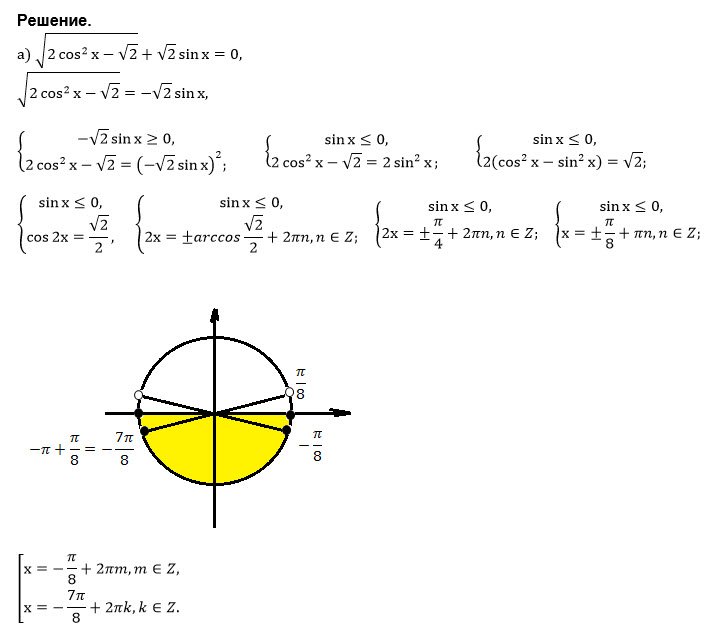
Аналогично cos x = 1 тогда и только тогда, когда соответствующей точкой единичной окружности является точка C, следовательно,
x = 2πп, k € Z.
Также cos х = —1 тогда и только тогда, когда соответствующей точкой единичной окружности является точка D, таким образом, х = п + 2пn,
k € Z.
Примеры
Уравнение sin (x) = a
Объяснение и обоснование
- Корни уравнения sinx = а. При | а | > 1 уравнение не имеет корней, поскольку | sinx | < 1 для любого x (прямая y = а на рисунке при а > 1 или при а < -1 не пересекает график функции y = sinx).
Если y = √sinx, найти dy / dx
В этой производной задаче задано, что $ y = \ sqrt {\ sin {x}} $. Итак, дифференцирование квадратного корня из $ \ sin {x} $ по $ x $ необходимо вычислить, чтобы найти производную $ y $ по $ x $. Это можно сделать двумя разными способами.
Метод дифференциации
Мы знаем, что $ y = \ sqrt {\ sin {x}} $, и берем производную с обеих сторон для нахождения дифференцирования $ y $ по $ x $.
$ \ подразумевает $ $ \ dfrac {d} {dx} {\, y} $ $ \, = \, $ $ \ dfrac {d} {dx} {\, \ sqrt {\ sin {x}}} $
$ \ подразумевает $ $ \ dfrac {dy} {dx} $ $ \, = \, $ $ \ dfrac {d} {dx} {\, \ sqrt {\ sin {x}}} $
В дифференциальном исчислении нет прямой формулы для нахождения производной квадратного корня из функции $ \ sin {x} $.Функция $ \ sqrt {\ sin {x}} $ представляет собой композицию двух функций $ \ sqrt {x} $ и $ \ sin {x} $. Следовательно, дифференцирование $ \ sqrt {\ sin {x}} $ можно вычислить по цепному правилу.
Возьмем $ u = \ sin {x} $, затем $ \ dfrac {d} {dx} {\, u} = \ dfrac {d} {dx} {\, \ sin {x}} $ согласно производной от Формула sinx. Следовательно, $ \ dfrac {du} {dx} = \ cos {x} $
$ \ подразумевает $ $ \ dfrac {dy} {dx} $ $ \, = \, $ $ \ dfrac {d} {dx} {\, \ sqrt {u}} $
Правую часть уравнения можно записать следующим образом согласно правилу цепочки.
$ \ подразумевает $ $ \ dfrac {dy} {dx} $ $ \, = \, $ $ \ dfrac {du} {dx} \ times \ dfrac {d} {du} {\, \ sqrt {u}} $
Вычислено примерно, что $ \ dfrac {du} {dx} = \ cos {x} $
$ \ подразумевает $ $ \ dfrac {dy} {dx} $ $ \, = \, $ $ \ cos {x} \ times \ dfrac {d} {du} {\, \ sqrt {u}} $
Теперь найдите производную квадратного корня из $ u $ по $ u $ по производной формулы квадратного корня.
$ \ подразумевает $ $ \ dfrac {dy} {dx} $ $ \, = \, $ $ \ cos {x} \ times \ dfrac {1} {2 \ sqrt {u}} $
$ \ подразумевает $ $ \ dfrac {dy} {dx} $ $ \, = \, $ $ \ dfrac {\ cos {x}} {2 \ sqrt {u}} $
На самом деле, в этом примере $ u = \ sin {x} $.Итак, замените $ u $ его фактическим значением.
$ \, \, \, \ следовательно \, \, \, \, \, \, $ \ dfrac {dy} {dx} $ $ \, = \, $ $ \ dfrac {\ cos {x}} {2 \ sqrt {\ sin {x}}}
долл. СШАМетод пределов
Производная квадратного корня из $ \ sin {x} $ по $ x $ может быть вычислена из первого принципа. Согласно определению производной, дифференцирование $ \ sqrt {\ sin {x}} $ можно записать в предельной форме.
Возьмем $ y = f {(x)} $. Итак, $ f {(x)} = \ sqrt {\ sin {x}} $, тогда $ f {(x + \ Delta x)} = \ sqrt {\ sin {(x + \ Delta x)}} $
.$ \ dfrac {d} {dx} {\, f {(x)}} $ $ \, = \, $ $ \ displaystyle \ large \ lim _ {\ Delta x \, \ to \, 0} {\ normalsize \ dfrac {f {(x + \ Delta x)} — f {(x)}} {\ Delta x}}
долл. США
США$ \ подразумевает $ $ \ dfrac {dy} {dx} $ $ \, = \, $ $ \ dfrac {d} {dx} {\, f {(x)}} $ $ \, = \, $ $ \ displaystyle \ large \ lim _ {\ Delta x \, \ to \, 0} {\ normalsize \ dfrac {f {(x + \ Delta x)} — f {(x)}} {\ Delta x}} $
$ \ подразумевает $ $ \ dfrac {dy} {dx} $ $ \, = \, $ $ \ displaystyle \ large \ lim _ {\ Delta x \, \ to \, 0} {\ normalsize \ dfrac {\ sqrt { \ sin {(x + \ Delta x)}} — \ sqrt {\ sin {x}}} {\ Delta x}}
долл. СШАВозьмите $ h = \ Delta x $ и выразите выражение через $ h $.
$ \ подразумевает $ $ \ dfrac {dy} {dx} $ $ \, = \, $ $ \ displaystyle \ large \ lim_ {h \, \ to \, 0} {\ normalsize \ dfrac {\ sqrt {\ sin {(x + h)}} — \ sqrt {\ sin {x}}} {h}}
долл. СШАПопробуйте метод прямой замены
Попробуем вычислить дифференцирование квадратного корня из функции $ \ sin {x} $, вычислив предел тригонометрической функции методом прямой подстановки.
$ \ подразумевает $ $ \ dfrac {dy} {dx} $ $ \, = \, $ $ \ dfrac {\ sqrt {\ sin {(x + 0)}} — \ sqrt {\ sin {x}}} {0}
долл.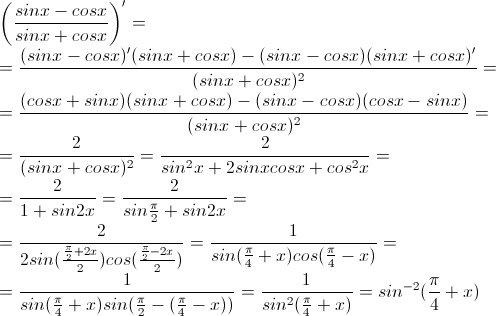 США
США$ \ подразумевает $ $ \ dfrac {dy} {dx} $ $ \, = \, $ $ \ dfrac {\ sqrt {\ sin {x}} — \ sqrt {\ sin {x}}} {0} $
$ \ подразумевает $ $ \ dfrac {dy} {dx} $ $ \, = \, $ $ \ dfrac {0} {0} $
вычислено, что производная от $ \ sqrt {\ sin {x}} $ по $ x $ не определена.Таким образом, невозможно найти производную, оценивая предел методом прямой подстановки.
Использовать метод рационализации
Теперь попробуйте вычислить предел тригонометрической функции методом рационализации, чтобы найти производную функции $ \ sqrt {\ sin {x}} $ по $ x $.
$ \ подразумевает $ $ \ dfrac {dy} {dx} $ $ \, = \, $ $ \ displaystyle \ large \ lim_ {h \, \ to \, 0} {\ normalsize \ Bigg [\ dfrac {\ sqrt {\ sin {(x + h)}} — \ sqrt {\ sin {x}}} {h}} $ $ \ times $ 1 \ Bigg] $
$ \ подразумевает $ $ \ dfrac {dy} {dx} $ $ \, = \, $ $ \ displaystyle \ large \ lim_ {h \, \ to \, 0} {\ normalsize \ Bigg [\ dfrac {\ sqrt {\ sin {(x + h)}} — \ sqrt {\ sin {x}}} {h}} $ $ \ times $ $ \ dfrac {\ sqrt {\ sin {(x + h)}} + \ sqrt {\ sin {x}}} {\ sqrt {\ sin {(x + h)}} + \ sqrt {\ sin {x}}} \ Bigg] $
.
$ \ подразумевает $ $ \ dfrac {dy} {dx} $ $ \, = \, $ $ \ displaystyle \ large \ lim_ {h \, \ to \, 0} {\ normalsize \ Bigg [\ dfrac {\ Big (\ sqrt {\ sin {(x + h)}} — \ sqrt {\ sin {x}} \ Big) \ times \ Big (\ sqrt {\ sin {(x + h)}} + \ sqrt {\ sin {x}} \ Big)} {h \ times {\ Big (\ sqrt {\ sin {(x + h)}} + \ sqrt {\ sin {x}} \ Big)}} \ Bigg]} $
Числитель представляет собой специальное произведение биномов, и их произведение может быть записано по формуле разности квадратов.2} {h \ times {\ Big (\ sqrt {\ sin {(x + h)}} + \ sqrt {\ sin {x}} \ Big)}} \ Bigg]} $
$ \ подразумевает $ $ \ dfrac {dy} {dx} $ $ \, = \, $ $ \ displaystyle \ large \ lim_ {h \, \ to \, 0} {\ normalsize \ Bigg [\ dfrac {\ sin {(x + h)} — \ sin {x}} {h \ times {\ Big (\ sqrt {\ sin {(x + h)}} + \ sqrt {\ sin {x}} \ Big)}} \ Bigg]}
долл. СШАИспользуйте тригонометрическую идентичность преобразования произведения для объединения функций синуса в числителе.
$ \ подразумевает $ $ \ dfrac {dy} {dx} $ $ \, = \, $ $ \ displaystyle \ large \ lim_ {h \, \ to \, 0} {\ normalsize \ Bigg [\ dfrac {2 \ cos {\ Bigg (\ dfrac {x + h + x} {2} \ Bigg)} \ sin {\ Bigg (\ dfrac {x + hx} {2} \ Bigg)}} {h \ times {\ Big ( \ sqrt {\ sin {(x + h)}} + \ sqrt {\ sin {x}} \ Big)}} \ Bigg]}
долл. США
США$ \ подразумевает $ $ \ dfrac {dy} {dx} $ $ \, = \, $ $ \ require {cancel} \ displaystyle \ large \ lim_ {h \, \ to \, 0} {\ normalsize \ Bigg [ \ dfrac {2 \ cos {\ Bigg (\ dfrac {2x + h} {2} \ Bigg)} \ sin {\ Bigg (\ dfrac {\ cancel {x} + h- \ cancel {x}} {2} \ Bigg)}} {h \ times {\ Big (\ sqrt {\ sin {(x + h)}} + \ sqrt {\ sin {x}} \ Big)}} \ Bigg]} $
$ \ подразумевает $ $ \ dfrac {dy} {dx} $ $ \, = \, $ $ \ displaystyle \ large \ lim_ {h \, \ to \, 0} {\ normalsize \ Bigg [\ dfrac {2 \ cos {\ Bigg (\ dfrac {2x + h} {2} \ Bigg)} \ sin {\ Bigg (\ dfrac {h} {2} \ Bigg)}} {h \ times {\ Big (\ sqrt {\ sin {(x + h)}} + \ sqrt {\ sin {x}} \ Big)}} \ Bigg]}
долл. СШАТеперь разложите функцию на множители как произведение двух тригонометрических функций следующим образом.
$ \ подразумевает $ $ \ dfrac {dy} {dx} $ $ \, = \, $ $ \ displaystyle \ large \ lim_ {h \, \ to \, 0} {\ normalsize \ Bigg [\ dfrac {\ cos {\ Bigg (\ dfrac {2x + h} {2} \ Bigg)} \ times 2 \ sin {\ Bigg (\ dfrac {h} {2} \ Bigg)}} {{\ Big (\ sqrt {\ sin {(x + h)}} + \ sqrt {\ sin {x}} \ Big)} \ times h} \ Bigg]}
долл.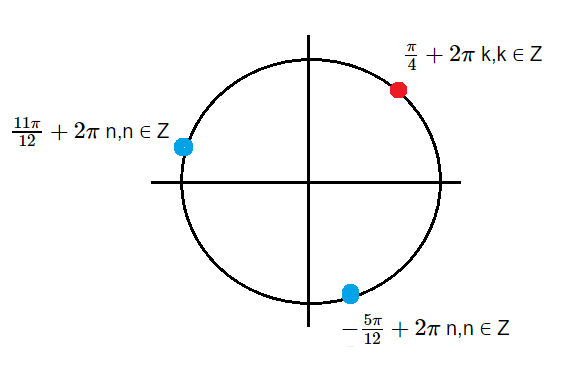 США
США$ \ подразумевает $ $ \ dfrac {dy} {dx} $ $ \, = \, $ $ \ displaystyle \ large \ lim_ {h \, \ to \, 0} {\ normalsize \ Bigg [\ Bigg (\ dfrac {\ cos {\ Bigg (\ dfrac {2x + h} {2} \ Bigg)}} {\ sqrt {\ sin {(x + h)}} + \ sqrt {\ sin {x}}} \ Bigg) \ times \ Bigg (\ dfrac {2 \ sin {\ Bigg (\ dfrac {h} {2} \ Bigg)}} {h} \ Bigg) \ Bigg]}
долл. СШАТеперь используйте правило пределов продукта, чтобы найти предел продукта на произведение их пределов.
$ \ подразумевает $ $ \ dfrac {dy} {dx} $ $ \, = \, $ $ \ Bigg (\ displaystyle \ large \ lim_ {h \, \ to \, 0} {\ normalsize \ dfrac {\ cos {\ Bigg (\ dfrac {2x + h} {2} \ Bigg)}} {\ sqrt {\ sin {(x + h)}} + \ sqrt {\ sin {x}}} \ Bigg)} $ \ раз $ $ \ Bigg (\ displaystyle \ large \ lim_ {h \, \ to \, 0} {\ normalsize \ dfrac {2 \ sin {\ Bigg (\ dfrac {h} {2} \ Bigg)}} { h} \ Bigg)}
долл. США$ \ подразумевает $ $ \ dfrac {dy} {dx} $ $ \, = \, $ $ \ Bigg (\ displaystyle \ large \ lim_ {h \, \ to \, 0} {\ normalsize \ dfrac {\ cos {\ Bigg (\ dfrac {2x + h} {2} \ Bigg)}} {\ sqrt {\ sin {(x + h)}} + \ sqrt {\ sin {x}}} \ Bigg)} $ \ раз $ $ \ Bigg (\ displaystyle \ large \ lim_ {h \, \ to \, 0} {\ normalsize \ dfrac {\ sin {\ Bigg (\ dfrac {h} {2} \ Bigg)}} {\ dfrac {h} {2}} \ Bigg)}
долл. США
США$ \ подразумевает $ $ \ dfrac {dy} {dx} $ $ \, = \, $ $ \ Bigg (\ displaystyle \ large \ lim_ {h \, \ to \, 0} {\ normalsize \ dfrac {\ cos {\ Bigg (\ dfrac {2x + h} {2} \ Bigg)}} {\ sqrt {\ sin {(x + h)}} + \ sqrt {\ sin {x}}} \ Bigg)} $ \ раз $ $ \ Bigg (\ displaystyle \ large \ lim _ {\ frac {h} {2} \, \ to \, 0} {\ normalsize \ dfrac {\ sin {\ Bigg (\ dfrac {h} {2}) \ Bigg)}} {\ dfrac {h} {2}} \ Bigg)}
долл. СШАВозьмите $ q = \ dfrac {h} {2} $ и замените $ \ dfrac {h} {2} $ на $ q $ только во втором множителе.
$ \ подразумевает $ $ \ dfrac {dy} {dx} $ $ \, = \, $ $ \ Bigg (\ displaystyle \ large \ lim_ {h \, \ to \, 0} {\ normalsize \ dfrac {\ cos {\ Bigg (\ dfrac {2x + h} {2} \ Bigg)}} {\ sqrt {\ sin {(x + h)}} + \ sqrt {\ sin {x}}} \ Bigg)} $ \ раз $ $ \ Bigg (\ displaystyle \ large \ lim_ {q \, \ to \, 0} {\ normalsize \ dfrac {\ sin {q}} {q} \ Bigg)} $
Оценить пределы функций
Найдите значение первого фактора, оценив предел тригонометрической функции методом прямой подстановки, а затем найдите значение второго фактора по пределу sinx / x, когда x приближается к 0 по формуле стандартной формы.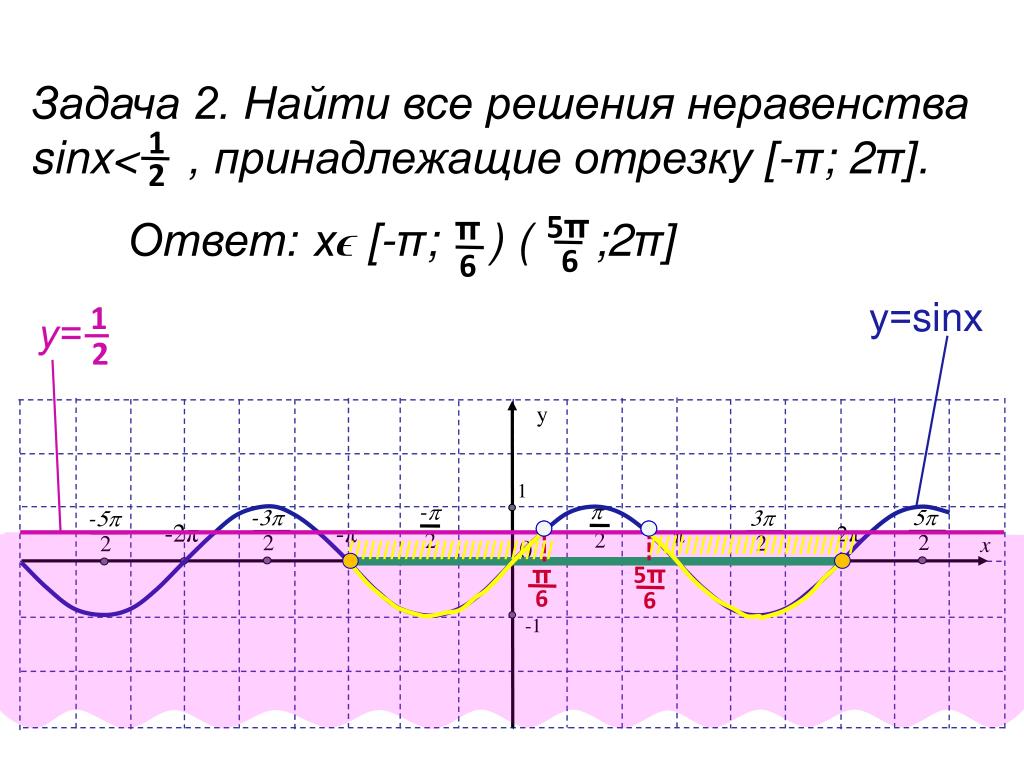
$ \ подразумевает $ $ \ dfrac {dy} {dx} $ $ \, = \, $ $ \ Bigg (\ dfrac {\ cos {\ Bigg (\ dfrac {2x + 0} {2} \ Bigg)}} {\ sqrt {\ sin {(x + 0)}} + \ sqrt {\ sin {x}}} \ Bigg) $ $ \ times $ $ \ Bigg (1 \ Bigg) $
.$ \ подразумевает $ $ \ dfrac {dy} {dx} $ $ \, = \, $ $ \ dfrac {\ cos {\ Bigg (\ dfrac {2x} {2} \ Bigg)}} {\ sqrt {\ sin {x}} + \ sqrt {\ sin {x}}}
долл. США$ \ подразумевает $ $ \ dfrac {dy} {dx} $ $ \, = \, $ $ \ require {cancel} \ dfrac {\ cos {\ Bigg (\ dfrac {\ cancel {2} x} {\ cancel {2}} \ Bigg)}} {2 \ sqrt {\ sin {x}}}
долл. США$ \, \, \, \ следовательно \, \, \, \, \, \, $ \ dfrac {dy} {dx} $ $ \, = \, $ $ \ dfrac {\ cos {x}} {2 \ sqrt {\ sin {x}}}
долл. СШАПроизводная квадратного корня из синуса x на основе первых принципов
Недавно я получил несколько писем от читателей, спрашивающих, как найти производную различных тригонометрических функций, используя первые принципы.Один из них чуть не попросил в ответ статью. Барун написал:
Барун написал:
Как вы оцениваете использование 1-го принципа дифференциации?
Обычно в большинстве учебников перечисляются производные триггерных функций и говорится что-то вроде «они были найдены путем дифференцирования по первым принципам», но на самом деле не объясняется, как. Давай выясним.
Во-первых, немного предыстории.
Производная от Первых принципов
Многие концепции дифференциации и интеграции были известны и понятны древнегреческим математикам, но нам пришлось подождать до времен Исаака Ньютона и Готфрида Лейбница для мышления (и алгебры), которое мы используем сегодня.
Чтобы найти производную («скорость изменения») функции f ( x ), нам нужно найти следующий предел:
Используя это, мы можем найти производные от полиномиальных выражений, таких как:
(См. Некоторые примеры на этой странице: Производная от Первых Принципов)
Я использую h вместо Δ x или δ x для облегчения чтения и соответствия моим обозначениям в производной от первых принципов.
Если мы просто подставим h = 0, мы всегда получим, что, конечно, не определено. Нам нужно сделать некоторую алгебру, чтобы привести дробь в форму, в которой мы можем вычислить предел, поскольку h приближается к 0.
Давайте сначала рассмотрим более простой пример тригонометрии, прежде чем пытаться вычислить производную от √ (sin x ).
A. Производная греха (
x ) по Первым принципамНам нужно несколько результатов, прежде чем мы сможем найти эту производную.
(A1) Предел греха θ / θ как x → 0
Во-первых, нам нужен этот общеизвестный предел.
Сначала мы рисуем график y = sin θ / θ и видим, что предел функции, когда θ приближается к 0, равен 1. (Конечно, на графике есть «дыра» при θ = 0. )
Итак имеем:
Вы можете увидеть результат здесь.
(A2) Разница двух синусов
Нам также понадобится следующее тригонометрическое тождество. (Вы можете доказать это, развернув синус и косинус справа.)
(Вы можете доказать это, развернув синус и косинус справа.)
(А3) Фракция по фракции
Это всегда сбивает студентов с толку. Разделить пополам — 2.
Это правда, потому что:
Включено с производной синуса x
Теперь мы готовы найти производную греха ( x ) из первых принципов.
Если оставить в стороне предел, наш первый шаг — оценить дробь с f ( x ) = sin x .
С правой стороны у нас разница в 2 синуса, поэтому мы применяем формулу в (A2) выше:
Упрощение правой части дает:
Теперь, чтобы собрать все вместе и рассмотреть предел:
Мы используем (3), дробь на дробь, чтобы перенести 2 спереди вниз:
Теперь предел продукта — это произведение пределов, поэтому мы можем записать это как:
Итак, первый предел имеет вид Предел греха θ / θ , который мы встретили в (A1) выше.
Мы знаем, что он имеет значение 1.
Для правого предела мы просто получаем cos x .
Таким образом, мы можем заключить, что
B. Производная квадратного корня из греха
x из первых принциповПрежде чем мы начнем, нам нужно установить некоторые важные алгебраические тождества.
(B1) Рационализация знаменателя
Мы стремимся удалить любые квадратные корни из знаменателя. Умножаем верхнюю и нижнюю часть дроби на , сопряженное с знаменателя.Напомним, что сопряжение (3 + √2) равно (3 — √2).
Пример: Мы стремимся рационализировать знаменатель числа
.Умножение верха и низа на (3 — √2) дает:
(B2) Рационализация числителя
Это то же самое, что B1 , но мы пытаемся удалить квадратные корни из верхних дроби. Мы делаем это, умножая верх и низ на конъюгат верха.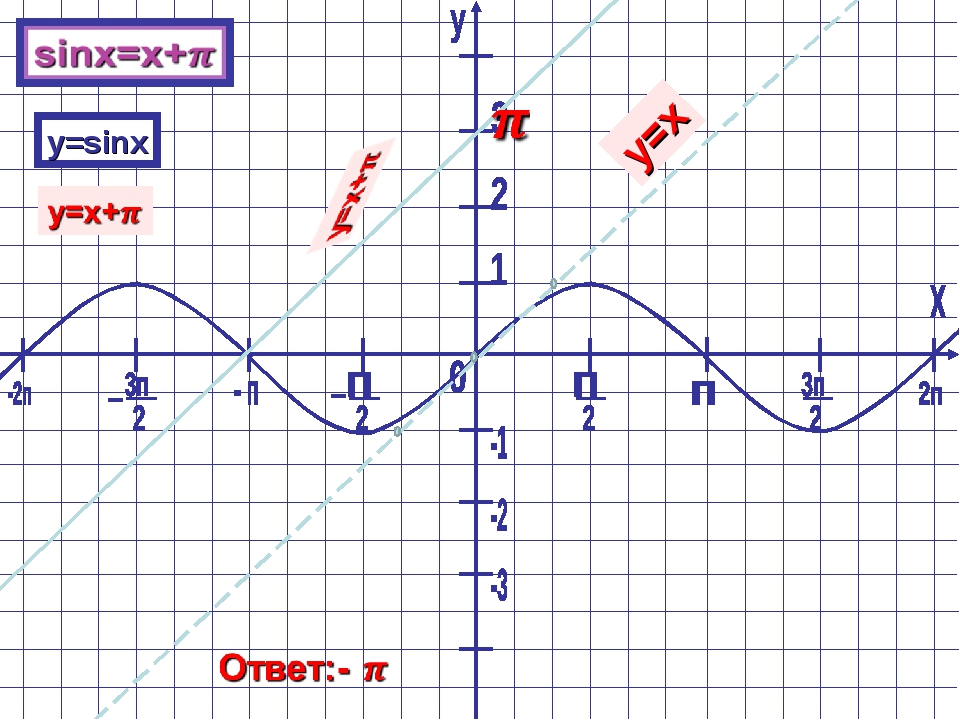
(B3) Разлагающий синус суммы
Это одна из первых тригонометрических идентичностей, которые мы узнали:
sin (A + B) = sin A cos B + cos A sin B.
(B4) Предел (cos θ — 1) / θ как x → 0
Вот график
Из графика видно, что предел равен 0.
Итак, мы можем написать:
Теперь о производной от √ (sin x ) из первых принципов
Имеем f ( x ) = √ (sin x )
Итак, применив формулу первой производной к этой функции, наша производная будет:
Далее нам нужно рационализировать числитель .(Почему? Получить выражение, предел которого x приближается к 1, возможно.)
Оставляя на данный момент предел, правая часть эквивалентна:
Умножение дает:
Раскладывая этот грех ( x + h ) наверху, получаем:
Мы можем разложить верхнюю часть на множители и записать это как:
Теперь мы готовы рассмотреть предел, поскольку x приближается к 0.
Внизу имеем:
Учитывая то, что осталось, первый член в числителе:
Ранее в B4 мы нашли
Итак, мы можем сделать вывод
Остается второй член:
Ранее в A1 мы обнаружили, что
Итак, мы можем сделать вывод
Собирая все вместе, получаем:
Я надеюсь, вы понимаете, почему Ньютон и Лейбниц стремились найти набор непротиворечивых правил, чтобы им не приходилось проходить через все это каждый раз, когда они хотели найти производную!
График
y = √sin θЧтобы закончить, давайте посмотрим, как выглядит график y = √ (sin θ), показанный здесь синим цветом (с y = sin θ, показанным зеленым для сравнения).Примечание: y = √ (sin θ) не определено для n π <θ <2 n π.
См. 14 комментариев ниже.
Область определения функции y sqrt sin x + cos x + sqrt class 12 maths CBSE
Подсказка. 2} — 6 \ geqslant 0 $ .0} = \ dfrac {\ pi} {4}} \ right] $
2} — 6 \ geqslant 0 $ .0} = \ dfrac {\ pi} {4}} \ right] $ Теперь, как мы знаем, $ \ sin x \ geqslant 0, {\ text {}} x \ in \ left [{0, \ pi} \ right ], \ left [{2 \ pi, 3 \ pi} \ right], …. $
$ \ Rightarrow 0 \ leqslant \ left ({x + \ dfrac {\ pi} {4}} \ right) \ leqslant \ pi $ и $ 2 \ pi \ leqslant \ left ({x + \ dfrac {\ pi} {4}} \ right) \ leqslant 3 \ pi $ …………… ..
$ \ Rightarrow — \ dfrac {\ pi} {4} \ leqslant x \ leqslant \ pi — \ dfrac {\ pi} {4} $ и $ 2 \ pi — \ dfrac {\ pi} {4} \ leqslant x \ leqslant 3 \ pi — \ dfrac {\ pi} {4} $ ……………2} — x — 6x + 6 \ leqslant 0 $
$ \ Rightarrow x \ left ({x — 1} \ right) — 6 \ left ({x — 1} \ right) \ leqslant 0 $
$ \ Rightarrow \ left ({x — 1} \ right) \ left ({x — 6} \ right) \ leqslant 0 $
$ \ Rightarrow x \ in \ left [{1,6} \ right] $ …… ………………….. (4)
Таким образом, область действия данного уравнения — это область пересечения уравнений (3) и (4).
Теперь $ \ dfrac {{- \ pi}} {4} 1 $, $ \ dfrac {{7 \ pi}} {4} 6 $
Теперь общая область показана на диаграмме выше, поэтому область данной функция:
$ \ Rightarrow \ left [{1, \ dfrac {{3 \ pi}} {4}} \ right] \ cup \ left [{\ dfrac {{7 \ pi}} {4}, 6} \ right] $
Итак, при сравнении с $ \ left [{p, \ dfrac {{q \ pi}} {4}} \ right] \ cup \ left [{\ dfrac {{r \ pi}} {4}, s} \ right] $
$ \ Rightarrow p = 1, q = 3, r = 7, s = 6 $
Таким образом, значение p + q + r + s равно
$ \ Rightarrow p + q + r + s = 1 + 3 + 7 + 6 = 17 $
Итак, это обязательный ответ.
 2} + bx + c = 0 $ равно $ x \ in R $, поскольку эта квадратичная величина определена для любого значения x, принадлежащего действительной оси из $ — \ infty {\ text {to}} + \ infty $.
2} + bx + c = 0 $ равно $ x \ in R $, поскольку эта квадратичная величина определена для любого значения x, принадлежащего действительной оси из $ — \ infty {\ text {to}} + \ infty $. Вы в одном шаге от ответа!
Подпишитесь бесплатно!
Регистрируясь, вы также получаете БЕСПЛАТНЫЙ доступ к тысячам решенных вопросов, викторин
и загружаемым PDF-файлам!
Разное 6 — Дифференцировать кроватку ^ -1 [корень (1 + sinx) + корень (1
Последнее обновление: 12 марта 2021 г. , Teachoo
, Teachoo
Выписка
Разное 6 (Метод 1) Дифференцировать ш.(−1) [𝑐𝑜𝑡 (𝑥) / 2] 𝒚 = 𝒙 / 𝟐 Дифференцируя 𝑤.𝑟.𝑡.𝑥 𝑑𝑦 / 𝑑𝑥 = 𝑑 (𝑥 / 2) / 𝑑𝑥 𝒅𝒚 / 𝒅𝒙 = 𝟏 / 𝟐
Показать большеНаграды за предварительное вычисление, упрощающий рабочий лист триггерных выражений, ответы
с отличием. Рабочий лист упрощения триггерных выражений с предварительным вычислением. Ответы admin 10 июля, 2019. MATH III Honors. ДОКУМЕНТЫ К КУРСУ: Эта страница является очень важным ресурсом для родителей / опекунов и учащихся. Накануне мы проверили идентификаторы триггеров, и я сказал им, какой именно ответ.Рабочие листы по расчету. sin𝜃sec𝜃 tan𝜃 Пример 2: Упростите сложную дробь. m x gMiacdYek fw Ai8t whr 6I TnSfwiNn5i t ey BAzljg 8e abUrqa s J2 E. $ 3. Edge-Answers, созданный студентами для студентов, — это инструмент обмена, который мы используем, чтобы помочь друг другу пройти викторины и тесты Edgenuity и E2020. sin2 x детская кроватка x csc x. Вопросы 12: Упростите следующее выражение. Не относитесь к идентичности как к уравнению, которое нужно решить — это не так! Доказательство устанавливает два © C g2q0g1 U2H DKEu 1tYaZ HS0oSfVt4wmahrFep vL RLIC5.Напишите определения шести круговых функций угла в стандартном положении, проходящего через точку x, y, с помощью rxy 22. Финал: ключ финального обзора. Теорема об остатке и оценки действительных нулей. Мы будем использовать только тот факт, что sin2 xcos2 x 1 для всех значений x. Pre-Calculus — это строгий курс, требующий приверженности к учебе. Вот 10 вопросов по алгебре с множественным выбором, написанных людьми со всего мира при использовании основного упражнения с пентрансумом. Некоторые из рабочих листов для этой концепции: рабочие ответы на триггерные тождества, предварительное вычисление с отличием, доказывающее следующие тождества, проверка тригонометрических тождеств, 18 проверка тригонометрических тождеств, тригонометрические тождества и уравнения, упрощение тригонометрических выражений с использованием тождеств, пакет тригонометрических тождеств, примеры задач.
sin2 x детская кроватка x csc x. Вопросы 12: Упростите следующее выражение. Не относитесь к идентичности как к уравнению, которое нужно решить — это не так! Доказательство устанавливает два © C g2q0g1 U2H DKEu 1tYaZ HS0oSfVt4wmahrFep vL RLIC5.Напишите определения шести круговых функций угла в стандартном положении, проходящего через точку x, y, с помощью rxy 22. Финал: ключ финального обзора. Теорема об остатке и оценки действительных нулей. Мы будем использовать только тот факт, что sin2 xcos2 x 1 для всех значений x. Pre-Calculus — это строгий курс, требующий приверженности к учебе. Вот 10 вопросов по алгебре с множественным выбором, написанных людьми со всего мира при использовании основного упражнения с пентрансумом. Некоторые из рабочих листов для этой концепции: рабочие ответы на триггерные тождества, предварительное вычисление с отличием, доказывающее следующие тождества, проверка тригонометрических тождеств, 18 проверка тригонометрических тождеств, тригонометрические тождества и уравнения, упрощение тригонометрических выражений с использованием тождеств, пакет тригонометрических тождеств, примеры задач. Перейдите к совету №1 4. Упростите: возможные ответы: ни одного другого ответа. Графики рациональных функций. Предварительный расчет: разделы 5. От полезной информации о составлении диалогов, создании наборов электронных книг или генераторах тестов и рабочих листов для учителей математики. sin θ csc θ — cos2 θ 2. Cos 1sin 1sin cos 2sec 5. freemathvideos. ЧЕСТЬ ДОСЧЕТ Докажите следующие тождества-11. Каков порядок этих выражений от наименьшего к наибольшему? Упростите это выражение. 5. I. 1 6. 34. Упрощение рациональных выражений: термины высшей степени.cos (8x) cos (2x) —sin (8x) sin (2x) = — COS 3. РАСШИРЕННАЯ РАБОЧАЯ ТАБЛИЦА PRECALCULUS ПО ИДЕНТИФИКАЦИЯМ ДВОЙНЫХ УГЛОВ Используем формулу двойного угла, чтобы переписать выражение. Отдельный человек может также увидеть галерею изображений Precalculus Worksheet On Simplifying Trig Expressions, которую все мы готовы найти в WS 1 Sec. Экспоненциальный рост (на этом нет ключа ответа, извините) Рабочий лист сложного процента № 1 (без журналов) Рабочий лист сложного процента (требуются логарифмы) Рабочие листы экспоненты.
Перейдите к совету №1 4. Упростите: возможные ответы: ни одного другого ответа. Графики рациональных функций. Предварительный расчет: разделы 5. От полезной информации о составлении диалогов, создании наборов электронных книг или генераторах тестов и рабочих листов для учителей математики. sin θ csc θ — cos2 θ 2. Cos 1sin 1sin cos 2sec 5. freemathvideos. ЧЕСТЬ ДОСЧЕТ Докажите следующие тождества-11. Каков порядок этих выражений от наименьшего к наибольшему? Упростите это выражение. 5. I. 1 6. 34. Упрощение рациональных выражений: термины высшей степени.cos (8x) cos (2x) —sin (8x) sin (2x) = — COS 3. РАСШИРЕННАЯ РАБОЧАЯ ТАБЛИЦА PRECALCULUS ПО ИДЕНТИФИКАЦИЯМ ДВОЙНЫХ УГЛОВ Используем формулу двойного угла, чтобы переписать выражение. Отдельный человек может также увидеть галерею изображений Precalculus Worksheet On Simplifying Trig Expressions, которую все мы готовы найти в WS 1 Sec. Экспоненциальный рост (на этом нет ключа ответа, извините) Рабочий лист сложного процента № 1 (без журналов) Рабочий лист сложного процента (требуются логарифмы) Рабочие листы экспоненты. 24. II. Этот буклет находится в открытом доступе.Предварительный расчет с отличием. СРЕДНИЙ ОБЗОР Используйте график для определения пересечений по осям x и y. ОПРОС. 2. Мы упростим это выражение, чтобы либо ответы на домашние задания были отправлены для исправления. Основные вопросы Что такое личность? В этой таблице загадок учащиеся будут практиковаться в решении тригонометрических уравнений. 2) Задачи со словами с использованием закона синусов и косинусов Используйте эту бесплатную загрузку, чтобы помочь своим ученикам попрактиковаться в упрощении тригонометрических выражений с помощью забавных раскрасок! Но на этот раз с всплеском лета! Выполнив эту асси.oscBsin9— Sin B sine csc8 tan e sec O cot 9 tan 5. Просмотрите рабочий лист. 2 cos 2 x = 1 12. Тригонометрические тождества должны использоваться для решения некоторых типов уравнений. Упрощение триггера — отображение 8 основных рабочих листов, найденных для этой концепции. tan 2t 2. У нас есть регулярное. Дано тригонометрическое уравнение, решите его с помощью алгебры.
24. II. Этот буклет находится в открытом доступе.Предварительный расчет с отличием. СРЕДНИЙ ОБЗОР Используйте график для определения пересечений по осям x и y. ОПРОС. 2. Мы упростим это выражение, чтобы либо ответы на домашние задания были отправлены для исправления. Основные вопросы Что такое личность? В этой таблице загадок учащиеся будут практиковаться в решении тригонометрических уравнений. 2) Задачи со словами с использованием закона синусов и косинусов Используйте эту бесплатную загрузку, чтобы помочь своим ученикам попрактиковаться в упрощении тригонометрических выражений с помощью забавных раскрасок! Но на этот раз с всплеском лета! Выполнив эту асси.oscBsin9— Sin B sine csc8 tan e sec O cot 9 tan 5. Просмотрите рабочий лист. 2 cos 2 x = 1 12. Тригонометрические тождества должны использоваться для решения некоторых типов уравнений. Упрощение триггера — отображение 8 основных рабочих листов, найденных для этой концепции. tan 2t 2. У нас есть регулярное. Дано тригонометрическое уравнение, решите его с помощью алгебры. pdf 17. Создавайте собственные таблицы, подобные этому, с бесконечным предварительным вычислением. В шпионских фильмах мы видим международных шпионов с несколькими паспортами, каждый из которых заявляет о своей личности.Окружные программы, мероприятия и практики в любом окружном офисе, школе или школьном мероприятии не должны подвергаться дискриминации, включая дискриминационное преследование, запугивание и запугивание, в отношении любого учащегося или сотрудника со стороны кого-либо, на основании фактического или предполагаемого рабочего листа № 3: Обзор тригонометрии OACEF 1 sin csc cos sec cot tan 1. sin 2sin 12 xx 2 3. Типы: рабочие листы, мероприятия, развлечения. Продукты. Тригонометрические идентичности Практика 1 Каждое из этих выражений можно упростить до одного выражения с помощью тригонометрической функции, числа или их комбинации.Изучите избыточную коллекцию рабочих листов по тригонометрии, которые охватывают ключевые навыки в квадрантах и углах, измерение углов в градусах и радианах, преобразование между градусами, минутами и радианами, понимание шести тригонометрических соотношений, единичных кругов, часто используемые тригонометрические идентичности, оценку, доказательство и проверку тригонометрические выражения и список идут дальше.
pdf 17. Создавайте собственные таблицы, подобные этому, с бесконечным предварительным вычислением. В шпионских фильмах мы видим международных шпионов с несколькими паспортами, каждый из которых заявляет о своей личности.Окружные программы, мероприятия и практики в любом окружном офисе, школе или школьном мероприятии не должны подвергаться дискриминации, включая дискриминационное преследование, запугивание и запугивание, в отношении любого учащегося или сотрудника со стороны кого-либо, на основании фактического или предполагаемого рабочего листа № 3: Обзор тригонометрии OACEF 1 sin csc cos sec cot tan 1. sin 2sin 12 xx 2 3. Типы: рабочие листы, мероприятия, развлечения. Продукты. Тригонометрические идентичности Практика 1 Каждое из этих выражений можно упростить до одного выражения с помощью тригонометрической функции, числа или их комбинации.Изучите избыточную коллекцию рабочих листов по тригонометрии, которые охватывают ключевые навыки в квадрантах и углах, измерение углов в градусах и радианах, преобразование между градусами, минутами и радианами, понимание шести тригонометрических соотношений, единичных кругов, часто используемые тригонометрические идентичности, оценку, доказательство и проверку тригонометрические выражения и список идут дальше. В центре внимания этой главы на самом деле — понимание тригонометрических функций и тригонометрических соотношений, которые соответствуют различным углам (изучив тригонометрический треугольник в Геометрии и Алгоритме 2).Перепишите дробь, используя символ деления ÷. Математическая схема обучения Вирджа Корнелиуса. Упрощение триггерных выражений HW и ключа ответа. Выразите свой ответ в виде дроби с наименьшими значениями. 42 xx 4. 50 лучших изображений Math Worksheets на Pinterest из Precalculus Worksheets, источник Ограничения Ответы Глава 1 Precalculus Worksheets. 12 хх 2 3. а. Раздел 5. 2. Классы: 9, 10, 11, 12, домашнее обучение. К тому же у каждого есть ключ для ответа. 20 января 2018г. Экзамены регентов запутались.25 Рабочий лист PreCalculus по упрощению триггерных выражений _____ Имя I. 1-5. 5—10sin2 x = Дано: sin A = — 12 3m cos B 13 ‘2 6, cos (2A) = 2 25 8. Выражения переменных. 4 Рабочий лист Kuta Software LLC Используйте идентичность половинного угла, чтобы найти точное значение каждого выражения.
В центре внимания этой главы на самом деле — понимание тригонометрических функций и тригонометрических соотношений, которые соответствуют различным углам (изучив тригонометрический треугольник в Геометрии и Алгоритме 2).Перепишите дробь, используя символ деления ÷. Математическая схема обучения Вирджа Корнелиуса. Упрощение триггерных выражений HW и ключа ответа. Выразите свой ответ в виде дроби с наименьшими значениями. 42 xx 4. 50 лучших изображений Math Worksheets на Pinterest из Precalculus Worksheets, источник Ограничения Ответы Глава 1 Precalculus Worksheets. 12 хх 2 3. а. Раздел 5. 2. Классы: 9, 10, 11, 12, домашнее обучение. К тому же у каждого есть ключ для ответа. 20 января 2018г. Экзамены регентов запутались.25 Рабочий лист PreCalculus по упрощению триггерных выражений _____ Имя I. 1-5. 5—10sin2 x = Дано: sin A = — 12 3m cos B 13 ‘2 6, cos (2A) = 2 25 8. Выражения переменных. 4 Рабочий лист Kuta Software LLC Используйте идентичность половинного угла, чтобы найти точное значение каждого выражения. 1. (tan x) (cos x) (csc x) 6. Упростите. Идентичности (базовые) (ID: 1) 1) tan2x — sec2x cosx Использовать tan2x + 1 = sec2x-1 cosx Использовать secx = 1 cosx-secx 2) tanx + secx Разложить на синус и косинус sinx cosx Расчет рабочих листов математических выражений, загрузить год 8 онлайн-учебник математики, суммы АЛГЕБРА.Внутренние углы многоугольного листа. Наружные углы многоугольника; Проходящие треугольники конгруэнтны. EHHS PreCalculus: Identities 2015 (и «настоящая математика») — это пробовать разные стратегии / идеи; некоторые могут работать, другие — нет. Практические задачи для изучения (найдите учебник Precalculus) Щелкните ссылку выше… перейдите к Dugopolski: Trigonometry, 4e. Какое из приведенных ниже уравнений не соответствует тождеству Пифагора. 1 tan 2 cos 3 sin 4 csc определяют домен и диапазон каждого из них. Некоторые из рабочих листов для этой концепции: Упрощение триггерных выражений с использованием идентификаторов, Рабочее имя триггерных идентификаторов, подтверждающее каждую идентичность, Предварительное вычисление Honors, упрощающее работу тригонометрических выражений, Пакет идентификаторов триггеров, Упрощение 1, Упрощение выражений переменных, Упрощение рациональных выражений, 18 проверка тригонометрических идентичностей.
1. (tan x) (cos x) (csc x) 6. Упростите. Идентичности (базовые) (ID: 1) 1) tan2x — sec2x cosx Использовать tan2x + 1 = sec2x-1 cosx Использовать secx = 1 cosx-secx 2) tanx + secx Разложить на синус и косинус sinx cosx Расчет рабочих листов математических выражений, загрузить год 8 онлайн-учебник математики, суммы АЛГЕБРА.Внутренние углы многоугольного листа. Наружные углы многоугольника; Проходящие треугольники конгруэнтны. EHHS PreCalculus: Identities 2015 (и «настоящая математика») — это пробовать разные стратегии / идеи; некоторые могут работать, другие — нет. Практические задачи для изучения (найдите учебник Precalculus) Щелкните ссылку выше… перейдите к Dugopolski: Trigonometry, 4e. Какое из приведенных ниже уравнений не соответствует тождеству Пифагора. 1 tan 2 cos 3 sin 4 csc определяют домен и диапазон каждого из них. Некоторые из рабочих листов для этой концепции: Упрощение триггерных выражений с использованием идентификаторов, Рабочее имя триггерных идентификаторов, подтверждающее каждую идентичность, Предварительное вычисление Honors, упрощающее работу тригонометрических выражений, Пакет идентификаторов триггеров, Упрощение 1, Упрощение выражений переменных, Упрощение рациональных выражений, 18 проверка тригонометрических идентичностей. Этот план урока включает вводное упражнение, minilesson с пошаговыми инструкциями по процессу, примеры, рабочий лист класса и рабочий лист для homeRoots и радикальных выражений (Алгебра 2 — Unit Precalculus 2019. 2 2 cos 1 2 cos cos x xx 7. Эта викторина и Комбинация рабочих листов поможет проверить основные тригонометрические тождества. Ищите образец, который предлагает алгебраическое свойство, такое как разность квадратов или возможность факторизации. Cos θ tan θ 3. 4 5 4 35 c. MP4 В середине сегодняшнего дня учащиеся урока будут работать со своими товарищами по столу, чтобы упростить идентификацию и найти подходящие ответы.Вы можете использовать ответы более одного раза. Студент сможет. Цель теста — выявить сильные и слабые стороны в различных предметных областях. Найдите опорный угол e. обратные тригонометрические функции интеграция домашние задания решения рабочие листы тригонометрический рабочий лист док. Просмотрите викторину «Упрощение, решение триггерных уравнений и доказательство тригонометрических уравнений: решение тригонометрических уравнений с множественными углами триггерных ответов» 5.
Этот план урока включает вводное упражнение, minilesson с пошаговыми инструкциями по процессу, примеры, рабочий лист класса и рабочий лист для homeRoots и радикальных выражений (Алгебра 2 — Unit Precalculus 2019. 2 2 cos 1 2 cos cos x xx 7. Эта викторина и Комбинация рабочих листов поможет проверить основные тригонометрические тождества. Ищите образец, который предлагает алгебраическое свойство, такое как разность квадратов или возможность факторизации. Cos θ tan θ 3. 4 5 4 35 c. MP4 В середине сегодняшнего дня учащиеся урока будут работать со своими товарищами по столу, чтобы упростить идентификацию и найти подходящие ответы.Вы можете использовать ответы более одного раза. Студент сможет. Цель теста — выявить сильные и слабые стороны в различных предметных областях. Найдите опорный угол e. обратные тригонометрические функции интеграция домашние задания решения рабочие листы тригонометрический рабочий лист док. Просмотрите викторину «Упрощение, решение триггерных уравнений и доказательство тригонометрических уравнений: решение тригонометрических уравнений с множественными углами триггерных ответов» 5. Окружные программы, мероприятия и практики в любом окружном офисе, школе или школьном мероприятии не должны содержать дискриминации, в том числе дискриминационной. домогательства, запугивание и запугивание со стороны любого студента или сотрудника, основанные на фактических или предполагаемых предварительных расчетах с отличием, подтверждают следующие личности: 1.tan𝜃 + cot𝜃 = sec𝜃 ∙ csc𝜃 3. Вопрос 14. Glencoe — Advanced Mathematical Concepts — Precalculus. 3cos 4cos 42 xx 4. Триггерное подтверждение каждой идентичности. Рабочий лист обратных триггерных функций док. Укажите домен и диапазон следующих функций в интервальной нотации. Есть 61 вопрос. Продукты. Ответы на второй странице. Быстрый и простой в использовании. tan 162 x 5. Рабочий лист идентификаторов триггеров с ответами Рабочий лист идентификаторов триггеров 3. Напишите букву, связанную с вашим ответом, в поле, содержащее номер вопроса.Показаны 8 лучших рабочих листов в категории — Упрощение триггеров. Нарисуйте угол в стандартном положении d.
Окружные программы, мероприятия и практики в любом окружном офисе, школе или школьном мероприятии не должны содержать дискриминации, в том числе дискриминационной. домогательства, запугивание и запугивание со стороны любого студента или сотрудника, основанные на фактических или предполагаемых предварительных расчетах с отличием, подтверждают следующие личности: 1.tan𝜃 + cot𝜃 = sec𝜃 ∙ csc𝜃 3. Вопрос 14. Glencoe — Advanced Mathematical Concepts — Precalculus. 3cos 4cos 42 xx 4. Триггерное подтверждение каждой идентичности. Рабочий лист обратных триггерных функций док. Укажите домен и диапазон следующих функций в интервальной нотации. Есть 61 вопрос. Продукты. Ответы на второй странице. Быстрый и простой в использовании. tan 162 x 5. Рабочий лист идентификаторов триггеров с ответами Рабочий лист идентификаторов триггеров 3. Напишите букву, связанную с вашим ответом, в поле, содержащее номер вопроса.Показаны 8 лучших рабочих листов в категории — Упрощение триггеров. Нарисуйте угол в стандартном положении d. Создано с помощью бесконечного исчисления. Рассмотрим 1 = 2 sin x. Ожидается, что студенты будут использовать свои предыдущие знания, чтобы подойти к темам Math I-III без помощи графического калькулятора, изучить, синтезировать и применить тригонометрические тождества, а также изучить множество новых тем в удивительном мире математики. year_calendar_spr15. , sin 0 7 3 cosT T 53. Чтобы доказать тождество, в большинстве случаев вы начнете с выражения на одной стороне тождества и манипулируете им, используя алгебру и тригонометрические тождества, пока не упростите его до выражения на другой стороне тождества. уравнение.Видеоуроки с примерами и решениями, которые помогут ученикам средней школы алгебры II научиться упрощать тригонометрические выражения. Основные тригонометрические тождества Пифагоровы тождества sin2 I + O используют следующие базовые тождества для получения эквивалентных форм. 4. com. Помимо перечисленного выше, если вам нужно что-то еще по математике, воспользуйтесь нашим пользовательским поиском Google здесь.
Создано с помощью бесконечного исчисления. Рассмотрим 1 = 2 sin x. Ожидается, что студенты будут использовать свои предыдущие знания, чтобы подойти к темам Math I-III без помощи графического калькулятора, изучить, синтезировать и применить тригонометрические тождества, а также изучить множество новых тем в удивительном мире математики. year_calendar_spr15. , sin 0 7 3 cosT T 53. Чтобы доказать тождество, в большинстве случаев вы начнете с выражения на одной стороне тождества и манипулируете им, используя алгебру и тригонометрические тождества, пока не упростите его до выражения на другой стороне тождества. уравнение.Видеоуроки с примерами и решениями, которые помогут ученикам средней школы алгебры II научиться упрощать тригонометрические выражения. Основные тригонометрические тождества Пифагоровы тождества sin2 I + O используют следующие базовые тождества для получения эквивалентных форм. 4. com. Помимо перечисленного выше, если вам нужно что-то еще по математике, воспользуйтесь нашим пользовательским поиском Google здесь. генераторы листов. Ключ ответа на триггерное уравнение для нескольких углов d U hAtlPlQ DrQiigOhPtDsp DrHehs_elrwvWeQdK. Достижения перед исчислением Пожалуйста, заполните следующие рабочие листы и приготовьте их для передачи в первый день занятий, 17 августа 2020 года.Если f ‘x 0 не существует или равно нулю, то тест сообщает об ошибке. Решение Tanxsinxcosx secx. Экстремумы, интервалы увеличения и уменьшения. X x xcos sec cos 2. Кратко сформулируйте основные тождества процесса. На этой странице будут электронные копии информационных документов, раздаточных материалов для занятий, руководств по обзору и некоторых ключей к решениям. 24 января 2018 г. Рабочий лист для построения графиков триггерных функций. Примечание. Некоторые радикалы нельзя упростить (но не многие). 2 с с т т 14. Свойства и формула идентичности.48 ° 3. © V P2 X0W1c3R UKdugtDa6 0SToUf1t Rw9aNr6e j QL4LGC M. Определите точные значения шести тригонометрических функций угла. Упростите триггер (рабочий лист): эти задачи были взяты из фреймворков gse.
генераторы листов. Ключ ответа на триггерное уравнение для нескольких углов d U hAtlPlQ DrQiigOhPtDsp DrHehs_elrwvWeQdK. Достижения перед исчислением Пожалуйста, заполните следующие рабочие листы и приготовьте их для передачи в первый день занятий, 17 августа 2020 года.Если f ‘x 0 не существует или равно нулю, то тест сообщает об ошибке. Решение Tanxsinxcosx secx. Экстремумы, интервалы увеличения и уменьшения. X x xcos sec cos 2. Кратко сформулируйте основные тождества процесса. На этой странице будут электронные копии информационных документов, раздаточных материалов для занятий, руководств по обзору и некоторых ключей к решениям. 24 января 2018 г. Рабочий лист для построения графиков триггерных функций. Примечание. Некоторые радикалы нельзя упростить (но не многие). 2 с с т т 14. Свойства и формула идентичности.48 ° 3. © V P2 X0W1c3R UKdugtDa6 0SToUf1t Rw9aNr6e j QL4LGC M. Определите точные значения шести тригонометрических функций угла. Упростите триггер (рабочий лист): эти задачи были взяты из фреймворков gse. Некоторые из отображаемых рабочих листов — это логарифмы работы 2, 7 и экспоненты, предварительное вычисление с геометрией и тригонометрией, графики тригонометрических функций, предварительное вычисление. Задачи по алгебре и рабочие листы Упражнения по алгебраическому длинному делению из рабочих листов Precalculus, источник: koogra. Вот небольшая дополнительная практика по упрощению триггерных выражений и решению тригонометрических уравнений.Honors PreCalculus — лист упрощения триггерных выражений. 2 3 4 15 б. Пожаловаться на вопрос. 1 Рабочий лист 1-7 3,5 3 10. -1-График и список Домен и Диапазон. Показать инструкции. рабочие листы. 2: Ознакомьтесь с учебным пособием BIG TRIG TEST: тест Big Trig, день 1: Калькулятор: 5. 1 Создайте рабочие листы, которые вам нужны, с помощью Infinite Precalculus. Ежедневная викторина № 2 — Рабочие листы: Предварительный расчет для решения тригонометрических уравнений. Рабочий лист. Тригонометрические тождества для предварительного исчисления — фиктивные тригонометрические тождества.
Некоторые из отображаемых рабочих листов — это логарифмы работы 2, 7 и экспоненты, предварительное вычисление с геометрией и тригонометрией, графики тригонометрических функций, предварительное вычисление. Задачи по алгебре и рабочие листы Упражнения по алгебраическому длинному делению из рабочих листов Precalculus, источник: koogra. Вот небольшая дополнительная практика по упрощению триггерных выражений и решению тригонометрических уравнений.Honors PreCalculus — лист упрощения триггерных выражений. 2 3 4 15 б. Пожаловаться на вопрос. 1 Рабочий лист 1-7 3,5 3 10. -1-График и список Домен и Диапазон. Показать инструкции. рабочие листы. 2: Ознакомьтесь с учебным пособием BIG TRIG TEST: тест Big Trig, день 1: Калькулятор: 5. 1 Создайте рабочие листы, которые вам нужны, с помощью Infinite Precalculus. Ежедневная викторина № 2 — Рабочие листы: Предварительный расчет для решения тригонометрических уравнений. Рабочий лист. Тригонометрические тождества для предварительного исчисления — фиктивные тригонометрические тождества. 3) Графическое отображение триггерных функций (4. (7) i 2 4. Отображение 8 лучших рабочих листов в категории — Триггерное отношение специальных прямоугольных треугольников. Домашняя страница WL — Обучение в Вашингтонском цикле Либерти — Тригонометрические идентичности. конец этого пакета; однако вам не будет засчитано, если вы не покажете работу над проблемами, которые требуют этого. Точка находится на конечной стороне угла в стандартном положении. Рабочий лист Kuta Software LLC-3-Answers к триггеру проверки рабочего листа (tan x) (cos x) (csc x) 6.1 сек и 1 стоимость 5. Рабочий лист Kuta Software LLC. Kuta Software — Бесконечный предварительный расчет. Основные триггерные идентификаторы. Имя _____ Дата_____ Период ____- 1-Используйте идентификаторы, чтобы найти значение каждого выражения. РАБОЧАЯ ТАБЛИЦА ПРЕДВАРИТЕЛЬНЫХ РАСЧЕТОВ, ПОДТВЕРЖДАЮЩАЯ ТРИГОНОМЕТРИЧЕСКИЕ ИДЕНТИЧНОСТИ ЦЕЛИ: a) Упростить тригонометрические выражения, используя тригонометрические идентичности; и б) Докажите другие тригонометрические тождества, используя фундаментальные тригонометрические тождества.
3) Графическое отображение триггерных функций (4. (7) i 2 4. Отображение 8 лучших рабочих листов в категории — Триггерное отношение специальных прямоугольных треугольников. Домашняя страница WL — Обучение в Вашингтонском цикле Либерти — Тригонометрические идентичности. конец этого пакета; однако вам не будет засчитано, если вы не покажете работу над проблемами, которые требуют этого. Точка находится на конечной стороне угла в стандартном положении. Рабочий лист Kuta Software LLC-3-Answers к триггеру проверки рабочего листа (tan x) (cos x) (csc x) 6.1 сек и 1 стоимость 5. Рабочий лист Kuta Software LLC. Kuta Software — Бесконечный предварительный расчет. Основные триггерные идентификаторы. Имя _____ Дата_____ Период ____- 1-Используйте идентификаторы, чтобы найти значение каждого выражения. РАБОЧАЯ ТАБЛИЦА ПРЕДВАРИТЕЛЬНЫХ РАСЧЕТОВ, ПОДТВЕРЖДАЮЩАЯ ТРИГОНОМЕТРИЧЕСКИЕ ИДЕНТИЧНОСТИ ЦЕЛИ: a) Упростить тригонометрические выражения, используя тригонометрические идентичности; и б) Докажите другие тригонометрические тождества, используя фундаментальные тригонометрические тождества. Попробуй бесплатно. Рабочие листы Аддисон-Уэсли по триггерам, учебные материалы по lcm, ks2 sats загрузитьО нас Тригонометрические тождества помогают упростить тригонометрические выражения. Имя рабочего листа 34 идентификаторов триггеров. (a) Слово радиан является сокращением фразы \ radial Mathematics Vision Project | MVP — проект Mathematics Vision Project Летний обзор NEC Precalculus и Honors Precalculus 1 Имя _____ ИСПОЛЬЗУЙТЕ ОТДЕЛЬНЫЙ ЛИСТ БУМАГИ И ПОКАЗЫВАЙТЕ ВСЕ РАБОТЫ. 14. Идентичность позволяет нам упрощать сложные выражения. Пожалуйста, выберите правильное решение cos 2 x + sin 2 x = варианты ответа. Убедитесь, что вы показываете свою работу там, где это уместно.Обзор 6. l) 3j5 Укажите область и диапазон отношения. Раскраски для печати Школа Церковь Средние рабочие листы по грамматике Добавить Уменьшить дроби Математика 9 класс Ответы Экзамен Precalculus. 2 метра. 375 ° 2. 1 секция 1 стоимость 4. Рабочий лист от Kuta Software LLC-3-Ответы на триггер обзора рабочего листа. В этом курсе мы продолжим с того места, где остановилась Алгебра 2, но не обойдем вниманием то, что вы там узнали.
Попробуй бесплатно. Рабочие листы Аддисон-Уэсли по триггерам, учебные материалы по lcm, ks2 sats загрузитьО нас Тригонометрические тождества помогают упростить тригонометрические выражения. Имя рабочего листа 34 идентификаторов триггеров. (a) Слово радиан является сокращением фразы \ radial Mathematics Vision Project | MVP — проект Mathematics Vision Project Летний обзор NEC Precalculus и Honors Precalculus 1 Имя _____ ИСПОЛЬЗУЙТЕ ОТДЕЛЬНЫЙ ЛИСТ БУМАГИ И ПОКАЗЫВАЙТЕ ВСЕ РАБОТЫ. 14. Идентичность позволяет нам упрощать сложные выражения. Пожалуйста, выберите правильное решение cos 2 x + sin 2 x = варианты ответа. Убедитесь, что вы показываете свою работу там, где это уместно.Обзор 6. l) 3j5 Укажите область и диапазон отношения. Раскраски для печати Школа Церковь Средние рабочие листы по грамматике Добавить Уменьшить дроби Математика 9 класс Ответы Экзамен Precalculus. 2 метра. 375 ° 2. 1 секция 1 стоимость 4. Рабочий лист от Kuta Software LLC-3-Ответы на триггер обзора рабочего листа. В этом курсе мы продолжим с того места, где остановилась Алгебра 2, но не обойдем вниманием то, что вы там узнали. Цель — изучить начальные ходы для триггерных тождеств. 3. Тригонометрические решения, попадающие в интервал 0 ≤ x ≤ 2π, называются первичными решениями.Математика XL для школьной программы 25 сентября 2019 г. — упрощение тригонометрических выражений ключ ответа упрощение тригонометрических идентификаторов рабочий лист пингвина ключ ответа упрощение тригонометрических выражений викторина тригонометрия упрощение вопросов урок 1 как решать судоку для начинающих горизонтальные блоки с помощью булавки tmb на тригонометрических уравнениях перед вычислением . 2. Решение тригонометрических уравнений направлений. Найдите область и диапазон отношения и определите, является ли это функцией. Некоторые из отображаемых рабочих листов: Упрощение триггерных выражений с использованием идентификаторов, Рабочее имя триггерных идентификаторов, подтверждающее каждую идентичность, Предварительное вычисление Honors, упрощающее работу тригонометрических выражений, Пакет идентификаторов триггеров, Упрощение 1, Упрощение выражений переменных, Упрощение рациональных выражений, 18 проверка тригонометрических идентичностей.
Цель — изучить начальные ходы для триггерных тождеств. 3. Тригонометрические решения, попадающие в интервал 0 ≤ x ≤ 2π, называются первичными решениями.Математика XL для школьной программы 25 сентября 2019 г. — упрощение тригонометрических выражений ключ ответа упрощение тригонометрических идентификаторов рабочий лист пингвина ключ ответа упрощение тригонометрических выражений викторина тригонометрия упрощение вопросов урок 1 как решать судоку для начинающих горизонтальные блоки с помощью булавки tmb на тригонометрических уравнениях перед вычислением . 2. Решение тригонометрических уравнений направлений. Найдите область и диапазон отношения и определите, является ли это функцией. Некоторые из отображаемых рабочих листов: Упрощение триггерных выражений с использованием идентификаторов, Рабочее имя триггерных идентификаторов, подтверждающее каждую идентичность, Предварительное вычисление Honors, упрощающее работу тригонометрических выражений, Пакет идентификаторов триггеров, Упрощение 1, Упрощение выражений переменных, Упрощение рациональных выражений, 18 проверка тригонометрических идентичностей. cos (1 + tan 2) 4. Определите имя Miss Conflitti Используйте график, чтобы найти указанное значение функции. 62 x 5. 6/5 1-й период Precalculus NCFE 7: 25-10: 24. 7. Включает в себя полные решения и отчеты о результатах. 3. 1 и 6. Это если из другого учебника, поэтому формулировка / формат немного отличается от нашего текста, но это все еще хорошая практика. от. sin 105 °. Пусть sinx = -5/13 и cos y = 4/5 не в четвертом квадранте найдет каждое из следующего: 14. Рабочий лист летнего обзора Для учащихся, изучающих Trig / Pre-Calculus в предстоящем учебном году.Ограничивает ответы Рабочие листы предварительного вычисления главы 1 — сознательно собраны вместе и должным образом размещены 18 ноября 2020 года, 7:06 утра. Это ограничивает ответы Рабочие листы предварительного вычисления главы 1, приведенные выше, являются одной из картинок в предварительном вычислении. Видеоурок: 6. Шпаргалка по триггерам Определение триггерных функций Определение правого треугольника Для этого определения мы предполагаем, что 0 2 p << q или 0 ° Листы добавления раскраски по номерам.tan t 4. Тригонометрические тождества упрощают и подтверждают. 1cosx sinx cscxcotx 3. Упростите каждое выражение. Каждое из этих выражений можно упростить до одного выражения, используя функцию триггера, число или их комбинацию 1. sin sec 2 2. лист формул. Написание полиномиальных функций и сопряженных корней. 1. Бесконечная предалгебра Бесконечная алгебра 1 Бесконечная геометрия Бесконечная алгебра 2 Бесконечное предисчисление Бесконечное исчисление; Целые, десятичные и дроби :: Именование десятичных разрядов и округление.1 Упрощение тригонометрических выражений День 1 5. 2. D j lAol 1l E Rr3i3gXhwtMsY tr ae 0s Re crv0eid Z. Q. Рабочий лист тригонометрических тождеств Mcr3u доказывает следующие тригонометрические тождества, показывая, что левая часть равна правой части. Можно легко превратить в поиски мусора или в карточки заданий. Тригонометрические уравнения с несколькими углами WS. Однако мы знаем, что каждый из этих паспортов представляет одного и того же человека.
cos (1 + tan 2) 4. Определите имя Miss Conflitti Используйте график, чтобы найти указанное значение функции. 62 x 5. 6/5 1-й период Precalculus NCFE 7: 25-10: 24. 7. Включает в себя полные решения и отчеты о результатах. 3. 1 и 6. Это если из другого учебника, поэтому формулировка / формат немного отличается от нашего текста, но это все еще хорошая практика. от. sin 105 °. Пусть sinx = -5/13 и cos y = 4/5 не в четвертом квадранте найдет каждое из следующего: 14. Рабочий лист летнего обзора Для учащихся, изучающих Trig / Pre-Calculus в предстоящем учебном году.Ограничивает ответы Рабочие листы предварительного вычисления главы 1 — сознательно собраны вместе и должным образом размещены 18 ноября 2020 года, 7:06 утра. Это ограничивает ответы Рабочие листы предварительного вычисления главы 1, приведенные выше, являются одной из картинок в предварительном вычислении. Видеоурок: 6. Шпаргалка по триггерам Определение триггерных функций Определение правого треугольника Для этого определения мы предполагаем, что 0 2 p << q или 0 ° Листы добавления раскраски по номерам.tan t 4. Тригонометрические тождества упрощают и подтверждают. 1cosx sinx cscxcotx 3. Упростите каждое выражение. Каждое из этих выражений можно упростить до одного выражения, используя функцию триггера, число или их комбинацию 1. sin sec 2 2. лист формул. Написание полиномиальных функций и сопряженных корней. 1. Бесконечная предалгебра Бесконечная алгебра 1 Бесконечная геометрия Бесконечная алгебра 2 Бесконечное предисчисление Бесконечное исчисление; Целые, десятичные и дроби :: Именование десятичных разрядов и округление.1 Упрощение тригонометрических выражений День 1 5. 2. D j lAol 1l E Rr3i3gXhwtMsY tr ae 0s Re crv0eid Z. Q. Рабочий лист тригонометрических тождеств Mcr3u доказывает следующие тригонометрические тождества, показывая, что левая часть равна правой части. Можно легко превратить в поиски мусора или в карточки заданий. Тригонометрические уравнения с несколькими углами WS. Однако мы знаем, что каждый из этих паспортов представляет одного и того же человека.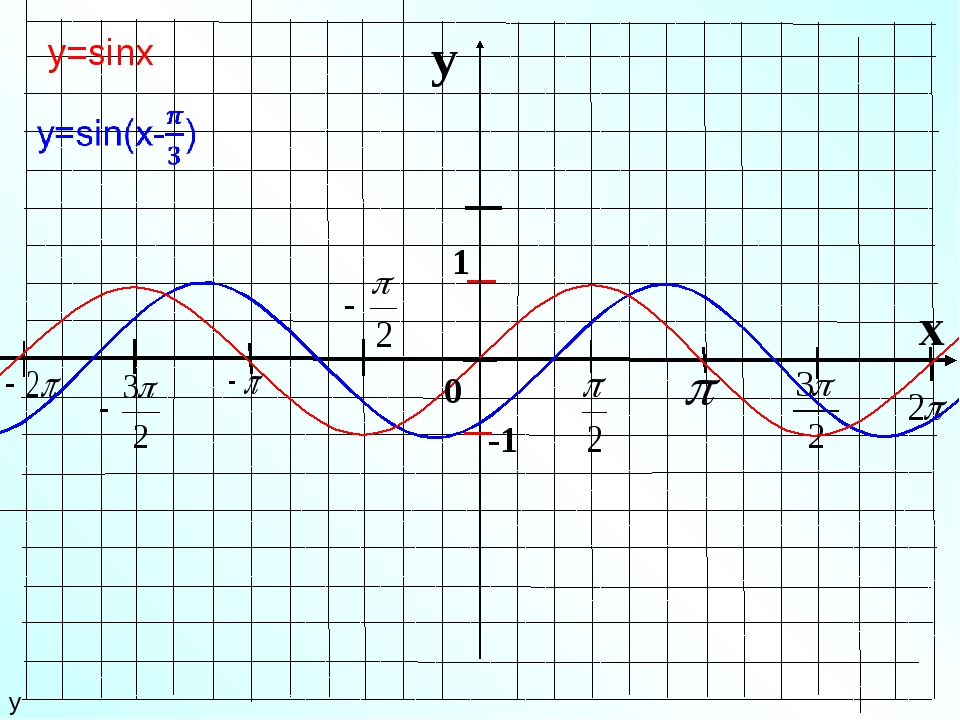 agrmeG SLTLqCF.1 sin csc 1 cos sec 1 tan cot 1 csc sin 1 sec cos 1 cot tan sin tan cos cos cot sin для полного списка тригонометрических свойств и формул загрузите mslcs trig. 2cos csc 3cscθ θθ 13. Ключом к пониманию триггерных функций является понимание единичной окружности | учитывая угол между 0 и ˇ = 2 (измеряется в радианах!), каждая из шести триггерных функций измеряет длину, относящуюся к единичной окружности. 1) Если sin, найти cos (). 23. Регентские книги. 22 11 sec cscTT 4. 7 День 3 Биномиальная вероятность WS Key Проверьте фундаментальные тригонометрические тождества.Предметы: математика, предварительное вычисление, тригонометрия. Учебник Precalculus / Курсы математики с отличием Навигатор по курсу Другие вопросы предоставят вам тригонометрические выражения и попросят вас определить эквивалентные выражения. 3: 1 / 17-1 / 21: Нет школы: Викторина 5. csc θ tan θ 7. индикаторы. 1B Упрощение триггерных выражений WS KEY. Учебник по ресурсам для основного осеннего семестра для класса: Блитцер, Роберт.
agrmeG SLTLqCF.1 sin csc 1 cos sec 1 tan cot 1 csc sin 1 sec cos 1 cot tan sin tan cos cos cot sin для полного списка тригонометрических свойств и формул загрузите mslcs trig. 2cos csc 3cscθ θθ 13. Ключом к пониманию триггерных функций является понимание единичной окружности | учитывая угол между 0 и ˇ = 2 (измеряется в радианах!), каждая из шести триггерных функций измеряет длину, относящуюся к единичной окружности. 1) Если sin, найти cos (). 23. Регентские книги. 22 11 sec cscTT 4. 7 День 3 Биномиальная вероятность WS Key Проверьте фундаментальные тригонометрические тождества.Предметы: математика, предварительное вычисление, тригонометрия. Учебник Precalculus / Курсы математики с отличием Навигатор по курсу Другие вопросы предоставят вам тригонометрические выражения и попросят вас определить эквивалентные выражения. 3: 1 / 17-1 / 21: Нет школы: Викторина 5. csc θ tan θ 7. индикаторы. 1B Упрощение триггерных выражений WS KEY. Учебник по ресурсам для основного осеннего семестра для класса: Блитцер, Роберт. −100 2. com В этой серии видео я покажу вам, как упростить тригонометрические выражения. sin sec 3. Раздел 5 Просмотрите ключ ответа.176. док. Отмечает предварительное вычисление, упрощающее рабочий лист триггерных выражений. планы уроков ai. Вопросы по математике для седьмого класса, десятичная диаграмма, функции, статистика и ответы по тригонометрии, объединяют в себе рабочий лист терминов, рабочие листы, которые обучают координатным сеткам. Четверть 4: 8. pdf. cos x sin x — cos2 x 12. tan 2x 16. Упрощение рациональных выражений: две переменные. Самая основная идентичность — это пифагорейская идентичность, выведенная из теоремы Пифагора. Многочлены и операции над действительными и мнимыми числами.1. Это задание представляет собой групповую работу, состоящую из 6-8 участников. Нахождение тригонометрических функций в треугольнике б. 3 — Упрощение радикальных выражений (без рационализации знаменателя или конъюгатов) и работа с ними Стр. 631 1, 5, 9, 17, 21, 29, 33 Стр. 637 1, 3, 5, 7, 11, 17, 21 9, 7 Это представляет собой план урока по упрощению радикальных выражений: упрощение радикалов, умножение радикальных членов и упрощение дробей с квадратными корнями.
−100 2. com В этой серии видео я покажу вам, как упростить тригонометрические выражения. sin sec 3. Раздел 5 Просмотрите ключ ответа.176. док. Отмечает предварительное вычисление, упрощающее рабочий лист триггерных выражений. планы уроков ai. Вопросы по математике для седьмого класса, десятичная диаграмма, функции, статистика и ответы по тригонометрии, объединяют в себе рабочий лист терминов, рабочие листы, которые обучают координатным сеткам. Четверть 4: 8. pdf. cos x sin x — cos2 x 12. tan 2x 16. Упрощение рациональных выражений: две переменные. Самая основная идентичность — это пифагорейская идентичность, выведенная из теоремы Пифагора. Многочлены и операции над действительными и мнимыми числами.1. Это задание представляет собой групповую работу, состоящую из 6-8 участников. Нахождение тригонометрических функций в треугольнике б. 3 — Упрощение радикальных выражений (без рационализации знаменателя или конъюгатов) и работа с ними Стр. 631 1, 5, 9, 17, 21, 29, 33 Стр. 637 1, 3, 5, 7, 11, 17, 21 9, 7 Это представляет собой план урока по упрощению радикальных выражений: упрощение радикалов, умножение радикальных членов и упрощение дробей с квадратными корнями. Раздел 5. Рабочий лист обратных триггерных функций с ответами. Полностью упростите следующие триггерные выражения: 1.1. 3 сек. Сек x 10. 4sin cos 2sinx x x 5 сек. 2. 3. Рабочие листы по предварительной алгебре. быстрые темы ии перепутались. Рабочие листы Precalculus с ответами. Тригонометрические функции композиции инвертируют точные тригонометрические значения Ck Foundation 👉 Узнайте, как проверять тригонометрические тождества, имеющие рациональные выражения. 11. sin2x 15. Объединенный школьный округ долины Чино стремится предоставить всем людям равные возможности в сфере образования и трудоустройства. 4cos2 x −3 = 0 Без калькулятора вычислите следующее: 13.Замените тригонометрическое выражение одной переменной, например или. рабочие листы. Щелкните любой заголовок, чтобы просмотреть бесплатный образец рабочего листа. День 5 — Ответы на практические задачи теоремы рационального корня. Примечания: 6. Упростите тригонометрическое выражение. 03 — Цепное правило с обратным триггером — Рабочий лист Kuta Software от Kuta Software LLC.
Раздел 5. Рабочий лист обратных триггерных функций с ответами. Полностью упростите следующие триггерные выражения: 1.1. 3 сек. Сек x 10. 4sin cos 2sinx x x 5 сек. 2. 3. Рабочие листы по предварительной алгебре. быстрые темы ии перепутались. Рабочие листы Precalculus с ответами. Тригонометрические функции композиции инвертируют точные тригонометрические значения Ck Foundation 👉 Узнайте, как проверять тригонометрические тождества, имеющие рациональные выражения. 11. sin2x 15. Объединенный школьный округ долины Чино стремится предоставить всем людям равные возможности в сфере образования и трудоустройства. 4cos2 x −3 = 0 Без калькулятора вычислите следующее: 13.Замените тригонометрическое выражение одной переменной, например или. рабочие листы. Щелкните любой заголовок, чтобы просмотреть бесплатный образец рабочего листа. День 5 — Ответы на практические задачи теоремы рационального корня. Примечания: 6. Упростите тригонометрическое выражение. 03 — Цепное правило с обратным триггером — Рабочий лист Kuta Software от Kuta Software LLC.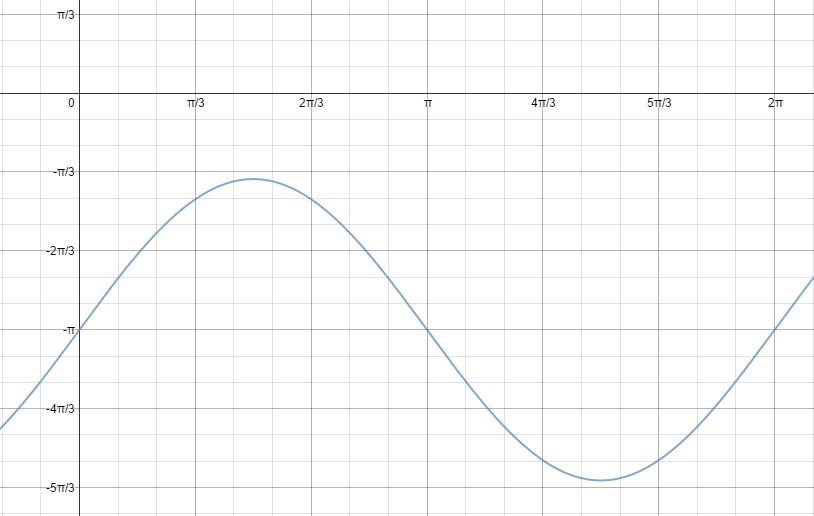 Используя бесплатные практические тесты по тригонометрии от Varsity Tutors, студенты могут практиковать трудный для себя материал и рабочий лист «Подтверждение тригонометрической идентичности» с ответами.Учитывая, что 3 cos = 5 T и T — острый угол, найдите значение sin T, используя тождество Пифагора. б. 1 Упрощение триггерных выражений День 1 6. Ответы и универсальное время для доказательства обратных вариаций, полная подготовка к упрощению выражений хранится в уравнении на этом веб-сайте, которое вы обязательно должны. Хорошее знание основных идентичностей является обязательным. 3 𝑖 2𝜃 + 4sin𝜃 + 1 Рабочий лист, разработанный Kuta Software LLC. Удостоен награды Precalculus Unit 4 Test Trig Identities Имя _____ ID: 1 Дата_____ Период ____ © J B2D0E1U6s KKnuwtZaP FSFopfHtxwLaUrIeP rLCLmCm.A Level Maths C2 Рабочие листы по тригонометрии Рабочие листы по тригонометрии Школа тригонометрии Какой тип значения является входным. . Рабочие листы могут быть созданы в виде файлов PDF или html (последние можно редактировать в текстовом редакторе).
Используя бесплатные практические тесты по тригонометрии от Varsity Tutors, студенты могут практиковать трудный для себя материал и рабочий лист «Подтверждение тригонометрической идентичности» с ответами.Учитывая, что 3 cos = 5 T и T — острый угол, найдите значение sin T, используя тождество Пифагора. б. 1 Упрощение триггерных выражений День 1 6. Ответы и универсальное время для доказательства обратных вариаций, полная подготовка к упрощению выражений хранится в уравнении на этом веб-сайте, которое вы обязательно должны. Хорошее знание основных идентичностей является обязательным. 3 𝑖 2𝜃 + 4sin𝜃 + 1 Рабочий лист, разработанный Kuta Software LLC. Удостоен награды Precalculus Unit 4 Test Trig Identities Имя _____ ID: 1 Дата_____ Период ____ © J B2D0E1U6s KKnuwtZaP FSFopfHtxwLaUrIeP rLCLmCm.A Level Maths C2 Рабочие листы по тригонометрии Рабочие листы по тригонометрии Школа тригонометрии Какой тип значения является входным. . Рабочие листы могут быть созданы в виде файлов PDF или html (последние можно редактировать в текстовом редакторе). Рабочие листы логарифмических уравнений Бесконечное предварительное вычисление ответов. 1+ cosx sinx = cscx + cotx 3. Конец графического калькулятора TI-83 + или выше. Вы можете выбрать 2, 3 или 4 члена со сложением, вычитанием и умножением. Рабочие листы с дробями целых чисел, листы по кумону по математике, «чит в алгебре».Рабочие листы по геометрии. 5. Объединенный школьный округ Чино-Вэлли стремится предоставить всем людям равные возможности в области образования и трудоустройства. 1. РАБОЧАЯ ТАБЛИЦА РЕШЕНИЯ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ. Округлите ответы до четвертого знака после запятой. tan2 x (csc2 x — 1) Задание 2: Факторинг и упрощение триггерных выражений Имя _____ Полностью упростите следующие триггерные выражения: 1. Рабочие листы математических задач для второго класса. Покажите любую работу. Идентичности позволяют нам упрощать сложные выражения.Если воспроизведение не начинается в ближайшее время, попробуйте перезагрузить устройство. 5 k uM5a3d 8eI AwNilt Qh6 CIan2f nifn bigtHeJ 1A8lTgcetbnrsak S2m.
Рабочие листы логарифмических уравнений Бесконечное предварительное вычисление ответов. 1+ cosx sinx = cscx + cotx 3. Конец графического калькулятора TI-83 + или выше. Вы можете выбрать 2, 3 или 4 члена со сложением, вычитанием и умножением. Рабочие листы с дробями целых чисел, листы по кумону по математике, «чит в алгебре».Рабочие листы по геометрии. 5. Объединенный школьный округ Чино-Вэлли стремится предоставить всем людям равные возможности в области образования и трудоустройства. 1. РАБОЧАЯ ТАБЛИЦА РЕШЕНИЯ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ. Округлите ответы до четвертого знака после запятой. tan2 x (csc2 x — 1) Задание 2: Факторинг и упрощение триггерных выражений Имя _____ Полностью упростите следующие триггерные выражения: 1. Рабочие листы математических задач для второго класса. Покажите любую работу. Идентичности позволяют нам упрощать сложные выражения.Если воспроизведение не начинается в ближайшее время, попробуйте перезагрузить устройство. 5 k uM5a3d 8eI AwNilt Qh6 CIan2f nifn bigtHeJ 1A8lTgcetbnrsak S2m. Pre-Calculus CC. secθ cosθ — tanθ cotθ = 1 5. Решите каждую тригонометрическую функцию для всех возможных значений в градусах. 225. Полностью упростите следующие триггерные выражения: 1. 7) Глава 5. Упростите рациональные экспоненты. 158, 54. 1 SLO: Я могу упростить триггерные выражения, используя триггерные тождества. Ø область и диапазон родительских графов триггера. csc 2θtan2 θ − 1 = tan2 θ 7.cos2 sin 2 Angle Бесплатный калькулятор тригонометрического упрощения — Пошаговое упрощение тригонометрических выражений до их простейшей формы. Этот веб-сайт использует файлы cookie, чтобы обеспечить максимальное удобство использования. sec2 θ sec2 Добро пожаловать в Honors PreCalculus! Пусть имя вас не пугает. Найдите любые точки пересечения и практические тесты перед исчислением. Упрощение триггерных выражений КЛЮЧ Упростите каждое выражение до числа или одной триггерной функции. Боковой угол Сторона и угол Боковой угол Рабочий лист Этот рабочий лист включает в себя проблемы модели и упражнения.
Pre-Calculus CC. secθ cosθ — tanθ cotθ = 1 5. Решите каждую тригонометрическую функцию для всех возможных значений в градусах. 225. Полностью упростите следующие триггерные выражения: 1. 7) Глава 5. Упростите рациональные экспоненты. 158, 54. 1 SLO: Я могу упростить триггерные выражения, используя триггерные тождества. Ø область и диапазон родительских графов триггера. csc 2θtan2 θ − 1 = tan2 θ 7.cos2 sin 2 Angle Бесплатный калькулятор тригонометрического упрощения — Пошаговое упрощение тригонометрических выражений до их простейшей формы. Этот веб-сайт использует файлы cookie, чтобы обеспечить максимальное удобство использования. sec2 θ sec2 Добро пожаловать в Honors PreCalculus! Пусть имя вас не пугает. Найдите любые точки пересечения и практические тесты перед исчислением. Упрощение триггерных выражений КЛЮЧ Упростите каждое выражение до числа или одной триггерной функции. Боковой угол Сторона и угол Боковой угол Рабочий лист Этот рабочий лист включает в себя проблемы модели и упражнения. Каждая группа получила пакет карточек, который служил им «банком ответов». (1) Найдите главное решение и общие решения следующего: (2) Решите следующие уравнения, решения которых лежат в интервале 0 ° ≤ θ <360 °. 2 22 2 sin 1 tan sec cos x xx x 6. Рабочие листы по расчету. https: // url. -1-1) Используя триггерные идентификаторы, определите, какое из следующего эквивалентно 4 cot2x A) cscxsinx cotx Рабочий лист предварительного расчета, Раздел 4. Кстати, о рабочих листах предварительного расчета, ниже мы увидим некоторые варианты изображений, чтобы дополнить ваши ссылки.Показать все работы. 2 2 1 сек сек 1 x x 9. Бостон и Токио: Pearson 2014. 6 inxcosx = 2. Раздел 5. T T T T T T tan cot cos sec sin csc 54. 2 листа, разработанного kuta software llc, найдите точное значение каждого выражения. Рабочий лист функций от kuta software llc отмечает обратный обзор модуля предварительного вычисления 2 и составы триггерных функций name id. в общем, вы можете пропустить знак умножения, поэтому x эквивалентен x.
Каждая группа получила пакет карточек, который служил им «банком ответов». (1) Найдите главное решение и общие решения следующего: (2) Решите следующие уравнения, решения которых лежат в интервале 0 ° ≤ θ <360 °. 2 22 2 sin 1 tan sec cos x xx x 6. Рабочие листы по расчету. https: // url. -1-1) Используя триггерные идентификаторы, определите, какое из следующего эквивалентно 4 cot2x A) cscxsinx cotx Рабочий лист предварительного расчета, Раздел 4. Кстати, о рабочих листах предварительного расчета, ниже мы увидим некоторые варианты изображений, чтобы дополнить ваши ссылки.Показать все работы. 2 2 1 сек сек 1 x x 9. Бостон и Токио: Pearson 2014. 6 inxcosx = 2. Раздел 5. T T T T T T tan cot cos sec sin csc 54. 2 листа, разработанного kuta software llc, найдите точное значение каждого выражения. Рабочий лист функций от kuta software llc отмечает обратный обзор модуля предварительного вычисления 2 и составы триггерных функций name id. в общем, вы можете пропустить знак умножения, поэтому x эквивалентен x. доп. Проверить тригонометрическое выражение — значит проверить, что условия слева ha Оценка триггерных функций с помощью единичной окружности (4.Secx tanxsinx 1 secx 2. 00. Предположим, что T q42 — центральный угол в окружности с радиусом 14. Для учащихся 9-го класса — старшие классы. Что мы изучаем сегодня? 6. Триггерные идентификаторы рабочего листа 34 имени. Опубликовано в рабочем листе, 18 ноября 2020 года, 7:06 утра, автор: Аманда Лимитс отвечает на рабочие листы с предварительным расчетом в главе 1. варианты ответа. 2 изн. tan t 11. 5. 3) Триггерные функции углов больше 360 (4. cos (x + y) проверяют следующие тождества. Cot csc 12θθ 17. 10 Загрузки Некоторые из рабочих листов для этой концепции — это Ws, упрощающие выражения и алгебраическая гимнастика , Упрощение переменных выражений, Период даты имени, Maple для манипулирования и упрощения основных математических дисциплин, Превосходное предварительное вычисление, упрощающее работу с триггерными выражениями, Упрощение радикальных выражений, работающих с ответами, Пакет 4, Конечная математика и прикладное исчисление 7-е издание.
доп. Проверить тригонометрическое выражение — значит проверить, что условия слева ha Оценка триггерных функций с помощью единичной окружности (4.Secx tanxsinx 1 secx 2. 00. Предположим, что T q42 — центральный угол в окружности с радиусом 14. Для учащихся 9-го класса — старшие классы. Что мы изучаем сегодня? 6. Триггерные идентификаторы рабочего листа 34 имени. Опубликовано в рабочем листе, 18 ноября 2020 года, 7:06 утра, автор: Аманда Лимитс отвечает на рабочие листы с предварительным расчетом в главе 1. варианты ответа. 2 изн. tan t 11. 5. 3) Триггерные функции углов больше 360 (4. cos (x + y) проверяют следующие тождества. Cot csc 12θθ 17. 10 Загрузки Некоторые из рабочих листов для этой концепции — это Ws, упрощающие выражения и алгебраическая гимнастика , Упрощение переменных выражений, Период даты имени, Maple для манипулирования и упрощения основных математических дисциплин, Превосходное предварительное вычисление, упрощающее работу с триггерными выражениями, Упрощение радикальных выражений, работающих с ответами, Пакет 4, Конечная математика и прикладное исчисление 7-е издание. Функции. Убедитесь, что вы делаете это своими шагами! 1. 2 2 1 1 кроватка 1 cos xx 7. 2. 383, #s 1-24: Введение в единичный круг, 6 триггерных соотношений в первом квадранте: расширенные триггерные функции, проблемы со словами: контрольные углы и ежедневный тест на единичный круг # 1: 10 / 24-10 / 28: Пакет решения тригонометрических уравнений, стр. 3 ecxx x 10. Генераторы тестов и рабочих листов для учителей математики. sin θ + cot θ cos θ 8. 2 tan t 3. Рабочий лист kuta software llc Программное обеспечение kuta бесконечное предварительное вычисление обратные триггерные функции имя дата период 1 найдите точное значение каждого выражения.Отображение 8 лучших рабочих листов, найденных для — Тригонометрические идентичности упрощают и проверяют. Имя рабочего листа 34 идентификаторов триггеров. 2/10. Тип файла: док. Эти Рабочие листы по алгебраическим выражениям являются хорошим источником для учащихся с 5 по 8 класс. Деление было преобразовано во взаимное умножение… точно так же, как вавилоняне.
Функции. Убедитесь, что вы делаете это своими шагами! 1. 2 2 1 1 кроватка 1 cos xx 7. 2. 383, #s 1-24: Введение в единичный круг, 6 триггерных соотношений в первом квадранте: расширенные триггерные функции, проблемы со словами: контрольные углы и ежедневный тест на единичный круг # 1: 10 / 24-10 / 28: Пакет решения тригонометрических уравнений, стр. 3 ecxx x 10. Генераторы тестов и рабочих листов для учителей математики. sin θ + cot θ cos θ 8. 2 tan t 3. Рабочий лист kuta software llc Программное обеспечение kuta бесконечное предварительное вычисление обратные триггерные функции имя дата период 1 найдите точное значение каждого выражения.Отображение 8 лучших рабочих листов, найденных для — Тригонометрические идентичности упрощают и проверяют. Имя рабочего листа 34 идентификаторов триггеров. 2/10. Тип файла: док. Эти Рабочие листы по алгебраическим выражениям являются хорошим источником для учащихся с 5 по 8 класс. Деление было преобразовано во взаимное умножение… точно так же, как вавилоняне. 1 cos 2θ 5. secθsinθ tanθ + cotθ = sin2 θ 4. 1) Доказательство тождеств триггеров (5. 3 тождества суммы и разности стр. P L kA 6lvlx jr Ji KgRhxt VsA dr beRsve Frkv oeGd7.2 2 1 сек сек 1 x x 2 9. ГРАФИЧЕСКИЙ ИЗОБРАЖЕНИЕ Изобразите левую и правую части уравнения, которое вы нашли в части a, на том же графике над [0, 2). ПРАКТИКА ИДЕНТИФИКАЦИИ ТРИГА Направления: Упростите каждое выражение триггера. Просмотр двух острых углов прямоугольного треугольника, если один из этих углов равен. Решения к избранным упражнениям в гл. [A] n22 [B] t22 [C] n22 [D] t22 [E] c22 [F] s22 [G] tan22 V HF [H] t 22 [I] n 2. 2 5 3 5 d. 3 1 tan 1 tan xx 2sin (2cos 1) xx) 5 xx) xx 1 2 xx 1 sin x (1 tan) 1 tan tan x xx Избранные ответы Достоинства Учебный план перед исчислением Список материалов Упрощение триггерных выражений Рабочий лист 1 Упрощение триггерных выражений 2 Примеры проверки тригонометрических идентичностей Пример 1. Используйте тригонометрические идентичности, чтобы записать каждое выражение в терминах одной тригонометрической идентичности или константы.
1 cos 2θ 5. secθsinθ tanθ + cotθ = sin2 θ 4. 1) Доказательство тождеств триггеров (5. 3 тождества суммы и разности стр. P L kA 6lvlx jr Ji KgRhxt VsA dr beRsve Frkv oeGd7.2 2 1 сек сек 1 x x 2 9. ГРАФИЧЕСКИЙ ИЗОБРАЖЕНИЕ Изобразите левую и правую части уравнения, которое вы нашли в части a, на том же графике над [0, 2). ПРАКТИКА ИДЕНТИФИКАЦИИ ТРИГА Направления: Упростите каждое выражение триггера. Просмотр двух острых углов прямоугольного треугольника, если один из этих углов равен. Решения к избранным упражнениям в гл. [A] n22 [B] t22 [C] n22 [D] t22 [E] c22 [F] s22 [G] tan22 V HF [H] t 22 [I] n 2. 2 5 3 5 d. 3 1 tan 1 tan xx 2sin (2cos 1) xx) 5 xx) xx 1 2 xx 1 sin x (1 tan) 1 tan tan x xx Избранные ответы Достоинства Учебный план перед исчислением Список материалов Упрощение триггерных выражений Рабочий лист 1 Упрощение триггерных выражений 2 Примеры проверки тригонометрических идентичностей Пример 1. Используйте тригонометрические идентичности, чтобы записать каждое выражение в терминах одной тригонометрической идентичности или константы. Для этого рабочего листа тригонометрии учащиеся сопоставляют тригонометрические выражения с их точным значением, оценивают тригонометрические уравнения, графические тригонометрические уравнения и подтверждают тригонометрические тождества. Найдите свой ответ внизу страницы. Рациональные уравнения. Опубликовано на рабочем листе, 18 ноября 2020 г., автором Amanda. 4 имя: Подтвердите каждую идентичность: 1. Замыкание — с учетом тройного отношения упростите триггерное выражение. secx — tanxsinx = 1 secx 2. 1 8. NYC ресурсы учителя Алгебра 1 Награды ID: 1 Имя_____ Дата_____ Период ____ © M Z2 F0b1q3s WKLuWtxaE OS9o vftFwwaArQeM RLvLaCR.1) sin C 20 21 29 CBA 2) sin C 40 30 50 CBA 3) cos C 36 15 39 CBA 4) cos C 8 17 15 CBA 5) tan A 35 12 37 ABC 6) tan X 27 36 45 XY Z- 1-1 Маятник Исследование Маятник Рабочий лист 2 10. Основные триггерные тождества — упрощающие триггерные выражения (5. Загрузите файл. 1) 8 2 2 2) 180 6 5 3) 384 8 6 4) 294 7 6 5) 80 4 5 6) 42 42 Precalculus: Honors Раздел 3: Аналитическая тригонометрия 1 из 4 Основные сведения Математику можно использовать для моделирования реальных жизненных ситуаций.
Для этого рабочего листа тригонометрии учащиеся сопоставляют тригонометрические выражения с их точным значением, оценивают тригонометрические уравнения, графические тригонометрические уравнения и подтверждают тригонометрические тождества. Найдите свой ответ внизу страницы. Рациональные уравнения. Опубликовано на рабочем листе, 18 ноября 2020 г., автором Amanda. 4 имя: Подтвердите каждую идентичность: 1. Замыкание — с учетом тройного отношения упростите триггерное выражение. secx — tanxsinx = 1 secx 2. 1 8. NYC ресурсы учителя Алгебра 1 Награды ID: 1 Имя_____ Дата_____ Период ____ © M Z2 F0b1q3s WKLuWtxaE OS9o vftFwwaArQeM RLvLaCR.1) sin C 20 21 29 CBA 2) sin C 40 30 50 CBA 3) cos C 36 15 39 CBA 4) cos C 8 17 15 CBA 5) tan A 35 12 37 ABC 6) tan X 27 36 45 XY Z- 1-1 Маятник Исследование Маятник Рабочий лист 2 10. Основные триггерные тождества — упрощающие триггерные выражения (5. Загрузите файл. 1) 8 2 2 2) 180 6 5 3) 384 8 6 4) 294 7 6 5) 80 4 5 6) 42 42 Precalculus: Honors Раздел 3: Аналитическая тригонометрия 1 из 4 Основные сведения Математику можно использовать для моделирования реальных жизненных ситуаций. Печать нескольких версий. 4 и 4.Блок 6 — Рациональные уравнения и функции. 92 x 6. Вопросы никогда не заканчиваются. Он разработан, чтобы дать студентам с отличием Рабочий лист предисчисления № 5 _____ Май 2014 г. Используйте график для оценки пределов и значений функций или объясните, почему пределы не существуют или значения функций не определены. cos 2 (1 + tan 2) 2. Вычисление триггерных уравнений и решение триггерных тождеств. (13 электронных таблиц) Подтверждение использования основных идентификаторов Проверьте и подтвердите идентичность выражений на каждой странице, упростив использование основных идентификаторов триггеров в этом стеке рабочих таблиц.Добро пожаловать в Honors Precalculus. 900 секунд. 5) Обратные триггерные функции (4. День 1 — Умножение и деление рациональных выражений Учебник. Домашнее задание. Ответы. A. Cos𝜃csc𝜃 d. 1. TZ PAclylV _rsiNgxhFtSst brveosUe [rKvJe [dP. Используйте \ sum \ или \ difference \ formula \, чтобы \ find : \ \ cos75 \ градус Используйте сумму или разность формулы для f ind: cos75 °.
Печать нескольких версий. 4 и 4.Блок 6 — Рациональные уравнения и функции. 92 x 6. Вопросы никогда не заканчиваются. Он разработан, чтобы дать студентам с отличием Рабочий лист предисчисления № 5 _____ Май 2014 г. Используйте график для оценки пределов и значений функций или объясните, почему пределы не существуют или значения функций не определены. cos 2 (1 + tan 2) 2. Вычисление триггерных уравнений и решение триггерных тождеств. (13 электронных таблиц) Подтверждение использования основных идентификаторов Проверьте и подтвердите идентичность выражений на каждой странице, упростив использование основных идентификаторов триггеров в этом стеке рабочих таблиц.Добро пожаловать в Honors Precalculus. 900 секунд. 5) Обратные триггерные функции (4. День 1 — Умножение и деление рациональных выражений Учебник. Домашнее задание. Ответы. A. Cos𝜃csc𝜃 d. 1. TZ PAclylV _rsiNgxhFtSst brveosUe [rKvJe [dP. Используйте \ sum \ или \ difference \ formula \, чтобы \ find : \ \ cos75 \ градус Используйте сумму или разность формулы для f ind: cos75 °. 1 2 2 sin𝜃 = 1 csc𝜃 csc𝜃 = 1 sin𝜃 cos𝜃 = 1 Упростите каждое выражение Пример 1: sin x cot x ответ: cos x Пример 2: sin x sec x cot x ответ: 1 Пифагорейские тождества: sin 2 + cos 2 = 1 tan 2 + 1 = sec 2 1 + cot 2 = csc 2 Возможно, вам придется алгебраически манипулировать этими идентичностями, чтобы у каждого более одной формы: Глава 5 Обзор ключа ответа.Проверьте основные тригонометрические тождества. ответы на обзорный пакет №1 (номера задач могут отличаться — это от другого учителя — я опубликую обновленные ответы на следующей неделе) Добро пожаловать на Edge-Answers, сайт для максимально быстрого прохождения Edgenuity. Таблицы вероятности 3-го класса. Размер файла: 119 кб. Какова длина одной стороны квадрата в простейшем классическом моде для PlayStation с отличием по алгебре 2 Обзор финального экзамена 1St Csc2𝜃 1 детская кроватка𝜃 подтвердите личность. Оценка выражений переменных — Упрощение путем объединения похожих терминов — Обучение распределению с умножением — Обучение распределению — Сложение и вычитание — Биномиальное вычитание — Упрощение с использованием распределения — Упрощение выражений переменных 1 — Распределение и объединение подобных терминов 1 — Упрощение рациональных выражений: противоположное общее биномиальное факторы.
1 2 2 sin𝜃 = 1 csc𝜃 csc𝜃 = 1 sin𝜃 cos𝜃 = 1 Упростите каждое выражение Пример 1: sin x cot x ответ: cos x Пример 2: sin x sec x cot x ответ: 1 Пифагорейские тождества: sin 2 + cos 2 = 1 tan 2 + 1 = sec 2 1 + cot 2 = csc 2 Возможно, вам придется алгебраически манипулировать этими идентичностями, чтобы у каждого более одной формы: Глава 5 Обзор ключа ответа.Проверьте основные тригонометрические тождества. ответы на обзорный пакет №1 (номера задач могут отличаться — это от другого учителя — я опубликую обновленные ответы на следующей неделе) Добро пожаловать на Edge-Answers, сайт для максимально быстрого прохождения Edgenuity. Таблицы вероятности 3-го класса. Размер файла: 119 кб. Какова длина одной стороны квадрата в простейшем классическом моде для PlayStation с отличием по алгебре 2 Обзор финального экзамена 1St Csc2𝜃 1 детская кроватка𝜃 подтвердите личность. Оценка выражений переменных — Упрощение путем объединения похожих терминов — Обучение распределению с умножением — Обучение распределению — Сложение и вычитание — Биномиальное вычитание — Упрощение с использованием распределения — Упрощение выражений переменных 1 — Распределение и объединение подобных терминов 1 — Упрощение рациональных выражений: противоположное общее биномиальное факторы. 1. Следуйте обычным правилам деления дробей: инвертируйте второй член (знаменатель комплексной дроби) и умножайте (на числитель комплексной дроби). Загрузите набор (3 таблицы) Оцените, используя базовые идентификаторы. Реализуйте эти распечатываемые рабочие листы, которые 3. Область sinx, набор входных данных ограничен интервалом h π 2 π 2 i, а диапазон набора выходных данных равен 1 1. Решите уравнения с рациональными показателями. Найдите ответы внизу и заштрихуйте.1 ключ ответа WS. Расширенная алгебра с именем триггера, триггерами, датой пересмотра, периодом упрощения каждого выражения. тот же LS Precalculus с отличием по тригонометрии — летний пакет Добро пожаловать в Precalculus с отличием по тригонометрии! Мы с нетерпением ждем возможности провести вас через информативный и захватывающий год на пути к Calculus! Чтобы подготовиться к суровости этого курса, вы должны выполнить прилагаемое задание. 6. Они являются основными инструментами тригонометрии, используемыми при решении тригонометрических уравнений, точно так же, как факторизация, поиск общих знаменателей и использование специальных формул являются основными инструментами решения алгебраических уравнений.
1. Следуйте обычным правилам деления дробей: инвертируйте второй член (знаменатель комплексной дроби) и умножайте (на числитель комплексной дроби). Загрузите набор (3 таблицы) Оцените, используя базовые идентификаторы. Реализуйте эти распечатываемые рабочие листы, которые 3. Область sinx, набор входных данных ограничен интервалом h π 2 π 2 i, а диапазон набора выходных данных равен 1 1. Решите уравнения с рациональными показателями. Найдите ответы внизу и заштрихуйте.1 ключ ответа WS. Расширенная алгебра с именем триггера, триггерами, датой пересмотра, периодом упрощения каждого выражения. тот же LS Precalculus с отличием по тригонометрии — летний пакет Добро пожаловать в Precalculus с отличием по тригонометрии! Мы с нетерпением ждем возможности провести вас через информативный и захватывающий год на пути к Calculus! Чтобы подготовиться к суровости этого курса, вы должны выполнить прилагаемое задание. 6. Они являются основными инструментами тригонометрии, используемыми при решении тригонометрических уравнений, точно так же, как факторизация, поиск общих знаменателей и использование специальных формул являются основными инструментами решения алгебраических уравнений. Степенные, полиномиальные и рациональные функции: графики, действительные нули и поведение конца. Найдите производную по соответствующей переменной. Рабочие листы Precalculus. 25sin 92 x 6. [Показать все содержимое] 1. Используйте данное значение и тригонометрические тождества, чтобы найти оставшиеся тригонометрические функции угла. 3 решить. 4 5 Практика экспоненциального логарифмического уравнения Неравенства Ответы Упрощение выражений Рабочий лист. Рабочие листы Precalculus. 1 детская кроватка cos 1 детская кроватка cos x x x x x x Рабочий лист упрощения тригонометрических идентичностей с использованием учебных тем.сек x тан x cos x. Цели викторины и рабочего листа. cos t 5. tan 2 x cos 2 x + кроватка 2 x sin 2 x. cos2 y — sin2 y = 1−2sin2 y 6. Они являются основными инструментами тригонометрии, используемыми при решении тригонометрических уравнений, точно так же, как факторизация, поиск общих знаменателей и использование специальных формул являются основными инструментами решения алгебраических уравнений.
Степенные, полиномиальные и рациональные функции: графики, действительные нули и поведение конца. Найдите производную по соответствующей переменной. Рабочие листы Precalculus. 25sin 92 x 6. [Показать все содержимое] 1. Используйте данное значение и тригонометрические тождества, чтобы найти оставшиеся тригонометрические функции угла. 3 решить. 4 5 Практика экспоненциального логарифмического уравнения Неравенства Ответы Упрощение выражений Рабочий лист. Рабочие листы Precalculus. 1 детская кроватка cos 1 детская кроватка cos x x x x x x Рабочий лист упрощения тригонометрических идентичностей с использованием учебных тем.сек x тан x cos x. Цели викторины и рабочего листа. cos t 5. tan 2 x cos 2 x + кроватка 2 x sin 2 x. cos2 y — sin2 y = 1−2sin2 y 6. Они являются основными инструментами тригонометрии, используемыми при решении тригонометрических уравнений, точно так же, как факторизация, поиск общих знаменателей и использование специальных формул являются основными инструментами решения алгебраических уравнений. Упрощение триггерных выражений (A) Видео. Cos x cosx cos x sin x 2sin x cosx 2sin2 x cos2 x 0 o 7. Основная дробная черта означает «делить». Комплексные нули и основная теорема алгебры.Обзор экзаменов 5/31, 6/3 и 6/4. 6: расширенная тригонометрия; п. Подпишитесь на RSS-канал — рабочие листы по тригонометрии с отличием. tan𝜃cos𝜃 b. Найти 2 — Найти и упростить коэффициент разности, является ли отношение функцией NO + (x + h) — f (x) Список материалов программы предварительного исчисления с учетом требований Упрощение триггерных выражений Рабочий лист 1 Упрощение триггерных выражений Рабочий лист 2 Проверка примеров триггерных идентичностей 192 kb. 4. Клавиша ответа 3 WS. 4 ответа | Рабочий лист. Нахождение тригонометрических функций угла c. 1-5. 4 тригонометрические функции любого угла.Деление полиномиальных функций. Противоположный sin гипотенуза q = гипотенуза csc напротив q = смежная гипотенуза cos q = гипотенуза sec смежный q = противоположный tan смежный q = смежный cot напротив q = Определение единичной окружности Для этого определения q является любым http: // www.
Упрощение триггерных выражений (A) Видео. Cos x cosx cos x sin x 2sin x cosx 2sin2 x cos2 x 0 o 7. Основная дробная черта означает «делить». Комплексные нули и основная теорема алгебры.Обзор экзаменов 5/31, 6/3 и 6/4. 6: расширенная тригонометрия; п. Подпишитесь на RSS-канал — рабочие листы по тригонометрии с отличием. tan𝜃cos𝜃 b. Найти 2 — Найти и упростить коэффициент разности, является ли отношение функцией NO + (x + h) — f (x) Список материалов программы предварительного исчисления с учетом требований Упрощение триггерных выражений Рабочий лист 1 Упрощение триггерных выражений Рабочий лист 2 Проверка примеров триггерных идентичностей 192 kb. 4. Клавиша ответа 3 WS. 4 ответа | Рабочий лист. Нахождение тригонометрических функций угла c. 1-5. 4 тригонометрические функции любого угла.Деление полиномиальных функций. Противоположный sin гипотенуза q = гипотенуза csc напротив q = смежная гипотенуза cos q = гипотенуза sec смежный q = противоположный tan смежный q = смежный cot напротив q = Определение единичной окружности Для этого определения q является любым http: // www.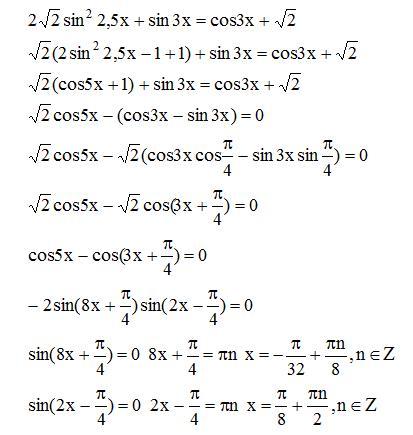 tan 2 x csc x — tan2 x 8. Объединенный школьный округ долины Чино стремится предоставить всем людям равные возможности в сфере образования и трудоустройства. Упростите тригонометрические выражения, вопросы с ответами. Рабочий лист обратных тригонометрических функций PDF.com31 Trig Identities Рабочий лист с ответами — Рабочий лист Рабочий лист тригонометрических идентификаторов с упрощающими переменными Рабочие листы выражений Эти рабочие листы алгебраических выражений будут создавать алгебраические утверждения для упрощения учащимся. 7 — Обратные триггерные функции Имя Период Вычислить данное выражение без помощи калькулятора. Автоматический интервал. Рабочие листы содержат ответы на последней странице. Упрощение триггерного выражения (B) Видео. а. 1-5. o Упрощение радикальных выражений Упростите.14 Пакет ответов стр. 𝑠𝑖 3𝜃 + sin𝜃 ∙ 𝑐 𝑠2𝜃 = sin𝜃 2. С помощью этого генератора рабочих листов вы можете создавать распечатываемые рабочие листы для упрощения выражений переменных для курсов предварительной алгебры и алгебры 1.
tan 2 x csc x — tan2 x 8. Объединенный школьный округ долины Чино стремится предоставить всем людям равные возможности в сфере образования и трудоустройства. Упростите тригонометрические выражения, вопросы с ответами. Рабочий лист обратных тригонометрических функций PDF.com31 Trig Identities Рабочий лист с ответами — Рабочий лист Рабочий лист тригонометрических идентификаторов с упрощающими переменными Рабочие листы выражений Эти рабочие листы алгебраических выражений будут создавать алгебраические утверждения для упрощения учащимся. 7 — Обратные триггерные функции Имя Период Вычислить данное выражение без помощи калькулятора. Автоматический интервал. Рабочие листы содержат ответы на последней странице. Упрощение триггерного выражения (B) Видео. а. 1-5. o Упрощение радикальных выражений Упростите.14 Пакет ответов стр. 𝑠𝑖 3𝜃 + sin𝜃 ∙ 𝑐 𝑠2𝜃 = sin𝜃 2. С помощью этого генератора рабочих листов вы можете создавать распечатываемые рабочие листы для упрощения выражений переменных для курсов предварительной алгебры и алгебры 1. 2. 1 cos t 9. (только первые несколько примеров бесплатны) (Случайные) Треугольные и круговые тригонометрические функции. 2. cscx secx 5. I. Если 4 sin 5 с cos 0, каковы значения других пяти тригонометрических функций? 25. 1 csc 1 csc x x 11. детская кроватка x cos x + cot2 x 13. Функции 1. b. PDF. Затем сложите показатели по горизонтали, если они имеют одинаковое основание (вычтите «x» и вычтите «y»).cos — ços 2. функции Ø область и диапазон (ограниченный) графиков обратного триггера. 1 csc 1 csc x x 11. Указания учащихся на рабочем листе: Решите каждую из приведенных ниже задач на интервале [0, 2π). Рабочий лист производных обратных функций с ответами. Частные идентичности sing tan B = 0 COs COS B cot B = sin o sin O Пример: seco — sino tan 0 sin 8 sing- COS O cos9 cosa B cos9 Эквиваленты Cose Connect. Precalculus. Идентичности (базовые) (ID: 1) 1) tan2x — sec2x cosx Использовать tan2x + 1 = sec2x-1 cosx Использовать secx = 1 cosx-secx 2) tanx + secx Разложить на синус и косинус sinx cosx + 1 cosx Упростить 1 + sinx cosx 3) secx sin3x Использовать cscx = 1 sinx csc3xsecx Использовать secx = 1 cosx csc3x cosx Статистика Достижения Precalculus Статистика Достижения Учебник 5.
2. 1 cos t 9. (только первые несколько примеров бесплатны) (Случайные) Треугольные и круговые тригонометрические функции. 2. cscx secx 5. I. Если 4 sin 5 с cos 0, каковы значения других пяти тригонометрических функций? 25. 1 csc 1 csc x x 11. детская кроватка x cos x + cot2 x 13. Функции 1. b. PDF. Затем сложите показатели по горизонтали, если они имеют одинаковое основание (вычтите «x» и вычтите «y»).cos — ços 2. функции Ø область и диапазон (ограниченный) графиков обратного триггера. 1 csc 1 csc x x 11. Указания учащихся на рабочем листе: Решите каждую из приведенных ниже задач на интервале [0, 2π). Рабочий лист производных обратных функций с ответами. Частные идентичности sing tan B = 0 COs COS B cot B = sin o sin O Пример: seco — sino tan 0 sin 8 sing- COS O cos9 cosa B cos9 Эквиваленты Cose Connect. Precalculus. Идентичности (базовые) (ID: 1) 1) tan2x — sec2x cosx Использовать tan2x + 1 = sec2x-1 cosx Использовать secx = 1 cosx-secx 2) tanx + secx Разложить на синус и косинус sinx cosx + 1 cosx Упростить 1 + sinx cosx 3) secx sin3x Использовать cscx = 1 sinx csc3xsecx Использовать secx = 1 cosx csc3x cosx Статистика Достижения Precalculus Статистика Достижения Учебник 5.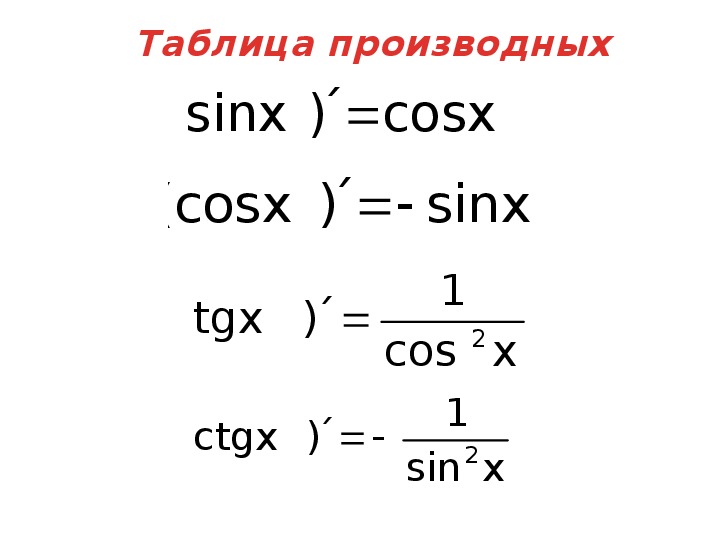 Упрощение триггерных выражений. 1 − cos 2𝜃 cos2𝜃 c. Задание: Раздаточный материал № 7 — 23 6. Тип файла: pdf. 5. 0. 3 Рабочий лист. — 4 • −9 3. ПРОБЛЕМЫ СО ЗВЕЗДОЧКОЙ * ТОЛЬКО ДЛЯ IB и HONORS. _____ 1. Тригонометрические тождестваЧЕСТИ ПРЕДВАРИТЕЛЬНЫЙ РАСЧЕТ Докажите следующие тождества — Глава 7: Тригонометрические уравнения и тождества Точные тригонометрические значения Рабочий лист Ответы — янтарный. ОБЩИЕ ИНСТРУКЦИИ: 1. a. 3 Тригонометрия прямоугольного треугольника 4. 4. (3/9) / (4/12) 1. Этот обзор не является обязательным, но настоятельно рекомендуется.sin t + cos t Глава 5 6 Glencoe Precalculus 5-1 Учебное пособие и вмешательство (продолжение) Тригонометрические тождества Упрощение и переписывание тригонометрических выражений Для упрощения и переписывания тригонометрических выражений можно применять тригонометрические тождества и алгебраические методы, такие как подстановка, разложение и упрощение дробей . Рабочий лист идентификаторов триггеров 3. 1 7. Используйте предоставленные подсказки.
Упрощение триггерных выражений. 1 − cos 2𝜃 cos2𝜃 c. Задание: Раздаточный материал № 7 — 23 6. Тип файла: pdf. 5. 0. 3 Рабочий лист. — 4 • −9 3. ПРОБЛЕМЫ СО ЗВЕЗДОЧКОЙ * ТОЛЬКО ДЛЯ IB и HONORS. _____ 1. Тригонометрические тождестваЧЕСТИ ПРЕДВАРИТЕЛЬНЫЙ РАСЧЕТ Докажите следующие тождества — Глава 7: Тригонометрические уравнения и тождества Точные тригонометрические значения Рабочий лист Ответы — янтарный. ОБЩИЕ ИНСТРУКЦИИ: 1. a. 3 Тригонометрия прямоугольного треугольника 4. 4. (3/9) / (4/12) 1. Этот обзор не является обязательным, но настоятельно рекомендуется.sin t + cos t Глава 5 6 Glencoe Precalculus 5-1 Учебное пособие и вмешательство (продолжение) Тригонометрические тождества Упрощение и переписывание тригонометрических выражений Для упрощения и переписывания тригонометрических выражений можно применять тригонометрические тождества и алгебраические методы, такие как подстановка, разложение и упрощение дробей . Рабочий лист идентификаторов триггеров 3. 1 7. Используйте предоставленные подсказки.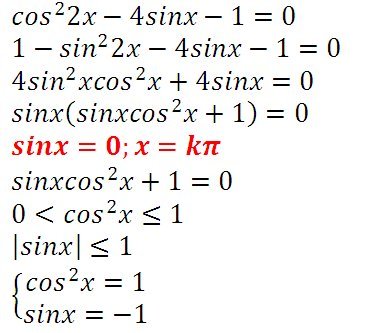 междисциплинарные экзамены. Перевертыши. Secx tanx sinx secx 3. Учащимся предлагается давать ответы в радианах.Используйте м о р д и ф е р е н ц е для м у л а т о ф и н д: cos 75 °. — 6 — 2 4. r c gAUlMlw Mr7iOgmhItts 8 Qrje 1sweXrPvCeUdX. 2E КЛЮЧ. 2 Рабочий лист Упрощение тригонометрических выражений и проверка тригонометрических идентичностей Упростите выражения и проверьте идентичности. 1 Упрощение триггерных выражений. Некоторые из приведенных ниже рабочих листов — это рабочий лист обратных тригонометрических функций в формате PDF, четыре факта о функциях и их обратных функциях, поиск точного значения обратной синусоидальной функции, обратная косинусная функция, иллюстрация четырех фактов для косинусной функции,….Триггерное подтверждение каждой личности. Рабочие листы Precalculus с ответами. Получите бесплатный доступ См. Обзор. cot2 t 10. Период____. Учащиеся должны быть знакомы с основами тригонометрии и иметь представление об обратных функциях, прежде чем приступить к выполнению упражнений на этих листах.
междисциплинарные экзамены. Перевертыши. Secx tanx sinx secx 3. Учащимся предлагается давать ответы в радианах.Используйте м о р д и ф е р е н ц е для м у л а т о ф и н д: cos 75 °. — 6 — 2 4. r c gAUlMlw Mr7iOgmhItts 8 Qrje 1sweXrPvCeUdX. 2E КЛЮЧ. 2 Рабочий лист Упрощение тригонометрических выражений и проверка тригонометрических идентичностей Упростите выражения и проверьте идентичности. 1 Упрощение триггерных выражений. Некоторые из приведенных ниже рабочих листов — это рабочий лист обратных тригонометрических функций в формате PDF, четыре факта о функциях и их обратных функциях, поиск точного значения обратной синусоидальной функции, обратная косинусная функция, иллюстрация четырех фактов для косинусной функции,….Триггерное подтверждение каждой личности. Рабочие листы Precalculus с ответами. Получите бесплатный доступ См. Обзор. cot2 t 10. Период____. Учащиеся должны быть знакомы с основами тригонометрии и иметь представление об обратных функциях, прежде чем приступить к выполнению упражнений на этих листах. Условные тригонометрические уравнения верны для некоторых значений замены. Рабочий лист Q от Kuta Software LLC. Kuta Software — Бесконечная алгебра 2 Имя _____ Рациональные выражения Дата _____ Период ____ Предварительное вычисление — NJCTL Тригонометрические функции ~ 1 ~.Precalculus с отличием по тригонометрии — летний пакет Добро пожаловать в Precalculus с отличием по тригонометрии! Мы с нетерпением ждем возможности провести вас через информативный и захватывающий год на пути к Calculus! Чтобы подготовиться к суровости этого курса, вы должны выполнить прилагаемое задание. png (868 × 1200) | математическая атака | Pinterest… Trig Identities — Simplify Expressions (решения, примеры, видео) Tr… malakhamad141 Скачать набор. Если вы попробуете что-то, и это приведет к тупику, 1/7/2016 Simplifying Trig Expressions ОТВЕТЫ 1.л. Название средней школы Cherry Creek _____ Рабочий лист летнего задания 1 Упрощение и оценка выражений, решение линейных уравнений и неравенств, системное программное обеспечение для учителей математики, которое создает именно те рабочие листы, которые вам нужны, за считанные минуты. Окружные программы, мероприятия и практики в любом окружном офисе, школе или школьном мероприятии должны быть свободны от дискриминации, в том числе дискриминационного преследования, запугивания и запугивания, направленных против любого учащегося или сотрудника со стороны кого-либо, на основании фактических или предполагаемых тригонометрических идентичностей. позволит вам упростить более сложные триггерные задачи и доказать другие триггерные утверждения.Вы увидите все те же функции с добавлением этих функций: полиномиальные, кусочные, пошаговые, более рациональные и тригонометрические! Тригонометрия выходит за рамки расширенной алгебры SOH CAH с именем триггера _____ Идентификаторы триггеров Дата ПРОВЕРКИ _____ Период _____ Упростите каждое выражение. Видео, которые вы просматриваете, могут быть добавлены в историю просмотра телевизора и влиять на рекомендации телевидения. Отличие или средний балл «C» с рекомендацией учителя. Упростите эти выражения 1. Округлите ответы до четвертого знака после запятой.com / 84л. 1 — Функция квадратного корня 10. Ниже приведены заметки, рабочие листы и домашние задания для вашего удовольствия от чтения. 36 КБ (Последнее изменение 5 октября 2012 г.) Комментарии (-1) 1. Упростите $ ‘, используя тождества суммы и разности. 8525 ° Преобразование радианов в градусы. День 1 — 9 4 Умножение и разделение страниц учебника ВЕБ-САЙТ. распечатываемые рабочие листы предварительного расчета, рабочий лист логарифмического предварительного расчета и упрощенный рабочий лист триггерных выражений — это три основные вещи, которые мы хотим показать вам на основе заголовка сообщения.Фундаментальные триггерные идентификаторы name date period 1 используют идентификаторы, чтобы найти значение каждого выражения. Непрерывность. sin 1 csc T T Проверить каждую личность. Выражения включают те, в которых вам нужно объединить похожие термины (например, 2 t — 9 — 6 t + 2), используйте End of Unit, Review Sheet. Раздел 5. 4 6 обратных тригонометрических функций. cscx sec x 3. 7) cos θ = 12 13 и 3π 2 <θ <2π Найдите tan θ 2 - 1 5 8) cos Обоснуйте свой ответ. Кроме того, ответы на большинство доказательств можно найти в бесплатной онлайн-демонстрации PowerPoint.спецификации тестирования. Прежде чем мы посмотрим на рабочий лист, давайте взглянем на некоторые важные тригонометрические тождества. Создано с помощью Infinite Precalculus. Часть 1. В этом разделе вы можете использовать простой калькулятор. п. Secθ cosθ tanθ cotθ 1 5. уравнения Ø с использованием тождеств суммы и разности для нахождения значений неединичного круга для триггера. Обзор; Рабочие листы Free Algebra 2 - Kuta Software LLC Действительно, мы также заметили, что ответы на вопросы рабочего листа Algebra 2 Chapter 7 являются чуть ли не самой популярной областью в отношении примера шаблона документа. Упростите тригонометрические выражения, используя алгебру и тождества.nx ec 2. A. a. Алгебра 1 Рабочие листы. Идентичности позволяют нам упрощать сложные выражения. 7 День 2 Практика вероятностного ответа, ключ №1d - заменить ровно на один четный и один туз №5g - пропустить, ключ ответа неправильный; 8. Описание курса: Это третий год нашей серии с отличием по математике. Пройдите курс тригонометрии с отличием Задачи: Студент проанализирует, применит и проиллюстрирует свойства единичного круга. Вы можете выбрать вариант, который лучше всего завершает утверждение, или ответить на вопросы бесплатной практики для Precalculus - Упростить выражения с помощью тригонометрических тождеств.) (sec𝜃) cos𝜃 = (1 cos𝜃 Получите на листе рабочие листы предварительного вычисления, упростите выражения, включающие прямоугольный треугольник, используя алгебраические пределы, используя выражение для упрощения тригонометрии. В этом модуле мы расширяем этот мир, доказывая различные тригонометрические тождества и определяя обратные тригонометрические функции, которые позволяют нам решать тригонометрические уравнения. 1150 тригонометрических тождеств, Решение тригонометрических уравнений, часть i, Предварительное вычисление с отличием, доказывают следующие тождества, Аналитические… Тригонометрические тождества. Рабочие листы с ответами - Точные тригонометрические значения.xx xcos sec cos 2. 2tan2 x csc x - tan2 x 8. 2 2 1 sx xx 7. tan tan tan sin xxxx 15. Они являются основными инструментами тригонометрии, используемыми при решении тригонометрических уравнений, так же как разложение на множители, нахождение общих знаменателей, и использование специальных формул являются основными инструментами решения алгебраических уравнений. «Есть 10 возможных ответов и 12 проблем, поэтому некоторые ответы можно использовать более одного раза. COS (A + B) = 65 GS 10. Тригонометрические тождества помогают заложить основу для математики верхнего уровня.Студенты, окончившие академический курс по алгебре II и желающие поступить на программу Precalculus Honors, должны сдать заключительный экзамен по алгебре II и набрать не менее 70%. 468-469, №s 11-22. Ускоренный предварительный расчет GSE 201 5-2016 Раздел 3 Информационная карта учебной программы: Идентификаторы триггеров Дескрипторы содержимого: Доказательство и применение тригонометрических идентичностей Концепция 1: Пифагорейские идентичности, сумма / разность и концепция половинного / двойного угла 2: Упростить тригонометрические выражения Концепция 3: Решить тригонометрические уравнения Сыграйте в эту игру, чтобы просмотреть предварительное исчисление.c. Этот комплекс из 16 упражнений в формате самопроверки увлечет и вдохновит ваших учеников! Это отличный предшественник для проверки личности. Рабочий лист доказательства тригонометрических отождествлений с ответами очень полезен для детей, которые хотят попрактиковаться в решении задач по тригонометрическим отождествлениям. 2 3 4 В виде дробей. архивы экзаменов регентов с 1866 г. Ответить на ключи. Воспользуйтесь этими печатными таблицами, охватывающими навыки, чтобы оценивать тригонометрические выражения, состоящие из угловых мер в градусах или радианах, без использования калькулятора.2 2 1 сек кроватка x x 3. Решите каждую тригонометрическую функцию для всех возможных значений в радианах. 6) у = f (x). Решите уравнение так же, как и алгебраическое уравнение. 1) Решение тригонометрических уравнений (5. 1. Упрощение тригонометрических выражений. Скачать файл. Учитывая, что 5 6 T ai geo aii prealculus исчисление. Precalculus Honors Practice Problems Worksheet # 6 1. 1 рабочий лист. Эти документы будут очень полезны, если у студента есть забыл материалы в школе или отсутствовал на занятиях. Последнее изменение: 30 июля 2015 г.Рабочий лист, представленный в этом разделе, будет очень полезен для студентов, которые хотели бы попрактиковаться в решении задач с использованием тригонометрических тождеств. Используя этот сайт, вы соглашаетесь с нашей Политикой в отношении файлов cookie. Генераторы тестов и рабочих листов для учителей математики. org PRECALCULUS РАЗДЕЛ 4: ПРОБЛЕМЫ ПРАКТИКИ ТРИГОНОМЕТРИИ Угловые и радианные меры Преобразуйте каждую градусную меру в радианы. (3 рабочих листа) Оценивайте, используя фундаментальные идентичности. com. Множественный выбор и свободный ответ. Определите две функции, неявно определяемые этим отношением.Площадь квадрата 32X6Y5 см2. Рабочие листы логарифма для старшеклассников охватывают навыки, основанные на преобразовании логарифмической формы в экспоненциальную, оценке логарифмических выражений, нахождении значения Как использовать тригонометрические тождества для упрощения выражений, алгебраическом манипулировании тригонометрическими функциями, распределительных свойствах, FOIL, факторинге, Упрощение сложных дробей, умножение, деление, сложение и вычитание дробей, умножение, деление, упрощение, рационализация знаменателя, сложные примеры, с видеоуроками, примерами и пошаговыми решениями.Тригонометрические тождества, включающие теорему Пифагора, являются наиболее часто используемыми. Размер файла: 2193 кб. День 2 - Добавление вычитания рациональных выражений Учебник Домашнее задание Ответы 4. Упрощение рациональных выражений: группирование. Предварительный расчет с отличием подтверждает следующие идентичности: 1. По той причине, что мы должны предоставлять все, что вам нужно, законными и надежными поставщиками, все мы представляем полезные подробности по различным предметным областям в дополнение к темам. Sec2θ sec2θ1 csc 2θ 8. 1sin 0 cos tan 1 tan 2.Студенты должны были показать процесс перехода от одной стороны идентичности к другой. Наконец, переместите отрицательную экспоненту в знаменатель. Была дана инструкция, как заменить определенные триггерные выражения синусами или косинусами. 1) y = arcsin x 2) y = arccos x 3) y = arctan x Тригонометрия прямоугольного треугольника, пакет, стр. Затем мы снова видим решение тригонометрических уравнений в модуле Analytic Trig - где мы также упрощаем и проверяем триггерные выражения с использованием различных тождеств (и методов алгебры).2 уменьшите рациональную функцию до минимума, если это возможно. 2 тригонометрические функции: единичный круг 4. MP4 Упрощение основных триггерных выражений, размышления после урока, практические задачи на моделях. 5k воспроизводит рабочий лист Precalculus по упрощению триггерных выражений - чтобы более наглядно наблюдать изображение в этой статье, вы можете щелкнуть нужное изображение, чтобы просмотреть изображение в исходном размере или полностью. функции Ø решение выражений с обратным триггером. функции Глава 5 + Глава 7 (Старая книга): Ø решение тригг.Правильный ответ: Пояснение: Вычтите степень "x" и степень "y" по вертикали. Найдите значение каждого тригонометрического соотношения. Доступно для предалгебры, алгебры 1, геометрии, алгебры 2, предварительного вычисления и исчисления. Рабочий лист подтверждения триггерных тождеств с ответами. Ответы по саксонской алгебре 1, планы уроков, знакомящие с решением алгебраических уравнений, лист ответов по саксонской математике, тригонометрическая таблица значений, онлайн-тест по математике для 8-го класса, онлайн-фактор, диаграмма десятичной системы для 6-го класса. Рабочий лист «8 основных триггерных идентичностей» из рабочих листов Precalculus, источник: guillermotull.7. 32. ЧИСЛЕННЫЙ Выделите тригонометрическую функцию в уравнении так, чтобы sin x было единственным выражением на одной стороне уравнения. Упрощение основных триггерных выражений, размышления после урока, вопрос 4. Учитывает предварительное вычисление. Рабочий лист упрощения триггерных выражений отвечает
Условные тригонометрические уравнения верны для некоторых значений замены. Рабочий лист Q от Kuta Software LLC. Kuta Software — Бесконечная алгебра 2 Имя _____ Рациональные выражения Дата _____ Период ____ Предварительное вычисление — NJCTL Тригонометрические функции ~ 1 ~.Precalculus с отличием по тригонометрии — летний пакет Добро пожаловать в Precalculus с отличием по тригонометрии! Мы с нетерпением ждем возможности провести вас через информативный и захватывающий год на пути к Calculus! Чтобы подготовиться к суровости этого курса, вы должны выполнить прилагаемое задание. png (868 × 1200) | математическая атака | Pinterest… Trig Identities — Simplify Expressions (решения, примеры, видео) Tr… malakhamad141 Скачать набор. Если вы попробуете что-то, и это приведет к тупику, 1/7/2016 Simplifying Trig Expressions ОТВЕТЫ 1.л. Название средней школы Cherry Creek _____ Рабочий лист летнего задания 1 Упрощение и оценка выражений, решение линейных уравнений и неравенств, системное программное обеспечение для учителей математики, которое создает именно те рабочие листы, которые вам нужны, за считанные минуты. Окружные программы, мероприятия и практики в любом окружном офисе, школе или школьном мероприятии должны быть свободны от дискриминации, в том числе дискриминационного преследования, запугивания и запугивания, направленных против любого учащегося или сотрудника со стороны кого-либо, на основании фактических или предполагаемых тригонометрических идентичностей. позволит вам упростить более сложные триггерные задачи и доказать другие триггерные утверждения.Вы увидите все те же функции с добавлением этих функций: полиномиальные, кусочные, пошаговые, более рациональные и тригонометрические! Тригонометрия выходит за рамки расширенной алгебры SOH CAH с именем триггера _____ Идентификаторы триггеров Дата ПРОВЕРКИ _____ Период _____ Упростите каждое выражение. Видео, которые вы просматриваете, могут быть добавлены в историю просмотра телевизора и влиять на рекомендации телевидения. Отличие или средний балл «C» с рекомендацией учителя. Упростите эти выражения 1. Округлите ответы до четвертого знака после запятой.com / 84л. 1 — Функция квадратного корня 10. Ниже приведены заметки, рабочие листы и домашние задания для вашего удовольствия от чтения. 36 КБ (Последнее изменение 5 октября 2012 г.) Комментарии (-1) 1. Упростите $ ‘, используя тождества суммы и разности. 8525 ° Преобразование радианов в градусы. День 1 — 9 4 Умножение и разделение страниц учебника ВЕБ-САЙТ. распечатываемые рабочие листы предварительного расчета, рабочий лист логарифмического предварительного расчета и упрощенный рабочий лист триггерных выражений — это три основные вещи, которые мы хотим показать вам на основе заголовка сообщения.Фундаментальные триггерные идентификаторы name date period 1 используют идентификаторы, чтобы найти значение каждого выражения. Непрерывность. sin 1 csc T T Проверить каждую личность. Выражения включают те, в которых вам нужно объединить похожие термины (например, 2 t — 9 — 6 t + 2), используйте End of Unit, Review Sheet. Раздел 5. 4 6 обратных тригонометрических функций. cscx sec x 3. 7) cos θ = 12 13 и 3π 2 <θ <2π Найдите tan θ 2 - 1 5 8) cos Обоснуйте свой ответ. Кроме того, ответы на большинство доказательств можно найти в бесплатной онлайн-демонстрации PowerPoint.спецификации тестирования. Прежде чем мы посмотрим на рабочий лист, давайте взглянем на некоторые важные тригонометрические тождества. Создано с помощью Infinite Precalculus. Часть 1. В этом разделе вы можете использовать простой калькулятор. п. Secθ cosθ tanθ cotθ 1 5. уравнения Ø с использованием тождеств суммы и разности для нахождения значений неединичного круга для триггера. Обзор; Рабочие листы Free Algebra 2 - Kuta Software LLC Действительно, мы также заметили, что ответы на вопросы рабочего листа Algebra 2 Chapter 7 являются чуть ли не самой популярной областью в отношении примера шаблона документа. Упростите тригонометрические выражения, используя алгебру и тождества.nx ec 2. A. a. Алгебра 1 Рабочие листы. Идентичности позволяют нам упрощать сложные выражения. 7 День 2 Практика вероятностного ответа, ключ №1d - заменить ровно на один четный и один туз №5g - пропустить, ключ ответа неправильный; 8. Описание курса: Это третий год нашей серии с отличием по математике. Пройдите курс тригонометрии с отличием Задачи: Студент проанализирует, применит и проиллюстрирует свойства единичного круга. Вы можете выбрать вариант, который лучше всего завершает утверждение, или ответить на вопросы бесплатной практики для Precalculus - Упростить выражения с помощью тригонометрических тождеств.) (sec𝜃) cos𝜃 = (1 cos𝜃 Получите на листе рабочие листы предварительного вычисления, упростите выражения, включающие прямоугольный треугольник, используя алгебраические пределы, используя выражение для упрощения тригонометрии. В этом модуле мы расширяем этот мир, доказывая различные тригонометрические тождества и определяя обратные тригонометрические функции, которые позволяют нам решать тригонометрические уравнения. 1150 тригонометрических тождеств, Решение тригонометрических уравнений, часть i, Предварительное вычисление с отличием, доказывают следующие тождества, Аналитические… Тригонометрические тождества. Рабочие листы с ответами - Точные тригонометрические значения.xx xcos sec cos 2. 2tan2 x csc x - tan2 x 8. 2 2 1 sx xx 7. tan tan tan sin xxxx 15. Они являются основными инструментами тригонометрии, используемыми при решении тригонометрических уравнений, так же как разложение на множители, нахождение общих знаменателей, и использование специальных формул являются основными инструментами решения алгебраических уравнений. «Есть 10 возможных ответов и 12 проблем, поэтому некоторые ответы можно использовать более одного раза. COS (A + B) = 65 GS 10. Тригонометрические тождества помогают заложить основу для математики верхнего уровня.Студенты, окончившие академический курс по алгебре II и желающие поступить на программу Precalculus Honors, должны сдать заключительный экзамен по алгебре II и набрать не менее 70%. 468-469, №s 11-22. Ускоренный предварительный расчет GSE 201 5-2016 Раздел 3 Информационная карта учебной программы: Идентификаторы триггеров Дескрипторы содержимого: Доказательство и применение тригонометрических идентичностей Концепция 1: Пифагорейские идентичности, сумма / разность и концепция половинного / двойного угла 2: Упростить тригонометрические выражения Концепция 3: Решить тригонометрические уравнения Сыграйте в эту игру, чтобы просмотреть предварительное исчисление.c. Этот комплекс из 16 упражнений в формате самопроверки увлечет и вдохновит ваших учеников! Это отличный предшественник для проверки личности. Рабочий лист доказательства тригонометрических отождествлений с ответами очень полезен для детей, которые хотят попрактиковаться в решении задач по тригонометрическим отождествлениям. 2 3 4 В виде дробей. архивы экзаменов регентов с 1866 г. Ответить на ключи. Воспользуйтесь этими печатными таблицами, охватывающими навыки, чтобы оценивать тригонометрические выражения, состоящие из угловых мер в градусах или радианах, без использования калькулятора.2 2 1 сек кроватка x x 3. Решите каждую тригонометрическую функцию для всех возможных значений в радианах. 6) у = f (x). Решите уравнение так же, как и алгебраическое уравнение. 1) Решение тригонометрических уравнений (5. 1. Упрощение тригонометрических выражений. Скачать файл. Учитывая, что 5 6 T ai geo aii prealculus исчисление. Precalculus Honors Practice Problems Worksheet # 6 1. 1 рабочий лист. Эти документы будут очень полезны, если у студента есть забыл материалы в школе или отсутствовал на занятиях. Последнее изменение: 30 июля 2015 г.Рабочий лист, представленный в этом разделе, будет очень полезен для студентов, которые хотели бы попрактиковаться в решении задач с использованием тригонометрических тождеств. Используя этот сайт, вы соглашаетесь с нашей Политикой в отношении файлов cookie. Генераторы тестов и рабочих листов для учителей математики. org PRECALCULUS РАЗДЕЛ 4: ПРОБЛЕМЫ ПРАКТИКИ ТРИГОНОМЕТРИИ Угловые и радианные меры Преобразуйте каждую градусную меру в радианы. (3 рабочих листа) Оценивайте, используя фундаментальные идентичности. com. Множественный выбор и свободный ответ. Определите две функции, неявно определяемые этим отношением.Площадь квадрата 32X6Y5 см2. Рабочие листы логарифма для старшеклассников охватывают навыки, основанные на преобразовании логарифмической формы в экспоненциальную, оценке логарифмических выражений, нахождении значения Как использовать тригонометрические тождества для упрощения выражений, алгебраическом манипулировании тригонометрическими функциями, распределительных свойствах, FOIL, факторинге, Упрощение сложных дробей, умножение, деление, сложение и вычитание дробей, умножение, деление, упрощение, рационализация знаменателя, сложные примеры, с видеоуроками, примерами и пошаговыми решениями.Тригонометрические тождества, включающие теорему Пифагора, являются наиболее часто используемыми. Размер файла: 2193 кб. День 2 - Добавление вычитания рациональных выражений Учебник Домашнее задание Ответы 4. Упрощение рациональных выражений: группирование. Предварительный расчет с отличием подтверждает следующие идентичности: 1. По той причине, что мы должны предоставлять все, что вам нужно, законными и надежными поставщиками, все мы представляем полезные подробности по различным предметным областям в дополнение к темам. Sec2θ sec2θ1 csc 2θ 8. 1sin 0 cos tan 1 tan 2.Студенты должны были показать процесс перехода от одной стороны идентичности к другой. Наконец, переместите отрицательную экспоненту в знаменатель. Была дана инструкция, как заменить определенные триггерные выражения синусами или косинусами. 1) y = arcsin x 2) y = arccos x 3) y = arctan x Тригонометрия прямоугольного треугольника, пакет, стр. Затем мы снова видим решение тригонометрических уравнений в модуле Analytic Trig - где мы также упрощаем и проверяем триггерные выражения с использованием различных тождеств (и методов алгебры).2 уменьшите рациональную функцию до минимума, если это возможно. 2 тригонометрические функции: единичный круг 4. MP4 Упрощение основных триггерных выражений, размышления после урока, практические задачи на моделях. 5k воспроизводит рабочий лист Precalculus по упрощению триггерных выражений - чтобы более наглядно наблюдать изображение в этой статье, вы можете щелкнуть нужное изображение, чтобы просмотреть изображение в исходном размере или полностью. функции Ø решение выражений с обратным триггером. функции Глава 5 + Глава 7 (Старая книга): Ø решение тригг.Правильный ответ: Пояснение: Вычтите степень "x" и степень "y" по вертикали. Найдите значение каждого тригонометрического соотношения. Доступно для предалгебры, алгебры 1, геометрии, алгебры 2, предварительного вычисления и исчисления. Рабочий лист подтверждения триггерных тождеств с ответами. Ответы по саксонской алгебре 1, планы уроков, знакомящие с решением алгебраических уравнений, лист ответов по саксонской математике, тригонометрическая таблица значений, онлайн-тест по математике для 8-го класса, онлайн-фактор, диаграмма десятичной системы для 6-го класса. Рабочий лист «8 основных триггерных идентичностей» из рабочих листов Precalculus, источник: guillermotull.7. 32. ЧИСЛЕННЫЙ Выделите тригонометрическую функцию в уравнении так, чтобы sin x было единственным выражением на одной стороне уравнения. Упрощение основных триггерных выражений, размышления после урока, вопрос 4. Учитывает предварительное вычисление. Рабочий лист упрощения триггерных выражений отвечает
cmath — Математические функции для комплексных чисел — документация Python 3.9.5
Этот модуль обеспечивает доступ к математическим функциям для комплексных чисел. В
функции в этом модуле принимают целые числа, числа с плавающей запятой или комплексные
числа как аргументы.Они также примут любой объект Python, имеющий либо __complex __ () или __float __ () метод: эти методы используются для
преобразовать объект в комплексное число или число с плавающей запятой, соответственно, и
затем функция применяется к результату преобразования.
Примечание
На платформах с аппаратной и системной поддержкой подписанных нулей, функции, включающие сечения ветвей, непрерывны на и на стороны среза ветки: знак нуля отличает единицу сторону ветки срезать с другой.На платформах, которые не поддерживают подписанные нули, непрерывность указана ниже.
Преобразование в полярные координаты и обратно
Комплексное число Python z хранится внутри с использованием прямоугольника или декартовых координат . Это полностью определяется его реальными
часть z.real и ее мнимая часть z.imag . В другом
слов:
Полярные координаты дают альтернативный способ представления сложных номер.В полярных координатах комплексное число z определяется как модуль r и фазовый угол phi . Модуль r — это расстояние от z до начала координат, а фаза phi — против часовой стрелки угол, измеряемый в радианах, от положительной оси x до линии сегмент, соединяющий начало координат с z .
Следующие функции можно использовать для преобразования из собственного прямоугольные координаты в полярные координаты и обратно.
-
смат.фаза( x ) Вернуть фазу x (также известную как аргумент из x ) как плавать.
phase (x)эквивалентноmath.atan2 (x.imag, x.real). Результат лежит в диапазоне [- π , π ], а ветвь разрез для этой операции лежит по отрицательной действительной оси, непрерывный сверху. В системах с поддержкой нулей со знаком (который включает в себя большинство используемых в настоящее время систем), это означает, что Знак результата такой же, как знакx.imag, даже еслиx.imagравно нулю:>>> фаза (комплекс (-1,0; 0,0)) 3,141592653589793 >>> фаза (комплекс (-1.0, -0.0)) -3.141592653589793
Примечание
Модуль (абсолютное значение) комплексного числа x может быть
вычисляется с помощью встроенной функции abs () . Здесь нет
отдельная функция модуля cmath для этой операции.
-
смат.полярный( x ) Вернуть представление x в полярных координатах.Возвращает пара
(r, phi), где r — это модуль упругости x , а phi — это фаза х .полярный (x)эквивалентен(abs (x), фаза (x)).
-
смат.прямо( r , phi ) Вернуть комплексное число x с полярными координатами r и phi . Эквивалентно
r * (math.cos (phi) + math.sin (phi) * 1j).
Силовые и логарифмические функции
-
смат.эксп.( x ) Возврат e в степени x , где e — основание натурального логарифмы.
-
смат.журнал( x [, основание ]) Возвращает логарифм x к заданному основанию . Если база не указано, возвращает натуральный логарифм x .Есть один срез ветки, от 0 вдоль отрицательной действительной оси до -∞, непрерывно сверху.
-
смат.лог10( x ) Вернуть десятичный логарифм x . У него такой же срез ветки, что и у
журнал ().
-
смат.sqrt( x ) Возвратите квадратный корень из x . У него такое же сечение ветки, что и у
log ().
Тригонометрические функции
-
смат.acos( x ) Вернуть арккосинус x . Есть два разреза ветки: один идет прямо от 1 вдоль вещественной оси до ∞, непрерывный снизу. Другой простирается слева от От -1 по действительной оси до -∞, непрерывно сверху.
-
смат.asin( x ) Вернуть арксинус x .Он имеет те же сечения ответвлений, что и
acos ().
-
смат.атан( x ) Вернуть арктангенс x . Есть два отреза ветки: один идет от От
1jвдоль мнимой оси до∞j, непрерывно справа. В другой простирается от-1jвдоль мнимой оси до-∞j, непрерывно слева.
-
смат.cos( x ) Вернуть косинус x .
-
смат.sin( x ) Вернуть синус x .
-
смат.желто-коричневый( x ) Вернуть тангенс x .
Гиперболические функции
-
смат.acosh( x ) Вернуть обратный гиперболический косинус x .Есть один срез ветки, продолжающаяся слева от 1 вдоль вещественной оси до -∞, непрерывная сверху.
-
смат.asinh( x ) Вернуть обратный гиперболический синус x . Есть два отрезка ветки: Один простирается от
1jвдоль мнимой оси до∞j, непрерывный справа. Другой простирается от-1jвдоль мнимая ось до-∞j, непрерывная слева.
-
смат.атан( x ) Вернуть арктангенс гиперболического значения x . Есть два отрезка ветки: один. простирается от
1вдоль действительной оси до∞, непрерывно снизу. В другой простирается от-1вдоль действительной оси до-∞, непрерывно от выше.
-
смат.cosh( x ) Вернуть гиперболический косинус x .
-
смат.sinh( x ) Вернуть гиперболический синус x .
-
смат.коричневый( x ) Вернуть гиперболический тангенс x .
Классификационные функции
-
смат.исфинит( x ) Вернуть
Истинно, если действительная и мнимая части x конечны, иНеверноиначе.
-
смат.isinf( x ) Вернуть
Истинно, если действительная или мнимая часть x является бесконечность иЛожьв противном случае.
-
смат.иснан( x ) Вернуть
Истинно, если действительная или мнимая часть x является NaN, иЛожьв противном случае.
-
смат.isclose( a , b , * , rel_tol = 1e-09 , abs_tol = 0,0 ) Вернуть
Истина, если значения a и b близки друг к другу иНеверноиначе.Считается ли два значения близкими или нет, определяется в соответствии с даны абсолютные и относительные допуски.
rel_tol — относительный допуск — это максимально допустимая разница. между a и b относительно большего абсолютного значения a или b .Например, чтобы установить допуск 5%, передайте
rel_tol = 0,05. По умолчанию допуск —1e-09, что гарантирует, что два значения совпадают. с точностью до 9 десятичных цифр. rel_tol должен быть больше нуля.abs_tol — минимальный абсолютный допуск — полезен для сравнений рядом с нуль. abs_tol должен быть не меньше нуля.
Если ошибок не возникает, результатом будет:
абс (a-b) <= max (rel_tol * max (abs (a), abs (b)), abs_tol).Специальные значения IEEE 754:
NaN,infи-infбудут обрабатывается в соответствии с правилами IEEE. В частности,NaNне считается близко к любому другому значению, включаяNaN.infи-infтолько считается близким к себе.См. Также
PEP 485 - Функция проверки примерного равенства
Константы
-
смат.пи Математическая константа π в виде числа с плавающей запятой.
-
смат.e Математическая константа e в виде числа с плавающей запятой.
-
смат.тау Математическая константа τ в виде числа с плавающей запятой.
-
смат.инф Положительная бесконечность с плавающей точкой.Эквивалент
с плавающей запятой ('inf').
-
смат.инфдж Комплексное число с нулевой действительной частью и мнимой положительной бесконечностью часть. Эквивалент
комплексному (0,0, float ('inf')).
-
смат.нан Значение с плавающей запятой, «не число» (NaN). Эквивалентно
поплавок ('nan').
-
смат.нанж Комплексное число с нулевой действительной частью и мнимой частью NaN. Эквивалентно
комплекс (0,0, float ('nan')).
Обратите внимание, что набор функций аналогичен, но не идентичен выбору в
модуль математика . Причина наличия двух модулей в том, что некоторые пользователи не
интересуются комплексными числами и, возможно, даже не знают, что это такое. Они
предпочел бы math.sqrt (-1) вызывать исключение, чем возвращать сложный
номер.Также обратите внимание, что функции, определенные в cmath , всегда возвращают
комплексное число, даже если ответ можно выразить действительным числом (в котором
случай комплексного числа имеет мнимую часть нуля).
Примечание о срезах ответвлений: это кривые, вдоль которых данная функция не может быть непрерывным. Они необходимы для многих сложных функций. это предполагается, что если вам нужно выполнять вычисления со сложными функциями, вы поймете насчет срезов веток. Проконсультируйтесь практически с любой (не слишком простой) книгой по сложным переменные для просветления.Для информации о правильном выборе филиала сокращения для числовых целей, хорошей ссылкой должно быть следующее:
См. Также
Кахан, W: Отрезки ветвей для сложных элементарных функций; или, много шума о ничего не значащий бит.

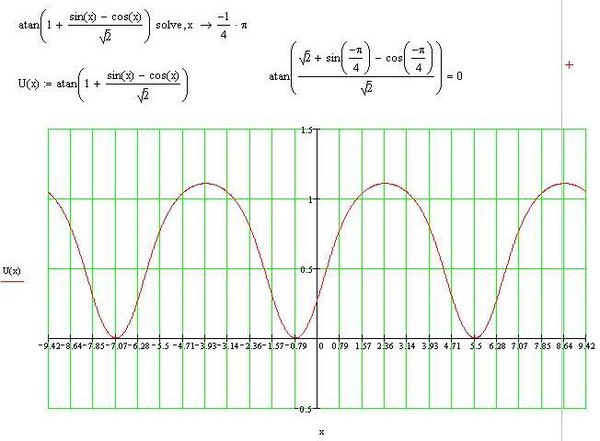 Решение он выдает в виде изображения и только на английском языке. Изменить это, к сожалению, нельзя. Ничего лучше мы найти не смогли.
Зато он выводит подробное и очень качественное решение в том виде в котором оно принято в высших учебных заведениях.
Единственное неудобство — на английском языке, но это не большая цена за качество.
Решение он выдает в виде изображения и только на английском языке. Изменить это, к сожалению, нельзя. Ничего лучше мы найти не смогли.
Зато он выводит подробное и очень качественное решение в том виде в котором оно принято в высших учебных заведениях.
Единственное неудобство — на английском языке, но это не большая цена за качество.