2+n-72)=1/(n+9)Функция y = sqrt(x) | Учебно-методический материал по алгебре (8 класс):
Учитель Вербовая Валерия Михайловна
Тема «Функция , ее свойства и график»
Цели:
- Образовательная – обобщение, систематизация знаний функции , ее графика и свойств, закрепление умения и навыков по применению полученных знаний к решению задач.
- Воспитательная – формирование целостного восприятия окружающего мира.
- Развивающая – развитие памяти, внимания, математической логики, познавательного интереса, применения учебной информации в нестандартных ситуациях.
Оборудование: набор инструментов, компьютер, проектор, экран.
ХОД УРОКА
1. Приветствие (Приложение 1, слайд 1)
2. Втупительное слово
Учитель: (Приложение 1, слайд 2) Вдумайтесь в слова русского ученого, основоположника аэродинамики Николая Егоровича Жуковского: «В математике есть своя красота, как в живописи и в поэзии».
Надеюсь сегодня на уроке мы сможем это прочувствовать.
Тема нашего обобщающего урока «Функция , ее свойства и график».
Открыли тетради и записали: Дата. Классная работа. Тему урока.
3. Опрос пройденного материала
– Для начала повторим, что мы знаем о функции
Задание 1. На доске построить график функции , и перечислить все ее свойства.(вызвать одного ученика)
4. Проверка домашней работы
– Пока ученик готовится, мы проверим домашнюю работу. Открыли тетради с выполненной домашней работой. Были заданы два номера.
№1. (Приложение 1, слайды 3, 4)
– Постройте график функции . По графику найдите:
а) наибольшее и наименьшее значения функции на отрезке [3; 9];
б) значение x при котором y > 1.
№2. (Приложение 1, слайд 5)
Дана функция . Решите уравнение
(Проверка д.р. на экране)
4. Устная работа (проводится, если ученик у доски еще не готов)
(Приложение 1, слайд 5).
1) Вычислите:
2) Решите уравнение:
(Приложение 1, слайд 6)
Выслушать 1-го ученика, поставить оценку.
5. Отработка знаний, умений, навыков (Приложение 1, слайд 7)
Зная функцию , ее свойства и график мы можем решать много разных и интересных задач. Рассмотрим одну из них.
№1. Решить уравнения:
(Приложение 1, слайд 8)
– Продолжить урок мне хотелось бы словами Гегеля: «То, чем в прежние эпохи занимались зрелые умы ученых мужей, в более поздние времена стало доступно пониманию мальчишек».
Двум учащимся было дано творческое задание, изучить одно из открытий Архимеда (Приложение 1, слайд 9) и применить его для решения задачи. Послушаем их сообщение.
1 ученик. Древнегреческий философ Архимед вычисляя площади разных фигур, получил следующий результат: (Приложение 1, слайд 10) если вершина графика у = х2 совпадет с вершиной прямоугольника, расположенного так как показано на рисунке 1, то площадь прямоугольника делится параболой в отношении 2 : 1.
Так как (Приложение 1, слайд 11) графики функций у = х2 и при симметричны относительно прямой у = х, то график функции также делит соответствующий прямоугольник в отношении 2 : 1.
2 ученик. Рассмотрим применение этого факта!
№3.(Приложение 1, слайд 12) Найти площадь фигуры ограниченной графиками функций , х = 9, у = 0.
Решение:
)
Рис 1 |
Учащиеся получают отметки.
– Решим задание из учебника. (Приложение 1, слайд 13)
№ 12.10.
Нарисуйте фигуру ограниченную графиками функций:
(вызвать ученика к доске)
– Мы можем найти площадь полученной фигуры? Давайте применим смекалку и новое свойство функции.
Решение:
(ученик получает оценку)
№ 13.47 (Приложение 1, слайд 14)
Решите уравнение:
(2-е учеников получают оценку)
№ 12.26 (если останется время) (Приложение 1, слайд 15)
Постройте на координатной плоскости фигуру, ограниченную графиком функции , прямой у = 6 – х и осью абсцисс, и укажите все точки с целыми координатами, принадлежащие этой фигуре.
6. Самостоятельная работа в виде теста (Приложение 2, Приложение 1, слайд 16)
7. Итог урока
– Сегодня на уроке мы применяли свойства и график функции к решению различных задач. Открыли дневники и записали домашнее задание:
№ 12.07(а), № 12.10(б), № 13.47(в, г). (Приложение 1, слайд 17)
№ 12.07 (а) Решите графически уравнение .
№ 12.10 (б) Нарисуйте фигуру ограниченную графиками функций y= и y = x2.
13.47(в,г) Решите уравнение: (x – 3)( + 1) = 0, (x – 3)( – 1) = 0
– Закончить урок (Приложение 1, слайд 18) мне хотелось бы поучительным стихотворением, где жизненная ситуация описывается функцией:
Вот предо мной кривая; абсциссы – это даты;
И следует запомнить, что деньги – ординаты.
Когда звенит в кармане, кривая – на подъем;
Когда карман пустеет – по ней мы вниз идем.
Когда-то при получке был ход кривой высок,
Но вскоре, волей-неволей, мы шли под изволок.
Все это – в милом прошлом, а нынче – тяжело!
Под ось абсцисс кривую, к несчастью, увлекло.
Конечно, в этой песне не новые слова:
И жизнь дороже стала, и денег-то едва!
Но вам моя кривая поможет затвердить:
Не трать ты больше денег, чем можешь получить!
(Франсуа Граф, известный архитектор-дизайнер)
(Приложение 1, слайд 19)
Литература:
- А.Г. Мордкович, Н.П. Николаев. Алгебра. 8 класс. В 2 ч. Ч. 1. Учебник;
- Л. И. Звавич, А.Р. Рязановский. Алгебра. 8 класс. В 2ч. Ч. 2. Задачник;
- Шейнина Щ.С., Соловьева Г.М. Математика. Занятия школьного кружка.
- Л.А.Александрова под редакцией А.Г.Мордковича. Алгебра. 8 класс. Самостоятельные работы для учащихся общеобразовательных учреждений.
Найдите область определения функции y= корень квадратный … -reshimne.ru
Новые вопросы
Ответы
ООФ то что под корнем ≥0 ⇒
х³-5х²+6х≥0
чтобы решить это неравенство разложим на множители левую часть
х(х²-5х+6)=х(х²-2х-3х+6)=х(х(х-2)-3(х-2))=х(х-2)(х-3)≥0
решим неравенство методом интервалов,
нанесем корни х={0;2;3} на числовую ось и определим знаки выражения х(х-2)(х-3) (1) на каждом из этих интервалов, для этого надо взять любое число из каждого интервала подставить вместо х в выражение 1 и посмотреть с каким знаком получится значение выражения если >0 то+ если <0 то —
например при х=10 10*(10-2)(10-3)=10*8*7=560>0 знак + , знаки на остальных интервалах можно не вычислять они будут чередоваться плюс с минусом так как функция у=х(х-2)(х-3) непрерывная см.
-1/3 помогите пожалуйста!!…
Математика
Литература
Алгебра
Русский язык
Геометрия
Английский язык
ХимияФизика
Биология
Другие предметы
История
Обществознание
Окружающий мир
География
Українська мова
Українська література
Қазақ тiлi
Беларуская мова
Информатика
Экономика
Музыка
Право
Французский язык
Немецкий язык
МХК
ОБЖ
Психология
3
Ключ к практическому экзамену II
Практический экзамен II
Без калькулятора
Задача 1: Нарисуйте график следующих функций
А.
Решение: Это тот, который у вас подозревается запомнил. График показан ниже.
Б.
Решение: Этот график также предполагается запомнить. График показан ниже.
С.
Решение: Это кусочная функция с лучом, слева от (2,1), сплошная точка на (2,3), и луч справа от (2,0).
Д.
Решение: Это график абсолютного значения в форма «V». «-» заставляет его перевернуться. Вершина находится в точка (2,1). «3» растягивает его до наклона 3 и -3.
г.
Задача 2: Определите пересечения, вершину и ось симметрии. Затем используйте эту информацию, чтобы нарисовать график.
Раствор
Чтобы найти перехват и , просто подключите x . = 0, чтобы получить:
y -пересечение: (0,6)
Чтобы найти точки пересечения, подставьте 0 для у получить:
0 = 2 x 2 — 8 x + 6
Теперь размножьте, чтобы получить
0 = 2( x -3)( x- 1)
Это имеет решение x = 3 или x = 1.
x -перехваты находятся по адресу:
x — пересечения: (1,0) и (3,0)
Чтобы найти координату вершины x , вычислите — б /2 а = -(-8)/[(2)(2)] = 2
Чтобы найти y -координату вершины, подключите обратно, чтобы получить
2(2) 2 -8(2) + 6 = -2
Вершина имеет координаты
вершин = (2,-2)
Ось симметрии проходит по координате x вершины, то есть
. ось симметрии: x = 2
Мы можем использовать всю информацию выше, чтобы получить график, показанный ниже:
г.
Задача 3: Решите неравенство.
Сначала вычтите 7 x с обеих сторон, чтобы установить правая часть равна 0,
x 2 — 7 x + 6 > 0
Следующий фактор
( х -1)( х -6) > 0
Ключевые значения x :
x = 1 и х = 6
Затем поместите эти значения в числовую строку.
Поместите параболу, которая
вогнутая вверх (так как коэффициент x 2 является положительным).
Так как нам нужна часть, которая больше или равна 0, решение — внешние части или
Задача 4: Рассмотрите многочлен ниже.
г.A. Перечислите действительные нули и кратности
Раствор
Нули — это когда функция равна нулю, а кратности полномочия. Следовательно, нули находятся по адресу:
.x = 0: Множественность 1
x = -1: Множественность 2
x = 1: Множественность 3
B. Определить, пересекает ли график 9 или касается его1815 x -ось на каждом x -перехвате.
Раствор
График будет пересекать ось x , если
кратность нечетная. Таким образом, график пересекает ось x в точке х = 0 и х = 1.
График касается оси x в точке x = -1.
C. Определите максимальное количество поворотных точек на графике.
Решение
Поскольку степень многочлена равна 6 = (1+2+3), граф имеет не более 5 поворотных точек.
D. Определите поведение. То есть найти силовую функцию, которая график f напоминает при больших значениях | х |.
Раствор
Поведение графика похоже на член высшей степени. термин высшей степени x 6 . Таким образом, она резко уменьшается вниз сверху в крайнем левом углу и резко возрастает вверх в крайнем правом углу.
г.Калькулятор
Проблема 5: Ниже показан график у = f ( х ). Эскиз график y = 1/3 f (- x ) — 2.
Раствор
Ключевыми точками этого графика являются (-3,-1),
(0,4) и (6,0).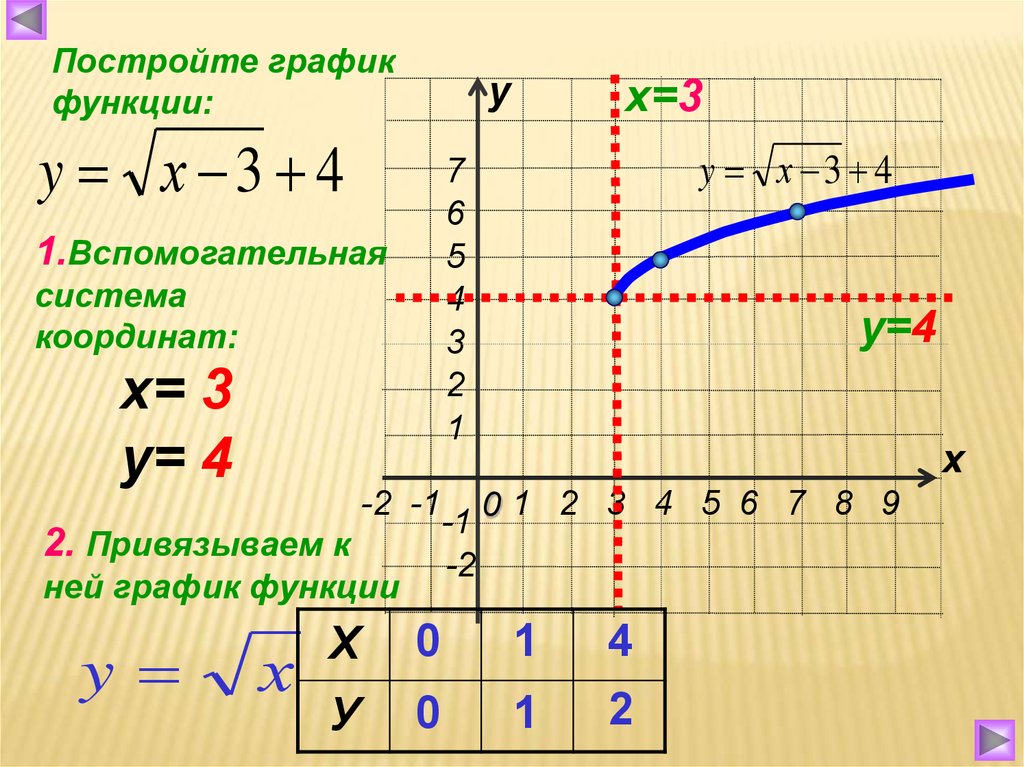
Соответствующие точки нового графика: (3,-2 1/3),
(0,-2/3) и (-6,-2).
Они получаются либо при подключении к новой функции, либо при первом
отражение по оси Y, затем деление на 3, а затем добавление
2. Форма будет включать отражение
вертикальная линия, масштаб на 1/3 и сдвиг вниз на
2. График показан ниже.
Задача 6: Прямоугольник вписан в полуокружность радиус 4, как показано ниже. Позволять P = ( x , y ) точка в первый квадрант, являющийся вершиной прямоугольника и лежащий на окружности.
А. Экспресс площадь А прямоугольник как функция x
Решение:
Поскольку площадь прямоугольника равна произведению основания на высоту, мы замечаем, что основание 2x, а высота y который является квадратным корнем из (16 -х 2 ). Сейчас площадь
B. Выразите периметр p прямоугольник как функция x .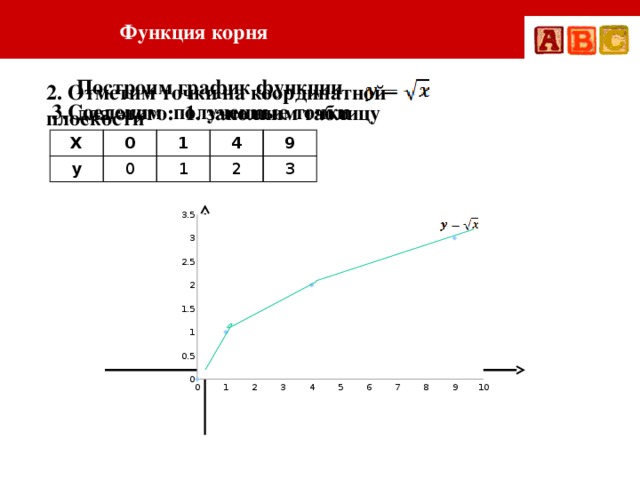
Раствор
Периметр равен сумме сторон. База 2x, а высота равна квадратному корню из (9-х 2 ). Таким образом, периметр равен
.
C. Для какого значения x A самый большой? Что это за самый большой A ?
Раствор
Для этого вопроса мы можем использовать наш калькулятор, чтобы построить график функции, а затем использовать максимальную функцию, чтобы найти, что это происходит примерно в x = 2,828 и A = 16,
.
Г. Для чего нужно значение 91 815 x 91 816? р самый большой? Какой самый большой p ?
Раствор
Для этого вопроса мы можем использовать наш калькулятор, чтобы построить график функции, а затем использовать максимальную функцию, чтобы найти, что это происходит примерно в x = 3,58 и p = 17.89.
Проблема 7: Два набора данных ниже представляют два
разные дистанции бегуна (в милях) в зависимости от времени (в секундах).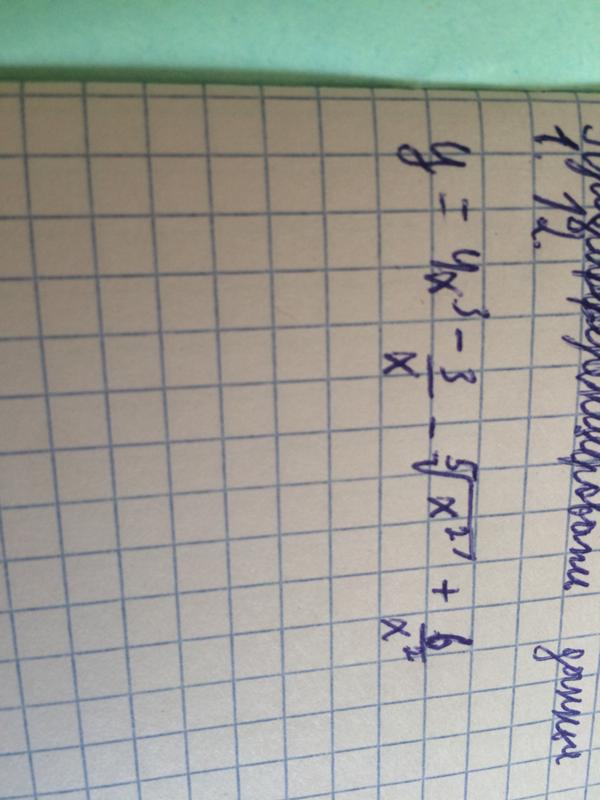
Для каждого из
на них зарисовать график диаграммы рассеяния. Затем определите, является ли линейный
модель или квадратичная модель лучше всего описывает график. Эскиз этих лучших
аппроксимирующая кривая на диаграмме рассеяния. Если это линия, интерпретируйте
склон. Затем используйте свою модель, чтобы предсказать время каждого на расстоянии
6 миль.
| Первый бегун | Второй бегун | ||||||||||||||||||||||||||||||||||||||||||||||
|
|
Раствор
График рассеяния первых бегунов показан ниже.
Поскольку точки почти
лежат на линии, мы используем линию линейной регрессии. Чтобы предсказать бегуна
время в 6 милях, мы подключаем 6
в линейное уравнение, чтобы получить:
Время = (7.1)(6) — 0,6 = 42
Обратите внимание, что точечная диаграмма для второго набора данных не близка к линейной, а близок к параболической форме. Мы используем кривую квадратичной регрессии, как показано ниже. Уравнение квадратичный равен
Время = 1,8x 2 — 5,39x + 15,65 = 48,4
Задача 8: Уравнение спроса на продажу х литров свежий морковный сок в магазине здоровой пищи по цене р долларов дает
x ( p ) = -6 p + 50
A. Найдите доход как функцию p .
Раствор
Доход равен количеству проданных товаров, умноженному на x цена р . Таким образом,
R(x) = (-6p + 50)p = -6p 2 + 50р
г.