Как найти квадратный корень из x график
Источник изображения: Pixabay.com
Вы столкнетесь с квадратным корнем x График. на уроках исчисления и геометрии. Работу, связанную с графиками, легко понять, даже если у вас нет большого математического опыта. Нарисуйте графики, чтобы сопровождать уравнения, чтобы помочь вам найти ответы без труда.
Быстрая навигация
Что такое квадратные корни?
Графики
Как учиться
Изучите все, что можно, о квадратных корнях, прежде чем использовать графики для решения поставленных задач. Квадратный корень — это число, умноженное само на себя. Квадратные корни используются для измерения пространств и зданий. Есть также много других научных и реальных применений квадратных корней.
Что такое квадратные корни?
Квадратные корни обозначаются добавлением двойки (обычно называемой возведением в квадрат или умножением числа на 2) над числом, которое вы умножаете.
Если вы вычисляете квадратный корень числа, вам нужно найти число, которое было возведено в квадрат в первую очередь. Например, три — это квадратный корень из девяти. Три в квадрате равно девяти, а квадратный корень из девяти равен трем. Все квадраты и квадратные корни отображаются парами.
Существует множество различных квадратных корней, включая десятичные квадраты, квадратные квадраты и квадратные корни для отрицательных чисел.
Квадратные корни большинства чисел не являются целыми и их легко определить. Вы, наверное, знаете наизусть квадратные корни из четырех и девяти, но как насчет пяти или семи? Квадратный корень из семи равен 2,64575131106!
Вы будете использовать калькулятор или таблицу для определения большинства квадратных корней. Тем не менее, некоторые учителя могут захотеть, чтобы вы поняли это от руки или, по крайней мере, знали ручной процесс определения нечетных квадратных корней.
Извлекать квадратные корни вручную можно по телефону:
Добавление нуля перед числами с нечетным количеством цифр перед запятой
Добавление нуля в конец, если после запятой стоит нечетное количество цифр
Убедитесь, что у вас есть четное количество цифр для работы с
После корректировки чисел нарисуйте диаграмму с областями и используйте ее для определения квадратного корня.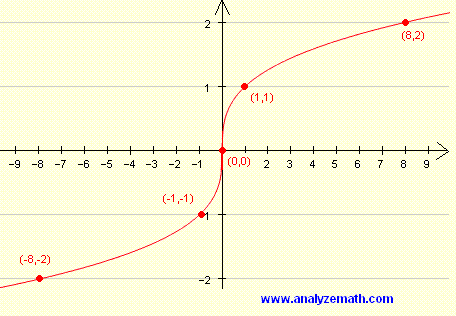 Вам, вероятно, не придется часто использовать этот метод, но он поможет вам понять метод, лежащий в основе определения квадратных корней. Ваш учитель может порекомендовать другие ручные методы.
Вам, вероятно, не придется часто использовать этот метод, но он поможет вам понять метод, лежащий в основе определения квадратных корней. Ваш учитель может порекомендовать другие ручные методы.
Квадратные корни используются фабричными рабочими, инженерами и учеными. Квадратные корни используются для вычисления объема и площади. Когда вы ищете новый дом или квартиру, квадратные корни помогают определить реальный размер комнаты. Например, квартира площадью 400 квадратных футов равна 20 на 20 футов.
Плотники используют квадратный корень для определения размеров здания и помещения.
Графики
Вы можете рисовать графики на своем компьютере или смартфоне. Придерживайтесь старой школы и используйте миллиметровую бумагу или калькулятор для решения задач, если хотите. Визуальное представление уравнения всегда поможет вам более эффективно рассчитать ответ.
Определите переменную в уравнении и найдите точку на графике для функции. Купите графический калькулятор, если вам нужно решить множество задач с квадратным корнем. Графический калькулятор показывает построенные графики и имеет возможности тангенса, синуса и косинуса. Вы можете купить эти калькуляторы онлайн или в Staples или Office Depot.
Купите графический калькулятор, если вам нужно решить множество задач с квадратным корнем. Графический калькулятор показывает построенные графики и имеет возможности тангенса, синуса и косинуса. Вы можете купить эти калькуляторы онлайн или в Staples или Office Depot.
Пример №1
Вот пример того, как найти квадратный корень из x-графика , который включает таблицу. Определите область для этого уравнения, определите таблицу значений функции f и начертите ее. Потом определитесь с диапазоном.
Уравнение: f(x) равно квадратному корню из (x квадрат минус 9). Найдите область определения функции, где х в квадрате минус 9 больше или равно нулю. Домен показан минусом 00 , минус 3 U (3 плюс 00 ).
Теперь найдите значения x в области f и составьте таблицу значений. Учтите, что f(x) равно f (отрицательный x). Проверьте симметрию графика и ось Y, чтобы определить ответ.
Диапазон F обозначается (0 плюс 00 ).
Пример #2
Определите график подкоренного числа (числа под радикалом) и составьте таблицу значений функции f, а также график f и определите его диапазон.
F(x) равно квадратному корню из x в квадрате плюс 4x плюс 6. Вы завершаете квадрат, переписывая числа под квадратным корнем следующим образом:
X в квадрате плюс 4x плюс шесть равно (x плюс 2) в квадрате плюс 2
Выражение под квадратным корнем положительное. Следовательно, область определения f состоит из всех действительных чисел. График (x плюс 2) в квадрате плюс 2 или парабола. График функции f имеет ту же ось симметрии. X равен двум вертикальным линиям, расположенным над графиком. Таблица графиков может быть записана численно как:
Х равно квадратному корню из (х плюс два в квадрате плюс 2). На графике минус 2 равняется 1,4, ноль равен 2,4, два равняется 4,2, а четыре равняется 6,2
Диапазон f показан интервалом квадратный корень из 2 плюс 00 .
Пример №3
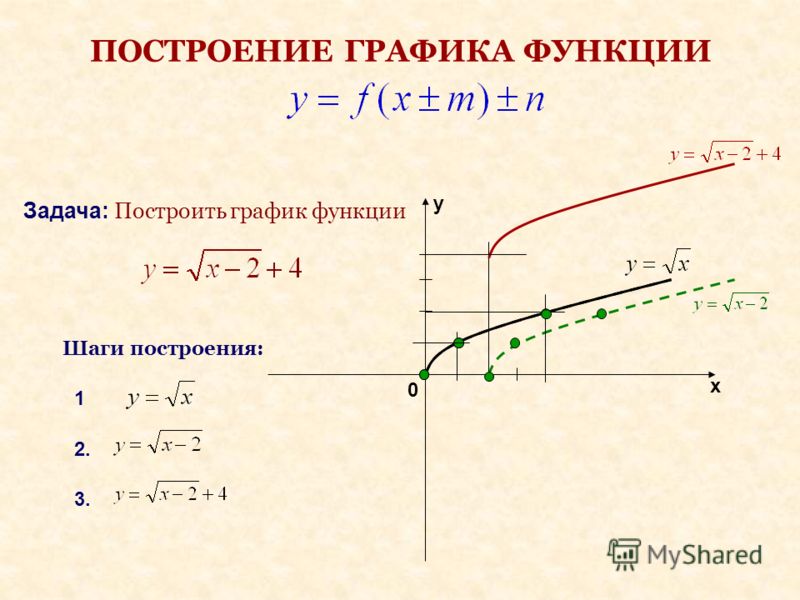
Здесь немного другое. Покажите, что график y равен квадратному корню из x минус один плюс два, поскольку расширение родительского графика y равно квадратному корню из x.
Нарисуйте график, представляющий, что y равно квадратному корню из x. Затем переместите график на единицу вправо, и вы получите y, равный квадратному корню из x минус один. Переместите график у, равного квадратному корню из единицы, на две единицы вверх, и вы получите у, равное квадратному корню из х минус один плюс два.
Визуальное представление графика позволяет легко увидеть ответы. Теперь вы можете понять, что x больше или равно единице, если область определения функции y равна квадратному корню из x минус один плюс два.
На графике также показан диапазон функции y, равный квадратному корню из x минус один плюс два больше или равному двум.
Как учиться
Большинству людей трудно готовиться к экзаменам по математике, геометрии или алгебре. Большинство проблем можно отнести к математическому беспокойству, распространенному заболеванию в классе. Математика сложна только в том случае, если вы так считаете. Как и в случае с любым другим предметом, ваше отношение будет влиять на ваши учебные привычки.
Большинство проблем можно отнести к математическому беспокойству, распространенному заболеванию в классе. Математика сложна только в том случае, если вы так считаете. Как и в случае с любым другим предметом, ваше отношение будет влиять на ваши учебные привычки.
Изучаете ли вы, как найти квадратный корень из графика x или что-то еще, вы столкнетесь с препятствиями, если не разбьете процесс на управляемые шаги.
Те, кто работает всю ночь, не добьются лучших результатов по какому-либо школьному предмету, а математика — самый сложный предмет для изучения в последнюю минуту. Спланируйте свой учебный график, даже если вам не предстоит контрольная. Ежедневная учеба — единственный способ ознакомиться с формулами и определениями исчисления.
Обязательно высыпайтесь и правильно питайтесь, особенно за день до экзамена. Если у вас затуманенное зрение и вы работаете на кофеине и сахаре, вы не сможете сосредоточиться на формулах и терминах, необходимых для решения задач.
Вы основываетесь на одной теории и наборе формул в алгебре, геометрии или математическом анализе, прежде чем перейти к другому, более сложному аспекту продвинутой математики. Вы не получите ответы с первой попытки, если только вы не математический гений или не работаете над простыми задачами. Будьте готовы к некоторым пробам и ошибкам.
Вы не получите ответы с первой попытки, если только вы не математический гений или не работаете над простыми задачами. Будьте готовы к некоторым пробам и ошибкам.
У вас есть несколько вариантов, помимо самостоятельного изучения и просмотра классных заметок, которые помогут вам в учебе. Нужна дополнительная помощь? Рассмотрите следующие варианты:
На YouTube и математических веб-сайтах есть множество видеоуроков, которые помогут вам, если письменные объяснения сбивают вас с толку. Проверьте веб-сайты колледжей и университетов, так как многие математические факультеты размещают раздаточные материалы в формате PDF с некоторых математических занятий.
Не игнорируйте концепции или проблемы, которые вы не понимаете, и переходите к другому уроку. Вам нужно полностью понять одну концепцию, прежде чем переходить к следующей главе или функции. Потренируйтесь на как можно большем количестве задач и определите, где вы допустили ошибку в своем мышлении.
Всегда просите своего учителя, репетитора или одноклассников помочь вам найти реальное применение математическим задачам. Когда вы знаете, как использовать исчисление или другие математические формулы в реальном мире, вы будете менее склонны испытывать математическую тревогу или жаловаться на то, что исчисление бесполезно и не поможет вам, когда вы закончите учебу.
Когда вы знаете, как использовать исчисление или другие математические формулы в реальном мире, вы будете менее склонны испытывать математическую тревогу или жаловаться на то, что исчисление бесполезно и не поможет вам, когда вы закончите учебу.
Исчисление используется в производстве, науке, технике, астрономии, авиации и других отраслях. Постарайтесь найти «общие точки соприкосновения» со своими математическими заданиями. Поищите, как вы можете использовать формулы в повседневной жизни, в хобби или в выбранной области.
Имейте в виду, что большинство математических задач можно решить несколькими способами. Может быть второй или третий способ, если вам трудно понять один метод. Если ваша книга или учитель предлагает только один способ решения проблемы, поищите другие методы в Интернете или спросите друга об альтернативных методах.
Управляйте своей тревожностью по математике, установив расписание домашних заданий. Всегда имейте хотя бы одного надежного человека, который поможет вам просмотреть задания и подготовиться к тестам.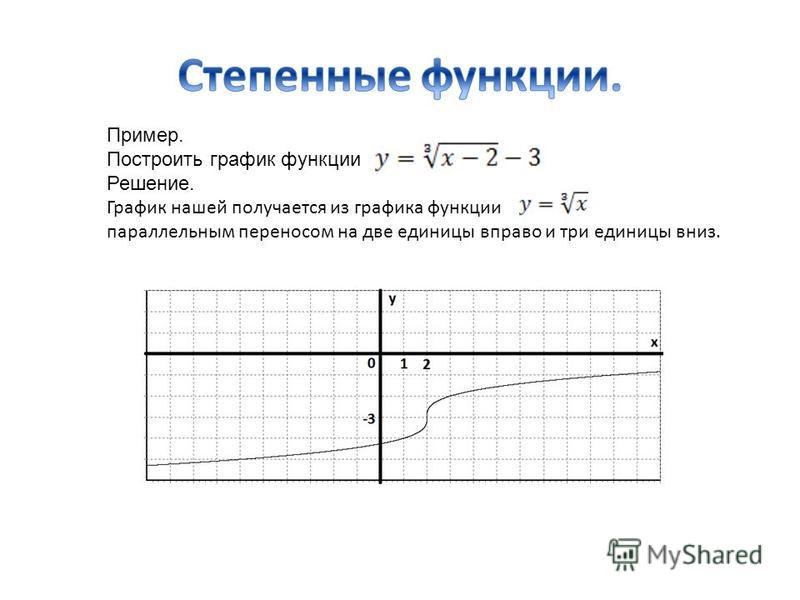
Будьте открыты для новых методов обучения и узнайте о практических способах использования математического анализа и других математических наук в вашей жизни за пределами классной комнаты.
Избранное изображение Герда Альтманна из Pixabay
Загрузка видео может занять несколько секунд.
Проблемы с просмотром видео? Некоторые браузеры не поддерживают эту версию — попробуйте другой браузер.
Функции извлечения квадратного корня
Функции извлечения квадратного корня
Преобразования
Функции квадратного корня также могут быть записаны в форме h,k. Функция квадратного корня содержит квадратный корень с независимой переменной (x) под радикалом. Родительская функция : f(x) = √x . График и таблица родительской функции показаны справа. Функции квадратного корня очень похожи. Обратите внимание на диаграмму справа: значения a, h и k выполняют те же преобразования, что и в квадратичной функции. Горизонтальное сжатие и растяжение (b) Отражение по оси Y (-b) Квадратичные функции также могут быть показаны со значением b, однако, поскольку парабола имеет горизонтальную симметрию, она обычно не включается. | Родительская функция квадратного корня |
Горизонтальное растяжение/сжатие | Вертикальное растяжение/сжатие | Горизонтальный перевод | Вертикальный перевод |
Посмотрите каждый пример ниже и сделайте заметки. Затем заполните рабочий лист.
Преобразования функций квадратного корня WS Преобразования Ключ ответа WS |
|
Домен и диапазон
Помните, что доменом являются все возможные значения x внутри функции. Функции квадратного корня не имеют неограниченного домена. Каждый раз, когда значение x дает отрицательное число под радикалом, результатом будет недействительное число. Поэтому эти значения x не будут частью домена. Чтобы найти домен, сосредоточьтесь на значении h (координата x исходной точки). Если график идет вправо (как в примере ниже), домен будет x ≥ h . Если график идет влево, домен будет Диапазоном будут все возможные выходные данные функции, поэтому сосредоточьтесь на k (значение y исходной точки). Ниже график идет вверх, поэтому диапазон будет y ≥ k . Если график идет вниз, диапазон будет равен г ≤ k.
| Примеры доменов и диапазонов |
Интервалы возрастания и убывания
Помните, что при определении интервалов увеличения и уменьшения вы находите значения x, которые заставляют график идти вверх, и значения x, которые заставляют график идти вниз. График справа только увеличивается. Оно будет возрастать при x ≥ 2 или в интервале [2, ∞). Это всегда будет соответствовать домену. Вам просто нужно определить, увеличивается она или уменьшается. | Интервалы Inc и Dec Примеры |
Конец поведения
Поведение конца показывает, что происходит на концах графа. Поскольку функция квадратного корня не является непрерывной (останавливается на одном конце), она отличается от знакомой вам квадратичной функции. Одна сторона останется, когда x приблизится к положительной или отрицательной бесконечности, это будет определяться стрелкой. См. пример справа. Однако, поскольку левая часть графика останавливается на (2, 0), конечное поведение здесь будет таким: когда x приближается к 2, y приближается к 0. Эти значения будут определяться из исходной точки (h, k). |
Конец Примеры поведения |
Рабочий лист | Ключ ответа |
Системы
Вы видели системы нелинейных уравнений до того, как занялись квадратичными уравнениями. Системы уравнений могут включать любую комбинацию функциональных правил. Вы будете использовать те же системные правила, что и всегда, единственная разница заключается в том, как вы решаете полученное уравнение. Нажмите кнопку примера, чтобы увидеть пример, составленный алгебраически.
Пример. Решение систем с радикальными уравнениями
ПОМНИТЕ!
Решением системы является точка пересечения. Здесь показаны общие значения x и y для двух правил функций.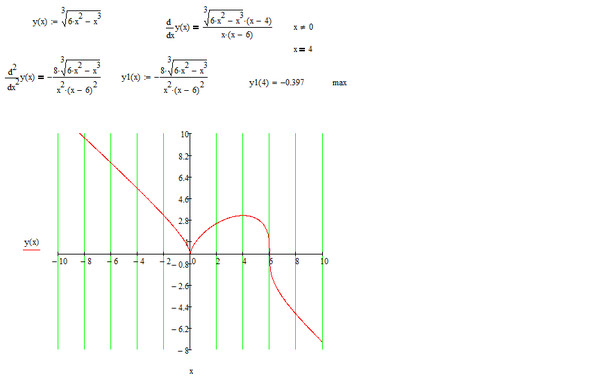

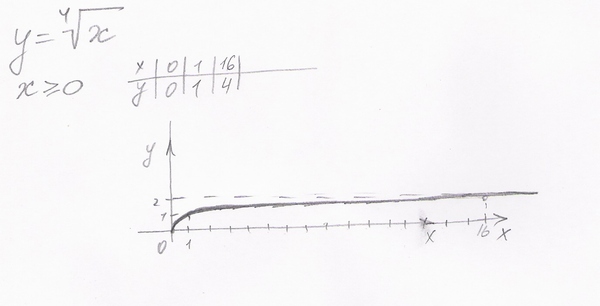 Обратите внимание, что в родительской функции нет отрицательных значений x. Это потому, что извлечение квадратного корня из отрицательного числа приводит к недействительному числу. Вот почему функция квадратного корня имеет начальную точку 92 и преобразования, примененные к этой родительской функции в форме h,k, определяют параболу после преобразований.
Обратите внимание, что в родительской функции нет отрицательных значений x. Это потому, что извлечение квадратного корня из отрицательного числа приводит к недействительному числу. Вот почему функция квадратного корня имеет начальную точку 92 и преобразования, примененные к этой родительской функции в форме h,k, определяют параболу после преобразований.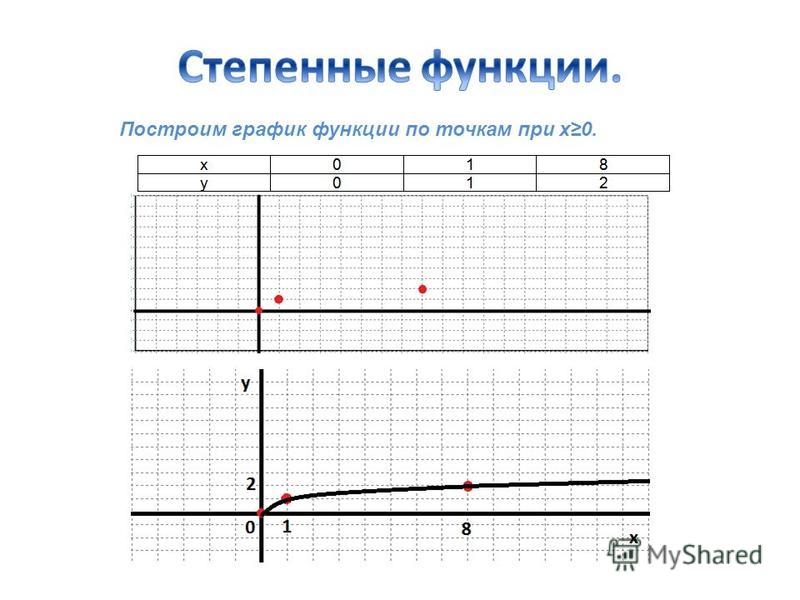
 С квадратичными функциями домен всегда состоял из действительных чисел, потому что набор значений x, которые можно ввести в правило квадратичной функции, может быть любым действительным числом.
С квадратичными функциями домен всегда состоял из действительных чисел, потому что набор значений x, которые можно ввести в правило квадратичной функции, может быть любым действительным числом. Функции квадратного корня будут делать только одно или другое.
Функции квадратного корня будут делать только одно или другое.