Y модуль x график: Функция y = |x| — урок. Алгебра, 8 класс.

Преобразования функций абсолютного значения

Функции, принадлежащие одному и тому же семейству функций, могут быть преобразованы друг в друга с помощью , растяжения и сжатия или отражения. Применяя одно или несколько преобразований к родительской функции, можно получить любую функцию из ее семейства функций. Этот урок будет посвящен преобразованиям функций абсолютного значения.

Вот несколько рекомендуемых материалов, прежде чем приступить к этому уроку.

Рассмотрим график .

Много разных можно получить, сдвигая график родительской функции абсолютного значения. Абсолютная величина, полученная таким образом, имеет следующий вид.

y=∣x−h∣+k​

При этом h и k равны . Используя следующий апплет, исследуйте, как значения h и k влияют на график родительской функции.

Те же типы преобразований, которые создают новые, также делают то же самое для функций абсолютного значения.

Точно так же они влияют на функции абсолютного значения. Однако, поскольку линейные функции и функции абсолютного значения имеют некоторые существенные различия, преобразования могут выглядеть по-разному графически.

График y=∣x∣ может быть по вертикали по а до — или от — .

Точно так же его можно также перевести по горизонтали , добавив число к правилу или вычтя его из него.

В таблице ниже приведены различные типы преобразований, которые можно выполнить для сдвига функции абсолютного значения.

Преобразования y=∣x∣
Вертикальные переводы	Перевод вверх на k единиц, k>0y=∣x∣+k​
	Перевод вниз на k единиц, k<0y=∣x∣+k​
Горизонтальные переводы	Перевод вправо h единиц, h>0y=∣x−h∣​
	Перевод влево h единиц, h<0y=∣x−h∣​

Тадео только что узнал о функциях абсолютного значения. Он верит в девиз, что практика ведет к совершенству, поэтому решает больше учиться. Следующие графики являются графиками после определенного перевода.

Помогите Тадео сопоставить каждый график с соответствующим .

Сравните данные графики с графиком родительской функции абсолютного значения, чтобы определить преобразование, примененное к каждому графику.

Начните с определения смещения каждого графика по сравнению с графиком родительской функции f(x)=∣x∣.

Теперь, когда переводы определены, вспомните правила перевода.

Преобразования y=f(x)
Горизонтальные переводы	Перевод вправо на h единиц, h>0y=f(x−h)​
	Перевод влево на h единиц, h<0y=f(x−h)​
Вертикальные переводы	Перевод вверх на k единиц, k>0y=f(x)+k​
	Перевод вниз на k единиц, k<0y=f(x)+k​

Используя эту таблицу, можно записать функциональные правила графиков.

График A: График B: График C: График D: ​  f(x)=∣x∣−3 f(x)=∣x+2∣  f(x)=∣x−4∣  f(x)= ∣x∣+1​

Тадео и Эмили — одноклассники Северной средней школы. Им было предложено пройти следующие 5 единиц вправо, а затем 3 единицы вниз.

f(x)=2∣x+2∣−1​ ​​

Тем не менее, они получили разные результаты.

Выполнив требуемые переводы, определите, кто прав!

График функции y=∣x∣ можно перевести по вертикали, добавив число к — или вычтя — из . Точно так же его можно перевести по горизонтали, добавив число к правилу или вычтя его из него.

Абсолютное значение можно перевести на 5 единиц вправо, вычитая 5 из ввода правила функции. Для этого подставьте x−5 вместо x в f(x)=2∣x+2∣−1.

f(x)=2∣x+2∣−1

f(x−5)=2∣x−5+2∣−1

f(x−5)=2∣x−3∣− 1

Далее, чтобы перевести полученную функцию на 3 единицы вниз, из правила функции нужно вычесть 3.

f(x−5)=2∣x−3∣−1

f(x−5)−3=2∣x−3∣−1−3

f(x−5)−3=2 ∣x−3∣−4

Наконец, результат можно упростить, заменив f(x−5)−3 на g(x).

г(х)=2∣х−3∣−4​

В результате Эмили права.

Следующий апплет показывает график функции an в виде f(x)=∣x−h∣+k, где h и k равны . Учитывая , определить значения h и k.

Помимо , new может быть создан путем сжатия или растяжения функции. Рассмотрим следующее.

Функция I​y=a(∣x−1∣−1)​Функция II​y=∣bx-1∣−1​

В этих примерах a и b больше 0. Исследуйте, как значения a и b изменяют график y=∣x−1∣−1.

График a можно растянуть по вертикали на 90 158 или сжать на 90 159, умножив a на a.

у=а⋅f(х)​

Расстояние по вертикали между графиком и осью абсцисс изменится на коэффициент а в каждой точке графика. Если a>1, это приведет к вертикальному растяжению графика. Точно так же a<1 приводит к сжатию графа по вертикали. Обратите внимание, что значение функции равно 0. Следовательно, это не влияет на них.

Общий вид этого преобразования показан в таблице.

Преобразования f(x)
Вертикальное растяжение или усадка	Вертикальное растяжение, a>1 y=af(x)
	Вертикальная усадка, 0 y=af(x)

С помощью a на b его график может быть растянут по горизонтали или сжат .

y=f(b⋅x)​

Если b>1, каждое входное значение будет изменено так, как если бы оно было дальше от оси Y, чем оно есть на самом деле. Это приводит к тому, что график сжимается по горизонтали — каждая часть графика перемещается ближе к оси Y. И наоборот, b<1 приводит к горизонтальному растяжению.

Горизонтальное расстояние между графиком и осью Y изменяется с коэффициентом b1​.

Обратите внимание, что значение x равно 0, поэтому это не влияет на них. Общий вид этого преобразования показан в таблице.

Преобразования f(x)
Горизонтальное растяжение или усадка	Горизонтальное растяжение, 0 y=f(bx)
	Горизонтальная усадка, b>1 y=f(bx)

Функция растяжения и сжатия абсолютного значения — это функция, которая изменяет ширину графика без его смещения. График y=∣x−1∣−1 может быть по a .

Точно так же график функции абсолютного значения y=∣x−0,5∣ можно построить, умножив правило на положительное число.

В таблице ниже приведены различные типы растяжения и сжатия, которые можно выполнять для функции абсолютного значения.

Преобразования y=∣x∣
Вертикальное растяжение или усадка	Вертикальное растяжение, a>1y=a∣x∣​
	Вертикальная усадка, 0
Горизонтальное растяжение или усадка	Растяжение по горизонтали, 0
	Горизонтальная усадка, b>1y=∣bx∣​

Эмили использует резервуар для воды объемом 10 кубометров, чтобы поливать растения. Она сливает воду из бака из одного крана, а затем наполняет его из другого такого же крана.

Следующий график моделирует уровень воды в баке, когда он опорожняется, а затем снова наполняется через t минут.

a Эмили замечает, что когда она удваивает количество воды и количество кранов, график функции увеличивается в 2 раза. Если это так, то каков будет преобразованный график.

b Если Эмили удвоит диаметр кранов, график функции сожмется по горизонтали. Какова будет в этом случае функция нового графика?

a График y=f(x) можно растянуть или сжать по вертикали, умножив на число.

b График функции y=f(x) можно растянуть или сжать по горизонтали, умножив правила на положительное число.

a Вспомним, что когда Эмили удваивает количество воды и диаметр кранов, график функции растягивается по вертикали на a, равное 2.

Чтобы растянуть график функции абсолютного значения по вертикали, нужно умножить на положительное число. В этом случае его следует умножить на 2. С помощью этой информации можно записать функцию преобразованного графа.

f(t)=21​∣t−20∣⇓f(t)=∣t−20∣​

b На этот раз Эмили удваивает только диаметр кранов. В результате график функции сжимается по горизонтали в 2 раза.

Чтобы сжать график функции абсолютного значения по горизонтали, ввод правила функции должен быть умножен на положительное число. В этом случае его следует умножить на 2.

f(t)=21​∣t−20∣⇓f(t)=21​∣2t−20∣​

Отражение функции — это , которое переворачивает график по некоторому . Эта линия называется и обычно является либо осью x, либо осью y. Отражение по оси абсцисс достигается изменением знака координаты у каждого на графике.

у=-f(x)​

Координата y у всех равна 0. Таким образом, изменение знака значения на точках пересечения с осью x не имеет значения — любые точки пересечения с осью x сохраняются при отражении графика по оси x.

Вместо этого отражение по оси Y достигается изменением знака каждого значения.

у=f(-x)​

Когда x=0, что соответствует , это отражение не влияет на входное значение. Следовательно, точка пересечения с осью y сохраняется за счет отражений по оси y.

В следующей таблице показаны различные типы отражений, которые можно применить к функции.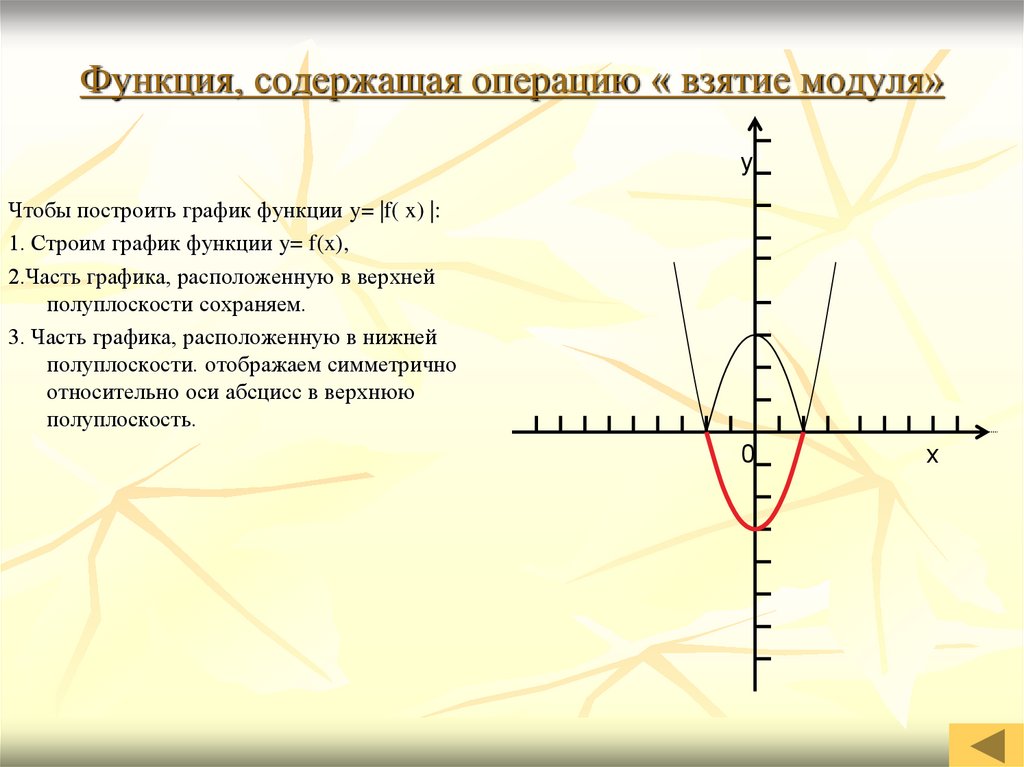

Преобразования f(x)
Отражения	По оси x y=-f(x)
	По оси Y y=f(-x)

Последнее, к чему можно применить отражений . Функция — это преобразование, которое переворачивает график без изменения его формы. График функции абсолютного значения y=∣x−1∣−1 можно отразить по оси x через -1.

Аналогичным образом график функции абсолютного значения y=∣2x−2∣−1 можно также отразить на оси y, умножив правило на -1.

В таблице ниже приведены различные типы отражений, которые могут быть выполнены для функции абсолютного значения.

Преобразования y=∣x∣
Отражения	По оси xy=-∣x∣​
	По оси Yy=∣-x∣​

a В результате можно получить некоторые цифры. В настоящее время Эмили работает над следующим.

f(x)=∣2x−5∣​

Отражая это, она хочет получить букву W. Запишите функцию отражения, определив тип отражения.

b Отражая функцию, можно также получить a. Рассмотрим следующую функцию абсолютного значения.

f(x)=21​∣x−4∣−2​

Как Эмили должна отразить эту функцию, чтобы получить четырехугольник? Каким будет уравнение отраженной функции?

a Начните с построения графика заданной функции. Обратите внимание, что график функции абсолютного значения y=f(x) можно отразить по оси x, умножив на -1. Аналогичным образом функцию можно отразить и по оси Y, умножив правило на -1.

b Начните с построения графика заданной функции. Обратите внимание, что график функции абсолютного значения y=f(x) можно отразить по оси x, умножив правило функции на -1. Аналогичным образом это можно отразить и на оси Y, умножив ввод правила на -1.

a Чтобы узнать, как получить букву W, начните с .

х	f(x)=∣2x−5∣	ф(х)
-1	f(x)=∣2(-1)−5∣	7
0	f(x)=∣2(0)−5∣	5
1	f(x)=∣2(1)−5∣	3
2,5	f(x)=∣2(2.5)−5∣	0
4	f(x)=∣2(4)−5∣	3
5	f(x)=∣2(5)−5∣	5
6	f(x)=∣2(6)−5∣	7

Теперь постройте и соедините их, чтобы построить график функции абсолютного значения.

Глядя на график функции, можно сделать вывод, что f(x) необходимо отразить по оси y.

Напомним, что график функции абсолютного значения можно отразить по оси Y, умножив ввод правила функции на -1.

Заданная функция​f(x)=∣2x−5∣⇓Отраженная функция​g(x)=∣-2x−5∣​

b Аналогичным образом нарисуйте график функции f(x), чтобы определить тип отражения.

х	f(x)=21​∣x−4∣−2	ф(х)
-2	f(x)=21​∣-2−4∣−2	1
0	f(x)=21​∣0−4∣−2	0
2	f(x)=21​∣2−4∣−2	-1
4	f(x)=21​∣4−4∣−2	-2
6	f(x)=21​∣6−4∣−2	-1
8	f(x)=21​∣8−4∣−2	0
10	f(x)=21​∣10−4∣−2	1

Постройте упорядоченные пары и нарисуйте график.

Видно, что для образования четырехугольника график функции нужно отразить по оси абсцисс.

Обратите внимание, что график функции абсолютного значения можно отразить по оси X, умножив правило функции на -1.

Заданная функция​f(x)=21​∣x−4∣−2⇓Отраженная функция​g(x)=-21​∣x−4∣+2​

На протяжении всего урока были рассмотрены преобразования. Было замечено, что различные функции абсолютного значения могут быть получены путем преобразования той или иной функции абсолютного значения. Однако это не единственный способ получить функцию. Рассмотрим в .

f(x)=21​x−1​

Нарисуйте график этого и отразите часть графика по оси X.

Полученная функция представляет собой функцию абсолютного значения вида g(x)=∣mx+b∣, где m и b равны, а m не может быть равно 0.

g(x)=∣∣∣∣∣​21​x−1∣∣∣∣∣​​

Следовательно, функции абсолютного значения в виде g(x)=∣mx+b∣ можно получить, отражая отрицательная часть графика линейной функции в виде f(x)=mx+b.

Размышления об осях и преобразовании абсолютного значения

Урок Графические инструменты: отражения и преобразование абсолютного значения в Учебная программа по алгебре II
дает подробное обсуждение осей $x$ и $y$, и преобразование абсолютного значения.

Упражнения в этом уроке дублируют упражнения в Графические инструменты: отражения и преобразование абсолютного значения.

• Точки на графике $\,y=f(x)\,$ имеют вид $\,\bigl(x,f(x)\bigr)\,$.
  Точки на графике $\,y=-f(x)\,$ имеют вид $\,\bigl(x,-f(x)\bigr)\,$.
  Таким образом, график $\,y=-f(x)\,$ находится по графику $\,y=f(x)\,$, и умножение значений $\,y$ на $\,-1\,$.
  Это отражает график относительно оси $\,x$.
• Преобразования, включающие $\,y\,$ , работают так, как вы ожидаете от них — они интуитивно понятны.
• Вот мыслительный процесс, который вы должны использовать, когда вам дан график $\,y=f(x)\,$
  и спросил о графике $\,y=-f(x)\,$: $$ \начать{выравнивать} \cssId{s23}{\text{исходное уравнение:}} &\quad \cssId{s24}{y=f(x)}\cr\cr \cssId{s25}{\text{новое уравнение:}} &\quad \cssId{s26}{y=-f(x)} \end{выравнивание} $$ $$ \начать{собирать} \cssId{s27}{\text{интерпретация нового уравнения:}}\cr\cr \overset{\cssId{s29}{\text{новые значения y}}}{\overbrace{ \стойка\\\cssId{s28}{y}\\}} \overset{\cssId{s31}{\text{are}}}{\overbrace{ \стойка\ \\cssId{s30}{=}\ \ }} \overset{\quad\cssId{s33}{\text{-1 раз}}\quad}{\overbrace{ \ стойка \ \ \ cssId {s32}{-}\ \ }} \overset{\qquad\cssId{s35}{\text{предыдущие значения y}}\quad}{\overbrace{ \ распорка \ \ \ cssId {s34} {f (x)} \ \ }} \конец{собрать} $$
• Размышляя об оси $\,x$, точка $\,(a,b)\,$ на графике $\,y=f(x)\,$ перемещается в точку $\,(a,-b)\,$ на графике $\,y=-f(x)\,$.

ИДЕИ, КАСАЮЩИЕСЯ РАЗМЫШЛЕНИЙ ОБ ОСИ $\,y$

Точки на графике $\,y=f(x)\,$ имеют вид $\,\bigl(x,f(x)\bigr)\,$. Точки на графике $\,y=f(-x)\,$ имеют вид $\,\bigl(x,f(-x)\bigr)\,$. Как мы можем найти эти искомые точки $\,\bigl(x,f(-x)\bigr)\,$? Выберите значение $\,x\,$. Во-первых, перейти к делу $\,\color{red}{\bigl(-x\,\,f(-x)\bigr)}\,$ на графике $\,\color{red}{y=f(x)}\,$. Эта точка имеет $\,y$ -значение, которое нам нужно, но оно имеет неправильное $\,x$ -значение. $\,x$-значение этой точки равно $\,-x\,$, но искомое $\,x$-значение равно $\,x\,$. Таким образом, текущий $\,\color{purple}{x}$-значение должно быть умножено на $\,\color{purple}{-1}\,$; то есть каждый $\,\color{purple}{x}$-значение должно быть отправлено в противоположное значение. Значение $\,\color{purple}{y}$ остается прежним. Это заставляет точку отражаться относительно оси $\,y$ и дает желаемая точка $\,\color{green}{\bigl(x,f(-x)\bigr)}\,$. Таким образом, график $\,y=f(-x)\,$ совпадает с графиком $\,y=f(x)\,$, за исключением того, что это было отражено относительно оси $\,y$. Вот мыслительный процесс, который вы должны использовать, когда вам дан график $\,y=f(x)\,$ и спросил о графике $\,y=f(-x)\,$: $$ \начать{выравнивать} \cssId{s54}{\text{исходное уравнение:}} &\quad \cssId{s55}{y=f(x)}\cr\cr \cssId{s56}{\text{новое уравнение:}} &\quad \cssId{s57}{y=f(-x)} \end{выравнивание} $$ $$ \начать{собирать} \cssId{s58}{\text{интерпретация нового уравнения:}}\cr\cr \cssId{s59}{у = е( \overset{\text{заменить x на -x}}{\overbrace{ \ \ -Икс\ \ }} )} \конец{собрать} $$ Замена каждого $\,x\,$ на $\,-x\,$ в уравнении заставляет график отражаться относительно оси $\,y$. Размышляя об оси $\,y$, точка $\,(a,b)\,$ на графике $\,y=f(x)\,$ перемещается в точку $\,(-a,b)\,$ на графике $\,y=f(-x)\,$.

ИДЕИ ОТНОСИТЕЛЬНО ПРЕОБРАЗОВАНИЯ АБСОЛЮТНОЙ ЦЕННОСТИ

• Точки на графике $\,y=f(x)\,$ имеют вид $\,\bigl(x,f(x)\bigr)\,$.
  Точки на графике $\,y=|f(x)|\,$ имеют вид $\,\bigl(x,|f(x)|\bigr)\,$.
• Таким образом, график $\,y=|f(x)|\,$ находится путем взятия графика $\,y=f(x)\,$ и взяв абсолютное значение $\,y$-значений.

  Точки с положительными значениями $\,y$ остаются прежними, поскольку абсолютное значение положительного числа есть оно само.
  То есть точки над осью $\,x$ не меняются.

  Точки с $\,y=0\,$ остаются прежними, поскольку абсолютное значение нуля есть оно само.
  То есть точки на оси $\,x$ не меняются.

  Точки с отрицательными значениями $\,y$ изменятся, поскольку взятие абсолютного значения отрицательного числа делает его положительным.
  То есть любая точка ниже оси $\,x$ отражает ось $\,x$.

  Эти действия резюмируются следующим образом: ‘любая часть графика ниже оси $\,x$ переворачивается’.

• Вот мыслительный процесс, который вы должны использовать, когда вам дан график $\,y=f(x)\,$
  и спросил о графике $\,y=|f(x)|\,$: $$ \начать{выравнивать} \cssId{s80}{\text{исходное уравнение:}} &\quad \cssId{s81}{y=f(x)}\cr\cr \cssId{s82}{\text{новое уравнение:}} &\quad \cssId{s83}{y=|f(x)|} \end{выравнивание} $$ $$ \начать{собирать} \cssId{s84}{\text{интерпретация нового уравнения:}}\cr\cr \overset{\cssId{s86}{\text{новые значения y}}}{\overbrace{ \стойка\ \\cssId{s85}{y}\ \ }} \overset{\cssId{s88}{\text{are}}}{\overbrace{ \стойка\ \\cssId{s87}{=}\ \ }} \overset{\quad\cssId{s90}{\text{абсолютное значение предыдущих значений y}}\quad}{\overbrace{ \стойка\ \ \cssId{s89}{|f(x)|}\ \ }} \конец{собрать} $$
• При преобразовании абсолютного значения точка $\,(a,b)\,$ на графике $\,y=f(x)\,$ перемещается в точку $\,(a,|b|)\,$ на графике $\,y=|f(x)|\,$.

ОБЗОР

по оси $\,x$:
переход от $\,y = f(x)\,$ к $\,y = -f(x)$

отражения по оси $\,y$:
переход от $\,y = f(x)\,$ к $\,y = f(-x)$

преобразование абсолютного значения:
переход от $\,y = f(x)\,$ к $\,y = |f(x)|$
Любая часть графика на оси $\,x$ или выше остается неизменной;
любая часть графика ниже оси $\,x$ переворачивается вверх.

УБЕДИТЕСЬ, ЧТО ВЫ ВИДИТЕ РАЗНИЦУ!

Убедитесь, что вы видите разницу между $\,y = -f(x)\,$ и $\,y = f(-x)\,$!

В случае $\,y = -f(x)\,$, знак минус стоит «снаружи»;
мы опускаем $\,x\,$ в ячейку $\,f\,$, получение соответствующего вывода, и , затем , умноженное на $\,-1\,$.