Интегральные функции:
- Si(x)
- Интегральный синус от x
- Ci(x)
- Интегральный косинус от x
- Shi(x)
- Интегральный гиперболический синус от x
- Chi(x)
- Интегральный гиперболический косинус от x
В выражениях можно применять следующие операции:
- Действительные числа
- вводить в виде 7.
 3
3- — возведение в степень
- x + 7
- — сложение
- x — 6
- — вычитание
- 15/7
- — дробь
- asec(x)
- Функция — арксеканс от x
- acsc(x)
- Функция — арккосеканс от x
- sec(x)
- Функция — секанс от x
- csc(x)
- Функция — косеканс от x
- floor(x)
- Функция — округление x в меньшую сторону (пример floor(4.5)==4.0)
- ceiling(x)
- Функция — округление x в большую сторону (пример ceiling(4.5)==5.0)
- sign(x)
- Функция — Знак x
- erf(x)
- Функция ошибок (или интеграл вероятности)
- laplace(x)
- Функция Лапласа
- asech(x)
- Функция — гиперболический арксеканс от
- csch(x)
- Функция — гиперболический косеканс от x
- sech(x)
- Функция — гиперболический секанс от x
- acsch(x)
- Функция — гиперболический арккосеканс от x
Постоянные:
- pi
- Число «Пи», которое примерно равно ~3.
 14159..
14159.. - e
- Число e — основание натурального логарифма, примерно равно ~2,7183..
- i
- Комплексная единица
- oo
- Символ бесконечности — знак для бесконечности
Как построить график функции y=f(x+m)+n, если известен график функции y=f(x) (28 слайдов)
Нажмите для просмотра |
Читать онлайн!
Слайд 1
Как построить график функции y=f(x+m)+n, если известен график функции y=f(x)
Слайд 2
Какая из формул задаёт:
— прямую пропорциональность;
-обратную пропорциональность;
-линейную функцию, график которой проходит через начало координат.
2)
1)
Слайд 3
На одном из рисунков изображена парабола. Укажите этот рисунок.
Слайд 4
На одном из рисунков изображена гипербола. Укажите этот рисунок.
Слайд 5
Соединить линиями соответствующие названия графиков функции:
гипербола
прямая
парабола
Слайд 6
Соединить линиями соответствующие названия графиков функции:
гипербола
прямая
парабола
Слайд 7
Повторим изученное
У
Опишите свойства
функции, используя
график.
-1
-2
Слайд 8
у
у= х²+ 3
Функция у = х² + 3; вершина (0; 3)
у= х²
Функция у = х²; вершина (0; 0)
х
Сдвиг графика функции у = х² вдоль оси ОУ на
3 единицы вверх.
Слайд 9
у
Функция у = х²; вершина (0; 0)
у= х²
Сдвиг графика функции у = х² вдоль оси ОУ на
5 единиц вниз.
х
у= х² 5
— 5
Функция у = х² — 5; вершина (0; -5)
Слайд 10
Построение графиков функций
y = f (x) и y = f (x + a)
Сдвиг вдоль оси абсцисс
y=(x+3)²
y=x²
y=(x-3)²
Слайд 11
Построение графиков функций
y = f (x) и y = f (x) +n
Сдвиг вдоль оси ординат
y=x²+3
y=x²
y=x²-3
Слайд 12
График функции График функции y = f(x + m) получается параллельным переносом графика функции y=f(x) вдоль оси х на |m| единиц масштаба влево, если m > 0 и вправо, если m
Слайд 13
График функции График функции y = f(x)+n получается параллельным переносом графика функции y=f(x) вдоль оси y на |n| единиц масштаба вверх, если n > 0 и вниз, если n
Слайд 14
Самостоятельная работа. №1. Постройте графики функций. Ответьте на вопросы.
Слайд 15
№2 Постройте графики функций. Ответьте на вопросы.
Ответьте на вопросы.
Запишите названия графиков_______________________
Какие изменения вы заметили у графика второй функции относительно основного графика?_____________
Слайд 16
Выводы: основные преобразования графиков элементарных функций:
Сжатие и растяжение графика вдоль
оси y у=k f(x).
Преобразование симметрии относительно оси x у = — f(x)
Сдвиг вдоль оси абсцисс y = f (x + a)
Сдвиг вдоль оси ординат y = f (x) +n
Слайд 17
вправо
вниз
вправо
вверх
Слайд 18
На одном из рисунков изображен график
функции
Укажите номер этого рисунка.
Слайд 19
Задайте формулой функцию по графику, изображенному на рисунке.
Слайд 20
Слайд 21
y
Алгоритм 1.
у=4
1. Построить график функции y=f(x)
4 ед.
2. Осуществить параллельный перенос графика y=f(x) вдоль оси х на |m| единиц масштаба влево, если m>0, и вправо, если mx
5 ед. 2
2
Построение графика квадратичной функций: алгоритм и примеры 9 класс онлайн-подготовка на Ростелеком Лицей
Тема 5.
Построение графика квадратичной функции с помощью преобразований.
Рассмотрим частные случаи
y = ax2 + n и y = a(x – m)2.
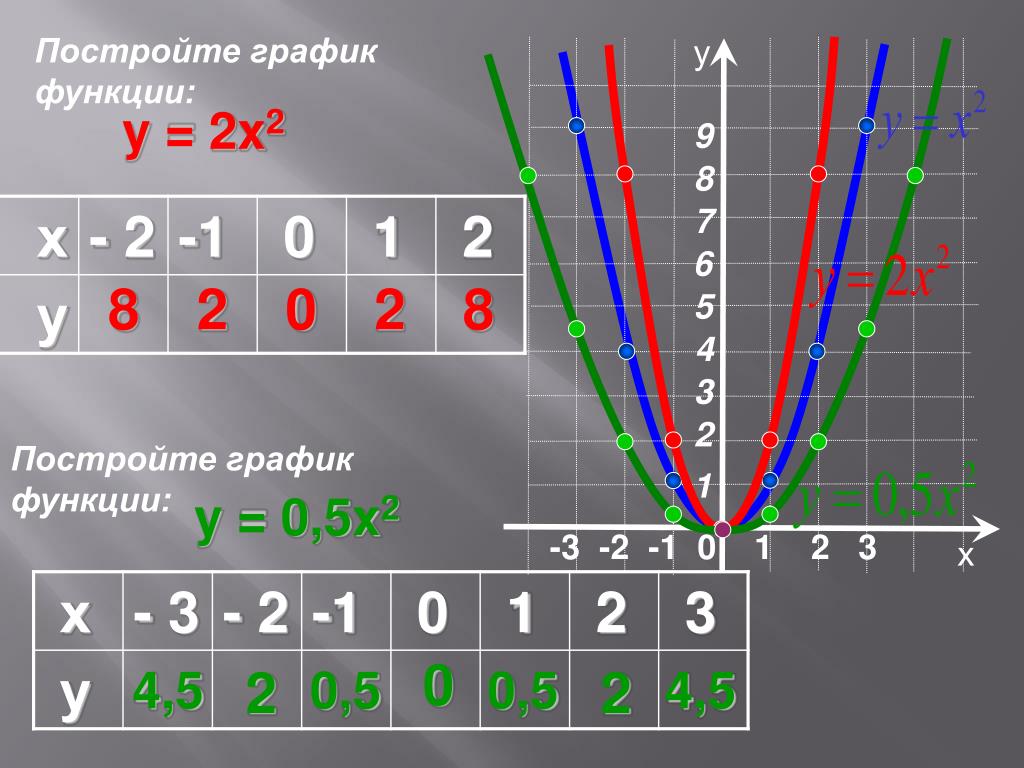
В одной системе координат построим графики функцийy=12×2 и y=12×2+5.
Составим таблицу значений функции: y=12×2
|
x |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
|
y |
4,5 |
2 |
0,5 |
0 |
0,5 |
2 |
4,5 |
Чтобы получить таблицу значений для функции y=12×2+5 для тех же значений аргумента, необходимо к найденным значениям функции y=12×2 прибавить 5.
|
x |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
|
y |
9,5 |
7 |
5,5 |
5 |
5,5 |
7 |
9,5 |
Получается, что каждую точку второго графика можно получить из некоторой точки первого графика с помощью параллельного переноса на 5 единиц вверх вдоль оси y.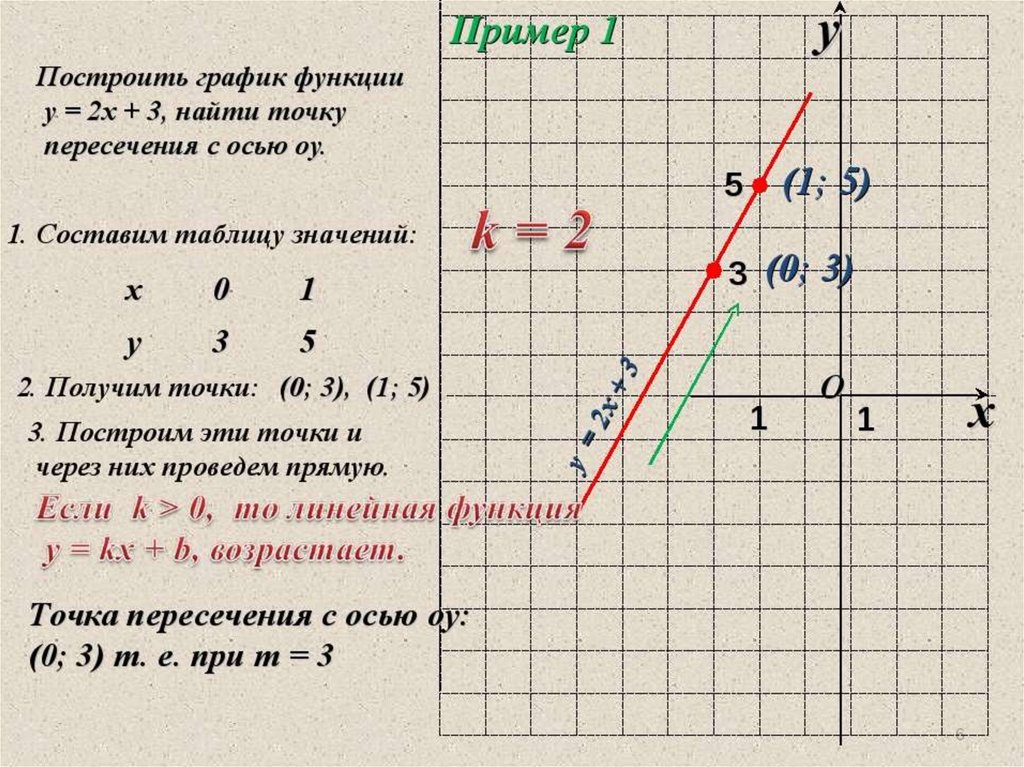
График функции y=12×2+5 – парабола, полученная в результате сдвига вверх графика функции y=12×2.
График функции y = ax2 + n – парабола, которую можно получить из графика функции y = ax2 с помощью параллельного переноса вдоль оси y на
В одной системе координат построим графики функций y=12×2 и y=12x-52. Составим таблицы значений для этих функций.
y=12×2
|
x |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
|
y |
4,5 |
2 |
0,5 |
0 |
0,5 |
2 |
4,5 |
y=12x-52
|
x |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
y |
4,5 |
2 |
0,5 |
0 |
0,5 |
2 |
4,5 |
Значит, если переместить каждую точку графика y=12×2 вправо на 5 единиц, то получим соответствующую точку графика функции y=12x-52.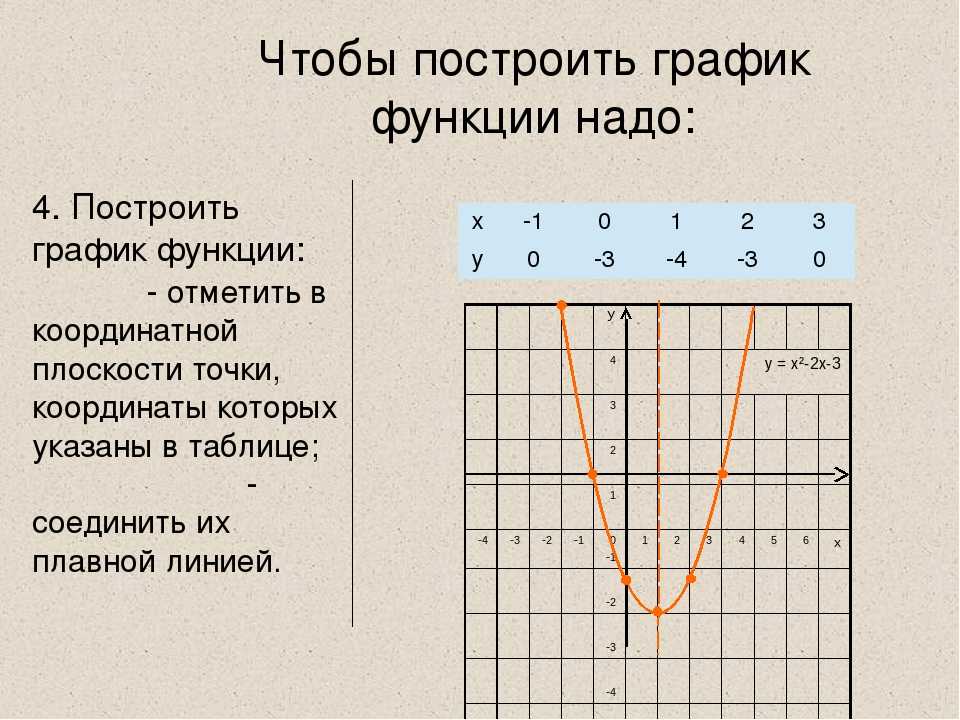 Иначе говоря, каждую точку второго графика можно получить из соответствующей точки первого графика с помощью параллельного переноса на 5 единиц вправо вдоль оси x.
Иначе говоря, каждую точку второго графика можно получить из соответствующей точки первого графика с помощью параллельного переноса на 5 единиц вправо вдоль оси x.
График функции y=12x-52 – парабола, полученная y=12x-52 в результате сдвига вправо графика функции y=12×2.
График функции y = a(x — m)2 – парабола, которую можно получить из графика функции y = ax2 с помощью параллельного переноса вдоль оси x на на m единиц вправо, если m > 0 или на – m единиц влево, если m
Полученные выводы позволяют понять, что представляет собой график функции y = a(x — m)2. Например, график функции y=12x-52+3 можно получить из графика функции y=12×2 с помощью двух параллельных переносов – сдвига вдоль оси x на 5 единиц вправо и вдоль оси y на 3 единицы вверх.
Таким образом, график функции y = a(x — m)2 можно получить из параболы y = ax2 с помощью двух параллельных переносов: сдвига вдоль x на m единиц вправо, если m > 0 или на – m единиц влево, если m n единиц вверх, если n > 0 или на – n единиц вниз, если n
Заметим, что данные преобразования можно производить в любом порядке: сначала выполнить параллельный перенос вдоль оси x, а затем вдоль оси y или наоборот.
Преобразования, которые мы рассмотрели применимы для любых функций.
Рассмотрим пример.
Построим график функции y = x2 — 4x двумя способами: с помощью преобразований, которые мы сегодня рассмотрели и с помощью таблицы значений функции.
Для того, чтобы построить график функции с помощью преобразований, необходимо его представить в виде y = a(x — m)2.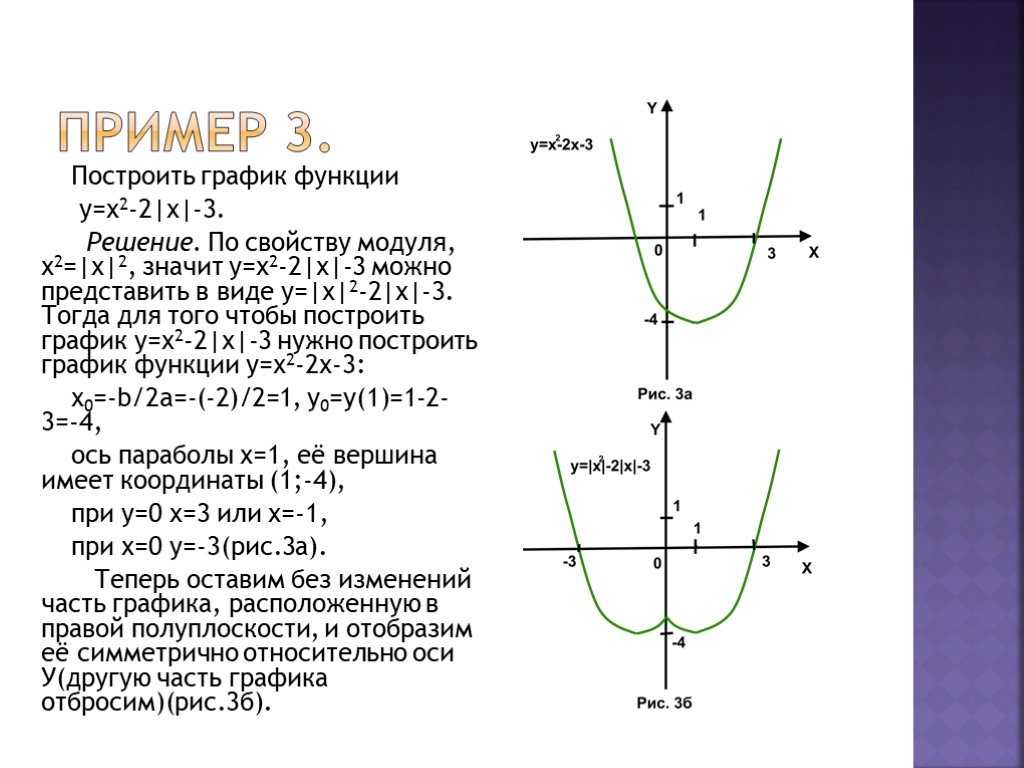 Для этого надо выделить полный квадрат. Итак, в нашу функцию y = x2 — 4x добавим 4 и вычтем 4. Получим:
Для этого надо выделить полный квадрат. Итак, в нашу функцию y = x2 — 4x добавим 4 и вычтем 4. Получим:
y=x2-4x+4-4=x-22-4
График данной функции можно получить из графика функции y = x2 с помощью двух параллельных переносов: сдвига вдоль оси x на 2 единицы вправо, и сдвига вдоль оси y на 4 единицы вниз.
Чтобы построить график функции вторым способом, составим таблицу ее значений. Возьми нечетное количество точек, например, пять и семь. В центре поставь координаты вершины параболы.
xв=-b2a=—42∙1=2
yв=22-4∙2=-4
График квадратичной функции симметричен относительно прямой, параллельной оси y, проходящей через вершину параболы. В данном случае прямая x = 2 является осью симметрии.
|
x |
-1 |
0 |
1 |
2 |
3 |
4 |
5 |
|
y |
5 |
0 |
-3 |
-4 |
-3 |
0 |
5 |
Построение графиков — Sage Tutorial in Russian v9.
 6
6Sage может строить двумерные и трехмерные графики.
Двумерные графики
В двумерном пространстве Sage может отрисовывать круги, линии и многоугольники; графики функций в декартовых координатах; также графики в полярных координатах, контурные графики и изображения векторных полей. Некоторые примеры будут показаны ниже. Для более исчерпывающей информации по построению графиков см. Решение дифференциальных уравнений и Maxima, а также документацию Sage Constructions.
Данная команда построит желтую окружность радиуса 1 с центром в начале:
sage: circle((0,0), 1, rgbcolor=(1,1,0)) Graphics object consisting of 1 graphics primitive
Также можно построить круг:
sage: circle((0,0), 1, rgbcolor=(1,1,0), fill=True) Graphics object consisting of 1 graphics primitive
Можно создавать окружность и задавать ее какой-либо переменной. Данный пример не будет строить окружность:
sage: c = circle((0,0), 1, rgbcolor=(1,1,0))
Чтобы построить ее, используйте Хороший способ создания заполненных фигур — создание списка точек ( Напечатайте Можно добавить текст на график: Учителя математики часто рисуют следующий график на доске: не одну
ветвь arcsin, а несколько, т. Так как функция тангенса имеет больший интервал, чем синус, при
использовании той же техники для перевертывания тангенса требуется
изменить минимальное и максимальное значения координат для оси x: Sage также может строить графики в полярных координатах, контурные
построения и изображения векторных полей (для специальных видов функций).
Далее следует пример контурного чертежа: Sage также может быть использован для создания трехмерных графиков. «Натуральный логарифм» - 0,1. Натуральные логарифмы. 4. «Логарифмический дартс». 0,04. 7. 121. «Степенная функция 9 класс» - У. Кубическая парабола. У = х3. 9 класс учитель Ладошкина И.А. У = х2. Гипербола. 0. У = хn, у = х-n где n – заданное натуральное число. Х. Показатель – четное натуральное число (2n). «Квадратичная функция» - 1 Определение квадратичной функции 2 Свойства функции 3 Графики функции 4 Квадратичные неравенства 5 Вывод. Свойства: Неравенства: Подготовил ученик 8А класса Герлиц Андрей. План: График: -Промежутки монотонности при а > 0 при а «Квадратичная функция и её график» - Решение.у=4x А(0,5:1) 1=1 А-принадлежит. При а=1 формула у=аx принимает вид. «8 класс квадратичная функция» - 1) Построить вершину параболы. Построение графика квадратичной функции. x. -7. Построить график функции. Выберем на плоскости прямоугольную систему координат и будем откладывать на оси абсцисс значения аргумента х , а на оси ординат - значения функции у = f (х) . Графиком функции y = f(x) называется множество всех точек, у которых абсциссы принадлежат области определения функции, а ординаты равны соответствующим значениям функции. Другими словами, график функции y = f (х) - это множество всех точек плоскости, координаты х, у которых удовлетворяют соотношению y = f(x) . На рис. 45 и 46 приведены графики функций у = 2х + 1 и у = х 2 - 2х . Строго говоря, следует различать график функции (точное математическое определение которого было дано выше) и начерченную кривую, которая всегда дает лишь более или менее точный эскиз графика (да и то, как правило, не всего графика, а лишь его части, расположенного в конечной части плоскости). С помощью графика можно находить значение функции в точке. Именно, если точка х = а принадлежит области определения функции y = f(x) , то для нахождения числа f(а) (т. е. значения функции в точке х = а ) следует поступить так. Нужно через точку с абсциссой х = а провести прямую, параллельную оси ординат; эта прямая пересечет график функции y = f(x) в одной точке; ордината этой точки и будет, в силу определения графика, равна f(а) (рис. 47). Например, для функции f(х) = х 2 - 2x с помощью графика (рис. 46) находим f(-1) = 3, f(0) = 0, f(1) = -l, f(2) = 0 и т. д. График функции наглядно иллюстрирует поведение и свойства функции. Например, из рассмотрения рис. 46 ясно, что функция у = х 2 - 2х принимает положительные значения при х и при х > 2 , отрицательные - при 0 наименьшее значение функция у = х 2 - 2х принимает при х = 1 . Для построения графика функции f(x) нужно найти все точки плоскости, координаты х , у которых удовлетворяют уравнению y = f(x) . В большинстве случаев это сделать невозможно, так как таких точек бесконечно много. Поэтому график функции изображают приблизительно - с большей или меньшей точностью. Самым простым является метод построения графика по нескольким точкам. Он состоит в том, что аргументу х придают конечное число значений - скажем, х 1 , х 2 , x 3 ,..., х k и составляют таблицу, в которую входят выбранные значения функции. Таблица выглядит следующим образом: Составив такую таблицу, мы можем наметить несколько точек графика функции y = f(x) . Затем, соединяя эти точки плавной линией, мы и получаем приблизительный вид графика функции y = f(x). Следует, однако, заметить, что метод построения графика по нескольким точкам очень ненадежен. В самом деле поведение графика между намеченными точками и поведение его вне отрезка между крайними из взятых точек остается неизвестным. Пример 1 . Для построения графика функции y = f(x) некто составил таблицу значений аргумента и функции: Соответствующие пять точек показаны на рис. 48. На основании расположения этих точек он сделал вывод, что график функции представляет собой прямую (показанную на рис. 48 пунктиром). Можно ли считать этот вывод надежным? Если нет дополнительных соображений, подтверждающих этот вывод, его вряд ли можно считать надежным. надежным. Для обоснования своего утверждения рассмотрим функцию . Вычисления показывают, что значения этой функции в точках -2, -1, 0, 1, 2 как раз описываются приведенной выше таблицей. Однако график этой функции вовсе не является прямой линией (он показан на рис. 49). Другим примером может служить функция y = x + l + sinπx; ее значения тоже описываются приведенной выше таблицей. Эти примеры показывают, что в «чистом» виде метод построения графика по нескольким точкам ненадежен. Поэтому для построения графика заданной функции,как правило, поступают следующим образом. Некоторые (наиболее простые и часто используемые) свойства функций, применяемые для нахождения эскиза графика, мы рассмотрим позже, а сейчас разберем некоторые часто применяемые способы построения графиков. График функции у = |f(x)|. Нередко приходится строить график функции y = |f(x) |, где f(х) - заданная функция. Напомним, как это делается. По определению абсолютной величины числа можно написать Это значит, что график функции y =|f(x)| можно получить из графика, функции y = f(x) следующим образом: все точки графика функции у = f(х) , у которых ординаты неотрицательны, следует оставить без изменения; далее, вместо точек графика функции y = f(x) , имеющих отрицательные координаты, следует построить соответствующие точки графика функции у = -f(x) (т. Пример 2. Построить график функции у = |х|. Берем график функции у = х (рис. 50, а) и часть этого графика при х (лежащую под осью х ) симметрично отражаем относительно оси х . В результате мы и получаем график функции у = |х| (рис. 50, б). Пример 3 . Построить график функции y = |x 2 - 2x|. Сначала построим график функции y = x 2 - 2x. График этой функции - парабола, ветви которой направлены вверх, вершина параболы имеет координаты (1; -1), ее график пересекает ось абсцисс в точках 0 и 2. На промежутке (0; 2) фукция принимает отрицательные значения, поэтому именно эту часть графика симметрично отразим относительно оси абсцисс. На рисунке 51 построен график функции у = |х 2 -2х| , исходя из графика функции у = х 2 - 2x График функции y = f(x) + g(x) Рассмотрим задачу построения графика функции y = f(x) + g(x). Заметим, что областью определения функции y = |f(x) + g(х)| является множество всех тех значений х, для которых определены обе функции y = f{x) и у = g(х), т. е. эта область определения представляет собой пересечение областей определения, функций f{x) и g{x). Пусть точки (х 0 , y 1 ) и (х 0 , у 2 ) соответственно принадлежат графикам функций y = f{x) и y = g(х) , т. е. y 1 = f(x 0), y 2 = g(х 0). Тогда точка (x0;. y1 + y2) принадлежит графику функции у = f(х) + g(х) (ибо f(х 0) + g(x 0 ) = y1 +y2 ),. причем любая точка графика функции y = f(x) + g(x) может быть получена таким образом. Следовательно, график функции у = f(х) + g(x) можно получить из графиков функций y = f(x) . и y = g(х) заменой каждой точки (х n , у 1) графика функции y = f(x) точкой (х n , y 1 + y 2), где у 2 = g(x n ), т. Такой метод построения графика функции y = f(x) + g(х ) называется сложением графиков функций y = f(x) и y = g(x) Пример 4 . На рисунке методом сложения графиков построен график функции При построении графика функции y = x + sinx мы полагали, что f(x) = x, а g(x) = sinx. Для построения графика функции выберем точки с aбциссами -1,5π, -, -0,5, 0, 0,5,, 1,5, 2. Значения f(x) = x, g(x) = sinx, y = x + sinx вычислим в выбранных точках и результаты поместим в таблице. Построение графиков функций, содержащих модули, обычно вызывает немалые затруднения у школьников. Однако, все не так плохо. Достаточно запомнить несколько алгоритмов решения таких задач, и вы сможете без труда построить график даже самой на вид сложной функции. 1. Построение графика функции y = |f(x)| Заметим, что множество значений функций y = |f(x)| : y ≥ 0. Таким образом, графики таких функций всегда расположены полностью в верхней полуплоскости. Построение графика функции y = |f(x)| состоит из следующих простых четырех этапов. 1) Построить аккуратно и внимательно график функции y = f(x). 2) Оставить без изменения все точки графика, которые находятся выше оси 0x или на ней. 3) Часть графика, которая лежит ниже оси 0x, отобразить симметрично относительно оси 0x. Пример 1. Изобразить график функции y = |x 2 – 4x + 3| 1) Строим график функции y = x 2 – 4x + 3. Очевидно, что график данной функции – парабола. Найдем координаты всех точек пересечения параболы с осями координат и координаты вершины параболы. x 2 – 4x + 3 = 0. x 1 = 3, x 2 = 1. Следовательно, парабола пересекает ось 0x в точках (3, 0) и (1, 0). y = 0 2 – 4 · 0 + 3 = 3. Следовательно, парабола пересекает ось 0y в точке (0, 3). Координаты вершины параболы: x в = -(-4/2) = 2, y в = 2 2 – 4 · 2 + 3 = -1. Следовательно, точка (2, -1) является вершиной данной параболы. Рисуем параболу, используя полученные данные (рис. 1) 2) Часть графика, лежащую ниже оси 0x, отображаем симметрично относительно оси 0x. 3) Получаем график исходной функции (рис. 2 , изображен пунктиром). 2. Построение графика функции y = f(|x|) Заметим, что функции вида y = f(|x|) являются четными: y(-x) = f(|-x|) = f(|x|) = y(x). Значит, графики таких функций симметричны относительно оси 0y. Построение графика функции y = f(|x|) состоит из следующей несложной цепочки действий. 1) Построить график функции y = f(x). 2) Оставить ту часть графика, для которой x ≥ 0, то есть часть графика, расположенную в правой полуплоскости. 3) Отобразить указанную в пункте (2) часть графика симметрично оси 0y. 4) В качестве окончательного графика выделить объединение кривых, полученных в пунктах (2) и (3). Пример 2. Изобразить график функции y = x 2 – 4 · |x| + 3 Так как x 2 = |x| 2 , то исходную функцию можно переписать в следующем виде: y = |x| 2 – 4 · |x| + 3. А теперь можем применять предложенный выше алгоритм. 1) Строим аккуратно и внимательно график функции y = x 2 – 4 · x + 3 (см. также рис. 1 ). 2) Оставляем ту часть графика, для которой x ≥ 0, то есть часть графика, расположенную в правой полуплоскости. 3) Отображаем правую часть графика симметрично оси 0y. (рис. 3) . Пример 3. Изобразить график функции y = log 2 |x| Применяем схему, данную выше. 1) Строим график функции y = log 2 x (рис. 4) . 3. Построение графика функции y = |f(|x|)| Заметим, что функции вида y = |f(|x|)| тоже являются четными. Действительно, y(-x) = y = |f(|-x|)| = y = |f(|x|)| = y(x), и поэтому, их графики симметричны относительно оси 0y. Чтобы построить график функции y = |f(|x|)|, необходимо: 1) Построить аккуратно график функции y = f(|x|). 2) Оставить без изменений ту часть графика, которая находится выше оси 0x или на ней. 3) Часть графика, расположенную ниже оси 0x, отобразить симметрично относительно оси 0x. 4) В качестве окончательного графика выделить объединение кривых, полученных в пунктах (2) и (3). Пример 4. Изобразить график функции y = |-x 2 + 2|x| – 1|. 1) Заметим, что x 2 = |x| 2 . Значит, вместо исходной функции y = -x 2 + 2|x| – 1 можно использовать функцию y = -|x| 2 + 2|x| – 1, так как их графики совпадают. Строим график y = -|x| 2 + 2|x| – 1. Для этого применяем алгоритм 2. a) Строим график функции y = -x 2 + 2x – 1 (рис. 6) . b) Оставляем ту часть графика, которая расположена в правой полуплоскости. c) Отображаем полученную часть графика симметрично оси 0y. d) Полученный график изображен на рисунке пунктиром (рис. 7) . 2) Выше оси 0х точек нет, точки на оси 0х оставляем без изменения. 3) Часть графика, расположенную ниже оси 0x, отображаем симметрично относительно 0x. 4) Полученный график изображен на рисунке пунктиром (рис. 8) . Пример 5. Построить график функции y = |(2|x| – 4) / (|x| + 3)| 1) Сначала необходимо построить график функции y = (2|x| – 4) / (|x| + 3). Для этого возвращаемся к алгоритму 2. a) Аккуратно строим график функции y = (2x – 4) / (x + 3) (рис. 9) . Заметим, что данная функция является дробно-линейной и ее график есть гипербола. Для построения кривой сначала необходимо найти асимптоты графика. Горизонтальная – y = 2/1 (отношение коэффициентов при x в числителе и знаменателе дроби), вертикальная – x = -3. 2) Ту часть графика, которая находится выше оси 0x или на ней, оставим без изменений. 3) Часть графика, расположенную ниже оси 0x, отобразим симметрично относительно 0x. 4) Окончательный график изображен на рисунке (рис. 11) . сайт,
при полном или частичном копировании материала ссылка на первоисточник обязательна. Визуализации Looker автоматически определяют, какие значения отображать по оси Y.
в зависимости от того, какие типы полей присутствуют в запросе. Возьмем, к примеру, этот Explore,
который разбивает пользователей с полным именем и пользователей с возрастом для
10 самых высоких значений Order Count : Первые два измерения — Полное имя пользователя и Возраст пользователя —
автоматически объединяются по оси x. Что делать, если вы хотите нанести размер по оси Y, когда Looker не делает этого автоматически?
Для этого необходимо преобразовать измерение, чтобы оно отображалось как показатель . Что делать, если вы хотите разделить пользователей, возраст и пользователей, полное имя , чтобы пользователей возраста были
на оси y, а Users Full Name и Orders Count отображаются на оси x, вот так? Два следующих решения описывают, как преобразовать измерение, например Users Age , в меру, чтобы ее можно было визуализировать на оси Y: Расчет таблицы
— это самый быстрый и простой способ нанести размер по оси Y. После добавления расчета таблицы и скрытия исходного измерения таблица Explore Data будет выглядеть примерно так: Вы можете настроить отображение полей с помощью визуализации.
варианты редактирования,
в том числе с использованием нескольких типов виз
в едином графике. В примере Orders Count визуализируется как линия, а Users Age как
столбец: Если вы планируете в будущем снова отобразить определенное измерение по оси Y, более устойчивым вариантом будет создание Включите измерение и в новую меру в запросе Исследовать. Цифры будут одинаковыми, так как
sum будет суммировать только одно значение — значение измерения рядом с ним. Мера будет выглядеть примерно так: Скройте измерение в визуализации «Исследовать», но обязательно оставьте измерение в
запрос, чтобы сумма не группировала несколько значений. Полученная визуализация Explore и Таблица данных будет выглядеть примерно так: Рисовать линейный график с возможностью нескольких смысловых группировок. Связь между Дополнительную информацию см. в руководстве. Обработка по умолчанию По умолчанию график агрегируется по нескольким значениям Структура входных данных. Либо полный набор векторов, который может быть
присваивается именованным переменным или набору данных широкой формы, который будет внутренне
изменен. Переменные, определяющие положения по осям x и y. Группирующая переменная, которая будет создавать линии разных цветов.
Может быть либо категориальным, либо числовым, хотя отображение цветов будет
в последнем случае ведут себя иначе. Группирующая переменная, которая будет создавать линии разной ширины.
Может быть либо категориальным, либо числовым, хотя сопоставление размеров
в последнем случае ведут себя иначе. Группирующая переменная, которая будет создавать линии с разными штрихами
и/или маркеры. Может иметь числовой тип dtype, но всегда будет обрабатываться
как категоричный. Группирующая переменная, идентифицирующая единицы выборки. При использовании отдельный
линия будет проведена для каждой единицы с соответствующей семантикой, но не
запись легенды будет добавлена. Полезно для отображения распределения
экспериментальные повторения, когда точные тождества не нужны. Метод выбора цветов для использования при отображении Укажите порядок обработки и построения графиков для категориальных уровней Любая пара значений, задающая диапазон нормализации в единицах данных
или объект, который будет отображать единицы данных в интервал [0, 1]. Применение
подразумевает числовое отображение. Объект, который определяет, как выбираются размеры при использовании Указанный порядок появления переменных уровней Нормализация в единицах данных для масштабирования объектов графика при Объект, определяющий способ рисования линий для разных уровней Объект, определяющий, как рисовать маркеры для разных уровней Указанный порядок появления переменных уровней Метод для агрегирования нескольких наблюдений Имя метода панели ошибок (либо «ci», «pi», «se» или «sd»), либо кортеж
с именем метода и параметром уровня или функцией, которая отображается из
вектор на интервал (мин., макс.). Количество бутстрапов, используемых для вычисления доверительного интервала. Seed или генератор случайных чисел для воспроизводимой начальной загрузки. Измерение, по которому данные сортируются/агрегируются. Эквивалентно,
«независимая переменная» результирующей функции. Если True, данные будут отсортированы по переменным x и y, иначе
линии будут соединять точки в том порядке, в котором они появляются в наборе данных. Следует ли рисовать доверительные интервалы с полупрозрачными полосами ошибок
или дискретные полосы ошибок. Дополнительные параметры для управления внешним видом полос ошибок.
kwargs передаются либо в Как нарисовать легенду. Если «краткое», числовой Размер доверительного интервала для построения при агрегировании. Устарело, начиная с версии 0.12.0: используйте новый параметр Существующие оси для графика. В противном случае вызовите Другие аргументы ключевого слова передаются в Оси matplotlib, содержащие график. См. также Нанесение данных на график с использованием точек. Постройте точечные оценки и CI, используя маркеры и линии. Примеры Набор данных c. 3),(x,0,2*pi),rgbcolor=hue(0.6))
sage: show(p1+p2+p3, axes=false)
3),(x,0,2*pi),rgbcolor=hue(0.6))
sage: show(p1+p2+p3, axes=false) L в следующем примере), а затем использование команды polygon для
построения фигуры с границами, образованными заданными точками. К
примеру, создадим зеленый дельтоид:sage: L = [[-1+cos(pi*i/100)*(1+cos(pi*i/100)),
....: 2*sin(pi*i/100)*(1-cos(pi*i/100))] for i in range(200)]
sage: p = polygon(L, rgbcolor=(1/8,3/4,1/2))
sage: p
Graphics object consisting of 1 graphics primitive
show(p, axes=false), чтобы не показывать осей на графике.sage: L = [[6*cos(pi*i/100)+5*cos((6/2)*pi*i/100),
....: 6*sin(pi*i/100)-5*sin((6/2)*pi*i/100)] for i in range(200)]
sage: p = polygon(L, rgbcolor=(1/8,1/4,1/2))
sage: t = text("hypotrochoid", (5,4), rgbcolor=(1,0,0))
sage: show(p+t)
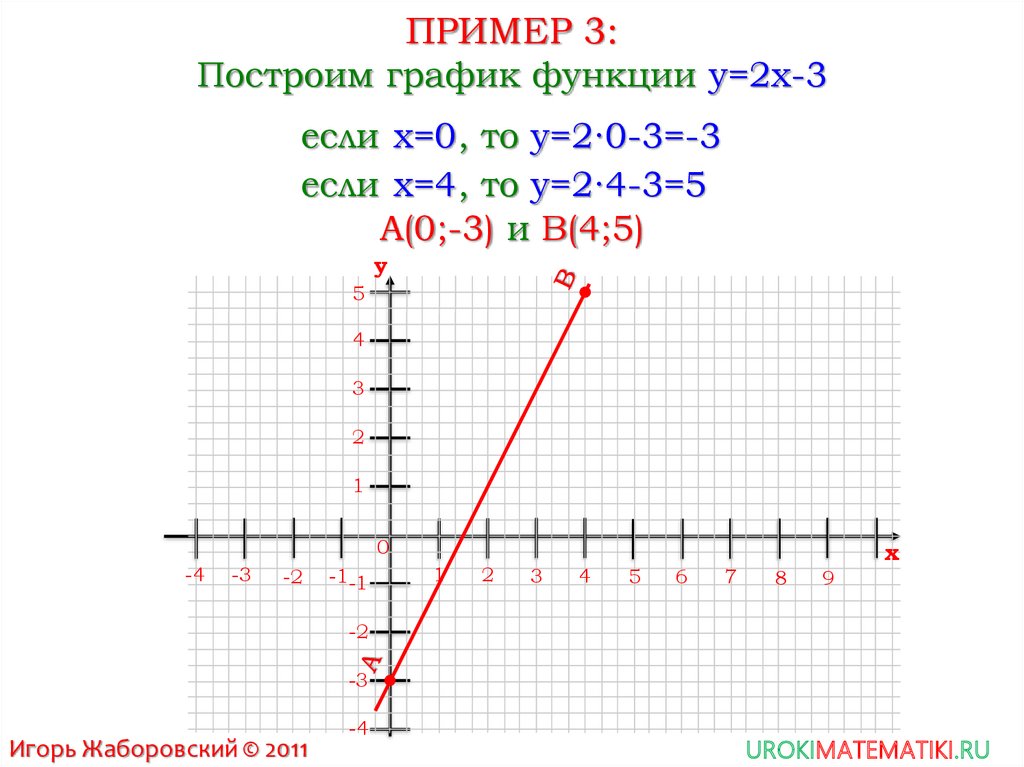 е. график функции \(y=\sin(x)\)
для \(x\) между \(-2\pi\) и \(2\pi\), перевернутый по
отношению к линии в 45 градусов. Следующая команда Sage построит
вышеуказанное:
е. график функции \(y=\sin(x)\)
для \(x\) между \(-2\pi\) и \(2\pi\), перевернутый по
отношению к линии в 45 градусов. Следующая команда Sage построит
вышеуказанное:sage: v = [(sin(x),x) for x in srange(-2*float(pi),2*float(pi),0.1)]
sage: line(v)
Graphics object consisting of 1 graphics primitive
sage: v = [(tan(x),x) for x in srange(-2*float(pi),2*float(pi),0.01)]
sage: show(line(v), xmin=-20, xmax=20)
sage: f = lambda x,y: cos(x*y)
sage: contour_plot(f, (-4, 4), (-4, 4))
Graphics object consisting of 1 graphics primitive
Трехмерные графики
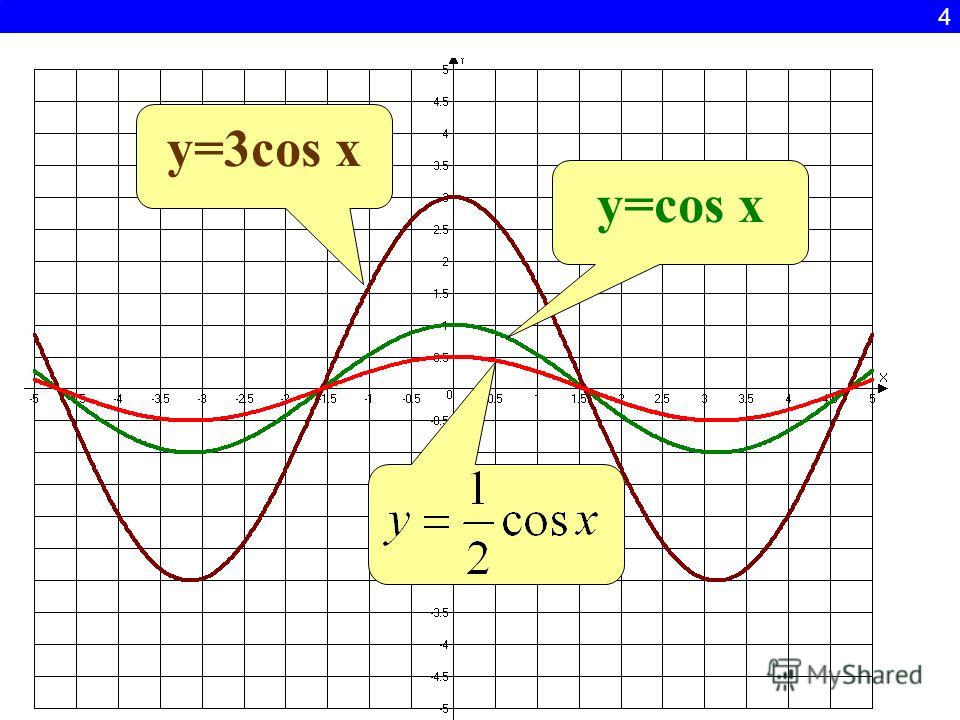 2 - 1)
sage: implicit_plot3d(f, (x, -0.5, 0.5), (y, -1, 1), (z, -1, 1))
Graphics3d Object
2 - 1)
sage: implicit_plot3d(f, (x, -0.5, 0.5), (y, -1, 1), (z, -1, 1))
Graphics3d Object Как построить график функции y 1 2. Функции и графики
 Алгебра 8 класс Учитель 496 школы Бовина Т. В. -1. План построения. 2) Построить ось симметрии x=-1. y.
Алгебра 8 класс Учитель 496 школы Бовина Т. В. -1. План построения. 2) Построить ось симметрии x=-1. y.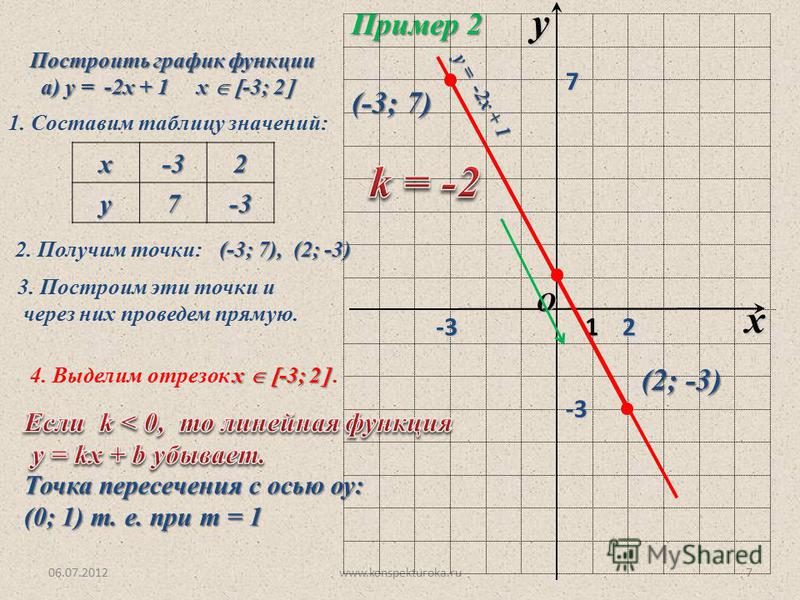 В дальнейшем, однако, мы обычно будем говорить «график», а не «эскиз графика».
В дальнейшем, однако, мы обычно будем говорить «график», а не «эскиз графика».
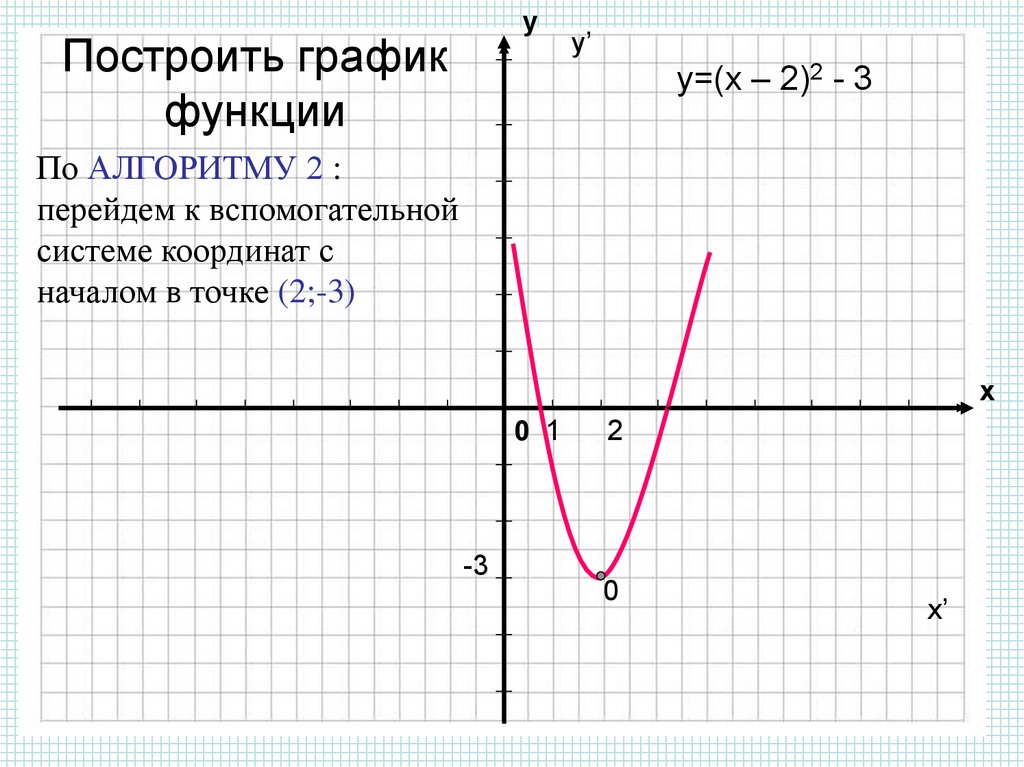
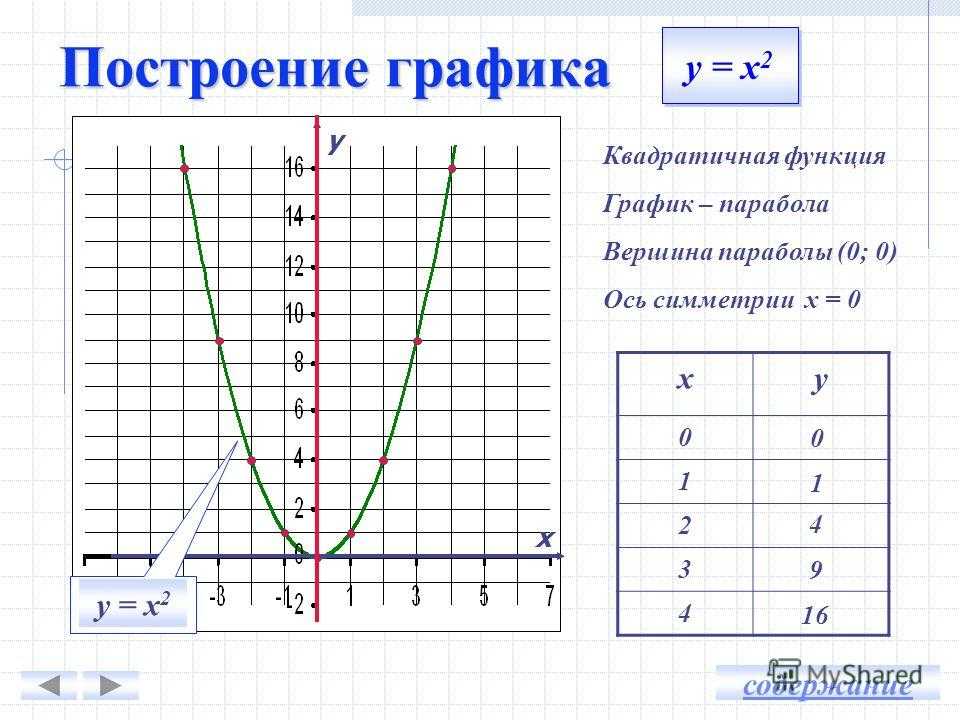 Сначала изучают свойства данной функции, с помощью которых можно построить эскиз графика. Затем, вычисляя значения функции в нескольких точках (выбор которых зависит от установленных свойств функции), находят соответствующие точки графика. И, наконец, через построенные точки проводят кривую, используя свойства данной функции.
Сначала изучают свойства данной функции, с помощью которых можно построить эскиз графика. Затем, вычисляя значения функции в нескольких точках (выбор которых зависит от установленных свойств функции), находят соответствующие точки графика. И, наконец, через построенные точки проводят кривую, используя свойства данной функции.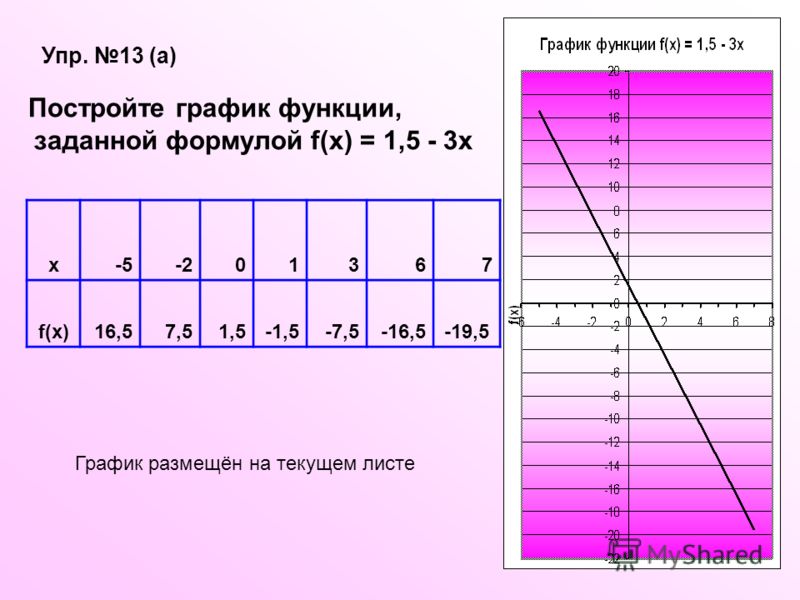 е. часть графика функции
е. часть графика функции
y = f(x) , которая лежит ниже оси х, следует симметрично отразить относительно оси х ). если заданы графики функций y = f(x) и y = g(x) .
если заданы графики функций y = f(x) и y = g(x) .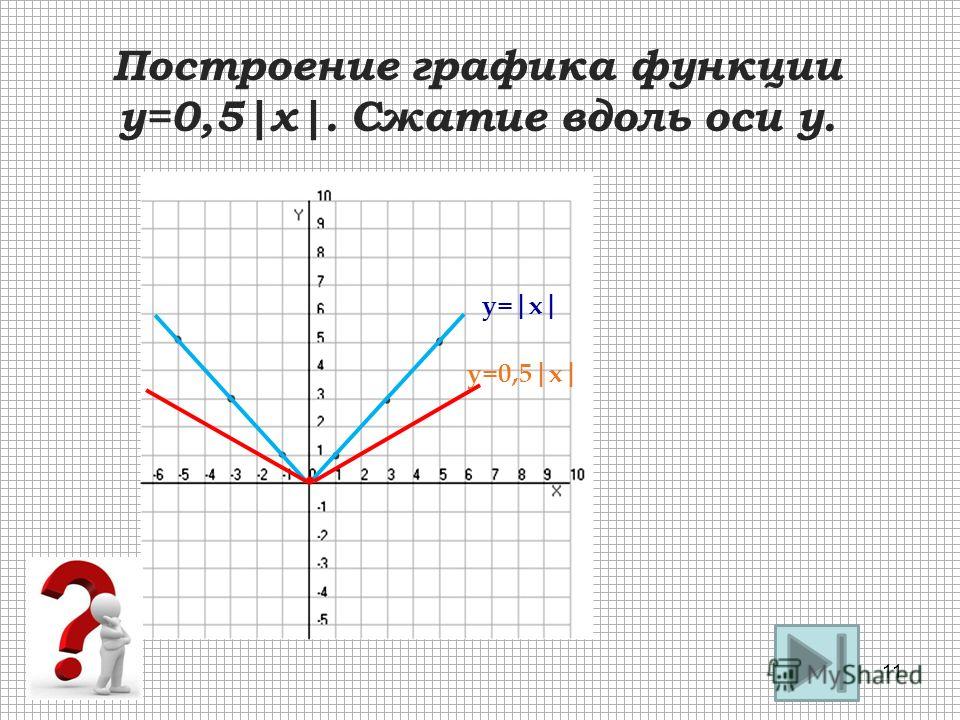 е. сдвигом каждой точки (х n , у 1 ) графика функции y = f(x) вдоль оси у на величину y 1 = g(х n ). При этом рассматриваются только такие точки х n для которых определены обе функции y = f(x) и y = g(x) .
е. сдвигом каждой точки (х n , у 1 ) графика функции y = f(x) вдоль оси у на величину y 1 = g(х n ). При этом рассматриваются только такие точки х n для которых определены обе функции y = f(x) и y = g(x) .
y = x + sinx .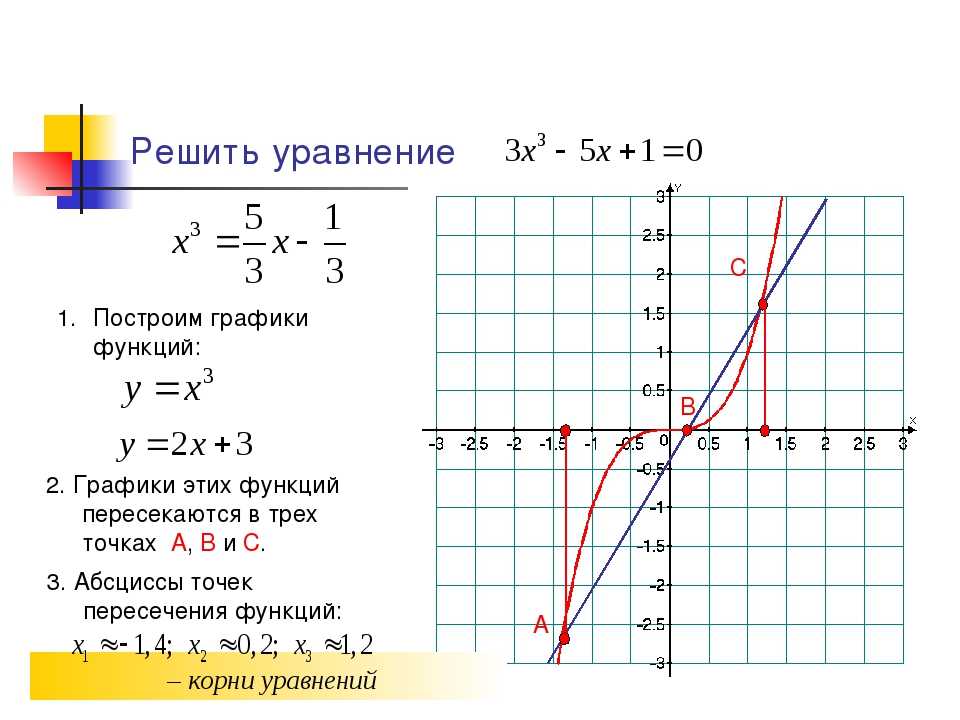 Давайте разберемся, что же это за алгоритмы.
Давайте разберемся, что же это за алгоритмы.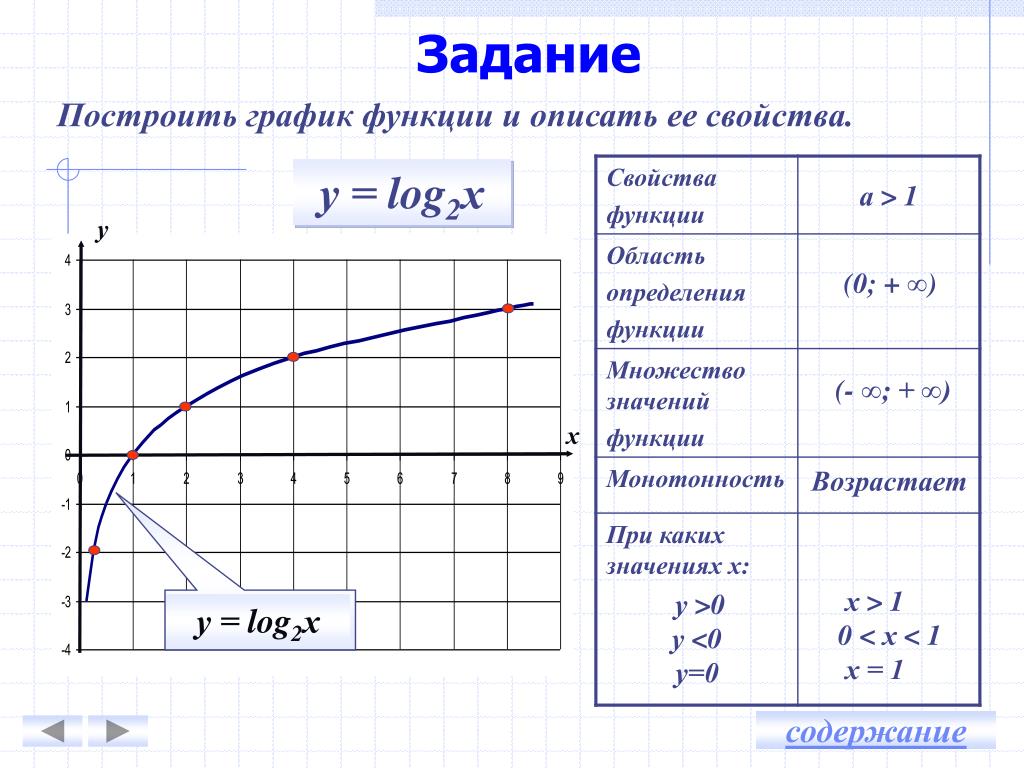
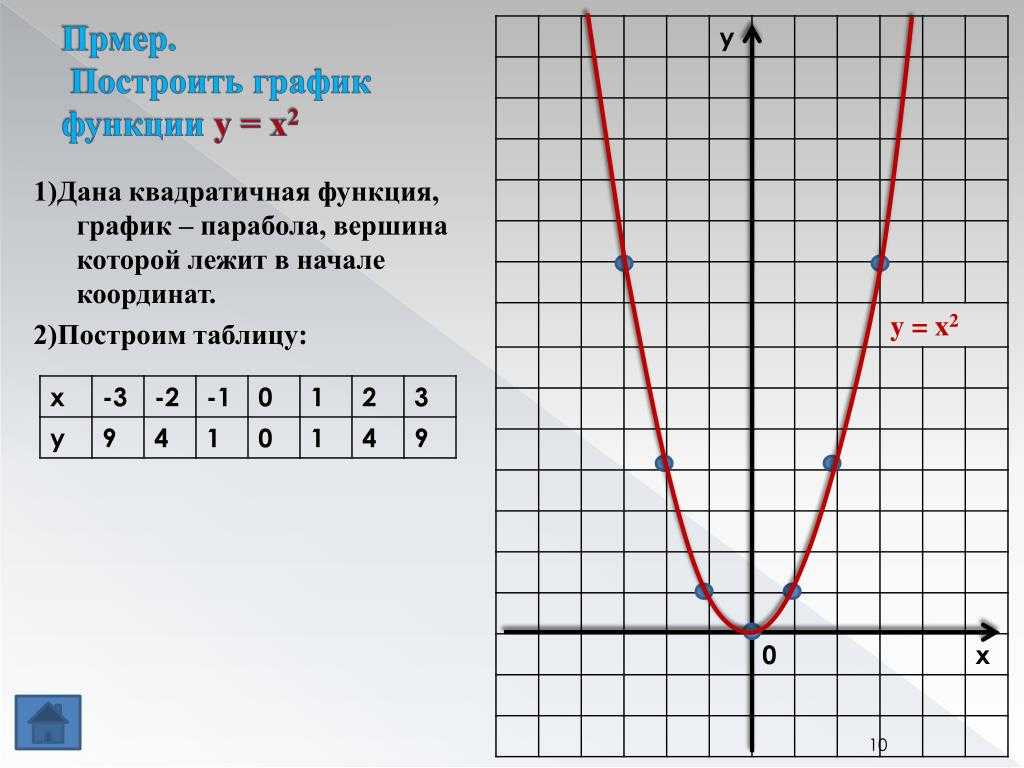
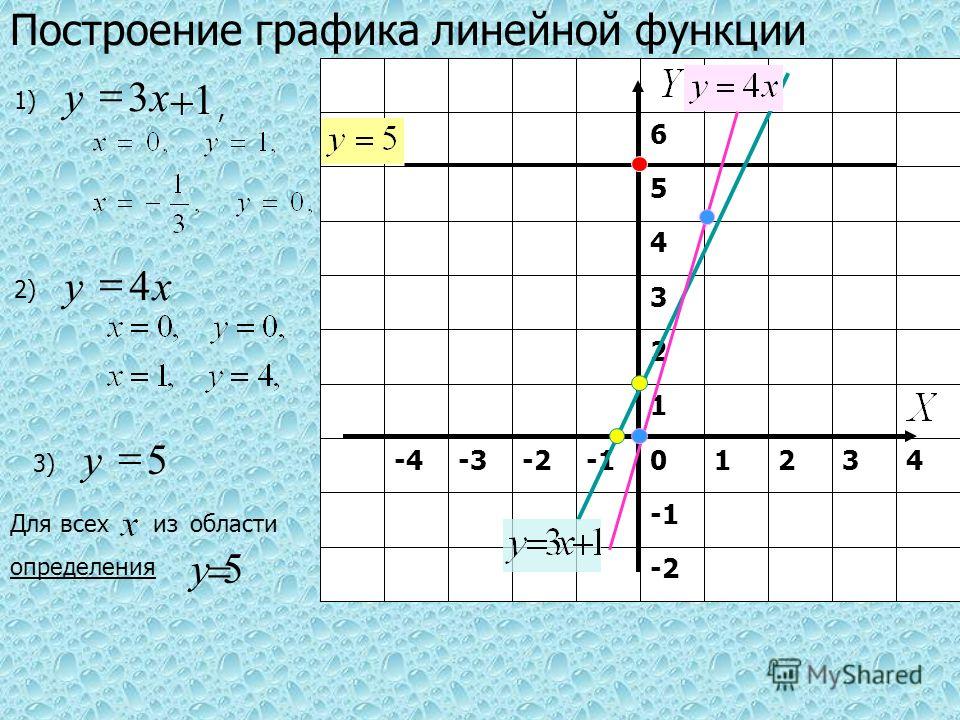 Множество значений таких функций: y ≥ 0. Значит, графики таких функций расположены полностью в верхней полуплоскости.
Множество значений таких функций: y ≥ 0. Значит, графики таких функций расположены полностью в верхней полуплоскости.

Как нанести размеры по оси Y | Смотритель
Все пользовательские данные, представленные в этой статье, приведены для примера.
 Два способа достижения
это изложено в этой статье.
Два способа достижения
это изложено в этой статье. sum — Разработайте LookML, чтобы можно было повторно использовать выражение в будущих исследованиях без создания табличных вычислений. Использование табличного расчета
 Вычисление обычно отображается в виде измерения, если в формулу не включены меры. Вы можете заставить табличное вычисление вести себя как меру, включив меру в выражение вычисления. Главное — убедиться, что мера не повлияет на значение исходного измерения.
Вычисление обычно отображается в виде измерения, если в формулу не включены меры. Вы можете заставить табличное вычисление вести себя как меру, включив меру в выражение вычисления. Главное — убедиться, что мера не повлияет на значение исходного измерения. ${mydimension} + (0 * ${mymeasure}) Расчет сохраняет исходное значение размера путем умножения
измерить на 0, if() и is_null() , вместо этого: если (is_null ($ {mymeasure}), $ {string_dimension}, $ {string_dimension}) Это выражение сообщает Looker, что всегда отображает значение размерности строки вместо
измерять значения.
Создание показателя суммы
в LookML сумма мера
в LookML, который суммирует измерение, которое вы хотите отобразить. Вместо того чтобы повторно создавать одно и то же табличное вычисление в Исследовании несколько раз, вы можете добавить поле в запрос из селектора полей.
Вместо того чтобы повторно создавать одно и то же табличное вычисление в Исследовании несколько раз, вы можете добавить поле в запрос из селектора полей.
мера: Measure_for_age { ## заменить новым именем
description: "Используйте это поле возраста для отображения возраста по оси Y"
тип: сумма
sql: ${возраст} ;; ## замените на свой размер
}
Добавление
описания к мере может помочь пользователям понять предполагаемое использование поля. seaborn.
 lineplot — документация seaborn 0.12.0
lineplot — документация seaborn 0.12.0 x и y может быть показана для разных подмножеств
данных с использованием параметров hue , size и style . Эти
параметры контролируют, какая визуальная семантика используется для идентификации различных
подмножества. Можно отображать до трех измерений независимо друг от друга.
используя все три семантических типа, но этот стиль сюжета может быть трудным для понимания.
интерпретируется и часто оказывается неэффективным. Использование избыточной семантики (т.е.
Эти
параметры контролируют, какая визуальная семантика используется для идентификации различных
подмножества. Можно отображать до трех измерений независимо друг от друга.
используя все три семантических типа, но этот стиль сюжета может быть трудным для понимания.
интерпретируется и часто оказывается неэффективным. Использование избыточной семантики (т.е. оттенок и стиль для одной и той же переменной) могут быть полезны для создания
графика более доступная. оттенка (и, в меньшей степени, размера )
семантика, если она присутствует, зависит от того, выводится ли переменная как
представляют «числовые» или «категориальные» данные. В частности, числовые переменные
представлены последовательной цветовой картой по умолчанию, а легенда
записи показывают обычные «галочки» со значениями, которые могут существовать или не существовать в
данные. Это поведение можно контролировать с помощью различных параметров, таких как
описаны и проиллюстрированы ниже.
y для каждого значения x и показывает оценку центральной тенденции и достоверность
интервал для этой оценки. pandas.DataFrame , numpy.ndarray , отображение или последовательность данных данных 
данных данных matplotlib. colors.Colormap
colors.Colormap оттенка семантики.
Строковые значения передаются в color_palette() . Список или словарные значения
подразумевают категориальное отображение, в то время как объект палитры подразумевает числовое отображение. оттенок семантический. matplotlib.colors.Normalize размера .
Аргументы list или dict должны указывать размер для каждого уникального значения данных,
что вынуждает к категоричной интерпретации. Аргумент также может быть
мин, макс кортеж.
Аргумент также может быть
мин, макс кортеж. size ,
в противном случае они определяются из данных. Не актуально, когда размер переменная является числовой. size переменная числовая. стиль переменный. При значении True будут использоваться дефисные коды по умолчанию или
вы можете передать список кодов тире или уровни сопоставления словаря стиль переменная для кодов тире. При установке на False будет использоваться сплошной
строки для всех подмножеств.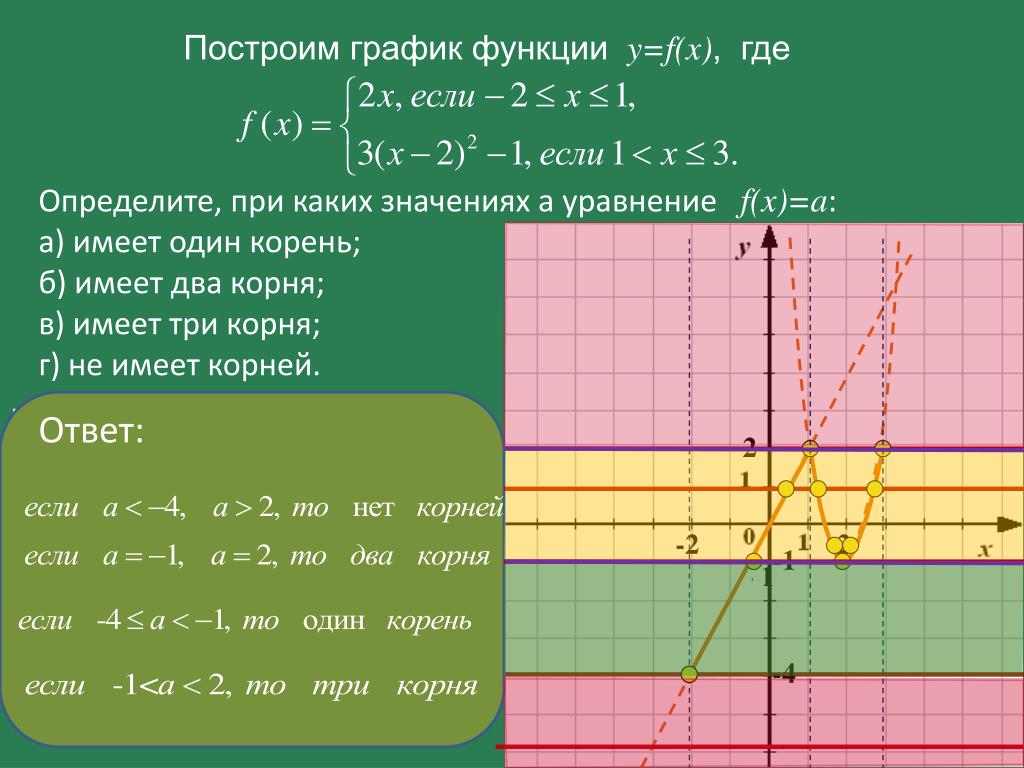 Тире указаны как в matplotlib: кортеж
из
Тире указаны как в matplotlib: кортеж
из (сегмент, разрыв) длин или пустая строка для рисования сплошной линии. стиль переменный. При значении True будут использоваться маркеры по умолчанию или
вы можете передать список маркеров или уровень сопоставления словаря стиль переменный для маркеров. Установка на False будет рисовать
линии без маркеров. Маркеры указаны как в matplotlib. стиля в противном случае они определяются из данных. Не актуально, когда
Переменная стиля является числовой. г переменная на том же уровне x . Если
Если None , все наблюдения будут
быть нарисованным.
matplotlib.axes.Axes.fill_between() или matplotlib.axes.Axes.errorbar() , в зависимости от err_style . оттенок и размер переменные будут представлены выборкой равномерно распределенных значений.
Если «полный», каждая группа получит запись в легенде. Если «авто»,
выберите между кратким или полным представлением в зависимости от количества уровней.
Если False , данные легенды не добавляются и легенда не рисуется.
errorbar для большей гибкости. matplotlib.axes.Axes matplotlib.pyplot.gca() внутри. matplotlib.axes.Axes.plot() . matplotlib.axes.Axes диаграмма рассеяния pointplot 
рейсов содержит ежемесячные данные о пассажирах авиакомпаний за 10 лет: рейса = sns.load_dataset("рейсы")
рейсы.голова()
год месяц пассажиров 0 1949 Январь 112 1 1949 фев 118 2 1949 март 132 3 1949 апр 129 4 1949 май 121
Чтобы построить линейный график с использованием полных данных, назначьте переменные x и y :
may_flights = рейсы.query("месяц == 'май'") sns.lineplot(data=may_flights, x="год", y="пассажиры")
Повернуть фрейм данных в широкоформатное представление:
рейсы_wide = рейсы.pivot("год", "месяц", "пассажиры")
рейсы_wide.head()
| месяц | Январь | фев | март | апр | май | июнь | июль | авг | сен | окт | ноябрь | декабрь |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| год | ||||||||||||
| 1949 | 112 | 118 | 132 | 129 | 121 | 135 | 148 | 148 | 136 | 119 | 104 | 118 |
| 1950 | 115 | 126 | 141 | 135 | 125 | 149 | 170 | 170 | 158 | 133 | 114 | 140 |
| 1951 | 145 | 150 | 178 | 163 | 172 | 178 | 199 | 199 | 184 | 162 | 146 | 166 |
| 1952 | 171 | 180 | 193 | 181 | 183 | 218 | 230 | 242 | 209 | 191 | 172 | 194 |
| 1953 | 196 | 196 | 236 | 235 | 229 | 243 | 264 | 272 | 237 | 211 | 180 | 201 |
Чтобы построить один вектор, передайте его в data .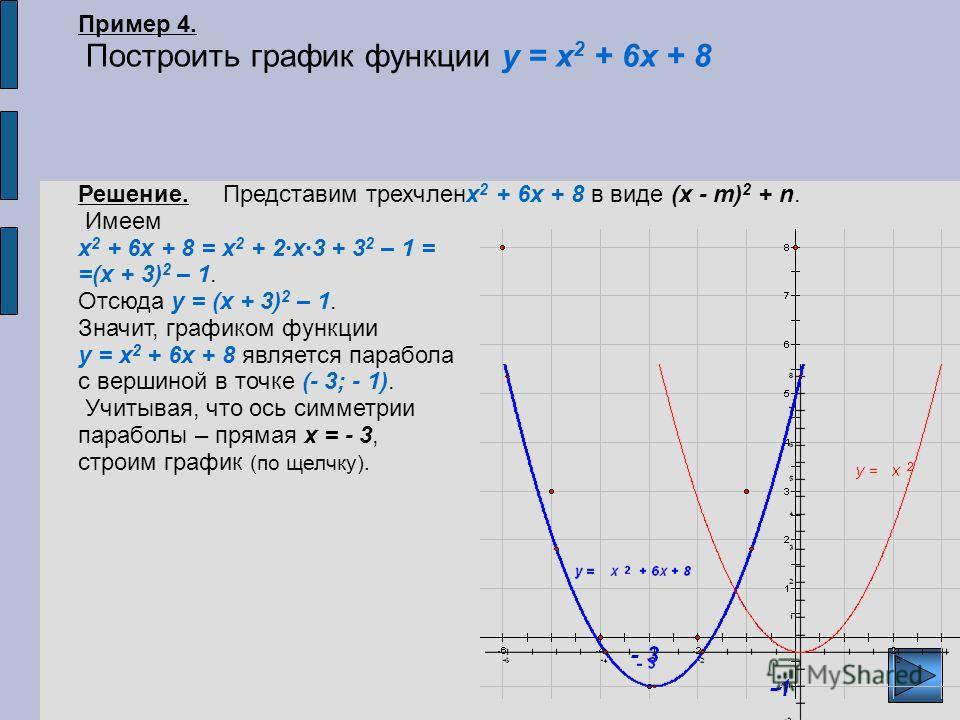 Если вектор представляет собой
Если вектор представляет собой pandas.Series , он будет построен по его индексу:
sns.lineplot(data=flights_wide["Май"])
Передача всего набора данных широкой формы в data строит отдельную строку для каждого столбца:
sns.lineplot(data=flights_wide)
При передаче всего набора данных в полном режиме будут агрегированы повторяющиеся значения (каждый год), чтобы показать среднее значение и 95% доверительный интервал:
sns.lineplot(data=рейсы, x="год", y="пассажиры")
Назначить семантику группировки ( оттенок , размер или стиль ) для построения отдельных линий
sns.lineplot(data=flights, x="год", y="пассажиры", hue="месяц")
Один и тот же столбец может быть назначен нескольким семантическим переменным, что может повысить доступность графика:
sns.lineplot(data=flights, x="год", y="пассажиры", hue="месяц",)
Используйте параметр ориентация для агрегирования и сортировки по вертикали графика:
sns.lineplot (данные = рейсы, x = "пассажиры", y = "год", ориентация = "y")
Каждая семантическая переменная также может представлять отдельный столбец. Для этого нам понадобится более сложный набор данных:
. ФМРИ = sns.load_dataset("ФМРИ")
fmri.head()
| тема | момент времени | событие | регион | сигнал | |
|---|---|---|---|---|---|
| 0 | с13 | 18 | стим | теменная | -0,017552 |
| 1 | с5 | 14 | стим | теменная | -0,080883 |
| 2 | с12 | 18 | стим | теменная | -0,081033 |
| 3 | с11 | 18 | стим | теменная | -0,046134 |
| 4 | с10 | 18 | стим | теменная | -0,037970 |
Повторные наблюдения агрегируются даже при использовании семантической группировки:
sns.lineplot(data=fmri, x="timepoint", y="signal", hue="event")
Назначьте оттенок и стиль для представления двух разных группирующих переменных:
sns.lineplot(data=fmri, x="timepoint", y="signal", hue="region",)
При назначении переменной стиля вместо дефисов (или вместе с ними) можно использовать маркеры для различения групп:
sns.lineplot(
данные = фмрт,
х = "точка времени", у = "сигнал", оттенок = "событие",
маркеры = Истина, тире = Ложь
)
Показать полосы ошибок вместо полос ошибок и расширить их до двух стандартных значений ширины ошибки:
sns.lineplot(
data=fmri, x="timepoint", y="signal", hue="event", err_style="bars", errorbar=("se", 2),
)
Присвоение переменной единиц приведет к построению нескольких линий без применения семантического отображения:
sns.lineplot(
data=fmri.query("регион == 'фронтальный'"),
x="точка времени", y="сигнал", оттенок="событие", блоки="тема",
оценщик = нет, lw = 1,
)
Загрузить другой набор данных с числовой переменной группировки:
точки = sns.load_dataset("dots").query("align == 'dots'") точки.голова()
| выровнять | выбор | время | когерентность | скорость стрельбы | |
|---|---|---|---|---|---|
| 0 | точек | Т1 | -80 | 0,0 | 33.189967 |
| 1 | точек | Т1 | -80 | 3,2 | 31.6 |
| 2 | точек | Т1 | -80 | 6,4 | 34.279840 |
| 3 | точек | Т1 | -80 | 12,8 | 32.631874 |
| 4 | точек | Т1 | -80 | 25,6 | 35.060487 |
Присвоение числовой переменной оттенок отображает его по-другому, используя другую палитру по умолчанию и количественное сопоставление цветов:
sns.lineplot( данные = точки, x = "время", y = "скорость стрельбы", оттенок = "когерентность", )
Управляйте сопоставлением цветов, установив палитру и передав объект matplotlib.colors.Normalize :
sns.lineplot(
данные = dots.query ("когерентность > 0"),
x = "время", y = "скорость стрельбы", оттенок = "когерентность",
палитра = «вспышка», hue_norm = mpl.colors.LogNorm (),
)
Или передать определенные цвета в виде списка или словаря Python:
палитра = sns.color_palette("mako_r", 6)
sns.lineplot(
данные = точки, x = "время", y = "скорость стрельбы",
оттенок = "когерентность",
палитра=палитра
)
Назначьте семантику размера для сопоставления ширины линий с числовой переменной:
sns.lineplot(
данные = точки, x = "время", y = "скорость стрельбы",
размер = "когерентность", оттенок = "выбор",
легенда = "полный"
)
Передать кортеж, размеров = (самый маленький, самый большой) , чтобы управлять диапазоном ширины линии, используемой для отображения семантики размера :
sns.lineplot( данные = точки, x = "время", y = "скорость стрельбы", размер = "когерентность", оттенок = "выбор", размеры = (0,25, 2,5) )
По умолчанию наблюдения сортируются по размеру x . Отключите это, чтобы построить линию в том порядке, в котором наблюдения появляются в наборе данных:
x, y = np.random.normal(size=(2, 5000)).cumsum(ось=1) sns.lineplot(x=x, y=y, sort=False, lw=1)
Использовать relplot() для объединения lineplot() и FacetGrid . Это позволяет группировать внутри дополнительных категориальных переменных. Использование relplot() безопаснее, чем непосредственное использование FacetGrid , поскольку оно обеспечивает синхронизацию семантических отображений между фасетами:
sns.relplot(
данные = fmri, x = "точка времени", y = "сигнал",
col="регион", оттенок="событие",
вид = "линия"
)
Построение графиков в Python | Набор 1
В этой серии статей вы познакомитесь с графическим представлением в Python с помощью Matplotlib, возможно, самой популярной библиотеки графического представления и визуализации данных для Python.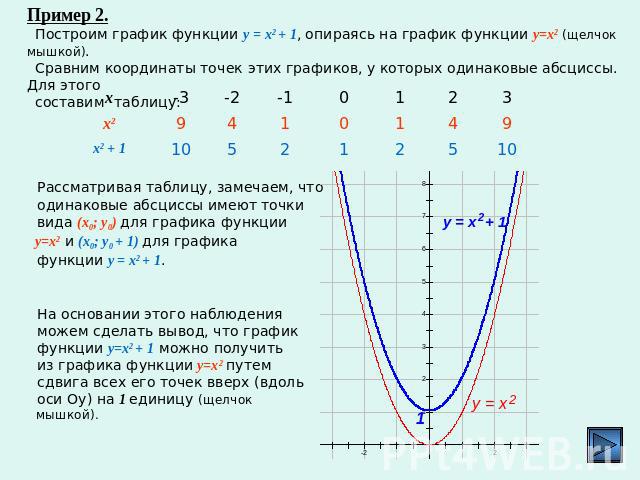
Установка
Самый простой способ установить matplotlib — использовать pip. Введите в терминал следующую команду:
pip install matplotlib
ИЛИ вы можете скачать ее отсюда и установить вручную.
Getting started ( Plotting a line)
Python
|
Output:
Код говорит сам за себя. Были выполнены следующие шаги:
- Определите оси X и соответствующие значения оси Y в виде списков.
- Нанесите их на холст с помощью функции .plot() .
- Дайте имя оси x и оси y, используя функции .xlabel() и .
 ylabel() .
ylabel() . - Дайте название вашему графику, используя функцию .title() .
- Наконец, чтобы просмотреть график, мы используем функцию .show() .
Plotting two or more lines on same plot
Python
|
Вывод:
- Здесь мы наносим две линии на один и тот же график. Мы различаем их, давая им имя ( label ), которое передается в качестве аргумента функции .plot().
- Маленькое прямоугольное поле, дающее информацию о типе линии и ее цвете, называется легендой. Мы можем добавить легенду к нашему графику, используя функцию .legend() .
Настройка графиков
Здесь мы обсудим некоторые элементарные настройки, применимые практически к любому графику.
Python
|
Выход:
Как вы можете увидеть, мы сделали несколько настройки, такие как
- 40045. цвет.
- настройка маркера, цвет лицевой стороны маркера, размер маркера.
- переопределяет диапазон осей x и y. Если переопределение не выполнено, модуль pyplot использует функцию автоматического масштабирования для установки диапазона и масштаба оси.
Bar Chart
Python
|
Output :
- Here, we use plt.
 bar() function to plot a гистограмма.
bar() function to plot a гистограмма. - x-координаты левой стороны стержней передаются вместе с высотами стержней.
- вы также можете дать некоторые имена координатам оси X, определив tick_labels
Histogram
Python
. = ( 0 , 100 ) |
. построить гистограмму. Диаграмма рассеяния Output: Pie-chart The output of вышеприведенная программа выглядит следующим образом: Plotting curves of given equation The output of above program looks like this: Здесь мы используем NumPy — универсальный пакет обработки массивов на Python. Итак, в этой части мы обсудили различные типы графиков, которые мы можем создавать в matplotlib. Есть и другие графики, которые не были рассмотрены, но наиболее важные из них обсуждаются здесь — Эта статья предоставлена Nikhil Kumar . Если вам нравится GeeksforGeeks и вы хотите внести свой вклад, вы также можете написать статью с помощью write.geeksforgeeks.org или отправить ее по адресу [email protected]. Посмотрите, как ваша статья появится на главной странице GeeksforGeeks, и помогите другим гикам. Графики x и y, также известные как оси x и y, — это две важные линии, составляющие график. График состоит из горизонтальной оси и вертикальной оси, на которых могут быть представлены данные. Точка может быть описана по горизонтали или по вертикали, что легко понять с помощью графика. Эти горизонтальные и вертикальные линии или оси на графике являются осью x и осью y соответственно. Давайте узнаем больше о графике x и y в математике, таблице, диаграммах и решим несколько примеров, чтобы лучше понять концепцию. Python
import matplotlib. pyplot as plt
pyplot as plt x = [ 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 7 7 , 9 7 .0197 10 ] y = [ 2 , 4 , 5 , 7 , 6 , 8 , 9 , 11 , 12 , 12 ] plt.  scatter(x, y, label
scatter(x, y, label = "stars , color = "green" , marker = "*" , s = 30 ) Plt.xlabel ( 'x - Axis' ) Plt.ylabel ( 'y - Axis' ) PLT.TIT. ) PLT.TIT. ) PLT.TIT. ) . ) plt.legend() plt. show()
show()
Python
import matplotlib.pyplot as plt activities = [ 'eat' , 'sleep' , 'work' , 'play' ] slices = [ 3 , 7 , 8 , 6 ] colors = [ ' r' , 'y' , 'g' , 'b' ] plt.  pie(slices, labels
pie(slices, labels = activities, colors = colors, startangle = 90 , shadow = True , explode = ( 0 , 0 , 0.1 , 0 ), radius = 1.2 , autopct = '%1.1f%%' ) plt.legend() plt.show()
 pie() .
pie() . Python
import matplotlib. pyplot as plt
pyplot as plt import numpy as np х = NP.Arange ( 0 , 2 * (NP.PI), 0,1 ) 97 ). plt.plot(x, y) plt.show()
 arange() , в котором первые два аргумента предназначены для диапазона, а третий — для пошагового увеличения. Результатом является массив NumPy.
arange() , в котором первые два аргумента предназначены для диапазона, а третий — для пошагового увеличения. Результатом является массив NumPy.

Пожалуйста, пишите комментарии, если вы обнаружите что-то неправильное, или вы хотите поделиться дополнительной информацией по теме, обсуждаемой выше.
Графики X и Y — определение, различия, уравнение на графике X и Y, примеры
1. Определение графика X и Y 2. Разница между графиками по осям X и Y 3. График уравнения по осям X и Y График 4. 
Уравнение оси Y 5. Уравнение оси X 6. Часто задаваемые вопросы по X и Y График Определение графика X и Y
График x и y может быть задан двумя осями, т. е. осью x и осью y, которые образуют координатную плоскость для графика. Горизонтальная ось представлена осью x, а вертикальная ось представлена осью y. Точка пересечения осей x и y называется началом координат и используется в качестве опорной точки для плоскости. На изображении ниже представлена координатная плоскость с обеими осями.
Ось X на графике также известна как абсцисса. Ось Y на графике также известна как ордината. Любая точка на координатной плоскости хорошо определяется упорядоченной парой, где упорядоченная пара записывается как (координата x, координата y) или (x, y), где координата x представляет точку на оси x или перпендикулярно расстояние от оси y и координата y представляет собой точку на оси y или перпендикулярное расстояние от оси x.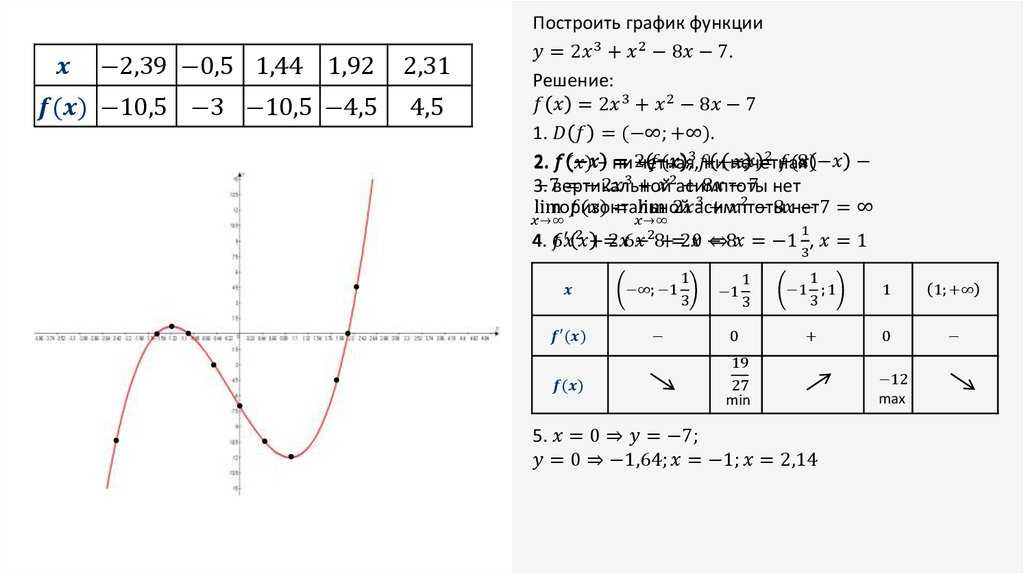 График x и y имеет 4 квадранта, то есть каждая перпендикулярная линия является одним квадрантом. Изображение ниже описывает график x и y как с положительными, так и с отрицательными координатами.
График x и y имеет 4 квадранта, то есть каждая перпендикулярная линия является одним квадрантом. Изображение ниже описывает график x и y как с положительными, так и с отрицательными координатами.
Например: Население города с 2015 по 2020 год указано в таблице X и Y как:
| Годы | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 |
| Люди в миллионах | 1 | 1,5 | 2 | 2,5 | 3 | 3,5 |
Чтобы найти любую точку на координатной плоскости, мы используем упорядоченную пару, где упорядоченная пара записывается как (координата x,координата y) или (x, y), где координата x представляет точку на координатной плоскости. ось x или перпендикулярное расстояние от оси y, а координата y представляет собой точку на оси y или перпендикулярное расстояние от оси x, поэтому сверху ясно, что ось x идет первой при записи упорядоченной пары в найти точку.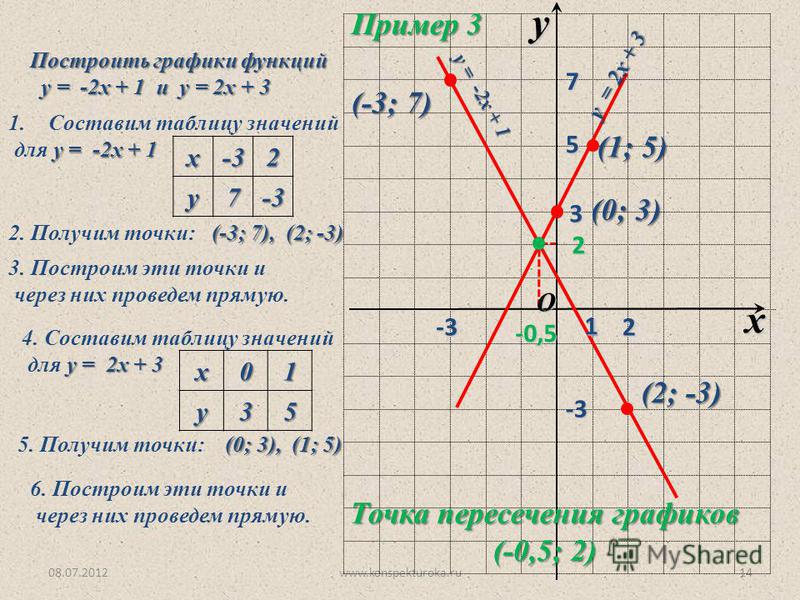 Здесь мы видим, что расположение каждой точки на графике отмечено как упорядоченная пара, где ось x или координата x опережает ось y или координату y. Затем представить эти точки на диаграмме x и y, используя годы на оси x и соответствующее население на оси y как:
Здесь мы видим, что расположение каждой точки на графике отмечено как упорядоченная пара, где ось x или координата x опережает ось y или координату y. Затем представить эти точки на диаграмме x и y, используя годы на оси x и соответствующее население на оси y как:
Разница между графиками по осям X и Y
График x и y состоит из осей x и y, которые образуют координатную плоскость графика, на котором представлены числа для сравнения или даже формирования линейных уравнений. Есть много различий между осью X и осью Y, даже если они имеют одну и ту же точку начала координат. Давайте посмотрим на различия:
| ось x графика | ось Y графика |
| Горизонтальная плоскость графика в декартовой системе координат, дающая числовое значение в каждой точке. | Это вертикальная плоскость графика в декартовой системе координат, дающая числовое значение в каждой точке. |
| Ось X называется абсциссой. | Ось Y называется ординатой. |
| Переменные на оси x представляют причину данных. | Переменные на оси Y представляют следствие данных. |
| Числа, размещенные на оси x, называются координатами x. | Числа, размещенные на оси Y, называются координатами Y. |
| Ось X представляет собой горизонтальную линию с 0 в качестве начала координат, положительными числами справа и отрицательными числами слева. | Ось Y рисуется вертикально снизу вверх с тем же началом, что и ось X, с положительными числами вверху и отрицательными числами внизу. |
| Координаты относительно оси x записываются как (x, y). | Координаты относительно оси Y записываются как (y, x). |
График уравнения по осям X и Y График
На графике x и y можно изобразить линейное уравнение, показывающее координаты как по оси x, так и по оси y. В геометрии линейное уравнение можно изобразить с помощью графика x и y, и оно представлено в виде прямой линии. Давайте посмотрим на пример, чтобы понять это лучше:
В геометрии линейное уравнение можно изобразить с помощью графика x и y, и оно представлено в виде прямой линии. Давайте посмотрим на пример, чтобы понять это лучше:
Рассмотрим линейное уравнение y = 2x + 1. Теперь, чтобы построить график этого уравнения, постройте таблицу с двумя столбцами для значений x и y. Выберем некоторые значения для переменной x и найдем соответствующие значения для y. Если x = 1, то y = 2 × 1 + 1 = 3. Если x = 2, то y = 2 × 2 + 1 = 5 и так далее. Здесь мы берем значения только трех точек, начиная с 0. Чтобы нарисовать график координат линейного уравнения по осям x и y, нам нужно нарисовать таблицу сетки осей x и y по крайней мере для двух точек.
| х | г |
| 0 | 1 |
| 1 | 3 |
| 2 | 5 |
Теперь нарисуйте точки на графике, где значения x лежат на оси x, а соответствующие значения y лежат на оси y. Затем соедините точки прямой линией, чтобы нарисовать график уравнения.
Затем соедините точки прямой линией, чтобы нарисовать график уравнения.
Уравнение оси Y
Ось Y — это линия, на которой значения координаты x равны нулю для всех значений y. Тогда точки данных для оси Y: (0, -1), (0, 0,5), (0, 1), (0, 1,5). Следовательно, уравнение оси y равно x = 0, и его график на графике x и y показан ниже. Если мы подставим значение x вместо 0 в общее уравнение y = mx + c, мы сможем найти координаты для y.
Уравнение оси X
Ось X — это линия, на которой значения координаты Y равны нулю для всех значений x. Тогда точки данных для оси x: (1,0), (-1,5, 0). Следовательно, уравнение оси x равно y = 0, и его график на графике x и y показан ниже. Если мы заменим значение y на 0 в общем уравнении y = mx + c, мы сможем найти координаты для x.
Связанные темы
Ниже перечислены несколько интересных тем, связанных с графиком x и y, посмотрите.
- Введение в графику
- Геометрия
- Полярные координаты
Часто задаваемые вопросы о графике X и Y
Что такое график X и Y?
График x и y — это визуальное представление данных, отображаемых на графике с осью x и y, образующими координатные плоскости. Ось X на графике также известна как абсцисса, тогда как ось Y известна как ордината. Любая точка на координатной плоскости хорошо определяется упорядоченной парой, где упорядоченная пара записывается как (координата x, координата y) или (x, y), где координата x представляет точку на оси x или перпендикулярно расстояние от оси y и координата y представляет собой точку на оси y или перпендикулярное расстояние от оси x. График x и y имеет 4 квадранта.
Ось X на графике также известна как абсцисса, тогда как ось Y известна как ордината. Любая точка на координатной плоскости хорошо определяется упорядоченной парой, где упорядоченная пара записывается как (координата x, координата y) или (x, y), где координата x представляет точку на оси x или перпендикулярно расстояние от оси y и координата y представляет собой точку на оси y или перпендикулярное расстояние от оси x. График x и y имеет 4 квадранта.
Как изобразить уравнение на графике X и Y?
Чтобы построить уравнение, сначала постройте таблицу с двумя столбцами для значений x и y, подставив значения x и y в уравнение, начиная с 0. Затем нарисуйте точки на графике, где значения x лежат на ось x и соответствующие значения y лежат на оси y. Затем соедините точки, чтобы нарисовать график уравнения. Обычно это прямая линия, диагональная, вертикальная или горизонтальная при построении линейного уравнения.
Какая точка находится на отрицательной оси Y на графике X и Y?
Точка с отрицательным значением координаты y находится на отрицательной оси y. Поскольку ось Y представляет собой вертикальную линию, которая начинается снизу вверх, отрицательные числа лежат в нижней части области и охватывают 3-й и 4-й квадранты графика.
Поскольку ось Y представляет собой вертикальную линию, которая начинается снизу вверх, отрицательные числа лежат в нижней части области и охватывают 3-й и 4-й квадранты графика.
Что является осью X и что является осью Y на графике X и Y?
Горизонтальная ось известна как ось X, а вертикальная ось известна как ось Y. Начало 0 является общим фактором для обеих осей. Ось X показывает причину данных, а ось Y показывает эффект данных. Например, при отображении температуры в Нью-Йорке ось X показывает недели, а ось Y показывает температуру. Каждая точка на обеих осях будет показывать предыдущее значение, начиная с 0,
Как построить график с осями X и Y?
Сначала мы рисуем и обозначаем оси x и y. Затем мы наносим координаты функции при различных значениях координат x и y. Затем соединяем координаты и строим график функции.
Как называются оси X и оси Y на графике X и Y?
Вертикальная ось, т. е. ось Y, известна как ось абсцисс. А ось x известна как ось ординат.
Линейный график Определение
Что такое линейный график?
Линейный график, также известный как линейный график или линейная диаграмма, представляет собой график, который использует линии для соединения отдельных точек данных. Линейный график отображает количественные значения за указанный интервал времени. В финансах линейные графики обычно используются для отображения исторической динамики цены актива или ценной бумаги.
Линейные графики можно сравнивать с другими визуализациями данных, включая гистограммы, круговые диаграммы и (в трейдинге) свечные диаграммы.
Ключевые выводы
- Линейный график соединяет отдельные точки данных, которые обычно отображают количественные значения за определенный интервал времени.
- Линейные графики состоят из двух осей: оси X (горизонтальной) и оси Y (вертикальной), которые графически обозначаются как (x,y).
- При инвестировании в область технического анализа линейные графики весьма информативны, позволяя пользователю визуализировать тенденции.

- Хотя линейные графики используются во многих различных областях для различных целей, их наиболее распространенная функция — создание графического изображения изменений значений с течением времени.
- В финансах линейные графики используются для визуального представления значений во времени, включая изменения цен на ценные бумаги.
Понимание линейных графиков
На линейных графиках используются «маркеры» точек данных, которые соединяются прямыми линиями. Эти точки данных, соединенные прямыми линиями, помогают в визуализации. Хотя линейные графики используются во многих различных областях для различных целей, они особенно полезны, когда необходимо создать графическое изображение изменений значений с течением времени.
Линейные графики часто используются в финансах для создания визуального представления значений во времени, включая изменения цен на ценные бумаги, отчеты о доходах компаний и истории основных фондовых индексов. Они также полезны для сравнения различных ценных бумаг. В инвестировании, особенно в области технического анализа, инвесторы используют линейные графики для визуализации тенденций, что может значительно помочь им в их анализе.
В инвестировании, особенно в области технического анализа, инвесторы используют линейные графики для визуализации тенденций, что может значительно помочь им в их анализе.
Есть некоторые ограничения для линейных графиков. Например, линейные графики часто теряют четкость, когда точек данных слишком много. Также легко манипулировать ими визуально для достижения определенных эффектов. Например, кажущейся степенью изменения можно визуально управлять, регулируя диапазон точек данных на осях.
Линейные графики можно построить вручную или с помощью программного обеспечения, такого как Microsoft Excel. Последнее значительно повышает скорость и точность конечного продукта.
Построение линейного графика
Линейные графики состоят из двух осей: оси X (горизонтальной) и оси Y (вертикальной). Каждая ось представляет другой тип данных, а точки их пересечения равны (0,0). Ось x является независимой осью, поскольку ее значения не зависят ни от чего измеряемого. Ось Y является зависимой осью, поскольку ее значения зависят от значений оси X.
Ось Y является зависимой осью, поскольку ее значения зависят от значений оси X.
Каждая ось должна быть помечена в соответствии с данными, измеренными вдоль этой оси. Затем каждую ось следует разделить на соответствующие приращения (например, первый день, второй день и т. д.). Например, при измерении изменений цен акций за предыдущие две недели ось X будет представлять измеренное время (торговые дни в течение периода), а ось Y — цены акций.
При использовании линейных графиков для отслеживания цены акции наиболее часто используемой точкой данных является цена закрытия акции.
Например, предположим, что в первый день торгов цена данной акции составляла 30 долларов, в результате чего точка данных была равна (1, 30 долларов). На второй день торгов цена акции составляла 35 долларов, в результате чего точка данных составила (2, 35 долларов).
Каждая точка данных нанесена на график и соединена линией, которая визуально показывает изменения значений с течением времени. Если бы стоимость акций увеличивалась ежедневно, линия наклонялась бы вверх и вправо. И наоборот, если бы цена акции неуклонно снижалась, то линия наклонялась бы вниз и вправо.
Если бы стоимость акций увеличивалась ежедневно, линия наклонялась бы вверх и вправо. И наоборот, если бы цена акции неуклонно снижалась, то линия наклонялась бы вниз и вправо.
Типы линейных графиков
Существует три основных типа линейных графиков. Хотя каждый тип основан на одних и тех же принципах, у каждого есть своя уникальная ситуация, в которой его лучше всего реализовать и использовать.
Простой линейный график
Простой линейный график является самым основным типом линейного графика. На этом графике отслеживается только одна зависимая переменная, поэтому есть только одна линия, соединяющая все точки данных на графике. Все точки на графике относятся к одному и тому же элементу, и единственная цель графика — отслеживать изменения этой переменной во времени. Этот график нельзя использовать для сравнения переменной с другой переменной, поскольку на графике отображается только переменная.
В приведенном ниже примере по оси X отложено время, а по оси Y — годовое изменение цен на все потребительские товары в США.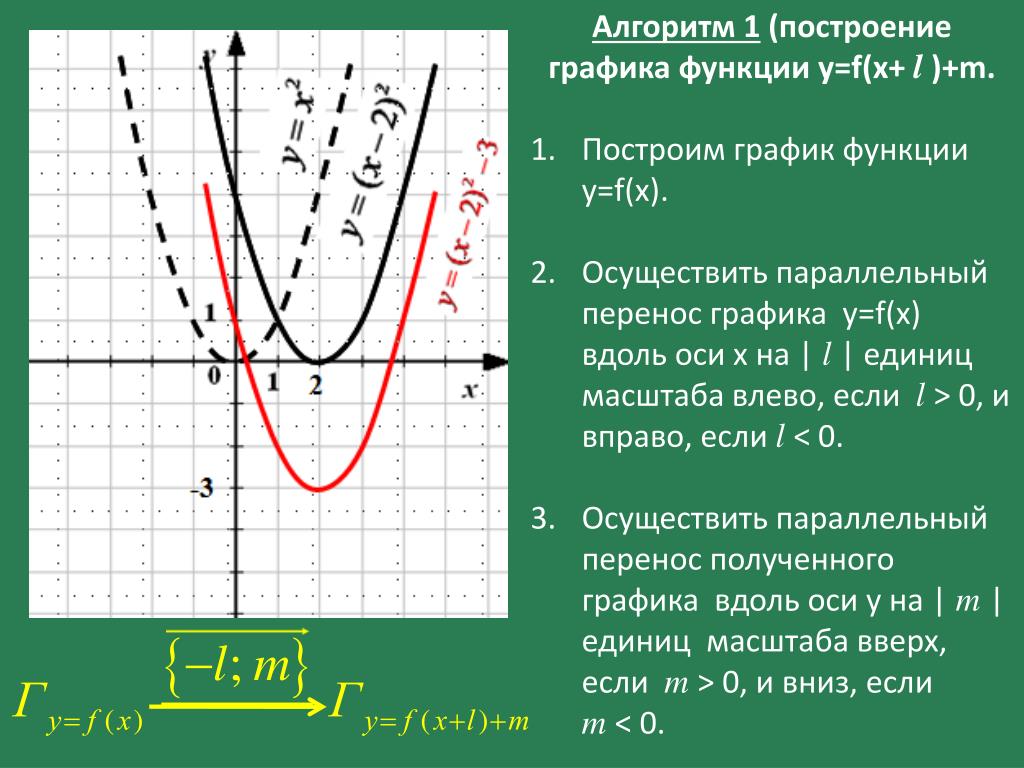 Этот график индекса потребительских цен показывает годовой уровень инфляции, и, поскольку он анализирует только один набор данных (все товары), здесь только одна линия.
Этот график индекса потребительских цен показывает годовой уровень инфляции, и, поскольку он анализирует только один набор данных (все товары), здесь только одна линия.
Бюро трудовой статистики
Многолинейный график
На многолинейном графике на график нанесено несколько зависимых переменных, которые сравниваются по одной независимой переменной (часто по времени). Различные зависимые переменные часто обозначаются линиями разного цвета, чтобы различать каждый набор данных. Каждая строка относится только к точкам в заданном наборе данных; линии не пересекаются между зависимыми переменными.
Например, линейный график ниже снова показывает индекс потребительских цен. Однако на этом графике показано изменение цен для трех различных категорий: медицинское обслуживание (красный цвет), товары (зеленый цвет) и жилье (синий цвет). На этом графике мы видим, что рост цен на товары был выше, чем на две другие категории в июле 2022 года.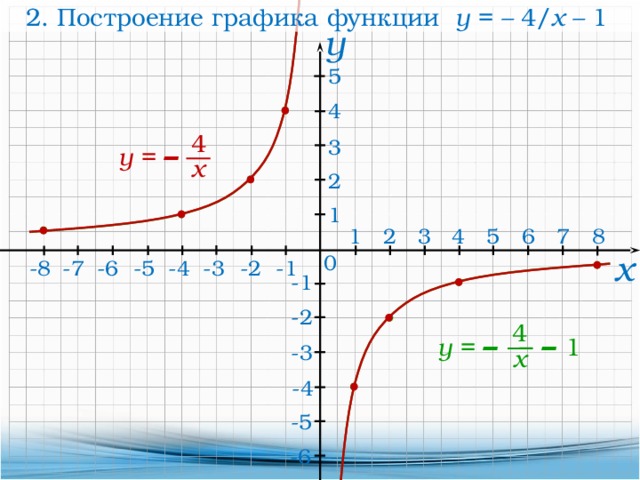 Однако расходы на жилье или медицинские расходы, как правило, были группами, которые испытали более высокую инфляцию за последнее десятилетие.
Однако расходы на жилье или медицинские расходы, как правило, были группами, которые испытали более высокую инфляцию за последнее десятилетие.
Бюро трудовой статистики
Составной линейный график
Составной линейный график использует несколько переменных, как и многострочный график. Однако переменные часто накладываются друг на друга, чтобы показать общее количество по всем переменным. Это не только информирует пользователей о взаимосвязи между каждой из переменных, но также информирует о том, как изменяется общая сумма.
В приведенном ниже примере от Агентства по охране окружающей среды (EPA) есть пять зависимых переменных, которые варьируются от аномально засушливых земель до исключительно засушливых районов. Сначала были нанесены данные о самой экстремальной засухе, а любое пустое место под этим линейным графиком было заштриховано темно-красным цветом. Затем были нанесены последующие наборы данных, при этом пустая область под каждой из этих линий была закрашена соответствующим цветом. В целом это показывает взаимосвязь между описаниями засухи, а также общим процентом земельной площади США в этих категориях по годам.
В целом это показывает взаимосвязь между описаниями засухи, а также общим процентом земельной площади США в этих категориях по годам.
Агентство по охране окружающей среды
Части линейного графика
Линейные графики могут различаться в зависимости от дополнительных функций или форматирования. Наиболее качественные и простые для понимания линейные графики обладают следующими характеристиками:
Название
Линейные графики могут иметь заголовок над графиком, чтобы кратко объяснить, что изображено на графике. Если вы не предоставите пользователю письменный контекст, пользователь часто будет полагаться на заголовок, чтобы лучше понять, какие данные извлекаются. В заголовке могут конкретно указываться временные рамки или ограничения для данных (т. может быть «Уровень засушливых земель США по годам, 2000–2015 гг.»).
Легенда
Легенда объясняет, что представляет собой каждая зависимая переменная и как различать разные наборы данных.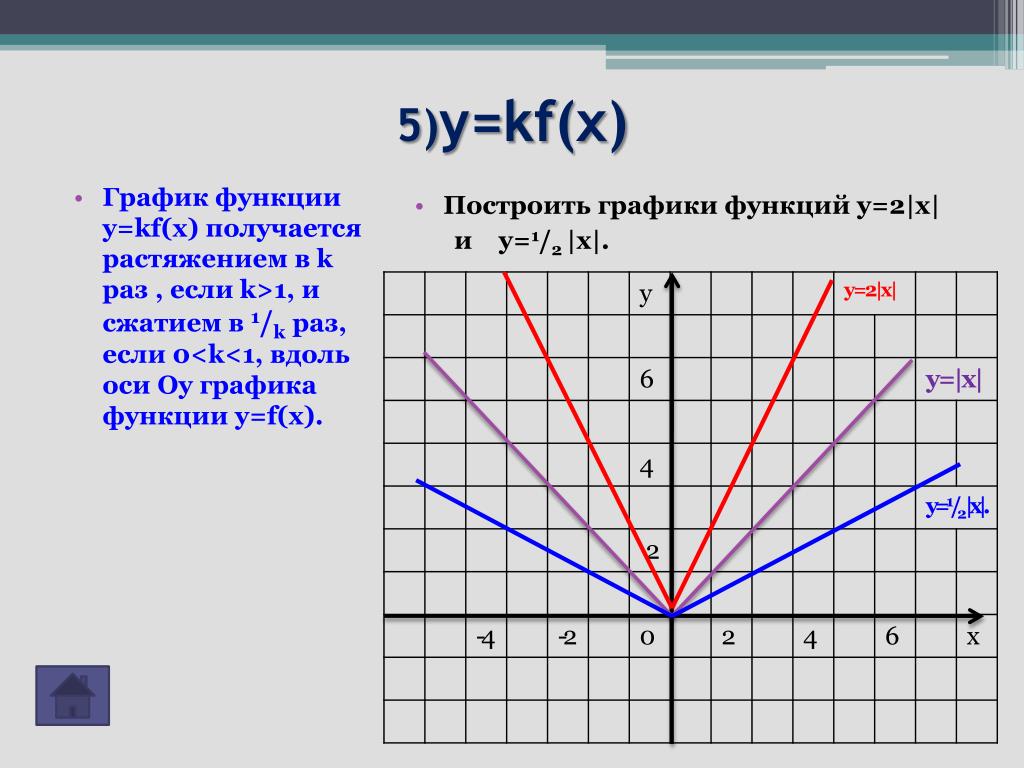 В приведенном выше примере каждая зависимая переменная отмечена своим цветом. Коробка, которая объясняет, что означает каждый цвет, является легендой.
В приведенном выше примере каждая зависимая переменная отмечена своим цветом. Коробка, которая объясняет, что означает каждый цвет, является легендой.
Данные
Каждый элемент данных на линейном графике является ссылкой на другой источник, который связывает зависимую переменную с независимой переменной. Это информация на вашем графике; это элемент, который создает точки, которые соединяются, чтобы сформировать линии на вашем графике. В некоторых примерах, как показано выше, может быть несколько наборов данных, объединенных в один график. Чтобы обеспечить защиту и точность данных, в компаниях могут быть специальные аналитики по целостности данных или аналогичные должности для мониторинга активности баз данных.
Ось X
Ось X — это набор информации, которая проходит вдоль горизонтальной плоской части в нижней части линейного графика. В большинстве линейных графиков ось X будет связана со временем, будь то разные месяцы в году или количество недель, прошедших с момента запуска продукта.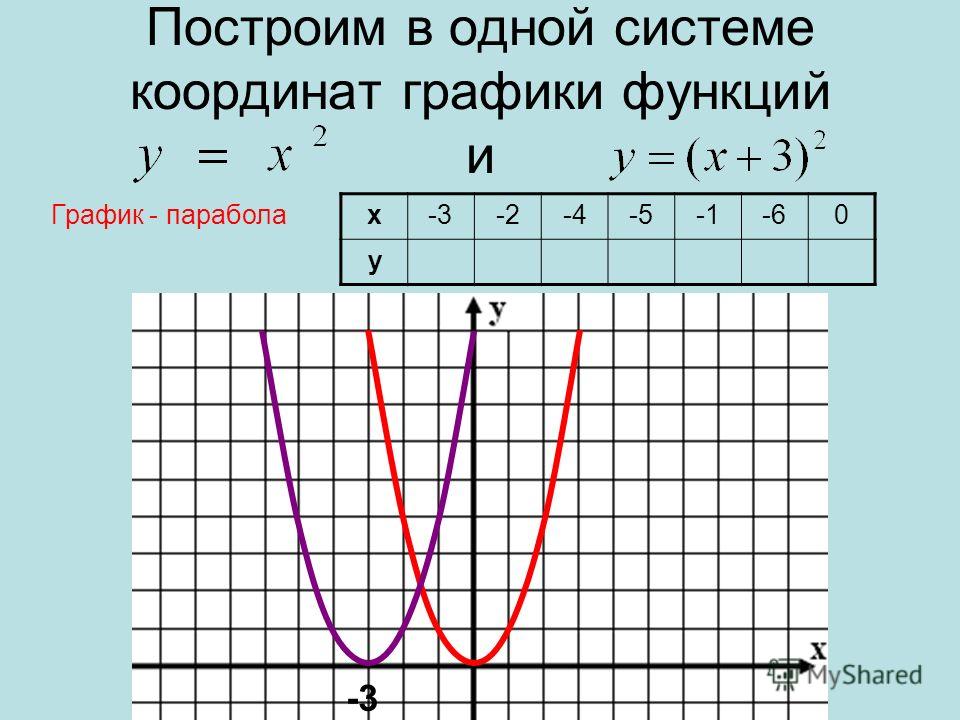
Ось Y
Ось Y — это набор информации, которая проходит по вертикали в левой части графика. Некоторые итерации линейных графиков имеют этот набор информации справа. В любом случае, эти числа учитывают измеряемые предметы. График может начинаться с нуля, хотя бывают случаи, когда имеет смысл начинать с большего числа.
Линия
Наконец, у нас есть линия. Линия соединяет все точки данных в одной зависимой переменной. Движение этой линии показывает увеличение и уменьшение информации во времени. Его также можно легко сравнить с другими линиями, если все наборы данных измеряются за аналогичные периоды времени. Несмотря на чрезмерное упрощение, эта линия может сообщать руководству, какие действия следует предпринять для улучшения операций или стратегического планирования.
Хотите отобразить несколько наборов данных, но один набор информации больше подходит для гистограммы? Такие программы, как Excel и Google Sheets, могут создавать комбинированные диаграммы, в которых одна зависимая переменная отображается в виде гистограммы, а другая зависимая переменная — в виде перекрывающейся линейной диаграммы.
Создание линейного графика в Excel
Вы можете использовать линейный график в Excel для отображения тенденций с течением времени. В Excel линейные графики подходят, если у вас есть текстовые метки, даты или несколько числовых меток на горизонтальной оси (ось X). Вот шаги для создания линейного графика в Excel. (Если вы используете числовые метки, очистите ячейку A1 перед созданием линейного графика):
- Введите желаемые заголовки столбцов в строке 1. Эти столбцы будут описывать различные наборы данных (т. е. в приведенном ниже примере заголовки различают данные по животным).
- Введите значение по оси X в столбец A. В приведенном ниже примере данные разбиты по годам, поэтому годы с 2017 по 2022 указаны в первом столбце.
- Введите свои данные. Для каждой ячейки, соответствующей заголовку и году, введите соответствующую цифру. Если данных нет, введите «0».
- После ввода значений выберите диапазон (любой диапазон, охватывающий эти значения).
 Если вы хотите, чтобы ваш график включал заголовки и метки, выберите первую строку и первый столбец. Например, выбрав A1: D7, ось X может быть помечена как «Годы», а ось Y может быть помечена как «Количество животных». '.
Если вы хотите, чтобы ваш график включал заголовки и метки, выберите первую строку и первый столбец. Например, выбрав A1: D7, ось X может быть помечена как «Годы», а ось Y может быть помечена как «Количество животных». '. - На вкладке «Вставка» в группе «Диаграммы» щелкните символ «Линия» («Вставить линейный график»).
- Щелкните "Линия с маркерами". Это создаст линейный график, аналогичный приведенному ниже, где каждая точка данных отмечена более крупной точкой, а эти точки соединены более тонкой линией. Многие из этих элементов форматирования можно настроить.
Использование линейного графика
Различные инструменты визуализации данных лучше всего использовать для конкретных целей, и линейный график не является исключением. В зависимости от исходных данных линейный график лучше всего подходит для:
- Отслеживание изменений во времени. Линейный график обычно форматируется с периодами времени по оси x и количеством событий по оси y.
 Каждый период равнялся году, но линейные платежи можно разбить на дни, недели, месяцы или другие периоды времени (т. е. дни с момента найма нового генерального директора).
Каждый период равнялся году, но линейные платежи можно разбить на дни, недели, месяцы или другие периоды времени (т. е. дни с момента найма нового генерального директора). - Отслеживание небольших изменений. Диапазон, отображаемый на графике, можно изменить, чтобы лучше увеличить масштаб данных, которые могут варьироваться не слишком сильно. По сравнению с другими типами диаграмм, линейный график может быть отформатирован так, чтобы иметь очень маленькие приращения по оси Y, что позволяет лучше понять, как крошечные изменения произошли во времени.
- Сравнение изменений более чем в одной группе. В приведенном выше примере очень легко сравнить количество трех разных типов затрат в одном визуальном элементе. Поскольку каждая строка представлена разным цветом, несколько типов или групп данных можно отслеживать одновременно и беспрепятственно сравнивать друг с другом.
- Непрерывные наборы данных. Поскольку линейный график основан на одном наборе непрерывных данных, по крайней мере одна переменная линейного графика должна быть непрерывной.
 В большинстве случаев этой переменной является время. Непрерывный набор данных (т. е. количество животных в 10 крупнейших зоопарках мира) не подходит, поскольку нет причин связывать каждую точку данных линией; гистограмма была бы более подходящей.
В большинстве случаев этой переменной является время. Непрерывный набор данных (т. е. количество животных в 10 крупнейших зоопарках мира) не подходит, поскольку нет причин связывать каждую точку данных линией; гистограмма была бы более подходящей.
Для чего используется линейный график?
Линейные графики используются для отслеживания изменений за разные периоды времени. Линейные графики также можно использовать в качестве инструмента для сравнения: для сравнения изменений за один и тот же период времени для более чем одной группы.
Чем линейный график полезен в финансах?
Линейные графики полезны в финансах, потому что они очень эффективны для визуального представления тенденций во времени. По этой причине они часто используются для отображения того, как акции работают в течение определенного периода времени.
Какие существуют 3 типа линейных графиков?
Линейный график может быть простым линейным графиком, многолинейным графиком или составным линейным графиком. Каждый тип графика имеет различную степень зависимых переменных и то, как пользователь хочет отобразить взаимосвязь между этими переменными.
Каждый тип графика имеет различную степень зависимых переменных и то, как пользователь хочет отобразить взаимосвязь между этими переменными.
Из каких частей состоит линейный график?
Линейные графики могут иметь широкие возможности настройки с точки зрения заголовка, меток, маркеров, стиля линии и других несущественных функций. Однако все линейные графики должны иметь ось X (независимая переменная), ось Y (количество зависимых переменных) и входные данные (зависимые переменные). Точки данных для каждой зависимой переменной отмечены на графике и соединены линией.
Практический результат
При анализе данных во времени одним из лучших графических изображений данных является линейный график. Линейный график часто использует время в качестве оси x и числовую величину на оси y. Когда точки данных отмечены на диаграмме, все точки данных в пределах одной зависимой переменной соединяются линией, что делает ее очень полезным инструментом для анализа изменений во времени для одной или нескольких переменных.
ПРОГРАММА ПРОГРАММЫ
СЮЖЕТ ПроцедураПримечание: Обратите внимание на более новую функцию PLOT, которая повторяет функциональность этой старой подпрограммы, но предлагает интерактивный интерфейс и обновленную функциональность.
Процедура PLOT рисует графики векторных аргументов. Если используется один параметр, параметр вектора откладывается по оси ординат в зависимости от номера точки по оси абсцисс. Чтобы построить один вектор как функцию другого, используйте два параметра. PLOT также можно использовать для создания полярных графиков, установив ключевое слово POLAR.
Синтаксис
График, [ x ,] y [/isotropic] [ max_value = Значение ] [ min_value = Значение 9328] [ NSNSUM = ] [NSNSUM = ] [NSNSUM = ] [NSNSUM = ] [NS NS = ] [NS NS = ] ] [ THICK= значение ] [ /XLOG] [ /YLOG] [ /YNOZERO]
Ключевые слова графики: [ BACKGROUND= color_index ] [ CHARSIZE= значение ] [ CHARTHICK = целое число ] [ CLIP = [X 0 , Y 0 , X 1 , Y 1 ] ] [ ЦВЕТ= значение ] [ /ДАННЫЕ| , /УСТРОЙСТВО| , /NORMAL] [ FONT= целое число ] [ LINESTYLE={0 | 1 | 2 | 3 | 4 | 5}] [ /NOCLIP] [ /NODATA] [ /NOERASE] [ POSITION= [X 0 , Y 0 , X 1 , Y 1 ] ] [ PSYM= целое число {от 0 до 10}] [ SUBTITLE= строка ] [ SYMSIZE= значение ] [ /T3D] [ THICK= значение ] [ TICKLEN= значение ] [ TITLE= строка ]
[ {X | Y | Z} CHARSIZE= значение ]
[ {X | Y | Z} GRIDSTYLE= целое число {от 0 до 5}]
[ {X | Y | Z}MARGIN= [слева , справа] ]
[ {X | Y | Z}MINOR= целое число ]
[ {X | Y | Z}RANGE= [минимум , максимум] ]
[ {X | Y | Z}STYLE= значение ]
[ {X | Y | Z}THICK= значение ]
[ {X | Y | Z}TICK_GET= переменная ]
[ {X | Y | Z}TICKFORMAT= строка ]
[ {X | Y | Z}TICKINTERVAL= значение ]
[ {X | Y | Z}TICKLAYOUT= скаляр ]
[ {X | Y| Z}TICKLEN= значение ]
[ {X | Y | Z}TICKNAME= string_array ]
[ {X | Y | Z}TICKS= целое число ]
[ {X | Y| Z}TICKUNITS= строка ]
[ {X | Y | Z}TICKV= массив ]
[ {X | Y | Z}TITLE= строка ]
[ ZVALUE= значение {от 0 до 1}]
Аргументы
X
Вектор, представляющий значения абсцисс для построения графика. Если X не указан, Y отображается как функция номера точки (начиная с нуля). Если предоставлены оба аргумента, Y отображается как функция X .
Если X не указан, Y отображается как функция номера точки (начиная с нуля). Если предоставлены оба аргумента, Y отображается как функция X .
Перед построением этот аргумент преобразуется в число с плавающей запятой двойной точности. Графики, созданные с помощью PLOT, ограничены диапазоном и точностью значений с плавающей запятой двойной точности.
Y
Данные ординат для построения графика. Перед построением этот аргумент преобразуется в число с плавающей запятой двойной точности.
Ключевые слова
Примечание: Многие графические параметры ключевых слов напрямую соответствуют полям в системных переменных !P, !X, !Y или !Z. При указании имени и значения ключевого параметра в вызове это значение влияет только на текущий вызов, соответствующее поле системной переменной не изменяется. Изменение значения поля системной переменной изменяет значение по умолчанию для этого конкретного параметра и остается в силе, пока не будет изменено явным образом.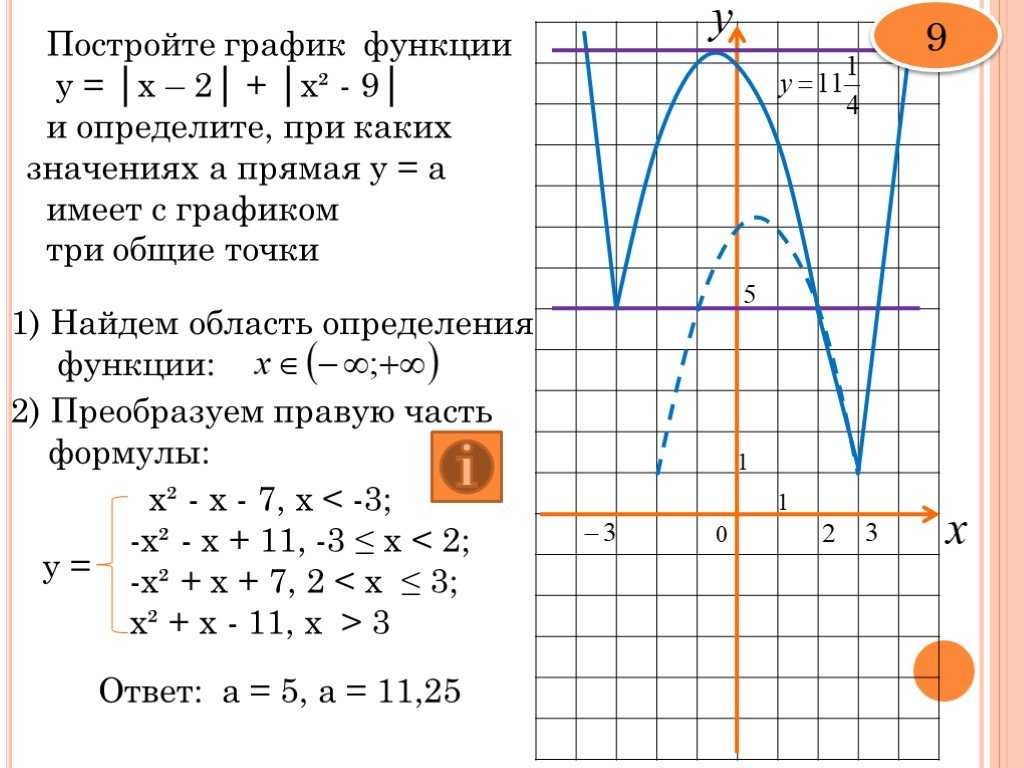
ИЗОТРОПИЧЕСКИЙ
Установите это ключевое слово, чтобы масштабирование осей X и Y было одинаковым.
Примечание: Оси X и Y будут масштабироваться изотропно, а затем помещаться в прямоугольник, определенный ключевым словом POSITION; одна из осей может быть укорочена. См. ПОЛОЖЕНИЕ для получения дополнительной информации.
MAX_VALUE
Максимальное отображаемое значение. Если присутствует это ключевое слово, значения данных, превышающие значение MAX_VALUE, считаются отсутствующими и не отображаются на графике. Обратите внимание, что значение с плавающей запятой IEEE NaN также рассматривается как отсутствующие данные.
MIN_VALUE
Минимальное отображаемое значение. Если присутствует это ключевое слово, значения данных, меньшие значения MIN_VALUE, считаются отсутствующими и не отображаются на графике. Обратите внимание, что значение с плавающей запятой IEEE NaN также рассматривается как отсутствующие данные.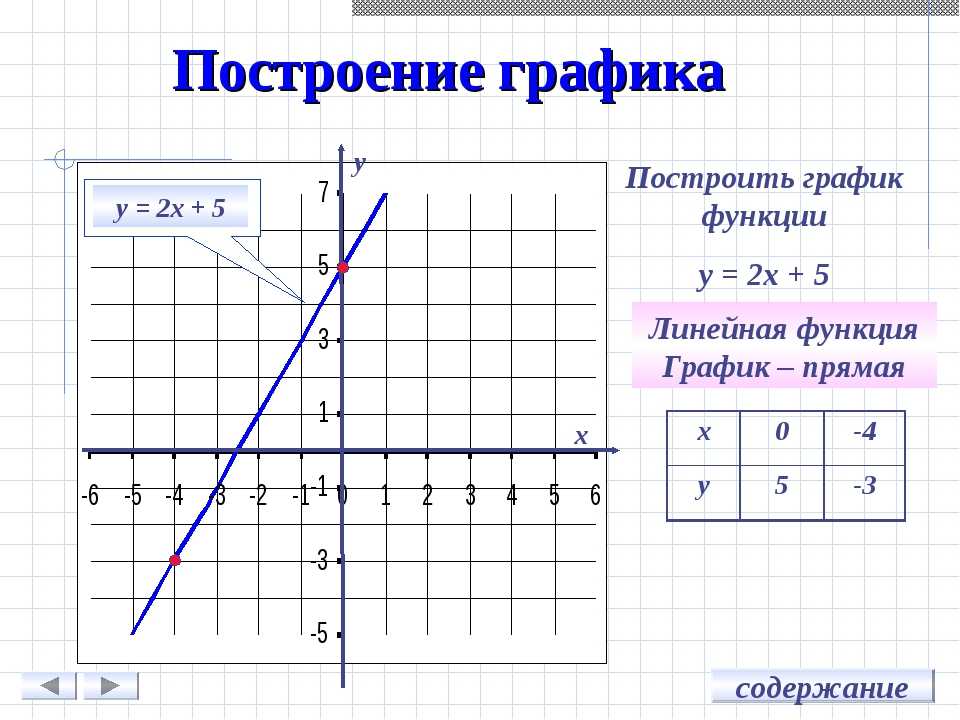
NSUM
Наличие этого ключевого слова указывает количество точек данных, которые необходимо усреднить при построении графика. Если NSUM больше 1, каждая группа точек NSUM усредняется для получения одной точки на графике. Если имеется м 9Отображается 3228 точек данных, затем m точек /NSUM. По логарифмическим осям выполняется среднее геометрическое.
Удобно использовать NSUM при очень большом количестве точек данных для построения графика, поскольку он отображает меньше точек, график менее загроможден и работает быстрее.
ПОЛЯРНЫЙ
Установите это ключевое слово для создания полярных графиков. Параметры вектора X и Y , оба из которых должны присутствовать, сначала преобразуются из полярных координат в декартовы. Первый параметр — радиус, а второй — угол (выражается в радианах). Например, чтобы сделать полярный график, вы должны использовать такую команду, как:
PLOT, /POLAR, R, THETA
Примечание: См.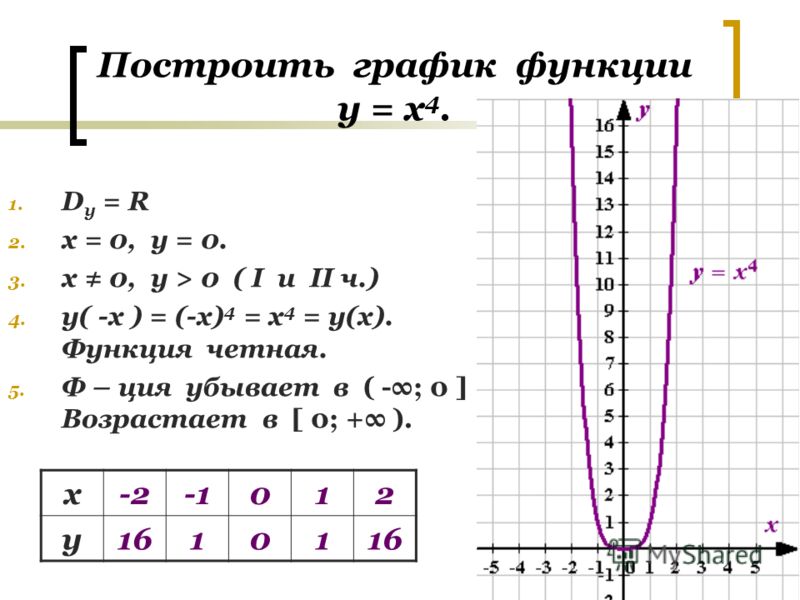 Использование AXIS с полярными графиками для примера добавления осей к полярному графику.
Использование AXIS с полярными графиками для примера добавления осей к полярному графику.
ТОЛЩИНА
Управляет толщиной линий, соединяющих точки. Толщина 1,0 — нормальная, 2 — двойная ширина и т. д.
XLOG
Установите это ключевое слово, чтобы указать логарифмическую ось X, создавая логарифмический график. Установите и XLOG, и YLOG, чтобы построить логарифмический график. Обратите внимание, что логарифмические оси, диапазоны которых меньше декады, не помечены.
YLOG
Установите это ключевое слово, чтобы указать логарифмическую ось Y, создающую линейно-логарифмический график. Установите и XLOG, и YLOG, чтобы построить логарифмический график. Обратите внимание, что логарифмические оси, диапазоны которых меньше декады, не помечены.
YNOZERO
Установите это ключевое слово, чтобы запретить установку минимального значения оси Y равным нулю, когда все данные Y положительные и ненулевые, и не задано явное минимальное значение Y (с помощью YRANGE или !Y. RANGE). По умолчанию ось Y охватывает диапазон от 0 до максимального значения 9.3227 Y , в случае положительных данных Y. Установите бит 4 в !Y.STYLE, чтобы сделать этот параметр значением по умолчанию.
RANGE). По умолчанию ось Y охватывает диапазон от 0 до максимального значения 9.3227 Y , в случае положительных данных Y. Установите бит 4 в !Y.STYLE, чтобы сделать этот параметр значением по умолчанию.
Примеры
Этот раздел включает следующие примеры:
Простой сюжет | Гистограммы |
X против Y | Указание делений |
Масштабирование оси | Логарифмическое масштабирование |
многострочных заголовков | Несколько графиков на странице |
Ключевое слово диапазона | Указание местоположения графика |
Графические символы | Построение отсутствующих данных |
Простой график
Процедура PLOT имеет много ключевых слов, позволяющих создавать самые разнообразные графики.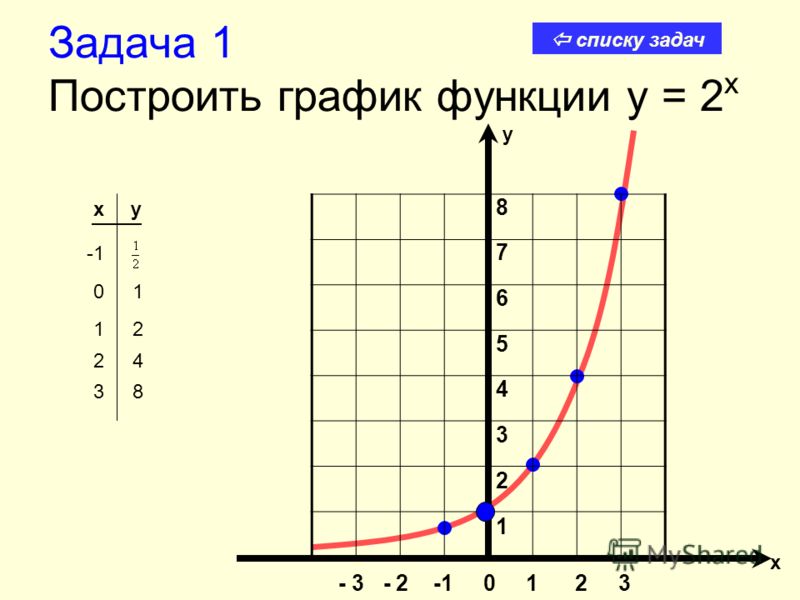 Вот несколько простых примеров использования команды PLOT.
Вот несколько простых примеров использования команды PLOT.
; Создайте простой набор данных:
D = FINDGEN(100)
; Создайте простой сюжет с названием «Простой сюжет»:
PLOT, D, TITLE = 'Простой участок'
; Постройте график сравнения одного аргумента с другим:
PLOT, SIN(D/3), COS(D/6)
; Создайте полярный график:
PLOT, D, D, /POLAR, TITLE = 'Полярный график'
; Использовать графические символы вместо соединительных линий
; путем включения ключевого слова PSYM. Пометьте оси X и Y
; с XTITLE и YTITLE:
PLOT, SIN(D/10), PSYM=4, XTITLE='Ось X', YTITLE='Ось Y'
X Versus Y Plots
В этом разделе показано использование основных процедур построения графиков x и y , PLOT и OPLOT. PLOT по умолчанию создает линейно-линейные графики и может создавать линейно-логарифмические, логарифмически-линейные или логарифмические графики с добавлением ключевых слов XLOG и YLOG.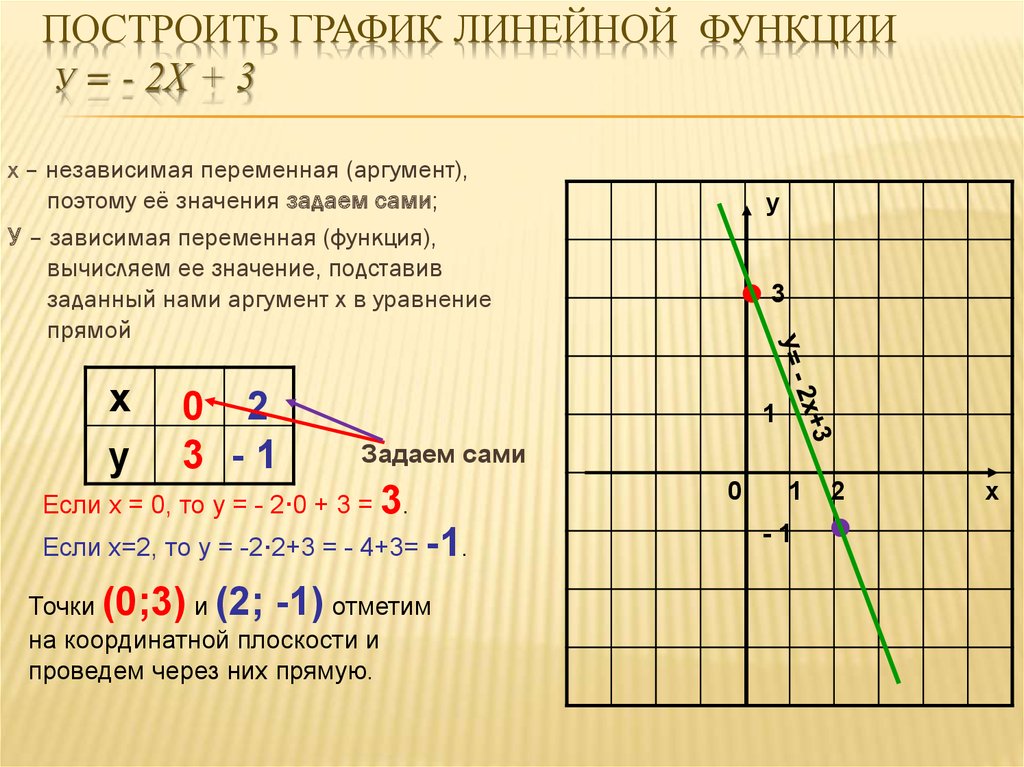
Данные, использованные в этих примерах, взяты из вымышленного исследования промысла лосося в северо-западной части Тихого океана. В примере мы предполагаем, что данные были собраны в 1967, 1970 и 19с 75 по 1983. Следующие операторы IDL создают и инициализируют переменные SOCKEYE, COHO, CHINOOK и HAMPBACK, которые содержат фиктивные значения популяции рыб в тысячах для 11 наблюдений:
SOCKEYE=[463, 459, 437, 433, 431, 433, 431, 428, 430, 431, 430]
COHO=[468, 461, 431, 430, 427, 425, 423, 420, 418, 421, 420]
ЧИНУК=[514, 509, 495, 497, 497, 494, 493, 491, 492, 493, 493]
ГОРБАН=[467, 465, 449, 446, 445, 444, 443, 443, 443, 443, 445]
; Построить вектор, в котором каждый элемент содержит
; год выборки:
YEAR = [1967, 1970, INDGEN(9) + 1975]
Этот код также содержится в пакетном файле plot01, расположенном в подкаталоге examples/doc/plot каталога установки IDL. Чтобы выполнить пакетный файл, введите в приглашении IDL следующую команду:
@plot01
Следующие команды IDL создают график популяции нерки по годам:
PLOT, YEAR, SOCKEYE, $
TITLE=' Популяция нерки', XTITLE='Год', $
YTITLE='Fish (thousands)'
Процедура PLOT, которая создает график x против y на новом наборе осей, требует одного или двух параметров: вектора y значений или вектора x значений, за которыми следует вектор из y значений. Первая попытка построить график дает рисунок, показанный ниже. Обратите внимание, что три заголовка, определяемые ключевыми словами TITLE, XTITLE и YTITLE, являются необязательными.
Первая попытка построить график дает рисунок, показанный ниже. Обратите внимание, что три заголовка, определяемые ключевыми словами TITLE, XTITLE и YTITLE, являются необязательными.
Масштабирование по осям
Колебания в данных трудно увидеть, поскольку оценки варьируются от 428 до 463, а ось y графика масштабируется от 0 до 500. Этот эффект вызывают два фактора. По умолчанию IDL устанавливает минимальное значение оси y линейных графиков равным нулю, если все данные y положительны. Максимальное значение оси автоматически устанавливается IDL из максимального значения данных и . Кроме того, IDL пытается создать от трех до шести интервалов меток, которые являются приращениями целочисленной степени 10, умноженной на 2, 2,5, 5 или 10. В этом примере этот эффект округления приводит к тому, что максимальное значение оси равно 500. , а не 463,
Параметр ключевого слова YNOZERO запрещает установку минимума оси y на ноль при наличии положительных, отличных от нуля данных. На рисунке ниже показаны данные, построенные с использованием этого ключевого слова. Ось y теперь находится в диапазоне от 420 до 470, а IDL создает интервалы делений равные 10.
На рисунке ниже показаны данные, построенные с использованием этого ключевого слова. Ось y теперь находится в диапазоне от 420 до 470, а IDL создает интервалы делений равные 10.
; Определите переменные:
@plot01
PLOT, YEAR, НЕРКА, /YNOZERO, $
TITLE='Популяция нерки', XTITLE='Year', $
YTITLE='Рыба (тысячи)'
Многострочные заголовки
Команда позиционирования графического текста !C запускает новую строку вывода текста. Заголовки, содержащие более одной строки текста, легко создаются путем разделения каждой строки с помощью этой команды позиционирования.
В приведенном выше примере основной заголовок можно было отобразить в двух центрированных строках, изменив параметр ключевого слова TITLE на следующий оператор:
TITLE = 'Sockeye!CPopulation'
может обнаружить, что поля по умолчанию неадекватны, в результате чего заголовки выходят за пределы страницы. В этом случае установите ключевые слова [XY]MARGIN или увеличьте значения !X.MARGIN или !Y.MARGIN.
В этом случае установите ключевые слова [XY]MARGIN или увеличьте значения !X.MARGIN или !Y.MARGIN.
Ключевое слово диапазона
Диапазон осей x , y или z может быть явно указан с помощью параметра ключевого слова [XYZ] RANGE. Аргумент параметра ключевого слова представляет собой двухэлементный вектор, содержащий минимальное и максимальное значения оси.
Как объяснялось выше, IDL пытается создать четные интервалы тактов, и диапазон осей, выбранный IDL, может быть немного больше, чем указанный с помощью ключевого слова RANGE. Чтобы получить точно указанный интервал, установите параметр стиля оси равным единице (YSTYLE = 1).
Эффект ключевого слова YNOZERO идентичен эффекту, полученному при включении параметра ключевого слова YRANGE = [MIN(Y), MAX(Y)] в вызове PLOT. Вы можете сделать /YNOZERO значением по умолчанию в последующих графиках, установив бит 4 !Y.STYLE в единицу (!Y.STYLE = 16).
Подробную информацию о поле STYLE системных переменных оси !X, !Y и !Z см. в разделе STYLE. Кратко: другие биты в поле STYLE расширяют оси, обеспечивая поле вокруг данных, подавляют ось и ее обозначения и подавляют оси прямоугольного стиля, рисуя только левую и нижнюю оси.
в разделе STYLE. Кратко: другие биты в поле STYLE расширяют оси, обеспечивая поле вокруг данных, подавляют ось и ее обозначения и подавляют оси прямоугольного стиля, рисуя только левую и нижнюю оси.
Например, чтобы ограничить ось X периодом с 1975 по 1983 год, в вызов PLOT включается параметр ключевого слова XRANGE = [1975, 1983]. Следующий рисунок иллюстрирует результат.
Обратите внимание, что ось x на самом деле простирается с 1974 по 1984 год, поскольку IDL решила сделать пять интервалов отметок, каждый из которых охватывает два года. Если, как объяснялось выше, стиль оси x установлен равным единице, график точно охватит заданный диапазон. Колл, объединяющий все эти варианты, выглядит следующим образом:
; Определите переменные:
@plot01
PLOT, YEAR, НЕРКА, /YNOZERO, $
TITLE='Популяция нерки', XTITLE = 'Год', $
YTITLE = 'Рыба (тысячи)', XRANGE = [1975, 1983], /XSTYLE
Примечание. Синтаксис параметра ключевого слова /XSTYLE является синонимом выражения XSTYLE = 1. Присвоение параметру ключевого слова значения 1 часто называют установкой ключевого слова.
Синтаксис параметра ключевого слова /XSTYLE является синонимом выражения XSTYLE = 1. Присвоение параметру ключевого слова значения 1 часто называют установкой ключевого слова.
Графические символы
Каждая точка данных может быть отмечена символом и/или соединена линиями. Значение ключевого параметра PSYM выбирает символ маркера, как описано в PSYM. Например, значение 1 помечает каждую точку данных знаком плюс (+), 2 — звездочкой (*) и т. д. Установка PSYM на минус число символа помечает точки символом и соединяет их линиями. Значение –1 помечает точки знаком плюс (+) и соединяет их линиями. Обратите также внимание на то, что установка PSYM на значение 10 приводит к созданию графиков в стиле гистограммы, на которых горизонтальная линия проводится через каждые 9 секунд.3227 x бин.
Часто, когда точки данных наносятся на график по результатам подбора или модели, символы используются для обозначения точек данных, когда модель строится с помощью линии. Рисунок ниже иллюстрирует это, подгоняя значения популяции нерки к квадратичной функции года. IDL-функция POLY_FIT используется для вычисления квадратичного уравнения.
IDL-функция POLY_FIT используется для вычисления квадратичного уравнения.
Операторы, используемые для построения приведенного выше графика, следующие:
; Определите переменные.
@plot01
; Используйте функцию LINFIT, чтобы подогнать данные к строке:
coeff = LINFIT(YEAR, SOCKEYE)
;YFIT — это подобранная строка:
YFIT = coeff[0] + coeff[1]*YEAR
; Нанесите исходные точки данных с PSYM = 4 для бриллиантов:
PLOT, YEAR, НЕРКА, /YNOZERO, PSYM = 4, $
TITLE = 'Quadratic Fit', XTITLE = 'Year', $
YTITLE = 'Популяция нерки'
; Постройте гладкую кривую с помощью простой линии:
OPLOT, YEAR, YFIT
Кроме того, вы можете запустить пакетный файл plot03 для создания графика, введя:
@plot03
Гистограммы
В следующем примере создается диаграмма в виде прямоугольников, на которой четыре популяции лосося представлены в виде прямоугольников разного цвета или оттенка.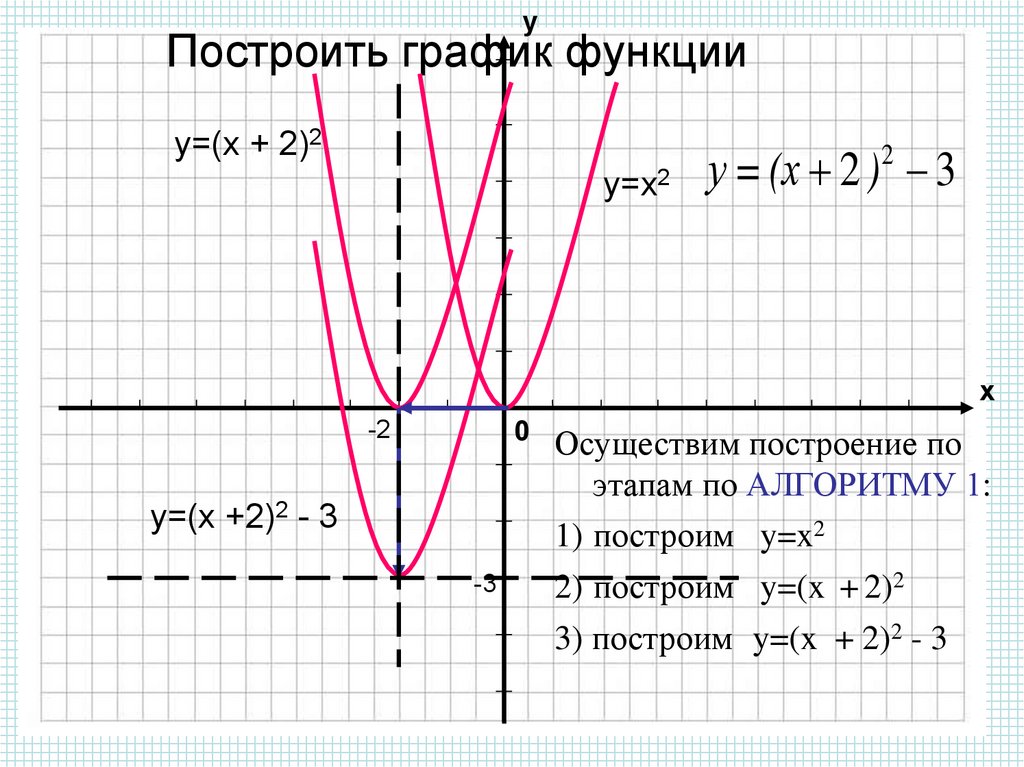 Команды, используемые для рисования следующего рисунка, показаны ниже с аннотацией.
Команды, используемые для рисования следующего рисунка, показаны ниже с аннотацией.
Вам не нужно вводить эти команды самостоятельно; они собраны в файлах plot05.pro, содержащих две процедуры, и пакетном файле plot06, создающем график. Эти файлы расположены в подкаталоге examples/doc/plot дистрибутива IDL. Запустите пример процедуры, введя plot05 в командной строке IDL, или просмотрите файл в окне редактора IDL, введя .EDIT plot05.pro.
Сначала мы определяем процедуру EX_BOX, которая рисует прямоугольник по координатам двух диагональных углов:
; Определите процедуру, рисующую прямоугольник, используя POLYFILL,
; чьи углы (X0, Y0) и (X1, Y1):
PRO EX_BOX, X0, Y0, X1, Y1, цвет
; Вызовите POLYFILL:
POLYFILL, [X0, X0, X1, X1], [Y0, Y1, Y1, Y0], COL = color
END
Затем создайте процедуру для рисования гистограммы:
PRO EX_BARGRAPH , минвал
; Определите переменные:
@plot01
; Ширина столбцов в единицах данных:
del = 1./5.
; Количество цветов, используемых в гистограмме:
; определяется количеством цветов, доступных в вашей системе:
ncol=!D.N_COLORS/5
; Создайте вектор индексов цвета, который будет использоваться в этой процедуре:
colors = ncol*INDGEN(4)+ncol
; Цикл для каждого образца:
FOR iscore = 0, 3 DO BEGIN
; Y значение аннотации. Вертикальное разделение: 20 data
; единицы:
yannot = minval + 20 *(iscore+1)
; Метка для каждого бара:
XYOUTS, 1984, yannot, names[iscore]
; Панель для аннотации:
EX_BOX, 1984, yannot - 6, 1988, yannot - 2, colors[iscore]
; Смещение x вертикальной полосы для каждой выборки:
xoff = iscore * del - 2 * del
; Нарисуйте вертикальную рамку для выборки каждого года:
FOR iyr=0, N_ELEMENTS(year)-1 DO $
EX_BOX, year[iyr] + xoff, minval, $
year[iyr] + xoff + del, $
core is[iyr], allpts $
colors[iscore]
ENDFOR
END
Введите в приглашении IDL следующее, чтобы скомпилировать эти две процедуры:
.run plot05.pro
Чтобы создать гистограмму, введите на экране следующие команды. .
; Загрузить таблицу цветов:
LOADCT, 39
Как и в предыдущем примере, процедура PLOT используется для построения осей и задания масштабирования с использованием ключевого слова NODATA.
PLOT, год, ЧИНУК, YRANGE = [MIN(allpts),MAX(allpts)], $
TITLE = 'Популяции лосося', /NODATA, $
XRANGE = [year[0], 1990]
; Получите значение y нижней оси x:
minval = !Y.CRANGE[0]
; Создайте гистограмму:
EX_BARGRAPH, minval
Указание делений
На следующем рисунке показана блочная диаграмма, иллюстрирующая непосредственную спецификацию значений отметок по оси x , количества отметок и имен отметок. Основываясь на предыдущей программе, эта программа показывает каждую из четырех оценок за 1967 год, первый год в наших данных. Он использует процедуру EX_BOX из предыдущего примера для рисования прямоугольника для каждого образца.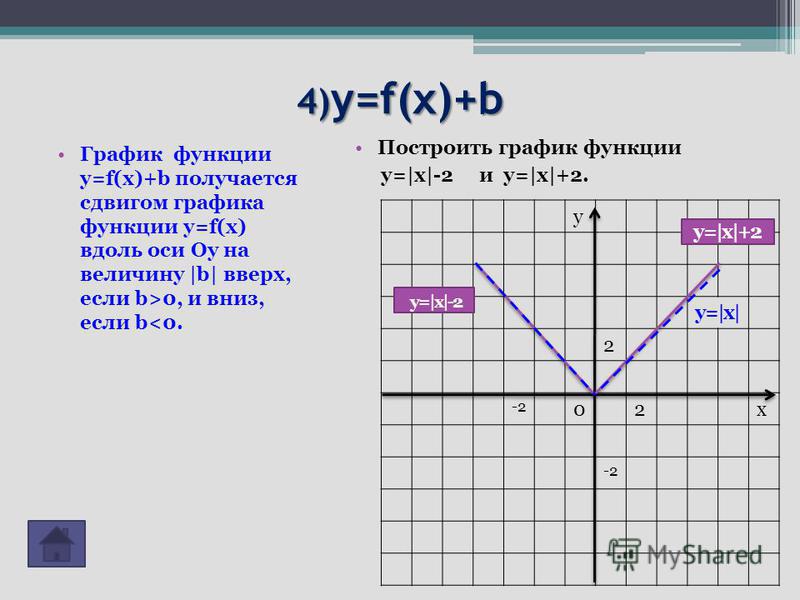
Введите следующую команду в приглашении IDL для компиляции процедур EX_BOX и EX_BARGRAPH (описанных в предыдущем примере):
.run plot05.pro
Введите следующие команды, чтобы создать блочную диаграмму:
; Определить переменные:
@plot01
; Отметьте значения x, 0,2, 0,4, 0,6, 0,8:
XVAL = FINDGEN(4)/5. + .2
; Составьте вектор баллов первого года обучения, соответствующий
; вектор имен сверху:
YVAL = [COHO[0], НЕРКА[0], ГОРБАН[0], ЧИНУК[0]]
; Сделайте оси без данных. Принудительно установить диапазон x в [0, 1],
; центрирующий xval, который также содержит значения галочки.
; Форсируйте три тиковых интервала, делая четыре тиковых метки.
; Укажите имена тиков из вектора имен:
PLOT, XVAL, YVAL, /YNOZERO, XRANGE = [0,1], XTICKV = XVAL, $
XTICKS = 3, XTICKNAME = NAMES, /NODATA, $
TITLE = 'Salmon Население, 1967'
; Нарисуйте прямоугольники, центрированные над делениями.
; !Y.CRANGE[0] — это значение y нижней оси x.
FOR I = 0, 3 DO EX_BOX, XVAL[I] - .08, !Y.CRANGE[0], $
XVAL[I] + 0,08, YVAL[I], 128
В качестве альтернативы вы можете ввести @plot07 в командной строке IDL, чтобы запустить пакетный файл plot07 и создать график.
Примечание: Данные о дате/времени можно отображать на графиках, изолиниях и поверхностях с помощью настроек деления оси даты/времени. Данные даты/времени могут отображаться на любой оси (x, y или z). Данные о дате/времени хранятся в виде дат по юлианскому календарю, но подпрограмма LABEL_DATE и ключевые слова оси позволяют отображать эти данные в виде календарных дат. Примеры см. на LABEL_DATE.
Логарифмическое масштабирование
Ключевые слова XLOG, YLOG и ZLOG можно использовать с процедурой PLOT для получения любой комбинации линейной и логарифмической осей. Процедура OPLOT использует то же масштабирование и преобразование, что и самый последний график.
На рисунке показано использование PLOT для построения линейно-логарифмического графика. Он был произведен со следующими операторами:
; Создать массив данных:
X = FLTARR(256)
; Сделайте ступенчатую функцию. Элементы массива с 80 по 120 устанавливаются равными 1:
X[80:120] = 1
; Сделать фильтр:
FREQ = FINDGEN(256)
; Сделайте фильтр симметричным относительно значения x = 128:
FREQ = FREQ < (256-FREQ)
; Баттерворт второго порядка, частота среза = 20,92)
; График с логарифмической осью x. Использовать точный диапазон осей:
PLOT, /YLOG, FREQ, ABS(FFT(X,1)), $
XTITLE = 'Относительная частота', YTITLE = 'Мощность', $
XSTYLE = 1
; График графика:
OPLOT, FREQ, FIL
Кроме того, вы можете запустить пакетный файл plot08 для создания графика:
@plot08
Несколько графиков на странице
Графики можно сгруппировать на дисплее или странице по горизонтали и /или вертикальные направления, используя поле системной переменной !P.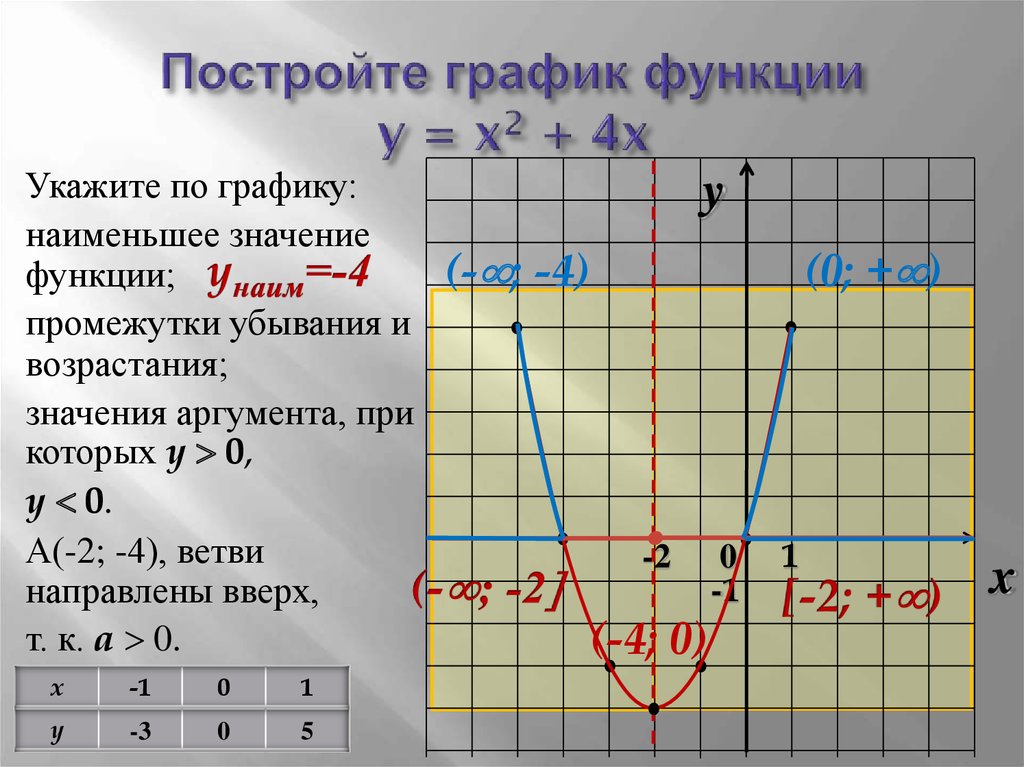 MULTI. IDL настраивает окно графика для создания заданного количества графиков на каждой странице и перемещает окно в новый сектор в начале каждого графика. Если страница заполнена, она сначала стирается. Если создается более двух строк или столбцов графиков, IDL уменьшает размер символа в 2 раза.
MULTI. IDL настраивает окно графика для создания заданного количества графиков на каждой странице и перемещает окно в новый сектор в начале каждого графика. Если страница заполнена, она сначала стирается. Если создается более двух строк или столбцов графиков, IDL уменьшает размер символа в 2 раза.
!P.MULTI управляет выводом нескольких графиков. Установите !P.MULTI равным целочисленному вектору, в котором:
- Первый элемент вектора содержит количество пустых секторов, оставшихся на странице. Дисплей стирается, если это поле равно нулю, когда начинается новый график.
- Второй элемент вектора содержит количество графиков на странице в горизонтальном направлении.
- Третий элемент содержит количество графиков на странице в вертикальном направлении.
- Четвертый элемент содержит количество графиков, сложенных по оси Z.
- Пятый элемент управляет порядком построения графиков.
 Установите пятый элемент равным нулю, чтобы построить графики слева направо (основной столбец) и сверху вниз. Установите пятый элемент равным единице, чтобы построить графики сверху вниз, слева направо (основной ряд).
Установите пятый элемент равным нулю, чтобы построить графики слева направо (основной столбец) и сверху вниз. Установите пятый элемент равным единице, чтобы построить графики сверху вниз, слева направо (основной ряд).
Исключение любого из пяти элементов вектора равносильно установке этого элемента равным нулю.
Например, чтобы настроить два графика по вертикали на каждой странице, используйте следующий оператор:
!P.MULTI = [0, 1, 2]
Обратите внимание, что первый элемент, !P.MULTI (0), устанавливается равным нулю, чтобы следующий график начинался с новой страницы. Чтобы сделать четыре графика на странице с двумя столбцами и двумя строками, используйте следующий оператор:
!P.MULTI = [0, 2, 2]
Чтобы сбросить значение по умолчанию для одного графика на страницу, установите значение ! P.MULTI в 0, как показано в следующем выражении:
!P.MULTI = 0
На этом рисунке показаны четыре графика в одном окне.
Для получения дополнительных сведений просмотрите пакетный файл plot09 в подкаталоге examples/doc/plot дистрибутива IDL или введите @plot09 в командной строке IDL, чтобы запустить пример.
Обратите внимание на следующие особенности графиков на рисунке:
- График в левом верхнем углу имеет деления в виде сетки. Это достигается установкой ключевого слова TICKLEN равным 1.0
- На графике в правом верхнем углу есть засечки, обращенные наружу. Это достигается установкой ключевого слова TICKLEN в отрицательное значение.
- График в левом нижнем углу имеет разные оси слева и справа, сверху и снизу. Это достигается путем раздельного рисования верхней и правой осей с использованием процедуры AXIS.
- График в правом нижнем углу вообще не использует оси по умолчанию. Центральные оси рисуются с помощью вызовов процедуры AXIS.
Указание местоположения графика
Окно данных графика — это область страницы или экрана, ограниченная осями. Область графика представляет собой поле, заключающее в себе окно данных графика, а также заголовки и аннотацию с отметками.
Область графика представляет собой поле, заключающее в себе окно данных графика, а также заголовки и аннотацию с отметками.
На рисунке показано соотношение окна данных графика, области графика и всей области устройства. Эти области определяются следующими системными переменными и параметрами ключевых слов в порядке убывания приоритета:
ПОЛОЖЕНИЕ |
!ПОЛОЖЕНИЕ |
!P.РЕГИОН |
!П.МУЛЬТИ |
[XYZ]МАРГИН |
![XYZ].ПОЛЯ |
Отображение отсутствующих данных
Ключевые слова MAX_VALUE и MIN_VALUE для PLOT можно использовать для создания графиков отсутствующих данных, на которых не отображаются неверные значения данных. Значения данных, превышающие значение ключевого слова MAX_VALUE или меньшие значения ключевого слова MIN_VALUE, рассматриваются как отсутствующие и не отображаются на графике. Следующий код создает набор данных с неправильными значениями данных и отображает его с этими ключевыми словами и без них:
Значения данных, превышающие значение ключевого слова MAX_VALUE или меньшие значения ключевого слова MIN_VALUE, рассматриваются как отсутствующие и не отображаются на графике. Следующий код создает набор данных с неправильными значениями данных и отображает его с этими ключевыми словами и без них:
; Создайте массив из 100 элементов, где каждый элемент равен
; установить равным его индексу:
A = FINDGEN(100)
; Установить 20 случайных точек в массиве равными 400.
; Это имитирует «плохие» значения данных выше диапазона
; "настоящих" данных.
A(RANDOMU(SEED, 20)*100)=400
; Установите 20 случайных точек в массиве равными -10.
; Это имитирует «плохие» значения данных ниже диапазона
; "настоящих" данных.
A(RANDOMU(SEED, 20)*100)=-10
; Постройте набор данных с неверными значениями. Выглядит очень плохо!
УЧАСТОК, А
; Нанесите на график набор данных, но не наносите значения выше 101.

 14159..
14159..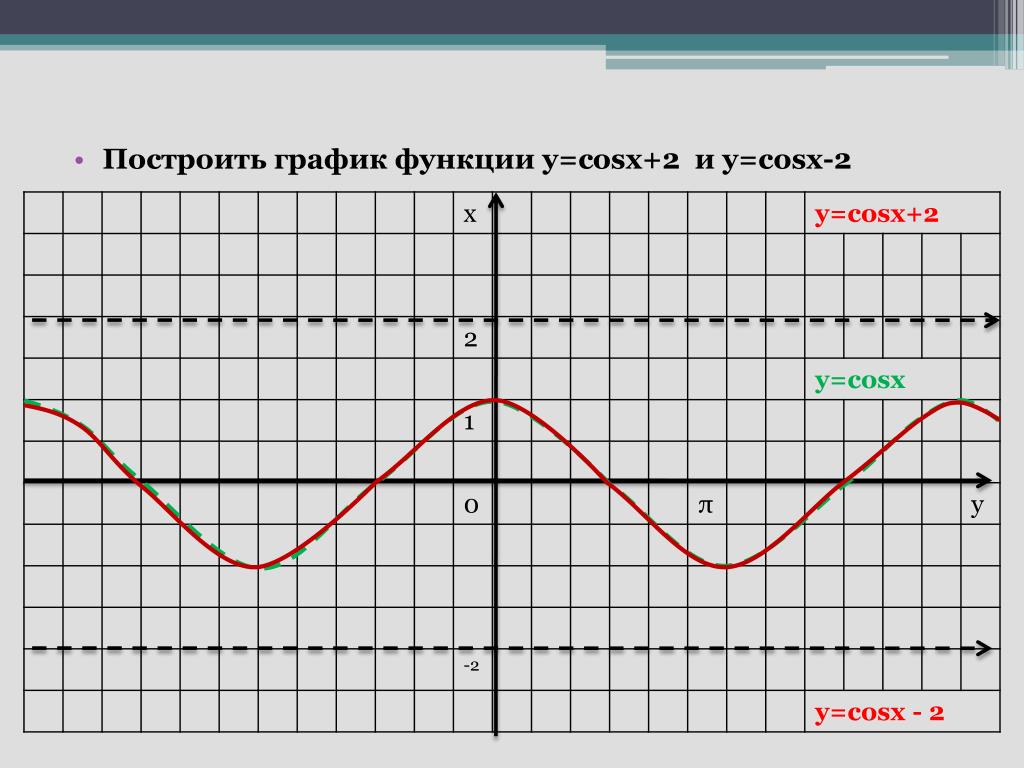 query("месяц == 'май'")
sns.lineplot(data=may_flights, x="год", y="пассажиры")
query("месяц == 'май'")
sns.lineplot(data=may_flights, x="год", y="пассажиры")
 lineplot (данные = рейсы, x = "пассажиры", y = "год", ориентация = "y")
lineplot (данные = рейсы, x = "пассажиры", y = "год", ориентация = "y")
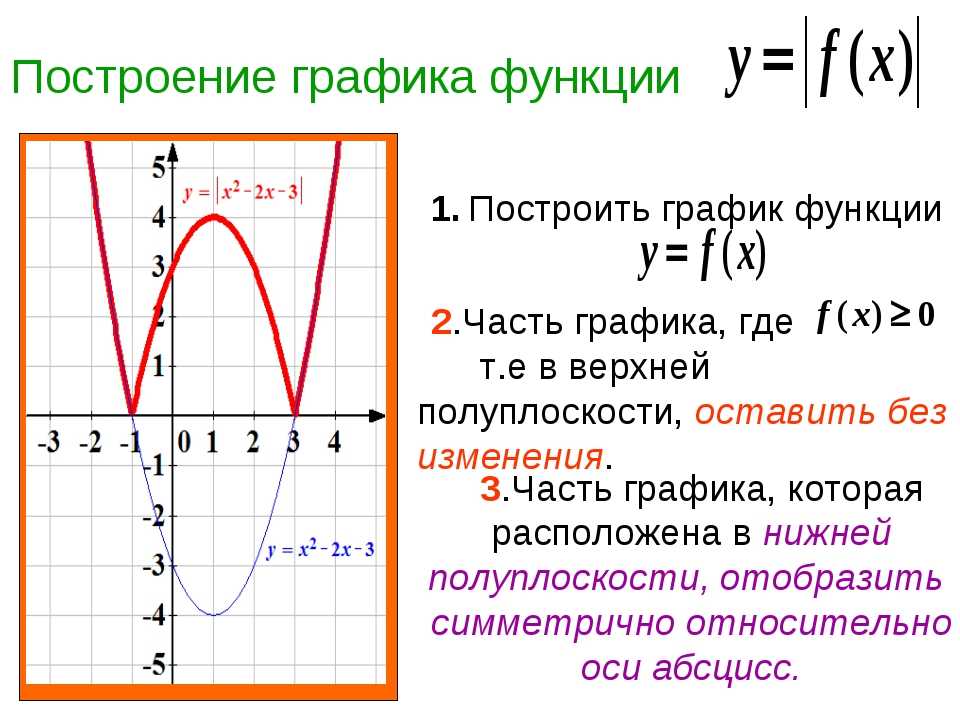 lineplot(data=fmri, x="timepoint", y="signal", hue="event")
lineplot(data=fmri, x="timepoint", y="signal", hue="event")
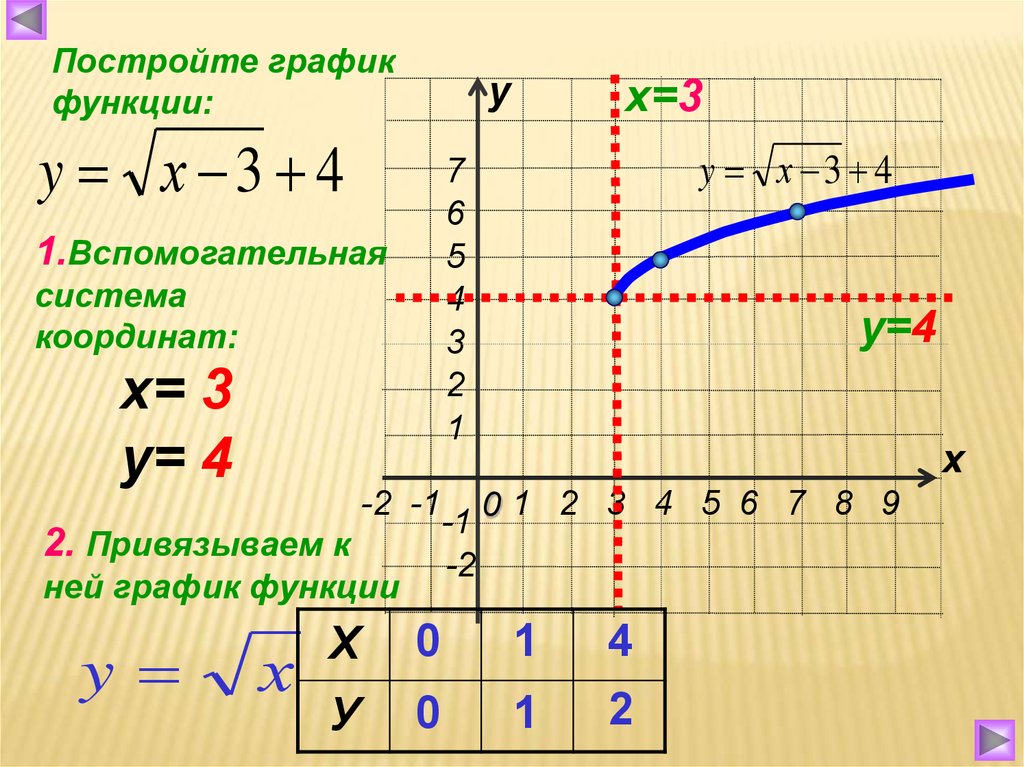 load_dataset("dots").query("align == 'dots'")
точки.голова()
load_dataset("dots").query("align == 'dots'")
точки.голова()
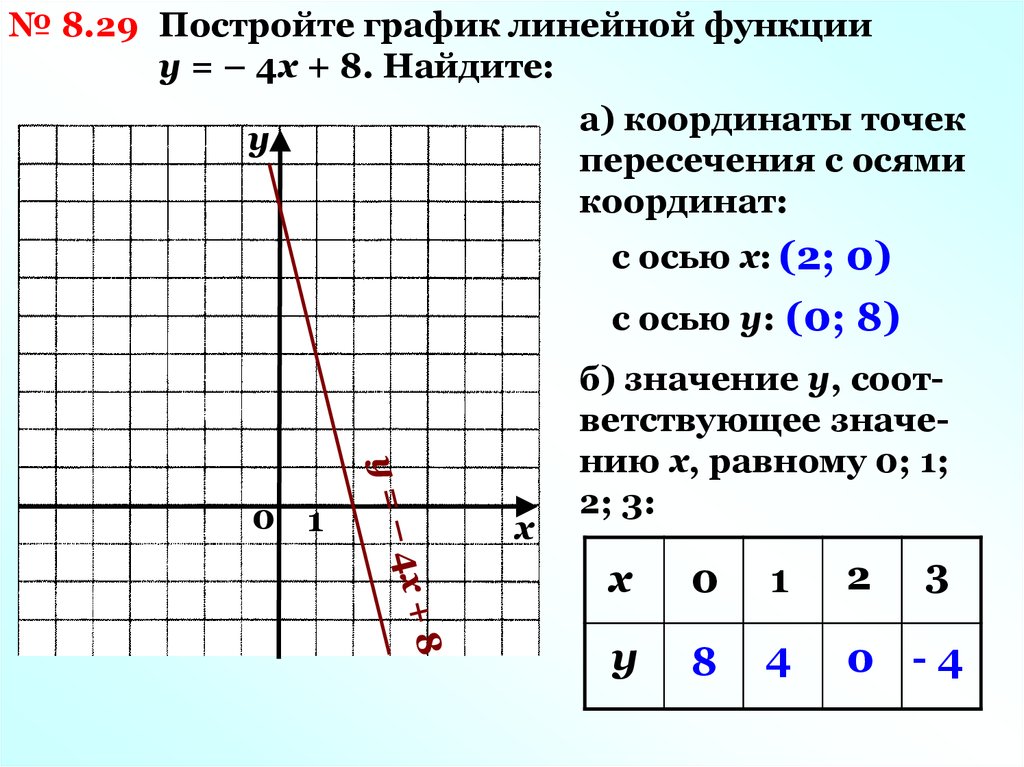 lineplot(
данные = точки, x = "время", y = "скорость стрельбы", оттенок = "когерентность",
)
lineplot(
данные = точки, x = "время", y = "скорость стрельбы", оттенок = "когерентность",
)
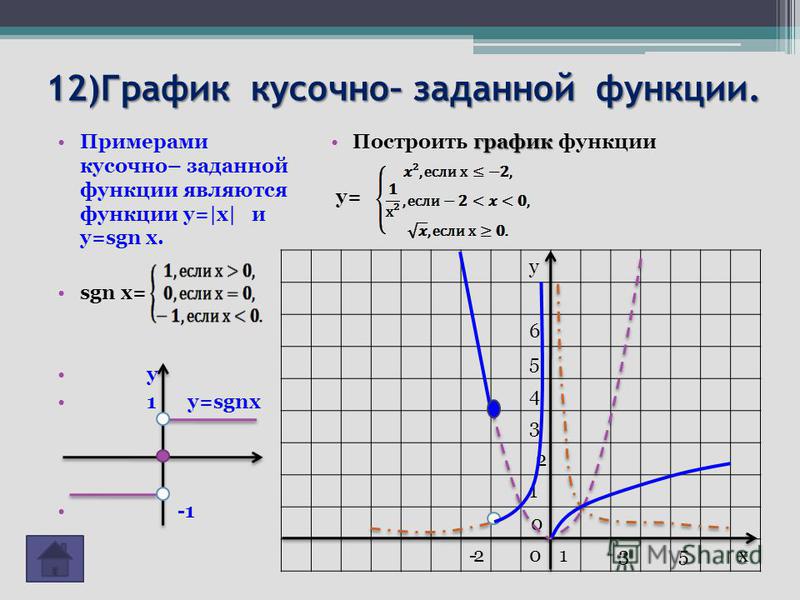 lineplot(
данные = точки, x = "время", y = "скорость стрельбы",
размер = "когерентность", оттенок = "выбор",
размеры = (0,25, 2,5)
)
lineplot(
данные = точки, x = "время", y = "скорость стрельбы",
размер = "когерентность", оттенок = "выбор",
размеры = (0,25, 2,5)
)
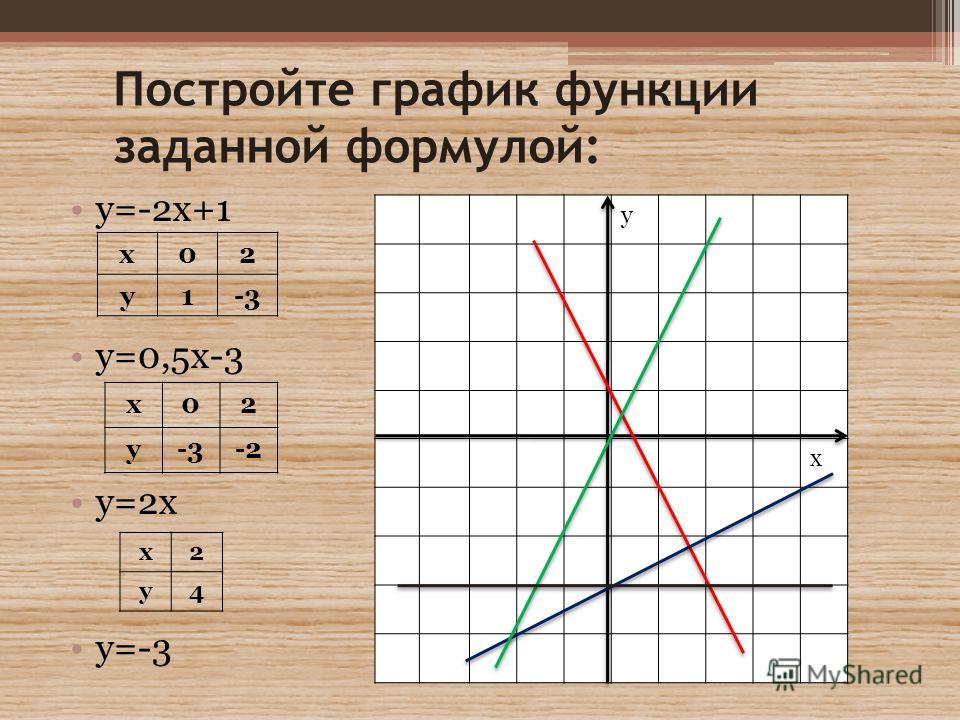 plot(x, y)
plot(x, y) 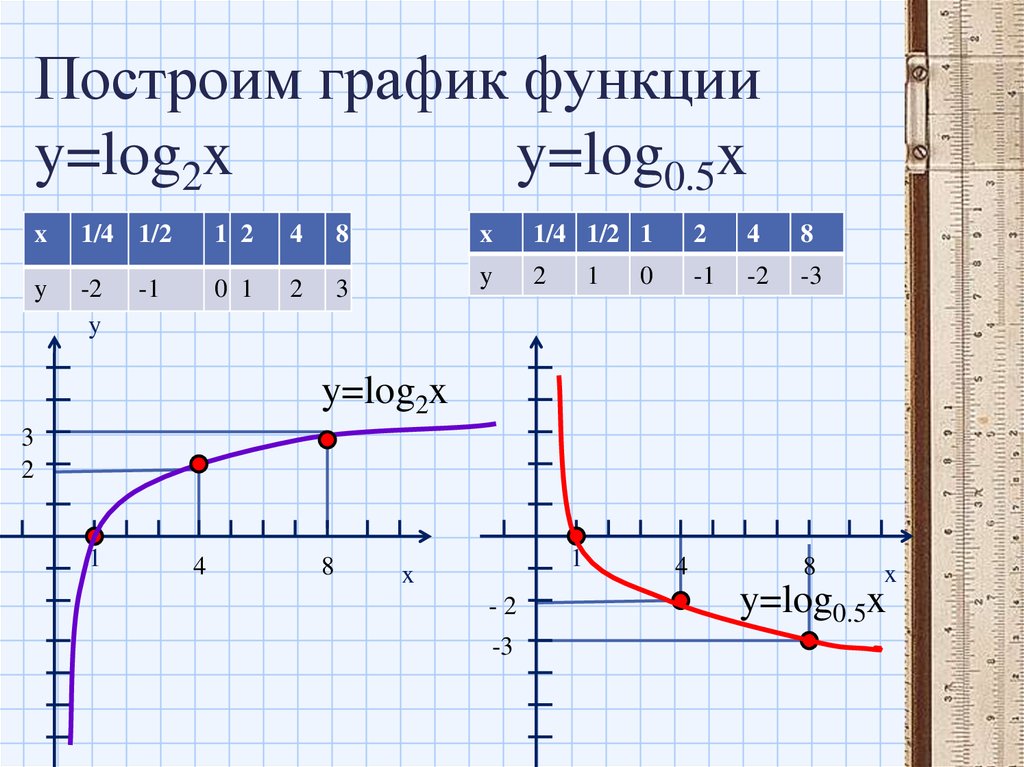 ylabel() .
ylabel() .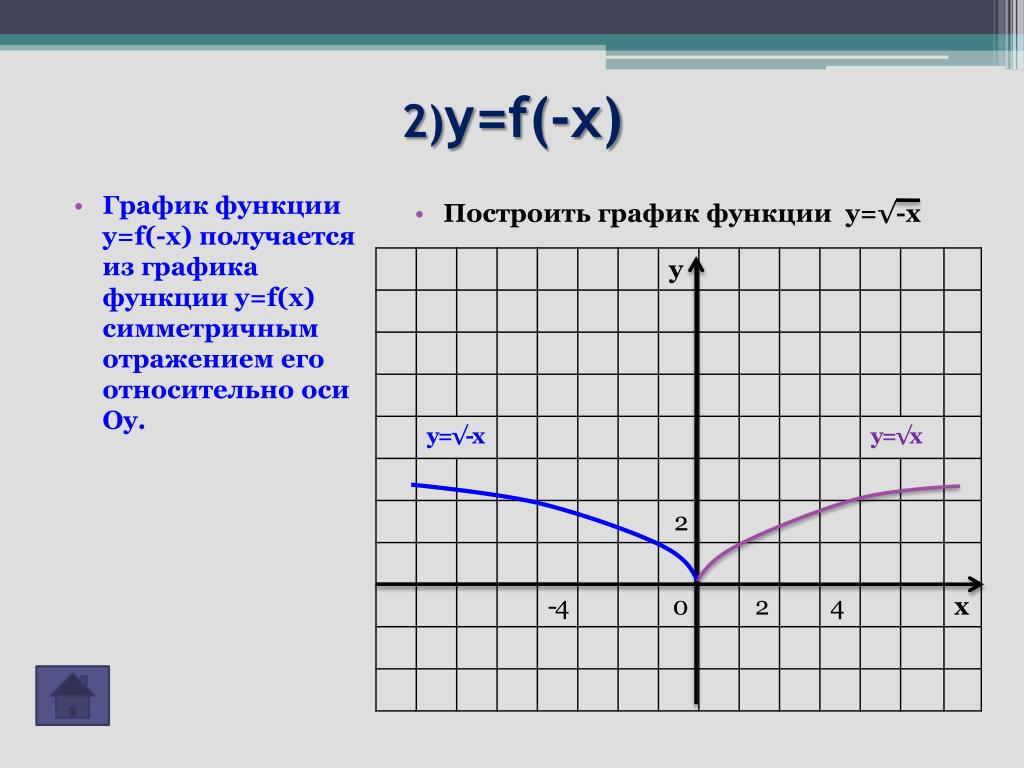 plot(x1, y1, label
plot(x1, y1, label  title(
title(  pyplot as plt
pyplot as plt 
 TITL (
TITL ( bar(left , высота, метка_галочки
bar(left , высота, метка_галочки  bar() function to plot a гистограмма.
bar() function to plot a гистограмма. 7 range
7 range  title(
title( 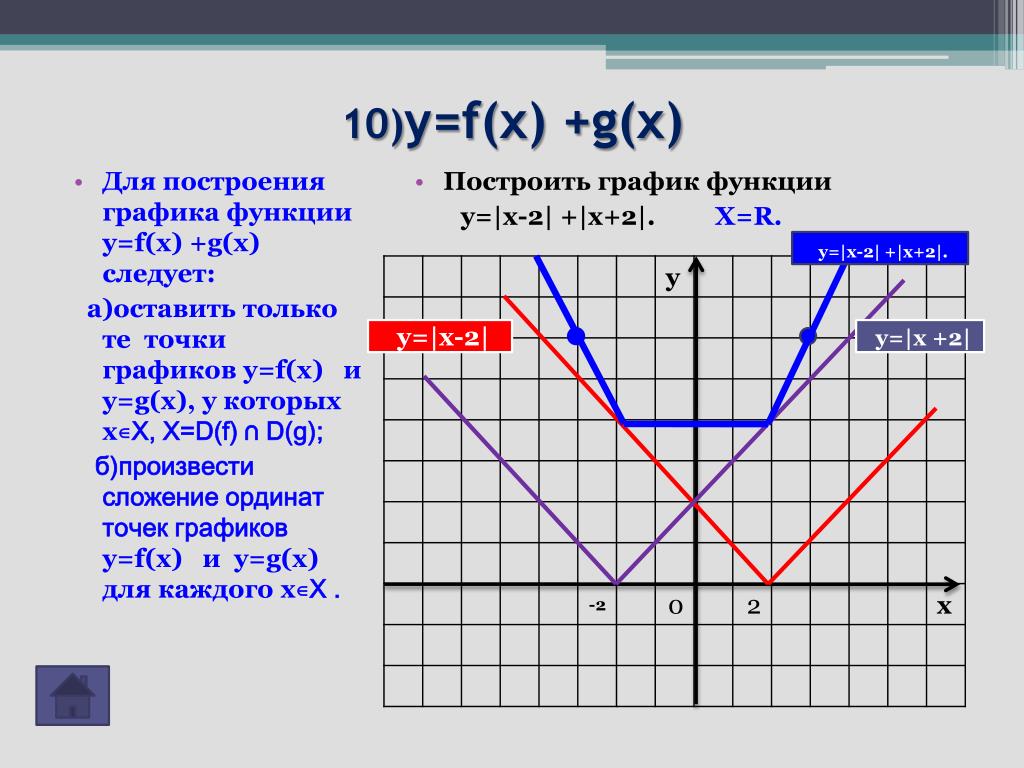
 Если вы хотите, чтобы ваш график включал заголовки и метки, выберите первую строку и первый столбец. Например, выбрав A1: D7, ось X может быть помечена как «Годы», а ось Y может быть помечена как «Количество животных». '.
Если вы хотите, чтобы ваш график включал заголовки и метки, выберите первую строку и первый столбец. Например, выбрав A1: D7, ось X может быть помечена как «Годы», а ось Y может быть помечена как «Количество животных». '. Каждый период равнялся году, но линейные платежи можно разбить на дни, недели, месяцы или другие периоды времени (т. е. дни с момента найма нового генерального директора).
Каждый период равнялся году, но линейные платежи можно разбить на дни, недели, месяцы или другие периоды времени (т. е. дни с момента найма нового генерального директора).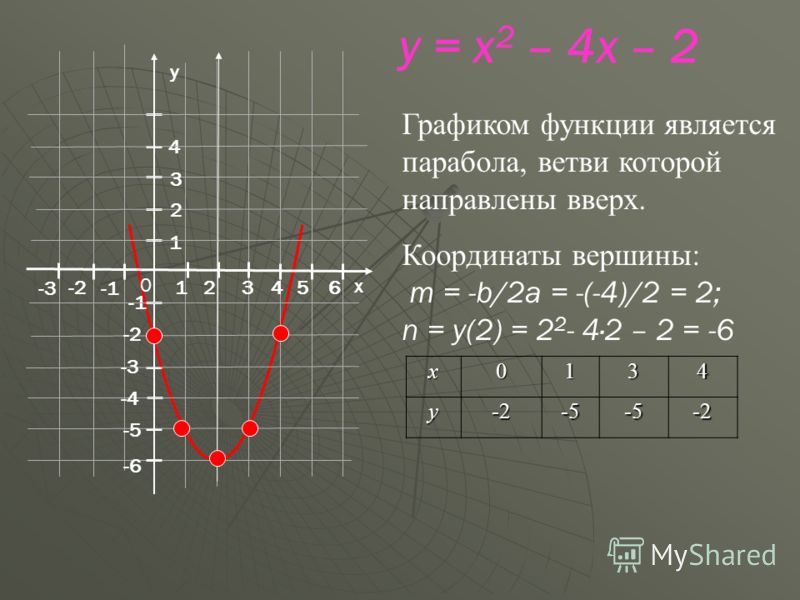 В большинстве случаев этой переменной является время. Непрерывный набор данных (т. е. количество животных в 10 крупнейших зоопарках мира) не подходит, поскольку нет причин связывать каждую точку данных линией; гистограмма была бы более подходящей.
В большинстве случаев этой переменной является время. Непрерывный набор данных (т. е. количество животных в 10 крупнейших зоопарках мира) не подходит, поскольку нет причин связывать каждую точку данных линией; гистограмма была бы более подходящей.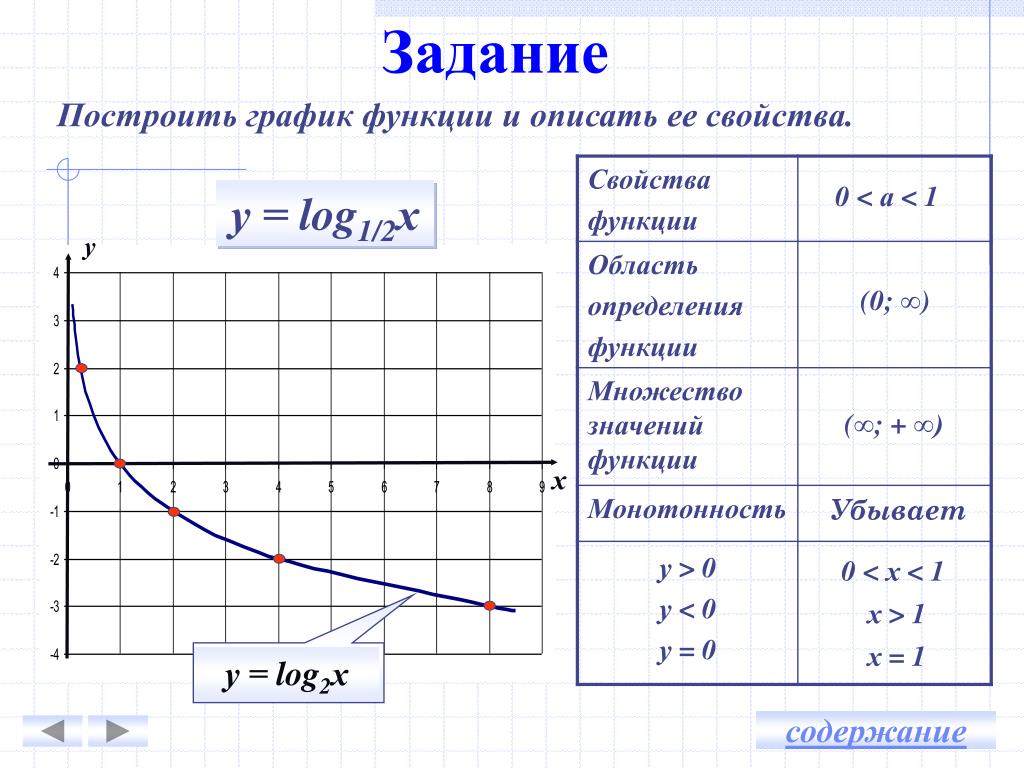 /5.
/5.  run plot05.pro
run plot05.pro