Производные элементарных функций — презентация онлайн
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
1. Производная
логарифмической
функции
Сначала
рассмотрим
частный
логарифмической функции:
y ln x
случай
Используем схему нахождения производной:
Дадим аргументу х приращение Δх и найдем
значение функции y+Δy:
y y ln( x x)
Находим приращение функции
y ln( x x) ln x
По свойству логарифма:
x x
x
ln
x
x
Составляем отношение
y 1 x
ln 1
x x
x
Находим предел этого отношения:
y
1 x
y lim
lim
ln 1
x 0 x
x 0 x
x
Сделаем замену:
x
y ; x xy
x
Тогда
1
1
1
1
1
ln 1 y y
lim
ln 1 y lim ln 1 y y lim
y 0 x
y 0 xy
x y 0
В силу непрерывности логарифмической
функции меняем местами знаки логарифма и
предела:
1
1
1
1
ln lim 1 y y ln e
x y 0
x
x
e
1
1
(ln x)
x
Для сложной функции:
1
(ln u ) u
u
ПРИМЕР.
y 3ln x
2
1
6
y (3 ln x ) 3 2 2 x
x
x
2
Найдем производную для общего случая
логарифмической функции:
y log a x
По свойству логарифма
ln x
log a x
ln a
Тогда
ln x
1
1
y (log a x)
(ln x)
ln a
x ln a
ln a
1
x
Отсюда окончательно имеем
1
(log a x)
x ln a
Для сложной функции:
1
(log a u )
u
u ln a
ПРИМЕР.
y log5 ( x 3x)
2
1
1
y (log 5 ( x 3x)) 2
(2 x 3)
x 3x ln 5
2
2. Производная
показательной
функции
Сначала
рассмотрим
показательной функции:
y e
частный
x
случай
Логарифмируем
основанию e:
обе
части
равенства
ln y ln e x ln e x
x
Дифференцируем обе части равенства по х:
1
y 1
(ln y ) x
y
Отсюда выражаем искомую производную:
y y
Т.к.
y e
x
то окончательно получаем:
y e
x
по
(e ) e
x
x
Для сложной функции:
(e ) e u
u
u
Кривая
y e
x
(экспонента) обладает свойством: в каждой
точке х ордината у равна угловому
коэффициенту касательной к кривой в этой
точке:
e tg
x
ПРИМЕР.
y x e
5x
y ( x e ) e x 5 e e (1 5x)
5x
5x
5x
5x
Найдем производную для общего случая
показательной функции:
y a
x
y (a )
x
Т.к.
a e
(e
e
ln a x
)
x ln a
a
x
ln a
(e
x ln a
)
ln a a ln a
x
(a ) a ln a
x
x
Для сложной функции:
(a ) a ln a u
u
u
ПРИМЕР.
y 7
y (7
3 x3 x
7
) 7
3 x3 x
3 x3 x
3 x3 x
ln 7 3x x
3
ln 7 (9 x 1)
2
3. Производная
степенной
функции
y x
n
Логарифмируем
основанию e:
обе
части
равенства
ln y ln x n ln x
n
Дифференцируем обе части равенства по х:
(ln y ) (n ln x)
1
1
y n
y
x
по
Отсюда выражаем искомую производную:
1
y y n
x
Т.к.
y x
n
то окончательно получаем:
1
n 1
y n x n x
x
n
( x ) n x
n
n 1
Для сложной функции:
(u ) n u u
n
n 1
4.
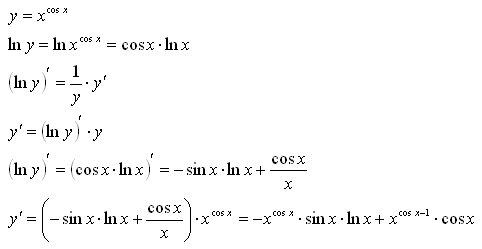Производнаястепеннопоказательной
функции
y f ( x)
( x)
Логарифмируем
основанию e:
обе
части
ln y ln f ( x)
( x)
равенства
по
( x) ln f ( x)
Дифференцируем обе части равенства по х,
учитывая, что в правой части стоит
произведение:
(ln y ) ( x ) ln f ( x )
1
y ( x) ln f ( x) ln f ( x) ( x)
y
1
1
y ( x) ln f ( x)
f ( x) ( x)
y
f ( x)
1
y y ( x) ln f ( x)
f ( x) ( x)
f ( x)
y f ( x)
( x)
Т.к.
то окончательно получаем:
y f ( x)
( x)
f ( x)
( x)
1
( x) ln f ( x)
f ( x) ( x)
f ( x)
( x) ln f ( x) f ( x)
( x ) 1
f ( x) ( x)
Чтобы продифференцировать
степенно-показательную функцию,
ее сначала нужно
продифференцировать как
показательную функцию, а затем
результаты сложить.
ПРИМЕР.
y x
x
x
n 1
x
x
y ( x ) x x x ln x x (1 ln x)
ЗАМЕЧАНИЕ
Производная логарифмической функции
1
(ln y) y
y
называется
логарифмической
производной.
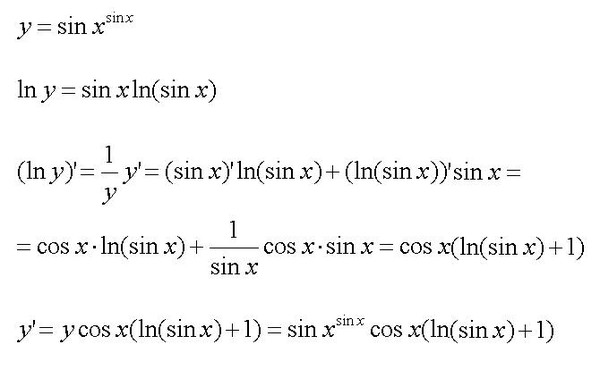Ее удобно использовать длядифференцирования
функции,
выражение
которой
существенно
упрощается при логарифмирования.
ПРИМЕР.
( x 1)( x 2)
y
3 x
2
Логарифмируем
основанию e:
обе
части
равенства
по
( x 1)( x 2)
ln y ln
3 x
2
Используем свойства логарифма:
1 ( x 1)( x 2 2)
ln
2
3 x
1
2
ln( x 1) ln( x 2) ln( 3 x)
2
Дифференцируем обе части равенства по х:
1
2
(ln y ) ln( x 1) ln( x 2) ln( 3 x)
2
1
1 1
2x
1
y
2
y
2 x 1 x 2 3 x
1 1
2x
1 ( x 1)( x 2 2)
y
2
2 x 1 x 2 3 x
3 x
5. Производные
тригонометрических
функций
y sin x
Используем схему нахождения производной:
Дадим аргументу х приращение Δх и найдем
значение функции y+Δy:
y y sin( x x)
Находим приращение функции
y sin( x x) sin x
Распишем разность синусов:
x
x
2 sin
cos x
2
2
Составляем отношение
x
x
2 sin
cos x
y
2
2
x
x
Находим предел этого отношения:
x
x
2 sin
cos x
y
2
2
y lim
lim
x 0 x
x 0
x
x
2 sin
x
2
lim
lim cos x
x 0
x 0
x
2
cos x
Первый
предел
замечательному:
сводим
к
x
sin
2
lim
cos x cos x
x 0 x
2
1
первому
(sin x) cos x
Для сложной функции:
(sin u ) cos u u
Аналогично
функции
можно
найти
y cos x
(cos x) sin x
Для сложной функции:
(cos u ) sin u u
ПРИМЕР.
sin 6 x
y
cos(x 2 1)
2
2
(sin 6 x) cos( x 1) sin 6 x (cos( x 1))
y
2
2
(cos( x 1))
6 cos 6 x cos( x 2 1) sin 6 x sin( x 2 1) 2 x
(cos( x 2 1)) 2
Найдем производную функции
y tgx
sin x
y (tgx)
cos x
Находим производную дроби:
(sin x) cos x sin x (cos x)
2
cos x
1
cos 2 x sin 2 x
1
2
2
cos x
cos x
1
(tgx)
cos 2 x
Для сложной функции:
1
(tgu)
u
cos2 u
Аналогично
функции
можно
найти
производную
y ctgx
1
(ctgx) 2
sin x
Для сложной функции:
1
(ctgu) 2 u
sin u
ПРИМЕР.
1
y tg 2
x 3x
1
2x 3
1
y tg 2
2
2
x 3x cos2 1 ( x 3x)
2
x
3x
6. Производные
обратных
тригонометрических
функций
y arcsin x
Обратной к ней функцией будет x sin y
Используем правило дифференцирования
обратной функции:
1
1
1
xy
y x
y x
x y
cos y
Теперь нужно выразить у через х с помощью
основного тригонометрического соотношения:
1
1
1
(arcsin x)
2
2
cos y
1 sin y
1 x
x2
Эта производная не существует при
x 1
(arcsin x)
1
1 x2
Для сложной функции:
1
(arcsin u )
u
2
1 u
Аналогично
функций
можно
найти
y arccos x
y arctgx
y arcctgx
производную
(arccos x)
1
1 x2
Для сложной функции:
1
(arccosu )
u
2
1 u
1
(arctgx)
2
1 x
Для сложной функции:
1
(arctgu)
u
2
1 u
1
(arcctgx)
1 x2
Для сложной функции:
(arcctgu)
1
u
2
1 u
ПРИМЕР.
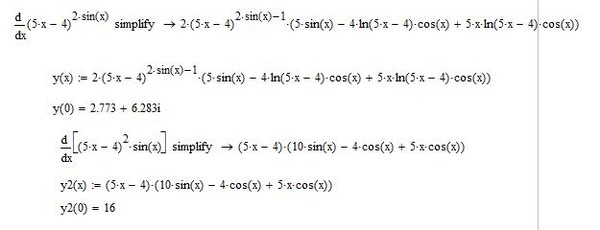
y arccos(lnx)
1
1
y (arccos(ln x))
2
1 ln x x
English Русский Правила
Дифференциал функции.
Приращение функции y=f(x) можно представить в виде суммы двух слагаемых: ∆y=y’·∆x + α(x) ·∆x, где α(x) — бесконечно малая при ∆x→0.
Второе слагаемое — бесконечно малая высшего порядка малости в сравнении с первым. Слагаемое y’·∆x составляет главную часть приращения функции.
Определение 8: Главная часть приращения функции, линейная относительно приращения аргумента, называется дифференциалом функции (dy): dy = y’·∆x
Учитывая, что при y=x имеем dx = x’·∆x, т.е. dx=∆x, получаем dy=y‘·dx, т.е. дифференциал функции равен произведению производной функции на дифференциал ее аргумента. Отсюда y’=dy/dx.
Решение типовых задач.
Задача: найти производную функцийа) y=(x5+x+8)·ctg3x
Решение.
Воспользуемся правилом 4 дифференцирования
произведения двух функций
y’=(x5+x+8)’·ctg3x+(x5+x+8)·(ctg3x)’
Далее используем правило 3 дифференцирования
суммы и правило 6 дифференцирования
сложной функции: (ctgu)’x=-(1/sin 2u)·u’x,
где u=3x.
Получаем: y’=(5x4+1)∙ctg3x-(x5+x+8)∙ = (5x4+1)∙ctg3x —
б)
Решение. Представим данную функция в виде степени y=[ln(2+sin5x)]1/3 и применим правило дифференцирования сложной функции: (U )’x=n·U n-1·U’x. В нашем примере u=ln(2+sin5x), n=1/3.
Получаем: y’=1/3 [ln(2+sin5x)]-2/3
Тогда y’ =1/3 [ln(2+sin5x)]-2/3·
Используем далее правило 3 и формулу: (sinu)’=cosu·u’, где u=5x получаем: y’=1/3 [ln(2+sin5x)]-2/3·
Задача:
найти вторую производную функции y=e 2x+1.
Решение. Найдем y’, используя формулу: (eu)’x =e u·u’x
В нашем примере u=2x+1. y’=e 2x+1·(2x+1)’ = 2e 2x+1
y»=(y’)’=(2e 2x+1)’=2(e2x+1)’=4e 2x+1.
Задача: найти дифференциал функции
Решение. Запишем функцию в виде: y=2(cos 2x)-2. Используем правило: dy=y’x·dx. dy= [2(cos 2x)-2]’·dx=2[(cos2x)-2]’·dx= =-4·(cos2x)-3 ·(cos2x)’·dx=-4(cos2x)-3·(-sin2x)·(2x)’·dx
Задача: Составить уравнение касательной к графику функции y=3x4+7 в точке x0=2.
Решение. Найдем ординату точки касания y0=f(x0):
y0=3·24+7=55.
Найдем угловой коэффициент касательной
k=f'(x0)
f'(x)=12x3,
f'(2)=12·23=96,
т.
е. k=96.
Запишем уравнение касательной в виде y=y0=k(x-x0): y-55=96(x-2) или y=96x-137.
3. Применение производных и исследование функций
Определение 1. Функция y=f(x) называется возрастающей на интервале ]a,b[, если для любых двух точек x1 и x2 этого интервала из неравенства x2>x1 следует неравенство f(x2)≥f(x1), т.е. приращение аргумента и приращение функций имеют одинаковые знаки.
Если из x2>x1 следует f(x2)>f(x1), то функцию называют строго возрастающей.
Определение
2. Функция
y=f(x)
называется убывающей на интервале
]a,b[,
если для любых двух точек x1 и x2 этого интервала из неравенства x2>x1 следует неравенство f(x2)≤f(x1),
т.е. приращение аргумента и приращение
функции имеют противоположные знаки.
Теорема 1 (о необходимых условиях возрастания и убывания функции на интервале)
Если дифференцируемая функция f(x) возрастает на ]a,b[, то в любой точке этого интервала f»(x)≥0;
Если дифференцируемая функция f(x) убывает на ]a,b[, то в любой точке этого интервала f»(x)≤0.
Если дифференцируемая функция f(x) на ]a,b[ не изменяется, то ее производная f»(x)=0.
Теорема 2. (о достаточных условиях возрастания и убывания функции). интервале строго возрастает,
Если производная f»(x) функции y=f(x) на интервале ]a,b[ отрицательна, то функция на этом интервале строго убывает.
Если производная f»(x) функции y=f(x) на интервале ]a,b[ равна нулю, то функция на этом интервале сохраняет постоянное значение.
Определение
3. Значение функции f(x0)
называется локальным максимумом функции
y=f(x)
на интервале ]a,b[,
если существует такая β-определенность
]x0-β,x0+β[
точки x0,
что для всех x≠x0 этой окрестности выполняется неравенство:
f(x)<f(x0).
Определение 4. Значение функции f(x0) называется локальным минимумом функции y=f(x) на интервале ]a,b[, если существует такая β-определенность ]x0 -β,x0+ β[ точки x0, что для всех x≠x0 этой окрестности выполняется неравенство: f(x)>f(x0).
Точку x0 называют, соответственно определению 3 (определению 4), точкой максимума (точкой минимума).
Если производная f»(x) функции y=f(x) на интервале ]a,b[ положительна, то функция на этом
Максимум и минимум функции называются локальным экстремумом функции.
Теорема 3 (о необходимом условии существования экстремума дифференцируемой функции)
Если функция y=f(x), дифференцируемая на интервале ]a,b[, имеет в точке x0є]a,b[ экстремум, то ее производная в этой точке равна нулю.
Теорема 4 (о достаточных условиях экстремума функции)
Если
производная функции y=f(x)
в точке x0 обращается в нуль (f'(x0)=0),
и при переходе через эту точку в
направлении возрастания x
меняет знак с плюса на минус, то в точке
x0 эта функция имеет максимум; если знак
производной меняется с минуса на плюс,
то в точке x0 функция имеет минимум; если же при
переходе через точку x0 производная f'(x)
не меняет знак, то в точке x0 функция экстремума не имеет.
Определение 5. Кривая y=f(x) называется выпуклой на интервале ]a,b[, если она лежит ниже касательной, проведенной к этой кривой в любой точке x этого интервала.
Определение 6. Кривая y=f(x) называется вогнутой на интервале ]a,b[, если она лежит выше касательной, проведенной к этой кривой в любой точке x этого интервала.
Теорема 5 (о достаточных условиях выпуклости и вогнутости кривой)
Если вторая производная f»(x) функции y=f(x) на интервале ]a,b[ положительна, то график функции на этом интервале вогнутый, а если вторая производная f»(x) отрицательна, то график функции выпуклый.
Определение 7. Точка непрерывной кривой, отделяющая участок выпуклости от участка вогнутости или наоборот, называется точкой перегиба.
Теорема 6 (о достаточных условиях наличия точки перегиба)
Если
вторая производная f»(x)
функции y=f(x)
в некоторой точке x0 обращается в нуль и при переходе через
нее меняет свой знак на обратный, то
точка (x0,f(x0))
является точкой перегиба графика
функции.
Правило 1 исследования функции на возрастание, убывание и экстремумы.
1. Указать область определения функции y=f(x).
2. Найти производную y’=f'(x).
3. Составить уравнение f'(x)=0 и найти его корни (критические значения.
4. Разбить область определения критическими значениями аргумента x на интервалы монотонности и найти знак производной на каждом интервале.
5. На основании теоремы 2 сделать вывод о возрастании или убывании функции на интервалах.
6. На основании теоремы 4 сделать вывод о наличии экстремумов в критических точках, разделяющих интервалы монотонности.
Правило 2 исследования функции на выпуклость, вогнутость и наличие точек перегиба.
1. Указать область определения функции y=f(x).
2. Найти вторую производную y»=f»(x).
3.
Составить уравнение f»(x)=0
и найти его корни.
4. Разбить область определения функции найденными корнями на интервалы и найти знак второй производной на каждом интервале.
5. На основании теоремы 5 сделать вывод о выпуклости или вогнутости графика функции на интервалах.
6. На основании теоремы 6 сделать вывод о наличии точек перегиба.
| 1 | Найти производную — d/dx | бревно натуральное х | |
| 2 | Оценить интеграл | интеграл натурального логарифма x относительно x | |
| 3 | Найти производную — d/dx | 92)||
| 21 | Оценить интеграл | интеграл от 0 до 1 кубического корня из 1+7x относительно x | |
| 22 | Найти производную — d/dx | грех(2x) | |
| 23 | Найти производную — d/dx | 9(3x) по отношению к x||
| 41 | Оценить интеграл | интеграл от cos(2x) относительно x | |
| 42 | Найти производную — d/dx | 1/(корень квадратный из х) | |
| 43 | Оценка интеграла 9бесконечность | ||
| 45 | Найти производную — d/dx | х/2 | |
| 46 | Найти производную — d/dx | -cos(x) | |
| 47 | Найти производную — d/dx | грех(3x) | 92+1|
| 68 | Оценить интеграл | интеграл от sin(x) по x | |
| 69 | Найти производную — d/dx | угловой синус(х) | |
| 70 | Оценить предел | ограничение, когда x приближается к 0 из (sin(x))/x 92 по отношению к х | |
| 85 | Найти производную — d/dx | лог х | |
| 86 | Найти производную — d/dx | арктан(х) | |
| 87 | Найти производную — d/dx | бревно натуральное 5х92x Производная
= $\sin x \cos x +\cos x \sin x$, так как мы знаем, что $\dfrac{d}{dx}(\sin x)=\cos x$ = $2\sin x \ cos x$ = $\sin 2x$, так как sin2x=2sinxcosx. Итак, производная квадрата sin x по правилу произведения равна sin2x. Производная sin2 x по первому принципуПроизводная f(x) по первому принципу равна следующему пределу: $\dfrac{d}{dx}(f(x))$ $=\lim\limits_{h \to 0} \dfrac{f(x+h)-f(x)}{h}$. 9092 x}{h}$ = $\lim\limits_{h \to 0} \dfrac{\sin(x+h+x)\sin(x+h-x)}{h}$, здесь мы использовали тригонометрическая формула sin 2 a-sin 2 b = sin(a+b) sin(a-b). = $\lim\limits_{h \to 0} \dfrac{\sin(2x+h)\sin(h)}{h}$ = sin(2x+0)$\lim\limits_{h \to 0} \dfrac{\sin(h)}{h}$ = sin2x ⋅ 1 = sin2x Итак, производная квадрата sinx x по первому принципу равна sin2x. Читайте также: Производная sin2 x по цепному правилуЦепное правило производной утверждает, что если y = f(u) и u = g(x), то производная y по x определяется формулой $\dfrac{dy}{dx}=\dfrac{dy}{du} \times \dfrac{du}{dx}$ …(I) См. |
