Главная → Видеоуроки → ЕГЭ по математике. Профильный уровень. Задание 14. Описание видеоурока: Задание №14 (В15) № 26695 (профильный уровень) и задача №14 (базовый уровень) ЕГЭ-2015 по математике. Производная, первообразная. Урок 5. Условие задачи: Найдите наибольшее значение функции y=15x-sin3x+5 на отрезке [-п/2; 0] 00:05:11 Валерий Волков 2 28.12.2014 Будем рады, если Вы поделитесь ссылкой на этот видеоурок с друзьями! Новости образования | ЕГЭ по математике Профильный уровень Задание 1 Задание 2 Задание 3 Задание 4 Задание 5 Задание 6 Задание 7 Задание 8 Задание 9 Задание 10 Задание 11 Задание 12 Задание 13 Задание 14 Задание 15 Задание 16 Задание 17 Задание 18 Задание 19 Задание 20 Задание 21 ГИА по математике Задача 1 Задача 2 Задача 3 Задача 4 Задача 5 Задача 6 Задача 7 Задача 8 Задача 9 Задача 10 Задача 11 Задача 12 Задача 13 Задача 14 Задача 15 Задача 16 Задача 17 Задача 18 Задача 19 Задача 20 Задача 21 Задача 22 Задача 23 Задача 24 Задача 25 Задача 26 Демонстрационные варианты ОГЭ по математике Математика. Натуральные числа Обыкновенные дроби Десятичные дроби Проценты Математика. 6 класс. Делимость чисел Сложение и вычитание дробей с разными знаменателями Умножение и деление обыкновенных дробей Отношения и пропорции Положительные и отрицательные числа Измерение величин Математика. 7 класс. Преобразование выражений Многочлены Формулы сокращенного умножения Математика. 8 класс. Модуль числа. Уравнения и неравенства. Квадратные уравнения Квадратные неравенства Уравнения с параметром Задачи с параметром Математика. 9 класс. Функции и их свойства Прогрессии Векторы Комбинаторика, статистика и теория вероятностей Математика. Числовые функции Тригонометрические функции Тригонометрические уравнения Преобразование тригонометрических выражений Производная Степенные функции Показательная функция Логарифмические функции Первообразная и интеграл Уравнения и неравенства Комбинаторика Создаёте видеоуроки? Если Вы создаёте авторские видеоуроки для школьников и учителей и готовы опубликовать их, то просим Вас связаться с администратором портала. Актуально Физкультминутки для школьников и дошкольников Подготовка к ЕГЭ Подготовка к ОГЭ |
Презентация «Преобразование графиков тригонометрических функций» | Презентация к уроку по алгебре (10 класс) по теме:
Опубликовано 26.11.2013 — 22:28 — Елена Александровна Пархоменко
Презентация «Преобразование графиков тригонометрических функций».
Скачать:
Предварительный просмотр:
Подписи к слайдам:
Слайд 1
Графики тригонометрических функций Функция у = sin x, ее свойства Преобразование графиков тригонометрических функций путем параллельного переноса Преобразование графиков тригонометрических функций путем сжатия и расширения Для любознательных…
Слайд 2
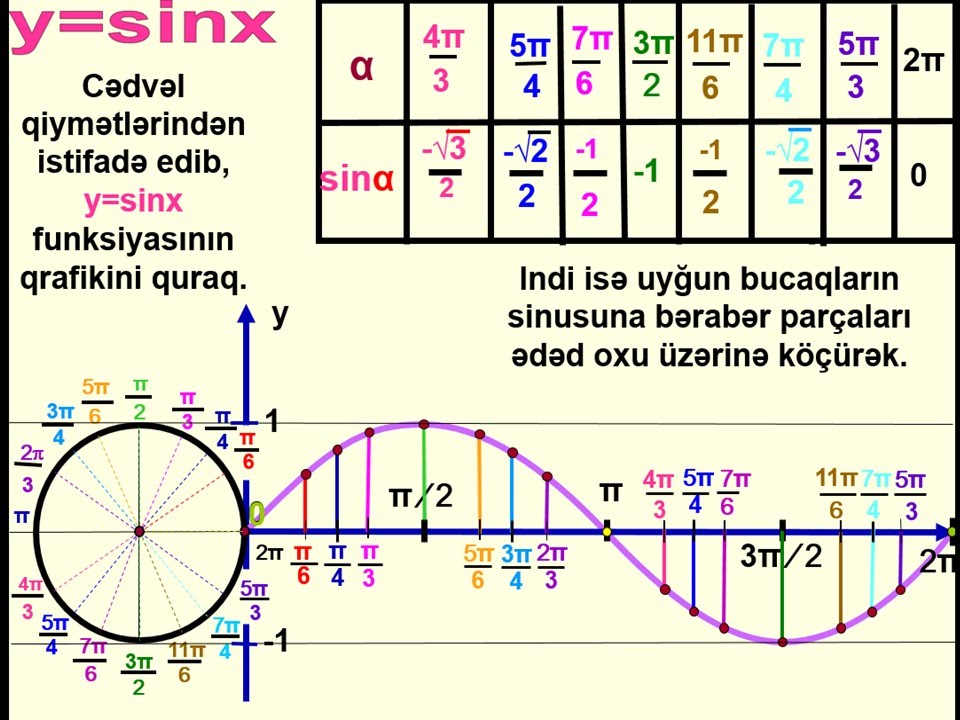
тригонометрические функции Графиком функции у = sin x является синусоида Свойства функции: D(y) =R Периодическая (Т=2 ) Нечетная ( sin(-x)=-sin x) Нули функции: у=0, sin x=0 при х = n, n Z y=sin x
Слайд 3
тригонометрические функции Свойства функции у = sin x 5. Промежутки знакопостоянства: У >0 при х ( 0+2 n ; +2 n ) , n Z У
Промежутки знакопостоянства: У >0 при х ( 0+2 n ; +2 n ) , n Z У
Слайд 4
тригонометрические функции Свойства функции у= sin x 6. Промежутки монотонности: функция возрастает на промежутках вида: — /2 +2 n ; / 2+2 n n Z y = sin x
Слайд 5
тригонометрические функции Свойства функции у= sin x Промежутки монотонности: функция убывает на промежутках вида: /2 +2 n ; 3 / 2+2 n n Z y=sin x
Слайд 6
тригонометрические функции Свойства функции у = sin x 7. Точки экстремума: Х мах = / 2 +2 n , n Z Х м in = — / 2 +2 n , n Z y=sin x
Слайд 7
тригонометрические функции Свойства функции у = sin x 8 . Область значений: Е(у) = -1;1 y = sin x
Слайд 8
тригонометрические функции Преобразование графиков тригонометрических функций График функции у = f (x +в) получается из графика функции у = f(x) параллельным переносом на (-в) единиц вдоль оси абсцисс График функции у = f (x )+а получается из графика функции у = f(x) параллельным переносом на (а) единиц вдоль оси ординат
Слайд 9
тригонометрические функции Преобразование графиков тригонометрических функций Постройте график Функции у = sin(x+ /4) вспомнить правила
Слайд 10
тригонометрические функции Преобразование графиков тригонометрических функций y =sin (x+ /4 ) Постройте график функции: y=sin (x — /6)
Слайд 11
тригонометрические функции Преобразование графиков тригонометрических функций y = sin x + Постройте график функции: y =sin (x — /6 )
Слайд 12
тригонометрические функции Преобразование графиков тригонометрических функций y= sin x + Постройте график функции: y=sin (x + /2) вспомнить правила
Слайд 13
тригонометрические функции Графиком функции у = cos x является косинусоида Перечислите свойства функции у = cos x sin(x+ /2)=cos x
Слайд 14
тригонометрические функции Преобразование графиков тригонометрических функций путем сжатия и растяжения График функции у = k f (x ) получается из графика функции у = f(x) путем его растяжения в k раз (при k>1) вдоль оси ординат График функции у = k f (x ) получается из графика функции у = f(x) путем его сжатия в k раз (при 0
Слайд 15
тригонометрические функции Преобразование графиков тригонометрических функций путем сжатия и растяжения y=sin2x y=sin4x Y=sin0. 5x вспомнить правила
5x вспомнить правила
Слайд 16
тригонометрические функции Преобразование графиков тригонометрических функций путем сжатия и растяжения График функции у = f (kx ) получается из графика функции у = f(x) путем его сжатия в k раз (при k>1) вдоль оси абсцисс График функции у = f (kx ) получается из графика функции у = f(x) путем его растяжения в k раз (при 0
Слайд 17
тригонометрические функции Преобразование графиков тригонометрических функций путем сжатия и растяжения y = cos2x y = cos 0.5x вспомнить правила
Слайд 18
тригонометрические функции Преобразование графиков тригонометрических функций путем сжатия и растяжения Графики функций у = -f (kx ) и у=- k f(x) получаются из графиков функций у = f(kx) и y= k f(x) соответственно путем их зеркального отображения относительно оси абсцисс синус – функция нечетная, поэтому sin(-kx) = — sin (kx) косинус –функция четная, значит cos(-kx) = cos(kx)
Слайд 19
тригонометрические функции Преобразование графиков тригонометрических функций путем сжатия и растяжения y = — sin3x y = sin3x вспомнить правила
Слайд 20
тригонометрические функции Преобразование графиков тригонометрических функций путем сжатия и растяжения y=2cosx y=-2cosx вспомнить правила
Слайд 21
тригонометрические функции Преобразование графиков тригонометрических функций путем сжатия и растяжения График функции у = f (kx+b ) получается из графика функции у = f(x) путем его параллельного переноса на (-в /k) единиц вдоль оси абсцисс и путем сжатия в k раз (при k>1) или растяжения в k раз ( при 0
Слайд 22
тригонометрические функции Преобразование графиков тригонометрических функций путем сжатия и растяжения Y= cos(2x+ /3) y=cos(x+ /6) y= cos(2x+ /3) y= cos(2(x+ /6)) y= cos(2x+ /3) y= cos(2(x+ /6)) Y= cos(2x+ /3) y=cos2x вспомнить правила
Слайд 23
тригонометрические функции Для любознательных… Посмотрите как выглядят графики некоторых других триг. функций : y = 1 / cos x или y=sec x ( читается секонс) y = cosec x или y= 1/ sin x читается косеконс
функций : y = 1 / cos x или y=sec x ( читается секонс) y = cosec x или y= 1/ sin x читается косеконс
По теме: методические разработки, презентации и конспекты
ЦОР «Преобразование графиков тригонометрических функций» 10-11 классы
Раздел учебной программы:«Тригонометрические функции».Тип урока:цифровой образовательный ресурс комбинированного урока алгебры. По форме изложения материала:Комбинированный (универсальный) ЦОР со…
Методическая разработка урока по математике:«Преобразование графиков тригонометрических функций»
Методическая разработка урока по математике: «Преобразование графиков тригонометрических функций» для учащихся десятого класса. Урок сопровождается презентацией….
Эффективное использование интерактивной доски при построении графиков тригонометрических функций
Презентация рассказывает о возможностях интерактивной доски Interwrite…
Преобразования графиков тригонометрических функций в среде Microsoft Excel.
 Свойства функций.
Свойства функций.Интегрированный (математика+информатика) урок. Цель урока: актуализация знаний и навыков учащихся по темам «Графики тригонометрических функций. Свойства функций». Развитие навыка применять знания в но…
Преобразования графиков тригонометрических функций в среде Microsoft Excel. Свойства функций.
Интегрированный (математика+информатика) урок. Цель урока: актуализация знаний и навыков учащихся по темам «Графики тригонометрических функций. Свойства функций». Развитие навыка применять знания в но…
Преобразования графиков тригонометрических функций в среде Microsoft Excel. Свойства функций.
Интегрированный (математика+информатика) урок. Цель урока: актуализация знаний и навыков учащихся по темам «Графики тригонометрических функций. Свойства функций». Развитие навыка применять знания в но…
Презентация к уроку по теме: «Графики тригонометрических функций. Их преобразование. Построение графиков в компьютерной программе GeoGebra»
Интегрированный урок математики и информатики. ..
..
Поделиться:
Синусоидальный график с преобразованиями
Стандартная форма функции синуса составляет Y = A SIN ( B x + C ) + D
.
, где A , B , C и D — параметры
(A) Предсказать, как будет выглядеть график для следующих функций:
1. а) y = 10 sin (x) b) y = -10 sin (x)
2. a) y = sin (10x) b) y = sin (-10x)
3. a) y = sin (x -10) b) y = sin (x + 10)
4.
(B) С помощью графического калькулятора нарисуйте графики от x = -2Π до x = 2Π:
1. y = 10 sin (x) 3. y = sin (x — 10)
2. y = sin (10x) 4. y = sin (x) + 10
(C) Что вы заметили по сравнению с родительской функцией y = sin(x)
1. Максимальное и минимальное значения были увеличены с 1 и -1 до 10 и -10 соответственно (амплитуда)
2. Синусоидальная кривая повторяется через более короткий промежуток времени (период)
3. Синусоида была преобразована по горизонтали вправо (фазовый сдвиг)
4.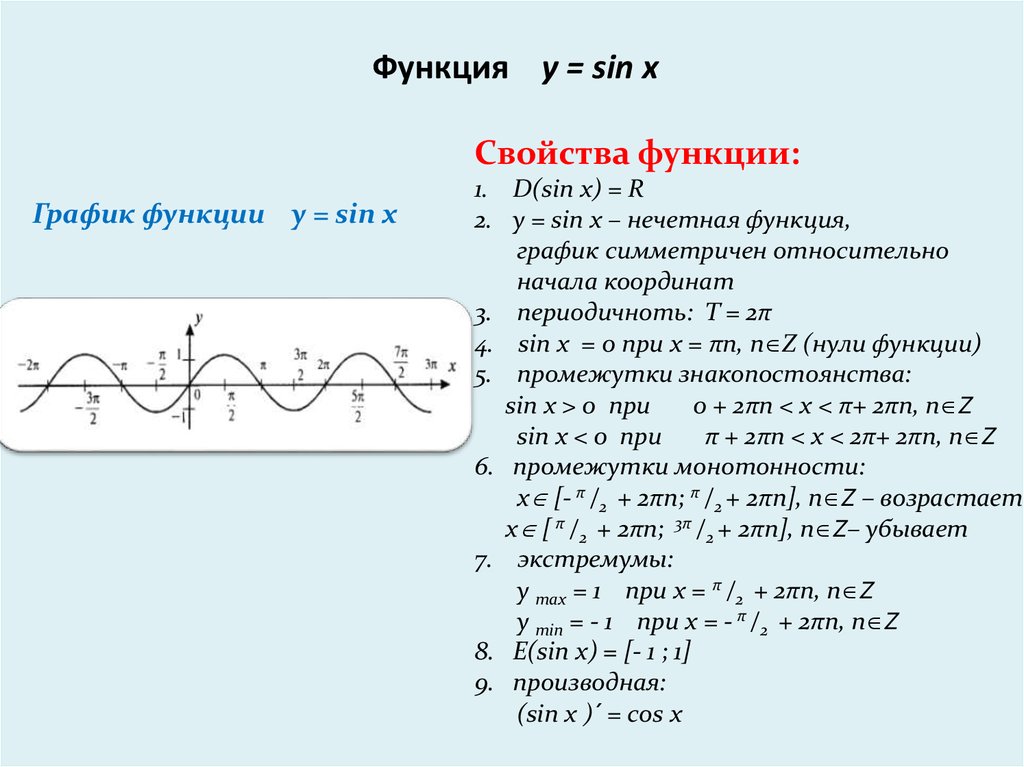 Синусоида смещена вверх на 10 (вертикальный перевод)
Синусоида смещена вверх на 10 (вертикальный перевод)
(D) Используя эскиз графического калькулятора от x = -2Π до x = 2Π, нарисуйте графики:
1. y = -10 sin (x) 3.y = sin (x +10)
2. y = sin (-10x) 4. y = sin (x) — 10
(E) Что вы заметили для каждой по сравнению с родительской функцией y = sin(x)
1. Максимальные и минимальные значения были растянуты от 1 и -1 до 10 и -10 соответственно (амплитуда), и график был отражен по оси X
2. Синусоидальная кривая повторяется через более короткий промежуток времени (период), и график отражается по оси x
3.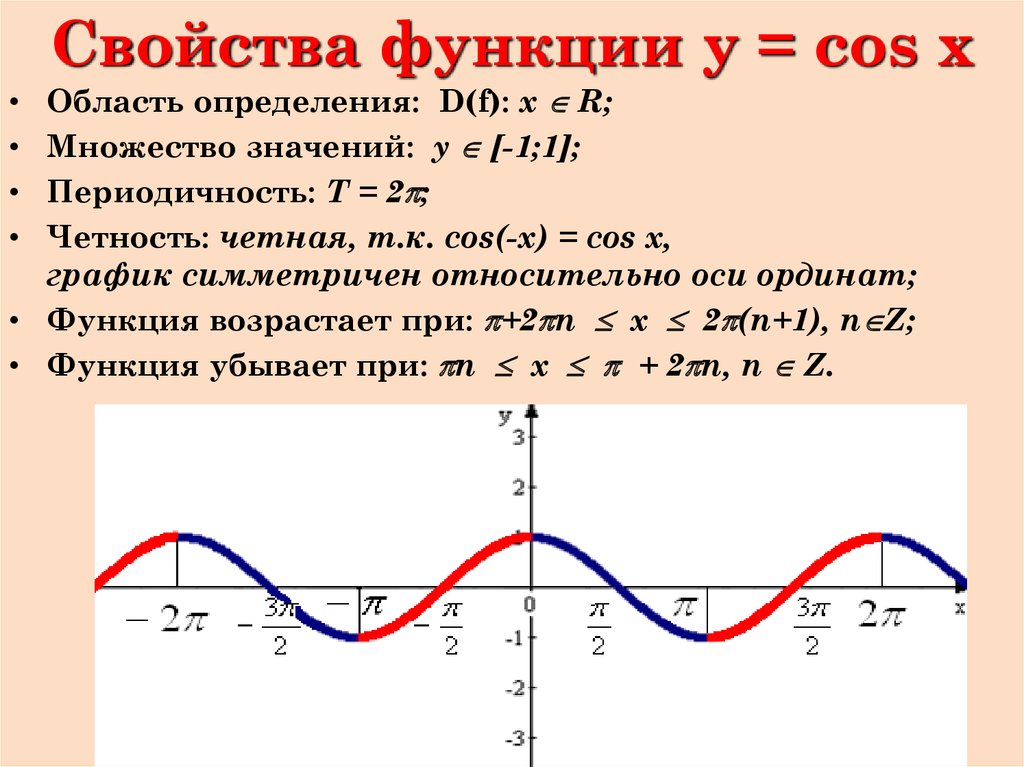 Синусоида была преобразована по горизонтали влево (фазовый сдвиг)
Синусоида была преобразована по горизонтали влево (фазовый сдвиг)
4. Синусоида смещена вверх на 10 (вертикальный перевод)
(F) Что, если хотя бы одно из ваших предсказаний окажется верным?
Надеюсь, учащиеся вспомнят предыдущие знания о других преобразованиях функций, таких как линейные и квадратичные функции. Предсказания учащихся могут быть точными в том, как график будет выглядеть визуально, однако, когда они обнаружат в ходе выполнения задания, те же самые преобразования, которые мы изучали ранее, означают разные вещи для синусоидальной функции, а также других тригонометрических функций.
(G) Сделать предположение, подробно описывающее преобразования графика синусоидальной функции, когда:
1. a ≠ 1 Когда a > 1. график растягивается по вертикали. Максимальное и минимальное значения расходятся дальше друг от друга. Когда a < 1, график сжимается по вертикали. Максимальное и минимальное значения ближе друг к другу.
Максимальное и минимальное значения ближе друг к другу.
2. b ≠ 1 Когда b > 1 время, необходимое для совершения одного оборота, меньше 2Π , а когда b < 1, время, необходимое для совершения одного оборота, больше 2Π
3. c ≠ 0 Если c не равно 0, график будет смещаться по горизонтали.
4. d ≠ 0 Когда d > 0, график будет перемещен вертикально вверх. При d < 0 график будет смещен вертикально вниз.
(H) Выберите три значения помимо 0,1,10 или -10, чтобы проверить свою гипотезу
Студент может выбрать любое число и получить аналогичные наблюдения за преобразованиями.
(I) Справились ли ваши предположения с тремя новыми значениями?
Они должны оставаться верными для любого значения.
(J) A,b,c,d — все параметры, влияющие на график y=sin (x).
1. A — амплитуда графика. В родительской функции A=1. Амплитуда равна половине расстояния от максимума до минимума. Поскольку амплитуда измеряет расстояние, она не может быть отрицательной, поэтому амплитуда синусоидального графика равна |A|.
а. Каковы максимальная и минимальная точки для синусоидального графика с A = 5? Макс= 5 Мин= -5
б. Каковы максимальные и минимальные точки для синусоидального графика с A = -4? Макс= 4 Мин= -4
2. b, используется для нахождения периода функции. Период функции – это время, за которое совершается один полный оборот. При y=sin(x) график начал повторяться после 2Π. Период функции находится по
а. Каков период для y = sin (2x)? Период = Π
б. Каков период для y = sin (x)? Период = 8Π
3. c, используется для нахождения горизонтального сдвига или фазового сдвига .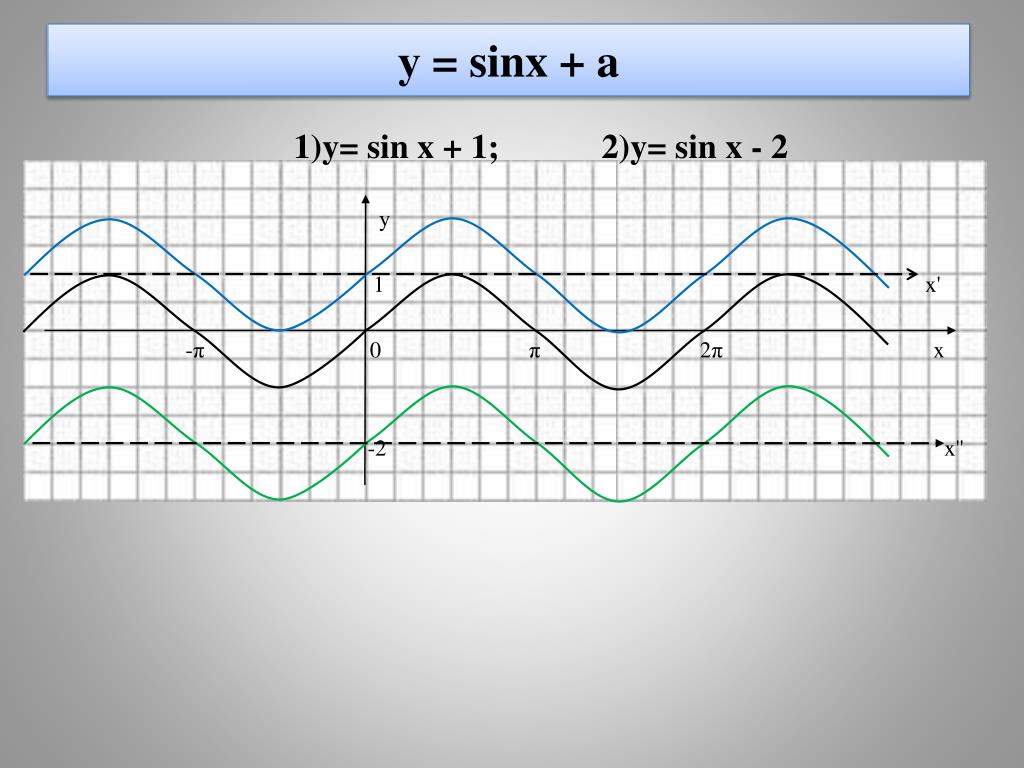 Фазовый сдвиг определяется как .
Фазовый сдвиг определяется как .
а. Для чего нужен фазовый сдвиг? Фазовый сдвиг = Π вправо
б. Для чего нужен фазовый сдвиг? Фазовый сдвиг =
4. d представляет вертикальное преобразование. Когда d > 0, график смещается вертикально вверх, а когда d < 0 — вертикально вниз.
а. Каково вертикальное преобразование для y = sin (x) -4? Вертикально: 4 вниз
б. Каково вертикальное преобразование для y = sin (3x) + 11? Вертикально: 11 вверх
5. Когда y = sin (x) преобразуется по вертикали, линия, равноудаленная от точек max и min, называется средней линией . Что происходит со средней линией, когда функция перемещается вверх или вниз?
Вертикальное перемещение определяет среднюю линию. Когда d = 0, средняя линия проходит по оси y = 0 или по оси x. Когда функция имеет вертикальный перевод, средняя линия перемещается вверх или вниз в зависимости от перевода.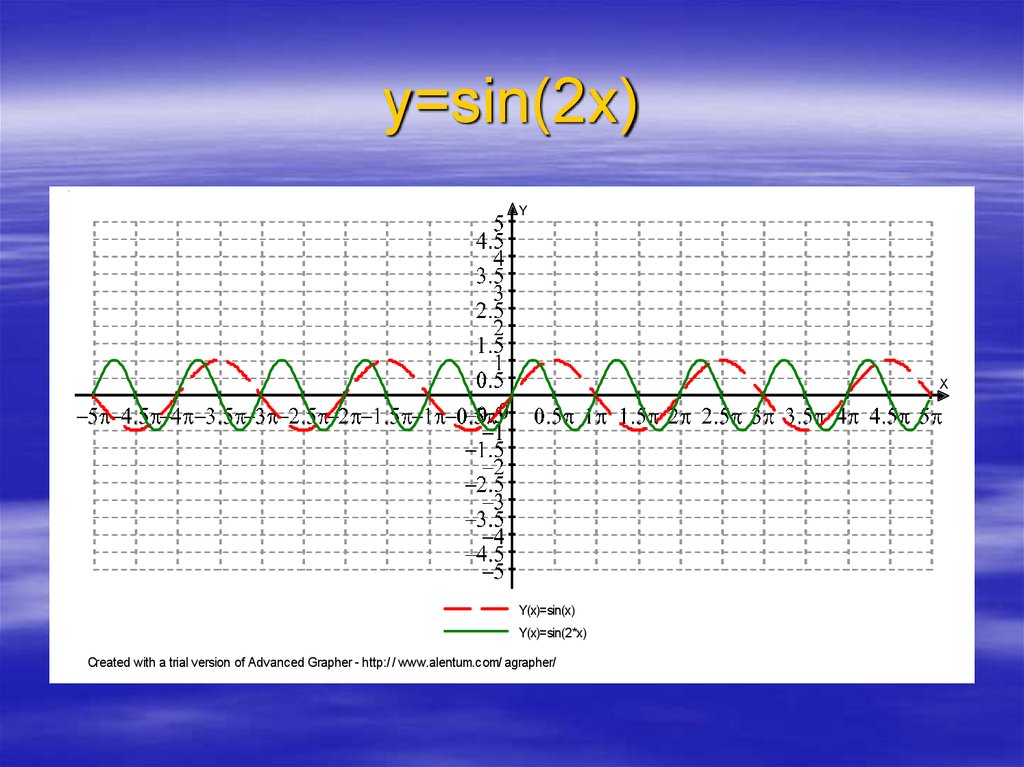
Сводка:
Сделайте следующие предсказания:
Что, если и a, и b не равны 1 или 0? а и в? а и г?
1. Функция имела бы другую амплитуду и период не был бы равен 2П.
2. Функция будет иметь другую амплитуду и сдвиг по горизонтали или фазе.
3. Функция будет иметь другую амплитуду и вертикальное смещение, поэтому средняя линия не будет находиться на y = 0 (ось x)
Повлияет ли изменение одного параметра на другой? Все или только некоторые?
Единственным преобразованием, на которое влияют другие параметры, является фазовый сдвиг. Поскольку фазовый сдвиг зависит как от c, так и от b, даже без изменения c, при изменении b фазовый сдвиг также будет другим.
График с использованием графического калькулятора:
y = -4 sin (-4x) y = -3 sin (x -3) y = -2 sin (x) -2
Каковы результаты?
Произошли ожидаемые нами преобразования.
Подведем итог:
1. Описать преобразования графика y = 2 sin (3x+Π)-10.
Функция синуса будет иметь амплитуду 2.
Период будет .
Фазовый сдвиг влево.
Наконец, среднюю линию можно найти при y = -10.
Другая информация, которую мы можем вывести:
Максимальное значение будет равно -8, а минимальное значение -12.
2. Описать преобразования графа .
Функция косинуса будет иметь амплитуду 6.
Будет отражение по оси x.
Период будет равен 6Π.
Фазовый сдвиг вправо на 8П.
Наконец, среднюю линию можно найти при y = 1,
Другая информация, которую мы можем вывести:
Максимальное значение будет равно 7, а минимальное -5.
Производная sin3x с формулой, правилом произведения и первым принципом
Производная sin3x равна 3cos3x. Это часть Дифференциации, которая является подтемой исчисления. В производной sin3x 3x — чисто алгебраическая функция, тогда как sin[f(x)] — тригонометрическая функция. Вместе они составляют составную функцию. Чтобы найти производную сложной функции, мы находим производную внешней функции, а затем умножаем ее на производную внутренней функции. В этой математической статье мы узнаем, как дифференцировать sin3x, используя различные правила дифференцирования, такие как первый принцип производной и правило произведения.
Производная от Sin3x
Как упоминалось выше, sin3x является составной функцией двух элементарных функций, а именно, алгебраической функции и тригонометрической функции. 3x — это чисто алгебраическая функция, а sin — тригонометрическая функция. Производную от sin3x можно производить по частям, т.е. дифференцировать по частям, так как это составная функция двух элементарных функций.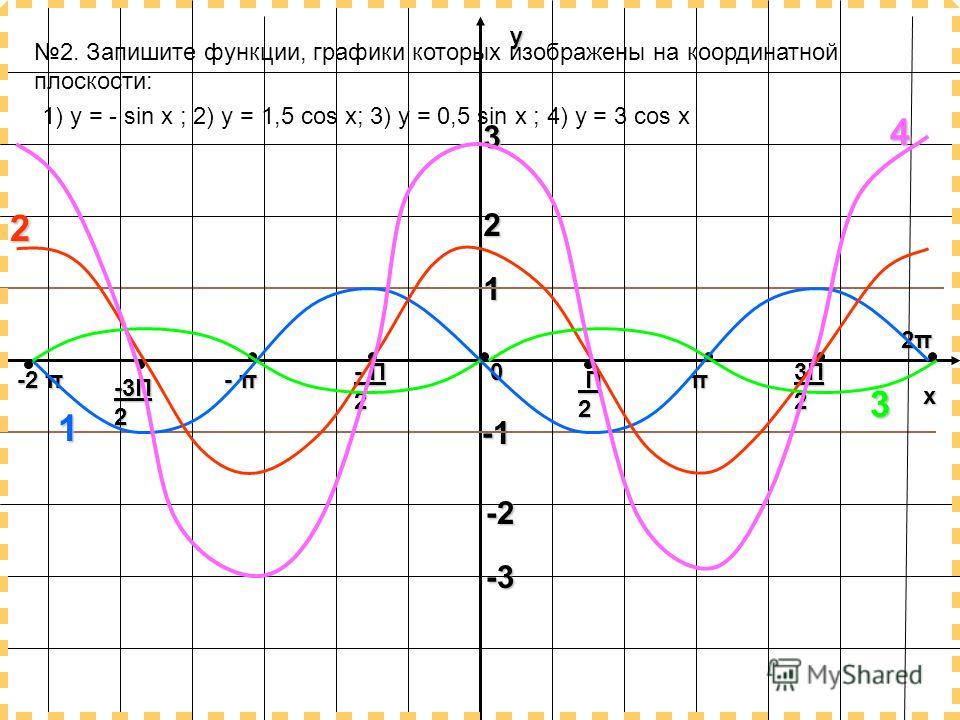 Здесь sin[f(x)] — внешняя функция, а 3x — внутренняя функция. Мы можем легко найти производную производных алгебраических функций и производных тригонометрических функций. Производные этих двух функций можно вычислить отдельно, как показано ниже:
Здесь sin[f(x)] — внешняя функция, а 3x — внутренняя функция. Мы можем легко найти производную производных алгебраических функций и производных тригонометрических функций. Производные этих двух функций можно вычислить отдельно, как показано ниже:
Производная от 3x
Производная переменной по той же переменной равна единице. Здесь 3 является константой и останется такой, какая она есть.
Таким образом, \({d\over{dx}}3x=3\)
Доказательство
Согласно определению производной, дифференцирование \((x)=3x\) по \ (x\) можно записать в форме с ограниченными операциями.
\(f'(x)={dy\over{dx}}=\lim _{h{\rightarrow}0}{f(x+h)–f(x)\over{h}}\)
\(f(x)=3x\)
\(f(x+h)=3(x+h)\)
\(f(x+h)=3x+3h\)
\(f(x+h)–f(x) =3x+3h-3x=3h\)
\({f(x+h)–f(x)\over{h}}=3\)
\(\lim _{h{\rightarrow}0 }{f(x+h)–f(x)\over{h}}=\lim _{h{\rightarrow}0}{3}\)
\(f'(x)={dy\over {dx}}=3\)
Точно так же у нас есть производная от \(sinx\), которая является тригонометрической функцией.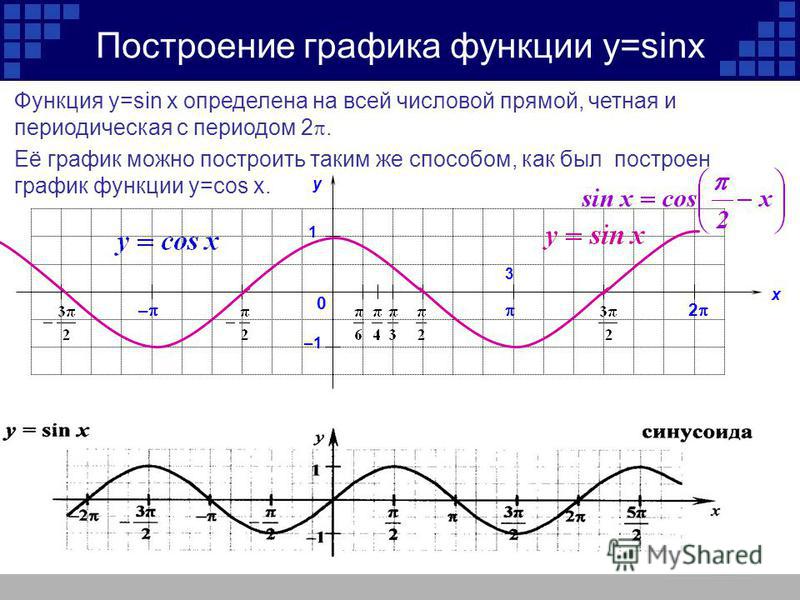
Производная sinx
Сначала рассмотрим простой \(sinx\).
Если \(f(x) = sinx\) , найти \(f'(x)\)
\(f'(x)={dy\over{dx}}=\lim _{h{\rightarrow}0}{f(x+h)–f(x)\over{h}}\)
\(f(x)=sinx\)
\(f(x+h)=sin(x+h)\)
\(f(x+h)–f(x)= sin(x+ h) – sin(x) = sinxch + cosxsinh – sinx\)
\(= sinx(ch-1) + cosxsinh\)
\({f(x+h) – f(x)\over{h }}={ sinx(cosh-1) + cosxsinh\over{h}}\)
\(\lim _{h{\rightarrow}0}{f(x+h) –f(x)\over{ h}} = \lim _{h{\rightarrow}0} {sinx(cosh-1) + cosxsinh\over{h}}\)
\(\lim _{h{\rightarrow}0}{f( x+h) –f(x)\over{h}} = \lim _{h{\rightarrow}0} {sinx(cosh-1)\over{h}} + \lim _{h{\rightarrow}} 0} {cosxsinh\over{h}}\)
\(= sinx \lim _{h{\rightarrow}0} {(cosh-1)\over{h}} + cosx \lim _{h{\rightarrow}0} {sinh\over{h}} \)
Поместите h = 0 в первый предел
\(sinx \lim _{h{\rightarrow}0} {(cosh-1)\over{h}} = sinx\times0 = 0\)
Используя Правило больниц L о втором пределе
\(\lim _ {h{\rightarrow}0}{f(x+h) –f(x)\over{h}} = cosx \lim _{h{\rightarrow} }0} {{d\over{dh}}sinh\over{{d\over{dh}}h}}\)
\(\lim _{h{\rightarrow}0}{f(x+h ) –f(x)\over{h}} = cosx \lim _{h{\rightarrow}0} {cosh\over{1}}\)
\(\lim _{h{\rightarrow}0}{f(x+h) –f(x)\over{h}} = cosx \times1 = cosx\)
\(f'(x) ={dy\over{dx}} = {d(sinx)\over{dx}} = cosx\)
Но в \(sin3x\) простое \(x\) заменяется на \(3x\) . Следовательно, применим правила дифференцирования композита. Самый простой способ — применить цепное правило. Цепное правило помогает нам дифференцировать составные функции, количество функций, составляющих композицию, определяет, сколько шагов дифференцирования необходимо. Цепное правило гласит, что
Следовательно, применим правила дифференцирования композита. Самый простой способ — применить цепное правило. Цепное правило помогает нам дифференцировать составные функции, количество функций, составляющих композицию, определяет, сколько шагов дифференцирования необходимо. Цепное правило гласит, что
\({d\over{dx}}f(g(x)) = f'(g(x))⋅g'(x)\)
\({d\over{dx}}f[ g(h(x))] = f'(g(h(x))⋅g'(h(x))h'(x)\)
\(g\) и \(h\), составляют составную функцию \(f(x)\), необходимо учитывать производные \(g′\) и \(h′\) при дифференцировании \(f(x)\).
Теперь давайте посмотрим на доказательства, используя первый принцип производной и цепное правило.
Производная sin3x по первому принципу
Производная по первому принципу относится к использованию алгебры для нахождения общего выражения для наклона кривой. Он также известен как дельта-метод. Производная является мерой мгновенной скорости изменения, которая равна:
\(f'(x)={dy\over{dx}}=\lim _{h{\rightarrow}0}{f(x+h)–f(x)\over{h}}\)
Вот пошаговое объяснение:
Пусть \(y = 3x\)
Пусть \(\delta{y}\) будет приращением в \(y, соответствующим приращению \(\) \дельта{х}\) в \(х\).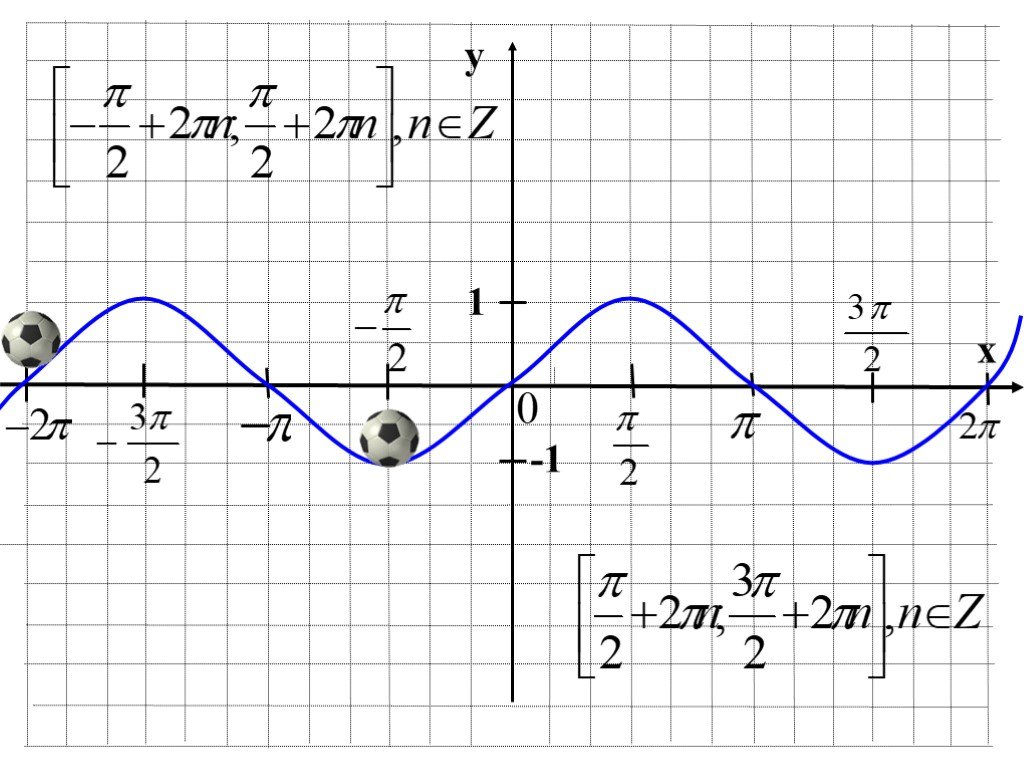
Тогда \(y+\delta{y}=sin3(x+\delta{x})\)
\(\delta{y}=sin(3x+3\delta{x})-sin3x\)
\(\frac{\delta{y}}{\delta{x}}=\frac{sin(3x+3\delta{x}) -sin3x}{\delta{x}}\)
\( \lim_{x\to0}\frac{\delta{y}}{\delta{x}}=\lim_{x\to0}\frac{sin(3x+3\delta{x}) -sin3x}{\ дельта{х}}\)
\(\frac{dy}{dx}=\lim_{x\to0}\frac{\delta{y}}{\delta{x}}=\lim_{x\to0}\frac{sin(3x +3\delta{x})-sin3x}{\delta{x}}\)
\(\frac{dy}{dx}=\lim_{x\to0}\frac{2cos(3x+\delta{x) })sin{\delta}x}{\delta{x}}\)
\(\frac{dy}{dx}=3\lim_{x\to0}\frac{2cos(3x+\delta{x}) )sin{\delta}x}{\delta{x}}\)
\(\frac{dy}{dx}=3cos3x\)
Следовательно, производная \(sin3x\) по первому принципу равна \(3cos3x\).
Производная от sin3x с использованием метода цепного правила
Цепное правило гласит, что мы должны дифференцировать выражение, как если бы оно было просто через x, чтобы выполнить дифференцирование \(sin(3x)\), до тех пор, пока мы умножаем этот результат на производную того, что выражение на самом деле в терминах (в данном случае производной от \(3x\)).
Назовем функцию с аргументом sin \(g(x)\), которая обозначает функцию с формой \(sin(x)\), но с другой функцией \(x(3x)\) в качестве угол вместо \(x\) как угол.
\(F'(x) = f'(g(x)).g'(x)\)
\(g(x) = 3x ⇒ g'(x) = 3\)
\( = f'(g(x))(3)\)
\(f(g(x)) = sin(3x) ⇒ f'(g(x)) = cos(3x)\)
\( = (cos(3x)).(3)\)
\(= 3cos(3x)\)
n-я производная от sin3x
Вот как мы вычисляем n-ю производную от \(sin3x\)
\( y=sin3x\)
Дифференцировать по \(x\), w get,
\(\frac{dy}{dx}=\frac{d}{dx}(sin3x)=3cos3x\)
Снова продифференцируем по \(‘x’\), получим 92x\)
Мы надеемся, что приведенная выше статья поможет вам понять и подготовиться к экзамену. Оставайтесь с нами в приложении Testbook, чтобы получать больше обновлений по связанным с математикой темам и другим подобным предметам. Кроме того, обратитесь к серии тестов, доступных для проверки ваших знаний по нескольким экзаменам.
Часто задаваемые вопросы о производной Sin3x
В.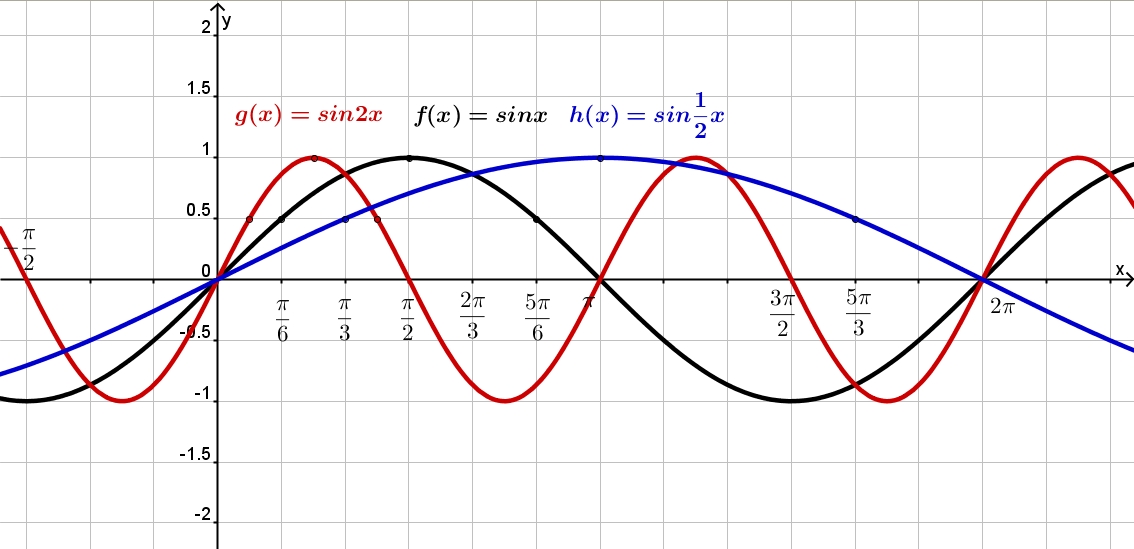

 5 класс.
5 класс.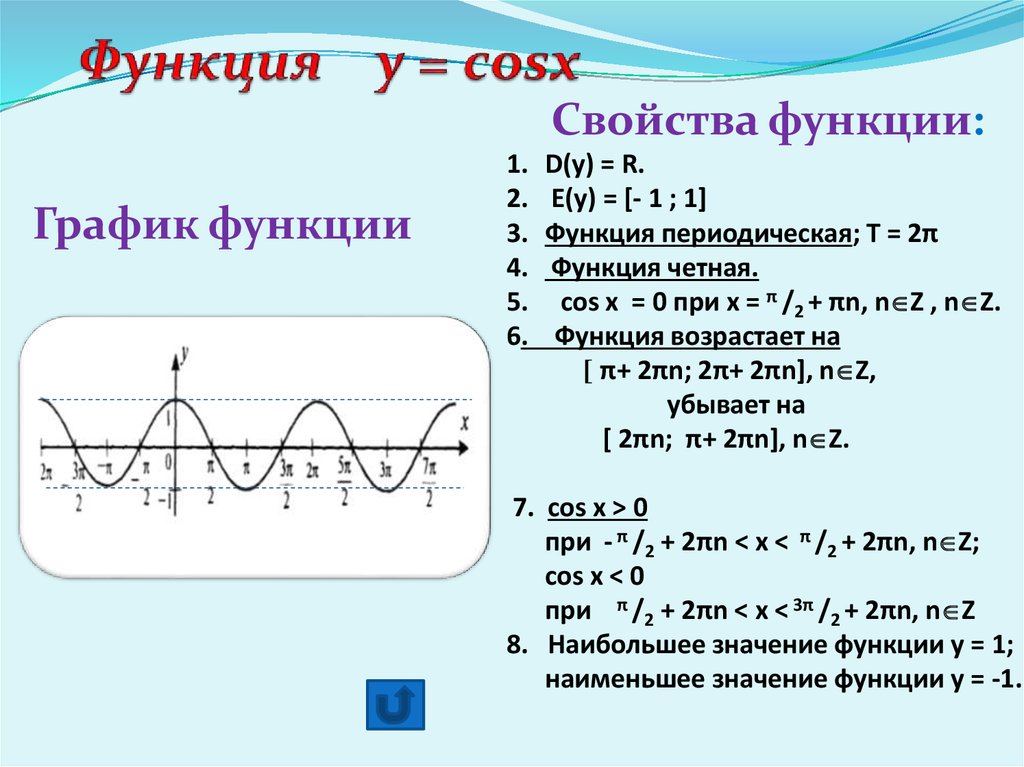 10 — 11 класс.
10 — 11 класс.