Y x2 1 функция: Постройте график функции y = x^2 – 1

Содержание

Функции y=x2 и y=x3 и их графики

Урок 23. Алгебра 7 класс

На этом уроке мы говорим о функциях y=x2и y=x3. Строим их графики. Выясняем некоторые свойства этих функций.

Конспект урока «Функции y=x2 и y=x3 и их графики»

Вопросы занятия:

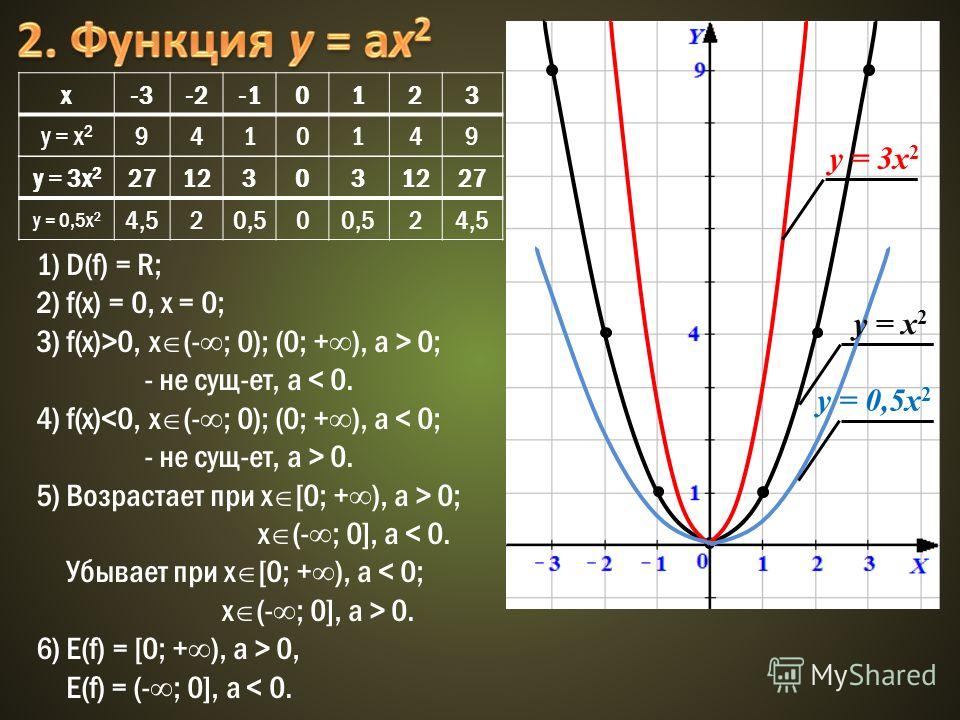
· рассмотреть функцию y = x², её свойства и график;

· рассмотреть функцию y = х³, её свойства и график.

Материал урока

На одном из предыдущих уроков мы с вами познакомились с линейной функцией, которую можно задать формулой вида:

Также вспомним, что графиком линейной функции является прямая.

На этом уроке мы рассмотрим функции:

А точнее, мы научимся строить графики этих функций и выясним некоторые их свойства.

Начнём с того, что выразим формулой зависимость площади квадрата от длины его стороны.

Таким образом, зависимость площади квадрата от его стороны является примером функции.

Давайте построим график этой функции.

Составим таблицу значений x, y.

Далее полученные точки изобразим на координатной плоскости и проведём через них плавную линию.

Обратите внимание, что этот график неограниченно продолжается вверх справа и слева от оси игрек.

Теперь выясним некоторые свойства функции y = x².

Из последнего свойства графика следует, что точки графика, имеющие противоположные абсциссы, симметричны относительно оси игрек.

Теперь давайте выразим формулой зависимость объёма куба от длины его ребра.

Если мы будем менять длину ребра, то и его объём будет меняться.

Зависимость объёма куба от длины его ребра является примером функции.

Построим график этой функции.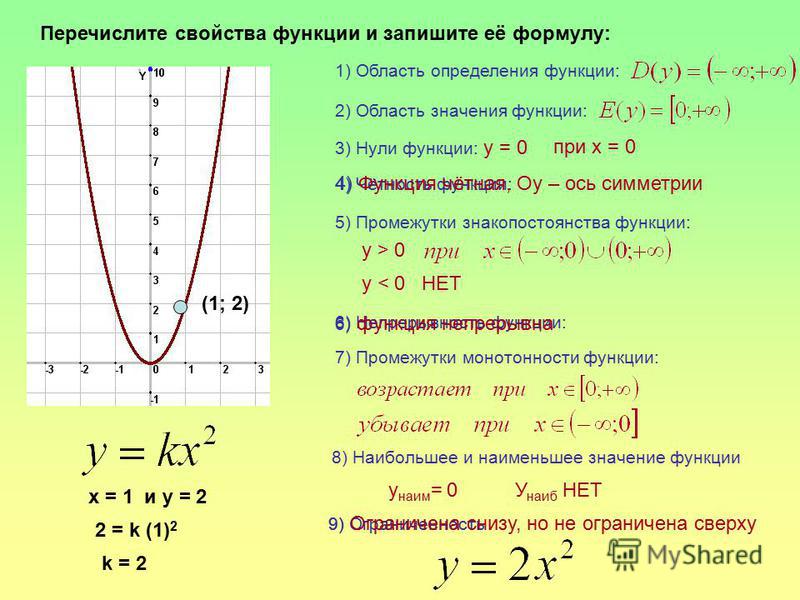

Для этого придадим несколько значений аргументу икс и вычислим соответствующие значения функции.

Изобразим точки с полученными координатами на координатной плоскости и проведём через них плавную линию.

Обратите внимание, что этот график можно неограниченно продолжать справа от оси игрек вверх и слева от оси игрек вниз.

Поговорим о свойствах функции игрек равняется икс в кубе.

Следовательно, точки графика, которые имеют противоположные абсциссы, расположены симметрично относительно начала координат.

В повседневной жизни представление о параболе дают нам, например, траектории прыжков животных, радуга. Тросы висячего моста напоминают нам параболы.

Также параболу часто можно встретить в архитектуре.

Предыдущий урок 22 Умножение одночленов. Возведение одночлена в степень

Следующий урок 24 Многочлен и его стандартный вид

Получите полный комплект видеоуроков, тестов и презентаций Алгебра 7 класс

Чтобы добавить комментарий зарегистрируйтесь или войдите на сайт

Y x2 3x график.

Постройте график функции y=

Построение графиков функций, содержащих модули, обычно вызывает немалые затруднения у школьников. Однако, все не так плохо. Достаточно запомнить несколько алгоритмов решения таких задач, и вы сможете без труда построить график даже самой на вид сложной функции. Давайте разберемся, что же это за алгоритмы.

1. Построение графика функции y = |f(x)|

Заметим, что множество значений функций y = |f(x)| : y ≥ 0. Таким образом, графики таких функций всегда расположены полностью в верхней полуплоскости.

Построение графика функции y = |f(x)| состоит из следующих простых четырех этапов.

1) Построить аккуратно и внимательно график функции y = f(x).

2) Оставить без изменения все точки графика, которые находятся выше оси 0x или на ней.

3) Часть графика, которая лежит ниже оси 0x, отобразить симметрично относительно оси 0x.

Пример 1. Изобразить график функции y = |x 2 – 4x + 3|

1) Строим график функции y = x 2 – 4x + 3.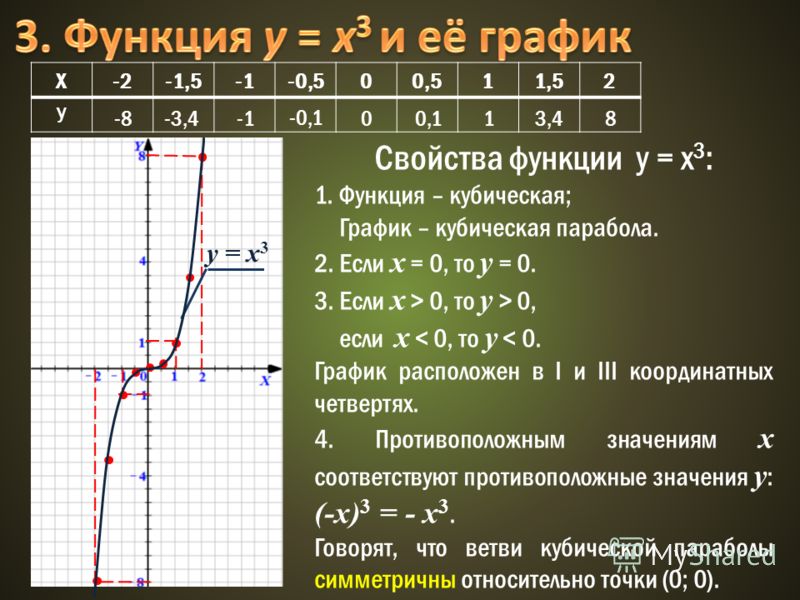 Очевидно, что график данной функции – парабола. Найдем координаты всех точек пересечения параболы с осями координат и координаты вершины параболы.

x 2 – 4x + 3 = 0.

x 1 = 3, x 2 = 1.

Следовательно, парабола пересекает ось 0x в точках (3, 0) и (1, 0).

y = 0 2 – 4 · 0 + 3 = 3.

Следовательно, парабола пересекает ось 0y в точке (0, 3).

Координаты вершины параболы:

x в = -(-4/2) = 2, y в = 2 2 – 4 · 2 + 3 = -1.

Следовательно, точка (2, -1) является вершиной данной параболы.

Рисуем параболу, используя полученные данные (рис. 1)

2) Часть графика, лежащую ниже оси 0x, отображаем симметрично относительно оси 0x.

3) Получаем график исходной функции (рис. 2 , изображен пунктиром).

2. Построение графика функции y = f(|x|)

Заметим, что функции вида y = f(|x|) являются четными:

y(-x) = f(|-x|) = f(|x|) = y(x). Значит, графики таких функций симметричны относительно оси 0y.

Построение графика функции y = f(|x|) состоит из следующей несложной цепочки действий.

1) Построить график функции y = f(x).

2) Оставить ту часть графика, для которой x ≥ 0, то есть часть графика, расположенную в правой полуплоскости.

3) Отобразить указанную в пункте (2) часть графика симметрично оси 0y.

4) В качестве окончательного графика выделить объединение кривых, полученных в пунктах (2) и (3).

Пример 2. Изобразить график функции y = x 2 – 4 · |x| + 3

Так как x 2 = |x| 2 , то исходную функцию можно переписать в следующем виде: y = |x| 2 – 4 · |x| + 3. А теперь можем применять предложенный выше алгоритм.

1) Строим аккуратно и внимательно график функции y = x 2 – 4 · x + 3 (см. также рис. 1 ).

2) Оставляем ту часть графика, для которой x ≥ 0, то есть часть графика, расположенную в правой полуплоскости.

3) Отображаем правую часть графика симметрично оси 0y.

(рис. 3) .

Пример 3. Изобразить график функции y = log 2 |x|

Применяем схему, данную выше.

1) Строим график функции y = log 2 x (рис.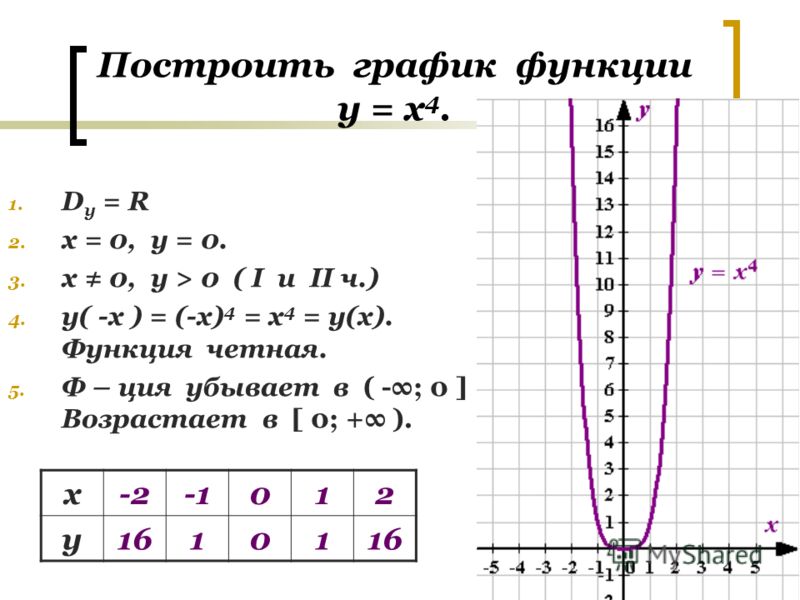 4) .

3. Построение графика функции y = |f(|x|)|

Заметим, что функции вида y = |f(|x|)| тоже являются четными. Действительно, y(-x) = y = |f(|-x|)| = y = |f(|x|)| = y(x), и поэтому, их графики симметричны относительно оси 0y. Множество значений таких функций: y ≥ 0. Значит, графики таких функций расположены полностью в верхней полуплоскости.

Чтобы построить график функции y = |f(|x|)|, необходимо:

1) Построить аккуратно график функции y = f(|x|).

2) Оставить без изменений ту часть графика, которая находится выше оси 0x или на ней.

3) Часть графика, расположенную ниже оси 0x, отобразить симметрично относительно оси 0x.

4) В качестве окончательного графика выделить объединение кривых, полученных в пунктах (2) и (3).

Пример 4. Изобразить график функции y = |-x 2 + 2|x| – 1|.

1) Заметим, что x 2 = |x| 2 . Значит, вместо исходной функции y = -x 2 + 2|x| – 1

можно использовать функцию y = -|x| 2 + 2|x| – 1, так как их графики совпадают.

Строим график y = -|x| 2 + 2|x| – 1. Для этого применяем алгоритм 2.

a) Строим график функции y = -x 2 + 2x – 1 (рис. 6) .

b) Оставляем ту часть графика, которая расположена в правой полуплоскости.

c) Отображаем полученную часть графика симметрично оси 0y.

d) Полученный график изображен на рисунке пунктиром (рис. 7) .

2) Выше оси 0х точек нет, точки на оси 0х оставляем без изменения.

3) Часть графика, расположенную ниже оси 0x, отображаем симметрично относительно 0x.

4) Полученный график изображен на рисунке пунктиром (рис. 8) .

Пример 5. Построить график функции y = |(2|x| – 4) / (|x| + 3)|

1) Сначала необходимо построить график функции y = (2|x| – 4) / (|x| + 3). Для этого возвращаемся к алгоритму 2.

a) Аккуратно строим график функции y = (2x – 4) / (x + 3) (рис. 9) .

Заметим, что данная функция является дробно-линейной и ее график есть гипербола. Для построения кривой сначала необходимо найти асимптоты графика.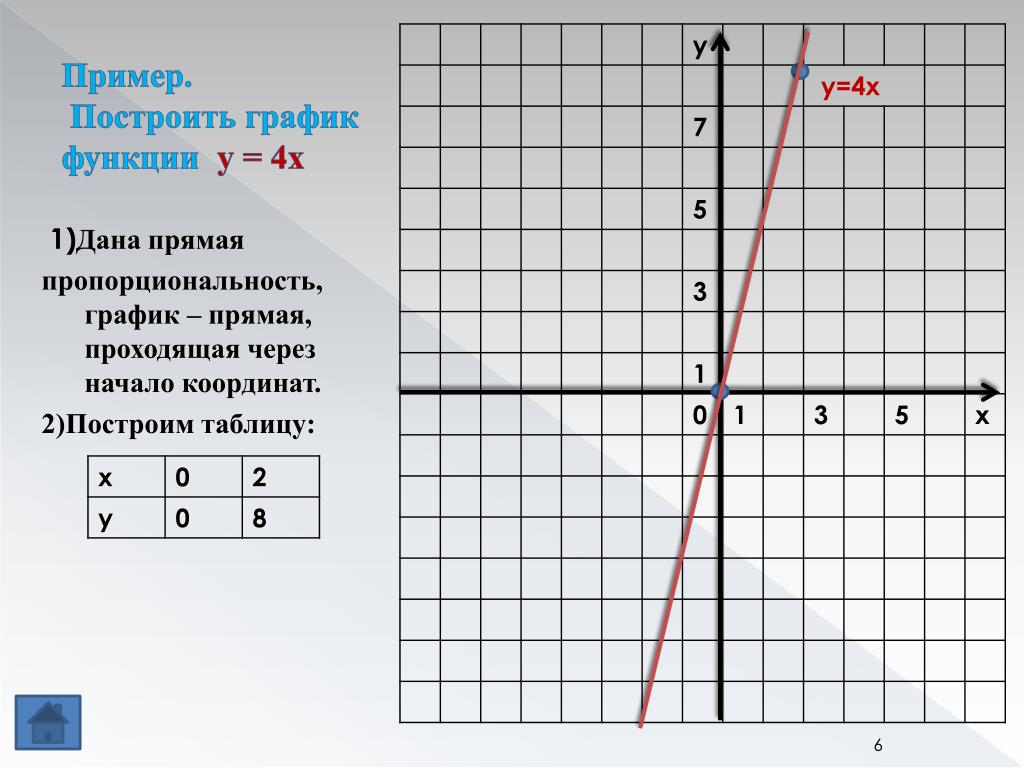

2 называется квадратичной функцией. Графиком квадратичной функции является парабола. Общий вид параболы представлен на рисунке ниже.

Квадратичная функция

Рис 1. Общий вид параболы

Как видно из графика, он симметричен относительно оси Оу. Ось Оу называется осью симметрии параболы. Это значит, что если провести на графике прямую параллельную оси Ох выше это оси. То она пересечет параболу в двух точках. Расстояние от этих точек до оси Оу будет одинаковым.

Ось симметрии разделяет график параболы как бы на две части. Эти части называются ветвями параболы. А точка параболы которая лежит на оси симметрии называется вершиной параболы. То есть ось симметрии проходит через вершину параболы. Координаты этой точки (0;0).

Основные свойства квадратичной функции

1. При х =0, у=0, и у>0 при х0

2. Минимальное значение квадратичная функция достигает в своей вершине. Ymin при x=0; Следует также заметить, что максимального значения у функции не существует.

3. Функция убывает на промежутке (-∞;0] и возрастает на промежутке , потому что прямая y=kx будет совпадать с графиком y=|x-3|-|x+3| на данном участке. Этот вариант нам не подходит.

Если k будет меньше -2, то прямая y=kx с графиком y=|x-3|-|x+3| будет иметь одно пересечение.Этот вариант нам подходит.

Если k=0, то пересечений прямой y=kx с графиком y=|x-3|-|x+3| также будет одно.Этот вариант нам подходит.

Ответ: при k принадлежащей интервалу (-∞;-2)U}

Инвертирование функций с ограниченными областями

Определения / инвертирование графикаЯвляется ли обратная функция?Поиск обратныхРабочие примерыДоказательство обратных

Purplemath

График параболы не пройдет тест горизонтальной линии; существует множество горизонтальных линий, которые пересекают график дважды. Таким образом, обратная квадратичная функция параболы сама по себе не будет функцией.

Однако иногда необратимую функцию можно преобразовать в обратимую, ограничив область определения.

Содержание продолжается ниже

MathHelp.com

Обратные функции

В случае параболы, если мы используем только одну «сторону» или одну «половину» параболы, тогда график пройдет Горизонтальную линию Тест.

Найдите обратную функцию y = x ² + 1, x ≤ 0,

Единственная разница между этой функцией и предыдущей заключается в том, что домен может включать только отрицательную половину х — ось; то есть функция была ограничена только левой половиной параболы. Из-за этого ограничения график выглядит следующим образом:

Эта функция проходит тест горизонтальной линии, поэтому она будет иметь обратную функцию, которая также является функцией.

(к вашему сведению: почти каждый раз, когда они дают вам задачу, в которой они потрудились ограничить домен, они также почти всегда давали вам что-то, обратная функция которого также будет. Однако вы должны быть осторожны с алгебру и нарисуйте красивую картинку, потому что может потребоваться дополнительное усилие, чтобы показать, что обратная функция является функцией, и, по крайней мере, ограниченная область определения функции потребует ограниченного диапазона.

)
В этом случае, поскольку домен равен x ≤ 0, а диапазон (из графика) равен y ≥ 1, то обратный будет иметь домен x ≥ 1 и диапазон y . ≤ 0,
Я начинаю с решения для » x =»:
y = x ² + 1
y 9001 8 − 1 = х ²
Выяснив область определения и диапазон обратной функции, я знаю, что должен выбрать отрицательный знак для квадратного корня в моей обратной функции:
Теперь я поменяю местами x и y ; новое » y =» является обратным:
(Ограничение » x ≥ 1″ подтверждается тем фактом, что выражение x — 1 находится внутри квадратного корня. Единственный способ для квадратный корень должен быть определен для x — 1 ≥ 0.)
Итак, мой ответ:
обратное: y = — sqrt ( x — 1), x 9 0018 ≥ 1
эта обратная функция также является функцией
Если вы изучали обозначения функций, вы можете начать с f ( x ) вместо y . В этом случае запустите процесс инверсии, переименовав f ( x ) в y . Затем выполните обычную процедуру. Как только вы найдете обратное, переименуйте полученное y как f ⁻¹ ( x ). (Обычно проще работать с y .)
Предупреждение: запись обратной функции вводит в заблуждение; степень «минус один» в обозначении обратной функции означает «обратное значение исходной функции», а не «обратное значение выражения». Не путайте два.
Найдите обратное число f ( x ) = − sqrt ( x − 2), x ≥ 2. Определите, является ли обратное также функция, и найти домен и диапазон обратного.
Ограничение домена связано с тем, что x находится внутри квадратного корня. Обычно я не стал бы записывать « x ≥ 2», потому что знаю, что значения x меньше 2 дадут мне отрицательные значения внутри квадратного корня.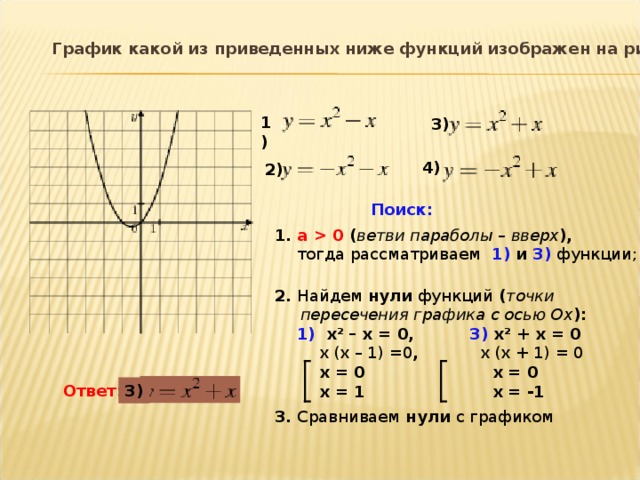 Но ограничение в данном случае полезно тем, что вместе с графиком оно поможет мне определить домен и диапазон на обратном:
Домен (указанный в инструкции по упражнению) x ≥ 2; диапазон (найденный из графика) равен y ≤ 0. Тогда областью обратного будет x ≤ 0; диапазон будет y ≥ 2.
Теперь мне нужно найти обратное:
y ² = x − 2
у ² + 2 = х
х ² + 2 = у
f ⁻¹ ( x ) = x ² + 2
График этой обратной функции представляет собой параболу, где я начал с половины (боковой) параболы. Так как я уже определился с областью и диапазоном — в частности, областью обратного является x ≤ 0 — я знаю, что мне нужно взять отрицательную половину параболы. Итак, мой ответ:
обратное: y = x ² + 2
обратная функция,
с доменом x ≤ 0
и диапазон y ≥ 2
Найдите обратное число f ( x ) = x ² − 3 x 90 018 + 2, x ≤ 1,5
С ограничением домена граф выглядит следующим образом:
Из того, что я знаю о графическом построении квадратичных уравнений, вершина находится в точке ( x , y ) = (1,5, −0,25), поэтому этот граф является левым. половина параболы. И эта половина параболы проходит тест горизонтальной линии, поэтому (ограниченная) функция обратима. Но как решить для обратного? Я начинаю как обычно:
f ( х ) = х ² — 3 х + 2
у = х ² − 3 x + 2
Теперь я решаю » x =» с помощью квадратичной формулы:
Так как x ≤ 1,5, то мне нужен *отрицательный* квадратный корень:
Затем, после переименования, обратное значение определяется как:
Да, иногда инверсия может быть грязной.
URL: https://www.purplemath.com/modules/invrsfcn4.htm
Страница 1Страница 2Страница 3Страница 5Страница 6
Обратная квадратичная функция | ChiliMath
Здесь мы хотим найти обратную функцию , из чего следует, что обратная ДОЛЖНА быть функцией. В противном случае мы получили обратную функцию, не являющуюся функцией.
Не всем функциям естественно «повезло» иметь обратные функции. Это происходит в случае с квадратичными уравнениями, потому что все они не проходят тест горизонтальной линии. Однако, если я ограничу их домен тем, где значения x создают график, который прошел бы тест горизонтальной линии, тогда у меня будет обратная функция. 9{ — 1}}\left( x \right), если ни одна горизонтальная линия не пересекает его график более одного раза.
Пример графика с обратной функцией
Пример графика без обратной функции
Ниже приведены основные стратегии алгебраического решения обратной функции .
Основные этапы поиска функции, обратной квадратичной функции
Замените f(x) на y.
Поменяйте местами \color{red}x и \color{blue}y. Другими словами, 92} + 2, если он существует. Укажите его домен и диапазон.
Первое, что я понял, это то, что эта квадратичная функция не имеет ограничения на область определения. Я уверен, что когда я нарисую это, я смогу нарисовать горизонтальную линию, которая будет пересекать его более одного раза. Следовательно, обратная функция не является. Я даже не буду применять ключевые шаги, описанные выше, чтобы найти его обратное.
Диаграмма показывает, что она не прошла тест горизонтальной линии, поэтому обратная функция не является функцией. Я остановлюсь здесь. 92} + 2,\,\,x \ge 0, если он существует. Укажите его домен и диапазон.
Эта же квадратичная функция, как показано в примере 1, имеет ограничение на область определения, которая равна x \ ge 0. После построения функции по оси xy я вижу, что график представляет собой параболу, разрезанную пополам для всех x значения равны или больше нуля. Это должно пройти тест горизонтальной линии, который говорит мне, что я действительно могу найти его обратную функцию, выполнив предложенные шаги.
На приведенном ниже графике я четко определил домен и диапазон, потому что мне понадобится эта информация, чтобы помочь мне определить правильную обратную функцию в конце.
Помните, что область определения и область значений обратной функции исходят из области значений и области значений исходной функции соответственно. Это называется обменом домена и диапазона .
Даже не находя пока обратной функции, я могу легко определить ее домен и диапазон, используя информацию из графика исходной функции: домен равен x ≥ 2 , а диапазон равен y ≥ 0 .
Видите, как я меняю местами домен и диапазон исходной функции, чтобы получить домен и диапазон обратного значения? 92} — 1,\,\,x \le 0 , если он существует. Укажите его домен и диапазон.
Эта задача очень похожа на пример 2. Диапазон начинается с \color{red}y=-1 и может опускаться как можно ниже.
Теперь, это шаги по решению для обратного.
Применение операции извлечения квадратного корня приводит к получению двух уравнений из-за положительного и отрицательного случаев. Чтобы выбрать правильную обратную функцию из двух, я предлагаю вам найти домен и диапазон каждого возможного ответа. Теперь правильная обратная функция должна иметь домен из диапазона исходной функции; и диапазон, исходящий из домена той же функции.
Ниже приведены графики исходной и обратной функции на одной оси координат.
Пример 4: Найдите обратную функцию ниже, если она существует. Укажите его домен и диапазон.
Я бы сначала построил график этой функции и четко определил домен и диапазон. Обратите внимание, что ограничение в области делит параболу на две равные половины. Я буду иметь дело с левой половиной этой параболы. Ясно, что это имеет обратную функцию, потому что проходит тест горизонтальной линии. 92} — 4ac} } \over {2a}}}}
, где a, b и c могут содержать переменные.
Это ожидаемо, так как мы ищем функцию, а не точные значения.
Ключевым шагом здесь является выбор подходящей обратной функции в конце, потому что у нас будут плюс (+) и минус (-) случаи. Мы можем сделать это, найдя домен и диапазон каждой функции и сравнив их с доменом и диапазоном исходной функции.
No related posts.