Y x2 2x 3 график функции: График функции y = x²-2x+3 (x во 2-ой степени (в квадрате) минус 2 умножить на x плюс 3) . Построить онлайн . Таблица точек .

Содержание

Математика — 9

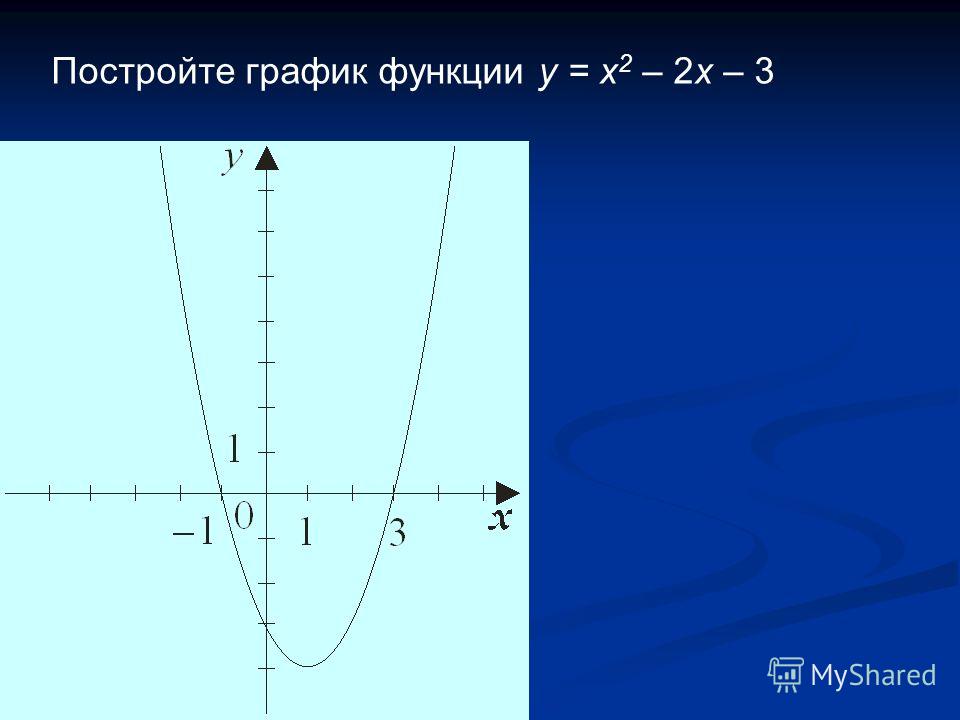
Исследование. 1) Найдите точки пересечения параболы y = x² — 2x — 3 с осью абсцисс: x² — 2x — 3 = 0 x = — 1, x = 3
2) Найдите координаты точки вершины:
m = -b
2a = 2
2 = 1, n = m² — 2 m — 3 = 1 — 2 — 3 = -4

3) Постройте параболу.
4) Определите знаки ординат для точек параболы с абсциссами:
x = 0, x = 1, x = 2
5) При каких значениях х парабола находится ниже оси абсцисс?
6) При каких значениях х парабола находится выше оси абсцисс?
7) Чтобы правильно ответить на вопросы в пунктах 5 и 6, что важнее: нахождение точки вершины, или нахождение точек пересечения параболы с осью абсцисс?

7-3	Квадратные неравенства

Неравенства вида:

• ax² + bx + c < 0
• ax² + bx + c ≤ 0
• ax² + bx + c > 0
• ax² + bx + c ≥ 0

являются квадратными
неравенствами (a ≠ 0).

Решение квадратных неравенств второй степени с одной переменной сводится к отысканию промежутков, на которых квадратичная функция принимает положительные или отрицательные значения.
При этом способе решения неравенств важно знать направление ветвей параболы и точки пересечения параболы с осью абсцисс.

Пример: По графику функции y = x² — x — 6 напишите множество решений нижеприведенных неравенств.

a) x² — x — 6 ≤ 0
b) x² — x — 6 ≥ 0

c) x² — x — 6 > 0
d) x² — x — 6 < 0

Решение. Поскольку x = — 2, x = 3 корни уравнения x² — x — 6 = 0 парабола функции y = x² — x- 6 пересекается с осью Ox в точках x = -2, x = 3 и делится на три промежутка, в которых принимает положительные и отрицательные значения. Определим значения выражения x² — x — 6 в каждом из промежутков.
a) График функции y = x² — x — 6 пересекает ось x в точках -2 и 3 и между этими значениями располагается ниже оси Ox .
Значит, неравенства x² — x — 6 ≤ 0 выполняется при -2 ≤ x ≤ 3.
b) При значениях x = -2 и x < -2 или же x=3 и x>3 значения функции (то есть значение выражения x² — x — 6) равны нулю или же больше нуля.
Решения неравенства x² — x — 6 ≥ 0 таковы: x ≤ -2 или x ≥ 3.
c) Решения неравенства x² — x — 6 > 0 таковы: x < -2 или же x > 3
d) Неравенства x² — x- 6 < 0 выполняется при -2 < x < 3.
Построение графика квадратичной функции — презентация онлайн
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
1. Построение графика квадратичной функции
Y = x2
Y = x2
Y = 3×2
Y = 0,3×2
Y = -0,5×2
2
y=ax
y=ax2+n
Y = x2
Y = x2 – 4
Y = x2 + 3
Как получить графики
функций Y = x2 – 4 и Y = x2 + 3
из графика функции Y = x2
4. y=a(x-m)2
2
y=a(x-m)
Y = x2
Y = ( x – 6 )2
Y = (x + 3)2
5. y=a(x-m)2 + n
Как получить график функции y=a(x-m)2 + n из графика функции y=ax2
Y = (x — 6)2 + 4
Найдите соответствия:
у х2 5
у 0,3х
2
у ( х 3)
2
у х 2 5
2
Параболу y = 5×2 cдвинули на 3
единицы вниз и на 6 единиц
вправо. Графиком какой функции
является полученная парабола?
Составьте уравнение параболы
Параболу y = -2×2 cдвинули на 7
единицы вверх и на 4 единицы
влево. Графиком какой функции
является полученная парабола?
Y = -2(x + 4)2 + 7
Y =5(x — 6)2 — 3
8. Построение графика функции у = ах2 + bх +с.
1. Определить направление ветвей параболы.
9. Построение графика функции у = ах2 + bх +с.
х т
Построение графика функции
у = ах2 + bх +с.
2. Найти координаты вершины параболы
(т; п).
b
т
2a
n y m
3. Провести ось
симметрии.
х т
О (т;п)
10. Построение графика функции у = ах2 + bх +с.
Определить точки пересечения графика
4. функции с осью Ох, т.е. найти нули
функции.
у 0
ах bx c 0
2
(х1;0)
(х2;0)
11. Построение графика функции у = ах2 + bх +с.
5.
Составить таблицу значений функции
с учетом оси симметрии параболы.
х
х1
х2
х3
х4
у
у1
у2
у3
у4
12.
Алгоритм построения графика функции у = ах2 + bх +с. 1. Определить направление ветвей параболы.
2. Найти координаты вершины параболы
(xв; yв).
3. Провести ось симметрии.
4. Определить точки пересечения графика
функции с осью Ох, т.е. найти нули
функции.
5. Составить таблицу значений функции
с учетом оси симметрии параболы.
Постройте график функции
y = x2 – 2x — 3.
С помощью графика
найдите:
1. Область определения
функции;
2. Область значений
функции;
3. Нули функции;
4. Промежутки, в которых
у>0, y<0;
5. Промежутки возрастания
и убывания функции;
6. Наибольшее
(наименьшее) значение
функции
Тест
y = -x2 — 4x — 5
y = x2 – 2x — 3.
y = x2 – 2x — 3.
y = x2 – 2x — 3.
English Русский Правила
График квадратичных функций Рабочий лист Ответы
ALLBILDERVIDEOSBüchermApsNewshopping
Sucoptionen
Bilder
Alle Anzeigen
Alle Anzeigen
[PDF] Graphing graphing. Alg1 › Graphing Quadratic Fu…
Worksheet by Kuta Software LLC. Kuta Software — Бесконечная алгебра 1 … Графики квадратичных функций. Нарисуйте график каждой функции. 1) у = 3х.
[PDF] Бесконечная алгебра 1 — Практика: построение графиков квадратичных функций
www.lcps.org › cms › lib › Centricity › предметная область › Алгебра 1 – примечания …
Практика: построение графиков квадратичных функций. Нарисуйте график каждой функции. 1) у = -2х² + 12х-17. −2x². 2) у = х²-6х+8.
[PDF] Ключ
tnelsonmath.weebly.com › graphing_quadratics_review_ws_answers
Практический рабочий лист: Графики квадратичных функций в стандартной форме. 1] Для любого квадратичного вида y = ax2 + c осью симметрии всегда является прямая X=0.
[PDF] День 1 — Графики квадратичных функций — Примечания — Ключ ответа
www.cbsd.org › cms › lib › Centricity › Domain › Day 1_2 — In class …
Алгебра 2/Тригл. Графики квадратных уравнений. Имя. КЛЮЧ… Запишите квадратное уравнение в стандартной форме и определите, открывается ли график вверх или вниз.
[PDF] 3 Графики квадратичных функций — City Tech OpenLab
openlab.citytech.cuny.edu › 1489642086-Graphing_Quadratic_Funct…
Графики квадратичных функций. 1. f(x) = x2. Вершина = точка пересечения y : точка пересечения x: 2. f(x) = x2 + 5. Вершина = точка пересечения y : точка пересечения x: 3. f(x) = (x + 3)2.
Рабочий лист для урока: Графики квадратичных функций — Nagwa
www.nagwa.com › рабочие листы
В этом рабочем листе мы будем практиковаться в построении графика любой квадратичной функции, заданной в ее стандартной, вершинной или факторизованной форме, с использованием ключевых функций из …
Ähnliche Fragen
Что представляет собой график ответа квадратичной функции?
Как построить график квадратичной функции?
Есть ли два ответа на квадратное уравнение?
Как решать квадратные уравнения?
Рабочие листы для построения графиков квадратичных функций — Tutoring Hour
www. tutoringhour.com › Рабочие листы › Graphing-qu…
Используйте наши рабочие листы для печати, чтобы улучшить навыки построения графиков квадратичных функций. Найдите выходные значения, нанесите точки и нарисуйте график.
Графики квадратичных функций
www.mathworksheets4kids.com › graphing-quadrati…
Графические рабочие листы с квадратичными функциями имеют идентифицирующие нули, чтение графика и запись квадратичной функции, построение графика с использованием значений x и y и многое другое.
[PDF] Рабочий лист обзора квадратичных графиков Имя ______
www.commackschools.org › Downloads › Graphing-Quadratics-Bonu…
Рабочий лист обзорных квадратичных графиков … Постройте график следующих квадратичных функций, используя критические значения и /или факторинг. … 9.1 Обзор ответов.
ähnliche sucaanfragen
Графический лист квадратичных функций с ответами PDF
График Квадратичные функции Рабочий лист Ответ Ключ Алгебра 1
График Квадратичный функции Рабочий лист Ответы Algebra 2
3 Graphing Functions Worksheet Workselet Workselet workselet. практический рабочий лист: построение графика квадратичных функций в стандартной форме, ключ ответа
Графики квадратичных функций, ответы на рабочий лист Kuta Software
Практический рабочий лист Построение графика квадратичных функций в вершинной форме
РЕШЕНО: a. Имея квадратичные функции y = x2 — 2x — 3 и y = -x + 4x — 1, преобразовать их в вид y = a(x — h)? + к. у=х²- 2х-3 у = -х2 + 4х
Вопрос
а. Имея квадратичные функции y = x2 — 2x — 3 и y = -x + 4x — 1, преобразовать их в вид y = a(x — h)? + к. y=x²- 2x-3 y = -x2 + 4x — 1
Шаг за шагом Ответ:
Шаг 1/7
y = x²- 2x-3
Шаг 2/7
1. Сначала нам нужно заполнить квадрат. Для этого нам нужно прибавить и вычесть из квадрата половину коэффициента при х. В этом случае коэффициент x равен -2, поэтому половина его равна -1. Складываем и вычитаем (-1)² = 1. y = x² — 2x — 3 + 1 — 1
Шаг 3/7
2. Мы можем сгруппировать первые три члена и упростить последний член. у = (х² — 2х + 1) — 4 y = (x — 1)² — 4
Видеорекомендация лучшего совпадения:
Решено проверенным экспертом 9{2}+3 x-1$$
Рекомендуемые видео
Стенограмма
Мы хотим защитить форму и эскизы. Сначала мы сделаем перехват Y, чтобы мы могли купить наши перехваты. перехват эквивалентен нулю. Это также будет причиной того, что это слишком негативно. Время ноль в квадрате плюс трижды ноль минус один — это отрицательная вещь. Давайте сначала построим эту точку. Нам должно быть интересно наше «Почему», вот что это говорит нам. Я пока отложу это. Невозможно сказать да. Давайте разберемся, что произошло. Это когда Х перехватывает? Почему у него будет ноль? Ноль равен двум X в квадрате плюс три X минус один и вспомнить. X равно минусу B плюс или минус B в квадрате минус четыре, и это формула, которую мы собираемся использовать. Это A.
Коэффициенты X в квадрате X и просто постоянная временная перспектива — вот что такое C-квадрат. Я собирался подключить все это сейчас, так что у нас будет X равно отрицательному трем, а квадратный корень хуже. Это будет девять минус или C, то есть четыре раза отрицательное, а также умноженное на один минус, будет всего восемь. Это даст нам минус четыре из-за двух отрицательных А и двух отрицательных В. Будет девять минус восемь — один облажался из одного отрицательно. У нас есть два решения после того, как вы закончите с этим. У нас либо минус три плюс один, либо минус три плюс один, что означает, что у нас минус расходы или мобильность. Отрицательный или сверхотрицательный для негативов, которые не могут быть проданы, — это то, что мы вычитаем. Мы получаем что, половина или один. Те будут шлепнуты вниз. Что тут пропустил, скажу. Один будет здесь, верно? Первое, что мы хотим сделать из этого термина, — это также выделить отрицательный фактор, чтобы мы могли завершить наш квадрат. Это будет как отрицательное, так и положительное значение X в квадрате.

Я оставляю немного места здесь и немного места минус один. Нам нужно привести наши условия в порядок, чтобы зачерпнуть это. Мы возьмем термин с квадратом X, разделенным на два, в рекламе, если она привлекательна. Это будет польза. Мне нужно было сохранить эту линию еще раз, зачерпнуть еще немного работы, а затем вычесть это. Три дома, разделенные на два, будут очень физическими. Этого должно быть достаточно для нас. Есть человек по имени Берт. Если этот член разделить на два плюс Х в квадрате, то это будет множитель. Мы также можем написать это нам отрицательно. Умножить на X, минус 1/3 в квадрате, и мы получим минус 9./16 здесь. Минус хочу что-то сделать. Давайте распространять и этот негатив. И делать это тоже. Это дало бы нам отрицательные два X минус 34 в квадрате, а затем это дало бы нам положительное 9/8 минус один. Просто +18 в конце сделает это проще, так что 98 минус один будет 18. Эта шлюха — одна из наших. Единственное, что нам нужно сделать, это выяснить, что Техас помнит X минус h.

No related posts.