2
Функция y = x2 и её график
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
1. Тема: Функция y = x2 и её график.
*y=
2
x
Назовите координаты точек, симметричных данным точкам
относительно оси y :
y
(- 2; 6)
( 2; 6)
(- 1; 4)
(1; 4)
(0; 0)
(0; 0)
(- 3; — 5)
(3; — 5)
х
На графике видно, что ось OY делит параболу на симметричные
левую и правую части (ветви параболы), в точке с координатами (0; 0)
(вершине параболы) значение функции x 2 — наименьшее.
Наибольшего значения функция не имеет. Вершина параболы — это
точка пересечения графика с осью симметрии OY .
На участке графика при x ∈ (– ∞; 0 ] функция убывает,
а при x ∈ [ 0; + ∞) возрастает.
График функции y = x 2 + 3 — такая же парабола, но её
вершина находится в точке с координатами (0; 3) .
Найдите значение функции
y = 5x + 4, если:
х=-1
y = — 1 y = 19
х=-2
y=-6
y = 29
х=3
х=5
Укажите
область определения функции:
y = 16 – 5x
10
y
х
х – любое
число
х≠0
1
y
х 7
4х 1
y
5
х≠7
Постройте графики функций:
1).У=2Х+3
2).У=-2Х-1;
3).
Математическое
исследование
Тема: Функция y = x2
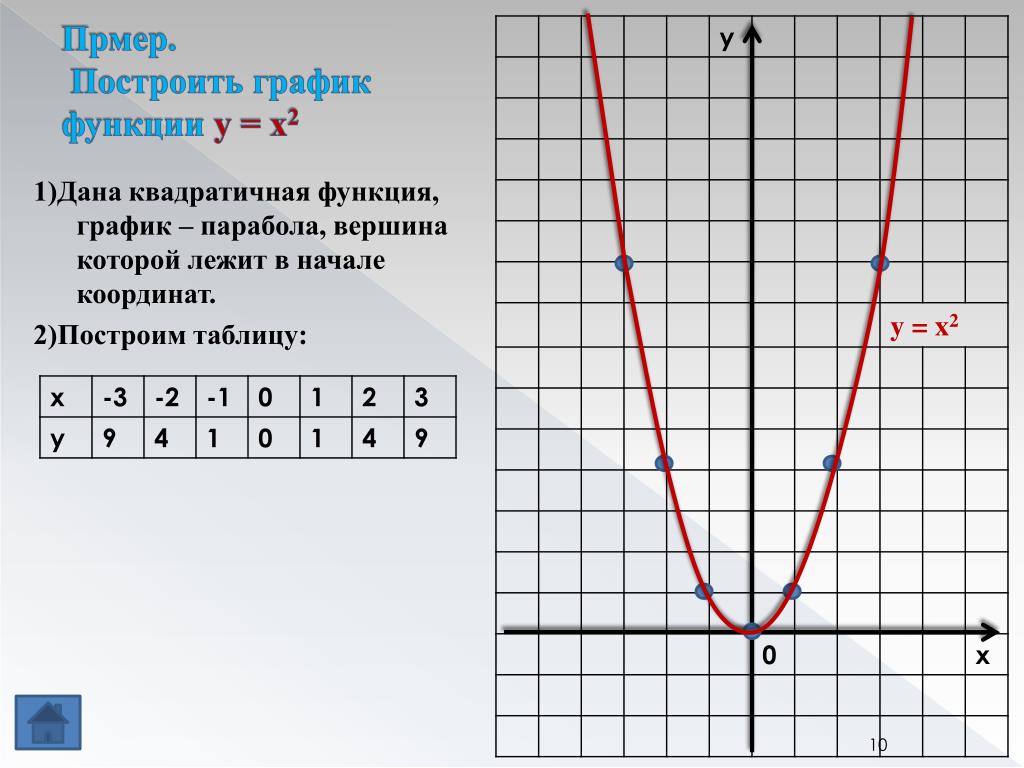
Постройте
график
функции
y = x2
Алгоритм построения параболы..
1.Заполнить таблицу значений Х и У.
2.Отметить в координатной плоскости точки,
координаты которых указаны в таблице.
3.Соедините эти точки плавной линией.
Невероятно,
но факт!
Перевал Парабола
Знаете ли вы?
Траектория камня, брошенного под
углом к горизонту, будет лететь по
параболе.
15. Свойства функции y = x2
*Свойства функции
y=
2
x
*Область определения
функции D(f):
х – любое число.
*Область значений
функции E(f):
все значения у ≥ 0.
*Если
х = 0, то у = 0.
График функции
проходит через
начало координат.
II
I
*Если
х ≠ 0,
то у > 0.
функции, кроме точки
(0; 0), расположены
выше оси х.
*Противоположным
значениям х
соответствует одно
и то же значение у.
График функции
симметричен
относительно оси
ординат.
Геометрические
свойства параболы
*Обладает симметрией
*Ось разрезает параболу на
две части: ветви
параболы
*Точка (0; 0) – вершина
параболы
*Парабола касается оси
абсцисс
Ось
симметрии
Найдите у, если:
«Знание – орудие,
а не цель»
Л. Н. Толстой
х = 1,4
— 1,4
у = 1,96
х = 2,6
-2,6
у = 6,76
х = 3,1
— 3,1
у = 9,61
Найдите х, если:
у=6
у=4
х ≈ 2,5 х ≈ -2,5
х=2 х=-2
постройте в одной
системе координат
графики двух функций
1.
Случай :у=х2
У=х+1
2. случай:
У=х2
у= -1
Найдите
несколько значений
х, при которых
значения функции :
меньше 4
больше 4
• Принадлежит ли графику функции у = х2 точка:
P(-18; 324)
R(-99; -9081)
принадлежит
не принадлежит
S(17; 279)
не принадлежит
• Не выполняя вычислений, определите, какие из
точек не принадлежат графику функции у = х2:
(-1; 1)
*
(-2; 4)
(0; 8)
(3; -9)
(1,8; 3,24)
При каких значениях а точка Р(а; 64) принадлежит графику функции у = х2.
а = 8; а = — 8
(16; 0)
Алгоритм решения уравнения
графическим способом
1. Построить в одной системе
координат графики функций, стоящих
в левой и правой части уравнения.
2. Найти абсциссы точек пересечения
графиков. Это и будут корни
уравнения.
3. Если точек пересечения нет, значит,
уравнение не имеет корней
Удачи вам!
English Русский Правила
3-8Математическая задача: Парабола 3 — вопрос № 3532, алгебра, уравнение
Найдите уравнение параболы с фокусом в точке (0,2) и вершиной в начале координат.
f:y=x2+bx+c
Нашли ошибку или неточность? Не стесняйтесь
написать нам. Спасибо!
Советы для связанных онлайн-калькуляторов
У вас есть линейное уравнение или система уравнений и вы ищете ее решение? Или у вас есть квадратное уравнение?
Для решения этой задачи по математике вам необходимо знать следующие знания:
- алгебра
- уравнение
- система уравнений
- арифметика
- квадрат (вторая степень, квадратичный)
- планиметрия
- парабола
Класс решения задачи:
- средняя школа
Мы рекомендуем вам посмотреть это обучающее видео по этой математической задаче: видео1
- Парабола
Найдите уравнение параболы, содержащей точки A[10; -5], Б[18; -7], С[20; 0]. (используйте y = ax²+bx+c) - Предположим, 10
Предположим, что 4+7i является решением 5z2+Az+B=0, где A, B∈R.
Найдите A и B. - Координата X 81737
В треугольнике ABC определите координаты точки B, если известно, что точки A и B лежат на прямой 3x-y-5=0, точки A и C лежат на прямой 2x +3y+4=0, точка C лежит на оси координат x, угол при вершине C прямой. - Найдите 5
Найдите уравнение окружности с центром в точке (1,20), которая касается прямой 8x+5y-19=0 - Пересечения 62784
Дана квадратичная функция: y = -x² + 2x + 3 a) определить точки пересечения с осью x, y и пиком V b) нарисовать график и описать c) для которого применяется x f (x) = 3 - В строке
В строке p: x = 4 + t , y = 3 + 2t, t есть R, найти точку C, которая находится на одинаковом расстоянии от точек A [1,2] и B [-1,0]. - Определить 80662
Дана функция y = x² — 4x + 3. Определить все действительные числа z такие, что g(x) = g(-2). - Вычислить 8
Вычислить координаты точки B, осесимметричной с точкой A[-1, -3] вдоль прямой линии p : x + y — 2 = 0. - Декартова система координат
1. В декартовой системе координат, функций f и g мы знаем, что: Функция (f) определяется как f (x) = 2x², функция (g) определяется как g (x) = x + 3, точка (O) является началом координат опорной, а точка (C) является точкой пересечения графа - Касательные эллипса
Найдите модуль угла, под которым эллипс x² + 5 y² = 5 виден из точки P[5, 1]. - Неравенства: 4229
Найдите количество всех целых чисел x, удовлетворяющих следующим двум неравенствам: | х + 2 | = 3 - Найдите
Найдите образ A’ точки A [1,2] в осевой симметрии с осью p: x = -1 + 3t, y = -2 + t (t = вещественное число) - Общие уравнения прямой
Во всех примерах запишите ОБЩЕЕ УРАВНЕНИЕ прямой, которая задана каким-либо образом. А) линия задана параметрически: х = — 4 + 2р, у = 2 — 3р Б) форма наклона дает линию: у = 3х — 1 В) линия задана двумя точками: А [3; -3], Б [-5; 2] D) линия - Квадратное уравнение
Найдите корни квадратного уравнения: 3x²-4x + (-4) = 0. - Окружность — AG
Найдите координаты окружности и ее диаметр, если ее уравнение: x² + y² — 6x- 4y=36 - Форма наклона
Найдите уравнение прямой с точкой X(8, 1) и наклоном -2,8.
Найдите A и B.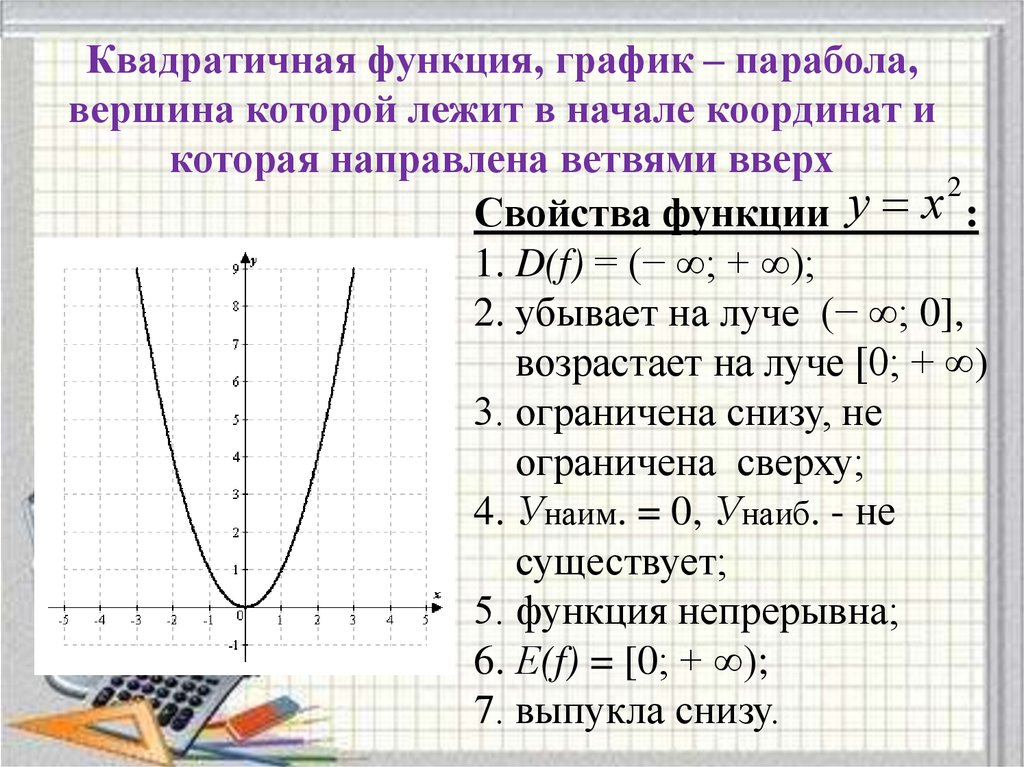
В декартовой системе координат, функций f и g мы знаем, что: Функция (f) определяется как f (x) = 2x², функция (g) определяется как g (x) = x + 3, точка (O) является началом координат опорной, а точка (C) является точкой пересечения графа