Y x5 график функции: Постройте график функции y=x-5

Степенная функция | Материалы для подготовки к ЕГЭ по математике ЕГЭ-Студия

Степенны́ми называют функции вида x^α, где α может быть целым, дробным, положительным или отрицательным. К ним относятся всем знакомая линейная функция y = kx + b, квадратичная парабола y = x² (в общем виде: y = ax² + bx + c), кубическая парабола y = x³. Степенными являются также гипербола , которую можно представить как y = x⁻¹, функция (ведь ),  и многие другие.

 

Расскажем подробно об этих функциях и их графиках.

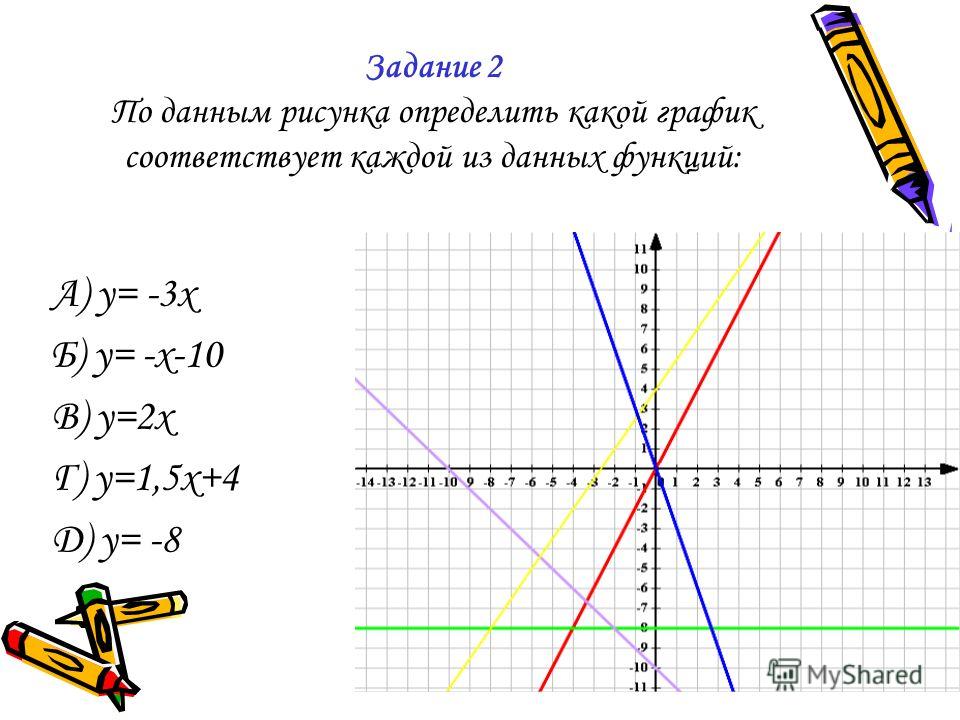
1. Линейная функция y = kx + b. График — прямая линия. Для её построения достаточно двух точек.

Если k > 0, линейная функция возрастает. Чем больше k, тем круче идет график. Число k называется угловым коэффициентом прямой и равно тангенсу угла наклона этой прямой к положительному направлению оси X:

Если k < 0, линейная функция убывает. Очевидно, в этом случае угол α — тупой и tgα < 0.

Если k = 0, мы получим прямую y = b, параллельную оси X.
Если угловые коэффициенты прямых равны — прямые параллельны.

2. О квадратичной функции (параболе) y = ax² + bx + c мы уже рассказывали.

Кратко повторим основные моменты:

— Если a > 0, ветви параболы направлены вверх. Если a < 0 — вниз.

— Координаты вершины параболы находятся по формулам:

— Точки пересечения параболы с осью X находятся как корни квадратного уравнения ax² + bx + c = 0. Если корней нет (дискриминант уравнения меньше нуля), парабола не пересекает ось X.

— Точку пересечения параболы с осью Y находим, подставив в её уравнение x = 0.

3. На рисунках функции y = x³ (кубическая парабола), y = x⁴ и y = x⁵.

4. Заметим, что между функциями y = x² и y = x⁴ есть определенное сходство. Оба этих графика симметричны относительно оси Y. Такие функции называются чётными.

Определение. Функция y = f(x) называется чётной, если:
1) область определения функции симметрична относительно нуля;
2) для каждого x из области определения выполняется равенство f(−x) = f(x).

Графики функций y = x³ и y = x⁵ симметричны относительно начала координат. Эти функции — нечётные.

Определение. Функция y = f(x) называется нечётной, если:
1) область определения функции симметрична относительно нуля;
2) для каждого x из области определения выполняется равенство f(-x) = -f(x).

Очевидно, функция y = x^α является чётной при чётных значениях α и нечётной при нечётных α.

5. Функция (гипербола) также относится к степенным. Ведь . Поскольку знаменатель не должен обращаться в ноль, эта функция не определена при x = 0. Гипербола является нечётной функцией. Её график симметричен относительно начала координат.

6. Построим график функции .

Выражение определено при x ≥ 0, поэтому область определения функции — все неотрицательные числа.

Кроме того, принимает только неотрицательные значения, поскольку ≥ 0.

Мы используем эти свойства при решении уравнений и неравенств. Уравнение вида имеет смысл только при f(x) ≥ 0 и g(x) ≥ 0. Это его область допустимых значений.

Существуют вопросы, ставящие в тупик почти любого абитуриента. Например, чему равен ?

Правильный ответ: .

Запомните это. Проверить легко: возьмём, например, a = −2.

Изобразим на одном графике параболу y = x² и функцию .

Сейчас нас интересует правая ветвь параболы, при x ≥ 0. Мы видим, что эта часть параболы и график функции словно нарисованы по одному шаблону, по-разному расположенному в координатной плоскости. Они симметричны относительно прямой y = x. То, что для одной из них — область определения, для другой — область значений.

Напомним, что такие функции называются взаимно обратными. Подробно об этом можно прочитать в статье «Логарифмическая функция».

7. Легко убедиться, что функция является обратной к функции y = x³.

 

Постройте графики функций — презентация онлайн

Похожие презентации:

Функция у=х2 и её график

Исследование функции и построение графика

Уравнение касательной к графику функции

Исследование функции. Построение графика

Функции и их графики

Свойства и графики тригонометрических функций

Функции и их графики. Задание №23

Функции и их свойства. Предел последовательности и функции. Производная функции и дифференциал

Графики тригонометрических функций

Графики тригонометрических функций. Преобразования графиков функций

Постройте графики функций. y = x5+x2–10, [-10;10],
Скачать https://author24shop.ru/readyworks/laboratornaya_rabota/informatika/454215/
Постройте графики функций. y = |tg(x)| x, [-1;1],
Скачать https://author24shop.ru/readyworks/laboratornaya_rabota/informatika/454216/
Постройте графики функций.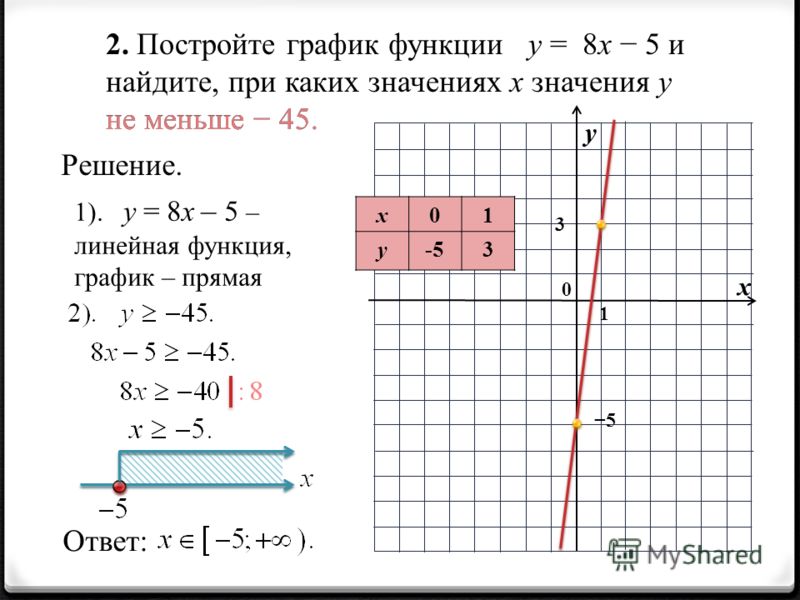 y = cos(x+x5)–2, [-2;2],

Скачать https://author24shop.ru/readyworks/laboratornaya_rabota/informatika/454217/
Постройте графики функций. y = |x3+x –10|, [-2;2],
Скачать https://author24shop.ru/readyworks/laboratornaya_rabota/informatika/454218/
Постройте графики функций. y = ex-3, [-1;1],
Скачать https://author24shop.ru/readyworks/laboratornaya_rabota/informatika/454219/
Постройте графики функций. y = ex·|x|, [-1;1],
Скачать https://author24shop.ru/readyworks/laboratornaya_rabota/informatika/454220/
Постройте графики функций. y = cos(x3)–5, [-2;2],
Скачать https://author24shop.ru/readyworks/laboratornaya_rabota/informatika/454221/
Постройте графики функций. y = x4-x2–х, [-5;5],
Скачать https://author24shop.ru/readyworks/laboratornaya_rabota/informatika/454222/
Постройте графики функций. y = |x|, [-10;10],
Скачать https://author24shop.ru/readyworks/laboratornaya_rabota/informatika/454223/
Постройте графики функций. y = |x|+5, [-10;10],
Скачать https://author24shop. ru/readyworks/laboratornaya_rabota/informatika/454225/
Постройте графики функций. y = tg(x), [-1;1],
Скачать https://author24shop.ru/readyworks/laboratornaya_rabota/informatika/454226/
Постройте графики функций. y = x3–2×2+5 , [-10;10],
Скачать https://author24shop.ru/readyworks/laboratornaya_rabota/informatika/454228/
Постройте графики функций. y = 3cos(x)·sin(2x+3), [-10;0],
Скачать https://author24shop.ru/readyworks/laboratornaya_rabota/informatika/454229/
Постройте графики функций. y = |x2+2x-5|, [-3;3],
Скачать https://author24shop.ru/readyworks/laboratornaya_rabota/informatika/454230/
Постройте графики функций. y = ex2-10, [-2;2],
Скачать https://author24shop.ru/readyworks/laboratornaya_rabota/informatika/454231/
Постройте графики функций. y = x3 – 5x–15, [-2;2],
Скачать https://author24shop.ru/readyworks/laboratornaya_rabota/informatika/454232/
Постройте графики функций. y = |tg(x)|, [-1;1],
Скачать https://author24shop.ru/readyworks/laboratornaya_rabota/informatika/454233/
Постройте графики функций. y = x3+5 |х|, [-5;5],
Скачать https://author24shop.ru/readyworks/laboratornaya_rabota/informatika/454234/
Постройте графики функций. y = |3tg(x) cos(x)|, [-1;1],
Скачать https://author24shop.ru/readyworks/laboratornaya_rabota/informatika/454235/
Постройте графики функций. y = |x2+5x-10|, [-10;5],
Скачать https://author24shop.ru/readyworks/laboratornaya_rabota/informatika/454236/

English     Русский Правила

3-8 9 Оценить квадратный корень из 12 10 Оценить квадратный корень из 20 11 Оценить квадратный корень из 50 94 18 Оценить квадратный корень из 45 19 Оценить квадратный корень из 32 20 Оценить квадратный корень из 18 92

Графики последовательностей

Нет сомнения, что при обучении математике мы используем графики функций, чтобы помочь учащимся понять, решить проблему или помочь учащимся понять новую концепцию.

Тогда возникает вопрос, должно ли быть полное представление нескольких разных графиков или последовательность этих графиков? Каким образом учащиеся лучше усвоят материал? Чтобы оценить эту проблему, я попытался изучить несколько случаев, когда в классе графически изображались несколько функций.

Первый случай, который я исследовал, связан с изменением коэффициента a при y=ax ² . Я изобразил следующее: y=-3x ² , y=-2x ² , y=-x ² , y=x ² и y=2x ² .

Сначала я построил график всех пяти функций одновременно, чтобы сравнить их с графиком пяти функций последовательно. Вот вид пяти функций одновременно,

Теперь я хотел бы показать последовательность графиков, состоящих из одних и тех же функций.

Я считаю, что в этом или в другом порядке учащиеся могут получить или выучить концепции более эффективно, чем когда графики представлены все сразу.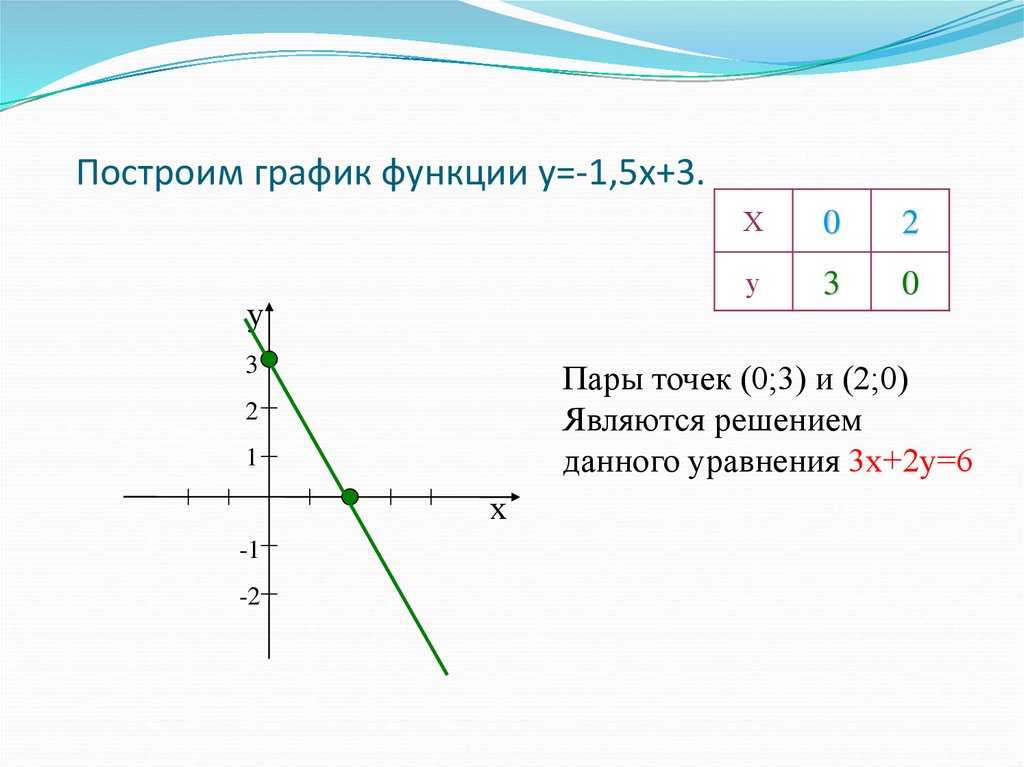 На первых трех графиках учащиеся могут визуализировать, как увеличивающийся коэффициент для отрицательной квадратичной функции расширяет график. Кроме того, на следующих двух графиках учащиеся видят, что делает возрастающий коэффициент для положительной квадратичной функции: сжимает график. В обоих случаях (последовательность или нет) учащиеся в конечном итоге поймут, как увеличивать и уменьшать коэффициент, но вопрос в том, как это сделать. Когда учащиеся могут просматривать графики в последовательности, у них больше шансов увидеть связь для себя. Учащиеся могут наблюдать за развитием графиков и делать наблюдения. После наблюдений и некоторого обсуждения учащиеся могут сделать определенные выводы о том, что они увидели на графиках. Важно то, что когда учащиеся могут учиться сами или делать определенные выводы и умозаключения, материал становится для них более важным и остается с ними на более длительный период времени. Этот тип процесса для студентов — это то, чего мы хотим достичь. Давайте посмотрим на другой пример функций.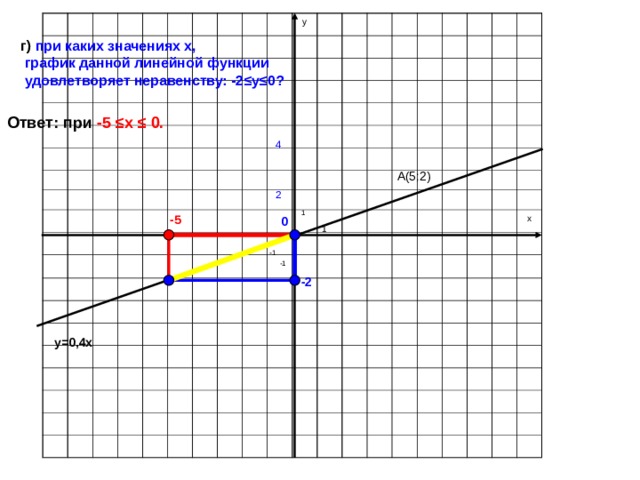

 

Теперь мы хотим рассмотреть пять новых функций: y=x, y=x ² , y=x ³ , y=x ⁴ и y=x ⁵ . Вот график всех функций сразу,

Теперь снова я хочу посмотреть на последовательность или развитие этих функций и их графиков.

Как видите, при попытке объяснить определенные свойства функций построение графиков функций в последовательности может быть очень полезным. Показатели этих полиномиальных функций чередуются с каждым новым графиком — сначала нечетные, затем четные, затем нечетные и так далее. Когда учащимся предоставляется такое представление графиков, они могут установить связь с четными/нечетными показателями и конечным поведением каждой функции. Этот тип заключения или заставить студентов собрать эту концепцию может быть довольно трудным, если рассматривать все пять функций одновременно.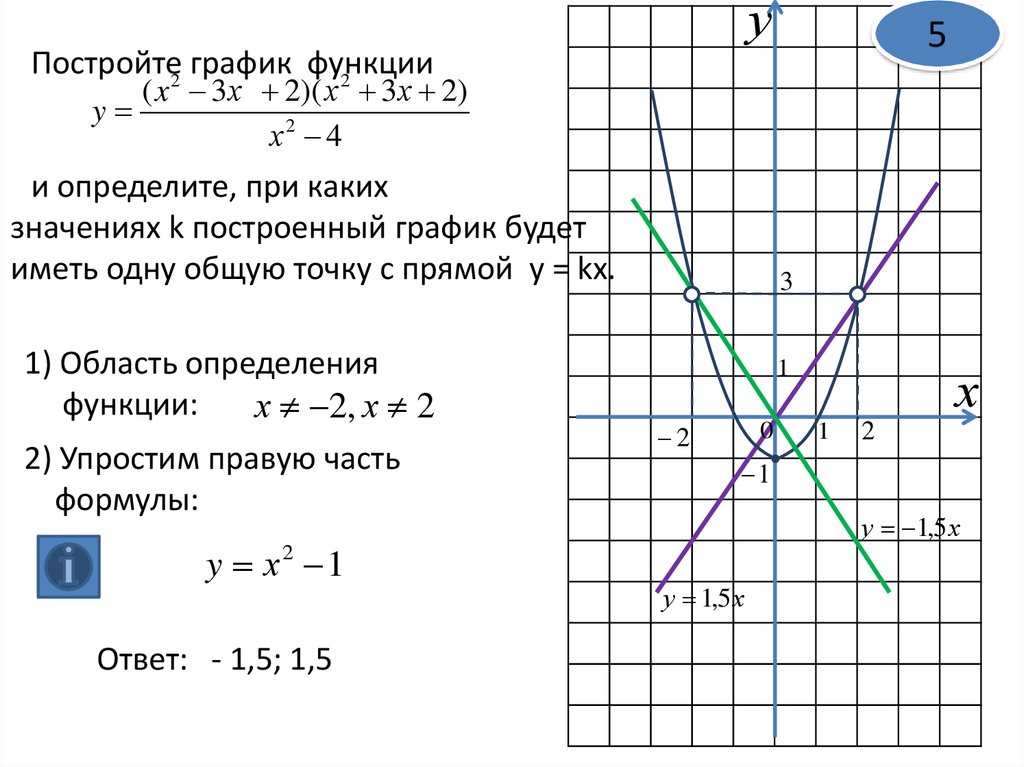 С этого момента учитель может показать пять новых функций той же природы, но со старшим коэффициентом -1: y = -x, y=-x ² , y=-x ³ , y=-x ⁴ , и y=-x ⁵ . Эти функции с похожи. Опять же, учащиеся узнают те же понятия, что и раньше, но, надеюсь, заметят разницу, вызванную отрицательным коэффициентом. Эту разницу также можно показать с помощью последовательности графиков. Последовательность показана ниже:

В заключение, упорядочивание графиков в определенном порядке дает учащимся возможность самостоятельно выводить, завершать или подвергать сомнению понятия. Как представлено в одном наборе графиков, учащиеся могут быть не в состоянии установить связи, необходимые для полного и полезного обучения. Когда учащиеся ищут ответы для себя, учителя не передают им информацию, а учащиеся могут не оценить материал и не сохранить его. Мы хотим, чтобы учащиеся устанавливали связи самостоятельно, и упорядочивание графиков функций дает еще один полезный выход для этого.