Геометрические задачи с ответами — BrainApps.ru
Геометрические задачи с ответами — BrainApps.ru- 940+ Все
- 125 Логика и рассуждения
- 78 Задачи с подвохом
- 233 Математические задачи
- 33 Взвешивания и переливания
- 15 Геометрические задачи
- 5 Детские задачи на логику со ответами: задачи для детей 1-3 класс
- 35 Загадки
- 7 Криптарифмы
- 21 На знания
- 43 О времени
- 41 Последовательности
- 7 Ребусы
- 56 Задачи со словами
- 9 Задачи со спичками
- 33 Задачи по физике
- 64 Что? Где? Когда?
- 1 Шахматные задачи
Мудрость
Я никогда не думаю о будущем. Оно приходит само достаточно скоро.
Альберт Эйнштейн
Топ-10 по просмотрам
- Середина
- Закономерность букв
- Секретная командировка
- Почему небо голубое?
- Страх и паника
- Расставить скобки и знаки
- Животное — рыба
- Собрать тракторы
- Умеете ли Вы считать в уме?
Топ-10 по рейтингу
- Умеете ли Вы считать в уме?
- Любовь на похоронах
- Середина
- Ничего не случилось
- Набор монет
- Детская загадка
- Задача Эйнштейна
- Волшебная фраза
- Цвет волос художника
- Шпионская история
Доказать параллельность
l1 и l2 — касательные к окружностям.
Доказать, что l3 и l4 — параллельны.
- 0
- 30
- 8 473
Узнать ответ
Объезд на дороге
Водителям приходится объезжать этот участок по запасному пути, отмеченному на плане пунктиром.
На сколько километров увеличивает путь этот объезд?
- 0
- 29
- 5 038
Узнать ответ
Складывание кубиков
На каждой грани бумажного кубика написана цифра 1, 2 или 3, причем цифры на противоположных гранях — одинаковые. Какая из фигурок может получиться. если этот кубик разрезать по некоторым ребрам и развернуть?
- 0
- 16
- 4 182
Узнать ответ
Толщина креста
На красном фоне датского флага изображен белый крест; правила требуют, чтобы площадь белого креста составляла ровно половину всей площади флага. Допустим, что длина флага составляет 7,5 фута, а ширина – 5 футов. Какова толщина белого креста, при условии, что его площадь составляет половину всего флага?
Допустим, что длина флага составляет 7,5 фута, а ширина – 5 футов. Какова толщина белого креста, при условии, что его площадь составляет половину всего флага?
- 29
- 5 047
Узнать ответ
Треугольные участки
На рисунке вы видите, как шахтеры спорят по поводу своих участков. Каждый участок имеет форму прямоугольного треугольника. Размеры этих треугольников не совпадают, но площади у них всех одинаковы и составляют точно 3360 квадратных футов.
Катеты одного треугольника равны 140 и 48 , а его гипотенуза – 148. У второго треугольника катеты равны 80 и 84, а гипотенуза 116. Можете ли вы указать длины сторон третьего треугольника при условии, что они выражаются целыми числами, а площадь этого треугольника равняется площади первых двух треугольников?
- 0
- 4
- 3 273
Узнать ответ
Одинаковые карточки
Найдите три одинаковые карточки
- 0
- 24
- 4 053
Узнать ответ
Куб
Если отпилить кубику одну вершину, на сколько измениться количество его вершин?
- 0
- -3
- 3 904
Узнать ответ
8 кусочков
Разделите приведенную фигуру на 8 одинаковых частей.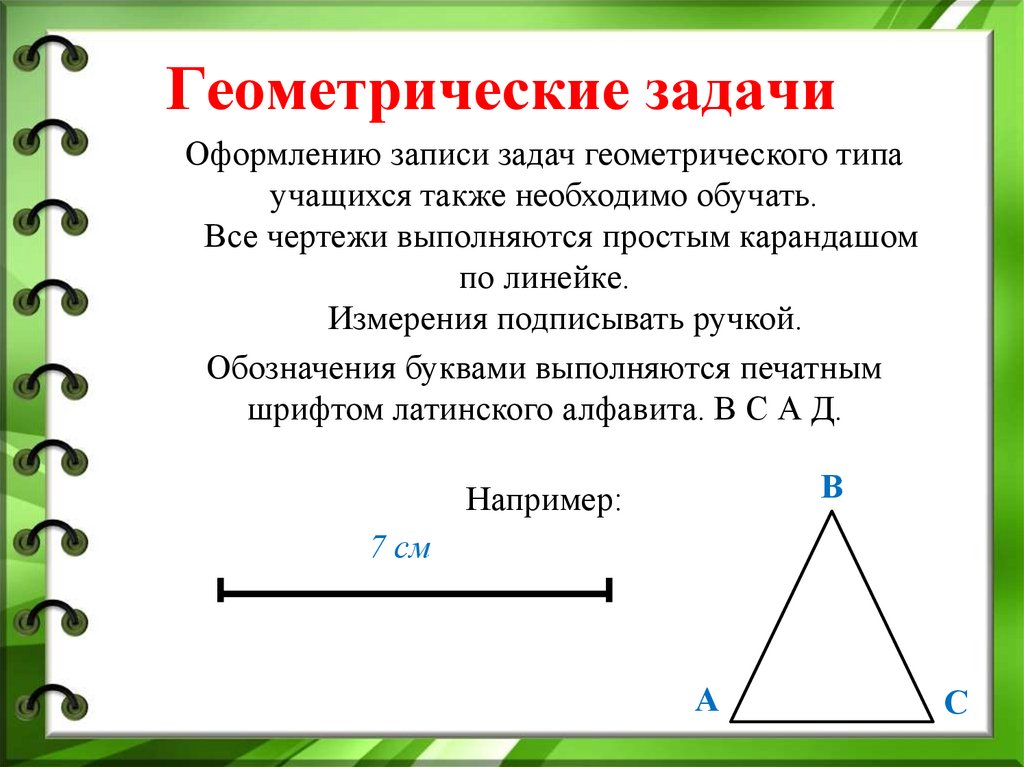
- 0
- 7
- 3 923
Узнать ответ
Площадь треугольника
Все высоты треугольника меньше 1. Может ли его площадь быть больше 10000 квадратных единиц?
- 0
- 3
- 2 818
Узнать ответ
Печать Царя Соломона
- 0
- 3
- 5 875
Узнать ответ
Заряжаем мозг каждый день
Раскройте весь потенциал вашего мозга вместе с BrainApps
- Оттачивайте свой ум
- Осваивайте полезные навыки
- Читайте лучшие книги в кратком изложении
Создайте аккаунт
Раскройте весь потенциал вашего мозга вместе с BrainApps
- Оттачивайте свой ум
- Осваивайте полезные навыки
- Читайте лучшие книги в кратком изложении
Или зарегистрируйтесь с помощью
Регистрируясь, вы соглашаетесь с Условиями использования и Политикой конфиденциальности.
Геометрическая задача про программиста и плитку
Программист решил у себя на квадратном участке сделать красиво: в центре сделать квадратную песочную зону отдыха, внизу слева — сделать угловую террасу, а справа — выложить плиткой круглую зону под мангал для шашлыков.
Когда он поехал за песком и плиткой, то уже в магазине вспомнил, что забыл записать площадь круга под мангал. Всё, что у него было, — это листок с такой схемой и площадью двух других участков. Но через пару минут программист уже оформлял нужное количество плитки. Как он это сделал?
Ключевой момент в этой задаче — это то, что у всех угловых треугольников площадь равна 24. А всё потому, что все эти треугольники — одинаковые. Как бы мы ни вращали один квадрат внутри другого, все угловые треугольники останутся одинаковыми между собой.
Если хотите в этом убедиться более точно — посчитайте противолежащие углы в треугольниках, если значение развёрнутого угла — 180°. А если в треугольниках одинаковые углы и хотя бы одна сторона — это одинаковые треугольники.
Также сразу посчитаем гипотенузу треугольника — она равна стороне жёлтого квадрата. Раз площадь квадрата равна 100, то сторона равна √100 = 10.
Теперь разберёмся с кругом. У нас получается, что нужно найти площадь окружности, вписанной в прямоугольный треугольник, у которого площадь равна 24, а гипотенуза равна 10.
Для площади круга нам нужно знать его радиус.Призываем на помощь школьную формулу радиуса окружности, вписанной в прямоугольный треугольник:
r = (a + b − c) / 2, где a и b — стороны треугольника, а c — гипотенуза.
Значение гипотенузы мы знаем, найдём длину двух оставшихся сторон. Площадь прямоугольного треугольника равна (a × b) / 2, получается:
(a × b) / 2 = 24 → a × b = 48 → a = 48 / b
Применим теперь формулу из теоремы Пифагора, которая гласит: a² + b² = c², и подставим туда значения a и c:
(48 / b)² + b² = 10²
2304 / b² + b² = 100
Так как у треугольника площадь не равна нулю, это значит, что ни одна из сторон тоже не равна нулю, поэтому умножаем обе части на b², чтобы избавиться от знаменателя:
2304 + b⁴ = 100 × b² → b⁴ − 100 × b² + 2304 = 0
Обозначим b² за x, чтобы получилось обычное квадратное уравнение:
x² − 100 × x + 2304 = 0
Решаем его и получаем, что x = 36 или x = 64.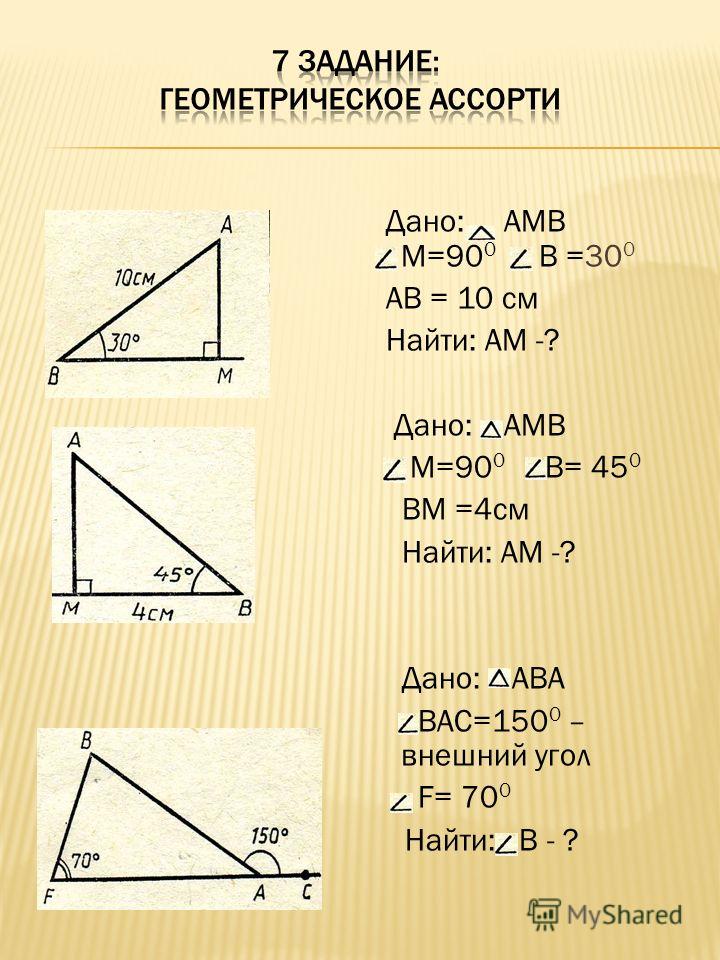 Это значит, что:
Это значит, что:
b² = 36 → b = 6
b² = 64 → b = 8
А раз a × b = 48, то выходит, что:
a = 48 / 6 = 8
или a = 48 / 8 = 6
Это значит, что стороны треугольника имеют размеры 6, 8 и 10. Подставим это в формулу нахождения радиуса:
r = (a + b − c) / 2 → r = (6 + 8 − 10) / 2 = 2
Теперь считаем площадь круга — это и будет нужное нам число:
S = π × r² → S = π × 4, что примерно равно 12,56.
Получается, программисту нужно взять 13 квадратов плитки. И немного останется на брак и доделки.
Еще одна распространенная геометрическая проблема связана с периметром или расстоянием вокруг объекта. Например, рассмотрим прямоугольник, для которого [латекс]\текст{периметр} = 2l + 2w.[/latex]
Например, рассмотрим прямоугольник, для которого [латекс]\текст{периметр} = 2l + 2w.[/latex]
Если длина прямоугольника на 5 м меньше удвоенной ширины, а периметр равен 44 м, найдите его длину и ширину.
Соотношения, описанные в виде уравнения, следующие:
[латекс]L = 2W — 5 \text{ и } P = 44[/латекс]
Для прямоугольника периметр определяется как:
[латекс ]P = 2 W + 2 L[/latex]
Замена [latex]L[/latex] и значения периметра дает:
[latex]44 = 2W + 2 (2W — 5)[/latex ]
Что упрощает до:
[латекс]44 = 2W + 4W — 10[/латекс]
Дальнейшее упрощение, чтобы найти длину и ширину:
[латекс]\begin{array}{rrrrlrrrr} 44&+&10&= &6W&&&& \\ \\ &&54&=&6W&&&& \\ \\ &&W&=&\dfrac{54}{6}&\text{or}&9&& \\ \\ &\text{So}&L&=&2(9)&-&5&\ text{or}&13 \\ \end{array}[/latex]
Ширина 9 м, длина 13 м.
Другие распространенные геометрические задачи:
Кабель длиной 15 м разрезается на две части так, что первая часть в четыре раза больше второй. Найдите длину каждой части.
Найдите длину каждой части.
Соотношения, описанные в виде уравнения, следующие:
[латекс]P_1 + P_2 = 15 \text{ и } P_1 = 4P_2[/latex]
Объединение этих выходов:
[латекс]\begin{array} {rrrrrrr} 4P_2&+&P_2&=&15&& \\ \\ &&5P_2&=&15&& \\ \\ &&P_2&=&\dfrac{15}{5}&\text{or}&3 \end{массив}[/latex]
Это означает, что [латекс]P_2 =[/латекс] 3 м и [латекс]P_1 = 4 (3),[/латекс] или 12 м.
Для вопросов с 1 по 8 напишите формулу, определяющую каждое отношение. Не решать.
- Длина прямоугольника на 3 см меньше, чем удвоенная ширина, а периметр равен 54 см.
- Длина прямоугольника на 8 см меньше его ширины в два раза, а периметр равен 64 см.
- Длина прямоугольника на 4 см больше его ширины в два раза, а периметр равен 32 см.
- Первый угол треугольника в два раза больше второго и на 10° больше третьего.
- Первый угол треугольника в два раза меньше второго и на 20° больше третьего.

- Сумма первого и второго углов треугольника вдвое меньше третьего угла.
- Кабель длиной 140 см разрезается на две части. Первая часть в пять раз длиннее второй.
- Кусок шланга длиной 48 м нужно разрезать на две части так, чтобы вторая часть была на 5 м длиннее первой.
Для вопросов с 9 по 18 напишите и решите уравнение, описывающее каждую взаимосвязь.
- Второй угол треугольника такой же величины, как и первый угол. Третий угол на 12° больше первого угла. Насколько велики углы?
- Два угла треугольника имеют одинаковую величину. Третий угол на 12° меньше первого угла. Найдите величину углов.
- Два угла треугольника имеют одинаковую величину. Третий угол в три раза больше первого. Насколько велики углы?
- Второй угол треугольника в два раза больше первого. Размер третьего угла на 20° больше первого. Насколько велики углы?
- Найдите размеры прямоугольника, если его периметр равен 150 см, а длина на 15 см больше ширины.

- Если периметр прямоугольника равен 304 см, а длина на 40 см больше ширины, найдите длину и ширину.
- Найдите длину и ширину прямоугольного сада, если его периметр равен 152 м, а ширина на 22 м меньше длины.
- Если периметр прямоугольника равен 280 м, а ширина на 26 м меньше длины, найдите его длину и ширину.
- Лаборант разрезает кусок трубки длиной 12 см на две части так, чтобы одна часть была в два раза длиннее другой. Как долго куски?
- Электрик разрезает 30-метровый кабель на две части. Одна часть на 2 м длиннее другой. Как долго куски?
Ключ ответа 4.5
задач по геометрии с решениями и пояснениями для 9 класса
Представлены подробные решения и полные пояснения к задачам по геометрии для 9 класса.
Ответы на вышеуказанные вопросы
|


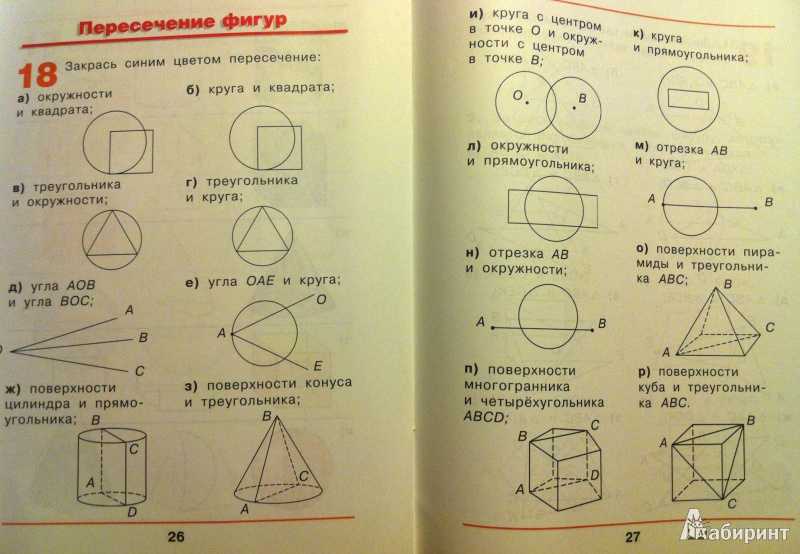
 Отсюда
Отсюда 



 Следовательно
Следовательно 
