Задача коши примеры решения: Решить задачу Коши для дифференциального уравнения с условиями: примеры

Содержание

Решение задачи Коши с примерами решения

Содержание:

Достаточное условие существования решения задачи Коши
Достаточные условия существования и единственности решения задачи Коши
Примеры с решением

Задача Коши. Одной из важнейших задач в теории дифференциальных уравнений является так называемая задача Коши. Для уравнения (2),

задача Коши, или начальная задача, ставится следующим образом: среди всех решений уравнения (2) найти такое решение

в котором функция у(х) принимает заданное числовое значение Уо при заданное числовом значении х0 независимой переменной х, т. е.

где и — заданные числа, так что решение (36) удовлетворяет условию:

При этом число называется начальным значением искомой функции, а число — начальным значением независимой переменной. В целом же числа и называются начальными данными решения (36), а условие (38) —начальным условием этого решения.

По этой ссылке вы найдёте полный курс лекций по высшей математике:

Высшая математика: лекции, формулы, теоремы, примеры задач с решением

Задачу Коши геометрически можно сформулировать так: среди всех интегральных кривых уравнения (2)’найти tj (рис. 6), которая проходит через заданную точку

Будем говорить, что задача Коши с начальными условиями (38) имеет единственное решение, если существует та кое число , что в интервале — определено решение такое, что и не существует решения, определенного в этом же интервале и не совпадающего с решением хотя бы в одной точке интервала

отличной от точки В противном случае, т. е. когда задача Коши с начальным условием (38) имеет не одно решение или же совсем не имеет решений, мы будем говорить, что в точке нарушается единственность решения задачи Коши.

Возможно вам будут полезны данные страницы:

Уравнения в полных дифференциалах

Аналитическое решение уравнения

Найти общее решение уравнения

Общее решение уравнения

Вопрос о единственности решения задачи Коши представляет исключительный интерес как для самой теории дифференциальных уравнений, так и для ее многочисленных приложений, ибо, зная, что решение задачи Коши единственно, мы, найдя решение, удовлетворяющее заданным начальным условиям, уверены, что других решений, удовлетворяющих тем же начальным условиям, нет.

В вопросах естествознания эго приводит к тому, что мы получаем вполне определенный, единственный закон явления, определяемый только дифференциальным уравнением и начальным условием. Иллюстрацией сказанного может служить хотя бы пример 1, рассмотренный во введении.

Заметим, что в простейшем случае задача Коши встречается нам уже в интегральном исчислении, именно там, по существу, доказывается, что если функция f(x) непрерывна в интервале (а, Ь),то единственным решением уравнения

принимающим значение принадлежит интервалу —любое заданное число, является функция*

Эго решение определено ео всем интервале (а, Ь).

Из формулы (40) легко усмотреть характер зависимости решения рассматриваемой задачи Коши как от независимой переменной, так и от начальных данных.

Прежде всего из курса анализа известно, что решение (40) является непрерывно дифференцируемой** функцией от независимой переменной х. Геометрически это означает, что через точку проходит одна и только одна интегральная кривая.

Эта интегральная кривая гладкая***. Она пересекается со всякой -прямой, параллельной оси Оу, не более чем в одной точке.

Из формулы (40) видно также, что решение задачи К о ш и дл я простейшего дифференциального уравнения (39) я в-ляется непрерывной и даже непрерывно дифференцируемой функцией начальных данных

Особые случаи задачи Коши. При постановке задачи Коши с начальными данными мы неявно предполагали, что числа х0 и уо конечны и что правая часть уравнения (2) определена и конечна в точке , т. е. уравнение (2) задает в точке определенное направление поля, причем последнее не параллельно оси Оу. Если правая часть уравнения (2) обращается в точке в бесконечность, то следует рассматривать перевернутое уравнение (.

и искать решение (рис. 7), удовлетворяющее начальному условию: . Единственная «особенность» решения этой задачи Коши состоит только в том, что в точке касательная к интегральной кривой параллельна оси Оу.

Совсем другое положение мы будем иметь, если в точке правая часть уравнения (2) по определена.

Предположим, что f(x, у) обращается в точке в неопределенность вида Тогда обычная постановка задачи Коши теряет смысл, так как через точку не проходит ни одна интегральная кривая.

В этом случае задача Коши ставится так:

найти решение вида [или обладающее свойством (28) [или (29)], т. е. найти решение, примыкающее к точке

Здесь, так же как и в основном случае задачи Коши, возникают вопросы существования и единственности решения.

Кроме того, здесь возникают и дополнительные вопросы:

1) имеют ли решения, примыкающие к точке , определенную касательную в этой точке? Дело в том, что само уравнение (2) в этом случае не предписывает никакого определенного направления касательной в такой точке ;

2) если интегральные кривые примыкают к точке с определенными направлениями касательной, то каковы эти направления? Сколько кривых входит по данному направлению? В примерах 3 и 4, рассмотренных в п. 4, все интегральные кривые уравнения (30) примыкают к точке (0,0) (где правая часть обращается в о — неопределенность вида ), имея в ней каждая свою касательную, в то время как ни одна из интегральных кривых уравнения (34) не примыкает к точке (0,0), так что для этого уравнения задача Коши с начальными данными не имеет ни одного решения.

В некоторых случаях возникает необходимость искать решения , удовлетворяющие условиям:

Указанные выше особые случаи задачи Коши исследуются в аналитической теории дифференциальных уравнений и в качественной теории дифференциальных уравнений. Во всех случаях задачи Коши наряду с вопросами существования и единственности возникают /вопросы о свойствах решения задачи Коши как функции независимой переменной (аналитический вид, дифференциальные и геометрические свойства и особенности «поведения во всей области существования) и как функции начальных данных. Рассмотрение этих вопросов составляет одну из основных задач теории дифференциальных уравнений.

Достаточное условие существования решения задачи Коши

Предположим, что правая часть уравнения (2) определена и непрерывна в некоторой области G изменения х и у. Тогда, как уже отмечалось раньше (п. 4), уравнение (2) определяет некоторое поле направлений, причем в силу только что сделанного предположения о непрерывности правой части уравнения (2) это ноле направлений непрерывно, так что направления в двух достаточно близких точках разнятся сколь угодно мало. Заметим, что из сделанного предположения о непрерывности

правой части уравнения (2) следует, что всякое решение этого уравнения (если оно существует) будет непрерывно дифференцируемым, так что всякая интегральная кривая будет гладкой. Всякая интегральная кривая, как уже было сказано в п. 4., обладает чем свойством, что в каждой ее точке направление карательной совпадает с направлением поля, определяемым дифференциальным уравнением в этой точке. Попытаемся, пользуясь этим свойством интегральной кривой, найти решение задачи Коши для уравнения (2) с начальными данными из области G.

Возьмем п области G некоторую точку (рис 8) Наклон поля в этой точке равен Проведем через точку -прямую с угловим коэффициентом

На этой прямой возьмем любую точку , принадлежащую области G, и через нее прощую области G, и через нее проведем прямую с угловым коэффициентом, равным наклону поля в этой точке, т. е. На последней прямой возьмем любую точку принадлежащую области G, и проведем через нее прямую с угловым коэффициентом и т. д. Такое же построение можно сделать и влево от точки . Построенная ломаная линия называется ломаной Эйлера.

Ясно, что можно построить бесчисленное множество ломаных Эйлера, проходящих через точку — Каждая из этих ломаных с достаточно короткими звеньями дает некоторое представление об интегральной кривой, проходящей через точку если эта интегральная кривая существует. Естественно ожидать, что .мы можем построить последовательность ломаных Эйлера, имеющую своим пределом (когда длины всех звеньев ломаной стремятся к пулю, а их число стремится к бесконечности) интегральную кривую, проходящую через точку Л<о(хо, Уо).

Можно доказать*, что при сделанном предположении относительно f(x, у) это действительно имеет место, так что для существования непрерывно дифференцируемого решения задачи Коши для уравнения (2) достаточно предположить, что его правая часть непрерывна в окрестности начальных данных (теорема Пеано).

Заметим, однако, что нс исключена возможность существования нескольких последовательностей ломаных Эйлера, проходящих через точку , каждая из которых стремится к своей интегральной кривой, так что в общем случае, нет оснований ожидать, что мы получим единственную интегральную кривую, проходящую через точку .

Более того, как показал М. Л. Лаврентьев**, единственность решения может нарушаться даже во всех точках непрерывности правой части уравнения (2).

Таким образом, теорема Пеано есть только теорема существования решения задачи Коши. Единственности решения она не гарантирует.

Достаточные условия существования и единственности решения задачи Коши

Поставим вопрос: каким условиям достаточно подчинить правую часть уравнения (2) в окрестности начальных данных чтобы через точку проходила одна и только одна интегральная кривая этого уравнения» В общем виде этот вопрос мы рассматриваем в гл. V, где пр* некоторых предположениях относительно правой части уравнения (2) мы доказываем существование и единственность решения задачи Коши и показываем, что свойства решения задачи Коши вполне определяются свойствами правой части уравнения (2) и начальными данным и. Сейчас мы приведем без дока-загельства основную теорему существования и единственности (теорему Пикара) для уравнения (2) в упрощенной формулировке.

Теорема. Пусть дано уравнение (2),

и поставлено начальное условие (38),

Предположим, что функция определена в некоторой замкнутой ограниченной области (рис. 9)

с точкой внутри (а и b — заданные положительные числа) и удовлетворяет в ней следующим двум условиям.

У 1. Функция непрерывна и следовательно, ограничена, т. е.

где М—постоянное положительное число, а(х, у) — любая точка области R;

II. Функция f(x, у) имеет ограничейную частную производную по аргументу у, т. е.:

где К — постоянное положительное число, а (х, у)—любая точка области R.

При этих предположениях уравнение (2) имеет единственное решение (36),

удовлетворяющее начальному условию (38). Это решение определено и непрерывно дифференцируемо в некоторой окрестности начального значения х0 независимой переменной х, а именно оно заведомо определено в интервале

где h есть наименьшее из чисел

Из этой теоремы, в частности, следует, что если правая часть уравнения (2) есть полином относительно х и у или любая другая функция, определенная и непрерывная относительно х и у вместе с частной производной по у при всех значениях х и у, то через любую точку проходит одна и только одна интегральная кривая, ибо во всяком прямоугольнике R с центром в точке (х0, уо) оба условия теоремы Пикара будут очевидно выполнены. В этом случае вся плоскость (х, у) будет заполнена не пересекающимися и не касающимися друг друга гладкими интегральными кривыми.

Примеры с решением

Пример 1.

Пусть дано уравнение

и поставлено начальное условие:

Так как правая часть уравнения (45) есть полином относительно х и у, то решение с любыми начальными условиями, в том числе и с начальным условием (46), существует и единственно.

Оценим область определения решения с начальным условием (46).

С этой целью построим прямоугольник R с центром в точке (0, 0),

причем в качестве а и b можно взять любые положительные числа. Будем иметь:

Отсюда видно, что h зависит от выбора чисел а к &*. В частности, при а = b — 1, получим:

Поэтому уравнение (45) имеет единственное решение, заведомо определенное в интервале и удовлетворяющее начальному условию (46). это решение непрерывно дифференцируемо.

С геометрической точки зрения полученный результат означает, что уравнение (45) имеет только одну интегральную кривую, проходящую через начало координат, причем эта интегральная кривая гладкая.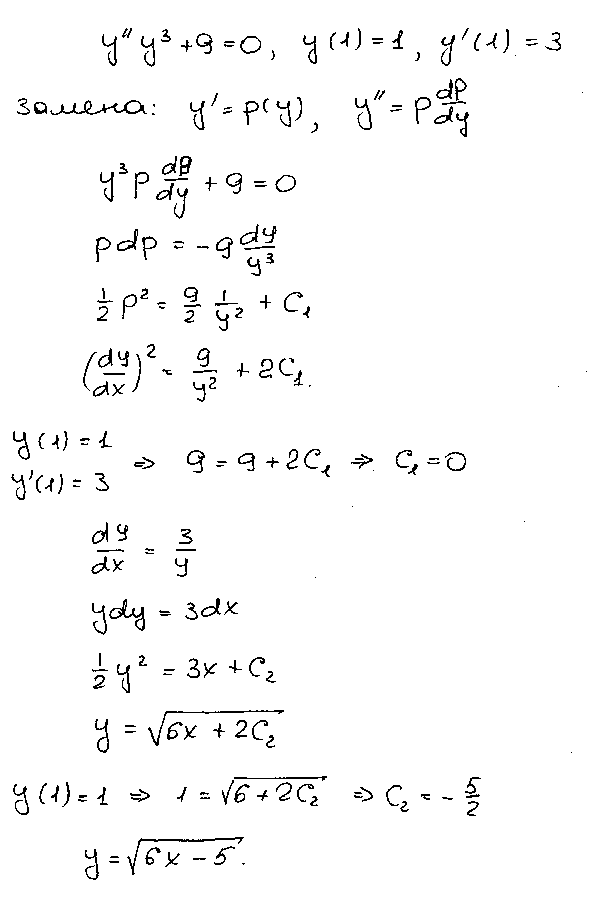

Этот результат приобретает особое значение, если принять во внимание, что уравнение (45) не интегрируется пи в элементарных функциях, пи в квадратурах от элементарных функций, в чем мы убедимся в п. 51. Установленный факт существования и единственноеги решения дает нам основание пытаться искать его другими методами и в том числе находить это решение приближенно.

Пример 2.

Найти решение уравнения

удовлетворяющее начальному условию:

Так как правая часть уравнения (50) вместе с ее частной производной по непрерывна при всех х и у, то через каждую точку плоскости (х, у) проходит единственная интегральная кривая. Это же будет иметь место и в начале координат. Но легко заметить, что у = 0 (ось Ох) есть решение уравнения (50) и это решение проходит через начало координат, так чго оно и будет искомым решением. В силу только что установленной единственности решения уравнение (50) не имеет других решений, проходящих через начало координат.

* Наибольшим значением h будет

Вообще, если в уравнении (2) функция f(x, у) удовлетворяет обоим условиям теоремы Пикара в некоторой окрестности заданной точки (х0, у0) и такова, что , то единственным решением этого уравнения, проходящим через точку , будет прямая

6.

02. Задача Коши для дифференциального уравнения первого порядка

Общее решение любого дифференциального уравнения первого порядка F(х; у; у’) = 0, как это следует из схемы его получения (1.3), содержит бесчисленное множество частных решений. Возникает естественный вопрос: как из этого множество частных решений выделить интересующее нас конкретное частное решение? Иначе говоря, как из множества интегральных кривых данного дифференциального уравнения выделить нужную интегральную кривую?

Ответ почти очевиден: для этого на плоскости Хоу нужно задать некоторую точку , через которую должна пройти искомая интегральная кривая. Тогда её уравнение и будет тем частным решением, которое выделяется из прочих (рис. 6.2).

Задание точки равносильно заданию условия для искомого, выделяемого из прочих, частного решения данного дифференциального уравнения. Это условие называется Начальным условием для дифференциального уравнения первого порядка F(х; у; у’) = 0. Начальным оно называется потому, что очень часто в реальных задачах по исследованию различного рода процессов роль независимой переменной Х играет время T, а начальным значением Х0 является начальный момент времени T0 (обычно T0 = 0). Тогда начальное условие показывает, какое значение У0 имела искомая функция , описывающая исследуемый процесс, в начальный момент времени Х0. Ну, а сама функция , если нас не интересует предистория процесса, то есть времена Х < х0, ищется для Х > х0.

Если дифференциальное уравнение первого порядка F(х; у; у’) = 0 задано вместе с начальным для него условием , То говорят, что для этого уравнения задана Задача Коши:

(2.1)

Решить её — это значит найти те частные решения дифференциального уравнения F(х; у; у’) = 0 , которые еще удовлетворяют и заданному начальному условию . С точки зрения рисунка 6.2 решить задачу Коши (2.1) – это значит найти уравнения всех интегральных кривых дифференциального уравнения F(х; у; у’) = 0, проходящих через начальную точку .

Как правило, задача Коши (2.1) имеет единственное решение . То есть через заданную начальную точку проходит единственная интегральная кривая дифференциального уравнения F(х; у; у’) = 0 (как на рис. 6.2). Но бывает, что задача Коши не имеет решений. То есть бывает, что ни одна из интегральных кривых не проходит через заданную начальную точку . Тогда такая точка называется Особой точкой дифференциального уравнения. А бывает, что задача Коши имеет несколько решений. То есть бывает, что через начальную точку проходит несколько интегральных кривых. Сколько решений будет у задачи Коши (2.1) и каковы они, выясняется в процессе её решения. А Схема решения задачи Коши (2.1) такова:

1. Решаем дифференциальное уравнение F(х; у; у’) = 0 и находим все его решения. То есть находим общее решение (общий интеграл) и возможные особые решения .

2. Подставляем начальные значения Х = х0 И У = у0 в общее решение и находим соответствующее значение (значения) константы С:

(2. 2)

3. Подставляем каждое из найденных значений С В общее решение и получаем частные решения

Являющиеся решением задачи Коши. Это те решения этой задачи, которые выделяются из общего решения дифференцированного уравнения F(х; у; у’) = 0.

4. Проверяем, нет ли среди особых решений Дифференциального уравнения F(х; у; у’) = 0 таких, которые удовлетворяют начальному условию У(х0) = у0. Если такие найдутся, они тоже будут решениями задачи Коши (2.1).

Пример1. Решить задачу Коши:

Решение.

1. Сначала решим дифференциальное уравнение . Оно уже решено ранее – его решение найдено в примере 3, §1:

— общее решение; – особое решение.

2. Подставим начальные значения В общее решение и найдем С:

3. Подставим в общее решение и получим частное решение

Эта функция является решением данной задачи Коши.

4. Обратим внимание на особое решение У=0. Начальному условию У(0)=1 оно не удовлетворяет, поэтому решением данной задачи Коши не является.

Ответ: — единственное решение поставленной задачи Коши.

Пример 2. Материальное тело поднято на высоту H и в начальный момент времени T=0 отпущено в свободное падение. Описать математически процесс падения тела. А именно, найти зависимость ν = ν(T) скорости ν падающего тела от времени T, и найти зависимость S = S(T) пути S, пройденного падающим телом, от времени T. Сопротивлением воздуха пренебречь.

Решение. Как известно, все свободно падающие тела падают с постоянным ускорением G ≈ 9,8 м/сек2 — с ускорением свободного падения. А так как ускорение – это производная от скорости, то получаем: . Это — дифференциальное уравнение первого порядка для искомой функции . Учтём еше, что в начальный момент времени T = 0 тело покоилось, а значит, выполняется начальное условие: . В итоге для определения функции Получаем задачу Коши:

Решим эту задачу.

1. Сначала решим дифференциальное уравнения:

Это – общее решение уравнения , содержащее все его решения. Особых решений у него нет.

2. Используем начальное условие и найдем С:

0 = G0+С => С = 0.

3. Подставим С=0 в общее решение V=Gt+C и получим окончательно: V=Gt. Это и есть решение поставленной задачи Коши (единственное). И заодно V=Gt — это искомая зависимость скорости V падающего тела от времени T.

А теперь займёмся поиском зависимости S=S(t) Пути S От времени T. Учтём, что и что . Тогда для определения этой зависимости получим следующую задачу Коши:

Решим эту задачу.

1. Сначала решим дифференциальное уравнение :

;

Это — общее решение уравнения , содержащее все его решения. Особых решений у него нет.

2. Используем начальное условие и найдём С:

3. Подставим С=0 в общее решение и получим окончательно: . Это и есть решение рассматриваемой задачи Коши. И заодно — это искомая зависимость пути S, проходимого свободно падающим телом, от времени T.

Ответ: — известные школьные формулы.

Пример3. Дать математическое описание демографического процесса (процесса изменение численности населения со временем) для достаточно крупного населённого региона, если в начальный момент времени численность населения региона составляла человек.

Решение. Пусть – искомая зависимость численности населения региона от времени . И пусть за время , прошедшее с некоторого момента до момента , родилось человек и умерло человек. Эти количества, очевидно, пропорциональны как исходной (в момент ) численности населения , так и величине временного промежутка . То есть

;

Здесь и – некоторые числовые коэффициенты, связанные соответственно с уровнем рождаемости и уровнем смертности в данном регионе. Тогда общее изменение численности населения за время найдется по формуле:

Здесь . Из получённого равенства следует: . Устремляя здесь (при этом, очевидно, и ), то есть переходя к бесконечно малым и , получим:

, или .

Это – дифференциальное уравнение первого порядка для искомой функции . Дополняя это заданным начальным условием , получим для этой функции задачу Коши:

Решим эту задачу.

1. Сначала решим дифференциальное уравнение . Функция является его очевидным частным решением. Но это, очевидно, не та функция, которую мы ищем – она не удовлетворяет начальному условию, да и вообще она означает, что население в регионе отсутствует.

Будем искать те решения уравнения для которых :

Итак, — общее решение дифференциального уравнения . В него, кстати, при С = 0 входит и отмеченное ранее нулевое решение . То есть в найденном общем решении содержатся все решения дифференциального уравнения.

2. Используем начальное условие и найдём С:

3. Подставим в общее решение и получим искомое решение задачи Коши:

Это и есть искомая зависимость Численности населения региона от времени .

Проанализируем эту зависимость.

а) Если , то численность населения экспоненциально растёт со временем (рис. 6.3(а)).

б) Если , то численность населения Экспоненциально убывает со временем (рис. 6.3(б)).

в) Если , то , то есть численность населения региона не меняется (рис. 6.3(в).

Какой именно будет величина для данного региона, можно выяснить опытным путём. Пусть, например, перепись населения показала, что в некоторый момент времени в регионе проживало человек. Подставляя эти данные в формулу , можем найти :

Примечание. Полученная формула будет верно описывать демографический процесс в регионе, если уровень рождаемости и уровень смертности в нем не меняются со временем. То есть если коэффициенты и рождаемости и смертности не меняются со временем. А значит, если не меняется со временем и итоговый коэффициент . Но это, как известно, не так: с течением времени, в силу разных причин, ситуация и со смертностью, и с рождаемостью может существенно измениться. Поэтому полученную формулу при конкретном числовом значении оправданно применять лишь на протяжении достаточно ограниченного периода времени. В другой период времени тоже можно применять эту формулу, но уже при другом значении .

Пример 4. Рассмотрим задачу о математической модели естественного роста выпуска продукции.

Пусть — объем продукции некоторого предприятия, реализованной моменту времени . Будем считать, что вся продукция реализуется по некоторой фиксированной цене за единицу продукции независимо от объема продаж . Это значит, что рынок данной продукции длительное время является насыщенным – удается продавать по фиксированной цене практически любые объемы этой продукции.

Доход от продаж составит: . Будем считать, что некоторая часть этого дохода используется в качестве инвестиций в производство выпускаемой продукции. То есть объем инвестиций составит:

(2.4)

Здесь – так называется Норма инвестиций. Она показывает, какая часть дохода возвращается в производство.

Чем больше объем инвестиций , тем быстрее растёт объем производства . В модели естественного роста это значит, что скорость роста объема производства (так называемая Акселерация производства) пропорциональна объему инвестиций :

. (2.5)

Здесь

(2.6)

— так называемая Норма акселерации, которая показывает, каким должен быть объём инвестиций , чтобы обеспечить единичную скорость роста объема производства (обеспечить рост на единицу продукции за единицу времени). Подставляя (2.4) в (2.5), получим

, (2.7)

Где – числовой коэффициент. Равенство (2.7) представляет собой дифференциальное уравнение первого порядка для функции . Дополняя его некоторым начальным условием , получим задачу Коши:

(2.8)

Эта задача полностью совпадает с задачей Коши для демографического процесса (см. пример 3). Значит, у них полностью совпадают и решения:

(2.9)

Заметим, что условие постоянства цены единицы продаваемой продукции, то есть условие насыщенности рынка, не может выполнятся всегда, при любых . С увеличением объема продаж на некотором этапе рынок насыщается, спрос на товар падает, и дальнейшее увеличении объема продаж возможно лишь при снижении цены на него – в соответствии с классической убывающей кривой спроса . Если учесть эту зависимость от , то выражение (2.4) для примет вид:

(2.10)

А вместо (2.7) из (2.5) получим:

, (2.11)

Где . Это дифференциальное уравнение вместе с начальным условием составит задачу Коши:

(2.12)

Для определения функции , характеризующей объем продаж при насыщенном спросе, когда рост объема продаж возможен лишь при снижении цены на продаваемую продукцию. Эта функция, естественно, будет отличаться от функции (2.9) (будет более сложной).

Упражнения

1. Сформулировать и решить задачу по определению скорости V=V(T) свободно падающего тела массой M при условии, что учитывается сопротивление воздуха, пропорциональное скорости падения тела.

Ответ: .

2. Сформулировать и решить задачу по определению объема У=y(t) реализованной продукции, если известно, что кривая спроса Р= р(у) задаётся уравнением Р=2-у; норма инвестиций M=0,5; норма акселерации ; У(0)=0,5 – начальное условие.

Ответ:

3. При условиях предыдущей задачи 2 найти эластичность объема продаж относительно цены Р и определить условия, при которых продажи продукции являются эластичными и неэластичными.

Ответ: .

Если 0,5<Y<1, то есть если , то , и продажи представляют собой эластичный процесс (продажи растут относительно быстрее снижения цены). Доход от продаж при снижении цены возрастает. А если 1<Y<2, то есть если , то , и продажи представляют собой неэластичный процесс (продажи растут относительно медленнее снижения цены). Доход от продаж растёт при увеличении цены товара (см. §7 главы 4).

< Предыдущая		Следующая >

Ошибка

Перейти к основному содержанию

Вся размещенная на ресурсе информационная продукция предназначена для детей, достигших возраста шестнадцати лет (16+)

Извините, не удалось найти запрашиваемый Вами файл

Подробнее об этой ошибке

Перейти на. .. Перейти на…Новостной форумКомплексные числа (с приложениями к задачам электротехники)Лекционный материал по теме «Комплексные числа»Разбор типовых задач задач по теме «Комплексные числа»Примеры решения задач по теме «Комплексные числа»КОМПЛЕКСНЫЕ ЧИСЛАКомплексные числа. Основы линейной алгебры. Системы линейных уравненийТеория функций комплексного переменного. Операционное исчислениеПрезентация по теме «Комплексные числа»Дополнительный материал к темеОсновы линейной алгебры с приложениями в других разделах математикиЛекционный материал по теме «Матрицы. Определители»Лекционный материал по теме «Системы линейных алгебраических уравнений (СЛАУ). Применение СЛАУ в экономике»Лекционный материал по теме «Линейные операторы»Примеры решения по теме «Системы линейных алгебраических уравнений»ЛИНЕЙНАЯ АЛГЕБРАКомплексные числа. Основы линейной алгебры. Системы линейных уравненийЛинейная алгебра для экономистовМатрицы. ОпределителиВекторная алгебра.Аналитическая геометрияЛекционный материал по теме «Векторная алгебра. Линейные операции над векторами»Лекционный материал по теме «Скалярное, векторное и смешанное произведения векторов»Примеры решения задач по теме «Векторная алгебра. Линейные операции над векторами»Примеры решения задач по теме «Скалярное, векторное и смешанное произведения векторов»ВЕКТОРНАЯ АЛГЕБРАВекторная алгебра и аналитическая геометрияПрезентация по теме «Векторная алгебра»Векторная алгебра.Аналитическая геометрияТеоретический материал по теме «Метод координат на плоскости и в пространстве»Лекционный материал по теме «Прямая на плоскости»Лекционный материал по теме «Кривые второго порядка»Лекционный материал по теме «Прямая в пространстве»Лекционный материал по теме «Плоскость в пространстве»Лекционный материал по теме «Поверхности второго порядка»Примеры решения задач по теме «Прямая на плоскости»Примеры решения задач по теме «Кривые второго порядка»Примеры решения задач по темам «Прямая и плоскость в пространстве»АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯВекторная алгебра и аналитическая геометрияСправочный материал «Прямая на плоскости»Справочный материал «Кривые второго порядка»Справочный материал «Прямая и плоскость в пространстве»Линейная алгебра для экономистовПрезентация по теме «Прямая на плоскости»Презентация по теме «Уравнения плоскости и прямой в пространстве»▶ Виртуальный тренажер «Прямая на плоскости» 👨‍🎓Введение в анализНачала анализаЛекционный материал по теме «Множества, функции, основные характеристики функций. Основные элементарные функции»Лекционный материал по теме «Предел функции, основные теоремы о пределах.Замечательные пределы. Бесконечно малые функции»Лекционный материал по теме «Непрерывность функции»Примеры решения задач по теме «Множества, функции, основные характеристики функций. Основные элементарные функции»Примеры решения задач по теме «Предел функции. Раскрытие математических неопределенностей»Примеры решения задач по теме «Непрерывность функции»ВВЕДЕНИЕ В АНАЛИЗУпражнения для самостоятельного решения Тест «Введение в анализ»Презентация по теме «Введение в анализ»1. Понятие функцииПрименение функций в экономической теории и практикеПрименение пределов в экономических расчетахПриложение понятия непрерывности функций в экономике▶ Виртуальная справочная «Тригонометрические функции» 👨‍🎓Дифференциальное исчисление функций одной переменнойПриложения дифференциального исчисления функции одной переменнойЛекционный материал по теме «Дифференциальное исчисление функции одной переменной»Лекционный материал по теме «Основные теоремы дифференциального исчисления. Правила Лопиталя»Лекционный материал по теме «Формулы Тейлора и Маклорена»Лекционный материал по теме «Приложения дифференциального исчисления»Примеры решения задач по теме «Дифференциальное исчисление функций одной переменной»ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙТест «Основные правила и формулы дифференцирования»Тест «Дифференциальное исчисление функций одной переменной»Основы дифференцирования. Часть 1Основы дифференцирования. Часть 2Основы дифференцирования. Часть 3Приложения производной Исследование функций, Примеры решения задачПрименение производных при решении экономических задачИнтегральное исчисление функции одной переменнойЛекционный материал по теме «Неопределенный интеграл»Лекционный материал по теме «Определенный интеграл»Практическое занятие 1. Непосредственное интегрирование (неопределённый интеграл)Практическое занятие 2. Интегрирование заменой переменной (неопределённый интеграл)Практическое занятие 3. Интегрирование по частям. Интегрирование выражений, содержащих квадратный многочлен (неопределённый интеграл)Практическое занятие 4. Интегрирование рациональных дробей (неопределенный интеграл)Практическое занятие 5. Определенный интегралПримеры решения задач по теме «Неопределенный интеграл»Примеры решения задач по теме «Определенный интеграл»ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙТест «Таблица основных неопределенных интегралов»Тест «Интегрирование функций одной переменной»1. Неопределенный интеграл. Основы интегрирования2. Интегрирование иррациональных выражений 3. Интегрирование тригонометрических выражений 4. Определенный интегралДифференциальное исчисление функций нескольких переменныхЛекционный материал по теме «Функции нескольких переменных»Примеры решения задач по теме «Функции нескольких переменных»ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХТест «Дифференциальное исчисление функций нескольких переменных»1. Функции нескольких переменныхПрименение функций нескольких переменных в экономикеОбыкновенные дифференциальные уравненияОбыкновенные дифференциальные уравнения и их приложенияДифференциальные уравнения первого порядкаДифференциальные уравнения высших порядковСистемы дифференциальных уравнений и устойчивость их решенийЛекционный материал по теме «Дифференциальные уравнения 1-го порядка»Лекционный материал по теме «Дифференциальные уравнения высших порядков»ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯТест «Обыкновенные дифференциальные уравнения»1. Дифференциальные уравнения 1-го порядка2. Дифференциальные уравнения высших порядковСпециальные разделы высшей математикиСпециальные разделы высшей математики: практикум Кратные, криволинейные и поверхностные интегралы. Элементы теории поляПоверхностные интегралы. Векторный анализЛекционный материал по теме «Двойные интегралы»Примеры решения задач по теме «Двойные интегралы»КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ2. Двойные интегралыРядыЛекционный материал по теме «Числовые ряды»Лекционный материал по теме «Функциональные ряды»Примеры решения задач по теме «Ряды»1. Числовые ряды2. Функциональные ряды3. Разложение функций в степенные рядыТеория функций комплексного переменного. Операционное исчисление.Основы теории функций комплексного переменногоОперационное исчисление.Теория функций комплексного переменного. Операционное исчислениеТеория вероятностей Теория вероятностей (случайные события)Вероятность, случайные процессы, математическая статистикаТеория вероятностей. Случайные процессы: практикумЛекционный материал по теме «Основные подходы к определению вероятности»Лекционный материал по теме «Алгебра событий. Основные теоремы о вероятности»Лекционный материал по теме «Дискретные случайные величины»Лекционный материал по теме «Непрерывные случайные величины»Лекционный материал по теме «Числовые характеристики случайных величин»Лекционный материал по теме «Моменты и другие характеристики распределений»Лекционный материал по теме «Нормальное распределение»Практическое занятие 1. КомбинаторикаПрактическое занятие 2. Действия над событиями. Вероятность событияПрактическое занятие 3. Теоремы умножения и сложения вероятностей событийПрактическое занятие 4. Формула полной вероятности Практическое занятие 5. Схема Бернулли. Локальная и интегральная теоремы ЛапласаПрактическое занятие 6. Дискретные случайные величины. Числовые характеристикиПрактическое занятие 7. Непрерывные случайные величины. Классические законы распределения НСВПримеры решения задач по теме «Комбинаторика»Примеры решения задач по теме «Классическое определение вероятности»Примеры решения задач по теме «Теоремы сложения и умножения»Примеры решения задач по теме «Формула полной вероятности. Формулы Байеса»Примеры решения задач по теме «Схема независимых испытаний Бернулли»Примеры решения задач по теме «Дискретные случайные величины»Примеры решения задач по теме «Основные числовые характеристики дискретных случайных величин»Примеры решения задач по теме «Непрерывные случайные величины»Примеры решения задач по теме «Основные числовые характеристики непрерывных случайных величин»Примеры решения задач по теме «Классические законы распределения дискретных случайных величин»Примеры решения задач по теме «Классические законы распределения непрерывных случайных величин»Таблица значений функции ЛапласаТЕОРИЯ ВЕРОЯТНОСТЕЙТест по разделу «Случайные события»Тест по теме «Числовые характеристики случайных величин»Тест по теме «Дискретные случайные величины»Тест по теме «Непрерывные случайные величины»Основные подходы к определению вероятностиАлгебра событий. Основные теоремы о вероятностиТеория вероятностей (Лыткина Е.М.,Чихачев А.С., 2013)Математическая статистикаОсновы математической статистикиМатематическая статистика: практикумПримеры решения задач по математической статистикиМАТЕМАТИЧЕСКАЯ СТАТИСТИКАТест по разделу «Математическая статистика». Тема «Статистическое распределение. Точечные и интервальные оценки параметров распределения»Тест по разделу «Математическая статистика». Тема «Статистические гипотезы. Корреляционный и регрессионный анализ»Вероятность, случайные процессы, математическая статистикаСтатистический метод и основы его примененияВероятностно-статистические методы на примере задач исследования работы железнодорожного транспорта Марковские процессы и СМО. Учебное пособиеЛекционный материал по теме «Марковский процесс с дискретным временем»Лекционный материал по теме «Марковский процесс с непрерывным временем»Лекционный материал по теме «Системы массового обслуживания»Примеры решения задач по теме «Марковские процессы»СЛУЧАЙНЫЕ ПРОЦЕССЫЛабораторные работы Вероятность, случайные процессы, математическая статистикаТеория вероятностей. Случайные процессы. ПрактикумЛекция «Марковские процессы»Цепи МарковаСистемы массового обслуживания (СМО)СМОВыбор группы*Тест «Таблица основных неопределенных интегралов»*Тест «Интегрирование функций одной переменной»*Тест «Дифференциальное исчисление функций нескольких переменных»*Тест «Обыкновенные дифференциальные уравнения»*Тест по разделу «Случайные события»*Тест по теме «Дискретные случайные величины»*Тест по теме «Непрерывные случайные величины»*Тест по теме «Числовые характеристики случайных величин»*Тест «Введение в анализ»*Тест «Основные правила и формулы дифференцирования»*Тест «Дифференциальное исчисление функций одной переменной»*Экзаменационный тест «Таблица основных неопределенных интегралов»*Экзаменационный тест «Интегрирование функций одной переменной»*Экзаменационный тест «Дифференциальное исчисление функций нескольких переменных»*Экзаменационный тест «Обыкновенные дифференциальные уравнения»Контрольная работа. Дифференциальное исчисление функций нескольких переменныхКонтрольная работа. Неопределенный интеграл (методы интегрирования)Контрольная работа. Неопределенный интеграл (интегрирование рациональных дробей)Контрольная работа. Определенный интегралКонтрольная работа. Обыкновенные дифференциальные уравненияКонтрольная работа 1. Теория вероятностей (случайные события)Контрольная работа 2. Теория вероятностей (характеристики дискретной случайной величины)Контрольная работа 3. Теория вероятностей (характеристики непрерывной случайной величины)Контрольная работа 4. Теория вероятностей (классические законы распределения дискретной случайной величины)Контрольная работа 5. Теория вероятностей (классические законы распределения непрерывной случайной величины)Экзамен Математика (2 семестр). СОД.1,2,3-19-1 (И,З)ЭКЗАМЕН. Математика (3 семестр)_СОД.1,2,3-19 (з)

Дифференциальные уравнения | Открытые видеолекции учебных курсов МГУ

Курс «Дифференциальные уравнения» читается студентам второго курса физического факультета МГУ имени М. В. Ломоносова в 4 семестре.

В рамках дисциплины «Дифференциальные уравнения» изложены основные понятия и теоремы, относящиеся к дифференциальным уравнениям, особое внимание уделяется приближенным методам решения и исследования дифференциальных уравнений, методам численного решения как начальных, так и краевых задач.

В курсе рассмотрены классические теоремы о существовании и единственности решений некоторых классов дифференциальных уравнений и систем, изложены традиционные методы исследования линейных задач. В курсе изучается качественная теория нелинейных дифференциальных уравнений, фазовая плоскость, теория устойчивости.

Список всех тем лекций

Лекция 1. Введение.
Основные понятия Решение обыкновенных дифференциальных уравнений

Лекция 2. Обыкновенные дифференциальные уравнения первого порядка.
Определение первого интеграла ОДУ и динамической системы Примеры физических задач, приводящие к дифференциальным уравнениям Простейшие ОДУ, интегрируемые в квадратурах Уравнения с разделяющимися переменными Автономные уравнения движения материальной точки на прямой Линейное уравнение (скалярное) Задача Коши для линейного ДУ однородного для неоднородного (метод вариации постоянной)

Лекция 3. Теорема существования и единственности решения задачи Коши.
Задача Коши для линейного ДУ неоднородного (продолжение) Теорема существования и единственности решения задачи Коши для скалярного ОДУ первого порядка Геометрическая интерпретация Эквивалентное интегральное уравнение (лемма 1) Метод последовательный приближений (метод Пикара) Доказательство существования решения задачи Коши О единственности решения интегрального уравнения

Лекция 4. Задача Коши для неоднородного ДУ. Теоремы Чаплыгина.
Доказательство единственности решения задачи Коши Теорема существования и единственности решения задачи Коши в случае, когда правая часть непрерывна и удовлетворяет условию Липшица в полосе Замечания и примеры Метод дифференциальных неравенств Теорема Чаплыгина о дифференциальных неравенствах Теорема Чаплыгина о существовании и единственности решения задачи Коши

Лекция 5. Задача Коши для нормальной системы ОДУ. ДУ n-го порядка.
Замечания к теоремам Чаплыгина Пример применения теоремы Чаплыгина Непрерывная зависимость решения задачи Коши от начальных условий и параметров в правой части Постановка задачи Теорема о непрерывной зависимости решения задачи Коши от параметров в правой части Теорема существования и единственности решения задачи Коши (без доказательства) Теорема существования и единственности решения задачи Коши в случае, когда правая часть непрерывна и удовлетворяет условию Липшица в полосе (без доказательства) Теорема о непрерывной зависимости решения задачи Коши от параметров в правой части (без доказательства) Сведение их к системе уравнений 1-го порядка Теорема существования и единственности решения задачи Коши Линейные ОДУ n-го порядка

Лекция 6. Линейные ОДУ n-го порядка. Однородное уравнение.
Теорема существования и единственности решения задачи Коши Следствия линейности уравнения Однородное уравнение Определитель Вронского Теорема о линейной зависимости системы функций Теорема о линейной независимости решений однородного уравнения Теорема о существовании фундаментальной системы решений (ФСР)

Лекция 7. Линейные ОДУ n-го порядка. Неоднородное уравнение.
Теорема о представлении общего решения через ФСР Общее решение неоднородного уравнения Функция Коши: построение частного решения неоднородного уравнения Общее решение однородного уравнения Структура ФСР в случае кратных корней характеристического уравнения

Лекция 8. Системы линейных уравнений..
Системы линейных уравнений Теорема существования и единственности решения задачи Коши Следствия линейности векторного уравнения Определитель Вронского Теорема о линейной зависимости системы вектор-функций Теорема о связи линейной независимости решений однородной системы с определителем Вронского Теорема о существовании ФСР Теорема о представлении общего решения через ФСР Общее решение неоднородной системы Матрица Коши

Лекция 9. Системы с постоянными коэффициентами. Краевые задачи.
Системы с постоянными коэффициентами Структура ФСР в случае простых собственных значений матрицы системы Структура ФСР в случае кратных собственных значений матрицы системы Постановка задачи Тождество Лагранжа Теорема единственности решения краевой задачи

Лекция 10. Функция Грина и её свойства.
Теоремы о достаточных условиях существования только тривиального решения у однородной задачи Необходимые условия разрешения неоднородной задачи Функция Грина и ее свойства Существование функции Грина Теорема о представлении решения с помощью функции Грина Единственность функции Грина Нелинейные задачи Метод стрельбы

Лекция 11. Теорема Нагумо. Теория устойчивости.
Теорема существования решения в случае ограниченной правой части (метод стрельбы) Понятие нижнего и верхнего решений краевой задачи, теорема Нагумо о существовании решения Примеры Асимптотическая устойчивость

Лекция 12. Устойчивость по Ляпунову. Классификация точек покоя.
Первый метод Ляпунова – исследование устойчивости решения по первому приближению Второй метод Ляпунова – метод функций Ляпунова Классификация точек покоя системы двух линейных уравнений первого порядка

Лекция 13. Фазовая плоскость и фазовые траектории. Асимптотические методы.
Постановка задачи Система первого приближения Фазовая плоскость Уравнение с квадратичной нелинейностью Понятие регулярно и сингулярно возмущенных задач Регулярные возмущения

Лекция 14. Регулярные и сингулярные возмущения. ДУ в частных производных.
Регулярные возмущения Теорема Тихонова Линейные однородные уравнения Квазилинейные уравнения

59.

Задача Коши, начальные условия. Теорема существования и единственности решения задачи Коши для уравнения . Особые точки. Особые решения. Примеры.

http://www.nsc.ru/rus/textbooks/akhmerov/ode_unicode/m-21/m-21.html

НАЧАЛЬНЫЕ УСЛОВИЯ

— условия при постановке задачи Коши для дифференциальных уравнений. Для обыкновенного дифференциального уравнения, разрешенного относительно старшей производной:

Н. у. состоят в задании производных (данных Коши)

где — произвольная фиксированная точка области определения функции F;эта точка наз. начальной точкой искомого решения. Задачу Коши (1), (2) часто наз. также начальной задачей.

Для дифференциального уравнения с частными производными, записанного в нормальной форме относительно выделенной переменной V.

Н. у. состоят в задании производных (данные Коши):

от искомого решения и( х, t )этого уравнения на гиперплоскости t=0 (носителя начальных условий).

60.Уравнение 1-го порядка с разделяющимися переменными.

Уравнением с разделенными переменными называется дифференциальное уравнение вида

f(x)dx + g(y)dy = 0

с непрерывными функциями f(х) и g(y).

Равенство

где C — произвольная постоянная, определяет общий интеграл уравнения с разделёнными переменными.

Начальное условие для уравнения f(x)dx + g(y)dy = 0 можно задавать в виде y(x₀) = y₀ или в виде x(y₀) = x₀ .

Уравнением с разделяющимися переменными называется дифференциальное уравнение вида

f₁(x)g₁ (y)dx + f₂(x) g₂(y)dy =0 .

Функции f₁(x), g₁(y), f₂(x), g₂(y) непрерывны в cвоих областях определения и g₁(y)f₂(x) ≠ 0 .

Разделив обе части уравнения на отличное от нуля произведение g₁(y)f₂(x), получим уравнение с разделенными переменными

Общий интеграл этого уравнения имеет вид

Решение уравнения в области, где g₁(y)f₂(x) = 0 требует специального обсуждения.

61. Однородное уравнение 1-го порядка. Определение однородной функции

Определение однородного дифференциального уравнения

Дифференциальное уравнение первого порядка

называется однородным, если правая часть удовлетворяет соотношению

для всех значений t. Другими словами, правая часть должна являться однородной функцией нулевого порядка по отношению к переменным x и y:

Однородное дифференциальное уравнение можно также записать в виде

или через дифференциалы:

где P(x,y) и Q(x,y) − однородные функции одинакового порядка.

Определение однородной функции

Функция P(x,y) называется однородной функцией порядка n, если для всех t > 0 справедливо следующее соотношение:

Решение однородных дифференциальных уравнений

Однородное дифференциальное уравнение можно решить с помощью подстановки y = ux, которая преобразует однородное уравнение в уравнение с разделяющимися переменными. Дифференциальное уравнение вида

преобразуется в уравнение с разделяющимися переменными посредством переноса начала системы координат в точку пересечения прямых линий, заданных в уравнении. Если указанные прямые параллельны, то дифференциальное уравнение сводится к уравнению с разделяющимися переменными путем замены переменной:

62. Линейное уравнение 1-го порядка. Методы решения: метод Лагранжа, метод Бернулли. Структура решения линейного уравнения.

Линейным дифференциальным уравнением первого порядка называется уравнение вида

Здесь a(x) и b(x) — известные, непрерывные на [a;b] функции.

Доказано, что если функции a(x) и b(x) непрерывны на [a;b] , то для любой начальной точки (x₀, y₀) , x₀∈ [a; b] , задача Коши

имеет единственное решение y = y(x) на [a;b].

Рассматривают однородные и неоднородные линейные уравнения первого порядка:

Общее решение линейного уравнения 1-го порядка можно найти с помощью замены y(x) = u(x) · v(x) .

История решения задачи Коши реферат по статистике | Сочинения Статистика

Скачай История решения задачи Коши реферат по статистике и еще Сочинения в формате PDF Статистика только на Docsity! История решения задачи Коши Задача Коши – это центральная задача в теории дифференциальных уравнений, так как является неотъемлемой частью моделирования систем и нахождения решения этой модели с целью возможности ее управления и прогнозирования. Поэтому рассматривать историю ее решения можно только совместно с историей развития общей теории дифференциальных уравнений. Теория дифференциальных уравнений является одним из самых больших разделов современной математики. Чтобы охарактеризовать ее место в современной математической науке, прежде всего, необходимо подчеркнуть основные особенности теории дифференциальных уравнений, состоящей из двух обширных областей математики: теории обыкновенных дифференциальных уравнений и теории уравнений с частными производными. Первая особенность — это непосредственная связь теории дифференциальных уравнений с приложениями. Характеризуя математику как метод проникновения в тайны природы, можно сказать, что основным путем применения этого метода является формирование и изучение математических моделей реального мира. Изучая какие-либо физические явления, исследователь, прежде всего создает его математическую идеализацию или, другими словами, математическую модель, то есть, пренебрегая второстепенными характеристиками явления, он записывает основные законы, управляющие этим явлением, в математической форме. Очень часто эти законы можно выразить в виде дифференциальных уравнений. Такими оказываются модели различных явлений механики сплошной среды, химических реакций, электрических и магнитных явлений и др. Исследуя полученные дифференциальные уравнения вместе с дополнительными условиями, которые, как правило, задаются в виде начальных и граничных условий (эти условия и есть главный компонент задачи Коши), математик получает сведения о происходящем явлении, иногда может узнать его прошлое и будущее. Изучение математической модели математическими методами позволяет не только получить качественные характеристики физических явлений и рассчитать с заданной степенью точности ход реального процесса, но и дает возможность проникнуть в суть физических явлений, а иногда предсказать и новые физические эффекты. Бывает, что сама природа физического явления подсказывает и подходы, и методы математического исследования. Критерием правильности выбора математической модели является практика, сопоставление данных математического исследования с экспериментальными данными. Для составления математической модели в виде дифференциальных уравнений нужно, как правило, знать только локальные связи и не нужна информация обо всем физическом явлении в целом. Математическая модель дает возможность изучать явление в целом, предсказать его развитие, делать количественные оценки изменений, происходящих в нем с течением времени. Напомним, что на основе анализа дифференциальных уравнений так были открыты электромагнитные волны, и только после экспериментального подтверждения Герцем фактического существования электромагнитных колебаний стало возможным рассматривать уравнения Максвелла как математическую модель реального физического явления. Как известно, теория обыкновенных дифференциальных уравнений начала развиваться в XVII веке одновременно с возникновением дифференциального и интегрального исчисления. Можно сказать, что необходимость решать дифференциальные уравнения для нужд механики, то есть находить траектории движений, в свою очередь, явилась толчком для создания Ньютоном нового исчисления. Органическая связь физического и математического ясно проявилась в методе флюксий Ньютона. Законы Ньютона представляют собой математическую модель механического движения. Через обыкновенные дифференциальные комплексного переменного и в различных областях математического анализа. Уравнение Лапласа является простейшим представителем широкого класса так называемых эллиптических уравнений. Здесь, может быть, уместно вспомнить слова А. Пуанкаре: «Математика — это искусство давать разным вещам одно наименование». Эти слова являются выражением того, что математика изучает одним методом, с помощью математической модели, различные явления действительного мира. Так же как и уравнение Лапласа, важное место в теории уравнений с частными производными и ее приложениях занимает уравнение теплопроводности. Это уравнение встречается в теории теплопередачи, в теории диффузии и многих других разделах физики, а также играет важную роль в теории вероятностей. Оно является наиболее простым представителем класса так называемых параболических уравнений. Некоторые свойства решений уравнения теплопроводности напоминают свойства решений уравнения Лапласа, что находится в согласии с их физическим смыслом, так как уравнение Лапласа описывает, в частности, стационарное распределение температуры. Уравнение теплопроводности было выведено и впервые исследовано в 1822 году в знаменитой работе Ж. Фурье «Аналитическая теория тепла», которая сыграла важную роль в развитии методов математической физики и теории тригонометрических рядов. Волновое уравнение описывает различные волновые процессы, в частности распространение звуковых волн. Оно играет важную роль в акустике. Это представитель класса так называемых гиперболических уравнений. Изучение основных уравнений математической физики дало возможность провести классификацию уравнений и систем с частными производными. И.Г. Петровским в 30-е годы были выделены и впервые изучены классы эллиптических, параболических и гиперболических систем, которые теперь носят его имя. В настоящее время это наиболее хорошо изученные классы уравнений. Важно отметить, что для проверки правильности математической модели очень важны теоремы существования решений соответствующих дифференциальных уравнений, так как математическая модель не всегда адекватна конкретному явлению и из существования решения реальной задачи (физической, химической, биологической) не следует существование решения соответствующей математической задачи. В настоящее время важную роль в развитии теории дифференциальных уравнений играет применение современных электронных вычислительных машин. Исследование дифференциальных уравнений часто облегчает возможность провести вычислительный эксперимент для выявления тех или иных свойств их решений, которые потом могут быть теоретически обоснованы и послужат фундаментом для дальнейших теоретических исследований. Вычислительный эксперимент стал также мощным средством теоретических исследований в физике. Он проводится над математической моделью физического явления, но при этом по одним параметрам модели вычисляются другие параметры и делаются выводы о свойствах изучаемого физического явления. Цель вычислительного эксперимента — построение с необходимой точностью с помощью ЭВМ за возможно меньшее машинное время адекватного количественного описания изучаемого физического явления. В основе такого эксперимента очень часто лежит численное решение системы уравнений с частными производными. Отсюда происходит связь теории дифференциальных уравнений с вычислительной математикой и, в частности, с такими ее важными разделами, как метод конечных разностей, метод конечных элементов и другие. Итак, первая черта теории дифференциальных уравнений — ее тесная связь с приложениями. Другими словами, можно сказать, что теория дифференциальных уравнений родилась из приложений. В этом своем разделе — теории дифференциальных уравнений – математика, прежде всего выступает как неотъемлемая часть естествознания, на которой основывается вывод и понимание количественных и качественных закономерностей, составляющих содержание наук о природе. Именно естествознание является для теории дифференциальных уравнений замечательным источником новых проблем, оно в значительной мере определяет направление их исследований, дает правильную ориентацию этим исследованиям. Более того, дифференциальные уравнения не могут плодотворно развиваться в отрыве от физических задач. И не только потому, что природа богаче человеческой фантазии. Развитая в последние годы теория о неразрешимости некоторых классов уравнений с частными производными показывает, что даже очень простые по форме линейные уравнения с частными производными с бесконечно дифференцируемыми коэффициентами могут не иметь ни одного решения не только в обычном смысле, но также и в классах обобщенных функций, и в классах гиперфункций, и, следовательно, для них не может быть построена содержательная теория (теория обобщенных функций, обобщающая основное понятие математического анализа — понятие функции, была создана в середине нашего века трудами С.Л. Соболева и Л. Шварца). Изучение уравнений с частными производными в общем случае — столь сложная задача, что если кто-нибудь наугад напишет какое-нибудь даже линейное дифференциальное уравнение с частными производными, то с большой вероятностью ни один математик не сможет о нем сказать что- либо и, в частности, выяснить, имеет ли это уравнение хотя бы одно решение. Задачи физики и других естественных наук снабжают теорию дифференциальных уравнений проблемами, из которых вырастают богатые содержанием теории. Однако бывает и так, что математическое исследование, рожденное в рамках самой математики, через значительное Начало качественной теории дифференциальных уравнений было положено в работах знаменитого французского математика Пуанкаре. Эти исследования Пуанкаре по обыкновенным дифференциальным уравнениям привели его к созданию основ современной топологии. Таким образом, дифференциальные уравнения находятся как бы на перекрестке математических дорог. С одной стороны, новые важные достижения в топологии, алгебре, функциональном анализе, теории функций и других областях математики сразу же приводят к прогрессу в теории дифференциальных уравнений и тем самым находят путь к приложениям. С другой стороны, проблемы физики, сформулированные на языке дифференциальных уравнений, вызывают к жизни новые направления в математике, приводят к необходимости совершенствования математического аппарата, дают начало новым математическим теориям, имеющим внутренние законы развития, свои собственные проблемы. В своих «Лекциях о развитии математики в XIX столетии» Ф. Клейн писал: «Математика в наши дни напоминает оружейное производство в мирное время. Образцы восхищают знатока. Назначение этих вещей отходит на задний план.» Несмотря на эти слова, можно сказать, что нельзя стоять за «разоружение» математики. Вспомним, например, что древние греки изучали конические сечения задолго до того, как было открыто, что по ним движутся планеты. Действительно, созданная древними греками теория конических сечений не находила своего применения почти две тысячи лет, пока Кеплер не воспользовался ею для создания теории движения небесных тел. Исходя из теории Кеплера, Ньютон создал механику, являющуюся основой всей физики и техники. Другим таким примером может служить теория групп, зародившаяся в конце XVIII века (Лагранж, 1771 год) в недрах самой математики и нашедшая лишь в конце XIX века плодотворное применение сначала в кристаллографии, а позднее в теоретической физике и других естественных науках. Возвращаясь к современности, заметим, что важнейшие научно- технические задачи, такие, как овладение атомной энергией, космические полеты, были успешно решены в Советском Союзе также благодаря высокому теоретическому уровню развития математики в нашей стране. Таким образом, в теории дифференциальных уравнений ясно прослеживается основная линия развития математики: от конкретного и частного через абстракцию к конкретному и частному. Как уже говорилось, в XVIII и XIX веках изучались в основном конкретные уравнения математической физики. Из общих результатов теории уравнений с частными производными в этот период следует отметить построение теории уравнений с частными производными первого порядка (Монж, Коши, Шарпи) и теорему Ковалевской. Теоремы о существовании аналитического (то есть представимого в виде степенного ряда) решения для обыкновенных дифференциальных уравнений, а также для линейных систем уравнений с частными производными были доказаны ранее Коши (Cauchy, 1789 — 1857). Эти вопросы рассматривались им в нескольких статьях. Но работы Коши не были известны Вейерштрассу, который предложил С.В. Ковалевской изучить вопрос о существовании аналитических решений уравнений с частными производными в качестве докторской диссертации. (Отмечу, что Коши опубликовал 789 статей и большое число монографий; его наследие огромно, поэтому неудивительно, что некоторые его результаты могли остаться некоторое время незамеченными. ) С.В. Ковалевская в своей работе опиралась на лекции Вейерштрасса, где рассматривалась задача с начальными условиями для обыкновенных дифференциальных уравнений. Исследование Ковалевской придало вопросу о разрешимости задачи Коши для уравнений и систем с частными производными в определенном смысле завершающий характер. Пуанкаре высоко ценил эту работу Ковалевской. Он писал: «Ковалевская значительно упростила доказательство и придала теореме окончательную форму». Теорема Ковалевской занимает важное место в современной теории уравнений с частными производными. Ей, пожалуй, принадлежит одно из первых мест по числу применений в различных областях теории уравнений с частными производными: теорема Хольмгрена о единственности решения задачи Коши, теоремы существования решения задачи Коши для гиперболических уравнений (Шаудер, Петровский), современная теория разрешимости линейных уравнений и многие другие результаты используют теорему Ковалевской. Важным достижением теории уравнений с частными производными явилось создание на рубеже XIX века теории интегральных уравнений Фредгольма и решение основных краевых задач для уравнения Лапласа. Можно считать, что основные итоги развития теории уравнений с частными производными XIX века подведены в учебнике Э. Гурса «Курс математического анализа», изданном в 20-е годы нашего века. Следует отметить большой вклад, который внесли в теорию дифференциальных уравнений и математическую физику труды М.В. Остроградского по вариационным методам, труды А.М. Ляпунова по теории потенциала и по теории устойчивости движения, труды В.А. Стеклова по обоснованию метода Фурье и другие. Тридцатые и последующие годы 20 века были периодом бурного развития общей теории уравнений с частными производными. В работах И.Г. Петровского были заложены основы общей теории систем уравнений с частными производными, выделены классы систем уравнений, которые в настоящее время носят название эллиптических, гиперболических и параболических по Петровскому систем, исследованы их свойства, изучены характерные для них задачи. В теорию уравнений с частными производными все глубже стали проникать идеи функционального анализа. Было введено понятие обобщенного решения как элемента некоторого функционального пространства. Идея обобщенного решения систематически проводилась в крайне затруднительно. Необходим асимптотический анализ задачи, что и приводит к задачам усреднения. Много работ в последние годы посвящено изучению поведения решений эволюционных уравнений (то есть уравнений, описывающих процессы, развивающиеся во времени, и удовлетворяющим условия задачи Коши) при неограниченном возрастании времени и возникающих при этом так называемых аттракторов. Продолжает привлекать внимание исследователей вопрос о характере гладкости решений краевых задач в областях с негладкой границей, большое число работ в последние годы посвящено изучению конкретных нелинейных задач математической физики. За последние полтора — два десятка лет сильно изменилось лицо качественной теории обыкновенных дифференциальных уравнений. Одним из важных достижений является открытие предельных режимов, которые получили название аттракторов. Оказалось, что наряду со стационарными и периодическими предельными режимами возможны предельные режимы совершенно иной природы, а именно такие, в которых каждая отдельная траектория неустойчива, а само явление выхода на данный предельный режим структурно устойчиво. Открытие и подробное изучение для систем обыкновенных дифференциальных уравнений таких предельных режимов, называемых аттракторами, потребовало привлечения средств дифференциальной геометрии и топологии, функционального анализа и теории вероятностей. В настоящее время происходит интенсивное внедрение этих математических понятий в приложения. Так, например, явления, происходящие при переходе ламинарного течения в турбулентное при повышении чисел Рейнольдса, описываются аттрактором. Изучение аттракторов предпринято также и для уравнений с частными производными. Другим важным достижением теории обыкновенных дифференциальных уравнений явилось изучение структурной устойчивости систем. При использовании любой математической модели возникает вопрос о корректности применения математических результатов к реальной действительности. Если результат сильно чувствителен к малейшему изменению модели, то сколь угодно малые изменения модели приведут к модели с совершенно иными свойствами. Такие результаты нельзя распространять на исследуемый реальный процесс, так как при построении модели всегда проводится некоторая идеализация и параметры определяются лишь приближенно. Это привело А.А. Андронова и Л.С. Понтрягина к понятию грубости системы обыкновенных дифференциальных уравнений или понятию структурной устойчивости. Это понятие оказалось очень плодотворным в случае малой размерности фазового пространства (1 или 2), и в этом случае вопросы структурной устойчивости были детально изучены. В 1965 году Смейл показал, что при большой размерности фазового пространства существуют системы, в некоторой окрестности которых нет ни одной структурно устойчивой системы, то есть такой, что при малом изменении векторного поля она остается в определенном смысле эквивалентной первоначальной. Этот результат имеет фундаментальное значение для качественной теории обыкновенных дифференциальных уравнений, так как показывает неразрешимость задачи топологической классификации систем обыкновенных дифференциальных уравнений, и может быть сравним по своему значению с теоремой Лиувилля о неразрешимости дифференциальных уравнений в квадратурах. К важным достижениям можно отнести построение А. Н. Колмогоровым теории возмущений гамильтоновых систем, обоснование метода усреднения для многочастичных систем, развитие теории бифуркаций, теории возмущений, теории релаксационных колебаний, дальнейшее глубокое изучение показателей Ляпунова, создание теории оптимального управления процессами, описываемыми дифференциальными уравнениями. Таким образом, теория дифференциальных уравнений в настоящее время представляет собой исключительно богатый содержанием, быстро развивающийся раздел математики, тесно связанный с другими областями математики и с ее приложениями. Бурбаки, говоря об архитектуре математики, так характеризует ее современное состояние: «Дать в настоящее время общее представление о математической науке — значит заниматься таким делом, которое, как кажется, с самого начала наталкивается на почти непреодолимые трудности благодаря обширности и разнообразию рассматриваемого материала. Статьи по чистой математике, публикуемые во всем мире в среднем в течение одного года, составляют многие тысячи страниц. Не все они, конечно, имеют одинаковую ценность; тем не менее, после очистки от неизбежных отбросов оказывается, что каждый год математическая наука обогащается массой новых результатов, приобретает все более разнообразное содержание и постоянно дает ответвления в виде теорий, которые беспрестанно видоизменяются, перестраиваются, сопоставляются и комбинируются друг с другом. Ни один математик не в состоянии проследить это развитие во всех подробностях, даже если он посвятит этому всю свою деятельность. Многие из математиков устраиваются в каком-либо закоулке математической науки, откуда они не стремятся выйти и не только почти полностью игнорируют все то, что не касается предмета их исследований, но не в силах даже понять язык и терминологию своих собратьев, специальность которых далека от них». (Н. Бурбаки, «Очерки по истории математики», М.: ИЛ, 1963 г.) Однако нельзя, как мне кажется, отрицать значение для математических исследований даже тех, кто находится «в закоулке» математической науки. Основное русло математики, как и большой реки, питают прежде всего небольшие ручейки. Крупные открытия, прорыв фронта исследований очень часто обеспечиваются и подготавливаются 0 0 1 Fприводили задачи о дви жении точки в сопротивляющейся среде, 0 0 1 Fрассмотренные впервые Ньюто ном, как и многие экстремальные задачи механики, физики, геометрии, явившиеся предметом развивающегося 0 0 1 Fвариационного исчисления, в част ности, важное для практических приложений нахождение геодезических линий на поверхности. Решение задач статики и динамики механических систем со сложными связями также требовало интегрирования нелинейных уравнений, удовлетворяющим условиям задачи Коши. Поэтому одним из направлений формировавшейся теории 0 0 1 Fобыкновен ных дифференциальных уравнений явилось разыскание методов решения нелинейных уравнений в конечной форме. Вопрос о самой 0 0 1 Fвозможности ре шения в таком виде еще не возникал. Именно в этом плане развивались методы понижения порядка и интегрирующего множителя. Наряду с этим назрела потребность в создании приемов решения линейных уравнений. Это объясняется тем, что в начале XVIII в. 0 0 1 Fприобре тает все большее значение исследование малых колебаний материальных систем с конечным числом степеней свободы, в первую 0 0 1 Fочередь в предпо ложении, что отсутствует сопротивление среды. В связи 0 0 1 Fс конструирова нием достаточно точных маятниковых часов, необходимых 0 0 1 Fдля астрономи ческих наблюдений, и с первыми гравиметрическими 0 0 1 Fпроблемами (опреде ление ускорения силы тяжести в зависимости от широты, выяснение сжатия Земли у полюсов) потребовалось дальнейшее 0 0 1 Fразвитие аналитической тео рии математического и физического маятников, начала которой положил ранее Гюйгенс. И если в XVII в. вопрос 0 0 1 Fограничивался, как правило, изу чением изохронного движения одной точки, то теперь в центр внимания встали системы любого конечного числа материальных точек. Отсюда берут начало и первые исследования в области колебательных процессов систем с бесконечным числом степеней свободы, начиная со знаменитой задачи о колебании струны. Весь этот комплекс вопросов требовал создания теории линейных 0 0 1 Fдиф ференциальных уравнений и их систем, как с постоянными, так и с переменными коэффициентами. Третье большое направление было обусловлено в значительной степени нуждами опять-таки небесной механики. Мы имеем в виду численные методы приближенного интегрирования дифференциальных уравнений, без которых невозможным оказалось изучение сложных нелинейных систем, не интегрируемых в конечном виде. Наряду с усовершенствованием метода степенных рядов, успешно применявшихся в 0 0 1 Fпредшествующем сто летии, уже в середине XVIII в. получают применение тригонометрические ряды. Несколько позже теория дифференциальных уравнений обогащается первым общим методом аппроксимации решения 0 0 1 Fдля любых уравнений пер вого и второго порядков. Наконец, четвертым направлением теории обыкновенных 0 0 1 Fдифферен циальных уравнений было изучение особых решений. Оно определялось главным образом запросами дифференциальной геометрии, 0 0 1 Fнапример ис следованием огибающих и изогональных траекторий 0 0 1 Fсемейств кривых (поз же семейств поверхностей). Это направление, связанное прежде всего с изучением семейств плоских кривых и, в 0 0 1 Fчастности, семейств интеграль ных линий, играло в XVIII в. меньшую роль, чем три названных ранее. Однако уже в начале второй четверти XIX в. тесно связанная с теорией особых решений проблема единственности решений задач с начальными условиями, а вместе с тем и общая проблема 0 0 1 Fсуществования решений задачи Коши при обрели в теории обыкновенных 0 0 1 Fдифференциальных уравнений первосте пенное значение. Список литературы 1. Одинец В.П. Зарисовки по истории математики. Сыктывкар, 2005г. 2. Депман И. Я. История арифметики., Гос.-уч. — пед.изд. М., 1959. 3. Стройк Д. Я. Краткий очерк истории математики., Наука, М., 1990. 4. Юшкевич А. П. История математики с древнейших времен до начала XIX века. т. I, II, III, Наука, М., 1970. 5. Математика XIX века // под. ред. Колмогорова А. Н. и Юшкевича А. П. т. I, II, III, Наука, М., 1978. 6. Гнеденко Б. В. Очерки по истории математики в России., ОГИЗ ТТЛ, М.- Л. 1946.

2.2.2: Задача Коши с начальным значением

Последнее обновление
Сохранить как PDF

Идентификатор страницы: 2169

Эрих Мирземанн
Университет Лейпцига

Рисунок 2.2.2.1: Начальная задача Коши

Определение. Кривая $\Gamma$ называется нехарактерной , если
$$
x_0′(s)a_2(x_0(s),y_0(s))-y_0′(s)a_1(x_0( с),у_0(с))\не=0.
\]

Теорема 2.1. Предположим, что $a_1,\ a_2,\ a_2\in C^1$ в их аргументах начальные данные $x_0,\ y_0,\ z_0\in C^1[s_1,s_2]$ и $ \Гамма$ нехарактерна.

Тогда существует окрестность $\cal{C}$ такая, что существует ровно одно решение $u$ начальной задачи Коши.

Доказательство. (i) Существование. Рассмотрим следующую начальную задачу для системы характеристических уравнений для ($\star$):
\begin{eqnarray*}
x'(t)&=&a_1(x,y,z)\\
y’ (t)&=&a_2(x,y,z)\\
z'(t)&=&a_3(x,y,z)
\end{eqnarray*}
с начальными условиями
\begin{eqnarray*}
x(s,0)&=&x_0(s)\\
y(s,0)&=&y_0(s)\\
z(s,0)&=&z_0(s) .
\end{eqnarray*}
Пусть $x=x(s,t)$, $y=y(s,t)$, $z=z(s,t)$ будет решением , $s_1\le s\le s_2$, $|t|<\eta$ для $\eta>0$. Мы покажем, что этот набор кривых, см. рис. 2.2.2.1, определяет поверхность. Чтобы показать это, рассмотрим функции, обратные $s=s(x,y)$, $t=t(x,y)$ функции $x=x(s,t)$, $ y=y(s,t)$ и показать, что $z(s(x,y),t(x,y))$ является решением исходной задачи Коши. Обратные функции $s$ и $t$ существуют в окрестности $t=0$, так как
$$
\det \frac{\partial(x,y)}{\partial(s,t)}\Big|_{t=0}=
\left|\begin{array}{cc}x_s&x_t\ \y_s&y_t\end{array}\right|_{t=0}
=x_0′(s)a_2-y_0′(s)a_1\not=0,
$$
и начальная кривая $\Gamma$ нехарактерно по предположению.

Установить
$$
u(x,y):=z(s(x,y),t(x,y)),
$$
тогда $u$ удовлетворяет начальному условию, так как
$$
u(x,y)|_{t=0}=z(s,0)=z_0(s).
$$
Следующее вычисление показывает, что $u$ также является решением дифференциального уравнения ($\star$).
\begin{eqnarray*}
a_1u_x+a_2u_y&=&a_1(z_ss_x+z_tt_x)+a_2(z_ss_y+z_tt_y)\\
&=&z_s(a_1s_x+a_2s_y)+z_t(a_1t_x+a_2t_y)\\ 9003 s_xx_t+s_yy_t)+z_t(t_xx_t+t_yy_t)\\
&=&a_3
\end{eqnarray*}
, так как $0=s_t=s_xx_t+s_yy_t$ и $1=t_t=t_xx_t+t_yy_t$.

(ii) Уникальность. Предположим, что $v(x,y)$ — второе решение. Рассмотрим точку $(x’,y’)$ в окрестности кривой $(x_0(s),y(s))$, $s_1-\epsilon\le s\le s_2+\epsilon $, $\epsilon>0$ маленький. Обратные параметры: $s’=s(x’,y’)$, $t’=t(x’,y’)$, см. рис. 2.2.2.2.

Рисунок 2.2.2.2: Доказательство единственности

Пусть
$$
{\mathcal{A}}:\ \ x(t):=x(s’,t),\ y(t):=y (s’,t),\ z(t):=z(s’,t)
$$
— решение указанной выше начальной задачи для характеристических дифференциальных уравнений с начальными данными
$$
x(s ‘,0)=x_0(s’),\ y(s’,0)=y_0(s’),\ z(s’,0)=z_0(s’).
$$
Согласно построению эта кривая лежит на поверхности $\mathcal{S}$, определяемой $u=u(x,y)$ и $u(x’,y’)=z (с’,т’)$. Набор
$$
\psi(t):=v(x(t),y(t))-z(t),
$$
затем
\begin{eqnarray*}
\psi'(t)&= &v_xx’+v_yy’-z’\\
&=&x_xa_1+v_ya_2-a_3=0
\end{eqnarray*}
и
$$
\psi(0)=v(x(s’,0),y (s’,0))-z(s’,0) =0
$$
, так как $v$ является решением дифференциального уравнения и по условию удовлетворяет начальному условию. Таким образом, $\psi(t)\equiv0$, т.е. е.,
$$
v(x(s’,t),y(s’,t))-z(s’,t)=0.
$$
Установить $t=t’$, затем
$$
v(x’,y’)-z(s’,t’)=0,
$$
что показывает, что $v(x’,y’)=u(x’,y’)$ из-за \(z(s’,t’)=u(x’,y’)\ ).

$\Box$

Примечание. В общем случае уникальности нет, если исходная кривая $\Gamma$ является характеристической кривой, см. упражнение и рис. 2.2.2.3, иллюстрирующий этот случай.

Рисунок 2. 2.2.3: Множественные решения

Примеры

Пример 2.2.2.1:

Рассмотрим задачу Коши с начальными значениями1\mbox{-функция}.
$$
Эти исходные данные нехарактеристичны, так как $y_0’a_1-x_0’a_2=-1$. Решение связанной системы характеристических уравнений
$$
x'(t)=1,\ y'(t)=1,\ u'(t)=0
$$
при начальных условиях
$$
x(s,0)=x_0(s),\ y(s,0)=y_0(s),\ z(s,0)=z_0(s)
$$
определяется как
$$
x= t+x_0(s),\ y=t+y_0(s),\ z=z_0(s) ,
$$
i. е.,
$$
x=t+s,\ y=t+1,\ z=z_0(s).
$$
Из этого следует, что $s=x-y+1,\ t=y-1$ и что $u=z_0(x-y+1)$ является решением начальной задачи Коши. 9{-k_1x}+k_2\right)(1-u)
$$
с начальными данными
$$
u(x,0)=0,\ x>0,\\mbox{and}\ u(0, у)=и_0(у),\у>0.
$$
Здесь константы $k_j$ положительны, эти константы определяют скорость рассматриваемых реакций и функция $u_0(y)$ задана. Переменная $х$ — это время, а $у$ — высота трубы, например, в которой происходит химическая реакция, а $и$ — концентрация химического вещества. 1\). Проекция ${\mathcal C}_1\cup {\mathcal C}_2$ исходной кривой на $(x,y)$-плоскость имеет угол в начале координат, см. рис. 2.2.2.4. 9{-k_1x}+k_2\справа)(1-z).
$$
Отсюда следует $x=t+c_1$, $y=t+c_2$ с константами $c_j$. Таким образом, проекцией характеристических кривых на $(x,y)$-плоскость являются прямые, параллельные $y=x$. Задачи с начальными значениями будем решать в доменах $\Omega_1$ и $\Omega_2$, см. рис. 2.2.2.4, отдельно.

(i) Проблема начального значения в $\Omega_1$. Исходные данные:
$$
x_0(s)=s,\ y_0(s)=0, \ z_0(0)=0,\ s\ge 0.
$$
Отсюда следует 9{-k_1x}-k_2x-\frac{k_0}{k_1}\right).
\end{eqnarray*}
Если $u_0(0)>0$, то \(u_1

Примечание. Такая задача с разрывными начальными данными называется задачей Римана . См. упражнение для другой задачи Римана.

Случай, когда известно решение уравнения

Здесь мы увидим, что мы немедленно получаем решение начальной задачи Коши, если решение однородное линейное уравнение
$$
a_1(x,y)u_x+a_2(x,y)u_y=0
$$
известно.

Пусть
$$
x_0(s),\ y_0(s),\ z_0(s),\ s_1 $$
начальные данные и $u=\phi(x,y )$ — решение дифференциального уравнения. Предположим, что
$$
\phi_x(x_0(s),y_0(s))x_0′(s)+\phi_y(x_0(s),y_0(s))y_0′(s)\not=0
$
$ доволен. Установите
$$
g(s)=\phi(x_0(s),y_0(s))
$$
и пусть $s=h(g)$ будет обратной функцией.

Решение исходной задачи Коши задается выражением $u_0\left(h(\phi(x,y))\right)$.

Это следует из того, что в рассматриваемой задаче композиция решения снова является решением, см. упражнение, а так как
$$
u_0\left(h(\phi(x_0(s),y_0(s))\ right)=u_0(h(g))=u_0(s).
\]

Пример 2.2.2.3:

Рассмотрим уравнение
$$
u_x+u_y=0
$$
с начальными данными
$$
x_0(s)=s,\ y_0(s)=1,\ u_0(s)\ \mbox{данная функция}.
$$
Решением дифференциального уравнения является $\phi(x,y)=x-y$. Таким образом,
$$
\phi((x_0(s),y_0(s))=s-1
$$
и
$$
u_0(\phi+1)=u_0(x-y+1)
$ $
— это решение проблемы

Авторы и ссылки

Профессор, доктор Эрих Мирземанн (Университет Лейпцига)
Интегрировано Джастином Маршаллом.

Эта страница под названием 2.2.2: Задача Коши с начальным значением распространяется по незаявленной лицензии, ее автором, ремиксом и/или куратором был Эрих Мирземанн.

Наверх

Была ли эта статья полезной?

Тип изделия
Раздел или Страница
Автор
Эрих Мирземанн
Показать страницу TOC
нет
Теги

Задача Коши для дифференциального уравнения

В этом разделе мы рассмотрим пример решения задачи с начальным значением (или задачи Коши) для неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами.

Проблема начального значения обычно возникает при анализе процессов, для которых известны дифференциальный закон эволюции и начальное состояние. Например, рассмотрим задачу подсчета населения. После многих лет наблюдений и обработки данных ученые придумали несколько дифференциальных уравнений, с помощью которых мы можем описать количество людей на Земле. Это называется популяционной моделью, и на самом деле существует несколько различных подходов к этой проблеме. Предположим, мы хотим узнать, сколько людей будет там до 2120 года. И здесь возникает проблема с начальным значением. Мы знаем текущую численность населения (наше начальное значение) и имеем дифференциальное уравнение, поэтому, чтобы найти будущее количество людей, мы должны решить задачу Коши. 2x 9{rx} и получаем характеристическое уравнение.

Как вы могли заметить, фактически мы получили квадратное уравнение для $r$. Его решения следующие:

r_{1,2}=\frac{-1\pm\sqrt{1-4}}{2}=\frac{-1\pm\sqrt{-3}}{2 }=\frac{-1\pm i \sqrt{3}}{2}=-\frac{1}{2}\pm i\frac{\sqrt{3}}{2}

, где i=\ sqrt{-1} — мнимая единица. Вспомните комплексные числа, если это звучит для вас незнакомо.

Таким образом, у нас есть два комплексных корня. В этом случае общее решение записывается в виде: 9{i=N}y_i

Давайте подробнее рассмотрим наше уравнение. В нашем случае неоднородным членом является g(x)=\frac{1}{2}-\frac{1}{2} \cos{2x}. Таким образом, мы можем разбить это неоднородное уравнение на два уравнения:

y” + y’ + y =\frac{1}{2} и y” + y’ + y =-\frac{1}{2} \ cos{2x}

Нам нужно найти частные решения этих уравнений, а затем сложить их, чтобы получить частное решение нашего исходного уравнения.

Рассмотрим первое уравнение y” + y’ + y =\frac{1}{2}

В этом случае \alpha=\beta=0

Следовательно, частным решением будет y=C

Подставим его в рассматриваемое уравнение:

C»+C’+C=\frac{1}{2 } => C=\frac{1}{2}.

Таким образом, частным решением этого уравнения является y=\frac{1}{2}.

Перейдем ко второму y” + y’ + y =-\frac{1}{2}\cos{2x}

В этом случае \alpha=0, \beta=2i и характеристическими корнями являются r_ {1,2}=\frac{1}{2}\pm\frac{\sqrt{3}}{2}i. Итак, запишем частное решение в виде: 9*:

y’=2A\cos{2x}-2B\sin{2x}

y”=-4A\sin{2x}-4B\cos{2x}

Теперь подставьте их в уравнение:

y” + y’ + y = -\frac{1}{2}\cos{2x}

-4A\sin{2x}-4B\cos{2x}+2A\cos{2x}-2B\sin{ 2x}+A\sin{2x}+B\cos{2x}=-\frac{1}{2}\cos{2x}

Перед \sin{2x} имеем: -4A-2B+A =0

Рядом \cos{2x}: -4B+2A+B=-\frac{1}{2}

Имеем систему двух линейных уравнений для нахождения неопределенных коэффициентов A,B:

\left\ { \begin{align}-4A-2B+A=0\\-4B+2A+B=-\frac{1}{2}\end{align}\right.

\left\{ \begin{align}A=-\frac{2}{3}B\\-3B-\frac{4}{3}B=-\frac{1}{2}\end{ выровнено}\справа.

\left\{ \begin{align}A=-\frac{2}{3}B=-\frac{1}{13}\\B=\frac{3}{26}\end{align} \Правильно.

Следовательно, частное решение для второго уравнения: y=-\frac{1}{13}\sin {2x}+\frac{3}{26} \cos{2x}

Мы нашли частное решения для обоих уравнений, так что теперь мы можем построить частное решение для всего исходного уравнения в виде суммы двух полученных:{\ frac {1} {2} x} \ sin ({\ frac {\ sqrt {3}} {2} x}) + \ frac {1} {2} — \ frac {1} {1} 3 \cos{2x}+\frac{3}{26}\sin{2x}

ШАГ 4. Начальные условия

Мы нашли решение с произвольными константами. По сути, это не одно решение, а куча. Однако, применяя начальные условия, мы можем зафиксировать значения этих констант.

Заданы следующие начальные условия: y(0)=1, y'(0)= -\frac{9}{2}:

Начиная с первого:

откуда

C_1=1-\frac{1}{2}-\frac{3}{26}=\frac{26-13-3}{26}=\frac{10}{26}=\frac {5}{13}

Чтобы применить второе условие, мы сначала должны найти производную y'(x):

\begin{aligned} y’=-\frac{1}{2}C_1 e^ {-\frac{1}{2} x} \cos(\frac{\sqrt{3}x}{2})-\frac{\sqrt{3}}{2} C_1 e^{-\frac{ 1}{2}x} \sin(\frac{\sqrt{3} x}{2})-\frac{1}{2} C_2 e^{-\frac{1}{2} x} \sin (\frac{\sqrt{3} x}{2})+&\\\frac{\sqrt{3} x}{2}C_2 e^{-\frac{1}{2} x} \cos( \frac{\sqrt{3} x}{2})-\frac{2}{13} \cos{2x}-\frac{3}{13} \sin{2x}\end{align} 9{-\frac{1}{2}\cdot 0} \cos(\frac{\sqrt{3}\cdot 0}{2})-\frac{2}{13} \cos(2\cdot 0) -\frac{3}{13} \sin(2\cdot 0)=-\frac{1}{2}C_1+\frac{\sqrt{3}}{2}C_2-\frac{2}{13} =-\frac{9}{2}\end{aligned}

откуда

\frac{\sqrt{3}}{2}C_2=-\frac{9}{2}+\frac{1}{ 2} C_1+\frac{2}{13}=-\frac{9}{2}+\frac{5}{26}+\frac{2}{13}=\frac{-9\cdot 13+5 +4}{26}=-\frac{108}{26}=-\frac{54}{13}

Наконец, мы можем найти значение второй константы C_2:

C_2=-\frac{54 }{13}\cdot \frac{2}{\sqrt{3} }=-\frac{108}{13\sqrt{3}} 9{-\frac{1}{2} x} \sin(\frac{\sqrt{3}x}{2})+\frac{1}{2}-\frac{1}{13}\sin{ 2x}+\frac{3}{26} \cos{2x}

, и это наш ответ.

Подведение итогов.

Если вас попросили решить задачу Коши для дифференциального уравнения, вот основные шаги:

1. Решите дифференциальное уравнение и получите общее решение.

2. Примените начальные условия, чтобы зафиксировать значения констант.

Хорошо, теперь немного подробнее о пункте 1. Сначала проверьте, однородно ли ваше уравнение. Если нет, то посмотрите на неоднородный термин. Помните, что описанный выше метод работает только для неоднородностей специального вида. Допустимые формы g(x) перечислены выше. Если это так, то вы можете продолжить.

Шаг 1. Найдите общее решение соответствующего однородного уравнения.

Шаг 2. Найти частное решение методом неопределенных коэффициентов.

Шаг 3. Найдите все решение, сложив результаты шагов 1 и 2.

Шаг 4. Задайте начальные условия, зафиксируйте значения констант.

Шаг 5. Подставляем все необходимое и получаем решение задачи Коши.

Когда закончите, проверьте свои ответы. Для этого подставьте ваш результат в исходное уравнение и условия. Также вы можете использовать математические онлайн-калькуляторы.

Имейте в виду, что если неоднородная часть вашего уравнения не в нужном виде и вы не можете применить неопределенные коэффициенты, есть еще другие варианты. Например, вы можете использовать метод вариаций параметров (иногда называемый методом вариаций констант), который является общим и применим для любой формы неоднородности.

0 Акции

Фейсбук
Твиттер
Копировать ссылку

Задача Коши — Математическая энциклопедия

Одна из фундаментальных задач теории дифференциальных уравнений (обыкновенных и в частных производных): найти решение (интеграл) дифференциального уравнения, удовлетворяющее так называемым начальным условиям (начальные данные ). Задача Коши обычно возникает при анализе процессов, определяемых дифференциальным законом и начальным состоянием, формулируемым математически в терминах дифференциального уравнения и начального условия (отсюда терминология и выбор обозначений: начальные данные заданы для $ t = 0 $ и решение требуется при $ t \geq 0 $). Задачи Коши отличаются от краевых задач тем, что область, в которой должно быть определено искомое решение, не указывается заранее. Тем не менее задачи Коши, как и краевые задачи, определяются наложением предельных условий для решения на (части) границы области определения.

Основные вопросы, связанные с задачами Коши, следующие:

1) Существует ли (хотя и локально) решение?

2) Если решение существует, то какому пространству оно принадлежит? В частности, какова его область существования?

3) Является ли решение уникальным?

4) Если решение единственно, то является ли задача корректной, т.е. является ли решение в каком-то смысле непрерывной функцией начальных данных?

Простейшая задача Коши — найти функцию $ u ( x) $ определяется на полупрямой $ x \geq x _ {0} $, удовлетворяющее обыкновенному дифференциальному уравнению первого порядка

$$ \тег{1} \ гидроразрыв {дю} {dx} знак равно f ( х, и) $$

($ ф $ — заданная функция) и принимающая заданное значение $ u _ {0} $ в $ х = х _ {0} $:

$$ \тег{2} ты ( Икс _ {0} ) знак равно ты _ {0} . $$

В геометрических терминах это означает, что, рассматривая семейство интегральных кривых уравнения (1) в $ ( x, u) $- плоскости нужно найти кривую, проходящую через точку $ ( x _ {0} , u _ {0} ) $.

Первое предложение о существовании такой функции (в предположении, что $ f $ непрерывна для всех $ x $ и непрерывно дифференцируемой по $u$) была доказана А. Л. Коши (1820–1830) и обобщена Э. Пикаром (1891–1896) (который заменил дифференцируемость условием Липшица по $u$). Оказывается, что в этих условиях задача Коши имеет единственное решение, которое к тому же непрерывно зависит от начальных данных. Современные представления о проблеме Коши по существу являются далеко идущим обобщением этой проблемы.

Тот факт, что вопросы с 1) по 4) глубоко затрагивают самую суть дела, т. е. для удовлетворительного ответа на них требуется наложение определенных условий, уже проиллюстрирован в теории обыкновенных дифференциальных уравнений. Таким образом, решение задачи Коши для уравнения (1) с условием (2), где $ f $ задано на открытом множестве $G$ и является только непрерывным, существует на некотором интервале, зависящем от $G$ и $ ( х _ {0} , и _ {0} ) $ ( см. теорему Пеано), но оно не обязательно должно быть уникальным. Решение не обязательно должно существовать во всех точках области определения $f$. 9{( п — 1) } , $$

стандартным устройством сводится к соответствующей задаче типа (1), (2).

В случае обыкновенных дифференциальных уравнений первого порядка, которые не могут быть выражены непосредственно через производную неизвестной функции (как в уравнении (1)), формулировка задачи Коши аналогична, за исключением того, что она опирается на высокая степень по геометрической интерпретации; однако реальное исследование уравнения может быть затруднено невозможностью (даже локально) приведения уравнения к нормальной форме (1).

Если ни постановка, ни исследование задачи Коши для обыкновенного дифференциального уравнения не вызывают существенных затруднений, то в случае уравнений в частных производных дело обстоит значительно сложнее (это касается, в частности, ответов на вопросы 1)–4) ). Это верно даже в том случае, если задействованные функции достаточно регулярны (гладки). Основным источником трудностей является тот факт, что пространство независимых переменных является многомерным, что приводит к проблемам (алгебраической) разрешимости. Например, рассмотрим задачу Коши для системы уравнений в полных дифференциалах, 9\альфа} знак равно ж (х) $$

Задача Коши может быть сформулирована следующим образом. В определенном регионе $G$ переменных $ x = ( x _ {1} \dots x _ {n} ) $ требуется найти решение, удовлетворяющее начальным условиям, т.е. принимающее заданные значения, вместе с его производными порядка до $m — 1$ включительно, на некотором $ ( n — 1) $- размерная гиперповерхность $ S $ в $Г$. Эта гиперповерхность известна как носитель начальных условий (или начальная поверхность). Начальные условия могут быть заданы в виде производных от $ u $ относительно направления единичной нормали $ \nu $ до $S$: 9{\ простое число \ альфа} } \Правильно ) ,\ \ \alpha = (\alpha _ {1} \dots \alpha _ {n}),\ \ \альфа _ {п} < м. $$

Задачи Коши обычно изучают, когда носителем исходных данных является нехарактеристическая поверхность, т. е. когда условие (5) выполняется для всех $ x _ {0} \in S $.

Теорема Коши–Ковалевской занимает важное место в теории задач Коши; это работает следующим образом. Если $S$ является аналитической поверхностью в окрестности одной из своих точек $ x _ {0} $, если функции $a_\alpha$, $ ж $ и $\phi_{k}$, $ 0 \leq k \leq m — 1 $, аналитичны в одной и той же окрестности, и если к тому же выполнено условие (5), то задача Коши (3), (4) имеет аналитическое решение $ u ( x) $ в окрестности точки; это решение единственно в классе аналитических функций. При допущении аналитичности эта теорема справедлива и для общих нелинейных уравнений, если последние можно привести к нормальной форме (6), а также для систем таких уравнений. Теорема носит универсальный характер, так как она применима к аналитическим уравнениям независимо от их типа (эллиптические, гиперболические и т. д.) и устанавливает локальное существование решения. Решение единственно в классе неаналитических функций. 9{2} } = 0 $$

с начальными условиями

$$ и (х, у, 0) = \ \фи _ {0} (х, у),\ \ \ гидроразрыва {\ парциальное ты} {\ парциальное г} (х, у, 0) = 0 $$

не имеет решения, если $ \phi _ {0} ( x, y) $ не является аналитической функцией. {k}$ метрика) по этим функциям. Для случаев $ n = 1, 2 $ и $n = 3$, явный вид решения задается формулами Даламбера, Пуассона и Кирхгофа соответственно: 9{2} } } , $$

где $ х = ( х _ {1} , х _ {2} ) $, $ у = ( у _ {1} , у _ {2} ) $;

$$ и (х, т) = \ \frac{1}{4 \pi } т \int\limits _ {| \xi | = 1 } \phi _ {1} ( x + t \xi ) \ д\сигма + $$

$$ + \frac{1}{4 \pi } \ гидроразрыв \ парциальное {\ парциальное т} \left [ т \int\limits _ {| \xi | = 1 } \phi _ {0} ( x + t \xi ) d \sigma \right ] , $$

где $ х = ( х _ {1} , х _ {2} , х _ {3} ) $, $ \xi = ( \xi _ {1} , \xi _ {2} , \xi _ {3} ) $, и $d\sigma$ элемент поверхности на единичной сфере $ | \xi | = 1$. 9{2} $( в зависимости от обстоятельств), лежит в $S$.

Эти результаты переносятся на более общий случай, когда носителем данных Коши является поверхность $ S $ пространственного типа, т.е. поверхность, для которой $ Q $( см. (5)) остается положительным на $S$.

Существуют и другие задачи, помимо задачи Коши, которые оказались корректными для гиперболических уравнений; примерами являются характеристическая задача Коши и смешанные начально-краевые задачи. В задаче последнего типа решение существует в $ ( n + 1) $- размерный цилиндр с образующей, параллельной $t$- ось и основание $S$ которая является некоторой областью в пространстве переменных $ x = ( x _ {1} \dots x _ {n} ) $ с границей $\Gamma$. Носителем начальных условий является $S$, а значение функции, ее нормальная производная (в случае уравнений второго порядка) или более общие краевые условия задаются на боковой поверхности $\Gamma\times\{t > 0\}$ цилиндра.

В случае вырождающихся уравнений формулировка задачи Коши также должна быть изменена. Например, если уравнение имеет гиперболический тип и носителем данных Коши является поверхность, на которой уравнение становится параболически вырожденным, то в зависимости от характера вырождения начальные условия могут включать использование некоторой весовой функции.

Список литературы

[1]

С. Ковалевская, «Научные труды», Москва (1948) (На русском языке) MR0049124

[2]

Ж.

Адамар, «Лекции по проблеме Коши в линейных дифференциальных уравнениях в частных производных», Довер, переиздание (1952) (Перевод с французского)

[3]

Л. Берс, Ф. Джон, М. Шехтер, «Уравнения в частных производных», Interscience (1964) MR0163043 Zbl 0126.00207

[4]

А.В. Бицадзе, «Уравнения математической физики», МИР (1980) (перевод с русского) MR0587310 MR0581247 Збл 0499.35002

[5]

Р. Курант, Д. Гильберт, «Методы математической физики. Уравнения в частных производных», 2 , Interscience (1965) (Перевод с немецкого) MR0195659 60780 9077

С. Мизохата, «Теория уравнений в частных производных», Кембриджский унив. Press (1973) (перевод с японского) MR0599580 Zbl 0263.35001

[7]

А.Н. [А.Н. Тихонов] Тихонов, А.А. Самарский, «Дифференциальные глэйхунген дер математической физики», Дойч.

Verlag Wissenschaft. (1959) (Translated from Russian) MR104888

[8]

L. Hörmander, «Linear partial differential operators» , Springer (1964) MR2512677 MR2304165 MR2108588 MR1996773 MR1481433 MR1313500 MR1065993 MR1065136 MR0961959 MR0925821 MR0881605 MR0862624 MR1540773 MR0781537 MR0781536 MR0717035 MR0705278 MR0404822 MR0248435 MR1533716 Zbl 1178.35003 Zbl 1115.35005 Zbl 1062.35004 Zbl 1028.35001 Zbl 0712.35001 Zbl 0687.35002 Zbl 0619.35002 Zbl 0619.35001 Zbl 0612.35001 Zbl 0601.35001 Zbl 0521.35002 Zbl 0521.35001 Zbl 0321.35001 Zbl 0175.39{2} } \} $. Актуальность этого замечания для общего определения области зависимости гиперболических уравнений в частных производных обсуждается в [5, разд. VI.7.

В современной практике гиперболичность оператора в частных производных определяется как необходимое условие корректности задачи Коши, см. [a2], Vol. 2, разд. 12.3.

Ссылки

[a1]	П. Р. Гарабедян, «Уравнения в частных производных», Wiley (1964) МР0162045 Збл 0124.30501
[а2]	Л.В. Hörmander, «Анализ линейных операторов дифференциального дифференциала», 1–2 , Springer (1985) MR1540773 MR0781537 MR0781536 ZBL 0612.35001 ZBL 0601.35001
9VER. . Press (1975) MR447753 Zbl 0305.35001

Как цитировать эту запись:
Задача Коши. Математическая энциклопедия. URL: http://encyclopediaofmath.org/index.php?title=Cauchy_problem&oldid=46284

Эта статья адаптирована из оригинальной статьи А.П. Солдатова (составитель), опубликованной в Encyclopedia of Mathematics — ISBN 1402006098. См. оригинальную статью

Дифференциальные уравнения – уравнения Эйлера

Онлайн-заметки Пола
Дом / Дифференциальные уравнения / Серийные решения для DE / Уравнения Эйлера

Показать мобильное уведомление Показать все примечания Скрыть все примечания

Уведомление для мобильных устройств

Похоже, вы используете устройство с «узкой» шириной экрана ( т. 2}y» + bxy’ + cy = 0\label{eq:eq1}\end{уравнение}\] 92}}}\]

имеют ряды Тейлора около ${x_0} = 0$. Однако из-за $x$ в знаменателе ни у одного из них не будет ряда Тейлора вокруг ${x_0} = 0$, и поэтому ${x_0} = 0$ является особой точкой. Итак, способ из предыдущего раздела не сработает, так как для него нужна обычная точка.

Однако можно получить решения этого дифференциального уравнения, которые не являются рядами. Начнем с предположения, что $x>0$ (причина этого станет очевидной после того, как мы проработаем первый пример) и что все решения имеют вид 9г} & = 0\конец{выравнивание*}\]

Теперь мы предположили, что $x>0$, поэтому это будет ноль, только если

\[\begin{equation}ar\left( {r — 1} \right) + b\left( r \right) + c = 0\label{eq:eq3}\end{equation}\]

Таким образом, решения будут иметь вид $\eqref{eq:eq2}$ при условии, что $r$ является решением $\eqref{eq:eq3}$. Это уравнение является квадратным относительно $r$, поэтому нам нужно будет рассмотреть три случая: вещественные, различные корни, двойные корни и комплексные корни. 9{- 3}}\]

Решив этот пример, мы теперь можем понять, почему нам требуется $x>0$. Второй член будет иметь деление на ноль, если мы допустим $x=0$, а первый член даст нам квадратные корни из отрицательных чисел, если мы допустим $x<0$.

Двойные корни

Этот случай приведет к той же проблеме, с которой мы сталкивались каждый раз, когда сталкивались с двойными корнями (или двойными собственными значениями). Мы получаем только одно решение, и нам понадобится второе решение. В этом случае можно показать, что вторым решением будет 9{ — 1}}\sin \left( {\sqrt 3 \ln x} \right)\]

Теперь мы должны поговорить о том, как поступить с $x < 0$, так как иногда это возможно. Чтобы справиться с этим, нам нужно использовать преобразование переменных,

\[\эта = — х\]

В этом случае, поскольку $x < 0$, мы получим $\eta > 0$.

Решение задачи Коши с примерами решения

Достаточное условие существования решения задачи Коши

Достаточные условия существования и единственности решения задачи Коши

Примеры с решением

Пример 1.

Пример 2.

6.

Ошибка

Дифференциальные уравнения | Открытые видеолекции учебных курсов МГУ

59.

60.Уравнение 1-го порядка с разделяющимися переменными.

61. Однородное уравнение 1-го порядка. Определение однородной функции

62. Линейное уравнение 1-го порядка. Методы решения: метод Лагранжа, метод Бернулли. Структура решения линейного уравнения.

История решения задачи Коши реферат по статистике | Сочинения Статистика

2.2.2: Задача Коши с начальным значением

Примеры

Авторы и ссылки

Задача Коши для дифференциального уравнения

Задача Коши — Математическая энциклопедия

Список литературы

Ссылки

Дифференциальные уравнения – уравнения Эйлера

Двойные корни

Добавить комментарий Отменить ответ