Задачи на нахождение периметра и сторон геометрических фигур | Материал по математике (2 класс):
Опубликовано 13.03.2019 — 17:05 — Фокина Ольга Николаевна
Данный материал предназначен для закрепления темы «Периметр» во 2 классе по программе «Школа России».
Скачать:
Предварительный просмотр:
ЗАДАЧИ НА НАХОЖДЕНИЕ ПЕРИМЕТРА И СТОРОН ГЕОМЕТРИЧЕСКИХ ФИГУР 1 вариант
- Длина прямоугольника 8 см, а ширина 6 см. Найди периметр.
- Длина прямоугольника 12 см, а ширина – на 3 см короче. Найди периметр.
- Одна сторона прямоугольника 5 см, а другая – на 16 см длиннее. Найди периметр.
- Сторона квадрата 4 см. Найди его периметр.
- Одна сторона треугольника 5 см, другая – 8 см, а третья – 4 см. Чему равен периметр треугольника?
- Периметр прямоугольника 20 см. Его длина 7 см. Чему равна ширина прямоугольника?
ЗАДАЧИ НА НАХОЖДЕНИЕ ПЕРИМЕТРА И СТОРОН ГЕОМЕТРИЧЕСКИХ ФИГУР 2 вариант
- Длина прямоугольника 9 см, а ширина 7 см.
 Найди периметр.
Найди периметр. - Длина прямоугольника 14 см, а ширина – на 5 см короче. Найди периметр.
- Одна сторона прямоугольника 6 см, а другая – на 13 см длиннее. Найди периметр.
- Сторона квадрата 5 см. Найди его периметр.
- Одна сторона треугольника 6 см, другая – 9 см, а третья – 3 см. Чему равен периметр треугольника?
- Периметр прямоугольника 18 см. Его длина 6 см. Чему равна ширина прямоугольника?
ЗАДАЧИ НА НАХОЖДЕНИЕ ПЕРИМЕТРА И СТОРОН ГЕОМЕТРИЧЕСКИХ ФИГУР 1 вариант
- Длина прямоугольника 8 см, а ширина 6 см. Найди периметр.
- Длина прямоугольника 12 см, а ширина – на 3 см короче. Найди периметр.
- Одна сторона прямоугольника 5 см, а другая – на 16 см длиннее. Найди периметр.
- Сторона квадрата 4 см. Найди его периметр.
- Одна сторона треугольника 5 см, другая – 8 см, а третья – 4 см. Чему равен периметр треугольника?
- Периметр прямоугольника 20 см. Его длина 7 см. Чему равна ширина прямоугольника?
ЗАДАЧИ НА НАХОЖДЕНИЕ ПЕРИМЕТРА И СТОРОН ГЕОМЕТРИЧЕСКИХ ФИГУР 2 вариант
- Длина прямоугольника 9 см, а ширина 7 см.
 Найди периметр.
Найди периметр. - Длина прямоугольника 14 см, а ширина – на 5 см короче. Найди периметр.
- Одна сторона прямоугольника 6 см, а другая – на 13 см длиннее. Найди периметр.
- Сторона квадрата 5 см. Найди его периметр.
- Одна сторона треугольника 6 см, другая – 9 см, а третья – 3 см. Чему равен периметр треугольника?
- Периметр прямоугольника 18 см. Его длина 6 см. Чему равна ширина прямоугольника?
ЗАДАЧИ НА НАХОЖДЕНИЕ ПЕРИМЕТРА И СТОРОН ГЕОМЕТРИЧЕСКИХ ФИГУР 1 вариант
- Длина прямоугольника 8 см, а ширина 6 см. Найди периметр.
- Длина прямоугольника 12 см, а ширина – на 3 см короче. Найди периметр.
- Одна сторона прямоугольника 5 см, а другая – на 16 см длиннее. Найди периметр.
- Сторона квадрата 4 см. Найди его периметр.
- Одна сторона треугольника 5 см, другая – 8 см, а третья – 4 см. Чему равен периметр треугольника?
- Периметр прямоугольника 20 см. Его длина 7 см. Чему равна ширина прямоугольника?
ЗАДАЧИ НА НАХОЖДЕНИЕ ПЕРИМЕТРА И СТОРОН ГЕОМЕТРИЧЕСКИХ ФИГУР 2 вариант
- Длина прямоугольника 9 см, а ширина 7 см.
 Найди периметр.
Найди периметр. - Длина прямоугольника 14 см, а ширина – на 5 см короче. Найди периметр.
- Одна сторона прямоугольника 6 см, а другая – на 13 см длиннее. Найди периметр.
- Сторона квадрата 5 см. Найди его периметр.
- Одна сторона треугольника 6 см, другая – 9 см, а третья – 3 см. Чему равен периметр треугольника?
- Периметр прямоугольника 18 см. Его длина 6 см. Чему равна ширина прямоугольника?
По теме: методические разработки, презентации и конспекты
Математический тренажер по решению задач на нахождение периметра.
математический тренажер по решению задач на нахождение периметра…
Тренажёр по математике 4 класс. «Решение задач на нахождение периметра и площади».
Разноуравневые задачи на нахождение периметра и площади….
Периметр и площадь геометрических фигур
Материал содержит тест-игру (задания закрытого типа)….
Интегрированный урок математики. «Сказка стала былью». 2 класс Тема: Решение задач на нахождение периметра прямоугольника.
 Интеграция с предметом: внеклассное чтение.
Интеграция с предметом: внеклассное чтение.формировать умение решать задачи на нахождение периметра прямоугольника, способствовать развитию учащихся памяти, внимания, логического и математического мышления, умения мечтать; обобщать знания дете…
Задачи на нахождение периметра.
Используя данный материал педагоги и родители помогут учащимся научиться решать задачи на нахождение периметра.Материал подобран в соответствии с требованияим ФГОС….
Периметр и площадь геометрических фигур
интерактивный тест по математике…
Технологическая карта урока математики по теме: Решение геометрических задач на нахождение периметра и площади (прямоугольника и квадрата).
Технологическая карта урока математики разработан в рамках ФГОС, полностью соответствует целям и содержанию урока, связан с материалом предыдущего и последующего уроков, учитывает возрастные и психоло…
Поделиться:
Этап урока, деятельность учителя
| Деятельность учащихся |
1. Самоопределение к деятельности. Организация класса. — Прозвенел звонок — начинаем мы урок. Ребята, сядьте удобно, правильно! Закройте глазки и повторяйте за мной. — Я готов к уроку! — Я собран! — Я все сумею! — Моя голова мыслит ясно! — Я все запомню надолго, навсегда! — Я хочу учиться!
-А девиз нашего урока будет таким: От каждого — по способностям, Каждому ̶ успех, всем — радость!
— Ребята, а чего вы ждете от этого урока? Посадите свои цветочки на полянке ожиданий. ( Учитель помогает оформить « Полянку ожиданий»
|
Настраиваются на урок.
Ответы детей, оформляют «Полянку ожидания». |
2. Мотивация учебной деятельности. Сообщение темы урока. — Итак, ребята, сегодня у нас с вами очень много работы: нам предстоит совершенствовать свои вычислительные навыки, развивать память, математическую речь, нас ждут игры, веселые задачи и новая тема: «Периметр треугольника, квадрата, прямоугольника». Причем ждет она нас ни где-нибудь, а в сказке. А в какой — вы узнаете сами, решив примеры устно и записывая ответы в строчку правильно и красиво.
|
|
3. Актуализация опорных знаний.
Игра « Молчанка» Учитель показывает карточки с примерами, дети устно решают их и записывают только ответы.
6 + 6 = 5 + 6 = 17 — 8 = 8 + 8 = 5 + 5 = 7 + 4 = 4 + 6 = 8 + 5 = 6 + 9 = 13 — 5 = 14 — 7 = 11 — 5 = Оценивание: 1 балл за правильный ответ.
(Минутка каллиграфии) (Ответы: 12, 11, 9, 16, 10, 11, 10, 13, 15, 8, 7, 6).
— На какие группы можно разделить данные числа? ( Однозначные и двузначные, четные и нечетные) — Назовите наибольшее число, наименьшее число. — Расшифровать название сказки нам поможет ключ к шифру: 12 — Т 10 — О 11 — Р 16 — П 9 — И 13 — С 15 — Ё 8 — Н 7 — К 6 — А Найдите буквы соответствующие числам (Ответ: «Три поросенка»).
— Да, ребята, нас ждет встреча с тремя братьями-поросятами. Жили — были три поросёнка. (На доске появляются рисунки трех поросят). Были они абсолютно одинаковые. Все трое одинакового роста, одинаково розовенькие, одинаково пухленькие, с одинаковыми хвостиками. — Ребята, подскажите мне имена поросят. Жили они в сказочном лесу, а деревья у них были такими:
Игра « Память» Выставляется набор картинок с изображением деревьев: рябина, береза, клен, ель, акация, дуб, сосна. |
Устно считают примеры.
Один ученик работает у доски.
Остальные записывают ответы в тетради.
Дети дают ответы.
Дети рассматривают набор, запоминают названия деревьев. |
Целыми днями поросята только и делали, что резвились, прыгали, бегали, грелись на солнышке, лежали в теплых лужах. И только старший из братьев, Наф — Наф, время от времени не давал им покоя, пытаясь научить их математике, придумывал разные задачи и говорил, что все должны быть грамотными, умными, наблюдательными, сообразительными. Поросята не хотели слушать брата, ничего не учили и не могли справиться даже с простыми заданиями. И теперь просят у вас помощи. Поможем? Первое задание: Математический диктант. — Сколько ушей у поросят? — Сколько ног у них? — Сколько глаз? — Сколько хвостиков? — Сколько деревьев росло у них в лесу? — Нуф — Нуф лежал в луже 25 минут, а Ниф — Ниф — 17минут. На сколько дольше лежал в луже Нуф — Нуф? ( Ответы: 6, 12, 6, 3, 7, 8) Оценивание: каждый правильный ответ- 1 балл. Второе задание: «Мозговой штурм» 1. 2. Как найти неизвестное слагаемое? (Из суммы вычесть известное слагаемое) 3. Можно ли утверждать, что фигура, в которой 4 стороны равны ̶ квадрат? (Можно) 4. Сколько углов у треугольника? (3) 5. Какие стороны равны у прямоугольника? (Противоположные) Оценивание: 1 балл за правильный ответ Так прошло лето. Но с наступлением холодов Наф — Наф сказал своим братьям, что пора подумать бы о жилье. Нуф -Нуф решил поступить очень просто: он построил дом, в котором было всего три угла и три стены. (3см, 3см, и 4,5 см) (Демонстрирует фигуру) — Ребята, какую геометрическую фигуру вам напоминает домик Нуф- Нуфа? (Треугольник) — По каким признакам вы определили это? (Три угла, три стороны)
Построив себе домик, брат отправился посмотреть на домики братьев. Ниф- Ниф не стал торопиться, как его брат, но и нагружать себя тоже не стал. (Демонстрирует фигуру) — Ребята, какую геометрическую фигуру вам напоминает домик второго брата? (Квадрат) По каким признакам вы определили это? (4 прямых угла и равные стороны)
Основательнее всех к строительству домика подошел Наф-Наф. Он отмерил длину своего домика (5см), а затем отмерил ширину (3 см). Его домик тоже имел 4 прямых угла,4 стены, но одинаковыми были только противоположные стороны. (Демонстрирует фигуру) — Ребята, какую геометрическую фигуру напоминает вам домик третьего брата? (Прямоугольник) — По каким признакам вы определили? ( 4 прямых угла, 4 стороны, одинаковые противоположные)
|
Записывают математический диктант.
Обмениваются тетрадями, проверяют ответы, сравнивая их с ответами выставленным учителем, на полях ставят оценку.
Отвечают на поставленные вопросы.
Дети отвечают на вопросы.
Дети дают ответы на вопросы.
Дети дают ответы на вопросы. |
4. Изучение нового материала. Создание проблемной ситуации. Не успели братья полюбоваться своими домиками, как Сорока принесла страшное известие: в лесу появился Волк! Однажды он уже разрушил их домики. Наф-Наф не растерялся и сказал, что свои домики им нужно срочно защитить прочной проволокой, и они отправились в магазин к Дятлу. — Хорошо, сказал Дятел. Я продам вам прочную проволоку. Сколько нужно проволоки каждому из вас? — Нам нужно столько, чтобы каждому хватило обтянуть свои домики. — Я не могу сразу отмерять вам проволоку. Для этого я должен знать … |
|
5. Решение проблемной ситуации. — Что же должен знать Дятел? Работа в группах. — Сейчас мы поработаем в группах. (Каждая группа собирается у столиков, на которых размещена такая же геометрическая фигура, какую дети получили до урока). (Практическая работа) (Первая группа ̶ треугольник, вторая ̶ прямоугольник, третья — квадрат). На столе ̶ шаблоны фигур. Размеры на листочке. С помощью ниток измеряют фигуру, находят решение проблемной ситуации. Оценивание: 2 балла ̶ правильное выполнение, 1 балл, если есть ошибки
|
Работают в группах. Дети рассуждают и приходят к выводу, что нужно знать длину каждой стены в каждом домике поросят, а также их сумму (периметр).
|
6. Первичное закрепление знаний.
— Сколько стен нужно измерять каждому поросенку? — Как узнать общую длину проволоки, необходимую для каждого домика? — Дети, помогите братьям. Посчитайте длину проволоки для каждого домика. — Ребята, какие результаты вы получили? Обратите внимание: у поросят получились мотки проволоки разной длины. А что было общего при решении задачи? (Они находили сумму длин всех сторон своих домиков). ( Вывод) — Ребята, нахождение суммы длин всех сторон геометрической фигуры в математике называется периметром и обозначается латинской буквой Р.
|
Дети дают ответы на вопросы.
Находят длину проволоки.
Вместе с учителем делают вывод.
|
Физкультминутка. Все хорошо работают. Но пора и отдохнуть. Мы в гостях у поросят, поэтому физкультминутку мы будем проводить с ними. Сначала как они: бегаем, прыгаем, приседаем, головой покрутим, пятачками землю пороем, глазками окошко обрисуем, покружимся, спинки солнышку подставим и тихонечко на место сядем.
|
|
7. Закрепление изученного на уроке. Самостоятельная работа с взаимопроверкой. Учитель раздает шаблоны треугольников, квадратов, прямоугольников каждому ученику. — Постройте в тетрадях свои фигуры, найдите периметр. Оценивание: 2 балла за правильно сделанное задание, 0 баллов, если есть ошибки.
|
Работают самостоятельно. Дети измеряют стороны фигур, находят периметр.
Делают взаимопроверку. |
8. Повторение. Метод «Микрофон»
( возвращаются к игре «Память»)
|
Дети дают ответы.
|
Я — ценю: (помощь товарища, помощь учителя, новые знания). Я — узнал: Я — умею: Я — верю: Я — хочу: — Всем ли сегодняшний урок принес радость? Просигнальте мне смайликами ваше настроение на уроке. |
Ответы детей. |
10. Оценивание учащихся по количеству жетонов. | Дети считают свои жетоны ( самооценивание). |
11. Домашнее задание.
Учащиеся 1 группы — чертят квадрат, 2 группы — треугольник, 3 группы — прямоугольник, находят периметр.
|
|
«Периметр прямоугольника», 2 класс — математика, уроки
В данном конспекте раскрыта тема периметра прямоугольника, которая изучается в начальной школе.
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
=> ПОЛУЧИТЬ СУПЕРСПОСОБНОСТИ УЧИТЕЛЯ
Просмотр содержимого документа
«»Периметр прямоугольника», 2 класс»
Технологическая карта урока
Предмет: математика
Класс: 2
Тема урока: «Периметр прямоугольника»
Цель урока: познакомить с разными способами нахождения периметра прямоугольника; совершенствовать вычислительные навыки и умение решать текстовые задачи; развивать внимание и логическое мышление.
Планируемые результаты:
Предметные: учащиеся научатся распознавать изученные геометрические фигуры и называть их отличительные особенности; находить периметр прямоугольника разными способами; выполнять письменные вычисления изученных видов в пределах 100; моделировать с помощью схематических рисунков и решать текстовые задачи; записывать решение задач уравнением; выполнять задания творческого и поискового характера; контролировать и оценивать свою работу и её результат.
Личностные: научатся осознавать свои возможности в учении; смогут адекватно судить о причинах своего успеха или неуспеха в учении, связывать успехи с усилиями, трудолюбием; научатся самостоятельно планировать и выполнять свои действия по учебному материалу, действовать в сотрудничестве с учителем.
Тип урока: урок «открытия» нового знания.
Оборудование: учебник математика 2 класс, часть № 2; учебная презентация; раздаточный материал.
Этап урока | Время | Содержание урока. Деятельность учителя | Деятельность учащихся | УУД |
1. Орг. момент | 1 мин | — Здравствуйте, ребята. — Тихо садятся девочки и ещё тише мальчики — Давайте настроимся на хорошую работу, соберём всё своё внимание. | Приветствовать учителя. | |
2. Актуализация знаний. | 5 мин | Устный счёт — Вам нужно найти ответы этих примеров и поставить ответы и соответствующие им буквы в порядке возрастания. И получите какое-то слово. 15 — (6+5) = 4 (М) 17 — (18-9) = 8 (Л) (4+8) — 7 = 5 (О) (90+5) — (43-40) = 92 (Е) (46-40) + (58-8) = 56 (Д) (3+8) + (12-6) = 17 (О) (80+10) + 7 = 97 (Ц) — Какое слово получилось? (Молодец) Логическая разминка — Расставьте вместо звёздочек знаки + и — так, чтобы получилось верное равенство. 2 * 6 * 3 * 4 * 5 * 8 = 12 — Кто покажет, как расставил знаки? (2+6-3+4-5+8 = 12) Работа над задачами 1) В книге 30 страниц. Таня прочитала 8 страниц. Сколько страниц ей осталось прочитать? 2) На полке было 20 книг. Сколько книг взяли с полки? Если их осталось 7? 3) В первой пачке 40 книг, во второй 30 книг. На сколько книг во второй пачке меньше, чем в первой? | Выполнять задание самостоятельно Решать задачи. Анализировать условие задачи. | Регулятивные: оценивать собственные успехи в вычислительной деятельности. |
3. Самоопределение к деятельности. | 7 мин | — Посмотрите на этот рисунок. Из каких фигур состоит этот замок? — На какие 2 группы можно разделить все эти фигуры? (Многоугольники и круг) — Если я уберу круг, как назвать оставшиеся фигуры? (Четырёхугольники) — На какие 2 группы можно их разделить? (Фигуры с прямыми углами и без прямых углов) — Если я уберу трапецию. — Докажите, что оставшиеся фигуры — прямоугольники. (4 стороны, 4 угла, все углы прямые, противоположные стороны равны) — А что можно узнать, зная длину сторон прямоугольника? (Периметр) — Сформулируйте тему сегодняшнего урока. — Какие задачи поставим перед собой? Что будем делать на сегодняшнем уроке? | Анализировать фигуры. Находить общие и различные признаки. Формулировать тему и цели урока. | |
4. Работа по теме урока. | 10 мин | — Постройте прямоугольник со сторонами 3 см. и 6 см. и подпишите длину каждой стороны. — Что такое периметр? (Сумма длин всех сторон) — Найдите периметр прямоугольника. (3+6+3+6 = 18 (см)) — Это первый способ нахождения периметра прямоугольника. — Сумму каких слагаемых мы можем заменить умножением? (3+3 и 6+6) — По 3 сколько раз взяли? (по 3 2 раза) — Как запишем? (3*2) — А по 6 сколько раз взяли? (по 6 2 раза) — Как запишем? (6*2) — А между этими выражениями какой знак поставим? (3*2+6*2) — Это 2-й способ нахождения периметра прямоугольника. — Но есть ещё один способ. — Посмотрите на свой прямоугольник. Сколько разных сторон у него? (Две: длина, ширина) — Как запишем их сумму? (3+6) — Сколько раз в прямоугольнике повторяется эта сумма? (2 раза) — (3+6) * 2 = 18 (см) — Это третий способ нахождения периметра прямоугольника. — А сейчас давайте повторим все 3 способа, но вместо цифр, мы поставим буквы. Обозначим длину прямоугольника буквой a, а ширину — буквой b. Подставим в наши решения. И мы получили 3 формулы нахождения периметра прямоугольника. P = a+b+a+b P = a*2+b*2 P = (a+b) * 2 | Выполнять чертёж Находить периметр Отвечать на вопросы. Заменять сложение умножением. Выводить формулы. | Познавательные: устанавливать закономерности и использовать их при выполнении заданий. Познавательные: понимать информацию, представленную в виде текста. |
5. | 2 мин | Мы становимся всё выше, Достаём руками крыши. На два счёта поднялись, Три-четыре — руки вниз. | ||
6. Продолжение работы по теме урока. | 15 мин | — Откройте учебники на странице 52 задание № 1. — Посмотрите, как находили периметр прямоугольника? Кто сможет объяснить? — Совпадают ли эти решения с теми формулами, которые вывели мы с вами? — А теперь давайте выполним задание № 2. Начертите в тетради прямоугольник со сторонами 3 см и 4 см. — Давайте найдём его периметр разными способами. — Кто покажет, как найти периметр первым способом? Вторым. Третьим. — Сколько способов нахождения периметра вы знаете? № 6. — Прочитайте задание. Что нужно сделать? Это вы уже умеете делать. — 1-й вариант находит значения выражения к — 8 при к = 14, 36, 58, 90 — 2-й вариант находит значения выражений к + 8 при к = 14, 36, 58, 90 — Давайте проверим. — Посмотрите на правильные ответы. — Поставьте себе на полях плюс те, кто выполнил всё верно. | Находить решение. Записывать решение самостоятельно. Проводить самопроверку. Выполнять письменное задание самостоятельно | Познавательные: перерабатывать полученную информацию: наблю-дать и делать самостоятельные выводы; Коммуникативные: организовывать самопроверку выполненной работы. |
7. Итог урока. | 3 мин | — Давайте подведём итог нашего урока. — Что мы делали сегодня на уроке? — Какие знания закрепили? — Какое задание было самым трудным? — А какое самым лёгким? — Что такое периметр? — Сколько способов нахождения периметра вы знаете? — Запишите домашнее задание: с 52 № 3, 7 | Подводить итог урока. Анализировать свою работу на уроке. | Регулятивные: оценивать собственные успехи и неуспехи. |
8. Рефлексия | 2 мин | — А сейчас посмотрите на слайд. Вы видите лесенку. — Поставьте себя на самую верхнюю ступень те, кому легко было справляться с заданиями. — Поставьте себя на среднюю ступень те, у кого возникали трудности. — Поставьте себя на самую нижнюю ступень те, кто очень сильно затруднялся. -Кто поставил себя на верхнюю ступень? На нижнюю? На среднюю? -Урок окончен. | Производить рефлексию. Проводить самоанализ. | Регулятивные: Осуществлять анализ своей работы на уроке. |
Советы, приемы и бесплатные задания упрощают изучение периметра и площади
Измерение — это очень увлекательная единица обучения, потому что она предлагает так много возможностей для реальных приложений. Одно из моих любимых понятий — площадь и периметр, потому что это единица, полная практических действий, возможностей для перемещения и совместной работы. Мне нравится выбирать действия, которые делают периметр и территорию конкретными для них. При этом изучение периметра и площади не всегда легко.
Мне нравится выбирать действия, которые делают периметр и территорию конкретными для них. При этом изучение периметра и площади не всегда легко.
Независимо от того, сколько увлекательных занятий я планирую, я обнаружил, что многим из моих учеников трудно отличить область от периметра. Вот почему так важно целенаправленно планировать занятия, которые дают учащимся возможность закрепить различия между этими понятиями.
В дополнение к придумыванию забавных способов обучения периметру и площади с использованием практического опыта, я также люблю давать своим ученикам несколько стратегий, которые помогут им различать их. Сегодня я собираюсь поделиться с вами некоторыми из этих трюков с периметром и площадью.
Что вы найдете на этой странице:
Учебная зона и периметр, чтобы учащиеся ДЕЙСТВИТЕЛЬНО поняли это
Приведенные ниже стратегии предназначены для определения учебной области и периметра и того, как вычислить каждую из них с использованием мультисенсорного подхода.
1. Используйте визуальные подсказки, чтобы отличить периметр от площади.
Может быть сложно понять, как объяснить площадь и периметр ребенку, который не знаком с этими понятиями. Вот почему я стараюсь помочь учащимся определить способы их различения. Предоставление визуального напоминания действительно может иметь огромное значение, помогая учащимся вспомнить два термина и их значение.
Вот как я использую наглядные изображения, чтобы термины запомнились:
Работая над уроком, мы записываем слово «периметр» в свои дневники. Тем не менее, мы используем заглавные буквы и выделяем жирным шрифтом цифру 9.0023 RIM , чтобы напомнить им о ре RIM eter — это измерение внешнего «ободка» формы.
Студенты также рисуют прямоугольник в своем математическом журнале и пишут слово «периметр», идя по всему периметру… снова и снова для моих друзей с небольшим почерком.
Мы также записываем ОБЛАСТЬ в наших журналах, и я позволяю им раскрасить внутреннюю часть букв А и П, чтобы напомнить им, что область находится внутри. Затем они возвращаются к нарисованному прямоугольнику и пишут 9.0023 ОБЛАСТЬ настолько большие, насколько они могут поместиться внутри.
Затем они возвращаются к нарисованному прямоугольнику и пишут 9.0023 ОБЛАСТЬ настолько большие, насколько они могут поместиться внутри.
2. Научить площадь и периметр как различные вычисления
Многие из моих детей понимают, что если все стороны имеют одинаковую длину, они могут умножить длину на количество сторон, чтобы получить периметр.
Тем не менее, для моих учеников, испытывающих затруднения, я призываю их всегда складывать с периметром и всегда умножать при вычислении площади, пока они не освоятся.
Это действительно помогает им различить их на раннем этапе, потому что они используют разные операции для решения.
3. Используйте цветовое кодирование
Наконец, если им дать форму и попросить найти периметр или площадь, я попрошу их помочь им с помощью цветных карандашей или мелков.
Если их просят найти периметр, учащиеся обрисовывают фигуры. Для вопросов, которые требуют от них найти площадь, учащиеся раскрашивают фигуру.
Один совет, который я усвоил на собственном горьком опыте, заключался в том, чтобы настаивать на том, чтобы ученики использовали цветные карандаши или мелки. Это позволяет легко увидеть нашу работу и предотвращает порванные страницы и беспорядок от маркеров.
Практика делает совершенным – Увлекательные способы преподавания периметра и области
Я также упорно работаю, чтобы дать своим ученикам МНОЖЕСТВО занятий и возможностей практиковать оба навыка вместе и по отдельности, потому что исследования подтверждают, что увеличение возможностей означает повышение уровня обучения (пока я дать содержательную обратную связь).
Вот несколько ресурсов, которые помогли мне преподавать площадь и периметр моим ученикам:
Площадь и периметр Вырезать, вставить и сопоставить — БЕСПЛАТНО!
Это задание предлагает учащимся попрактиковаться в поиске, узнавая, как вычислять площадь и периметр для квадратов и прямоугольников.
Всего 8 комплектов – 4 базовых и 4 продвинутых.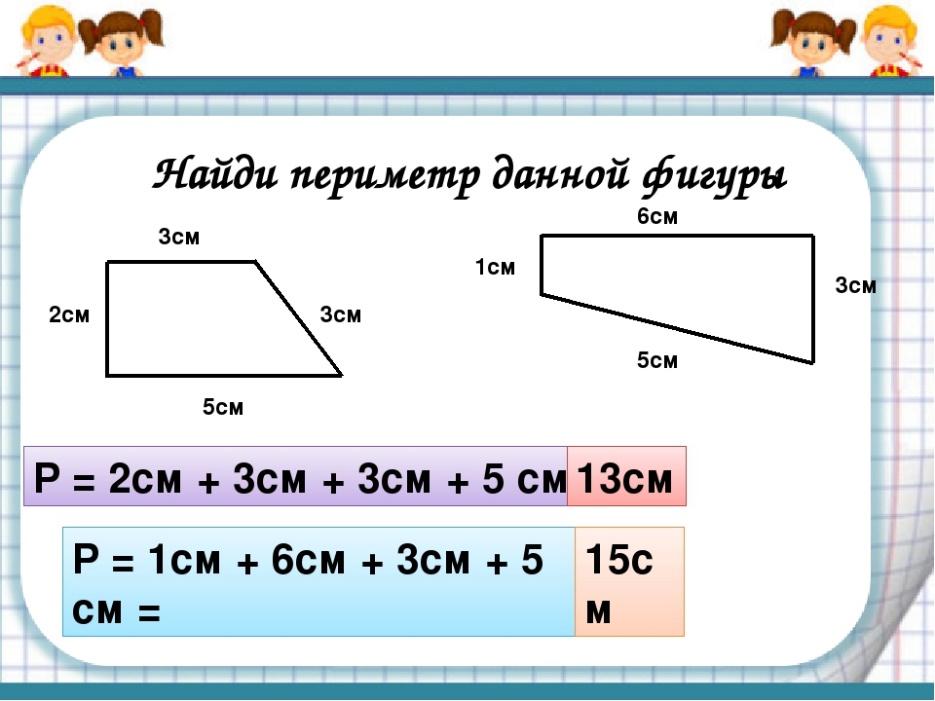 Вы можете разнообразить это занятие, дав учащимся меньше карточек.
Вы можете разнообразить это занятие, дав учащимся меньше карточек.
Ученики сопоставляют набор игровых карточек, чтобы найти наборы из 4 карточек, описывающих один и тот же четырехугольник. Набор включает в себя набор для начинающих и набор для продвинутых.
Набор для начинающих идеально подходит для учащихся, которым трудно владеть фактами. Расширенный набор требует, чтобы учащиеся вычисляли более сложные факты.
Я использую это задание как часть повторного обучения в небольшой группе. Мои учащиеся, испытывающие затруднения, рассматривают вместе со мной один набор карточек во время мини-урока с гидом. Второй набор завершается как формирующее оценивание. Мои ученики приклеивают их к сортировочному коврику, чтобы мне было легче искать распространенные заблуждения для повторного обучения.
Введите адрес электронной почты, чтобы получить мгновенный доступ к этому увлекательному занятию.
Карты задач по площади и периметру
Я использую эти карты задач ближе к концу нашего отряда.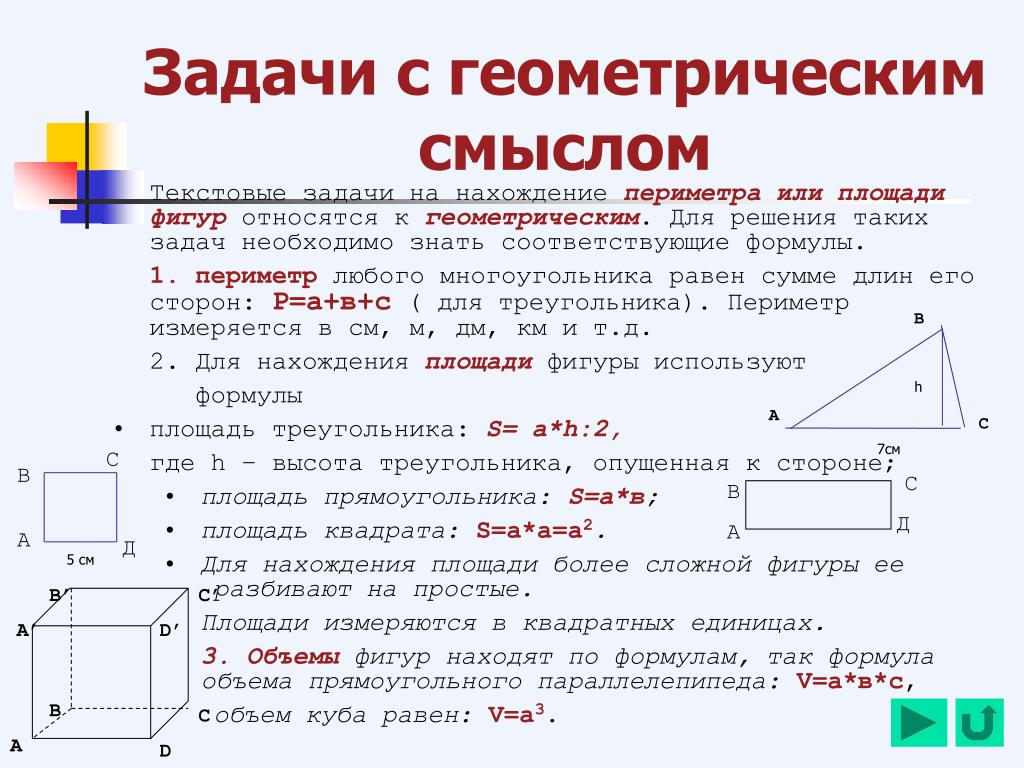 Это отличный способ включить движение, пока я оцениваю прогресс.
Это отличный способ включить движение, пока я оцениваю прогресс.
Самое замечательное то, что это может быть самостоятельным заданием, которое ваши ученики могут выполнять, пока вы занимаетесь повторным обучением в небольшой группе. Единственное, что вам нужно сделать, это установить таймер для вращения.
Я также использовал их в качестве полнофункционального обзора перед нашей оценкой, так что они определенно универсальны.
Набор содержит как обычные (стандартные), так и метрические единицы измерения для 36 карточек с заданиями.
Карточки различаются по сложности, а также включают в себя некоторые сюжетные задания, похожие на те, что встречаются при оценке состояния. Набор идеально подходит для ламинирования и использования из года в год для оценки мастерства учащихся в области площади и периметра.
Ищете другие стратегии и инструменты для обучения математике? В этих статьях содержится много полезной информации для старшеклассников по математике.

Практические манипуляции для обучения области и периметру. Для преподавания и изучения математики в реальном мире требуются строительные леса, которые разбивают большие концепции. Вот почему я всегда использую манипуляторы для поддержки концептуального понимания площади и периметра. И есть некоторые манипуляторы I
не может обучать без.Сегодня я составил список из пяти моих лучших манипуляций для обучения области и периметру с помощью манипуляций. Этот список отвечает ряду потребностей в обучении. Прочитайте и решите, какие из них лучше всего подходят для ваших учеников.
Введение площади и периметра с помощью цветных квадратных плиток
Цветные квадратные плитки — святой Грааль манипуляторов. Это одни из первых манипуляторов, которые я использую в своей области и подразделениях по периметру, и они, как правило, являются фаворитами среди моих учеников. Почему? Простота и гибкость!
Отличное средство для переписки 1-1
Если вы новичок, знайте, что квадратные цветные плитки — настоящий фаворит. Я использую квадратные цветные плитки для обучения массивам. Они представляют собой прямую визуализацию равных строк или столбцов. Студенты могут легко переставлять и разбирать плитки. Самое главное, студенты могут использовать индивидуальную переписку в зависимости от их уровня владения языком. Вот лучшая часть: Использование квадратных цветных плиток для массивов легко перейдет к их использованию для площади.
Я использую квадратные цветные плитки для обучения массивам. Они представляют собой прямую визуализацию равных строк или столбцов. Студенты могут легко переставлять и разбирать плитки. Самое главное, студенты могут использовать индивидуальную переписку в зависимости от их уровня владения языком. Вот лучшая часть: Использование квадратных цветных плиток для массивов легко перейдет к их использованию для площади.
Преобразование массивов в площадь
Ваши учащиеся готовы развить свое понимание массивов в умножении. Пришло время применить его к области. Вначале понятие площади мало чем отличается от понятия массивов при умножении. Когда учащиеся строят массивы, я ввожу в них родственные словарные слова с этими массивами. Учащиеся изучают площадь, длину, ширину и квадратные единицы.
Различение периметра
Хотя я использую множество манипулятивных приемов для обучения области, инструменты для периметра на удивление более ограничены. Некоторым учащимся трудно понять разницу между площадью и периметром. Они требуют манипулятивных действий, которые облегчают их идентификацию. Изучение периметра включает в себя взаимно однозначное соответствие и понимание массивов.
Они требуют манипулятивных действий, которые облегчают их идентификацию. Изучение периметра включает в себя взаимно однозначное соответствие и понимание массивов.
По мере того, как мы переходим к построению прямоугольников из квадратных цветных плиток и именованию областей, мы начинаем обсуждать периметр. «Если бы мы ходили только по внешним плиткам, сколько плиток потребовалось бы, чтобы обойти весь прямоугольник?»
За прошедшие годы я обнаружил, что есть два способа выделить периметр по сравнению с площадью с помощью квадратных цветных плиток:
- Замените внешние плитки другим цветом.
- Удалите внутренние плитки, оставив только периметр.
Бесконечная дифференциация
Вот еще одна причина, по которой я люблю квадратную плитку. Они позволяют легко и просто дифференцировать. У меня были классы, где ученики широко разбирались в понимании площади и периметра.
Для учащихся, обучающихся на более ранних стадиях математического развития, можно продолжать использовать квадратные плитки для создания меньших массивов/областей и называть их.
Готовы ли ваши ученики применить свои знания к более значимому, творческому мышлению? Возможно, пришло время представить дизайн плана этажа. Квадратные цветные плитки — отличный инструмент для определения площади и периметра, когда учащиеся строят план этажа. Они могут использовать разные цвета для разных комнат и построить пол дома своей мечты, а также найти площадь каждой комнаты и весь план этажа.
Площадь и периметр заметок Post-It
Еще одним действительно конкретным манипулятивным средством являются квадратные заметки Post-It! (А кто не любит яркие цвета?) Они особенно хороши для групповых обсуждений, потому что вы можете моделировать и управлять площадью и периметром на доске. Вы также можете легко добавлять и удалять квадратные единицы!
Их можно использовать для простого создания визуальных элементов для анкорных диаграмм, досок объявлений, групповой работы и многого другого. Единственное предостережение: убедитесь, что учащиеся используют стикеры SQUARE.
Исследование площади и периметра с помощью ленты и напольных плиток
Квадратные цветные плитки поддерживают построение области и периметра в миниатюрном мире. Теперь пришло время для реального применения.
Можно сказать, мне повезло. Полы в большинстве моих классов покрыты линолеумом размером 1×1 кв. Это не самое красивое зрелище, но они полезны для изучения области и периметра.
Учащиеся объединяются в команды, чтобы оценить наш класс и его разделенные пространства. Студенты могут выполнить это задание двумя способами:
- Учащиеся заклеивают периметр классной комнаты вдоль напольной плитки. Они считают периметр и вычисляют площадь всего класса, используя квадратные футы.
- Учащиеся используют рулетку для измерения определенных областей в классе. Вы можете попросить учащихся измерить часть классной комнаты, а затем измерить ее. Или вы можете дать учащимся конкретное измерение площади (например, 12 квадратных футов или прямоугольник с периметром 8), чтобы записать их на пленку.

Добавлен бонус, позволяющий учащимся заклеивать разделы лентой: всякий раз, когда учащиеся перемещаются по классу, понятие площади и периметра усиливается. Выстроиться? Учащиеся передают пример площади и периметра. Отложить свою работу? Они должны передать пример площади и периметра. Это отличный способ разместить эти визуальные эффекты (и не занимать тонны драгоценного места на доске объявлений).
Блоки паттернов как продвинутое манипулятивное средство для периметра
Блоки паттернов — это манипуляторы, поддерживающие более глубокое понимание периметра. Блоки шаблонов пригодятся, когда учащиеся будут готовы выйти за рамки прямоугольников и больше думать о сторонах. Почему? Блоки шаблонов бывают разных форм (шестиугольник, трапеция, квадрат, треугольник, параллелограмм и ромб), но имеют стандартную длину стороны. Для занятий со студентами я использую разноцветные плитки: шестиугольник, трапецию, квадрат, треугольник и ромб. Треугольник является базовой фигурой, которая может составить все остальные четыре.
Как я ввожу узорные блоки для периметра
Я добавляю узорные блоки так же, как квадратные цветные плитки. Однако на этот раз мы сосредоточимся ТОЛЬКО на периметре. Иногда полезно разделить два навыка, чтобы действительно помочь усвоить, что есть что.
Исследовать: Всей группой (или небольшой группой) мы исследуем различные формы и определяем сходство.
- Стороны треугольника и квадрата равны.
- Трапеция состоит из 3-х треугольников.
- Шестиугольник состоит из шести треугольников.
- Ромб – это два треугольника.
Практика : Учащиеся выполняют определенные задания. Они используют шаблонные блоки в качестве манипулятивного средства для создания определенных периметров. При нахождении периметра длина одной стороны треугольника равна 1 единице. Вот некоторые примеры задач:
- Создайте фигуру с периметром 16 единиц.
- Создайте фигуру с периметром 20 единиц.

- Создайте фигуру с периметром 20 единиц.
Запись : Используя свои математические журналы, они записывают подсказку и решение. Быстрый финишер? Пусть они найдут и запишут другой способ выполнить ту же подсказку.
Расширение: Разрешить учащимся создавать свои собственные изображения из блоков шаблонов. Это задание с низким полом и высоким потолком позволяет учащимся бросить вызов самим себе. Когда они закончат, попросите их найти периметр своего творения. Вы даже можете сфотографировать их проекты и распечатать их, чтобы повесить в классе или создать дополнительные математические задачи для их сверстников.
Отличия с геобордами
Одним словом: геоборды — это фантастика. Они отлично подходят для манипулирования площадью, периметром и всеми геометрическими понятиями.
Геоборды представляют собой деревянные или пластмассовые квадраты с набором колышков. Ленты петляют и тянутся от одного стержня к другому, создавая сегменты линии. Эти линейные сегменты образуют фигуры с простыми для расчета площадями и периметрами.
Эти линейные сегменты образуют фигуры с простыми для расчета площадями и периметрами.
Продвинутые математические мыслители возрадуются. Геоборды обладают гибкостью использования, что позволяет учащимся исследовать новые, связанные задачи. (Бонус: с помощью этой манипуляции вы можете создать половину квадратного элемента, чего нельзя сделать с квадратными плитками или блоками узоров.)
Использование геобордов в качестве средства управления площадью и периметром
Начните с простых задач. Попросите учащихся создать простые фигуры, используя только горизонтальные и вертикальные линии (это позволит избежать обсуждения половинных единиц сначала).
Предложите учащимся вычислить периметр. Расчет периметра зачастую менее сложен, чем расчет площади с геобордами. Студентам, возможно, придется разделить свои фигуры на квадраты, чтобы найти их площадь.
Когда учащиеся поймут, как находить площадь и периметр с помощью вертикальных и горизонтальных линий, вы можете начать вводить диагональные линии и частичные квадраты.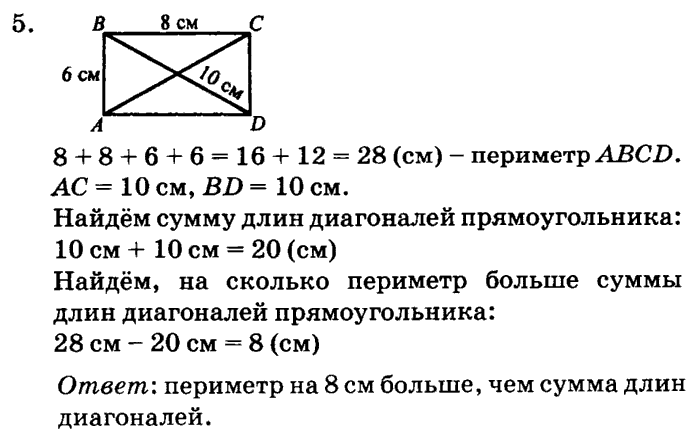 Это может оказаться прекрасным дополнением для студентов, которые продвинулись дальше в своем понимании. (Просто помните, что стороны диагоналей на самом деле больше одной единицы, поэтому сосредоточьтесь на площади этого расширения.)
Это может оказаться прекрасным дополнением для студентов, которые продвинулись дальше в своем понимании. (Просто помните, что стороны диагоналей на самом деле больше одной единицы, поэтому сосредоточьтесь на площади этого расширения.)
Геоборды — моя любимая работа для тех, кто быстро финиширует.
Геоборды предлагают бесконечное исследование местности, периметра и форм. Вы никогда не услышите страшное «Я готов!» исходит от студента. Открытые задачи для геобордов предлагают бесконечное исследование и множество решений одной задачи.
Примечание: Предпочтительны физические геоборды. Однако есть несколько виртуальных вариантов, если у вас нет набора физических плат. Веб-сайт Центра обучения математике имеет три бесплатные версии, в зависимости от доступной технологии.
Исследование крупной моторики: квадратные салфетки
Некоторым учащимся требуется дополнительная поддержка. Иногда я замечаю, что студенты не усваивают понятия. Поэтому я ищу способы задействовать все их тело и крупную моторику. И получать удовольствие!
И получать удовольствие!
Квадратные салфетки — отличный предшественник квадратных цветных плиток. Кроме того, они идеально подходят для полноценных демонстраций.
Во-первых, ученики могут создавать гигантские массивы с помощью квадратных салфеток. Подобно квадратным цветным плиткам, учащиеся начинают с задания на площадь или периметр. Например, создайте прямоугольник площадью 10. Они строят форму с помощью салфеток.
Вот тогда и начнется настоящее веселье и исследование! Ваши ученики построили большую фигуру. Тем не менее, они должны увидеть, соответствует ли он спецификациям задачи. Чтобы найти периметр, учащиеся могут физически обойти периметр этих массивов. Они могут вести переписку 1-1, используя собственное тело, переходя от одной плитки к другой. Затем они могут найти площадь, наступив на каждую квадратную салфетку.
Упрощенное использование квадратных салфеток включает прямоугольные формы. Более сложные версии этих задач могут включать фигуры, которые можно разбить на прямоугольники разного размера.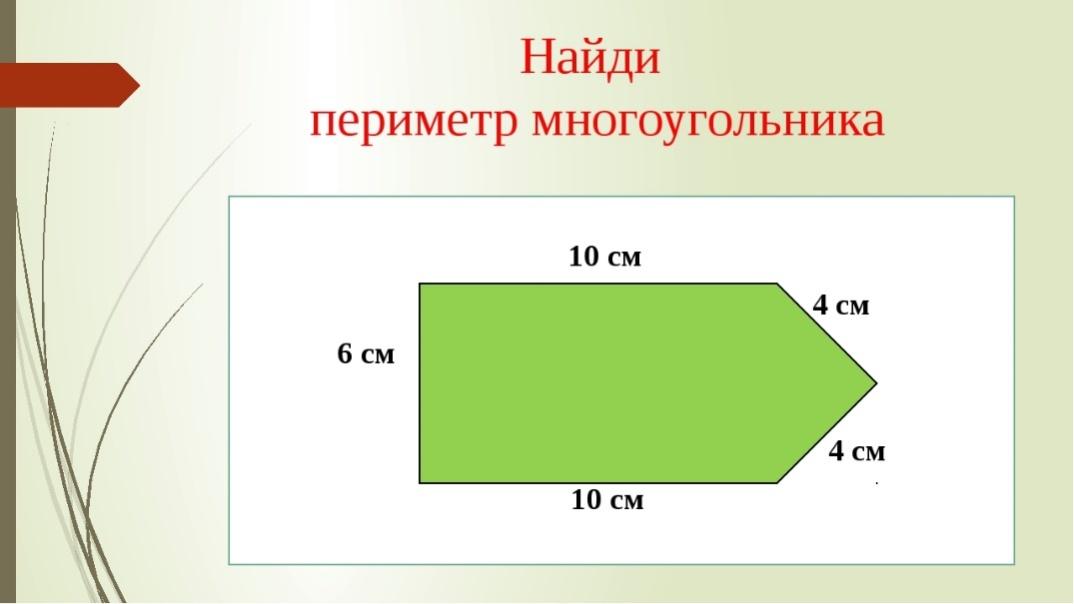
Соедините исследование крупной моторики с абстрактным мышлением
Квадратные салфетки — это манипулятор, который помогает учащимся использовать свои навыки крупной моторики для исследования пространства и периметра. Но учащимся по-прежнему необходимо связать физические исследования с конечной целью абстрактного мышления. Как и другие манипуляторы, я заставляю студентов записывать свои исследования в математических журналах.
Все математические мыслители могут заниматься практическим изучением области и периметра. Я надеюсь, что этот пост даст вам различные идеи, чтобы поддержать ваших учеников. Как ваш виртуальный товарищ по команде, я также хотел бы услышать об инновационных манипуляциях для обучения области и периметру, которые вы реализуете в своем классе.
План урока 5+ — Площадь и периметр
Модифицированный урок 5 — итоговый проект Отличный способ привлечь учащихся, в том числе учащихся ELL, к изучению материала — дать им свободу выбора способа обучения. Этот заключительный урок посвящен использованию всего, что было изучено до сих пор, для создания проекта, демонстрирующего их понимание материала. Как указано в первоначальном плане модуля, у учащихся есть выбор между тремя заданиями, которые они могут выбрать, чтобы продемонстрировать свое понимание площади и периметра. Три задания: практический , творческий и аналитический . Есть две из трех задач, указанных в плане модуля, которые, по нашему мнению, заставляют учащихся ELL серьезно задуматься.
Этот заключительный урок посвящен использованию всего, что было изучено до сих пор, для создания проекта, демонстрирующего их понимание материала. Как указано в первоначальном плане модуля, у учащихся есть выбор между тремя заданиями, которые они могут выбрать, чтобы продемонстрировать свое понимание площади и периметра. Три задания: практический , творческий и аналитический . Есть две из трех задач, указанных в плане модуля, которые, по нашему мнению, заставляют учащихся ELL серьезно задуматься.
ПРАКТИЧЕСКИЙ : Нарисуйте планы дома своей мечты на листе миллиметровой бумаги размером 100 x 100. Каждый квадрат сетки будет представлять собой 1 метр на 1 метр.
Правила: Каждая комната должна быть достаточно большой, чтобы вместить предметы, которые обычно находятся внутри (например, ванная комната должна быть достаточно большой, чтобы вместить унитаз, раковину и ванну). Дома должны быть только одноэтажными, но учащиеся могут пойти дальше, если захотят. Это будет зависеть от того, что они хотят делать. Их идеи могут быть слишком грандиозными, и их реализация может занять слишком много времени.
Это будет зависеть от того, что они хотят делать. Их идеи могут быть слишком грандиозными, и их реализация может занять слишком много времени.
Пометьте каждую комнату и запишите размеры комнат на миллиметровой бумаге. Приклейте эту бумагу в свой математический журнал.
На следующей странице своего математического журнала составьте список всех комнат в доме, который вы нарисовали (включая кладовые), и перечислите периметр и площадь каждой комнаты. На следующей странице своего математического журнала составьте список каждой комнаты в доме, который вы нарисовали (включая кладовые), и перечислите периметр и площадь каждой комнаты.
В каждой комнате должны быть стены, окружающие внешний край комнаты. Каждая комната также должна быть оснащена половыми досками и ковровым покрытием. Материалы для возведения стен стоят 10 долларов за метр стены. Материалы для пола стоят 10 долларов за квадратный метр пола. Сколько будет стоить построить каждую комнату в вашем доме? Добавьте цену к каждому номеру в списке, который вы составили. Изучите самую большую комнату в вашем доме и ответьте на следующий вопрос: есть ли способ сделать комнату такого же размера, но с меньшими затратами на строительство? Если есть, покажи как. Если нет способа сделать самую большую комнату менее дорогой, докажите, откуда вы это знаете.
Изучите самую большую комнату в вашем доме и ответьте на следующий вопрос: есть ли способ сделать комнату такого же размера, но с меньшими затратами на строительство? Если есть, покажи как. Если нет способа сделать самую большую комнату менее дорогой, докажите, откуда вы это знаете.
Это задание, которое учащиеся могут выбрать, является отличным заданием для учащихся ELL. Дома разные по всему миру, и не так много домов одинаковы по дизайну. Это задание побуждает учащихся к творчеству в создании плана дома своей мечты. Это задание — отличный способ для учащихся ELL создать нечто, включающее их культуру. Это отличный способ для учащихся, не изучающих ELL, увидеть, как будут выглядеть дома разных культур.
ТВОРЧЕСКИЙ : Создайте продукт, чтобы научить аудиторию второклассников периметру и площади. Учащиеся должны продемонстрировать, что они знают все термины, которые они уже выучили, как найти периметр и площадь, как они измеряются, почему каждый из них важен для повседневной жизни (связь с реальным миром), а также продемонстрировать понимание соотношение между периметром и площадью. Примеры проектов, которые могут создать учащиеся: плакат, сборник рассказов о периметре и площади, театр для читателей, картина с рецензией, объясняющей картину, или песня. Студенты могут придумывать свои собственные идеи для творческого задания, если они согласуют их с преподавателем.
Примеры проектов, которые могут создать учащиеся: плакат, сборник рассказов о периметре и площади, театр для читателей, картина с рецензией, объясняющей картину, или песня. Студенты могут придумывать свои собственные идеи для творческого задания, если они согласуют их с преподавателем.
Это задание дает учащимся гораздо больше свободы в выборе того, что они хотят создать, чтобы выразить свое понимание периметра и площади. Студенты ELL особенно выиграют от свободы выполнения этого задания. Это задание поможет учащимся ELL включить все, чему они научились, и поделиться этим с аудиторией. Это лучший способ для студентов и преподавателя узнать, как они продвинулись на данный момент, не только с материалом, но и с их английским языком.
Окончательная оценка :
Учащиеся будут оцениваться по их знаниям и точности по площади и периметру. Учащиеся будут представлять свои проекты либо перед классом своим сверстникам, либо перед учащимися других классов младше 4 класса.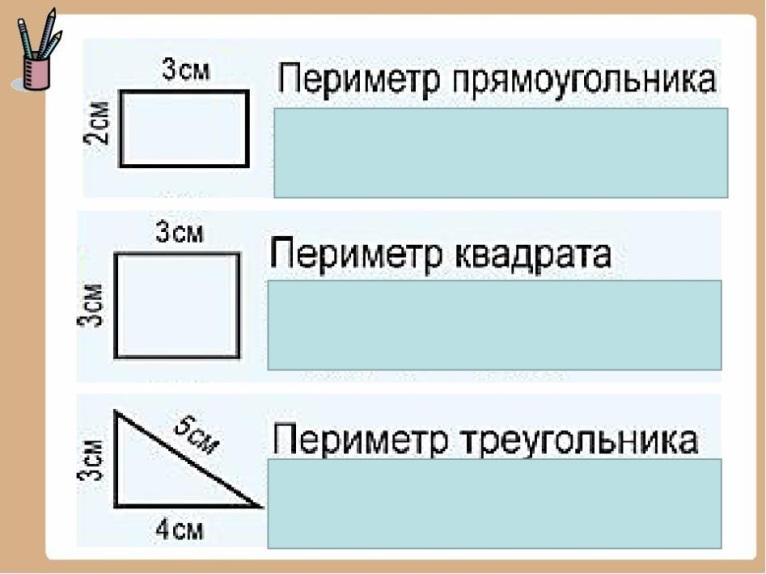
Материалы:
N/A
Список словарного запаса:
N/A
Действия:
Добавляя области вместе, чтобы найти общую площадь
. показать, чему учат на уроке. Прослушивание и просмотр видео также является хорошим способом для изучающих ELL сопоставить слова, которые они выучили, с изображениями, которые они увидят. Это, конечно, уже достигается с помощью уроков, которые также будут преподавать инструкторы. Это просто еще одна альтернатива для учащихся ELL и больше знакомства с английским языком.
Рабочие листы, над которыми учащиеся будут работать, чтобы лучше понять новый материал. Ниже приведен пример рабочего листа, над которым они будут работать.
Ниже приведен пример рабочего листа, над которым они будут работать.
Оценка:
Этот урок считается дополнительным уроком, который учащиеся могут использовать для своего итогового проекта. Этот урок будет помещен в математические журналы учащихся, чтобы они могли вернуться к нему при необходимости. Учащиеся старших классов могут лучше понять информацию на этом уроке, чем другие учащиеся, поэтому они могут помочь своим сверстникам, когда дело доходит до понимания материала.
Урок 5.2 – ОбъемЦели урока:
В продолжение урока, проведенного на уроке 5.1, учащиеся познакомятся с определением объема. Учащиеся смогут определять объем и применять его в реальных приложениях.
Материалы:
Соединительные кубики, вода, квадратные емкости, мерный стакан.
Словарь:
Объем, высота, миллилитры.
Упражнения:
Вода и объем
Хороший способ для учащихся узнать, что такое объем, наглядно показать им, как найти объем. Один соединительный куб имеет ширину 1 см, длину 1 см и высоту 1 см. Значит, один из этих кубиков равен 1 мл. Теперь, когда это объяснено учащимся, вы можете объединить их в группы. Каждая группа измерит квадратный контейнер и предскажет, каким, по их мнению, будет объем их квадратного контейнера. Затем вы предлагаете учащимся налить воду в свои квадратные сосуды, а затем налить эту воду в мерную чашку, чтобы подтвердить объем квадратных сосудов. Это занятие — отличный способ для учащихся ELL выучить новый словарный запас и материал. Имея возможность визуально распознавать слова из словарного списка, они могут эффективно изучать новые слова и материал.
Объем и кубы
После вводного задания учащиеся могут работать с различными рабочими листами.
Пример рабочего листа:
Оценка:
Этот урок считается дополнительным уроком, который учащиеся могут использовать для своего итогового проекта. Этот урок будет помещен в математические журналы учащихся, чтобы они могли вернуться к нему при необходимости. Учащиеся старших классов могут лучше понять информацию на этом уроке, чем другие учащиеся, поэтому они могут помочь своим сверстникам, когда дело доходит до понимания материала.
Этот урок будет помещен в математические журналы учащихся, чтобы они могли вернуться к нему при необходимости. Учащиеся старших классов могут лучше понять информацию на этом уроке, чем другие учащиеся, поэтому они могут помочь своим сверстникам, когда дело доходит до понимания материала.
Цели урока:
На этом уроке учащиеся узнают, как найти периметр и площадь прямоугольного треугольника.
Материалы:
нет данных
Словарь:
Прямоугольный треугольник, гипотенуза, противоположный, смежный.
Действия:
Площадь прямоугольного треугольника
Учащиеся познакомятся с прямоугольными треугольниками с помощью диаграмм. Затем учащиеся научатся находить площади прямоугольных треугольников. У учащихся могут возникнуть трудности с формулой. Учащиеся должны умножить противоположные и соседние, а затем разделить на 2, чтобы найти площадь прямоугольного треугольника. Учащихся также можно научить тому, что 2 прямоугольных треугольника составляют квадрат, поэтому учащиеся могут узнать площадь квадрата, найдя площадь прямоугольного треугольника и умножив ее на 2.
Учащиеся должны умножить противоположные и соседние, а затем разделить на 2, чтобы найти площадь прямоугольного треугольника. Учащихся также можно научить тому, что 2 прямоугольных треугольника составляют квадрат, поэтому учащиеся могут узнать площадь квадрата, найдя площадь прямоугольного треугольника и умножив ее на 2.
Словесные задачи для учащихся ELL:
- Периметр треугольника равен 30 см. Высота 10 см. Гипотенуза равна 15. Какова площадь треугольника?
- Периметр треугольника равен 10 см. Высота 5 см. Гипотенуза равна 4. Какова площадь треугольника?
- Периметр треугольника равен 20 см. Высота 9 см. Гипотенуза равна 8. Какова площадь треугольника?
Оценка:
Этот урок считается дополнительным уроком, который учащиеся могут использовать для своего итогового проекта. Этот урок будет помещен в математические журналы учащихся, чтобы они могли вернуться к нему при необходимости. Учащиеся старших классов могут лучше понять информацию на этом уроке, чем другие учащиеся, поэтому они могут помочь своим сверстникам, когда дело доходит до понимания материала.

 Найди периметр.
Найди периметр. Найди периметр.
Найди периметр. Найди периметр.
Найди периметр. Урок-сказка на тему: «Периметр»
Урок-сказка на тему: «Периметр»


 Даже имена у них были похожие.
Даже имена у них были похожие.
 Как называются компоненты действия сложения? (Слагаемое, слагаемое, сумма)
Как называются компоненты действия сложения? (Слагаемое, слагаемое, сумма) Он отмерял длину 1 раз (это 3 см) и сделал все четыре стороны одинаковой длины, а все углы прямыми.
Он отмерял длину 1 раз (это 3 см) и сделал все четыре стороны одинаковой длины, а все углы прямыми.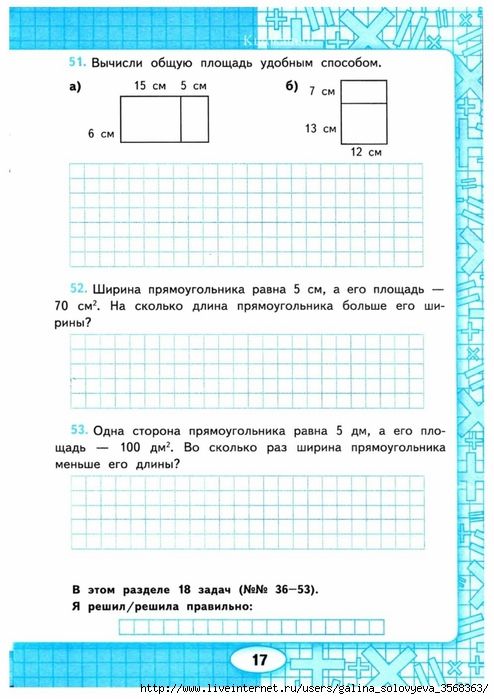 (Только ответы).
(Только ответы). Нельзя допустить этого снова.
Нельзя допустить этого снова.




 Какие фигуры остались? (Прямоугольники)
Какие фигуры остались? (Прямоугольники)
 Физ. минутка.
Физ. минутка.