Касательная к окружности — свойства, теорема, правила
Касательная к окружности, секущая и хорда — в чем разница
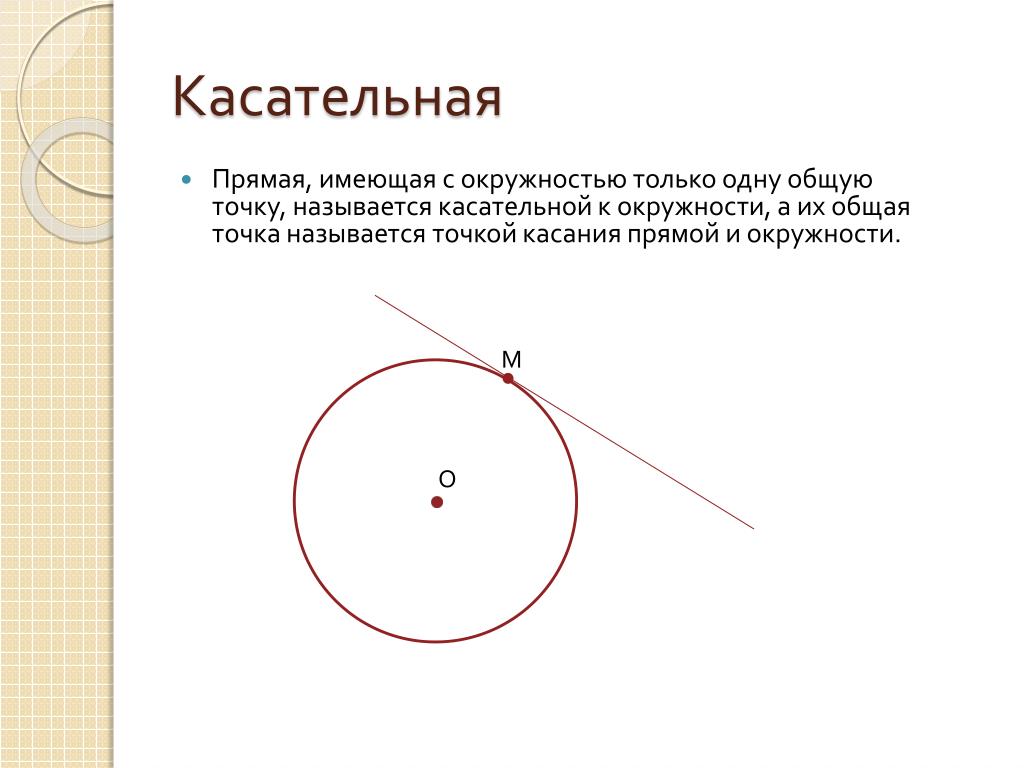
В самом названии касательной отражается суть понятия — это прямая, которая не пересекает окружность, а лишь касается ее в одной точке. Взглянув на рисунок окружности ниже, несложно догадаться, что точку касания от центра отделяет расстояние, в точности равное радиусу.
Касательная к окружности — это прямая, имеющая с ней всего одну общую точку. |
Если мы проведем прямую поближе к центру окружности — так, чтобы расстояние до него было меньше радиуса — неизбежно получится две точки пересечения. Такая прямая называется секущей, а отрезок, расположенный между точками пересечения, будет хордой (на рисунке ниже это ВС ).
Секущая к окружности — это прямая, которая пересекает ее в двух местах, т. |
Практикующий детский психолог Екатерина Мурашова
Бесплатный курс для современных мам и пап от Екатерины Мурашовой. Запишитесь и участвуйте в розыгрыше 8 уроков
Свойства касательной к окружности
Выделяют четыре свойства касательной, которые необходимо знать для решения задач. Два из них достаточно просты и легко доказуемы, а вот еще над двумя придется немного подумать. Рассмотрим все по порядку.
Касательная к окружности и радиус, проведенный в точку касания, взаимно перпендикулярны.
Не будем принимать это на веру, попробуем доказать. Итак, у нас даны:
- окружность с центральной точкой А;
- прямая а — касательная к ней;
- радиус АВ, проведенный к касательной.

Докажем, что касательная и радиус АВ взаимно перпендикулярны, т.е. а ⟂ АВ.
Пойдем от противного — предположим, что между прямой а и радиусом АВ нет прямого угла и проведем настоящий перпендикуляр к касательной, назвав его АС.
В таком случае наш радиус АВ будет считаться наклонной, а наклонная, как известно, всегда длиннее перпендикуляра. Получается, что АВ > АС. Но если бы это было на самом деле так, наша прямая а пересекалась бы с окружностью два раза, ведь расстояние от центра А до нее — меньше радиуса. Но по условию задачи а — это касательная, а значит, она может иметь лишь одну точку касания.
Итак, мы получили противоречие. Делаем вывод, что настоящим перпендикуляром к прямой а будет вовсе не
Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.
Задача
У нас есть окружность, центр которой обозначен О. Из точки С проведена прямая, и она касается этой окружности в точке А. Известно, что ∠АСО = 28°. Найдите величину дуги АВ.
Решение:
Мы знаем, что касательная АС ⟂ АО, следовательно ∠САО = 90°.
Поскольку нам известны величины двух углов треугольника ОАС, не составит труда найти величину и третьего угла.
∠АОС = 180° — ∠САО — ∠АСО = 180° — 90° — 28° = 62°
Поскольку вершина угла АОС лежит в центре окружности, можно вспомнить свойство центрального угла — как известно, он равен дуге, на которую опирается. Следовательно, АВ = 62°.
Ответ: АВ = 62°.
Если провести две касательных к окружности из одной точки, лежащей вне этой окружности, то их отрезки от этой начальной точки до точки касания будут равны.
Докажем и это свойство на примере. Итак, у нас есть окружность с центром А, давайте проведем к ней две касательные из точки D. Обозначим эти прямые как ВD и CD . А теперь выясним, на самом ли деле BD = CD.
Для начала дополним наш рисунок, проведем еще одну прямую из точки D в центр окружности. Как видите, у нас получилось два треугольника: ABD и ACD . Поскольку мы уже знаем, что касательная и радиус к ней перпендикулярны, углы
Итак, у нас есть два прямоугольных треугольника с общей гипотенузой AD. Учитывая, что радиусы окружности всегда равны, мы понимаем, что катеты AB и AC у этих треугольников тоже одинаковой длины. Следовательно, ΔABD = ΔACD (по катету и гипотенузе).. Значит, оставшиеся катеты, а это как раз наши BD и CD (отрезки касательных к окружности), аналогично равны.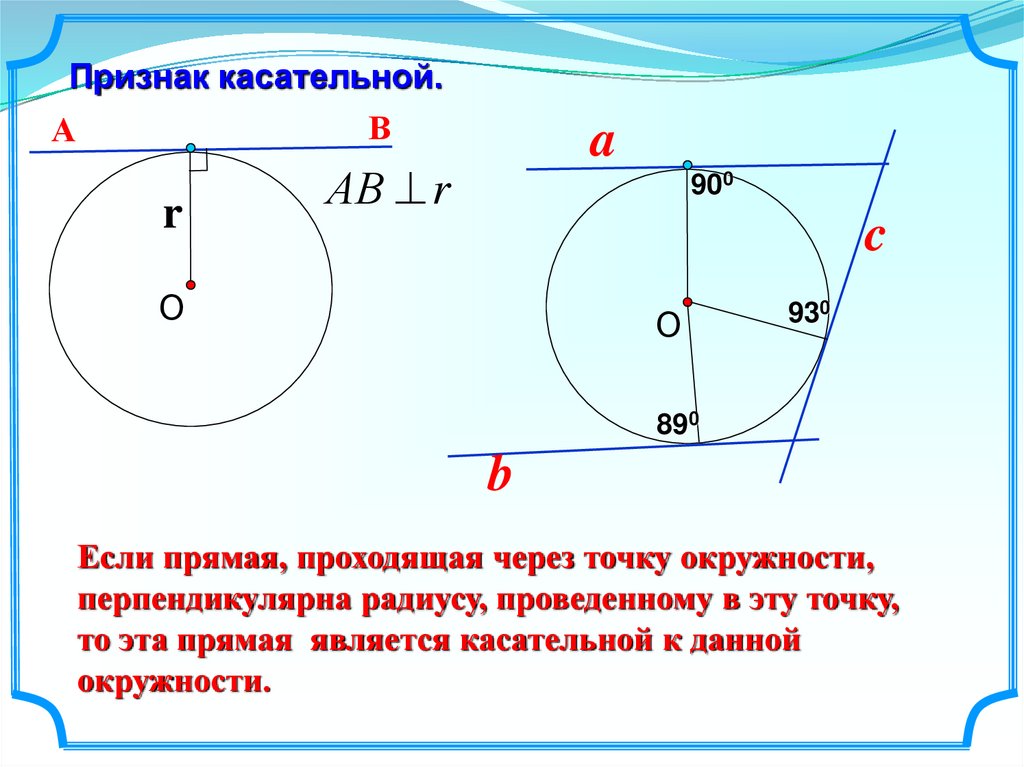
Важно: прямая, проложенная из стартовой точки до центра окружности (в нашем примере это AD), делит угол между касательными пополам.
Задача 1
У нас есть окружность с радиусом 4,5 см. К ней из точки D, удаленной от центра на 9 см, провели две прямые, которые касаются окружности в точках B и C. Определите градусную меру угла, под которым пересекаются касательные.
Решение
Для этой задачи вполне подойдет уже рассмотренный выше рисунок окружности с радиусами АВ и АC. Поскольку касательная ВD перпендикулярна радиусу АВ , у нас есть прямоугольный треугольник АВD. Зная длину его катета и гипотенузы, определим величину ∠BDA.
∠BDA = 30° (по свойству прямоугольного треугольника: угол, лежащий напротив катета, равного половине гипотенузы, составляет 30°).
Мы знаем, что прямая, проведенная из точки до центра окружности, делит угол между касательными, проведенными из этой же точки, пополам. Другими словами:
Другими словами:
∠BDC = ∠BDA × 2 = 30° × 2 = 60°
Итак, угол между касательными составляет 60°.
Ответ: ∠BDA = 60°.
Задача 2
К окружности с центром О провели две касательные КМ и КN. Известно, что ∠МКN равен 50°. Требуется определить величину угла ∠NМК.
Решение
Согласно вышеуказанному свойству мы знаем, что КМ = КN. Следовательно, треугольник МNК является равнобедренным.
Углы при его основании будут равны, т.е. ∠МNК = ∠NМК.
∠МNК = (180° — ∠МКN) : 2 = (180° — 50°) : 2 = 65°
Ответ: ∠NМК = 65°.
Соотношение между касательной и секущей: если они проведены к окружности из одной точки, лежащей вне окружности, то квадрат расстояния до точки касания равен произведению длины всей секущей на ее внешнюю часть.
Данное свойство намного сложнее предыдущих, и его лучше записать в виде уравнения.
Начертим окружность и проведем из точки А за ее пределами касательную и секущую. Точку касания обозначим В, а точки пересечения — С и D. Тогда CD будет хордой, а отрезок AC — внешней частью секущей.
AB2 = AD × AC
Задача 1
Из точки М к окружности проведены две прямые, пусть одна из них будет касательной МA, а вторая — секущей МB. Известно, что хорда ВС = 12 см, а длина всей секущей МB составляет 16 см. Найдите длину касательной к окружности МA.
Решение
Исходя из соотношения касательной и секущей МА 2 = МВ × МС.
Найдем длину внешней части секущей:
МС = МВ — ВС = 16 — 12 = 4 (см)
МА2 = МВ × МС = 16 х 4 = 64
МА = √ 64= 8 (см)
Ответ: MA = 8 см.
Задача 2
Дана окружность с радиусом 6 см. Из некой точки М к ней проведены две прямые — касательная МA и секущая МB . Известно, что прямая МB пересекает центр окружности O. При этом МB в 2 раза длиннее касательной МA . Требуется определить длину отрезка МO.
Решение
Допустим, что МО = у, а радиус окружности обозначим как R.
В таком случае МВ = у + R, а МС = у – R.
Поскольку МВ = 2 МА, значит:
МА = МВ : 2 = (у + R) : 2
Согласно теореме о касательной и секущей, МА 2 = МВ × МС.
Значит:
(у + R)2 : 4 = (у + R) × (у — R)
Сократим уравнение на (у + R), так как эта величина не равна нулю, и получим:
(у + R) : 4 = (у — R)
у = 5R : 3
Поскольку R = 6, у = 5R : 3 = 30 : 3 = 10 (см).
Ответ: MO = 10 см.
Угол между хордой и касательной, проходящей через конец хорды, равен половине дуги, расположенной между ними.
Это свойство тоже стоит проиллюстрировать на примере: допустим, у нас есть касательная к окружности, точка касания В и проведенная из нее хорда AВ. Отметим на касательной прямой точку C, чтобы получился угол AВC.
∠АВС = ½ АВ
Задача 1
Угол АВС между хордой АВ и касательной ВС составляет 32°. Найдите градусную величину дуги между касательной и хордой.
Решение
Согласно свойствам угла между касательной и хордой, ∠АВС = ½ АВ.
АВ = ∠АВС × 2 = 32° × 2 = 64°
Ответ: АВ = 64°.
Задача 2
У нас есть окружность с центром О, к которой идет прямая, касаясь окружности в точке K. Из этой точки проводим хорду KM, и она образует с касательной угол MKB, равный 84°. Давайте найдем величину угла ОMK.
Из этой точки проводим хорду KM, и она образует с касательной угол MKB, равный 84°. Давайте найдем величину угла ОMK.
Решение
Поскольку ∠МКВ равен половине дуги между KM и КВ, следовательно:
КМ = 2 ∠МКВ = 2 х 84° = 168°
Обратите внимание, что ОМ и ОK по сути являются радиусами, а значит, ОМ = ОК. Из этого следует, что треугольник ОMK равнобедренный.
∠ОКМ = ∠ОМК = (180° — ∠КОМ) : 2
Так как центральный угол окружности равен угловой величине дуги, на которую он опирается, то:
∠КОМ = КМ = 168°
∠ОМК = (180° — ∠КОМ) : 2 = (180° — 168°) : 2 = 6°
Ответ: ∠ОМК = 6°.
Внеклассный урок — Касательная к графику функции
Касательная к графику функции
Касательная – это прямая, проходящая через точку кривой и совпадающая с ней в этой точке с точностью до первого порядка (рис. 1).
1).
Другое определение: это предельное положение секущей при Δx→0.
Пояснение: Возьмем прямую, пересекающую кривую в двух точках: А и b (см.рисунок). Это секущая. Будем поворачивать ее по часовой стрелке до тех пор, пока она не обретет только одну общую точку с кривой. Так мы получим касательную.
Строгое определение касательной:
Касательная к графику функции f, дифференцируемой в точке xо, — это прямая, проходящая через точку (xо; f(xо)) и имеющая угловой коэффициент f ′(xо).
Угловой коэффициент имеет прямая вида y = kx + b. Коэффициент k и является угловым коэффициентом этой прямой.
Угловой коэффициент равен тангенсу острого угла, образуемого этой прямой с осью абсцисс:
|
Здесь угол α – это угол между прямой y = kx + b и положительным (то есть против часовой стрелки) направлением оси абсцисс. Он называется углом наклона прямой (рис.1 и 2).
Он называется углом наклона прямой (рис.1 и 2).
Если угол наклона прямой y = kx + b острый, то угловой коэффициент является положительным числом. График возрастает (рис.1).
Если угол наклона прямой y = kx + b тупой, то угловой коэффициент является отрицательным числом. График убывает (рис.2).
Если прямая параллельна оси абсцисс, то угол наклона прямой равен нулю. В этом случае угловой коэффициент прямой тоже равен нулю (так как тангенс нуля есть ноль). Уравнение прямой будет иметь вид y = b (рис.3).
Если угол наклона прямой равен 90º (π/2), то есть она перпендикулярна оси абсцисс, то прямая задается равенством x = c, где c – некоторое действительное число (рис.4).
Уравнение касательной к графику функции y = f(x) в точке xо:
|
Алгоритм решения уравнения касательной к графику функции y = f(x):
1. 2. Вычислить производные f ′(x) и f ′(xо). 3. Внести найденные числа xо, f(xо), f ′(xо) в уравнение касательной и решить его. |
Пример: Найдем уравнение касательной к графику функции f(x) = x3 – 2x2 + 1 в точке с абсциссой 2.
Решение.
Следуем алгоритму.
1) Точка касания xо равна 2. Вычислим f(xо):
f(xо) = f(2) = 23 – 2 ∙ 22 + 1 = 8 – 8 + 1 = 1
2) Находим f ′(x). Для этого применяем формулы дифференцирования, изложенные в предыдущем разделе. Согласно этим формулам, х2 = 2х, а х3 = 3х2. Значит:
Значит:
f ′(x) = 3х2 – 2 ∙ 2х = 3х2 – 4х.
Теперь, используя полученное значение f ′(x), вычислим f ′(xо):
f ′(xо) = f ′(2) = 3 ∙ 22 – 4 ∙ 2 = 12 – 8 = 4.
3) Итак, у нас есть все необходимые данные: xо = 2, f(xо) = 1, f ′(xо) = 4. Подставляем эти числа в уравнение касательной и находим окончательное решение:
у = f(xо) + f ′(xо) (x – xо) = 1 + 4 ∙ (х – 2) = 1 + 4х – 8 = –7 + 4х = 4х – 7.
Ответ: у = 4х – 7.
Касательная прямая — Вики
График функции (чёрная кривая) и касательная прямая (красная прямая)
Каса́тельная пряма́я — прямая, проходящая через точку кривой и совпадающая с ней в этой точке с точностью до первого порядка.
Содержание
- 1 Строгое определение
- 2 Замечание
- 3 Касательная как предельное положение секущей
- 4 Касательная к окружности
- 4.1 Свойства
- 5 Вариации и обобщения
- 5.1 Односторонние полукасательные
- 6 См. также
- 7 Литература
Строгое определение
- Пусть функция f:U(x0)⊂R→R{\displaystyle f\colon U(x_{0})\subset \mathbb {R} \to \mathbb {R} } определена в некоторой окрестности точки x0∈R{\displaystyle x_{0}\in \mathbb {R} }, и дифференцируема в ней: f∈D(x0){\displaystyle f\in {\mathcal {D}}(x_{0})}. Касательной прямой к графику функции f{\displaystyle f} в точке x0{\displaystyle x_{0}} называется график линейной функции, задаваемый уравнением
- y=f(x0)+f′(x0)(x−x0),x∈R{\displaystyle y=f(x_{0})+f'(x_{0})(x-x_{0}),\quad x\in \mathbb {R} }.
- Если функция f{\displaystyle f} имеет в точке x0{\displaystyle x_{0}} бесконечную производную f′(x0)=±∞,{\displaystyle f'(x_{0})=\pm \infty ,} то касательной прямой в этой точке называется вертикальная прямая, задаваемая уравнением
- x=x0.
 {\displaystyle x=x_{0}.}
{\displaystyle x=x_{0}.}
- x=x0.
Замечание
Прямо из определения следует, что график касательной прямой проходит через точку (x0,f(x0)){\displaystyle (x_{0},f(x_{0}))}. Угол α{\displaystyle \alpha } между касательной к кривой и осью Ох удовлетворяет уравнению
- tgα=f′(x0)=k,{\displaystyle \operatorname {tg} \,\alpha =f'(x_{0})=k,}
где tg{\displaystyle \operatorname {tg} } обозначает тангенс, а k{\displaystyle \operatorname {k} } — коэффициент наклона касательной. Производная в точке x0{\displaystyle x_{0}} равна угловому коэффициенту касательной к графику функции y=f(x){\displaystyle y=f(x)} в этой точке.
Касательная как предельное положение секущей
Пусть f:U(x0)→R{\displaystyle f\colon U(x_{0})\to \mathbb {R} } и x1∈U(x0).{\displaystyle x_{1}\in U(x_{0}).} Тогда прямая линия, проходящая через точки (x0,f(x0)){\displaystyle (x_{0},f(x_{0}))} и (x1,f(x1)){\displaystyle (x_{1},f(x_{1}))} задаётся уравнением
- y=f(x0)+f(x1)−f(x0)x1−x0(x−x0).
 {\displaystyle y=f(x_{0})+{\frac {f(x_{1})-f(x_{0})}{x_{1}-x_{0}}}(x-x_{0}).}
{\displaystyle y=f(x_{0})+{\frac {f(x_{1})-f(x_{0})}{x_{1}-x_{0}}}(x-x_{0}).}
Эта прямая проходит через точку (x0,f(x0)){\displaystyle (x_{0},f(x_{0}))} для любого x1∈U(x0),{\displaystyle x_{1}\in U(x_{0}),} и её угол наклона α(x1){\displaystyle \alpha (x_{1})} удовлетворяет уравнению
- tgα(x1)=f(x1)−f(x0)x1−x0.{\displaystyle \operatorname {tg} \,\alpha (x_{1})={\frac {f(x_{1})-f(x_{0})}{x_{1}-x_{0}}}.}
В силу существования производной функции f{\displaystyle f} в точке x0,{\displaystyle x_{0},} переходя к пределу при x1→x0,{\displaystyle x_{1}\to x_{0},} получаем, что существует предел
- limx1→x0tgα(x1)=f′(x0),{\displaystyle \lim \limits _{x_{1}\to x_{0}}\operatorname {tg} \,\alpha (x_{1})=f'(x_{0}),}
а в силу непрерывности арктангенса и предельный угол
- α=arctgf′(x0).{\displaystyle \alpha =\operatorname {arctg} \,f'(x_{0}).}
Прямая, проходящая через точку (x0,f(x0)){\displaystyle (x_{0},f(x_{0}))} и имеющая предельный угол наклона, удовлетворяющий tgα=f′(x0),{\displaystyle \operatorname {tg} \,\alpha =f'(x_{0}),} задаётся уравнением касательной:
- y=f(x0)+f′(x0)(x−x0).
 {\displaystyle y=f(x_{0})+f'(x_{0})(x-x_{0}).}
{\displaystyle y=f(x_{0})+f'(x_{0})(x-x_{0}).}
Касательная к окружности
Отрезки касательных
Прямая, имеющая одну общую точку с окружностью и лежащая с ней в одной плоскости, называется касательной к окружности.
Свойства
- Касательная к окружности перпендикулярна к радиусу, проведённому в точку касания.
- Отрезки касательных к окружности, проведённые из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.
- Длина отрезка касательной, проведённой к окружности единичного радиуса, взятого между точкой касания и точкой пересечения касательной с лучом, проведённым из центра окружности, является тангенсом угла между этим лучом и направлением от центра окружности на точку касания. «Тангенс» от лат. tangens — «касательная».
Вариации и обобщения
Односторонние полукасательные
- Если существует правая производная f+′(x0)<∞,{\displaystyle f’_{+}(x_{0})<\infty ,} то пра́вой полукаса́тельной к графику функции f{\displaystyle f} в точке x0{\displaystyle x_{0}} называется луч
- y=f(x0)+f+′(x0)(x−x0),x⩾x0.
 {\displaystyle y=f(x_{0})+f’_{+}(x_{0})(x-x_{0}),\quad x\geqslant x_{0}.}
{\displaystyle y=f(x_{0})+f’_{+}(x_{0})(x-x_{0}),\quad x\geqslant x_{0}.}
- Если существует левая производная f−′(x0)<∞,{\displaystyle f’_{-}(x_{0})<\infty ,} то ле́вой полукаса́тельной к графику функции f{\displaystyle f} в точке x0{\displaystyle x_{0}} называется луч
- y=f(x0)+f−′(x0)(x−x0),x⩽x0.{\displaystyle y=f(x_{0})+f’_{-}(x_{0})(x-x_{0}),\quad x\leqslant x_{0}.}
- Если существует бесконечная правая производная f+′(x0)=+∞(−∞),{\displaystyle f’_{+}(x_{0})=+\infty \;(-\infty ),} то правой полукасательной к графику функции f{\displaystyle f} в точке x0{\displaystyle x_{0}} называется луч
- x=x0,y⩾f(x0)(y⩽f(x0)).{\displaystyle x=x_{0},\;y\geqslant f(x_{0})\;(y\leqslant f(x_{0})).}
- Если существует бесконечная левая производная f−′(x0)=+∞(−∞),{\displaystyle f’_{-}(x_{0})=+\infty \;(-\infty ),} то правой полукасательной к графику функции f{\displaystyle f} в точке x0{\displaystyle x_{0}} называется луч
- x=x0,y⩽f(x0)(y⩾f(x0)).
 {\displaystyle x=x_{0},\;y\leqslant f(x_{0})\;(y\geqslant f(x_{0})).}
{\displaystyle x=x_{0},\;y\leqslant f(x_{0})\;(y\geqslant f(x_{0})).}
См. также
- Дифференцируемая функция
- Касательное пространство
- Нормаль, бинормаль
- Теорема о секущих
Литература
- Топоногов В. А. Дифференциальная геометрия кривых и поверхностей. — Физматкнига, 2012. — ISBN 9785891552135.
- Касательная // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
— Проблема с базовым определением касательной.
Спросил
Изменено 6 лет, 4 месяца назад
Просмотрено 11 тысяч раз
$\begingroup$
Я только начал впервые заниматься исчислением, и тут я вижу что-то, что называется касательной. Говорят, касательная — это линия, которая пересекает кривую ровно в одной точке. Но есть много линий, которые могут пересекать одну и ту же точку, как показано на рисунке-
Говорят, касательная — это линия, которая пересекает кривую ровно в одной точке. Но есть много линий, которые могут пересекать одну и ту же точку, как показано на рисунке-
ПОЧЕМУ мы не говорим, что прямые М и С тоже касательные?
Каково реальное определение касательной?
«Касательная — это прямая, проходящая через две бесконечно малые точки» Верно ли это определение? Спасибо!
- исчисление
- определение
- бесконечно малые
- касательная
$\endgroup$
11
$\begingroup$
Анимации, показывающие, что предел секанс по мере того, как переменная точка стремится к фиксированной точке, становится касательной.
Во-первых, когда переменная точка (красная) приближается к фиксированной точке (черная) снизу:
Во-вторых, когда переменная точка приближается к фиксированной точке сверху:
В обоих случаях секанс линия становится той же касательной. Это говорит о том, что производная четко определена в черной точке (которая выделяется зеленым, когда происходит касание).
Это говорит о том, что производная четко определена в черной точке (которая выделяется зеленым, когда происходит касание).
Формально это дает нам следующее определение производной. Для вещественнозначной функции $f(x)$ производная в точке $x = a$ есть предел наклона секущей, проходящей через две точки $$P_a = (a, f(a)), \ quad P_b = (b, f(b))$$, когда $b$ приближается к $a$, если такой предел существует. Поскольку наклон равен просто $$\frac{f(b)-f(a)}{b-a},$$, мы имеем $$f'(a) = \lim_{b \to a} \frac{f( b) — f(a)}{b-a}.$$ Таким образом, уравнение касательной в точке $P_a$ имеет вид $$y — f(a) = f'(a)(x-a),$$, если линия не имеет бесконечного наклона; в противном случае $1/f'(a) = 0$, и мы можем записать уравнение касательной в виде $x = a$.
$\endgroup$
3
$\begingroup$
Когда мы говорим о линии, касательной к кривой, мы имеем в виду линию, касающуюся окружности, соответствующей радиусу кривизны. Это связано с тем, что линия может взаимодействовать с окружностью только тремя способами:
Это связано с тем, что линия может взаимодействовать с окружностью только тремя способами:
- Линия не пересекает окружность.
- Линия пересекает окружность, т.е. пересекается в двух точках. Мы называем это секущей линией.
- Линия пересекает окружность в одной точке. Это называется касательной линией.
Для гладкой кривой в любой точке мы можем вычислить ее кривизну с помощью окружности. Линия, касающаяся этой окружности, является касательной к кривой.
$\endgroup$
16
$\begingroup$
Это соответствует ответам Кристиана Блаттера и блохи. Касательная линия к кривой в точке — это, неформально, линия, которая лучше всего аппроксимирует поведение кривой в этой точке . Линия, пересекающая кривую под углом, не очень хорошо аппроксимирует кривую, но линия, идущая в том же направлении, что и кривая в этой точке, дает хорошее приближение. 3$ при $x = 0$, но в точке касания ее поведение максимально близко к поведению кривой насколько это возможно.
3$ при $x = 0$, но в точке касания ее поведение максимально близко к поведению кривой насколько это возможно.
Это неформально, так как возникает вопрос, что значит аппроксимировать кривую. На это можно ответить через определение производной. Мы аппроксимируем кривую линией, проходящей не только через точку интереса, но и через вторую близлежащую точку на кривой. Затем переместите вторую точку к первой. На правильной кривой чем ближе вторая точка к первой, тем угол линии будет приближаться к определенному углу, который представляет собой касательную. Производная — это просто средство точного выражения этой идеи.
$\endgroup$
4
$\begingroup$
Говорят, касательная — это линия, которая пересекает кривую ровно в одной точке.
Нет, это линия, которая касается в одной точке.
Только представьте, что кривая — это кожа части вашего тела, а линии в вопросах — это ножи. 2\sin{1\ над x}$, но не $y=|x|$. В примере $y=|x|$ строка $y=0$ — это поддерживающая линия графика, но не касательная.
2\sin{1\ над x}$, но не $y=|x|$. В примере $y=|x|$ строка $y=0$ — это поддерживающая линия графика, но не касательная.
$\endgroup$
5
$\begingroup$
Характерным свойством касательной к кривой в данной точке является то, что эта линия наилучшим образом аппроксимирует кривую вблизи точки.
Это означает, что по любой другой прямой можно найти окрестность точки (диска с центром в этой точке), где касательная всегда ближе к кривой, чем ее соперник.
Кстати, кто-то упомянул понятие круга кривизны. Можно применить те же рассуждения, только теперь мы принимаем также окружности, кроме линий, для аппроксимации кривой.
$\endgroup$
$\begingroup$
Чтобы ответить на ваш вопрос, является ли Касательная линия линией, проходящей через две бесконечно малые точки , стоит указать, что это было первоначальное определение касательной линии Лейбницем в первой публикации по математическому анализу, появившейся в 1684 г. , озаглавленной 92$. Линия, проходящая через эти две точки, будет иметь наклон $2+dx$ по простому вычислению. Поскольку термин $dx$ не может быть присвоен в терминологии Лейбница, он опускается, чтобы получить окончательный ответ $2$ для наклона.
, озаглавленной 92$. Линия, проходящая через эти две точки, будет иметь наклон $2+dx$ по простому вычислению. Поскольку термин $dx$ не может быть присвоен в терминологии Лейбница, он опускается, чтобы получить окончательный ответ $2$ для наклона.
В современной системе бесконечно малых величин, разработанной Абрахамом Робинсоном, это достигается за счет применения принципа стандартной части, согласно которому каждое конечное гипердействительное число бесконечно близко к уникальному действительному числу.
Таким образом, строгое определение касательной не требует знания ни производной, ни исчисления, а скорее предшествует и мотивирует и то, и другое, как это было исторически. См. учебник Кейслера Элементарное исчисление для получения подробной информации.
$\endgroup$
$\begingroup$
Если принять интуитивное представление о том, что кривая имеет две стороны (см., например, теорему Жордана о кривой), то можно определить касательную в точке $P$ на кривой как линию, которая в достаточно малой окрестности $P$:
1 .
Проходит через $P$ и никакую другую точку кривой
2 . Лежит на одной стороне кривой.
$\endgroup$
6
$\begingroup$
Хорошо, мои два цента:
Для точного определения «касательной» линии требуется исчисление.
На интуитивном уровне касательная «просто» касается кривой и «идет вместе с ней». Ваши встречные примеры не «просто касаются» — они бьют в лоб и проходят через это. Они не «идут вместе» с кривой — они пересекают ее под значительным углом.
Но, очевидно, это не строгое определение. Это даже не близко.
Если бы это зависело от меня, я бы определил это как линию, которая касается кривой в точке, и в этой точке наклон линии (который измеряет скорость изменения линий) такой же, как мгновенная скорость изменения кривой.
Это намекает на грядущие расчеты, а именно на то, что «гладкие» кривые будут иметь мгновенные скорости изменения, и имеет смысл говорить о них.
Лейбниц определил касательную линию как линию, проходящую через две бесконечно близкие точки на кривой, так что вы находитесь в очень хорошей компании. Однако я не думаю, что это работает как определение . Нет двух точек, бесконечно близких друг к другу. Есть только одна точка, но результирующая линия является пределом серии линий, состоящих из двух точек, пары которых становятся бесконечно ближе.
Но я действительно думаю, что эта концепция обеспечивает механику вывода касательной и определения производной… как только установлены фундаментальные понятия исчисления (пределы и бесконечности).
$\endgroup$
6
$\begingroup$
Способ, которым меня учили и который оказался очень полезным с интуитивной точки зрения, — это идея «приближения» точки, к которой вы хотите найти касательную на кривой.
Идея в основном такая же, как и в Интуитивном описании касательной в Википедии (эту страницу стоит прочитать для получения информации о касательных), но развивайте это дальше, представляя, как выглядит кривая в этом масштабе (когда они говорят «около точка» в $a + h$, представьте, что h — это значение, которое становится все меньше и меньше, но никогда не достигает $0$, очень-очень маленькое значение).
По мере того, как вы будете подходить все ближе и ближе, кривая будет выглядеть все прямее и прямее! Вы можете подобраться к точке сколь угодно близко, но кривая все равно будет кривой.
Если теперь вы можете найти уравнение (в форме $y = Cx + D$, прямая линия), которое соответствует «прямой» части этой кривой в точке $a$, вы нашли касательную для эта точка. Технически эта линия пересекается с кривой только в точке а, но при таком масштабе линия и кривая будут казаться одинаковыми.
Из этого вы можете получить представление о том, что значение скорости изменения кривой в любой точке — это просто наклон этой касательной в этой точке.
$\endgroup$
1
$\begingroup$
Я не буду говорить об определении или формальном способе описания касательной. Но именно так касательная обрела для меня больший смысл, когда я впервые узнал об этом. Допустим, вам нужно найти касательную точки P на изображении ниже. Теперь возьмите эту точку и любую другую точку Q на графике и соедините их линией. Теперь приближайте точку Q все ближе и ближе к точке P . Когда две точки настолько близки, что представляют собой почти одну и ту же точку, вы получаете линию, которая является касательной к точке P
Допустим, вам нужно найти касательную точки P на изображении ниже. Теперь возьмите эту точку и любую другую точку Q на графике и соедините их линией. Теперь приближайте точку Q все ближе и ближе к точке P . Когда две точки настолько близки, что представляют собой почти одну и ту же точку, вы получаете линию, которая является касательной к точке P
$\endgroup$
$\begingroup$
Это определение просто не работает.
Первой попыткой исправить это было бы сказать, что локально касательная и кривая пересекаются только один раз. Даже тогда, согласно этому определению, две пересекающиеся прямые будут касаться друг друга.
Более интуитивное, но не строгое определение состоит в том, что прямая $\tau$ касается функции $f$ в точке $(a, f(a))$, если
- $\ тау(а) = f(а)$
- Чем больше вы приближаете точку $(a, f(a))$, тем лучше линия $y = \tau(x)$ аппроксимирует кривую $y = f(x)$.
 92)$, что можно интерпретировать как утверждение, что прямая $\tau(x) = f(a) + (x-a)f'(a)$ удовлетворяет условиям $(1.)$ и $(2.)$, указанным выше .
92)$, что можно интерпретировать как утверждение, что прямая $\tau(x) = f(a) + (x-a)f'(a)$ удовлетворяет условиям $(1.)$ и $(2.)$, указанным выше .$\endgroup$
1
$\begingroup$
Касательная проходит между двумя совпадающими точками $d=0$, секущая проходит между двумя различными точками на расстоянии $d>0$. Как и скимминг и (ныряние/погружение) они совершенно разные.
$ M,C$ являются не касательными . Но $B$ это касательная .
Что касается нарисованных вами вращающихся стрелок, то $B$ имеет нулевой или минимальный наклон, а $C$ имеет максимальный или бесконечный наклон.
Например, представьте, что вы нарисовали апельсин, который вы разрезаете ножом, весь апельсин будет разрезан по направлению стрелки $C$, но только тонкий круглый круг диаметром 1 дюйм вокруг касательной, вырезанной вдоль направления $C$.

$\endgroup$
1
$\begingroup$
Тангенс – это отношение противолежащей и прилежащей сторон прямоугольного треугольника. Если вокруг треугольника с диаметром гипотенузы треугольника провести окружность, то прямая, перпендикулярная гипотенузе, в точке пересечения с окружностью будет касательной к окружности, т. е. она проходит через одну и только одну точку на окружности .
$\endgroup$
1
$\begingroup$
Может быть полезно сначала взглянуть на определение «секущей» линии. Секущая линия — это просто линия, которая проходит через график функции в двух точках. Чтобы найти касательную в определенной точке (x, y), мы смотрим на все секущие, содержащие (x, y). Другими словами, зафиксируйте эту точку и позвольте второй точке изменяться вдоль кривой.
 3$ в точке (0,0), когда функция может разделиться на обе стороны.
3$ в точке (0,0), когда функция может разделиться на обе стороны.$\endgroup$
$\begingroup$
Касательная в точке P лучше всего определяется как предельное положение секущей, пересекающей кривую в точках P и Q, когда точка Q приближается к P вдоль кривой.
Ни системы координат, ни координат, ни исчисления (ну почти).
И он также работает в 3D и более высоких измерениях. 🙂$\endgroup$
$\begingroup$
Пусть $f$ — кривая, а $l$ — прямая. Тогда $l$ является касательной к кривой $f$ на интервале $I$ в точке $P=(x_0,y_0)$. Если он содержит оба следующих условия:
- $f(x)=l(x)$ тогда и только тогда, когда $ x=x_0 $
- $f(x) \geq l(x) $ или $ f(x) \leq l(x) $ для каждого $x \in I$
Другими словами, $l$ касается $f$, если она пересекает $f$ только в одной точке и кривая находится либо на верхней, либо на нижней стороне прямой.

$\endgroup$
2
$\begingroup$
Вы работаете с неверным определением касательной. Ваше утверждение «Говорят, касательная — это линия, пересекающая кривую ровно в одной точке» — ошибка, это не определение касательной. Правильное утверждение состоит в том, что a касается кривой в точке и НЕ пересекает кривую в этой точке. Если считается, что кривая имеет две стороны, то касательной называется линия, которая приближается к кривой в такой точке, которая пересекает кривую, но не пересекает кривую в этой точке. Существует бесконечное число линий, которые могут пересекать кривую, но в любой точке будет только одна, которая может коснуться ее, не пересекая ее, и это будет касательной в этой точке.
Нет необходимости определять тангенс с точки зрения исчисления, скорее, это определение является основой для многих понятий в исчислении, попытка использовать исчисление для его определения будет круговым рассуждением.
 Скорее, ваша проблема связана с неверным определением, которое никогда не может быть согласовано с тем, что на самом деле представляет собой касательная. Обратите также внимание, что это не означает, что касательная не может пересекать кривую, она может и часто пересекает сложные кривые. Он просто не может пересечь кривую в точке касания.
Скорее, ваша проблема связана с неверным определением, которое никогда не может быть согласовано с тем, что на самом деле представляет собой касательная. Обратите также внимание, что это не означает, что касательная не может пересекать кривую, она может и часто пересекает сложные кривые. Он просто не может пересечь кривую в точке касания.$\endgroup$
3
$\begingroup$
Касательная линия — это уникальная линия, которая «касается» точки, фактически не пересекая ее. Для других линий в вашем примере есть пересечение в точке; линия идет от точки над кривой к точке под ней. Линия касания остается под ним.
Очевидно, что это не строгое определение, но для тех, кто только начинает заниматься исчислением, это, вероятно, самый простой способ осмыслить его.
$\endgroup$
1
Историческая деятельность по математическому анализу.
 Модуль 2. Касательные прямые тогда и сейчас изучая кривые, они интересовались построением их касательных. Аполлоний, живший более двух тысяч лет назад и широко изучавший конические кривые, нашел геометрические методы построения касательных линий к параболам, эллипсам и гиперболам. На самом деле предложения 33 и 34 Книги I великого труда Аполлония, The Conics, дают рецепты построения касательных к этим кривым.
Модуль 2. Касательные прямые тогда и сейчас изучая кривые, они интересовались построением их касательных. Аполлоний, живший более двух тысяч лет назад и широко изучавший конические кривые, нашел геометрические методы построения касательных линий к параболам, эллипсам и гиперболам. На самом деле предложения 33 и 34 Книги I великого труда Аполлония, The Conics, дают рецепты построения касательных к этим кривым.Рецепт Аполлония для построения касательных к параболам следующий:
Предложение I-33. Пусть \(P\) — точка на параболе с вершиной \(E,\) с \(PD\), перпендикулярной оси симметрии. Если \(A\) лежит на оси симметрии так, что \(AE=ED,\), то \(AP\) будет касаться параболы в точке \(P.\)
Рис. 11. Аполлоний ‘ рецепт построения касательных к параболам. Перетащите \(F,\) фокус, чтобы изменить форму параболы. Перетащите \(P,\) точку касания, чтобы увидеть касательную линию в любой точке параболы.
Рецепт Аполлония для построения касательных к эллипсам и гиперболам следующий:Предложение I-34.
 Пусть \(P\) точка на эллипсе или гиперболе и \(PB\) перпендикуляр из этой точки к главной оси. Пусть \(G\) и \(H\) будут пересечениями оси с кривой и выберем \(A\) на оси так, чтобы \[\frac{|AH|}{|AG|}=\frac {|BH|}{|BG|}.\] Тогда \(AP\) будет касаться кривой в точке \(P.\)
Пусть \(P\) точка на эллипсе или гиперболе и \(PB\) перпендикуляр из этой точки к главной оси. Пусть \(G\) и \(H\) будут пересечениями оси с кривой и выберем \(A\) на оси так, чтобы \[\frac{|AH|}{|AG|}=\frac {|BH|}{|BG|}.\] Тогда \(AP\) будет касаться кривой в точке \(P.\) Рис. 12. Рецепт Аполлония для построения касательных линий к эллипсам. Перетащите \(H\) по горизонтали и/или \(C\) по вертикали, чтобы изменить форму эллипса. Перетащите \(P,\) точку касания, чтобы увидеть касательную линию в любой точке эллипса.
Рис. 13. Рецепт Аполлония для построения касательных к гиперболам. Перетащите \(H\) по горизонтали и/или \(C\) по вертикали, чтобы изменить форму гиперболы. Перетащите \(P,\) точку касания, чтобы увидеть касательную линию в любой точке (правой половины) гиперболы.
Рецепты Аполлония по построению касательных линий к коническим кривым легко реализовать, но его методы были ограничены тем, что их можно было применить только к небольшому количеству кривых. Конечно, во времена античности было не так уж много кривых, которые интересовали бы людей, и поэтому не было особой необходимости в общем методе.
Конечно, во времена античности было не так уж много кривых, которые интересовали бы людей, и поэтому не было особой необходимости в общем методе.К началу семнадцатого века коллекция известных кривых разрослась. Кривые часто описывались как путь движущейся точки; например, круг можно рассматривать как путь, очерченный точкой на внешнем краю прялки. Действительно, инструменты, которые использовались для рисования кривых, некоторые из которых обсуждались в Модуле 1, подчеркивали это понятие кривой как пути движущейся точки. Именно Жиль Персонн де Роберваль (1602-1675) использовал это определение кривой, рассматривая касательную линию как направление, в котором точка движется в определенный момент.
Рис. 14. Тангенс как направление движения (щелкните изображение, чтобы анимировать)
Рассмотрим, например, параболу, которую, вспоминая «Рисунок параболы» Франса ван Шутена из Модуля 1, можно определить как путь точки \(D\), когда \(G\) движется вдоль \(AC,\), как показано ниже на рисунке 15.

,\) точка \(D\) одновременно тянется к точке \(B\) и к горизонтальной линии \(AC.\). Так как \(|GD|=|BD|,\) две силы равны равно: если \(D\) немного сместится к \(B,\), то оно должно сместиться на такое же расстояние к прямой \(AC\). По закону параллелограмма направление движения \(D\) должно быть биссектрисой угла \(\угла BDG.\). Эта биссектриса угла на самом деле является диагональю \(FH\) ромба \(FGHB.\)
И Аполлоний, и де Роберваль использовали геометрические методы для построения касательных линий. Один из первых алгебраических методов принадлежит Рене Декарту, одному из изобретателей аналитической геометрии. Хорошо известно, что касательная к окружности всегда перпендикулярна радиусу окружности. Итак, идея Декарта заключалась в том, чтобы сначала найти окружность, касающуюся данной кривой. Тогда касательная к этой окружности является искомой касательной к кривой.
Рис. 16. Метод Декарта: Касательная к кривой перпендикулярна радиусу касательной окружности.
 (Щелкните изображение, чтобы его оживить.)
(Щелкните изображение, чтобы его оживить.)Именно Пьер де Ферма в основном придумал метод, используемый сегодня для построения касательных линий, рассматривая касательную как предел секущих, проходящих через заданную точку \(A\) и близлежащую точку \(B\) на кривая, где \(B\) приближается и в конечном итоге становится \(A.\)
, не обошлось без споров. Если \(A=(a,f(a))\) является точкой на кривой \(y=f(x),\) и \(B=(a+e,f(a+e))\ ) является близкой точкой, наклон линии \(AB\) совершенно точно определен, пока \(A\) и \(B\) различны, т. е. \(e\neq 0\), но как Определим ли мы наклон, когда \(e=0\) так, чтобы \(B=A?\) Это кажущееся несоответствие вызвало много критики, наиболее известная из которых исходила от ирландского философа и епископа Джорджа Беркли (1685-1753) в памфлет, который он опубликовал в 1734 году под названием Аналитик. Здесь епископ Беркли высмеял приращения \(e,\), назвав их «призраками ушедших количеств». Фактически, Декарт разработал свой метод, рассмотренный выше, как способ обойти эти трудности.
 Ниже вы можете увидеть, как, как \( B\) приближается к \(A,\) к окружности с центром \(O\) на оси \(x\), которая проходит через \(A\) и \(B\) четко определена, даже когда \ (A=B.\) Однако линия, проходящая через \(A\) и \(B\), не может быть четко определена, когда \(A=B.\)
Ниже вы можете увидеть, как, как \( B\) приближается к \(A,\) к окружности с центром \(O\) на оси \(x\), которая проходит через \(A\) и \(B\) четко определена, даже когда \ (A=B.\) Однако линия, проходящая через \(A\) и \(B\), не может быть четко определена, когда \(A=B.\)Рис. 18. Сравнение метода Декарта с методом Ферма (щелкните изображение, чтобы его оживить)
К сожалению, метод Декарта работал не очень хорошо, за исключением некоторых простых кривых, из-за обременительной алгебры, связанной с поиском уникальной окружности с центром на ось \(x\), которая пересекает кривую только один раз в точке \(A.\)
Несмотря на проблемы с логическими основами предмета, никто не мог оспорить, что методы работали. Итак, Ферма приписывают изобретение дифференциального исчисления, поскольку он разработал этот метод в 1629 году.и успешно использовал его для вычисления подкасательных большой коллекции кривых. Только в девятнадцатом веке споры и проблемы были удовлетворительно разрешены французским математиком Огюстеном-Луи Коши (1789-1857), который дал точное определение производной в терминах новой концепции, называемой пределом .
 Это привело к определению, которое мы используем сегодня.
Это привело к определению, которое мы используем сегодня.Упражнения
Рисунок 19. Этот апплет для упражнения 5 реализует рецепты Аполлония для построения касательных к параболам, эллипсам и гиперболам. 92}{9}=1\) в точке \((5,2.25).\)
Упражнение 6.
В этом упражнении вы будете использовать метод де Роберваля для построения касательных к нескольким кривым.
Рисунок 20. Этот апплет для упражнения 6, часть а, иллюстрирует стандартное построение параболы с использованием фокуса \(F\) и директрисы \(OB\).
(a) Апплет на рис. 20 выше иллюстрирует построение параболы как геометрического места точек \(P\), равноудаленных от фиксированной точки \(F\) ( фокус ) и фиксированная линия \(OB\) ( директриса ). Вы можете видеть, что при перетаскивании точки \(B,\) расстояния \(BP\) и \(PF\) всегда равны.
На \(P\) действуют две силы: одна по направлению к \(F\) и одна по направлению к горизонтальной линии \(OB.
 \). Так как \(|FP|=|BP|,\), то две силы равны равны, что означает, что если \(P\) немного сместится к \(F,\), он должен сместиться на такое же расстояние к линии. Следовательно, направление движения по закону параллелограмма должно быть биссектрисой угла \(\угол FPB.\) Постройте биссектрису угла, чтобы убедиться, что она действительно касается кривой в каждой точке параболы. Для этого:
\). Так как \(|FP|=|BP|,\), то две силы равны равны, что означает, что если \(P\) немного сместится к \(F,\), он должен сместиться на такое же расстояние к линии. Следовательно, направление движения по закону параллелограмма должно быть биссектрисой угла \(\угол FPB.\) Постройте биссектрису угла, чтобы убедиться, что она действительно касается кривой в каждой точке параболы. Для этого:Нажмите на инструмент биссектрисы угла на панели инструментов, затем на отрезок \(FP,\) и затем на отрезок \(PB.\). Вы получите две линии, перпендикулярные друг другу. Щелкните инструмент «Перемещение», затем щелкните правой кнопкой мыши ненужную линию и выберите «Показать объект», чтобы скрыть ее. Вы можете перетащить \(B\), чтобы убедиться, что эта конструкция работает для каждой точки параболы.
Рисунок 21. Этот апплет для упражнения 6, часть b, иллюстрирует стандартное построение эллипса с использованием двух фокусов \(F_1\) и \(F_2.\)
(b) Апплет на рис. 21 выше иллюстрирует построение эллипса как геометрического места точек \(P\), таких, что сумма расстояний \(P\) от двух фиксированных точек \(F_1\ ) и \(F_2\) является константой.
 Обратите внимание, что при перетаскивании точки \(P,\) сумма \(|PF_1|+|PF_2|\) остается постоянной.
Обратите внимание, что при перетаскивании точки \(P,\) сумма \(|PF_1|+|PF_2|\) остается постоянной.Так как \(|PF_1|+|PF_2|\) постоянна, каждый раз, когда \(P\) движется к \(F_1\), он должен перемещаться на одно и то же расстояние от \(F_2.\). на \(P,\) действуют две равные силы: одна по направлению к одному из фокусов, вторая — по направлению от другого фокуса. Итак, снова вы можете построить касательную как биссектрису угла. Постройте касательную к эллипсу в любой точке \(P.\) Убедитесь, что ваша конструкция работает во всех точках эллипса.
Рисунок 22. Этот апплет для упражнения 6, часть c, иллюстрирует стандартное построение гиперболы с использованием двух фокусов \(F_1\) и \(F_2.\)
(c) Апплет на рисунке 22 выше , является построением гиперболы как геометрического места точек \(P\), таких, что разность расстояний \(P\) от двух фиксированных точек \(F_1\) и \(F_2\) постоянна. Обратите внимание, что при перетаскивании точки \(P,\) разница \(|PF_1-PF_2|\) остается постоянной.
 Постройте касательную к гиперболе в любой точке \(P.\) Убедитесь, что ваша конструкция работает в каждой точке гиперболы.
Постройте касательную к гиперболе в любой точке \(P.\) Убедитесь, что ваша конструкция работает в каждой точке гиперболы.Рисунок 23. Этот апплет к упражнению 6, часть d, иллюстрирует циклоиду как путь, прочерченный точкой на окружности окружности, катящейся по горизонтальной линии.
(d) Циклоида, показанная на рис. 23 выше, сыграла очень важную роль в истории исчисления, и ее свойства широко изучались в шестнадцатом и семнадцатом веках. Это путь, прочерченный точкой на окружности круга, когда круг катится по горизонтальной линии. Воспользуйтесь методом де Роберваля, чтобы построить касательную в любой точке \(P\) циклоиды.
Рис. 24. Этот апплет для упражнения 6, часть e, иллюстрирует эпициклоиду как путь, прочерченный точкой на окружности одной окружности, катящейся по внешней стороне другой окружности.
(e) Эпициклоида, показанная на рисунке 24 выше, представляет собой путь, прочерченный точкой на окружности круга, когда круг катится по внешней стороне другого круга.
 Воспользуйтесь методом де Роберваля, чтобы построить касательную в любой точке \(P\) циклоиды.
Воспользуйтесь методом де Роберваля, чтобы построить касательную в любой точке \(P\) циклоиды.Упражнение 7.
В этом упражнении вы будете использовать метод Декарта для нахождения касательных к кривой \(y=\sqrt{4x}.\) Метод состоит в том, чтобы сначала найти окружность, касающуюся кривой. Тогда касательная к кривой будет такой же, как касательная к окружности, которую легко построить, поскольку она перпендикулярна радиусу.
Рисунок 25. Апплет для упражнения 7
(a) Апплет, показанный выше на рисунке 25, содержит: график \(y=\sqrt{4x},\) точку \(A=(1,2 )\), которая находится на этой кривой, точка \(О\) на оси \(х\) и окружность с центром \(О\) и радиусом \(ОА.\). В общем, в зависимости от того, где точка \(O\), эта окружность будет пересекать кривую в двух точках \(A\) и \(B.\). Теперь перетащите \(O\) вдоль оси \(x\), пока две точки пересечения \(A\) и \(B\) сливаются в одно. Полученная окружность касается кривой в одной точке и, таким образом, касается кривой.
 Теперь вы можете вычислить наклон касательной, так как она перпендикулярна \(OA.\). Введите уравнение касательной в фиолетовое поле ввода, чтобы отобразить ее и убедиться, что она действительно касается \(y=\sqrt {4x}\) в \(A=(1,2).\)
Теперь вы можете вычислить наклон касательной, так как она перпендикулярна \(OA.\). Введите уравнение касательной в фиолетовое поле ввода, чтобы отобразить ее и убедиться, что она действительно касается \(y=\sqrt {4x}\) в \(A=(1,2).\)(b) Повторите с \(A=(9,6)\) и введите уравнение касательной в синее поле ввода.
Ссылки
Дж. Л. Кулидж, История касательных, The American Mathematical Monthly, Vol. 58, № 7. (1951), стр. 449-462.
Пол Р. Вольфсон, Изогнутое сделано прямым: Роберваль и Ньютон о касательных, The American Mathematical Monthly, Vol. 108, № 3 (2001), стр. 206-216.
Габриэла Р. Санчис (Элизабеттаунский колледж), «Исторические занятия по исчислению — модуль 2: касательные линии тогда и сейчас», Конвергенция (июнь 2014 г.)
Касательная линия к кривой
Эндрю Эллинор, Хобарт Пао, Тан Джун Вэй, а также
способствовал
Содержимое
- Введение
- Коэффициент разницы
- Нахождение касательной
- Смотрите также
Нам нужно найти наклон прямой, проходящей через (c,f(c))\big(c,f(c)\big)(c,f(c)), касающейся f(x) е (х) е (х).
 В общем, мы знаем, что мы можем найти наклон, mmm, через любые две точки, вычислив изменение y (Δy)y\, (\Delta y)y(Δy), деленное на изменение x (Δx),x \, (\Delta x),x(∆x), которое описывается формулой
В общем, мы знаем, что мы можем найти наклон, mmm, через любые две точки, вычислив изменение y (Δy)y\, (\Delta y)y(Δy), деленное на изменение x (Δx),x \, (\Delta x),x(∆x), которое описывается формулойm=ΔyΔx=y2−y1x2−x1.m = \frac{\Delta y}{\Delta x}=\frac{y_2 — y_1}{x_2 — x_1}.m=ΔxΔy=x2−x1 у2-у1.
Однако в данном случае мы пытаемся найти наклон в единственной точке (c,f(c))\big(c, f(c)\big)(c,f(c)), что означает что, если бы мы использовали приведенную выше формулу, мы бы нашли m=00,m=\frac00,m=00, что не определено. Чтобы найти наклон нашей касательной, нам нужно будет использовать разностное частное.
Коэффициент разности — это выражение, описывающее наклон линии в одной точке. Давайте еще раз рассмотрим нашу формулу наклона:
m=ΔyΔx=y2−y1x2−x1.m = \frac{\Delta y}{\Delta x}=\frac{y_2 — y_1}{x_2 — x_1}.m=ΔxΔy=x2−x1 у2-у1.
Мы хотим найти изменение yyy, деленное на изменение xxx. Рассмотрим, что произойдет, если мы воспользуемся нашей точкой (c,f(c))\big(c,f(c)\big)(c,f(c)) и еще одной близкой к ней точкой, (c+∆x, f(c+Δx))\big(c+\Delta x,f(c+\Delta x)\big)(c+Δx,f(c+Δx)).
 Мы можем провести секущую, которая дважды пересекает функцию (представленную ниже пунктирной красной линией):
Мы можем провести секущую, которая дважды пересекает функцию (представленную ниже пунктирной красной линией):Обратите внимание, что эта секущая линия не имеет того же наклона, что и касательная, но ее наклон на близок к наклону касательной на . Мы можем легко вычислить наклон секущей: )Δx.m = \frac{\Delta y}{\Delta x}=\frac{y_2 — y_1}{x_2 — x_1}=\frac{f(c+\Delta x) — f(c)}{c+\ Дельта x — c}=\frac{f(c+\Delta x) — f(c)}{\Delta x}.m=ΔxΔy=x2−x1y2−y1=c+Δx−cf (c+Δx)−f(c)=Δxf(c+Δx)−f(c).
Большое понимание разностного отношения здесь заключается в том, что по мере того, как Δx\Delta xΔx становится меньше, наклон секущей становится все ближе и ближе к наклону касательной, которую мы пытаемся найти. На самом деле, используя пределы, мы можем найти точный наклон касательной к кривой f(x)f(x)f(x) в точке x=cx=cx=c, используя разностное частное: 92) \\ & = 3. \end{выровнено}m=h→0limhf(1+h)−f(1)=h→0limh(1+h)3−(1)2=h→0limh2+3h +3h3+h4−1=h→0limh4h+3h3+h4=h→0lim(3+3h+h3)=3.


 е. имеет с ней две общие точки. Часть секущей, расположенная внутри окружности, будет называться
е. имеет с ней две общие точки. Часть секущей, расположенная внутри окружности, будет называться 
 Вычислить f(xо).
Вычислить f(xо). {\displaystyle x=x_{0}.}
{\displaystyle x=x_{0}.} {\displaystyle y=f(x_{0})+{\frac {f(x_{1})-f(x_{0})}{x_{1}-x_{0}}}(x-x_{0}).}
{\displaystyle y=f(x_{0})+{\frac {f(x_{1})-f(x_{0})}{x_{1}-x_{0}}}(x-x_{0}).} {\displaystyle y=f(x_{0})+f'(x_{0})(x-x_{0}).}
{\displaystyle y=f(x_{0})+f'(x_{0})(x-x_{0}).} {\displaystyle y=f(x_{0})+f’_{+}(x_{0})(x-x_{0}),\quad x\geqslant x_{0}.}
{\displaystyle y=f(x_{0})+f’_{+}(x_{0})(x-x_{0}),\quad x\geqslant x_{0}.} {\displaystyle x=x_{0},\;y\leqslant f(x_{0})\;(y\geqslant f(x_{0})).}
{\displaystyle x=x_{0},\;y\leqslant f(x_{0})\;(y\geqslant f(x_{0})).}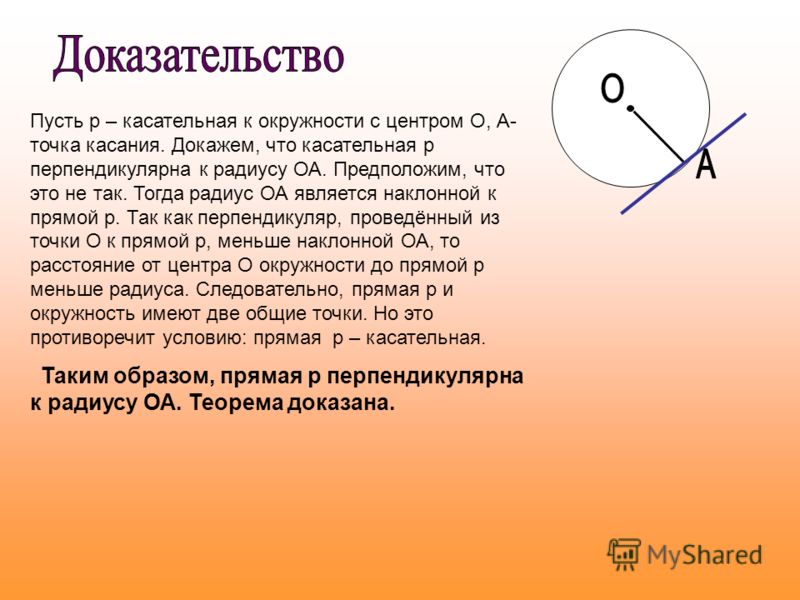 Проходит через $P$ и никакую другую точку кривой
Проходит через $P$ и никакую другую точку кривой 92)$, что можно интерпретировать как утверждение, что прямая $\tau(x) = f(a) + (x-a)f'(a)$ удовлетворяет условиям $(1.)$ и $(2.)$, указанным выше .
92)$, что можно интерпретировать как утверждение, что прямая $\tau(x) = f(a) + (x-a)f'(a)$ удовлетворяет условиям $(1.)$ и $(2.)$, указанным выше .
 3$ в точке (0,0), когда функция может разделиться на обе стороны.
3$ в точке (0,0), когда функция может разделиться на обе стороны.
 Скорее, ваша проблема связана с неверным определением, которое никогда не может быть согласовано с тем, что на самом деле представляет собой касательная. Обратите также внимание, что это не означает, что касательная не может пересекать кривую, она может и часто пересекает сложные кривые. Он просто не может пересечь кривую в точке касания.
Скорее, ваша проблема связана с неверным определением, которое никогда не может быть согласовано с тем, что на самом деле представляет собой касательная. Обратите также внимание, что это не означает, что касательная не может пересекать кривую, она может и часто пересекает сложные кривые. Он просто не может пересечь кривую в точке касания. Модуль 2. Касательные прямые тогда и сейчас изучая кривые, они интересовались построением их касательных. Аполлоний, живший более двух тысяч лет назад и широко изучавший конические кривые, нашел геометрические методы построения касательных линий к параболам, эллипсам и гиперболам. На самом деле предложения 33 и 34 Книги I великого труда Аполлония, The Conics, дают рецепты построения касательных к этим кривым.
Модуль 2. Касательные прямые тогда и сейчас изучая кривые, они интересовались построением их касательных. Аполлоний, живший более двух тысяч лет назад и широко изучавший конические кривые, нашел геометрические методы построения касательных линий к параболам, эллипсам и гиперболам. На самом деле предложения 33 и 34 Книги I великого труда Аполлония, The Conics, дают рецепты построения касательных к этим кривым. Пусть \(P\) точка на эллипсе или гиперболе и \(PB\) перпендикуляр из этой точки к главной оси. Пусть \(G\) и \(H\) будут пересечениями оси с кривой и выберем \(A\) на оси так, чтобы \[\frac{|AH|}{|AG|}=\frac {|BH|}{|BG|}.\] Тогда \(AP\) будет касаться кривой в точке \(P.\)
Пусть \(P\) точка на эллипсе или гиперболе и \(PB\) перпендикуляр из этой точки к главной оси. Пусть \(G\) и \(H\) будут пересечениями оси с кривой и выберем \(A\) на оси так, чтобы \[\frac{|AH|}{|AG|}=\frac {|BH|}{|BG|}.\] Тогда \(AP\) будет касаться кривой в точке \(P.\)  Конечно, во времена античности было не так уж много кривых, которые интересовали бы людей, и поэтому не было особой необходимости в общем методе.
Конечно, во времена античности было не так уж много кривых, которые интересовали бы людей, и поэтому не было особой необходимости в общем методе.
 (Щелкните изображение, чтобы его оживить.)
(Щелкните изображение, чтобы его оживить.) Ниже вы можете увидеть, как, как \( B\) приближается к \(A,\) к окружности с центром \(O\) на оси \(x\), которая проходит через \(A\) и \(B\) четко определена, даже когда \ (A=B.\) Однако линия, проходящая через \(A\) и \(B\), не может быть четко определена, когда \(A=B.\)
Ниже вы можете увидеть, как, как \( B\) приближается к \(A,\) к окружности с центром \(O\) на оси \(x\), которая проходит через \(A\) и \(B\) четко определена, даже когда \ (A=B.\) Однако линия, проходящая через \(A\) и \(B\), не может быть четко определена, когда \(A=B.\) Это привело к определению, которое мы используем сегодня.
Это привело к определению, которое мы используем сегодня. \). Так как \(|FP|=|BP|,\), то две силы равны равны, что означает, что если \(P\) немного сместится к \(F,\), он должен сместиться на такое же расстояние к линии. Следовательно, направление движения по закону параллелограмма должно быть биссектрисой угла \(\угол FPB.\) Постройте биссектрису угла, чтобы убедиться, что она действительно касается кривой в каждой точке параболы. Для этого:
\). Так как \(|FP|=|BP|,\), то две силы равны равны, что означает, что если \(P\) немного сместится к \(F,\), он должен сместиться на такое же расстояние к линии. Следовательно, направление движения по закону параллелограмма должно быть биссектрисой угла \(\угол FPB.\) Постройте биссектрису угла, чтобы убедиться, что она действительно касается кривой в каждой точке параболы. Для этого: Обратите внимание, что при перетаскивании точки \(P,\) сумма \(|PF_1|+|PF_2|\) остается постоянной.
Обратите внимание, что при перетаскивании точки \(P,\) сумма \(|PF_1|+|PF_2|\) остается постоянной. Постройте касательную к гиперболе в любой точке \(P.\) Убедитесь, что ваша конструкция работает в каждой точке гиперболы.
Постройте касательную к гиперболе в любой точке \(P.\) Убедитесь, что ваша конструкция работает в каждой точке гиперболы. Воспользуйтесь методом де Роберваля, чтобы построить касательную в любой точке \(P\) циклоиды.
Воспользуйтесь методом де Роберваля, чтобы построить касательную в любой точке \(P\) циклоиды. Теперь вы можете вычислить наклон касательной, так как она перпендикулярна \(OA.\). Введите уравнение касательной в фиолетовое поле ввода, чтобы отобразить ее и убедиться, что она действительно касается \(y=\sqrt {4x}\) в \(A=(1,2).\)
Теперь вы можете вычислить наклон касательной, так как она перпендикулярна \(OA.\). Введите уравнение касательной в фиолетовое поле ввода, чтобы отобразить ее и убедиться, что она действительно касается \(y=\sqrt {4x}\) в \(A=(1,2).\) В общем, мы знаем, что мы можем найти наклон, mmm, через любые две точки, вычислив изменение y (Δy)y\, (\Delta y)y(Δy), деленное на изменение x (Δx),x \, (\Delta x),x(∆x), которое описывается формулой
В общем, мы знаем, что мы можем найти наклон, mmm, через любые две точки, вычислив изменение y (Δy)y\, (\Delta y)y(Δy), деленное на изменение x (Δx),x \, (\Delta x),x(∆x), которое описывается формулой Мы можем провести секущую, которая дважды пересекает функцию (представленную ниже пунктирной красной линией):
Мы можем провести секущую, которая дважды пересекает функцию (представленную ниже пунктирной красной линией):