Метод Гомори. Решение задач и контрольных работ по линейному программированию онлайн
Краткая теория
Метод Гомори является одним из методов решения задач целочисленного линейного программирования. Идея метода Гомори заключается в следующем.
Отбрасывается условие целочисленности и полученная задача линейного программирования решается симплекс-методом. Если оптимальное решение задачи является целочисленным, то оно является и решением исходной задачи. Если оптимальное решение задачи не является целочисленным, то к основным ограничениям добавляется новое линейное ограничение, обладающее следующими свойствами:
1) оптимальный нецелочисленный план задачи ему не удовлетворяет;
2) любой целочисленный план задачи ему удовлетворяет.
Затем решается расширенная
задача. Процесс повторяется до получения целочисленного решения. Способы
построения дополнительного линейного ограничения различны для полностью и
частично целочисленных задач линейного программирования.
Если задача разрешима в целых числах, то через конечное число итераций оптимальный целочисленный план будет найден.
Если в процессе решения появится строка с нецелым свободным членом и целыми остальными коэффициентами, то соответствующее уравнение не имеет решения в целых числах. В таком случае и исходная задача неразрешима в целых числах.
Несмотря на точность метода Гомори, он имеет ограниченное применение. С его помощью целесообразно решать задачи небольшой размерности, поскольку число итераций может быть очень большим.
Алгоритм метода Гомори рассмотрим на конкретном примере.
Пример решения задачи
Решить задачу целочисленного программирования методом Гомори.
– целые
Решение
Приведем задачу к каноническому виду.
Решаем задачу симплекс-методом.
Заполняем симплексную таблицу 0-й итерации.
| БП |
Симплексные отношения |
|||||||
| 7 | -9 | 0 | 0 | |||||
| 0 | 9 | 2 | 1 | 1 | 0 | 0 | 9/2 | |
| 0 | 7 | 0 | 3 | 0 | 1 | 0 | — | |
| 0 | 5 | 4 | 5 | 0 | 0 | 1 | 5/4 | |
| 0 | -7 | 9 | 0 | 0 | 0 | |||
Переходим к таблице 1-й итерации:
| БП |
Симплексные отношения |
|||||||
| 7 | -9 | 0 | 0 | 0 | ||||
| 0 | 13/2 | 0 | -3/2 | 1 | 0 | -1/2 | ||
| 0 | 7 | 0 | 3 | 0 | 1 | 0 | ||
| 7 | 5/4 | 1 | 5/4 | 0 | 0 | 1/4 | ||
| 35/4 | 0 | 71/4 | 0 | 0 | 7/4 | |||
В индексной строке все члены неотрицательные, поэтому получено следующее решение задачи линейного программирования (выписываем из столбца свободных членов):
Так как оптимальное решение не удовлетворяет условию целочисленности, продолжим решение, используя алгоритм
Гомори.
Выбираем базисную переменную с наибольшей дробной частью.
По 1-й строке строим дополнительное ограничение:
Ограничение принимает вид:
Введем в ограничение дополнительную переменную:
Домножим последнее ограничение на -1:
Припишем это ограничение к последней симплексной таблице, и, следуя методу Гомори, выполним симплексные преобразования:
| БП |
Симплексные |
||||||||
| 7 | -9 | 0 | 0 | 0 | 0 | ||||
| 0 | 13/2 | 0 | -3/2 | 1 | 0 | -1/2 | 0 | — | |
| 0 | 7 | 0 | 3 | 0 | 1 | 0 | 0 | 7/3 | |
| 7 | 5/4 | 1 | 5/4 | 0 | 0 | 1/4 | 0 | 1 | |
| 0 | -1/2 | -1/2 | 0 | 0 | -1/2 | 1 | 1 | ||
| 35/4 | 0 | 71/4 | 0 | 0 | 7/4 | 0 | |||
Просматриваем строку, содержащую отрицательное число в столбце
свободных членов, и выбираем любое отрицательное число в этой строке. Выбранное
число будет определять разрешающий столбец.
Выбранное
число будет определять разрешающий столбец.
Ключевой столбец соответствует .
Находим ключевую строку, для этого определяем:
На пересечении ключевого столбца и ключевой строки находим разрешающий элемент, т.е. 5/4.
Вектор выводим из базиса и вводим вектор .
Если не находите примера, аналогичного вашему, если сами не успеваете выполнить работу, если впереди экзамен по предмету и нужна помощь — свяжитесь со мной:
ВКонтакте
WhatsApp
Telegram
Я буду работать с вами, над вашей проблемой, пока она не решится.
Переходим к таблице 1-й итерации:
| БП |
Симплексные отношения |
||||||||
| 7 | -9 | 0 | 0 | 0 | 0 | ||||
| 0 | 8 | 6/5 | 0 | 1 | 0 | -1/5 | 0 | 20/3 | |
| 0 | 4 | -12/5 | 0 | 0 | 1 | -3/5 | 0 | — | |
| -9 | 1 | 4/5 | 1 | 0 | 0 | 1/5 | 0 | 5/4 | |
| 0 | 0 | 2/5 | 0 | 0 | 0 | -2/5 | 1 | 0 | |
| -9 | -71/5 | 0 | 0 | 0 | -9/5 | 0 | |||
Переходим к таблице 2-й итерации:
| БП |
Симплексные отношения |
||||||||
| 7 | -9 | 0 | 0 | 0 | 0 | ||||
| 0 | 8 | 0 | 0 | 1 | 0 | 1 | -3 | 8 | |
| 0 | 4 | 0 | 0 | 0 | 1 | -3 | 6 | — | |
| -9 | 1 | 0 | 1 | 0 | 0 | 1 | -2 | 1 | |
| 7 | 0 | 1 | 0 | 0 | 0 | -1 | 5/2 | — | |
| -9 | 0 | 0 | 0 | 0 | -16 | 71/2 | |||
Переходим к таблице 3-й итерации:
| БП |
Симплексные отношения |
||||||||
| 7 | -9 | 0 | 0 | 0 | 0 | ||||
| 0 | 7 | 0 | -1 | 1 | 0 | 0 | -1 | ||
| 0 | 7 | 0 | 3 | 0 | 1 | 0 | 0 | ||
| 0 | 1 | 0 | 1 | 0 | 0 | 1 | -2 | ||
| 7 | 1 | 1 | 1 | 0 | 0 | 0 | 1/2 | ||
| 7 | 0 | 16 | 0 | 0 | 0 | 7/2 | |||
В индексной строке все члены неотрицательные, поэтому получено следующее решение задачи линейного программирования (выписываем из столбца свободных членов):
Найденное оптимальное решение удовлетворяет условию целочисленности и является решением исходной задачи.
Метод Гомори
Метод Гомори решения задач целочисленного программирования является методом отсечения.
Суть метода заключается в построении ограничений, отсекающих нецелочисленные решения задачи линейного программирования, но не отсекающих ни одного целочисленного плана. Для этого сначала решается ослабленная задача линейного программирования без учета условия целочисленности переменных.
Если
полученное решение задачи линейного
программирования является целочисленным,
то задача целочисленного программирования
также решена и найденное решение является
оптимальным и для нее. Если же в найденном
решении задачи линейного программирования
одна или большее число переменных не
целые, то для отыскания целочисленного
решения задачи добавляются новое
линейное ограничение, которое отсекает
нецелочисленные решения. При продолжении
решения расширенной задачи двойственным
симплексным методом с учетом этого
ограничения получается целочисленный
план.
Для нахождения целочисленного решения задачи методом Гомори используется следующий алгоритм.
Решаем ослабленную задачу симплексным методом без учета условия целочисленности. Если все компоненты оптимального плана целые, то он является оптимальным и для задачи целочисленного программирования. Если обнаруживается неразрешимость задачи, то и неразрешима задача целочисленного программирования.
Если в результате решения задачи линейного программирования в полученном оптимальном плане есть нецелая базисная переменная, то к ограничениям задачи добавляется новое ограничение, обладающее следующими свойствами:
— оно должно быть линейным;
— должно отсекать найденный оптимальный нецелочисленный план;
— не должно отсекать ни одного целочисленного плана.
Если
нецелых базисных переменных несколько,
то для составления ограничения выбираем
компоненту оптимального плана с
наибольшей дробной частью (если таких переменных несколько, то
выбираем любую).
Этой переменной соответствует строка симплексной таблицы, называемая строкой, производящей отсечение (производящей строкой).
Для изложения метода вводим следующие понятия. Пусть a – действительное число.
Под целой частью некоторого числа а понимается максимальное целое число [a], не превосходящее данного.
Под дробной частью некоторого числа а понимается наименьшее неотрицательное число такое, что разность между ним иа есть [a] – целая часть числа).
Для выбранной базисной переменной с наибольшей дробной частью находим дробную часть этой переменной и дробные части всех коэффициентов при переменныхi — й строки системы ограничений (производящей строкой).
Обозначим ицелые части чисел и . Величины дробных частейи() определяются следующим образом
Составляем неравенство Гомори и включаем его в систему ограничений исходной задачи.

Для этого по производящей строке симплексной таблицы выписывается уравнение, предполагая, что первые m переменных являются базисными для данного оптимального плана
или
Переносим все целые части коэффициентов в одну сторону, оставляя все дробные в другой:
Так как <1, то заменяя в правой части , получим строгое неравенство
Так как левая часть неравенства должна принимать целые значения, то, следовательно, необходимое условие ее целочисленности можно записать только в следующем виде:
Неравенство преобразуется в уравнение путем введения дополнительной неотрицательной переменной и включается в оптимальную симплексную таблицу.
Решаем задачу, используя двойственный симплексный метод. Если новый оптимальный план расширенной задачи будет целочисленным, то задача решена.
 Если
же решение нецелое, то нужно повторять
алгоритм метода Гомори вплоть до
получения целочисленного решения.
Если
же решение нецелое, то нужно повторять
алгоритм метода Гомори вплоть до
получения целочисленного решения.
Пример. Методом Гомори найти решение задачи целочисленного программирования, состоящей в определении максимального значения функции при условии
Решение. Выравнивая неравенства с помощью вспомогательных переменных х3, х4, получаем задачу линейного программирования в канонической форме:
Решаем задачу линейного программирования симплексным методом, используя поэтапный переход от одного базиса к другому. Ход решения задачи и полученное оптимальное решение представлены в таблицах.
Б | СБ | В | С1=5 | С2=11 | С3=0 | С4=0 |
а1 | а2 | а3 | а4 | |||
а3 | 0 | 3 | 4 | 1 | 0 | |
а4 | 0 | 10 | 2 | 5 | 0 | 1 |
∆j =Zj–Сj | 0 | -5 | -11 | 0 | 0 | |
СБ | В | С1=5 | С2=11 | С3=0 | С4=0 | |
а1 | а2 | а3 | а4 | |||
а2 | 11 | 1 | 0 | |||
а4 | 0 | 0 | 1 | |||
∆j =Zj–Сj | 0 | 0 | ||||
В
найденном оптимальном плане значение
переменной х2 равно дробному числу. Находим его дробную
часть и дробные части всех элементов
строки, содержащей переменную х2 , а именно:
Находим его дробную
часть и дробные части всех элементов
строки, содержащей переменную х2 , а именно:
Теперь составляем для найденных значений дробных частей неравенство Гомори:
.
Выравниваем неравенство Гомори с помощью новой вспомогательной переменной х5, переносим свободный член уравнения в правую часть и получаем новое ограничение:
.
Добавляем в симплексную таблицу строку, содержащую новое ограничение, и столбец, содержащий новую переменную, и продолжаем решать задачу двойственным симплексным методом, так как теперь в таблице записан псевдоплан.
Б | СБ | В | С1=5 | С2=11 | С3=0 | С4=0 | С5=0 |
а1 | а2 | а3 | а4 | а5 | |||
а2 | 110 | 1 | 0 | 0 | |||
а4 | 0 | 0 | 1 | 0 | |||
а5 | 0 | 0 | 0 | 1 | |||
∆j=Zj–Сj | 0 | 0 | 0 | ||||
Б | СБ | В | С1=5 | С2=11 | С3=0 | С4=0 | С5=0 |
а1 | а2 | а3 | а4 | а5 | |||
а2 | 11 | 1 | 0 | 1 | 0 | 0 | 1 |
а4 | 0 | 0 | 0 | 1 | |||
а1 | 0 | 1 | 0 | 0 | |||
∆j=Zj–Сj | 0 | 0 | 0 | ||||
Полученное оптимальное решение расширенной задачи содержит нецелое значение переменной х1, поэтому находим для этой строки дробные части всех нецелых чисел, а именно:
и новое неравенство Гомори имеет вид:
Выравниваем
неравенство Гомори с помощью новой
вспомогательной переменной х6,
переносим свободный член уравнения в
правую часть и получаем новое ограничение:
.
Добавляем его к решаемой задаче, выравниваем с помощью вспомогательной переменной и решаем расширенную задачу
Б | СБ | В | С1=5 | С2=11 | С3=0 | С4=0 | С5=0 | С6=0 |
а1 | а2 | а3 | а4 | а5 | а6 | |||
а2 | 110 | 1 | 0 | 1 | 0 | 0 | 1 | 0 |
а4 | 0 | 0 | 0 | 1 | 0 | |||
а1 | 0 | 1 | 0 | 0 | 0 | |||
а6 | 0 | 0 | 0 | 0 | 1 | |||
∆j=Zj–Сj | 0 | 0 | 0 | 0 | ||||
Б | СБ | В | С1=5 | С2=11 | С3=0 | С4=0 | С5=0 | С6=0 |
а1 | а2 | а3 | а4 | а5 | а6 | |||
а2 | 110 | 1 | 0 | 1 | 0 | 0 | 1 | 0 |
а4 | 0 | 5 | 0 | 0 | 0 | 1 | -1 | -2 |
а1 | 0 | 0 | 1 | 0 | 0 | 0 | -2 | 1 |
а3 | 0 | 0 | 0 | 1 | 0 | 2 | -3 | |
∆j=Zj–Сj | 11 | 0 | 0 | 0 | 0 | 1 | 5 | |
Таким
образом, найдено оптимальное решение
задачи целочисленного программирования: Zmax =11 при
.
Замечания:
Если в процессе решения в симплексной таблице появится уравнение с нецелой компонентой и целыми коэффициентами в соответствующей строке системы ограничений, то данная задача не имеет целочисленного решения.
6 Целочисленное программирование. Метод отсекающих плоскостей (метод…
Привет, сегодня поговорим про целочисленное программирование, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое целочисленное программирование, метод отсекающих плоскостей, метод гомори, метод ветвей и границ , настоятельно рекомендую прочитать все из категории Математические методы исследования операций .Теория игр и расписаний..
целочисленное программирование .
Общая постановка задачи целочисленного программирования отличается от общей задачи ЛП лишь наличием дополнительного ограничения. Этим ограничением является требование целочисленности: значения всех или части переменных модели в оптимальном решении являются целыми неотрицательными числами, то есть принадлежат множеству N. Если это требование распространяется на все переменные, то задачу ЦП называют полностью целочисленной задачей. Если оно относится лишь к части переменных, задача называется частично целочисленной. Задача ЛП, отличающаяся от задачи ЦП лишь отсутствие требований целочисленности, называют задачей с ослабленными ограничениями, соответствующей данной задаче ЦП.
Если это требование распространяется на все переменные, то задачу ЦП называют полностью целочисленной задачей. Если оно относится лишь к части переменных, задача называется частично целочисленной. Задача ЛП, отличающаяся от задачи ЦП лишь отсутствие требований целочисленности, называют задачей с ослабленными ограничениями, соответствующей данной задаче ЦП.
Задача целочисленного программирования — это задача математической оптимизации или выполнимости, в которой некоторые или все переменные должны быть целыми числами. Часто термин адресуется к целочисленному линейному программированию (ЦЛП), в котором целевая функция и ограничения (за исключением требования целочисленности) линейны.
Целочисленное программирование является NP-трудной задачей. Специальный случай, 0-1 целочисленное линейное программирование, в которой переменные принимают значения 0 или 1, является одной из 21 NP-полных задач Карпа.
Каноническая и стандартная виды ЦЛП
Задача целочисленного линейного программирования в каноническом виде выражается как
| максимизировать | |
| при условиях | |
| и | , |
а в стандартном виде
| максимизировать | |
| при условиях | |
| и |
где — векторы, а — матрица, все элементы которых являются целыми числами. Заметьте, что, как и в случае линейного программирования, ЦЛП-задача, не находящаяся в стандартном виде, может быть приведена к стандартному виду путем исключения неравенств введением дополнительных и искусственных переменных и заменой переменных, на которые не наложено ограничение неотрицательности, двумя переменными.
Заметьте, что, как и в случае линейного программирования, ЦЛП-задача, не находящаяся в стандартном виде, может быть приведена к стандартному виду путем исключения неравенств введением дополнительных и искусственных переменных и заменой переменных, на которые не наложено ограничение неотрицательности, двумя переменными.
Пример
Целочисленный многогранник с линейным ослаблением
Рисунок справа показывает следующую задачу.
Допустимые целые точки показаны красным и красные пунктирные линии показывают выпуклую оболочку этих точек, которая является наименьшим многоугольником, содержащим все эти точки. Синие линии вместе с координатными осями определяют многоугольник линейного ослабления, который задается неравенствами без требования целочисленности. Цель оптимизации — сдвинуть черную пунктирную линию так, чтобы она была как можно выше, но касалась многоугольника. Оптимальные решения целочисленной задачи — точки и , на которых целевая функция принимает значение 2. Единственное решение ослабленной (линейной) задачи — точка , в которой целевая функция принимает значение 2.8. Заметим, что если мы округлим решение задачи линейного программирования до ближайших целых, решение будет недопустимо для ЦЛП.
Единственное решение ослабленной (линейной) задачи — точка , в которой целевая функция принимает значение 2.8. Заметим, что если мы округлим решение задачи линейного программирования до ближайших целых, решение будет недопустимо для ЦЛП.
Доказательство NP-трудности
Следующее рассуждение является сведением задачи минимизации вершинного покрытия к задаче целочисленного программирования, что доказывает NP-трудность.
Пусть — неориентированный граф. Определим задачу линейного программирования следующим образом:
Если наложить требование, чтобы принимали значения 0 или 1, любое допустимое решение для целочисленного программирования является подмножество вершин. Из первого ограничения следует, что по меньшей мере один конец каждого ребра включена в подмножество. Таким образом, решение дает покрытие вершин. Кроме того, если задано вершинное покрытие C, можно присвоить значение 1 для любого и 0 для любого , что дает нам допустимое решение задачи целочисленного программирования. Отсюда мы может заключить, что при минимизации суммы мы получим также минимальное вершинное покрытие.
Отсюда мы может заключить, что при минимизации суммы мы получим также минимальное вершинное покрытие.
Варианты
В смешанном целочисленном линейном программировании (СЦЛП) только для части переменных требуется целочисленность, в то время как остальные переменные могут быть нецелочисленными.
В булевом программировании переменные должны принимать значения 0 или 1. Заметим, что любая ограниченная целочисленная переменная может быть выражена как комбинация булевых переменных. Например, если есть целочисленная переменная , ее можно выразить через булевых переменных:
Приложения
Есть две основные причины для использования целых переменных при моделировании задач линейного программирования:
- Целочисленные переменные представляют величины, которые могут быть исключительно целыми. Например, невозможно построить 3.7 автомобилей.
- Целочисленные переменные представляют решения, которые принимают значения 0 или 1.

Эти соглашения на практике встречаются часто и, таким образом, целочисленное линейное программирование может быть использовано во многих областях, некоторые из которых коротко освещены ниже.
Производственное планирование
Смешанное целочисленное программирование имеет много приложений в производстве, включая моделирование календарного планирования. Один из примеров встречается при производственном планировании[en] в сельском хозяйстве для определения выхода продукции, которая может иметь общие ресурсы (такие как земля, труд, расходы, семена, удобрения и т.д.). Возможной целью оптимизации может быть максимизация дохода без выхода за границы имеющихся ресурсов. В некоторых случаях задача может быть выражена как задача линейного программирования, но переменные при этом должны быть целыми.
Планирование
В этих задачах нужно обеспечить обслуживание и расписание работы транспортной сети . Об этом говорит сайт https://intellect.icu . Например, задача может состоять в расстановке автобусов или поездов по маршрутам, чтобы соблюсти расписание, а также обеспечить подвижный состав водителями. Здесь булевы переменные (т.е. принимающее значение 0 или 1) определяют, назначен ли автобус или поезд на маршрут, и назначен ли водитель на конкретный автобус/поезд.
Здесь булевы переменные (т.е. принимающее значение 0 или 1) определяют, назначен ли автобус или поезд на маршрут, и назначен ли водитель на конкретный автобус/поезд.
Сети передачи данных
Целью этой задачи является построение сети передачи данных так, чтобы обеспечить предопределенные требования за минимальную цену. В этой задаче требуется оптимизация как топологии сети, так и пропускной возможности элементов сети. Во многих случаях пропускная способность выражается дискретными величинами, что приводит к целочисленным переменным. Обычно накладываются зависящие от применяемой технологии другие ограничения, которые могут моделироваться целочисленными или булевыми переменными.
Сотовые сети
Задача планирования частот в мобильных сетях GSM требует распределение допустимых частот по антеннам, чтобы обеспечить связь и минимизировать интерференцию между антеннами. Эту задачу можно сформулировать как задачу линейного программирования, в которой булевы переменные отражают, назначена ли конкретная частота конкретной антенне.
Методы решения задач ЛП.
Наивный путь решения задачи ЦЛП — просто игнорировать ограничение целочисленности на переменные
x, решить соответствующую задачу ЛП (которая называется линейным ослаблением ограничений задачи ЦЛП), а затем округлить компоненты решения полученной задачи. Однако полученное решение может оказаться не только не оптимальным, оно может оказаться даже недопустимым, то есть некоторые ограничения могут быть нарушены.На первый взгляд естественным методом решения задачи ЦП является метод округления, реализация которого состоит из двух этапов. На первом этапе находят оптимальное решение задачи ЛП с ослабленными ограничениями. На втором этапе значения переменных в оптимальном решении X*, не являющиеся целыми, округляют так, чтобы получить допустимое решение X** с целочисленными значениями.
Состоятелен ли такой метод?
Пример. Рассмотрим полностью целочисленную задачу:
x1 + 1,5x2 max
2x1 + 4x2 17, 10x1 + 4x245
x1, x20, x1, x2 N.
Задача ЛП с ослабленными ограничениями получается снятием ограничений
x1, x2 N. Ее оптимальное решение может быть получено графическим методом.
Оптимальное решение достигается в точке А. Целевая функция равна при этом f=7,25. Оптимальное решение X*=(7/2, 5/2)Т. По методу округления примем X**=(3, 2) Т. Значение целевой функции при этом равно 6. Однако на самом деле оптимальное решение Xo=(2, 3) Т, а fопт=6,5.
Итак, метод округления дает неоптимальное решение. Поэтому он не состоятелен как общий метод решения задач ЦП. Кроме того, многие задачи ИО могут быть сформулированы как задачи ЦП, в которых переменные модели принимают значения из множества .
Рассмотрим метод, известный как метод отсечений.
Рассмотрим целочисленную задачу.
Допустимым решениям этой задачи соответствуют не все точки множества допустимых решений G, а лишь те, которые удовлетворяют требованиям целочисленности. Теоретически из множества G всегда можно выделить множество G* такое, что:
Теоретически из множества G всегда можно выделить множество G* такое, что:
а) оно содержит все точки множества G, удовлетворяющие требованию целочисленности;
б) оно является выпуклым множеством;
в) координаты всех его крайних точек удовлетворяют требованиям целочисленности.
Если множество G допустимых решений заменить множеством G*, это не может привести к изменению оптимального решения, так как G* получено из G путем отсечения от него подмножества, заведомо не содержащего допустимых решений, удовлетворяющих требованию целочисленности. Но в этом случае оптимальное решение задачи ЛП с ослабленными ограничениями и множеством G* допустимых решений соответствует крайней точке множества G*. Как следствие, оно удовлетворяет требованию целочисленности и обеспечивает экстремальное значение не только на G*, но и на G.
В основе комбинаторных методов решения задач ЦП лежит идея перебора всех элементов множества G допустимых решений, удовлетворяющих требованию целочисленности.
Наиболее известным комбинаторным методом является метод ветвей и границ . Он начинается с решением задачи ЛП с ослабленными ограничениями. Если оптимальное решение X* (точка B) не удовлетворяет требованию целочисленности, то из множества G выделяют два пересекающихся выпуклых подмножества K1 иK2, содержащих все допустимые решения из G, удовлетворяющие требованию целочисленности, но не содержащие X*. Этим задача ЦП заменяется совокупностью двух эквивалентных ей (в смысле оптимального решения Xo G) задач с множествами допустимых решений K1 и K2, т.к. XoK1 или XoK2.
Разработано много методов решения задач ЦП. Почти все эти методы можно описать на основе единой принципиальной схемы, состоящей из трех элементов.
Элемент 1. Предусматривается процедура формирования и решения последовательности взаимосвязанных задач, которые называют задачами, порожденными исходной задачей или задачами – истоками. При этом оптимальное решение по крайней мере одной из задач – истоков должно совпадать с оптимальным решением породившей их задачи.
При этом оптимальное решение по крайней мере одной из задач – истоков должно совпадать с оптимальным решением породившей их задачи.
Элемент 2. Каждой задаче, порожденной исходной задачей, ставится в соответствие так называемая ослабленная задача (задача с ослабленными ограничениями). Ее оптимальное решение может быть найдено с гораздо меньшими затратами, чем оптимальное решение соответствующей ей задачи – истока.
Элемент 3. В результате анализа решения ослабленной задачи принимается решение, относящееся к задаче – истоку:
а) исключить ее из рассмотрения;
б) заменить одной порожденной задачей, выбранной по определенному правилу;
в) заменить системой порожденных задач.
Использование полной унимодулярностиХотя, в общем случае, целочисленность решения ослабленной задачи не гарантирована, если ЦЛП имеет вид при условиях , где и имеют в качестве элементов целых чисел и является вполне унимодулярной, тогда любое базисное допустимое решение будет целочисленным. Следовательно, решение, которое дает симплекс-метод, будет заведомо целочисленным. Чтобы показать, что любое базисное решение такой задачи целочисленно, пусть — произвольное допустимое решение. Поскольку допустимо, мы знаем, что . Пусть — элементы, соответствующие базисным столбцам базисного решения . По определению базиса существует некоторая квадратная подматрица матрицы с линейно независимыми столбцами, такая, что .
Следовательно, решение, которое дает симплекс-метод, будет заведомо целочисленным. Чтобы показать, что любое базисное решение такой задачи целочисленно, пусть — произвольное допустимое решение. Поскольку допустимо, мы знаем, что . Пусть — элементы, соответствующие базисным столбцам базисного решения . По определению базиса существует некоторая квадратная подматрица матрицы с линейно независимыми столбцами, такая, что .
Поскольку столбцы линейно независимы и матрица квадратная, матрица неособенная, а потому при предположениях, что унимодулярна, выполняется . Поскольку не является особенной, матрица обратима, а потому . По определению, . Здесь означает союзную матрицу для и она целочисленна, поскольку целочисленна. Таким образом,
целочисленна
целочисленен
Любое базисное допустимое решение целочисленно.
Таким образом, если матрица ЦЛП вполне унимодулярна, вместо решения задачи ЦЛП можно использовать линейное ослабление задачи, которое даст целочисленное решение.
Если матрица не является вполне унимодулярной, существует ряд алгоритмов, решающих задачу целочисленного линейного программирования точно. Один из классов таких алгоритмов — методы секущих плоскостей (методы Гомори), которые работают путем решения ослабленной линейной задачи с последующим добавлением линейных ограничений, которые отсекают нецелочисленное решение задачи без отсечения целочисленных допустимых решений.
Другой класс алгоритмов — варианты метода ветвей и границ. Например, метод ветвей и отсечений[en], комбинирующий метод ветвей и границ с методами секущих плоскостей. Методы ветвей и границ имеют ряд преимуществ перед алгоритмами, использующими исключительно отсекающие плоскости. Одно из преимуществ — алгоритм можно завершить рано, как только хотя бы одно допустимое целочисленное решение найдено, хотя и не оптимальное. Кроме того, решение ослабленной линейной задачи может быть использовано для оценки, насколько далеко полученное от оптимального. Наконец, методы ветвей и границ можно использовать, чтобы получить несколько оптимальных решений.
Наконец, методы ветвей и границ можно использовать, чтобы получить несколько оптимальных решений.
Ленстра в 1983 показал, что в случае фиксированного числа переменных допустимое решение задачи целочисленного программирования может быть найдено за полиномиальное время.
Эвристические методыПоскольку задачи целочисленного линейного программирования NP-трудны, многие задачи трудноразрешимы, так что приходится использовать эвристические методы. Например, может быть использован поиск с запретами. Для использования поиска с запретами для решения задачи ЦЛП шаг алгоритма можно определить как увеличение или уменьшение целочисленной переменной, в то время как остальные целочисленные переменные остаются неизменными. Затем находится решение для переменных, на которых ограничение целочисленности не наложено. Для хранения предыдущих попыток может использоваться кратковременная память, в то время как более долговременная память может состоять из значений целочисленных переменных, для которых получены бо́льшие значения целевой функции (в предположении задачи максимизации).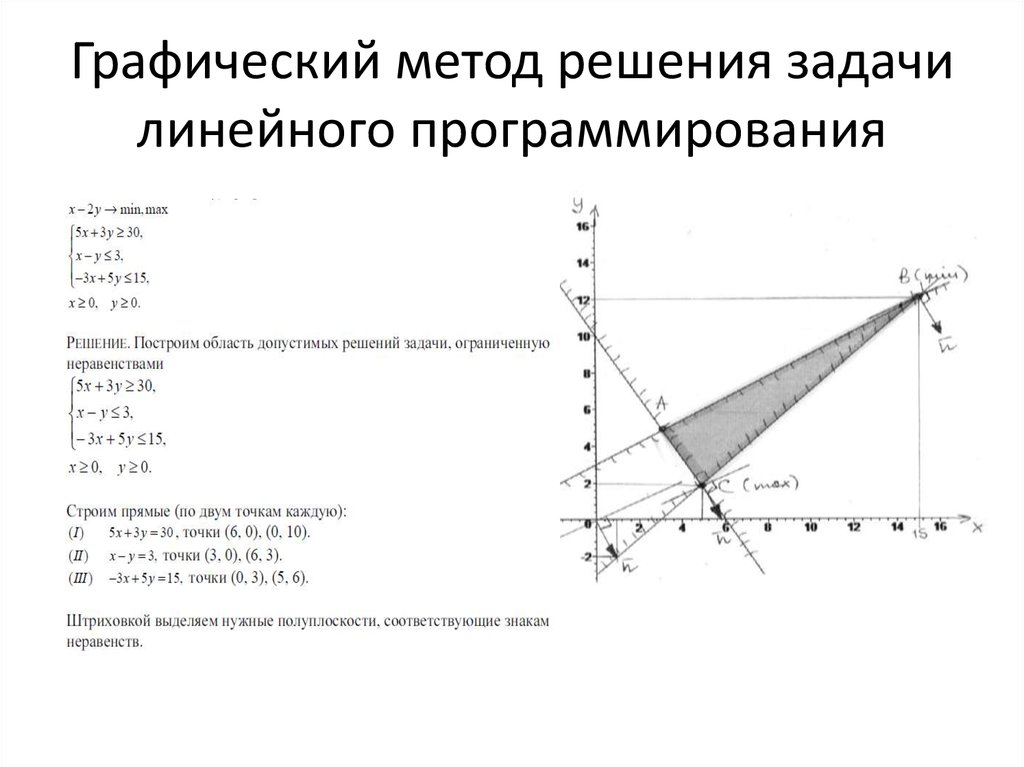 Наконец, долгая память может быть использована для поиска целочисленных значений, которые еще не пробовали.
Наконец, долгая память может быть использована для поиска целочисленных значений, которые еще не пробовали.
Другие эвристические методы, которые могут быть применены для решения ЦЛП
- Восхождение по выпуклой поверхности[en]
- Алгоритм имитации отжига
- Пассивная поисковая оптимизация
- Муравьиный алгоритм
- Нейронная сеть Хопфилда
Есть также некоторые другие, зависящие от задачи эвристические методы, такие как k-opt эвристика для задачи коммивояжера. Заметим, что недостатком эвристических методов является то, что в случае неудачи поиска решения метод не определяет, произошло это вследствие отсутствия допустимого решения, или просто алгоритм его найти не может. Далее обычно невозможно определить, насколько близко к оптимальному полученное этим методом решение.
метод отсекающих плоскостей ( метод гомори ).
Метод разработан Р. Гомори в 1957- 1958 гг. МОП относится к методам отсечений и называется методом правильных отсечений.
Пример. Пусть необходимо найти решение полностью целочисленной задачи:
2x1 + x2max
0,75x1 + 1,5x2 4,8 (1)
x1, x2 0, x1, x2 N.
Пусть есть некоторая задача ЛП:
с ограничениями:
, i= (2)
xj 0, j= (3)
с целочисленными ограничениями:
xj N, j= (4)
Целой частью вещественного числа а называется наибольшее целое число [a], не превышающее а. Дробная часть а есть число {a}=a – [a].
Метод Гомори состоит в следующем. Пусть решена ослабленная задача (1) – (3) и на последней итерации получена система:
Пусть решена ослабленная задача (1) – (3) и на последней итерации получена система:
x1+α1m+1xm+1+…+ α1nxn=β1,
x2+α2m+1xm+1+…+ α2nxn=β2, (5)
. . . . . . . . . . . . . .
xm+αnm+1xm+1+…+ αmnxn=βm
т.е. решение задачи есть
(β1,…, βm, 0, …,0) (6)
Предположим, что это решение не удовлетворяет условию целочисленности (4), т.е. некоторое βi, i=1,…, m, нецелое.
Добавим к системе (6), которая эквивалентна системе (2) ограничение:
{ βi } — (7)
Строка i называется производящей. Это ограничение отсекает от исходного многогранника решений оптимальную точку (β1,…, βm, 0, …,0), не затрагивая ни одной из целочисленных точек множества.
Это ограничение отсекает от исходного многогранника решений оптимальную точку (β1,…, βm, 0, …,0), не затрагивая ни одной из целочисленных точек множества.
Покажем, что допустимое целочисленное решение удовлетворяет соотношению (7). Из системы (5) мы имеем:
xi+, или xi+
Пусть x=(x1, …,xn) – целочисленное допустимое решение. Тогда левая часть последнего выражения целочисленна, т.е. целочисленным является и значение:
{βi} —
Тогда, если бы соотношение (7), не выполнялось, т.е. выполнялось бы:
{ βi } — ,
то в силу того, что 0 {βi}<1 , 0{αik}<1, xk 0, должно было бы выполняться соотношение:
{ βi } — ,
а это противоречит целочисленности {βi} — .
Теперь проверим условие отсечения. Т.к. для оптимального решения { βi }>0, xi=0, i=m+1, …,n, т. е. это решение действительно не удовлетворяет (7).
е. это решение действительно не удовлетворяет (7).
Итак, если к (6) или к (2) – что равносильно – добавить ограничение (7) и решить задачу (1) – (3) и (7), то получим решение, отличное от (β1,…, βm, 0, …,0), которое тоже может оказаться нецелочисленным. Это потребует добавления новых ограничений вида (7). Если при этом каждый раз индекс i в ограничениях (7) выбирать так, чтобы это был индекс первый по порядку переменной с нецелочисленным значением, допустимое множество задачи (1) – (3) ограниченно и не пусто, значит алгоритм Гомори конечен, т.е. заканчивается за конечное число шагов решением целочисленной задачи.
Несмотря на то, что метод Гомори – надежное решение для задач ЦП, его практическое применение нецелесообразно, если исходная задача имеет большую размерность.
Иллюстрация метода Гомори.
Z=7x1+10x2,
-x1+3x2 6,
7x1+x235,
x1, x2 0, x1, x2 N.
Отсечения не отбрасывают ни одной исходной допустимой целочисленной точки, но должны проходить, по меньшей мере, через одну целочисленную точку (допустимую или недопустимую).
Метод ветвей и границ.
Впервые его предложили Ленд и Дойч в 1960г. затем усовершенствовали Литтл, Мурти, Суни, Кэрол.
Рассмотрим следующую целочисленную задачу ЛП:
z=5x1+4x2max
x1+x2 5
10x1+6x245
x1,x20,
Соответствующая ослабленная задача ЛП имеет решение: x1=3.75, x2=1.25, z=23.75
Оптимальное решение задачи ЛП0 (обозначим ее так) не удовлетворяет условию целочисленности.
Метод ветвей и границ изменяет пространство решений задачи ЛП так, что в конечном счете образуется оптимальное решение задачи ЦП. Для этого сначала выбирается одна из целочисленных переменных, значение которой в оптимальном решении ЛП0 не является целочисленным. Например, выбирая x1(=3.75), замечаем, что область 31<4 пространства допустимых решений задачи ЛП0 не содержит целочисленных значений x1, и следовательно ее можно исключить из рассмотрения как бесперспективную. Это эквивалентно замене исходной задачи ЛП0 двумя новыми задачами ЛП1 и ЛП2:
Например, выбирая x1(=3.75), замечаем, что область 31<4 пространства допустимых решений задачи ЛП0 не содержит целочисленных значений x1, и следовательно ее можно исключить из рассмотрения как бесперспективную. Это эквивалентно замене исходной задачи ЛП0 двумя новыми задачами ЛП1 и ЛП2:
Пространство допустимых решений ЛП1=Пространство допустимых решений ЛП0+(x1 3),
Пространство допустимых решений ЛП2=Пространство допустимых решений ЛП0+(x14).
Все допустимые решения задачи ЦП остались, задачи ЛП1 и ЛП2 «не потеряют» ни одного решения.
Новые ограничения (x13) и (x14) взаимно исключаемы, так что задачи ЛП1 и ЛП2 нужно рассматривать как независимые. Дихотомизация задач ЛП — основа концепции ветвления в методе ветвей и границ. В этом случае x1 называется переменной ветвления.
Оптимальное решение находится либо в ПДЗ задачи ЛП1, либо задачи ЛП2. Следовательно обе задачи должны быть решены.
Решаем ЛП1:
z=5x1+4x2max
x1+x2 5
10x1+6x245
x13
x1,x20
Решение: x1=3, x2=2, z=23.
Оптимальное решение задачи ЛП1 удовлетворяет условию целочисленности переменных x1 и x2 . В этом случае говорят, что задача ЛП1 прозондирована. Это значит, что задача ЛП1 не должна больше зондироваться, она не может содержать лучшего решения задачи ЦП, чем уже есть.
Пока мы можем сказать, что z=23 – нижняя граница.
Теперь переходим к задаче ЛП2. Так как в задаче ЛП0 оптимальное значение z=23,75 и все ее коэффициенты целые числа, невозможно получить целочисленное решение в задаче ЛП2. Задачу ЛП2 отбрасываем и считаем ее прозондированной.
Реализация метода ветвей и границ завершена. Оптимальное решение: x1=3, x2=2, z=23.
Остались без ответа два вопроса:
1) Можно ли было в задаче ЛП0 выбрать переменную x2 в качестве переменной ветвления вместо x1?
2) Можно ли было сначала решить задачу ЛП2 вместо ЛП1?
Оба ответа положительные, но дальнейший ход решения может отличаться. Если решать задачу ЛП2, то получим такую схему:
Если решать задачу ЛП2, то получим такую схему:
Последовательность подзадач наихудшая. Пример указывает на основную слабость метода ветвей и границ: как выбирать переменную ветвления и как выбирать следующую подзадачу? На этот счет нет строгой теории.
См. также
- Метод наименьших квадратов с ограничениями
- Методы оптимизации
- Метод золотого сечения
- Дихотомия
- Метод парабол
- Перебор по сетке
- Метод равномерного блочного поиска
- Метод Фибоначчи
- Троичный поиск
- Метод Пиявского
- Метод Стронгина
Я хотел бы услышать твое мнение про целочисленное программирование Надеюсь, что теперь ты понял что такое целочисленное программирование, метод отсекающих плоскостей, метод гомори, метод ветвей и границ
и для чего все это нужно, а если не понял, или есть замечания,
то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу.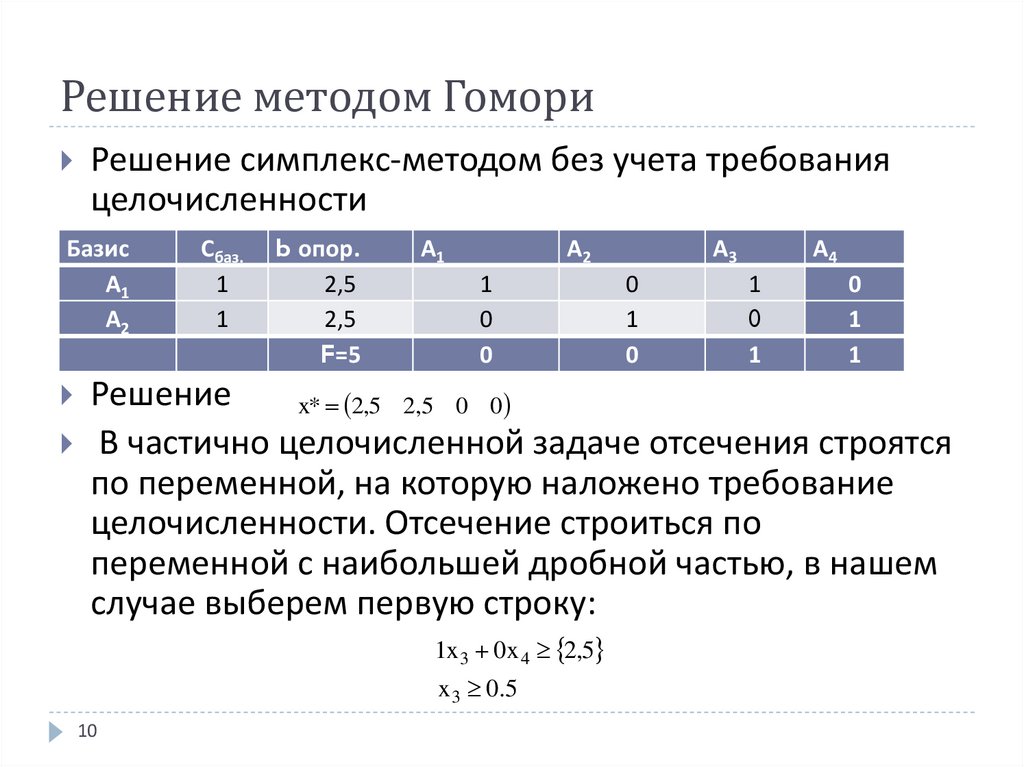 Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Математические методы исследования операций .Теория игр и расписаний.
Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Математические методы исследования операций .Теория игр и расписаний.
|
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Генеалогическое древо Султанов Османской империи: Османские правители, вначале, будучи еще бейлербеями Анатолии, женились на дочерях византийских императоров… Особенности труда и отдыха в условиях низких температур: К работам при низких температурах на открытом воздухе и в не отапливаемых помещениях допускаются лица не моложе 18 лет, прошедшие… Отражение на счетах бухгалтерского учета процесса приобретения: Процесс заготовления представляет систему экономических событий, включающих приобретение организацией у поставщиков сырья… Интересное: Мероприятия для защиты от морозного пучения грунтов: Инженерная защита от морозного (криогенного) пучения грунтов необходима для легких малоэтажных зданий и других сооружений. Наиболее распространенные виды рака: Раковая опухоль — это самостоятельное новообразование, которое может возникнуть и от повышенного давления… Уполаживание и террасирование склонов: Если глубина оврага более 5 м необходимо устройство берм. Варианты использования оврагов для градостроительных целей… Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция |
⇐ ПредыдущаяСтр 5 из 6Следующая ⇒
Если в задаче целочисленного программирования количество управляющих переменных равно двум, а ограничения имеют вид неравенств, то ее можно решить графическим методом.
Этап 1. Решение исходной задачи обычным графическим методом. Если найденное оптимальное решение является целочисленным, то решение прекращают. Если же найденное оптимальное решение содержит хотя бы одно дробное значение, то переходят к этапу 2. Этап 2. В непосредственной близости от границ ОДР задачи со стороны, где расположена вершина оптимального решения нецелочисленной задачи (т.е. вблизи тех границ ОДР, куда указывает вектор градиента целевой функции), строят точки, координатами которых являются целые числа. Дальнейшее решение в точности повторяет графическое решение обычной задачи линейного программирования, с тем лишь отличием, что, продвигая в направлении вектора градиента линию уровня целевой функции, находят последнюю из целочисленных точек на пути продвижения. Именно ее координаты и будут являться оптимальным целочисленным решением исходной задачи.
ПРИМЕР: Найдите графическим методом оптимальное решение целочисленной задачи линейного программирования, заданной моделью вида: Вначале решим поставленную задачу графическим методом без ограничения на целочисленность управляющих переменных. Рис. 4.
Как следует из рассмотрения рис. 4, ОДР задачи есть трапеция ОАВС, а оптимальным решением задачи будут являться координаты точки В, т.е. получено нецелочисленное оптимальное решение задачи в виде: . Построим внутри ОДР целочисленную сетку и примем во внимание точки D, E и F, имеющие целые значения координат. Очевидно, что наиболее близкой к точке В оказывается точка Е, координаты которой и будут являться искомым целочисленным решением: и при этом . Метод Гомори решения задач целочисленного Программирования
Для решения задач целочисленного программирования с любым количеством управляющих переменных может быть успешно применен метод Гомори.
Этап 1. Решение задачи линейного программирования без условия целочисленности управляющих переменных обычным симплекс – методом. Если все значения управляющих переменных оптимального плана – целые числа, то решение заканчивают. Если же полученное оптимальное решение содержит хотя бы одно дробное значение управляющих переменных, то переходят к этапу 2.
Этап 2. Составление дополнительного ограничения (сечения) и решение расширенной задачи обычным симплекс – методом. При этом дополнительное ограничение (сечение) отсекает нецелочисленные решения, оставляя только целочисленные.
Целой частью [r] рационального числа r называется наибольшее целое число, не превосходящее числа r. Дробной частью числа r называется правильная дробь {r}, определяемая соотношением: {r} = r – [r]. Пример 1. Для числа 5 имеем: [5] = 5 и {5} = 0. Пример 2. Для числа 4/5 имеем: [4/5] = 0 и {4/5} = 4/5. Пример 3. Для числа 8/3 имеем: [8/3] = 2 и {8/3} = 2/3. Пример 4. Для числа – 4/5 имеем: [- 4/5] = — 1 и {- 4/5} = 1/5. Пример 5. Для числа – 8/3 имеем: [- 8/3] = — 3 и {- 8/3} = 1/3. Поясним, каким образом составляется сечение (дополнительное ограничение). Пусть выполнен этап 1, т.е. найдено оптимальное решение задачи в виде: и пусть некоторое — дробное число. Рассмотрим i-ое ограничение задачи:
С учетом обозначений: и дополнительное ограничение (сечение) для переменной можно записать в виде: , где . Очевидно, что при дополнении исходной задачи этим ограничением, получают задачу большей размерности. На практике поступают так: последнюю симплекс-таблицу, содержащую оптимальное (нецелочисленное) решение дополняют еще одной строкой с переменной в списке базисных переменных и еще одним столбцом, соответствующим этой же дополнительной переменной, а в дополнительную строку записывают числовые коэффициенты сечения, включая значение свободного члена. Если при решении целочисленной задачи симплекс – методом (на этапе 1) получено несколько дробных значений, то дополнительное ограничение следует составлять для значения, имеющего максимальную дробную часть. ПРИМЕР: Найдите методом Гомори целочисленное решение задачи примера подраздела 3.3.1. Решив поставленную задачу симплекс-методом, получим последнюю симплекс-таблицу, содержащую оптимальное (не целочисленное) решение, (убедитесь в этом сами) в виде:
Поскольку оба свободных члена имеют одинаковую дробную часть, равную 1/2, для определенности будем составлять сечение по Гомори для переменной .
. Введя это ограничение и дополнительную базисную переменную в приведенную симплекс-таблицу, получим новую симплекс-таблицу, из которой в одну итерацию получим искомое целочисленное решение поставленной задачи.
Из последней симплекс-таблицы следует и при этом: .
Рекомендуемая литература по теме 3: [1 ÷ 4].
ВОПРОСЫ для самопроверки знаний по теме 3: 1. Чем отличаются целочисленные задачи от обычных задач линейного программирования?
2. В чем суть графического метода решения задач целочисленного программирования?
3. В чем суть метода Гомори решения задач целочисленного программирования?
4. Для какой управляющей переменной составляется дополнительное ограничение по Гомори?
⇐ Предыдущая123456Следующая ⇒ Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого… Папиллярные узоры пальцев рук — маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни… Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰). Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой… |
Целочисленное решение задач линейного программирования методом ветвей и границ с помощью Excel
В большинстве экономико-математических моделей, сформулированных как задачи линейного программирования, часть или все компоненты вектора-решения должны выражаться в целых числах, т. е. быть целочисленными. К ним относятся, например, задачи, в которых переменные означают количество единиц неделимой продукции, число станков при закупке оборудования, количество домов при очередности строительства и т. д. [3, c. 180]
С другой стороны, это могут быть задачи, в которых при моделировании используются логические (булевы) переменные со значениями 1 и 0, что означает, например, взимать или не взимать арендную плату, создавать или не создавать дополнительный пункт производства и т. д. Покажем особенности фактора целочисленности на следующем примере, который в учебных целях генерируется на компьютере в виде индивидуальных заданий. Оптимальное решение в примере, в принципе, не может быть получено каким-либо округлением решения соответствующей задачи линейного программирования.
д. Покажем особенности фактора целочисленности на следующем примере, который в учебных целях генерируется на компьютере в виде индивидуальных заданий. Оптимальное решение в примере, в принципе, не может быть получено каким-либо округлением решения соответствующей задачи линейного программирования.
Для решения рассмотренного класса задач математического программирования, как правило, используется универсальный метод решения под названием «метод ветвей и границ». [2, с. 158]
Продемонстрируем основные идеи этого метода на примере решения задачи целочисленного линейного программирования (ЦЛП).
Эти задачи включают в себя требования целочисленности ко всем искомым переменным. Они относятся к классу задач полностью целочисленного линейного программирования (задача ЦЛП). В свою очередь, эти задачи являются частным случаем задачи частично целочисленного линейного программирования (ЧЦЛП). [2, с. 160]
При решении задач частично-целочисленного линейного программирования методом ветвей и границ на определенных этапах решаются вспомогательные задачи линейного программирования (ЛП), для которых применяется симплекс-метод.
Рассмотрим развернутую экономико-математическую модель задачи.
Система переменных: x1, x2
Система ограничений: 2x1 + x2 ≤ 9
5x1 + 4x2 ≤ 29
Целевая функция: F = 27x1 + 21x2 → max
Решение задачи осуществляется симплексным методом [1, с. 176] с помощью сервисной функции MS Excel «Поиск решения».
Описание шагов алгоритма «метода ветвей и границ»
- Решение вспомогательной задачи линейного программирования.
Вспомогательная задача № 1 получается из данной задачи целочисленного линейного программирования путём игнорирования требования целочисленности. Решим задачу симплексным методом с помощью Excel. В результате получим: х1=2,3, х2=4,3, Fmax=154 (схема 1).
2.Очередное ветвление вспомогательной задачи на две вспомогательные подзадачи нижнего уровня.
Так как вышеполученное решение нецелочисленное, то оно дает верхнюю границу F = 154 для максимума целевой функции искомого оптимального решения исходной задачи.
В этом случае одна из переменных, имеющих дробное значение, в данном случае x1, берется за основу для разбиения (ветвления) данной вспомогательной задачи № 1 на вспомогательные подзадачи под номерами 1.1 и 1.2 по нижеприведенной методике:
Так как 2
задача 1.1. → задача 1.2.
2×1 + x2 ≤ 9 → 2×1 + x2 ≤ 9
5×1 + 4×2 ≤ 29 → 5×1 + 4×2 ≤ 29
х1=3
х1>=0, х2>=0х1>=0, х2>=0
F = 27×1+21×2 → max → F = 27×1+21×2 → max
При решении подзадачи 1.1. в Excel добавим ограничение х1
В результате получим:
х1=2, х2=4,75 Fмах=153,75.
153,75 — уточненная верхняя граница
При решении подзадачи 1.2. в Excel добавим ограничение х2>=3
В результате получим:
х1=3, х2=3, Fмах=144
Таким образом, получим первый целочисленный рекорд.
- Проверка оптимальности текущего целочисленного рекорда после очередного ветвления на основе формулировки критерия оптимальности текущего целочисленного рекорда по методу ветвей и границ:Текущий целочисленный рекорд объявляется оптимальным решением исходной задачи в том и только том случае, если при данном состоянии дерева решений на концах других ветвей не существует верхних границ, превосходящих значение рекорда.

В данном случае критерий не выполняется, так как 153,75 больше 144.
- Ветвление следует продолжить по подзадаче № 1.1, которая дает наибольшую на данный момент верхнюю границу из подзадач, находящихся на концах ветвей. В качестве основы для ветвления выбирается дробное значение переменной х2 = 4,75.
Так как 4
задача 1.1.1. → задача 1.1.2.
2×1+x2≤9 → 2×1+x2≤9
5×1+4×2≤29 → 5×1+4×2≤29
х2=5
х1
х1>=0, х2>=0х1>=0, х2>=0
F=27×1+21×2 → max → F=27×1+21×2 → max
При решении подзадачи 1.1.1. в Excel добавим ограничение х2
В результате получим:
х1=2, х2=4, Fмах=138
При решении подзадачи 1.1.2. в Excel добавим ограничение х2>=5
В результате получим:
х1=1,8, х2=5, Fмах=153,6
153,6 — уточненная верхняя граница.
- Проверка оптимальности текущего целочисленного рекорда после очередного ветвленияпоказывает, что критерий вновь не выполняется, так как 153,6 больше 138.

- Продолжаем ветвление по подзадаче 1. Рассмотрим подзадачу 1.3.В качестве основы для ветвления выбирается дробное значение переменной х2 =4,3.
Так как 3
задача 1.3. → задача 1.4.
2×1+x2≤9 → 2×1+x2≤9
5×1+4×2≤29 → 5×1+4×2≤29
х2=5
х1>=0, х2>=0х1>=0, х2>=0
F=27×1+21×2 → max → F=27×1+21×2→ max
При решении подзадачи 1.3. в Excel добавим ограничение х2
В результате получим:
х1=2,5, х2=4, Fмах=151,5
При решении подзадачи 1.4. в Excel добавим ограничение х2>=5
В результате получим:
х1=1,8, х2=5, Fмах=153,6
- Продолжим ветвление по подзадаче 1.4.
В качестве основы для ветвления выбирается дробное значение переменной х1 = 1,8.
Так как 1
2×1+x2≤9 → 2×1+x2≤9
5×1+4×2≤29 → 5×1+4×2≤29
х2>=5 х2>=2
х1
х1>=0, х2>=0 → х1>=0, х2>=0
F=27×1+21×2 →max → F=27×1+21×2 → max
При решении подзадачи 1. 4.2. — поиск не может найти подходящего решения.
4.2. — поиск не может найти подходящего решения.
При решении подзадачи 1.4.1. в Excel добавим ограничение х2
В результате получим: х1=1, х2=6, Fмах=153
Таким образом, значение 153 является новым текущим целочисленным рекордом, отменяющим прежний рекорд 144.
Оптимальным решением этой задачи будет Fмах=153, при х1=1, х2=6.
Следует отметить, что никаким округлением решения вспомогательной задачи № 1 (х1=2,3, х2=4,3) в принципе невозможно получить оптимальное решение х1=1, х2=6.
Рис. 1. Алгоритм «метода ветвей и границ» Дерево решений
Литература:
- Гармаш А. Н., Орлова И. В. Математические методы в управлении: Учебное пособие. — М.: Вузовский учебник: ИНФРА-М, 2014. — 272 — c.
- Математическое моделирование экономических процессов в сельском хозяйстве / Гатаулин А. М., Гаврилов Г. В., Сорокина Т. М. и др.
 ; Под ред. А. М. Гатаулина. — СПБ.: ООО «ИТК ГРАНИТ», 2009. — 432 с.
; Под ред. А. М. Гатаулина. — СПБ.: ООО «ИТК ГРАНИТ», 2009. — 432 с. - Савиных В. Н. Математическое моделирование производственного и финансового менеджмента [Текст]: учеб. пособие / В. Н. Савиных. — Новосибирск: СГГА, 2007. — 219 с.
- Алексеев Г. В. Численное экономико-математическое моделирование и оптимизация [Электронный ресурс]: учебное пособие / Алексеев Г. В., Холявин И. И.— С.: Вузовское образование, 2013. 195— c. — Режим доступа: http://www.iprbookshop.ru/16905. — ЭБС «IPRbooks».
Основные термины (генерируются автоматически): задача, решение подзадачи, вспомогательная задача, линейное программирование, целочисленное линейное программирование, ветвление, дробное значение переменной, качество основы, метод ветвей, текущий целочисленный рекорд.
Автоматизация табличного симплекс-метода решения задач линейного программирования с использованием программы С++
Глава 1. Аналитическая часть
1.1 История развития экономико-математического планирования
В 1938-1939 гг. ленинградский математик (впоследствии академик, лауреат Ленинской, Государственных и Нобелевской премий) Л.В. Канторович в результате анализа ряда проблем организации и планирования производства сформулировал новый класс условно-экстремальных задач и предложил методы их решения. Так было положено начало новой отрасли прикладной математики линейному программированию. В более поздних работах Л. В. Канторович расширил область применения линейного программирования в социалистической экономике, сформулировав задачи отраслевого и народнохозяйственного оптимального планирования. А через два десятилетия после своего возникновения линейное программирование стало основным инструментом планово-экономических решений на всех уровнях социалистического народного хозяйства. [1]
В том же 1939 г. ленинградский экономист В. В. Новожилов, рассматривая эффективность плановых и проектных решений, сформулировал важные теоретические положения, ставшие потом органической частью теории оптимального планирования социалистической экономики.
Аналитическая часть
1.1 История развития экономико-математического планирования
В 1938-1939 гг. ленинградский математик (впоследствии академик, лауреат Ленинской, Государственных и Нобелевской премий) Л.В. Канторович в результате анализа ряда проблем организации и планирования производства сформулировал новый класс условно-экстремальных задач и предложил методы их решения. Так было положено начало новой отрасли прикладной математики линейному программированию. В более поздних работах Л. В. Канторович расширил область применения линейного программирования в социалистической экономике, сформулировав задачи отраслевого и народнохозяйственного оптимального планирования. А через два десятилетия после своего возникновения линейное программирование стало основным инструментом планово-экономических решений на всех уровнях социалистического народного хозяйства. [1]
В том же 1939 г. ленинградский экономист В. В. Новожилов, рассматривая эффективность плановых и проектных решений, сформулировал важные теоретические положения, ставшие потом органической частью теории оптимального планирования социалистической экономики. Далее методы планирования продолжали совершенствоваться, но только развитие вычислительной техники в конце 50-х гг. позволило сделать плановые многовариантные расчеты достаточно распространенными. Важную роль в организации и пропаганде экономико-математических исследований в этот период сыграл академик В. С. Немчинов. Именно в эти годы получают развитие некоторые разделы прикладной математики, связанные с решением оптимизационных задач: линейное и нелинейное программирование, теория оптимального управления и др. В 60-е гг. основное внимание исследователей сосредоточивается на разработке оптимизационных моделей различных типов и их практическом применении к решению задач планирования. Было построено большое количество экономико-математических моделей, на основе которых проведены расчеты по составлению реальных оптимальных планов (оптимальные планы перевозок, эксплуатации подвижного состава транспорта, использования топлива, загрузки оборудования предприятий; оптимальное размещение отдельных отраслей промышленности и предприятий отрасли; оптимальное планирование и распределение капиталовложений и т.
Далее методы планирования продолжали совершенствоваться, но только развитие вычислительной техники в конце 50-х гг. позволило сделать плановые многовариантные расчеты достаточно распространенными. Важную роль в организации и пропаганде экономико-математических исследований в этот период сыграл академик В. С. Немчинов. Именно в эти годы получают развитие некоторые разделы прикладной математики, связанные с решением оптимизационных задач: линейное и нелинейное программирование, теория оптимального управления и др. В 60-е гг. основное внимание исследователей сосредоточивается на разработке оптимизационных моделей различных типов и их практическом применении к решению задач планирования. Было построено большое количество экономико-математических моделей, на основе которых проведены расчеты по составлению реальных оптимальных планов (оптимальные планы перевозок, эксплуатации подвижного состава транспорта, использования топлива, загрузки оборудования предприятий; оптимальное размещение отдельных отраслей промышленности и предприятий отрасли; оптимальное планирование и распределение капиталовложений и т. д.), что дало большой народнохозяйственный эффект. Наряду с расширением сферы применения математических моделей в экономике и планировании осуществляется процесс усовершенствования моделей и использования более адекватного математического аппарата: переход от статических моделей к динамическим, от жестко детерминированных к стохастическим моделям, учитывающим случайность и неопределенность экономических процессов, применение дискретного программирования, методов статистического моделирования, создание новых алгоритмов, позволяющих решать задачи большой размерности.
1.2 Необходимость решения задач линейного программирования
Применение экономико-математических методов и моделей позволяет существенно улучшить качество планирования и получить дополнительный экономический эффект без вовлечения в общественное производство дополнительных ресурсов, что чрезвычайно важно в условиях перехода экономики на преимущественно интенсивный путь развития.
В настоящее время область возможного применения экономико-математических методов в планировании чрезвычайно велика и с каждым годом она расширяется.
д.), что дало большой народнохозяйственный эффект. Наряду с расширением сферы применения математических моделей в экономике и планировании осуществляется процесс усовершенствования моделей и использования более адекватного математического аппарата: переход от статических моделей к динамическим, от жестко детерминированных к стохастическим моделям, учитывающим случайность и неопределенность экономических процессов, применение дискретного программирования, методов статистического моделирования, создание новых алгоритмов, позволяющих решать задачи большой размерности.
1.2 Необходимость решения задач линейного программирования
Применение экономико-математических методов и моделей позволяет существенно улучшить качество планирования и получить дополнительный экономический эффект без вовлечения в общественное производство дополнительных ресурсов, что чрезвычайно важно в условиях перехода экономики на преимущественно интенсивный путь развития.
В настоящее время область возможного применения экономико-математических методов в планировании чрезвычайно велика и с каждым годом она расширяется. Однако область фактического их применения в практике плановых расчетов намного скромнее. Это объясняется трудностями широкого внедрения экономико-математических методов.
К числу их следует отнести: сложность определения критерия оптимальности в ряде экономических задач; трудности при решении проблемы «встраивания» математических моделей в существующую систему планирования и управления, приводящие к необходимости создания новой технологии планирования, базирующегося на системном использовании экономико-математических методов и ЭВМ; стохастический и динамический характер экономических процессов, требующий усложнения используемого математического аппарата и программного обеспечения ЭВМ, увеличения объема вычислений; трудность измерений многих экономических явлений и получения массовой достоверной информации для наполнения разработанных моделей; трудность проверки правильности (верификации) экономико-математических моделей, ориентированных не столько на подтверждение действительности, сколько на решение новых социально-экономических задач (это в первую очередь относится к моделям планирования и прогнозирования), и т.
Однако область фактического их применения в практике плановых расчетов намного скромнее. Это объясняется трудностями широкого внедрения экономико-математических методов.
К числу их следует отнести: сложность определения критерия оптимальности в ряде экономических задач; трудности при решении проблемы «встраивания» математических моделей в существующую систему планирования и управления, приводящие к необходимости создания новой технологии планирования, базирующегося на системном использовании экономико-математических методов и ЭВМ; стохастический и динамический характер экономических процессов, требующий усложнения используемого математического аппарата и программного обеспечения ЭВМ, увеличения объема вычислений; трудность измерений многих экономических явлений и получения массовой достоверной информации для наполнения разработанных моделей; трудность проверки правильности (верификации) экономико-математических моделей, ориентированных не столько на подтверждение действительности, сколько на решение новых социально-экономических задач (это в первую очередь относится к моделям планирования и прогнозирования), и т. д.
Но главная трудность заключается в сложности моделируемых экономических процессов и явлений. Большинство объектов, изучаемых экономической наукой, может быть охарактеризовано кибернетическим понятием «сложная система». При изучении систем недостаточно (а иногда и невозможно) пользоваться методом расчленения на элементы с последующим изучением этих элементов в отдельности.
Кроме того, моделирование существенно усложняется тем, что экономика охватывает не только производственные процессы, но и производственные отношения. Моделировать производственные отношения невозможно, не учитывая поведение людей, их интересы и индивидуально принятые решения.
В результате производственно-хозяйственная или социально-экономическая ситуация, в которой приходится принимать плановые решения, часто оказывается намного богаче и сложнее тех моделей, которые используются в планировании в этой ситуации.
В настоящее время линейное программирование является одним из наиболее употребительных аппаратов математической теории оптимального принятия решений, в том числе и в финансовой математике.
д.
Но главная трудность заключается в сложности моделируемых экономических процессов и явлений. Большинство объектов, изучаемых экономической наукой, может быть охарактеризовано кибернетическим понятием «сложная система». При изучении систем недостаточно (а иногда и невозможно) пользоваться методом расчленения на элементы с последующим изучением этих элементов в отдельности.
Кроме того, моделирование существенно усложняется тем, что экономика охватывает не только производственные процессы, но и производственные отношения. Моделировать производственные отношения невозможно, не учитывая поведение людей, их интересы и индивидуально принятые решения.
В результате производственно-хозяйственная или социально-экономическая ситуация, в которой приходится принимать плановые решения, часто оказывается намного богаче и сложнее тех моделей, которые используются в планировании в этой ситуации.
В настоящее время линейное программирование является одним из наиболее употребительных аппаратов математической теории оптимального принятия решений, в том числе и в финансовой математике. Для решения задач линейного программирования разработано сложное программное обеспечение, дающее возможность эффективно и надежно решать практические задачи больших объемов. Эти программы и системы снабжены развитыми системами подготовки исходных данных, средствами их анализа и представления полученных результатов. В развитие и совершенствование этих систем вложен труд и талант многих математиков, аккумулирован опыт решения тысяч задач. Владение аппаратом линейного программирования необходимо каждому специалисту в области прикладной математики.
1.3 Линейное программирование
Линейное программирование — математическая дисциплина, посвященная теории и методам решения задач об экстремумах линейных функций на множествах n-мерного векторного пространства, задаваемых системами линейных уравнений и неравенств.
Линейное программирование — это наука о методах исследования и отыскания наибольших и наименьших значений линейной функции, на неизвестные которой наложены линейные ограничения.
Для решения задач линейного программирования разработано сложное программное обеспечение, дающее возможность эффективно и надежно решать практические задачи больших объемов. Эти программы и системы снабжены развитыми системами подготовки исходных данных, средствами их анализа и представления полученных результатов. В развитие и совершенствование этих систем вложен труд и талант многих математиков, аккумулирован опыт решения тысяч задач. Владение аппаратом линейного программирования необходимо каждому специалисту в области прикладной математики.
1.3 Линейное программирование
Линейное программирование — математическая дисциплина, посвященная теории и методам решения задач об экстремумах линейных функций на множествах n-мерного векторного пространства, задаваемых системами линейных уравнений и неравенств.
Линейное программирование — это наука о методах исследования и отыскания наибольших и наименьших значений линейной функции, на неизвестные которой наложены линейные ограничения. Таким образом, задачи линейного программирования относятся к задачам на условный экстремум функции. Казалось бы, что для исследования линейной функции многих переменных на условный экстремум достаточно применить хорошо разработанные методы математического анализа, однако невозможность их использования можно довольно просто проиллюстрировать. [17]
Целевая функция задачи линейного программирования достигает своего экстремума (минимума или максимума) в вершине допустимой области. Если целевая функция достигает экстремального значения более, чем на одной вершине, то она достигает того же значения в любой точке, являющейся выпуклой комбинацией этих вершин.
К задачам линейного программирования сводится множество практических задач, встречающихся в разных областях экономики и техники. Теоретическая и практическая сторона решения задачи линейного программирования на сегодняшний день хорошо разработана однако отдельные вопросы, связанные с так называемой проблемой вырожденности были разрешены не так давно.
Таким образом, задачи линейного программирования относятся к задачам на условный экстремум функции. Казалось бы, что для исследования линейной функции многих переменных на условный экстремум достаточно применить хорошо разработанные методы математического анализа, однако невозможность их использования можно довольно просто проиллюстрировать. [17]
Целевая функция задачи линейного программирования достигает своего экстремума (минимума или максимума) в вершине допустимой области. Если целевая функция достигает экстремального значения более, чем на одной вершине, то она достигает того же значения в любой точке, являющейся выпуклой комбинацией этих вершин.
К задачам линейного программирования сводится множество практических задач, встречающихся в разных областях экономики и техники. Теоретическая и практическая сторона решения задачи линейного программирования на сегодняшний день хорошо разработана однако отдельные вопросы, связанные с так называемой проблемой вырожденности были разрешены не так давно. Полученные в рамках борьбы с вырожденностью результаты представляют самостоятельный интерес и являются основой для предлагаемого в настоящей работе нового алгоритма.
Термин «программирование» нужно понимать в смысле «планирования». Он был предложен в середине 1940-х годов Джорджем Данцигом, одним из основателей линейного программирования, еще до того, как компьютеры были использованы для решения линейных задач оптимизации. Первым исследованием по линейному программированию является работа Л.B. Kантфовича “Математические методы организации и планирования производства”, опубликованная в 1939 г. В нем дана постановка задач линейного программирования, разработан метод разрешающих множителей решения задач линейного программирования и дано его теоретическое обоснование.
Прямая задача линейного программирования является математической формулировкой проблемы составления такого плана использования различных способов производства, который позволяет получить максимальное количество однородного продукта при имеющихся в наличии ресурсах.
Полученные в рамках борьбы с вырожденностью результаты представляют самостоятельный интерес и являются основой для предлагаемого в настоящей работе нового алгоритма.
Термин «программирование» нужно понимать в смысле «планирования». Он был предложен в середине 1940-х годов Джорджем Данцигом, одним из основателей линейного программирования, еще до того, как компьютеры были использованы для решения линейных задач оптимизации. Первым исследованием по линейному программированию является работа Л.B. Kантфовича “Математические методы организации и планирования производства”, опубликованная в 1939 г. В нем дана постановка задач линейного программирования, разработан метод разрешающих множителей решения задач линейного программирования и дано его теоретическое обоснование.
Прямая задача линейного программирования является математической формулировкой проблемы составления такого плана использования различных способов производства, который позволяет получить максимальное количество однородного продукта при имеющихся в наличии ресурсах. Математическое программирование — это прикладная отрасль математики, которая является теоретической основой решения задач оптимального планирования.
Существуют следующие разделы математического программирования: линейное, параметрическое, нелинейное и динамическое программирование. Наиболее разработанным и широко применяемым разделом математического программирования является линейное программирование, целью которого служит отыскивание оптимума (max, min) заданной линейной функции при наличии ограничений в виде линейных уравнений или неравенств.
Линейное программирование – наиболее разработанный и широко применяемый раздел математического программирования (кроме того, сюда относят: целочисленное, динамическое, нелинейное, параметрическое программирование).
Это объясняется следующим:
— математические модели большого числа экономических задач линейны относительно искомых переменных;
— данный тип задач в настоящее время наиболее изучен. Для него разработаны специальные методы, с помощью которых эти задачи решаются, и соответствующие программы для ЭВМ;
— многие задачи линейного программирования, будучи решенными, нашли широкое применение;
— некоторые задачи, которые в первоначальной формулировке не являются линейными, после ряда дополнительных ограничений и допущений могут стать линейными или могут быть приведены к такой форме, что их можно решать методами линейного программирования.
Математическое программирование — это прикладная отрасль математики, которая является теоретической основой решения задач оптимального планирования.
Существуют следующие разделы математического программирования: линейное, параметрическое, нелинейное и динамическое программирование. Наиболее разработанным и широко применяемым разделом математического программирования является линейное программирование, целью которого служит отыскивание оптимума (max, min) заданной линейной функции при наличии ограничений в виде линейных уравнений или неравенств.
Линейное программирование – наиболее разработанный и широко применяемый раздел математического программирования (кроме того, сюда относят: целочисленное, динамическое, нелинейное, параметрическое программирование).
Это объясняется следующим:
— математические модели большого числа экономических задач линейны относительно искомых переменных;
— данный тип задач в настоящее время наиболее изучен. Для него разработаны специальные методы, с помощью которых эти задачи решаются, и соответствующие программы для ЭВМ;
— многие задачи линейного программирования, будучи решенными, нашли широкое применение;
— некоторые задачи, которые в первоначальной формулировке не являются линейными, после ряда дополнительных ограничений и допущений могут стать линейными или могут быть приведены к такой форме, что их можно решать методами линейного программирования. 1.4 Математическая формулировка задачи линейного программирования
Прямая задача линейного программирования является математической формулировкой. Проблемы составления такого плана использования различных способов производства позволяет получить максимальное количество однородного продукта при имеющихся в наличии ресурсах.
Математическое программирование — это прикладная отрасль математики, которая является теоретической основой решения задач оптимального планирования.
Математическим программированием принято называть науку о моделях и методах отыскания таких значений переменных некоторой целевой функции, при которых она достигает своего наибольшего или наименьшего значения в рамках поставленных ограничений (условий). Целевая функция – это математическое представление зависимости критерия оптимальности от искомых переменных.
Существуют следующие разделы математического программирования: линейное, параметрическое, нелинейное и динамическое программирование.
1.4 Математическая формулировка задачи линейного программирования
Прямая задача линейного программирования является математической формулировкой. Проблемы составления такого плана использования различных способов производства позволяет получить максимальное количество однородного продукта при имеющихся в наличии ресурсах.
Математическое программирование — это прикладная отрасль математики, которая является теоретической основой решения задач оптимального планирования.
Математическим программированием принято называть науку о моделях и методах отыскания таких значений переменных некоторой целевой функции, при которых она достигает своего наибольшего или наименьшего значения в рамках поставленных ограничений (условий). Целевая функция – это математическое представление зависимости критерия оптимальности от искомых переменных.
Существуют следующие разделы математического программирования: линейное, параметрическое, нелинейное и динамическое программирование. Наиболее разработанным и широко применяемым разделом математического программирования является линейное программирование, целью которого служит отыскивание оптимума (max, min) заданной линейной функции при наличии ограничений в виде линейных уравнений или неравенств.
Математическое выражение целевой функции и ее ограничений называется математической моделью экономической задачи.
В общем виде математическая модель задачи линейного программирования (ЛП) записывается как:
L(?x)= c_1 x_1+ c_2 x_2+?+ c_j x_j+?+ c_n x_(n )>max?? (min)?
при ограничениях:
a_11 x_1+ a_12 x_2+?+ a_1j x_j+?+ a_1n x_n=b_1,
a_21 x_1+ a_22 x_2+?+ a_2j x_j+?+ a_2n x_(n )=b_2
…………………………………………………………
a_i1 x_1+ a_i2 x_2+?+ a_ij x_j+?+ a_in x_n=b_i
…………………………………………………………
a_m1 x_1+ a_m2 x_2+?+ a_mj x_j+?+ a_mn x_n=b_m
x_j?0,i=?(1,m,j),j=?(1,n)
где xj — неизвестные; aij, bi, cj— заданные постоянные величины.
Все или некоторые уравнения системы ограничений могут быть записаны в виде неравенств.
Наиболее разработанным и широко применяемым разделом математического программирования является линейное программирование, целью которого служит отыскивание оптимума (max, min) заданной линейной функции при наличии ограничений в виде линейных уравнений или неравенств.
Математическое выражение целевой функции и ее ограничений называется математической моделью экономической задачи.
В общем виде математическая модель задачи линейного программирования (ЛП) записывается как:
L(?x)= c_1 x_1+ c_2 x_2+?+ c_j x_j+?+ c_n x_(n )>max?? (min)?
при ограничениях:
a_11 x_1+ a_12 x_2+?+ a_1j x_j+?+ a_1n x_n=b_1,
a_21 x_1+ a_22 x_2+?+ a_2j x_j+?+ a_2n x_(n )=b_2
…………………………………………………………
a_i1 x_1+ a_i2 x_2+?+ a_ij x_j+?+ a_in x_n=b_i
…………………………………………………………
a_m1 x_1+ a_m2 x_2+?+ a_mj x_j+?+ a_mn x_n=b_m
x_j?0,i=?(1,m,j),j=?(1,n)
где xj — неизвестные; aij, bi, cj— заданные постоянные величины.
Все или некоторые уравнения системы ограничений могут быть записаны в виде неравенств. n-a_ij x_j=b_i,x_i?0,i=?(1,m),j=?(1,n).
Допустимым решением (планом) зада¬чи линейного программирования называется вектор x ? = (x1, x2,…, xп), удовлетворяющий системе ограничений.
Множество допустимых решений образует область допус¬тимых решений (ОДР).
Допустимое решение, при котором целевая функция достигает своего экстремального значения, называ¬ется оптимальным решением задачи линейного программиро¬вания и обозначается ?xопт.
Иногда на xi также накладывается некоторый набор ограничений в виде равенств, но от них можно избавиться, последовательно выражая одну переменную через другие и подставляя ее во всех остальных равенствах и неравенствах (а также в функции f).
Такую задачу называют «основной» или «стандартной» в линейном программировании.
Базисное допустимое решение x ?(х1, х2,…, xr, 0, …, 0) яв¬ляется опорным решением, где r — ранг системы ограничений.
Математическая модель задачи ЛП может быть каноничес¬кой и неканонической.
Если все ограничения системы заданы урав¬нениями и переменные xj неотрицательные, то такая модель задачи называется канонической.
n-a_ij x_j=b_i,x_i?0,i=?(1,m),j=?(1,n).
Допустимым решением (планом) зада¬чи линейного программирования называется вектор x ? = (x1, x2,…, xп), удовлетворяющий системе ограничений.
Множество допустимых решений образует область допус¬тимых решений (ОДР).
Допустимое решение, при котором целевая функция достигает своего экстремального значения, называ¬ется оптимальным решением задачи линейного программиро¬вания и обозначается ?xопт.
Иногда на xi также накладывается некоторый набор ограничений в виде равенств, но от них можно избавиться, последовательно выражая одну переменную через другие и подставляя ее во всех остальных равенствах и неравенствах (а также в функции f).
Такую задачу называют «основной» или «стандартной» в линейном программировании.
Базисное допустимое решение x ?(х1, х2,…, xr, 0, …, 0) яв¬ляется опорным решением, где r — ранг системы ограничений.
Математическая модель задачи ЛП может быть каноничес¬кой и неканонической.
Если все ограничения системы заданы урав¬нениями и переменные xj неотрицательные, то такая модель задачи называется канонической. Если хотя бы одно ограничение является неравенством, то модель задачи линейного программирования является неканонической. Чтобы перейти от неканонической модели к канонической, необходимо в каждое неравенство ввести балансовую переменную xn+i. Если знак неравенства ?, то балансовая переменная вводится со знаком плюс, если знак неравенства ?, то — минус. В целевую функ¬цию балансовые переменные не вводятся.
Чтобы составить математическую модель задачи ЛП, не¬обходимо:
— ввести обозначения переменных;
— исходя из цели экономических исследований, составить целевую функцию;
— учитывая ограничения в использовании экономических показателей задачи и их количественные закономернос¬ти, записать систему ограничений.
1.5 Постановка задачи целочисленного программирования
Значительная часть задач оптимального планирования по смыслу может иметь решения только в целых числах. Такие задачи связаны с определением количества единиц неделимой продукции, например, числа станков при загрузке оборудования, численности работников в структурных подразделениях предприятия и т.
Если хотя бы одно ограничение является неравенством, то модель задачи линейного программирования является неканонической. Чтобы перейти от неканонической модели к канонической, необходимо в каждое неравенство ввести балансовую переменную xn+i. Если знак неравенства ?, то балансовая переменная вводится со знаком плюс, если знак неравенства ?, то — минус. В целевую функ¬цию балансовые переменные не вводятся.
Чтобы составить математическую модель задачи ЛП, не¬обходимо:
— ввести обозначения переменных;
— исходя из цели экономических исследований, составить целевую функцию;
— учитывая ограничения в использовании экономических показателей задачи и их количественные закономернос¬ти, записать систему ограничений.
1.5 Постановка задачи целочисленного программирования
Значительная часть задач оптимального планирования по смыслу может иметь решения только в целых числах. Такие задачи связаны с определением количества единиц неделимой продукции, например, числа станков при загрузке оборудования, численности работников в структурных подразделениях предприятия и т. д.
Такие задачи решаются методами целочисленного программирования, где общая постановка задачи линейного программирования дополняется требованием о том, чтобы найденные переменные в оптимальном плане были целыми.
Под задачей целочисленного программирования (ЦП) понимается задача, в которой все или некоторые переменные должны принимать целые значения. В том случае, когда ограничения и целевая функция задачи представляют собой линейные зависимости, задачу называют целочисленной задачей линейного программирования. В противном случае, когда хотя бы одна зависимость будет нелинейной, это будет целочисленной задачей нелинейного программирования.
Если функция и ограничения в таких задачах линейны и на переменные задачи наложено условие целочисленности, то такие задачи называются задачами линейного целочисленного программирования.
Сформулируем основную задачу линейного программирования, в которой переменные могут принимать только целые значения. В общем виде эту задачу можно записать следующим образом.
д.
Такие задачи решаются методами целочисленного программирования, где общая постановка задачи линейного программирования дополняется требованием о том, чтобы найденные переменные в оптимальном плане были целыми.
Под задачей целочисленного программирования (ЦП) понимается задача, в которой все или некоторые переменные должны принимать целые значения. В том случае, когда ограничения и целевая функция задачи представляют собой линейные зависимости, задачу называют целочисленной задачей линейного программирования. В противном случае, когда хотя бы одна зависимость будет нелинейной, это будет целочисленной задачей нелинейного программирования.
Если функция и ограничения в таких задачах линейны и на переменные задачи наложено условие целочисленности, то такие задачи называются задачами линейного целочисленного программирования.
Сформулируем основную задачу линейного программирования, в которой переменные могут принимать только целые значения. В общем виде эту задачу можно записать следующим образом. n-c_ij x_j=b_i, (i=?(1,m))
x_j?0 (j=?(1,n))
x_j-цели (j=?(1,n))
Если найти решение задачи симплексным методом, оно может быть как целочисленным, так и нет. В таком случае для нахождения оптимального плана задачи нужны специальные методы. В настоящее время есть несколько таких методов, из которых наиболее известны графический метод и метод Гомори.
Особый интерес к задачам ЦП вызван тем, что во многих практических задачах необходимо находить целочисленное решение ввиду дискретности ряда значений искомых переменных. В сфере лесного комплекса к их числу относятся следующие задачи:
задачи оптимизации раскроя;
оптимальное проектирование лесных машин и оборудования;
оптимизации системы сервиса и технического обслуживания машинно-тракторного парка;
и т.д.
Как уже отмечалось, часто задачу ЦП решают без учета условий целочисленности переменных, а затем округляют полученное решение с избытком или недостатком. Это не гарантирует получение оптимального целочисленного решения задачи.
n-c_ij x_j=b_i, (i=?(1,m))
x_j?0 (j=?(1,n))
x_j-цели (j=?(1,n))
Если найти решение задачи симплексным методом, оно может быть как целочисленным, так и нет. В таком случае для нахождения оптимального плана задачи нужны специальные методы. В настоящее время есть несколько таких методов, из которых наиболее известны графический метод и метод Гомори.
Особый интерес к задачам ЦП вызван тем, что во многих практических задачах необходимо находить целочисленное решение ввиду дискретности ряда значений искомых переменных. В сфере лесного комплекса к их числу относятся следующие задачи:
задачи оптимизации раскроя;
оптимальное проектирование лесных машин и оборудования;
оптимизации системы сервиса и технического обслуживания машинно-тракторного парка;
и т.д.
Как уже отмечалось, часто задачу ЦП решают без учета условий целочисленности переменных, а затем округляют полученное решение с избытком или недостатком. Это не гарантирует получение оптимального целочисленного решения задачи. Поэтому для нахождения оптимального решения целочисленных задач применяют специальные методы, в которых учитывается, что число возможных решений любой целочисленной задачи является конечным. Следовательно, можно рассмотреть все возможные сочетания целочисленных переменных и проверить, удовлетворяют ли они ограничениям, и из числа удовлетворяющих ограничениям, выбрать наилучшее с точки зрения целевой функции. Такой метод называют методом полного перебора. Его трудоемкость с ростом числа переменных и расширением области граничных условий значительно возрастает. Поэтому для реальных задач он неприменим.
На практике для решения реальных задач следует использовать методы, в котором все возможные альтернативы не рассматриваются. Наиболее распространенным является метод ветвей и границ.
Поэтому для нахождения оптимального решения целочисленных задач применяют специальные методы, в которых учитывается, что число возможных решений любой целочисленной задачи является конечным. Следовательно, можно рассмотреть все возможные сочетания целочисленных переменных и проверить, удовлетворяют ли они ограничениям, и из числа удовлетворяющих ограничениям, выбрать наилучшее с точки зрения целевой функции. Такой метод называют методом полного перебора. Его трудоемкость с ростом числа переменных и расширением области граничных условий значительно возрастает. Поэтому для реальных задач он неприменим.
На практике для решения реальных задач следует использовать методы, в котором все возможные альтернативы не рассматриваются. Наиболее распространенным является метод ветвей и границ.
Решатели NEOS
Ниже перечислены доступные решатели, организованные по типу проблемы. Ан
дополнительный список доступен для поиска с помощью Solver, если вы предпочитаете.
Если вам нужна помощь в выборе решателя, обратитесь к Дерево оптимизации руководства НЕОС. Затем выбор решателя определяет доступные параметры ввода для определения задачи оптимизации.
Каждый решатель содержит примеры задач и справочную информацию о решателе. Обязательно отправьте образец задачи, чтобы понять, как ее отправить. проблемы с оптимизацией для NEOS. Если у вас возникнут проблемы, обратитесь к Часто задаваемые вопросы по серверу NEOS, или свяжитесь с нами, нажав на кнопку Комментарии и вопросы ссылка внизу страницы.
- Тип проблемы
- Решатель
- Просмотр очереди заданий
- Просмотр результатов задания / Завершение задания
- ПРЕОБРАЗОВАТЬ [ГАМС]
- Домино [jpeg]
- ЕСМ [CSV] [один_текст] [zip]
- Фишверкс [CSV]
- Приложение для планирования [JSON]
- Л-БФГС-Б [АМПЛ]
- БикМак [РАЗДЕЛЬНЫЙ]
- согласие [TSP]
- Вязание [АМПЛ]
- МИЛЬ [ГАМС]
- НЛПЭК [ГАМС]
- ПУТЬ [АМПЛ] [ГАМС]
- Германия [ГАМС]
- ДЖЕМ [ГАМС]
- АНТИГОНА [ГАМС]
- АСА [АМПЛ]
- БАРОН [АМПЛ] [ГАМС]
- Куэнн [АМПЛ] [ГАМС]
- значков [АМПЛ]
- ЛГО [АМПЛ]
- ЛИНДОГлобал [АМПЛ] [ГАМС]
- ОКТЕРАКТ [АМПЛ] [ГАМС] [Нидерланды]
- ПГАПакет [АМПЛ]
- PSтеплый [АМПЛ]
- РАПОСа [АМПЛ]
- код [АМПЛ] [КОМПЛЕКС] [ГАМС] [MPS] [ОСИЛ] [ЗИМПЛ]
- РЕЛАКС4 [ДИМАКС] [РЕЛАКС4]
- ударов в минуту [АМПЛ] [LP] [MPS] [QPS]
- клп [MPS]
- КОПТ [АМПЛ] [ГАМС] [LP] [MPS] [Нидерланды]
- КОМПЛЕКС [АМПЛ] [ГАМС] [LP] [MPS] [Нидерланды]
- ФИКО-Экспресс [АМПЛ] [ГАМС] [МОЗЕЛЬ] [MPS] [Нидерланды]
- Гуроби [АМПЛ] [ГАМС] [LP] [MPS] [Нидерланды]
- Высокие [АМПЛ] [ГАМС] [LP] [MPS]
- МОСЕК [АМПЛ] [ГАМС] [LP] [MPS] [Нидерланды]
- ОКТЕРАКТ [АМПЛ] [LP] [MPS] [Нидерланды]
- ООКП [АМПЛ]
- Соплекс 80 бит [LP] [MPS]
- фильтрМПЭК [АМПЛ]
- Вязание [АМПЛ] [ГАМС]
- НЛПЭК [ГАМС]
- КВС [АМПЛ] [ГАМС] [MPS]
- КОПТ [АМПЛ] [ГАМС] [LP] [MPS] [Нидерланды]
- КОМПЛЕКС [АМПЛ] [ГАМС] [LP] [MPS] [Нидерланды]
- feaspump [АМПЛ] [КОМПЛЕКС] [MPS]
- ФИКО-Экспресс [АМПЛ] [ГАМС] [МОЗЕЛЬ] [MPS] [Нидерланды]
- Гуроби [АМПЛ] [ГАМС] [LP] [MPS] [Нидерланды]
- Высокие [АМПЛ] [ГАМС] [LP] [MPS]
- МИНТО [АМПЛ]
- МОСЕК [АМПЛ] [ГАМС] [LP] [MPS] [Нидерланды]
- ОКТЕРАКТ [АМПЛ] [LP] [MPS] [Нидерланды]
- прокси [КОМПЛЕКС] [MPS]
- qsopt_ex [АМПЛ] [LP] [MPS]
- код [АМПЛ] [КОМПЛЕКС] [ГАМС] [MPS] [ОСИЛ] [ЗИМПЛ]
- СИМФОНИЯ [MPS]
- АльфаЭКП [ГАМС]
- АНТИГОНА [ГАМС]
- БАРОН [АМПЛ] [ГАМС]
- Бонмин [АМПЛ] [ГАМС]
- Куэнн [АМПЛ] [ГАМС]
- ДИКОПТ [ГАМС]
- ФилМИНТ [АМПЛ]
- Вязание [АМПЛ] [ГАМС]
- ЛИНДОГлобал [АМПЛ] [ГАМС]
- МИНЛП [АМПЛ]
- ОКТЕРАКТ [АМПЛ] [ГАМС] [Нидерланды]
- СББ [ГАМС]
- код [АМПЛ] [КОМПЛЕКС] [ГАМС] [MPS] [ОСИЛ] [ЗИМПЛ]
- ВЫСТРЕЛ [ГАМС]
- МУСКОД-II [АМПЛ]
- кондор [АМПЛ]
- АНТИГОНА [ГАМС]
- КОНОПТ [АМПЛ] [ГАМС]
- ФИКО-Экспресс [МОЗЕЛЬ]
- фильтр [АМПЛ]
- Ипопт [АМПЛ] [ГАМС] [Нидерланды]
- Вязание [АМПЛ] [ГАМС] [Нидерланды]
- ЛАНСЕЛОТ [АМПЛ]
- ЛОКО [АМПЛ]
- МИНОС [АМПЛ] [ГАМС]
- ОКТЕРАКТ [АМПЛ] [ГАМС] [Нидерланды]
- ПАТНЛП [ГАМС]
- СНИМОК [АМПЛ] [ГАМС] [Нидерланды]
- КОПТ [MPS]
- КОМПЛЕКС [АМПЛ] [ГАМС] [MPS] [Нидерланды]
- ФИКО-Экспресс [АМПЛ] [ГАМС] [МОЗЕЛЬ] [MPS] [Нидерланды]
- Гуроби [АМПЛ] [ГАМС] [MPS] [Нидерланды]
- МОСЕК [КБФ] [ГАМС] [MPS]
- код [АМПЛ] [КОМПЛЕКС] [MPS]
- нсипс [АМПЛ]
- csdp [MATLAB_BINARY] [SPARSE_SDPA]
- мосек [MATLAB_BINARY] [SPARSE_SDPA]
- пенсдп [MATLAB_BINARY] [SPARSE_SDPA]
- scipsdp [SPARSE_SDPA]
- СДПА [MATLAB_BINARY] [SPARSE_SDPA]
- сдплр [СДПЛР] [SPARSE_SDPA]
- сдпт3 [MATLAB_BINARY] [SPARSE_SDPA]
- седуми [MATLAB_BINARY] [SPARSE_SDPA]
- бнбс [SMPS]
- ддсип [LP] [MPS]
- ДСП [SMPS]
- сд [SMPS]
Целочисленное программирование – Оптимизация онлайн
Многоцелевые целочисленные программы (MOIP) одновременно оптимизируют несколько целевых функций по набору линейных ограничений и целочисленных переменных. В этой статье мы представляем непрерывную релаксацию выпуклой оболочки и лагранжеву релаксацию для MOIP и исследуем взаимосвязь между ними. Релаксация выпуклой оболочки точна на поддерживаемых решениях, т. Е. На тех, которые можно получить путем скаляризации … Читать далее
Вдохновленные приложениями в облачных вычислениях, мы изучаем временную проблему упаковки корзины с заданиями, которые занимают половину емкости корзины. Экземпляр задается набором заданий, каждое из которых имеет время начала и окончания, в течение которых оно должно быть обработано, т. е. назначено ячейке. Мусорный бак может вместить два рабочих места … Читать далее
Экземпляр задается набором заданий, каждое из которых имеет время начала и окончания, в течение которых оно должно быть обработано, т. е. назначено ячейке. Мусорный бак может вместить два рабочих места … Читать далее
Руководствуясь важностью социальной устойчивости как решающего элемента в каскадном уходе пользователей из социальной сети, мы изучаем определение наибольшего расслабленного варианта связанного подграфа на основе степеней: проблема k-core с максимальным закреплением. Учитывая граф G = (V, E) и целые числа k и b, задача k-ядра с максимальной привязанностью стремится найти наибольшее… Читать далее
Мы рассматриваем проблему в контексте энергоэффективного расписания метрополитена, в котором существующий проект расписания улучшается за счет незначительного изменения времени отправления и движения. На практике синхронизация между ускоряющимися и тормозящими поездами для использования рекуперативного торможения играет важную роль для энергоэффективности расписания. Поскольку отклонения от запланированного графика … Читать дальше
Мы рассматриваем упаковку двухгистограмм (2-BCPP), недавнюю задачу комбинаторной оптимизации, цель которой состоит в том, чтобы упаковать набор одномерных элементов в минимальное количество ячеек. В отличие от хорошо известной проблемы упаковки в контейнеры, пары предметов группируются в гистограммы, и решение возможно только в том случае, если первое и… Читать далее
В отличие от хорошо известной проблемы упаковки в контейнеры, пары предметов группируются в гистограммы, и решение возможно только в том случае, если первое и… Читать далее
Хотя большинство методов решения задач оптимизации со смешанными целыми числами вычисляют единственное оптимальное решение, разнообразный набор почти оптимальных решений часто может быть более полезным. Мы представляем новый метод поиска набора разнообразных решений, подчеркивая разнообразие в поиске решений, близких к оптимальным. В частности, в рамках схемы ветвей и границ мы исследуем параметризованный выбор узлов… Подробнее
Задача планирования проекта с ограниченными ресурсами с гибкой структурой проекта (RCPSP-PS) является обобщением проблемы планирования проекта с ограниченными ресурсами (RCPSP). Цель RCPSP-PS состоит в том, чтобы найти минимальное расписание выполнения с учетом приоритета и ограничений ресурсов, при этом необходимо выполнить только подмножество всех действий. Представляем общий … Читать дальше 9{N-p}_+\}$, в котором подзадача, возникающая при фиксированном $x$, имеет специальную структуру. Одним из таких примеров является задача размещения мощностей с единым источником, в которой релаксация линейного программирования подзадачи представляет собой транспортировку … Читать далее
уже более 50 лет находится в центре работы энергосистемы. Однако эту проблему нельзя считать решенной из-за ее масштабности и сложности. Сегодня операторы полагаются на готовые решения для оптимизации, чтобы решить эту сложную проблему, и часто прибегают к упрощениям, чтобы сделать проблему более понятной и решаемой в … Подробнее
Мы рассматриваем реальную проблему мультимодальных грузовых перевозок, которая возникает в организации по производству продовольственного зерна в Индии. Эта задача направлена на то, чтобы удовлетворить спрос на набор складов для различных видов продовольственного зерна из другого набора складов с избыточными количествами в течение нескольких периодов времени железнодорожным и автомобильным транспортом, при этом минимизируя … Читать далее
Оптимизация с помощью Python — настоящий Python
Линейное программирование — это набор методов, используемых в математическое программирование , иногда называемое математической оптимизацией, для решения систем линейных уравнений и неравенств при максимизации или минимизации некоторой линейной функции. Это важно в таких областях, как научные вычисления, экономика, технические науки, производство, транспорт, военные, менеджмент, энергетика и так далее.
Это важно в таких областях, как научные вычисления, экономика, технические науки, производство, транспорт, военные, менеджмент, энергетика и так далее.
Экосистема Python предлагает несколько всеобъемлющих и мощных инструментов для линейного программирования. Вы можете выбирать между простыми и сложными инструментами, а также между бесплатными и коммерческими. Все зависит от ваших потребностей.
В этом уроке вы узнаете:
- Что такое линейное программирование и почему оно важно
- Какие инструменты Python подходят для линейного программирования
- Как построить модель линейного программирования на Python
- Как решить задачу линейного программирования с помощью Python
Сначала вы изучите основы линейного программирования. Затем вы узнаете, как реализовать методы линейного программирования в Python. Наконец, вы познакомитесь с ресурсами и библиотеками, которые помогут вам в дальнейшем развитии линейного программирования.
Бесплатный бонус: 5 Thoughts On Python Mastery, бесплатный курс для Python-разработчиков, который показывает вам дорожную карту и образ мышления, которые вам понадобятся, чтобы вывести свои навыки Python на новый уровень.
Объяснение линейного программирования
В этом разделе вы познакомитесь с основами линейного программирования и родственной дисциплины — линейного программирования смешанных целых чисел. В следующем разделе вы увидите несколько практических примеров линейного программирования. Позже вы будете решать задачи линейного программирования и смешанно-целочисленного линейного программирования с помощью Python.
Удалить рекламу
Что такое линейное программирование?
Представьте, что у вас есть система линейных уравнений и неравенств. Такие системы часто имеют множество возможных решений. Линейное программирование представляет собой набор математических и вычислительных средств, позволяющих найти частное решение данной системы, соответствующее максимуму или минимуму какой-либо другой линейной функции.
Что такое смешанно-целочисленное линейное программирование?
Смешанное целочисленное линейное программирование является расширением линейного программирования. Он обрабатывает проблемы, в которых по крайней мере одна переменная принимает дискретное целое число, а не непрерывное значение. Хотя задачи со смешанными целыми числами на первый взгляд похожи на задачи с непрерывными переменными, они предлагают значительные преимущества с точки зрения гибкости и точности.
Целочисленные переменные важны для правильного представления величин, естественно выраженных целыми числами, таких как количество произведенных самолетов или количество обслуженных клиентов.
Особенно важным типом целочисленной переменной является двоичная переменная . Он может принимать только значения ноль или единица и полезен при принятии решений «да» или «нет», например, следует ли строить завод или включать или выключать машину. Вы также можете использовать их для имитации логических ограничений.
Вы также можете использовать их для имитации логических ограничений.
Почему важно линейное программирование?
Линейное программирование — это фундаментальный метод оптимизации, который десятилетиями использовался в наукоемких и математических областях. Он точен, относительно быстр и подходит для целого ряда практических приложений.
Смешанно-целочисленное линейное программирование позволяет преодолеть многие ограничения линейного программирования. Вы можете аппроксимировать нелинейные функции кусочно-линейными функциями, использовать полунепрерывные переменные, моделировать логические ограничения и многое другое. Это инструмент, требующий значительных вычислительных ресурсов, но прогресс в компьютерном оборудовании и программном обеспечении делает его более применимым с каждым днем.
Часто, когда люди пытаются сформулировать и решить задачу оптимизации, первый вопрос заключается в том, могут ли они применить линейное программирование или смешанно-целочисленное линейное программирование.
Некоторые примеры использования линейного программирования и линейного программирования со смешанными целыми числами проиллюстрированы в следующих статьях:
- Практические примеры оптимизации Gurobi
- Пять областей применения методов линейного программирования
Значение линейного программирования, и особенно линейного программирования смешанных целых чисел, с течением времени возрастало по мере того, как компьютеры становились более производительными, алгоритмы совершенствовались, а более удобные программные решения становились доступными.
Линейное программирование с помощью Python
Основной метод решения задач линейного программирования называется симплекс-метод , который имеет несколько вариантов. Другим популярным подходом является метод внутренних точек .
Задачи линейного программирования со смешанными целыми числами решаются с помощью более сложных и ресурсоемких методов, таких как метод ветвей и границ , в котором используется линейное программирование. Некоторые варианты этого метода метод ветвей и отсечений , который включает использование секущих плоскостей, и метод ветвей и цен .
Некоторые варианты этого метода метод ветвей и отсечений , который включает использование секущих плоскостей, и метод ветвей и цен .
Существует несколько подходящих и хорошо известных инструментов Python для линейного программирования и линейного программирования смешанных целых чисел. Некоторые из них с открытым исходным кодом, а другие являются проприетарными. Нужен ли вам бесплатный или платный инструмент, зависит от размера и сложности вашей проблемы, а также от потребности в скорости и гибкости.
Стоит отметить, что почти все широко используемые библиотеки линейного программирования и смешанно-целочисленного линейного программирования являются родными и написаны на Fortran, C или C++. Это связано с тем, что линейное программирование требует интенсивной вычислительной работы с (часто большими) матрицами. Такие библиотеки называются решатели . Инструменты Python — это просто оболочки для решателей.
Python подходит для создания оболочек нативных библиотек, поскольку хорошо работает с C/C++. Для этого руководства вам не понадобится язык C/C++ (или Fortran), но если вы хотите узнать больше об этой замечательной функции, ознакомьтесь со следующими ресурсами:
Для этого руководства вам не понадобится язык C/C++ (или Fortran), но если вы хотите узнать больше об этой замечательной функции, ознакомьтесь со следующими ресурсами:
- Создание модуля расширения Python C
- Внутреннее устройство CPython
- Расширение Python с помощью C или C++
По сути, когда вы определяете и решаете модель, вы используете функции или методы Python для вызова низкоуровневой библиотеки, которая выполняет реальную работу по оптимизации и возвращает решение вашему объекту Python.
Несколько бесплатных библиотек Python специализированы для взаимодействия с решателями линейного или смешанно-целочисленного линейного программирования:
- Оптимизация SciPy и поиск корней
- Пульпа
- Пиомо
- CVXOPT
В этом руководстве вы будете использовать SciPy и PuLP для определения и решения задач линейного программирования.
Удалить рекламу
Примеры линейного программирования
В этом разделе вы увидите два примера задач линейного программирования:
- Небольшая задача, иллюстрирующая, что такое линейное программирование
- Практическая задача, связанная с распределением ресурсов, которая иллюстрирует концепции линейного программирования в реальном сценарии
В следующем разделе вы будете использовать Python для решения этих двух задач.
Небольшая задача линейного программирования
Рассмотрим следующую задачу линейного программирования:
Нужно найти x и y такие, что выполняются красное, синее и желтое неравенства, а также неравенства x ≥ 0 и y ≥ 0. При этом ваше решение должно соответствовать максимально возможному значению z .
Независимые переменные, которые вам нужно найти — в данном случае x и y — называются переменными решения . Функция переменных решения, которую необходимо максимизировать или минимизировать, — в данном случае z — называется целевой функцией , функцией стоимости или просто целью . Неравенства, которые вам необходимо удовлетворить, называются ограничениями неравенства . Вы также можете иметь уравнения среди ограничений, называемых ограничениями равенства .
Вот как вы можете визуализировать проблему:
Красная линия представляет функцию 2 x + y = 20, а красная область над ним показывает, где выполняется красное неравенство , а не . Точно так же синяя линия представляет собой функцию −4 x + 5 y = 10, а синяя область запрещена, поскольку нарушает синее неравенство. Желтая линия — это — 90 540 x 90 541 + 2 90 540 y 90 541 = —2, а желтая область под ней — это место, где желтое неравенство неверно.
Точно так же синяя линия представляет собой функцию −4 x + 5 y = 10, а синяя область запрещена, поскольку нарушает синее неравенство. Желтая линия — это — 90 540 x 90 541 + 2 90 540 y 90 541 = —2, а желтая область под ней — это место, где желтое неравенство неверно.
Если не учитывать красную, синюю и желтую области, останется только серая область. Каждая точка серой области удовлетворяет всем ограничениям и является потенциальным решением проблемы. Эта область называется допустимая область , а ее точки допустимые решения . В этом случае существует бесконечное количество возможных решений.
Вы хотите максимизировать z . Допустимое решение, соответствующее максимальному z , является оптимальным решением . Если бы вместо этого вы пытались минимизировать целевую функцию, то оптимальное решение соответствовало бы ее допустимому минимуму.
Обратите внимание, что z является линейным. Вы можете представить его как плоскость в трехмерном пространстве. Вот почему оптимальное решение должно быть на вершина или угол допустимой области. В этом случае оптимальным решением будет точка пересечения красной и синей линий, как вы увидите позже.
Вы можете представить его как плоскость в трехмерном пространстве. Вот почему оптимальное решение должно быть на вершина или угол допустимой области. В этом случае оптимальным решением будет точка пересечения красной и синей линий, как вы увидите позже.
Иногда целое ребро допустимой области или даже вся область может соответствовать одному и тому же значению z . В этом случае у вас есть много оптимальных решений.
Теперь вы готовы расширить задачу дополнительным ограничением равенства, показанным зеленым цветом:
Уравнение − x + 5 y = 15, написанное зеленым цветом, является новым. Это ограничение равенства. Вы можете визуализировать это, добавив соответствующую зеленую линию к предыдущему изображению:
Теперь решение должно удовлетворять зеленому равенству, поэтому допустимая область больше не является всей серой областью. Это часть зеленой линии, проходящая через серую область от точки пересечения с синей линией до точки пересечения с красной линией. Последний пункт является решением.
Последний пункт является решением.
Если вы вставите требование, чтобы все значения x должны быть целыми числами, тогда вы получите смешанно-целочисленную задачу линейного программирования, и набор допустимых решений снова изменится:
У вас больше нет зеленой линии, только точки вдоль линии, где значение x является целым числом. Допустимые решения — это зеленые точки на сером фоне, а оптимальное в данном случае находится ближе всего к красной линии.
Эти три примера иллюстрируют разрешимых задач линейного программирования , потому что они имеют ограниченные допустимые области и конечные решения.
Удалить рекламу
Неразрешимая задача линейного программирования
Задача линейного программирования неразрешима , если она не имеет решения. Обычно это происходит, когда ни одно решение не может удовлетворить сразу всем ограничениям.
Например, рассмотрим, что произойдет, если вы добавите ограничение x + y ≤ −1. Тогда по крайней мере одна из переменных решения ( x или y ) должен быть отрицательным. Это противоречит заданным ограничениям x ≥ 0 и y ≥ 0. Такая система не имеет допустимого решения, поэтому она называется недопустимой.
Другим примером может быть добавление второго ограничения равенства параллельно зеленой линии. У этих двух линий не будет общей точки, поэтому не будет решения, удовлетворяющего обоим ограничениям.
Неограниченная задача линейного программирования
Задача линейного программирования равна неограниченный , если его допустимая область не ограничена и решение не является конечным. Это означает, что по крайней мере одна из ваших переменных не ограничена и может достигать положительной или отрицательной бесконечности, что также делает цель бесконечной.
Например, предположим, что вы берете исходную задачу, описанную выше, и отбрасываете красные и желтые ограничения. Удаление ограничений из проблемы называется ослаблением проблемы. В таком случае 90 540 x 90 541 и 90 540 y 90 541 не будут ограничены с положительной стороны. Вы могли бы увеличить их до положительной бесконечности, получив бесконечно большое число 9.0540 z значение.
Удаление ограничений из проблемы называется ослаблением проблемы. В таком случае 90 540 x 90 541 и 90 540 y 90 541 не будут ограничены с положительной стороны. Вы могли бы увеличить их до положительной бесконечности, получив бесконечно большое число 9.0540 z значение.
Проблема распределения ресурсов
В предыдущих разделах вы рассмотрели абстрактную задачу линейного программирования, которая не была привязана к какому-либо реальному приложению. В этом подразделе вы найдете более конкретную и практическую проблему оптимизации, связанную с распределением ресурсов в производстве.
Предположим, что фабрика производит четыре различных продукта, и ежедневное количество первого продукта составляет 90 540 x 90 541 ₁, а количество второго продукта составляет x ₂ и так далее. Цель состоит в том, чтобы определить максимизирующий прибыль ежедневный объем производства каждого продукта, принимая во внимание следующие условия:
Прибыль на единицу продукта составляет 20, 12, 40 и 25 долларов для первого, второго, третьего и четвертого продукта соответственно.

Из-за нехватки рабочей силы общее количество единиц, производимых в день, не может превышать пятидесяти.
На каждую единицу первого продукта расходуется три единицы сырья А. Для каждой единицы второго продукта требуется две единицы сырья А и одна единица сырья В. Для каждой единицы третьего продукта требуется одна единица А и две единицы В. Наконец, для каждой единицы четвертого продукта требуется три единицы сырья. ед. Б.
Из-за ограничений по транспортировке и хранению фабрика может потреблять до ста единиц сырья А и девяноста единиц сырья В в день.
Математическая модель может быть определена следующим образом:
Целевая функция (прибыль) определяется в условии 1. Ограничение по рабочей силе следует из условия 2. Ограничения на сырье А и В могут быть получены из условий 3 и 4 путем суммирования потребностей в сырье для каждого продукта.
Наконец, количество продуктов не может быть отрицательным, поэтому все переменные решения должны быть больше или равны нулю.
В отличие от предыдущего примера, вы не можете удобно визуализировать этот пример, потому что он имеет четыре переменные решения. Однако принципы остаются неизменными независимо от размерности задачи.
Реализация линейного программирования Python
В этом руководстве вы будете использовать два пакета Python для решения задачи линейного программирования, описанной выше:
- SciPy — это пакет общего назначения для научных вычислений с помощью Python.
- PuLP — это API линейного программирования Python для определения задач и вызова внешних решателей.
SciPy легко настроить. После установки у вас будет все необходимое для запуска. Его подпакет scipy.optimize можно использовать как для линейной, так и для нелинейной оптимизации.
PuLP позволяет выбирать решатели и формулировать задачи более естественным образом. Решатель по умолчанию, используемый PuLP, — это COIN-OR Branch and Cut Solver (CBC). Он подключен к решателю линейного программирования COIN-OR (CLP) для линейной релаксации и библиотеке генератора разрезов COIN-OR (CGL) для генерации разрезов.
Он подключен к решателю линейного программирования COIN-OR (CLP) для линейной релаксации и библиотеке генератора разрезов COIN-OR (CGL) для генерации разрезов.
Еще одним отличным решателем с открытым исходным кодом является GNU Linear Programming Kit (GLPK). Некоторыми хорошо известными и очень мощными коммерческими и проприетарными решениями являются Gurobi, CPLEX и XPRESS.
Помимо обеспечения гибкости при определении задач и возможности запуска различных решателей, PuLP проще в использовании, чем такие альтернативы, как Pyomo или CVXOPT, для освоения которых требуется больше времени и усилий.
Удаление рекламы
Установка SciPy и PuLP
Чтобы следовать этому руководству, вам необходимо установить SciPy и PuLP. В приведенных ниже примерах используется версия 1.4.1 SciPy и версия 2.1 PuLP.
Вы можете установить оба, используя pip :
$ python -m pip install -U "scipy==1.4.*" "pulp==2.1"
Возможно, вам потребуется запустить Pulptest или sudo Pulptest , чтобы включить решатели по умолчанию для PuLP, особенно если вы используете Linux или Mac:
$ тест пульпы
При желании вы можете загрузить, установить и использовать GLPK. Это бесплатное приложение с открытым исходным кодом, которое работает на Windows, MacOS и Linux. Позже в этом руководстве вы увидите, как использовать GLPK (в дополнение к CBC) с PuLP.
В Windows можно скачать архивы и запустить установочные файлы.
В MacOS вы можете использовать Homebrew:
$ варить установить glpk
В Debian и Ubuntu используйте apt для установки glpk и glpk-utils :
$ sudo apt установить glpk glpk-utils
В Fedora используйте dnf с glpk-utils :
$ sudo dnf установить glpk-utils
Вы также можете найти conda полезным для установки GLPK:
$ conda install -c conda-forge glpk
После завершения установки вы можете проверить версию GLPK:
$ glpsol --версия
Дополнительную информацию см. в руководствах GLPK по установке с помощью исполняемых файлов Windows и пакетов Linux.
в руководствах GLPK по установке с помощью исполняемых файлов Windows и пакетов Linux.
Использование SciPy
В этом разделе вы узнаете, как использовать библиотеку оптимизации и поиска корня SciPy для линейного программирования.
Чтобы определить и решить проблемы оптимизации с помощью SciPy, вам необходимо импортировать scipy.optimize.linprog() :
>>>
>>> из scipy.optimize import linprog
Теперь, когда вы импортировали linprog() , вы можете начать оптимизацию.
Пример 1
Давайте сначала решим задачу линейного программирования сверху:
linprog() решает только задачи минимизации (не максимизации) и не допускает ограничений неравенства со знаком больше или равно (≥). Чтобы обойти эти проблемы, вам нужно изменить свою проблему перед началом оптимизации:
- Вместо максимизации z = x + 2 y можно минимизировать его отрицательное значение (− z = − х − 2 y).

- Вместо знака больше или равно вы можете умножить желтое неравенство на −1 и получить противоположное знаку меньше или равно (≤).
После внесения этих изменений вы получаете новую систему:
Эта система эквивалентна исходной и будет иметь такое же решение. Единственная причина применить эти изменения — преодолеть ограничения SciPy, связанные с постановкой задачи.
Следующим шагом является определение входных значений:
>>>
>>> объект = [-1, -2] >>> # ─┬ ─┬ >>> # │ └┤ Коэффициент для y >>> # └────┤ Коэффициент для x >>> lhs_ineq = [[ 2, 1], # Красное ограничение слева ... [-4, 5], # Синее ограничение слева ... [ 1, -2]] # Желтое ограничение слева >>> rhs_ineq = [20, # Красное ограничение справа ... 10, # Синее ограничение справа ... 2] # Желтая правая сторона ограничения >>> lhs_eq = [[-1, 5]] # Зеленое ограничение слева >>> rhs_eq = [15] # Зеленое ограничение справа
Вы помещаете значения из системы выше в соответствующие списки, кортежи или массивы NumPy:
-
objсодержит коэффициенты целевой функции.
-
lhs_ineqсодержит левые коэффициенты из ограничений неравенства (красный, синий и желтый). -
rhs_ineqсодержит правые коэффициенты из ограничений неравенства (красного, синего и желтого). -
lhs_eqсодержит левые коэффициенты ограничения равенства (зеленого). -
rhs_eqсодержит правые коэффициенты ограничения равенства (зеленого).
Примечание: Обратите внимание на порядок строк и столбцов!
Порядок строк для левой и правой сторон ограничений должен быть одинаковым. Каждая строка представляет одно ограничение.
Порядок коэффициентов целевой функции и левых частей ограничений должен совпадать. Каждый столбец соответствует одной переменной решения.
Следующим шагом является определение границ для каждой переменной в том же порядке, что и коэффициенты. В данном случае они оба находятся между нулем и положительной бесконечностью:
.
>>>
>>> bnd = [(0, float("inf")), # Границы x
... (0, float("inf"))] # Границы y
Этот оператор является избыточным, поскольку linprog() использует эти границы (от нуля до положительной бесконечности) по умолчанию.
Примечание: Вместо float("inf") , вы можете использовать math.inf , numpy.inf или scipy.inf .
Наконец, пришло время оптимизировать и решить интересующую вас проблему. Вы можете сделать это с помощью linprog() :
>>>
>>> opt = linprog(c=obj, A_ub=lhs_ineq, b_ub=rhs_ineq,
... A_eq=lhs_eq, b_eq=rhs_eq, bounds=bnd,
... метод = "пересмотренный симплекс")
>>> выбрать
против: массив ([0.])
весело: -16.818181818181817
сообщение: «Оптимизация успешно завершена».
нит: 3
слабина: массив ([ 0. , 18.18181818, 3.36363636])
статус: 0
успех: правда
х: массив ([7. 72727273, 4.54545455])
72727273, 4.54545455])
Параметр c относится к коэффициентам целевой функции. A_ub и b_ub связаны с коэффициентами из левой и правой частей ограничений неравенства соответственно. Аналогично, A_eq и b_eq относятся к ограничениям равенства. Вы можете использовать границ , чтобы задать нижнюю и верхнюю границы для переменных решения.
Вы можете использовать параметр , метод , чтобы определить метод линейного программирования, который вы хотите использовать. Есть три варианта:
-
method="interior-point"выбирает метод внутренней точки. Этот параметр установлен по умолчанию. -
method="пересмотренный симплекс"выбирает пересмотренный двухфазный симплексный метод. -
method="simplex"выбирает устаревший двухфазный симплексный метод.
linprog() возвращает структуру данных со следующими атрибутами:
.— остатки ограничений равенства. кон
кон .fun— оптимальное значение целевой функции (если оно найдено)..message— статус решения..nit— количество итераций, необходимых для завершения вычисления..slack— это значения переменных резерва или разница между значениями левой и правой частей ограничений..status— целое число от0до4, которое показывает состояние решения, например0, когда оптимальное решение найдено..success— логическое значение, показывающее, найдено ли оптимальное решение..x— это массив NumPy, содержащий оптимальные значения переменных решения.
Вы можете получить доступ к этим значениям отдельно:
>>>
>>> опт.удовольствие -16,818181818181817 >>> опт.успех Истинный >>> опт.х массив ([7.72727273, 4.54545455])
Вот как вы получаете результаты оптимизации. Вы также можете показать их графически:
Как обсуждалось ранее, оптимальные решения задач линейного программирования лежат в вершинах допустимых областей. В этом случае возможная область — это только часть зеленой линии между синей и красной линиями. Оптимальным решением является зеленый квадрат, представляющий собой точку пересечения зеленой и красной линий.
Если вы хотите исключить ограничение равенства (зеленый), просто удалите параметры A_eq и b_eq из вызова linprog() :
>>>
>>> opt = linprog(c=obj, A_ub=lhs_ineq, b_ub=rhs_ineq, bounds=bnd,
... метод = "пересмотренный симплекс")
>>> выбрать
против: массив ([], dtype = float64)
весело: -20. 714285714285715
сообщение: «Оптимизация успешно завершена».
нит: 2
слабина: массив([0. , 0. , 9.85714286])
статус: 0
успех: правда
х: массив ([6.42857143, 7.14285714]))
714285714285715
сообщение: «Оптимизация успешно завершена».
нит: 2
слабина: массив([0. , 0. , 9.85714286])
статус: 0
успех: правда
х: массив ([6.42857143, 7.14285714]))
Решение отличается от предыдущего случая. Вы можете увидеть это на графике:
В этом примере оптимальным решением является фиолетовая вершина допустимой (серой) области, где пересекаются красные и синие ограничения. Другие вершины, например желтая, имеют более высокие значения целевой функции.
Пример 2
Вы можете использовать SciPy для решения проблемы распределения ресурсов, указанной в предыдущем разделе:
Как и в предыдущем примере, вам нужно извлечь необходимые векторы и матрицу из задачи выше, передать их в качестве аргументов в .linprog() и получить результаты:
>>>
>>> obj = [-20, -12, -40, -25] >>> lhs_ineq = [[1, 1, 1, 1], # Рекруты ... [3, 2, 1, 0], # Материал А ... [0, 1, 2, 3]] # Материал B >>> rhs_ineq = [ 50, # Рекруты ... 100, # Материал А ... 90] # Материал В >>> opt = linprog(c=obj, A_ub=lhs_ineq, b_ub=rhs_ineq, ... метод = "пересмотренный симплекс") >>> выбрать против: массив ([], dtype = float64) удовольствие: -1900.0 сообщение: «Оптимизация успешно завершена». нит: 2 слабина: массив ([ 0., 40., 0.]) статус: 0 успех: правда х: массив ([ 5., 0., 45., 0.])
Результат говорит о том, что максимальная прибыль составляет 1900 и соответствует х ₁ = 5 и х ₃ = 45. Вторую и четвертую продукцию при данных условиях производить невыгодно. Здесь можно сделать несколько интересных выводов:
Третий продукт приносит наибольшую прибыль на единицу, поэтому фабрика будет производить его больше всего.
Первый резерв равен
0, что означает, что значения левой и правой частей ограничения рабочей силы (первого) одинаковы. Фабрика производит50штук в сутки, и это ее полная мощность.
Второй резерв равен
40, потому что фабрика потребляет 60 единиц сырья А (15 единиц для первого продукта плюс 45 единиц для третьего) из потенциального100шт.Третий резерв равен
0, что означает, что фабрика потребляет все90единиц сырья B. Все это количество потребляется для третьего продукта. Поэтому фабрика вообще не может произвести второй или четвертый продукт и не может произвести более45единиц третьего продукта. Не хватает сырья B.
опт.статус это 0 и опт.успех равно True , что указывает на то, что задача оптимизации была успешно решена с помощью оптимального допустимого решения.
SciPy полезны в основном для небольших задач. Для более крупных и сложных задач вам могут подойти другие библиотеки по следующим причинам:
SciPy не может запускать различные внешние решатели.

SciPy не может работать с целочисленными переменными решения.
SciPy не предоставляет классы или функции, облегчающие построение моделей. Вы должны определить массивы и матрицы, что может быть утомительной и подверженной ошибкам задачей для больших задач.
SciPy не позволяет напрямую определять задачи максимизации. Вы должны преобразовать их в задачи минимизации.
SciPy не позволяет вам определять ограничения, используя знак «больше или равно» напрямую. Вместо этого вы должны использовать меньше или равно.
К счастью, экосистема Python предлагает несколько альтернативных решений для линейного программирования, которые очень полезны для решения более крупных задач. Одним из них является PuLP, который вы увидите в действии в следующем разделе.
Удаление рекламы
Использование PuLP
PuLP имеет более удобный API линейного программирования, чем SciPy. Вам не нужно математически модифицировать вашу задачу или использовать векторы и матрицы. Все чище и меньше подвержено ошибкам.
Вам не нужно математически модифицировать вашу задачу или использовать векторы и матрицы. Все чище и меньше подвержено ошибкам.
Как обычно, вы начинаете с импорта того, что вам нужно:
из импорта целлюлозы LpMaximize, LpProblem, LpStatus, lpSum, LpVariable
Теперь, когда вы импортировали PuLP, вы можете решить свои проблемы.
Пример 1
Теперь вы решите эту систему с помощью PuLP:
Первым шагом является инициализация экземпляра LpProblem для представления вашей модели:
# Создать модель модель = LpProblem (имя = «маленькая проблема», смысл = LpMaximize)
Вы используете параметр sense , чтобы выбрать, следует ли выполнять минимизацию ( LpMinimize или 1 , что является значением по умолчанию) или максимизацию ( LpMaximize или -1 ). Этот выбор повлияет на результат вашей проблемы.
Когда у вас есть модель, вы можете определить переменные решения как экземпляры класса LpVariable :
# Инициализировать переменные решения x = LpVariable (имя = "x", lowBound = 0) y = LpVariable(name="y", lowBound=0)
Необходимо указать нижнюю границу с lowBound=0 , поскольку значение по умолчанию равно отрицательной бесконечности. Параметр
Параметр upBound определяет верхнюю границу, но здесь его можно опустить, поскольку по умолчанию он равен положительной бесконечности.
Необязательный параметр cat определяет категорию переменной решения. Если вы работаете с непрерывными переменными, вы можете использовать значение по умолчанию «Continuous» .
Вы можете использовать переменные x и y для создания других объектов PuLP, представляющих линейные выражения и ограничения:
>>>
>>> выражение = 2 * х + 4 * у >>> тип(выражение) <класс 'pulp.pulp.LpAffineExpression'> >>> ограничение = 2 * x + 4 * y >= 8 >>> тип(ограничение) <класс 'pulp.pulp.LpConstraint'>
Когда вы умножаете переменную решения на скаляр или строите линейную комбинацию нескольких переменных решения, вы получаете экземпляр pulse.LpAffineExpression , который представляет собой линейное выражение.
Примечание: Вы можете складывать или вычитать переменные или выражения, а также умножать их на константы, потому что классы PuLP реализуют некоторые специальные методы Python, которые эмулируют числовые типы, такие как __add__() , __sub__() и __mul__() . Эти методы используются для настройки поведения таких операторов, как
Эти методы используются для настройки поведения таких операторов, как +, - и *.
Точно так же вы можете комбинировать линейные выражения, переменные и скаляры с операторами == , <= или >= , чтобы получить экземплярыpulse.LpConstraint, представляющие линейные ограничения вашей модели.
Примечание: Также можно создавать ограничения с помощью расширенных методов сравнения .__eq__() , .__le__() и .__ge__() , которые определяют поведение операторов == 0 , 3 <= и >= .
Имея это в виду, следующим шагом будет создание ограничений и целевой функции, а также назначение их вашей модели. Вам не нужно создавать списки или матрицы. Просто напишите выражения Python и используйте оператор += , чтобы добавить их к модели:
# Добавляем ограничения в модель модель += (2 * x + y <= 20, "red_constraint") модель += (4 * x - 5 * y >= -10, "blue_constraint") модель += (-x + 2 * y >= -2, "yellow_constraint") модель += (-x + 5 * y == 15, "green_constraint")
В приведенном выше коде вы определяете кортежи, содержащие ограничения и их имена.
LpProblem позволяет добавлять ограничения в модель, указывая их как кортежи. Первый элемент — это экземпляр LpConstraint . Второй элемент — это удобочитаемое имя для этого ограничения.
Настройка целевой функции очень похожа:
# Добавляем в модель целевую функцию obj_func = х + 2 * у модель += obj_func
В качестве альтернативы вы можете использовать более короткое обозначение:
# Добавляем в модель целевую функцию модель += х + 2 * у
Теперь у вас есть добавленная целевая функция и определенная модель.
Примечание: Вы можете добавить ограничение или цель к модели с помощью оператора += , потому что его класс LpProblem реализует специальный метод .__iadd__() , который используется для указания поведения += .
Для больших задач часто удобнее использовать lpSum() со списком или другой последовательностью, чем повторять оператор + . Например, вы можете добавить целевую функцию в модель с помощью этого оператора:
Например, вы можете добавить целевую функцию в модель с помощью этого оператора:
# Добавляем в модель целевую функцию модель += lpSum([x, 2 * y])
Выдает тот же результат, что и предыдущий оператор.
Теперь вы можете увидеть полное определение этой модели:
>>>
>>> модель небольшая проблема: МАКСИМИЗИРОВАТЬ 1*х + 2*у + 0 ПРИ УСЛОВИИ red_constraint: 2 х + у <= 20 blue_constraint: 4 x - 5 y >= -10 yellow_constraint: - x + 2 y >= -2 green_constraint: - х + 5 у = 15 ПЕРЕМЕННЫЕ х Непрерывный г Непрерывный
Строковое представление модели содержит все необходимые данные: переменные, ограничения, цель и их имена.
Наконец-то вы готовы решить проблему. Вы можете сделать это, вызвав .solve() для объекта вашей модели. Если вы хотите использовать решатель по умолчанию (CBC), вам не нужно передавать никаких аргументов:
# Решаем проблему статус = модель.решить()
. вызывает базовый решатель, изменяет модель  solve()
solve() и возвращает целочисленный статус решения, который будет равен 1 , если оптимум найден. Остальные коды состояния см. в разделе LpStatus[] .
Вы можете получить результаты оптимизации как атрибуты модели . Функция value() и соответствующий метод .value() возвращают фактические значения атрибутов:
>>>
>>> print(f"status: {model.status}, {LpStatus[model.status]}")
статус: 1, Оптимальный
>>> print(f"цель: {model.objective.value()}")
цель: 16.8181817
>>> для var в model.variables():
... print(f"{var.name}: {var.value()}")
...
х: 7,7272727
г: 4,5454545
>>> для имени, ограничения в model.constraints.items():
... print(f"{name}: {constraint.value()}")
...
red_constraint: -9.999999939e-08
blue_constraint: 18.181818300000003
yellow_constraint: 3.3636362999999996
green_constraint: -2.0000000233721948e-07)
model. содержит значение целевой функции,  objective
objective model.constraints содержит значения резервных переменных, а объекты x и y имеют оптимальные значения переменных решения. model.variables() возвращает список с переменными решения:
>>>
>>> модель.переменные() [х, у] >>> model.variables()[0] равно x Истинный >>> model.variables()[1] есть у Истинный
Как видите, этот список содержит в точности объекты, созданные с помощью конструктора LpVariable .
Результаты примерно такие же, как у SciPy.
Примечание: Будьте осторожны с методом .solve() — он меняет состояние объектов x и и !
Вы можете увидеть, какой решатель использовался, вызвав .solver :
>>>
>>> модель.решатель <объект pulp.apis.coin_api.PULP_CBC_CMD по адресу 0x7f60aea19e50>
Вывод информирует вас о том, что решатель — CBC. Вы не указали решатель, поэтому PuLP назвал его по умолчанию.
Вы не указали решатель, поэтому PuLP назвал его по умолчанию.
Если вы хотите запустить другой решатель, вы можете указать его в качестве аргумента .solve() . Например, если вы хотите использовать GLPK и он уже установлен, вы можете использовать Solr=GLPK(msg=False) в последней строке. Имейте в виду, что вам также нужно будет импортировать его:
из целлюлозы импортной ГЛПК
Теперь, когда вы импортировали GLPK, вы можете использовать его внутри .solve() :
# Создать модель модель = LpProblem (имя = «маленькая проблема», смысл = LpMaximize) # Инициализировать переменные решения x = LpVariable (имя = "x", lowBound = 0) y = LpVariable(name="y", lowBound=0) # Добавляем ограничения в модель модель += (2 * x + y <= 20, "red_constraint") модель += (4 * x - 5 * y >= -10, "blue_constraint") модель += (-x + 2 * y >= -2, "yellow_constraint") модель += (-x + 5 * y == 15, "green_constraint") # Добавляем целевую функцию в модель модель += lpSum([x, 2 * y]) # Решать проблему статус = model.solve(решатель=GLPK(msg=False))
Параметр msg используется для отображения информации от решателя. msg=False отключает отображение этой информации. Если вы хотите включить информацию, просто опустите msg или установите msg=True .
Ваша модель определена и решена, поэтому вы можете проверить результаты так же, как и в предыдущем случае:
>>>
>>> print(f"status: {model.status}, {LpStatus[model.status]}")
статус: 1, Оптимальный
>>> print(f"цель: {model.objective.value()}")
цель: 16.81817
>>> для var в model.variables():
... print(f"{var.name}: {var.value()}")
...
х: 7,72727
г: 4,54545
>>> для имени, ограничения в model.constraints.items():
... print(f"{name}: {constraint.value()}")
...
red_constraint: -1.0000000000509601е-05
blue_constraint: 18.181830000000005
yellow_constraint: 3.3636299999999997
green_constraint: -2.000000000279556e-05
Вы получили практически тот же результат с GLPK, что и с SciPy и CBC.
Давайте посмотрим, какой решатель использовался на этот раз:
>>>
>>> модель.решатель <объект pulp.apis.glpk_api.GLPK_CMD по адресу 0x7f60aeb04d50>
Как вы определили выше с помощью выделенного оператора model.solve(solver=GLPK(msg=False)) , решатель — GLPK.
Вы также можете использовать PuLP для решения задач линейного программирования со смешанными целыми числами. Чтобы определить целочисленную или двоичную переменную, просто передайте cat="Integer" или cat="Binary" в LpVariable . Все остальное остается прежним:
# Создать модель модель = LpProblem (имя = «маленькая проблема», смысл = LpMaximize) # Инициализировать переменные решения: x — целое число, y — непрерывное x = LpVariable(name="x", lowBound=0, cat="Integer") y = LpVariable(name="y", lowBound=0) # Добавляем ограничения в модель модель += (2 * x + y <= 20, "red_constraint") модель += (4 * x - 5 * y >= -10, "blue_constraint") модель += (-x + 2 * y >= -2, "yellow_constraint") модель += (-x + 5 * y == 15, "green_constraint") # Добавляем целевую функцию в модель модель += lpSum([x, 2 * y]) # Решать проблему статус = модель.решить()
В этом примере у вас есть одна целочисленная переменная, и вы получаете другие результаты:
>>>
>>> print(f"status: {model.status}, {LpStatus[model.status]}")
статус: 1, Оптимальный
>>> print(f"цель: {model.objective.value()}")
цель: 15,8
>>> для var в model.variables():
... print(f"{var.name}: {var.value()}")
...
х: 7,0
у: 4,4
>>> для имени, ограничения в model.constraints.items():
... print(f"{name}: {constraint.value()}")
...
red_constraint: -1,5999999999999996
blue_constraint: 16.0
yellow_constraint: 3.8000000000000007
green_constraint: 0.0)
>>> модель.решатель
Теперь x является целым числом, как указано в модели. (Технически он содержит значение с плавающей запятой с нулем после запятой.) Этот факт меняет все решение. Покажем это на графике:
Как видите, оптимальное решение — крайняя правая зеленая точка на сером фоне. Это допустимое решение с наибольшими значениями обоих
Это допустимое решение с наибольшими значениями обоих x и y , что дает максимальное значение целевой функции.
ГЛПК способен решить и такие задачи.
Пример 2
Теперь вы можете использовать PuLP для решения проблемы распределения ресурсов сверху:
Подход к определению и решению проблемы такой же, как и в предыдущем примере:
# Определить модель
модель = LpProblem(name="resource-allocation", смысл=LpMaximize)
# Определяем переменные решения
x = {i: LpVariable(name=f"x{i}", lowBound=0) для i в диапазоне (1, 5)}
# Добавляем ограничения
модель += (lpSum(x.values()) <= 50, "рабочая сила")
модель += (3 * x[1] + 2 * x[2] + x[3] <= 100, "material_a")
модель += (x[2] + 2 * x[3] + 3 * x[4] <= 90, "материал_б")
# Установите цель
модель += 20 * х[1] + 12 * х[2] + 40 * х[3] + 25 * х[4]
# Решаем задачу оптимизации
статус = модель.решить()
# Получить результаты
print(f"статус: {model.status}, {LpStatus[model.status]}")
print(f"цель: {model. objective.value()}")
для var в x.values():
print(f"{var.name}: {var.value()}")
для имени ограничение в model.constraints.items():
печать (f"{имя}: {ограничение.значение()}")
objective.value()}")
для var в x.values():
print(f"{var.name}: {var.value()}")
для имени ограничение в model.constraints.items():
печать (f"{имя}: {ограничение.значение()}")
В этом случае вы используете словарь x для хранения всех переменных решения. Этот подход удобен тем, что словари могут хранить имена или индексы переменных решения в качестве ключей и соответствующих LpVariable объектов в качестве значений. Также могут быть полезны списки или кортежи экземпляров LpVariable .
Приведенный выше код дает следующий результат:
статус: 1, Оптимальный цель: 1900.0 х1: 5,0 х2: 0,0 х3: 45,0 х4: 0,0 рабочая сила: 0.0 материал_а: -40.0 материал_б: 0.0
Как видите, решение совпадает с решением, полученным с помощью SciPy. Наиболее выгодное решение – произвести 5,0 единиц первого продукта и 45,0 единиц третьего продукта в сутки.
Давайте сделаем эту задачу более сложной и интересной. Скажем, фабрика не может производить первый и третий продукты параллельно из-за проблем с оборудованием. Какое самое выгодное решение в этом случае?
Скажем, фабрика не может производить первый и третий продукты параллельно из-за проблем с оборудованием. Какое самое выгодное решение в этом случае?
Теперь у вас есть еще одно логическое ограничение: если x ₁ положительно, то x ₃ должно быть равно нулю, и наоборот. Здесь очень полезны бинарные переменные решения. Вы будете использовать две бинарные переменные решения, y ₁ и y ₃, которые будут обозначать, генерируются ли вообще первый или третий продукты:
1model = LpProblem(name="resource-allocation", смысл=LpMaximize)
2
3# Определите переменные решения
4x = {i: LpVariable(name=f"x{i}", lowBound=0) для i в диапазоне (1, 5)}
5y = {i: LpVariable(name=f"y{i}", cat="Binary") для i в (1, 3)}
6
7# Добавить ограничения
8model += (lpSum(x.values()) <= 50, "рабочая сила")
9model += (3 * x[1] + 2 * x[2] + x[3] <= 100, "material_a")
10модель += (x[2] + 2 * x[3] + 3 * x[4] <= 90, "материал_б")
11
12М = 100
13model += (x[1] <= y[1] * M, "x1_constraint")
14model += (x[3] <= y[3] * M, "x3_constraint")
15model += (y[1] + y[3] <= 1, "y_constraint")
16
17# Установить цель
18модель += 20 * х[1] + 12 * х[2] + 40 * х[3] + 25 * х[4]
19
20# Решить задачу оптимизации
21статус = модель. решить()
22
23print(f"статус: {model.status}, {LpStatus[model.status]}")
24print(f"цель: {model.objective.value()}")
25
26для var в model.variables():
27 print(f"{var.name}: {var.value()}")
28
29для имени ограничение в model.constraints.items():
30 print(f"{name}: {constraint.value()}")
решить()
22
23print(f"статус: {model.status}, {LpStatus[model.status]}")
24print(f"цель: {model.objective.value()}")
25
26для var в model.variables():
27 print(f"{var.name}: {var.value()}")
28
29для имени ограничение в model.constraints.items():
30 print(f"{name}: {constraint.value()}")
Код очень похож на предыдущий пример, за исключением выделенных строк. Вот отличия:
Строка 5 определяет двоичные переменные решения
y[1]иy[3], содержащиеся в словареy.Строка 12 определяет произвольно большое число
M. Значение100в этом случае достаточно, потому что вы не можете иметь более100единиц в день.Строка 13 говорит, что если
y[1]равно нулю, тоx[1]должно быть равно нулю, иначе это может быть любое неотрицательное число.Строка 14 говорит, что если
y[3]равно нулю, тоx[3]должно быть равно нулю, иначе это может быть любое неотрицательное число.
Строка 15 говорит, что либо
y[1], либоy[3]равно нулю (или оба равны), поэтому либоx[1], либоx[3]также должны быть равны нулю.
Вот решение:
статус: 1, Оптимальный цель: 1800.0 х1: 0,0 х2: 0,0 х3: 45,0 х4: 0,0 у1: 0,0 у3: 1.0 рабочая сила: -5,0 материал_а: -55.0 материал_б: 0.0 x1_constraint: 0.0 x3_constraint: -55.0 у_ограничение: 0.0
Получается, что оптимальный подход — исключить первый продукт и произвести только третий.
Удалить рекламу
Ресурсы по линейному программированию
Линейное программирование и линейное программирование смешанных целых чисел — очень важные темы. Если вы хотите узнать о них больше — а узнать можно гораздо больше, чем то, что вы видели здесь, — то вы можете найти множество ресурсов. Вот несколько для начала:
- Статья Википедии о линейном программировании
- Статья Википедии о целочисленном программировании
- MIT Введение в курс математического программирования
- Линейное программирование Brilliant.
 org Статья
org Статья - CalcWorkshop Что такое линейное программирование?
- Линейное программирование BYJU Артикул
Gurobi Optimization — компания, которая предлагает очень быстрый коммерческий решатель с Python API. Он также содержит ценные ресурсы по линейному программированию и линейному программированию со смешанными целыми числами, в том числе следующие:
- Линейное программирование (LP) — введение в основы
- Смешанно-целочисленное программирование (MIP) — введение в основы
- Учебники
- Выбор решателя для математического программирования
Если вы настроены изучать теорию оптимизации, то существует множество математических книг. Вот несколько популярных вариантов:
- Линейное программирование: основы и расширения
- Выпуклая оптимизация
- Построение моделей в математическом программировании
- Инженерная оптимизация: теория и практика
Это лишь часть того, что доступно. Линейное программирование и линейное программирование смешанных целых чисел являются популярными и широко используемыми методами, поэтому вы можете найти бесчисленное количество ресурсов, которые помогут углубить ваше понимание.
Линейное программирование и линейное программирование смешанных целых чисел являются популярными и широко используемыми методами, поэтому вы можете найти бесчисленное количество ресурсов, которые помогут углубить ваше понимание.
Решатели линейного программирования
Так же, как существует множество ресурсов, которые помогут вам изучить линейное программирование и линейное программирование смешанных целых чисел, существует также широкий спектр решателей с доступными оболочками Python. Вот неполный список:
- ГЛПК
- LP Решить
- КЛП
- КВС
- CVXOPT
- SciPy
- SCIP с PySCIPOPt
- Оптимизатор Гуроби
- КОМПЛЕКС
- ЭКСПРЕСС
- МОСЕК
Некоторые из этих библиотек, например Gurobi, включают собственные оболочки Python. Другие используют внешние оболочки. Например, вы видели, что вы можете получить доступ к CBC и GLPK с помощью PuLP.
Заключение
Теперь вы знаете, что такое линейное программирование и как использовать Python для решения задач линейного программирования. Вы также узнали, что библиотеки линейного программирования Python — это всего лишь оболочки для нативных решателей. Когда решатель завершает свою работу, оболочка возвращает статус решения, значения переменных решения, резервные переменные, целевую функцию и т. д.
Вы также узнали, что библиотеки линейного программирования Python — это всего лишь оболочки для нативных решателей. Когда решатель завершает свою работу, оболочка возвращает статус решения, значения переменных решения, резервные переменные, целевую функцию и т. д.
В этом уроке вы узнали, как:
- Определите модель , которая представляет вашу проблему
- Создайте программу Python для оптимизации
- Запустите программу оптимизации, чтобы найти решение проблемы
- Получить результат оптимизации
Вы использовали SciPy с его собственным решателем, а также PuLP с CBC и GLPK, но вы также узнали, что существует множество других решателей линейного программирования и оболочек Python. Теперь вы готовы погрузиться в мир линейного программирования!
Если у вас есть какие-либо вопросы или комментарии, оставьте их в разделе комментариев ниже.
Средства линейного программирования
Этот JavaScript хорошо работает в Netscape Navigator версии 4 (например, 4.7). Если это для вас невыполнимо, вы можете загрузить (бесплатно) программный пакет, который решает модели линейных программ с помощью симплексного метода и/или метода двухтактного взаимодействия:
Профессор Хоссейн Аршам
Другие учебные объекты JavaScript для принятия решений в этой серии классифицируются по разным областям применения на уровне 9.0007 Раздел МЕНЮ на этой странице.
При вводе данных для перехода от ячейки к ячейке в матрице данных используйте клавишу Tab , а не клавиши со стрелками или клавиши ввода.
Инструкции и предварительные сведения:
- Этот JavaScript предназначен для экспериментов по углублению понимания концепций и методов LP. Поэтому он предназначен для задач LP с не более чем 3 переменными решения и не более чем с 3 ограничениями. То есть 3 на 3 — это самый большой размер задачи.
- Имена переменных решения должны состоять из одной буквы, например, X, Y, Z.
- Преобразовать задачу минимизации в задачу максимизации (умножив целевую функцию на -1).
- Каждая переменная решения, фигурирующая в любых ограничениях, должна также фигурировать в целевой функции, возможно, с нулевым коэффициентом, если это необходимо.
- Все переменные решения должны быть неотрицательными.
Чтобы выполнить это требование, преобразуйте любую неограниченную переменную X в две неотрицательные переменные, заменив X на T — X. Это увеличит размерность задачи только на единицу (введите одну переменную y) независимо от того, сколько переменных не ограничено. Например, если Y также неограниченная переменная, то замена — Y вместо Y.
Например, если Y также неограниченная переменная, то замена — Y вместо Y.
Если какая-либо переменная, скажем, X ограничена неположительностью, замените — X на каждый X. Это уменьшит сложность задачи. - Все переменные решения должны появляться в левой части ограничений, а числовые значения должны появляться в правой части ограничений (поэтому эти числа называются значениями RHS).
- Все значения RHS должны быть неотрицательными. Умножьте обе части ограничения на -1, если необходимо.
- Для нецелочисленных коэффициентов для переменных решения, целевой функции и ограничений используйте дробный эквивалент в скобках, например, для X/5 используйте (1/5)X.
- Все ограничения должны быть в форме ≤ и/или ≥. Вы можете войти в условия неотрицательности, если хотите.
- Любое строгое ограничение равенства должно быть заменено двумя одновременными неравенствами формы ≤ и ≥ с одинаковым значением RHS.
- Выходные данные включают оптимальное значение и оптимальную стратегию для переменных решения.
 Оптимальное значение резерва/излишка для каждого ограничения может быть найдено путем оценки каждого ограничения с использованием доступной оптимальной стратегии для переменных решения.
Оптимальное значение резерва/излишка для каждого ограничения может быть найдено путем оценки каждого ограничения с использованием доступной оптимальной стратегии для переменных решения. - Выходные данные также содержат необходимые инструменты для выполнения различных анализов чувствительности коэффициентов целевой функции и правых значений ограничений. Эти инструменты применимы к любой задаче ЛП, имеющей единственное оптимальное решение.
Решите стандартную отформатированную задачу, а затем подставьте эти изменения обратно, чтобы получить значения исходных переменных и оптимальное значение.
Пример: Рассмотрим следующую задачу с ограничением равенства:
Максимизация 3x + 2y + z
при условии:
4x + 2y + 3z = 12
х + г ≥ 1
х, у и г ≥ 0.
Преобразовывая ограничения равенства в два ограничения неравенства, мы получаем следующую эквивалентную задачу:
Максимизация 3x + 2y + z
при условии:
4x + 2y + 3z ≤ 24
4x + 2y + 3z ≥ 24
х + г ≥ 1
х, у и г ≥ 0.
Введите стандартную задачу LP в следующую таблицу, затем нажмите кнопку «Рассчитать».
| При вводе данных для перехода от ячейки к ячейке в матрице данных используйте клавишу Tab , а не клавиши со стрелками или клавиши ввода. | Введите свой LP с помощью Netscape Navigator. Нажмите на «Пример», чтобы увидеть, как: | г.|
| В соответствии с | ||
| Вы можете ввести ограничения неотрицательности ниже: | ||
| Оптимальная ценность и оптимальные стратегические решения: | ||
| Инструменты анализа чувствительности для LP с уникальным решением: | ||
Linear Optimization
Для получения технических сведений о построении области чувствительности см. Вернуться к:
Вернуться к:
Построение области чувствительности для LP-моделей.
Пожалуйста, отправьте ваши комментарии по электронной почте:
Профессор Хоссейн Аршам
24 Лучшие услуги линейного программирования для покупки онлайн
24 лучших сервиса линейного программирования для покупки онлайн | Fiverr114 Услуги доступны
MMUHAMMED_AZMAT
Уровень 1 Продавец
I будет моделировать и выполнять исследования, линейное задание программирования
5,0 (
5
)
, начиная с . 5)
, начиная с . 5)
.Уровень 1 Продавец
Я буду моделировать, кодировать операции и задачи линейного программирования
5.0(
3
)
, начиная с € 15 75 SSHEHROZ_29
Уровень 1 Продавец
Я буду решать проблемы с линейным программированием.

BestOne786
I будет моделировать, исследования по эксплуатации и линейные задачи программирования
5,0 (
5
)
Начиная с € 10 50 H. оптимизационная задача
5.0(
1
)
Starting at €5 25 mmaster_alfa
I will assist operation research linear programming excel solver
5.0(
4
)
Starting at € 15 75 ddatasci_master
Продавец 1-го уровня
Я займусь линейным программированием и оптимизацией исследования операций
5.0(
17
) Начиная с
8 8€ 15 75 E
ENGR_EJAZ
Уровень 2 Продавец
I помогу вам в линейном программировании с использованием Excel Solver
5,0 (
3
)
, начиная с 3)
, начиная с 3)
68, начиная с 3) .
Уровень 2 Продавец
Я буду моделировать, кодировать, исследовать операции и решать задачи линейного программирования
5.0(
30
)
Начиная с €15 75 iiftiarka, excel linear3, excel 904, iftiarka 904 программирование и исследование операций
5.0(
4
)
Starting at €5 25 ddr_saffina
I will tutor operation research, linear programming, asset management, complex networks
5.0(
2
)
Начиная с €5 25 ffarzanbashir
Продавец 1-го уровня
Выполню экспертные задачи по линейному программированию и исследованию операций см.
мои отзывы
5.0(
9
33) , начиная с € 15 75 IIOTTIO
I будет делать линейные не линейные целочисленные программирование оптимизация Excel Solver и Lingo
4.9 (
6
)
4.9 (
6
)
4.9 (
6
)
4.9.
lakshmanphd
Level 1 Seller
I will model operations research and linear programming tasks
4.7(
1
)
Starting at €21aalfasol2022
Level 1 Seller
Я буду линейным программированием в исследовании операций
5,0 (
1
)
Начиная с € 10 50 JGOEYJONES03
I DRAIT ARGING RESHING RESSIC
1
)
Начиная с €5 25 eexamassignmen
Я буду заниматься исследованием операций, линейным программированием, решателем Excel, оптимизацией
5.
0(
1
)
, начиная с € 5 25 CCharli_BRO
Уровень 1 Продавец
I поможет исследованию программы Excel Excel Optimization
5.0 (
211
9111111111119919191919191999999.5.0. €10 50 a
albertochave956
Продавец 1-го уровня
Я сделаю линейные, смешанные целочисленные или логические модели оптимизации программирования
4.9(
19
3 )
31868, начиная с
€ 5 25 AAlijanjua1
Уровень 2 Продавец
I будет провести исследование операций Линейное программирование и связанные с ними проекты
5,0 (
123
)
5,0 (
123
)
5,0 (
123
)
5,0 (
123
)
5,0 (
123
)5,0 (
.
Solver Solver Решение проблем Оптимизация Исследование операций Исследование операций Управление операциями Minitab Microsoft excel Матлаб Программное обеспечение и решатели для линейного и смешанно-целочисленного программирования с открытым исходным кодом
Посмотреть видео
Узнайте, как производительность, надежность, интерфейсы и поддержка являются ключевыми отличиями Gurobi Optimizer от бесплатных решателей.
Изучение вариантов среди решателей с открытым исходным кодом
Мы знаем, что существует целый ряд решателей, бесплатных и платных, на выбор.
Мы также знаем, что в некоторых ситуациях вам может понадобиться бесплатный решатель. Эта страница предназначена для того, чтобы помочь вам лучше понять свой выбор среди бесплатных решателей, их относительную производительность и задать некоторые вопросы, чтобы решить, какой тип решателя вам подходит. В частности, на этой странице мы рассмотрим следующие темы:
- список некоторых из ведущих бесплатных решателей линейного и смешанного целочисленного программирования
- относительное сравнение производительности решателя
- когда бесплатный решатель может быть лучшим выбором
- общее сравнение бесплатных и коммерческих решателей
Обратите внимание: поскольку вы изучаете бесплатные решатели, мы предполагаем, что вы не академик. Если да, мы предлагаем несколько типов лицензий Gurobi совершенно бесплатно для академических пользователей, соответствующих определенным критериям. Если вы являетесь академическим пользователем (студентом, преподавателем или сотрудником) в учебном заведении, присуждающем ученую степень, или если вы в настоящее время проходите онлайн-курс по оптимизации, загляните на нашу академическую страницу.
Распространенные бесплатные решатели для линейного и смешанного целочисленного программирования
Вы обнаружите, что доступно множество бесплатных решателей. Ниже приведен краткий обзор двух наиболее популярных решателей с открытым исходным кодом:
Solver Общий обзор ГЛПК
- GLPK ( GNU L inear P rogramming K it) представляет собой набор подпрограмм, написанных на C и организованных в виде вызываемой библиотеки
- GLPK решает задачи линейного программирования (LP) и смешанного целочисленного программирования (MIP)
- Ссылка: GLPK (сторонний веб-сайт)
LP_Solve
- LP_Solve написан на C и компилируется как в Linux, так и в Windows
- LP_Solve решает задачи линейного программирования (LP), смешанно-целочисленного программирования (MIP), полунепрерывных и специальных упорядоченных множеств (SOS)
- Ссылка: LP_Solve (сторонний веб-сайт)
Сравнение относительной производительности решателя
Производительность обычно является решающим фактором при выборе решателя.
Чтобы дать представление об относительной производительности различных вариантов решателя, перечисленных выше, мы обобщили результаты независимых эталонных тестов, проведенных Хансом Миттельманном из штата Аризона. Если мы посмотрим на производительность моделей смешанного целочисленного программирования (MIP) в широком наборе тестовых моделей, в таблице ниже показаны результаты по двум ключевым параметрам: а) смог ли решатель решить модель, и б) как быстро модель решено?
Решатель # решенных задач эталона (из 87) Относительная производительность MIP ГЛПК 0 н/д (GLPK решила 0 моделей тестового набора) г.LP_Solve 5 н/д (LP_Solve решила 5 моделей тестового набора) Гуроби 87 1,0X (самый быстрый) Как видно из результатов, производительность разных решателей сильно различается. Хотя в приведенной выше таблице производительность представлена в количественном выражении, мы видели несколько случаев, когда производительность решателя имела очень качественный эффект. В частности, мы знаем нескольких человек, которые построили модели оптимизации с помощью бесплатных решателей и не смогли решить полученные модели за приемлемое время. Из этого они сделали вывод, что технология оптимизации не подходит для решения их задач, хотя, по всей вероятности, более способный решатель без труда решил бы их.
Когда бесплатный решатель может быть лучшим выбором
Как видно из приведенных выше данных, бесплатные решатели имеют тенденцию бороться с практическими моделями, либо не решая их вообще, либо решая их относительно медленно. Однако мы не хотим создать у вас впечатление, что бесплатные решатели никогда не будут правильным выбором. Ниже приведены несколько сценариев, в которых вы можете рассмотреть возможность использования бесплатного решателя.
Нет утвержденного бюджета
- Часто, когда компания впервые рассматривает возможность использования оптимизационного решателя в своем бизнесе, может не быть утвержденного бюджета. Руководство, возможно, все еще пытается определить, какую роль оптимизация может сыграть в планировании и принятии решений, а команда, выполняющая работу, все еще «накачивает ноги».
- Хотя бесплатная пробная версия Gurobi (с ограничением до 2000 переменных решений и 2000 ограничений) или неограниченная временная ознакомительная лицензия Gurobi могут удовлетворить ваши потребности, если ваша проблема больше, чем позволяет пробная версия, и/или ваш временной горизонт больше, чем подходит для ознакомительной версии, бесплатный решатель может быть хорошим способом начать работу.
Вы предпочитаете программировать на C или C++
- Большинство бесплатных решателей написаны на C или C++ и не предлагают других API. GLPK требует, чтобы вы использовали C.
- Gurobi предлагает API-интерфейсы C и C++, а также полный набор других API-интерфейсов, включая Python, на ваш выбор.
Решаемая(ые) модель(и) малы и относительно легко решаются вы уверены, что ваша проблема не станет более сложной в будущем, то бесплатное решение может быть разумным выбором.
Мы хотим подчеркнуть, что вы должны учитывать будущий рост модели. Мы видели много ситуаций, когда бесплатные решатели хорошо работали на небольшом прототипе, но не могли справиться с производственной моделью. Это может привести к большому количеству переделок, которых можно избежать. Прежде чем сделать выбор в пользу использования бесплатного решателя, мы предлагаем вам оценить относительную производительность моделей такого же размера и сложности, как и те, которые вы, вероятно, захотите решить в конечном итоге. Мы рады помочь, если хотите. У нас есть очень большая библиотека моделей, и мы можем провести конкретное сравнение.
Как избежать ловушки «ложноотрицательного результата»…
Один из самых важных вопросов, который обычно задают люди, впервые изучающие решатели, — подходит ли оптимизация для их бизнеса. Мы видели случаи, когда кто-то выбирал бесплатный решатель, пытался построить модель, а решатель просто не мог решить проблему. В результате они решили, что их проблема слишком сложна, чтобы использовать методы оптимизации. С другой стороны, они обнаружили, что его слишком сложно использовать, учитывая, что решатель не поддерживает предпочитаемый ими язык программирования, они не могут получить поддержку и т. д. Затем команда завершает проект и движется дальше. Это печально, так как при наличии правильных инструментов и поддержки проект мог бы иметь большой успех. Если вы оказались в такой ситуации, пожалуйста, свяжитесь с нами. Возможно, мы сможем помочь направить вас в правильном направлении, чтобы вы получили результаты, необходимые для поддержки продолжения проекта.
Обзор бесплатных и платных решателей
Существует несколько важных различий между бесплатными и коммерческими решателями, которые следует учитывать при сравнении бесплатных и платных решателей.
Класс решателя Деталь Бесплатные решатели
- Без платы за лицензию или обслуживание
- Нет прямой поддержки, необходимо ответить в «сообществе» для получения поддержки
- Уровни обслуживания и постоянного улучшения различаются в зависимости от бесплатных решателей
- Способен решать более мелкие/простые модели в рамках этих типов задач, но может быть не в состоянии решать более сложные модели или может решать их очень медленно
Платные решатели
- Плата за лицензию и обслуживание (для поддержки и обновлений)
- Прямая поддержка доступна от компании
- Отсутствие риска нарушения кода
- Активно поддерживается и совершенствуется с течением времени
- Способность решать более широкий спектр задач, включая задачи линейного программирования (LP) и смешанно-целочисленного программирования (MIP), а также задачи квадратичного (QP) и квадратичного программирования с ограничениями (QCP)
- Предложение широкого спектра API языков программирования и моделирования
- Предлагайте функции распределенной оптимизации
- Гораздо лучше решает сложные модели и решает их быстрее
Тестируйте Gurobi бесплатно
Мы уверены, что когда вы сами попробуете, вы придете к такому же выводу, что и многие другие компании: Gurobi — разумная альтернатива «бесплатным» решателям.


 Если
же решение нецелое, то нужно повторять
алгоритм метода Гомори вплоть до
получения целочисленного решения.
Если
же решение нецелое, то нужно повторять
алгоритм метода Гомори вплоть до
получения целочисленного решения.
 ..
.. При этом процесс решения состоит из двух этапов.
При этом процесс решения состоит из двух этапов.