Задачи динамического программирования онлайн: Динамическое программирование

alexxlab / / Разное

Как решать задачи по динамическому программированию

Методы динамического программирования применяются при решении оптимизационных задач, в которых целевая функция или ограничения, или же и первое, и второе одновременно характеризуются нелинейными зависимостями.

Данный раздел представлен следующими калькуляторами:

  1. Задача распределения инвестиций. Распределении инвестиций между предприятиями П1, П2,…, Пn. Инвестируемая сумма E усл. ден. ед.
  2. Задача распределения ресурсов. Планируется работа двух предприятий на n лет. Начальные ресурсы равны s0.
  3. Метод прогонки.
  4. Задача замены оборудования.
  5. Складская задача: составить оптимальную программу выпуска продукции X, которая минимизирует суммарные издержки предприятия.
  6. Задача Джонсона.
  7. Задача о рюкзаке (решение задачи о загрузке транспортного средства).
  8. Динамическая оптимизация в планировании работ
    В условиях задачи производственного планирования найти оптимальные сроки начала строительства каждого из объектов так, чтобы суммарный срок строительства всех объектов был бы минимальным.
    Объекты / Стадии№1№2№3№4
    A12543
    A21426
    A33434

Задача распределения инвестиций

В задачах данного типа заданы сумма инвестиций (или сумма для распределения) и таблица планируемой прибыли.
Если сумма для распределения явно не задана, то ее можно найти из таблицы — она равна максимальному значению xi (последняя строчка таблицы).

Таблицы могут иметь разный вид.
Таблица 1 — Первый вариант таблицы исходных данных

xf1(x)f2(x)f3(x)
16.345
25.267
34.34.67.8
4563
5*76.38.2
* — здесь значение 5 — максимальное значение (сумма для распределения).

Таблица 2 — Второй вариант таблицы исходных данных

x010203040
f1(x)04578
f2(x)03346
f3(x)04456

Пример задачи.
Для двух предприятий выделено A единиц средств. Как распределить все средства в течение 4 лет, чтобы доход был наибольшим, если известно, что доход от x единиц средств, вложенных в первое предприятие, равен f1(х), а доход от y единиц средств, вложенных во второе предприятие, равен f2(y). Остаток средств к концу года составляет g1(x) для первого предприятия и g2(y) для второго предприятия. Задачу решить методом динамического программирования.

При вводе данных первую нулевую строку можно не заполнять.

В сервисе Задача распределения инвестиций используется метод обратной прогонки.

Метод прогонки

Данная задача соответствует задаче распределения инвестиций. Разница состоит в оформлении результатов полученного решения и применения метода прямой прогонки.

В сервисе Метод прогонки необходимо также выбрать метод решения: процедура прямой или обратной прогонки.

Задача замены оборудования

Цель решения — определить на каких шагах алгоритма (в какие годы) необходимо заменить оборудование. Для этого вводятся Период эксплуатации (в годах) и Стоимость нового оборудования. После этого необходимо заполнить таблицу дохода r(t) и остаточной стоимости S(t).
Задача замены оборудования

Планирование производственной линии

Задача последовательной обработки на двух машинах N различных деталей, если известно время A
i и Bi обработки i-й детали на соответствующих машинах. Требуется найти порядок обработки, минимизирующий время простоя второй машины и тем самым сокращающий общее время обработки деталей.
Задача Джонсона

Mетод динамического программирования. Примеры решения задач

Mетод динамического программирования

Задача1. Для двух предприятий выделено 1400 единиц денежных средств. Как распределить все средства в течение 4 лет, чтобы доход был наибольшим, если известно, что доход от х единиц, вложенных в первое предприятие равен , а доход от у единиц, вложенных в первое предприятие равен . Остаток средств к концу года составляет  - для первого предприятия,  - для второго предприятия. Решить задачу методом динамического программирования.

Решение

Процесс распределения средств разобъем на 4 этапа – по соответствующим годам.
Обозначим  — средства, которые распределяются на к–ом шаге как сумма средств по предприятиям.

Суммарный доход от обоих предприятий на к–ом шаге:

Остаток средств от обоих предприятий на к–ом шаге:

Обозначим  — максимальный доход, полученный от распределения средств  между двумя предприятиями с к-го шага до конца рассматриваемого периода.
Рекуррентные соотношения Беллмана для этих функций

Проведем оптимизацию, начиная с четвертого шага:

4-й шаг.
Оптимальный доход равен: , т.к. линейная убывающая функция достигает максимума в начале рассматриваемого промежутка, т.

е. при .

3-й шаг.

 т.к. линейная убывающая функция достигает максимума в начале рассматриваемого промежутка, т.е. при .

2-й шаг.

 т.к. линейная возрастающая функция достигает максимума в конце рассматриваемого промежутка, т.е. при .

1-й шаг.

 т.к. линейная возрастающая функция достигает максимума в конце рассматриваемого промежутка, т.е. при .

Результаты оптимизации:



         Определим количественное распределение средств по годам:

Т.к. , получаем


         Представим распределение средств в виде таблицы:

предприятие

год

1

2

3

4

1

1400

700

0

0

2

0

0

350

105

 

При таком распределении средств за 4 года будет получен доход, равный

 

Задача 2.

Предприятие изготавливает продукцию, спрос на которую в каждом из месяцев планируемого периода Dt  (t =) тыс. ед. Запас продукции на складе на начало планируемого периода i0 тыс.ед. Затраты на производство продукции складываются из условно постоянных затрат, равных kден.ед., и пропорциональных затрат, равных Lxt. Затраты на хранение 1 тыс. ед. продукции составляют h ден.ед. Складские площади позволяют хранить не более М тыс.ед. продукции. Производственные мощности ограничены, и в каждом месяце предприятие может произвести не более В тыс.ед. продукции. Требуется разработать производственную программу изготовления продукции xt  удовлетворяющую спрос в каждом из месяцев планируемого периода и обеспечивающую минимальные затраты на производство продукции и содержание запасов. Запас продукции на складе в конце планируемого периода должен быть равен нулю.
Все необходимые числовые данные приведены в таблице.

T

D1

D2

D3

D4

i0

k

L

h

M

B

3

3

5

4

-

2

4

1

1

6

7

Решение
Для решения задачи методом динамического программирования и записи рекуррентного соотношения будем использовать следующие обозначения: n — номер планового отрезка времени периода; j — уровень запаса на конец отрезка;

dn— спрос на продук­цию на n-м отрезке;

cn(x,j)= c(x)+j h — затраты, связанные с выпуском х единиц продукции на n-м отрезке и содержанием запасов, объем которых на конец n-го отрезка равен единицу j;  fn(i)— значение функции, равное затратам на производство и хранение продук­ции за последние n месяцев при условии, что уровень запасов на начало n-гo месяца составляет i единиц; xn(i)— производство про­дукции на n-м отрезке, если уровень запасов на начало отрезка равен i единиц.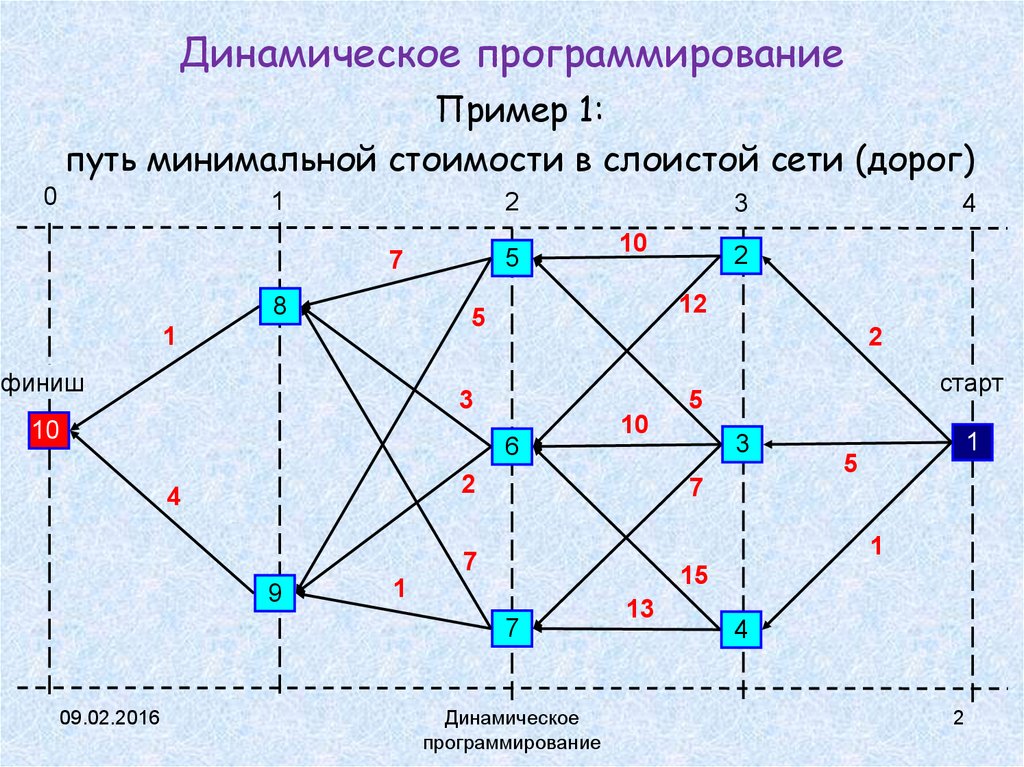 Изобразим плановый период на рисунке и для на­глядности нанесем на него числовые данные

          D1 = 3             D2 = 5            D3 = 4                 
 

  i 0 = 2   n =3           n = 2                n = 1     j 4 = 0
d3 = 3              d2 = 5                      d1 = 4
x3                      x2                            x1

Т.к. c(x)=k+Lxто c(0)=0; c(l)=5; c(2)=6; c(3)=7; c (4)=8; c(5)=9; c(6)=10; c(7)=11; Уровень запасов на конец планового периода должен быть равен нулю, то для n=0 имеем f0(0)=0. Перейдем к рассмотрению первого отрезка, т.е. n=1.
Тогда функциональные уравнения Беллмана для рассматриваемой задачи имеют следующий вид: для n =1
f1(i)=c1(d1-i, 0) = c1(d1-i, 0)  , где  i может принимать значения 0, 1, 2, 3, 4.
Расчет всех значений выполним в виде таблицы.

x
i    

X1* (i)

f1 (i)

0

4

8

1

3

7

2

2

6

3

1

5

4

0

0

Переходим к анализу периода, состоящего из двух последних месяцев, т.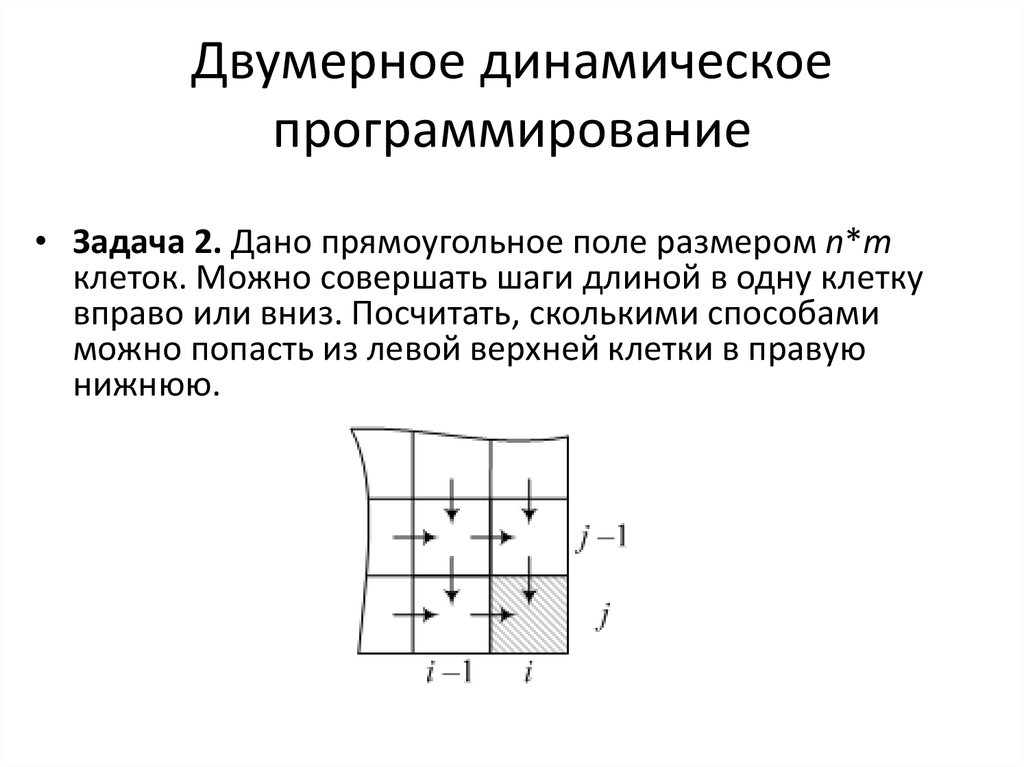 е. n= 2. Тогда уравнение Беллмана примет вид:
(с2(x) + h(i +x- d2 ) + f1(i +x — d2)) ,  где i — уровень запаса сырья на начало предпоследнего месяца может принимать значения 0, 1, 2, 3, 4, 5, 6,

x будет равняться   7, 6, 5, 4 ,3, 2, 1, 0.
Расчет всех значений выполним в виде таблицы.

x
i    

0

1

2

3

4

5

6

7

X2(i)

f2(i)

0

—

—

—

—

—

9+0+8=17

10+1+7=18

11+2+6=19

5

17

1

—

—

—

—

8+0+8=16

9+1+7=17

10+2+6=18

11+3+5=19

4

16

2

—

—

—

7+0+8=15

8+1+7=16

9+2+6=17

10+3+5=18

11+4+0=15

3

15

3

—

—

6+0+8=14

7+1+7=15

8+2+6=16

9+3+5=17

10+4+0=14

—

2

14

4

—

5+0+8=13

6+1+7=14

7+2+6=15

8+3+5=16

9+4+0=13

—

—

1

13

5

0+0+8=8

5+1+7=13

6+2+6=14

7+3+5=15

8+4+0=12

—

—

—

0

8

6

0+1+7=8

5+2+6=13

6+3+5=14

7+4+0=14

—

—

—

—

0

8

      Последнему шагу (n=3) будет соответствовать функциональное уравнение,  
(с3(x) + h(2 +x- d3 ) + f2(2 +x – d3)),  где i — уровень запаса сырья на начало предпоследнего месяца может принимать значение 2, а  x будет равняться  7, 6, 5, 4 , 3, 2, 1.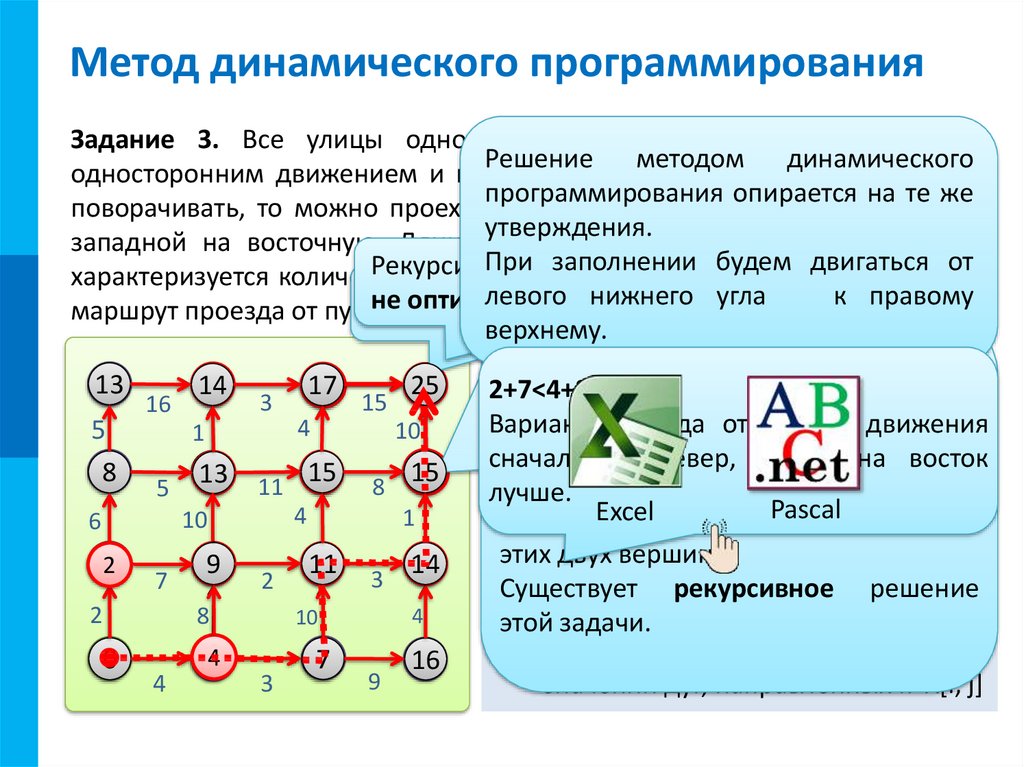

Расчет всех значений выполним в виде таблицы. Таб. 4.4

     x
i    

1

2

3

4

5

6

7

x4(i)

f4(х)

i 0 = 2     

5+0+17

6+1+16

7+2+15

8+3+14

9+4+13

10+5+8

11+6+8

1

22

Из таблицы видно, что в первом месяце оптимальной будет поставка x3(2)=1 единицам. С учетом запаса 2 единиц, общее коли­чество составит 3. За этот месяц будет израсходовано 3 единицы, так что к началу второго месяца запас составит i=0 единиц. По таб. 4.3 находим x2(0)=5, за этот месяц будет израсходовано 5 единиц. Останется 0 единица. В третьем   месяце с учетом остатка 0 единиц будет поставка x1(0)=4 единицы, что достаточно для удовлетворения потребностей в третьем   месяце. При этом к концу третьего   месяца уровень запаса будет равен  0 ед. 
Минимальные затраты, связанные с производством и хранением продукции за три месяца, составят 22 единицы.

 

Топ 50 практических задач динамического программирования | Кодирование Freak | Techie Delight

50 лучших практических задач динамического программирования | Кодирование Freak | Технарь Восторг | Средний

Динамическое программирование — это метод решения сложной проблемы путем разбиения ее на набор более простых подзадач, решения каждой из этих подзадач только один раз и сохранения их решений с использованием структуры данных в памяти (массив, карта и т. д.). Каждое из решений подзадачи каким-то образом индексируется, обычно на основе значений его входных параметров, чтобы облегчить его поиск. Таким образом, в следующий раз, когда возникает та же самая подзадача, вместо повторного вычисления ее решения просто просматривается ранее вычисленное решение, тем самым экономя время вычислений. Этот метод хранения решений подзадач вместо их пересчета называется мемоизацией.

Вот блестящее объяснение концепции динамического программирования на Quora. Ответ Джонатана Полсона на вопрос «Как объяснить динамическое программирование четырехлетнему ребенку?»

Ниже приведены 50 самых распространенных проблем со структурами данных, которые можно решить с помощью динамического программирования —

  1. Самая длинная общая подпоследовательность | Введение и длина LCS
  2. Самая длинная общая подпоследовательность | Поиск всех LCS
  3. Проблема с самой длинной общей подстрокой
  4. Самая длинная палиндромная подпоследовательность с использованием динамического программирования
  5. Проблема с самой длинной повторяющейся подпоследовательностью
  6. Утилита Diff для реализации
  7. Самая короткая общая суперпоследовательность | Введение и длина SCS
  8. Кратчайшая общая суперпоследовательность | Поиск всех SCS
  9. Самая длинная возрастающая подпоследовательность с использованием динамического программирования
  10. Самая длинная битоническая подпоследовательность
  11. Возрастающая подпоследовательность с максимальной суммой
  12. Задача о расстоянии Левенштейна (расстояние редактирования)
  13. Найти размер наибольшей квадратной подматрицы из 1-х присутствующих в заданной двоичной матрице
  14. Умножение цепочки матриц с помощью динамического программирования
  15. Найти минимальную стоимость достижения последней ячейки матрицы из ее первой ячейки
  16. Найти самую длинную последовательность, образованную соседними числами в матрице
  17. Подсчитать количество путей в матрице с заданной стоимостью до достичь ячейки назначения
  18. 0–1 Задача о рюкзаке
  19. Максимизация значения выражения
  20. Задача о разбиении | Решение динамического программирования
  21. Проблема суммы подмножеств
  22. Задача о разделе минимальной суммы
  23. Найти все двоичные строки из N цифр без последовательных единиц
  24. Задача обрезания стержня
  25. Обрезка стержня максимального продукта
  26. Задача о размене монет (неограниченное количество монет)
  27. Задача о размене монет (общее количество) способов получить номинал монет)
  28. Задача о самой длинной чередующейся подпоследовательности
  29. Подсчитайте, сколько раз образец появляется в заданной строке в виде подпоследовательности
  30. Соберите максимальное количество точек в матрице, удовлетворяя заданным ограничениям
  31. Подсчитайте общее количество возможных комбинаций N-значных чисел на клавиатуре мобильного телефона
  32. Найдите оптимальную стоимость построения двоичного дерева поиска
  33. Задача с разрывом слов | Динамическое программирование
  34. Проблема разрыва слов | Использование структуры данных Trie
  35. Всего возможных решений линейного уравнения k переменных
  36. Сопоставление шаблонов с подстановочными знаками
  37. Найти вероятность того, что человек выживет после N шагов на острове
  38. Вычислить сумму всех элементов в подматрице в константе время
  39. Найти подматрицу максимальной суммы в заданной матрице
  40. Найти подматрицу максимальной суммы, присутствующую в данной матрице
  41. Найти максимальную сумму подпоследовательности без соседних элементов
  42. Задача о максимальном подмассиве (алгоритм Кадане) Алгоритм Форда
  43. Кратчайшие пути для всех пар — Алгоритм Флойда Уоршалла
  44. Игра Pots of Gold с использованием динамического программирования
  45. Найдите минимальные разрезы, необходимые для палиндромного разбиения строки
  46. Змеиная последовательность максимальной длины
  47. Задача с тремя разделами
  48. Вычислить размер наибольшего плюса 1 в двоичной матрице
  49. Проверить, является ли данная строка чередованием двух других заданных строк

Программирование

0 Алгоритмы

Структуры данных

Динамическое программирование

Вопросы для интервью

Ведущая платформа для подготовки технических интервью.

No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *