Графический метод — линейное программирование
Описание метода
Если в задаче линейного программирования имеется только две переменные, то ее можно решить графическим методом.
Рассмотрим задачу линейного программирования с двумя переменными и :
(1.1) ;
(1.2)
Здесь , есть произвольные числа. Задача может быть как на нахождение максимума (max), так и на нахождение минимума (min). В системе ограничений могут присутствовать как знаки , так и знаки .
Построение области допустимых решений
Графический метод решения задачи (1) следующий.
Вначале мы проводим оси координат и и выбираем масштаб. Каждое из неравенств системы ограничений (1.2) определяет полуплоскость, ограниченную соответствующей прямой.
Так, первое неравенство
(1.2.1)
определяет полуплоскость, ограниченную прямой . С одной стороны от этой прямой , а с другой стороны . На самой прямой . Чтобы узнать, с какой стороны выполняется неравенство (1. 2.1), мы выбираем произвольную точку, не лежащую на прямой. Далее подставляем координаты этой точки в (1.2.1). Если неравенство выполняется, то полуплоскость содержит выбранную точку. Если неравенство не выполняется, то полуплоскость расположена с другой стороны (не содержит выбранную точку). Заштриховываем полуплоскость, для которой выполняется неравенство (1.2.1).
2.1), мы выбираем произвольную точку, не лежащую на прямой. Далее подставляем координаты этой точки в (1.2.1). Если неравенство выполняется, то полуплоскость содержит выбранную точку. Если неравенство не выполняется, то полуплоскость расположена с другой стороны (не содержит выбранную точку). Заштриховываем полуплоскость, для которой выполняется неравенство (1.2.1).
Тоже самое выполняем для остальных неравенств системы (1.2). Так мы получим заштрихованных полуплоскостей. Точки области допустимых решений удовлетворяют всем неравенствам (1.2). Поэтому, графически, область допустимых решений (ОДР) является пересечением всех построенных полуплоскостей. Заштриховываем ОДР. Она представляет собой выпуклый многоугольник, грани которого принадлежат построенным прямым. Также ОДР может быть неограниченной выпуклой фигурой, отрезком, лучом или прямой.
Может возникнуть и такой случай, что полуплоскости не содержат общих точек. Тогда областью допустимых решений является пустое множество. Такая задача решений не имеет.
Такая задача решений не имеет.
Можно упростить метод. Можно не заштриховывать каждую полуплоскость, а вначале построить все прямые
(2)
Далее выбрать произвольную точку, не принадлежащую ни одной из этих прямых. Подставить координаты этой точки в систему неравенств (1.2). Если все неравенства выполняются, то область допустимых решений ограничена построенными прямыми и включает в себя выбранную точку. Заштриховываем область допустимых решений по границам прямых так, чтобы оно включало в себя выбранную точку.
Если хотя бы одно неравенство не выполняется, то выбираем другую точку. И так далее, пока не будет найдены одна точка, координаты которой удовлетворяют системе (1.2).
Нахождение экстремума целевой функции
Итак, мы имеем заштрихованную область допустимых решений (ОДР). Она ограничена ломаной, состоящей из отрезков и лучей, принадлежащих построенным прямым (2). ОДР всегда является выпуклым множеством. Оно может быть как ограниченным множеством, так и не ограниченным вдоль некоторых направлений.
Теперь мы можем искать экстремум целевой функции
(1.1) .
Для этого выбираем любое число и строим прямую
(3) .
Для удобства дальнейшего изложения считаем, что эта прямая проходит через ОДР. На этой прямой целевая функция постоянна и равна . такая прямая называется линией уровня функции . Эта прямая разбивает плоскость на две полуплоскости. На одной полуплоскости
.
На другой полуплоскости
.
То есть с одной стороны от прямой (3) целевая функция возрастает. И чем дальше мы отодвинем точку от прямой (3), тем больше будет значение . С другой стороны от прямой (3) целевая функция убывает. И чем дальше мы отодвинем точку от прямой (3) в другую сторону, тем меньше будет значение . Если мы проведем прямую, параллельную прямой (3), то новая прямая также будет линией уровня целевой функции, но с другим значением .
Таким образом, чтобы найти максимальное значение целевой функции, надо провести прямую, параллельную прямой (3), максимально удаленную от нее в сторону возрастания значений , и проходящую хотя бы через одну точку ОДР. Чтобы найти минимальное значение целевой функции, надо провести прямую, параллельную прямой (3) и максимально удаленную от нее в сторону убывания значений , и проходящую хотя бы через одну точку ОДР.
Чтобы найти минимальное значение целевой функции, надо провести прямую, параллельную прямой (3) и максимально удаленную от нее в сторону убывания значений , и проходящую хотя бы через одну точку ОДР.
Если ОДР неограниченна, то может возникнуть случай, когда такую прямую провести нельзя. То есть как бы мы ни удаляли прямую от линии уровня (3) в сторону возрастания (убывания) , то прямая всегда будет проходить через ОДР. В этом случае может быть сколь угодно большим (малым). Поэтому максимального (минимального) значения нет. Задача решений не имеет.
Рассмотрим случай, когда крайняя прямая, параллельная произвольной прямой вида (3), проходит через одну вершину многоугольника ОДР. Из графика определяем координаты этой вершины. Тогда максимальное (минимальное) значение целевой функции определяется по формуле:
.
Решением задачи является
.
Также может встретиться случай, когда прямая параллельна одной из граней ОДР. Тогда прямая проходит через две вершины многоугольника ОДР. Определяем координаты и этих вершин. Для определения максимального (минимального) значения целевой функции, можно использовать координаты любой из этих вершин:
Определяем координаты и этих вершин. Для определения максимального (минимального) значения целевой функции, можно использовать координаты любой из этих вершин:
.
Задача имеет бесконечно много решений. Решением является любая точка, расположенная на отрезке между точками и , включая сами точки и .
Пример решения задачи линейного программирования графическим методом
Фирма выпускает платья двух моделей А и В. При этом используется ткань трех видов. На изготовление одного платья модели А требуется 2 м ткани первого вида, 1 м ткани второго вида, 2 м ткани третьего вида. На изготовление одного платья модели В требуется 3 м ткани первого вида, 1 м ткани второго вида, 2 м ткани третьего вида. Запасы ткани первого вида составляют 21 м, второго вида — 10 м, третьего вида — 16 м. Выпуск одного изделия типа А приносит доход 400 ден. ед., одного изделия типа В — 300 ден. ед.
Составить план производства, обеспечивающий фирме наибольший доход. Задачу решить графическим методом.
Решение
Пусть переменные и означают количество произведенных платьев моделей А и В, соответственно. Тогда количество израсходованной ткани первого вида составит:
(м)
Количество израсходованной ткани второго вида составит:
(м)
Количество израсходованной ткани третьего вида составит:
(м)
Поскольку произведенное количество платьев не может быть отрицательным, то
и .
Доход от произведенных платьев составит:
(ден. ед.)
Тогда экономико-математическая модель задачи имеет вид:
Решаем графическим методом.
Проводим оси координат и .
Строим прямую .
При .
При .
Проводим прямую через точки (0; 7) и (10,5; 0).
Строим прямую .
При .
При .
Проводим прямую через точки (0; 10) и (10; 0).
Строим прямую .
При .
При .
Проводим прямую через точки (0; 8) и (8; 0).
Прямые и являются осями координат.
Область допустимых решений (ОДР) ограничена построенными прямыми и осями координат.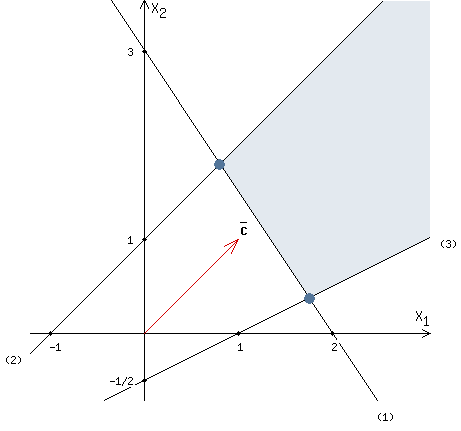 Чтобы узнать, с какой стороны, замечаем, что точка принадлежит ОДР, поскольку удовлетворяет системе неравенств:
Чтобы узнать, с какой стороны, замечаем, что точка принадлежит ОДР, поскольку удовлетворяет системе неравенств:
Заштриховываем область, чтобы точка (2; 2) попала в заштрихованную часть. Получаем четырехугольник OABC.
Строим произвольную линию уровня целевой функции, например,
(П1.1) .
При .
При .
Проводим прямую через точки (0; 4) и (3; 0).
Далее замечаем, что поскольку коэффициенты при и целевой функции положительны (400 и 300), то она возрастает при увеличении и . Проводим прямую, параллельную прямой (П1.1), максимально удаленную от нее в сторону возрастания , и проходящую хотя бы через одну точку четырехугольника OABC. Такая прямая проходит через точку C. Из построения определяем ее координаты.
.
Решение задачи: ;
Ответ
.
То есть, для получения наибольшего дохода, необходимо изготовить 8 платьев модели А. Доход при этом составит 3200 ден. ед.
Пример 2
Решить задачу линейного программирования графическим методом.
Решение
Решаем графическим методом.
Проводим оси координат и .
Строим прямую .
При .
При .
Проводим прямую через точки (0; 6) и (6; 0).
Строим прямую .
Отсюда .
При .
При .
Проводим прямую через точки (3; 0) и (7; 2).
Строим прямую .
Строим прямую (ось абсцисс).
Область допустимых решений (ОДР) ограничена построенными прямыми. Чтобы узнать, с какой стороны, замечаем, что точка принадлежит ОДР, поскольку удовлетворяет системе неравенств:
Заштриховываем область по границам построенных прямых, чтобы точка (4; 1) попала в заштрихованную часть. Получаем треугольник ABC.
Строим произвольную линию уровня целевой функции, например,
.
При .
При .
Проводим прямую линию уровня через точки (0; 6) и (4; 0).
Поскольку целевая функция увеличивается при увеличении и , то проводим прямую, параллельную линии уровня и максимально удаленную от нее в сторону возрастания , и проходящую хотя бы через одну точку треугольника АВC. Такая прямая проходит через точку C. Из построения определяем ее координаты.
Такая прямая проходит через точку C. Из построения определяем ее координаты.
.
Решение задачи: ;
Ответ
.
Пример отсутствия решения
Решить графически задачу линейного программирования. Найти максимальное и минимальное значение целевой функции.
Решение
Решаем задачу графическим методом.
Проводим оси координат и .
Строим прямую .
При .
При .
Проводим прямую через точки (0; 8) и (2,667; 0).
Строим прямую .
При .
При .
Проводим прямую через точки (0; 3) и (6; 0).
Строим прямую .
При .
При .
Проводим прямую через точки (3; 0) и (6; 3).
Прямые и являются осями координат.
Область допустимых решений (ОДР) ограничена построенными прямыми и осями координат. Чтобы узнать, с какой стороны, замечаем, что точка принадлежит ОДР, поскольку удовлетворяет системе неравенств:
Заштриховываем область, чтобы точка (3; 3) попала в заштрихованную часть. Получаем неограниченную область, ограниченную ломаной ABCDE.
Строим произвольную линию уровня целевой функции, например,
(П3.1) .
При .
При .
Проводим прямую через точки (0; 7) и (7; 0).
Поскольку коэффициенты при и положительны, то возрастает при увеличении и .
Чтобы найти максимум, нужно провести параллельную прямую, максимально удаленную в сторону возрастания , и проходящую хотя бы через одну точку области ABCDE. Однако, поскольку область неограниченна со стороны больших значений и , то такую прямую провести нельзя. Какую бы прямую мы не провели, всегда найдутся точки области, более удаленные в сторону увеличения и . Поэтому максимума не существует. можно сделать сколь угодно большой.
Ищем минимум. Проводим прямую, параллельную прямой (П3.1) и максимально удаленную от нее в сторону убывания , и проходящую хотя бы через одну точку области ABCDE. Такая прямая проходит через точку C. Из построения определяем ее координаты.
.
Минимальное значение целевой функции:
Ответ
Максимального значения не существует.
Минимальное значение
.
Графическое решение задач линейного программирования с примерами
Оглавление:
Для решения задач линейного программирования разработано множество методов, но наиболее популярными из них являются графический, симплексный и двойственный методы, которые мы и рассмотрим далее в нашей исследовательской работе.
| Если что-то непонятно — вы всегда можете написать мне в WhatsApp и я вам помогу! |
Возможно эта страница вам будет полезна:
Рассмотрим задачу линейного программирования в стандартной форме записи с двумя переменными
при условиях:
Необходимо найти вектор , удовлетворяющий данной математической модели.
При решении, прежде всего, необходимо найти область допустимых решений системы неравенств (3.2). Рассмотрим декартову систему координат . Заменив каждое из неравенств (3.2) равенством, строим соответствующую ему граничную прямую . На рисунке 1 видно, как эта прямая делит плоскость на две полуплоскости [3].
Чтобы определить, какую именно полуплоскость определяет данное неравенство, достаточно взять произвольную точку плоскости () (например, начало координат) и подставить в неравенство числа . Если оно удовлетворится, то полуплоскость, в которой лежит данная точка — искомая. В противном случае нужная полуплоскость лежит по другую сторону прямой [26].
Для нахождения области допустимых решений строим граничные прямые полуплоскости, соответствующие всем неравенствам. Общая часть («пересечение») всех этих полуплоскостей будет решением системы неравенств данной задачи.
При нахождении области допустимых решений (ОДР) задачи линейного программирования может встретиться один из четырех случаев, рассмотренных в таблице 4:
Рассмотренные примеры позволяют сделать вывод о том, что область допустимых решений системы неравенств может быть пустой, одной точкой, выпуклым многоугольником или неограниченной выпуклой областью.
Согласно теореме, описанной в предыдущем параграфе, оптимальное решение ЗЛП находится в одной из угловых точек многоугольника допустимых решений.
Рассмотрим целевую функцию
Уравнение
при фиксированном значении определяет прямую, а при изменении — семейство параллельных прямых с параметром . Вдоль каждой из этих прямых функция цели принимает одно и то же фиксированное значение, поэтому эти линии называют линиями уровня целевой функции [24].
Для решения задачи необходимо среди точек области допустимых решений найти такую точку (точки), в которой целевая функция принимает максимальное значение.
Для этого построим вектор-градиент , компонентами которого являются коэффициенты при неизвестных целевой функции, и линию уровня целевой функции, которая имеет уравнение и обладает тем свойством, что она перпендикулярна вектору .
Линию уровня в направлении вектора перемещаем до тех пор, пока она не сместится в область недопустимых значений, и все еще будет иметь одну общую точку с ОДР, координаты которой находим из пересечения соответствующих прямых [5].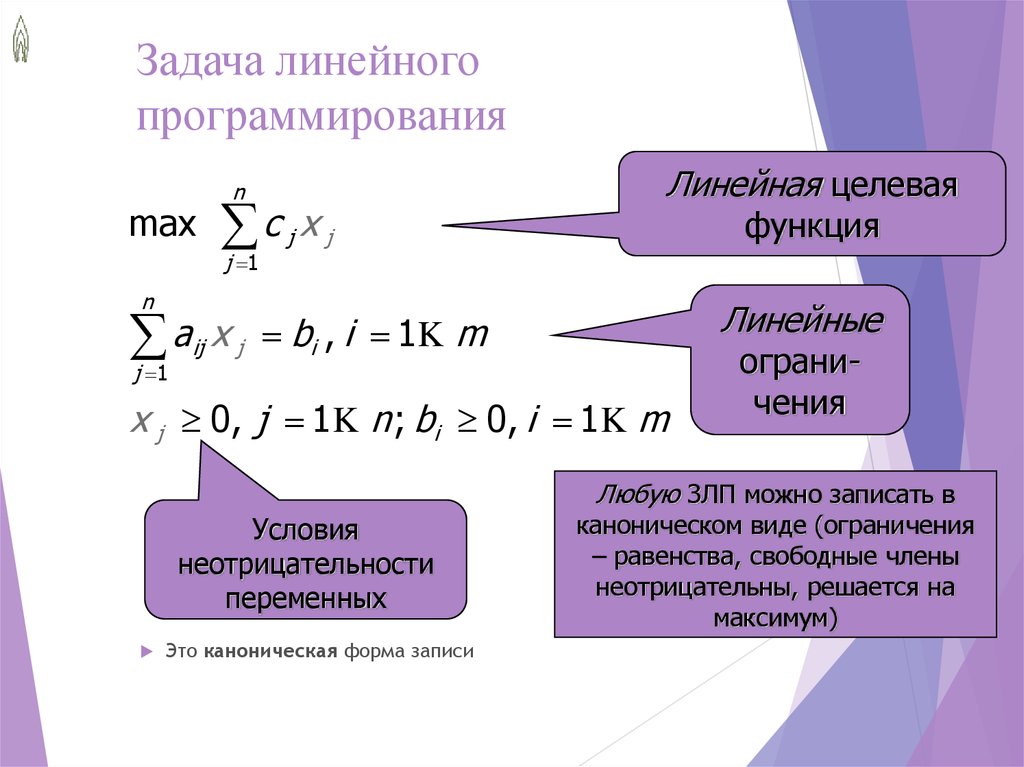
Таким образом, можно определить алгоритм геометрического (графического) решения задач линейного программирования:
- Записать уравнения прямых, соответствующих ограничениям, и построить их на плоскости .
- Определить области, в которых выполняются ограничения задачи.
- Определить область допустимых решений задачи как область пересечения полуплоскостей, соответствующих ограничениям задачи.
- Определить направление возрастания (убывания) целевой функции
- Определить граничную точку или точки области допустимых решений, в которых целевая функция принимает максимальное (минимальное) значение.
- Определить координаты найденной точки, решая систему уравнений, состоящую из уравнений прямых, на пересечении которых находится эта точка, или выявляя уравнение граничной прямой области допустимых решений, с которой совпадает линия уровня целевой функции.
Графический метод решения задачи линейного программирования состоит из двух этапов:
- Построение пространства допустимых решений, удовлетворяющих всем ограничениям модели.

- Поиск оптимального решения среди всех точек пространства допустимых решений.
Применение графического метода удобнее рассмотреть на конкретных примерах в двух постановках: для максимума и минимума целевой функции.
Примеры с решениемПример решения задачи №1:Задана стандартная математическая модель задачи с двумя неизвестными:
Нахождение решения этой модели на основе ее геометрической интерпретации включает следующие этапы.
- В плоскости строят прямые, уравнения которых получаются в результате замены в ограничениях (2.1) модели знаков неравенств на знаки точных равенств.
- Находят полуплоскости, определенные каждым неравенством системы.
- Находят выпуклый многоугольник решений всей системы (2.1).
- Строят нормальный вектор целевой функции , причем, начало вектора совмещают с началом координат и строят прямую .
- Передвигают эту прямую в направлении вектора , в результате либо находят вершину или отрезок, в которой целевая функция принимает наибольшее значение, либо устанавливают неограниченность сверху этой функции на множестве допустимых решений.

- Если функция ограничена, то определяют , вычисляют значение функции в этой точке .
При геометрической интерпретации задач ЛП могут встретиться случаи, изображенные на рис. 2.1. — 2.4.
Рис. 2.1. Задача ЛП имеет единственное решение .
Рис. 2.2. Задача ЛП имеет бесчисленное множество решений, т.к. целевая функция достигает максимума на отрезке .
Рис. 2.3. Задача ЛП не имеет решения, т.к. функция неограниченна сверху.
Рис. 2.4. Задача ЛП не имеет решения, т.к. система (2.1) несовместна.
Для производства двух видов изделий и предприятие использует три вида сырья . Нормы расхода сырья каждого вида на изготовление единицы продукции данного вида приведены в табл. 2.1.
Прибыль от реализации одного изделия каждого вида равна и , а общее количество сырья вида равно . Считая, что изделия и могут производиться в любых соотношениях (сбыт обеспечен), требуется составить такой план их выпуска, при котором прибыль предприятия от реализации всех изделий будет максимальной.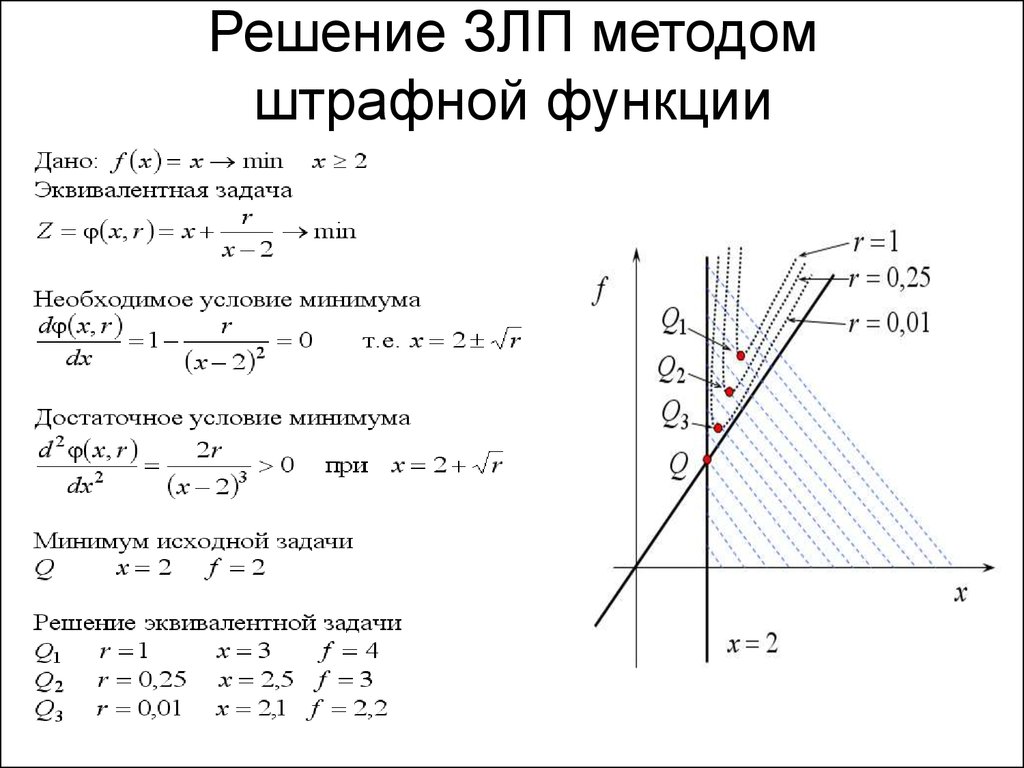
Решение. Обозначим через и количество изделий первого и второго вида в плане предприятия. Поскольку производство продукции ограничено только сырьем каждого типа то получим условия:
Переменные и не могут быть отрицательными по смыслу задачи. Вычислим прибыль от реализации продукции и получим:
Итак, мы получили стандартную модель с двумя переменными.
Решим задачу линейного программирования геометрически, придерживаясь плана, приведенного ранее.
- Строим прямые :
Обратимся к неравенствам (2.3). Отмстим те полуплоскости, которые им удовлетворяют. Учтем на чертеже и неотрицательность переменных и , и получим многоугольник решений данной системы неравенств (см. рис. 2.5).
- Построим линию уровня — прямую и нормальный вектор .
- Передвигая линию уровня в направлении вектора , получим, что в точке (12, 18) целевая функция будет иметь наибольшее значение. Координаты этой точки находим как координаты точки пересечения прямых и , решая систему уравнений:
- Запишем окончательный ответ:
Наибольшая прибыль будет равна 1080 (у. е).
е).
Минимизировать функцию
при ограничениях
Допустимой областью, изображенной на рис. 1.2, является чегырехугольник . Два последних ограничения усиливают условия неотрицательности. Функция убывает в направлении вектора
Минимальное значение функции = — 68 и достигается в точке = (12,8). Заметим, что, как и в примере разд. 1.1, минимум достигается в вершине допустимой области. Оптимальным решением задачи является точках = 2, = 8 с минимальным значением функции = — 68.
Иногда задача имеет более чем одно оптимальное решение.
Пример решения задачи №4:Минимизировать функцию
при ограничениях
На рис. 1.3 чегырехугольник изображает допустимую область , , и, таким образом, вектор указывает направление убывания функции .
Любая точка на отрезке является оптимальным решением. В частности, в вершинах достигаются оптимальные решения, соответствующие одному и тому же минимальному значению функции =-12.
Любая точка на отрезке представляется формулой
где
Для каждой такой точки значение функции равно
Функция имеет единственное минимальное значение.
Иногда решение задачи не ограничено.
Пример решения задачи №5:Максимизировать функцию
при ограничениях
Допустимая область, изображенная на рис. 1.4, не ограничена в направлении, в котором функция возрастает, т. е. в допустимой области не существует конечной точки, в которой функция достигала бы максимума. Решение, как и максимальное значение функции , не ограничено. Однако некоторые задачи с неограниченными допустимыми областями имеют конечные решения. Например, задача максимизации функции при ограничениях из примера 3 имеет конечное решение.
Разумеется, если бы задача состояла в минимизации функции , при тех же ограничениях, то минимум достигался бы в единственной точке в вершине допустимой области .
Иногда задача не имеет решения, поскольку допустимой области не существует.
Минимизировать функцию
при ограничениях
Ограничения задачи противоречивы, поэтому нет допустимых решений (рис. 1.5).
Уже из рассмотренных выше примеров можно вывести несколько характерных черт задач линейного программирования. Во-первых, допустимая область всегда является выпуклым многоугольником, даже в случае, когда она не ограничена. Во-вторых, оптимальное решение всегда достигается в вершинах допустимой области. В примере 2 и вершина , и вершина являются оптимальными точками.
Эти результаты могут быть обобщены. Сначала покажем, что задачи линейного программирования могут быть приведены к стандартной форме.
Пример решения задачи №7:Найти максимум функции при ограничениях
На рис. 3 изображены: неограниченная многогранная область решений данной системы ограничений-неравенств, линия уровня , вектор . Функция может неограниченно возрастать при заданной системе ограничений, поэтому .
Найти максимум функции при ограничениях
Изображенная на рис. 4 область не содержит ни одной общей точки, которая удовлетворяла бы всем неравенствам системы ограничений, т.е. система ограничений противоречива и не может содержать ни одного решения, в том числе и оптимального.
Пример решения задачи №9:Найти максимум функции при ограничениях
Всем неравенствам системы ограничений удовлетворяют точки треугольника , который и является областью решений (рис. 5). Максимальное значение . При построении треугольника не использовали прямые , хотя все точки этого треугольника удовлетворяют неравенствам . Таким образом, эти неравенства лишние в системе ограничений.
Пример решения задачи №10:Найти минимум функции при ограничениях
Областью решений данной системы ограничений является треугольник (рис. 7).
На рис. 7 также изображены исходная линия уровня и вектор . Так как требуется найти минимум функции, то будем передвигать исходную линию уровня в сторону, противоположную . Минимум функции достигается в угловой точке , координаты которой служат решением системы уравнений
Так как требуется найти минимум функции, то будем передвигать исходную линию уровня в сторону, противоположную . Минимум функции достигается в угловой точке , координаты которой служат решением системы уравнений
т.е.
Опорнои прямой называется линия уровня, которая имеет хотя бы одну общую точку с областью допустимых решений и по отношению к которой эта область находится в одной из полуплоскостей.
Область допустимых решений любой задачи имеет не более двух опорных прямых, на одной из которых может находиться оптимальное решение.
На основании приведенных примеров и определения опорной прямой запишем этапы нахождения решения задачи линейного программирования с двумя переменными графическим методом:
- Изображаем область допустимых решений.
- Если область допустимых решений является пустым множеством, то задача не имеет решения ввиду несовместности системы ограничений.
- Если область допустимых решений является непустым множеством, то изображаем нормальный вектор линий уровня и одну из линий уровня, имеющую общие точки с этой областью.

- Линию уровня перемещаем до опорной прямой в задаче на максимум в направлении нормали, в задаче на минимум — в противоположном направлении.
- Если при перемещении линии уровня по области допустимых решений в направлении, соответствующем приближению к максимуму (минимуму) целевой функции, линия уровня уходит в бесконечность, то .
- Если задача линейного программирования имеет оптимальное решение, то для его нахождения решаем систему из уравнений прямых, ограничивающих область допустимых решений и имеющих общие точки с соответствующей опорой прямой. Если целевая функция достигает экстремума в двух угловых точках, то задача имеет бесконечное множество решений. Оптимальным решением является любая выпуклая линейная комбинация этих точек.
- Вычисляем значение целевой функции на оптимальном решении.
Графическим методом решаются задачи линейного программирования, записанные в каноническом виде и удовлетворяющие условию , где — число неизвестных системы ограничений; — ранг системы векторов условий.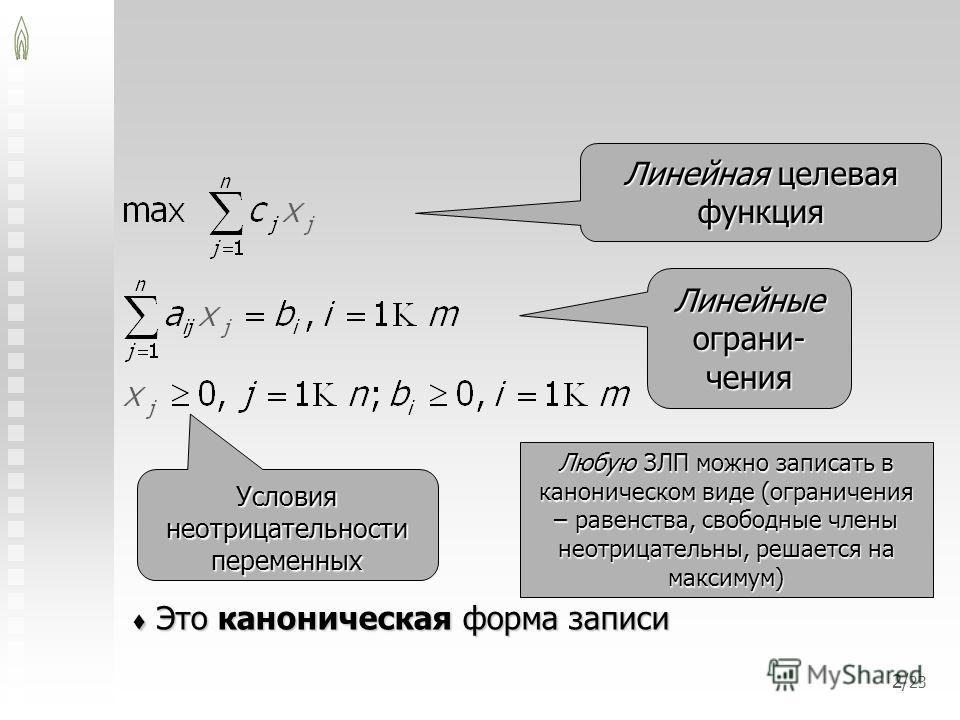 Если уравнения системы ограничений линейно независимы, то ранг равен числу уравнений системы .
Если уравнения системы ограничений линейно независимы, то ранг равен числу уравнений системы .
Возможно эти страницы вам будут полезны:
Примеры решения задач линейного программирования графическим методом
Z=2x1+x2
при ограничениях:
Построим область L допустимых решений. Для этого сначала необходимо построить области решений каждого ограничения-неравенства задачи. После этого находим пересечение таких областей, что дает область L.
Заменим в каждом неравенстве задачи знак неравенства на знак равенства. Получим уравнения прямых, ограничивающих соответствующие полуплоскости решений:
Для
того, чтобы определить, точки какой из
полуплоскостей удовлетворяют данному
неравенству, берем любую точку плоскости,
например точку O(0,0),
и подставляем ее координаты в неравенство.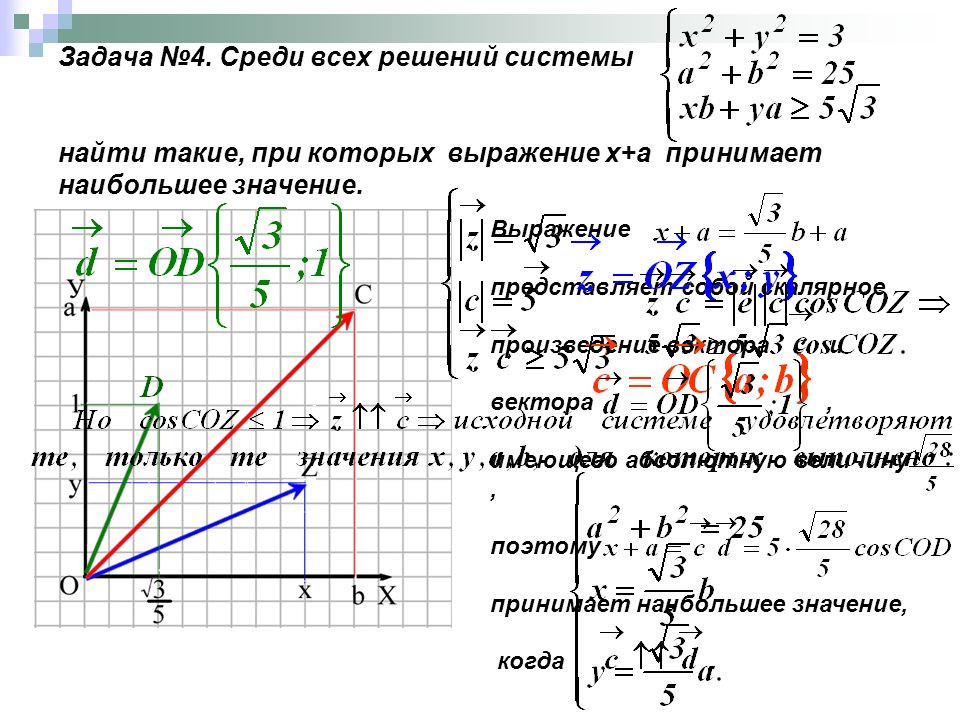 Если окажется, что неравенство
удовлетворяется, то все точки плоскости,
лежащие по ту сторону от прямой, что и
данная, составляют множество решений
соответствующего неравенства. Если же
неравенство не выполняется, то
противоположные точки образуют множество
решений данного неравенства. Будем
штриховать ту сторону разграничивающей
прямой, которая обращена к соответствующему
множеству решений. Кроме того, будем
также указывать стрелками положение
таких множеств решений.
Если окажется, что неравенство
удовлетворяется, то все точки плоскости,
лежащие по ту сторону от прямой, что и
данная, составляют множество решений
соответствующего неравенства. Если же
неравенство не выполняется, то
противоположные точки образуют множество
решений данного неравенства. Будем
штриховать ту сторону разграничивающей
прямой, которая обращена к соответствующему
множеству решений. Кроме того, будем
также указывать стрелками положение
таких множеств решений.
В рассматриваемом примере область L выглядит как на рисунке 2. Область допустимых решений определяется как общая часть полуплоскостей, соответствующих данным неравенствам. Она представляет собой многоугольник ABDEFK.
Для нахождения экстремума строим разрешающую прямую, приравнивая линейную форму нулю: Z=2x1+x2=0. Кроме того, строим градиент C=(2;1) целевой функции.
О
чевидно,
что максимальное значение функция
принимает в вершине (крайней точке)  Координаты этих точек найдем как
пересечение соответствующих прямых.
Так точка А — точка пересечения прямых:
Координаты этих точек найдем как
пересечение соответствующих прямых.
Так точка А — точка пересечения прямых:
x1+x2=1, x1=0.
Очевидно, А(0;1)=Xmin(0;1), minZ=2.0+1=1.
Аналогично можно получить координаты точки Е, решив совместно второе и третье уравнения:
x1=3, 3x1+2x2=12, E(3;1.5)=Xmax(3;1.5),
maxZ=23+1.5=7.5.
Пример 2. Найти максимум и минимум линейной формы
Z=x1+3x2при ограничениях:
Построим
область L допустимых решений. Заменим в каждом
неравенстве задачи знак неравенства
на знак равенства. Получим уравнения
прямых:
Получим уравнения
прямых:
О бласть допустимых решений L определяется как общая часть полуплоскостей, соответствующих неравенствам. Она представляет собой неограниченную область (рисунок 3).
Для нахождения экстремумов строим разрешающую прямую, приравнивая линейную форму нулю: Z=x1+3x2=0. Строим градиент С(1;3) целевой функции.
Минимальное значение функция Z принимает в вершине A, координаты которой соответствуют точке пересечения прямых:
3x1+5x2
Решая систему, получим:
A(10/3;1)=Xmin(10/3;1), minZ=10/3+3.1=6.
Область
допустимых решений L неограниченна, а линейная форма
неограниченно возрастает и максимума
не имеет.
Найти максимум и минимум линейной формы графическим методом по исходным данным задачи ЛП (таблица 1).
Таблица 1
Номер варианта | Целевая функция | Ограничения задачи линейного программирования |
| 1 2 | 2x1+5x2 -5x1+2x2 | |
3 4 | 5x1+3x2 -3x1+5x2 | |
5 6 | 2x1—4x2 2x1+4x2 | |
7 | 3x1+2x2 -2x1+3x2 | |
9 10 | x1—2x2 2x1+x2 |
|
⇐ ПредыдущаяСтр 3 из 15Следующая ⇒ Задача с двумя переменными Графическим методом могут быть решены задачи линейного программирования с двумя переменными и некоторые задачи с большим числом переменных при выполнении определенных условий. Задача линейного программирования с двумя переменными должна иметь систему ограничений, представляющую собой систему неравенств. Неравенства могут быть как вида » £ «, так и » ³ «. Условия неотрицательности могут отсутствовать. Математическая модель должна иметь вид (2.1) (2.2) . Метод решения данной задачи основывается на возможности графического изображения области допустимых решений (ОДР) и нахождения в этой области оптимального решения. Для обоснования метода докажем две теоремы. Теорема 2.1. О виде области решений линейного неравенства. Областью решений линейного неравенства является одна из двух полуплоскостей, на которые разбивает всю координатную плоскость прямая , соответствующая этому неравенству. Доказательство. В системе координат О построим прямую (L) и ее нормаль (рис. 2.1). Рис. 2.1 Прямая (L) разбивает плоскость О на две полуплоскости: верхнюю ( ), соответствующую направлению нормали , и нижнюю ( ). Пусть произвольно выбранная точка М( ) принадлежит ( ), ее проекцией на прямую (L) является точка . Вектор . Координаты векторов и совпадают с координатами точек М и А, т. е. = ( ), . Вектор коллинеарен вектору , поэтому = ×l, где l некоторое число. Найдем скалярное произведение . Запишем это равенство через координаты векторов . Так как точка А принадлежит прямой (L), то , получаем . Отсюда следует, что если l>0, т. е. M Î( ), то и тогда . Если же l<0, M Î( ), то и . Пример 2.1. Найти область решений неравенства . Решение. Строим прямую (рис. 2.2).
Чтобы определить какая из двух полуплоскостей является областью решений, выбираем произвольно «пробную» точку, не лежащую на прямой, и подставляем ее координаты в неравенство. Если неравенство выполняется, то область, содержащая эту «пробную» точку, является областью решений. Если же неравенство не выполняется, то областью решений будет полуплоскость, не содержащая «пробную» точку. В рассматриваемом примере в качестве «пробной» точки возьмем О(0, 0). Подставляем координаты этой точки в неравенство, получаем 2 × 0 + 3 × 0 £ 6 Û 0 £ 6, следовательно, областью решений является полуплоскость, содержащая начало координат. Этот факт отмечаем на рисунке стрелками. В общем случае, когда система ограничений состоит из нескольких неравенств, область допустимых решений (ОДР) находят как пересечение полуплоскостей – решений каждого из неравенств-ограничений. ОДР может быть пустым множеством, многоугольником и многоугольным множеством (многоугольником, неограниченным с одной из сторон). Линией уровня называется прямая, в точках которой целевая функция постоянна Z(X) = . Уравнение линий уровня , с = const. Теорема 2.2. Об изменении значений функции. Значения целевой функции в точках линий уровня возрастают, если линии уровня перемещать в направлении их нормали, и убывают при перемещении линий уровня в противоположном направлении. Рис. 2.3 Доказательство. Пусть целевая функция задачи линейного программирования имеет вид Z(X) = . В системе координат О построим две линии уровня (L ) и (L ) (рис. 2.3). Их общая нормаль . Пусть точка М( ) Î (L ), а точка Î(L ) является проекцией М на (L ). Вектор , = ( ), . Так как коллинеарен вектору , то вектор = ×l, где l число. Скалярное произведение . Используя координаты векторов и , можно записать . Отсюда получаем следующие выводы: 1) если линия уровня перемещается в направлении нормали из положения (L ) к (L ), то l > 0 и, следовательно, ; 2) если же линия уровня перемещается в направлении противоположном направлению нормали из положения (L ) к (L ), то l < 0 и, следовательно, . Таким образом, если задача линейного программирования на максимум, то для нахождения оптимального решения линии уровня надо перемещать по ОДР в направлении нормали, а в задаче на минимум наоборот – в противоположном направлении. Для нахождения оптимального решения задачи необходимо использовать опорную прямую. Опорной прямой называется линия уровня, относительно которой ОДР находится в одной из полуплоскостей и которая имеет хотя бы одну общую точку с ОДР. Если ОДР является замкнутым многоугольником, то независимо от вида целевой функции имеется две опорных прямых. Если же ОДР – многоугольное множество (незамкнутый многоугольник), то в зависимости от направления нормали линий уровня ОДР может иметь как две, так и одну опорную прямую. Алгоритм графического метода решения задач линейного программирования с двумя переменными заключается в следующем. 1. Строится область допустимых решений. 2. Если область допустимых решений является пустым множеством, то ввиду несовместности системы ограничений задача не имеет решения. 3. Если область допустимых решений – это непустое множество, то строится нормаль линий уровня и одна из линий уровня, имеющая общие точки с этой областью. 4. Линия уровня перемещается до опорной прямой в задаче на максимум в направлении нормали, в задаче на минимум – в противоположном. 5. Если при перемещении линии уровня по области допустимых решений в направлении, соответствующем приближению к экстремуму целевой функции, линия уровня уходит в бесконечность, то задача не имеет решения ввиду неограниченности целевой функции. 6. Если задача линейного программирования имеет оптимальное решение, то для его нахождения решаются совместно уравнения прямых, ограничивающих область допустимых решений и имеющих общие точки с соответствующей опорной прямой. Пример 2.2. Решить задачу линейного программирования Рис. 2.4 Решение. Изобразим на плоскости систему координат (рис. 2.4) и построим граничные прямые области допустимых решений. Прямые, ограничивающие ОДР: Область допустимых решений определяется многоугольником ОАВСD. Для линий уровня (с = const) строим нормальный вектор . Перпендикулярно вектору построим одну из линий уровня (на рисунке она проходит через начало координат). Так как задача на максимум, то перемещаем ее в направлении вектора до опорной прямой. На рисунке видно, что опорная прямая проходит через точку B, являющуюся точкой пересечения первой и второй граничных прямых, . Получаем = 3, = 6. Данному оптимальному решению Ответ: max Z(X) = 30 при X = (3; 6). Пример 2.3 Решить задачу линейного программирования.
Рис. 2.5 Решение. Строим область допустимых решений, нормаль линий уровня и одну из линий уровня, имеющую общие точки с этой областью (рис. 2.5). Перемещаем линию уровня в направлении противоположном направлению нормали , так как решается задача на отыскание минимума функции. Нормаль линии уровня и нормаль = (2; 1) второй граничной прямой, в направлении которой перемещаются линии уровня, параллельны, так как их координаты пропорциональны 4/2 = 2/1. Следовательно, опорная прямая совпадает со второй граничной прямой области допустимых решений, проходит через две угловые точки этой области и . Вычисляем Ответ: при Пример 2.4. Решить задачу линейного программирования. Рис. 2.6 Прямые, ограничивающие ОДР: Решение. Строим область допустимых решений, нормаль и одну из линий уровня (рис. 2.6). В данной задаче необходимо найти максимум целевой функции, поэтому линию уровня перемещаем в направлении нормали. Ввиду того, что в этом направлении область допустимых решений не ограничена, линия уровня уходит в бесконечность. Задача не имеет решения по причине неограниченности целевой функции. Ответ: . Пример 2.5. Решить задачу линейного программирования. Рис. 2.7 Решение. Строим прямые линии, соответствующие неравенствам системы ограничений и находим полуплоскости, являющиеся областями решений этих неравенств (рис. Ответ: система ограничений несовместна. Лекция №3 ГРАФИЧЕСКИЙ МЕТОД РЕШЕНИЯ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ Графический метод решения задач линейного Данным методом решаются задачи линейного программирования, имеющие каноническую форму и удовлетворяющие условию , где n – число неизвестных системы, r – ранг системы векторов-условий (число линейно независимых уравнений системы). Если уравнения системы ограничений линейно независимые, то r = m. Рассмотрим алгоритм метода на конкретном примере. Пример 2.6. Решить графическим методом. , . Решение. 1. Проверяем условие применимости графического метода. Нетрудно видеть, что любые два из векторов-столбцов системы ограничений, например, , являются линейно независимыми, так как их координаты непропорциональны, поэтому ранг системы векторов-условий r = 2. 2. Приведем систему ограничений-уравнений к равносильной, разрешенной с помощью метода Жордана – Гаусса. Одновременно исключим разрешенные неизвестные из целевой функции. Для этого Т а б л и ц а 2.1
запишем коэффициенты целевой функции в последней (третьей) строке таблицы, под матрицей системы. 3. Отбросим в уравнениях-ограничениях неотрицательные разрешенные неизвестные и и заменим знаки равенства знаками » «, получим эквивалентную задачу линейного программирования с двумя переменными которая решается графическим методом (рис. 2.8).
Рис. 2.8 Оптимальное решение ; = (2; 0). Значение целевой функции = 4 × 2 + 0 + 5 = 13. 4. Используем систему ограничений исходной задачи, приведенную к каноническому виду, и оптимальное решение задачи с двумя переменными = (2; 0) для нахождения оптимального решения исходной задачи ; . Записываем оптимальное решение исходной задачи Ответ: max Z(X) = 13 при = (3; 0; 2; 0). Задания для самостоятельного решения Решить задачи линейного программирования графическим методом. Пример 2.7. , Пример 2.8. , Пример 2.9. , Пример 2.10. ,
Пример 2.11. ,
Пример 2.12. ,
Лекция№4. СВОЙСТВА РЕШЕНИЙ ЗАДАЧ ЛИНЕЙНОГО ⇐ Предыдущая12345678910Следующая ⇒ |
Графические методы решения задач — Энциклопедия по экономике
На последующих примерах мы рассмотрим графический метод решения задачи линейного программирования. В предыдущем примере мы рассматривали задачу максимизации, где все ограничения были выражены в виде неравенств, т. е. задачи линейного программирования могут иметь различные по виду ограничения, то есть там может быть сочетание >,задачи минимизации также важны. Так, компания может поставить задачу минимизировать затраты, рабочее время и убытки. На последующих примерах мы и рассмотрим применение графического метода в таких случаях.
[c.272]
е. задачи линейного программирования могут иметь различные по виду ограничения, то есть там может быть сочетание >,задачи минимизации также важны. Так, компания может поставить задачу минимизировать затраты, рабочее время и убытки. На последующих примерах мы и рассмотрим применение графического метода в таких случаях.
[c.272] Графические методы решения задач [c.472]
| Рис. 1.2. Графический метод решения задачи |
ЭВМ семейства СМ, профессиональных персональных ЭВМ. При всех вариантах проектирования АРМ пользователь должен иметь возможность использовать лично устройства, позволяющие ему выполнять должностные функции. К таким устройствам относятся алфавитно-цифровые или графические дисплеи, устройства ввода-вывода, накопители на магнитных носителях. Опосредованное использование могут находить устройства связи ЭВМ между собой и с ЭВМ верхнего уровня, средства передачи и приема информации на расстоянии. Экон. эффект от внедрения АРМ складывается из двух составляющих. Во-первых, это повышение качества управленческих решений, принимаемых с помощью информации, предоставляемой АРМ. Во-вторых, эффект, получаемый за счет снижения трудоемкости выполнения личной работы сотрудников. С помощью АРМ р. целесообразно решать задачи, ограниченные по своим информационным связям на входе и выходе с др. задачами, т.е. локальные в информационном отношении задачи. АРМ р. присущ диалоговый метод решения задач, позволяющий использовать производственный опыт руководителей и специалистов при решении задач с недостаточно четко формализованным алгоритмом. Проектирование и внедрение АРМ р. основывается на принципах проектирования систем обработки данных, основными из которых являются принцип максимальной ориентации на конечного пользователя (реализация данного принципа достигается созданием средств адаптации АРМ к уровню подготовки пользователя и возможностью его обучения (самообучения) непосредственно на данном АРМ) принцип проблемной ориентации — обеспечивает ориентацию АРМ на решение определенного класса задач, объединенных общей технологией обработки данных, единством режимов работы и эксплуатации принцип соответствия информационным потребностям пользователя.
Экон. эффект от внедрения АРМ складывается из двух составляющих. Во-первых, это повышение качества управленческих решений, принимаемых с помощью информации, предоставляемой АРМ. Во-вторых, эффект, получаемый за счет снижения трудоемкости выполнения личной работы сотрудников. С помощью АРМ р. целесообразно решать задачи, ограниченные по своим информационным связям на входе и выходе с др. задачами, т.е. локальные в информационном отношении задачи. АРМ р. присущ диалоговый метод решения задач, позволяющий использовать производственный опыт руководителей и специалистов при решении задач с недостаточно четко формализованным алгоритмом. Проектирование и внедрение АРМ р. основывается на принципах проектирования систем обработки данных, основными из которых являются принцип максимальной ориентации на конечного пользователя (реализация данного принципа достигается созданием средств адаптации АРМ к уровню подготовки пользователя и возможностью его обучения (самообучения) непосредственно на данном АРМ) принцип проблемной ориентации — обеспечивает ориентацию АРМ на решение определенного класса задач, объединенных общей технологией обработки данных, единством режимов работы и эксплуатации принцип соответствия информационным потребностям пользователя. К определению состава и функций АРМ р. следует приступать только после установления информационных потребностей пользователя, которые обеспечивают выполнение им возложенных на него функций. Обязательным условием разработки эффективного АРМ р. является совместное участие будущего пользователя и разработчика в этом процессе. Это обеспечивает лучшее осознание всех проблемных ситуаций, стимулирует творческую дея-
[c.3]
К определению состава и функций АРМ р. следует приступать только после установления информационных потребностей пользователя, которые обеспечивают выполнение им возложенных на него функций. Обязательным условием разработки эффективного АРМ р. является совместное участие будущего пользователя и разработчика в этом процессе. Это обеспечивает лучшее осознание всех проблемных ситуаций, стимулирует творческую дея-
[c.3]
Q графические методы решения экономических задач и представления результатов анализа [c.436]
Таким образом, графическое решение никоим образом нельзя рассматривать как практический метод решения задач линейного программирования. Однако проведенный графический анализ дает [c.59]
Первая геометрическая интерпретация ЗЛП и графический метод решения. Рассмотрим следующий пример. Пусть дана задача максимизации линейной целевой функции [c.23]
Несмотря на свою очевидную ограниченность, графический метод решения ЗЛП часто оказывается полезным. В частности, он может быть применен не только к задачам с двумя переменными и ограничениями в виде неравенств, но и к каноническим задачам вида (1. 7), у которых п — т = 2, где п — количество переменных, am — ранг матрицы А.
[c.26]
7), у которых п — т = 2, где п — количество переменных, am — ранг матрицы А.
[c.26]
Графические методы решения игр. Следует отметить, что применение для решения задач (6.16)-(6.17), (6.18)-(6.19) стандартных алгоритмов линейного программирования далеко не всегда является рациональным. Помимо этого существуют иные методы, которые основываются на использовании специфики данных задач. В настоящем пункте мы остановимся на очень простом классическом способе поиска оптимальных смешанных стратегий в матричных играх, где один из участников имеет только две стратегии (это так называемые 2 х п и т х 2 игры). [c.194]
Б. Какая комбинация принтеров и компьютеров будет максимизировать операционную прибыль корпорации IT . Используйте для решения задачи графический метод и метод проб и ошибок. [c.389]
Три первые задачи уже рассмотрены в главе о производственной деятельности. Решение проблемы расчета прибыли предприятия может быть представлено несколькими вариантами применение формул для расчета, графический метод отражения взаимосвязи прибыли и объема производства. [c.258]
[c.258]
При использовании многих аналитических методов на первом этапе часто полезно попытаться графически отобразить полученные данные. Такой подход может привести к решению задачи, и отпадет необходимость прибегать к сложным аналитическим приемам. Но, к сожалению, графическое отображение данных часто недооценивают в качестве инструмента делового общения. График разброса полезен с точки зрения иллюстрации возможного соотношения наборов данных. На последующих примерах мы рассмотрим, как пользоваться этим графиком. [c.100]
Мы рассмотрим графическое решение задач линейного программирования на данных тех примеров, что приведены в предыдущем разделе. В принципе, метод состоит из двух этапов [c.266]
Как мы уже отмечали, графические методы, описанные в предыдущих разделах, приемлемы только в отношении задач с не более чем двумя неизвестными (например, х и у). В большинстве практических ситуаций число неизвестных может быть гораздо большим. Симплексный метод — один из наиболее известных подходов к решению задач линейного программирования через алгебраические методы. Симплексный метод применяется в самых разнообразных компьютерных программах, предназначенных для решений таких задач.
[c.279]
Симплексный метод применяется в самых разнообразных компьютерных программах, предназначенных для решений таких задач.
[c.279]
В этой главе мы рассмотрели приемы линейного программирования при решении задач оптимизации. Типичный пример — максимизация прибыли предприятия за счет определения соответствующей номенклатуры производства. Кроме того, задачи линейного программирования могут быть направлены на минимизацию переменных, в частности затрат. Выражение, которое необходимо оптимизировать, называется объективной функцией. Эта функция высчитывается при наличии ряда ограничений. Одна из самых больших трудностей при решении такого рода задач состоит в исходной постановке задачи, когда необходимо определить ограничения, представить их в виде неравенств и выдать выражение объективной функции. При решении простых задач только с двумя переменными можно применить графический метод. Для более сложных задач применяется симплексный метод. [c.304]
Известно, что в случае двух переменных решение задачи математического программирования можно провести не только аналитически (например, используя симплекс-метод), но и графически. В нашем примере интерес представляет только целочисленное решение.
[c.221]
В нашем примере интерес представляет только целочисленное решение.
[c.221]
Линейное программирование — математический метод, предназначенный для выявления оптимального решения из большого числа возможных вариантов решения задачи, у которой условия позволяют запись в виде линейных соотношений. Линейное программирование применяется для решения задач типа распределение ресурсов, формирование комбинации кормов, составление портфеля инвестиций, выбор производственной программы. Для постановки задачи линейного программирования необходимо ввести переменные (определяемые) величины, выразить через эти переменные ограничивающие условия и целевую функцию. Для решения задач линейного программирования используют симплекс-метод или графический метод (при наличии двух переменных в решаемой задаче). [c.122]
В результате проведенных исследований разработаны аналитический и графический методы, позволяющие обосновывать и принимать решения по масштабу, фондоемкости производства, затратам, цене, обеспечивающим заданную прибыльность выпуска продукции. Эти методы позволяют решать и обратную задачу определять уровень относительной прибыли (по отношению к себестоимости) по двум отношениям отношению по-
[c.59]
Эти методы позволяют решать и обратную задачу определять уровень относительной прибыли (по отношению к себестоимости) по двум отношениям отношению по-
[c.59]
Широкое распространение в мире получила система методов управления проектами, известная в России под названием сетевое планирование и управление (СПУ). Аппарат СПУ предназначен для решения двух основных проблем формирования календарного графика выполнения работ проекта и принятия эффективных решений в процессе его реализации. Эффект, достигаемый при использовании системы СПУ, обусловлен формализацией структуры проекта и количественным выражением его параметров, в первую очередь — временных. Это позволяет использовать строгий математический аппарат и средства вычислительной техники для анализа и синтеза сетевых графиков проектов. Система СПУ — один из наиболее известных примеров использования математического аппарата к решению задач экономико-управленческого характера. Она основана на графическом представлении комплекса работ в виде сетевой модели проекта, которая отражает логические последовательности и взаимосвязи между отдельными работами. Для формального отображения сетевых моделей применяется математический аппарат теории графов.
[c.120]
Для формального отображения сетевых моделей применяется математический аппарат теории графов.
[c.120]
Такая же задача ставится и при составлении бизнес-плана по вновь начинаемому деловому проекту на существующем предприятии. Решение ее позволяет сбалансировать доходы и расходы в рамках утверждаемого и контролируемого бюджета данного проекта. Поставленная задача может быть решена как аналитическим ( формульным ), так и графическим методами. [c.82]
Вероятностные сетки удобны для решения многих задач прикладной статистики графическими методами, не требующими вычислений. В частности с их помощью можно осуществлять оценку согласия опытного распределения с теоретическим, выполнять операции статистического приемочного контроля по количественному признаку и т. п. Они обладают большой наглядностью. [c.26]
При графическом решении задачи мы ограничивались двумя компонентами. Но для составления смеси требуемого состава могли быть использованы и другие компоненты. Для решения задачи при п компонентах, если заданы т ограничений, целесообразно применить симплексный метод. Он позволяет находить допускаемое решение и осуществлять последующие систематические переходы к другим допустимым решениям, предусматривающим меньшую стоимость. При этом необходимо установить, является ли данное решение оптимальным и каким образом следует производить переходы от одной точки к другой, чтобы уменьшить стоимость требуемой смеси. Симплекс метод дает ответы на эти вопросы, и решение будет оптимальным, если какой-либо использованный компонент дает чистый выигрыш.
[c.191]
Он позволяет находить допускаемое решение и осуществлять последующие систематические переходы к другим допустимым решениям, предусматривающим меньшую стоимость. При этом необходимо установить, является ли данное решение оптимальным и каким образом следует производить переходы от одной точки к другой, чтобы уменьшить стоимость требуемой смеси. Симплекс метод дает ответы на эти вопросы, и решение будет оптимальным, если какой-либо использованный компонент дает чистый выигрыш.
[c.191]
Второй этап — постановка экстремальных задач раскроя, их приближенное и точное решение. Здесь в центре внимания научный анализ возможностей экономии материала при раскрое. Одновременно анализируется роль налагаемых ограничений, а также свобода в технологической реализации оптимальных раскроев. Выделяются подлежащие внедрению решающие моменты в изменении технологии. На первом шаге расчеты ведутся вручную с привлечением подбора и графических методов. Второй шаг — перенос части расчетов на ЭВМ. К этому уровню анализа задач раскроя относится наша книга и большая часть упоминаемой во всем этом обзоре литературы. [c.229]
[c.229]
Выбор методов анализа собранной информации о рынке во многом обусловлен целью работы, квалификацией исследователей, качеством первичной информации, содержанием конкретной задачи. Традиционно для решения задач исследования рынка используются в различных сочетаниях следующие методы группировка, индексный и графический методы, выравнивание и прогнозирование временных рядов, корреляционный и регрессионный анализ, экспертные оценки. Несколько реже применяется метод моделирования [21]. [c.51]
Рассмотрим несколько примеров решения задач графическим методом. [c.347]
Если бы количество заготовок было больше двух, то такой графический способ решения оказался бы слишком сложным, практически трудно реализуемым, так как для изображения множества осуществимых планов потребовалось бы построить многогранник в многомерном пространстве. Для решения задачи в этих случаях на помощь приходят аналитические методы и, в частности, эффективный метод разрешающих множителей— оценок, особых показателей, характеризующих оптимальный план. [c.13]
[c.13]
Если бы количество заготовок было больше двух, то графический способ решения (рис. 3) оказался бы практически трудно реализуемым. Дело в том, что для изображения множества осуществимых планов нужно построить очень сложную геометрическую фигуру — многогранник в многомерном пространстве. Поэтому для решения задачи более рационально использовать аналитические методы и, в частности, эффективный метод разрешающих множителей — оценок, особых показателей, характеризующих оптимальный план. [c.15]
Таким образом, с геометрической точки зрения задача максимизации сводится к определению такой точки области Д через которую проходит линия уровня, соответствующая наибольшему из возможных значений. Последнее означает, что для нахождения точки экстремума в задаче линейного программирования мы должны сначала построить линию уровня для некоторого произвольного значения целевой функции. Затем необходимо осуществлять ее параллельное передвижение (так, чтобы она оставалась перпендикулярной вектору с) до тех пор, пока не достигнем такой точки области допустимых планов Д из которой смещение в направлении вектора с было бы невозможно. Такой метод решения получил название графического. Заметим, что решение задачи поиска минимума линейной функции осуществляется аналогично, с той лишь разницей, что движение по линиям уровня должно производиться в направлении, обратном градиенту целевой функции, т. е. по вектору (-с).
[c.25]
Такой метод решения получил название графического. Заметим, что решение задачи поиска минимума линейной функции осуществляется аналогично, с той лишь разницей, что движение по линиям уровня должно производиться в направлении, обратном градиенту целевой функции, т. е. по вектору (-с).
[c.25]
Практическое значение теорем двойственности состоит в том, что они позволяют заменить процесс решения основной задачи на решение двойственной, которое в определенных случаях может оказаться более простым. Например, задача, область допустимых значений которой описывается двумя уравнениями, связывающими шесть переменных (т = 2, п = 6), не может быть решена графическим методом. Однако данный метод может быть применен для решения двойственной к ней задачи, которая имеет только две переменные. [c.62]
Решение задач с помощью графического метода содержит элементы не только аналитического, но и графического порядка. Большая наглядность является основным достоинством рассматриваемого метода. Однако область его применения ограничена решением задач с двумя и тремя переменными.
[c.188]
Однако область его применения ограничена решением задач с двумя и тремя переменными.
[c.188]
Задача об использовании оборудования. Ход решения задач симплексным методом рассмотрим на примере загрузки оборудования, который был использован в одной из предыдущих глав, при изложении графического метода линейного программирования. [c.298]
Среди них можно выделить традиционные логические способы, которые широко применяются и в других дисциплинах для обработки и изучения информации (сравнение, графический, балансовый, средних и относительных величин, аналитических группировок, эвристические методы решения экономических задач на основании интуиции, прошлого опыта, экспертных оценок специалистов и т.д.). [c.15]
Решение задачи произвести аналитическим и графическим методами. [c.364]
В этом разделе мы рассмотрим решение задачи линейного программирования с помощью графических методов. Необходимо отметить, что такой метод имеет практический смысл только при рассмотрении двух неизвестных переменных (например, х и у), и он непригоден при решении задач с более, чем двумя неизвестными. Так, если руководитель производства Стенлюкс захочет определиться по количеству трех и более различных моделей холодильников, то в этом случае графический метод применять нельзя. Аналогично, аналитик по инвестициям Вили-Макен не сможет пользоваться графическим методом при оптимизации портфеля из более чем двух акций. То есть вы видите, что графический метод крайне ограничен. Однако он дает полезное представление о том, как вести поиск оптимальных решений, что может оказать помощь при анализе более сложных задач с большим количеством переменных.
[c.266]
Так, если руководитель производства Стенлюкс захочет определиться по количеству трех и более различных моделей холодильников, то в этом случае графический метод применять нельзя. Аналогично, аналитик по инвестициям Вили-Макен не сможет пользоваться графическим методом при оптимизации портфеля из более чем двух акций. То есть вы видите, что графический метод крайне ограничен. Однако он дает полезное представление о том, как вести поиск оптимальных решений, что может оказать помощь при анализе более сложных задач с большим количеством переменных.
[c.266]
Теоретической основой применения графических методов и моделей, по мнению В.М.Цимбалова1, является прежде всего теория графов, которая зародилась в XVIII в. как математическая задача Эйлера о прогулке по замкнутому маршруту в прусском городе Кенигсберге и была развита в XIX в. в связи с возникшей в Англии математической задачей о четырех красках, решенной лишь совсем недавно. В XX в. теория графов прошла определенные стадии формирования и была признана самостоятельной дисциплиной. [c.59]
[c.59]
Графический метод решения одноиндексных задач
Лабораторная работа №2
ЛАБОРАТОРНАЯ РАБОТА №2
“ГРАФИЧЕСКИЙ МЕТОД РЕШЕНИЯ ОДНОИНДЕКСНЫХ ЗАДАЧ ” 2.1. ЦЕЛЬ РАБОТЫ
Приобретение навыков решения задач линейного программирования графическим методом.
2.2. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Согласно номеру своего варианта выберите условие задачи и найдите оптимальное решение графическим методом.
2. Найдите оптимальное решение задачи в Excel.
3. Оформите отчет по лабораторной работе, который должен содержать:
титульный лист;
исходные данные варианта;
решение задачи;
результаты решения задачи.
2. 3. ИНСТРУКЦИЯ ПО ИСПОЛЬЗОВАНИЮ Microsoft Excel ДЛЯ РЕШЕНИЯ ЗАДАЧ ЛП ГРАФИЧЕСКИМ МЕТОДОМ
3. ИНСТРУКЦИЯ ПО ИСПОЛЬЗОВАНИЮ Microsoft Excel ДЛЯ РЕШЕНИЯ ЗАДАЧ ЛП ГРАФИЧЕСКИМ МЕТОДОМ
Рассмотрим пример нахождения оптимального решения графическим методом для следующей задачи линейного программирования:
Для того чтобы решить задачу ЛП в табличном редакторе Microsoft Excel, необходимо выполнить следующие действия.
1. В столбце А, начиная с ячейки А2, задаем последовательность значений переменной x1 как арифметическую прогрессию с первым членом, равным нулю, разностью 0,2, предельным значением 6.
2. В ячейке В2 вводим формулу =10-А2 и копируем ее в столбце В. Прямые х1=6, х2=8 зададим позже, как границы рисунка.
3. Вводим в ячейку С2 формулу линии уровня =($D$2-5-A2)/3 и копируем ее в столбце С.
4. В ячейке D2 вводим значение 0.
5. Выделяем диапазон А2:С32 и «Мастером диаграмм» строим точечную диаграмму:
6. Убираем лишнее через контекстное меню:
Командами Формат оси Шкала открываем диалоговое окно:
Устанавливаем в нем максимальное значение: 6, нажимаем ОК. Аналогично по оси Y задаем минимальное значение 0, максимальное значение 8.
Приводим диаграмму к виду, показанному на рисунке:
7. Изменяя значения ячейки D2, передвигаем линию уровня в сторону выхода из области допустимых решений:
Из диаграммы видно, что точкой выхода линии уровня из многоугольника допустимых решений является точка (2; 8).
Графическим методом можно решить задачи ЛП, записанные в каноническом виде и удовлетворяющие условию , где n – число неизвестных системы ограничений; r – ранг системы векторов условий.
Рассмотрим пример решения задачи ЛП:
Графический метод применим, так как . Методом Жордана-Гаусса приведем систему уравнений-ограничений задачи к равносильной разрешенной.
Введем расширенную матрицу системы ограничений и коэффициенты целевой функции в диапазон B2:G5:
В ячейке В7 зададим формулу =B2/$B$2 и методом «протаскивания» маркера заполнения скопируем ее в ячейки С7:G7:
Тем самым первая строка расширенной матрицы системы ограничений разделена на -1 и выделен разрешающий элемент 1.
Замечание. Если в диапазоне В7:G7 окажутся результаты в форме десятичных дробей, то откройте контекстное меню и в диалоговом окне «Формат ячеек» установите формат числа «Дробный», со знаменателем до двух (или трех) цифр.
Далее в ячейку В8 вводим формулу =B3-B$7*$B3. Копируем ее, методом «протаскивания» маркера заполнения, в остальные ячейки диапазона С8:G8, делаем такие же элементарные преобразования диапазонов (строк) В4:G4 и В5:G5, получаем нули ниже разрешающего элемента:
В ячейку С13 вводим формулу =C8/$C$8 и методом «протаскивания» маркера заполнения копируем ее в остальные ячейки диапазона В13:G13, что дает:
В ячейке С14 задаем формулу =C9-C$13*$C9 и копируем ее в остальные ячейки диапазона В14:G14. Далее проводим аналогичные элементарные преобразования диапазонов В12:G12 и В15:G15:
Повторяя алгоритм, приходим к окончательному результату:
Задача ЛП после преобразований имеет вид:
Отбросим в уравнениях-ограничениях неотрицательные разрешенные неизвестные х1, х2, х3 и заменим знак равенства знаками неравенства «», получим вспомогательную задачу ЛП с двумя переменными
Далее она решается аналогично, как в первом примере, графическим методом.
2.4. ПРИМЕРНЫЕ ВОПРОСЫ НА ЗАЩИТЕ РАБОТЫ
1. Каковы основные этапы решения задач ЛП графическим методом?
2. Как определить, какая полуплоскость отвечает линейному неравенству?
3. Что называется областью допустимых решений?
4. Какая линия называется линией уровня?
5. Как определить максимальное и минимальное значения линейной целевой функции в области допустимых решений?
6. Какие случаи возможны при решении задачи ЛП графическим методом?
7. В каких случаях задачу линейного программирования можно решить графическим методом?
2.5. ВАРИАНТЫ
Используя MS Excel, найти решение графическим методом для задачи ЛП, соответствующей заданному варианту (табл.3.1).
Таблица 3. 1
1
Варианты задач к лабораторной работе №3
№ варианта | Математическая модель |
1 | |
2 |
3 | |
4 | |
5 | |
6 | |
7 |
8 | |
9 | |
10 | |
11 | |
12 |
9
Графическое решение задач линейного программирования
Линейное программирование — самый простой способ оптимизации задачи. С помощью этого метода мы можем сформулировать реальную проблему в виде математической модели. С помощью линейного программирования мы можем решить огромное количество задач в различных секторах, но обычно оно используется для задач, в которых мы должны максимизировать прибыль, минимизировать затраты или минимизировать использование ресурсов.
С помощью этого метода мы можем сформулировать реальную проблему в виде математической модели. С помощью линейного программирования мы можем решить огромное количество задач в различных секторах, но обычно оно используется для задач, в которых мы должны максимизировать прибыль, минимизировать затраты или минимизировать использование ресурсов.
Типы задач линейного программирования
Существуют в основном три типа задач, основанных на линейном программировании. Они следующие:
Производственная задача: В задаче этого типа некоторые ограничения, такие как рабочая сила, единицы продукции в час, машино-часы, задаются в виде линейного уравнения. И мы должны найти оптимальное решение, чтобы получить максимальную прибыль или минимальные затраты.
Диетическая проблема: Такого рода проблемы, как правило, просты для понимания и имеют меньше переменных. Наша главная цель в этом виде проблемы состоит в том, чтобы свести к минимуму стоимость диеты и сохранить минимальное количество каждого компонента в рационе.
Транспортная задача: В этих задачах мы должны найти самый дешевый способ транспортировки, выбрав кратчайший маршрут/оптимизированный путь.
Некоторые часто используемые термины в задачах линейного программирования:
Целевая функция: Прямая функция формы Z = ax + by, где a и b являются постоянными, которая уменьшается или увеличивается, называется целевой функцией. Например, если Z = 10x + 7y. Переменные x и y называются переменной решения.
Ограничения: Ограничения, которые применяются к линейному неравенству, называются ограничениями.
- Неотрицательные ограничения: x > 0, y > 0 и т. д.
- Общие ограничения: x + y > 40, 2x + 9y ≥ 40 и т. д.
Задача оптимизации: Минимизация переменных задачи линейного неравенства называется задачей оптимизации.
Допустимая область: Общая область, определяемая всеми заданными задачами, включая неотрицательное (x ≥ 0, y ≥ 0) ограничение, называется допустимой областью (или областью решения) задачи. Область, отличная от допустимой области, известна как недопустимая область.
Область, отличная от допустимой области, известна как недопустимая область.
Возможные решения: Эти точки внутри или на границе области представляют возможные решения проблемы. Любая точка вне сценария называется невозможным решением.
Оптимальное (наиболее возможное) решение: Любая точка в появляющейся области, которая обеспечивает правильное количество (максимум или минимум) целевой функции, называется оптимальным решением.
Теоремы задачи линейного программирования
Теорема 1: Пусть Y будет допустимой областью (выпуклым многоугольником) для задачи линейного программирования, т.е. Y = ax + by (целевая функция). Итак, когда Y имеет оптимальное значение (максимальное или минимальное), где x и y подчиняются ограничениям, описываемым линейными неравенствами, то это оптимальное значение возникает в угловых точках допустимой области, т. е. в вершинах.
Теорема 2: . Пусть Y — допустимая область задачи линейного программирования, т. е. Y = ax + by (целевая функция). Если X ограничено, то целевая функция Y имеет как максимальное, так и минимальное значение на X, и каждое из них происходит в угловой точке X.
е. Y = ax + by (целевая функция). Если X ограничено, то целевая функция Y имеет как максимальное, так и минимальное значение на X, и каждое из них происходит в угловой точке X.
ПРИМЕЧАНИЕ:
- должны учитывать самые внутренние точки пересечения всех уравнений.
- Если нам нужно найти минимальный выход, мы рассматриваем самые внешние точки пересечения всех уравнений.
- Если в линейном неравенстве нет общих точек, то нет допустимого решения.
Графическое решение задач линейного программирования
Мы можем решать задачи линейного программирования двумя разными методами:
- Угловая точка
- Метод затрат по изо-стоимости
Шаг 1: Создать математическую формулировку из данной задачи. Если не дано.
Шаг 2: Теперь постройте график, используя заданные ограничения, и найдите достижимую область.
Шаг 3: Найдите координаты допустимой области (вершин), которые мы получили из шага 2.
Шаг 4: Теперь оцените целевую функцию в каждой угловой точке допустимой области. Предположим, что N и n обозначают наибольшее и наименьшее значения этих точек.
Шаг 5: Если допустимая область ограничена, то N и n являются максимальным и минимальным значением целевой функции. Или, если допустимая область неограничена, то:
- N — максимальное значение целевой функции, если открытый полуплан получен по оси + by > N не имеет общих точек с допустимой областью. В противном случае целевая функция не имеет решения.
- n — минимальное значение целевой функции, если открытый полуплан получается по оси + by < n не имеет общих точек с допустимой областью. В противном случае целевая функция не имеет решения.
Примеры:
Вопрос 1. Решите заданные задачи линейного программирования графически:
Maximize: z = 8x + Y
, а ограничения:
x + y ≤ 40,
2x + y ≤ 60, .
x ≥ 0, y ≥ 0
Решение:
Шаг 1: Ограничения:
x + y ≤ 40,
2x + y ≤ 60,
x ≥ 0, y ≥
0
Шаг 2: Нарисуйте график, используя эти ограничения.
Здесь оба ограничения меньше или равны, поэтому они удовлетворяют области ниже (в направлении начала координат). Вы можете найти вершину допустимой области по графу или рассчитать, используя заданные ограничения:
x + y = 40 … (i)
2x + y = 60 … (ii)
Теперь умножьте уравнение (i) на 2, а затем вычтем оба уравнения (i) и (ii), мы получим
y = 20
Теперь подставим значение y в любое из уравнений, мы получим
x = 20
Итак, третья точка допустимая область (20, 20)
Шаг 3: Найти максимальное значение Z = 8x + y. Compare each intersection point of the graph to find the maximum value
Points Z = 8x + y (0, 0) 0 (0, 40) 40 (20, 20) 180 (30, 0) 240 So the maximum value of Z = 240 at point x = 30, y = 0.
Вопрос 2. Для одного торта требуется 200 г муки и 25 г жира, а для другого вида торта требуется 100 г муки и 50 г жира Найдите максимальное количество тортов, которое можно приготовить из 5 кг муки. муки и 1 кг жира при условии, что в других ингредиентах, используемых при приготовлении лепешек, недостатка нет.
Решение:
Шаг 1. Создайте подобную таблицу для облегчения понимания (не обязательно).
Floor(g) Fat(g) Cake of first kind (x) 200 25 Cake of second kind (y) 100 50 Доступность 5000 1000 Шаг 2: Создать линейное уравнение с использованием vianairatial
.
1000 или x + 2y ≤ 40
- Кроме того, x > 0 и y > 0
Шаг 3: Создайте график, используя неравенство (помните, что оси x и y должны быть положительными)
Шаг 4: Найдите максимальное количество тортов ( Z) = х + у. Сравните каждую точку пересечения графика, чтобы найти максимальное количество тортов, которые можно испечь.
x Y Z (x+Y) 0 20 0 20 0 20 0 20 0 20187 0 017720 10 30 908 25 0 25 ясно. Таким образом, максимальное количество тортов, которое можно испечь, равно Z = 20 + 10 = 30.
Метод изо-затратТермин «изо-затраты» или «метод изо-прибыли» представляет собой комбинацию баллов, которая дает одинаковую стоимость /профит как любая другая комбинация на той же линии.
Это делается путем построения линий, параллельных наклону уравнения.
Для решения задачи методом Изо-затрат необходимо выполнить следующие шаги:
Шаг 1: Создать математическую формулировку данной задачи. Если не дано.
Шаг 2: Теперь постройте график, используя заданные ограничения, и найдите допустимую область.
Шаг 3: Теперь найдите координаты допустимой области, которые мы получили из шага 2.
Шаг 4: Найдите подходящее значение Z (целевая функция) и нарисуйте линию этой целевой функции.
Шаг 5: Если целевая функция максимального типа, нарисуйте линию, параллельную линии целевой функции, и эта линия будет дальше всего от начала координат и имеет только одну общую точку с допустимой областью. Или, если целевая функция минимального типа, то нарисуйте прямую, параллельную прямой целевой функции, и эта линия является ближайшей к началу координат и имеет хотя бы одну общую точку с допустимой областью.
Шаг 6: Теперь получите координаты общей точки, которую мы нашли на шаге 5.
Теперь эта точка используется для нахождения оптимального решения и значения целевой функции.
Примеры:
Вопрос 1. Решите заданные задачи линейного программирования.
x + y ≤ 50,
x ≥ 0, y ≥ 0
Решение:
Дано:
5x + y ≤ 100,
x + y ≤ 500003
х ≥ 0, у ≥ 0
Шаг 1: Поиск точек
Мы также можем записать как
5x + y = 100 ….(i)
x + y = 50 ….(ii)
Теперь мы находим точки
поэтому берем
eq(i), теперь в этом уравнении
Когда x = 0, y = 100
и когда y = 0, x = 20
Итак, точки (0, 100) и (20, 0)
Аналогично , в уравнении (ii)
Когда x = 0, y = 50
Когда y = 0, x = 50
Итак, точки (0, 50) и (50, 0)
Шаг 2: Теперь нанесите эти точки на график и найдите достижимую область.
Шаг 3: Теперь мы находим удобное значение Z (целевая функция)
Итак, чтобы найти удобное значение Z, мы должны взять lcm коэффициента 50x + 15y, т.
е. 150. Итак, значение Z кратно 150, т. е. 300. Отсюда
50x + 15y = 300
Теперь найдем точки
Положим x = 0, y = 20
Положим y = 0, x = 6
нарисуйте линию этой целевой функции на графике:
Шаг 4: Поскольку мы знаем, что целевая функция является максимальным типом, мы рисуем линию, которая параллельна линии целевой функции и находится дальше всего от начала координат и имеет только одну общую точку с допустимой областью.
Шаг 5: У нас есть общая точка (12,5, 37,5) с допустимой областью. Итак, теперь находим оптимальное решение целевой функции:
Z = 50x + 15y
Z = 50(12,5) + 15(37,5)
Z = 625 + 562,5
z = 1187
Вопрос 2. Решите заданные задачи линейного программирования графически:
Минимизация: z = 20x + 10y
, а ограничения:
x + 2y ≤ 40, 40,
x + 2y ≤ 40.

3x + y ≥ 30,
4x + 3y ≥ 60,
x ≥ 0, y ≥ 0
Решение:
Дано:
x + 2y 2. ,
3х + у ≥ 30,
4x + 3y ≥ 60,
x ≥ 0, y ≥ 0
Шаг 1: Поиск точек + y = 30 ….(ii)
l3 = 4x + 3y = 60 ….(iii)
Теперь мы находим точки
Итак, мы берем уравнение (i), теперь в этом уравнении
Когда x = 0 , y = 20
и когда y = 0, x = 40
Таким образом, точки (0, 20) и (40, 0)
Аналогично, в уравнении (ii)
Когда x = 0, y = 30
Когда y = 0, x = 10
Итак, точки (0, 30) и (10, 0)
Аналогично, в уравнении (iii)
Когда x = 0, y = 20
Когда y = 0, x = 15
Итак, точки (0, 20) и (15, 0)
Шаг 2: Теперь нанесите эти точки на график и найдите допустимую область.
Шаг 3: Теперь мы находим подходящее значение Z (целевая функция)
Предположим, что z = 0 целевая функция на графике:
Шаг 4: Поскольку мы знаем, что целевая функция является минимальной, мы рисуем прямую, параллельную прямой целевой функции, ближайшую к началу координат и имеющую хотя бы одну общую точку с допустимой областью.
Эта параллельная линия касается допустимой области в точке A. Итак, теперь мы находим координаты точки A:
Как видно из графика в точке A линии l2 и l3 пересекаются, поэтому мы находим координату точки A путем решения этих уравнений:
l2 = 3x + y = 30 ….(iv)
l3 = 4x + 3y = 60 ….(v)
Теперь умножьте eq(iv) на 4 и eq(v) на 3, мы получим
12x + 4y = 120
12x + 9y = 180
Теперь вычтем оба уравнения, и мы получим координаты (6, 12)
Шаг 5: У нас есть общая точка (6, 12) с допустимой областью. Итак, теперь находим оптимальное решение целевой функции:
Z = 20x + 10y
Z = 20(6) + 10(12)
Z = 120 + 120
Z = 240
Линейное программирование | Приложения линейного программирования
Введение
Оптимизация — это образ жизни. У всех нас есть ограниченные ресурсы и время, и мы хотим максимально использовать их. От продуктивного использования вашего времени до решения проблем с цепочками поставок для вашей компании — везде используется оптимизация.
Это особенно интересная и актуальная тема в науке о данных.
Это тоже очень интересная тема — она начинается с простых задач, но может стать очень сложной. Например, разделить плитку шоколада между братьями и сестрами — простая проблема оптимизации. Мы не думаем математическими терминами, решая ее. С другой стороны, разработка стратегии инвентаризации и складирования для интернет-магазина может быть очень сложной. Миллионы SKU с разной популярностью в разных регионах, которые будут доставлены в определенные сроки и ресурсы — вы понимаете, что я имею в виду!
Линейное программирование (ЛП) — один из самых простых способов оптимизации. Это поможет вам решить некоторые очень сложные задачи оптимизации, сделав несколько упрощающих предположений. Как аналитик, вы обязательно столкнетесь с приложениями и проблемами, которые должны быть решены с помощью линейного программирования.
По какой-то причине LP не уделяется должного внимания при изучении науки о данных. Итак, я подумал, позвольте мне отдать должное этой удивительной технике.
Я решил написать статью, объясняющую линейное программирование простым английским языком. Я максимально упростил содержание. Идея состоит в том, чтобы вы начали и увлеклись линейным программированием.
Примечание — Если вы хотите изучить это в формате курса, мы подготовили для вас этот бесплатный курс — «Линейное программирование для специалистов по науке о данных»
Содержание
- Что такое линейное программирование?
- Основные термины
- Процесс определения проблемы LP
- Решение линейной программы графическим методом
- Решение линейной программы с использованием R
- Решение линейной программы с использованием OpenSolver
- Симплексный метод
- Метод северо-западного угла и метод наименьшей стоимости
- Приложения линейного программирования
1. Что такое линейное программирование?
Итак, что такое линейное программирование? Линейное программирование — это простая техника, в которой мы изображаем сложных отношений через линейные функции, а затем находим оптимальные точки.
Изображено важное слово в предыдущем предложении. Реальные отношения могут быть намного сложнее, но мы можем упростить их до линейных отношений.
Приложения линейного программирования повсюду вокруг вас. Вы используете линейное программирование в личных и профессиональных целях. Вы используете линейное программирование, когда едете из дома на работу и хотите выбрать кратчайший маршрут. Или, когда у вас есть сдача проекта, вы разрабатываете стратегии, чтобы ваша команда работала эффективно для своевременной доставки.
Пример задачи линейного программирования
Допустим, курьеру FedEx нужно доставить 6 посылок в день. Склад находится в точке А. 6 пунктов доставки обозначены буквами U, V, W, X, Y и Z. Цифры в строках обозначают расстояние между городами. Чтобы сэкономить на топливе и времени, курьер хочет выбрать кратчайший маршрут.
Итак, курьер рассчитает разные маршруты для всех 6 пунктов назначения, а затем придумает кратчайший маршрут. Этот метод выбора кратчайшего маршрута называется линейным программированием.
В этом случае задача курьера — вовремя доставить посылку во все 6 пунктов назначения. Процесс выбора наилучшего маршрута называется Operation Research. Исследование операций — это подход к принятию решений, который включает в себя набор методов управления системой. В приведенном выше примере моей системой была модель доставки.
Линейное программирование используется для получения наиболее оптимального решения задачи с заданными ограничениями. В линейном программировании мы формулируем нашу реальную проблему в виде математической модели. Он включает в себя целевую функцию, линейные неравенства с учетом ограничений.
Является ли линейное представление 6 точек выше репрезентативным для реального мира? Да и нет. Это упрощение, так как реальный маршрут не будет прямой линией. Скорее всего, у него будет несколько поворотов, разворотов, сигналов и пробок. Но с помощью простого предположения мы резко уменьшили сложность проблемы и создаем решение, которое должно работать в большинстве сценариев.
Формулировка задачи – Изготовим несколько шоколадных конфет
Пример: Рассмотрим компанию по производству шоколада, которая производит только два типа шоколада — A и B. Для обоих видов шоколада требуется только молоко и шоколад. Для производства каждой единицы A и B требуется следующее количество:
- Для каждой единицы А требуется 1 единица молока и 3 единицы шоколада
- Для каждой единицы B требуется 1 единица молока и 2 единицы шоколада
На кухне компании есть в общей сложности 5 единиц молока и 12 единиц шоколада. С каждой продажи компания получает прибыль в размере
.
- 6 рупий за единицу продано
- 5 рупий за проданную единицу B.
Теперь компания хочет максимизировать свою прибыль. Сколько единиц продукции A и B она должна производить соответственно?
Решение: Первое, что я собираюсь сделать, это представить задачу в табличной форме для лучшего понимания.
Молоко Шоколад Прибыль на единицу А 1 3 6 рупийБ 1 2 5 рупийИтого 5 12
Пусть общее количество единиц, произведенных А, будет = X
Пусть общее количество единиц, произведенных B, равно Y
Теперь общая прибыль представлена Z
Общая прибыль, которую получает компания, определяется как общее количество произведенных единиц продукции А и В, умноженное на ее прибыль на единицу продукции в размере 6 и 5 рупий соответственно.
Прибыль: макс. Z = 6X+5Y
, что означает, что мы должны максимизировать Z.
Компания постарается произвести столько единиц товаров А и В, чтобы максимизировать прибыль. А вот ресурсы Milk и Choco доступны в ограниченном количестве.
Согласно приведенной выше таблице, для каждой единицы продуктов А и В требуется 1 единица молока. Общее количество доступного молока составляет 5 единиц. Чтобы представить это математически,
X+Y ≤ 5
Кроме того, для каждой единицы A и B требуется 3 единицы и 2 единицы Choco соответственно. Общее количество доступных Choco составляет 12 единиц. Чтобы представить это математически,
3X+2Y ≤ 12
Кроме того, значения единиц A могут быть только целыми числами.
Итак, у нас есть еще два ограничения: X ≥ 0 и Y ≥ 0
Чтобы компания получила максимальную прибыль, необходимо, чтобы выполнялись указанные выше неравенства.
Это называется преобразованием реальной проблемы в математическую модель.
Общие термины, используемые в линейном программировании
Давайте определим некоторые термины, используемые в линейном программировании, используя приведенный выше пример.
- Переменные решения: Переменные решения — это переменные, которые будут определять мой результат. Они представляют мое окончательное решение. Чтобы решить любую проблему, нам сначала нужно определить переменные решения. Для приведенного выше примера общее количество единиц для A и B, обозначенное X и Y соответственно, является моими переменными решения.
- Цель Функция: Определяется как цель принятия решений. В приведенном выше примере компания хочет увеличить общую прибыль, представленную Z. Итак, прибыль — это моя целевая функция.
- Ограничения: Ограничения — это ограничения или ограничения на переменные решения. Обычно они ограничивают значение переменных решения. В приведенном выше примере ограничение на доступность ресурсов Молоко и Шоколад — это мои ограничения.
- Ограничение на неотрицательность: Для всех линейных программ переменные решения всегда должны принимать неотрицательные значения.
Это означает, что значения переменных решения должны быть больше или равны 0.
Процесс формулирования задачи линейного программирования
Давайте рассмотрим шаги определения задачи линейного программирования в общем виде:
- Определите переменные решения
- Запись целевой функции
- Упомянуть ограничения
- Явно указать ограничение неотрицательности
Чтобы задача была задачей линейного программирования, все переменные решения, целевая функция и ограничения должны быть линейными функциями.
Если все три условия выполнены, это называется Задача линейного программирования .
2. Решение линейных программ графическим методом
Линейная программа может быть решена несколькими способами. В этом разделе мы рассмотрим графический метод решения линейной программы. Этот метод используется для решения линейной программы с двумя переменными. Если у вас есть только две переменные решения, вы должны использовать графический метод, чтобы найти оптимальное решение.
Графический метод включает формулировку набора линейных неравенств с учетом ограничений. Затем неравенства наносятся на плоскость X-Y. После того, как мы нанесли все неравенства на график, область пересечения дает нам допустимую область. Допустимая область объясняет, какие значения может принимать наша модель. И это также дает нам оптимальное решение.
Давайте разберемся с этим на примере.
Пример: Фермер недавно приобрел участок земли площадью 110 га. Он решил выращивать на этой земле пшеницу и ячмень. Благодаря качеству солнца и прекрасному климату региона, все производство пшеницы и ячменя может быть продано. Он хочет знать, как посадить каждый сорт на 110 гектарах, учитывая затраты, чистую прибыль и потребность в рабочей силе в соответствии с данными, показанными ниже:
Разнообразие Стоимость (Цена/Гек) Чистая прибыль (Цена/Гектар) Человеко-дней/Гек Пшеница 100 50 10 Ячмень 200 120 30 Бюджет фермера составляет 10 000 долларов США, а наличие 1 200 человеко-дней в течение горизонта планирования.
Найдите оптимальное решение и оптимальное значение.
Решение: Чтобы решить эту задачу, сначала мы сформулируем нашу линейную программу.
Формулировка линейной задачи
Шаг 1. Определите переменные решения
Общая площадь для выращивания пшеницы = X (в гектарах)
Общая площадь для выращивания ячменя = Y (в гектарах)
X и Y — переменные моего решения.
Шаг 2: Напишите целевую функцию
Так как продукцию со всей земли можно продать на рынке. Фермер хотел бы максимизировать прибыль от общего объема производства. Нам дают чистую прибыль как по пшенице, так и по ячменю. Фермер получает чистую прибыль в размере 50 долларов США за каждый гектар пшеницы и 120 долларов США за каждый ячмень.
Наша целевая функция (заданная Z) равна Max Z = 50X + 120Y
Шаг 3. Запись ограничений
1.
Учитывая, что общий бюджет фермера составляет 10 000 долларов США. Стоимость производства пшеницы и ячменя на гектар также предоставляется нам. У нас есть верхний предел общих затрат, потраченных фермером. Таким образом, наше уравнение становится:
100X + 200Y ≤ 10 000
2. Следующим ограничением является верхний предел доступности общего количества человеко-дней для горизонта планирования. Общее количество доступных человеко-дней составляет 1200. Согласно таблице, нам дано количество человеко-дней на гектар для пшеницы и ячменя.
10X + 30Y ≤ 1200
3. Третьим ограничением является общая площадь плантаций. Общая доступная площадь составляет 110 га. Таким образом, уравнение становится
X + Y ≤ 110
Шаг 4: Ограничение неотрицательности
Значения X и Y будут больше или равны 0. Это само собой разумеется.
X ≥ 0, Y ≥ 0
Мы сформулировали нашу линейную программу.
Пришло время решить это.
Решение ЛП графическим методом
Так как мы знаем, что X, Y ≥ 0. Мы будем рассматривать только первый квадрант.
Чтобы построить график для приведенных выше уравнений, сначала я упростю все уравнения.
100X + 200Y ≤ 10 000 можно упростить до X + 2Y ≤ 100 путем деления на 100.
10X + 30Y ≤ 1200 можно упростить до X + 3Y ≤ 120 путем деления на 10.
Третье уравнение в упрощенной форме, X + Y ≤ 110.
Постройте первые 2 линии на графике в первом квадранте (как показано ниже)
Оптимальное допустимое решение достигается в точке пересечения, где действуют ограничения бюджета и человеко-дней. Это означает, что точка, в которой пересекаются уравнения X + 2Y ≤ 100 и X + 3Y ≤ 120, дает нам оптимальное решение.
Значения X и Y, дающие оптимальное решение, равны (60,20).
Чтобы максимизировать прибыль, фермер должен выращивать пшеницу и ячмень на 60 га и 20 га земли соответственно.
Максимальная прибыль, которую получит компания,
Макс. Z = 50 * (60) + 120 * (20)
= 5400 долларов США
Примечание: Все, чему здесь учат, также преподается в формате курса этого бесплатного курса «Линейное программирование для специалистов по науке о данных»
3. Решить линейную программу с помощью R
R — это инструмент с открытым исходным кодом, который очень популярен среди специалистов по обработке и анализу данных для решения основных задач обработки данных. Выполнение линейного программирования очень просто, и мы можем получить оптимальное решение всего за несколько шагов. Приходите учиться.
Пример: Организация по производству игрушек производит два типа игрушек A и B. Обе игрушки продаются по цене 25 и 20 рупий соответственно. Ежедневно доступно 2000 единиц ресурсов, из которых для игрушки А требуется 20 единиц, а для игрушки В — 12 единиц. Обе эти игрушки требуют времени производства 5 минут.
Общее рабочее время 9 часов в день. Каким должен быть объем производства каждой из труб, чтобы максимизировать прибыль?
Здесь:
Целевая функция:
Макс.Z=25x+20y, где х — единицы измерения трубы А
y — единицы трубы B
Ограничения:
20x+12y<=20005x+5y<=540
Теперь посмотрим часть кода:
Посмотреть код на Gist.
Выход
сводка(опция) Режим класса длины направление 1 -нет-числовое x.count 1 -нет-числовой цель 2 - нечисловая const.count 1 -none- числовой ограничения 8 -нет- числовой int.count 1 -нет-числовой int.vec 1 -нет-числовой bin.count 1 -нет-числовой двоичный.vec 1 -нет-числовой num.bin.solns 1 -нет- числовой objval 1 -нет- числовой решение 2 - не числовое presolve 1 -нет- числовой Compute.sens 1 -нет- числовой sens.coef.from 1 -none- числовой sens.coef.to 1 -none- числовой двойные 1 -нет-числовой duals.from 1 -none- числовой duals.to 1 -none- числовой шкала 1 - нет - числовая use.dense 1 -none- числовой плотный.col 1 -нет-числовой плотно.val 1 -нет- числовой плотно.const.nrow 1 -нет- числовой плотный.ctr 1 -нет-числовой use.rw 1 -нет-числовой tmp 1 -none- символ статус 1 -нет-числовой > выбрать $ решение [1] 88 20 > opt$objval [1] 2600
Таким образом, на выходе мы видим, что организация должна произвести 88 единиц игрушки А и 20 единиц игрушки В, а максимальная прибыль организации составит 2600 рупий.
4. Решение линейной программы с помощью OpenSolver
В действительности линейная программа может содержать от 30 до 1000 переменных, и решить ее ни графически, ни алгебраически практически невозможно. Компании обычно используют OpenSolver для решения этих реальных проблем. Здесь я покажу вам, как решить линейную программу с помощью OpenSolver.
OpenSolver — линейный оптимизатор с открытым исходным кодом для Microsoft Excel. Это расширенная версия встроенного Решателя Excel. Вы можете скачать OpenSolver здесь и следовать руководству по установке.
Я хочу, чтобы вы получили практические навыки использования OpenSolver. Итак, для ясности поясню на примере.
Пример: Ниже приведена таблица диеты, в которой указано содержание калорий, белков, углеводов и жиров для 4 продуктов питания. Сара хочет диету с минимальными затратами. Схема диеты выглядит следующим образом:
Продукт питания 1 Еда 2 Продукт питания 3 Продукт питания 4 Калории 400 200 150 500 Протеин (в граммах) 3 2 0 0 Углеводы (в граммах) 2 2 4 4 Жир (в граммах) 2 4 1 5 Стоимость 0,50 $ 0,20 долл. США 0,30 долл. США
0,80 $ В таблице указано содержание питательных веществ, а также удельная стоимость каждого продукта питания. Диета должна быть спланирована таким образом, чтобы она содержала не менее 500 калорий, 6 граммов белков, 10 граммов углеводов и 8 граммов жиров.
Решение. Сначала я сформулирую свою линейную программу в электронной таблице.
- Шаг 1: Определите переменные решения. Здесь переменными моего решения являются продукты питания. Добавьте заголовки. В пробных целях мы вводим произвольные значения. Допустим, Сара потребляет 3 единицы продукта питания 1, 0 единиц продукта питания 2, 1 единицу продукта питания 3 и 0 единиц продукта питания 4. Они называются переменными ячейками.
- Шаг 2: Теперь напишем нашу целевую функцию. Чтобы диета была оптимальной, мы должны иметь минимальную стоимость наряду с необходимыми калориями, белками, углеводами и жирами.
В ячейке B7:E7 берем ссылку на количество единиц. А в ячейку B8:E8 мы помещаем стоимость единицы каждого продукта питания.
В ячейке B10 нам нужна общая стоимость рациона. Общая стоимость определяется как сумма произведений количества съеденных единиц и затрат на единицу. Суммарное произведение равно B7*B8+C7*C8+D7*D8+E7*E8. Давайте посмотрим на это в электронной таблице.
- Шаг 3: Теперь мы введем ограничения. Столбец F содержит общее количество калорий, белков, углеводов и жиров. Общее количество потребляемых калорий, определяемое суммой продуктов, количество съеденных продуктов и количество калорий, потребленных на каждый продукт питания. Для ячейки F13= Sumprodcut($B$7:$F$7, B13:F13). Аналогично для других. Столбец G дает неравенство, поскольку задача требует, чтобы Калории, Белки, Углеводы и Жиры были не менее 500, 6, 10 и 8 соответственно. Колонка H дает требуемое содержание питательных веществ.
- Шаг 4: Теперь мы введем линейную программу в решатель. Теперь, когда вы установили OpenSolver. Когда вы нажмете на вкладку «Данные», справа вы увидите «Модель». Нажмите на модель, затем введите значения по одному. Во-первых, мы введем целевую функцию, $ B10, то есть в целевую ячейку. Выберите «Свернуть», потому что мы хотим минимизировать стоимость диеты.
- Шаг 5: Теперь введите переменные решения в ячейки переменных.
- Шаг 6: Теперь мы добавим ограничения. Первое ограничение — это F13 ≥ h23. Добавьте все ограничения по одному.
- Шаг 7: Теперь вам нужно ввести одно важное ограничение. Ограничение неотрицательности. Все переменные решения будут больше 0,
.
- Шаг 8: Теперь нажмите «Сохранить модель», чтобы завершить процесс моделирования. После сохранения модели она будет выглядеть примерно так.
- Шаг 9: После сохранения модели щелкните вкладку «Данные», затем нажмите «Решить». Оптимальное решение и значения отображаются в соответствующих ячейках. Оптимальная минимальная стоимость составляет 0,90 доллара США. Сара должна потреблять 3 единицы пищевого продукта 2 и 1 единицу пищевого продукта 3 для требуемого содержания питательных веществ с минимальными затратами. Это решает нашу линейную программу.
5. Симплексный метод
Симплекс-метод— один из самых мощных и популярных методов линейного программирования. Симплекс-метод представляет собой итеративную процедуру для получения наиболее приемлемого решения. В этом методе мы продолжаем преобразовывать значения основных переменных, чтобы получить максимальное значение целевой функции.
Функция линейного программирования имеет стандартную форму , если она стремится максимизировать целевую функцию. с ограничениями,
.
. . . . .
. . . . . .
где, и . После добавления резервных переменных соответствующая система уравнений ограничений будет равна
.. . . .
где,
Переменные, ………………. называются слабыми переменными. Это неотрицательные числа, которые добавляются для устранения неравенств из уравнения.
Приведенное выше объяснение дает теоретическое объяснение симплекс-метода. Теперь я объясню, как использовать симплекс-метод в реальной жизни с помощью Excel.
Пример: Рекламные альтернативы компании включают рекламу на телевидении, в газетах и на радио. Стоимость для каждого средства с его охватом аудитории приведена ниже.
Телевидение Газета Радио Стоимость рекламы ($) 2000 600 300 Аудитория на рекламу 100 000 40 000 18 000 Местная газета ограничивает количество объявлений от одной компании до десяти.
При этом, чтобы сбалансировать рекламу среди трех видов СМИ, на радио должно появляться не более половины от общего количества рекламы. И не менее 10% должно происходить на телевидении. Еженедельный рекламный бюджет составляет 18 200 долларов. Сколько рекламных объявлений следует размещать в каждом из трех типов СМИ, чтобы максимально увеличить общую аудиторию?
Решение: Сначала я собираюсь сформулировать свою проблему для ясного понимания.
Шаг 1: Определение переменных решения
Пусть , , представляет собой общее количество рекламных объявлений на телевидении, в газете и на радио соответственно.
Шаг 2: Целевая функция
Цель компании – максимально увеличить аудиторию. Целевая функция определяется выражением:
Шаг 3: Запишите ограничения
Теперь я упомяну каждое ограничение по очереди.
Понятно, что у нас есть бюджетное ограничение.
Общий бюджет, который может быть выделен, составляет 18 200 долларов. А индивидуальные затраты на телевизионную, газетную и радиорекламу составляют 2000, 600 и 300 долларов соответственно. Это может быть представлено уравнением
Для рекламы в газете существует верхний предел количества рекламных объявлений до 10. Мои первые ограничения:
Следующим ограничением является количество рекламы на телевидении. Компания хочет, чтобы по телевидению показывалось не менее 10% всей рекламы. Таким образом, это можно представить как:
Последнее ограничение — количество рекламы на радио не может быть больше половины от общего количества рекламы. Его можно представить как
Итак, я сформулировал свою задачу линейного программирования. Мы используем симплексный метод, чтобы решить эту проблему. Я проведу вас по симплексному методу один за другим.
Повторюсь, все ограничения следующие. Я упростил последние два уравнения, чтобы привести их к стандартной форме.
Всего у нас есть 4 уравнения. Чтобы сбалансировать каждое уравнение, я ввожу 4 резервные переменные, , и .
Таким образом, наши уравнения выглядят следующим образом:
Надеюсь, теперь вы готовы разобраться во всей рекламной проблеме. Все приведенные выше уравнения предназначены только для вашего лучшего понимания. Теперь, если вы решите эти уравнения, вы получите значения для X1 = 4, X2 = 10 и X3 = 14.
Решив целевую функцию, вы получите максимальную еженедельную аудиторию 1 052 000 человек. Вы можете следовать учебнику здесь, чтобы решить уравнение. Чтобы решить линейную программу в Excel, следуйте этому руководству.
6. Метод северо-западного угла и метод наименьших затрат
6.1 Метод северо-западного угла
Метод северо-западного угла — это метод специального типа, используемый для транспортных задач в линейном программировании. Он используется для расчета возможного решения для транспортировки товаров из одного места в другое.
Всякий раз, когда вам дают реальную проблему, которая включает в себя спрос и предложение из одного источника из разных источников. Модель данных включает в себя следующее:
- Дан уровень спроса и предложения в каждом источнике
- Единица перевозки товара из каждого источника в каждый пункт назначения
Модель предполагает наличие только одного товара. Спрос на который может исходить из разных источников. Цель состоит в том, чтобы удовлетворить общий спрос с минимальными затратами на транспортировку. Модель основана на гипотезе о том, что общий спрос равен общему предложению, т.е. модель сбалансирована. Давайте разберемся в этом с помощью примера.
Пример: Предположим, что есть 3 бункера, которые необходимы для удовлетворения потребности 4 мельниц. (Силосохранилище — это складское помещение фермы, используемое для хранения зерна, а Мельница — это мельница для зерна).
Решение: Давайте разберемся, что объясняет приведенная выше таблица.
Стоимость транспортировки из бункера и на мельницу и определяется стоимостью в каждой ячейке, соответствующей поставке из каждого бункера 1 и спросу на каждой мельнице. Например, стоимость транспортировки из бункера 1 на мельницу 1 составляет 10 долларов, из бункера 3 на мельницу 5 — 18 долларов. Также дается общий спрос и предложение для мельниц и силосов. Цель состоит в том, чтобы найти минимальную транспортную стоимость, при которой спрос на все мельницы будет удовлетворен.
Как следует из названия, метод северо-западного угла — это метод размещения единиц измерения, начиная с верхней левой ячейки. Спрос на мельницу 1 составляет 5, а общее предложение силоса 1 составляет 15. Таким образом, 5 единиц могут быть выделены мельнице 1 по цене 10 долларов за единицу. Спрос на Mill1 удовлетворен. затем мы переходим к верхней левой ячейке мельницы 2. Спрос на мельницу 2 составляет 15 единиц, из которых она может получить 10 единиц из бункера 1 по цене 2 доллара за единицу и 5 единиц из бункера 2 по цене 7 долларов за единицу.
Ед. изм. Затем переходим на мельницу 3, северо-западная ячейка S2M3. Спрос на мельницу 3 составляет 15 единиц, которые он может получить из бункера 2 по цене 9 долларов.за единицу. Переходя к последней мельнице, потребность мельницы 4 составляет 15 единиц. Он получит 5 единиц из хранилища 2 по цене 20 долларов за единицу и 10 единиц из хранилища 3 по цене 18 долларов за единицу.
Общая стоимость перевозки = 5*10+(2*10+7*5)+9*15+(20*5+18*10) = 520$
6.2 Метод наименьших затрат
Метод наименьшей стоимости — это еще один метод расчета наиболее подходящего решения задачи линейного программирования. Этот метод дает более точные результаты, чем метод северо-западного угла. Он используется для транспортных и производственных задач. Для простоты я объясню приведенную выше транспортную проблему.
В соответствии с методом наименьших затрат вы начинаете с ячейки, содержащей наименьшие удельные затраты на транспортировку. Итак, для вышеуказанной задачи я поставляю 5 единиц из бункера 3 по цене 4 доллара за единицу.
Спрос на Mill1 удовлетворен. Для мельницы 2 мы поставляем 15 единиц продукции из бункера 1 по цене 2 доллара за единицу. Затем для мельницы 3 мы поставляем 15 единиц из бункера 2 по цене 9 долларов за единицу. Затем для мельницы 4 мы поставляем 10 единиц продукции из бункера 2 по цене 20 долларов США за единицу и 5 единиц продукции из бункера 3 по цене 18 долларов США за единицу. Общие транспортные расходы составляют 475 долларов.
Приведенный выше метод объясняет, что мы можем дополнительно оптимизировать наши расходы, используя лучший метод. Давайте проверим это с помощью Excel Solver. Решатель — это встроенная надстройка в Microsoft Excel. Это надстройка, доступная в Excel. Перейдите в файл-> параметры-> надстройки-> выберите решатель-> нажмите «Управление»-> выберите решатель-> нажмите «ОК». Теперь ваш решатель добавлен в Excel. Вы можете проверить это на вкладке «Данные».
Первое, что я собираюсь сделать, это ввести свои данные в Excel. После ввода данных в Excel я вычислил сумму C3:F3.
Аналогично для других. Это делается для того, чтобы взять общий спрос из бункера 1 и других.
После этого я разобью свою модель на две части. Первая таблица дает мне поставляемые единицы, а вторая таблица дает мне стоимость единицы.
Теперь я вычисляю общую стоимость, которая будет получена как Суммарное произведение стоимости единицы продукции и поставленных единиц.
Теперь я буду использовать Solver для расчета моей модели. Аналогичен вышеописанному способу. Добавьте целевую функцию, переменные ячейки, ограничения.
Теперь ваша модель готова к решению. Нажмите «Решить», и вы получите оптимальную стоимость. Минимальная стоимость перевозки составляет $435.
7. Приложения линейного программирования
Линейное программирование и оптимизация используются в различных отраслях промышленности. Производство и сфера услуг регулярно используют линейное программирование. В этом разделе мы рассмотрим различные приложения линейного программирования.
- Производственные отрасли используют линейное программирование для анализа операций цепочки поставок . Их мотивом является максимальная эффективность при минимальных эксплуатационных затратах. В соответствии с рекомендациями модели линейного программирования производитель может перенастроить схему хранения, настроить рабочую силу и устранить узкие места. Вот небольшой пример Warehouse американской компании Cequent. Посмотрите это видео, чтобы получить более четкое представление.
- Линейное программирование также используется в организованной розничной торговле для оптимизации полочного пространства . Поскольку количество продуктов на рынке увеличилось как на дрожжах, важно понимать, чего хочет клиент. Оптимизация агрессивно используется в таких магазинах, как Walmart, Hypercity, Reliance, Big Bazaar и т. д. Товары в магазине размещаются стратегически с учетом покупательского поведения покупателей. Цель состоит в том, чтобы облегчить покупателю поиск и выбор нужных продуктов.
Это связано с такими ограничениями, как ограниченное пространство на полках, разнообразие продуктов и т. д.
- Оптимизация также используется для оптимизации маршрутов доставки . Это расширение популярной задачи коммивояжера. Сфера услуг использует оптимизацию для поиска наилучшего маршрута для нескольких продавцов, путешествующих в разные города. С помощью кластеризации и жадного алгоритма маршруты доставки определяются такими компаниями, как FedEx, Amazon и т. д. Цель состоит в том, чтобы минимизировать эксплуатационные расходы и время.
- Оптимизация также используется в Machine Learning . Обучение с учителем работает на основе линейного программирования. Система обучается соответствовать математической модели функции на основе размеченных входных данных, которая может предсказывать значения на основе неизвестных тестовых данных.
На этом возможности линейного программирования не заканчиваются. Есть много других приложений линейного программирования в реальном мире, таких как акционеры, спорт, фондовые рынки и т.
д. Продолжайте изучать дальше.
Конечные примечания
Надеюсь, вам понравилось читать эту статью. Я попытался объяснить все основные понятия линейного программирования. Если у вас есть какие-либо сомнения или вопросы, не стесняйтесь оставлять их в разделе комментариев. Для простоты понимания мы разбили эту длинную статью на более короткий формат курса — Linear Programming for Data Science Professionals
.Я объяснил каждую концепцию на примере из реальной жизни. Я хочу, чтобы вы попробовали их на своем конце и получили практический опыт. Дайте мне знать, что вы думаете!
Графический метод линейного программирования – задачи с решениями
Не секрет, что симплекс-метод является хорошо изученным и широко используемым методом решения задач линейного программирования. Но что касается нелинейного программирования, такого универсального метода не существует. С помощью графических методов легко решаются любые задачи оптимизационного программирования, состоящие только из двух переменных.
Эти переменные можно обозначить как x₁ и x₂, и с помощью этих переменных большую часть анализа можно выполнить на двумерном графике. Хотя мы не можем обобщить большое количество переменных с помощью графического подхода, можно легко продемонстрировать основные концепции линейного программирования в контексте с двумя переменными. Мы всегда можем обратиться к задачам с двумя переменными, если проблемы кажутся сложными и мы оказываемся в пучке вопросов. И мы всегда можем искать ответы в случае с двумя переменными, используя графы, то есть графически решая задачи линейного программирования.
Графический подход обладает еще одним преимуществом, и это его визуальная природа. Это дает нам картину, чтобы разобраться с алгеброй линейного программирования. Эта картинка может утолить нашу жажду понимания основных определений и возможностей. Эти причины являются доказательством того, что графический подход хорошо работает с концепциями линейного программирования.
Теперь для графического решения задач линейного программирования нам необходимо две вещи:
Неравенство ограничений
И целевая функция.
Графический метод решения задач линейного программирования основан на четко определенном наборе логических шагов. С помощью этих шагов мы можем освоить графическое решение задач линейного программирования.
Методы, используемые для решения линейного программирования
Следующие два метода, используемые для графического метода решения линейного программирования:
Важные моменты
Набор значений переменных xj (j = 1, 2,3…, N), который удовлетворяет проблемам LP, называется решением этой проблемы LP.
Потенциальное решение Набор значений переменных xj (j = 1, 2,3.., N), который одновременно удовлетворяет всем барьерам и неотрицательным условиям задачи ЛП, называется возможным решение этой проблемы LP.
Маловероятное решение Набор значений переменных xj (j = 1, 2,3.
.., N), которые не удовлетворяют одновременно всем барьерам и неотрицательным условиям задачи ЛП, называется сформировать невозможное решение для этого. проблема с ЛП.
При m-группе одновременных n (n > m) переменных в задаче ЛП решение, полученное путем размещения (n — m) равных нулю переменных и решения оставшихся m-переменных m, называется базовым решением. этой проблемы LP. Переменные (n — m), значение которых не фигурировало в базовом решении, называются неосновными переменными, а остальные переменные m называются базовыми переменными.
Возможное основное решение Возможное решение задачи ЛП и основное решение называется возможным основным решением. То есть все основные изменения принимают неотрицательные значения.
Базовое решение двух типов
Вырожденное Возможное базовое решение называется вырожденным, если значение хотя бы одного базового элемента равно нулю.
Неразлагаемый Основное практическое решение называется невырожденным, если значение всех основных переменных равно нулю и положительно.
Способы решения задачи LP
Точечный метод
Чтобы решить проблему с помощью существующего точечного метода, вам необходимо выполнить следующие шаги:
Шаг 1: Создайте статистический план на основе заданной проблемы. Если не предусмотрено.
Шаг 2: Теперь спланируйте график, используя заданные препятствия, и найдите область, которую вы можете использовать.
Шаг 3: Найдите возможные связи местоположения (вершины), которые мы нашли на шаге 2.
Шаг 4: Теперь проверьте целевую функцию в каждой из возможных областей местоположения. Предположим, что N и n представляют наибольшее и наименьшее значения в этих точках.
Шаг 5: Если возможная область ограничена, то N и n являются максимальным и минимальным значениями целевой функции.
Или, если область, вероятно, не будет иметь границ, то:
N — наибольшее значение целевой функции, если открытая полусистема получается топором + by>N без общей точки в возможной области. Если нет, то целевая работа не имеет решения.
n небольшой объем объективной работы, если открытая полусистема найдена по оси + по
3 Теперь постройте линию ограничения древесины (x 1 = 10 и x 2 = 15) и линию ограничения труда (x 1 = 22Метод изо-затрат
Термин «метод изо-затрат» или «метод изо-прибыли» обеспечивает комбинацию точек, которые дают такие же затраты/прибыль, как и любая другая комбинация в той же строке. Это делается путем расположения линий, соответствующих наклону уравнения.
Выполните следующие шаги для решения методом затрат по Изо:
Шаг 1: Создайте статистический план на основе заданной задачи. Если не предусмотрено.
Шаг 2: Теперь спланируйте график, используя заданные препятствия, и найдите область, которую вы можете использовать.
Шаг 3: Теперь найдите возможные связи местоположения, которые мы нашли на шаге 2.
Шаг 4: Найдите правильное Z (целевую функцию) и нарисуйте линию для этой целевой деятельности.
Шаг 5: Если целевая функция высокого типа, начертите линию, соответствующую линии целевых характеристик, и эта линия будет дальше от корня и будет иметь только одну общую точку в возможной области. Или, если целевая функция имеет небольшой тип, то нарисуйте линию, которая соответствует линии целевой производительности, и эта линия очень близка к источнику и имеет одну общую точку в возможном положении.
Шаг 6: Теперь найдите ссылки на общую точку, которую мы нашли на шаге 5. Теперь эта точка используется для поиска правильного решения и объема объективной работы.
Information for the Wooden Tables and Chairs Linear Programming Problem
Resource
Table(X₁)
Chair(X₂)
Available
Древесина (ч/б)
30
20
300
Labor(hr)
5
10
110
Unit Profit $6 $8
Таблица 1 дает нам информацию для задачи линейного программирования.
Мы можем шаг за шагом решать задачи линейного программирования графически.
Шаг 1) Приведенная выше таблица поможет нам сформулировать задачу. Нижняя строка будет выполнять целевую функцию. Целевой функцией компании является максимизация прибыли на единицу продукции. Леса и рабочие являются набором ограничений. Сформулированы также условия неотрицательности.
Maximize z = 6x 2 +8x 2 (является целевой функцией)
При условии: 30x 1 +20x 2 ≤ 300 (300 BF доступны)
57778 ≤ 300 (300 BF)1578 +10x 2 ≤ 110 (доступно 110 часов)
x 1 +x 2 ≥ 0 (неотрицательные переменные)
две.
Шаг 2) Это шаг построения графика. С осью x в качестве количества столов и осью y в качестве количества стульев мы можем найти две линии ограничений. Это можно найти, если мы найдем точки пересечения x и y для двух уравнений связи.
Но перед этим мы должны переписать неравенства ограничений в виде равенств.
Wood
30x 1 +20x 2 = 300
Установка x₂ = 0 для решения X₁
30x = 300
X₁ = 300/30 = 10 Tables (Wood используется для Moke Total :
Setting x₁ = 0 to solve x₂
20x₂ = 300
x₂ =300/20 = 15 chairs (Wood used to make chairs)
Labor
50x 1 +10x 2 = 110
Установка x₂ = 0 для решения x₁
5x₁ = 110
x₁ = 110/5= 22 стола (затраты труда на изготовление столов)
Установка x₁ = 0 для решения x₂
10x₂ = 110
x₂ = 110/10= 11 стульев (трудозатраты на изготовление стульев)
3и x 2 = 11)
(изображение будет загружено).
скоро)
Шаг 3) Чтобы проверить действительную сторону для обеих линий ограничений, используйте исходную точку (0,0).
30(0) + 20(0) < 300 — допустимая сторона линии ограничения древесины. Точно так же 5(0) + 10(0) < 110 также является действительной стороной линии трудовых ограничений. Теперь нарисуйте стрелки, указывающие действительную сторону каждой линии ограничения.
(Изображение будет загружено в ближайшее время)
Шаг 4) Определите допустимую область, которая является областью с допустимой стороны обеих ограничительных линий.
Шаг 5) Найдите x 1 и x 2 , используя Z = 48 и 72.
В первом случае значения будут x 1 = 8 и x2= 12
Во втором случае значения будут x 1 = 6 и x 2 = 9
Постройте линии целевой функции, когда Z = 48 и Z = 72.
Две линии целевой функции удаляются от начала координат (0,0), Z увеличивается.
(Изображение скоро будет загружено)
Шаг 6) Найдите самый привлекательный угол.
(Изображение скоро будет загружено)
Шаг 7) Вычислите координаты и найдите значения x и y.
Таким образом, по оптимальному решению компании можно изготовить четыре стола и девять стульев.
Шаг 8) наконец, определите значение целевой функции для оптимального решения, подставив число столов и стульев и решите для Z: , производя четыре стола и девять стульев, мы можем получить максимальную прибыль в размере 96 долларов.
Графический метод линейного программирования | Бухгалтерский учет упрощенный
Введение
Графический метод линейного программирования используется для решения задач путем нахождения самой высокой или самой низкой точки пересечения между линией целевой функции и допустимой областью на графике.
Этот процесс можно разбить на 7 простых шагов, описанных ниже .
Шаг 1: определение ограничений
Все ограничения, относящиеся к задаче линейного программирования, должны быть определены в виде неравенств.
Что такое неравенства?
Неравенства – это математические выражения, подобные уравнениям, за исключением одного отличия. В отличие от уравнений, в которых утверждается, что чему-то равно (например, x = y), неравенства выражают, что больше или меньше чего-то (например, x > y).
Неравенства обозначаются следующими символами:
> Больше
≥ Больше или равно
< Меньше 1326
≤ Меньше или равноШаг 2. Определение целевой функции
Цель решения задачи выражается в форме математического уравнения.
Например, если цель состоит в том, чтобы максимизировать вклад от продажи Продуктов A и B с доходом на единицу 10 и 5 долларов соответственно, целевая функция должна быть:
10A + 5B = Максимальный вклад
что цель решения проблемы состоит в том, чтобы максимизировать общий вклад бизнеса за счет продажи оптимального сочетания продуктов А и В.
Проблема с приведенным выше уравнением заключается в том, что мы не можем просто изобразить его на графике (как требуется на шаге 5). Чтобы обойти эту проблему, мы определяем случайное число вместо «Максимального вклада». Поскольку нам требуется только наклон (градиент) целевой функции, мы можем изобразить целевую функцию на графике, используя любое случайное значение вместо максимального вклада.
Используя предыдущий пример, целевую функцию можно переписать как:
10A + 5B = 100
Обратите внимание, что 100 выше — просто случайное число. Вместо этого можно использовать любое другое значение.
Шаг 3: Нанесите ограничения на миллиметровую бумагу
Неравенства ограничений, определенные на шаге 1, следует нанести на график.
Вы можете построить ограничения таким же образом, как и уравнение.
Пример
Ограничение: 1A + 2B ≤ 100
Для построения приведенного выше ограничения на графике вы можете преобразовать неравенство в уравнение:
1A + 2B = 100
Теперь вам нужны координаты любых двух точек из приведенного выше уравнения.
Как найти координаты точки из уравнения?
Чтобы найти координаты, просто вставьте случайное значение для A или B. Решение уравнения после вставки случайных значений может быть использовано для нахождения значения другой координаты.
Например, мы можем найти значение B, когда A = 0, вставив ноль вместо A и решив уравнение следующим образом:
1 (0) + 2b = 100
0 + 2b = 100
2b = 100
B = 50, так что координаты первых — это первые точки. 50, который можно записать как
(0, 50).Аналогично, вставка нуля в качестве значения B может дать нам значение A для второй точки следующим образом:1326
1A = 100
A = 100Следовательно, координаты второй точки равны A = 100 и B = 0 или (100, 0).
После того, как вы определили координаты любых двух точек из уравнения, вы просто отмечаете их на графике и проводите через них прямую линию, как показано ниже.
Шаг 4: Выделите допустимую область на графике
После того, как вы нанесли на график неравенства ограничений, вам нужно заштриховать область графика, которая находится за пределами ограничений, т.е. которая невозможна.
Например, ограничение 1A + 2B ≤ 100 будет заштриховано следующим образом:
Область на графике, которая находится на или ниже предельной линии ограничения , допустима и поэтому не заштрихована. После того, как все линии ограничений будут одинаково заштрихованы, незаштрихованная часть графика будет представлять допустимую область.
Иногда бывает сложно понять, какую сторону ограничивающей линии следует заштриховать. В таких случаях полезно рассмотреть, возможна ли конкретная комбинация (например, 0 единиц A, 0 единиц B) выше или ниже линии или не учитывать только это ограничение. Если комбинация выполнима, необходимо заштриховать противоположную сторону линии и наоборот.
Шаг 5: Нанесите целевую функцию на график
Линия целевой функции может быть нанесена на график так же, как и линии ограничения, за исключением того, что вы можете отличить ее от линий ограничения, например.
нарисовав пунктирную линию вместо обычной линии.
Линия целевой функции 10A + 5B = 100 будет проведена следующим образом:
Рабочая
Точка A:
10(0) + 5B = 100
B = 5 100 00002 B = 20
(0, 20)
Точка B:
10 (A) + 5 (0) = 100
A = 100 ÷ 10
A = 10
(10 , 0)
Шаг 6: Найдите оптимальную точку
Оптимальная точка задачи линейного программирования всегда лежит в одной из угловых точек допустимой области графа.
Чтобы найти оптимальную точку, нужно провести линейкой по графику по градиенту целевой функции. Если цель состоит в том, чтобы максимизировать (например, вклад), вы должны сдвинуть линейку до точки в допустимой области, которая находится дальше всего от начала координат. И наоборот, если цель состоит в том, чтобы минимизировать (например, стоимость), вы должны сдвинуть линейку до точки в допустимой области, ближайшей к началу координат.
В обоих случаях вы должны помнить о перемещении линейки по градиенту линии целевой функции.
Обратите внимание, что линейка параллельна пунктирной линии (т.е. линии целевой функции). Красная точка, отмеченная на графике (100, 0), — это последняя точка, которой касается линейка, оставаясь при этом в допустимой области, и, следовательно, это оптимальная точка.
Шаг 7: Найдите координаты оптимальной точки
В приведенном выше примере координаты оптимальной точки можно легко определить, поскольку точка лежит на оси X.
Если оптимальная точка задачи линейного программирования не лежит ни на оси x, ни на оси y, вы можете найти ее координаты, проведя вертикальную и горизонтальную линии от оптимальной точки к двум осям.
Графический метод решения линейного программирования
Графический метод решения задач ЛП
Графический метод линейного программирования используется для решения задач ЛП путем нахождения максимальной или минимальной точки пересечения линии целевой функции с допустимой областью на график.
Графический метод используется для оптимизации задач ЛП с двумя переменными.
Допустимая область:
Замкнутая плоская область, полученная пересечением плоскостей, определяемых набором ограничений в задаче ЛП, называется допустимой областью.
Угловые точки допустимой области известны как вершины допустимой области.
Значения набора переменных решения, которые удовлетворяют заданным ограничениям, являются допустимым решением.
Решение данной задачи ЛП:
Сформулируйте задачу, используя целевую функцию и ограничения.
Выразите неравенства в виде уравнений.
Постройте график из точек, полученных из уравнений.
Определите правильную сторону каждой плоскости на графике.
Определите вершины допустимой области.
Оценить значение целевой функции в каждой из вершин допустимой области.
Найдите вершину, в которой целевая функция достигает оптимального (максимального или минимального) значения.
Интерпретация оптимального значения.
Упражнение:
Найдите допустимую область, определяемую следующими неравенствами. Кроме того, найдите вершины области.
x + y ≤ 6,
2x + y ≥ 8,
y ≥ 0
Решение:
Соответствующие уравнения данных неравенств:
x + y = 6 —-(i)
2x + y = 8 —-(ii)
y = 0 —-(iii)
Из уравнения (i)
Когда x=0, y=6 и
Когда y= 0, х=6.
Итак, граничная линия (i) проходит через (0,6) и (6,0).
Принимая (0,0) в качестве контрольной точки для неравенства;
0+0 ≤ 6
или, 0 ≤ 6 (Истина)
∴ Полуплоскость, определяемая x + y ≤ 6, направлена к началу координат.
Из уравнения (ii),
Когда x=0, y=8 и
Когда y=0, x=4.
Итак, граничная линия (ii) проходит через (0,8) и (4,0).
Принимая (0,0) в качестве контрольной точки для неравенства;
0+0 ≥ 8
или, 0 ≥ 8 (Ложь)
∴ Полуплоскость, определяемая 2x + y ≥ 8, лежит в стороне от начала координат.
Из уравнения (iii)
y=0 — это линия, параллельная оси X.
∴ Полуплоскость, определяемая y ≥ 0, лежит над осью X.
Допустимая область, определяемая данными неравенствами, представлена заштрихованной областью на графике ниже:
Вершинами допустимой области ABC являются A (4,0), B (6,0) и C (2 ,4).
Упражнение 2:
Максимизировать и минимизировать:
F (x, y) = 6x + 9y
.
Решение:
Данная целевая функция Z= 6x + 9y
Соответствующие уравнения данных неравенств таковы:
2x + y = 9 —-(i)
y = x —- (ii)
x = 1 —-(iii)
Из уравнения (i),
Когда x=0, y=9 и
При y=0, x=
Итак, граничная линия (i) проходит через (0,9) и (,0).
Принимая (0,0) в качестве контрольной точки для неравенства;
0+0 ≤ 9
или, 0 ≤ 9 (Истина)
∴ Полуплоскость, определяемая 2x + y ≤ 9, направлена к началу координат.
Из уравнения (ii),
Когда x=0, y=0 и
Когда y=1, x=1.
Итак, граничная линия (ii) проходит через (0,0) и (1,1).
Принимая (1,0) в качестве контрольной точки для неравенства;
0 ≥ 1 (Ложь)
∴ Полуплоскость, определяемая y ≥ x, лежит вдали от (1,0).
Из уравнения (iii)
x=1 — это линия, параллельная оси y.
∴ Полуплоскость, определяемая x ≥ 1, лежит справа от x=1.
Допустимая область, определяемая данными неравенствами, представлена заштрихованной областью на графике ниже:
Вершинами допустимой области ABC являются A (1,1), B (3,3) и C (1 ,7).
Таблица оценки целевой функции:
Вершины: х г Целевая функция: F (x,y) = 6x + 9y Замечания А (1,1) 1 1 6,1 + 9,1 = 15 Минимум
Б (3,3)3 3 6,3 + 9,3 = 45
С (1,7)1 7 6,1 + 9,7 = 69 Максимум Следовательно, максимальное значение равно 69 при C (1,7), а минимальное значение равно 15 при A (1,1).
Упражнение 3:
Фабрика выпускает два изделия A и B, каждое из которых обрабатывается на двух машинах X и Y. A требует два часа X и 4 часа Y; B требует 4 часа X и 2 часов Y
Если x — это количество A, а y — это количество B, производимое ежедневно, запишите два неравенства относительно x и y, отметив, что ни X, ни Y не могут работать более 24 часов в сутки.
Если предположить, что все произведенные товары проданы и каждый товар A приносит прибыль в размере рупий. 60, и каждая статья B приносит прибыль в размере рупий. 100, найдите, сколько каждого изделия нужно производить ежедневно, чтобы прибыль была максимальной.
Решение:
Данный вопрос может быть сведен в таблицу следующим образом:
А (х) Б (у) Ограничение Х 2 часа 4 часа 24 часа Д 4 часа 2 часа 24 часа Прибыль рупий. 60
рупий. 100
для x, 2x + 4y ≤ 24
или, x + 2y ≤ 12
для Y, 4x + 2y ≤ 24
OR, 2x + y ит.
Целевая функция F(x,y) = 60x + 100y
Математическая модель :
Макс. F(x,y) = 60x + 100y
с учетом,
x + 2y ≤ 12
2x + y ≤ 12
x,y ≥ 0
Соответствующие уравнения данных неравенств:
x + 2y = 12 —-(i)
2x + y =12 —- (ii)
x,y = 0 —-(iii)
Из уравнения (i), x + 2y = 12
Когда x=0, y=6 и
Когда y=0, x= 12
Итак, граничная линия (i) проходит через (0,6) и (12,0).
Принимая (0,0) в качестве контрольной точки для неравенства;
0+0 ≤ 12
или, 0 ≤ 12 (верно)
∴ Полуплоскость, определяемая x + 2y ≤ 12, направлена к началу координат.
Из уравнения (ii), 2x + y =12
Когда x=0, y=12 и
Когда y=0, x=6.
Итак, граничная линия (ii) проходит через (0,12) и (6,0).
Принимая (0,0) в качестве контрольной точки для неравенства;
0+0 ≤ 12
или, 0 ≤ 12 (Истина)
∴ Полуплоскость, определяемая 2x + y ≤12, направлена к началу координат.
Из уравнения (iii)
x=0 — это линия, параллельная оси Y.
∴ Полуплоскость, определяемая x ≥ 0, лежит справа от оси Y.
y=0 — линия, параллельная оси X.
∴ Полуплоскость, определяемая y ≥ 0, лежит над осью X.
Допустимая область, определяемая данными неравенствами, представлена заштрихованной областью на графике ниже:
Вершинами допустимой области OABC являются O (0,0), A (6,0), B (4, 4) и С (0,6).
Таблица оценки целевой функции:
Вершины: х г Целевая функция: F (x,y) = 60x + 100y Замечания О (0,0) 0 0 60,0 + 100,0 = 0 А (6,0) 6 0 60,6 + 100,0 = 360
Б (4,4)4 4 60,4 + 100,4 = 640 Максимум
С (0,6)0 6 60,0 + 100,6 = 600 Следовательно, максимальная прибыль составляет рупий.
640, где произведено 4 единицы статьи А и 4 единицы статьи Б.
двенадцать математика Программирование 2
Примеры линейного программирования | Superprof
Что такое линейное программирование?
Линейное программирование используется для оптимизации линейной целевой функции и системы линейных неравенств или уравнений. Ограничения, накладываемые на целевую функцию, называются ограничениями. Целевая функция представляет количество, которое необходимо минимизировать или максимизировать. Основной целью линейного программирования является оптимизация целевой функции.
Ниже приведены допущения для задачи линейного программирования:
- Ограничения целевой функции, известные как ограничения, записываются в виде количественных значений.
- Целевая функция должна быть линейной функцией.
- Связь между целевой функцией и ограничениями должна быть линейной.
Задачи линейного программирования можно решать несколькими способами.
Наиболее распространенными методами являются симплексный метод, решение задач с использованием R или открытого решателя, а также графический метод. В этой статье мы будем решать задачи линейного программирования графическим методом.
Пример 1
Магазин заказал производителю штаны и спортивные куртки.
Для материалов, которые производитель предлагает из хлопчатобумажной ткани и полиэстера. Каждая пара брюк (1 шт.) должна быть из хлопка и полиэстера. Каждая куртка должна быть из хлопка и полиэстера. Цена брюк зафиксирована на уровне 40. Какое количество брюк и курток производитель должен отдать в магазины, чтобы эти товары получили максимальную продажу?
Лучшие репетиторы по математике
Приступим
Решение
Шаг 1. Определите переменные решения
Выберите неизвестные.
x = количество брюк
y = количество курток
Шаг 2 —
Запишите целевую функцию .
Шаг 3.
Определите набор ограничений
Для записи ограничений используйте таблицу:
брюки куртки2554 available cotton 1 1,5 750 polyester 2 1 1,000 As the number of pants and жакеты — натуральные числа, есть еще два ограничения:
x ≥ 0
y ≥ 0
Шаг 4 — Выберите метод решения задачи
Существует множество методов решения метода линейного программирования. В этой задаче мы найдем решение задачи графически.
Шаг 5. Построение графа
Графически изобразите ограничения.
При x ≥ 0 и y ≥ 0 работать в первом квадранте.
Изобразите прямые линии из точек их пересечения с осями.
Пример 1 — ГрафикРешить неравенство графически: , и взять точку на плоскости, например (0,0).
С этого момента точка (0,0) находится в полуплоскости, где выполняется неравенство.
Аналогично решить .
Шаг 6. Определите допустимую область
Область пересечения решений неравенств будет решением системы неравенств, которая представляет собой набор из допустимых решений .
Шаг 7. Найдите оптимальную точку
Вычислите координаты вершин из совокупности допустимых решений.
Оптимальное решение, если оно единственное, находится в вершине. Это решения для систем:
;
Теперь вычислим значение целевой функции в каждой из вершин, чтобы определить, какая из них имеет максимальное или минимальное значение. Необходимо учитывать возможное отсутствие решения, если соединение не ограничено.
В целевой функции поместите каждую из вершин, которые были определены на предыдущем шаге.
20000f(500, 0) = 50 cdot 500 + 40 cdot 0 =
2875028 750.
Решение не всегда единственное, поэтому можно найти и другие решения.
Пример 2
У Марии есть интернет-магазин, где она продает картины и открытки ручной работы. Она продает картину за 20. Ей требуется 2 часа, чтобы нарисовать 1 картину, и 45 минут, чтобы сделать одну карту. У нее также есть дневная работа, а в свободное время она рисует картины и делает открытки. Она не может тратить более 15 часов в неделю на создание картин и открыток. Дополнительно она должна делать не более 10 картин и открыток в неделю.
Она получает прибыль в размере 15 с каждой карты. Сколько картин и открыток она должна делать каждую неделю, чтобы максимизировать свою прибыль.
Решение
Выполните следующие действия, чтобы решить описанную выше проблему.
Шаг 1. Определите переменные решения
x = количество картин
y = количество карточек
Шаг 2. Запишите целевую функцию
функция:
Шаг 3.




 ГРАФИЧЕСКИЙ МЕТОД РЕШЕНИЯ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
ГРАФИЧЕСКИЙ МЕТОД РЕШЕНИЯ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
 2.2
2.2 Для нахождения среди допустимых решений оптимального используют линии уровня.
Для нахождения среди допустимых решений оптимального используют линии уровня. Так как , , то .
Так как , , то .
 Если целевая функция задачи достигает экстремума в двух угловых точках, то задача имеет бесконечное множество решений. Оптимальным решением является любая выпуклая линейная комбинация этих точек. После нахождения оптимальных решений вычисляется значение целевой функции на этих решениях.
Если целевая функция задачи достигает экстремума в двух угловых точках, то задача имеет бесконечное множество решений. Оптимальным решением является любая выпуклая линейная комбинация этих точек. После нахождения оптимальных решений вычисляется значение целевой функции на этих решениях. Для определения координат точки В решаем систему уравнений
Для определения координат точки В решаем систему уравнений Задача имеет бесконечное множество оптимальных решений, являющихся точками отрезка . Находим точки , , решая соответствующие системы уравнений.
Задача имеет бесконечное множество оптимальных решений, являющихся точками отрезка . Находим точки , , решая соответствующие системы уравнений.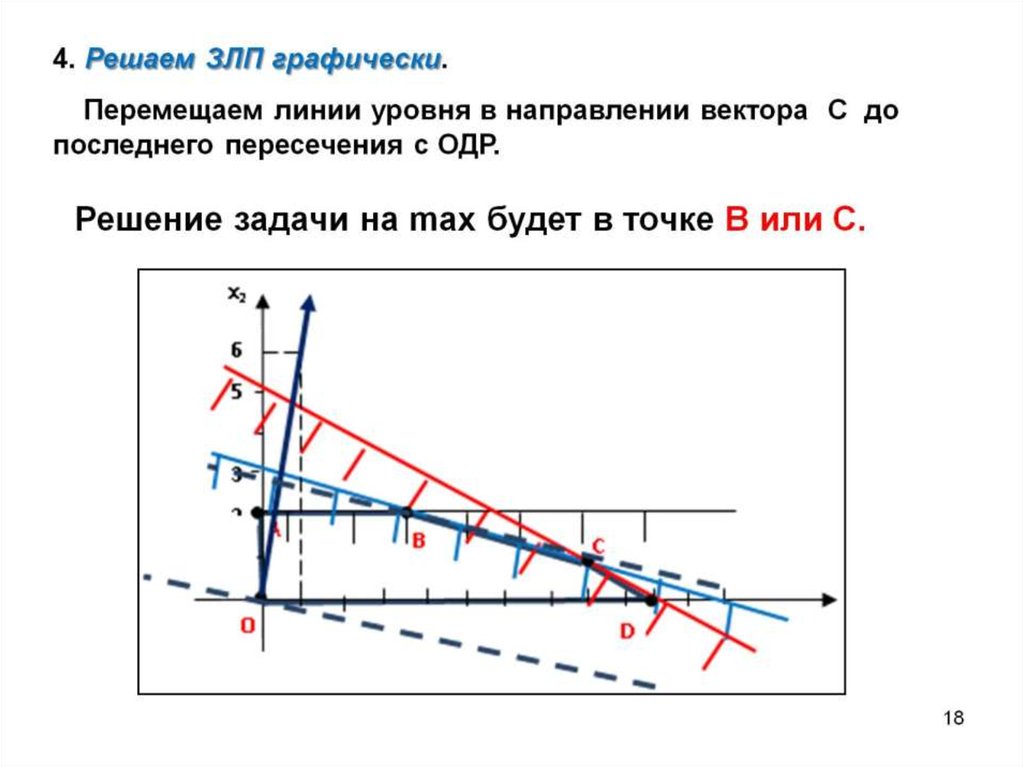 2.7). Область допустимых решений задачи – пустое множество. Задача не имеет решения ввиду несовместности системы ограничений.
2.7). Область допустимых решений задачи – пустое множество. Задача не имеет решения ввиду несовместности системы ограничений. Находим n — r = 4 — 2 =2 £ 2. Следовательно, метод применим.
Находим n — r = 4 — 2 =2 £ 2. Следовательно, метод применим. Вычисления приведены в табл. 2.1. Задача после проведенных преобразований
Вычисления приведены в табл. 2.1. Задача после проведенных преобразований
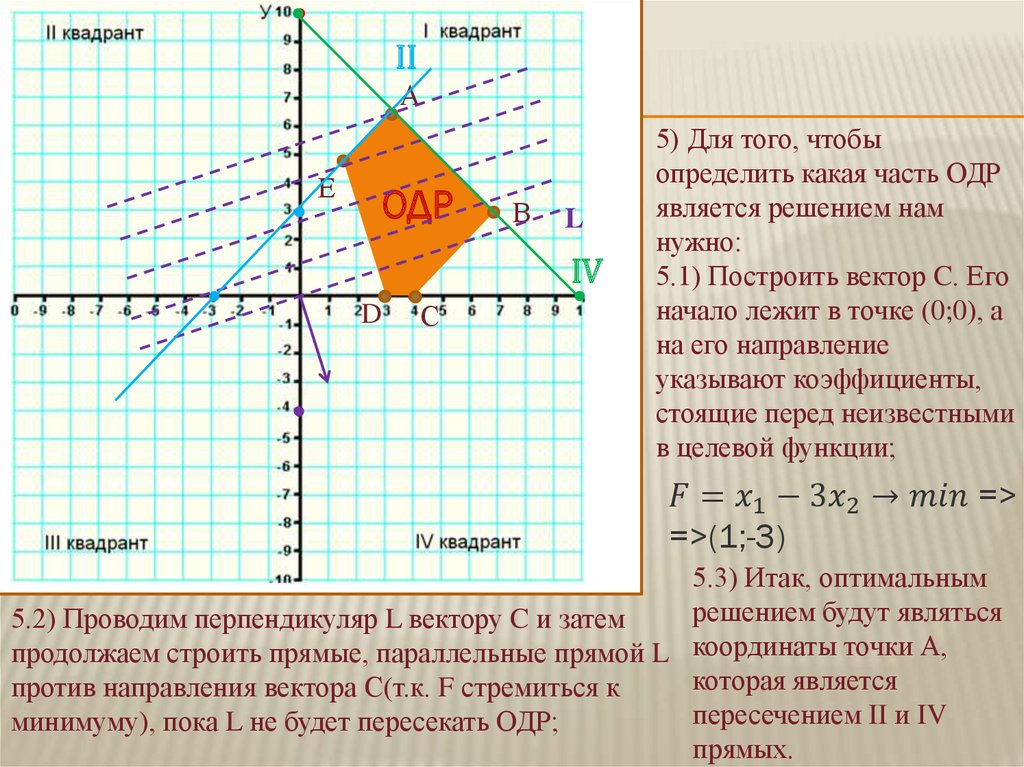
 1000 или x + 2y ≤ 40
1000 или x + 2y ≤ 40 Это делается путем построения линий, параллельных наклону уравнения.
Это делается путем построения линий, параллельных наклону уравнения. Теперь эта точка используется для нахождения оптимального решения и значения целевой функции.
Теперь эта точка используется для нахождения оптимального решения и значения целевой функции. е. 150. Итак, значение Z кратно 150, т. е. 300. Отсюда
е. 150. Итак, значение Z кратно 150, т. е. 300. Отсюда

 Это особенно интересная и актуальная тема в науке о данных.
Это особенно интересная и актуальная тема в науке о данных.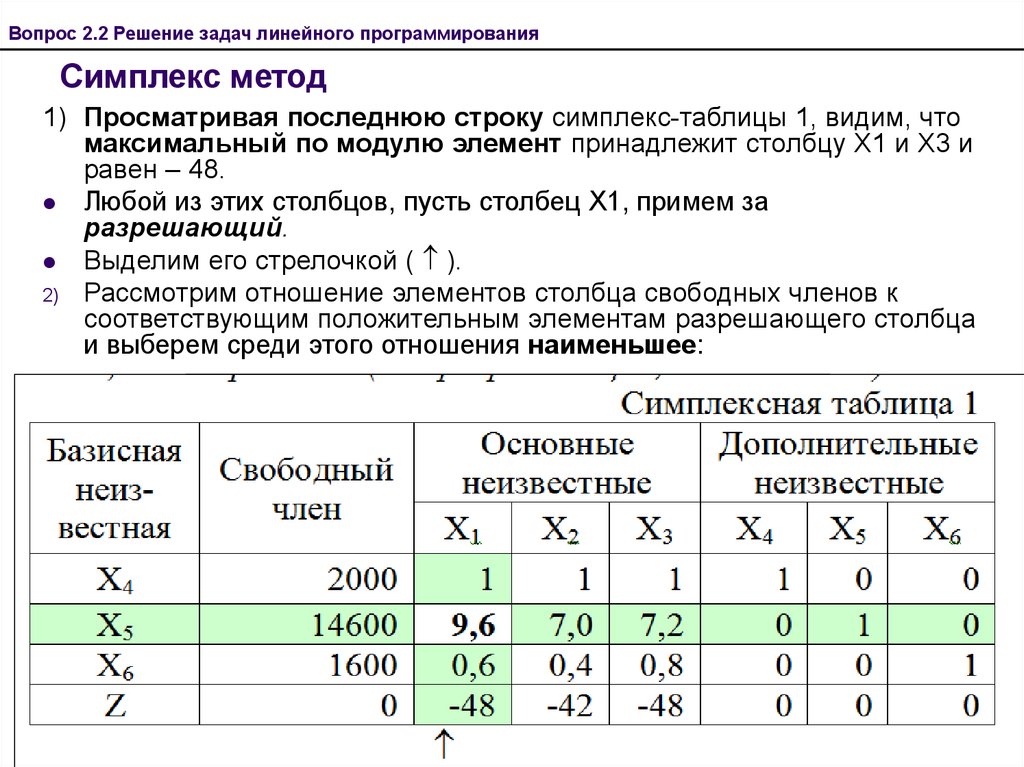 Я решил написать статью, объясняющую линейное программирование простым английским языком. Я максимально упростил содержание. Идея состоит в том, чтобы вы начали и увлеклись линейным программированием.
Я решил написать статью, объясняющую линейное программирование простым английским языком. Я максимально упростил содержание. Идея состоит в том, чтобы вы начали и увлеклись линейным программированием. Изображено важное слово в предыдущем предложении. Реальные отношения могут быть намного сложнее, но мы можем упростить их до линейных отношений.
Изображено важное слово в предыдущем предложении. Реальные отношения могут быть намного сложнее, но мы можем упростить их до линейных отношений.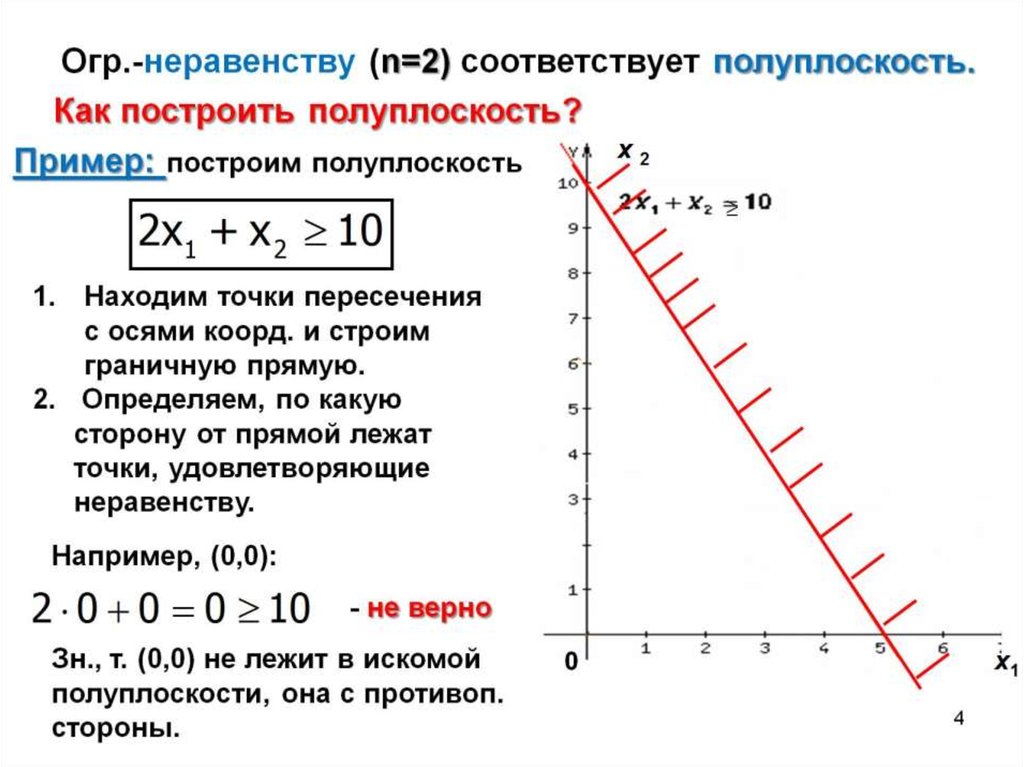




 Это означает, что значения переменных решения должны быть больше или равны 0.
Это означает, что значения переменных решения должны быть больше или равны 0.
 Найдите оптимальное решение и оптимальное значение.
Найдите оптимальное решение и оптимальное значение. Учитывая, что общий бюджет фермера составляет 10 000 долларов США. Стоимость производства пшеницы и ячменя на гектар также предоставляется нам. У нас есть верхний предел общих затрат, потраченных фермером. Таким образом, наше уравнение становится:
Учитывая, что общий бюджет фермера составляет 10 000 долларов США. Стоимость производства пшеницы и ячменя на гектар также предоставляется нам. У нас есть верхний предел общих затрат, потраченных фермером. Таким образом, наше уравнение становится: Пришло время решить это.
Пришло время решить это.
 Общее рабочее время 9 часов в день. Каким должен быть объем производства каждой из труб, чтобы максимизировать прибыль?
Общее рабочее время 9 часов в день. Каким должен быть объем производства каждой из труб, чтобы максимизировать прибыль? dense 1 -none- числовой
плотный.col 1 -нет-числовой
плотно.val 1 -нет- числовой
плотно.const.nrow 1 -нет- числовой
плотный.ctr 1 -нет-числовой
use.rw 1 -нет-числовой
tmp 1 -none- символ
статус 1 -нет-числовой
> выбрать $ решение
[1] 88 20
> opt$objval
[1] 2600
dense 1 -none- числовой
плотный.col 1 -нет-числовой
плотно.val 1 -нет- числовой
плотно.const.nrow 1 -нет- числовой
плотный.ctr 1 -нет-числовой
use.rw 1 -нет-числовой
tmp 1 -none- символ
статус 1 -нет-числовой
> выбрать $ решение
[1] 88 20
> opt$objval
[1] 2600

 США
США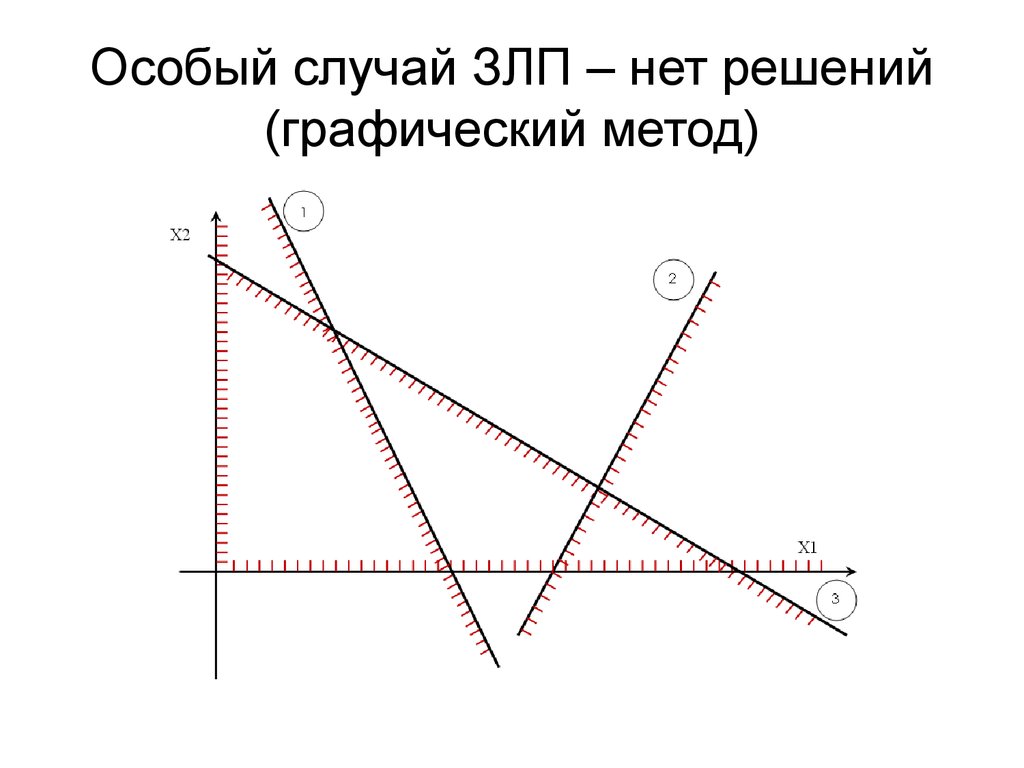
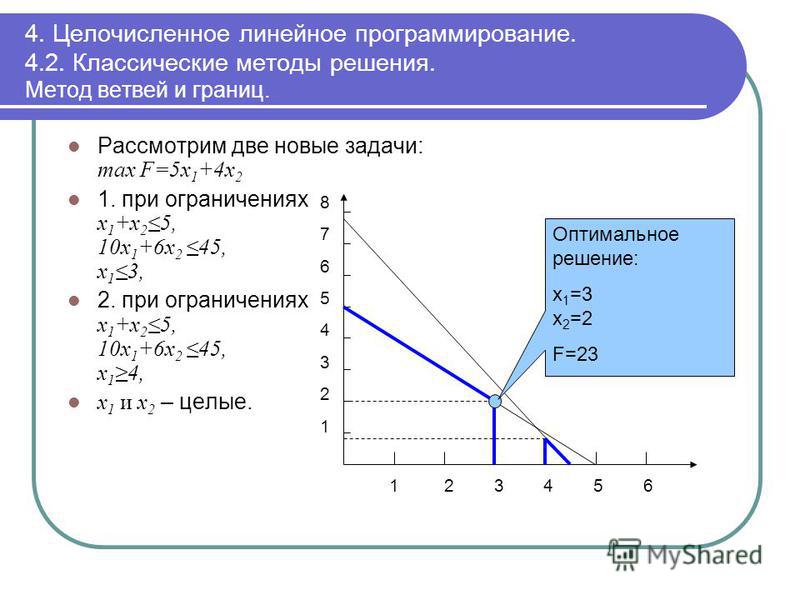
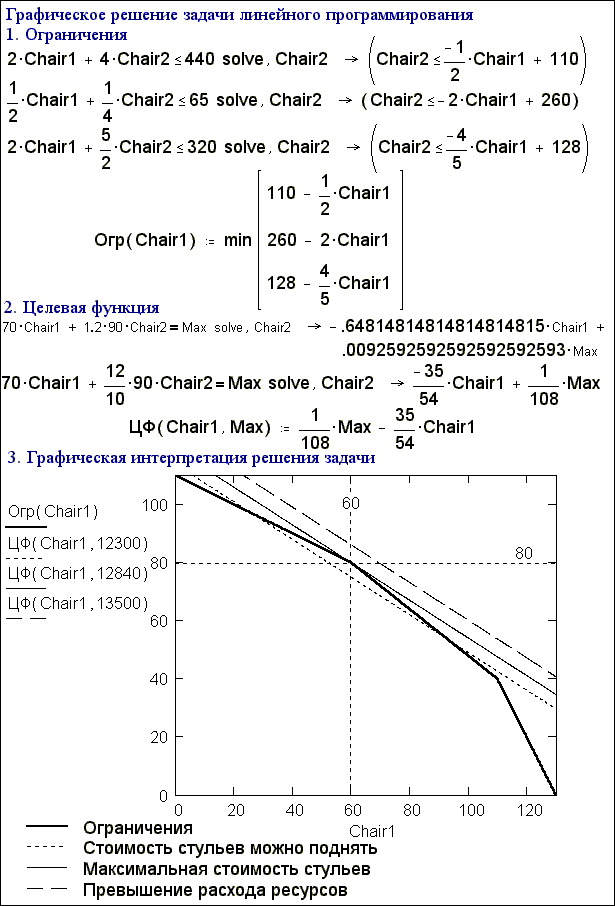
 . . . . .
. . . . . При этом, чтобы сбалансировать рекламу среди трех видов СМИ, на радио должно появляться не более половины от общего количества рекламы. И не менее 10% должно происходить на телевидении. Еженедельный рекламный бюджет составляет 18 200 долларов. Сколько рекламных объявлений следует размещать в каждом из трех типов СМИ, чтобы максимально увеличить общую аудиторию?
При этом, чтобы сбалансировать рекламу среди трех видов СМИ, на радио должно появляться не более половины от общего количества рекламы. И не менее 10% должно происходить на телевидении. Еженедельный рекламный бюджет составляет 18 200 долларов. Сколько рекламных объявлений следует размещать в каждом из трех типов СМИ, чтобы максимально увеличить общую аудиторию?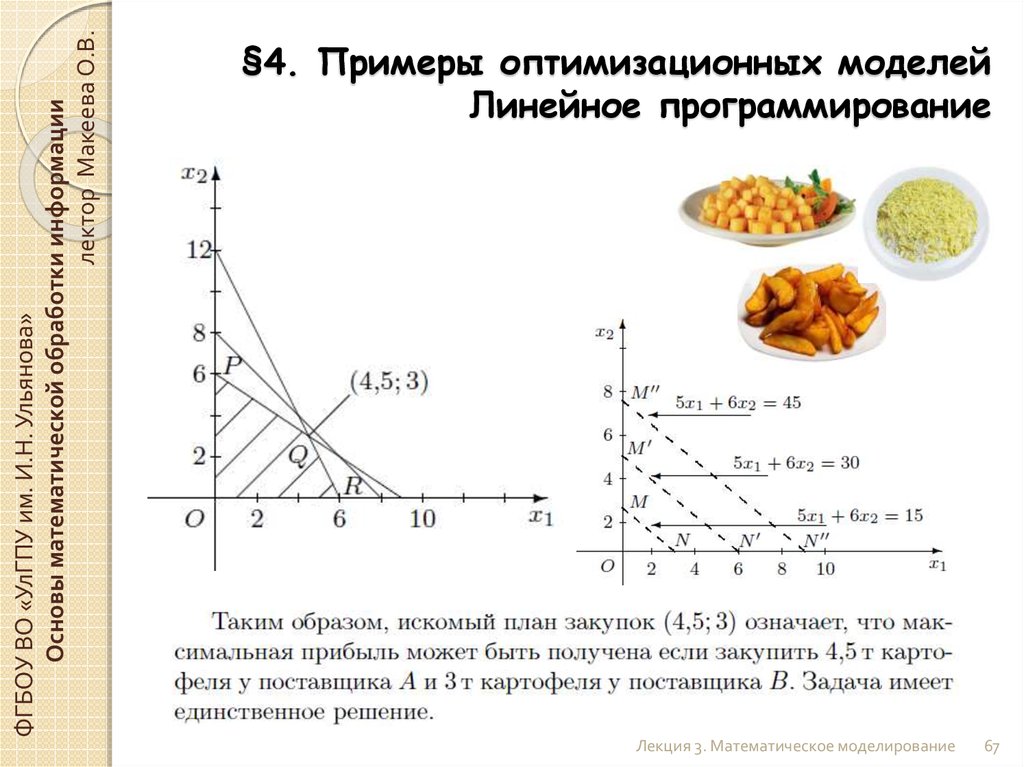 Общий бюджет, который может быть выделен, составляет 18 200 долларов. А индивидуальные затраты на телевизионную, газетную и радиорекламу составляют 2000, 600 и 300 долларов соответственно. Это может быть представлено уравнением
Общий бюджет, который может быть выделен, составляет 18 200 долларов. А индивидуальные затраты на телевизионную, газетную и радиорекламу составляют 2000, 600 и 300 долларов соответственно. Это может быть представлено уравнением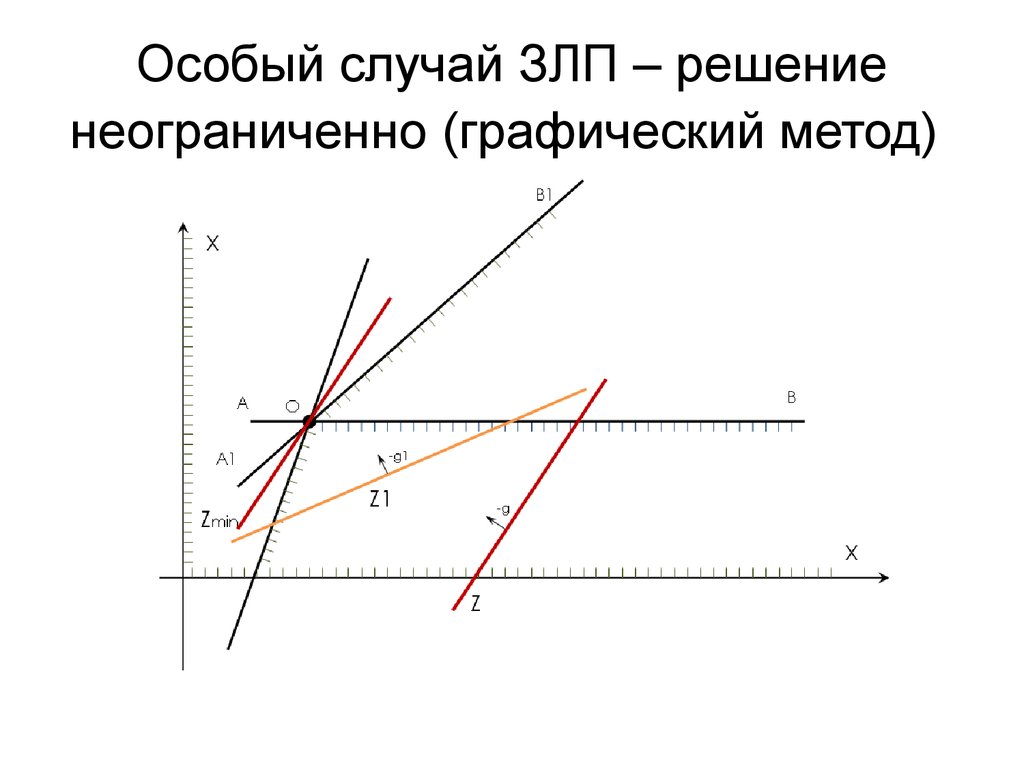
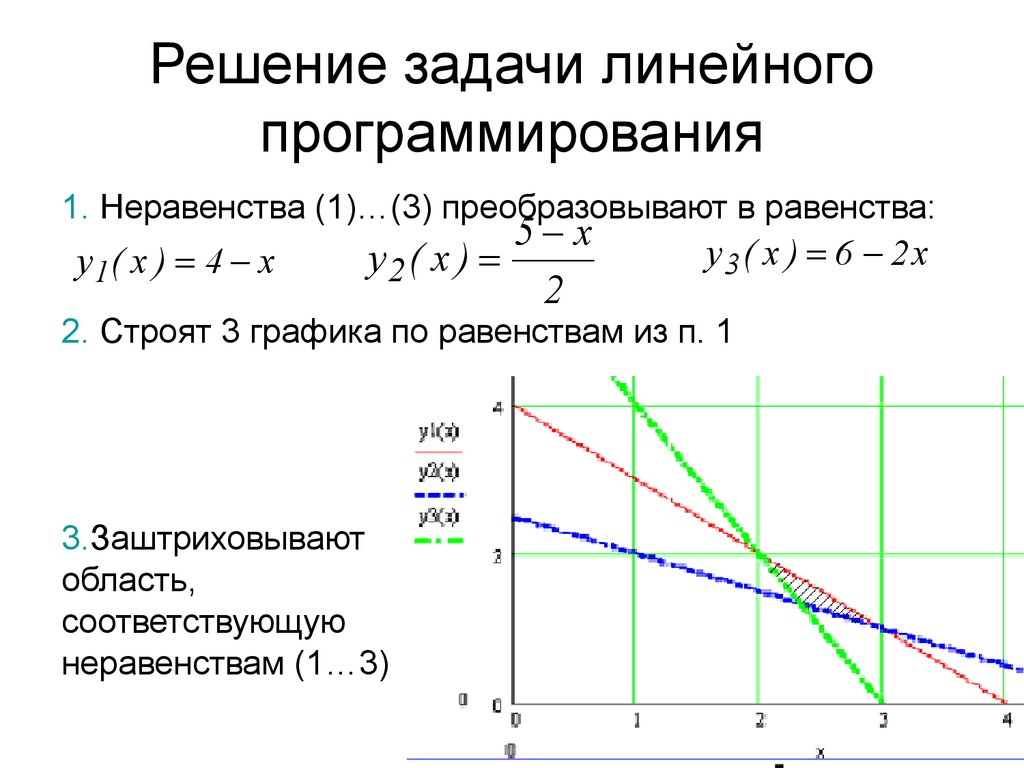 Всякий раз, когда вам дают реальную проблему, которая включает в себя спрос и предложение из одного источника из разных источников. Модель данных включает в себя следующее:
Всякий раз, когда вам дают реальную проблему, которая включает в себя спрос и предложение из одного источника из разных источников. Модель данных включает в себя следующее: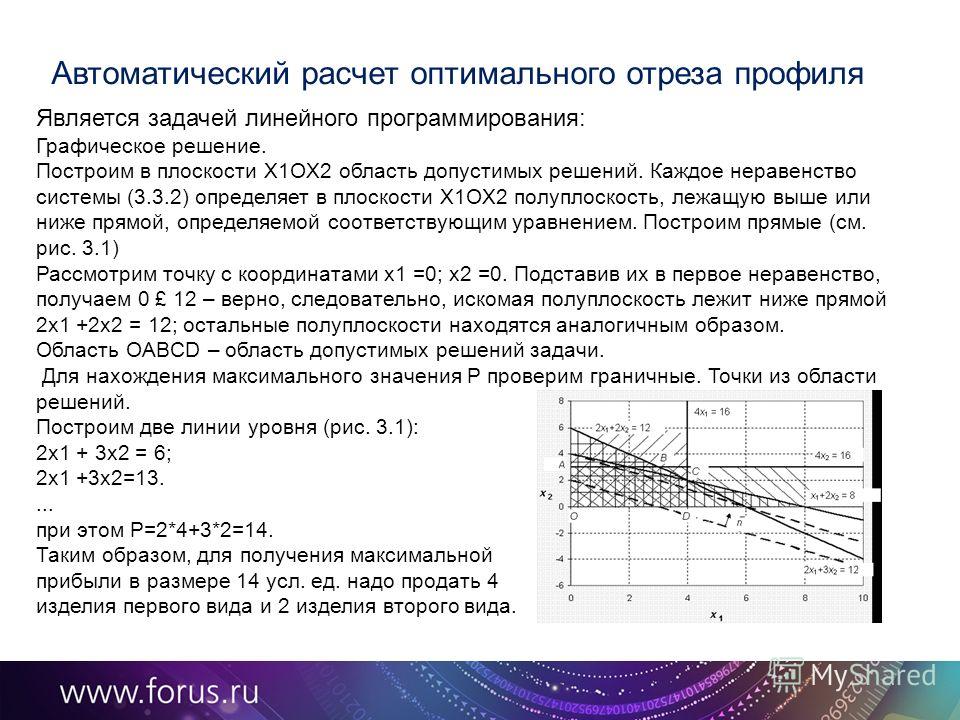
 Ед. изм. Затем переходим на мельницу 3, северо-западная ячейка S2M3. Спрос на мельницу 3 составляет 15 единиц, которые он может получить из бункера 2 по цене 9 долларов.за единицу. Переходя к последней мельнице, потребность мельницы 4 составляет 15 единиц. Он получит 5 единиц из хранилища 2 по цене 20 долларов за единицу и 10 единиц из хранилища 3 по цене 18 долларов за единицу.
Ед. изм. Затем переходим на мельницу 3, северо-западная ячейка S2M3. Спрос на мельницу 3 составляет 15 единиц, которые он может получить из бункера 2 по цене 9 долларов.за единицу. Переходя к последней мельнице, потребность мельницы 4 составляет 15 единиц. Он получит 5 единиц из хранилища 2 по цене 20 долларов за единицу и 10 единиц из хранилища 3 по цене 18 долларов за единицу. Спрос на Mill1 удовлетворен. Для мельницы 2 мы поставляем 15 единиц продукции из бункера 1 по цене 2 доллара за единицу. Затем для мельницы 3 мы поставляем 15 единиц из бункера 2 по цене 9 долларов за единицу. Затем для мельницы 4 мы поставляем 10 единиц продукции из бункера 2 по цене 20 долларов США за единицу и 5 единиц продукции из бункера 3 по цене 18 долларов США за единицу. Общие транспортные расходы составляют 475 долларов.
Спрос на Mill1 удовлетворен. Для мельницы 2 мы поставляем 15 единиц продукции из бункера 1 по цене 2 доллара за единицу. Затем для мельницы 3 мы поставляем 15 единиц из бункера 2 по цене 9 долларов за единицу. Затем для мельницы 4 мы поставляем 10 единиц продукции из бункера 2 по цене 20 долларов США за единицу и 5 единиц продукции из бункера 3 по цене 18 долларов США за единицу. Общие транспортные расходы составляют 475 долларов. Аналогично для других. Это делается для того, чтобы взять общий спрос из бункера 1 и других.
Аналогично для других. Это делается для того, чтобы взять общий спрос из бункера 1 и других.
 Это связано с такими ограничениями, как ограниченное пространство на полках, разнообразие продуктов и т. д.
Это связано с такими ограничениями, как ограниченное пространство на полках, разнообразие продуктов и т. д. д. Продолжайте изучать дальше.
д. Продолжайте изучать дальше. Эти переменные можно обозначить как x₁ и x₂, и с помощью этих переменных большую часть анализа можно выполнить на двумерном графике. Хотя мы не можем обобщить большое количество переменных с помощью графического подхода, можно легко продемонстрировать основные концепции линейного программирования в контексте с двумя переменными. Мы всегда можем обратиться к задачам с двумя переменными, если проблемы кажутся сложными и мы оказываемся в пучке вопросов. И мы всегда можем искать ответы в случае с двумя переменными, используя графы, то есть графически решая задачи линейного программирования.
Эти переменные можно обозначить как x₁ и x₂, и с помощью этих переменных большую часть анализа можно выполнить на двумерном графике. Хотя мы не можем обобщить большое количество переменных с помощью графического подхода, можно легко продемонстрировать основные концепции линейного программирования в контексте с двумя переменными. Мы всегда можем обратиться к задачам с двумя переменными, если проблемы кажутся сложными и мы оказываемся в пучке вопросов. И мы всегда можем искать ответы в случае с двумя переменными, используя графы, то есть графически решая задачи линейного программирования.
 .., N), которые не удовлетворяют одновременно всем барьерам и неотрицательным условиям задачи ЛП, называется сформировать невозможное решение для этого. проблема с ЛП.
.., N), которые не удовлетворяют одновременно всем барьерам и неотрицательным условиям задачи ЛП, называется сформировать невозможное решение для этого. проблема с ЛП.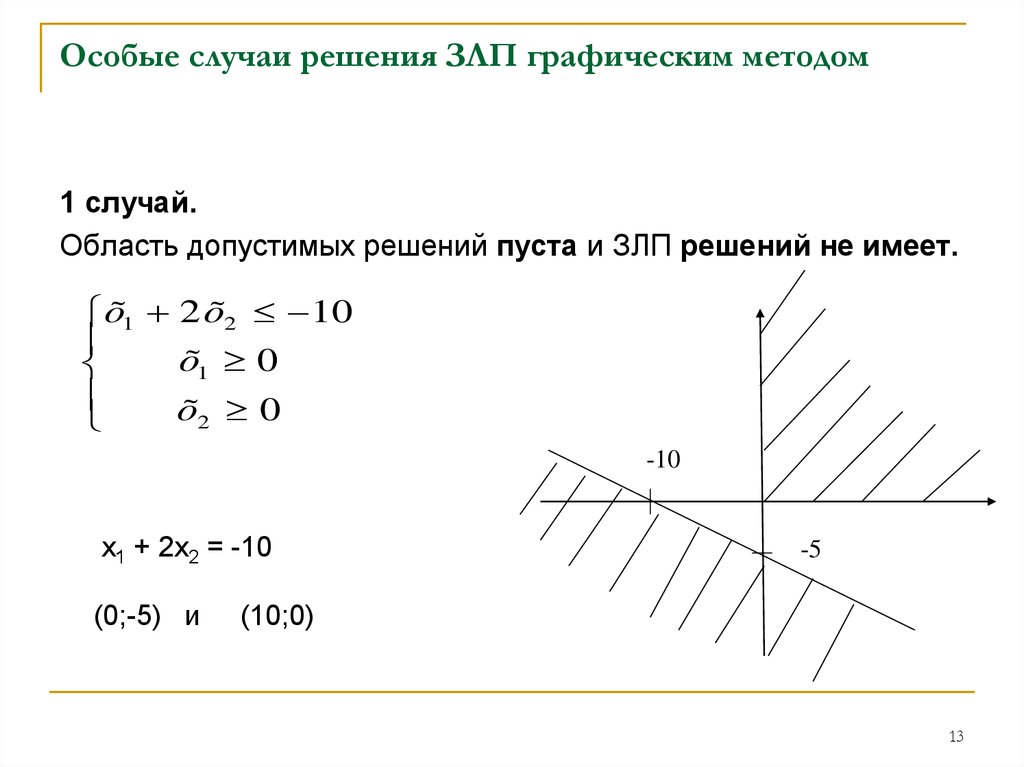
 Или, если область, вероятно, не будет иметь границ, то:
Или, если область, вероятно, не будет иметь границ, то:
 Мы можем шаг за шагом решать задачи линейного программирования графически.
Мы можем шаг за шагом решать задачи линейного программирования графически. Но перед этим мы должны переписать неравенства ограничений в виде равенств.
Но перед этим мы должны переписать неравенства ограничений в виде равенств. скоро)
скоро)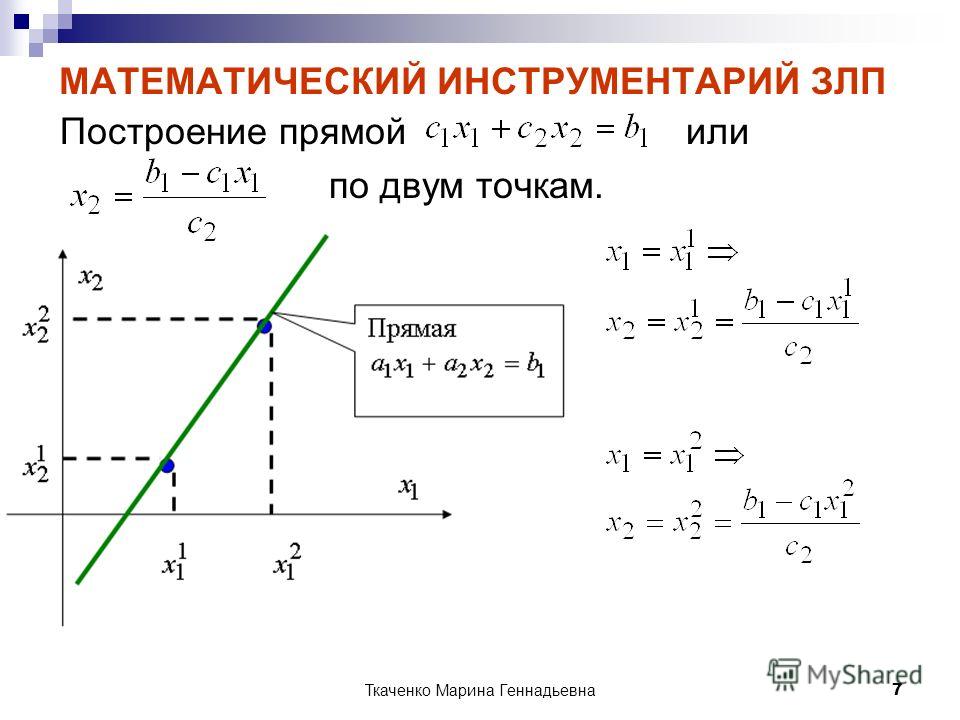

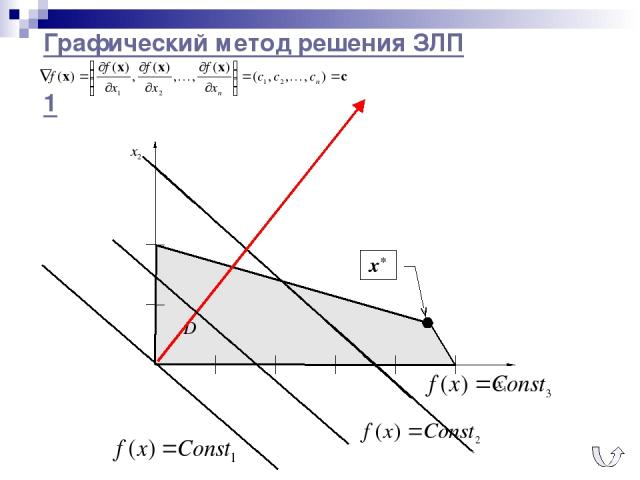
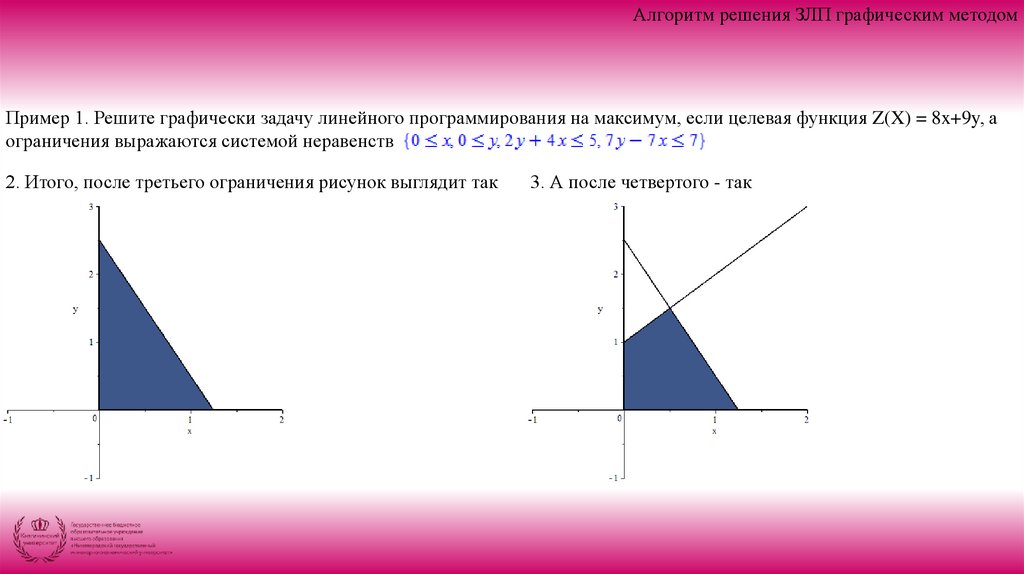
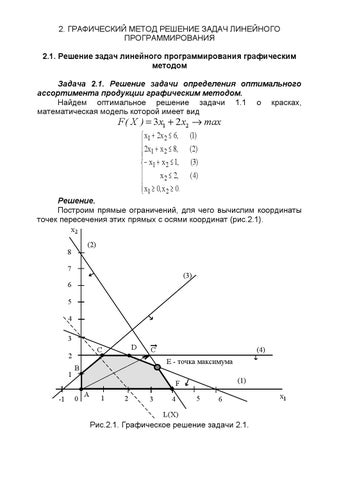
 нарисовав пунктирную линию вместо обычной линии.
нарисовав пунктирную линию вместо обычной линии. В обоих случаях вы должны помнить о перемещении линейки по градиенту линии целевой функции.
В обоих случаях вы должны помнить о перемещении линейки по градиенту линии целевой функции.




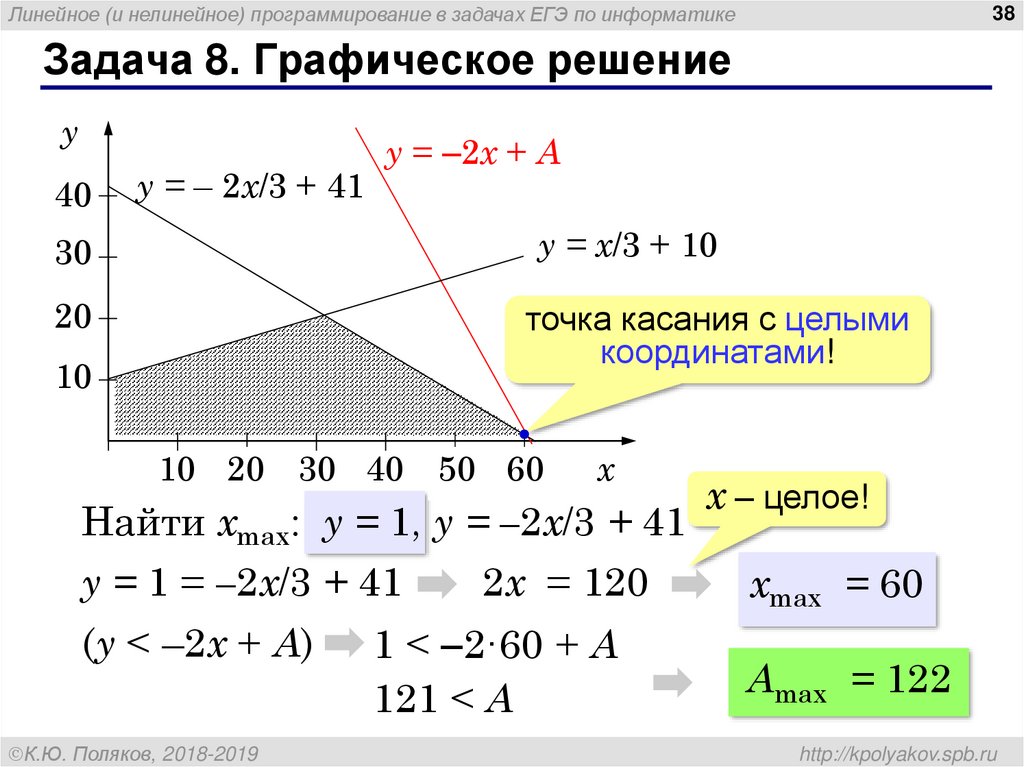 60
60
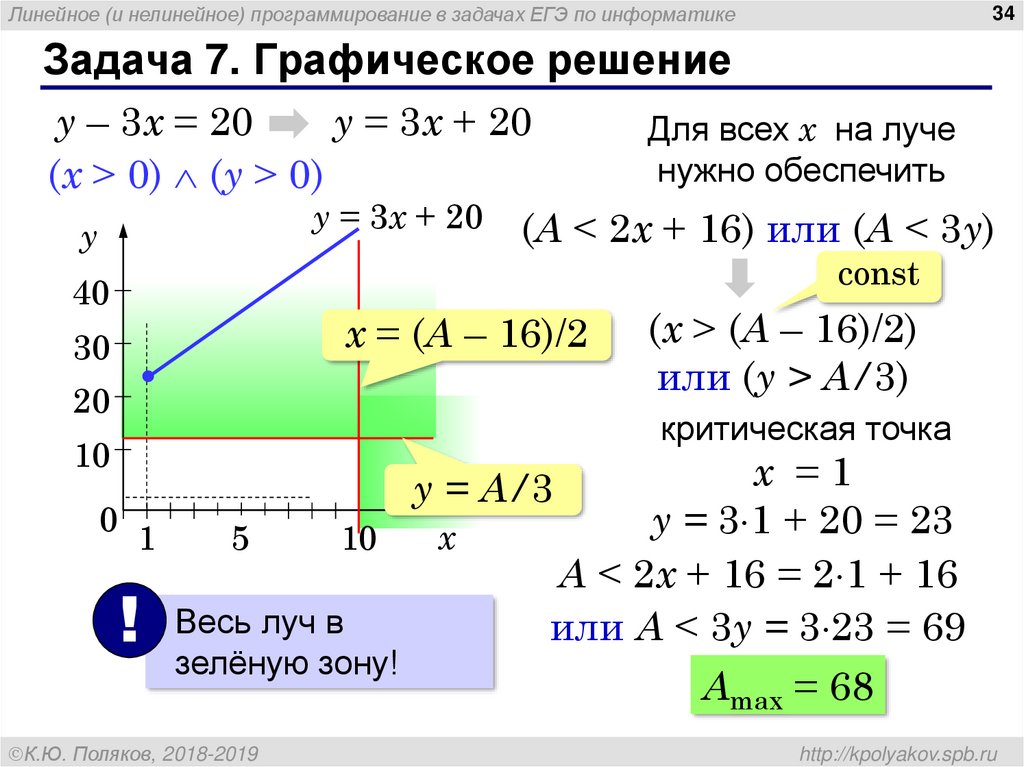 640, где произведено 4 единицы статьи А и 4 единицы статьи Б.
640, где произведено 4 единицы статьи А и 4 единицы статьи Б.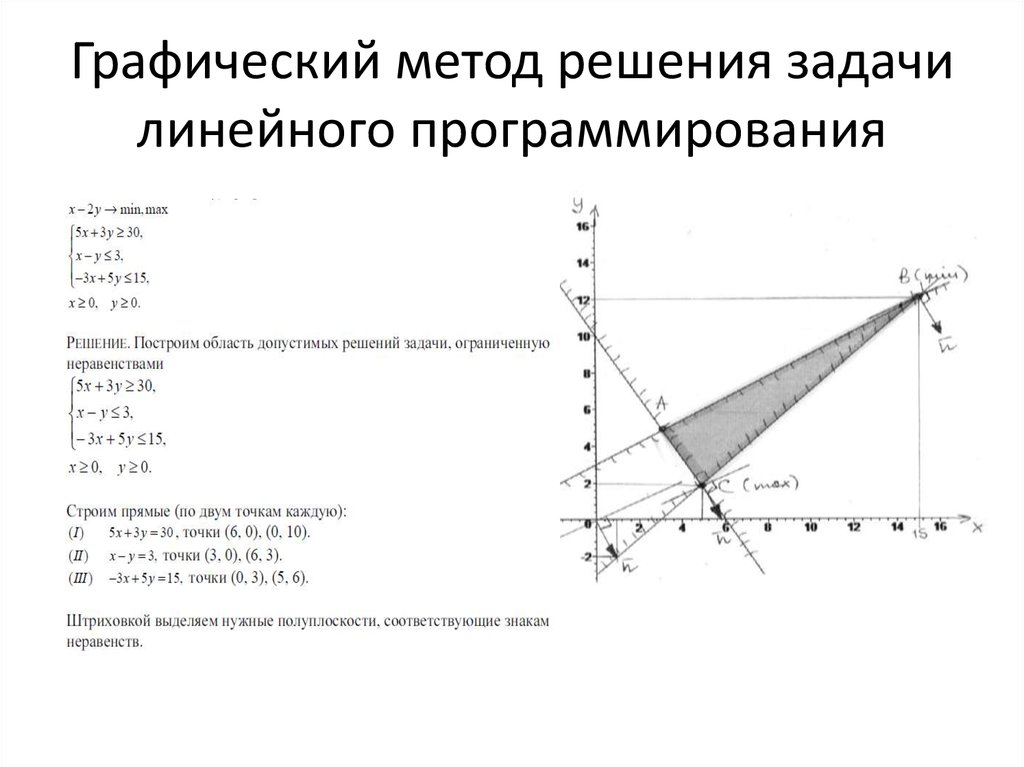 Наиболее распространенными методами являются симплексный метод, решение задач с использованием R или открытого решателя, а также графический метод. В этой статье мы будем решать задачи линейного программирования графическим методом.
Наиболее распространенными методами являются симплексный метод, решение задач с использованием R или открытого решателя, а также графический метод. В этой статье мы будем решать задачи линейного программирования графическим методом.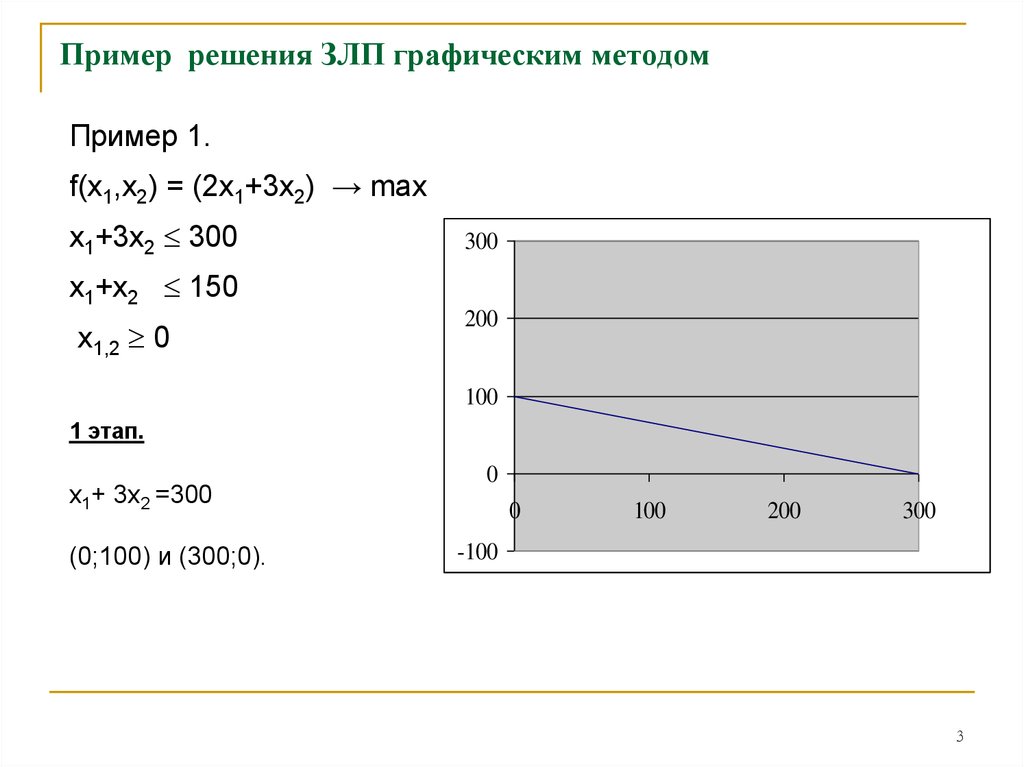 Определите набор ограничений
Определите набор ограничений