Задачи линейного программирования примеры: Математическое Бюро. Страница 404

Пример решения задачи линейного программирования графическим методом

Find:

Highlight allMatch case

Current View

Current View

Automatic ZoomActual SizeFit PageFull Width50%75%100%125%150%200%300%400%

Enter the password to open this PDF file:

File name:

—

File size:

—

Title:

—

Author:

—

Subject:

—

Keywords:

—

Creation Date:

—

Modification Date:

—

Creator:

—

PDF Producer:

—

PDF Version:

—

Page Count:

—

Ваулина В. А., УрГЭУ Пример решения задачи линейного программирования графическим методом Линейное программирование — это раздел математики, в котором рассматриваются методы решения экстремальных задач с линейным функционалом и линейными ограничениями. Существуют два наиболее распространенных способа решения задач линейного программирования: графический метод и симплекс-метод. Графический метод существенно нагляднее и обычно проще для понимания решения. Также этот метод позволяет практически одновременно найти решение на минимум и максимум. Основные шаги по решению ЗПЛ графическим методом следующие: построить область допустимых решений задачи (выпуклый многоугольник), который определяется как пересечение полуплоскостей, соответствующих неравенствам задачи, построить линию уровня целевой функции, и, наконец, двигать линию уровня в нужном направлении, пока не достигнем крайней точки области — оптимальной точки (или множества). В отличие от графического метода, симплексный метод практически не имеет ограничений на задачу, может быть любое количество переменных и т.

п. При решении задачи симплексным методом вычисления ведутся в таблицах. Решение задачи данным методом дает не только оптимальное решение, но и решение двойственной задачи, остатки ресурсов и т.п. Рассмотрим решение задачи линейного программирования графическим методом. Для производства столов и стульев мебельная фабрика использует три вида древесины. Норма затрат для каждого вида древесины на один стол составляет 1; 2; 5; на один стул – 1; 5; 2. Запасы древесины – 150; 600; 600. Прибыль от реализации одного стола – 200р, одного стула – 100р. Составить оптимальный план производства, обеспечивающий максимальную прибыль. Решение. Составим математическую модель задачи. Пусть Х — столы, У — стулья, I,II,III – виды древесины соответственно. I II III Прибыль X 1 2 5 200 Y 1 5 2 100 150 600 600 Общий запас Составим неравенства по полученной таблице: { x 1+ x2 ≤150, 2 x 1+5 x 2 ≤600, 5 x 1 +2 x 2 ≤600, x1,2 ≥ 0. } F ( x )=200 x 1+100 x 2 → max Применим описанные выше шаги решения. Построим область допустимых решений. Рассмотрим целевую функцию задачи F = 200×1+100×2 → max и построим вектор-градиент, составленный из коэффициентов целевой функции. Так как нас интересует максимальное решение, то опорную прямую двигаем прямую до последнего касания обозначенной области. Получаем оптимальную точку D. Так как точка D получена в результате пересечения прямых (1) и (3), то ее координаты удовлетворяют уравнениям этих прямых: x1+x2=150 5×1+2×2=600 Решив систему уравнений, получим: x1 = 100, x2 = 50 Откуда найдем максимальное значение целевой функции: F(X) = 25000. На примере данной задачи мы рассмотрели решение задачи линейного программирования графическим методом. Этот метод наглядно показывает область дополнительных решений и нахождение оптимальной точки. Руководитель: Кныш А.А.

Примеры задач линейного программирования.

1. Сущность методов оптимизации. Определение. Предмет изучения. Цель. Примеры оптимизации. Оптимальное, т.е. самое наилучшее. Особенность – кол-во возможных вариантов решения является бесконечным. Критерий качества оптимальности либо целевая функция будет показывать в каком направлении надо двигаться. Методы оптимизации – наука, занимающаяся разработкой либо практическим применением методов более эффективного оптимального управления организационными системами.

   Решение – выбор из ряда возможных альтернатив. Предмет изучения – системы организационного управления или организации, кот состоят из большого числа подразделений. Цели отдельных подразделений могут не совпадать. Цель МО – количественное обоснование принимаемых решений по управлению организацией.

2. Основные понятия и особенности методов оптимизации. Операция, решение, элементы решения. Этапы исследования. Операция – любое мероприятие, направленное на достижение цели. Решение – выбор, зависящий от заданных параметров. Параметры, совокупность кот образует решение, называются элементами решения. Особенности МО: 1. Системный подход к анализу проблемы(любая задача рассматривается комплексно, с т.з. функционирования всего коллектива) 2. Непременное желание найти экстремальное (оптимальное) решение. 3. МО проводятся комплексно по многим направлениям одновременно. 4. Количество вариантов решения м.б. неограниченным. 5. Обязательное наличие функции качества(оптимальности), целевой функции. 6. При решении каждой проблемы могут возникать новые задачи. Наибольший эффект при непрерывном переходе от первой проблемы к другой. Многие задачи решаются поэтапным циклическим способом

   , алгоритм становится неизменным. Этапы исследования операций: 1. Построение экономических и математических моделей для задач принятия решений в сложных ситуациях или условиях неопределенности. 2. Изучение взаимосвязей, определяющих в последствии принятия решений и установления критериев эффективности, позволяющих оценить преимущество того или иного варианта действия.

3. Общая характеристика методов оптимизации.

   Линейное программирование. Нелинейное программирование. Динамическое программирование. Стохастическое программирование. Дискретное программирование. Эвристическое программирование. Прямые и обратные задачи методов оптимизации. Параметры при решении задач оптимизации6 1.ЦФ (целевая функция) ЦФ: Z=f(x1,x1,…,xn)→max(min) 2. СО (Система ограничений) ∑g(x1,x2,..,xn)≤bi – уровень запасов. 3. УНО (условия неотрицательности) xi≥I, i=1,n. Классические МО (исходные данные не заданы таблично, дискретно) :1Линейное программирование. ЦФ, СО — линейный характер. 2. Нелинейное программирование. ЦФ, СО — нелинейный характер. 3.Целочисленное программирование. 4.Динамическое программирование. Исходные параметры зависят от времени. 5.Параметрическое программирование. 6.Стахостическое программирование. 7. Эвристическое программирование (количество возможных вариантов решения слишком велико)

4. Типичные классы задач методов оптимизации. Классы:1 задача сетевого программирования и управления. 2. Задачи массового обслуживания. 3. Задача управления запасами. 4. задача распределения ресурсов. 5. Задача ремонта и замены оборудования. 6. Задача составления расписания. 7. Задача планирования и размещения. 8. Задача выбора маршрута.

5. Общая постановка задачи линейного программирования. Экономико-математическая модель. Этапы проведения экономико-математического моделирования. Под моделью будем понимать условный образ какого либо объекта приближенно воссоздающий этот объект с помощью некоторого языка. Процесс приближенного воссоздания объекта будем называть формализацией. Экономико-математическая модель – это математическое описание исследуемого экономического процесса или объекта. Рассматривается 3 этапа проведения экономико-математического моделирования: 1. Ставятся цели и задачи исследования, проводится качественное описание объекта виде экономической модели.

   2. Формируется математическая модель осуществляется выбор или разработка методов исследования. Проводится программирование модели на ЭВМ. 3. Основной. Осуществляется анализ математической модели, проводятся машинные расчеты, анализ и обработка полученных результатов, системы ограничений и условий неотрицательности.

7. Общая задача линейного программирования. Общая постановка задачи при ограничениях. Оптимальное решение (план).

8. Решение систем m линейных неравенств с двумя переменными. Область решения. Область допустимых решений. Методика решения системы.

L(x) =c₁x₁ + c₂x₂ + … + c_n x_n → max

а₁₁x₁+ a₁₂ x₂ =< b ₁

а₂₁x₁+ a₂₂ x₂ =< b ₂

…

а_m1x₁+ a_m2 x₂ =< b _m

x₁>=0; x₂>=0 – область первого квадрата

a₁₁x₁ + a₁₂x₂=b₁ – граничная прямая, так как x₂=0 -> b₁/a₁₂ и x₁=0 -> b₁/a₁₁

Неравенство характеризует одну из двух плоскостей

X = (x₁; x₂)

Решением каждого неравенства системы является полуплоскость, содержащая граничную прямую и расположенную по одну сторону от неё.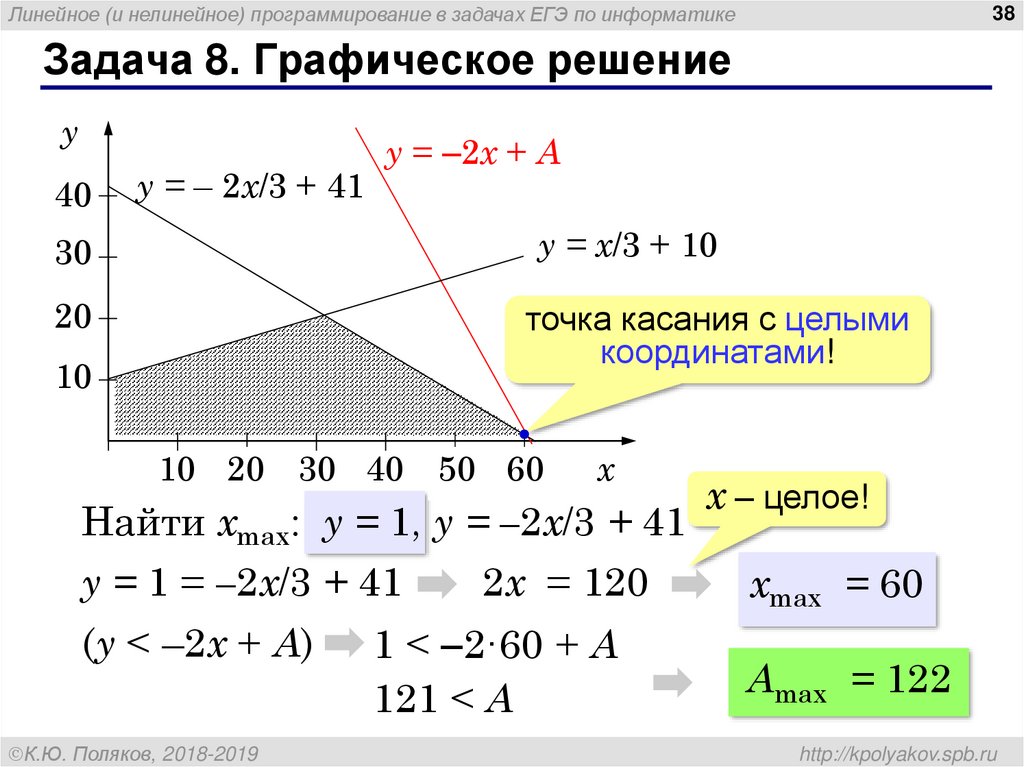

ОР (область решений системы) – это пересечение полуплоскостей, каждая из которых определяется неравенством системы. ОДР (область доступных решений)

– это область решений системы + условия неотрицательности.

Виды возможных решений:

9. Геометрическая интерпретация задач линейного программирования. Типы решений злп на плоскости.

Графический метод, несмотря на свою очевидность и применимость лишь в случае малой размерности задачи, позволяет понять качественные особенности задачи линейного программирования, характерные для любой размерности пространства переменных и лежащие в основе численных методов ее решения. Поясним графический метод на примере задачи ЛП в основной форме для n = 2

Для нахождения единственного оптимального решения используется градиентный метод, вектор-градиент (градиент) указывает направление максимально быстрого вырастания целевой функции

Вектор-градиент начинается в начале координат и заканчивается в координате, обозначенной С = (с₁, с₂)

с₁ = d F / d x₁

с₂ = d F / d x₂, где F – целевая функция

Для построения вектора С необходимо построить линию уровня (она перпендикулярна Z₀)

Z_c — перемещается, Z₀ – самая крайняя точка

Точка С – результат пересечения двух переменных (2) и (1), с = (1)∩(2)

Максимальная прибыль достигнута в точки С.

Минимальные затраты достигаются с помощью С с инверсией.

10. Понятие линейного программирования. Матричная форма экономико-математической модели злп.

Линейное программирование — математическая дисциплина, посвященная теории и методам решения задач об экстремумах линейных функций на множествах n-мерного векторного пространства, задаваемых системами линейных уравнений и неравенств.

Линейное программирование является частным случаем выпуклого программирования, которое в свою очередь является частным случаем математического программирования. Одновременно оно — основа нескольких методов решения задач целочисленного и нелинейного программирования. Одним из обобщений линейного программирования является дробно-линейное программирование.

Многие свойства задач линейного программирования можно интерпретировать также как свойства многогранников

Матричные модели [matrix models] — экономико-математические модели, построенные в виде таблиц (матриц). Они отображают соотношения между затратами на производство и его результатами, нормативы затрат, производственную и экономическую структуру хозяйства. Применяются в межотраслевом балансе, при решении отраслевых задач оптимального планирования развития и размещения производства, в эколого-экономическом моделировании и т. д.

Широкое распространение матричные модели связано, в частности, с тем, что запись данных в табличной форме облегчает их введение в компьютер и дает наглядное представление о результатах расчета (на самом деле ввиду большой размерности моделей они обычно не изображаются непосредственно в виде таблиц, а содержащаяся в них информация хранится в памяти ЭВМ — см. ст. “Массив данных”). Для перехода между Матричные модели различных звеньев (уровней хозяйства) применяются вариантные матрицы.

Матричные модели применяются и в теоретических исследованиях экономики, поскольку она представляется как процесс преобразования затрат в результаты. Элементами матрицы при этом являются величины затрат при разных технологических способах.

Примеры решения для линейного программирования

Примеры решения для линейного программирования

OR-Notes — это серия вводных заметок по темам, широкий заголовок области исследования операций (ИЛИ). Они были изначально используется мной во вводном курсе ИЛИ, который я веду в Имперском колледже. Они теперь доступны для использования любыми студентами и преподавателями, заинтересованными в ИЛИ при соблюдении следующих условий.

Полный список тем, доступных в OR-Notes, можно найти здесь.

---

Примеры решения для линейного программирования

Пример линейного программирования 1997 г. экзамен UG

Компания производит два продукта (X и Y) на двух машинах (A и B). Каждая произведенная единица X требует 50 минут обработки на машина A и 30 минут обработки на машине B. Каждая единица Y, которая производится требует 24 минут обработки на машине А и 33 минуты время обработки на станке Б.

В начале текущей недели имеется 30 единиц X и 90 единиц Y в наличии. Ожидается, что доступное время обработки на машине A составит 40 часов, а на машине B прогнозируется 35 часов.

Спрос на X на текущей неделе прогнозируется на уровне 75 единиц и для Y прогнозируется 95 единиц. Политика компании заключается в максимизации совокупного сумма единиц X и единиц Y на складе в конце недели.

• Сформулируйте задачу, чтобы решить, сколько каждого продукта производить на текущей неделе в виде линейной программы.
• Решите эту линейную программу графически.

Раствор

Пусть

• x количество единиц X, произведенных за текущую неделю
• y — количество единиц Y, произведенных за текущую неделю

тогда ограничения:

50x + 24y <= 40(60) машинное время

30x + 33y <= 35(60) машинное время B

х >= 75 — 30

т. е. x >= 45, поэтому производство X >= спрос (75) — начальный запас (30), что гарантирует удовлетворение спроса

г >= 95 — 90

т. е. y >= 5, поэтому производство Y >= спроса (95) — начальный запас (90), что гарантирует удовлетворение спроса

Цель: максимизировать (x+30-75) + (y+90-95) = (х+у-50)
т. е. максимизировать количество единиц, оставшихся на складе в конце недели

Из диаграммы ниже видно, что максимум приходится на пересечение из х=45 и 50х + 24у = 2400

Решение одновременно, а не чтение значений с графика, мы имеем, что x = 45 и y = 6,25 со значением целевой функции 1,25

---

Пример линейного программирования 1995 УГ экзамен

Показан спрос на два продукта в каждую из последних четырех недель ниже.

 неделя
                      1 2 3 4
Спрос - продукт 1 23 27 34 40
Спрос - продукт 2 11 13 15 14
 

Применить экспоненциальное сглаживание с константой сглаживания 0,7 для получения прогноза спрос на эти товары на неделе 5.

Эти продукты производятся с использованием двух машин, X и Y. Каждая единица произведенный продукт 1 требует 15 минут обработки на машине X и 25 минут обработки на машине Y. Каждая единица продукта 2, произведено требует 7 минут обработки на машине X и 45 минут обработки на машине Y. Ожидается, что доступное время на машине X на неделе 5 составит будет 20 часов, а на машине Y на неделе 5 прогнозируется 15 часов. Каждый единица продукта 1, проданная на 5-й неделе, дает вклад в прибыль в размере 10 фунтов стерлингов. и каждая единица продукта 2, проданная на неделе 5, дает вклад в прибыль от 4 фунтов стерлингов.

Может быть невозможно произвести достаточно, чтобы удовлетворить ваш прогнозируемый спрос на эти товары в неделю 5 и на каждую единицу неудовлетворенного спроса на товар 1 стоит 3 фунта стерлингов, каждая единица неудовлетворенного спроса на продукт 2 стоит 1 фунт стерлингов.

• Сформулируйте задачу, чтобы решить, сколько каждого продукта производить на 5 неделе по линейной программе.
• Решите эту линейную программу графически.

Раствор

Обратите внимание, что первая часть вопроса — это прогнозирование вопрос так решается ниже.

Для продукта 1 применяется экспоненциальное сглаживание с константой сглаживания из 0,7 получаем:

М ₁ = Д ₁ = 23
M ₂ = 0,7Y ₂ + 0,3M ₁ = 0,7(27) + 0,3(23) = 25,80
M ₃ = 0,7Y ₃ + 0,3M ₂ = 0,7(34) + 0,3(25,80) = 31,54
M ₄ = 0,7Y ₄ + 0,3M ₃ = 0,7(40) + 0,3(31,54) = 37,46

Прогноз на пятую неделю — это среднее значение на 4-ю неделю = M ₄ = 37,46 = 31 (поскольку у нас не может быть дробного спроса).

Для продукта 2 применяется экспоненциальное сглаживание с константой сглаживания из 0,7 получаем:

М ₁ = Д ₁ = 11
М ₂ = 0,7Г ₂ + 0,3М ₁ = 0,7(13) + 0,3(11) = 12,40
M ₃ = 0,7Y ₃ + 0,3M ₂ = 0,7(15) + 0,3(12,40) = 14,22
M ₄ = 0,7Y ₄ + 0,3M ₃ = 0,7(14) + 0,3(14,22) = 14. 07

Прогноз на пятую неделю — это среднее значение на 4-ю неделю = M ₄ = 14,07 = 14 (поскольку у нас не может быть дробного спроса).

Теперь мы можем сформулировать LP для недели 5, используя две цифры спроса. (37 для продукта 1 и 14 для продукта 2), полученные выше.

Пусть

x ₁ количество произведенных единиц продукта 1

x ₂ количество произведенных единиц продукта 2

где х ₁ , х ₂ >=0

Ограничения:

15x ₁ + 7x ₂ <= 20(60) станок X

25x ₁ + 45x ₂ <= 15(60) станок Y

x ₁ <= 37 спрос на продукт 1

x ₂ <= 14 спрос на продукт 2

Цель состоит в максимизации прибыли, т.е.

увеличить 10x ₁ + 4x ₂ — 3(37-x ₁ ) — 1(14-x ₂ )

т.е. максимизировать 13x ₁ + 5x ₂ — 125

График показан ниже, из графика мы имеем, что решение происходит по горизонтальной оси (x ₂ =0) в x ₁ =36 в какой точке максимальная прибыль 13(36) + 5(0) — 125 = £343

---

Пример линейного программирования 1994 UG экзамен

Компания занимается производством двух изделий (X и Y). ресурсы, необходимые для производства X и Y, двояки, а именно машинное время для автоматическая обработка и время мастера для ручной отделки. Таблица ниже дает количество минут, необходимых для каждого элемента:

 Машинное время Время мастера
Пункт Х 13 20
     Д 19 29 

У компании есть 40 часов машинного времени в наличии на следующем рабочем месте. неделю, но только 35 часов рабочего времени. Машинное время стоит 10 фунтов стерлингов за час работы, а время мастера стоит 2 фунта стерлингов за час работы. Время простоя машины и мастера не требует затрат. Полученный доход за каждый произведенный товар (все производство продано) составляет 20 фунтов стерлингов для X и 30 фунтов стерлингов за Y. У компании есть конкретный контракт на производство 10 изделий. X в неделю для конкретного клиента.

• Сформулируйте задачу о том, сколько производить в неделю, как линейная программа.
• Решите эту линейную программу графически.

Раствор

Пусть

• x количество элементов X
• y количество элементов Y

тогда LP:

увеличить

• 20x + 30y — 10(время работы машины) — 2(время работы мастера)

предмет:

• 13x + 19y <= 40(60) машинного времени
• 20x + 29y <= 35(60) времени мастера
• х >= 10 контракт
• х, у >= 0

так, чтобы целевая функция стала

увеличить

• 20x + 30y — 10(13x + 19y)/60 — 2(20x + 29y)/60

т. е. максимизировать

• 17,1667х + 25,8667у

предмет:

• 13x + 19y <= 2400
• 20x + 29y <= 2100
• х >= 10
• х, у >= 0

Из диаграммы ниже видно, что максимум приходится на пересечение из х=10 и 20х + 29у <= 2100

Решение одновременно, а не чтение значений с графика, имеем, что x=10 и y=65,52 со значением целевой функции £1866,5

---

Пример линейного программирования 1992 UG экзамен

Компания производит два продукта (А и В) и прибыль на единицу продано 3 и 5 фунтов стерлингов соответственно. Каждое изделие должно быть собрано на конкретной машине каждая единица продукта А собирается за 12 минут. времени и каждой единицы продукта B 25 минут времени сборки. Компания оценивает, что машина, используемая для сборки, имеет эффективную рабочую неделю всего 30 часов (из-за технического обслуживания/поломки).

Технологические ограничения означают, что на каждые пять единиц продукции Произведено не менее двух единиц продукта В.

• Сформулируйте задачу о том, сколько каждого продукта нужно произвести, в виде линейной программа.
• Решите эту линейную программу графически.
• Компании была предложена возможность арендовать дополнительную машину, тем самым удвоение эффективного доступного времени сборки. Что такое максимум сумма, которую вы готовы платить (в неделю) за аренду этой машины и почему?

Раствор

Пусть

x _A = количество произведенных единиц A

x _B = количество произведенных единиц B

, тогда ограничения:

12x _A + 25x _B <= 30(60) (время сборки)

х _В >= 2(х _А /5)

т. е. x _B — 0,4x _A >= 0

т.е. 5x _B >= 2x _A (технологический)

где х _А , х _В >= 0

и цель

увеличить 3x _A + 5x _B

Из диаграммы ниже видно, что максимум приходится на пересечение из 12х _А + 25х _В = 1800 и х _В — 0,4х _А = 0

Решение одновременно, а не чтение значений с графика, у нас это:

х _А = (1800/22) = 81,8

х _В = 0,4 х _А = 32,7

со значением целевой функции £408,9

Удвоение доступного времени сборки означает, что ограничение времени сборки (в настоящее время 12x _A + 25x _B <= 1800) становится 12x _A + 25x _B <= 2(1800) Это новое ограничение будет параллельно существующее ограничение по времени сборки, так что новое оптимальное решение будет лежать на пересечении 12х _А + 25х _В = 3600 и х _В — 0,4х _А = 0

т. е. при х _А = (3600/22) = 163,6

х _В = 0,4 х _А = 65,4

со значением целевой функции £817,8

Следовательно, мы получили дополнительную прибыль в размере £(817,8-408,9) = £408,9. и это максимальная сумма, которую мы готовы заплатить за аренда станка для удвоения времени сборки.

Это потому, что если мы заплатим больше этой суммы, мы уменьшим наша максимальная прибыль ниже 408,9 фунтов стерлингов, которые мы получили бы без новая машина.

---

Пример линейного программирования 1988 г. экзамен UG

Решить

свернуть

4а + 5б + 6с

с учетом

Решение

Чтобы решить эту LP, мы используем уравнение c-a-b=0, чтобы положить c=a+b (>= 0 как a >= 0 и b >= 0), поэтому LP уменьшается до

.

свернуть

при условии

а + б >= 11

а — б <= 5

7а + 12б >= 35

а >= 0 б >= 0

На приведенной ниже диаграмме минимум приходится на пересечение — б = 5 и а + б = 11

т. е. a = 8 и b = 3 с c (= a + b) = 11 и значением цели функция 10а + 11б = 80 + 33 = 113.

---

---

Пример линейного программирования 1987 г. экзамен UG

Решите следующую линейную программу:

увеличить 5x ₁ + 6x ₂

при условии

x ₁ + x ₂ <= 10

x ₁ — x ₂ >= 3

5x ₁ + 4x ₂ <= 35

x ₁ >= 0

x ₂ >= 0

Решение

Из диаграммы ниже видно, что максимум приходится на пересечение из

5x ₁ + 4x ₂ = 35 и

х ₁ — х ₂ = 3

Решение одновременно, а не чтение значений с графика, у нас есть

5 (3 + х ₂ ) + 4 х ₂ = 35

т.е. 15 + 9x ₂ = 35

т.е. х ₂ = (20/9) = 2,222 и

х ₁ = 3 + х ₂ = (47/9) = 5,222

Максимальное значение равно 5(47/9) + 6(20/9) = (355/9) = 39,444.

---

---

Пример линейного программирования 1986 UG экзамен

Плотник делает столы и стулья. Каждый стол можно выгодно продать 30 фунтов стерлингов и каждый стул с прибылью 10 фунтов стерлингов. Плотник может позволить себе тратить до 40 часов в неделю на работу, и на это уходит шесть часов. сделать стол и три часа сделать стул. Потребительский спрос требует что он производит как минимум в три раза больше стульев, чем столов. Столы принимают в четыре раза больше места для хранения, чем стулья, и есть место для почти четыре стола каждую неделю.

Сформулируйте эту задачу как задачу линейного программирования и решите ее. графически.

Решение

Переменные

Пусть

x _T = количество столов, сделанных за неделю

x _C = количество стульев, изготовленных за неделю

Ограничения

• общее рабочее время

6x _T + 3x _C <= 40

• покупательский спрос

x _C >= 3x _T

• место для хранения

(х _С /4) + х _Т <= 4

• все переменные >= 0

Объектив

увеличить 30x _T + 10x _C

Графическое представление проблемы приведено ниже и из что имеем что решение лежит на пересечении

(x _C /4) + x _T = 4 и 6x _T + 3x _C = 40

Решая эти два уравнения одновременно, получаем x _C = 10,667, x _T = 1,333 и соответствующая прибыль = 146,667 фунтов стерлингов.

---

---

Типы задач линейного программирования: концепции и решения

Задачи линейного программирования состоят из линейной функции, которую необходимо максимизировать или минимизировать. Линейное программирование — это метод оптимизации, который используется для поиска наилучшего результата в математической модели. В линейном программировании целевая функция (линейная функция, представляющая величины, которые необходимо максимизировать или минимизировать) и ограничения (система равенств или неравенств, описывающих ограничения на переменные решения) представлены линейными отношениями.

Смотреть: Как решить задачу линейного программирования с помощью графического метода!

Проблемы линейного программирования Терминологии

СОДЕРЖАНИЕ

• Проблемы линейного программирования
• .
  • • Постановка задачи:
    • Решение:
• Решение линейной программы с использованием R
• Проблемы и решения Food Sportings
. и управление сельским хозяйством

Ниже приведены термины, с которыми вы должны ознакомиться, прежде чем приступить к решению задач линейного программирования:

Целевая функция

Определяется как некоторое числовое значение, которое следует максимизировать или минимизировать. Например, если вы занимаетесь каким-то бизнесом, то ваша основная цель — максимизировать прибыль и сократить убытки.

Ограничения

Ограничения определяются как ограничения переменных решения. Например, если вы занимаетесь каким-то бизнесом, то ограничениями или ограничениями являются бюджет, количество рабочих, производственные мощности, площадь и т.д.

Переменные решения

Переменные решения — это переменные, определяющие результат. Например, если вы фермер, который хочет выращивать пшеницу и ячмень, то вычисление общей площади для выращивания пшеницы и ячменя является переменными решения.

Ограничение на неотрицательность

Ограничение на неотрицательность означает, что значения переменных решения должны быть больше или равны 0.0634 ?

Загрузите подробную брошюру и получите бесплатный доступ к интерактивному демонстрационному классу с отраслевым экспертом

Как определить задачу линейного программирования?

Чтобы задача была определена как задача линейного программирования, все переменные решения, целевая функция и ограничения должны быть линейными функциями. Ниже приведены шаги для определения задачи как задачи линейного программирования:

(1) Определите количество переменных решения
(2) Определите ограничения на переменные решения
(3) Запишите целевую функцию в виде линейного уравнения
(4) Явно укажите ограничение неотрицательности
(5) Линейный Задачи программирования

Задача линейного программирования имеет дело с линейной функцией, которую необходимо максимизировать или минимизировать с учетом определенных ограничений в виде линейных уравнений или неравенств.

В этом разделе мы узнаем, как сформулировать задачу линейного программирования и какие методы используются для ее решения.

Постановка задачи:

Компания-производитель калькуляторов производит два типа калькуляторов: портативный калькулятор и научный калькулятор. Статистические данные прогнозируют, что ожидается спрос не менее чем на 100 научных и 80 портативных калькуляторов каждый день. Поскольку у компании есть определенные ограничения на производственные мощности, компания может производить только 200 научных и 170 карманных калькуляторов в день. Компания получила контракт на поставку минимум 200 калькуляторов в день. Если каждый проданный научный калькулятор приносит убыток в размере 2 индийских рупий и прибыль в размере 5 индийских рупий с каждого портативного калькулятора, то сколько калькуляторов каждого типа компания должна производить ежедневно, чтобы максимизировать чистую прибыль?

Решение:

Чтобы решить эту проблему, давайте сначала сформулируем ее правильно, выполнив шаги, указанные выше.

Шаг 1: Определите количество переменных решения. В этой задаче, поскольку мы должны рассчитать, сколько калькуляторов каждого типа следует производить ежедневно, чтобы максимизировать чистую прибыль, количество научных и портативных калькуляторов является нашими переменными решения.

X = количество произведенных научных калькуляторов

Y = количество произведенных портативных калькуляторов

Следовательно, у нас есть две переменные решения в этой задаче.

Шаг 2: Определите ограничения на переменные решения.

Нижняя граница, упомянутая в задаче (ожидаемый спрос не менее чем на 100 научных и 80 карманных калькуляторов каждый день), выглядит следующим образом.

Следовательно,

X >= 100

Y >= 80

Верхняя граница из-за ограничений, указанных в постановке задачи (компания может производить только 200 научных и 170 карманных калькуляторов в день) такова:

Следовательно,

X<=200

Y<=170

В постановке задачи также видно, что существует совместное ограничение на значения X и Y из-за минимального заказа на отгрузочную партию, которая можно записать как:

X + Y >= 200

Шаг 3: Запишите целевую функцию в виде линейного уравнения. В этой задаче четко сказано, что мы должны оптимизировать чистую прибыль. Как указано в задаче (если на каждом научном калькуляторе, который вы продали, есть убыток в размере 2 индийских рупий и прибыль в размере 5 индийских рупий на каждом портативном калькуляторе), функция чистой прибыли может быть записана как:

Прибыль (P) = -2X + 5Y

Шаг 4: Явно укажите ограничение неотрицательности. Поскольку компания-производитель калькуляторов не может производить отрицательное количество калькуляторов, ограничений на неотрицательность нет.

Следовательно,

X ≥ 0

Y ≥ 0

Поскольку мы сформулировали задачу, давайте приведем ее к математическому виду для дальнейшего ее решения.

Максимизация P = -2X + 5Y при условии:

100 ≤ X ≤ 200

80 ≤ Y ≤ 170

X + Y ≥ 200

Графический метод решения задачи линейного программирования график.

Этот метод решает постановку задачи, разбивая ее на следующие шаги:

Шаги с 1 по 4 аналогичны упомянутым при формулировании задачи линейного программирования.

Шаг 5: Нанесите ограничения на график. Давайте нанесем все ограничения, определенные на шаге 2, на график так же, как мы строим уравнение.

Чтобы отобразить ограничение, упомянутое в шаге 2, на графике, вы должны преобразовать неравенство в уравнение:

X + Y = 200

Отметьте координаты на графике и проведите прямую через координаты.

Шаг 6: Выделите допустимую область на графике. После нанесения координат на график заштрихуйте область, выходящую за пределы ограничений (что невозможно). Выделенная допустимая область будет выглядеть так:

Шаг 7: Найдите координаты оптимальной точки. Чтобы найти координаты оптимальной точки, мы будем решать одновременную пару линейных уравнений, взяв некоторые случайные значения.

P = -2x + 5y

Угловые точки

Уравнение, P = -2x + 5y

A (100, 170)

P = 650

B (200, 170)

P = 450

C (200, 80)

P = 0

D (120, 80)

P = 160

E (100, 100)

P = 300

Эти угловые точки получают координатами двух перпендикулярных линий. из точки на оси координат.

Шаг 8: Найдите оптимальную точку.

В приведенной выше таблице показано, что максимальное значение P равно 650, полученное при (X, Y) = A (100, 170).

Решение линейной программы с помощью R

Чтобы решить задачу линейного программирования с помощью R, вы должны быть знакомы с пакетом lp_solve. Этот пакет содержит несколько функций для решения задач линейного программирования и получения значимого статистического анализа. Давайте разберем этот метод на примере.

Пример:  Производственная компания продает два товара А и Б по 25 и 20 долларов соответственно. Компания имеет только 1800 единиц ресурсов, доступных каждый день. Для продукта А требуется 20 единиц ресурсов, а для продукта Б — 12 единиц ресурсов, а время производства обоих продуктов — 4 минуты. Общее количество доступных рабочих часов, доступных в день, равно 8. Каким должен быть объем производства каждого из продуктов, чтобы максимизировать прибыль.

Решение: Целевая функция в приведенной выше задаче равна

Max(Sales) = Max(25A + 20B)

Где,

A – количество произведенных единиц продукта A

B – количество единиц продукта B произведено

A и B также называются переменными решения

В задаче есть два ограничения: ресурсы и время.

20A + 12B <= 1800 (ограничение ресурсов)

4A + 4B <= 8*60 (ограничение времени)

Давайте посмотрим на часть кода:

install.packages(«lpSolve»)

## Загрузить пакет lpsolve

library(lpSolve)

## Установить коэффициенты переменных решения ## Создать ограничение martix

const.mat <- matrix(c(20, 12, 4, 4), nrow=2, byrow=TRUE)

## определить ограничения

time_constraint <- (8*60)

resource_constraint <- 1800

## RHS для ограничений

const.rhs <- c(resource_constraint, time_constraint)

## Направление ограничений

const.dir  <- c("<=", "<=")

## Найти оптимальное решение

оптимальный <- lp(direction="max", target. in, const.mat, const.dir, const.rhs)

## Отображение оптимальных значений для A и B

optimum$solution

Вывод вышеуказанной программы: :

## [1] 45 75

## Проверить значение целевой функции в оптимальной точке

оптимальный $objval

## [1] 2625

Вывод: Из приведенного выше результата видно, что компания должна произвести 45 единиц продукта A и 75 единиц продукта B, чтобы получить продажи на сумму 2625 долларов, что составляет максимальные продажи, которые компания может получить при данных ограничениях.

Постановка задачи линейного программирования и ее решение

Постановка задачи:

Вы представляете ИТ-организацию, которая хочет оборудовать свой офис новыми шкафами. Вы связались с мебельной компанией, и они сообщили вам, что шкаф X стоит 10 долларов за единицу, требует 6 квадратных футов площади и вмещает восемь кубических футов файлов. Стоимость шкафа Y составляет 20 долларов за единицу, требуется восемь квадратных футов площади и вмещает двенадцать кубических футов файлов. У вас есть место только для шкафов площадью 72 квадратных фута, а бюджет на эту покупку составляет 140 долларов. Сколько моделей какой модели вы должны купить, чтобы максимизировать объем хранилища?

Решение:

Чтобы решить эту задачу, давайте сначала правильно сформулируем ее, выполнив шаги, указанные выше.

Шаг 1: Определите количество переменных решения. В этой задаче, поскольку нам нужно рассчитать, сколько шкафов той или иной модели мы должны купить, чтобы максимизировать объем хранилища, количество шкафов X и Y являются нашими переменными решения.

X = количество приобретенных шкафов модели X

Y = количество приобретенных шкафов модели Y

Следовательно, в этой задаче есть две переменные решения.

Шаг 2: Определите ограничения на переменные решения. Затраты и пространство являются двумя ограничениями в этой проблеме.

Стоимость = 10X + 20Y < 140 или Y < –( 1/2 )X + 7

Пробел = 6X + 8Y < 72 или Y < –( 3/4 )X + 9

Шаг 3: Запись целевая функция в виде линейного уравнения. В этой задаче четко указано, что мы должны оптимизировать объем, который можно записать как:

Объем (V) = 8X + 12Y

Шаг 4: Явно укажите ограничение неотрицательности. Естественно,

X ≥ 0

Y ≥ 0

Поскольку мы сформулировали задачу, давайте для дальнейшего решения приведем ее к математической форме.

Шаг 5: Выделите допустимую область на графике. После нанесения координат на график заштрихуйте область, выходящую за пределы ограничений (что невозможно). Выделенная допустимая область будет выглядеть так:

Шаг 6: Найдите координаты оптимальной точки. Чтобы найти координаты оптимальной точки, мы будем решать одновременную пару линейных уравнений, взяв некоторые случайные значения.

V = 8x + 12y

Угловые точки

Уравнение, V = 8x + 12y

A (8, 3)

P = 100

B (0, 7)

P = 84

C ( 12, 0)

P = 96

Координаты этих угловых точек получаются проведением двух перпендикулярных линий из точки на оси координат.

Шаг 7: Найдите оптимальную точку.

В приведенной выше таблице показано, что максимальное значение V равно 100, которое получается при (X, Y) = A (8, 3).

Хотите узнать, как стать
экспертом по науке о данных ?

Загрузите подробную брошюру и получите бесплатный доступ к интерактивному демонстрационному классу с отраслевым экспертом

Постановка задачи:

Представьте, что вы лаборант и ваша работа — ежедневно кормить кроликов. Их ежедневный рацион содержит минимум 24 г (г) жира, 36 г углеводов и 4 г белка. Вы можете кормить только 5 унций пищи в день. В соответствии с бюджетом можно заказать два продукта питания и смешать их для получения оптимальной смеси. Продукт X состоит из 8 г жира, 12 г углеводов и 2 г белка на унцию и стоит 0,20 доллара за унцию. Продукт Y включает 12 г жиров, 12 г углеводов и 1 г белков на унцию по цене 0,30 доллара США за унцию. Какая оптимальная смесь?

Решение:

Чтобы решить эту задачу, давайте сначала правильно сформулируем ее, выполнив шаги, указанные выше.

Шаг 1: Определите количество переменных решения. В этой задаче, поскольку мы должны рассчитать количество унций каждого продукта, необходимого для оптимальной дневной смеси, количество унций продуктов X и продуктов Y являются нашими переменными решения.

X = количество унций еды X

Y = количество унций еды Y

Следовательно, в этой задаче у нас есть две переменные решения.

Шаг 2: Определите ограничения на переменные решения. Граммы жира, углеводов и белков на унцию — три ограничения в этой задаче.

Жир = 8X + 12Y > 24

Углеводы = 12X + 12Y > 36

Белок = 2X + 1Y > 4

В постановке задачи также видно, что существует совместное ограничение на значения X и Y, потому что максимальный вес еды составляет пять унций. Следовательно,

X + Y <=5

Шаг 3: Запишите целевую функцию в виде линейного уравнения. В этой задаче четко сказано, что мы должны оптимизировать стоимость для минимального значения.

Отношение затрат, C = 0,2X + 0,3Y

Шаг 4: Явно укажите ограничение неотрицательности. Так как вы не можете использовать отрицательное количество любого из продуктов,

Следовательно,

X ≥ 0

Y ≥ 0

Поскольку мы сформулировали задачу, давайте преобразуем ее в математическую форму для дальнейшего решения.

Шаг 5: Выделите допустимую область на графике. После нанесения координат на график заштрихуйте область, выходящую за пределы ограничений (что невозможно). Выделенная допустимая область будет выглядеть так:

Шаг 6: Найдите координаты оптимальной точки. Чтобы найти координаты оптимальной точки, мы будем решать одновременную пару линейных уравнений, взяв некоторые случайные значения.

C = 0,2X + 0,3Y

Угловые точки

Уравнение, C = 0,2X + 0,3Y

A (0,4)

C = 1,2

B (0, 5)

C = 1,5

C (3, 0)

3

3

D (5,0 )

C = 1,0

E (1,2)

C = 0,8

Координаты этих угловых точек получаются путем проведения двух перпендикулярных линий из точки на оси координат.

Шаг 7: Найдите оптимальную точку.

Из приведенной выше таблицы видно, что минимальное значение стоимости = 0,6 и получается при (X, Y) = A (3, 0). Следовательно, вы должны получать минимальную стоимость 60 центов за ежедневную порцию, используя только 3 унции Food X.

Применение задач линейного программирования

Линейное программирование используется для поиска оптимальных решений для исследования операций. Линейное программирование требует создания неравенств, а затем их графического отображения для решения задач.

Вот список областей, в которых используется линейное программирование.

Управление маркетингом

Линейное программирование позволяет маркетологам анализировать охват аудитории рекламой на основе таких ограничений, как доступные средства массовой информации, рекламный бюджет и т. д. Линейное программирование также помогает продавцам (полевым агентам) определять кратчайший маршрут до пункта назначения. Руководитель отдела логистики может легко найти оптимальный график распределения для транспортировки продукта с разных складов в различные точки рынка таким образом, чтобы общие транспортные расходы были минимальными.

Финансовый менеджмент

Линейное программирование помогает финансовым фирмам, фирмам взаимных фондов и банкам выбирать инвестиционный портфель акций, облигаций и т. д. таким образом, чтобы доход от инвестиций был максимальным.

Управление запасами

Линейное программирование также помогает складским фирмам лучше управлять сырьем и готовой продукцией. Они могут найти оптимальное решение для минимизации стоимости запасов на основе пространства и спроса как ограничений.

Управление человеческими ресурсами

Линейное программирование позволяет менеджеру по подбору персонала решать проблемы, связанные с наймом, отбором, обучением и размещением рабочей силы в различных отделах фирмы. Линейное программирование можно использовать для определения минимального количества сотрудников, необходимых в различные смены для выполнения производственного графика в рамках графика.

Управление продовольствием и сельским хозяйством

Линейное программирование помогает фермерам определить, какие культуры выращивать и в каком количестве следует выращивать конкретные культуры, чтобы увеличить свои доходы.

No related posts.