Летняя математическая школа . 5 класс
- Презентации
- Летняя математическая школа . 5 класс
Автор публикации: Миньковская И.Н.
Дата публикации: 05.06.2016
Краткое описание:
загрузить презентацию
1
Графы Это — один из способов решения логических задач По условию задачи составляется схема, состоящая из линий(ребер) и точек (вершин).
2
История возникновения графов Термин граф впервые появился в книге венгерского математика Д. Кенига в 1936 г., хотя начальные важнейшие теоремы о графах восходят к Л. Эйлеру. Математические графы с дворянским титулом «граф» связывает общее происхождение от латинского слова « графио » — пишу.
Благодаря этой рекламе сайт может продолжать свое существование, спасибо за просмотр.
загрузить презентацию
3
Задача о Кенигсбергских мостах Город Кенигсберг (после мировой войны он называется Калининград) стоит на реке Прегель. Некогда там было 7 мостов, которые связывали между собой берега и два острова. Жители города заметили, что они никак не могут совершить прогулку по всем семи мостам, пройдя по каждому из них ровно один раз. Так возникла головоломка: “можно ли пройти все семь кенигсбергских мостов ровно один раз и вернуться в исходное место?”. Выстроив алгоритм, Эйлер получил отрицательный ответ в задаче о мостах.
4
Впервые над задачами такого типа задумался Леонард Эйлер после посещения города Кенигсберга (теперь Калининград). В городе было семь мостов через реку Прегель.
5
Гостям города предлагали задачу: пройти по всем мостам, причём по каждому мосту ровно один раз.
Никому из гостей не удавалось совершить подобные путешествия. Эйлер отметил на карте города по одной точке на каждом острове. Затем он соединил эти точки в соответствии с расположением мостов. Получилось следующая картина.6
Что такое граф Для решения задачи о мостах Эйлер ввёл следующие определения: Графом называется конечное множество точек, некоторые из которых соединены линиями. Точки называются вершинами графа, а соединяющие линии – рёбрами. Рёбра графа Вершина графа
7
Что такое граф Количество рёбер, выходящих из вершины графа, называется степенью вершины. Вершина графа, имеющая нечётную степень, называется нечетной, а чётную степень – чётной. Нечётная степень Чётная степень
8
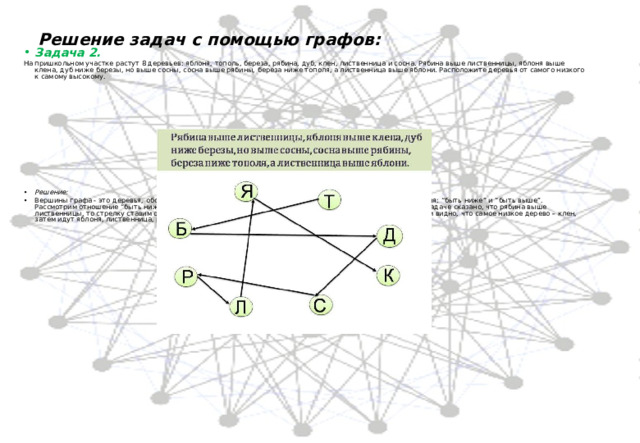Эйлеров путь — путь в графе, проходящий через каждое ребро ровно один раз. Граф, который можно нарисовать, не отрывая карандаша от бумаги, называется эйлеровым. Фигура (граф), которую можно начертить, не отрывая карандаш от бумаги, называется уникурсальной.9
Уникурсальные фигуры Уникурсальная фигура – это фигура, которую можно начертить одним росчерком, то есть, не отрывая карандаша от бумаги и не проводя одну и ту же линию дважды. Существует правило, позволяющее определить, можно ли начертить фигуру одним росчерком. Оно основывается на понятиях четной и нечетной вершины графа: вершину графа называют четной, если из нее исходит четное число ребер, и нечетной, если из нее исходит нечетное число ребер. Граф – это фигура, состоящая из конечного множества точек плоскости и отрезков, соединяющих некоторые из этих точек. Точки называются вершинами графа, а отрезки – ребрами графа. Правило: фигуру можно начертить одним росчерком, если: все ее вершины четные, при этом движение можно начинать с любой вершины и закончить в той же вершине(Нечетных вершин нет) у нее только две нечетные вершины, при этом движение нужно начать с одной из этих нечетных вершин и закончить другой.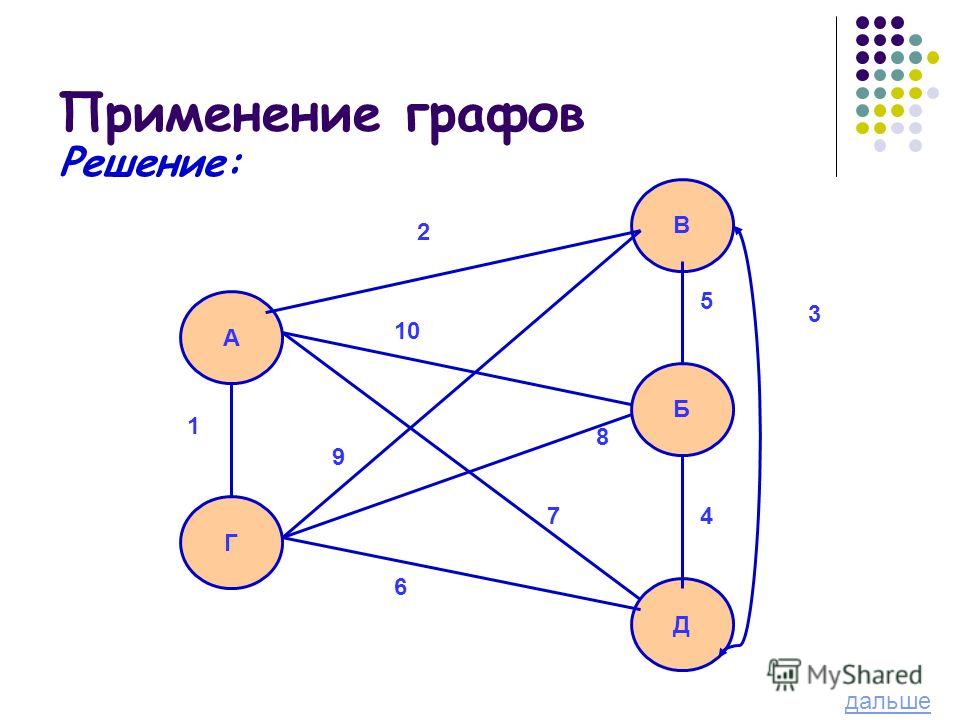
10
Теперь задача обхода мостов свелась к задаче изображения полученной картинки одним росчерком. Неудивительно, что гостям не удавалось выполнить подобное путешествие, так как решить эту задачу невозможно.
11
Докажите, что если в задаче о кёнигсбергских мостах добавить еще один мост в любом месте реки Прегель, то полученный граф будет уникурсальным
12
Одним росчерком Благодаря Леонарду Эйлеру существует общий прием решения подобных задач: преобразовать рисунок в граф (определить его вершины и рёбра), определить степень каждой вершины, посчитать количество нечётных вершин, сделать выводы: а) заданный обход возможен, если — все вершины чётные (его можно начать с любой вершины), — две вершины нечётные (его нужно начать с одной из нечётных вершин), б) заданный обход невозможен, если нечётных вершин больше двух, указать начало и конец пути.
13
14
А,Б,В можно Г,Д нельзя
15
16
Одним росчерком Говорят, что Магомет вместо подписи (он был неграмотен) описывал одним росчерком состоящий из двух рогов луны знак, представленный на рисунке. Возможно ли это?
17
Решение. Да, потому что в данном случае мы имеем дело с вершинами четного порядка.
18
Некоторые буквы, например, С, легко нарисовать одной чертой, не отрывая карандаш от бумаги и не проходя дважды по одному и тому же месту. А вот нарисовать печатную букву Ю, не отрывая карандаш от бумаги и не проводя ни одну линию дважды у вас вряд ли получится. А можно ли написать таким образом букву Р? Букву Х или букву К? В чём разница между этими буквами? А печатную букву А? Какие из русских букв можно написать, не отрывая карандаш от бумаги? Очевидно, легко нарисовать буквы типа Г, З, И, С, Л, М, П. Их можно выпрямить в одну линию
19
20
Начинаем выкладывать А, но получается только Л — чтобы попасть к перекладине, надо или оторвать карандаш, или пройти ножку два раза.
21
22
23
Рассмотрим примеры решения задач с помощью графов
24
Одним росчерком Муха в банке. Муха забралась в банку из-под сахара. Банка имеет форму куба. Сможет ли муха последовательно обойти все 12 ребер куба, не проходя дважды по одному ребру? Подпрыгивать и перелетать с места на место не разрешается. Решение. Ребра и вершины образуют граф, все 8 вершин которого имеют 3 степень, и, следовательно, требуемый обход невозможен.
25
Задачи с лабиринтом Лабиринт — это граф. А исследовать его — это найти путь в этом графе. дальше
26
Задачи с лабиринтом Можно ли обойти все данные комнаты, пройдя через каждую дверь ровно один раз и выйти на улицу через комнату 1 или 10? С какой комнаты надо начинать?27
Пусть комнаты – вершины графа, а двери – ребра. Проверим степени вершин: Решение: Только две вершины имеют нечетную степень.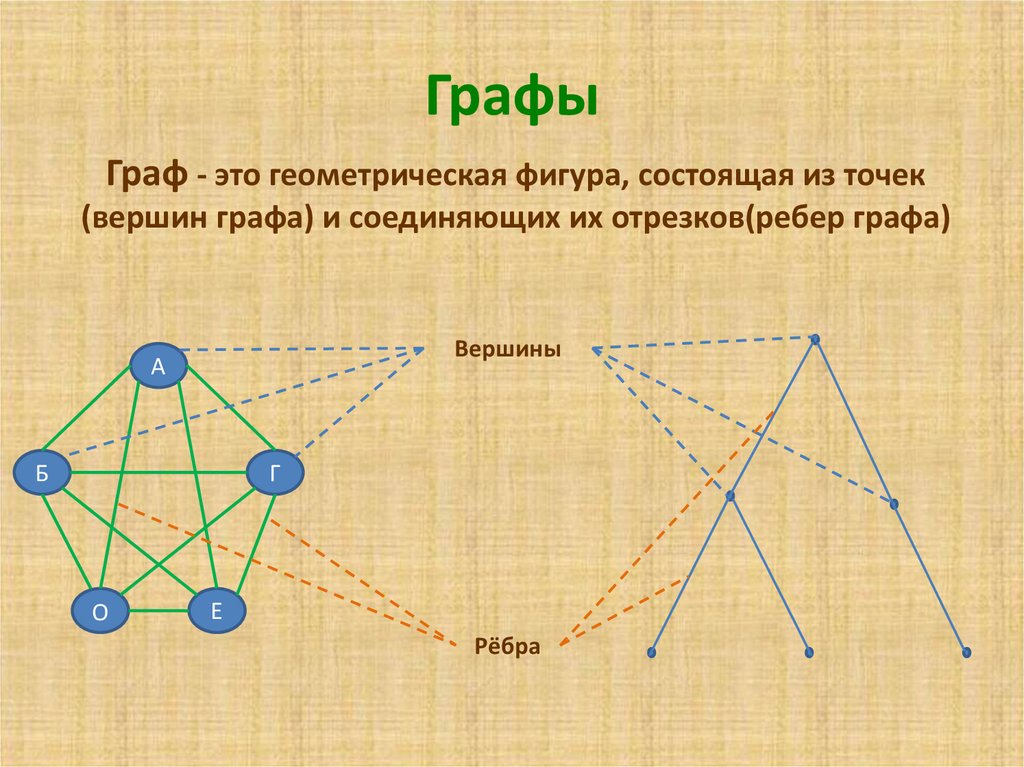
Начать движение можно из комнаты 10, а закончить в комнате 8, либо наоборот.
28
Но, чтобы выйти на улицу (из комнаты 10), надо начинать из комнаты 8. В этом случае пройдём все двери один раз и попадём в комнату 10, но окажемся внутри комнаты, а не снаружи: Решение:
29
Почтальон Печкин разнес почту во все дома деревни и зашел к Дяде Фёдору выпить молока. На рисунке показаны все тропинки, которые проходил Печкин, причем по каждой тропинке он прошёл только один раз. Укажи номерами порядок прохождения тропинок, а стрелками – направление. В каком доме живёт Дядя Фёдор? Применим вышеизложенное правило к данной задаче: Вершина — является четной, т.к. она имеет четное число рёбер (четыре). Вершины 2, 3, 4, 6, 7 – также четные. Вершина 5 и вершина под названием «почта» – нечетные, т.к. они имеют нечетное количество рёбер (по три каждая). Согласно пункту 2 вышеизложенного правила, мы имеет возможность весь путь «начертить одним росчерком», т.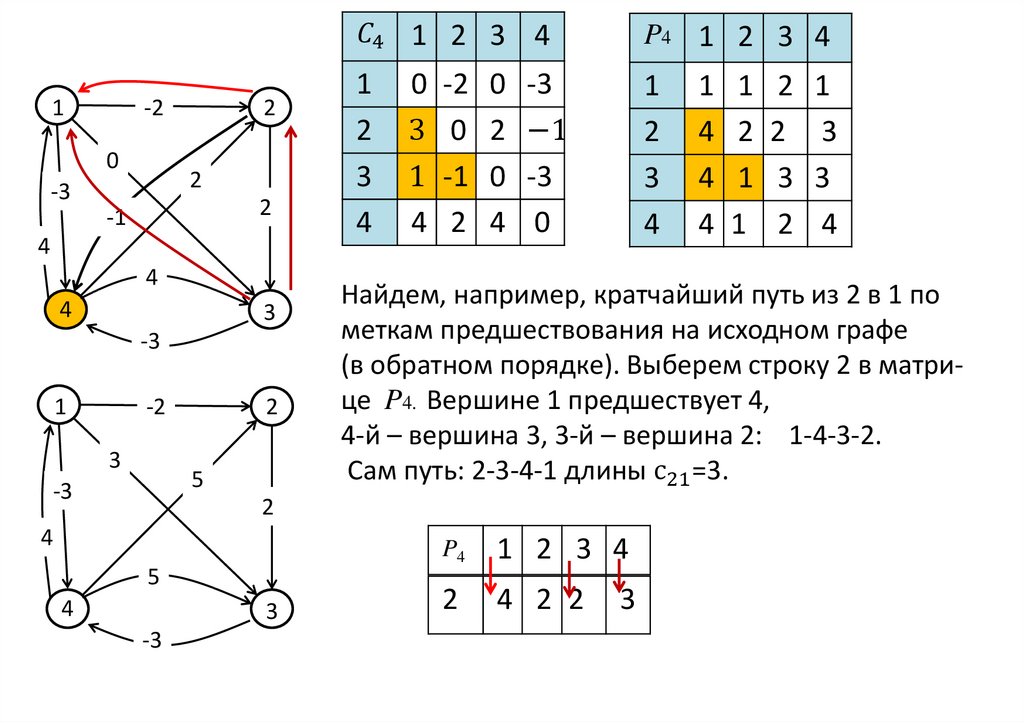
30
Логические задачи Аркадий, Борис. Владимир, Григорий и Дмитрий при встрече обменялись рукопожатиями (каждый пожал руку каждому по одному разу). Сколько всего рукопожатий было сделано? Решение: Пусть каждому из пяти молодых людей соответствует определенная точка на плоскости, названная первой буквой его имени, а производимому рукопожатию — отрезок или часть кривой, соединяющая конкретные точки — имена. Если подсчитать число ребер графа, изображенного на рисунке, или по формуле n(n-1)/2, это число и будет равно количеству совершенных рукопожатий между пятью молодыми людьми. Их 10.
31
Логические задачи В деревне 10 домов, и из каждого выходит по 7 тропинок, идущих к другим домам.
Сколько всего тропинок приходит между домами? Решение. Пусть дома- вершины графа, тропинки- рёбра. По условию из каждого дома (вершины) выходит 7 тропинок (рёбер), тогда степень каждой вершины 7, сумма степеней вершин 7×10=70, а число рёбер 70 : 2= 35. Таким образом, между домами проходит 35 тропинок. Ответ. 35 тропинок
32
Применение графов Инженер чертит схемы электрических цепей. Химик рисует структурные формулы, чтобы показать, как в сложной молекуле с помощью валентных связей соединяются друг с другом атомы. Историк прослеживает родословные связи по генеалогическому дереву. Военачальник наносит на карту сеть коммуникаций, по которым из тыла к передовым частям доставляется подкрепление. Социолог по сложнейшей диаграмме показывает, как подчиняются друг другу различные отделы одной огромной корпораций. В каждом из них фигурирует схема, состоящая из точек, соединённых между собой линиями.
33
Применение графов Теория графов сейчас одна из самых развиваемых частей математики, так как современная жизнь требует появление новых профессий.
Одна из них – специалист по логистике. Менеджер по логистике занимается доставкой товаров, грузов, планирует транспортные маршруты, рассчитывает стоимость перевозок, организует хранение товаров, грузов и т.д. Одна из главных задач специалиста по логистике- анализ ситуации, по этому он должен уметь хорошо считать, владеть математическим анализом
34
Графом является и система улиц города. Его вершины – площади и перекрестки, а ребра – улицы. дальше Применение графов
35
Схема линий московского метрополите-на
36
Применение графов Графы есть и на картах звездного неба.
37
Применение графов Графами являются блок – схемы программ для ЭВМ. дальше
38
Применение графов При графическом изображении формул веществ указывается последовательность расположения атомов в молекуле с помощью, так называемых валентных штрихов (термин «валентный штрих» предложил в 1858 г.
А. Купер для обозначения химических сил сцепления атомов), иначе называемых валентной чертой
39
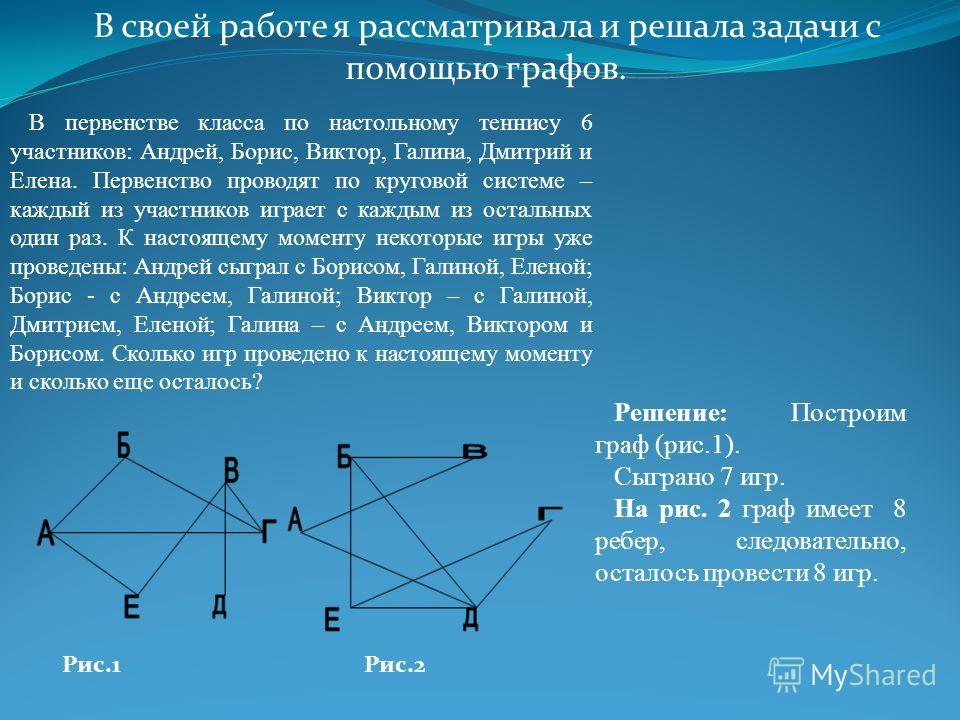
Задача 1 В первенстве класса по настольному теннису 6 участников: Андрей, Борис, Виктор, Галина, Дмитрий и Елена. Первенство проводится по круговой системе – каждый из участников играет с каждым только один раз. К настоящему моменту некоторые игры уже проведены: Андрей сыграл с Борисом, Галиной и Еленой, Борис – с Андреем и с Галиной, Виктор – с Галиной, Дмитрием и Еленой, Галина — с Андреем и Борисом, Дмитрий – с Виктором, Елена – с Андреем и Виктором. Сколько игр проведено к настоящему моменту и сколько еще осталось? Решение Соединим зелеными отрезками тех, кто уже играл. Сколько получилось отрезков(ребер? То есть сколько проведено уже игр? Ответ: 7
40
Продолжим решение задачи 1 Покажем синим цветом еще не проведенные игры. Сколько еще нужно провести игр? Ответ: 8.
41
Задача 2 В школьном кружке решили ставить гоголевского «Ревизора».
И тут разгорелся жаркий спор. Ляпкина-Тяпкина хотели играть: Гена, Дима. Гена согласен уступить, если ему дадут роль Хлестакова. А Дима уступит, если ему дадут роль Осипа. Вова хочет быть Городничим или Земляникой. Алик и Боря хотят быть Городничим или Хлестаковым. Удастся ли распределить роли так, чтобы все были довольны? Составьте схему для решения этой задачи
42
Ответ к задаче 2 Ответ: Играют: Гена – Ляпкина-Тяпкина, Дима – Осипа, Вова – Землянику, Алик – Хлестакова, Боря – Городничего.
43
Решение
44
Задача 4 Корзины, полные яблок. В пяти корзинах лежат яблоки пяти разных сортов. Яблоки первого сорта лежат в корзинах Г и Д, яблоки второго сорта в корзинах А, Б и Г, в корзинах А, Б и В имеются яблоки пятого сорта, в корзине В имеются к тому же яблоки четвертого сорта, а в корзине Д — третьего. Требуется дать каждой корзине номер, но так, чтобы в корзине №1 были яблоки первого сорта (хотя бы одно), в корзине №2 — второго и т.
д.
45
Решение задачи 4 Составим схему по условию задачи
46
Решение задачи 4
47
Решение задачи 4 и ответ
48
Задача 5 В автомобильных гонках Коля, Боря, Юра заняли первые четыре места. На вопрос, какие места они заняли, трое из них ответили: 1)Коля ни первое, ни четвертое, 2)Боря второе, 3)Вова не был последним. Какое место занял каждый мальчик? Решите самостоятельно
49
К решению задачи 5 В автомобильных гонках Коля, Боря, Юра заняли первые четыре места. На вопрос, какие места они заняли, трое из них ответили: 1)Коля ни первое, ни четвертое, 2)Боря второе, 3)Вова не был последним. Какое место занял каждый мальчик?
50
Решение задачи 5
51
Ответ к задаче 5 Ответ: I место — Вова II место — Боря III место — Коля IV место — Юра
52
Геометрические искажения Иллюзия Геринга (иллюзия веера).
Прямые, на самом деле, параллельны.
53
Иллюзия Вундта (1896). Линии в центре, в действительности, параллельны.
54
Здесь тоже линии параллельны.
55
56
Иллюзия Поггендорфа (Poggendorf, 1860) На одной прямой лежат линии BC, а не AC, как кажется.
57
58
Иллюзия Перельмана. Буквы на самом деле параллельны друг другу.
59
горизонтальные линии параллельны.
60
61
Круги или спирали?
62
Задача 1. Три друга — Алеша, Боря и Витя — учатся в одном классе. Один из них ездит домой из школы на автобусе, один — на трамвае, один — на троллейбусе. Однажды после уроков Алеша пошел проводить своего друга до остановки автобуса. Когда мимо них проходил троллейбус, третий друг крикнул из окна: «Боря, ты забыл в школе тетрадку!».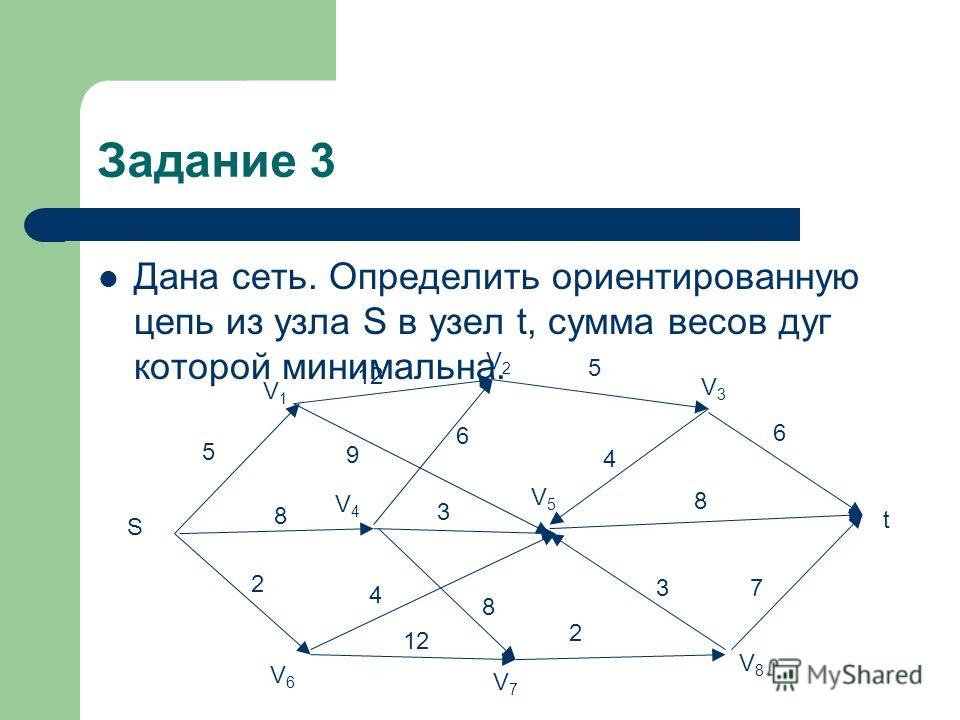
Кто на чем ездит домой?
63
Алеша поедет на трамвае, Боря — на автобусе, Витя — на троллейбусе.
64
Задача 2. Каникулы в школе птиц и зверей началась большим карнавалом. Медведь, волк, лиса и заяц явились в маскарадных костюмах волка, медведя, лисы и зайца. На балу зверь в маскарадном костюме зайца выиграл в лотерее банку меда и остался этим очень недоволен. Известно также, что медведь не любит лису и никогда не берет в лапы картинок, где она нарисована. Зверь в маскарадном костюме лисы выиграл в лотерее пучок моркови, но это тоже не доставило ему никакой радости. Не могли бы вы сказать, какой маскарадный костюм смастерил себе каждый из зверей?
65
медведь — в костюме волка, лиса — в костюме зайца, волк — в костюме лисы, заяц — в костюме медведя.
66
Задача 3. В бутылке, стакане, кувшине и банке находятся молоко, лимонад, квас и вода.
Известно, что вода и молоко не в бутылке, сосуд с лимонадом стоит между кувшином и сосудом с квасом, в банке не лимонад и не вода, стакан стоит между банкой и сосудом с молоком. В каком сосуде находится каждая из жидкостей?
67
Ответ: лимонад — в бутылке, вода — в стакане, молоко — в кувшине, квас — в банке.
68
Задача 4. В небольшом районном городе живут пять друзей: Иванов, Петренко, Сидорчук, Гришин и Капустин. Профессии у них разные: один из них маляр, другой — мельник, третий — плотник, четвертый — почтальон, а пятый — парикмахер. Петренко и Гришин никогда не держали в руках малярной кисти. Иванов и Гришин собираются посетить мельницу, на которой работает их товарищ. Петренко и Капустин живут в одном доме с почтальоном. Сидорчук был недавно в ЗАГСе одним из свидетелей, когда Петренко и дочь парикмахера сочетались законным браком. Иванов и Петренко каждое воскресенье играют в городки с плотником и маляром.
Гришин и Капустин по субботам обязательно встречаются в парикмахерской, где работает их друг. Почтальон предпочитает бриться сам. Кто есть кто?
69
Иванов — парикмахер, Петренко — мельник, Сидорчук — почтальон, Гришин — плотник, Капустин — маляр.
70
Беседуют трое друзей: Белокуров, Рыжов и Чернов. Брюнет сказал Белокурову: «Любопытно, что один из нас блондин, другой — брюнет, третий — рыжий, но ни у кого цвет волос не соответствует фамилии». Какой цвет волос у каждого из друзей?
71
Задача №3. Таблицы и схемы, поиск оптимального маршрута по таблице и по расписанию.
Автор — Лада Борисовна Есакова.
В своей деятельности человек повсеместно использует модели, то есть создает образ, упрощенную копию того объекта, с которым ему приходится иметь дело.
Модель — это искусственно созданный объект, дающий упрощенное представление о реальном объекте, процессе или явлении, отражающий существенные стороны изучаемого объекта с точки зрения цели моделирования.
Моделирование — это построение моделей, предназначенных для изучения и объектов, процессов или явлений.
Распространенными информационными моделями являются графики, схемы, таблицы, диаграммы. Одним из распространенных видов моделей являются графы. Граф – это один из способов графического едставления информации. Объекты представлены в нем как вершины (узлы), а связи между объектами как ребра (дуги). Т.е. граф – это набор вершин и связывающих их ребер.
Путь в графе – это конечная последовательность вершин, каждая из которых (кроме последней) соединена со следующей ребром. Граф может содержать циклы (первая вершина пути может совпадать с последней).
Обычно в задачах используют взвешенный граф, т.е. граф, в котором с каждым ребром связано число (вес). Например, расстояние, стоимость и т.д.
Граф может задаваться таблицей, в которой на пересечении строки и столбца с наименованиями вершин записано числовое значение (вес) ребра, соединяющего эти вершины.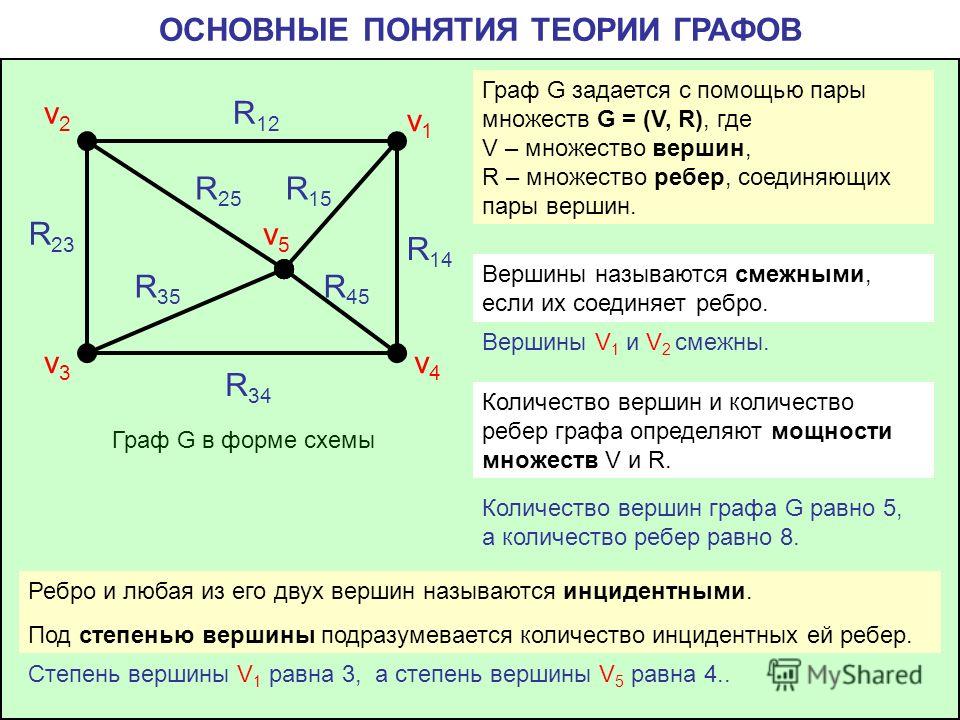
Дерево – это граф, не имеющий циклов. В дереве существует один единственный путь между любой парой вершин. Одна из вершин дерева (корень) не имеет входящих ребер, все остальные имеют ровно одно входящее ребро. Вершины, у которых нет исходящих ребер, называются листьями.
1. Поиск графа, соответствующего таблице
Пример 1.
В таблице приведена стоимость перевозок между соседними железнодорожными станциями. Укажите схему, соответствующую таблице.
Решение:
Сравним значения таблицы и схем:
Согласно таблице вершина A должна быть связана с вершинами B (значение 4) и D (значение 5). Т.е. AB=4, AD=5. На схеме значения указаны около соответствующего ребра. Сразу отбрасываем 1),2),3) схемы, т.к. на них AD не равно 5.
Для уверенности проверим все остальные ребра схемы 4): BC=3, BD=6, что совпадает со значениями таблицы. Правильная схема 4).
Ответ: 4
2.
Анализ информации в таблице и графе
Пример 2.
На рисунке справа схема дорог Н-ского района изображена в виде графа, в таблице содержатся сведения о длинах этих дорог (в километрах).
Так как таблицу и схему рисовали независимо друг от друга, то нумерация населенных пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите, какова длина дороги из пункта В в пункт Е. В ответе запишите целое число – так, как оно указано в таблице.
Решение:
На графе из вершины В выходит 5 ребер, значит в таблице соответствующий пункт должен иметь дороги в 5 других (строка должна содержать 5 заполненных клеток). Такой пункт в таблице один: П6.
На графе из вершины Е выходит 4 ребра, значит в таблице соответствующий пункт должен иметь дороги в 4 других (строка должна содержать 4 заполненные клетки). Такой пункт в таблице один: П4.
Таким образом, нам нужно найти расстояние между П6 и П4. Согласно таблице оно равно 20.
Ответ: 20
3. Поиск информации в таблице по условию
Пример 3.
Между четырьмя местными аэропортами: ЛУГОВОЕ, ДЯТЛОВО, НИКИТИНО и ОРЕХОВО, ежедневно выполняются авиарейсы. Приведён фрагмент расписания перелётов между ними:
Путешественник оказался в аэропорту ЛУГОВОЕ в полночь. Определите самое раннее время, когда он может попасть в аэропорт ОРЕХОВО. Считается, что путешественник успевает совершить пересадку в аэропорту, если между временем прилета в этот аэропорт и временем вылета проходит не менее часа.
1) 12:05 2) 12:50 3)12:55 4) 13:30
Решение:
Можно, конечно, решить эту задачу просто глядя на таблицу и перебирая подходящие варианты, но есть риск ошибиться или пропустить нужную строчку. Поэтому рекомендую нарисовать дерево всех возможных путей из аэропорта ЛУГОВОЕ в ОРЕХОВО:
Средняя ветка не подходит, т.к. между прилетом в аэропорт ДЯТЛОВО (11:15) и вылетом из ДЯТЛОВО в ОРЕХОВО (12:00) интервал меньше часа.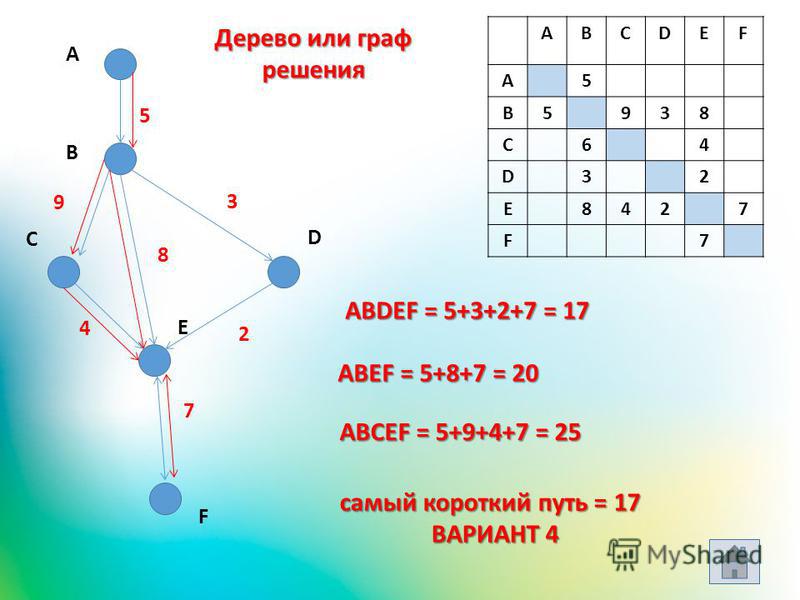
Из оставшихся двух выбираем раннее время прилета: 12:55.
Ответ: 3
4. Выбор таблицы по условию
Пример 4.
В таблицах приведена протяженность автомагистралей между соседними населенными пунктами. Если пересечение строки и столбца пусто, то соответствующие населенные пункты не являются соседними. Укажите номер таблицы, для которой выполняется условие «Максимальная протяженность маршрута от пункта C до пункта B не больше 6». Протяженность маршрута складывается из протяженности автомагистралей между соответствующими соседними населенными пунктами. При этом через любой насеченный пункт маршрут должен проходить не более одного раза.
Решение:
По каждой из схем построим дерево с корнем в точке C и листьями в точке B. При этом нам не нужно строить дерево полностью. Как только найдена ветка с протяженностью больше 6, делаем вывод, что таблица не удовлетворяет указанному условию:
Таблицы 1), 2) и 4) отвергаем уже при анализе первой ветки дерева.
В таблице 3) две ветки вообще не приведут в B, а две другие имеют суммарную длину, не превышающую 6.
Ответ: 3
5. Поиск кратчайшего пути по таблице
Пример 5.
Между населёнными пунктами A, B, C, D, E, F, Z построены дороги, протяжённость которых приведена в таблице. (Отсутствие числа в таблице означает, что прямой дороги между пунктами нет.)
Определите длину кратчайшего пути между пунктами A и Z (при условии, что передвигаться можно только по построенным дорогам).
1) 13 2) 16 3) 19 4) 21
Решение:
При решении этой задачи тоже не следует полагаться на простой визуальный анализ таблицы. Чтобы избежать ошибок, построим дерево с корнем в вершине A и листьями в вершине Z. При этом нам не нужно выписывать все ветки. Второй путь из A в С (AC=6) длиннее первого (ABC=5), значит и весь маршрут через него будет длиннее.
Второй путь из C в E (CE=10) длиннее первого (CDE=6), значит и весь маршрут через него будет длиннее.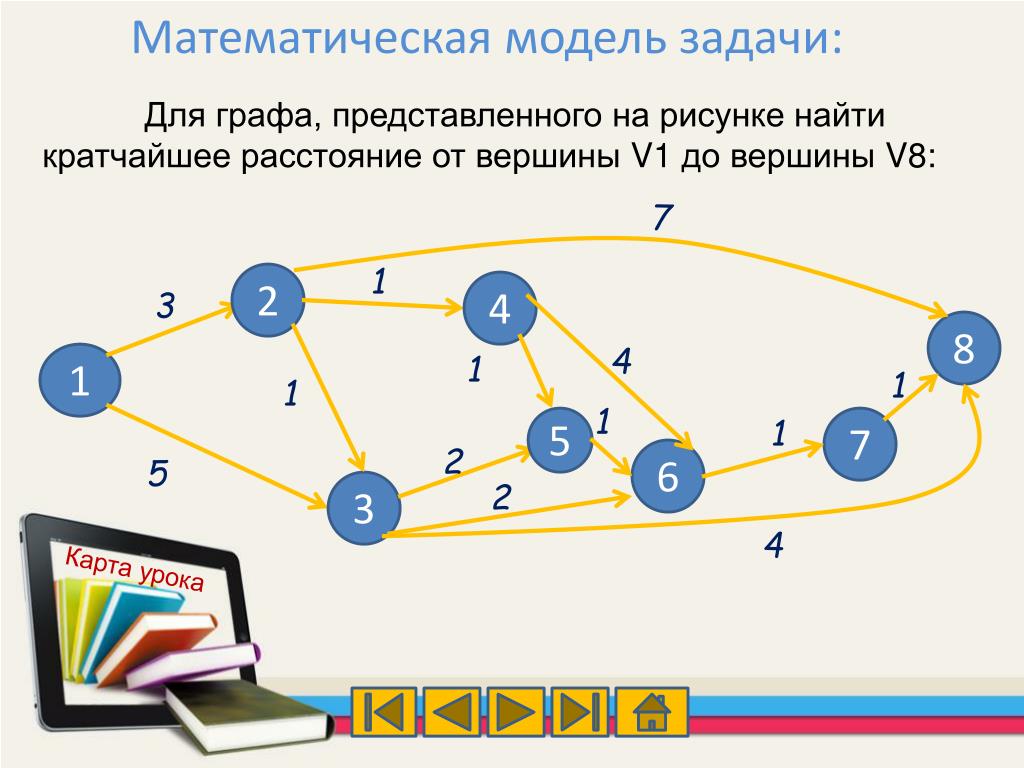
Нам остается сложить длины всех отрезков и выбрать маршрут с наименьшей длиной.
Это верхняя ветка дерева с длиной 16.
Ответ: 2
Графы (7 класс) — презентация онлайн
ГРАФЫ. 7 КЛАСС
Презентация к § 24*-26* учебника
«Геометрия. 7-9 классы»
И.М. Смирновой и В.А. Смирнова
ВЕДУЩИЙ: Смирнов Владимир Алексеевич, профессор, доктор физико-математических
наук, заведующий кафедрой элементарной математики МПГУ, автор учебников
по геометрии для 5-6 7-9 и 10-11 классов
E-mail: [email protected]
Сайт: vasmirnov.ru
Авторский сайт: vasmirnov.ru
24. Графы
Теория графов
Теория графов зародилась в ходе решения головоломок двести с лишним
лет назад. Одной из таких задач-головоломок была задача о кенигсбергских
мостах, которая привлекла к себе внимание Леонарда Эйлера (1707-1783), долгое
время жившего и работавшего в России (с 1727 по 1741 год и с 1766 до конца
жизни).
Л.Эйлер был действительным членом
Петербургской Академии наук, оказал большое
влияние на развитие отечественной математической
школы и в деле подготовки кадров ученыхматематиков и педагогов в России.
Поражает своими
размерами научное наследие ученого. При жизни им
опубликовано 530 книг и статей, а сейчас их известно
уже более 800. Причем последние 12 лет своей жизни
Эйлер тяжело болел, ослеп и, несмотря на тяжелый
недуг, продолжал работать и творить. Статистические
подсчеты показывают, что Эйлер в среднем делал одно
открытие в неделю. Трудно найти математическую
проблему, которая не была бы затронута в произведениях Эйлера. Все математики последующих
поколений так или иначе учились у Эйлера, и недаром
известный французский ученый П.С. Лаплас сказал:
«Читайте Эйлера, он – учитель всех нас».
Почему нужны графы в геометрии?
1. Геометрические графы являются, в некотором смысле
обобщением понятия ломаной.
2. Теория графов – одно из современных направлений
развития математики, имеющих приложения в различных
её областях.
3. С графами связаны классические задачи, знакомство
с которыми должно входить в математическое образование
учащихся.
4. Задачи, связанные с графами, включаются в различные
олимпиады по математике.
5. Решение таких задач развивает геометрические
и комбинаторные представления учащихся, повышает мотивацию
к обучению геометрии.
Задача Эйлера о Кёнигсбергских мостах
Задача. В г. Кёнигсберге (ныне Калининград) было семь
мостов через реку Прегель (Л — левый берег, П — правый берег, А и Б
— острова). Можно ли, прогуливаясь вдоль реки, пройти по каждому
мосту ровно один раз?
Для решения задачи Эйлера введем понятие графа.
Фигура, образованная конечным набором точек плоскости и
отрезков, соединяющих некоторые пары из этих точек, называется
плоским графом, или просто графом. Точки называются вершинами,
а отрезки – рёбрами графа.
Вместо отрезков в качестве рёбер графов рассматриваются
также кривые линии.
Индексом вершины графа называется число ребер,
сходящихся в данной вершине графа.
Например, на рисунке 1 индекс вершины А равен 5,
индекс вершин Л, Б, П равен 3.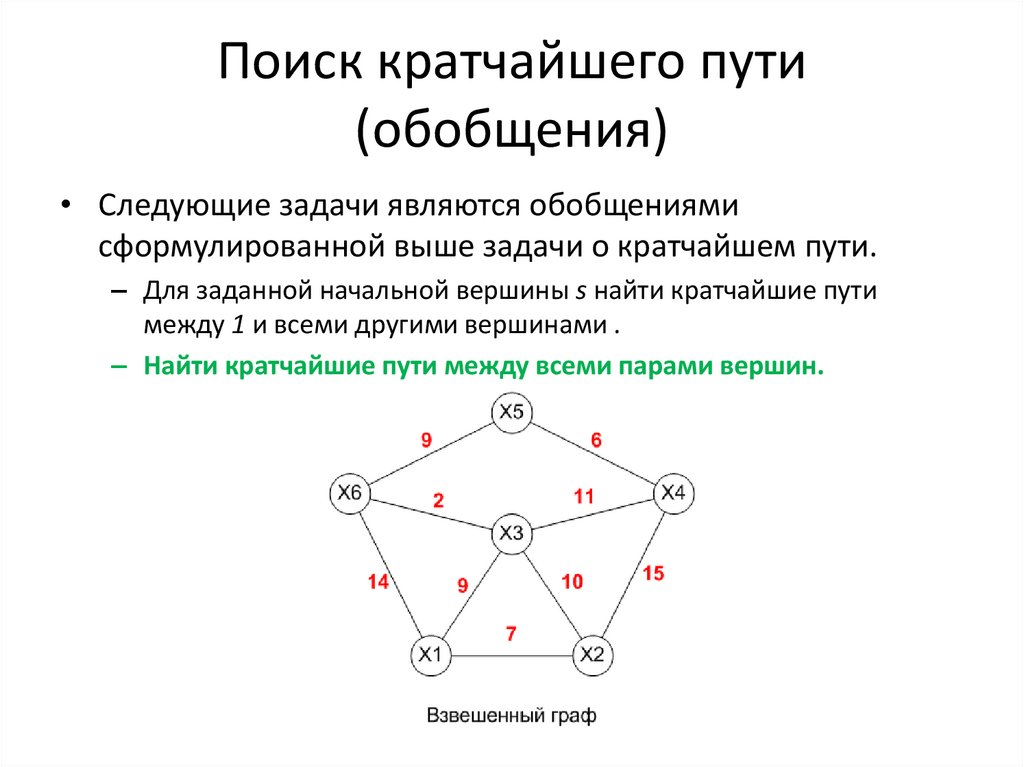
При этом, при подсчёте индекса ребро-петля
учитывается дважды. Например, на рисунке 2 индекс
вершины A равен 2.
1)
2)
Теорема. Сумма индексов всех вершин графа равна
удвоенному числу ребер этого графа.
Доказательство. Индекс вершины это число ребер,
выходящих из этой вершины. Сумма индексов всех
вершин это число ребер, выходящих из всех вершин. Так
как ребра имеют две вершины, то при таком подсчете мы
каждое ребро посчитаем дважды. Следовательно, сумма
индексов всех вершин графа равна удвоенному числу
ребер этого графа.
Следствие 1. Сумма индексов всех вершин графа
четна.
Следствие 2. Число вершин с нечетным индексом
четно.
Доказательство. Действительно, если бы оно было
нечетно, то сумма индексов вершин графа с нечетными
индексами была бы нечетна. С другой стороны, сумма
индексов вершин графа с четными индексами четна. Но
тогда сумма всех индексов вершин графа была бы нечетна,
что противоречит теореме.
Упражнения
1. В графе 3 вершин, каждая из которых
имеет индекс 2. Сколько у него ребер? Нарисуйте
такой граф.
Ответ: 3.
2. В графе 4 вершин, каждая из которых
имеет индекс 3. Сколько у него ребер? Нарисуйте
такой граф.
Ответ: 6.
3. В графе 5 вершин, каждая из которых
имеет индекс 4. Сколько у него ребер? Нарисуйте
такой граф.
Ответ: 10.
4. В графе 12 рёбер, а каждая вершина имеет
индекс 3. Сколько у него вершин? Нарисуйте такой
граф.
Ответ: 6.
5. Может ли граф иметь:
а) одну вершину нечетного индекса;
б) две вершины нечетного индекса;
в) три вершины нечетного индекса;
г) четыре вершины нечетного индекса?
Ответ: а), в) нет; б), г) да.
6. Может ли граф иметь пять вершин,
в каждой из которых сходится три ребра?
Ответ: Нет. Число вершин с нечетным индексом
должно быть четным.
7. В классе 15 компьютеров. Можно ли их
соединить друг с другом так, чтобы каждый
компьютер был соединен ровно с пятью другими?
Ответ: Нет.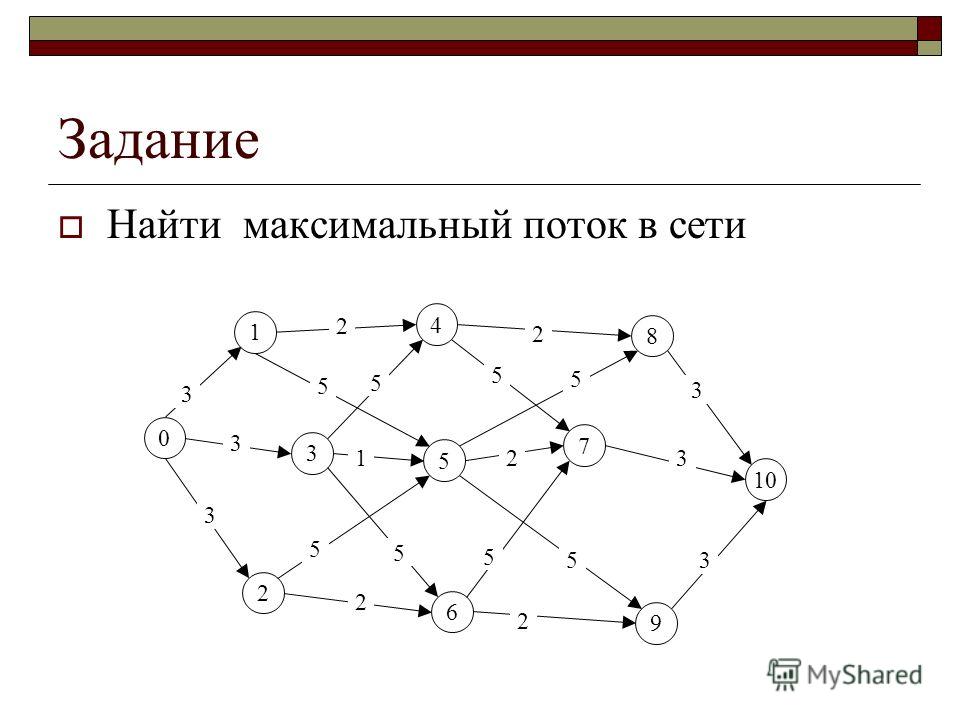
Уникурсальные графы
Граф называется уникурсальным, если можно пройти
по каждому ребру этого графа ровно один раз, или, что то же самое,
можно нарисовать этот граф «одним росчерком», т. е. не отрывая
карандаша от бумаги и проходя по каждому ребру ровно один раз.
На рисунке представлен граф, соответствующий задаче
Эйлера, в котором ребра соответствуют мостам, а вершины –
берегам и островам.
Для решения задачи Эйлера требуется выяснить, является ли
этот граф уникурсальным.
Теорема Эйлера
Теорема. Для уникурсального графа число вершин
нечетного индекса равно двум или нулю.
Доказательство. Если граф уникурсален, то у него есть
начало и конец обхода. Остальные вершины имеют четный индекс,
так как с каждым входом в такую вершину есть и выход. Если
начало A и конец B не совпадают, то они являются единственными
вершинами нечетного индекса. У начала выходов на один больше,
чем входов, а у конца входов на один больше, чем выходов.
Если
начало A совпадает с концом B, то вершин с нечетным индексом нет.
Решение задачи Эйлера. Найдем индексы вершин
графа задачи Эйлера. Вершина А имеет индекс 5, Б — 3,
П — 3 и Л — 3. Таким образом, мы имеем четыре вершины
нечетного индекса, и, следовательно, данный граф
не является уникурсальным. Значит, нельзя пройти
по каждому из семи мостов только один раз.
8. Выясните, какие графы, изображенные
на рисунке, являются уникурсальными?
Ответ: а), б), г), д), ж), з).
9. Выясните, какие графы, изображенные
на рисунке, являются уникурсальными?
Ответ: б).
10. Решите задачу, аналогичную задаче Эйлера,
с пятнадцатью мостами.
11. На рисунке изображен план подземелья, в одной
из комнат которого находится клад, для отыскания
которого нужно войти в одну из крайних комнат, пройти
через все двери ровно по одному разу через каждую. Клад
будет в комнате за последней дверью. В какой комнате
находится клад?
Ответ: 18.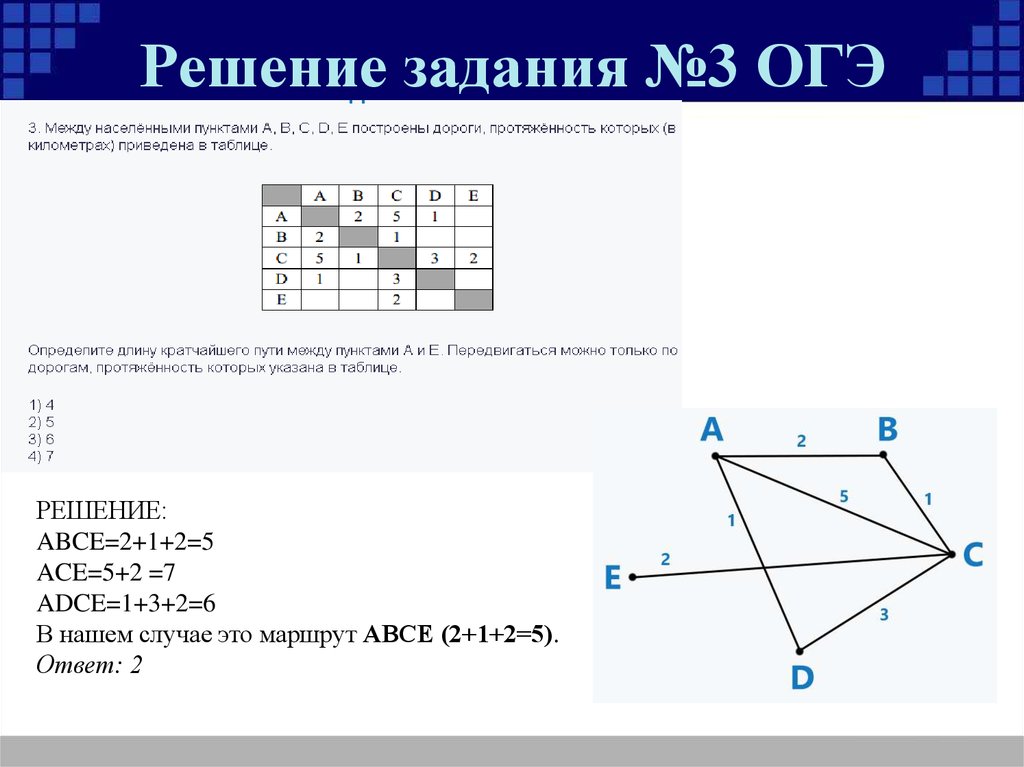
12. Какое наименьшее число мостов в задаче
о кёнигсбергских мостах придется пройти дважды,
чтобы пройти по каждому мосту?
Ответ: Один.
13.
Докажите,
что
если
в
задаче
о кёнигсбергских мостах добавить еще один мост
в любом месте реки Прегель, то полученный граф
будет уникурсальным.
14. Можно ли обойти все рёбра тетраэдра,
пройдя по каждому ребру ровно один раз?
Ответ: Нет.
15. Какое наименьшее число рёбер придется
пройти дважды, чтобы обойти все рёбра тетраэдра?
Ответ: Одно.
16. Какое наименьшее число рёбер придется
пройти дважды, чтобы обойти все рёбра тетраэдра
и вернуться в исходную вершину?
Ответ: Два.
17. Имеется проволока длины 48 см. Можно
ли сложить из неё рёберную модель тетраэдра
с ребром 8 см?
Ответ: Нет.
18. Какой наименьшей длины должна быть
проволока, чтобы из неё можно было сложить
рёберную модель тетраэдра с ребром 8 см?
Ответ: 56 см.
19. Можно ли обойти все рёбра куба, пройдя
по каждому ребру ровно один раз?
Ответ: Нет.
20. Какое наименьшее число рёбер придется
пройти дважды, чтобы обойти все рёбра куба?
Ответ: Три.
21. Какое наименьшее число рёбер придется
пройти дважды, чтобы обойти все рёбра куба
и вернуться в исходную вершину?
Ответ: Четыре.
22. Какой наименьшей длины должна быть
проволока, чтобы из неё можно было сложить
рёберную модель куба с ребром 4 см?
Ответ: 60 см.
23. Сколько имеется кратчайших путей,
проходящих по рёбрам куба, из одной его вершины
в противоположную?
Ответ: 6.
24. Можно ли обойти все рёбра октаэдра,
пройдя по каждому ребру ровно один раз?
Ответ: Да.
25. Какой наименьшей длины должна быть
проволока, чтобы из неё можно было сложить
рёберную модель октаэдра с ребром 4 см?
Ответ: 48 см.
26. Сколько имеется кратчайших путей,
проходящих по рёбрам октаэдра, из одной его
вершины в противоположную?
Ответ: 4.
27. Можно ли обойти все рёбра икосаэдра,
пройдя по каждому ребру ровно один раз?
Ответ: Нет.
28. Какое наименьшее число рёбер придется
пройти дважды, чтобы обойти все рёбра
икосаэдра?
Ответ: Пять.
29. Какое наименьшее число рёбер придется
пройти дважды, чтобы обойти все рёбра икосаэдра
и вернуться в исходную вершину?
Ответ: Шесть.
30. Какой наименьшей длины должна быть
проволока, чтобы из неё можно было сложить
рёберную модель икосаэдра с ребром 4 см?
Ответ: 140 см.
31. Сколько имеется кратчайших путей,
проходящих по рёбрам икосаэдра, из одной его
вершины в противоположную?
Ответ: 10.
32. Можно ли обойти все рёбра додекаэдра,
пройдя по каждому ребру ровно один раз?
Ответ: Нет.
33. Какое наименьшее число рёбер придется
пройти дважды, чтобы обойти все рёбра
додекаэдра?
Ответ: Девять.
34. Какое наименьшее число рёбер придется
пройти дважды, чтобы обойти все рёбра
додекаэдра и вернуться в исходную вершину?
Ответ: Десять.
35. Какой наименьшей длины должна быть
проволока, чтобы из неё можно было сложить
рёберную модель додекаэдра с ребром 4 см?
Ответ: 156 см.
36. Сколько имеется кратчайших путей,
проходящих по рёбрам додекаэдра, из одной его
вершины в противоположную?
Ответ: 6.
37*. Докажите, что у любого графа, у которого
больше одной вершины и ребрами являются отрезки,
имеются хотя бы две вершины одинакового индекса.
Доказательство. Пусть A – вершина графа
с наибольшим индексом, равным n. Если среди вершин
A1, …, An имеется вершина индекса n, то мы получим две
вершины индекса n. Если индексы всех вершин A1, …, An
меньше n, то среди этих вершин найдутся две вершины
одинакового индекса, так как количество вершин равно n,
а индексы этих вершин могут принимать значения только
1, 2, …, n – 1.
Граф называется связным, если любые две его
вершины можно соединить ломаной, состоящей из ребер
графа. На рисунках изображены связные графы.
Связный граф, не содержащий ни одной замкнутой
ломаной, называется деревом. На рисунках изображены
деревья.
38. Докажите, что для любого дерева, имеющего
В вершин и Р ребер, справедливо соотношение Эйлера:
В — Р = 1.
Доказательство. Рассмотрим какое-нибудь крайнее ребро
дерева, т. е. такое, у которого имеется вершина индекса 1
(самостоятельно обоснуйте существование такого ребра).
Удалим это ребро. При этом граф останется деревом,
а число вершин и число рёбер уменьшатся на единицу. Значит, В –
Р не изменится.
Повторяя удаление крайних рёбер, мы придём к графу,
состоящему из одного ребра и двух его вершин. Для этого графа
В – Р = 1. Следовательно, В – Р = 1 и для исходного графа.
39. Граф, не содержащий ни одной замкнутой
ломаной, называется лесом. Пусть лес состоит из n
деревьев и имеет В вершин и Р ребер. Чему равно В — Р?
Ответ: n.
Одной из задач, связанных с графами, является
задача прокладки сетей (дорог, трубопроводов и др.),
соединяющих данные пункты и имеющих наименьшую
возможную длину.
40*. Попробуйте изобразить сеть дорог (связный
граф), соединяющих данные населённые пункты A, B, C,
D, с наименьшей суммарной длиной.
41. Оцените, какой из графов, изображённых
на рисунке, имеет наименьшую сумму длин рёбер.
Проверьте ответ с помощью линейки.
Ответ: в). Оказывается, что этот граф имеет
наименьшую сумму длин рёбер из всех связных графов,
соединяющих вершины A, B, C, D. Углы, образованные
рёбрами этого графа, с вершинами в точках E и F, равны
120о.
25. Теорема Эйлера
Граф называется простым, если его ребра или
не имеют общих точек, или имеют только общие
вершины.
Теорема Эйлера. Для связного простого графа
имеет место равенство В — Р + Г = 2, где В — число
вершин, Р — общее число ребер, Г — число областей,
на которые граф разбивает плоскость.
Например, для графа, изображенного на рисунке,
В = 8, Р = 12, Г = 6.
Доказательство теоремы. Стянем какое-нибудь ребро
связного простого графа, соединяющее две его вершины, в точку.
При этом число ребер и число вершин уменьшаться на единицу,
а число областей не изменится. Следовательно, В – Р + Г
не измениться.
Продолжая стягивать ребра, мы придем к графу,
у которого имеется одна вершина, а ребрами являются петли.
Уберем какое-нибудь ребро. При этом число ребер и число областей
уменьшаться на единицу. Следовательно, В – Р + Г не изменится.
Продолжая убирать ребра, мы придем к графу, у которого имеется
одна вершина и одно ребро. У этого графа В = 1, Р = 1, Г = 2 и,
следовательно, В – Р + Г = 2. Значит, для исходного графа также
выполняется равенство В – Р + Г = 2.
Задача Эйлера
Задача. Три соседа имеют три общих колодца.
Можно ли провести непересекающиеся дорожки
от каждого дома к каждому колодцу?
То, что не получилось на рисунке, не является
доказательством невозможности соединения дорожками
домиков и колодцев. Для доказательства воспользуемся
следующей теоремой Эйлера.
Решение.
Предположим,
что
можно
провести
непересекающиеся дорожки от каждого дома к каждому колодцу.
Рассмотрим граф, вершинами которого являются домики
и колодцы, а ребрами – дорожки.
У него В = 6, Р = 9 и,
следовательно, Г = 5. Каждая из пяти областей ограничена,
по крайней мере, четырьмя ребрами, поскольку, по условию задачи,
ни одна из дорожек не должна непосредственно соединять два дома
или два колодца. Так как каждое ребро разделяет две области,
то количество ребер должно быть не меньше (5∙4)/2 = 10,
что противоречит тому, что их число равно 9.
Упражнения
1. Посчитайте число вершин (В), ребер (Р)
и областей (Г) для графов, изображенных
на рисунке. Убедитесь, что В – Р + Г = 2.
Ответ: а) В = 6, Р = 12, Г = 8;
б) В = 20, Р = 30, Г = 12; в) В = 12, Р = 30, Г = 20.
2. Посчитайте число вершин (В), ребер (Р)
и граней (Г) для многогранников, изображенных
на рисунке. Чему равно В – Р + Г?
Ответ: а) В = 4, Р = 6, Г = 4; б) В = 8, Р = 12, Г = 6;
в) В = 6, Р = 12, Г = 8; г) В = 20, Р = 30, Г = 12;
д) В = 12, Р = 30, Г = 20.
3. Два соседа имеют: а) три общих колодца;
б) четыре общих колодца.
Можно ли провести непересекающиеся дорожки от
каждого дома к каждому колодцу?
Ответ: а), б) Да.
4. Три соседа имеют: а) два общих колодца;
б) четыре общих колодца.
Можно ли провести непересекающиеся дорожки
от каждого дома к каждому колодцу?
Ответ: а) да; б) нет.
5. Четыре соседа имеют четыре общих
колодца. Можно ли провести непересекающиеся
дорожки так, чтобы каждый домик был соединен
с тремя колодцами и каждый колодец соединен
с тремя домиками?
Ответ: Да.
6. Докажите, что пять домиков нельзя соединить
непересекающимися дорожками так, чтобы каждый домик
был соединен со всеми другими домиками.
Предположим,
что
это
сделать можно. Тогда мы имеем
связный простой граф, у которого
В = 5, Р = 10 и, следовательно,
Г = 7.
С другой стороны,
поскольку
каждая
область
ограничена, по крайней мере тремя
ребрами, то число ребер должно
быть больше или равно 7 3 10.
2
Противоречие.
7. Пять соседей имеют пять общих колодцев. Можно
ли провести непересекающиеся дорожки так, чтобы
каждый домик был соединен с четырьмя колодцами
и каждый колодец соединен с четырьмя домиками?
Решение.
Если это сделать можно, то для
соответствующего графа В = 10, Р = 20, следовательно,
Г = 12. С другой стороны, поскольку каждая область
ограничена, по крайней мере четырьмя ребрами, то число
ребер должно быть больше или равно 24. Противоречие.
8. Шесть соседей имеют шесть общих колодцев.
Можно ли провести непересекающиеся дорожки так,
чтобы каждый домик был соединен с четырьмя колодцами
и каждый колодец соединен с четырьмя домиками?
Ответ. Нет. Решение аналогично предыдущему.
9. Имеется 100 домиков и 100 колодцев. Можно ли
провести непересекающиеся дорожки так, чтобы каждый
домик был соединен с тремя колодцами и каждый колодец
соединен с тремя домиками?
Ответ. Да. Разобьем домики и колодцы на 25 групп
по 4 домика и 4 колодца в каждой. В этих группах,
согласно упражнению 5, можно провести дорожки.
Следовательно, дорожки можно провести для всех
домиков и колодцев.
10. Имеется 100 домиков и 100 колодцев. Можно ли
провести непересекающиеся дорожки так, чтобы каждый
домик был соединен с четырьмя колодцами и каждый
колодец соединен с четырьмя домиками?
Ответ.
Нет.
26. Проблема четырех красок
В 1850 году шотландский физик Фредерик Гутри
обратил внимание на то, что задачи раскрашивания карт
очень популярны среди студентов-математиков в Лондоне,
а сформулировал проблему четырех красок его брат
Фрэнсис Гутри, который, раскрасив карту графств Англии
четырьмя красками, выдвинул гипотезу о том, что этого
количества красок достаточно для раскраски любой карты.
Он привлек к проблеме внимание своего преподавателя
математики А. Де Моргана, а тот сообщил о ней своему
другу В. Гамильтону и тем самым способствовал
ее широкому распространению.
Годом рождения проблемы четырех красок
считается 1878 год (в некоторых изданиях указывается
1879). Именно тогда на одном из заседаний Британского
географического общества выдающийся английский
математик А.Кэли четко сформулировал поставленную
задачу: «Доказать, что любую географическую карту
на плоскости (или на глобусе) можно правильно закрасить
четырьмя красками».
Раскраска карты называется
правильной, если любые две страны, имеющие на карте
общую границу, окрашены в различные цвета. Именно
с этого момента проблема привлекла к себе внимание
многих крупных математиков.
В 1890 году английский математик П. Хивуд доказал, что
любую карту на плоскости можно раскрасить пятью красками.
Однако долгое время проблема четырех красок не поддавалась
решению.
В 1968 году американские математики Оре и Стемпл
показали, что любую карту, имеющую не более 40 стран, можно
раскрасить четырьмя красками.
В 1976 году американскими учеными К. Аппелем и В.
Хакеном было получено решение проблемы четырех красок.
С помощью компьютера они просматривали различные типы карт,
и для каждого из них компьютер решал, может ли в данном типе
найтись карта, которая не раскрашивается четырьмя красками. Было
просмотрено почти 2000 типов карт, и для всех был получен ответ:
«Нет», — что и позволило объявить о компьютерном решении
проблемы четырех красок.
Определение карты
Пусть на плоскости задан связный простой граф,
каждая вершина которого имеет индекс, больший двух.
Этот граф разбивает плоскость на несколько областей.
Области будем называть странами, а само разбиение –
картой на плоскости.
Примеры карт приведены на рисунке.
Помимо
плоскости,
карты
рассматривают
и на других поверхностях, например, на сфере.
Поверхность многогранника можно рассматривать
как карту, странами которой являются грани
многогранника, а границами – его ребра.
На рисунке показаны карты, образованные
поверхностями правильных многогранников: тетраэдра,
куба, октаэдра, икосаэдра и додекаэдра.
Упражнения
1. Какое наименьшее число красок
потребуется для правильной раскраски карты,
изображенной на рисунке?
Ответ: 2.
2. Какое наименьшее число красок
потребуется для правильной раскраски карт,
изображенных на рисунке?
Ответ: а) 3; б) 4.
3. Какое наименьшее число красок
потребуется для правильной раскраски карты,
образованной
двумя
концентрическими
окружностями, имеющими n перегородок?
Ответ: 3, если n четно и 4, если n нечетно.
4.
Докажите,
что
любую
карту,
образованную прямыми, можно правильно
раскрасить двумя красками.
Доказательство. Ясно, что карту, образованную одной прямой
можно раскрасить в два цвета (рис. а). Докажем, что если карта,
образованная прямыми, раскрашена в два цвета, то карта, полученная
из нее добавлением новой прямой также может быть раскрашена в два
цвета (рис. б).
Действительно, новая прямая делит раскрашенную карту на две
карты, каждая из которых раскрашена в два цвета. Однако к самой
прямой примыкают пары областей, закрашенные в один цвет.
Перекрасим одну из карт-половинок, изменив цвет каждой области
на противоположный. Получим раскраску в два цвета всей карты (рис. в).
Поскольку любую карту, образованную прямыми можно получить
последовательным добавлением прямых, то всякая такая карта может
быть раскрашена в два цвета.
5.
Докажите,
что
любую
карту,
образованную окружностями, можно правильно
раскрасить двумя красками.
Решение аналогично решению предыдущей
задачи.
6. Докажите, что если карту можно правильно
раскрасить двумя красками, то каждая её вершина имеет
четный индекс (т. е. в ней сходится четное число ребер).
Доказательство. Если хотя бы одна вершина карты имела
бы нечетный индекс, то для правильной раскраски такой карты
потребовалось бы более двух красок.
Верно и обратное. Если каждая вершина карты имеет
четный индекс, то такую карту можно правильно раскрасить двумя
красками.
Попробуйте доказать это самостоятельно.
7. Докажите, что если регулярную карту (т. е. такую,
в каждой вершине которой сходится три ребра), можно
правильно раскрасить тремя красками, то каждая
её страна имеет четное число сторон.
Доказательство. Если хотя бы одна страна карты имела
бы нечетное число сторон, то для правильной раскраски такой
карты потребовалось бы более трёх красок.
Верно и обратное. Если каждая
страна регулярной карты имеет
четное число сторон, то такую
карту
можно
правильно
раскрасить тремя красками.
Попробуйте
доказать
самостоятельно.
это
8. Какое наименьшее
потребуется для правильной
изображенных на рисунке?
Ответ: а) 4; б) 4; в) 2.
число красок
раскраски карт,
9. Какое наименьшее число красок
потребуется для правильной раскраски паркетов,
части которых изображены на рисунке?
Ответ: а) 2; б) 3; в) 3; г) 2.
10. Какое наименьшее число красок
потребуется для правильной раскраски карт,
изображенных на рисунке?
Ответ: а) 3; б) 2; в) 4; г) 3.
11. Какое наименьшее число красок
потребуется для правильной раскраски граней
правильных многогранников?
Ответ: а) 4; б) 3; в) 2; г) 3; д) 4.
Контактная
информация
Издательство «Мнемозина»:
105043, Москва, ул. 6-я Парковая, д. 29 Б
Тел.: 8 (499) 367–67–81
E-mail: [email protected]
Сайт: mnemozina.ru
Интернет-магазин: shop.mnemozina.ru
Торговый дом:
E-mail: [email protected]
Тел.: 8 (495) 644–20–26
Электронные формы учебников и пособий представлены
на сайте «Школа в кармане»:
http://pocketschool.
ru
решений: данные и графики | Математические вкусности
Форма поиска
Поиск
Данные и линейные графики
| Упражнение | Проблема | Ответить |
| 1 | В каком месяце вандалов было больше всего? | июнь |
| 2 | В каком месяце вандалов было меньше всего? | январь |
| 3 | Сколько вандалов было в марте? | 19 |
| 4 | В каком месяце было 24 вандала? | апрель |
| 5 | Сколько вандалов было в феврале? | 15 |
Построение линейных графиков
| Упражнение 1: | В 2000 году был принят закон, запрещающий использование сотовых телефонов за рулем в Anytown, штат Нью-Йорк. С тех пор количество людей, использующих сотовые телефоны за рулем в Anytown, менялось каждый год, как показано в таблице ниже. Постройте линейный график, чтобы визуально отобразить эти данные. | ||||||||||||||||||||
| |||||||||||||||||||||
| Решение: | Ответы будут различаться в зависимости от используемых шкал. Образец линейного графика показан ниже. | ||||||||||||||||||||
| Упражнение 2: | Всего в школе было проведено 7 соревнований по бегу на 50 метров. Время выигрыша было записано в секундах, как показано в таблице ниже. Постройте линейный график, чтобы визуально отобразить эти данные. | ||||||||||||||||||
| |||||||||||||||||||
| Решение: | Ответы будут различаться в зависимости от используемых шкал. Образец линейного графика показан ниже. | ||||||||||||||||||
1
Данные и гистограммы
Учащихся класса миссис Глоссер опрашивали о закусках и просили выбрать из перечня закуску, которая им больше всего нравится. Гистограмма ниже обобщает данные, собранные в ходе этого опроса.
| Упражнение | Проблема | Ответить |
| 1 | Какая закуска понравилась больше всего? | Файлы cookie |
| 2 | Какую закуску предпочли 2 ученика? | Крекеры |
| 3 | Сколько студентов предпочитали крендельки? | 5 |
| 4 | Какую закуску предпочли 3 ученика? | Чипсы |
| 5 | Какому значению согласно графику соответствует количество учащихся, одинаково предпочитающих фрукты и овощи? | 1 |
Построение гистограмм
| Упражнение 1: | Средняя высота различных деревьев в США была записана в метрах, как показано в таблице ниже. Постройте гистограмму, чтобы визуально отобразить эти данные. | ||||||||||||||||||
| |||||||||||||||||||
| Решение: | Ответы будут различаться в зависимости от используемого масштаба и от того, расположены ли полосы горизонтально или вертикально. Примеры графиков показаны ниже. | ||||||||||||||||||
| Упражнение 2: | Были опрошены шесть детей, чтобы выяснить, на какой процент прибавки получает каждый из них в своем пособии, как показано в таблице ниже. Постройте гистограмму, чтобы визуально отобразить эти данные. | ||||||||||||||||
| |||||||||||||||||
| Решение: | Ответы будут различаться в зависимости от используемого масштаба и от того, расположены ли полосы горизонтально или вертикально. Примеры графиков показаны ниже. | ||||||||||||||||
1
Данные и круговые диаграммы
| Упражнение | Проблема | Ответить |
| 1 | Сколько секторов в графе? | 6 |
| 2 | Какой тип питомца покупают чаще всего? | Собаки |
| 3 | Какой тип питомца покупают меньше всего? | Другое |
| 4 | Какой процент клиентов покупает песчанок? | 9 |
| 5 | Какой процент клиентов покупает птиц? | 18 |
Построение круговых графов
| Упражнение 1: | Источники доходов федерального правительства были зарегистрированы, как показано в таблице ниже. Постройте круговую диаграмму, чтобы визуально отобразить эти данные. | ||||||||||||
| |||||||||||||
| Решение: | Образец круговой диаграммы показан ниже. | ||||||||||||
| Упражнение 2: | Учащиеся небольшой школы были опрошены, чтобы определить, какой вид транспорта используется, чтобы добраться до школы и обратно, как показано в таблице ниже. Постройте круговую диаграмму, чтобы визуально отобразить эти данные. | ||||||||||||||
| |||||||||||||||
| Решение: | Пример круговой диаграммы показан ниже. | ||||||||||||||
Сравнение графиков
| Упражнение | Проблема | Ответить |
| 1 | Возраст 7 трубачей в оркестре: 13, 12, 11, 12, 11, 10 и 12 лет. Какой тип графика подходит для сравнения возраста этих трубачей? | бар |
| 2 | Федеральная почасовая минимальная заработная плата регистрировалась каждый год с 1990 по 2007 год. Какой тип графика лучше всего покажет изменения минимальной заработной платы за этот период времени? | строка |
| 3 | На вопрос, состоит ли словосочетание «антидисистеблишментарианство» из 28 букв, 50 человек ответили да , 35 человек ответили нет и 15 человек ответили Не знаю. Какой тип диаграммы лучше всего подходит для сравнения этих ответов друг с другом и с итоговым значением? | круг |
| 4 | Рост 7 разных растений был записан в сантиметрах. Какой тип графика лучше всего подходит для сравнения роста каждого растения? | бар |
| 5 | В городе каждый месяц в течение 12 месяцев регистрировалось количество осадков в дюймах. Какой тип графика лучше всего отображает изменение количества осадков? | строка |
Практические упражнения
См. линейный график ниже для упражнений 1–3.
| Упражнение | Проблема | Ответить |
| 1 | Какое самое большое число на вертикальной шкале? | 140 |
| 2 | Какая частота пульса была зарегистрирована через 2 минуты? | 95 |
| 3 | Во сколько минут была зарегистрирована частота пульса 121 удар в минуту? | 3 |
См.
гистограмму ниже для упражнений 4–6.
См. круговую диаграмму ниже для упражнений 7–10.
Упражнения с вызовом
1. | Класс миссис Глоссер проголосовал за свою любимую игрушку. Каждый студент проголосовал один раз. Вот голосование: кукла 4, фигурка 4, обучающая игрушка 3, видеоигра 6, электроника 5, строительные блоки 1. Какая из следующих гистограмм правильно отображает все эти факты? (Обратите внимание, что заголовок каждого графика опущен.) |
Вариант 1 неверен, поскольку он показывает 6 для куклы, а не 4; и потому что он показывает 4 для видеоигры, а не 6.
Вариант 2 неверен, потому что он показывает 2 для электроники, а не 5.
Вариант 3 правильный, потому что он правильно показывает все факты.
| 2. | Вес младенца регистрировали в фунтах для каждой из 7 недель. Вот данные: 1-я неделя : 7,5 фунтов; Неделя 2 : 7,1 фунта; Неделя 3 : 7,4 фунта; Неделя 4 : 7,7 фунта; Неделя 5 : 8,2 фунта; Неделя 6 : 8,6 фунта; Неделя 7 : 9,0 фунтов. Какой из следующих линейных графиков правильно отображает все эти факты? (Обратите внимание, что заголовок каждого графика опущен. Кроме того, значения для каждой точки не обозначены.) |
Вариант 1 неверен, так как значение, которое он показывает для недели 1, составляет около 9фунтов, а не 7,5 фунтов.
Вариант 3 неверен, так как значение, которое он показывает для недели 4, составляет около 9 фунтов, а не 7,7 фунтов.
Вариант 2 правильный, поскольку он правильно показывает все факты.
| 3. | Количество времени, затрачиваемого на повседневную деятельность, указано в часах следующим образом: школа 8, сон 6, развлечения 5, домашняя работа 3, приемы пищи 2. Какая из следующих круговых диаграмм правильно отображает все эти факты? (Обратите внимание, что все заголовки опущены.) |
Вариант 1 неверен, поскольку: [1] Проценты для каждого сектора не соответствуют заданным данным.
[2] Сектора имеют номер , а не , они нарисованы от большего к меньшему по часовой стрелке.
Вариант 2 неверен, потому что: [1] Проценты для каждого сектора не соответствуют заданным данным. [2] Сектора имеют номер , а не , они нарисованы от большего к меньшему по часовой стрелке.
Вариант 3 правильный, поскольку он правильно показывает все факты.
| Упражнение | Проблема | Ответить |
| 4 | Какой график вы бы использовали для представления скорости в км в час 20 самых быстрых животных в мире? | бар |
| 5 | Какой график вы бы использовали для представления годового количества ДТП со смертельным исходом в вашем штате за последние 10 лет? | строка |
| 6 | Какой график вы бы использовали для представления количества пользователей Интернета в 10 разных странах? | бар |
| 7 | Какой график вы бы использовали для представления процентной доли учащихся в вашей школе по классам? | круг |
Обратитесь к линейному графику ниже, чтобы ответить на упражнение 8.
Шкала начинается с 60 вместо 0,
Обратитесь к гистограмме ниже, чтобы ответить на упражнение 9.
На вертикальной шкале нет меток.
Обратитесь к круговой диаграмме ниже, чтобы ответить на упражнение 10.
Эта круговая диаграмма состоит из 7 секторов. Он загроможден и его трудно читать. На этом графике представлено слишком много данных.
| Уроки по данным и графикам |
| Данные и графики |
| Построение линейных графиков |
| Данные и гистограммы |
| Построение гистограмм |
| Данные и круговые диаграммы |
| Построение круговых диаграмм |
| Сравнение графиков |
| Практические упражнения |
| Упражнения с вызовом |
| Решения |
Подпишитесь на нашу БЕСПЛАТНУЮ рассылку новостей!
Подпишитесь на нашу БЕСПЛАТНУЮ рассылку новостей!
Адрес электронной почты *
Texas Go Math, 5 класс, урок 15.
4 Ключ к ответу Анализ гистограмм – Ключ к ответу в Go MathЧтобы получить хорошие оценки на экзаменах, обратитесь к нашему Pdf-файлу ответов на вопросы по математике для 5-го класса Texas Go Math. Проверьте себя, решая задачи из урока 15.4 для 5-го класса Texas Go Math, ключ к ответу, анализ гистограмм.
Раскрыть проблему
Гистограмма полезна для сравнения и анализа данных.
Иногда можно сделать прогноз на основе данных. Предсказание — это разумное предположение о том, что может произойти, и может оказаться верным или ложным.
Пример 1.
Миссис Марципан продавала крендельки в закусочной в городском парке.
Она записывала количество кренделей, продаваемых каждый день в течение 5 дней.
• Сколько дней миссис Марципан записывала количество проданных кренделей?
Ответ:
• Что сравнивается на этой гистограмме?
Ответ:
А. Сделайте вывод.
В какой день было продано наибольшее количество кренделей?
Вывод: Наибольшее количество кренделей было продано
____
B.
Сделайте прогноз.
В какой день на следующей неделе
Миссис Марципан продаст больше всего кренделей?
Прогноз: На следующей неделе миссис Марципан
продаст больше всего кренделей ___
Пример 2
Решите многошаговую задачу.
Студенты зарабатывают 3 доллара за каждую проданную ими подписку на журнал. Насколько больше денег зарабатывает Аарон, чем Карла?
Шаг 1
Используйте график, чтобы найти количество подписок, проданных Аароном и Карлой.
Аарон: ___ подписок
Карла: ____ подписок
Шаг 2
Умножьте, чтобы найти сумму денег, которую каждый из них зарабатывает.
Аарон: ___ × $3 = $____
Карла: ___ × $3 = $ ____
Шаг 3:
$___ – $___ = $____
Итак, Аарон зарабатывает на $___ больше, продавая подписки на журналы, чем Карла.
Делитесь и показывайте
Используйте гистограмму для 1-2.
Вопрос 1.
На сколько моллюсков больше, чем раковин гребешков, у Барба?
количество ракушек: ____
количество раковин гребешков: ____
___ – ___ = ___
___ ракушек
Ответ:
Вопрос 2.
Каково общее количество ракушек в коллекции Барба?
Ответ:
Math Talk
Mathematical Processes
Опишите, как бы выглядели столбцы на графике, если бы у Барб было в 2 раза больше раковин, чем раковин моллюсков.
Шарики в мешке красного, синего, желтого и зеленого цвета. Альберт достает из мешка 20 шариков и записывает результаты на гистограмме. Используйте гистограмму для 3-4.
Вопрос 3.
Соединить Когда вы суммируете количество шариков двух цветов, которые вытягивает Альберт, оно равно общему количеству шариков другого цвета, которые он вытаскивает. Напишите уравнение, используя цветные слова, чтобы представить эту связь.
Ответ:
Вопрос 4.
Какого цвета в мешочке, скорее всего, больше, чем любого другого цвета в мешочке? Обосновать ответ.
Ответ:
Используйте график для 5-6.
Вопрос 5.
Многошаговый В статье в школьной газете говорится, что Гектор получил более половины голосов на выборах.
Это утверждение верно? Объяснять.
Ответ:
Вопрос 6.
Г.О.Т. Анализ Двадцать студентов не голосовали на выборах. Если бы эти студенты проголосовали за других кандидатов, а не за Гектора, как могли бы отличаться результаты выборов? Дайте три различных возможности.
Ответ:
Ежедневная оценка
Используйте гистограмму для 7-9. Заполните кружок полностью, чтобы показать свой ответ.
Вопрос 7.
Учителя школы Марти участвуют в соревновании по приготовлению пасты. Гистограмма показывает количество соуса, которое они используют в своих рецептах. В чем разница между наибольшим и наименьшим количеством соуса?
(A) 7 чашек
(B) 2 чашки
(C) 1 чашка
(D) 6 чашек
Ответ:
Вопрос 8.
Проанализируйте Кто мог наполнить соусом более одной литровой банки? Подсказка: 1 кварта = 4 чашки
(A) Стив
(B) Эрл
(C) Ана
(D) Хайме
Ответ:
Вопрос 9.
Сколько соуса используют все учителя в своих рецептах?
(A) 5 чашек
(B) 7 чашек
(C) 15 чашек
(D) 14 чашек ферма. Животные едят сено каждый день. Каждая лошадь съедает 15 фунтов; каждая корова съедает 30 фунтов; и каждая свинья съедает 1 фунт. Сколько сена съедают все сельскохозяйственные животные за 1 день?
(A) 46 фунтов
(B) 636 фунтов
(C) 591 фунт
(D) 33 фунта
Ответ:
Texas Go Math, 5 класс, урок 15.4 график для записи и сравнения результатов первых четырех игр. Используйте гистограмму для 1-3.
Вопрос 1.
На сколько больше очков команда набрала в игре 4, чем во второй? ______
Ответ:
Вопрос 2.
Сколько очков набрала команда в первых трех играх? ____
Ответ:
Вопрос 3.
Какое общее количество очков набрала команда? ____
Ответ:
Решение проблем
В субботу учащиеся участвуют в уборке в парке. Директор записывает посещаемость на гистограмме.
Используйте график для 4-5.
Вопрос 4.
Тайлер говорит, что у пятиклассников в два раза больше участников, чем у второклассников. Тайлер прав? Объяснять.
Ответ:
Вопрос 5.
‘Что, если после обеда придут еще 27 третьеклассников, чтобы помочь с уборкой? В чем разница между количеством учеников в классе с наибольшей посещаемостью и количеством учеников в классе с наименьшей посещаемостью? Объяснять.
Ответ:
Техасская подготовка к экзаменам
Заполните кружок полностью, чтобы показать свой ответ.
Вопрос 6.
Гистограмма показывает количество часов, отработанных каждым человеком в кинотеатре в пятницу. Эл зарабатывает 8 долларов в час, Боб зарабатывает 10 долларов в час, а Елена зарабатывает 9 долларов.0,50 в час. Сколько владелец театра заплатит всем трем работникам в пятницу?
(A) 158 $
(B) 168 $
(C) 171 $
(D) 181 $
Ответ:
Питомник заботится о собаках, пока их владельцы находятся в отпуске.
На графике показано количество пищи, которое каждая собака получает каждый день, в зависимости от ее веса и уровня активности. Используйте график для 7-9.
1 пинта = 2 чашки
1 кварта = 2 пинты
1 галлон = 4 кварты еда каждый день?
(A) Buster
(B) Abe
(C) Pepper
(D) Benji
Ответ:
Вопрос 8.
Multi-Step Сколько еды дается Pepper за одну неделю?
(A) 7 пинт
(B) 7 кварт
(C) 25 чашек
(D) 7 галлонов
Ответ:
Вопрос 9.
Multi-Step Что из следующего эквивалентно общему количеству собаки еды всех четырех собак кормят за один день?
(A) 1 галлон и 1 пинта
(B) 8 пинтов
(C) 3 галлона
(D) 2 кварты и 2 пинты
Ответ:
Графики и данные, рабочий лист по математике для 5-го класса, PDF
для 5-го класса, данные и графики / by math5childrenplus График и рабочий лист с данными для детей 5-го класса. Это математический PDF-лист с несколькими упражнениями, который можно распечатать.
На второй странице прикреплен ключ ответа. Этот рабочий лист является дополнительным ресурсом для пятого класса, который поможет учителям, родителям и детям дома и в школе.
Печать рабочего листа
Первый набор упражнений в этом вопросе предлагается учащимся для нахождения координат объектов на координатной плоскости. Эти упражнения предназначены для того, чтобы дать учащимся четкое представление о том, как двигаться по декартовой плоскости, а также дать учащимся достаточную практику и знакомство с системой координат. Дети, которые в состоянии успешно выполнить эти упражнения, найдут новые упражнения по мере продвижения вперед. Вопросы по диаграммам были тщательно разработаны, чтобы еще больше расширить представление ребенка о координатных плоскостях, а также о том, как правильно использовать пустое пространство на диаграмме. Дополнительные сведения: графики и диаграммы, гистограммы, построить диаграмму, типы диаграмм, круговая диаграмма, создать гистограмму.
Связанные рабочие листы
Расчетный лист по математике для детей 5-го класса – PDF для печати
Рабочий лист по добавлению денег для детей 5-го класса. Это математика…
https://math5childrenplus.com/wp-content/uploads/2013/11/adding-money-002.png 237 168 математика5детиплюс https://math5childrenplus.com/wp-content/uploads/2013/04/logo.png math5childrenplus2013-11-28 07:11:172014-06-20 03:48:11Добавление денежного листа по математике для детей 5-го класса – PDF для печатиЛист с дополнительными упражнениями по математике для детей 5-го класса – PDF для печати
Лист с дополнительными упражнениями по кругу для детей 5-х классов. Это…
https://math5childrenplus.com/wp-content/uploads/2013/11/addition-circle-drill-0021.png 237 168 математика5детиплюс https://math5childrenplus.com/wp-content/uploads/2013/04/logo.png math5childrenplus2013-11-28 07:11:002014-06-20 03:51:09Сложение с заданием по математике для детей 5-го класса – PDF для печатиДобавление 4-значного задания по математике для детей 5-го класса – PDF-печать
Добавление 4-значного задания для детей 5-го класса. Это…
https://math5childrenplus.com/wp-content/uploads/2013/11/дополнение-из-4-чисел-002.png 237 168 математика5детиплюс https://math5childrenplus.com/wp-content/uploads/2013/04/logo.png math5childrenplus2013-11-28 07:10:392014-06-20 03:51:33Добавление рабочего листа по математике с 4 числами для детей 5-го класса – PDF для печатиДобавление рабочего листа с 3 числами по математике для детей 5-го класса – PDF для печати
Добавление 3 чисел рабочий лист для детей 5 класса. Это…
https://math5childrenplus.com/wp-content/uploads/2013/11/дополнение-из-3-чисел-002.png 237 168 математика5детиплюс https://math5childrenplus.com/wp-content/uploads/2013/04/logo.png math5childrenplus2013-11-28 07:10:222014-06-20 03:51:37Добавление 3 чисел по математике для детей 5-го класса – PDF для печатиДобавление до ста тысяч листов по математике для детей 5-го класса – PDF для печати
Добавление до сотен тысяч листов для детей 5-х классов.…
https://math5childrenplus.com/wp-content/uploads/2013/11/дополнение-до-сотни-тысяч-002.png 237 168 математика5детиплюс https://math5childrenplus.com/wp-content/uploads/2013/04/logo.png math5childrenplus2013-11-28 07:10:022014-06-20 03:51:40Добавление до ста тысяч математических листов для детей 5-го класса – PDF для печатиДобавление рабочего листа по математике до миллионов для детей 5-го класса – PDF для печати
Добавление рабочего листа до миллионов для детей 5-го класса. Это…
https://math5childrenplus.com/wp-content/uploads/2013/11/дополнение-до-миллионов-002.png 237 168 математика5детиплюс https://math5childrenplus.com/wp-content/uploads/2013/04/logo.png math5childrenplus2013-11-28 07:09:432014-06-20 03:51:44Добавление до миллионов математических листов для детей 5-го класса – PDF для печатиДополнение с перегруппировкой, рабочий лист по математике для 5-го класса, PDF для печати
Дополнение с перегруппировкой рабочего листа для детей 5-го класса. Это…
https://math5childrenplus.com/wp-content/uploads/2013/11/дополнение-с-перегруппировкой-002.png 237 168 математика5детиплюс https://math5childrenplus.com/wp-content/uploads/2013/04/logo.png math5childrenplus2013-11-28 07:09:172015-09-01 06:49:07Дополнение с перегруппировкой, рабочий лист по математике для 5-го класса, PDF для печатиАлгебра, оценка выражений, математический лист для детей 5-го класса – PDF для печати
Алгебра, оценка выражений, рабочий лист для детей 5-го класса.…
https://math5childrenplus.com/wp-content/uploads/2013/11/алгебра-оценка-выражений-002.png 237 168 математика5детиплюс https://math5childrenplus.com/wp-content/uploads/2013/04/logo.png math5childrenplus2013-11-28 07:06:062014-06-20 03:51:58Алгебра, вычисляющая выражения, математический лист для детей 5-го класса – PDF для печатиЛист математических задач по алгебре для детей 5-го класса – PDF для печати
Рабочий лист с задачами по алгебре для детей 5-го класса. Это…
https://math5childrenplus.com/wp-content/uploads/2013/11/алгебра-число-задач-002.png 237 168 математика5детиплюс https://math5childrenplus.com/wp-content/uploads/2013/04/logo.png math5childrenplus2013-11-28 07:05:412014-06-20 03:52:06Рабочая тетрадь по математике с числами по алгебре для детей 5-го класса – PDF для печатиРешение по алгебре для задания по математике с переменной для детей 5-го класса – PDF для печати
Решение по алгебре для задания по математике с переменными для детей 5-го класса.…
https://math5childrenplus.com/wp-content/uploads/2013/11/алгебра-решение-для-переменной-002.png 237 168 математика5детиплюс https://math5childrenplus.com/wp-content/uploads/2013/04/logo.png math5childrenplus2013-11-28 07:05:082014-06-20 03:52:13Решение по алгебре для задания по математике с переменной для детей 5-го класса – PDF для печатиПредыдущийСледующий
Похожие сообщения:
Поделитесь этой записью
