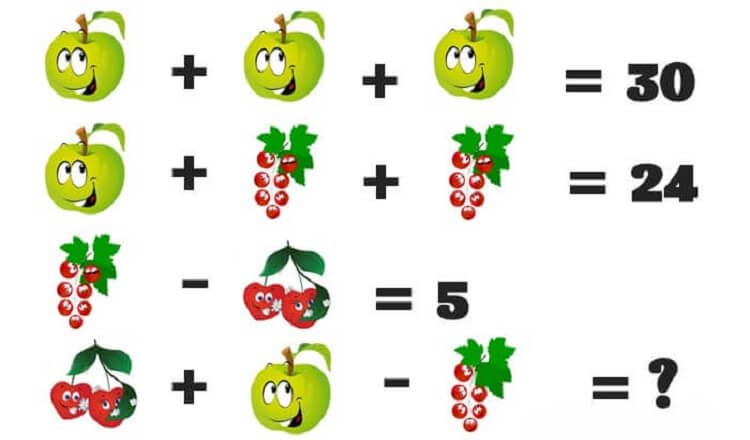Логика и логические задачи — презентация онлайн
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
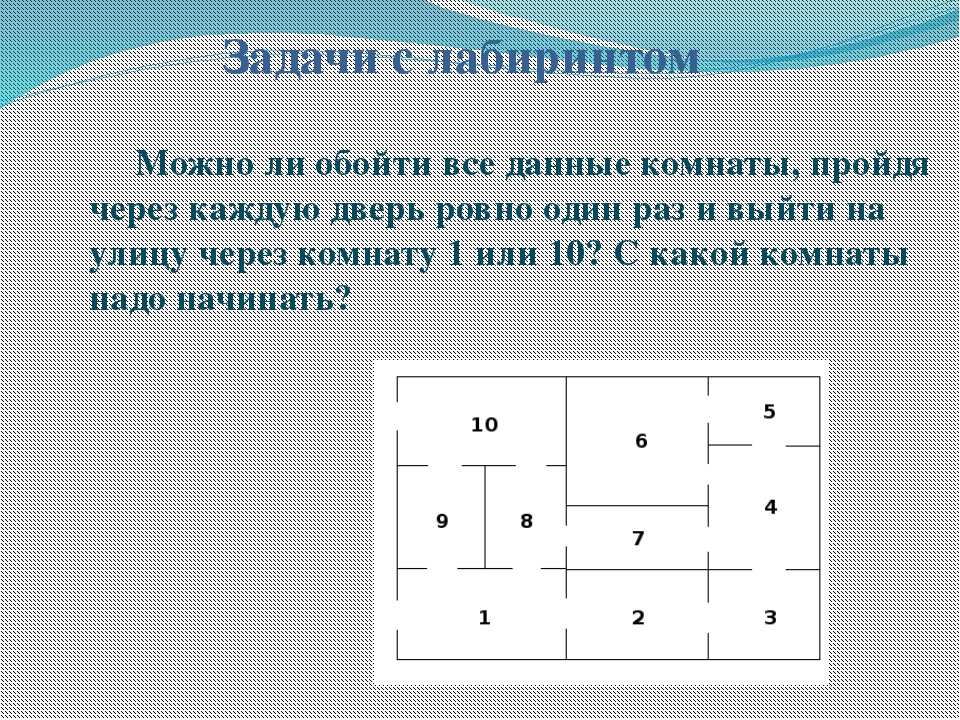
1. Логика и Логические задачи
Логика есть искусство, которое упорядочиваети связывает мысли. Люди ошибаются именно
потому, что им недостает логики.
Немецкий философ Иммануил Кант
2. Что такое логика? Немного истории
Что такое?
Как самостоятельная наука логика
оформилась в трудах греческого философа
Аристотеля (384-322г.
 г. до н.э.). Он обобщил и
г. до н.э.). Он обобщил исистематизировал известные до него сведения,
и эта система позже стала называться
формальной, или Аристотелевой логикой.
Формальная логика просуществовала без
серьезных
изменений
более
двадцати
столетий.
Естественно,
что
развитие
математики
выявило
недостаточность Аристотелевой логики и потребовало
дальнейшего ее развития.
3. Что такое логика? Немного истории
Что такое?
Впервые в истории идеи о построении логики
на математической основе были высказаны
немецким математиком Г. Лейбницем (1646-1716) в
конце XVII века. Он считал, что основные понятия
логики должны быть обозначены символами,
которые соединяются по особым правилам. Это
позволит
всякое
рассуждение
заменить
вычислением.
4. Что такое логика? Немного истории
Что такое?
Впервые идеи Лейбница реализовал
английский ученый Джордж Буль (18151864). Он создал алгебру, в которой
буквами обозначены высказывания, и это
привело к алгебре высказываний.
 Этот
Этотраздел математики стали называть
булевой
алгеброй
или
алгеброй
высказываний.
Введение символических обозначений
в логику имело для этой науки такое же
решающее значение, как введение
буквенных обозначений для математики.
Именно благодаря введению символов в логику была получена
основа для создания новой науки — математической логики.
5. Что такое логика? Немного истории
Что такое?
Применение математики к логике
позволило представить логические теории в
новой удобной форме. К концу XIX
столетия актуальное значение для
математики приобрели вопросы
обоснования ее основных понятий и идей.
Эти задачи имели логическую природу и,
естественно, привели к дальнейшему
развитию математической логики.
Современную математическую логику определяют
как раздел математики, посвященный изучению
математических доказательств и вопросов оснований
математики.
6. Что такое логическая задача?
-наука о способах иформах правильного мышления.

–описание реальной это задача, в которой с
ситуации с числовыми данными,
помощью верных
в котором с помощью
арифметических действий,
рассуждений, без всяких
формул, уравнений (систем
вычислений
или
с
уравнений) или неравенств
(систем неравенств) надо найти помощью наименьшего
неизвестную величину или
их количества надо
ответить на главный вопрос
ответить на главный
задачи с помощью найденной
вопрос задачи.
величины.
7. Особенности логической задачи
логической задачиЛогические задачи отличаются от привычных школьных задач
тем, что
, а решаются
.
Почти всегда логические задачи
и этим
даже тех, кто не любит математику.
Решение логических задач
, что
не только лучшему
, но и успешному
любой
.
основ
8. Как научиться решать логические задачи
логические задачиосновными
логических задач.
логических задач.
как можно
логических задач
полном овладении этой темы.

в
9. Основные Виды логических задач
логических задачзадачи
одного или
;
нескольких других
задачи
;
на переливание;
задачи
;
задачи
.
10. методы решения логических задач
логических задач;
;
;
;
11. Значение решения логических задач
решения логических задачПри решении логических задач
, который пригодится в
различных жизненных ситуациях.
Логические задачи
научиться
,
приводящие к единственно верному решению.
Основные методы решения
данных и выведении основных выводов
на их основе.
Решение логических задач побуждает ученика, чтобы он
разнообразными
, на первый
взгляд,
, без которых решение будет неправильным.
А теперь перейдём к
На этом этапе ты научишься применять в
решении логических задач
English Русский Правила
Задания на логику для детей 7-8 лет
1 уровень сложности
- 10
.
 ..
..
2 уровень сложности
- 10
.
 ..
..
3 уровень сложности
-
10
.
 ..
..
Вспомним знакомую с детства сценку. Мальвина говорит Буратино: «У вас в кармане два яблока». «Врете, ни одного…» — отвечает озорной деревянный мальчишка. Эта сценка в полной мере отражает возрастную особенность детского мышления, а именно конкретность. Свойство детского ума воспринимать все конкретно, буквально, неумение подняться над ситуацией и понять ее общий смысл — одна из основных трудностей детского мышления, ярко проявляющаяся при изучении таких абстрактных школьных дисциплин, как математика или грамматика. Однако к моменту поступления в первый класс образное мышление детей перестает быть сугубо конкретным и ситуативным. Ребенок способен не только представить предмет во всей полноте и разнообразии характеристик, но также способен выделить его существенные свойства и отношения. У него формируется наглядно-схематическое мышление. Это особый вид мышления, который выражается в том, что ребенок понимает и успешно использует различные схематические изображения предмета (план, макет, простейший чертеж).
Процесс отвлечения в возрасте 7–8 лет совершается не только при восприятии ряда предметов, но и под влиянием словесных описаний и объяснений. Однако ребенок все еще находится в плену образов конкретных предметов. Зная из опыта, что железные предметы тонут в воде, он говорит, что гвоздь утонет, но этот вывод он подкрепляет не общим положением («Все железные предметы тонут»), а ссылкой на единичный случай: «Я сам видел, как гвоздь тонул».
Об активности мышления детей красноречиво говорят их многочисленные вопросы, в которых ребенок выражает любознательность к тому, что его окружает: «Почему теперь ночь? Почему капель падает? Отчего огонь в спичке, где он спрятан?» и т. д. Мысль почемучки теперь направлена на различение и обобщение предметов, явлений, событий, наблюдаемых ими.
д. Мысль почемучки теперь направлена на различение и обобщение предметов, явлений, событий, наблюдаемых ими.
В протекании мыслительного процесса также выступает наметившийся еще у пяти-, шестилетних детей способ мышления методом «короткого замыкания». Ребенок не анализирует всю задачу в целом (житейскую, орфографическую или математическую), т.е. не выделяет всех ее условий, всех данных и не видит связи между ними. Он выхватывает какое-то одно условие и устанавливает прямую связь с любым другим условием или с заданным вопросом. Так, отгадывая загадку «Я все знаю, всех учу, но сама всегда молчу», первоклассник часто отвечает, что это учительница. Фразы «Я все знаю, всех учу…» достаточно, чтобы найти решение, т.е. подставить знакомый образ. И хотя дальше следует дополнение — «…но сама всегда молчу», — т.е. налицо как будто прямо противоположное условие найденной отгадке, ребенок просто отбрасывает это условие.
Поступление в школу меняет содержание деятельности детей. Значительно расширяется круг предметов и явлений, о которых они должны думать, повышаются и требования к самим процессам мышления. Преподаватель учит детей внимательно следить за ходом рассуждения, точно выражать мысли в словах, сначала думать, а потом делать что-либо и пр. Хотя мышление младших школьников в целом остается еще конкретно-образным, элементы абстрактного мышления выражены все заметнее. Дети могут мыслить на уровне общих понятий о том, что им хорошо известно, о знакомых животных, растениях, людях и их труде.
Преподаватель учит детей внимательно следить за ходом рассуждения, точно выражать мысли в словах, сначала думать, а потом делать что-либо и пр. Хотя мышление младших школьников в целом остается еще конкретно-образным, элементы абстрактного мышления выражены все заметнее. Дети могут мыслить на уровне общих понятий о том, что им хорошо известно, о знакомых животных, растениях, людях и их труде.
Темп развития мышления детей школьного возраста в значительной мере зависит от того, как их обучают. Опытное обучение младших школьников по специальным программам повышенной трудности доказывает, что уже у детей 7–8 лет способность к отвлеченному рассуждению и последовательному выполнению умственных действий достаточно высока. Применение научно разработанных методов обучения детей убыстряет развитие мышления.
Таким образом, в формировании мышления школьников решающее значение принадлежит учебной деятельности, постепенное усложнение которой ведет за собой развитие умственных способностей учащихся.
Однако для активизации и развития мыслительной деятельности детей бывает целесообразно использовать неучебные задания, которые в целом ряде случаев оказываются для школьников более привлекательными. Неоценимую помощь в развитии логического мышления окажут задания и упражнения на поиск закономерностей, логические задачи, головоломки. Пусть ребенок отгадывает загадки и придумывает их сам. Знакомьте его с пословицами, но не в абстрактной форме, а применительно к жизненной ситуации (например, если ребенок разбросал игрушки, скажите: «Любишь кататься — люби и саночки возить», и объясните обобщенный смысл пословицы).
Сделайте занятия по развитию мышления ребенка не только полезными, но и увлекательными. В этом вам обязательно поможет наш сайт!
Удачи и гордости за достижения вашего ребенка!
3E Пазлы Льюиса Кэрролла
3E Пазлы Льюиса Кэрролла3E Пазлы Льюиса Кэрролла
| |
Льюис Кэрролл, чистка объектива |
Как только вы овладеете механизмом символической логики, у вас всегда под рукой будет умственное занятие, занимающее интерес и действительно полезное для вас в любом предмете, за который вы возьметесь. Это даст вам ясность мысли, способность видеть путь сквозь головоломку, привычку упорядочивать свои идеи в упорядоченной и удобной форме и, что важнее всего, способность обнаруживать ошибки и разорвите в клочья нелепые нелогичные рассуждения, которые вы так постоянно будете встречать в книгах, в газетах, в речах и даже в проповедях и которые так легко вводят в заблуждение тех, кто никогда не утруждал себя овладением этим увлекательным Искусством.
Это даст вам ясность мысли, способность видеть путь сквозь головоломку, привычку упорядочивать свои идеи в упорядоченной и удобной форме и, что важнее всего, способность обнаруживать ошибки и разорвите в клочья нелепые нелогичные рассуждения, которые вы так постоянно будете встречать в книгах, в газетах, в речах и даже в проповедях и которые так легко вводят в заблуждение тех, кто никогда не утруждал себя овладением этим увлекательным Искусством.
Льюис Кэрролл
Льюис Кэрролл, возможно, немного преувеличил, как это часто делают профессора математики в отношении полезности своего предмета. Кэрролл наиболее известен своими бессмысленными книгами, в том числе печально известной «Алисой в стране чудес», написанной для детей в возрасте от пяти до девяноста лет; но его основная работа была профессором математики в Оксфордском университете в Англии. Он изучал логику как призвание и играл с логикой в своих произведениях. Его рассказы о маленьких девочках и странных существах полны дурных каламбуров и других игр со словами, нелепыми подтекстами, противоречиями и многочисленными и разнообразными оскорблениями здравого смысла. Создается впечатление, что он писал свои глупые рассказы не столько для того, чтобы развлечь себя, сколько для того, чтобы развлечь свою аудиторию.
Создается впечатление, что он писал свои глупые рассказы не столько для того, чтобы развлечь себя, сколько для того, чтобы развлечь свою аудиторию.
|
| Согласно |
|
Будучи учителем логики и любителем чепухи, Кэрролл разработал занимательные головоломки, чтобы обучать людей систематическому мышлению. В этих головоломках он составляет список выводов, намеренно бессмысленных, чтобы на читателя не влияли какие-либо предвзятые мнения. Задача читателя — использовать все перечисленные импликации, чтобы прийти к неизбежному заключению. Вы получите общее представление после нескольких примеров.
Мы начинаем с одной из самых простых головоломок Льюиса Кэрролла и переходим к более сложным.
Головоломка №1
(а) Все дети нелогичны.
(b) Никого не презирают, кто может управлять крокодилом.
(c) Нелогичных людей презирают.
Поскольку субъектами этой головоломки являются люди, мы принимаем вселенную за совокупность всех людей. Мы перепишем каждое утверждение в головоломке как следствие. Сначала определим более простые операторы,
B : это ребенок |
| L : логично |
М: может управлять крокодилом | D : презирается , |
, где «это» в данном контексте относится к обычному лицу. Тогда эти три утверждения можно перефразировать как
.(a) B → ~L : Если это ребенок, то это нелогично. |
(b) M → ~D : Если он может управлять крокодилом, то его не презирают. |
(c) ~L → D : Если это не логично, то это презирается. |
Наша цель состоит в том, чтобы использовать транзитивное рассуждение несколько раз, выстраивая цепочку следствий, используя все данные утверждения. У нас есть стрелка, указывающая от B к ~L, и точно так же стрелка, указывающая от ~L к D; таким образом, мы можем начать с B и прийти к заключению D. Однако второе утверждение все еще не используется. Но поскольку любая импликация эквивалентна своему контрапозитиву, мы можем заменить второе утверждение его контрапозитивом D → ~M. Тогда мы получаем транзитивную цепочку рассуждений
B → ~L → D → ~M .
Мы считаем, что если B истинно, то ~L истинно, следовательно, D истинно, и, следовательно, ~M истинно. Наш окончательный вывод — утверждение
.B → ~M: Если это младенец, то он не может справиться с крокодилом.
На обычном языке мы бы скорее перефразировали этот ответ на загадку как
.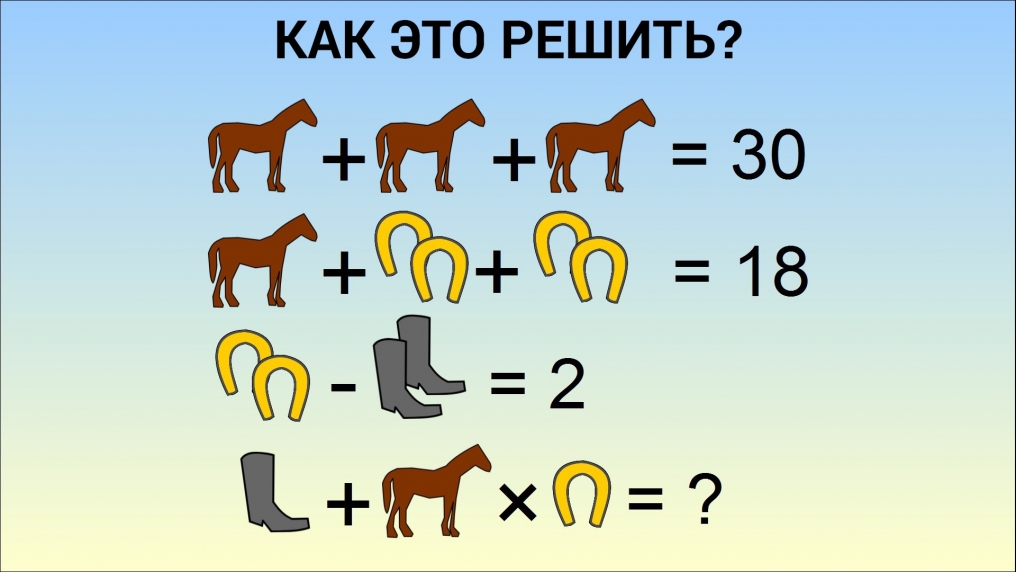
«Ни один ребенок не может справиться с крокодилом».
В качестве альтернативы мы могли бы записать ответ как противопоставленное утверждение
M → ~B : Если он может управлять крокодилом, то это не ребенок.
Перевод в слова тогда будет примерно таким:
«Тот, кто может управлять крокодилом, не ребенок».
|
|
Далее мы рассмотрим головоломку Льюиса Кэрролла с четырьмя утверждениями.
Головоломка №2
(а) Ни одно из незамеченных существ, встреченных в море, не является русалкой.
(b) Вещи, записанные в журнале, встречающиеся в море, обязательно заслуживают запоминания.
(c) В путешествии я никогда не встречал ничего, что стоило бы помнить.
(d) Вещи, встреченные в море, замеченные, обязательно записываются в журнал.
|
После внимательного прочтения утверждений мы делаем вывод, что обсуждаемые предметы принадлежат к несколько расплывчатой категории «вещи, встречающиеся в море», и поэтому принимаем это множество за универсальное множество. Наши более простые операторы
N : замечено |
М : это русалка |
L : внесено в журнал |
R : стоит запомнить |
Я: Я встречался с ним в море. |
Мы запишем каждое из утверждений (a) — (d) символически вместе с противопоставлением каждого утверждения:
(а) ~N → ~M | , | М → N |
(b) L → R | , | ~R → ~L |
(в) I → ~R | , | R → ~I |
(г) N → L | , | ~L → ~N . |
Затем мы смотрим на символические операторы, пока не обнаружим, что можем связать их все вместе как
.I → ~ R → ~ L → ~ N → ~ M .
Значит, решением головоломки является следствие
I → ~M: Если я встречался с ней в море, то это не русалка.
В качестве альтернативы мы могли бы выбрать контрапозитив
M → ~I: Если это русалка, то я не встречал ее в море.
Предпочтительным переводом на обычный язык является
.«Я никогда не встречал русалку в море».
Наконец, мы решаем головоломку Льюиса Кэрролла с пятью утверждениями.
Головоломка №3
(a) Нет интересных стихотворений, которые бы не пользовались популярностью среди людей с настоящим вкусом.
(б) Ни одна современная поэзия не свободна от жеманства.
(c) Все ваши стихотворения посвящены мыльным пузырям.
(d) Ни одна напыщенная поэзия не пользуется популярностью среди людей с настоящим вкусом.
(e) Ни одна древняя поэма не посвящена мыльным пузырям.
|
Вселенная в этой головоломке представляет собой собрание всех стихотворений, а пять утверждений являются импликациями, включающими более простые утверждения
Я : интересно | , | P: популярен среди людей с хорошим вкусом |
М : современно | , | A : затронуто |
Y : это твоя поэма | , | S: это на тему мыльных пузырей. |
Опять же, мы записываем каждое утверждение символически вместе с его противоположностью:
(а) I → P | , | ~П → ~И |
(б) М → А | , | ~А → ~М |
(в) Y → S | , | ~S → ~Y |
(г) A → ~P | , | П → ~А |
(д) ~M → ~S | , | С → М . |
В наших предыдущих двух головоломках вы могли заметить, что цепочка импликаций, соединяющая все утверждения, начинается с буквы, встречающейся только в одном из утверждений. В этой головоломке буквы Y и I соответствуют этому критерию. Если мы начнем с буквы I, мы получим цепь
.I → P → ~A → ~M → ~S → ~Y ,
, и если мы начнем с буквы Y, мы создадим противоположную цепочку,
Y → S → M → A → ~P → ~I .
Таким образом, решением головоломки является I → ~Y или эквивалентное противоположное Y → ~I. Самым простым переводом обратно в слова является, пожалуй, жестокое утверждение
.«Ваша поэзия неинтересна».
УПРАЖНЕНИЯ 3E
Эти головоломки создал Льюис Кэрролл. В каждой головоломке вы должны записать утверждения символически как импликации вместе с их контрапозитивами, а затем связать вместе стрелками все утверждения, чтобы прийти к окончательному заключению. Ваш ответ будет конечным следствием, которое вы затем должны умело перевести обратно на обычный язык.
Ваш ответ будет конечным следствием, которое вы затем должны умело перевести обратно на обычный язык.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Математические логические головоломки Shapes — осеннее издание
Используйте код купона SAVE10, чтобы получить дополнительную скидку 10% на первый заказ!
Заработайте 4,00 бонусных балла
4,00 $
Поощряйте своих учеников настойчиво выполнять сложные задачи с помощью этих логических головоломок FALL Pattern Block! Простые в использовании и простые в подготовке, эти головоломки представляют собой увлекательный, дифференцированный математический центр, который развивает у учащихся логику и визуальное различение!
Всего страниц: 30 головоломок + дополнения
Размер файла: 1 МБ
ПРЕДПРОСМОТР
КоличествоMath Logic Puzzles Shapes — Fall Edition
Также доступен в НАБОРАХ СО СКИДКОЙ:
Категория: математические логические головоломки
- Описание
- Бонусные очки
- Задайте вопрос
- Отзывы (0)
- часто задаваемые вопросы
Описание
Этот набор интерактивных логических головоломок «Осенний рисунок» заставит ваших первоклассников просить еще! Простые в использовании, эти головоломки являются отличным практическим центром математики, который будет увлекать детей, улучшая навыки ваших учеников, необходимые для решения логических задач, а также развивая их навыки визуального различения. Эти ДИФФЕРЕНЦИИРОВАННЫХ головоломок идеально подходят для того, чтобы помочь вашим ученикам научиться настойчиво выполнять сложные задания.
Эти ДИФФЕРЕНЦИИРОВАННЫХ головоломок идеально подходят для того, чтобы помочь вашим ученикам научиться настойчиво выполнять сложные задания.
★★★ Сохранить 20%, купив математическую логику головоломки Год. Пакет ★★★
Вы можете узнать больше об этом ресурсе в этом посте в блоге
. В комплекте в этом ресурсе:- советы учителю
- распечатка блоков выкройки (при необходимости)
- якорная диаграмма настойчивости
- карточки-ключи для ответов
30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 303 пазлы — по 10 на каждом из 3-х уровней
Вам также может понравиться эти другие растущих мозга Ресурсы:
Рост мышления
Рост.
Математические логические головоломки – Набор для подсчета монет
Наградные баллы
Я разработал простую систему начисления баллов для постоянных клиентов!
- За каждый потраченный доллар (доллар США) вы получаете 1 балл!
- 20 баллов можно обменять на 1 доллар США при следующей покупке!
- Когда вы оставляете отзыв (review), вы получаете 5 баллов!
- бонусных баллов можно просмотреть в разделе «Моя учетная запись».

Это означает, что вы фактически получаете 5% обратно на все, что покупаете, а также дополнительные баллы за отзыв. Баллы действительны в течение одного года и могут быть использованы для чего угодно в магазине!
Примечание. Система начисления баллов может быть изменена. Посмотреть полные условия здесь.
Только зарегистрированные клиенты, которые приобрели этот продукт, могут оставить отзыв.
Есть два способа получить доступ к купленным загрузкам:
- Автоматическое электронное письмо со ссылкой для скачивания генерируется каждый раз, когда вы совершаете покупку, поэтому проверьте папку «Входящие» и «Спам», а затем щелкните ссылку в письме.
- Войдите в свою учетную запись, и вы найдете список своих покупок, который вы можете загрузить в любое время на любое из ваших устройств.


 ..
.. ..
.. ..
..