1.10. Деревья решений — scikit-learn
Деревья решений (DT) — это непараметрический контролируемый метод обучения, используемый для классификации и регрессии . Цель состоит в том, чтобы создать модель, которая предсказывает значение целевой переменной, изучая простые правила принятия решений, выведенные из характеристик данных. Дерево можно рассматривать как кусочно-постоянное приближение.
Например, в приведенном ниже примере деревья решений обучаются на основе данных, чтобы аппроксимировать синусоидальную кривую с набором правил принятия решений «если-то-еще». Чем глубже дерево, тем сложнее правила принятия решений и тем лучше модель.
Некоторые преимущества деревьев решений:
- Просто понять и интерпретировать. Деревья можно визуализировать.
- Требуется небольшая подготовка данных. Другие методы часто требуют нормализации данных, создания фиктивных переменных и удаления пустых значений. Однако обратите внимание, что этот модуль не поддерживает отсутствующие значения.

- Стоимость использования дерева (т. Е. Прогнозирования данных) является логарифмической по количеству точек данных, используемых для обучения дерева.
- Может обрабатывать как числовые, так и категориальные данные. Однако реализация scikit-learn пока не поддерживает категориальные переменные. Другие методы обычно специализируются на анализе наборов данных, содержащих только один тип переменных. См. Алгоритмы для получения дополнительной информации.
- Способен обрабатывать проблемы с несколькими выходами.
- Использует модель белого ящика. Если данная ситуация наблюдаема в модели, объяснение условия легко объяснить с помощью булевой логики. Напротив, в модели черного ящика (например, в искусственной нейронной сети) результаты могут быть труднее интерпретировать.
- Возможна проверка модели с помощью статистических тестов. Это позволяет учитывать надежность модели.
- Работает хорошо, даже если его предположения несколько нарушаются истинной моделью, на основе которой были сгенерированы данные.

К недостаткам деревьев решений можно отнести:
- Обучающиеся дереву решений могут создавать слишком сложные деревья, которые плохо обобщают данные. Это называется переобучением. Чтобы избежать этой проблемы, необходимы такие механизмы, как обрезка, установка минимального количества выборок, необходимых для конечного узла, или установка максимальной глубины дерева.
- Деревья решений могут быть нестабильными, поскольку небольшие изменения в данных могут привести к созданию совершенно другого дерева. Эта проблема смягчается за счет использования деревьев решений в ансамбле.
- Как видно из рисунка выше, предсказания деревьев решений не являются ни гладкими, ни непрерывными, а являются кусочно-постоянными приближениями. Следовательно, они не годятся для экстраполяции.
- Известно, что проблема обучения оптимальному дереву решений является NP-полной с точки зрения нескольких аспектов оптимальности и даже для простых концепций. Следовательно, практические алгоритмы обучения дереву решений основаны на эвристических алгоритмах, таких как жадный алгоритм, в котором локально оптимальные решения принимаются в каждом узле.
 Такие алгоритмы не могут гарантировать возврат глобального оптимального дерева решений. Это можно смягчить путем обучения нескольких деревьев в учащемся ансамбля, где функции и образцы выбираются случайным образом с заменой.
Такие алгоритмы не могут гарантировать возврат глобального оптимального дерева решений. Это можно смягчить путем обучения нескольких деревьев в учащемся ансамбля, где функции и образцы выбираются случайным образом с заменой. - Существуют концепции, которые трудно изучить, поскольку деревья решений не выражают их легко, например проблемы XOR, четности или мультиплексора.
- Ученики дерева решений создают предвзятые деревья, если некоторые классы доминируют. Поэтому рекомендуется сбалансировать набор данных перед подгонкой к дереву решений.
1.10.1. Классификация
DecisionTreeClassifier — это класс, способный выполнять мультиклассовую классификацию набора данных.
Как и в случае с другими классификаторами, DecisionTreeClassifier принимает в качестве входных данных два массива: массив X, разреженный или плотный, формы (n_samples, n_features), содержащий обучающие образцы, и массив Y целочисленных значений, формы (n_samples,), содержащий метки классов для обучающих образцов:
>>> from sklearn import tree >>> X = [[0, 0], [1, 1]] >>> Y = [0, 1] >>> clf = tree.DecisionTreeClassifier() >>> clf = clf.fit(X, Y)
После подбора модель можно использовать для прогнозирования класса образцов:
>>> clf.predict([[2., 2.]]) array([1])
В случае, если существует несколько классов с одинаковой и самой высокой вероятностью, классификатор предскажет класс с самым низким индексом среди этих классов.
В качестве альтернативы выводу определенного класса можно предсказать вероятность каждого класса, которая представляет собой долю обучающих выборок класса в листе:
>>> clf.predict_proba([[2., 2.]]) array([[0., 1.]])
DecisionTreeClassifier поддерживает как двоичную (где метки — [-1, 1]), так и мультиклассовую (где метки — [0,…, K-1]) классификацию.
Используя набор данных Iris, мы можем построить дерево следующим образом:
>>> from sklearn.datasets import load_iris >>> from sklearn import tree >>> iris = load_iris() >>> X, y = iris.data, iris.target >>> clf = tree.DecisionTreeClassifier() >>> clf = clf.fit(X, y)
После обучения вы можете построить дерево с помощью plot_tree функции:
>>> tree.plot_tree(clf)
Мы также можем экспортировать дерево в формат Graphviz с помощью export_graphviz экспортера. Если вы используете Conda менеджер пакетов, то Graphviz бинарные файлы и пакет питон может быть установлен conda install python-graphviz.
В качестве альтернативы двоичные файлы для graphviz можно загрузить с домашней страницы проекта graphviz, а оболочку Python установить из pypi с помощью pip install graphviz.
Ниже приведен пример экспорта graphviz вышеуказанного дерева, обученного на всем наборе данных радужной оболочки глаза; результаты сохраняются в выходном файле iris.pdf:
>>> import graphviz >>> dot_data = tree.export_graphviz(clf, out_file=None) >>> graph = graphviz.Source(dot_data) >>> graph.render("iris")
Экспортер export_graphviz также поддерживает множество эстетических вариантов, в том числе окраски узлов их класс (или значение регрессии) и используя явные имена переменных и классов , если это необходимо. Блокноты Jupyter также автоматически отображают эти графики встроенными:
>>> dot_data = tree.export_graphviz(clf, out_file=None, ... feature_names=iris.feature_names, ... class_names=iris.target_names, ... filled=True, rounded=True, ... special_characters=True) >>> graph = graphviz.Source(dot_data) >>> graph
В качестве альтернативы дерево можно также экспортировать в текстовый формат с помощью функции export_text. Этот метод не требует установки внешних библиотек и более компактен:
>>> from sklearn.datasets import load_iris >>> from sklearn.tree import DecisionTreeClassifier >>> from sklearn.tree import export_text >>> iris = load_iris() >>> decision_tree = DecisionTreeClassifier(random_state=0, max_depth=2) >>> decision_tree = decision_tree.fit(iris.data, iris.target) >>> r = export_text(decision_tree, feature_names=iris['feature_names']) >>> print(r) |--- petal width (cm) <= 0.80 | |--- class: 0 |--- petal width (cm) > 0.80 | |--- petal width (cm) <= 1.75 | | |--- class: 1 | |--- petal width (cm) > 1.75 | | |--- class: 2
Примеры
- Постройте поверхность принятия решений дерева решений на наборе данных радужной оболочки глаза
- Понимание структуры дерева решений
1.10.2. Регрессия
Деревья решений также могут применяться к задачам регрессии с помощью класса DecisionTreeRegressor .
Как и в настройке классификации, метод fit будет принимать в качестве аргументов массивы X и y, только в этом случае ожидается, что y будет иметь значения с плавающей запятой вместо целочисленных значений:
>>> from sklearn import tree >>> X = [[0, 0], [2, 2]] >>> y = [0.5, 2.5] >>> clf = tree.DecisionTreeRegressor() >>> clf = clf.fit(X, y) >>> clf.predict([[1, 1]]) array([0.5])
Пример:
- Регрессия дерева решений
1.10.3. Проблемы с несколькими выходами
Задача с несколькими выходами — это проблема контролируемого обучения с несколькими выходами для прогнозирования, то есть когда Y — это 2-й массив формы (n_samples, n_outputs).
Когда нет корреляции между выходами, очень простой способ решить эту проблему — построить n независимых моделей, то есть по одной для каждого выхода, а затем использовать эти модели для независимого прогнозирования каждого из n выходов. Однако, поскольку вполне вероятно, что выходные значения, относящиеся к одному и тому же входу, сами коррелированы, часто лучшим способом является построение единой модели, способной прогнозировать одновременно все n выходов. Во-первых, это требует меньшего времени на обучение, поскольку строится только один оценщик. Во-вторых, часто можно повысить точность обобщения итоговой оценки.
Что касается деревьев решений, эту стратегию можно легко использовать для поддержки задач с несколькими выходами. Для этого требуются следующие изменения:
- Сохранять n выходных значений в листьях вместо 1;
- Используйте критерии разделения, которые вычисляют среднее сокращение для всех n выходов.
Этот модуль предлагает поддержку для задач с несколькими выходами, реализуя эту стратегию как в, так DecisionTreeClassifier и в DecisionTreeRegressor. Если дерево решений соответствует выходному массиву Y формы (n_samples, n_outputs), то итоговая оценка будет:
- Вывести значения n_output при
predict; - Выведите список массивов n_output вероятностей классов на
predict_proba.
Использование деревьев с несколькими выходами для регрессии продемонстрировано в разделе «Регрессия дерева решений с несколькими выходами» . В этом примере вход X — это одно действительное значение, а выходы Y — синус и косинус X.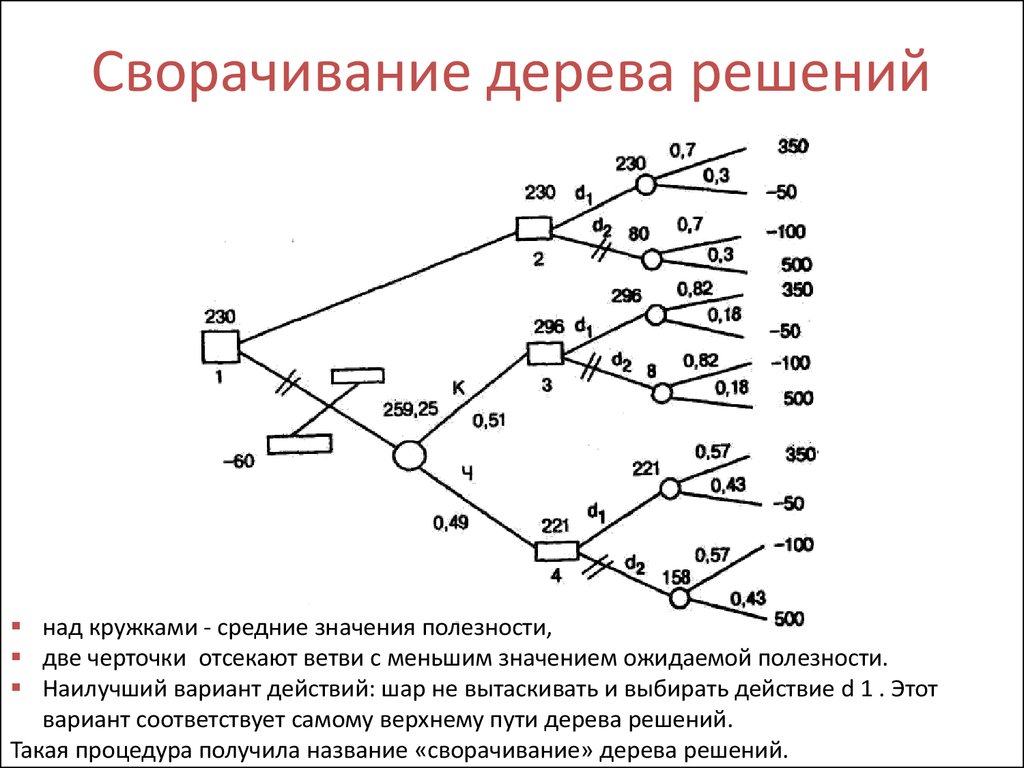
Использование деревьев с несколькими выходами для классификации демонстрируется в разделе «Завершение лица с оценками с несколькими выходами» . В этом примере входы X — это пиксели верхней половины граней, а выходы Y — пиксели нижней половины этих граней.
Примеры:
- Регрессия дерева решений с несколькими выходами
- Завершение лица с помощью многовыходных оценщиков
Рекомендации:
- М. Дюмон и др., Быстрая мультиклассовая аннотация изображений со случайными подокнами и множественными выходными рандомизированными деревьями , Международная конференция по теории и приложениям компьютерного зрения, 2009 г.
1.10.4. Сложность
В общем, время выполнения для построения сбалансированного двоичного дерева составляет $O(n_{samples}n_{features}\log(n_{samples}))$ и время запроса $O(\log(n_{samples}))$. Хотя алгоритм построения дерева пытается генерировать сбалансированные деревья, они не всегда будут сбалансированными. Предполагая, что поддеревья остаются примерно сбалансированными, стоимость на каждом узле состоит из перебора $O(n_{features})$ найти функцию, обеспечивающую наибольшее снижение энтропии.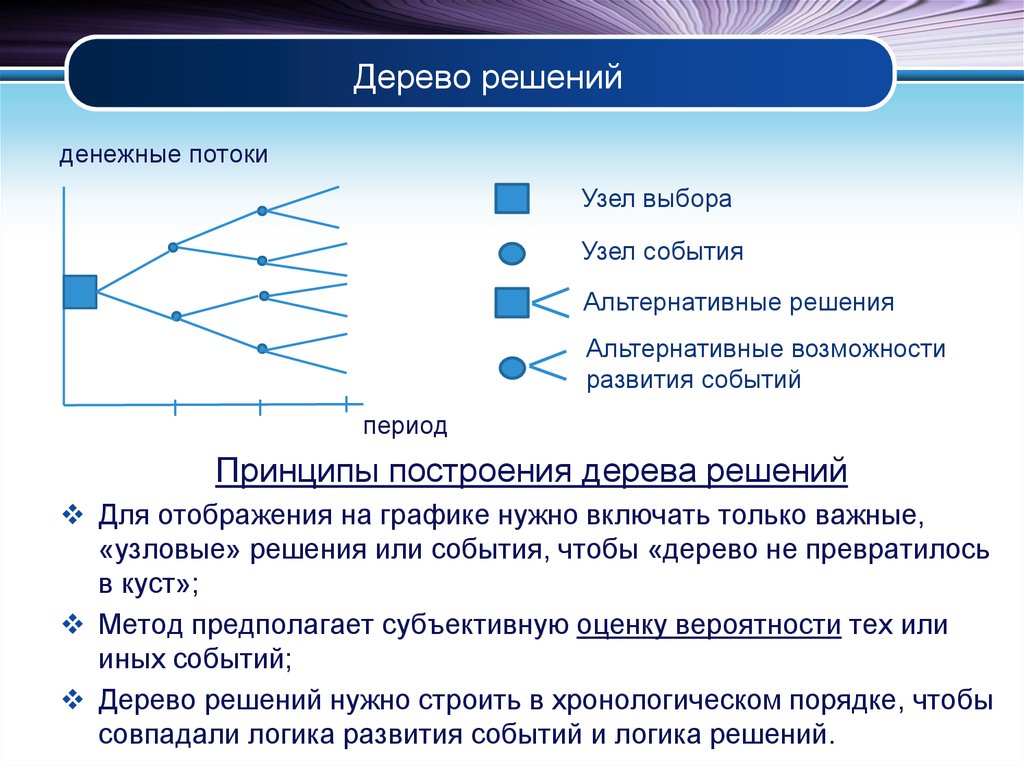 {2}\log(n_{samples}))$
{2}\log(n_{samples}))$
1.10.5. Советы по практическому использованию
- Деревья решений имеют тенденцию чрезмерно соответствовать данным с большим количеством функций. Получение правильного соотношения образцов к количеству функций важно, поскольку дерево с небольшим количеством образцов в многомерном пространстве, скорее всего, переоборудуется.
- Предварительно рассмотрите возможность уменьшения размерности (PCA, ICA, или Feature selection), чтобы дать вашему дереву больше шансов найти отличительные признаки.
- Понимание структуры дерева решений поможет лучше понять, как дерево решений делает прогнозы, что важно для понимания важных функций данных.
- Визуализируйте свое дерево во время тренировки с помощью
exportфункции. Используйтеmax_depth=3в качестве начальной глубины дерева, чтобы понять, насколько дерево соответствует вашим данным, а затем увеличьте глубину. - Помните, что количество образцов, необходимых для заполнения дерева, удваивается для каждого дополнительного уровня, до которого дерево растет.
 Используйте
Используйте max_depthдля управления размером дерева во избежание переобучения. - Используйте
min_samples_splitили,min_samples_leafчтобы гарантировать, что несколько выборок информируют каждое решение в дереве, контролируя, какие разделения будут учитываться. Очень маленькое число обычно означает, что дерево переоборудуется, тогда как большое число не позволяет дереву изучать данные. Попробуйтеmin_samples_leaf=5в качестве начального значения. Если размер выборки сильно различается, в этих двух параметрах можно использовать число с плавающей запятой в процентах. В то время какmin_samples_splitможет создавать произвольно маленькие листья,min_samples_leafгарантирует, что каждый лист имеет минимальный размер, избегая малодисперсных, чрезмерно подходящих листовых узлов в задачах регрессии. Для классификации с несколькими классамиmin_samples_leaf=1это часто лучший выбор.Обратите внимание, что
min_samples_splitвыборки рассматриваются напрямую и независимо от нихsample_weight, если они предусмотрены (например, узел с m взвешенными выборками по-прежнему обрабатывается как имеющий ровно m выборок). Рассмотрим
Рассмотрим min_weight_fraction_leafилиmin_impurity_decreaseесли учет образцов весов требуются при расколах. - Перед обучением сбалансируйте набор данных, чтобы дерево не смещалось в сторону доминирующих классов. Балансировка классов может быть выполнена путем выборки равного количества выборок из каждого класса или, предпочтительно, путем нормализации суммы весов выборок (
sample_weight) для каждого класса к одному и тому же значению. Также обратите внимание, что критерии предварительного отсечения на основе веса, такие какmin_weight_fraction_leaf, будут менее смещены в сторону доминирующих классов, чем критерии, которые не знают весов выборки, напримерmin_samples_leaf. - Если выборки взвешены, будет проще оптимизировать древовидную структуру, используя основанный на весе критерий предварительной отсечения, например
min_weight_fraction_leaf, который гарантирует, что конечные узлы содержат по крайней мере часть общей суммы весов выборки.
- Все деревья решений
np.float32внутренне используют массивы. Если данные обучения не в этом формате, будет сделана копия набора данных. - Если входная матрица X очень разреженная, рекомендуется преобразовать ее в разреженную
csc_matrixперед вызовом соответствия и разреженнуюcsr_matrixперед вызовом предсказания. Время обучения может быть на порядки меньше для входной разреженной матрицы по сравнению с плотной матрицей, когда функции имеют нулевые значения в большинстве выборок.
1.10.6. Алгоритмы дерева: ID3, C4.5, C5.0 и CART
Что представляют собой различные алгоритмы дерева решений и чем они отличаются друг от друга? Какой из них реализован в scikit-learn?
ID3 (Iterative Dichotomiser 3) был разработан Россом Куинланом в 1986 году. Алгоритм создает многостороннее дерево, находя для каждого узла (т. Е. Жадным образом) категориальный признак, который даст наибольший информационный выигрыш для категориальных целей.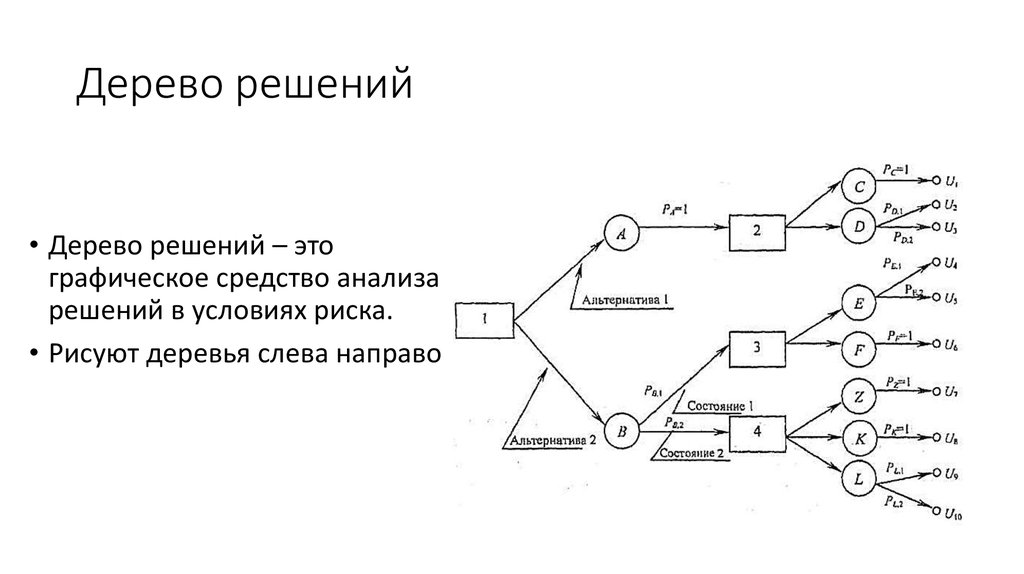 Деревья вырастают до максимального размера, а затем обычно применяется этап обрезки, чтобы улучшить способность дерева обобщать невидимые данные.
Деревья вырастают до максимального размера, а затем обычно применяется этап обрезки, чтобы улучшить способность дерева обобщать невидимые данные.
C4.5 является преемником ID3 и снял ограничение, что функции должны быть категориальными, путем динамического определения дискретного атрибута (на основе числовых переменных), который разбивает непрерывное значение атрибута на дискретный набор интервалов. C4.5 преобразует обученные деревья (т. Е. Результат алгоритма ID3) в наборы правил «если-то». Затем оценивается точность каждого правила, чтобы определить порядок, в котором они должны применяться. Удаление выполняется путем удаления предусловия правила, если без него точность правила улучшается.
C5.0 — это последняя версия Quinlan под частной лицензией. Он использует меньше памяти и создает меньшие наборы правил, чем C4.5, но при этом является более точным.
CART (Classification and Regression Trees — деревья классификации и регрессии) очень похож на C4.5, но отличается тем, что поддерживает числовые целевые переменные (регрессию) и не вычисляет наборы правил.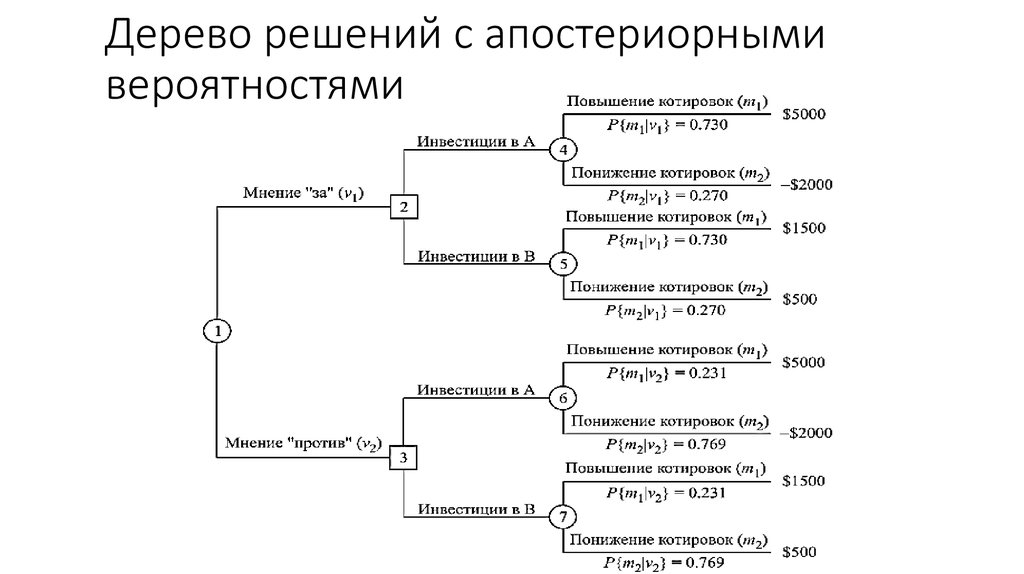 *)$ пока не будет достигнута максимально допустимая глубина, $N_m < \min_{samples}$ или же $N_m = 1$.
*)$ пока не будет достигнута максимально допустимая глубина, $N_m < \min_{samples}$ или же $N_m = 1$.
1.10.7.1. Критерии классификации
Если целью является результат классификации, принимающий значения 0,1,…, K-1, для узла m, позволять
$$p_{mk} = 1/ N_m \sum_{y \in Q_m} I(y = k)$$
быть пропорцией наблюдений класса k в узле m. Еслиmявляется конечным узлом, predict_proba для этого региона установлено значение $p_{mk}$. Общие меры примеси следующие.
Джини:
$$H(Q_m) = \sum_k p_{mk} (1 — p_{mk})$$
Энтропия:
$$H(Q_m) = — \sum_k p_{mk} \log(p_{mk})$$
Неверная классификация:
$$H(Q_m) = 1 — \max(p_{mk})$$
1.10.7.2. Критерии регрессии
Если целью является непрерывное значение, то для узла m, общими критериями, которые необходимо минимизировать для определения местоположений будущих разделений, являются среднеквадратичная ошибка (ошибка MSE или L2), отклонение Пуассона, а также средняя абсолютная ошибка (ошибка MAE или L1). 2$$
2$$
Половинное отклонение Пуассона:
$$H(Q_m) = \frac{1}{N_m} \sum_{y \in Q_m} (y \log\frac{y}{\bar{y}_m} — y + \bar{y}_m)$$
Настройка criterion="poisson" может быть хорошим выбором, если ваша цель — счетчик или частота (количество на какую-то единицу). В любом случае, y>=0 является необходимым условием для использования этого критерия. Обратите внимание, что он подходит намного медленнее, чем критерий MSE.
Средняя абсолютная ошибка:
$$median(y)m = \underset{y \in Q_m}{\mathrm{median}}(y)$$
$$H(Q_m) = \frac{1}{N_m} \sum{y \in Q_m} |y — median(y)_m|$$
Обратите внимание, что он подходит намного медленнее, чем критерий MSE.
1.10.8. Обрезка с минимальными затратами и сложностью
Сокращение с минимальными затратами и сложностью — это алгоритм, используемый для сокращения дерева во избежание чрезмерной подгонки, описанный в главе 3 [BRE] . Этот алгоритм параметризован $\alpha\ge0$ известный как параметр сложности. Параметр сложности используется для определения меры затрат и сложности, $R_\alpha(T)$ данного дерева $T$:
$$R_\alpha(T) = R(T) + \alpha|\widetilde{T}|$$
где $|\widetilde{T}|$ количество конечных узлов в $T$ а также $R(T)$ традиционно определяется как общий коэффициент ошибочной классификации конечных узлов. В качестве альтернативы scikit-learn использует взвешенную общую примесь конечных узлов для $R(T)$. Как показано выше, примесь узла зависит от критерия. Обрезка с минимальными затратами и сложностью находит поддеревоT что сводит к минимуму $R_\alpha(T)$.
В качестве альтернативы scikit-learn использует взвешенную общую примесь конечных узлов для $R(T)$. Как показано выше, примесь узла зависит от критерия. Обрезка с минимальными затратами и сложностью находит поддеревоT что сводит к минимуму $R_\alpha(T)$.
Оценка сложности стоимости одного узла составляет $R_\alpha(t)=R(t)+\alpha$. Ответвление $T_t$, определяется как дерево, в котором узел $t$ это его корень. В общем, примесь узла больше, чем сумма примесей его конечных узлов, $R(T_t)<R(t)$. Однако мера стоимости и сложности узла, $t$, и его ветвь, $T_t$, может быть равным в зависимости от $\alpha$. Определяем эффективныйα узла быть значением, где они равны, $R_\alpha(T_t)=R_\alpha(t)$ или же $\alpha_{eff}(t)=\frac{R(t)-R(T_t)}{|T|-1}$. Нетерминальный узел с наименьшим значением $\alpha_{eff}$ является самым слабым звеном и будет удалено. Этот процесс останавливается, когда обрезанное дерево минимально $\alpha_{eff}$ больше ccp_alpha параметра.
Примеры:
- Публикация деревьев решений об обрезке с сокращением сложности затрат
Рекомендации:
- BRE Л.
 Брейман, Дж. Фридман, Р. Олшен и К. Стоун. Деревья классификации и регрессии. Уодсворт, Белмонт, Калифорния, 1984.
Брейман, Дж. Фридман, Р. Олшен и К. Стоун. Деревья классификации и регрессии. Уодсворт, Белмонт, Калифорния, 1984. - https://en.wikipedia.org/wiki/Decision_tree_learning
- https://en.wikipedia.org/wiki/Predictive_analytics
- JR Quinlan. C4. 5: программы для машинного обучения. Морган Кауфманн, 1993.
- Т. Хасти, Р. Тибширани и Дж. Фридман. Элементы статистического обучения, Springer, 2009.
понятие, алгоритм работы, сферы применения метода
Что это такое? Дерево решений является весьма эффективной методикой, применяемой для анализа больших массивов данных. Инструмент работает по четкому алгоритму и в соответствии со строго определенными принципами.
Где применяется? Дерево решений как способ обработки имеющейся информации и одно из средств предсказательной аналитики используется во многих сферах человеческой деятельности: банковской и медицинской, предпринимательской и промышленной.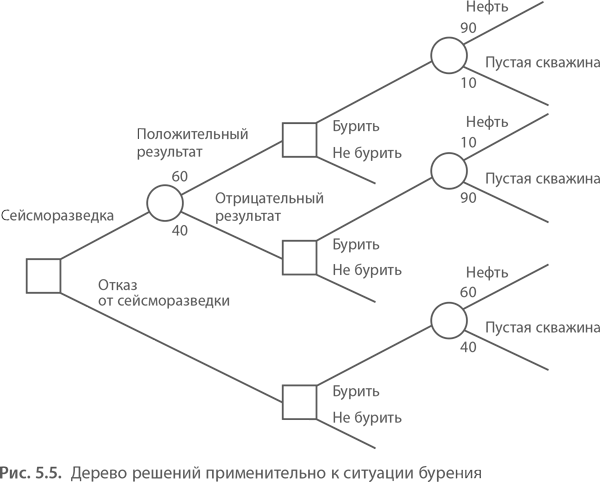 Часто инструмент бывает полезен в машинном обучении.
Часто инструмент бывает полезен в машинном обучении.
В статье рассказывается:
- Общее описание метода дерева решений
- Алгоритм работы инструмента
- Задачи, решаемые с помощью дерева методики
- Сферы применения инструмента
- Дерево решений в машинном обучении
- Этапы построения дерева решений
- Преимущества и недостатки методики
-
Пройди тест и узнай, какая сфера тебе подходит:
айти, дизайн или маркетинг.Бесплатно от Geekbrains
Общее описание метода дерева решений
Сама идея создания и дальнейшего развития моделей дерева решений появилась в середине XX века после исследований вероятного человеческого поведения киберсистемами. Работы К. Ховеленда «Компьютерное моделирование мышления» и Е. Ханта «Эксперименты по индукции» сыграли ведущую роль в развитии этого направления.
Дальнейшее увеличение популярности этому методу обеспечили работы Джона Р. Куинлена, который разработал алгоритм ID3 и его усовершенствованные модификации С4.5 и С5.0, а также Лео Бреймана, предложившего алгоритм CART и метод случайного леса.
Куинлена, который разработал алгоритм ID3 и его усовершенствованные модификации С4.5 и С5.0, а также Лео Бреймана, предложившего алгоритм CART и метод случайного леса.
Если говорить простыми словами, то дерево решений представляет собой задачу с несколькими вариантами действий. На карте прорабатываются возможные результаты каждого шага, а также следующие на них реакции. Этот метод особенно актуален в тех ситуациях, в которых нужно сделать вывод о ряде последовательных решений, ведущих к оптимальному исходу.
Общее описание метода дерева решенийАлгоритм работы инструмента
Дерево принятия решений — это метод, дающий представление о действиях и их последствиях в виде упорядоченной иерархии. Оно включает в себя элементы двух типов: узлы (node) и листья (leaf). Узлы представляют собой совокупность решающих правил и осуществляют проверку гипотетических ситуаций на соответствие выбранным показателям.
Если говорить проще, то примеры, которые попадают в узел, после прохождения проверки разделяются на два типа:
- Первый — те, которые подходят под назначенные правила.

- Второй — те, которые не подходят под назначенные правила.
Затем к каждому подтипу опять применяется правило, и процедура повторяется до тех пор, пока не произойдёт остановка алгоритма дерева решений. Последний узел, который больше не нуждается в проверке и разделении на подмножество, становится листом.
Лист представляет собой решение для примера, который в нём находится. Таким образом, там содержится не одно общее правило, а подмножество объектов, которые удовлетворяют всем правилам данной ветви. Ведь пример оказывается в листе, только если будет соответствовать всем установленным критериям на пути к нему. Очевидно, что к каждому листу ведёт только одна «дорога», что предполагает единственное верное решение и следование одному оптимальному алгоритму.
Задачи, решаемые с помощью методики
Задачи составления дерева решений заключаются в следующем:
- Классификация. Анализ предложенных объектов и решение о соответствии их определённому классу из заявленных ранее.
 При этом целевая переменная имеет дискретные задачи.
При этом целевая переменная имеет дискретные задачи. - Регрессия (численное предсказание). Прогнозирование конкретного числового значения независимой переменной для заданного вектора.
- Описание объектов. Позволяет ёмко и лаконично описывать объекты при помощи использования ряда конкретных правил.
Сферы применения
Огромное количество аналитических платформ включают в себя различные модули для построения деревьев решений. Этот метод анализа данных является очень удобным и позволяет выявить оптимальный алгоритм действий для решения заданной проблемы. Дерево решений, например, используется для составления готовых скриптов для общения с потребителями в сфере продаж товаров и услуг.
Сферы примененияРассмотрим следующую ситуацию: пользователь захотел оплатить услугу через приложение банка. Операция была отклонена. После этого клиент написал в службу поддержки банка для выяснения обстоятельств. Сотрудник, который ответит ему в чате, будет следовать определённому алгоритму. Для начала он спросит у клиента идентификатор платежа. В дальнейшем, согласно дереву решений, варианты общения будут разветвляться в зависимости от ответа на этот вопрос.
Для начала он спросит у клиента идентификатор платежа. В дальнейшем, согласно дереву решений, варианты общения будут разветвляться в зависимости от ответа на этот вопрос.
Отдел продаж также пользуется деревьями решений: менеджер задает клиенту вопросы и выстраивает своё дальнейшее общение с ним в зависимости от его ответов.
В общем, практически в любой службе поддержки или работы с клиентами пользуются деревьями решений, будь то интернет-провайдер или отдел претензий к качеству товара.
В статистике данный инструмент также очень полезен, ведь с его помощью можно прогнозировать ситуации и описывать данные, разделяя их на взаимосвязанные группы. Самой простой и популярной задачей, которая ставится перед деревом решений, является бинарная классификация. Она представляет собой деление заявленных примеров на два типа, один из которых является положительным (успех), а второй — отрицательным (неудача).
Топ-30 самых востребованных и высокооплачиваемых профессий 2023
Поможет разобраться в актуальной ситуации на рынке труда
Подборка 50+ ресурсов об IT-сфере
Только лучшие телеграм-каналы, каналы Youtube, подкасты, форумы и многое другое для того, чтобы узнавать новое про IT
ТОП 50+ сервисов и приложений от Geekbrains
Безопасные и надежные программы для работы в наши дни
pdf 3,7mb
doc 1,7mb
Уже скачали 20013
Например, метеорологам требуется составить прогноз о том, будет ли завтра дождь. Для анализа предлагаются данные о предшествующих пятидесяти днях. Чтобы составить дерево решений, нужно разделить все эти дни на две группы, которые будут соответствовать следующим значениям: 1 — на следующий день шёл дождь, 0 — на следующий день дождя не было.
Для анализа предлагаются данные о предшествующих пятидесяти днях. Чтобы составить дерево решений, нужно разделить все эти дни на две группы, которые будут соответствовать следующим значениям: 1 — на следующий день шёл дождь, 0 — на следующий день дождя не было.
Кроме того, анализируются все сопутствующие условия: влажность, атмосферное давление, направление ветра, средняя температура и т. д. Использование алгоритма дерева решений дает возможность выявить в общем объёме информации те условия, которые позволят разделить дни на предложенные два типа. Таким образом, будет выявлена ситуация, позволяющая максимально верно составить прогноз на следующий день.
Дерево решений в машинном обучении
Этот инструмент используется и при составлении автоматизированных моделей прогнозирования. Они активно применяются в машинном обучении. Применение дерева решений даёт возможность предсказать вероятную ценность объекта с учётом всей известной о нём информации.
Дерево решений в машинном обученииЭтот тип называется «дерево классификации». В данной схеме узлы представляют собой данные, а не решение. Каждая ветвь такого дерева содержит определённый набор правил, которые соответствуют выбранному классу.
В данной схеме узлы представляют собой данные, а не решение. Каждая ветвь такого дерева содержит определённый набор правил, которые соответствуют выбранному классу.
Такие правила принятия решений обычно выражаются в условии соответствия, которое кратко можно описать формулой «если — то». Условия формулируются отдельно по каждому решению или значению и прогнозируют вероятность определённого результата при соблюдении условий.
Любая дополнительная информация увеличивает достоверность прогнозирования того, насколько выбранный объект соответствует заявленным условиям. Полученные данные могут быть использованы для составления более масштабного дерева решений в выбранной области.
Точный инструмент «Колесо компетенций»
Для детального самоанализа по выбору IT-профессии
Список грубых ошибок в IT, из-за которых сразу увольняют
Об этом мало кто рассказывает, но это должен знать каждый
Мини-тест из 11 вопросов от нашего личного психолога
Вы сразу поймете, что в данный момент тормозит ваш успех
Регистрируйтесь на бесплатный интенсив, чтобы за 3 часа начать разбираться в IT лучше 90% новичков.
Только до 20 марта
Осталось 17 мест
Иногда применяется сразу несколько видов деревьев решений. Это позволяет наиболее точно предсказать результат и выявить оптимальный алгоритм для достижения желаемого итога. В качестве комбинированного подхода используются следующие методы:
- Бэггинг. Включает в себя создание нескольких деревьев решений для анализа повторной выборки исходных данных. На основе полученных результатов формулируется единое решение заданного вопроса.
- Метод случайного леса. В данном случае несколько деревьев применяются для увеличения количества успешно классифицированных объектов.
- Бустинг. Используется в отношении регрессионных и классификационных деревьев.
- Ротационный лес. Деревья решений выстраиваются на основе метода анализа главных компонентов (PCA) на случайной выборке данных.
Идеально составленное дерево решений должно выдавать максимум информации при минимальном количестве уровней.
В машинном обучении модель дерева решений используется особенно часто, так как она дает множество преимуществ. Этот инструмент экономически выгоден, так как затраты на его использование уменьшаются с каждой дополнительной точкой данных. Деревья решений позволяют анализировать как числовые, так и категориальные данные.
Кроме того, данный метод даёт возможность формировать вопросы с несколькими вероятными ответами. Он даёт максимально точные результаты даже при искажении предпосылок исходных данных.
Этапы построения дерева решений
Составление деревьев решений для машинного обучения и анализа давно автоматизировано. Для этого можно воспользоваться специальными библиотеками, созданными при помощи двух языков программирования: R и Python. В рамках Python существует бесплатная библиотека стандартных моделей машинного обучения scikit-learn, которая активно используется аналитиками для решения задач. В ней также существует возможность использования предподготовленного кода.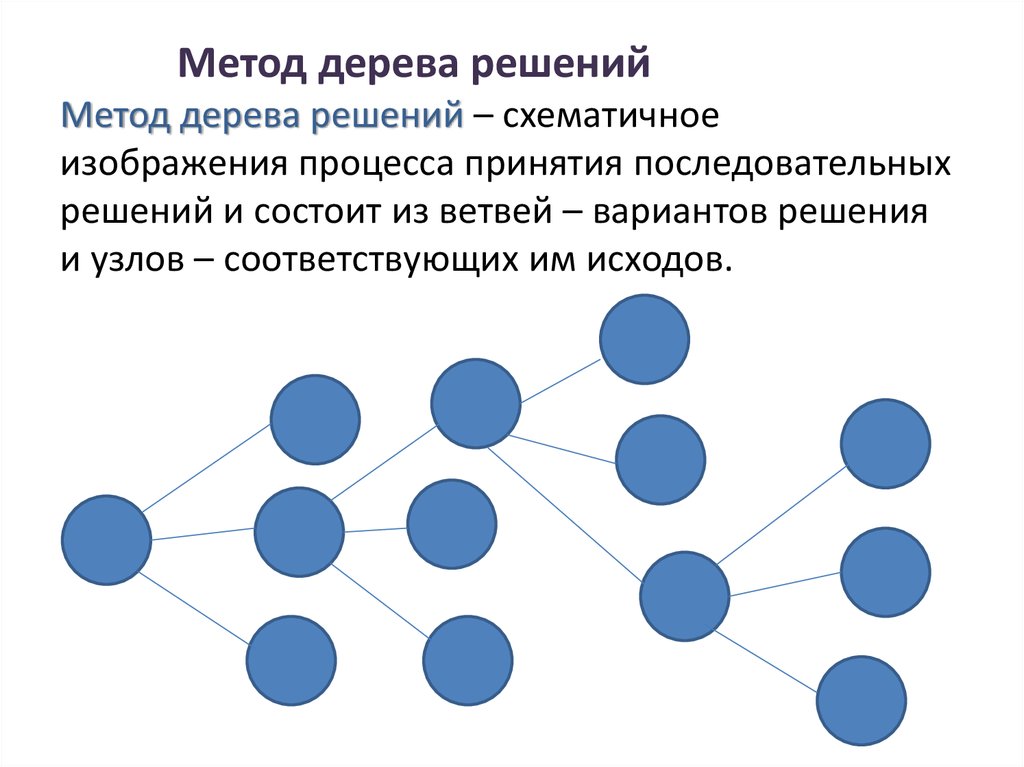
Для того чтобы составить дерево решений с помощью предподготовленного кода, необходимо выполнить следующие действия:
Сбор данных и их анализ
Сначала аналитики оценивают исходные данные и ищут в них общие закономерности. Затем они формируют ответ на вопрос о том, почему для решения данной задачи должен использоваться именно такой инструмент. Кроме того, на этом этапе вычисляются факторы, которые оказывают влияние на зависимую переменную.
Проведение предподготовки
На этом этапе специалисты очищают данные от аномалий. Это действие необходимо для того, чтобы представить информацию в нужном формате. Существуют специализированные алгоритмы для данной работы:
- Заполнение пропусков средними значениями.
- Нормирование показателей относительно друг друга.
- Удаление аномалий.
- Категоризация переменных данных.
Формирование отложенной выборки
Некоторую часть представленных данных необходимо проанализировать самостоятельно, чтобы определить ожидаемое значение для итогового результата.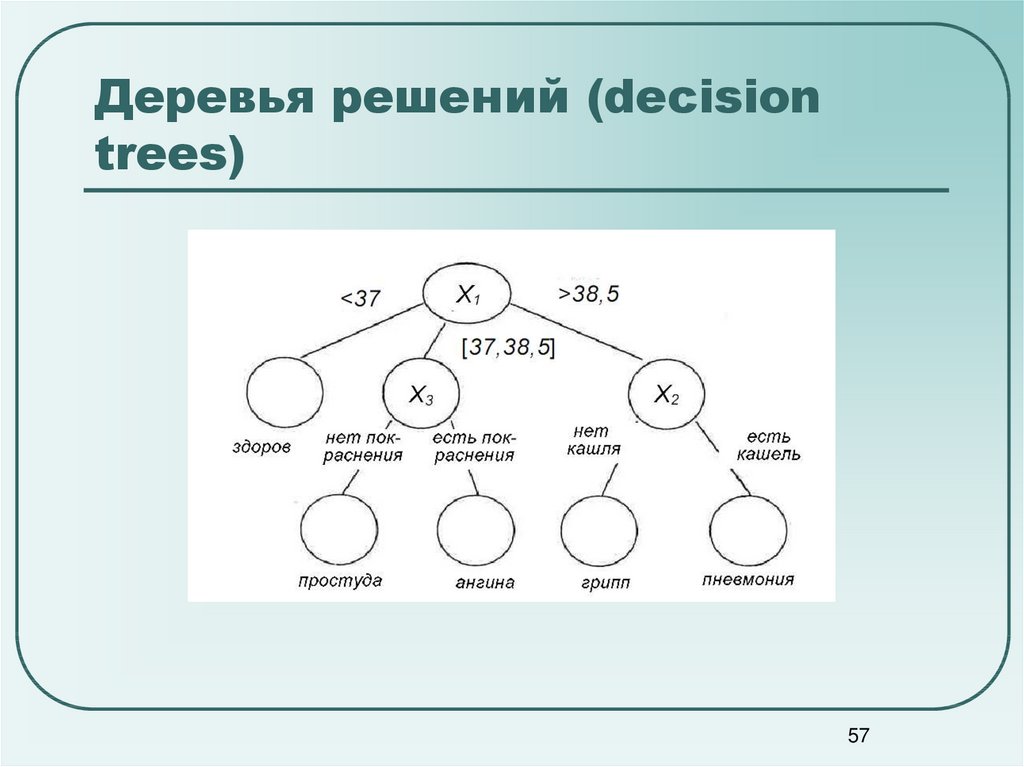 Это позволяет проверить качество работы алгоритма дерева решений при анализе ситуации, с которыми обученная модель ранее не сталкивалась.
Это позволяет проверить качество работы алгоритма дерева решений при анализе ситуации, с которыми обученная модель ранее не сталкивалась.
Составление дерева решений и начало обучение модели
Специалисты загружают в библиотеку необходимые данные и условия задачи. На основе представленной информации происходит автоматическая генерация правил работы дерева решений.
Сравнение результатов на обучающей и на отложенной выборке
Если результаты совпадают, значит, модель дерева решений обучена верно и пригодна для дальнейшей работы. В этом случае можно сохранить код обученной модели и применять его в будущем.
Преимущества и недостатки методики
Преимущества метода дерева решений:
- Правила создания таких моделей просты и понятны, а интерпретировать полученные результаты легко.
- Есть возможность работать с разными видами переменных.
- Деревья решений допускают пропуски данных и способны заполнять их наиболее вероятным в данной ситуации значением.

- Этот инструмент помогает выявить, какие данные наиболее важны для достижения нужного результата.
- Деревья решений способны самостоятельно формировать правила в малознакомых специалисту областях.
- Их легко визуализировать, что позволяет воспринимать не только модель в целом, но и прогнозировать результат для отдельных субъектов в дереве.
- Не требуют большого количества изначально заданных параметров.
- Способны работать с категориальными и числовыми идентификаторами.
- Позволяют быстро решить проблему благодаря качественному прогнозированию результата.
Но данный метод имеет не только преимущества, но и недостатки, которые тоже необходимо учитывать при работе с ним:
- В задачах на классификацию объектов существует вероятность ошибок. Это связано с большим количеством классов при маленьком числе обучающих примеров.
- Важно учитывать то, что изменения параметров в одном узле дерева решений может привести к полному изменению всей его структуры.

- Составление дерева решений может быть весьма трудоёмким. Это связано с тем, что в каждом узле каждый элемент должен анализироваться до тех пор, пока не станет возможным принятие наилучшего возможного в данной ситуации решения.
Несмотря на ряд недостатков, создание дерева решений является очень востребованной методикой. Она актуальна в различных ситуациях и способна сослужить хорошую службу. Если вы являетесь новичком в данной сфере, то попробуйте начать с небольших задач. Постепенно вы наберетесь опыта и сможете грамотно использовать этот инструмент для работы с более глобальными вопросами.
Продвижение блога — Генератор продаж
Рейтинг: 5
( голосов 1 )
Поделиться статьей
Что такое дерево решений
Деревья решений
Дерево решений — это непараметрический контролируемый алгоритм обучения, который используется как для задач классификации, так и для задач регрессии.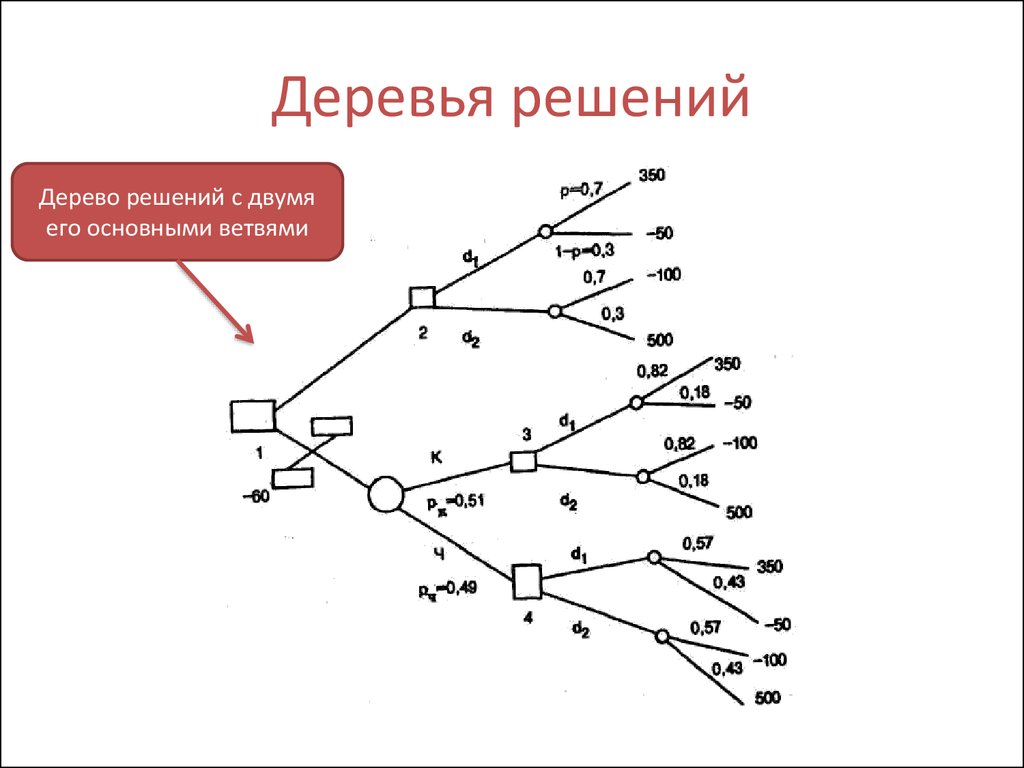 Он имеет иерархическую древовидную структуру, которая состоит из корневого узла, ветвей, внутренних узлов и конечных узлов.
Он имеет иерархическую древовидную структуру, которая состоит из корневого узла, ветвей, внутренних узлов и конечных узлов.
Как видно из диаграммы выше, дерево решений начинается с корневого узла, который не имеет входящих ветвей. Исходящие ветви от корневого узла затем направляются во внутренние узлы, также известные как узлы принятия решений. На основе доступных функций оба типа узлов выполняют оценку для формирования однородных подмножеств, которые обозначаются конечными узлами или конечными узлами. Листовые узлы представляют все возможные результаты в наборе данных. В качестве примера, давайте представим, что вы пытаетесь оценить, стоит ли вам заниматься серфингом, вы можете использовать следующие правила принятия решений, чтобы сделать выбор:
Этот тип структуры блок-схемы также создает легкое для восприятия представление о принятии решений, позволяя различным группам в организации лучше понять, почему было принято решение.
Изучение дерева решений использует стратегию «разделяй и властвуй» путем проведения жадного поиска для определения оптимальных точек разделения в дереве. Затем этот процесс разделения повторяется рекурсивно сверху вниз до тех пор, пока все или большинство записей не будут отнесены к определенным меткам классов. Классифицируются ли все точки данных как однородные наборы, во многом зависит от сложности дерева решений. Меньшие деревья легче могут получить чистые листовые узлы, т.е. точки данных в одном классе. Однако по мере роста дерева становится все труднее поддерживать эту чистоту, и это обычно приводит к тому, что в данное поддерево попадает слишком мало данных. Когда это происходит, это называется фрагментацией данных и часто может привести к переоснащению. В результате деревья решений отдают предпочтение маленьким деревьям, что согласуется с принципом экономии в бритве Оккама; то есть «сущности не должны умножаться сверх необходимости». Иными словами, деревья решений должны усложнять только в случае необходимости, поскольку самое простое объяснение часто является лучшим. Чтобы уменьшить сложность и предотвратить переоснащение, обычно используется обрезка; это процесс, который удаляет ветви, разделяющиеся на объекты с низкой важностью.
Затем этот процесс разделения повторяется рекурсивно сверху вниз до тех пор, пока все или большинство записей не будут отнесены к определенным меткам классов. Классифицируются ли все точки данных как однородные наборы, во многом зависит от сложности дерева решений. Меньшие деревья легче могут получить чистые листовые узлы, т.е. точки данных в одном классе. Однако по мере роста дерева становится все труднее поддерживать эту чистоту, и это обычно приводит к тому, что в данное поддерево попадает слишком мало данных. Когда это происходит, это называется фрагментацией данных и часто может привести к переоснащению. В результате деревья решений отдают предпочтение маленьким деревьям, что согласуется с принципом экономии в бритве Оккама; то есть «сущности не должны умножаться сверх необходимости». Иными словами, деревья решений должны усложнять только в случае необходимости, поскольку самое простое объяснение часто является лучшим. Чтобы уменьшить сложность и предотвратить переоснащение, обычно используется обрезка; это процесс, который удаляет ветви, разделяющиеся на объекты с низкой важностью.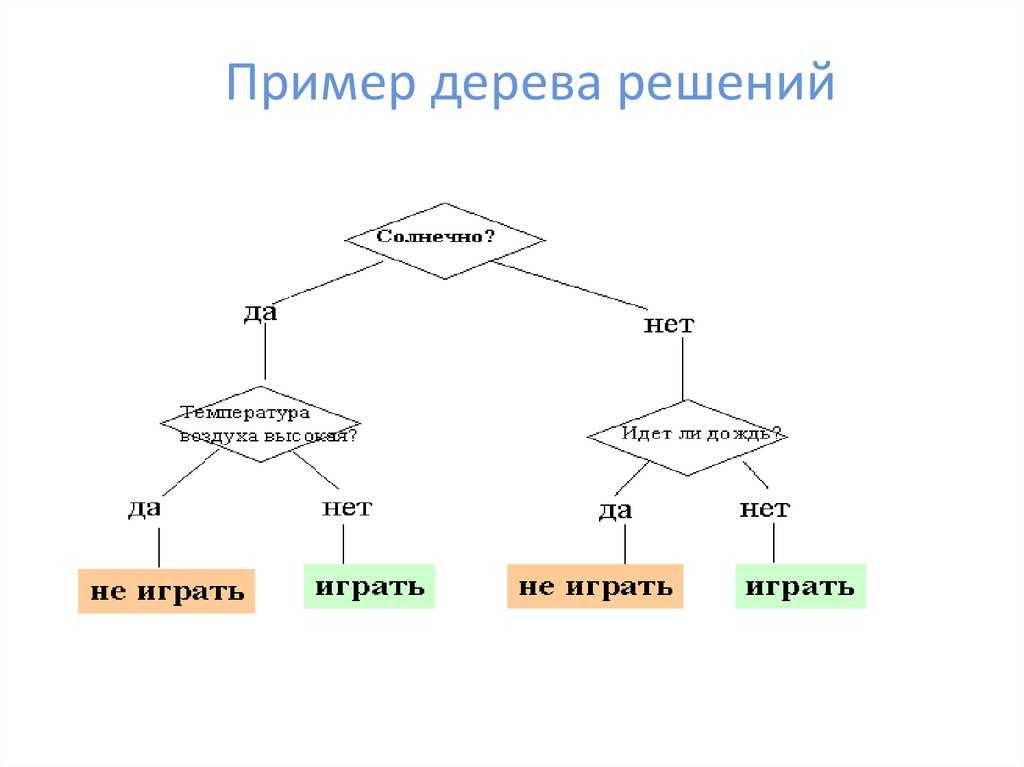 Затем соответствие модели можно оценить в процессе перекрестной проверки. Другой способ, которым деревья решений могут поддерживать свою точность, — это формирование ансамбля с помощью алгоритма случайного леса; этот классификатор предсказывает более точные результаты, особенно когда отдельные деревья не коррелируют друг с другом.
Затем соответствие модели можно оценить в процессе перекрестной проверки. Другой способ, которым деревья решений могут поддерживать свою точность, — это формирование ансамбля с помощью алгоритма случайного леса; этот классификатор предсказывает более точные результаты, особенно когда отдельные деревья не коррелируют друг с другом.
Типы деревьев решений
Алгоритм Ханта, разработанный в 1960-х годах для моделирования человеческого обучения в психологии, формирует основу многих популярных алгоритмов дерева решений, таких как: является сокращением от «Итеративный дихотомайзер 3». Этот алгоритм использует энтропию и прирост информации в качестве метрик для оценки расщеплений-кандидатов. Некоторые из исследований Куинлана по этому алгоритму от 1986 можно найти здесь (PDF, 1,4 МБ) (ссылка находится за пределами ibm.com).
— C4.5: Этот алгоритм считается более поздней итерацией ID3, который также был разработан Куинланом.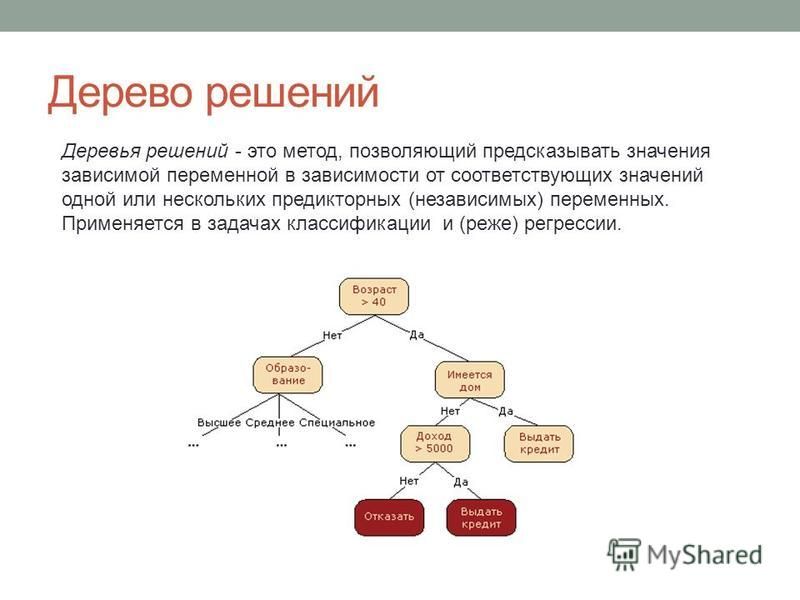 Он может использовать прирост информации или коэффициент усиления для оценки точек разделения в деревьях решений.
Он может использовать прирост информации или коэффициент усиления для оценки точек разделения в деревьях решений.
— CART: Термин CART является аббревиатурой для «деревьев классификации и регрессии» и был введен Лео Брейманом. Этот алгоритм обычно использует примесь Джини для определения идеального атрибута для разделения. Примесь Джини измеряет, как часто случайно выбранный атрибут неправильно классифицируется. При оценке с использованием примеси Джини более низкое значение является более идеальным.
Как выбрать лучший атрибут в каждом узле
Хотя существует несколько способов выбора наилучшего атрибута в каждом узле, два метода, прирост информации и примесь Джини, действуют как популярные критерии разделения для моделей дерева решений. Они помогают оценить качество каждого условия тестирования и то, насколько хорошо оно сможет классифицировать образцы по классам.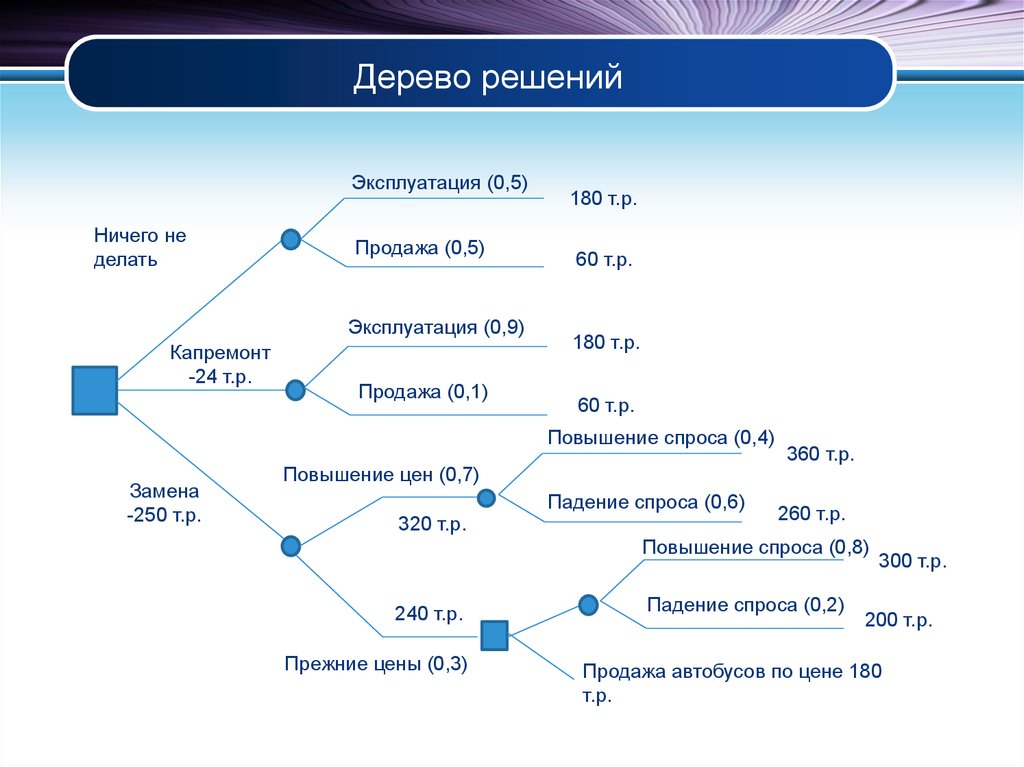
Энтропия и прирост информации
Трудно объяснить получение информации без обсуждения энтропии. Энтропия — это концепция, вытекающая из теории информации, которая измеряет нечистоту выборочных значений. Он определяется по следующей формуле, где:
- S представляет набор данных, для которого рассчитывается энтропия
- c представляет классы в наборе, S
- p(c) представляет долю точек данных, принадлежащих классу c, к общему количеству точек данных в наборе, S
Значения энтропии могут находиться в диапазоне от 0 до 1. Если все выборки в наборе данных S принадлежат одному классу, то энтропия будет равна нулю. Если половина выборок относится к одному классу, а другая половина — к другому классу, энтропия будет максимальной, равной 1. Чтобы выбрать лучший признак для разделения и найти оптимальное дерево решений, атрибут с наименьшим следует использовать количество энтропии. Прирост информации представляет собой разницу в энтропии до и после разделения по данному атрибуту.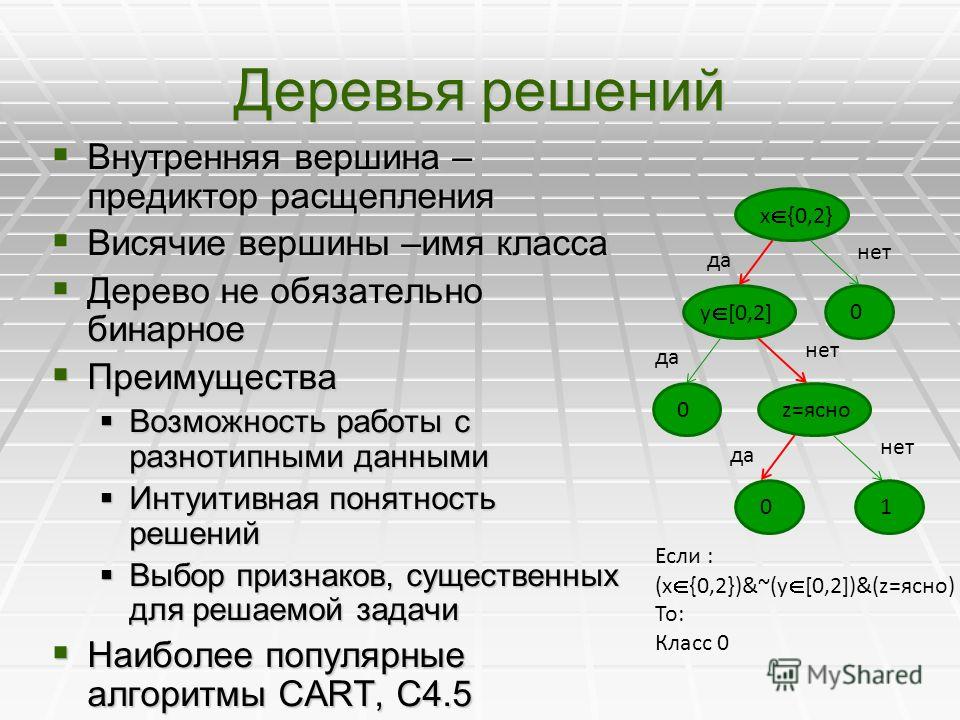 Атрибут с наибольшим приростом информации даст наилучшее разделение, поскольку он лучше всего справляется с классификацией обучающих данных в соответствии с его целевой классификацией. Прирост информации обычно представляется следующей формулой, где:
Атрибут с наибольшим приростом информации даст наилучшее разделение, поскольку он лучше всего справляется с классификацией обучающих данных в соответствии с его целевой классификацией. Прирост информации обычно представляется следующей формулой, где:
- a представляет определенный атрибут или метку класса
- Entropy(S) — энтропия набора данных, S
- |Зв|/ |С| представляет пропорцию значений в S и к количеству значений в наборе данных, S
- Энтропия (S v ) — энтропия набора данных, S v
Давайте рассмотрим пример, чтобы закрепить эти понятия. Представьте, что у нас есть следующий произвольный набор данных:
Для этого набора данных энтропия равна 0,94. Это можно рассчитать, найдя долю дней, когда «Играть в теннис» — «Да», что составляет 9/14, и долю дней, когда «Играть в теннис» — «Нет», что составляет 5/14. Затем эти значения можно подставить в приведенную выше формулу энтропии.
Энтропия (теннис) = -(9/14) log2(9/14) – (5/14) log2 (5/14) = 0,94
Затем мы можем вычислить прирост информации для каждого из атрибутов в отдельности. Например, прирост информации для атрибута «Влажность» будет следующим:
Коэффициент усиления (теннис, влажность) = (0,94)-(7/14)*(0,985) – (7/14)*(0,592) = 0,151 доля значений, где влажность равна «высокой», к общему количеству значений влажности. В этом случае количество значений, в которых влажность равна «высокой», равно количеству значений, в которых влажность равна «нормальной».
— 0,985 — энтропия при влажности = «высокая»
— 0,59 — энтропия при влажности = «нормальная»
Затем повторите расчет прироста информации для каждого атрибута в приведенной выше таблице и выберите атрибут с наибольшим приростом информации в качестве первой точки разделения в дереве решений. В этом случае Outlook дает наибольший прирост информации. Оттуда процесс повторяется для каждого поддерева.
Примесь Джини
Примесь Джини — это вероятность неправильной классификации случайных точек данных в наборе данных, если они были помечены на основе распределения классов набора данных.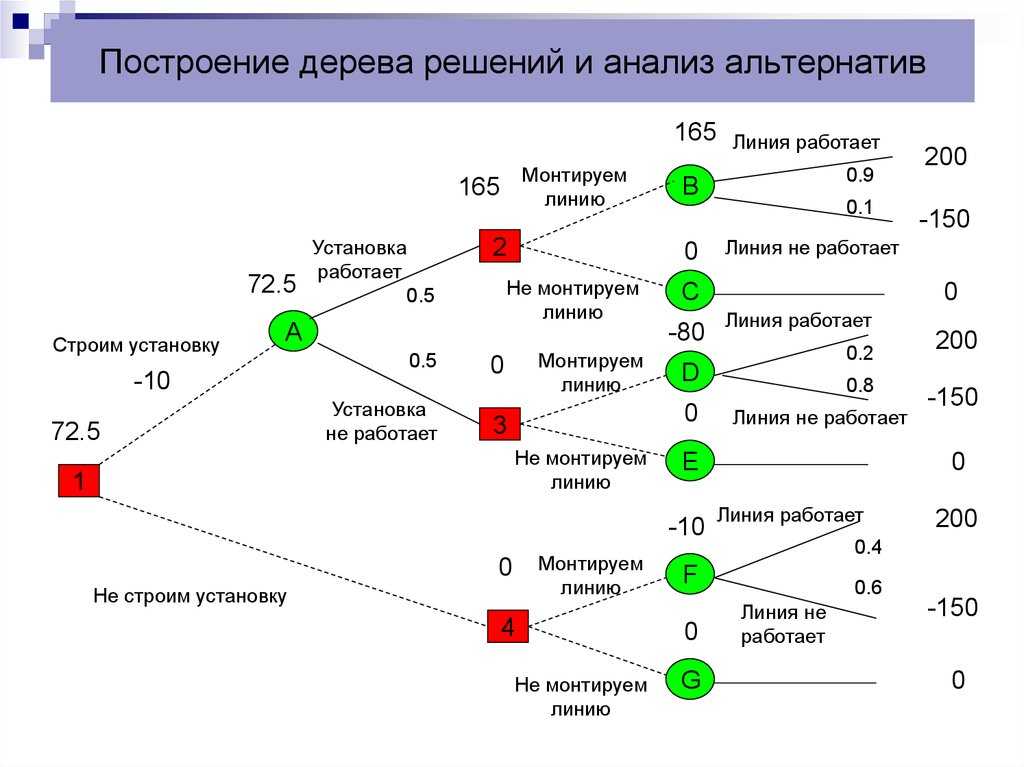 Подобно энтропии, если набор S является чистым, т.е. принадлежащий одному классу), то его примесь равна нулю. Это обозначается следующей формулой:
Подобно энтропии, если набор S является чистым, т.е. принадлежащий одному классу), то его примесь равна нулю. Это обозначается следующей формулой:
Преимущества и недостатки деревьев решений
Хотя деревья решений можно использовать в различных случаях, другие алгоритмы обычно превосходят алгоритмы деревьев решений. Тем не менее, деревья решений особенно полезны для задач интеллектуального анализа данных и поиска знаний. Давайте рассмотрим основные преимущества и проблемы использования деревьев решений ниже:
Преимущества — Простота интерпретации: Булева логика и визуальное представление деревьев решений упрощают их понимание и использование. Иерархическая природа дерева решений также позволяет легко увидеть, какие атрибуты являются наиболее важными, что не всегда понятно с другими алгоритмами, такими как нейронные сети.
— Подготовка данных практически не требуется: Деревья решений обладают рядом характеристик, которые делают его более гибким, чем другие классификаторы. Он может обрабатывать различные типы данных, т.е. дискретные или непрерывные значения, а непрерывные значения могут быть преобразованы в категориальные значения с помощью порогов. Кроме того, он также может обрабатывать значения с отсутствующими значениями, что может быть проблематичным для других классификаторов, таких как наивный байесовский метод.
— Более гибкий: Деревья решений можно использовать как для задач классификации, так и для задач регрессии, что делает его более гибким, чем некоторые другие алгоритмы. Он также нечувствителен к лежащим в основе отношениям между атрибутами; это означает, что если две переменные сильно коррелированы, алгоритм выберет только одну из функций для разделения.
Недостатки — Склонность к переоснащению: Сложные деревья решений склонны к переоснащению и плохо обобщают новые данные.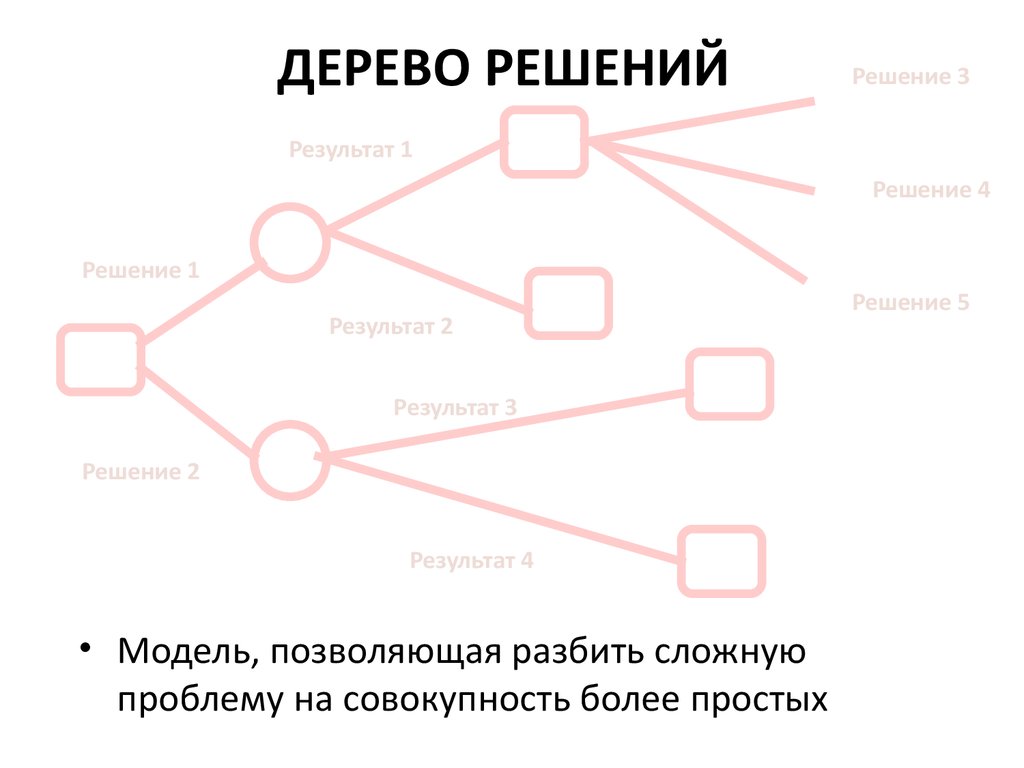 Этого сценария можно избежать с помощью процессов предварительной обрезки или последующей обрезки. Предварительная обрезка останавливает рост дерева при недостатке данных, а постобрезка удаляет поддеревья с неадекватными данными после построения дерева.
Этого сценария можно избежать с помощью процессов предварительной обрезки или последующей обрезки. Предварительная обрезка останавливает рост дерева при недостатке данных, а постобрезка удаляет поддеревья с неадекватными данными после построения дерева.
— Оценщики с высокой дисперсией: Небольшие вариации в данных могут привести к совершенно другому дереву решений. Бэггинг или усреднение оценок может быть методом уменьшения дисперсии деревьев решений. Однако этот подход ограничен, поскольку он может привести к сильно коррелированным предикторам.
— Дороже: Учитывая, что деревья решений используют жадный поиск во время построения, их обучение может быть более дорогим по сравнению с другими алгоритмами.
— Не полностью поддерживается в scikit-learn: Scikit-learn — это популярная библиотека машинного обучения на основе Python. Хотя в этой библиотеке есть модуль дерева решений (DecisionTreeClassifier, ссылка находится за пределами ibm. com), текущая реализация не поддерживает категориальные переменные.
com), текущая реализация не поддерживает категориальные переменные.
Деревья решений и IBM
IBM SPSS Modeler — это инструмент интеллектуального анализа данных, который позволяет разрабатывать прогностические модели для развертывания их в бизнес-операциях. Разработанный на основе модели CRISP-DM, являющейся отраслевым стандартом, IBM SPSS Modeler поддерживает весь процесс интеллектуального анализа данных, от обработки данных до улучшения бизнес-результатов.
Деревья решений IBM SPSS содержат визуальную классификацию и деревья решений, которые помогают вам представлять результаты по категориям и более четко объяснять анализ нетехнической аудитории. Создавайте модели классификации для сегментации, стратификации, прогнозирования, сокращения данных и скрининга переменных.
Чтобы получить дополнительную информацию об инструментах и решениях IBM для интеллектуального анализа данных, подпишитесь на IBMid и создайте учетную запись IBM Cloud сегодня.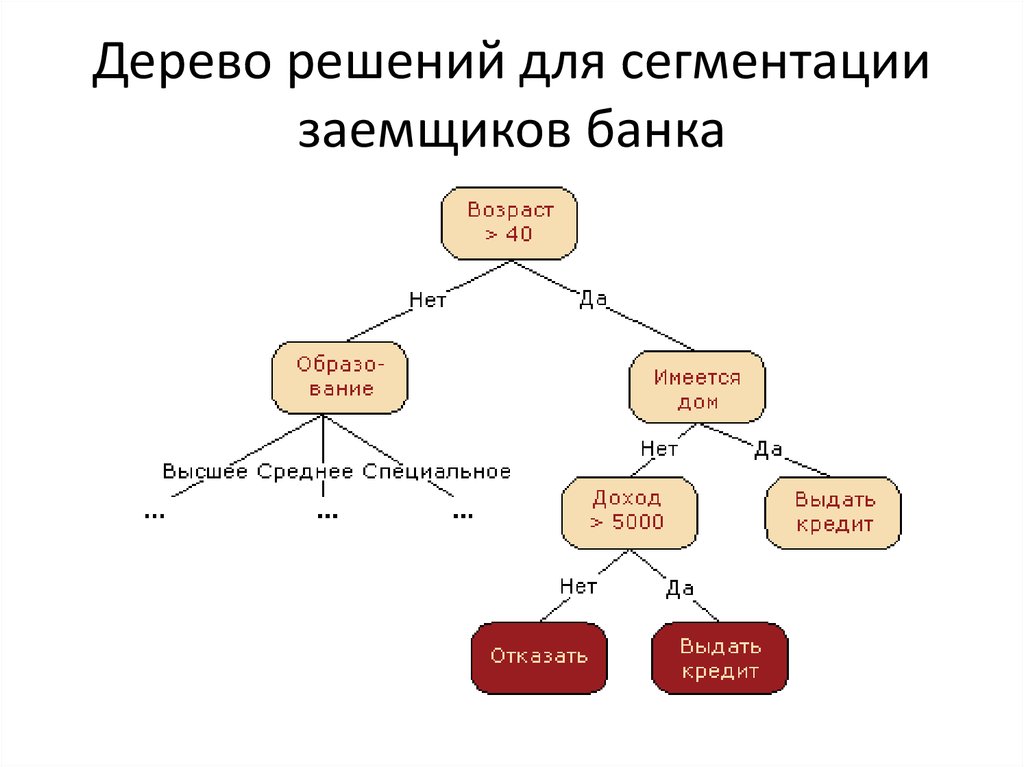
Связанные решения
IBM SPSS Modeler
IBM SPSS Modeler — это инструмент интеллектуального анализа данных, который позволяет разрабатывать прогностические модели для развертывания их в бизнес-операциях. Разработанный на основе модели CRISP-DM, являющейся отраслевым стандартом, IBM SPSS Modeler поддерживает весь процесс интеллектуального анализа данных, от обработки данных до улучшения бизнес-результатов.
Деревья решений IBM SPSS
IBM SPSS Decision Trees предлагает визуальную классификацию и деревья решений, которые помогают вам представлять результаты по категориям и более четко объяснять анализ нетехнической аудитории. Создавайте модели классификации для сегментации, стратификации, прогнозирования, сокращения данных и скрининга переменных.
Создавайте модели классификации для сегментации, стратификации, прогнозирования, сокращения данных и скрининга переменных.
Ресурсы
Узнайте больше о решениях IBM для интеллектуального анализа данных
Чтобы получить дополнительную информацию об инструментах и решениях IBM для интеллектуального анализа данных, подпишитесь на IBMid и создайте учетную запись IBM Cloud уже сегодня. Завести аккаунтДеревья решений для принятия решений
Обучение на испанском языке
Ler em português
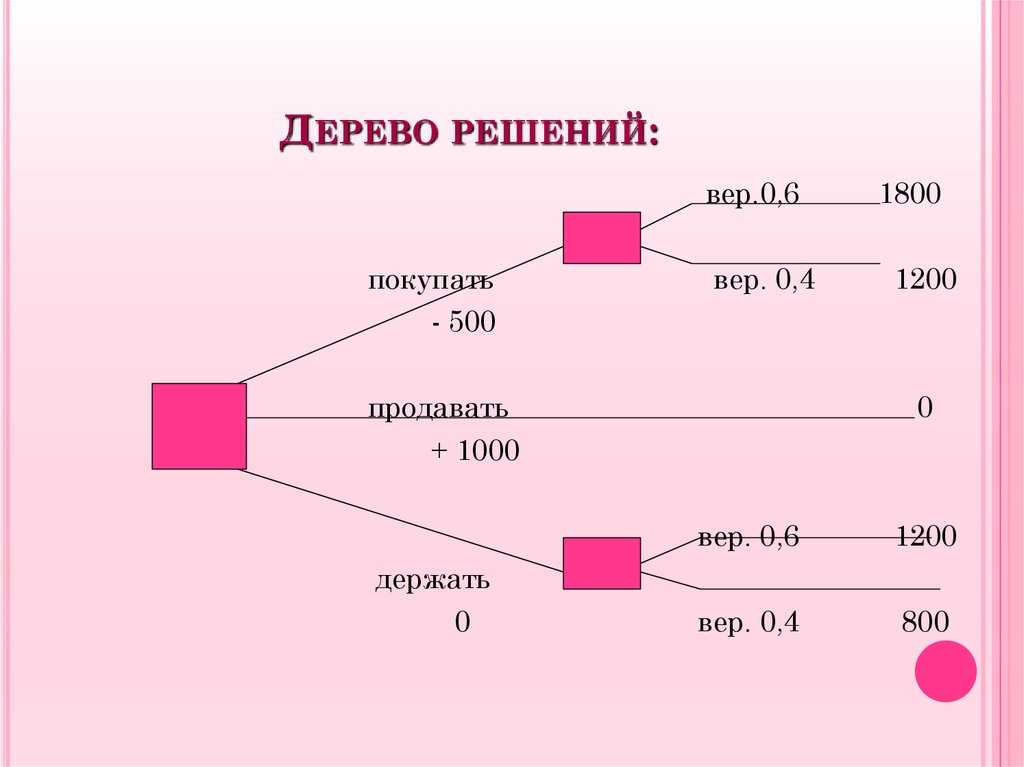
Руководство компании, которую я назову Stygian Chemical Industries, Ltd., должно решить, строить ли небольшой или крупный завод для производства нового продукта с ожидаемым рыночным сроком службы 10 лет. Решение зависит от размера рынка продукта.
Возможно, спрос будет высоким в течение первых двух лет, но, если многие первоначальные пользователи сочтут продукт неудовлетворительным, впоследствии он упадет до низкого уровня. Или высокий первоначальный спрос может указывать на возможность устойчивого рынка с большим объемом. Если спрос будет высоким, а компания не будет расширяться в течение первых двух лет, обязательно будет представлена конкурентоспособная продукция.
Если компания строит большой завод, она должна жить с ним независимо от размера рыночного спроса. Если он строит небольшой завод, у руководства есть возможность расширить завод через два года, если спрос будет высоким в течение вводного периода; в случае, если спрос будет низким в течение вводного периода, компания продолжит работу на небольшом заводе и получит приличную прибыль от небольшого объема.
Руководство не знает, что делать. Компания быстро росла в 1950-е годы; она шла в ногу с химической промышленностью в целом. Новый продукт, если рынок окажется большим, дает нынешнему руководству шанс подтолкнуть компанию к новому периоду прибыльного роста. Отдел разработки, в частности инженер-проектировщик, настаивает на строительстве крупномасштабного завода, чтобы использовать первую крупную разработку продукта, которую отдел произвел за несколько лет.
Отдел разработки, в частности инженер-проектировщик, настаивает на строительстве крупномасштабного завода, чтобы использовать первую крупную разработку продукта, которую отдел произвел за несколько лет.
Председатель совета директоров, главный акционер, опасается, что производственные мощности могут оказаться ненужными. Он выступает за меньший размер завода, но признает, что последующее расширение для удовлетворения больших объемов спроса потребует больше инвестиций и будет менее эффективным в эксплуатации. Председатель также признает, что если компания не примет срочных мер для удовлетворения растущего спроса, у конкурентов возникнет соблазн перейти на рынок с эквивалентными продуктами.
Проблема Stygian Chemical, как бы она ни была упрощена, иллюстрирует неопределенности и проблемы, которые бизнес-менеджмент должен решать при принятии инвестиционных решений. (Я использую термин «инвестиции» в широком смысле, имея в виду затраты не только на новые заводы и оборудование, но и на крупные, рискованные заказы, специальные маркетинговые услуги, исследовательские программы и другие цели. ) Эти решения приобретают все большее значение в в то же время, что они увеличиваются в сложности. Бесчисленное количество руководителей хотят сделать их лучше, но как?
) Эти решения приобретают все большее значение в в то же время, что они увеличиваются в сложности. Бесчисленное количество руководителей хотят сделать их лучше, но как?
В этой статье я представлю одну недавно разработанную концепцию под названием «дерево решений», которая обладает огромным потенциалом в качестве инструмента для принятия решений. Дерево решений может прояснить для руководства, как никакой другой известный мне аналитический инструмент, выбор, риски, цели, денежную прибыль и информационные потребности, связанные с инвестиционной проблемой. В ближайшие годы мы еще много услышим о деревьях решений. Несмотря на то, что сегодня они являются новинкой для большинства деловых людей, они, несомненно, войдут в обычную управленческую терминологию еще до того, как пройдет много лет.
Позже в этой статье мы вернемся к проблеме, стоящей перед Stygian Chemical, и посмотрим, как руководство может решить ее, используя деревья решений. Однако сначала более простой пример проиллюстрирует некоторые характеристики подхода дерева решений.
Отображение альтернатив
Предположим, субботнее утро довольно пасмурное, а после обеда 75 человек пришли выпить коктейли. У вас есть красивый сад, и ваш дом не слишком велик, поэтому, если позволяет погода, вы хотели бы устроить в саду прохладительные напитки и устроить там вечеринку. Было бы и приятнее, и вашим гостям было бы удобнее. С другой стороны, если вы устроите вечеринку в саду, а после того, как все гости соберутся, пойдет дождь, угощение будет испорчено, ваши гости промокнут, и вы от души пожалеете, что решили устроить вечеринку. в доме. (Мы могли бы усложнить эту проблему, рассмотрев возможность частичной приверженности тому или иному курсу и возможность корректировать оценки погоды в течение дня, но нам нужна простая проблема.)
Это конкретное решение может быть представлено в виде таблицы «выигрышей»:
Гораздо более сложные вопросы, связанные с принятием решений, могут быть представлены в виде таблицы выплат. Однако, особенно для сложных инвестиционных решений, другое представление информации, относящейся к проблеме, — дерево решений — полезно, чтобы показать пути достижения различных возможных результатов. Пьер Массе, генеральный комиссар Национального агентства по планированию производительности и оборудования во Франции, отмечает:
Пьер Массе, генеральный комиссар Национального агентства по планированию производительности и оборудования во Франции, отмечает:
Проблема принятия решения не ставится ни в терминах изолированного решения (поскольку сегодняшнее решение зависит от того, которое мы примем завтра), ни в терминах последовательности решений (поскольку в условиях неопределенности решения, принимаемые в будущем, будут зависеть от того, что мы научились за это время). Задача ставится в виде дерева решений.
В приложении I показано дерево решений для задачи о коктейльной вечеринке. Это дерево представляет собой другой способ отображения той же информации, что и в таблице выплат. Однако, как покажут более поздние примеры, в сложных решениях дерево решений часто является гораздо более ясным средством представления соответствующей информации, чем таблица выигрышей.
Дерево состоит из ряда узлов и ветвей. В первом узле слева у хоста есть выбор: провести вечеринку внутри или снаружи. Каждая ветвь представляет альтернативный образ действий или решение. В конце каждой ветви или альтернативного пути находится еще один узел, представляющий случайное событие — будет дождь или нет. Каждый последующий альтернативный ход вправо представляет собой альтернативный исход этого случайного события. С каждым полным альтернативным ходом в дереве связан выигрыш, показанный в конце самой правой или конечной ветви хода.
Каждая ветвь представляет альтернативный образ действий или решение. В конце каждой ветви или альтернативного пути находится еще один узел, представляющий случайное событие — будет дождь или нет. Каждый последующий альтернативный ход вправо представляет собой альтернативный исход этого случайного события. С каждым полным альтернативным ходом в дереве связан выигрыш, показанный в конце самой правой или конечной ветви хода.
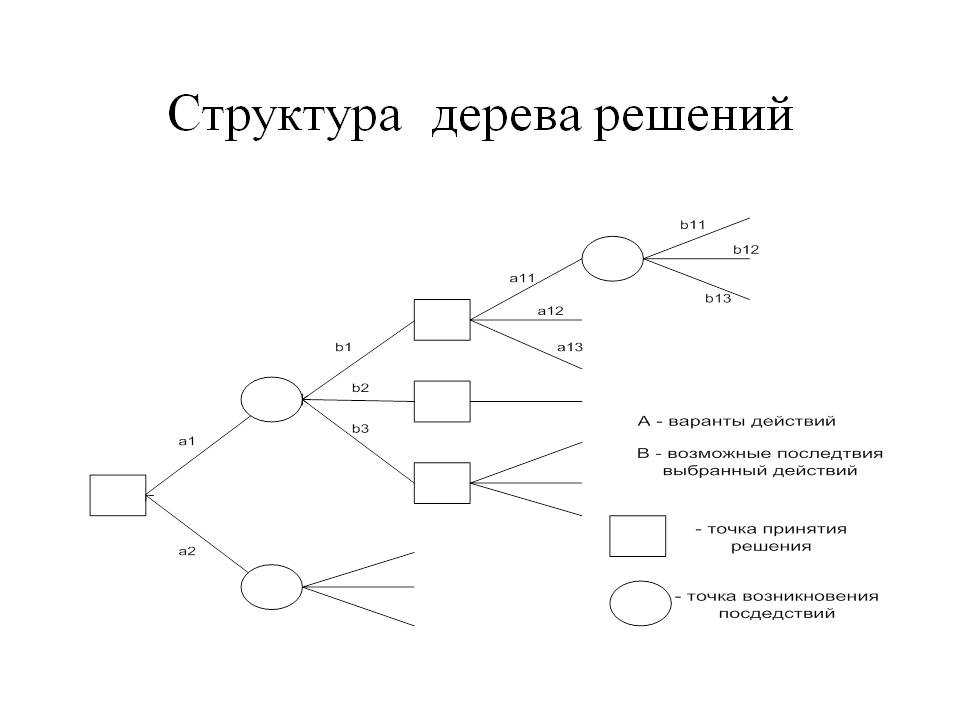
Когда я рисую деревья решений, мне нравится обозначать ответвления действий или решений квадратными узлами, а ответвления случайных событий — круглыми. Вместо этого могут использоваться другие символы, такие как однострочные и двухстрочные ответвления, специальные буквы или цвета. Не так важно, какой метод различения вы используете, пока вы используете тот или иной. Дерево решений любого размера всегда будет сочетать (a) действия вариантов выбора с (b) различными возможными событиями или результаты действий, на которые частично повлияли случайность или другие неконтролируемые обстоятельства.
Цепочки событий-решений.
Предыдущий пример, хотя и включает только один этап принятия решения, иллюстрирует элементарные принципы, на которых строятся более крупные и сложные деревья решений. Возьмем чуть более сложную ситуацию.
Вы пытаетесь решить, утвердить ли бюджет на разработку улучшенного продукта. Вам настоятельно рекомендуется сделать это на том основании, что разработка, в случае успеха, даст вам конкурентное преимущество, но если вы не разработаете продукт, ваш конкурент может серьезно подорвать вашу долю на рынке. Вы набрасываете дерево решений, похожее на то, что показано на рисунке 2.
Ваше первоначальное решение показано слева. После принятия решения о продолжении проекта, если разработка прошла успешно, следует второй этап принятия решения в точке А. Предполагая, что между настоящим моментом и моментом точки А в ситуации нет существенных изменений, вы решаете сейчас, какие альтернативы будут для вас важны. в это время. Справа от дерева результаты различных последовательностей решений и событий. Эти результаты также основаны на вашей текущей информации. По сути, вы говорите: «Если то, что я знаю сейчас, верно тогда, то это то, что произойдет».
Эти результаты также основаны на вашей текущей информации. По сути, вы говорите: «Если то, что я знаю сейчас, верно тогда, то это то, что произойдет».
Конечно, вы не пытаетесь определить все события, которые могут произойти, или все решения, которые вам придется принять по анализируемому предмету. В дереве решений вы размещаете только те решения и события или результаты, которые важны для вас и имеют последствия, которые вы хотите сравнить. (Дополнительные иллюстрации см. в Приложении.)
Добавление финансовых данных
Теперь мы можем вернуться к проблемам, с которыми столкнулось руководство Stygian Chemical. Дерево решений, характеризующее инвестиционную проблему, как обрисовано в общих чертах во введении, показано в Приложении III. В Решении № 1 компания должна выбрать между большим и малым заводом. Это все, что нужно решить сейчас. Но если компания решит построить небольшой завод, а затем обнаружит высокий спрос в начальный период, она может через два года — в Решении № 2 — принять решение о расширении своего завода.
Но давайте не будем ограничиваться простым наброском альтернатив. Принимая решения, руководители должны учитывать вероятности, затраты и прибыль, которые кажутся вероятными. На основании имеющихся у них данных и при условии, что ситуация в компании не изменится, они рассуждают следующим образом:
- Маркетинговые оценки указывают на 60-процентную вероятность большого рынка в долгосрочной перспективе и на 40-процентную вероятность низкого спроса, первоначально развивающегося следующим образом:
- Первоначально высокий спрос, устойчивый высокий: 60%
Первоначально высокий спрос, долгосрочный низкий: 10%
Первоначально низкий уровень и продолжающийся низкий уровень: 30%
Первоначально низкий, а затем высокий: 0%
- Таким образом, вероятность того, что спрос изначально будет высоким, составляет 70% (60 + 10). Если спрос на изначально высок, по оценке компании, вероятность того, что он сохранится на высоком уровне, составляет 86% (60 ÷ 70).
 Сравнивая 86% с 60%, становится очевидным, что высокий начальный уровень продаж изменяет расчетную вероятность высоких продаж в последующие периоды. Точно так же, если продажи в начальный период низкие, вероятность того, что продажи в последующие периоды будут низкими, равна 100% (30 ÷ 30). Таким образом, ожидается, что уровень продаж в начальный период будет достаточно точным индикатором уровня продаж в последующие периоды.
Сравнивая 86% с 60%, становится очевидным, что высокий начальный уровень продаж изменяет расчетную вероятность высоких продаж в последующие периоды. Точно так же, если продажи в начальный период низкие, вероятность того, что продажи в последующие периоды будут низкими, равна 100% (30 ÷ 30). Таким образом, ожидается, что уровень продаж в начальный период будет достаточно точным индикатором уровня продаж в последующие периоды.
- Оценки годового дохода сделаны в предположении каждого альтернативного результата:
- Крупный завод с большими объемами производства будет приносить ежегодный денежный поток в размере 1 000 000 долларов.
- Большой завод с небольшим объемом производства принесет всего 100 000 долларов из-за высоких постоянных затрат и неэффективности.
- Небольшой завод с низким спросом был бы экономичным и приносил бы годовой денежный доход в размере 400 000 долларов.
- Небольшой завод в начальный период высокого спроса будет приносить 450 000 долларов в год, но в долгосрочной перспективе он упадет до 300 000 долларов в год из-за конкуренции.
 (Рынок был бы больше, чем при Альтернативе 3, но был бы разделен между большим количеством конкурентов.)
(Рынок был бы больше, чем при Альтернативе 3, но был бы разделен между большим количеством конкурентов.) - Если бы небольшой завод был расширен, чтобы удовлетворить устойчивый высокий спрос, он бы приносил денежный поток в размере 700 000 долларов США в год и, таким образом, был бы менее эффективным, чем большой завод, построенный изначально.
- Если бы небольшой завод был расширен, но высокий спрос не был бы устойчивым, расчетный годовой денежный поток составил бы 50 000 долларов.
- Кроме того, предполагается, что ввод в эксплуатацию крупного завода обойдется в 3 миллиона долларов, небольшого завода — в 1,3 миллиона долларов, а расширение малого завода будет стоить дополнительно 2,2 миллиона долларов.
При включении вышеизложенных данных у нас есть дерево решений, показанное в Приложении IV. Имейте в виду, что здесь не показано ничего такого, чего руководители Stygian Chemical не знали раньше; ни одного номера из шляпы не вытащили. Тем не менее, мы начинаем видеть убедительные доказательства ценности деревьев решений в , излагающих то, что известно руководству, таким образом, который позволяет проводить более систематический анализ и приводит к лучшим решениям. Подводя итог требованиям построения дерева решений, руководство должно:
Тем не менее, мы начинаем видеть убедительные доказательства ценности деревьев решений в , излагающих то, что известно руководству, таким образом, который позволяет проводить более систематический анализ и приводит к лучшим решениям. Подводя итог требованиям построения дерева решений, руководство должно:
- Определите точки принятия решений и альтернативы, доступные в каждой точке.
- Определите точки неопределенности и тип или диапазон альтернативных результатов в каждой точке.
- Оцените значения, необходимые для проведения анализа, особенно вероятности различных событий или результатов действий, а также затраты и выгоды от различных событий и действий.
- Проанализируйте альтернативные значения, чтобы выбрать курс.
Выбор курса действий
Теперь мы готовы к следующему шагу анализа — сравнить последствия различных действий. Дерево решений не дает руководству ответа на инвестиционную проблему; скорее, это помогает руководству определить, какая альтернатива в любой конкретной точке выбора принесет наибольшую ожидаемую денежную выгоду, учитывая информацию и альтернативы, относящиеся к решению.
Конечно, прибыль нужно рассматривать с риском. В Stygian Chemical, как и во многих других корпорациях, менеджеры по-разному относятся к риску; следовательно, они придут к разным выводам в обстоятельствах, описанных деревом решений, показанным в Приложении IV. Многие люди, участвующие в принятии решения — те, кто предоставляет капитал, идеи, данные или решения и подвергает риску различные ценности, — будут по-разному воспринимать неопределенность, окружающую это решение. Если эти различия не будут признаны и устранены, те, кто должен принимать решение, платить за него, предоставлять данные и анализы и жить с этим, будут судить о проблеме, актуальности данных, необходимости анализа и критерии успеха в различных областях. и противоречивые пути.
Например, акционеры компании могут рассматривать конкретную инвестицию как одну из ряда возможностей, некоторые из которых сработают, а другие потерпят неудачу. Крупные инвестиции могут представлять риск для менеджера среднего звена — для его работы и карьеры — независимо от того, какое решение будет принято. Другой участник может много выиграть от успеха, но мало что потеряет от провала проекта. Характер риска — как его видит каждый человек — будет влиять не только на предположения, которые он готов сделать, но и на стратегию, которой он будет следовать в отношении риска.
Другой участник может много выиграть от успеха, но мало что потеряет от провала проекта. Характер риска — как его видит каждый человек — будет влиять не только на предположения, которые он готов сделать, но и на стратегию, которой он будет следовать в отношении риска.
Наличие многочисленных, неустановленных и противоречащих друг другу целей, безусловно, будет способствовать «политике» решения Stygian Chemical, и можно быть уверенным, что политический элемент существует всякий раз, когда затрагиваются жизни и амбиции людей. Здесь, как и в подобных случаях, неплохо было бы продумать, кто является сторонами инвестиционного решения, и попытаться сделать следующие оценки:
- Чему грозит риск? Прибыль или стоимость капитала, выживание бизнеса, сохранение работы, возможность сделать крупную карьеру?
- Кто несет риск? Акционер обычно несет риск в одной форме. Руководство, сотрудники, общество — все они могут подвергаться разным рискам.

- Каков характер риска, который несет каждый человек? Является ли он, в его терминах, уникальным, единственным в жизни, последовательным, застрахованным? Влияет ли это на экономику, отрасль, компанию или часть компании?
Соображения, подобные вышеприведенным, несомненно, придут в голову высшему руководству, и дерево решений в Приложении IV не устранит их. Но дерево покажет руководству, какое сегодняшнее решение будет больше всего способствовать достижению его долгосрочных целей. Инструментом для этого следующего шага в анализе является концепция «отката».
Концепция «отката».
Вот как работает откат в описанной ситуации. Во время принятия Решения № 1 (см. Приложение IV) руководство не обязано принимать Решение № 2 и даже не знает, будет ли у него возможность это сделать. Но если бы было , чтобы иметь вариант в Решении № 2, компания расширила бы завод, принимая во внимание ее текущие знания. Анализ показан в Таблице V. (На данный момент я проигнорирую вопрос о дисконтировании будущих прибылей, который будет представлен позже.) Мы видим, что общая ожидаемая стоимость альтернативы расширения на 160 000 долларов больше, чем альтернативы без расширения, в течение осталось восемь лет жизни. Следовательно, это альтернатива, которую выбрало бы руководство, столкнувшись с Решением № 2 с существующей информацией (и думая только о денежной выгоде в качестве стандарта выбора).
(На данный момент я проигнорирую вопрос о дисконтировании будущих прибылей, который будет представлен позже.) Мы видим, что общая ожидаемая стоимость альтернативы расширения на 160 000 долларов больше, чем альтернативы без расширения, в течение осталось восемь лет жизни. Следовательно, это альтернатива, которую выбрало бы руководство, столкнувшись с Решением № 2 с существующей информацией (и думая только о денежной выгоде в качестве стандарта выбора).
Читатели могут удивиться, почему мы начали с решения №2, если сегодняшняя проблема — это решение №1. Причина в следующем: нам нужно иметь возможность оценить решение № 2 в денежном выражении, чтобы «откатиться» к решению № 1 и сравнить выигрыш от выбора нижней ветки («Построить малый завод») с выигрышем от взятия верхней ветки («Построить большой завод»). Давайте назовем это денежное значение для Решения № 2 значением позиции . Позиционное значение решения — это ожидаемое значение предпочтительной ветви (в данном случае вилки-расширения). Ожидаемая стоимость — это просто своего рода среднее значение результатов, которые вы ожидаете, если будете повторять ситуацию снова и снова: получить доход в размере 5,6 миллиона долларов в 86% случаев и доход в размере 400 000 долларов в 14% случаев.
Ожидаемая стоимость — это просто своего рода среднее значение результатов, которые вы ожидаете, если будете повторять ситуацию снова и снова: получить доход в размере 5,6 миллиона долларов в 86% случаев и доход в размере 400 000 долларов в 14% случаев.
Другими словами, Stygian Chemical стоит 2 672 000 долларов, чтобы занять позицию, на которой она сможет принять Решение №2. Вопрос в следующем: учитывая это значение и другие данные, показанные в Приложении IV, что теперь кажется лучшим действием в Решении №1?
Перейдем к экспонату VI. Справа от ветвей в верхней половине мы видим доходность для различных событий, если будет построен большой завод (это просто перемноженные цифры в Приложении IV). В нижней половине мы видим небольшие цифры завода, включая стоимость позиции по Решению № 2 плюс урожайность за два года до Решения № 2. Если мы уменьшим все эти доходности по их вероятностям, мы получим следующее сравнение:
Построить большой завод:
(10 миллионов долларов × 0,60) + (2,8 миллиона долларов × 0,10) + (1 миллион долларов × 0,30) – 3 миллиона долларов = 3,6 миллиона долларов
Построить небольшой завод:
(3,6 миллиона долларов) × 0,70) + (4 миллиона долларов × 0,30) – 1,3 миллиона долларов = 2,4 миллиона долларов
Таким образом, выбор, который максимизирует ожидаемый общий денежный доход в Решении № 1, состоит в том, чтобы сначала построить большой завод.
Учет времени
Как насчет учета разницы в времени будущих доходов? Время между последовательными этапами принятия решений в дереве решений может быть значительным. На любом этапе нам, возможно, придется сопоставлять разницу в немедленных затратах или доходах с разницей в стоимости на следующем этапе. Какой бы стандарт выбора ни применялся, мы можем поставить две альтернативы на сопоставимую основу, если снизим ценность, присвоенную следующему этапу, на соответствующий процент. Процент дисконтирования, по сути, является поправкой на стоимость капитала и аналогичен использованию ставки дисконтирования в приведенной стоимости или методам дисконтирования денежных потоков, уже хорошо известным деловым людям.
При использовании деревьев решений процедура дисконтирования может применяться пошагово. И денежные потоки, и стоимость позиций дисконтируются.
Для простоты предположим, что ставка дисконтирования 10 % в год для всех стадий установлена руководством Stygian Chemical. Применяя принцип отката, мы снова начинаем с Решения №2. Взяв те же цифры, что и в предыдущих приложениях, и дисконтировав денежные потоки по ставке 10%, мы получим данные, показанные в Части А Приложения VII. Обратите внимание, что это текущие значения на момент принятия Решения №2.
Применяя принцип отката, мы снова начинаем с Решения №2. Взяв те же цифры, что и в предыдущих приложениях, и дисконтировав денежные потоки по ставке 10%, мы получим данные, показанные в Части А Приложения VII. Обратите внимание, что это текущие значения на момент принятия Решения №2.
Теперь мы хотим пройти ту же процедуру, что и в Приложении V, когда мы получили ожидаемые значения, только на этот раз с использованием значений дисконтированной доходности и получением дисконтированного ожидаемого значения. Результаты показаны в Части B Приложения VII. Поскольку дисконтированная ожидаемая стоимость альтернативы без расширения выше, , то цифра на этот раз становится значением позиции Решения №2.
Сделав это, снова возвращаемся к работе по Решению №1, повторяя ту же аналитическую процедуру, что и раньше, только с дисконтированием. Расчеты показаны в Приложении VIII. Обратите внимание, что значение позиции в Решении № 2 обрабатывается во время Решения № 1, как если бы это была единовременная сумма, полученная в конце двух лет.
Вариант с крупным заводом снова является предпочтительным на основе ожидаемого дисконтированного денежного потока. Но предел разницы по сравнению с альтернативой с небольшим заводом (290 000 долларов) меньше, чем без дисконтирования.
Альтернативы неопределенности
При иллюстрации концепции дерева решений я рассматривал альтернативы неопределенности, как если бы они были дискретными, четко определенными возможностями. В своих примерах я использовал неопределенные ситуации, зависящие в основном от одной переменной, такой как уровень спроса или успех или неудача проекта разработки. Я стремился избежать ненужных осложнений, делая акцент на ключевых взаимосвязях между нынешним решением, будущим выбором и промежуточными неопределенностями.
Во многих случаях неопределенные элементы принимают форму дискретных альтернатив с одной переменной. В других, однако, возможности потока наличности на этапе могут варьироваться по всему спектру и могут зависеть от ряда независимых или частично связанных переменных, подверженных случайным влияниям, — затрат, спроса, доходности, экономического климата и т. д. В этих случаях мы обнаружили, что диапазон изменчивости или вероятность того, что денежный поток попадет в заданный диапазон на этапе, можно легко рассчитать, зная ключевые переменные и окружающие их неопределенности. Затем диапазон возможных денежных потоков на этапе можно разбить на два, три или более «подмножеств», которые можно использовать в качестве дискретных случайных альтернатив.
д. В этих случаях мы обнаружили, что диапазон изменчивости или вероятность того, что денежный поток попадет в заданный диапазон на этапе, можно легко рассчитать, зная ключевые переменные и окружающие их неопределенности. Затем диапазон возможных денежных потоков на этапе можно разбить на два, три или более «подмножеств», которые можно использовать в качестве дискретных случайных альтернатив.
. . .
Питер Ф. Друкер лаконично выразил связь между текущим планированием и будущими событиями: «Долгосрочное планирование не связано с будущими решениями. Он имеет дело с будущим нынешних решений». Сегодняшнее решение должно приниматься с учетом предполагаемого влияния, которое оно и исход неопределенных событий окажут на будущие ценности и решения. Поскольку сегодняшнее решение готовит почву для завтрашнего решения, сегодняшнее решение должно сочетать экономичность с гибкостью; она должна уравновешивать потребность в извлечении выгоды из возможностей получения прибыли, которые могут существовать, со способностью реагировать на будущие обстоятельства и потребности.
Для читателей, заинтересованных в дополнительных примерах структуры дерева решений, я опишу в этом приложении две репрезентативные ситуации, с которыми я знаком, и покажу деревья, которые можно использовать для анализа альтернатив принятия решений руководством. Мы не будем заниматься здесь затратами, доходами, вероятностями или ожидаемыми значениями.
Новое предприятие
Выбор альтернатив при строительстве завода зависит от рыночных прогнозов. Выбранная альтернатива, в свою очередь, повлияет на результат рынка. Например, подразделение военной продукции диверсифицированной фирмы после некоторого периода низкой прибыли из-за острой конкуренции выиграло контракт на производство военного двигателя нового типа, подходящего для армейских транспортных машин. Подразделение имеет контракт на наращивание производственных мощностей и производство в соответствии с контрактом на уровне в течение трех лет.
Рисунок A иллюстрирует ситуацию. Пунктирная линия показывает курс контракта. Сплошная линия показывает предлагаемое наращивание производства для вооруженных сил. Некоторые другие возможности показаны пунктирными линиями. Компания не уверена, будет ли контракт продолжен по относительно высокой ставке после третьего года, как показано в строке А, или военные обратятся к другой, более новой разработке, как показано в строке В. Компания не гарантирует компенсация после третьего года. Существует также возможность, указанная линией C, большого дополнительного коммерческого рынка для продукта, причем эта возможность в некоторой степени зависит от затрат, по которым продукт может быть произведен и продан.
Сплошная линия показывает предлагаемое наращивание производства для вооруженных сил. Некоторые другие возможности показаны пунктирными линиями. Компания не уверена, будет ли контракт продолжен по относительно высокой ставке после третьего года, как показано в строке А, или военные обратятся к другой, более новой разработке, как показано в строке В. Компания не гарантирует компенсация после третьего года. Существует также возможность, указанная линией C, большого дополнительного коммерческого рынка для продукта, причем эта возможность в некоторой степени зависит от затрат, по которым продукт может быть произведен и продан.
Если бы этот коммерческий рынок можно было использовать, это означало бы новый крупный бизнес для компании и существенное повышение прибыльности подразделения и его значимости для компании.
Руководство хочет изучить три способа производства продукта, а именно:
- Оно может заключить субподряд на все производство и организовать простую сборку с ограниченной потребностью в инвестициях в заводы и оборудование; затраты, как правило, будут относительно высокими, а инвестиции и возможности получения прибыли компании будут ограничены, но активы компании, подверженные риску, также будут ограничены.

- Он может взять на себя большую часть производства самостоятельно, но использовать станки общего назначения на заводе универсального строительства. Подразделение имело бы шанс сохранить за собой больше наиболее прибыльных операций, используя некоторые технические разработки, которые он сделал (на основании которых он получил контракт). Хотя себестоимость производства по-прежнему будет относительно высокой, характер инвестиций в заводы и оборудование будет таким, что их, вероятно, можно будет использовать для других целей или ликвидировать, если бизнес исчезнет.
- Компания могла бы построить высокомеханизированный завод со специализированным производственным и сборочным оборудованием, что потребовало бы самых больших инвестиций, но дало бы значительно более низкую себестоимость единицы продукции, если бы объем производства был адекватным. Следование этому плану повысило бы шансы на продолжение военного контракта и проникновение на коммерческий рынок, а также повысило бы прибыльность любого бизнеса, который можно было бы получить на этих рынках.
 Однако неспособность поддерживать военный или коммерческий рынок приведет к значительным финансовым потерям.
Однако неспособность поддерживать военный или коммерческий рынок приведет к значительным финансовым потерям.
Любой из первых двух вариантов лучше подходит для мелкосерийного производства, чем третий.
Некоторыми основными неопределенностями являются: соотношение затрат и объема при альтернативных методах производства; размер и структура будущего рынка — это зависит отчасти от стоимости, но степень и степень зависимости неизвестны; и возможности конкурентоспособных разработок, которые сделают продукт конкурентоспособным или технологически устаревшим.
Как эта ситуация будет показана в виде дерева решений? (Прежде чем идти дальше, вы можете сами нарисовать дерево для решения задачи.) На рисунке B показана моя версия дерева. Заметим, что в этом случае случайные альтернативы в некоторой степени зависят от принятого решения. Например, решение построить более эффективный завод откроет возможности для расширения рынка.
Модернизация завода
Руководству компании необходимо принять решение по предложению ее инженерно-технического персонала, который после трех лет обучения хочет установить компьютерную систему управления на главном заводе компании. Ожидаемая стоимость системы управления составляет около 30 миллионов долларов. Заявленными преимуществами системы будут снижение трудозатрат и повышение выхода продукции. Эти преимущества зависят от уровня производительности продукта, который, вероятно, возрастет в течение следующего десятилетия. Предполагается, что программа установки займет около двух лет и будет стоить значительную сумму сверх стоимости оборудования. Инженеры подсчитали, что проект автоматизации принесет 20% прибыли от инвестиций после уплаты налогов; прогноз основан на 10-летнем прогнозе спроса на продукцию, сделанном отделом маркетинговых исследований, и на предположении о восьмилетнем сроке службы системы управления технологическим процессом.
Ожидаемая стоимость системы управления составляет около 30 миллионов долларов. Заявленными преимуществами системы будут снижение трудозатрат и повышение выхода продукции. Эти преимущества зависят от уровня производительности продукта, который, вероятно, возрастет в течение следующего десятилетия. Предполагается, что программа установки займет около двух лет и будет стоить значительную сумму сверх стоимости оборудования. Инженеры подсчитали, что проект автоматизации принесет 20% прибыли от инвестиций после уплаты налогов; прогноз основан на 10-летнем прогнозе спроса на продукцию, сделанном отделом маркетинговых исследований, и на предположении о восьмилетнем сроке службы системы управления технологическим процессом.
Что даст это вложение? Будут ли фактические продажи продукта выше или ниже прогнозируемых? Будет ли работать процесс? Достигнет ли это ожидаемой экономии? Последуют ли конкуренты, если компания будет успешной? Они все-таки собираются механизироваться? Приведут ли новые продукты или процессы к устареванию основной установки до того, как удастся окупить инвестиции? Продержится ли контроль восемь лет? Появится ли что-то лучшее раньше?
Первоначальные варианты решения: (а) установить предлагаемую систему управления, (б) отложить действие до тех пор, пока тенденции на рынке и/или конкуренция не прояснятся, или (в) инициировать дополнительное расследование или независимую оценку. За каждой альтернативой последует разрешение какого-то неопределенного аспекта, отчасти зависящего от предпринятого действия. Эта резолюция, в свою очередь, приведет к новому решению. Пунктирные линии в правой части рисунка C показывают, что дерево решений продолжается бесконечно, хотя альтернативы решений имеют тенденцию повторяться. В случае отсрочки или дальнейшего изучения принимаются решения об установке, отсрочке или повторном изучении; в случае установки принимаются решения о продолжении эксплуатации или отказе от нее.
За каждой альтернативой последует разрешение какого-то неопределенного аспекта, отчасти зависящего от предпринятого действия. Эта резолюция, в свою очередь, приведет к новому решению. Пунктирные линии в правой части рисунка C показывают, что дерево решений продолжается бесконечно, хотя альтернативы решений имеют тенденцию повторяться. В случае отсрочки или дальнейшего изучения принимаются решения об установке, отсрочке или повторном изучении; в случае установки принимаются решения о продолжении эксплуатации или отказе от нее.
Немедленное решение часто является одним из последовательных. Это может быть одна из нескольких последовательностей. Необходимо учитывать как влияние настоящего решения на сужение будущих альтернатив, так и влияние будущих альтернатив на ценность настоящего выбора.
Уникальная особенность дерева решений заключается в том, что оно позволяет руководству сочетать аналитические методы, такие как методы дисконтированных денежных потоков и методов приведенной стоимости, с четким изображением влияния будущих альтернативных решений и событий.


 Такие алгоритмы не могут гарантировать возврат глобального оптимального дерева решений. Это можно смягчить путем обучения нескольких деревьев в учащемся ансамбля, где функции и образцы выбираются случайным образом с заменой.
Такие алгоритмы не могут гарантировать возврат глобального оптимального дерева решений. Это можно смягчить путем обучения нескольких деревьев в учащемся ансамбля, где функции и образцы выбираются случайным образом с заменой.
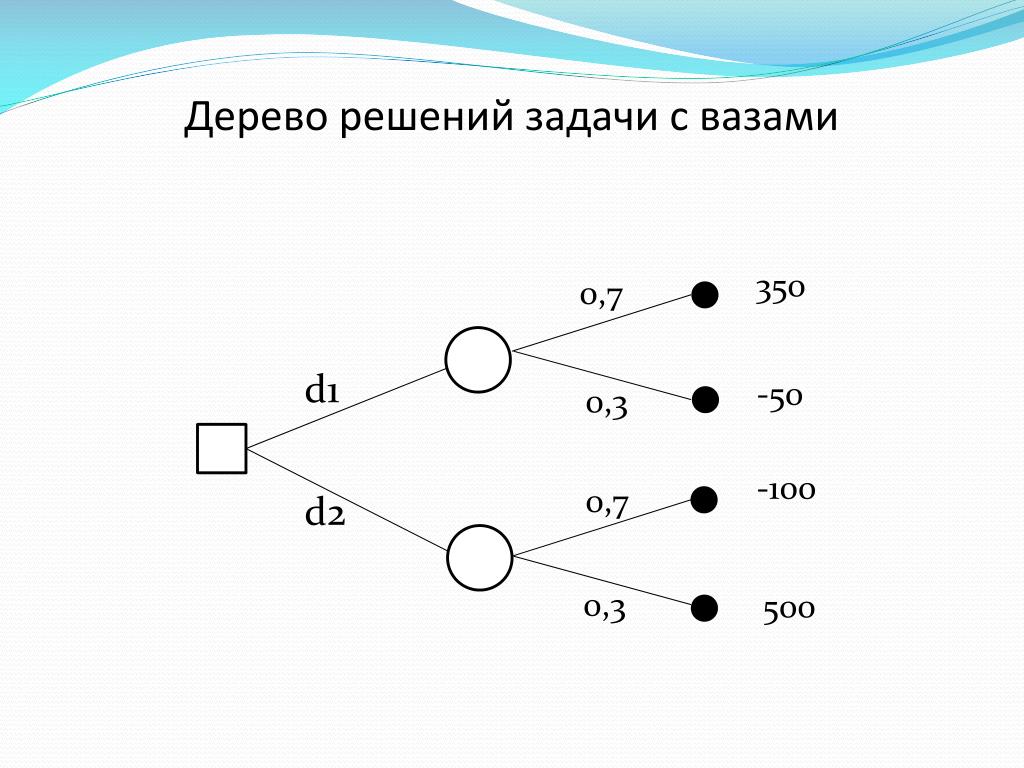 predict_proba([[2., 2.]])
array([[0., 1.]])
predict_proba([[2., 2.]])
array([[0., 1.]]) plot_tree(clf)
plot_tree(clf)  export_graphviz(clf, out_file=None)
>>> graph = graphviz.Source(dot_data)
>>> graph.render("iris")
export_graphviz(clf, out_file=None)
>>> graph = graphviz.Source(dot_data)
>>> graph.render("iris") 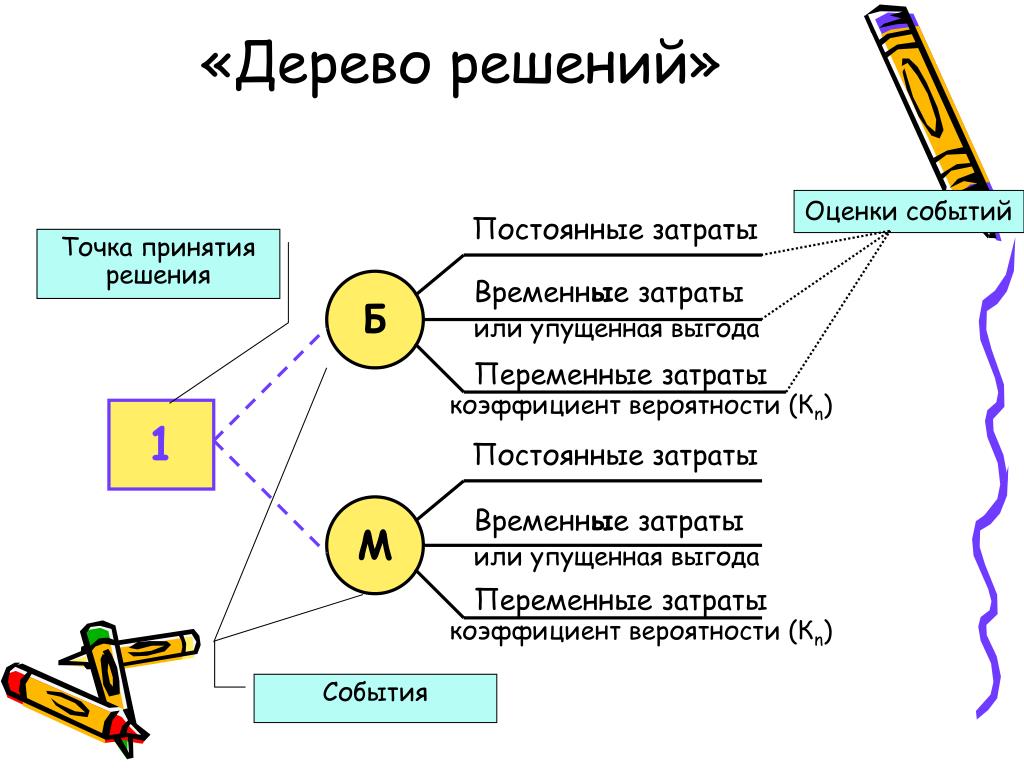 .. special_characters=True)
>>> graph = graphviz.Source(dot_data)
>>> graph
.. special_characters=True)
>>> graph = graphviz.Source(dot_data)
>>> graph 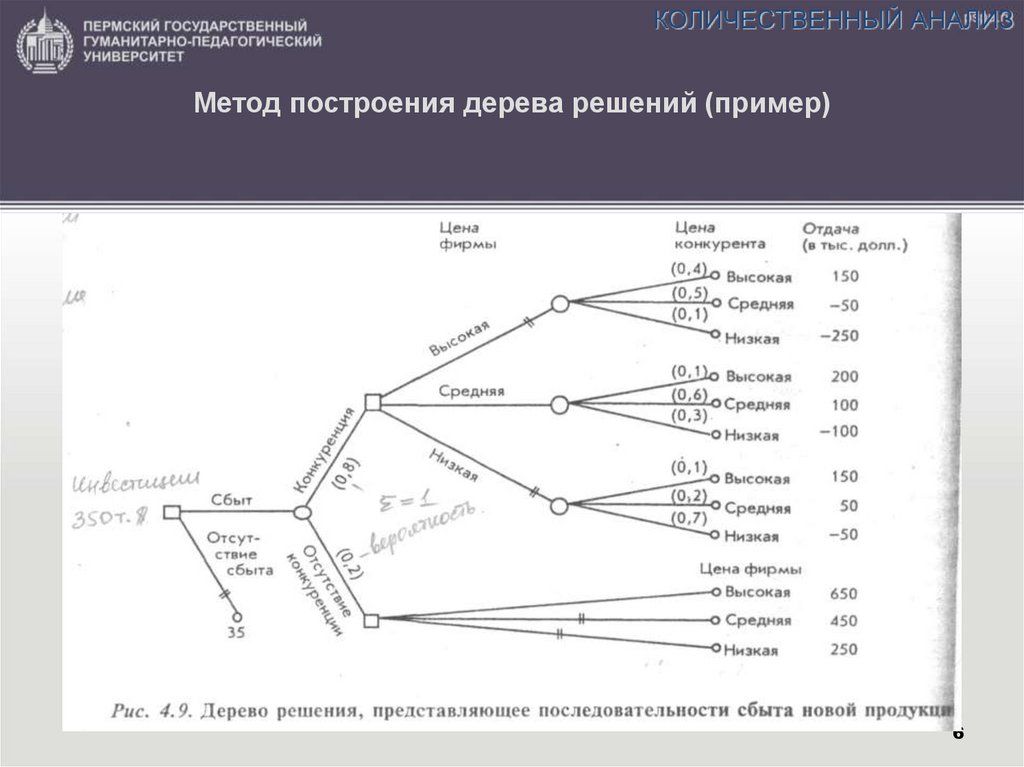
 5, 2.5]
>>> clf = tree.DecisionTreeRegressor()
>>> clf = clf.fit(X, y)
>>> clf.predict([[1, 1]])
array([0.5])
5, 2.5]
>>> clf = tree.DecisionTreeRegressor()
>>> clf = clf.fit(X, y)
>>> clf.predict([[1, 1]])
array([0.5]) Используйте
Используйте 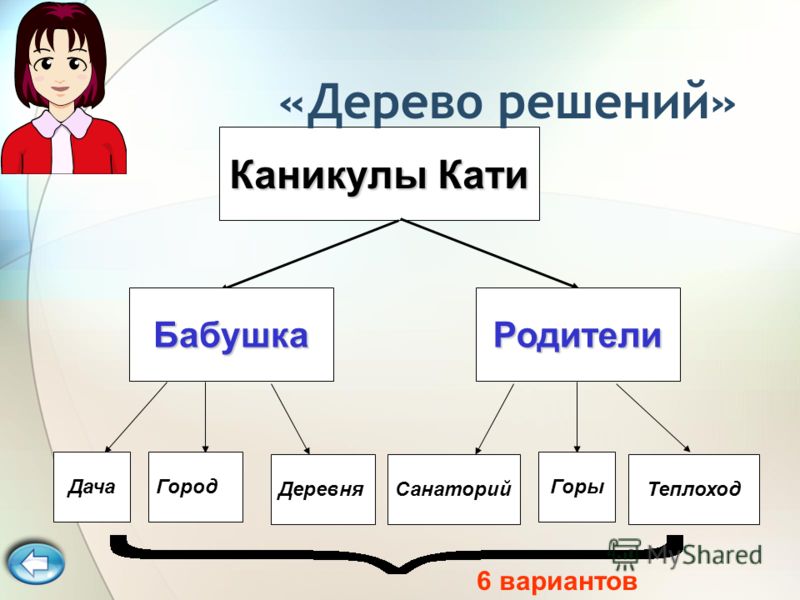 Рассмотрим
Рассмотрим 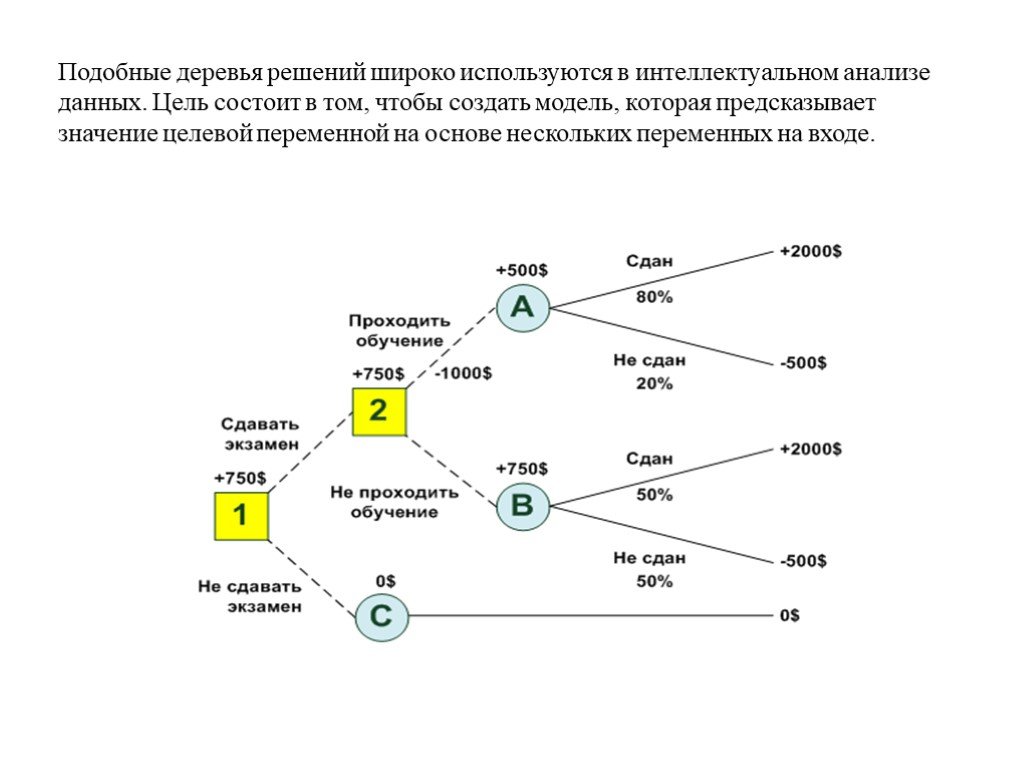
 Брейман, Дж. Фридман, Р. Олшен и К. Стоун. Деревья классификации и регрессии. Уодсворт, Белмонт, Калифорния, 1984.
Брейман, Дж. Фридман, Р. Олшен и К. Стоун. Деревья классификации и регрессии. Уодсворт, Белмонт, Калифорния, 1984.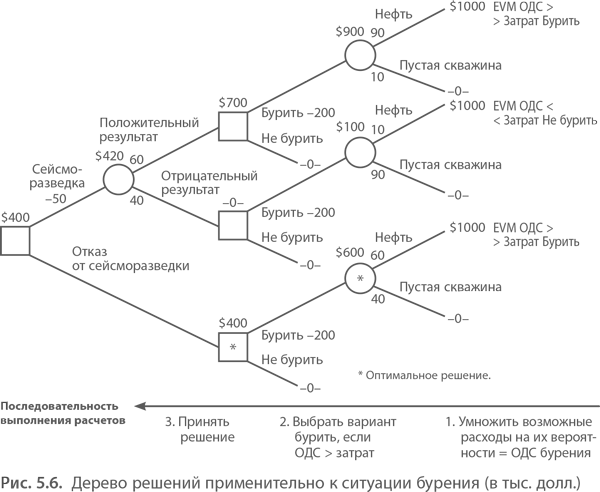
 При этом целевая переменная имеет дискретные задачи.
При этом целевая переменная имеет дискретные задачи.