Конспект урока математики в 5 классе «Задачи на нахождение процентного отношения чисел»
Муниципальное казенное общеобразовательное учреждение
Бугаевская средняя общеобразовательная школа
Кантемировского муниципального района, Воронежской области
Конспект урока математики
в 5 классе на тему:
Учитель математики МКОУ Бугаевская сош:
Воронько Владимир Иванович
2013 г.
Урок математики в 5 классе на тему:
«Задачи
на нахождение процентного
отношения чисел»
Цель урока: организовать деятельность учащихся по восприятию, осмыслению и
первичному закреплению знаний и способов деятельности по решению задач на проценты.
Задачи урока
обучающие: научить учащихся обозначать, читать и находить процент чисел и величин, переводить процент в десятичную дробь и обратно, решать задачи на проценты;
развивающие: формирование и развитие познавательной активности, логического мышления учащихся, навыков устного счёта, самостоятельной работы;
воспитывающие: экономическое воспитание в современных условиях формирования рыночных отношений.
Технология: тестирование.
Продолжительность урока: 45 минут
Ход урока
Организационный момент
Создание проблемной ситуации
Учитель: если вы правильно выполните вычисления, то узнаете тему сегодняшнего урока.
1,5 | 3,5 | 0,8 | 0,36 | 1,6 | 0,25 | 0,1 | 13,6 |
Учащиеся дают ответы. Появляется тема урока.
Появляется тема урока.
Учитель: Итак, ребята, тема сегодняшнего урока – «Задачи на нахождение процентного отношения чисел». Это универсальная величина, которая появилась из практической необходимости измерения различных величин. Она очень важная в курсе математики. В этом году мы начнём эту тему. В 6-ом классе мы к ней вернёмся при изучении пропорций.
– Ребята, как вы думаете, в повседневной жизни, где встречаются проценты? Примерные ответы учащихся:
– В банках, на вкладах с разной процентной ставкой, при получении кредитов.
Учитель: Верно, в современных условиях формирования рыночных отношений, мы правильно должны уметь обращаться деньгами, выбирать сберегательные банки, где нам будут предоставлять вклады по более высоким процентным ставкам.
А также в повседневной жизни встречается очень много задач на нахождение процентного отношения чисел, и не только денежных. Полученные знания на уроках математики вам помогут в дальнейшем при решении задач по химии, физике. При сдаче ЕГЭ часто дают текстовые задачи на проценты. Поэтому, наша цель, научиться решать их уже сейчас, и в дальнейшем уметь применять полученные знания.
Полученные знания на уроках математики вам помогут в дальнейшем при решении задач по химии, физике. При сдаче ЕГЭ часто дают текстовые задачи на проценты. Поэтому, наша цель, научиться решать их уже сейчас, и в дальнейшем уметь применять полученные знания.
Повторение.
Вопросы:
1) Сколько килограммов в одном центнере? Какую часть центнера составляет 1 кг?
2) Сколько сантиметров в одном метре? Какую часть метра составляет 1 см?
3) Сколько ар в одном гектаре? Какую часть гектара составляет 1 а?
Учащиеся дают ответы.
1 ц=100 кг;
1 м=100 см;
1 га = 100 а;
Записывают в тетради.
Объяснение нового материала.
Учитель: ребята, мы рассмотрели величины, которые связаны с одной сотой частью.
Сотая часть любой величины принято называть процентом.
Слово «процент» происходит от латинского «центи» (по-французски «санти»), указывающего на уменьшение единицы измерения в 100 раз. Для краткости слово «процент» после числа заменяется знаком «%».
Предлагается ученикам найти определение процента в учебнике, прочитать и запомнить. В тетради записывается:
Выводы: 1 кг – 1% центнера;
1 см – 1 % метра;
1 а – 1 % га;
0,05 – 1 % от 5.
Примеры.
Записать в тетради:
Учитель: Итак, что нужно делать, чтобы десятичную дробь выразить в процентах или проценты представить в виде десятичной дроби?
Выводы: (отвечают ученики)
1) Чтобы обратить десятичную дробь в проценты, надо её умножить на 100.
2) Чтобы перевести проценты в десятичную дробь, надо разделить число процентов на 100.
Находят эти правила в учебнике.
Решение примеров и задач.
Учитель: теперь, ребята, вспомним
Ребята рассказывают правила.
Решаем №№ 1532, 1533
Два ученика по очереди на доске показывают решения. После выполнения ответы появляются на экране, учащиеся проверяют свои ответы.
Ответы: №1532: 0,01; 0,06; 0,45; 1,23; 0,025; 0,004
№1533: 87%; 7%; 145%; 3,5%; 267,2%; 90,7%
Решаем задачи (условия задач на экране)
Задача 1. При помоле пшеницы получается 80% муки. Сколько муки получится из 90 тонн пшеницы?
Решение:
90 :100=0,9(т) – 1%
0,9 * 80= 72(т) – 80%
Ответ: 72 т муки получится из 90 т пшеницы.
Задача 2. Контрольную работу выполнили 20 учеников.
Из них на «5» – 4 ученика,
на «4» – 8 учеников,
на « 3» – 6 учеников,
на «2» – 2 ученика.
Какой процент всех учащихся получили соответствующие оценки?
Решение:
4:20*100=0,2*100=20(%) – на «5»
8:20*100=0,4*100=40(%) – на «4»
6:20*100=0,3*100=30(%) – на «3»
2:20*100=0,1*100=10(%) – на «2»
Ответ: написали на «5» — 20%, на «4» — 40 %, на «3» — 30% и на «2» — 10% всех учащихся.
7. Физкультминутка. Дети, прямо все вставайте,
Руки вверх все поднимайте.
Их немножко потрясите,
Медленно вниз опустите.
Плечи прямо вы держите,
А головку поверните
То налево, то направо…
Ох, как здорово, как браво!
8. Закрепление.
Закрепление.
Проверочный тест:
I вариант | |||
5 % – это | 1) 0,05 | 2) 0,5 | 3) 0,005 |
0, 134 – это | 1) 134% | 2) 1,34% | 3) 13,4% |
25% класса – это | 1) половина класса | 2) пятая часть класса | 3) четверть класса |
5,68 – это | 1) 56,8% | 2) 568% | 3) 5680% |
40% от 70 равно | 1) 28 | 2) 30 | 3) 175 |
II вариант | |||
7 % – это | 1) 0,7 | 2) 0,07 | 3) 0,007 |
0, 976 – это | 1) 97,6% | 2) 9,76% | 3) 976% |
50% класса – это | 1)четверть класса | 2) половина класса | 3) пятая часть класса |
13,5 – это | 1) 135% | 2) 1,35% | 3) 1350% |
30% от 80 равно | 1) 50 | 2) 110 | 3) 24 |
Ответы:
I вариант: 1) – 1; II вариант: 1) – 2;
2) – 3; 2) – 1;
3) – 3; 3) – 2;
4) – 2; 4) – 3;
5) – 1. 5) – 3.
5) – 3.
Учащиеся обмениваются тетрадями, проверяют работы, выставляют оценки.
Заключение.
Учитель: Итак, ребята, сегодня мы с вами ознакомились с понятием процента. Выяснили, где он применяется. Научились обозначать эту величину, выражать десятичную дробь в процентах и процент представлять в виде десятичной дроби. Рассмотрели, как решаются простейшие задачи на проценты.
Проверочное тестирование показало, как вы усвоили и закрепили этот материал. На следующих уроках мы с вами будем решать более сложные задачи на проценты.
10. Итоги урока.
Выставляются оценки за активную работу на уроке, все получают оценку за тест.
11. Домашнее задание.
Выучить определение и правила. Решить №№1569, 1560, 1583(а).
Литература.
1. З.С. Стромова, О. В. Пожарская. Поурочные разработки по математике. 5 класс. – Волгоград: Учитель, 2006
В. Пожарская. Поурочные разработки по математике. 5 класс. – Волгоград: Учитель, 2006
2. Н.Я. Виленкин, В.И. Жохов и др. Математика: учебник для 5 класса общеобразовательных учреждений. – М.: Мнемозина, 2006
Математика
«Математику уже затем учить следует, что она ум в порядок приводит», говорил великий ученый М.В.Ломоносов. Эта наука пригодится во многих отраслях повседневной жизни. Математика в первую очередь учит логически мыслить, чего очень не хватаем многим современным детям, которые привыкли списывать домашку с интернета, не пошевелив ни единой извилиной. Для пытливых умов, для тех, кто хочет разобраться в математике, узнать ее получше, научиться решать сложные задачи, для сознательных детей и их родителей создан этот раздел нашей энциклопедии «7гуру».
Курс математики с 1 по 4 класс рассмотрен в разделе
МАТЕМАТИКА НАЧАЛЬНОЙ ШКОЛЫ >>
- Категория: Математика
Иногда в жизни требуется выяснить, сколько дней прошло с начала какого-либо события, или осталось до начала события.
- Категория: Математика
Пропорциональными называются две взаимно зависимые величины, если отношение их значений остаётся неизменным. Пропорция – это равенство двух отношений. Отношение – это частное двух чисел. Отношение показывает, во сколько раз одно число больше другого или какую часть одно число составляет от другого. Полезно напомнить и основное свойство пропорции: в верной пропорции произведение крайних членов равно произведению средних.
- Категория: Математика
В шестом классе изучается тема деления чисел в данном отношении.
- Категория: Математика
Дробь называют правильной, если ее числитель меньше знаменателя, и неправильной, если числитель больше знаменателя.
- Категория: Математика
Чтобы умножить одну обыкновенную дробь на другую, нужно перемножить их числители и записать как числитель, затем перемножить их знаменатели и записать как знаменатель. При возможности полученную дробь нужно сократить.
Все отрицательные числа, и только они, меньше, чем ноль. На числовой оси отрицательные числа располагаются слева от нуля. Для них, как и для положительных чисел, определено отношение порядка, позволяющее сравнивать одно целое число с другим.
Для них, как и для положительных чисел, определено отношение порядка, позволяющее сравнивать одно целое число с другим.
- Категория: Математика
Если одно натуральное число нацело делится на другое натуральное число, то первое число называют кратным второму числу, а второе число называют делителем первого числа. Весь материал по этой теме вы можете повторить на странице «Делители и кратные числа» >>
- Категория: Математика
Цифры в записи многозначных чисел разбивают справа налево на группы по три цифры в каждой. Эти группы называют классами. В каждом классе цифры справа налево обозначают единицы, десятки и сотни этого класса. Каждая цифра в записи многозначного числа занимает определённое место — позицию. Место (позицию) в записи числа, на котором стоит цифра, называют разрядом.
- Категория: Математика
Деление с остатком обычно ведут в столбик, как и любое другое деление. Разница лишь в том, что внизу вы получите число, которое больше не делится на делитель, это и есть остаток. Помните, что остаток всегда будет меньше делителя. Почитать о делении с остатком и потренироваться на тренажере у нас на 7 гуру можно тут >>
- Категория: Математика
Подробнее с правилами деления на двузначное число вы можете ознакомиться тут >>
- Категория: Математика
Повторим и закрепим понятия секунды, минуты, часы, сутки, месяц, год, век.
- Категория: Математика
Чтобы округлить число до целого (или округлить число до единиц), надо отбросить запятую и все числа, стоящие после запятой. Если первая из отброшенных цифр 0, 1, 2, 3 или 4, то число не изменится. Если первая из отброшенных цифр 5, 6, 7, 8 или 9, предыдущую цифру нужно увеличить на единицу.
- Категория: Математика
Существуют разные типы чисел — четные числа, нечетные числа, простые числа, составные числа. Также на основе знака числа могут быть двух видов — положительные числа и отрицательные числа. Эти числа могут быть представлены на числовой прямой. Среднее число в этой строке равно нулю. С левой стороны от нуля находятся отрицательные числа, а с правой стороны — положительные. С тало быть, при сложении двух отрицательных чисел двигаемся по числовой прямой влево от первого числа на количество делений, соответствующих второму числу.
- Категория: Математика
Одна из сложнейших для восприятия детьми в пятом классе тема — нахождение дроби от числа. Как и все другие темы в математике, она будет пригождаться в вычислениях до самого 11-го класса, поэтому периодически повторяется и в шестом, и в седьмом, и в последующих годах обучения. Обобщить или восстановить знания о нахождении дроби от числа вы можете в нашей статье по этой ссылке >> В тесте участвуют и обыкновенные, и десятичные дроби.
- Категория: Математика
Наибольший общий делитель нескольких чисел (НОД) – это наибольшее натуральное целое число, на которое все исходные числа делятся без остатка. Чтобы найти НОД, нужно разложить числа на простые множители, подчеркнуть одинаковые множители, перемножить их, не дублируя. Нахождение НОД очень нам пригодится при нахождении значения выражений с участием обыкновенных дробей и решении неравенств.
- Категория: Математика
«Школа России» учится по учебникам Моро. Как правило, к этому УМК прилагаются контрольно-измерительные материалы — набор контрольных работ, которые дает учитель после изучения очередной темы, авторы которых Глаголева и Волковская. Если у учителя нет цели дать детям уникальную контрольную и он просто нормально выполняет свою работу, не желая сильно загружаться, конечно, он даст задания именно по этому учебному пособию. Именно эти рядовые контрольные работы мы и рассмотрим, а вернее проработаем ответы к ним, поскольку в современной школе зачастую учителя не делают с детьми работу над ошибками.
- Категория: Математика
То, каким образом мы будем складывать или вычитать дроби, напрямую зависит от знаменателей этих дробей. Самое простое: сложение и вычитание дробей с одинаковыми знаменателями. С него и начнем.
Самое простое: сложение и вычитание дробей с одинаковыми знаменателями. С него и начнем.
- Категория: Математика
Простое число — это натуральное число, единственными делителями которого являются только оно само и единица. Все остальные натуральные числа называются составными. Натуральное число 1 не является ни простым, ни составным.
- Категория: Математика
Наименьшее общее кратное двух и более чисел (НОК) — это самое маленькое целое число, которое делится нацело на любое из этих чисел. К примеру, узнаем наименьшее общее кратное чисел 6 и 9. Числа, кратные 6-ти: 6, 12, 18, 24 … Числа, кратные 9-ти: 9, 18, 27… Самое меньшее число, которое в этих разложениях совпадает — это 18. НОК(6;9) = 18
- Категория: Математика
Наибольший общий делитель нескольких чисел (НОД) – это наибольшее натуральное целое число, на которое все исходные числа делятся без остатка. И как вы заметили, если одно число делится без остатка на другое, то меньшее число и будет наибольшим общим делителем. Если НОД чисел равен 1, такие числа называют взаимно простыми.
И как вы заметили, если одно число делится без остатка на другое, то меньшее число и будет наибольшим общим делителем. Если НОД чисел равен 1, такие числа называют взаимно простыми.
- Категория: Математика
Если одно натуральное число нацело делится на другое натуральное число, то первое число называют кратным второму числу, а второе число называют делителем первого числа.
- Категория: Математика
Объектом наших исследований стали системы счисления, которых оказалось гораздо больше, чем мы даже могли предположить. Стало очень интересно узнать о жизни предков и попробовать считать как они. По мере изучения выяснилось, что и в наши дни осталось достаточно много «воспоминаний» о канувших в лета системах счислений.
- Категория: Математика
Контрольные работы по математике к учебнику УМК Мерзляк А. Г., Полонский В.Б., Якир М.С. за пятый класс. 4 варианта, задания типовые, подобные задания были разобраны в учебнике, а потому никаких сложностей при выполнении контрольной работы возникнуть не должно.
Г., Полонский В.Б., Якир М.С. за пятый класс. 4 варианта, задания типовые, подобные задания были разобраны в учебнике, а потому никаких сложностей при выполнении контрольной работы возникнуть не должно.
- Категория: Математика
Итоговая контрольная работа проводится в конце изучения темы «Проценты» по учебнику математики за пятый класс авторов Мерзляк, Полонский, Якир. Эта работа не из стандартной методички, но довольно распространенный вариант дополнения к курсу математики в 5 классе, поэтому, не исключено, что учитель выберет именно эту контрольную работу для проверки знаний учащихся по темам «Среднее арифметическое» и «Проценты». Зачастую родители и дети не видят свою работу после выставления оценок (что на наш взгляд в корне неправильно, потому как так невозможно узнать, в чем же ученик ошибался и исправиться в будущем), поэтому для вас, родители и дети, ответы к контрольной, чтобы проверить себя, когда в классе вы ее уже написали и сдали на проверку.
- Категория: Математика
Среднее арифметическое нескольких чисел — довольно сложная тема, с которой ученики впервые знакомятся в пятом классе, и не все и не всегда понимают ее с первого раза. Для взрослого понимания тема проста, но детям, порой, она дается нелегко. Так что же такое среднее арифметическое? Как его найти? Как решать типовые задачи на среднее арифметическое? Все эти вопросы разберем и на каждый дадим ответы в этой статье.
- Категория: Математика
Чтобы найти дробь от числа, нужно это число разделить на знаменатель дроби и умножить на числитель. Чтобы найти число по его дроби, нужно число разделить на числитель и умножить на знаменатель.
- Категория: Математика
Тему «Проценты» начинают изучать в четвертом-пятом классе, именно тогда ученики знакомятся с понятием процентов и учатся находить процент по числу и число по процентам. Потренироваться на заданиях изученной темы поможет наш тест для 5 класса по теме «Проценты».
Потренироваться на заданиях изученной темы поможет наш тест для 5 класса по теме «Проценты».
- Категория: Математика
Уже во втором классе на уроках математики дети сталкиваются с такими величинами, как площадь и объем. Учителя рассказывают, что площадь измеряется в квадратных сантиметрах или метрах и так далее, а объем — в кубических. Дети просто запоминают и пишут см2 или м2 или мм3. Очень немногие в тот момент задумывались, что же означает приписанная в верхнем уголке единицы длины цифра. По-настоящему со степенью мы познакомимся в пятом классе, а если хотите это сделать самостоятельно, можете и раньше :))
- Категория: Математика
Задачник по математике за пятый класс, автор Бунимович Е.А., в центре нашего внимания, а это значит, что теперь и к нему у нас на 7 гуру есть ГДЗ с ответами на задания. По этой книженции частенько задают домашнее задание, и поэтому мы посчитали своим долгом помочь вам решебником. Темы те же, что и в учебнике, идут в том же порядке. Разница в том, что тут не описана никакая теория, даны лишь задания друг за другом, которые нужно решать и еще раз решать. Кстати, в конце вашего задачника есть краткие ответы, кому-то и их будет достаточно. Ну а если тех ответов вам мало и нужно сверить весь процесс решения, добро пожаловать на 7гуру!
По этой книженции частенько задают домашнее задание, и поэтому мы посчитали своим долгом помочь вам решебником. Темы те же, что и в учебнике, идут в том же порядке. Разница в том, что тут не описана никакая теория, даны лишь задания друг за другом, которые нужно решать и еще раз решать. Кстати, в конце вашего задачника есть краткие ответы, кому-то и их будет достаточно. Ну а если тех ответов вам мало и нужно сверить весь процесс решения, добро пожаловать на 7гуру!
- Категория: Математика
Ответы к учебнику за пятый класс «математика. Арифметика и геометрия», авторы учебника: Е.А.Бунимович, Г.В.Дорофеев, С.Б.Суворова. Основное внимание в этом учебнике математики посвящено геометрии, геометрическим фигурам и вычислениям, с ними связанными. Но для начала повторяем пройденный в начальной школе материал, ведь все учились по разным программам и учителю нужно выяснить уровень знания учеников по разным темам. Дорогие родители, в первую очередь этот решебник для вас. Мы ни на минуту не сомневаемся, что вы можете с легкостью выполнить все эти задания и решить все задачи. Просто ГДЗ поможет вам очень быстро проверить, правильно ли ваш ребенок выполнил домашнее задание, не отвлекаясь от своих домашних дел и работы.
Дорогие родители, в первую очередь этот решебник для вас. Мы ни на минуту не сомневаемся, что вы можете с легкостью выполнить все эти задания и решить все задачи. Просто ГДЗ поможет вам очень быстро проверить, правильно ли ваш ребенок выполнил домашнее задание, не отвлекаясь от своих домашних дел и работы.
- Категория: Математика
В учебниках математики за пятый класс много теории, дети к такому еще не привыкли, да и родителям сложно ориентироваться в толстом учебнике при проверке домашнего задания. Уже с самого начала учебника математики автора Мерзляк, Полонский, Якир, за 5 класс, повторяем и систематизируем понятия из начальной школы, вводим новые правила и свойства. Учителя часто задают выучить правила и возвращаются к пройденному снова и снова. Детям и родителям зачастую неудобно выискивать давно пройденное в учебнике, а дети забывают материал и, конечно же, забывают, в какой теме учили нужное правило и на какой странице. Вам в помощь — все правила и определения из этого учебника.
Вам в помощь — все правила и определения из этого учебника.
- Категория: Математика
Дорофеев Г.В., Шарыгин И.Ф., Суворова С.Б., Е.А.Бунимович и другие из бомонда математиков приложили руку к созданию этого учебника за пятый класс. Листаешь учебник, и складывается впечатление, что это какая-то брошюра по математике, а не серьезное издание для обучения пятиклассников. Где уравнения? Где примеры на сложение, вычитание, умножение, деление с миллионами, да хотя бы с тысячами? Где нормальные на уровне пятого класса примеры с дробями? Это что, учебник для детей с отклонениями в развитии? Так или иначе, не удивлюсь, что ГДЗ по этому учебнику все же могут кому-то пригодиться, всякие ситуации бывают. Да и многие родители сейчас не видят смысла в таких глубоких знаниях, в том числе по математике. ГДЗ на 7 гуру поможет вам с математикой.
- Категория: Математика
Рабочая тетрадь по математике за пятый класс, авторы которой Потапов М. К. и Шевкин А.В., сделана к учебнику по математике Никольского С.М., так же за 5 класс, это одна линия УМК. В тетради даются задания по основным темам параллельно учебнику, нужно вписать ответы в пустые строки или окошки. Большое внимание в рабочей тетради Потапова за 5 класс уделяется решению задач, и это просто отлично, поскольку современные школьники зачастую с ними справляются не с такой легкостью, как хотелось бы. Мало того, родители современных школьников так же не все могут быстро найти правильное решение. Для вас, родители, мы сделали решебник к рабочей тетради Потапова. На этой странице 7 гуру — ГДЗ к первой части рабочей тетради.
К. и Шевкин А.В., сделана к учебнику по математике Никольского С.М., так же за 5 класс, это одна линия УМК. В тетради даются задания по основным темам параллельно учебнику, нужно вписать ответы в пустые строки или окошки. Большое внимание в рабочей тетради Потапова за 5 класс уделяется решению задач, и это просто отлично, поскольку современные школьники зачастую с ними справляются не с такой легкостью, как хотелось бы. Мало того, родители современных школьников так же не все могут быстро найти правильное решение. Для вас, родители, мы сделали решебник к рабочей тетради Потапова. На этой странице 7 гуру — ГДЗ к первой части рабочей тетради.
- Категория: Математика
В некоторых УМК по математике, к коим относится «Перспектива» с учебниками Дорофеева, критически мало времени уделено обучению детей умножению чисел столбиком. В третьем классе этого касаемся лишь вскользь, в четвертом рассматриваем простейшие примеры. А ведь умножать столбиком пригодится до самого 9 — 11-го. Можно умножать и в уме, но быстрее обычно будет — в столбик. Ничего не остается, как отработать навык дома, самостоятельно. Хороший учитель распечатает и задаст на дом карточки из тренажера, а что делать, если нет? Тогда распечатайте их сами у себя дома! Наши тренажеры 7 гуру на умножение столбиком рассчитаны на печать в формате А4 как на цветном, так и на монохромном принтере.
А ведь умножать столбиком пригодится до самого 9 — 11-го. Можно умножать и в уме, но быстрее обычно будет — в столбик. Ничего не остается, как отработать навык дома, самостоятельно. Хороший учитель распечатает и задаст на дом карточки из тренажера, а что делать, если нет? Тогда распечатайте их сами у себя дома! Наши тренажеры 7 гуру на умножение столбиком рассчитаны на печать в формате А4 как на цветном, так и на монохромном принтере.
- Категория: Математика
Задачи человеку в жизни приходится решать практически ежедневно, и взрослые это делают не задумываясь. Посчитать стоимость покупки, количество необходимых материалов во время ремонта — всему этому мы научились в школе. В четвертом классе пройдены уже практически все типы математических текстовых задач, дети научились логически находить решение и вычислять ответ. Логически, значит без буквенных неизвестных, без построения уравнения, что в какой-то мере даже сложнее, чем считать через х и у. А мы в свою очередь хотим поддержать полученные в школе навыки и даже развить их с помощью тренажера на 7 гуру. Скачивайте и занимайтесь.
А мы в свою очередь хотим поддержать полученные в школе навыки и даже развить их с помощью тренажера на 7 гуру. Скачивайте и занимайтесь.
- Категория: Математика
В четвертом классе темы «части» и «дроби» изучаются по всем существующим на данный момент УМК по математике, то есть по всем программам. В каких-то поверхностно, как в программе «Перспектива», учебники Дорофеева, в каких-то основательно, как в учебниках Петерсон. Но в любом случае дети за лето забывают, как оперировать с дробями, находить часть от целого и тому подобное. Цели нашего тренажера — не дать забыть за время каникул эту тему, либо потренироваться в решении заданий с дробями и задач на части целого во время изучения этого материала в школе в качестве дополнения к учебнику.
- Категория: Математика
Тренажер содержит задания на сложение и вычитание, умножение и деление разного уровня сложности. Один лист тренажера рассчитан на печать в формате А4. Задания разбиты на столбцы. Если используете тренажер в качестве пособия, позволяющего ученику 3-4 класса не забыть за лето математику, можно решать по одному столбцу в день. Если же нужно улучшить вычислительные навыки, столбика будет недостаточно, как минимум задание на день — половина страницы. Вы можете разрезать листы на столбцы и дозировать ребенку на свое усмотрение, в том числе вперемешку (столбец на +-, столбец на *:, к примеру). Скачивать как обычную картинку.
Один лист тренажера рассчитан на печать в формате А4. Задания разбиты на столбцы. Если используете тренажер в качестве пособия, позволяющего ученику 3-4 класса не забыть за лето математику, можно решать по одному столбцу в день. Если же нужно улучшить вычислительные навыки, столбика будет недостаточно, как минимум задание на день — половина страницы. Вы можете разрезать листы на столбцы и дозировать ребенку на свое усмотрение, в том числе вперемешку (столбец на +-, столбец на *:, к примеру). Скачивать как обычную картинку.
- Категория: Математика
Контрольные работы за пятый класс в соответствии с темами учебника математики, автором которого является Дорофеев. Критерии оценки этих контрольных следующие. Если решены все задания как обязательной, так и дополнительной части, ставится оценка пять. Не решено или решено неправильно одно или 2 задания из разных частей — четыре. Не решена дополнительная часть, а в обязательной нет одного задания — три.
- Категория: Математика
Итак, если у вас на уроках математики используется учебник автора по фамилии Виленкин, то предложенные ниже контрольные работы могут вам подойти. Контрольные подобраны в соответствии с изучаемым на уроках математики в пятом классе материалом, в соответствии с данным учебником. Контрольные работы разбиты по темам и даны в порядке изучения этих тем от вводной до итоговой контрольной работы.
- Категория: Математика
Примерные контрольные работы, специально разработанные для УМК к учебнику «Математика. 5 класс», авторы которого Мерзляк, Полонский, Якир. Контрольные охватывают все темы учебника. В каждой контрольной работе по два варианта с похожими заданиями.
- Категория: Математика
С задачами на движение дети знакомятся в четвертом классе начальной школы и решают их систематически до самого одиннадцатого. Эти задачи от класса к классу все усложняются, добавляется новый способ решения — с помощью уравнения, но сами задачи остаются неизменными. Приводим для вас тексты таких задач на движение от самых простых до усложненных.
Эти задачи от класса к классу все усложняются, добавляется новый способ решения — с помощью уравнения, но сами задачи остаются неизменными. Приводим для вас тексты таких задач на движение от самых простых до усложненных.
- Категория: Математика
Н.Я.Виленкин, В.И.Жохов, А.С.Чесноков и С.И.Шварцбург приложили свои руки к этому учебнику математики, напридумывали заданий, а мы с вами все их должны по порядочку решить и решить правильно, корректно оформить и написать ответы. Будем решать вместе!
- Категория: Математика
Рассмотрим основные свойства деления в математике.
- Категория: Математика
Поговорим о свойствах, или законах умножения.
- Категория: Математика
В этой статье мы рассмотрим все свойства вычитания, которые могут понадобиться при упрощении выражений и решении уравнений.
- Категория: Математика
Прибавить одно число к другому довольно просто. Рассмотрим пример, 6+3=9. Это выражение означает, что к шести единицам добавили три единицы и в итоге получили девять единиц. Или, если рассмотреть числовой отрезок: сначала по нему передвинулись на 6 единиц, а затем на 3. Числа 6 и 3, которые мы сложили, называются слагаемыми. А результат сложения — число 9 — называется суммой. В виде буквенного выражения этот пример будет выглядеть так: a+b=c, где a — слагаемое, b — слагаемые, c – сумма.
- Категория: Математика
Чтобы правильно переводить одну величину в другую, нужно знать, сколько в чем чего. В школьной программе меры длины, объема, площади, массы и времени изучаются вразброс по мере знакомства с новым разрядом чисел. Давайте соберем эту информацию воедино и оформим для наглядности в виде табличек. Картинки с таблицами можно скачать и распечатать для работы с детьми или учебы.
Картинки с таблицами можно скачать и распечатать для работы с детьми или учебы.
- Категория: Математика
Вот и вступили вы уже на взрослую дорожку взрослого пути через среднюю школу. Позади начальная школа, начальные классы, но это совершенно не означает, что впереди будет труднее и сложнее. Касается это как раз того самого учебника математики за пятый класс авторов Мерзляк, Полонский, Якир. Ну ладно, если вы учились по программе Перспектива или Школа России, тогда этот учебник вам в самый раз по нарастающей. А если же у вас были в четвертом классе учебники Истоминой, а уж тем более Петерсон, вам можно смело переходить по математике вместо пятого сразу в шестой. Учебник довольно простой, если у ребенка развита логика. ГДЗ к этому учебнику Математики за 5 класс, 3-е издание (2012-2018 год включительно).
- Категория: Математика
Скобки используются для указания на порядок выполнения действий в числовых и буквенных выражениях, а также в выражениях с переменными. От выражения со скобками удобно перейти к тождественно равному выражению без скобок. Этот прием носит название раскрытия скобок.
От выражения со скобками удобно перейти к тождественно равному выражению без скобок. Этот прием носит название раскрытия скобок.
- Категория: Математика
Деление столбиком или, правильнее сказать, письменный прием деления уголком, школьники проходят уже в третьем классе начальной школы, но зачастую этой теме уделяется так мало внимания, что к 9-11 классу не все ученики могут им свободно пользоваться. Деление столбиком на двузначное число проходят в 4 классе, как и деление на трехзначное число, а далее этот прием используется только как вспомогательный при решении каких-либо уравнений или нахождении значения выражения.
Математика и гармония: Задачи на «высушивание»
На страницах блога я уже писала о различных способах решения задач на смеси «Переливаем, смешиваем» и «Задачи на понижение концентрации».
Сегодня хочу рассмотреть так называемые задачи на «высушивание».
При решении этих задач следует помнить, что все тела, вещества, продукты содержат в себе воду, которая частично испаряется. Поэтому в решении надо каждый раз разделять данное нам вещество на воду и «сухой остаток». Количество воды может меняться, масса же сухого вещества остаётся неизменной.
Задача 1. Собрали 8 кг свежих цветков ромашки, влажность которых 85%. После того как цветки высушили, их влажность составила 20%. Чему равна масса цветков ромашки после сушки?
Решение. Заполним таблицу по условию задачи:
Масса, в кг | Содержание, в % | ||
воды | Сухого вещества | ||
Свежие цветы | 8 | 85 | 100 — 85 = 15 |
Высушенные | х | 20 | 100 — 20 = 80 |
1) 0,15 · 8 = 1,2 (кг) — масса сухого вещества в 8 кг;
2) 1,2 кг — 80%
x кг — 100%
Отсюда, х = 1,2 · 100 : 80 = 1,5 (кг).
Ответ: 1,5 кг
Задача 2. Из 22 кг свежих грибов получается 2,5 кг сухих грибов, содержащих 12% воды. Каков процент воды в свежих грибах?
Решение. Заполним таблицу по условию задачи:
Масса, в кг | Содержание, в % | ||
воды | Сухого вещества | ||
Свежие грибы | 22 | х | |
Сухие грибы | 2,5 | 12 | 100 — 12 |
Определим процент сухого вещества в высушенных грибах: 100-12 = 88% = 0, 88.
1) 2,5 · 0,88 = 2,2 (кг) — масса сухого вещества;
2) 2,2 кг : 22 · 100 = 10% сухого вещества содержится в свежих грибах;
3) 100 — 10 = 90% воды в свежих грибах.
Ответ: 90%
Задача 3. Свежие яблоки содержат 80% воды, а сушёные 10%. Сколько надо взять свежих яблок, чтобы получить 6 кг сушёных?
Решение.
Если в сушёных яблоках содержится 10% воды, то сухое вещество составляет 90%.
Найдём массу сухого вещества в 6 кг сушёных яблок:
6 · 0,9 = 5,4 9 (кг).
Та же масса сухого вещества была и в свежих яблоках, и она составляла 20% от их массы. Найдём массу свежих яблок:
5,4 : 0,2 = 27 (кг).
Ответ: 27 кг
Задача 4. Только что добытый каменный уголь содержит 2% воды, а после двухнедельного пребывания на воздухе он содержит 12% воды. На сколько килограммов увеличится масса одной добытой тонны угля после того, как она две недели пролежит на воздухе?
Эта задача обратна предыдущим: здесь влажность угля увеличивается за счёт поглощения влаги из воздуха.
Решение. Заполним таблицу по условию задачи:
Масса, в т | Содержание, в % | ||
воды | Сухого вещества | ||
Было | 1 | 2 | 100 — 2 |
Стало | х | 12 | 100 — 12 |
1) 1000 · 0,98 = 980 (кг) — масса сухого вещества в добытом угле;
2) 980 кг — это 88%, 980 : 0,88 ≈ 1114 (кг) — масса угля после двух недель пребывания на воздухе;
3)
1114
— 1000
= 114
(кг) — увеличение массы одной
добытой
тонны угля.
Ответ: 114 кг
Задача 5. В свежих грибах 70% влаги, а в сушёных 10%. Сколько килограммов свежих грибов надо собрать для того, чтобы получить 30 кг сушёных?
Решение.
1) В сушёных грибах сухое вещество составляет 90%.
90% от 30 кг — это 30 : 100 · 90 = 27 (кг).
2) 27 кг сухого вещества в свежих грибах составляют 30%.
1% от 27 кг — это 27 : 30 = 0,9 (кг). Тогда 100% составляют 0,9 · 100 = 90 (кг).
Ответ: 90 кг
Задачи для самостоятельного решения.
- Свежие грибы содержат 90% воды, а сухие — 12% воды. Сколько получится сухих грибов из 22 кг свежих грибов?
- Трава при высыхании теряет около 28% своей массы. Сколько было накошено травы, если из неё было получено 1,44 т сена?
- На
складе хранилась 51 т зерна, влажность
которого была 20%. Перед закладкой зерна
в зернохранилище его просушили, доведя
влажность до 15%.
 Сколько тонн зерна
засыпали в зернохранилище?
Сколько тонн зерна
засыпали в зернохранилище? - Имеется 0,5 т целлюлозной массы, содержащей 85% воды. После выпаривания получили массу, содержащую 25% целлюлозы. Сколько килограммов воды было выпарено?
- Пчёлы перерабатывают цветочный нектар в мёд, освобождая его от воды. Нектар обычно содержит 84% воды, а полученный из него мёд — 20%. Сколько килограммов нектара приходится перерабатывать пчёлам для получения одного килограмма мёда?
О трудолюбивом человеке, который практически не сидит без дела, говорят: «Трудится как пчёлка». Понять почему так говорят вам помогут следующие цифры.
Для выработки 100 граммов меда пчела облетает приблизительно миллион цветов.
Скорость полета пчелы составляет 65 км/ч, что приблизительно равно скорости движения автомобиля по городу.
Пчела за один полет набирает нектара практически столько, сколько она весит сама. С полным медовым желудочком пчела способна развивать скорость до 30 км/ч.
Чтобы
набрать 1 кг нектара, пчеле придется
совершить до 150 тысяч вылетов из улья.
В среднем за один вылет пчела преодолевает до 3 километров.
Чтобы произвести килограмм меда, пчеле необходимо пролететь в среднем до 450 тысяч километров. Это значит, что расстояние, которое пролетает пчела, аналогично расстоянию, которое необходимо пролететь, чтобы обогнуть экватор Земли примерно 10 раз.
Информация взята с сайта о животных.
процентов | Математика Новой Зеландии
Цель
Цель этой серии уроков состоит в том, чтобы обобщить знания учащихся о дробях и десятичных разрядах, чтобы дать им возможность работать с процентами с пониманием и компетентностью. Активно используются конкретные материалы для закрепления понимания учащихся.
Цели достижения
NA3-1: используйте ряд аддитивных и простых мультипликативных стратегий с целыми числами, дробями, десятичными дробями и процентами.
Разработка AO и другие учебные ресурсы
NA4-3: Найдите дроби, десятичные дроби и проценты от сумм, выраженных целыми числами, простыми дробями и десятичными дробями.
Разработка AO и другие учебные ресурсы
NA4-5: Знать эквивалентные десятичные и процентные формы для повседневных дробей.
Разработка AO и другие учебные ресурсы
NA5-5: Знать часто используемые дроби, десятичные дроби и процентные преобразования.
Разработка АО и другие учебные ресурсы
Конкретные результаты обучения
- Выражайте дробные и десятичные числа в процентах.
- Вычислите суммы в процентах, используя знание обыкновенных дробей и их процентных эквивалентов.
- Вычислите 100% из заданного процента.
- Создавайте контекстные процентные задачи для решения другими.
- Преобразование «неудобной» дроби в десятичную и отображение в процентах.
- Используйте и объясните вычисление процентов.
- Работа с процентами выше 100% и их объяснение.
- Понять и рассчитать процентное увеличение и уменьшение проблем.
Описание математики
Способность понимать проценты и грамотно работать с ними зависит от того, хорошо ли учащиеся понимают разрядное значение, нашу десятичную систему счисления, дроби и операции с ними. Важно, чтобы учащиеся имели возможность исследовать, распознавать, демонстрировать и формулировать эти связи для себя, а также иметь возможность свободно работать между ними.
Важно, чтобы учащиеся имели возможность исследовать, распознавать, демонстрировать и формулировать эти связи для себя, а также иметь возможность свободно работать между ними.
Реляционное мышление лежит в основе способности учащегося понять, что процент используется для выражения того, насколько велика или мала одна величина по отношению к другой величине (которая больше нуля). Процент – это отношение части к целому.
Процент — это способ выражения доли от 100 или другой способ записи сотых. Процент, от латинского per centum , буквально означает из (на) сто (процентов). Символ % состоит из знака / и двух нулей (00) из числа 100. Важно использовать ряд физических представлений, чтобы учащиеся могли четко видеть и устанавливать связи между дробями: например, . 75/100 (или 3/4), 75% в процентах и десятичное представление 0,75 той же суммы.
Проценты — это третий способ записи десятичных и дробных чисел. Таким образом, процент — это не новое понятие, а скорее новый способ выражения понятия «из 100» с использованием обозначения %.
Здравое понимание числа в десятичном разряде помогает учащимся работать с процентами. При этом учащийся может легко увидеть, например, что 0,6 составляет 6 десятых, а также 60 сотых и, следовательно, 60%, тогда как 0,06 составляет 6 сотых и, следовательно, составляет всего 6%. Студенты осознают преимущества работы с десятичными дробями, а не с дробями при преобразовании в проценты, особенно когда отношение не может быть представлено в виде обыкновенной дроби.
Формирование готовых знаний о обычных эквивалентных дробях для процентов , (1/4 = 25%, 1/2 = 50%, 3/4 = 75%, 1/10 = 10%, 1/5 = 20% , 1/8 = 12,5%), имея возможность использовать их в качестве эталона для расчета некоторых других процентов (например, 15% = 10% + половина 10%), а также упрощая дроби и выражая их в процентах (например, 9/36). = 1/4 = 25%) и являются ключевыми результатами. Использование формулы для расчета процента требует понимания того, что происходит: числитель дроби делится на знаменатель, что дает десятичную дробь, которая затем умножается на 100, чтобы выразить процент. Например, 72/120 х 100/1 = 0,6 х 100 = 60%. Это также можно представить как 6/10 из 100, что, конечно же, равно 60.
Например, 72/120 х 100/1 = 0,6 х 100 = 60%. Это также можно представить как 6/10 из 100, что, конечно же, равно 60.
Как и в любой математике, важны оценки навыков. Студенты должны предвидеть, какой ответ будет разумным. Например, если учащегося просят найти 9 % от 450, учащийся должен понимать, что он может найти 10 %, что равно 45, и 1 %, что равно 4,5, и предположить, что 9 %, таким образом, будет близко к 40.
В отвечая на вопросы, связанные с процентным увеличением или уменьшением , учащийся должен понимать, к чему относится процент. Например, увеличение на 100 % означает, что конечная сумма составляет 200 % от исходной суммы, а уменьшение на 100 % означает, что конечная сумма равна нулю. Необходимо соблюдать осторожность при расчете процентного изменения. Если, например, цену в 50 долларов увеличить на 10%, она вырастет на 5 долларов до 55 долларов. Если бы она была затем уменьшена на 10%, она уменьшилась бы на 10% от 55 долларов, или 5,50 долларов, в результате чего цена составила бы 49 долларов. .50. Два изменения здесь относятся к разным количествам.
.50. Два изменения здесь относятся к разным количествам.
Вычисление процентного изменения может быть сложной задачей, когда проблемы связаны с обратными процентами. Например, при нахождении исходной цены товара, за который вы заплатили 15 долларов после скидки 25%.
Важно обеспечить реалистичный контекст для задач на проценты. Полезно, чтобы учащиеся определяли, где в их собственной жизни появляются проценты. Если они соберут примеры из школьных данных, CensusAtschool, рекламных материалов и средств массовой информации (газеты, Интернет), это поможет им понять, насколько часто проценты используются в повседневной жизни.
Эти идеи представлены на пяти занятиях, однако, поскольку они включают в себя сложные концепции, которые необходимы учащимся для успешной работы с дробями, эти занятия можно растянуть на более длительный период времени.
Несмотря на то, что игры вводятся и используются на занятиях для закрепления идей, их также можно добавить к занятиям в классе или группе или отправить домой для решения семейных задач и развлечений.
Ссылки на систему нумерации
Этапы 7–8 (от расширенного мультипликативного до расширенного пропорционального)
Этот модуль поддерживает преподавание и обучение в разделе «Дроби для учащихся» e-ako 12 и дополняет учебные мероприятия в Книге 7 «Обучение дробям, десятичным числам и процентам» .
Необходимые ресурсы
- Доска счастливых сотен
- Метровая линейка
- Вращающиеся регионы
- Несколько счетов
- 10 x 10 квадратная бумага
- Карточки с десятичными стрелками
Деятельность
Сессия 1: Вводная сессия
SLO:
- Продемонстрировать понимание десятичной системы.
- Понимание языка процентов.
- Выражайте десятичные числа в процентах.
- Сформулируйте связь между десятичными дробями и процентами.
Занятие 1
- Проведите мозговой штурм по таблице группы/класса, что учащиеся знают о десятичных дробях.

Запишите их идеи. (например: «между целыми числами и частями стоит десятичная точка», «есть десятые, сотые, тысячные», «десятичные числа вы продолжаете делить на 10 по мере того, как идете вправо», «деци равно десяти» ….).
- Предоставьте учащимся следующее оборудование:
10 х 10 квадратная бумага, счеты, вращающаяся область, метровая линейка, доска счастливых сотен.Предложите учащимся поработать в парах. Каждый человек выбрал разное оборудование.
Напишите на таблице несколько десятичных дробей (например: 0,1, 0,01, 0,23, 0,5, 0,99, 0,001). Попросите пары учащихся показать и обсудить, как каждый из них выглядит на их оборудовании, и согласиться. (nb, 0,001 будет 1/10 от 1 квадрата, бусины, круга, сантиметра и счастливой сотни).
Слушайте язык и комментируйте услышанное.
- Предложите учащимся вернуть часть своего снаряжения в центр, выбрать другую часть и повторить.
- В группе выберите учащегося, который продемонстрирует каждое из десятичных чисел на своей единице оборудования, затем обсудите и наметьте общие характеристики всех единиц оборудования (например: они показывают 100 частей, каждая из которых равна 0,01 или одной сотой) .
 Обратите внимание, что линейка метра показывает тысячные доли (мм), а квадраты на сетке легче разделить на 0,001, чем в других представлениях.
Обратите внимание, что линейка метра показывает тысячные доли (мм), а квадраты на сетке легче разделить на 0,001, чем в других представлениях.
Занятие 2
- Напишите слово процентов в таблице класса/группы. Проведите коллективный мозговой штурм и запишите, что это означает для учащихся и контексты, в которых они слышат использование выражения «процент/процент». (Например: скидки на покупки, спортивные результаты, политические предпочтения, индикаторы загрузки и отображения на их компьютере/iPad).
- Запишите процентное значение рядом с десятичными числами из действия 1, шага 2 выше. (10%, 1%, 23%, 50%, 99% и 0,1%) и предложите учащимся показать это на выбранном ими оборудовании.
- Предложите им сосредоточиться на двух числовых представлениях и записать то, что заметили учащиеся. Например: 0,1 — это 1/10 и 10/100 или 10%.
- Попросите пары учащихся написать собственное определение «процента» и объяснить, почему мы используем слово «процент» и символ %.

Убедитесь, что обсуждение включает следующие моменты:
Процент – это способ выражения доли от 100 или другой способ записи сотых. Процент, от латинского per centum буквально означает из (за) сто (процентов). Символ % состоит из знака / и двух нулей (00) из числа 100.
Упражнение 3
- Раздайте каждой паре учащихся набор десятичных стрелок и бумагу.
Попросите их составить с помощью своих карточек со стрелками десятичное число меньше 1 и только до двух знаков (например, 0,15, 0,7, 0,05), записать его, сделать на оборудовании и записать в процентах.
- Предложите парам поделиться и обсудить то, что они заметили (при записи десятичного числа в процентах десятичная точка «перемещается» на два знака вправо), и объяснить, почему с помощью оборудования. (например, 0,15: 0,1 равно 1/10 или 10/100, а 0,05 равно 5/100. В сумме это 15/100 или 15%)
- Попросите пары учеников повторить это с трехзначными десятичными числами меньше единицы.

Задание 4
Завершите занятие, попросив учащегося записать в диаграмме класса дробное представление десятичных дробей и процентов, записанных в Упражнении 1, Шаге 2 и Задании 2, Шаге 2 выше: 10/100, 1 /100, 23/100, 50/100, 99/100 и 1/1000 (или 0,1 от 1/100). Пусть учащиеся прочитают их, чтобы убедиться, что они правильно произносят дробь (сотни dth s и тысяча dth s).
Запишите итоговые утверждения учащихся о связи между десятичной дробью, дробями и процентами.
Сессия 2
SLO:
- Демонстрация эквивалентов обыкновенных дробей для процентов.
- Вычислите суммы в процентах, используя знание обыкновенных дробей и их процентных эквивалентов.
- Вычислите 100% из заданного процента.
- Создавайте контекстные процентные задачи для решения другими.
Предоставьте учащимся процент оборудования из Упражнения 1, Шага 2 выше.
Задание 1
- Запишите эти проценты в таблицу классов.
 25%, 50%, 75%, 10%, 20%.
25%, 50%, 75%, 10%, 20%.
Передайте славянские счеты по классу/группе. Пока один ученик моделирует процентное соотношение на счетах, другой записывает долю сдвинутых бусинок в в обе стороны .25% 25/100 1/4 50% 50/100 1/2 75% 75/100 3/4 10% 10/100 1/10 20% 20/100 1/5 - Спросите, что учащиеся замечают в дробях (они упрощены до 9).0049 обыкновенные дроби, которые мы используем каждый день ).
Занятие 2
- Поставьте парам учащихся следующие задачи, чтобы решить их с использованием обыкновенных дробей. Скажите учащимся, что они должны быть в состоянии объяснить свои решения группе.
Дэнни съел 10% из 20 слив. Сколько он съел?
Лили получила 20% из 40 голосов. Сколько голосов она набрала?
Сколько голосов она набрала?
Айрини собрал 50% из 60 яблок. Сколько она выбрала?
Стиви косил 25% из 28 гектаров городских газонов. Сколько гектаров он скосил?
- Пусть они попарно поделятся своими решениями и обсудят. Послушайте их обсуждения и выделите любые ключевые моменты и использование ими обыкновенных дробей.
- Поставьте эти проблемы и повторите шаг 2 выше.
Кири съела 5% из 20 слив. Сколько она съела?
Энди получил 15% из 40 голосов. Сколько голосов она набрала?
Марк собрал 40% из 60 яблок. Сколько он выбрал?
Джо косил 65% из 28 гектаров общественных газонов в городе. Сколько гектаров она скосила?
- В классе обсудите, запишите и смоделируйте на счетах стратегии нахождения 5 %, (половина 10 %), 15 %, (10 % + половина 10 %), 40 % (4 x 10 % или 50 % — 10%), 65% (6 x 10% + половина 10% или 50% + 10% + половина 10%).
- Предоставьте учащимся несколько счетов и попросите их написать для одноклассников, чтобы решить (как минимум) 3 задачи, используя личные интересы, и процент, который вы можете вычислить, используя обыкновенные дроби или комбинации этих .
 Им нужно показать и записать решения проблем.
Им нужно показать и записать решения проблем.
Соберите их письменные задачи и объясните, что из них будет создан лист группового задания для распространения на следующем занятии.
Упражнение 3
- Поставьте задачу:
Сколько будет 100%, если Ману съест 15 вишен и это 5% полного мешка?
Предложите учащимся обсудить решение в парах. Поделитесь и продемонстрируйте один способ мышления, используя счеты, чтобы посмотреть на проценты и вычисления, а затем применить их к проблеме.
Смоделируйте еще дважды с другим номером, например. 7 — 5 %, 12 — 5 %
5% x 2 = 10%
10 х 10 = 100 %15 х 2 = 30 = 10 % 30 x 10 = 300 = 100 %
- Раздайте Приложение 1.
(Цель: попрактиковаться в вычислении 100% от заданного процента)
Попросите учащихся выполнить это задание самостоятельно или в парах. Пусть они продемонстрируют свое мышление в отведенном для этого свободном месте.
Пусть они продемонстрируют свое мышление в отведенном для этого свободном месте.
- Обсудите решения в парах.
- Запишите заключительные замечания учащихся об использовании обыкновенных дробей, в частности 1/10 и 10%, чтобы облегчить решение задач.
Перед занятием 3 скомпилируйте (выберите) задачи учащихся, созданные в Упражнении 2, шаг 4.
Занятие 3
SLO:
- Решите процентные задачи, созданные учащимися.
- Используйте знание эквивалентных дробей, чтобы упростить отношения до обыкновенных дробей и дать процентное значение (например, 9из 36 составляет 25%).
- Исследуйте и смоделируйте 1/8 и 1/3 как десятичные дроби и проценты.
- Преобразование «неудобной» дроби в десятичную и отображение в процентах.
- Используйте и объясните вычисление процентов.
Упражнение 1
Просмотрите выводы по Занятию 2 в виде схемы.
Раздайте учащимся задачи, созданные на Занятии 2, Упражнении 2, Шаге 4.
Предложите учащимся решить их самостоятельно или в парах. В группе обсудите решения и попросите студентов-писателей проверить их.
Занятие 2
- Просмотрите список в виде диаграмм из Занятия 2, Задания 1, Шага 1.
Имейте записи учащихся рядом с каждым их десятичным эквивалентом.25% 25/100 1/4 0,25 50% 50/100 1/2 (5/10) 0,5 75% 75/100 3/4 0,75 10% 10/100 1/10 0,1 20% 20/100 1/5 (2/10) 0,2 - Укажите, что, как они знают, некоторые задачи на процентов можно просто решить, упростив дробь, чтобы найти общую дробь, которую легко преобразовать в проценты.
- Поставьте эти три процентные задачи:
Том забил 9 из 36 голов, забитых его командой. Какой это был процент?
Какой это был процент?
Марни съела 4 из 40 слив в миске. Какой это был процент?
21 из 28 голосов были за Меле. Какой это был процент голосов?
Пусть учащиеся поработают в парах, чтобы решить задачи, и пары поделятся своими результатами.
Том забил 9/36 = 1/4 = 25% голов.
Марни съела 4/40 = 1/10 = 10% слив.
Меле набрал 21/28 = 3/4 = 75% голосов.
- Предложите учащимся предложить другие числа, которые они могли бы упростить до обыкновенных дробей или их кратных, и процентов из списка . Запишите это. (например, 12/16, 10/20, 4/8, 9/90, 3/30 и т. д.)
Занятие 3
- Задайте эти вопросы:
В распродаже говорилось, что цена снижена с 27 до 18 долларов. Какой процент скидки был?
Натан заплатил 8 долларов за небольшой пакет грибов. 1 доллар из них был налогом на товары и услуги. Какой процент от общей цены составлял налог на товары и услуги?
- Попросите другого ученика смоделировать и объяснить каждому ответ, используя счеты.
 В результате обсуждения учащийся разделит 100 бусинок на трети и восьмые, что приведет к необходимости найти 1/3 бусины и 1/2 бусины соответственно.
В результате обсуждения учащийся разделит 100 бусинок на трети и восьмые, что приведет к необходимости найти 1/3 бусины и 1/2 бусины соответственно.
Пусть учащийся запишет проценты (33,33% и 12,5%) в таблице класса/группы и запишет это в виде десятичной дроби (0,3333 и 0,125).
- Обратитесь к выводам, сделанным о взаимосвязи между десятичными знаками и процентами в Занятии 1, Упражнении 3.
- Напишите на схеме дробь 9/27 и упростите ее до 1/3. Попросите одного из учащихся объяснить 1/3. (выявить язык 1, разделенный или разделенный на 3).
Решите задачу на деление 1 ÷ 3, показав результат 0,3333.
0,3333 r
3) 1,0000
Предложите учащимся также вычислить 1 ÷ 3 на калькуляторе. Обсудите это в процентах.
Попросите учеников заменить 0,3333 на 33,33 на калькуляторе. Спросите, что они сделали, и выясните «умножить на 100».
- Повторите это с 1/8 и покажите, как 1/8 становится процентом.
Попросите учащихся предложить, как это можно записать и получить: 1/8 x 100/1.
- Используя эту «процедуру», изучите вычисления для известных обыкновенных дробей, таких как 1/2, 1/4, 3/4, 1/5, 2/3.
Например:
1/2 : 1 разделить на 2 = 0,5 0,5 x 100 = 50 %
1/4 : 1 разделить на 4 = 0,25 0,25 x 100 = 25 %
Упражнение 4
- Спросите: может ли это помочь нам, если в задаче нет знаменателя или дроби? Поставьте эту задачу:
7 из 49 человек в зале проголосовали против. Какой это процент?
Сначала попросите учащихся оценить процент.
(7/49 = 1/7 : 1/8 равно 12,5%, а 1/5 равно 20%, поэтому оно будет между 12,5% и 20%, но ближе к 12,5%) Посмотрите на это на счетах.? 1/5 1/7 1/8
Предложите учащимся вычислить процентное значение, используя деление в большую сторону и калькулятор.
(1 ÷ 7 = 0,1428 0,1428 x 100 = 14,28 % Это: 1/7 x 100/1 = 14,28 %)Обратитесь к исходной задаче и запишите ответ:
7 из 49 человек в комнате проголосовал против идеи. Какой это процент? 14,28 % или округлить до 14,3 %
Какой это процент? 14,28 % или округлить до 14,3 %
- Исследуйте эту задачу таким же образом:
Зоя забила 19 голов из 29 бросков. Каков был ее процент успеха?
(19/29 x 100/1 = 65,5%)
- Запишите несколько предложений учеников по решению дальнейших задач, включающих более сложные отношения, но с использованием их собственного интересного контекста .
- Предложите учащимся решить эти задачи с помощью вычислений.
Занятие 5
Завершите это занятие повторением знаний, полученных на сегодняшнем занятии.
(Обратите внимание, что мы можем использовать обыкновенные дроби для вычисления некоторых процентов. Если дробь сложная, мы можем вычислить ее десятичное значение, разделив числитель на знаменатель и преобразовав десятичную дробь в проценты, умножив ее на 100).
Сессия 4
SLO:
- Обзор подходов к решению процентных задач.

- Вычислите проценты путем пропорциональной корректировки коэффициентов, включающих множители 100.
- Работа с процентами выше 100% и их объяснение.
Занятие 1
- Начните это занятие с рассмотрения выводов Занятия 3.
- Передайте группе счеты и попросите учащихся смоделировать некоторые распространенные дроби/десятичные числа/проценты, назвав все три «названия».
- Предложите учащимся описать два способа вычисления процента от заданной дроби/отношения. Запишите эти:
1. Найдите дроби они могут упростить , чтобы сделать эквивалентные дроби, для которых они знают или могут вычислить проценты.
2. Рассчитайте, разделив числитель на знаменатель, чтобы найти десятичную сумму, и умножив ее на 100.
Занятие 2
Раздайте наборы карточек из Приложения 2 каждой паре учащихся.
(Цель: попрактиковаться в решении наилучших способов решения процентных задач. )
)
Предложите им рассортировать их по двум указанным стопкам, давая процентные решения для группы «наиболее обыкновенных дробей, которые они знают».
Задание 3
- Скажите учащимся, что сейчас будет изучен третий способ нахождения процентов.
Покажите счеты и спросите, каковы множители 100? (1, 2, 4, 5, 10, 20, 25, 50, 100)
Запишите идеи учащегося в таблице класса/группы и попросите их продемонстрировать свои ответы: 1 x 100, 2 x 50, 4 x 25 , 5 х 20, 10 х 10 на счетах.
- Поставьте задачу:
Таху решил 7 из 20 задач. Какой это процент?
Предложите учащимся обсудить в парах решение задачи.
- Попросите одного из учеников смоделировать это на счетах.
Напишите 7/20 х 5/5 = 35/100.Установите 20 в 100 раз
5 x 20 = 100Модель 7/20
(сито 80 бисерин)Модель 7/20 пять раз 
Смоделируйте это снова на счетах.
Попросите учащихся сформулировать, что значение не изменилось, поскольку и , и знаменатель, и числитель умножаются на 5 (и 5/5 = 1).
Вернуться к задаче:
Таху решил 7 из 20 задач. Какой это процент? 35%
- Изучите и попросите учащихся смоделировать на счетах, например:
Сколько процентов составляет:
14 из 50? (14/50 x 2/2 = 28/100 = 28%)
17 из 25? (17/25 х 4/4 = 68/100 = 68%)
3 из 10? ( 3/10 x 10/10 = 30/100 = 30%)
13 из 20? (13/20 x 5/5 = 65/100 = 65%)
- Предложите учащимся поработать в парах, чтобы обсудить и решить следующий набор задач, изображающих счеты.
Сколько процентов составляет:
35 из 50?
21 из 25?
7 из 10?
9 из 20?
Подтвердите решение, попросив ученика смоделировать его на счетах.
Упражнение 4
Раздайте приложение 3.
(Цель: попрактиковаться в выборе наилучшего решения задач на проценты.)
Перечислите три способа решения задач на проценты:
- Найдите дробей, которые они могут упростить , чтобы сделать эквивалентные дроби, для которых они знают или могут вычислить проценты.
- Рассчитайте, разделив числитель на знаменатель, чтобы найти десятичную сумму, и умножив ее на 100.
- Найдите знаменатели, которые являются множителями 100, и умножьте числитель и знаменатель на одно и то же число, чтобы получить дробь 100.
Предложите учащимся поработать в парах, как в Приложении 2 к Упражнению 2, шагу 1 выше, на этот раз распределив задачи по на три группы по . Пусть они выберут несколько задач из каждой группы для решения, а затем напишут несколько своих задач.
Деятельность 5
- Напишите 200% на графике. Предложите учащимся обсудить, возможно ли превысить 100%.
Обсудите некоторые примеры:
Предсказанная температура достигнет 25 o C. Она достигла 30 o C.
Она достигла 30 o C.
Это было 120% предсказания. (1/5 выше 100%, 30/25)
Моя цель состояла в том, чтобы сэкономить 100 долларов. Я сэкономил 130 долларов.
Это было на 130% моей цели. (130/100)
Я рассчитывал, что работа займет у меня 15 минут, но на это ушло полчаса.
Это было 200% ожидаемого времени. (двойной, 30/15)
Ожидалось, что число погибших составит 80 человек. К сожалению, окончательное число погибших составило 200 человек.
Это было 250% от ожидаемых потерь. (2 1/2 раза, 200/80)
- Попросите учащихся предложить примеры и записать их.
Занятие 6
Раздайте Приложение 4 парам учащихся.
В парах они должны решить, верны утверждения или нет.
Они должны в парах разделить и по очереди работать с примерами, продемонстрировать и объяснить их обоснование. Сделать оборудование доступным.
Занятие 7
Завершите занятие, записав основные идеи, выработанные на занятии.
Занятие 5
SLO:
- Оцените решения десятичных задач и объясните их обоснование.
- Вычислить процент от общей суммы.
- Понимание, расчет и демонстрация процентного увеличения и уменьшения проблем.
- Вычислите первоначальную цену из заданной процентной скидки и суммы скидки.
- Просмотр процента обучения.
Упражнение 1
- Поставьте задачу и сделайте калькуляторы доступными.
Штеффи забила 23% из 78 голов. Сколько голов она забила?
Попросите пары учащихся сначала записать оценку, а затем вычислить решение.
Дайте им время понять, как это сделать.
- Обсудите , почему решение равно 0,23 х 78 = 17,94, округлить до 18 ( 0,23 равно 23 сотым, так что это 23/100, или 23% от 78). Так Штеффи забила 18 мячей.
- Предложите учащимся предложить (как минимум) еще три похожие задачи из их собственного контекста.
 Запишите это. Попросите пары учащихся решить их, поделитесь и объясните свои решения.
Запишите это. Попросите пары учащихся решить их, поделитесь и объясните свои решения.
Деятельность 2
- В таблице классов напишите « оценка ». Попросите учащихся дать определение оценки и причин оценки.
- Предложите учащимся объяснить в парах, как бы они оценили следующее:
9,5% от 165 долларов (10% — это 16,50 долларов, поэтому 9,5% — около 15,50 долларов)
14% от 360 (10% — это 36, 5% — 18, поэтому 15% — это 36 + 18 = 54, поэтому 14 процентов — это около 50)
26% от 164 (25% — это 41, поэтому 26% — это около 43)
82% от 600 (80% — это 4/5, 1/5 — это 120, 4/5 — это 480, поэтому 82 % составляет около 490)
Запишите оценки учащихся.
Раздайте калькуляторы и попросите учащихся проверить.
Обсудите разумное округление.
Запишите расчеты учащихся рядом с оценками и сравните.
- Раздайте игру Оцените матч (Приложение 5) для 2-4 игроков.

(Цель: дальнейшее развитие навыков вычисления процентов).
Попросите тех, кто быстро закончит, написать новые задачи на предоставленных запасных карточках.
- Завершите игру, затем обсудите самые сложные оценки, исследуя причины этого.
Занятие 4
- Напишите « процентное увеличение/уменьшение » в таблице класса/группы и раздайте Приложение 6. Создайте пары учащихся обсудите и решите эти проблемы, связанные с процентным увеличением и уменьшением.
- Предложите им попарно поделиться и объяснить свои мысли.
При необходимости эти концепции могут быть смоделированы на счетах учителем или учениками.
Например:
Это 100% бус.
Это 200% бисера.
Бусины увеличились на 100%.
Произошло увеличение с на 100%.
Это увеличение до 200% (исходные 100%, +100%)
Это 300% бусинок.
Бусины увеличились на 200%.
Произошло увеличение с 200% .
Это увеличение до 300% (исходные 100%, + 200%) - Поставьте дополнительные задачи.
Первоначальная цена бруса для забора составляла 397 долларов.
Через два года цена увеличилась на 200%. Сколько сейчас будет стоить брус для забора? Обсудить.
Что, если бы цена в 397 долларов была снижена на 100%?
Это 100% бус.Вот так они выглядят при уменьшении на 100%. Нуль. - Из-за популярности фасона цена футболки в размере 30 долларов США была увеличена на 40%. Через две недели он был снижен на 40%. Рик сказал: «Цена снова вернулась к 29 долларам». Он прав?
Предложите учащимся обсудить это и обосновать свое решение Да/Нет.
Это можно легко смоделировать на счетах.
Например:
Показать 30 бисерин, добавить 12 бисерин (увеличение 40% от 30, что равно 12)
Показать 42 бисерины
Показать 42 бисеринки и вычесть 17 бисерин (уменьшение 40% от 42, что равно 16,8, округлить до 17)
Показать 25 бусин
Нет, Рик не прав.
Подчеркните, что процентное увеличение и уменьшение относятся к разным суммам.
- Вернуться к Приложению 6, внимательно изучив формулировку « to, by, of » и суммы, к которым относится увеличение или уменьшение.
Поставьте и попробуйте другие примеры, параллельные приведенным в Приложении 6.
Упражнение 5
- Вы можете поставить и исследовать эту последнюю задачу, хотя она концептуально сложная:
Вы получаете 15% скидку на футболку и платите 24 доллара. Какая была первоначальная цена?
Спросите, как учащиеся могут решить эту проблему.
Переформулируйте это так:
Если вы получили скидку 15%, значит, вы заплатили 85% от первоначальной цены. Как узнать первоначальную цену?
Как узнать первоначальную цену?
Предложите учащимся исследовать это с помощью калькулятора.
(Студенты могут найти 15% от 24, вычислив 24 x 0,15, а затем добавить это к 24. Но это не дает , а не исходную цену, потому что вычисленные 15% относятся к цене со скидкой, а не к первоначальной цене. )Посмотрите на это так:
Первоначальная цена $? был умножен на 0,85, чтобы получить цену со скидкой.
Следовательно, чтобы найти первоначальную цену, этот процесс выполняется в обратном порядке.
Цена со скидкой делится на 0,85, чтобы получить первоначальную цену $? цена.Например: 40 долларов (исходная) x 0,85 = 34 доллара (цена со скидкой)
(40 долларов были снижены на 15% путем умножения 40 на 0,85)Следовательно, чтобы найти исходную цену (в данном случае мы знаем, что она составляет 40 долларов) , должно произойти обратное .
То есть 34 доллара (цена со скидкой) ÷ 0,85 = 40 долларов (исходная цена).Таким образом, разделив 24 на 0,85, мы получим первоначальную цену = 28,24 доллара.

15% от 28,24 = 4,24.
28,24 доллара – 4,24 доллара = 24 доллара (цена со скидкой).
- Попросите учащихся предложить диаграмму, чтобы показать, что происходит.
Вместе исследуйте несколько примеров из жизни учащихся, чтобы понять, что происходит.
- Завершите это занятие записью размышлений учащихся о том, чему они научились, работая с процентами.
Домашняя ссылка
Уважаемые родители и Ванау,
В классе мы работали с процентами. Ваш ребенок хотел бы рассказать вам о том, чему он научился, и предложить вам поиграть в игру под названием «9».0049 Estimate Match , который находится в прилагаемом пластиковом пакете.
Мы верим, что вы найдете это одновременно сложным и увлекательным.
Приложения
Добавить в план
Третий уровень
Четвертый уровень
Пятый уровень
Рабочие листы по математике для пятого класса с ответами PDF
Бесплатные PDF-файлы для печати по математике
Поощряйте математическую гибкость вашего ребенка, когда он работает с нашими Рабочие листы по математике для пятого класса с ответами pdf . Эти рабочие листы были специально разработаны, чтобы улучшить их навыки решения математических задач, а также предложить им большие таланты для логической разработки решений. На самом деле, наши усилия по разработке и упрощению бесплатных печатных листов по математике для 5 класса заключались в том, чтобы предоставить вашим детям очень быстрые и простые стратегии решения, которые помогут им легко усваивать основные математические факты, концепции и закономерности.
Эти рабочие листы были специально разработаны, чтобы улучшить их навыки решения математических задач, а также предложить им большие таланты для логической разработки решений. На самом деле, наши усилия по разработке и упрощению бесплатных печатных листов по математике для 5 класса заключались в том, чтобы предоставить вашим детям очень быстрые и простые стратегии решения, которые помогут им легко усваивать основные математические факты, концепции и закономерности.
Все рабочие листы по математике для 5 класса по категориям
ЧИСЛО ЧИСЛА
ДОПОЛНЕНИЕ & ВЫЧИТАНИЕ
УМНОЖЕНИЕ
ОТДЕЛ
ЭКСПОНЕНТЫ
ТЕОРИЯ ЧИСЕЛ
ДЕСЯТИЧНЫЕ ЗНАЧЕНИЯ
ДОБАВИТЬ & ВЫЧИТАТЬ ДЕСЯТИЧНЫЕ
УМНОЖЕНИЕ ДЕСЯТИЧНЫХ ЗНАЧЕНИЙ
ДЕЛИТЬ ДЕСЯТИЧНЫЕ ДОЛЯ
ДРОБЕЙ И AMP; СМЕШАННЫЕ ЧИСЛА
ДОБАВИТЬ & ВЫЧИТАНИЕ ДРОБЕЙ
УМНОЖЕНИЕ ДРОБЕЙ
ДЕЛИТЬ ДРОИ
СМЕШАННЫЕ ОПЕРАЦИИ
РЕШЕНИЕ ПРОБЛЕМ
СООТНОШЕНИЯ И КОЭФФИЦИЕНТЫ
ПРОЦЕНТЫ
ДЕНЕЖНАЯ МАТЕМАТИКА
ПОСЛЕДОВАТЕЛЬНОСТЬ ЧИСЛОВ
ГРАФИК КООРДИНАТ
ПЕРЕМЕННЫЕ & ВЫРАЖЕНИЯ
ДАННЫЕ И AMP; ГРАФИК
ВЕРОЯТНОСТЬ & СТАТИСТИКА
ВРЕМЯ ГОВОРЯ
ЕДИНИЦЫ ИЗМЕРЕНИЯ
2D ЦИФРЫ
ТРЕУГОЛЬНИКИ & ЧЕТЫРЕХСТОРОННИЕ
СИММЕТРИЯ & ПРЕОБРАЗОВАНИЯ
3D ЦИФРЫ
ГЕОМЕТРИЧЕСКИЕ РАЗМЕРЫ
Важные факты о математических печатных формах для 5
-го -го класса Как мы знаем, математика является очень важным компонентом 5 -го класса, поэтому, поощряя домашнее обучение детей с помощью наших фантастических рабочих листов, они не только подготовят и укрепят уверенность в математике в их математическом классе, но в равной степени позволят им достичь нужное 5 -й класс математических понятий в приятной форме.
Убедитесь, что ваши дети понимают математические концепции, с нашими бесплатными печатными PDF-файлами для занятий по математике
Поскольку этот ресурс предоставляет все, что вам нужно знать в учебной программе по математике в пятом классе, просто убедитесь, что ваши дети понимают математические концепции с помощью наших бесплатных печатных PDF-файлов для занятий по математике .
Это так, потому что мы практически сформулировали очень простые упражнения с ответами через каждые 5 -й класс математических понятий. К таким понятиям относятся:
Разрядное значение и смысл числа; сложение, вычитание, умножение и деление целых чисел, десятичных дробей и дробей; проценты; коэффициенты; измерения; алгебра; геометрия; координаты; вероятность; данные; раз.
Кроме того, эти рабочие листы считаются идеальным руководством для преодоления страха перед математикой у детей из-за нашего замечательного дизайна, который сделает математику веселой, приятной и интересной для ваших 5 -й класс .
Word Problems on Percentage
Задача 1 :
Джейкоб правильно ответил на 50% вопросов в тесте из 30 вопросов и 90% в тесте из 50 вопросов. Какой процент всех вопросов Джейкоб ответил правильно?
Решение:
Общее количество вопросов в обоих тестах:
= 30 + 50
= 80
Количество вопросов, на которые он ответил правильно в тесте из 30 вопросов:
= 50% ⋅ 900 300002 = 0,5 ⋅ 30
= 15
Количество вопросов, на которые он ответил правильно в тесте из 50 вопросов:
= 90% ⋅ 50
= 0,9 ⋅ 50
= 4 правильно ответил в обоих тестах:
= 15 + 45
= 60
Процент правильных ответов Джейкоба:
= (60/80) ⋅ 100 %
= 75 %
все вопросы правильные.
Задача 2 :
В этом году куры на ферме снесли на 30% яиц меньше, чем в прошлом году. Если в этом году они снесли 3500 яиц, то сколько яиц они снесли в прошлом году?
Решение:
Пусть x будет количеством яиц, отложенных в прошлом году.
Дано : В этом году куры снесли на 30% яиц меньше, чем в прошлом году, и в этом году они снесли 3500 яиц.
Тогда мы имеем
(100-30)% x = 3500
70% x = 3500
0,7 ⋅ x = 3500
0,7x = 3500
Разделите каждую сторону на 0,7
x = 3500
. 5000
Итак, в прошлом году куры снесли 5000 яиц.
Задача 3 :
Мигель следует рецепту соуса маринара, для которого требуется половина столовой ложки уксуса. Если одна чашка эквивалентна 16 столовым ложкам, сколько примерно процентов от чашки уксуса составляет количество, указанное в рецепте?
Раствор:
Процент на чашку уксуса — это количество по рецепту:
= (Количество уксуса требуется/1 чашка уксуса) ⋅ 100%
= (Половина столовой ложки/16 столовых ложек) ⋅ 100 %
= (0,5/16) ⋅ 100%
≈ 3,1%
Итак, примерно 3,1 % на чашку уксуса — это количество, указанное в рецепте.
Задача 4 :
Цена книги со скидкой на 20% меньше розничной цены. Алексу удается купить книгу со скидкой 30% на специальной книжной распродаже. Какой процент от розничной цены заплатил Алекс?
Алексу удается купить книгу со скидкой 30% на специальной книжной распродаже. Какой процент от розничной цены заплатил Алекс?
Решение:
Пусть 100 долларов — розничная цена книги.
Цена книги после 20% скидки:
= (100 — 20)% ⋅ 100
= 80% ⋅ 100
= 0,8 ⋅ 100
= 80 долл.
= 0,7 ⋅ 80
= 56 долларов
Розничная цена составляет 100 долларов, и Алекс купил книгу за 56 долларов.
Итак, процент от розничной цены, которую заплатил Алекс, составляет 56%.
Задача 5 :
Каждый день Джейкоб съедает 40% фисташек, оставшихся в его банке на тот момент. В конце второго дня остается 27 фисташек. Сколько фисташек было в банке в начале первого дня?
Решение:
Пусть x будет количеством фисташек в начале первого дня.
Количество фисташек в конце первого дня:
= (100 — 40)% ⋅ x
= 60% ⋅ x
= 0,6x
= 80 долларов
Количество фистахий в конце второй день :
= (100 — 40)% ⋅ 0,6x
= 60% ⋅ 0,6x
= 0,6 ⋅ 0,6x
= 0,36x
: Число оставшихся секунд на конец дня 27.
Тогда у нас есть
0,36x = 27
Разделите каждую сторону на 0,36.
x = 75
Итак, в начале первого дня в банке было 75 фисташек.
Задача 6 :
Лили покупает куклу с 10-процентной скидкой от первоначальной цены в 105,82 доллара. Однако она должна заплатить налог с продаж в размере x% от цены со скидкой. Если общая сумма, которую она заплатила за куклу, составляет 100 долларов, найдите значение x.
Решение:
Цена куклы после 10%скидка:
= (100 — 10)%⋅ 105,82
= 90%⋅ 105,82
= 0,9 ⋅ 105,82
= 95,238 долл. США
. Налог с продаж по сниженной цене:
= (100 + x)%⋅ 95,238
= (100 + x)/100 ⋅ 95,238
= (1 + 0,01x) ⋅ 95,238
= 95,238 + 0,95238x
= 95,238 + 0,95238x
= 95,238 + 0,95238x
Дано : Общая сумма, которую Лили платит за куклу, составляет 100 долларов.
Тогда у нас есть
95,238 + 0,95238x = 100
Вычесть 95,238 с каждой стороны.
0,95238x = 4,762
Разделите каждую сторону на 0,95238 (Используйте калькулятор).
x ≈ 5
Таким образом, значение x равно примерно 5.
Задача 7 :
За две недели Джеймс съел 20 фунтов куриных крылышек и 15 фунтов хот-догов. Андерсон съел на 20 процентов больше куриных крылышек и на 40 процентов больше хот-догов. Учитывая только куриные крылышки и хот-доги, сколько процентов еды Андерсон съел больше, чем Джеймс, по весу (округлив до ближайшего процента).
Решение:
Всего фунтов куриных крылышек и хот-догов, съеденных Джеймсом:
= 20 + 15
= 35
Количество фунтов куриных крылышек, съеденных Андерсоном:
= (0) + 100 + %⋅ 20
= 120%⋅ 20
= 1,2 ⋅ 20
= 24
Компания фунтов хот -догов, съеденных Андерсоном:
= (100 + 40)%⋅ 15
= 140%⋅ 15
= 1,4 ⋅ 15
= 21
Всего фунтов куриных крылышек и хот-догов, съеденных Андерсоном:
= 24 + 21
= 45
Количество фунтов еды, съеденных Андерсоном больше, чем Джеймс:
= 45 — 35
= 10
Процентное увеличение от Джеймса к Андерсону:
2 =
2 35) ⋅ 100 % 90 134 ≈ 29 %
Итак, Андерсон съел примерно на 29 процентов больше еды, чем Джеймс, по весу.
Задача 8 :
Уильям играет в настольную игру, в которой он должен собрать как можно больше карточек. В свой первый ход он теряет 18 процентов своих карт. На втором ходу он увеличивает количество своих карт на 36 процентов. Если его последнее количество карт после этих двух ходов равно n, что из следующего представляет его начальное количество карт в виде n?
A) н/[(1,18)(0,64)]
B) (1,18)(0,64)n
C) н/[(1,36)(0,82)]
D) (0,82)(1,36)n
Решение:
Пусть x будет начальным количеством карт.
Количество карт после потери 18% карт в первый ход:
= (100 — 18)% ⋅ x
= 82% ⋅ x
= 0,82x
Количество карт после увеличения 36% карт на второй ход:
= (100 + 36)% ⋅ 0,82x
= 136% ⋅ 0,82x
= 1,36 ⋅ 0,82x
= (1,36)(0,82)x
Дано: Окончательное количество карт после этих двух ходов равно n.
Тогда у нас есть
(1,36)(0,82)x = n
Разделите каждую сторону на (1,36)(0,82).
x = n/[(1,36)(0,82)]
Таким образом, начальное количество карт в пересчете на n равно
n/[(1,36)(0,82)]
Следовательно, вариант C верен.
Задача 9 :
Исследователи ожидают, что из-за обезлесения популяция оленей будет сокращаться на 6 процентов каждый год. если текущая популяция оленей составляет 12 000, то найдите приблизительную ожидаемую численность популяции через 10 лет (с округлением до ближайших десятков).
Решение:
Популяция оленей через 1 год через 1 год:
= (100 — 6)%⋅ 12000
= 94%⋅ 12000
= 0,94 ⋅ 12000
Население оленя через 2 года. :
= 0,94 ⋅ 0,94 ⋅ 12000
= (0,94) 2 ⋅ 12000
Таким образом, популяция оленей через 10 лет после:
= (0,94) 10 ⋅ 12000
≈ 64606060731 10 ⋅ 12000
≈ 64606060606060731 10 ⋅ 12000
≈ 646060606060731 10 ⋅
Таким образом, ожидаемая численность оленей через 10 лет составляет около 6 460 особей.
Задача 10 :
Небольшой магазин одежды продает аксессуары 3 разных типов. 20% — шарфы, 60% — галстуки, а остальные 40 аксессуаров — ремни. Если половину галстуков заменить шарфами, сколько шарфов останется в магазине?
Решение:
Пусть x будет общим количеством аксессуаров в магазине.
Шарфы и галстуки составляют 80% всех аксессуаров.
Итак, оставшиеся 20% аксессуаров должны быть ремнями.
Тогда у нас есть
20% от x = 40
20% ⋅ x = 40
0,2x = 40
Разделите каждую сторону на 0,2.
x = 200
Всего в магазине 200 аксессуаров.
Количество шарфов в магазине:
= 20%⋅ 200
= 0,2 ⋅ 200
= 40
Количество связей в магазине:
= 60%⋅ 200
= 0,6 вно 200
. = 120
Половина из 120 завязок (60 завязок) заменяется косынками.
Теперь количество шарфов в магазине:
= 40 + 60
= 100
Итак, после замены половины галстуков на шарфы, в магазине будет 100 шарфов.
Пожалуйста, отправьте ваш отзыв на [email protected]
Мы всегда ценим ваши отзывы.
©Все права защищены. onlinemath5all.com
Как рассчитать проценты в Excel – примеры формул процентов
В этом уроке вы узнаете быстрый способ расчета процентов в Excel, найдете основную формулу процентов и еще несколько формул для расчета процентного увеличения, процентов всего и многое другое.
Расчет процента полезен во многих сферах жизни, будь то чаевые в ресторане, комиссия реселлера, подоходный налог или процентная ставка. Скажем, вам посчастливилось получить промокод на скидку 25% на новый плазменный телевизор. Это хорошая сделка? И сколько в итоге придется заплатить?
В этом уроке мы рассмотрим несколько методов, которые помогут вам эффективно вычислять проценты в Excel, и изучим основные процентные формулы, которые избавят вас от догадок при расчетах.
- Процентные основы
- Процентная формула Excel
- Расчет процента от общего числа
- Расчет процентного изменения (увеличение/уменьшение в процентах)
- Рассчитать сумму и итог в процентах
- Увеличение/уменьшение числа на процент
Основы расчета процентов
Термин «проценты» происходит от латинского per centum , что означает «на сто». Как вы, наверное, помните из школьного курса математики, процент — это дробь от 100, которая рассчитывается путем деления числителя на знаменатель и умножения результата на 100.
Как вы, наверное, помните из школьного курса математики, процент — это дробь от 100, которая рассчитывается путем деления числителя на знаменатель и умножения результата на 100.
Основная формула процентов выглядит следующим образом:
(Часть/Целое)*100 = Процент
Например, если у вас было 20 яблок, и вы отдали 5 своим друзьям, сколько вы отдали в процентах? Выполнив простой расчет =5/20*100 вы получите ответ — 25%.
Так обычно считают проценты в школе и в повседневной жизни. Вычислять проценты в Microsoft Excel еще проще, поскольку Excel выполняет некоторые операции автоматически в фоновом режиме.
К сожалению, универсальной формулы Excel для расчета процентов, которая охватывала бы все возможные сценарии, не существует. Если вы спросите кого-нибудь: «Какую формулу процентов я использую, чтобы получить желаемый результат?», скорее всего, вы получите ответ типа «Ну, это зависит от того, какого именно результата вы хотите достичь».
Итак, позвольте мне показать вам несколько простых формул для расчета процентов в Excel, таких как формула процентного увеличения, формула для получения процентов от общей суммы и многое другое.
Базовая процентная формула Excel
Основная формула для расчета процентов в Excel выглядит следующим образом:
Часть/Сумма = Проценты
Если вы сравните ее с основной математической формулой для вычисления процентов, то заметите, что в процентной формуле Excel отсутствует часть *100. При вычислении процента в Excel не нужно умножать полученную дробь на 100, так как Excel делает это автоматически, когда к ячейке применяется формат Процент.
А теперь давайте посмотрим, как можно использовать процентную формулу Excel на реальных данных. Предположим, у вас есть число » Заказанный товар » в столбце B и « Доставленный товар » в столбце C. Чтобы узнать процент доставленных товаров, выполните следующие действия:
- Введите формулу
=C2/B2 в ячейку D2, и скопируйте его на столько строк, сколько вам нужно. - Нажмите кнопку Percent Style (вкладка Home > группа Number ), чтобы отобразить полученные десятичные дроби в процентах.

- Не забудьте при необходимости увеличить количество знаков после запятой, как описано в разделе Советы по работе с процентами.
- Готово! 🙂
Та же последовательность шагов должна быть выполнена при использовании любой другой процентной формулы в Excel.
В следующем примере в столбце D отображается округленный процент доставленных товаров без указания десятичных знаков.
Вычисление процентов от суммы в Excel
По сути, приведенный выше пример является частным случаем вычисления процентов от суммы. Теперь давайте рассмотрим еще несколько примеров, которые помогут вам быстро вычислить процент от общей суммы в Excel для разных наборов данных.
Пример 1. Сумма находится в конце таблицы в определенной ячейке
Очень распространен сценарий, когда у вас есть сумма в одной ячейке в конце таблицы. В этом случае процентная формула будет аналогична той, которую мы только что обсудили, с той лишь разницей, что ссылка на ячейку в знаменателе является абсолютной ссылкой (с $). Знак доллара фиксирует ссылку на данную ячейку, поэтому что она никогда не меняется, где бы ни копировалась формула.
Знак доллара фиксирует ссылку на данную ячейку, поэтому что она никогда не меняется, где бы ни копировалась формула.
Например, если у вас есть некоторые значения в столбце B и их сумма в ячейке B10, вы должны использовать следующую формулу для расчета процентов от суммы:
=B2/$B$10
Вы используете относительную ссылку на ячейку B2, потому что хотите, чтобы она менялась при копировании формулы в другие ячейки столбца B. Но вы вводите $B$10 как абсолютную ячейку ссылка, потому что вы хотите оставить знаменатель фиксированным на B10 при автоматическом заполнении формулы до строки 9.
Совет. Чтобы сделать знаменатель абсолютной ссылкой, либо введите знак доллара ($) вручную, либо щелкните ссылку на ячейку в строке формул и нажмите F4.
На приведенном ниже снимке экрана показаны результаты, возвращаемые формулой. Столбец Проценты от общего числа отформатирован как проценты с двумя десятичными знаками.
Пример 2. Части общей суммы находятся в нескольких строках
В приведенном выше примере предположим, что у вас есть несколько строк для одного и того же продукта, и вы хотите знать, какую часть общей суммы составляют все заказы на этот конкретный продукт.
В этом случае вы можете использовать функцию СУММЕСЛИ, чтобы сначала сложить все числа, относящиеся к данному продукту, а затем разделить это число на общую сумму, например:
=СУММЕСЛИ(диапазон, критерий, сумма_диапазон) / итог
Учитывая, что столбец A содержит все названия продуктов, столбец B перечисляет соответствующие количества, ячейка E1 — это название интересующего вас продукта, а общее количество находится в В ячейке B10 ваша реальная формула может выглядеть примерно так:
=СУММЕСЛИ(A2:A9 ,E1, B2:B9) / $B$10
Естественно, вы можете указать название продукта непосредственно в формуле, вот так:
=СУММЕСЛИ(A2:A9, "вишня", B2:B9) / $B$10
Если вы хотите узнать, какую часть суммы составляют несколько различных продуктов, сложите результаты, возвращаемые несколькими функциями СУММЕСЛИ, а затем разделите это число на общее количество. Например, следующая формула вычисляет процент вишни и яблок:
=(СУММЕСЛИ(A2:A9, "вишня", B2:B9) + СУММЕСЛИ(A2:A9, "яблоки", B2:B9)) / $B$10
Дополнительные сведения о функции СУММ см. в следующих руководствах:
в следующих руководствах:
- Как использовать функцию СУММЕСЛИ в Excel
- Excel СУММЕСЛИМН и СУММЕСЛИ с несколькими критериями
Как рассчитать процентное изменение в Excel
Из всех формул для расчета процентного соотношения в Excel наиболее часто используется формула процентного изменения.
Формула Excel для процентного изменения (процентное увеличение/уменьшение)
Для расчета процентного изменения между значениями A и B используйте следующую формулу:
Процентное изменение = (B — A) / A
При применении этой формулы к реальным данным важно правильно определить, какое значение А, а какое В. Например, вчера у вас было 80 яблок, а у вас 100, значит, теперь у вас на 20 яблок больше, чем раньше , что на 25% больше. Если у вас было 100 яблок, а теперь у вас 80, то количество яблок уменьшилось на 20, то есть на 20%.
Учитывая вышеизложенное, наша формула Excel для процентного изменения принимает следующий вид:
(Новое значение — Старое значение) / Старое значение
А теперь давайте посмотрим, как вы можете использовать эту формулу процентного изменения (также известную как формула процентного увеличения Excel) в ваших электронных таблицах.
Пример 1. Расчет процентного изменения между двумя столбцами
Предположим, что у вас есть цены за последний месяц в столбце B и цены за этот месяц в столбце C. Затем вы можете ввести следующую формулу в ячейку D2 для расчета процентного изменения на листе Excel :
=(C2-B2)/B2
Эта формула процентного изменения вычисляет процентное увеличение/уменьшение в этом месяце (столбец C) по сравнению с предыдущим месяцем (столбец B).
После копирования формулы в другие строки не забудьте нажать кнопку Percent Style на ленте, чтобы отобразить десятичные дроби в процентах, и вы получите результат, аналогичный тому, что вы видите на снимке экрана ниже. В этом примере положительные проценты, которые показывают процентное увеличение, отформатированы обычным черным цветом, а отрицательные проценты (процентное уменьшение) — красным с использованием метода, описанного в этом совете.
Пример 2. Расчет процентного изменения между строками
Если у вас есть один столбец чисел, скажем, столбец C, в котором перечислены еженедельные или ежемесячные продажи, вы можете рассчитать процентное изменение, используя следующую формулу:
= (C3-C2)/C2
Где C2 — это 1 st и C3 2 nd ячейка с данными.
Примечание. Обратите внимание, что вы должны пропустить первую строку с данными и поместить процентную формулу Excel в ячейку 2 nd , в данном примере это D3.
После применения процентного формата к столбцу с формулой процентного изменения вы получите следующий результат:
Если вы хотите рассчитать процентное изменение по сравнению с определенной ячейкой, вам необходимо исправить ссылку на эту ячейку, используя абсолютную ссылку на ячейку со знаком $, например. $С$2.
Например, вот формула процентного изменения Excel, которая вычисляет процентное увеличение / уменьшение для каждого месяца по сравнению с январем (C2):
= (C3-$C$2)/$C$2
формулу вниз, чтобы скопировать ее в другие ячейки, абсолютная ссылка ($C$2) останется прежней, а относительная ссылка (C3) изменится на C4, C5 и так далее.
Вычисление суммы и итога в процентах
Как вы только что видели, вычислять проценты в Excel легко, как и вычислять суммы и итоги, если вы знаете проценты.
Пример 1. Рассчитать сумму по итогу и в процентах
Предположим, вы покупаете новый ноутбук за 950 долларов, и они взимают с этой покупки НДС 11%. Вопрос в том, сколько вы должны заплатить сверх чистой цены? Другими словами, что такое 11% от 950 долларов?
Поможет следующая формула:
Итого * Процент = Сумма
Предполагая, что общее значение находится в ячейке A2, а проценты в ячейке B2, приведенная выше формула превращается в простую =A2*B2 и возвращает 104,50.
Помните, что когда вы вводите число, за которым следует знак процента (%) в Excel, число интерпретируется как сотая часть его значения. Например, 11% на самом деле хранится как 0,11, и Excel использует это базовое значение во всех формулах и вычислениях.
Другими словами, формула =A2*11% эквивалентно =A2*0,11 . Естественно, вы можете использовать десятичное число, соответствующее проценту, непосредственно в формуле, если это лучше подходит для ваших рабочих листов.
Пример 2. Расчет суммы по сумме и процентам
Например, ваш друг предложил вам свой старый компьютер за 400 долларов, что на 30% меньше первоначальной цены. Вы хотите знать, какова была первоначальная цена.
Так как 30% — это скидка, вы сначала вычтите ее из 100%, чтобы узнать, какой процент вы действительно должны заплатить (100% — 30% = 70%). Теперь вам нужна формула для расчета исходной цены, т.е. для нахождения числа, 70% которого равняется 400.
Формула выглядит следующим образом:
Сумма / Процент = Итого
Применительно к реальным данным, может принимать любую из следующих форм:
=A2/B2
или
92/664 = A или
=A2/70%
Как увеличить/уменьшить число в процентах
Приближается сезон отпусков, и это указывает на изменение ваших обычных еженедельных расходов. Возможно, вы захотите рассмотреть различные варианты, чтобы узнать свое оптимальное недельное пособие.
Для увеличьте сумму в процентах, используйте следующую формулу:
= Сумма * (1 + %)
Например, чтобы увеличить значение в ячейке A1 на 20%, используйте следующую формулу:
= A1*(1+20%)
К уменьшите сумму в процентах:
= Сумма * (1 — %)
Например, чтобы уменьшить значение в ячейке A1 на 20%, формула :
=A1*(1-20%)
В нашем примере, если A2 — ваши текущие расходы, а B2 — процент, на который вы хотите увеличить или уменьшить эту сумму, вот формулы, которые вы должны ввести в ячейка С2:
Увеличение в процентах:
=A2*(1+B2)
Уменьшение в процентах:
=A2*(1-B2)
Как увеличить/уменьшить весь столбец на процент
Предположим, у вас есть столбец чисел, который вы хотите увеличить или уменьшить на определенный процент, и вы хотите иметь обновленные числа в том же столбце, а не добавлять новый столбец с формулой.
Вот 5 быстрых шагов для решения этой задачи:
- Введите все числа, которые вы хотите увеличить или уменьшить, в каком-либо столбце, в данном примере столбце B.
- В пустую ячейку введите одну из следующих формул:
Увеличение в процентах:
=1+20%
Уменьшить на процент:
=1-20%
Естественно, вы можете заменить 20% в приведенных выше формулах на желаемый процент.
- Выделите ячейку с формулой (в нашем случае C2) и скопируйте ее, нажав Ctrl + C.
- Выберите диапазон ячеек, который вы хотите изменить, щелкните правой кнопкой мыши выделение и выберите Специальная вставка…
- В диалоговом окне Специальная вставка выберите Значения под Вставить , Умножить под Операция и нажмите OK .
И вот результат — все числа в столбце B увеличены на 20%:
Таким же образом можно умножить на или разделить на столбец чисел на определенный процент. Просто введите желаемый процент в пустую ячейку и выполните шаги, описанные выше.
Просто введите желаемый процент в пустую ячейку и выполните шаги, описанные выше.
Так вы вычисляете проценты в Excel. И даже если работа с процентами никогда не была вашим любимым видом математики, с помощью этих основных процентных формул вы можете заставить Excel делать всю работу за вас. На сегодня все, спасибо за прочтение!
Вас также могут заинтересовать
Рабочие листы по математике для 5-го класса
Секрет того, как стать ботаником в математике, заключается в практике, предлагаемой нашими печатными рабочими листами по математике для 5-го класса, включающими такие упражнения, как использование порядка операций со скобками, фигурными скобками и фигурными скобками. решать выражения, генерировать шаблоны из двух правил, выполнять операции с многозначными целыми числами, а также с десятичными дробями до сотых и дробями. Преобразование между стандартными единицами измерения разного размера в заданной системе измерения, построение линейного графика для отображения набора данных, измерение объема путем подсчета кубов единиц измерения, графических точек на плоскости координат и многое другое. Попробуйте наши бесплатные рабочие листы по математике для 5 класса и начните свою практику!
Попробуйте наши бесплатные рабочие листы по математике для 5 класса и начните свою практику!
All
Order of Operations
Patterns
Place Value
Multiplication & Division
Decimals
Fractions
Measurement
Time
Money
Data & Graphs
Coordinate Planes
Shapes
Volume и площадь поверхности
Исследуйте более 5600 рабочих листов по математике для пятого класса
Порядок операций: скобки, квадратные скобки, фигурные скобки
Знайте порядок операций: сначала вычисляются самые внутренние скобки ( ), затем [ ] следующий слой скобок, и, наконец, вычисляются операции внутри фигурных скобок { }.
Завершение выкройки | Увеличение и уменьшение
Поразмышляйте над правилом, определяющим каждый шаблон в этих pdf-файлах с рабочими листами по математике для 5-го класса, и выясните, увеличивается оно или уменьшается, и напишите следующее число в последовательности.
Написание названий номеров | Миллиарды
По мере того, как в ваш словарный запас добавляются слова «миллиарды», «десять миллиардов» и «сотни миллиардов», становится важным также знать их написание. Выразите числительные в виде числовых слов без особых усилий с помощью этих упражнений.
Умножение 3-значного числа на 2-значное | Standard
Сделайте наши распечатанные листы по математике для 5-го класса вашим любимым местом, если вы хотите укрепить навыки умножения. Находить произведение трехзначных и двузначных чисел точно и быстро с практикой.
Сложение десятичных знаков в числовой строке | Десятки
Читать модель числового ряда, понимать целую часть числа, десятичную часть: десятые доли и сумму. Лучше всего подходит для ознакомления вашей команды с десятичным сложением.
Сложение правильных дробей по горизонтали
Обильные упражнения для практики сложения правильных дробей с разными знаменателями ждут ваших детей 5-го класса в этих математических рабочих листах в формате pdf. Бери, ставь и тренируйся!
Преобразование дюймов, футов и ярдов
Изобилие упражнений для преобразования единиц длины между дюймами и футами в первой части, ярдами и футами в следующей и между ярдами и дюймами в последней, эти PDF-файлы представляют собой навязчивую печать.
Преобразование часов, минут и секунд в секунды
Повторение мантры 1 час = 3600 с, а минута = 60 с обеспечит детям 5-го класса беспрепятственное изучение этих распечатываемых математических листов. Умножьте и сложите, чтобы выразить время в секундах.
Подсчет монет и банкнот
Сэкономленный пенни — это заработанный пенни. Подчеркните привычку экономить, пока дети считают монеты и купюры в каждой копилке и отвечают на вопросы, исходя из суммы, сэкономленной или потраченной пятью друзьями.
Построение линейного графика
Богатые множеством упражнений по построению линейных графиков, наши PDF-файлы с рабочими листами по математике для 5-го класса удобны тем, что помогают учащимся упорядочивать собранные данные, маркировать оси и давать подходящие названия.
Определение положения реальных объектов
Реальные объекты размещаются в разных точках 1-го квадранта декартовой плоскости. Запишите координаты x-y или упорядоченные пары в части A и определите элемент, расположенный в указанной точке в части B.
Классификация треугольников по сторонам | Без мер
Изучите стороны каждого треугольника в наших печатных листах по математике для 5 класса, используйте линейку для измерения сторон или доверьтесь своему наблюдению и классифицируйте треугольники как равносторонние, равнобедренные или разносторонние.
Подсчет кубов для нахождения объема прямоугольных призм
Проанализируйте слои и подсчитайте количество единичных кубов, заполняющих пространство в каждом слое прямоугольной призмы, и просуммируйте их для определения объема.
Традиционные единицы США
Метрические единицы
Порядок операций с вложенными скобками | PEMDAS
Ускоренная практика решения выражений с помощью наших рабочих листов по математике для 5-го класса в формате PDF. Сначала выполняйте операции в скобках, а затем возведение в степень, умножение, деление, сложение и вычитание.
Идентификация шаблона с двумя правилами
Может ли ваш пятиклассник сделать вывод о двух основных правилах сложения и вычитания в каждом ряду чисел? Пусть они понаблюдают за образцом, найдут задействованные операции и закончат узор.
Далее »
CBSE Class 5 Математика Процентные вопросы MCQ, вопросы с несколькими вариантами ответов по математике
Скачать PDF
- Математика
CBSE Class 5 Mathematics Percentage MCQ с ответами доступны в формате Pdf для бесплатной загрузки. Вопросы MCQ по математике для класса 5 с ответами были подготовлены в соответствии с последними учебными планами, книгами NCERT и шаблонами экзаменов, предложенными в Стандарте 5 CBSE, NCERT и KVS. Вопросы с несколькими вариантами ответов являются важной частью экзаменов за семестр 1 и семестр 2 по математике для 5-го класса и при правильном выполнении могут помочь вам получить более высокие оценки. Обратитесь к дополнительным MCQ по главам для NCERT Class 5 Mathematics, а также загрузите более свежие учебные материалы по всем предметам
Percentage Class 5 Mathematics MCQ
Учащиеся 5 класса, изучающие математику, должны обратиться к следующим вопросам с несколькими вариантами ответов и ответами на проценты в стандарте 5. Эти вопросы MCQ с ответами на математику 5 класса будут представлены на экзаменах и помогут вам получить хорошие оценки
Эти вопросы MCQ с ответами на математику 5 класса будут представлены на экзаменах и помогут вам получить хорошие оценки
Процент вопросов MCQ Класс 5 Математика с ответами
Вопрос: 25% =
- а) 0,25
- б) 25
- в) 2,5
9,0028
2 Ответ:320084
Question: 9% =
- a) 0.09
- b) 9
- c) 0.9
Answer: 0.09
Question: 1.5 =
- a) 150%
- b) 0.15 %
- C) 15%
Ответ: 150%
ВОПРОС: 50% из 200 =
- A) 100
- B) 50
- C) 10
34343444444444444444444444444444444444444444444444444444444444444444444444н. Вопрос: 0,06% от 800 =
- а) 0,48
- B) 48
- C) 4,8
Ответ: 0,48
ВОПРОС: 5% из рупий 5 =
- A) 0,25 P
- B) 2,5 P
- C) C) C) C) C) 0,25 P
- B) 2,5 P
- C) C) C) C) C) C) C)
- B).

Ответ: 0,25 P
Вопрос: В слове КЛАСС сколько процентов буквы S =
- а) 40%
- б) 20%
- в) 4%
3 %
Вопрос: 20% от 1 часа 30 минут составляет
- а) 18 минут
- b) 30 минут
- c) 26 минут
Ответ: 18 минут
Вопрос: Рина правильно написала 22 из 50 слов. Какой процент слов Рина написала правильно?
- a) 44%
- b) 40%
- c) 50%
Answer: 44%
Question: 23/100 =
- a) 23%
- b) 0.23%
- в) 2,3%
Ответ: 23%
Вопрос: Анил сказал, что 3/4 его друзей носят очки. Какой процент его друзей носит очки?
- а) 75%
- б) 30%
- в) 25%
Ответ: 75%
Вопрос. 25%
б) 20% в) 15% Ответ: 25%
Вопрос: В школе 600 учеников.
 60% — мальчики. Сколько учениц в школе?
60% — мальчики. Сколько учениц в школе?- а) 240
- б) 360
- в) 100
Ответ: 240
Вопрос: В школе 120 учеников явились на экзамен X класса. Если 90 % учащихся сдали первый дивизион, сколько студентов сдали первый дивизион?
- а) 108
- б) 105
- в) 100
Ответ: 108
Вопрос: Что из следующего эквивалентно 2,02?
- а) 202%
- б) 20,2%
- в) 0,02%
Ответ: 202%
Вопрос: Что из следующего эквивалентно 8%?
- а) 0,08
- б) 0,008
- в) 0,8
Ответ: 0,08
Вопрос: Сколько процентов от 20 составляет 16?
- а) 80%
- б) 20%
- в) 30%
Ответ: 80%
Вопрос: Сколько процентов от рупии составляет 40 пайсов?
- а) 40%
- б) 60%
- в) 50%
Ответ: 40%
Вопрос: Сколько процентов от 6 литров составляют 20 мл?
- а) 1/3 %
- б) 2/3 %
- в) 3/3 %
Ответ: 1/3 %
Вопрос: 9026 9026 9026 9026 9026 9026 9026
3 3 б) 0,021 в) 0,21 Ответ: 0,69
Вопрос: Что больше (i) 12% от 400 или (ii) 18% от 200?
- a) (i)
- b) (ii)
- c) оба числа равны
Ответ: (i)
Вопрос: В наборе чисел 1, 2, 3, 4, 5 , 6, 7, 9, 11, 12 процентов четных чисел составляет
- а) 40%
- б) 20%
- в) 11%
Ответ: 40%
9 8 это 2?- а) 25%
- б) 20%
- в) 40%
Ответ: 25%
Вопрос: Какой процент от 140 рупий составляет 7 рупий?
- A) 5%
- B) 0,5%
- C) 20%
Ответ: 5%
Теги:
- CBS pdf MCQ
- Класс 5 Математика MCQ pdf
- CBSE Класс 5 Математика
- Математика Класс 5 MCQ
- CBSE Класс 5 Глава Математика MCQ
- MCQ для Класса 5 Математика
Click for more Mathematics Study Material › MCQs for Class 5 Mathematics CBSE Class 5 Mathematics Average MCQs CBSE Class 5 Mathematics Decimals MCQs CBSE MCQ по математике: расстояние, время и скорость, класс 5 MCQ: математические коэффициенты и множители CBSE, класс 5 CBSE, класс 5: математические дроби, MCQ CBSE Class 5 Mathematics Geometric Constructions MCQs CBSE Class 5 Mathematics Geometry MCQs CBSE Class 5 Mathematics Integer MCQs CBSE Class 5 Mathematics Introduction to Algebra MCQs CBSE Class 5 MCQ по математике для больших чисел MCQ по математике CBSE класса 5 MCQ по математике для измерения CBSE класса 5 CBSE Class 5 Mathematics Measuring Temperature MCQs CBSE Class 5 Mathematics Operations on Large Numbers MCQs CBSE Class 5 Mathematics Order of Operations MCQs CBSE Class 5 Mathematics Patterns MCQs CBSE MCQ по математике класса 5 MCQ по математике периметра и площади CBSE класса 5 MCQ по математике класса 5 CBSE по прибылям и убыткам CBSE Class 5 Mathematics Ratio MCQs CBSE Class 5 Mathematics Rounding off Numbers MCQs CBSE Class 5 Mathematics Symmetry and Nets of Solids MCQs CBSE Class 5 Mathematics Unitary Method MCQs CBSE Class 5 Mathematics Volume MCQ CBSE Class 5 Math Question Bank MCQs Set A
Вопросы с несколькими вариантами ответов для компьютеров класса V
Вопросы с множественным выбором для класса V английский
Вопросы с множественным выбором для математики класса V
Вопросы с множественным выбором для науки класса V наука
Вопросы с множественным выбором для Class V Social Science
NCERT.
 Решения
Решения Образцы документов
Вопросы для заполнения
Рабочие листы для печати
Книги NCERT
Задания для печати
Latest Syllabus
Useful Resources
Online Test
Practice Worksheets
Tags:
- CBSE MCQ
- CBSE Class 5 Mathematics MCQ
- CBSE Class 5 Mathematics pdf MCQ
- Class 5 Mathematics MCQ pdf
- CBSE Математика для 5-го класса
- Математика для 5-го класса MCQ
- CBSE 5-й курс по математике Глава MCQ
- MCQ для 5-го класса по математике
Таблица дат экзаменов для 10-го и 12-го классов
Информационная таблица для экзаменов Совета CBSE, класс 10
(Прокрутите вниз, чтобы просмотреть лист данных для класса 12)
Дата сдачи экзаменов CBSE Board Class 12
Подробнее
Уведомление CBSE 40/2021 Программа «Посол инноваций»
Это со ссылкой на уведомление CBSE № 40/2021 от 04. 05.2021 о программе «Посол инноваций» — программа онлайн-обучения для учителей CBSE в сотрудничестве с Инновационной ячейкой Министерства образования (MIC) и AICTE.
В связи с текущим…
05.2021 о программе «Посол инноваций» — программа онлайн-обучения для учителей CBSE в сотрудничестве с Инновационной ячейкой Министерства образования (MIC) и AICTE.
В связи с текущим…
Подробнее
Викторина «Наследие Индии» 2021 2022
Викторина CBSE «Наследие Индии» проводится каждый год для повышения осведомленности о сохранении человеческого наследия, разнообразия и уязвимости памятников и объектов наследия Индии. Это попытка Совета мотивировать будущие поколения этой страны…
Подробнее
Процесс переоценки 10-го и 12-го семестров 2 2022
Оценка сборников ответов осуществляется в соответствии с четко установленной политикой. Чтобы гарантировать, что оценка будет безошибочной, CBSE предпринимает несколько шагов. После строгого соблюдения этих действий результат готов. Хотя в CBSE есть отлаженная система оценивания,…
Подробнее
Парикша Пе Чарча 2022
5-й выпуск Парикхас Пе Чарча, уникальная интерактивная программа достопочтенного премьер-министра со студентами, учителями и родителями, будет проходить в виртуальном режиме в феврале 2022 года.




 Как вы, наверное, помните из школьного курса математики, процент — это дробь от 100, которая рассчитывается путем деления числителя на знаменатель и умножения результата на 100.
Как вы, наверное, помните из школьного курса математики, процент — это дробь от 100, которая рассчитывается путем деления числителя на знаменатель и умножения результата на 100. =5/20*100 вы получите ответ — 25%.
=C2/B2 в ячейку D2, и скопируйте его на столько строк, сколько вам нужно.
 Знак доллара фиксирует ссылку на данную ячейку, поэтому что она никогда не меняется, где бы ни копировалась формула.
Знак доллара фиксирует ссылку на данную ячейку, поэтому что она никогда не меняется, где бы ни копировалась формула. =B2/$B$10 
=СУММЕСЛИ(диапазон, критерий, сумма_диапазон) / итог =СУММЕСЛИ(A2:A9 ,E1, B2:B9) / $B$10 =СУММЕСЛИ(A2:A9, "вишня", B2:B9) / $B$10 =(СУММЕСЛИ(A2:A9, "вишня", B2:B9) + СУММЕСЛИ(A2:A9, "яблоки", B2:B9)) / $B$10  в следующих руководствах:
в следующих руководствах:
=(C2-B2)/B2 = (C3-C2)/C2 
= (C3-$C$2)/$C$2 
=A2*B2 и возвращает 104,50. =A2*11% эквивалентно =A2*0,11 . Естественно, вы можете использовать десятичное число, соответствующее проценту, непосредственно в формуле, если это лучше подходит для ваших рабочих листов.
=A2/B2 =A2/70% 
= A1*(1+20%) =A1*(1-20%) =A2*(1+B2) =A2*(1-B2) 
Увеличение в процентах:
=1+20%
Уменьшить на процент:
=1-20%
Естественно, вы можете заменить 20% в приведенных выше формулах на желаемый процент.
 Просто введите желаемый процент в пустую ячейку и выполните шаги, описанные выше.
Просто введите желаемый процент в пустую ячейку и выполните шаги, описанные выше. Попробуйте наши бесплатные рабочие листы по математике для 5 класса и начните свою практику!
Попробуйте наши бесплатные рабочие листы по математике для 5 класса и начните свою практику!




 Эти вопросы MCQ с ответами на математику 5 класса будут представлены на экзаменах и помогут вам получить хорошие оценки
Эти вопросы MCQ с ответами на математику 5 класса будут представлены на экзаменах и помогут вам получить хорошие оценкиВопрос: 0,06% от 800 =
- а) 0,48
- B) 48
- C) 4,8
Ответ: 0,48
ВОПРОС: 5% из рупий 5 =
- A) 0,25 P
- B) 2,5 P
- C) C) C) C) C) 0,25 P
- B) 2,5 P
- C) C) C) C) C) C) C)
- B).

Ответ: 0,25 P
Вопрос: В слове КЛАСС сколько процентов буквы S =
- а) 40%
- б) 20%
- в) 4%
3 %
Вопрос: 20% от 1 часа 30 минут составляет
- а) 18 минут
- b) 30 минут
- c) 26 минут
Ответ: 18 минут
Вопрос: Рина правильно написала 22 из 50 слов. Какой процент слов Рина написала правильно?
- a) 44%
- b) 40%
- c) 50%
Answer: 44%
Question: 23/100 =
- a) 23%
- b) 0.23%
- в) 2,3%
Ответ: 23%
Вопрос: Анил сказал, что 3/4 его друзей носят очки. Какой процент его друзей носит очки?
- а) 75%
- б) 30%
- в) 25%
Ответ: 75%
Вопрос. 25%
Вопросы с несколькими вариантами ответов для компьютеров класса V
Вопросы с множественным выбором для класса V английский
Вопросы с множественным выбором для математики класса V
Вопросы с множественным выбором для науки класса V наука
Вопросы с множественным выбором для Class V Social Science
 05.2021 о программе «Посол инноваций» — программа онлайн-обучения для учителей CBSE в сотрудничестве с Инновационной ячейкой Министерства образования (MIC) и AICTE.
В связи с текущим…
05.2021 о программе «Посол инноваций» — программа онлайн-обучения для учителей CBSE в сотрудничестве с Инновационной ячейкой Министерства образования (MIC) и AICTE.
В связи с текущим…

 Сколько тонн зерна
засыпали в зернохранилище?
Сколько тонн зерна
засыпали в зернохранилище?
 Обратите внимание, что линейка метра показывает тысячные доли (мм), а квадраты на сетке легче разделить на 0,001, чем в других представлениях.
Обратите внимание, что линейка метра показывает тысячные доли (мм), а квадраты на сетке легче разделить на 0,001, чем в других представлениях.

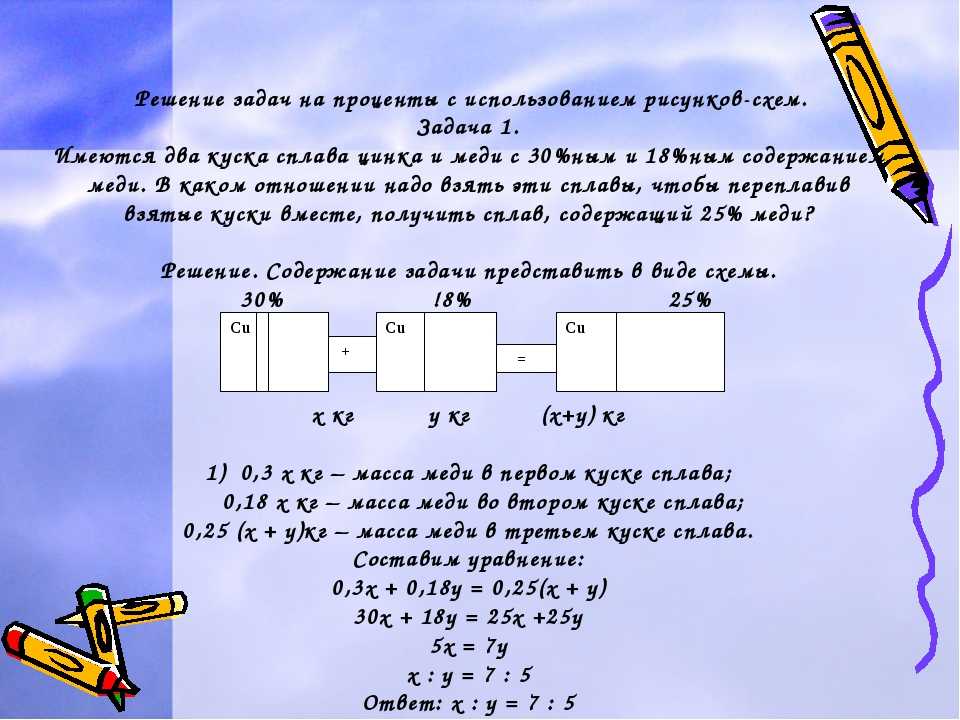 25%, 50%, 75%, 10%, 20%.
25%, 50%, 75%, 10%, 20%.  Сколько голосов она набрала?
Сколько голосов она набрала?  Им нужно показать и записать решения проблем.
Им нужно показать и записать решения проблем.  Пусть они продемонстрируют свое мышление в отведенном для этого свободном месте.
Пусть они продемонстрируют свое мышление в отведенном для этого свободном месте.  Какой это был процент?
Какой это был процент?  В результате обсуждения учащийся разделит 100 бусинок на трети и восьмые, что приведет к необходимости найти 1/3 бусины и 1/2 бусины соответственно.
В результате обсуждения учащийся разделит 100 бусинок на трети и восьмые, что приведет к необходимости найти 1/3 бусины и 1/2 бусины соответственно. 
 Какой это процент? 14,28 % или округлить до 14,3 %
Какой это процент? 14,28 % или округлить до 14,3 % 
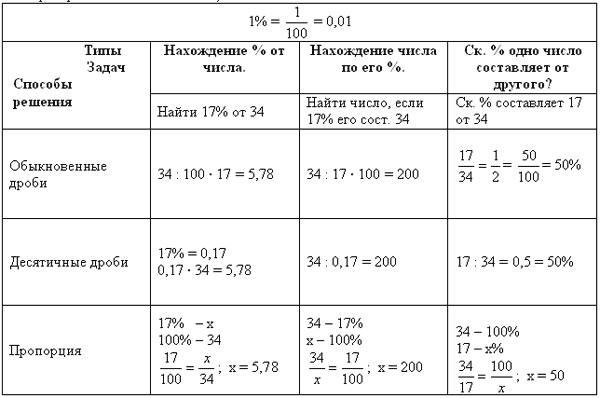
 Она достигла 30 o C.
Она достигла 30 o C.  Запишите это. Попросите пары учащихся решить их, поделитесь и объясните свои решения.
Запишите это. Попросите пары учащихся решить их, поделитесь и объясните свои решения.
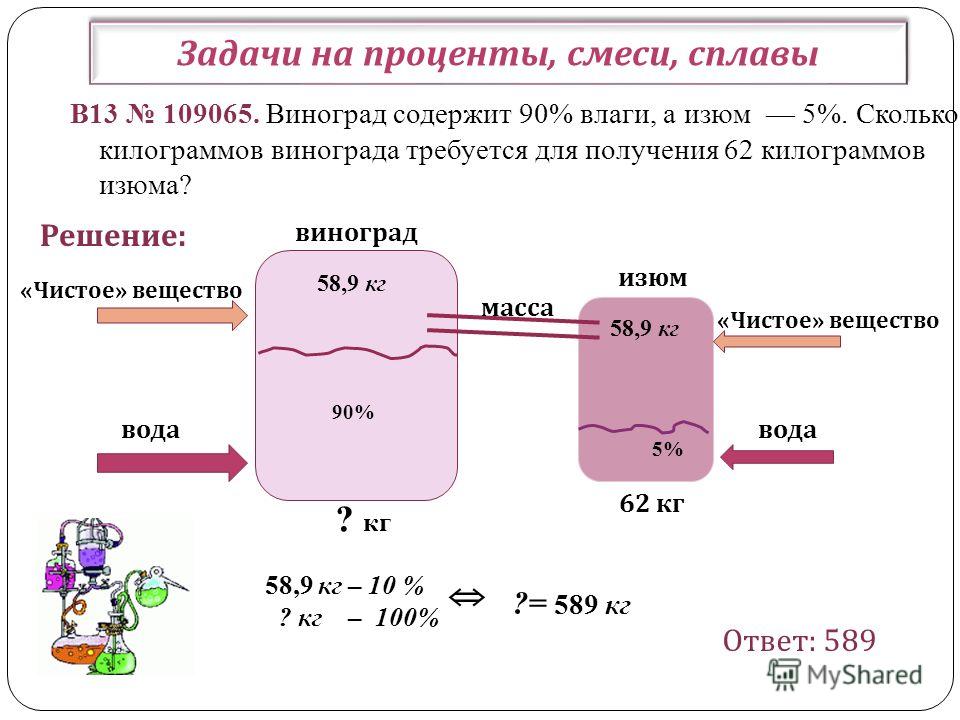

 Как узнать первоначальную цену?
Как узнать первоначальную цену? 