Задачи на простые проценты: Простые проценты. Решение задач

Содержание

что это, как рассчитать, формула, примеры

Проценты – это плата, уплачиваемая за сумму денег, независимо от того, предоставлена ли она взаймы, заимствована или инвестирована. Простые проценты – это особый тип расчета процентов, который не учитывает сложные проценты. Начисление сложных процентов – это повторяющийся процесс получения (или начисления) процентов, добавления этой суммы процентов к основной сумме денег, а затем получения еще большего количества процентов в следующем периоде из-за увеличения остатка на счете.

Продолжайте читать, чтобы узнать, как рассчитать простые проценты и почему этот расчет иногда не является точным представлением ваших процентных платежей.

Определение и примеры простых процентов

Проценты представляют собой комиссию, которую вы платите по кредиту, или доход, который вы получаете по депозитам. Простые проценты – это особый способ измерения процентов, который не учитывает несколько периодов процентных платежей или начислений. Другими словами, процентная ставка будет применяться только к основной сумме кредита или инвестиции – на нее не будут влиять какие-либо начисленные проценты.

Проценты могут повлиять на вас в различных аспектах вашей финансовой жизни:

Когда вы берете деньги взаймы: вы должны погасить сумму, которую вы взяли взаймы, и внести дополнительные платежи по процентам, которые представляют собой стоимость заимствования.
Когда вы даете деньги взаймы: вы обычно устанавливаете процентную ставку и получаете процентный доход в обмен на то, что ваши деньги становятся доступными для других людей.
При внесении денег на депозит: по процентным счетам, таким как сберегательные счета, выплачивается процентный доход, потому что вы предоставляете свои деньги банку для ссуды другим.

Как рассчитать простые проценты?

Это уравнение является самым простым способом расчета процентов. Как только вы поймете, как рассчитать простые проценты, вы можете перейти к другим расчетам, таким как годовая процентная доходность (APY), годовая процентная ставка (APR) и сложные проценты.

Чтобы рассчитать простые проценты, умножьте основную сумму на процентную ставку и время. Вот формула простых процентов:

Простые проценты = Основная сумма × Процентная ставка × Время

Использование калькуляторов

Если вы не хотите выполнять эти расчеты самостоятельно, вы можете воспользоваться калькулятором или попросить Google выполнить расчеты за вас. В Google просто введите формулу в поле поиска, нажмите «Ввод», и вы увидите результаты. Например, поиск «5/100» выполнит для вас ту же функцию (результат должен быть 0,05).

Для простого расчета процентов используйте любой онлайн-калькулятор простых процентов, которых в сети Интернет предостаточно.

Как работают простые проценты

Понимание простых процентов – одна из самых фундаментальных концепций для управления вашими финансами. Это включает в себя простую математику, но калькуляторы могут сделать всю работу за вас, если вы предпочитаете упрощение задачи. Понимая, как работают проценты, вы получаете возможность принимать более эффективные финансовые решения, которые экономят ваши деньги.

Например, предположим, что вы инвестируете 100 долларов (основная сумма) по ставке 5% годовых на один год. Простой расчет процентов:

$100 долларов × 0,05 процентной ставки × 1 год = $5 простых процентов, полученных через год.

Обратите внимание, что процентная ставка (5%) отображается в виде десятичной дроби (0,05). Чтобы сделать свои собственные вычисления, вам нужно будет преобразовать проценты в десятичные дроби. Например, чтобы преобразовать 5% в десятичную дробь, разделите пять на 100, чтобы получить 0,05.

Легкий трюк, чтобы запомнить это, состоит в том, чтобы думать о слове «процент» как о делении «на 100». Вы можете преобразовать процент в десятичную форму, разделив его на 100. Или просто переместите десятичную точку на две позиции влево.

Если вы хотите рассчитать простые проценты за более чем 1 год, рассчитайте процентный доход, используя основную сумму за первый год, умноженную на процентную ставку и общее количество лет.

$100 × 0,05 процентной ставки × 3 года = $15 простых процентов за три года

Ограничения простых процентов

Расчет простых процентов обеспечивает очень простой способ взглянуть на проценты. Это введение в понятие процентов в целом. В реальном мире ваши проценты – независимо от того, платите вы их или зарабатываете – обычно рассчитываются с использованием более сложных методов.

В кредит могут быть включены и другие расходы, кроме процентов. Эти расходы повлияют на общую сумму, которую вы потратите на кредит в течение года, но они могут не быть включены в процентную ставку, которую вам назначит кредитор.

Например, для таких кредитов, как 30-летняя ипотека, расчет простых процентов не является полностью точным способом расчета ваших затрат, поскольку они не учитывают затраты на закрытие, которые могут повлиять на вашу годовую процентную ставку.

Эффекты сложных процентов со временем становятся более выраженными, и это еще одна причина, по которой 30-летняя ипотека – плохой кандидат для расчета простых процентов. В течение 30-летнего срока действия кредита процентные расходы значительно добавятся к общей стоимости, уплачиваемой заемщиком.

Когда вы начинаете учитывать начисление процентов, вам нужно использовать более сложные расчеты, которые измеряют «частоту начисления процентов» или как часто начисляются проценты. Это может быть ежедневно, ежемесячно, ежегодно или с какой-либо другой периодичностью. Каждая частота будет давать разные результаты.

Например, когда вы занимаете средства с помощью кредитной карты, вы можете оценить, сколько процентов вы платите, используя простые проценты. Тем не менее большинство кредитных карт указывают годовую процентную ставку (APR) для клиентов, но на самом деле они начисляют проценты ежедневно, и общая сумма основной суммы долга и процентов за каждый день становится основой для следующего начисления процентов. В результате вы накапливаете намного больше в процентах, чем вы бы подсчитали, рассчитывая простые проценты.

Подведем итог

Простые проценты – это самый простой способ рассчитать сумму, которую вы заработаете или заплатите за инвестиции или кредит.

Вы можете рассчитать простые проценты, умножив основную сумму на процент процентной ставки и измеряемое время.

Хотя простые проценты являются отличным инструментом для получения приблизительных оценок, обычно гораздо точнее рассматривать расчет процентов, учитывающий эффекты начисления сложных процентов.

Игорь Титов

Экономист, финансовый аналитик, трейдер, инвестор. Личные интересы – финансы, трейдинг, криптовалюты и инвестирование.

Простые проценты — определение термина

закономерность роста величины (капитала), если определенный заданным процентом прирост прибавляется к исходной величине лишь в конце определенного срока; напр., при p% годовых исходный капитал K превратится через n лет в капитал K(1 + np/100)

Научные статьи на тему «Простые проценты»

, которая может определяться простыми и сложными процентами….
Декурсивная ставка процента называется ссудным процентом и представляет собой выраженное в процентах. ..
Учетные ставки могут быть простыми и сложными….
Простую учетную ставку рассчитывают по формулам: Рисунок 1. Формула….

С позиции кредитора при проведении краткосрочных финансовых операций выгодно использование простых процентов

Статья от экспертов

Рассмотрено динамическое моделирование при решении сюжетных математических задач. Доказано, что моделирование задачной ситуации является доминирующей эвристикой, которая значительно облегчает поиск решения задачи. Автором презентовано методику работы над задачами на простые и составные проценты с использованием динамического моделирования задачи. Этапы вывода формул простых и составных процентов проиллюстрированы при помощи схем.

Creative Commons

Научный журнал

Например, как проценты на проценты; проценты эффективности; композиционный процент; доходности с учетом.

..
= X • (1 + p • d / y) n Рассмотрим два варианта вложений с использованием простых и сложных процентов…
; простой процент….
Так, вложения с использованием сложного процента гораздо выгоднее, чем с простым процентом….
В случае простого процента график увеличения капитала получается линейный, поскольку вы снимаете прибыль

Статья от экспертов

Автор сравнивает наращение по схеме простых и сложных процентов при кратном начислении, и показывает, что сложные проценты становятся выгоднее простых после первого начисления.

Creative Commons

Научный журнал

Еще термины по предмету «Высшая математика»

Аликвотная дробь

дробь вида 1 n, где n > 1 — натуральное число

Замыкание (множества)

пересечение всех замкнутых множеств, содержащих данное множество M топологического пространства; множество всех точек прикосновения данного множества M; обозначается M̅ или [M], или cl M;

Нормальная кривизна

(нормальная кривизна поверхности в направлении данной кривой на поверхности) — проекция вектора кривизны кривой на нормаль к поверхности

Проценты простые
Простой процент
Схема простых процентов

Простые ставки ссудных процентов
Проценты
Процент
Простой
Простая
Прость

Простая дуга, простая кривая, простая линия
Сложный процент
Процент выполненного
Процент (interest)
Процент сложный
Ставка процента

Процент за кредит
Процент раскрываемости
Проценты обычные
Проценты сложные
Накопленный процент

Смотреть больше терминов

Повышай знания с онлайн-тренажером от Автор24!

Напиши термин
Выбери определение из предложенных или загрузи свое
Тренажер от Автор24 поможет тебе выучить термины с помощью удобных и приятных карточек

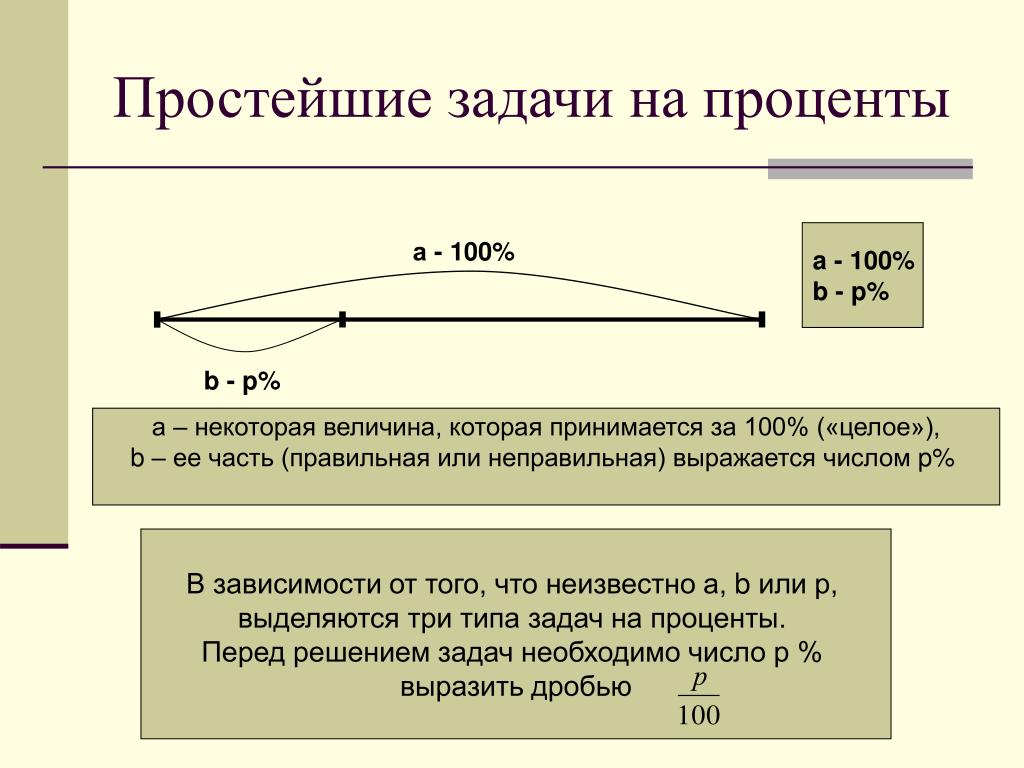
Задачи на простые проценты: примеры с решениями

Ключевые понятия

Простые проценты, проценты и основная сумма.
Найти простые проценты.
Найти процентную ставку.
Найти директора.

Решение простых процентных задач

Что такое основная сумма?

Когда физическое или юридическое лицо берет взаймы определенную сумму денег в виде кредита, заемная сумма называется основной суммой.

Пример: Мэдди хочет построить свой дом; оценка была рассчитана в размере 40000 долларов. Он решает занять 10000 долларов в банке. Эта заемная сумма называется основной суммой.

Что такое простые проценты?

Простые проценты — это метод расчета суммы процентов на некоторую основную сумму денег. Обычно мы занимаем деньги у наших братьев и сестер или друзей, когда наши карманные деньги иссякают, или одалживаем деньги. Мы используем эти деньги для наших целей и возвращаем их, когда получаем им карманные деньги в следующем месяце. Вот как кредитование и заимствование работает дома.

Но в реальном мире деньги нельзя брать взаймы бесплатно. Мы часто занимаем деньги в банках в виде кредита. При возврате, помимо суммы кредита, мы платим дополнительную сумму, которая зависит от суммы кредита и периода времени, на который мы взяли кредит. Эта дополнительная выплачиваемая сумма называется простыми процентами.

Что такое проценты?

Процентная ставка — это процент, используемый для расчета процентов на основную сумму.

Пример:

Мэдди занимает 10000 долларов под 4% годовых на два года.

Здесь мы понимаем, что основная сумма = 10000 долларов США, а процентная ставка = 4%.

Давайте разберемся, что значит 4%?

4% записывается как 4/100

Здесь банкир хочет передать, что если Мэдди займет 100 долларов, то он должен заплатить дополнительно 4 доллара во время выплаты. Но Мэдди занимает 10000 долларов.

Процент, который должен быть выплачен = 10000 × 4%

= 10000 × 0,04

= 400 долл. США.

Следовательно, Мэдди должна заплатить 400 долларов во время окупаемости дополнительно вместе с основной суммой в 10000 долларов.

Найти простые проценты

Пример 1: Энн открывает сберегательный счет с депозитом в размере 670 долларов. Она будет зарабатывать 1,5% годовых на свои деньги. Сколько процентов она заработает за 10 лет? (при условии, что она не добавляет и не берет деньги).

Решение:

Шаг 1:

Используйте уравнение процентов, чтобы найти сумму процентов, заработанных за один год.

Мы знаем, что часть = проценты × целое

Возьмем сумму процентов как I, часть = I, процент = 1,5%, а целое = сумму вклада.

I = 1,5% × 670

I = 0,015 × 670

I = 10,05 долл. США

Шаг 2: Умножьте проценты, полученные за один год, на 10, чтобы рассчитать общую сумму процентов, которую Энн заработает за 10-летний период.

Общая сумма процентов, заработанных Анной за 10 лет = 10,05 × 100019

Следовательно, через десять лет Энн получит 100,5 долларов.

Пример 2: Дэйв занимает 1500 долларов на ремонт своего дома. Он погасит кредит через 3 года, выплачивая основную сумму плюс 3,5% годовых. Сколько он заплатит в виде процентов и сколько она упакует вместе

Решение:

Шаг 1:

Используйте уравнение процентов, чтобы найти сумму процентов, заработанных за один год.

Мы знаем, что часть = проценты × целое

Возьмем процентную сумму как I, часть = I, процент = 3,5% и целое = сумма займа.

I = 3,5% × 1500

I = 0,035 × 1500

I = 52,5 долл. 3-летний период.

Общая сумма процентов за 3 года = 52,5 × 3

= 157,50019

= 1500 + 157,5

= 1657,5

Следовательно, проценты, которые должны быть выплачены Дейвом, составляет 157,5 долл. США, а общая сумма составляет 1657,5 долл. США

. кредит предпринимателю под простые проценты. Если он обещает платить 20 долларов каждый месяц в течение двух лет. Какая процентная ставка по кредиту в год?

Решение:
Шаг 1:
Умножьте проценты на 12, чтобы получить проценты за 1 год.
20 × 12 = 240 долларов
Проценты, подлежащие выплате через два года = 240 × 2
= 480 долларов.
Шаг 2: Используйте процентное уравнение, чтобы найти процентную ставку.
Мы знаем, что часть = проценты × целое
Здесь мы понимаем, что часть = проценты, целое = основная сумма и процентная ставка = p.
Возьмем в качестве p процентную ставку, которую мы собираемся найти.
Проценты = процентная ставка × основная сумма.
480 = p × 4000
Разделите уравнение на 4000 в обе стороны.
480/4000 = p
p = 0,12
Выразите десятичную дробь в процентах, умножив ее на 100.
P = 12%.
Таким образом, процентная ставка, взимаемая банком с кредита, составляет 12%.
Пример 2: Лицо вносит 5000 долларов в банк под простые проценты; он находит 6200 долларов через два года на счету. Какова процентная ставка в год?
Решение:
Шаг 1:
Найдите проценты, выплачиваемые банком за эти два года
Проценты, выплаченные за два года = 6200 — 5000
= 1200 долл. США.
Проценты, выплаченные за один год = 1200/2
Проценты, выплаченные за один год = 600
Шаг 2: Используйте уравнение процентов, чтобы найти процентную ставку.
Мы знаем, что часть = проценты × целое
Здесь мы понимаем, что часть = проценты, целое = основная сумма и процентная ставка = р.
Возьмем в качестве p процентную ставку, которую мы собираемся найти.
Проценты = процентная ставка × основная сумма.
600 = p × 5000
Разделите уравнение на 1200 в обе стороны.
600/5000 = p
p = 0,12
Выразите десятичную дробь в процентах, умножив ее на 100.
P = 12%.
Таким образом, процентная ставка, взимаемая банком с депозита, составляет 12%
Найти основную сумму
Пример 1: Британец открыл сберегательный счет, который приносит ему 4% годовых. По оценкам Брит, если он не пополняет и не снимает средства со своего счета, он заработает 300 долларов в виде процентов через 5 лет. Сколько Брит вложил, когда открыл счет?
Решение:
Шаг 1:
Сначала найдите проценты, которые он заработает за 1 год.
300 ÷ 4 = 75
Проценты за год составляют 75 долларов.
Шаг 2: Используйте процентное уравнение, чтобы найти депозит или основную сумму.
Мы знаем, что часть = проценты × целое
Возьмем в качестве p основную сумму, которую мы собираемся найти.
Здесь мы понимаем, что часть = сумма процентов, целое = основная сумма и проценты = процентная ставка.
Сумма процентов в год = процентная ставка × основная сумма.
75 = 4% × P
75 = 0,04 × P
Разделите уравнение на 0,04 в обе стороны.
75/0,04 = 0,04/0,04 = × P
P × 1 = 1875
P = 1875 $
Таким образом, Брит вносит на счет $1875 под 4% простых процентов, чтобы заработать $300 процентов в течение 4 лет.
Пример 2: Алекс занял деньги на учебу. Он взял кредит под 5% простых процентов. В конечном итоге он заплатит 800 долларов в виде процентов через 5 лет. Сколько Алекс занял для школы?
Решение:
Шаг 1:
Сначала найдите проценты, которые он заработает за 1 год.
800 ÷ 5 = 160
Проценты за год составляют 160 долларов США.
Шаг 2: Используйте процентное уравнение, чтобы найти депозит или основную сумму.
Мы знаем, что часть = проценты × целое
Возьмем в качестве p основную сумму, которую мы собираемся найти.
Здесь мы понимаем, что часть = сумма процентов, целое = основная сумма и проценты = процентная ставка.
Сумма процентов в год = процентная ставка × основная сумма.
160 = 5% × P
160 = 0,05 × P
Разделите уравнение на 0,05 в обе стороны.
160/0,05 = 0,05/0,05 = × P
P × 1 =3300
P = 3300 долларов США
Таким образом, Алекс занимает 3300 долларов США для школы под 5% простых процентов в течение 5 лет и выплачивает 800 долларов США процентов.
Упражнение
Банк ссужает 1000 долларов под 2,5% простых процентов. Через 5 лет сколько денег нужно вернуть банку?
Адам занимает 6600 долларов у своего друга под 1,5% простых процентов; он обещает вернуть его через 3 года. Сколько процентов он платит?
Рассчитайте проценты, полученные по кредиту в размере 500 долларов США на два года под 3% годовых в виде простых процентов?
Грег платит 100 долларов в год в течение 8 лет за заимствование 12000 долларов в виде простых процентов; какова процентная ставка?
Банк требует платить 50 долларов США в год в течение 2 лет по займу 1000 долларов США. Определить процентную ставку.
Компания одалживает Майе 4000 долларов. Каждый месяц она будет платить $11,88 процентов в течение 1 года. Какова процентная ставка?
Проценты, полученные по ставке 2%, составляют 320 долларов США за 2 года. Что такое главный?
Проценты, полученные по ставке 5%, составляют 1000 долларов США в течение 10 лет. Определить принципала.
Ребекка занимает деньги, чтобы оплатить медицинские расходы. Она заплатила 400 долларов в течение 10 лет, взяв кредит под 2% простых процентов. Сколько она заняла?
Адам решил положить 8000 долларов в банк под простые проценты в размере 3% на срок до 12 лет, чтобы потом использовать их для расширения своего бизнеса. Сколько денег будет у него на счету через 12 лет, если предположить, что он ничего не снимает и не добавляет?
Чему мы научились?
Простые проценты, проценты и основная сумма.
Нахождение простых процентов.
Нахождение процентной ставки.
Поиск директора.
Задачи на простые проценты с решениями
Задача 1 :
Человек кладет 5000 долларов на банковский счет, который выплачивает 6% простых процентов в год. Найдите стоимость его вклада через 4 года.
Решение:
Формула для простых процентов:
I = Prt
Замена P = 5000, t = 4, r = 6%.
I = 5000 ⋅ 6/100 ⋅ 4
I = 1200
Накопленная стоимость = Принципал + процент
= 5000 + 1200
= 6200
Проблема 2:
GLEN GLEN GLEN. Через шесть месяцев он вернул 2295 долларов и закрыл кредит. Найдите процентную ставку.

Решение:
Проценты = Сумма — Основная сумма
I = 2295 — 2250
I = 45
Дано: период времени 6 месяцев.
В формуле простых процентов мы используем период времени в годах. Но период времени, указанный в вопросе, указан в месяцах.
Итак, изменим заданный период времени в годах.
6 месяцев = 6/12 года = 1/2 года
Таким образом, период времени равен 1/2 года.
Формула простых процентов:
I = Prt
Замена I = 45, P = 2250, t = 1/2.
45 = 2250 ⋅ r ⋅ 1/2
45 = 1125 ⋅ R
Разделение обеих сторон на 1125.
45/1125 = R
0,04 = R
, чтобы преобразовать десятичный 0,04 в процент, умножьте его на 100.
0,0%. r
4% = r
Задача 3:
Человек вкладывает 16 500 долларов в казначейские билеты двух видов, доходность которых составляет 7,5% и 6% годовых. Через два года он зарабатывает 2442 доллара в виде процентов. Сколько он инвестирует при ставке 6%?

Решение:
Пусть x будет суммой инвестиций по ставке 6%.
Тогда сумма, вложенная в счет 7,5%, составит
= 16500 — x
Дано: через два года общая сумма процентов, заработанных на обоих счетах, составит 2442 доллара США.
Проценты по ставке 6% + Проценты по ставке 7,5% = 2442
x ⋅ 6/100 ⋅ 2 + (16500 — x) ⋅ 7,5/100 ⋅ 2 = 2442
x ⋅ 0,06 x 600 2 + (1 ) ⋅ 0,075 ⋅ 2 = 2442
0,12x + (16500 — x) ⋅ 0,15 = 2442
0,12x + 2475 — 0,15x = 2442
2475 — 0,03x = 2442
2475 — 2442 = 0,03x
33 = 0,03x
Разделите обе части на 0,03.
33/0,03 = x
3300/3 = x
1100 = x
Следовательно, сумма инвестиций по ставке 6% составляет 1100 долларов.

Задача 4 :
Человек вложил 25 200 долларов на два счета, которые выплачивают 5% и 10% годовых. Сумма, инвестированная по ставке 10%, составляет 110% от суммы, инвестированной по ставке 5%. Через три года он зарабатывает 2442 доллара в виде процентов. Сколько он инвестировал при ставке 5%?
Решение:
Пусть x будет суммой инвестиций по ставке 5%.
Тогда сумма, вложенная в 10-процентный счет, равна
= 110% x
= 1,10 ⋅ x
= 1,1 x
. Дано: через три года общая сумма процентов, заработанных на обоих счетах, составляет 5760 долларов США.
Проценты по ставке 5% + Проценты по ставке 10% = 5760
x ⋅ 5/100 ⋅ 3 + 1,1x ⋅ 10/100 ⋅ 3 = 5760
x ⋅ 0,05 ⋅ 3 = ⋅ 3 + 1,1x 1. 5760
0,15x + 0,33x = 5760
0,48x = 5760
Разделите обе части на 0,48.
x = 5760/0,48
x = 576000/48
x = 12000
Следовательно, сумма инвестиций по ставке 5% составляет 12000 долларов США.
Задача 5 :
В простых процентах сумма денег удваивается за 10 лет. Найдите количество лет, которое потребуется, чтобы увеличить себя втрое.
Решение:
Пусть P будет суммой вложенных денег.
Дано : Сумма денег удваивается за 10 лет.
Тогда P станет 2P через 10 лет.
Теперь мы можем рассчитать проценты за десять лет, как показано ниже.
Из приведенного выше расчета P — это проценты за первые 10 лет.
В случае простых процентов заработанные проценты будут одинаковыми каждый год.
Таким образом, проценты, полученные в следующие 10 лет, также будут P.
Это было объяснено ниже.
Следовательно, потребуется 20 лет, чтобы принципал стал тройным.
Задача 6 :
Сумма простых процентов составляет 6200 долларов через 2 года и 7400 долларов через 3 года. Найдите главного.
Решение:
По истечении 2 лет мы получим 6200 долларов
По истечении 3 лет мы получим 7400 долларов
Из этих двух данных мы можем получить проценты, полученные за 3-й год, как показано ниже.
No related posts.