Задачи на равенство треугольников 7 класс: Задачи на признаки равенства треугольников (7 класс)

Второй и третий признаки равенства треугольников 7 класс онлайн-подготовка на Ростелеком Лицей

Повторение понятия «равные треугольники», первого признака равенства треугольников

 

Для начала вспомним из материалов предыдущих уроков, что две фигуры называются равными, если их можно совместить наложением. На рисунке указаны два равных отрезка и два равных угла.

 

              

Рис. 1. Углы А и А₁ равны, АВ = CD

 

Доказательство признаков равенства треугольников

 

 

Рассмотрим теперь равенство треугольников. Треугольники называются равными, если их можно совместить наложением. В таком случае совместятся все стороны и углы треугольников.

 

 

Рис. 2. Равные треугольники АВС и А₁В₁С₁

         

Теперь мы готовы сформулировать и доказать второй признак равенства треугольников.

Второй признак равенства треугольников:

Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, такие треугольники равны.

Теорема: Дано . Доказать: АВС и .      

Доказательство: Выполним наложение данных в условии фигур. В результате данного действия вершины А и А₁, , отрезки АС и А₁С₁ совпадают. Если рассматривать треугольники в целом, то  совпадет с .

Теорема доказана.

Рис. 3. Равные треугольники АВС и А₁В₁С₁

Третий признак равенства треугольников:

Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.

Теорема: Дано . Доказать: АВС и . 

Доказательство: Выполним наложение данных в условии фигур. В результате

данного действия имеем три случая:

1. Луч СС₁ внутри .

Рис. 4. Равные треугольники АВС и А₁В₁С₁

В таком случае по первому признаку.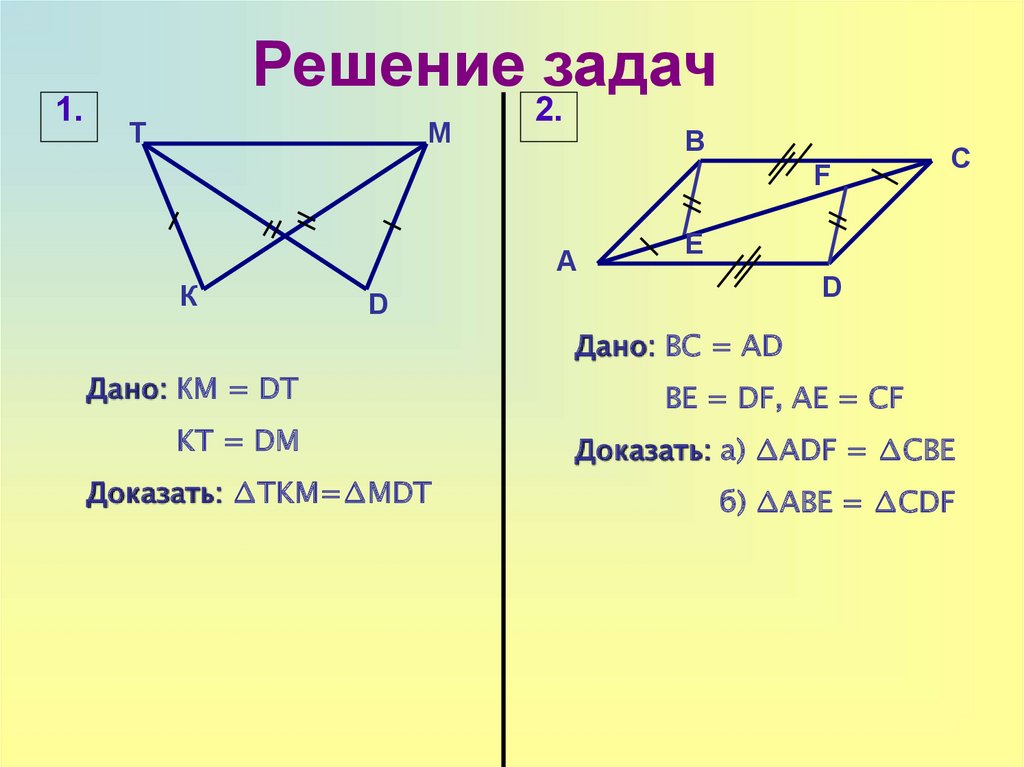

1. Луч СС₁ совпадает с одной из сторон .

2. Луч СС₁ лежит вне угла .

 

Рис. 5. Равные треугольники АВС и А₁В₁

С₁. Случаи 2, 3

Случаи 2 и 3 предлагаем рассмотреть самостоятельно.

Теорема доказана.

 

 

  

Рис. 6. Третий признак равенства треугольников

 

Решение задач

 

 

Рассмотрим некоторые задачи, чтобы закрепить пройденный материал.

 

Пример 1: Известно, что . Найти стороны АВ и ВС.

Решение: Выполним пояснительный рисунок к задаче.

Рис. 7. Чертеж к примеру 1

Поскольку , то треугольники АВС и ADC равны по второму признаку. Из равенства треугольников следует, что .

Ответ: 11 см, 19 см.

Пример 2: В изображенных треугольниках  , , и медианы ВМ и ВМ₁ тоже равны.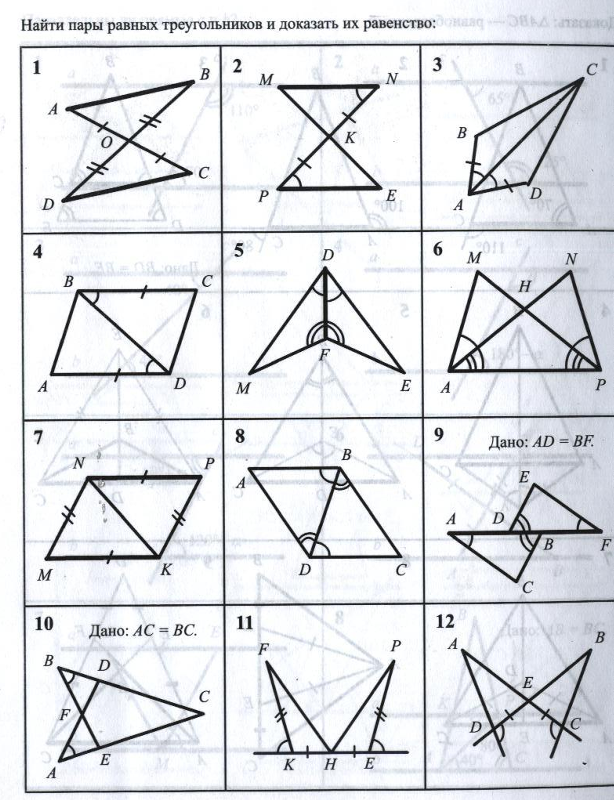

Доказать равенство треугольников: .

Рис. 8

Доказательство:                                                    

Вследствие того, что М и М₁ – середины равных отрезков, то А₁М₁ = АМ. , ВМ = ВМ₁  (по условию). Следовательно,  по третьему признаку. Из равенства треугольников следует равенство углов .

,  (по условию),  (по доказанному). Следовательно,  по первому признаку.

Что и требовалось доказать.

 

Рекомендованные ссылки на интернет-ресурсы

1. Математика (Источник).
2. School.xvatit.com (Источник).

 

Рекомендованное домашнее задание

1. № 37. Бутузов В.Ф., Кадомцев С.Б., Прасолова В.В. Геометрия 7 / В.Ф. Бутузов, С.Б. Кадомцев, В.В. Прасолова, под ред. Садовничего В.А.  – М.: Просвещение, 2010.

2. На рисунке РC = QR, CR = QP. Докажите, что ∠CQP = ∠QCR.

3.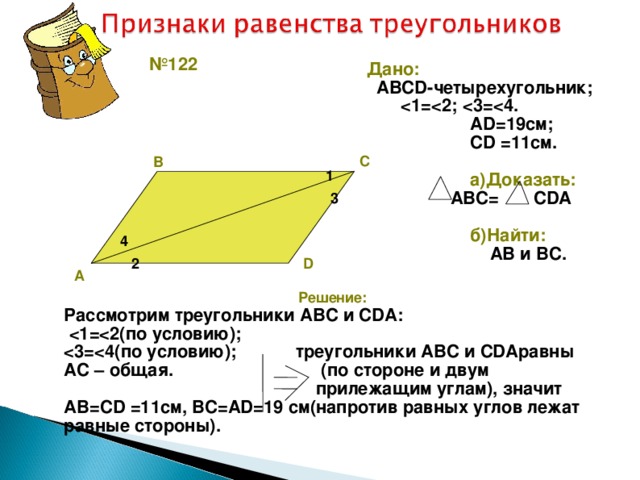 На рисунке задачи № 2 CP = RQ, CR = PQ. Докажите, что CO = OQ, PO = OR.

4. Докажите перпендикулярность прямых СQ и BА, если AC = BC, а OA = OB.

 

Решение задач по теме «Первый признак равенства треугольников» 7 класс онлайн-подготовка на Ростелеком Лицей

Повторение первого признака равенства треугольников

 

Вспомним предварительно формулировку первого признака равенства треугольников.

 

                                    

Рис. 1. Первый признак равенства треугольников

Определение: Первый признак равенства треугольников – это равенство их по углу и прилежащим сторонам.

Из этих трех равенств и вытекает равенство самих треугольников.

Смысл равенства треугольников заключается в том, что при совмещении этих трех элементов гарантируется совмещение, то есть равенство всех остальных элементов двух треугольников.

 

Решение задач

 

 

Рассмотрим следующие задачи:

 

Пример 1: Измерить на местности расстояние между двумя точками A и B, между которыми нельзя пройти по прямой.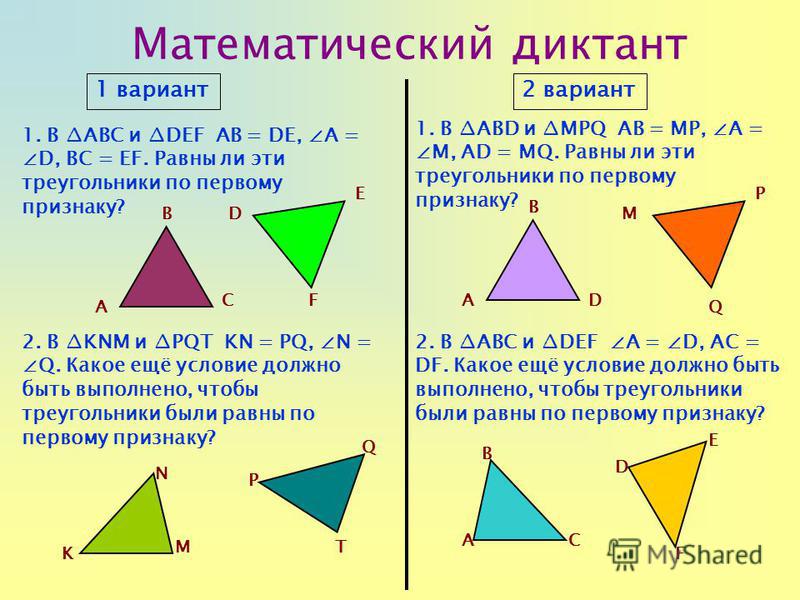 Для этого выбирают такую точку С, из которой можно пройти и к точке А, и к точке В, и из которой видны обе эти точки. Провешивают расстояния АС и ВС, продолжают их за точку С и отмеряют СD = AC и ЕС = СВ. Тогда отрезок ED равен искомому расстоянию. Объясните, почему.

Решение:

Выполним пояснительный рисунок:

                

Рис. 2. Чертеж к примеру 1

Продлим отрезки АС и ВС. Отмеряем СЕ = СВ и CD = CA. ∆CDE = ∆CAB по первому признаку.

.

Из равенства треугольников следует, что ED = AB.

Ответ: Задача решена.

Пример 2: Через середину О отрезка АВ проведена прямая р, перпендикулярная прямой АВ. Докажите, что каждая точка Х этой прямой одинаково удалена от точек А и В (каждая точка серединного перпендикуляра к отрезку АВ равноудалена от его концов).

Решение:

Рис. 3. Чертеж к примеру 2

Рассмотрим треугольники АОХ и ВОХ. ∆АОХ = ∆ВОХ – по первому признаку.

Из равенства треугольников следует, что АХ = ВХ для любой произвольной точки Х, которая принадлежит прямой р.

Ответ: Доказано.

Пример 3: На стороне АВ треугольника АВС взята точка D, а на стороне треугольника  взята точка . Известно, что треугольники ADC и  равны и отрезки DB и  равны. Докажите равенство треугольников АВС и .

Решение:

                                             

Рис. 4. Чертеж к примеру 3

Рассмотрим треугольники АВС и . В них . АС =  (поскольку треугольники ADC и  равны по условию). В нашем случае для доказательства необходимо лишь, чтобы АВ =  . Докажем, что это действительно так.

 

AD =  из равенства треугольников. DB =  по условию. Отсюда следует, что АВ = .  и прилежащие к ним стороны тоже равны у двух треугольников, значит, АВС = .

Ответ: Доказано.

Пример 4: На сторонах ВС и  равных треугольников АВС и  взяты соответственно точки М и , причем ВМ : BС = : = 1 : 3. Доказать, что АМ = .

Решение:

Рис. 5. Чертеж к примеру 4

Из равенства треугольников АВС и  следует, что , АВ = , ВС = . Для доказательства того, что ∆АВМ = ∆, у нас есть уже два необходимых элемента, это равенство углов  и равенство сторон АВ = , значит, нам необходимо доказать, что ВМ = .                                                           =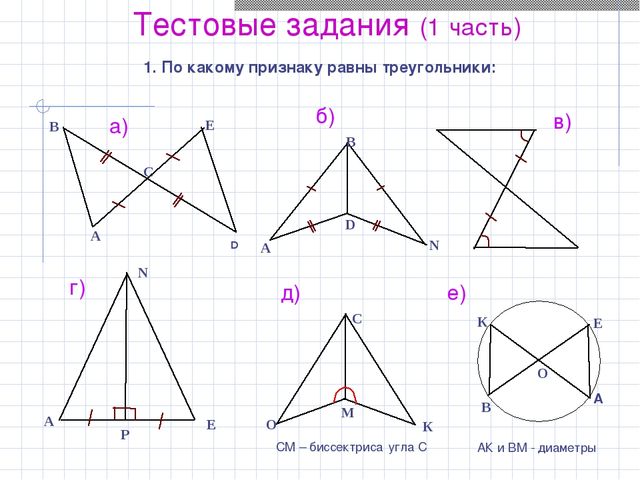

Треугольники ∆АВМ = ∆ по первому признаку. А значит, АМ = .

Ответ: Доказано.

Пример 5: На сторонах угла CAD отмечены точки В и Е так, что точка В лежит на отрезке АС, а точка Е – на отрезке AD, причем АС = AD и АВ = АЕ. Докажите, что .

Решение:

Рис. 6. Чертеж к примеру 5

Обозначим  как  и как . Доказать, что , – это то же самое, что доказать равенство смежных с ними углов и . ∆BAD = ∆EAC по первому признаку, поскольку у них общий, ВА = ЕА и AD = AC. , так как они лежат напротив равных сторон AD и AC соответственно. Мы доказали равенство смежных углов, а значит, и доказали равенство искомых. .

Ответ: Доказано.

На сегодняшнем уроке мы рассмотрели несколько примеров на первый признак равенства треугольника. На следующем уроке мы познакомимся с перпендикуляром, проведенным к прямой.

 

Список рекомендованной литературы

1. Александров А.Д., Вернер А. Л., Рыжик В.И. и др. Геометрия 7. – М.: Просвещение.
2. Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. Геометрия 7. 5-е изд. – М.: Просвещение.
3. Бутузов В.Ф., Кадомцев С.Б., Прасолова В.В. Геометрия 7 / В.Ф. Бутузов, С.Б. Кадомцев, В.В. Прасолова, под ред. Садовничего В.А. – М.: Просвещение, 2010.

 

Рекомендованные ссылки на интернет-ресурсы

1. Обобщающий урок по геометрии в 7-м классе (Источник).
2. Прямая линия, отрезок (Источник).

 

Рекомендованное домашнее задание

1. №35 (д). Бутузов В.Ф., Кадомцев С.Б., Прасолова В.В. Геометрия 7 / В.Ф. Бутузов, С.Б. Кадомцев, В.В. Прасолова, под ред. Садовничего В.А. – М.: Просвещение, 2010.
2. Постройте треугольник по заданному углу и двум прилежащим к нему сторонам.
3. Докажите по первому признаку равенства треугольников, что диагональ квадрата делит его на 2 равных треугольника.

 

Конгруэнтность треугольников 7 класс Дополнительные вопросы по математике Глава 7

Дополнительные вопросы к 7 классу Математика Глава 7 Конгруэнтность треугольников

Конгруэнтность треугольников 7 класс Дополнительные вопросы Очень короткий тип ответа имя

(a) сторона, противоположная вершине A
(b) вершина, противоположная A стороне AB
(c) угол, противоположный стороне AC
(d) угол, образованный сторонами CB и CA.

Решение:
(a) Сторона, противоположная вершине A, равна BC.
(b) Вершина, противоположная стороне AB, равна C.
(c) Угол, противоположный стороне AB, равен ∠ACB.
(d) Угол между сторонами CB и CA равен ∠ACB.

Вопрос 2.
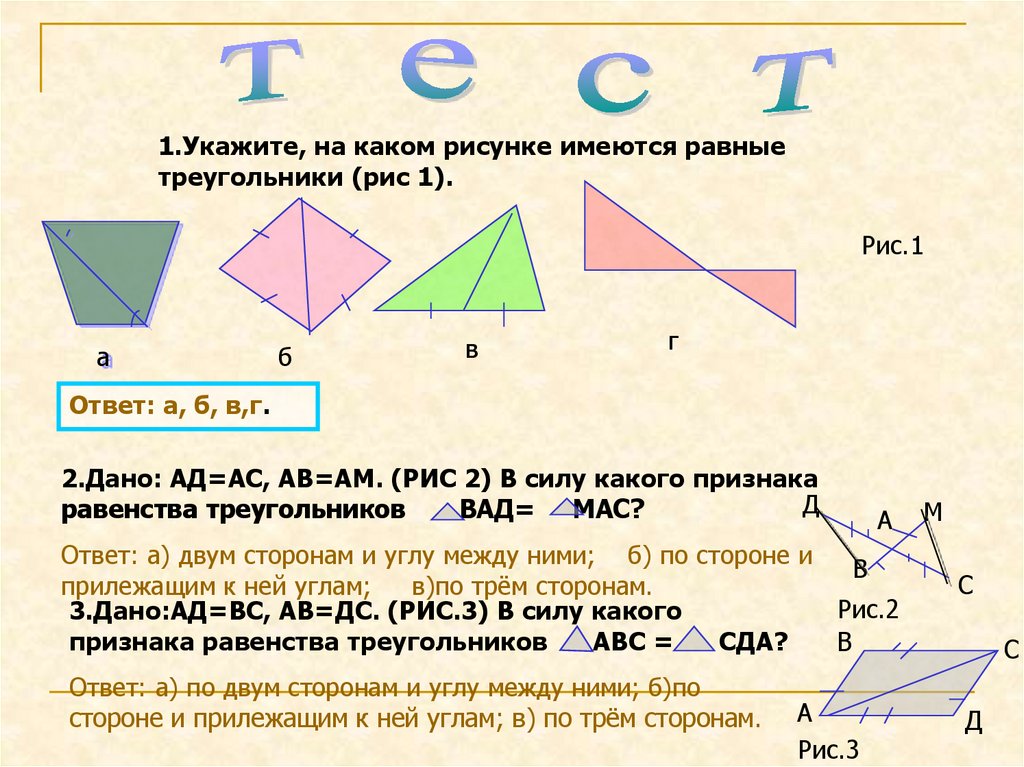
Проверьте, равны ли данные треугольники.
Решение:
Здесь
AB = DE = 3 см
BC = DF = 3,5 см
AC = EF = 4,5 см
ΔABC = ΔEDF (по правилу SSS)

Итак, ΔABC и ΔEDF конгруэнтны.

Вопрос 3.
В данных равных треугольниках при ASA найти значение x и y, ΔPQR = ΔSTU.

Решение:
Дано: ΔPQR = ΔSTU (по правилу ASA)
∠Q = ∠T = 60° (дано)
\(\bar { QR }\) = \(\bar { TU }\) = 4 см (дано)
∠x = 30° (для правила ASA)
Теперь в ΔSTU,
∠S + ∠T + ∠U = 180° (свойство суммы углов)
∠y + 60° + ∠x = 180°
∠y + 60° + 30° = 180°
∠y + 90° = 180°
∠y = 180° – 90° = 90°
Следовательно, x = 30° и y = 90°.

Вопрос 4.
Покажите на следующем рисунке, что ΔPSQ = ΔPSR.

Решение:
В ΔPSQ и ΔPSR
\(\bar {PQ}\) = \(\bar {PR}\) = 6,5 см (данные)
\(\bar {PS}\) = \(\bar {PS}\) (общие)
∠PSQ = ∠PSR = 90° (Дано)
ΔPSQ = ΔPSR (По правилу RHS)

Вопрос 5.
Могут ли два равносторонних треугольника всегда быть конгруэнтными? Назови причины.
Решение:
Нет, любые два равносторонних треугольника не всегда равны.
Причина: Каждый угол равностороннего треугольника равен 60°, но их соответствующие стороны не всегда могут быть одинаковыми.

Вопрос 6.
На данном рисунке AP = BQ, PR = QS. Покажите, что ΔAPS = ΔBQR

Решение:
In ΔAPS и ΔBQR
AP = BQ (дано)
PR = QS (дано)
PR + RS = QS + RS (Добавление RS с обеих сторон)
PS = QR
∠APS = ∠BQR = 90 ° (Дано)
ΔAPS = ΔBQR (по правилу SAS)

Вопрос 7.
Не рисуя фигуры треугольников, запишите все шесть пар равных мер в каждой из следующих пар конгруэнтных треугольников.
(i) ΔABC = ADEF
(ii) ΔXYZ = ΔMLN
Решение:
(i) Дано: ΔABC = ΔDEF
Здесь AB = DE
BC = EF
AC = DF
∠A = ∠D, ∠B = ∠E и ∠C = ∠F
(ii) Дано ΔXYZ = ΔMLN
Здесь XY = ML
YZ = LN
XZ = MN
∠X = ∠M, ∠Y = ∠L и ∠Z = ∠N

Вопрос 8.
Длины двух сторон равнобедренного треугольника равны 5 см и 8 см, найдите периметр треугольника.
Решение:
Поскольку длины любых двух сторон равнобедренного треугольника равны, то
Случай I: три стороны треугольника равны 5 см, 5 см и 8 см.
Периметр треугольника = 5 см + 5 см + 8 см = 18 см
Случай II: три стороны треугольника равны 5 см, 8 см и 8 см.
Периметр треугольника = 5 см + 8 см + 8 см = 21 см
Следовательно, искомый периметр равен 18 см или 21 см.

Вопрос 9.
Запишите правило конгруэнтности в следующих парах конгруэнтных треугольников.

Решение:
(i) Здесь AB = ST = 3 см
BC = TU = 4,5 см
∠ABC = ∠STU = 110°
ΔABC = ΔSTU (по правилу SAS)
(ii) Здесь ∠PQR = ∠ MNL = 90°
гип. PR = гипноз. ML
QR = NL = 3 см
ΔPQR = ΔMNL (По правилу RHS)

Вопрос 10.
На данном рисунке сформулируйте правило конгруэнтности, которому следуют конгруэнтные треугольники LMN и ONM. 11 треугольник, в котором PQ = PR.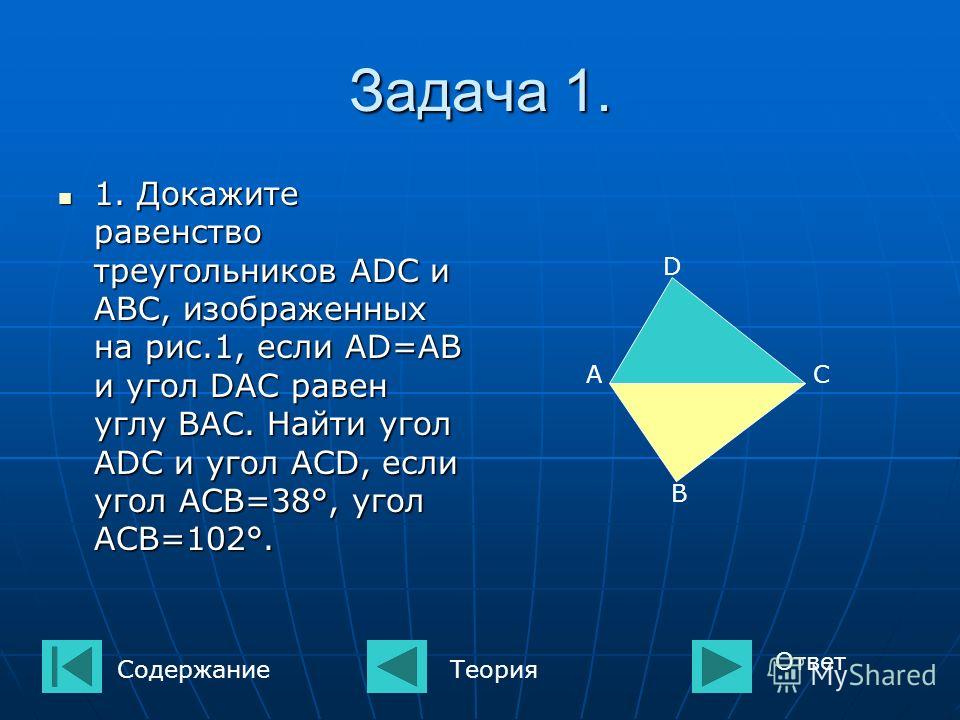 QM и RN — медианы треугольника. Докажите, что
(i) ΔNQR = ΔMRQ
(ii) QM = RN
(iii) ΔPMQ = ΔPNR

Решение:
ΔPQR — равнобедренный треугольник. [∵ PQ = PR]
⇒ \(\frac { 1 }{ 2 }\) PQ = \(\frac { 1 }{ 2 }\) PR
⇒ NQ = MR и PN = PM
(i) In ΔNQR и ΔMRQ
NQ = MR (половина равных сторон)
∠NQR = ∠MRQ (углы, противоположные равным сторонам)
QR = RQ (общий)
ΔNQR = ΔMRQ (по правилу SAS) частей конгруэнтных треугольников)
(iii) В ΔPMQ и ΔPNR
PN = PM (Половина равных сторон)
PR = PQ (Дано)
∠P = ∠P (Общий)
ΔPMQ = ΔPNR (По правилу SAS)

Вопрос 12.
На данном рисунке PQ = CB, PA = CR, ∠P = ∠C. Является ли ΔQPR = ΔBCA? Если да, укажите критерий соответствия.

Решение:
Дано:
PQ = CB, PA = CR
и ∠P = ∠C
В ΔQPR и ΔBCA
PQ = CB (Дано)
∠QPR = ∠BCA (Дано)
G PA = CR )
PA + AR = CR + AR (Добавление AR к обеим сторонам)
или PR = CA
ΔQPR = ΔBCA (по правилу SAS)

Вопрос 13.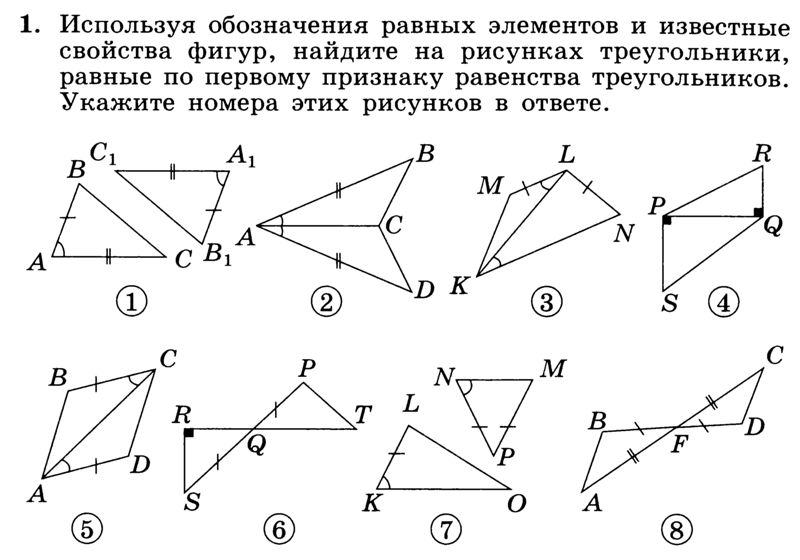
На данном рисунке укажите, является ли ΔABC = ΔEOD или нет. Если да, укажите критерий соответствия.

Решение:
In ΔABC и ΔEOD
AB = OE
∠ABC = ∠EOD = 90°
AC = ED
ΔABC = ΔEOD
Следовательно, ΔABC = ΔEOD
RHS является критерием конгруэнтности.

Вопрос 14.
На данном рисунке PQ || RS и PQ = RS. Докажите, что ∆PUQ = ∆SUR.

Решение:
In ΔPUQ и ΔSUR
PQ = SR = 4 см
∠UPQ = ∠USR (чередующиеся внутренние углы)
∠PQU = ∠SRU (альтернативные внутренние углы)
ΔPUQ = 06g 9005 Conruence 9005 Conruence 9005 Треугольников Класс 7 Дополнительные вопросы Длинный ответ Тип

Вопрос 15.
На данном рисунке ΔBAC = ΔQRP по критерию конгруэнтности SAS. Найдите значение x и y.

Решение:
Дано: ΔBAC = ΔQRP (по правилу SAS)
Итак, BA = QR
⇒ 3x + 10 = 5y + 15 ……(i)
∠BAC = ∠QRP
⇒ 2x + 15° = 5x – 60° ……(ii)
Из ур. (ii), мы имеем
2x + 15 = 5x – 60
⇒ 2x – 5x = -15 – 60
⇒ -3x = -7 5
⇒ x = 25
Из уравнения.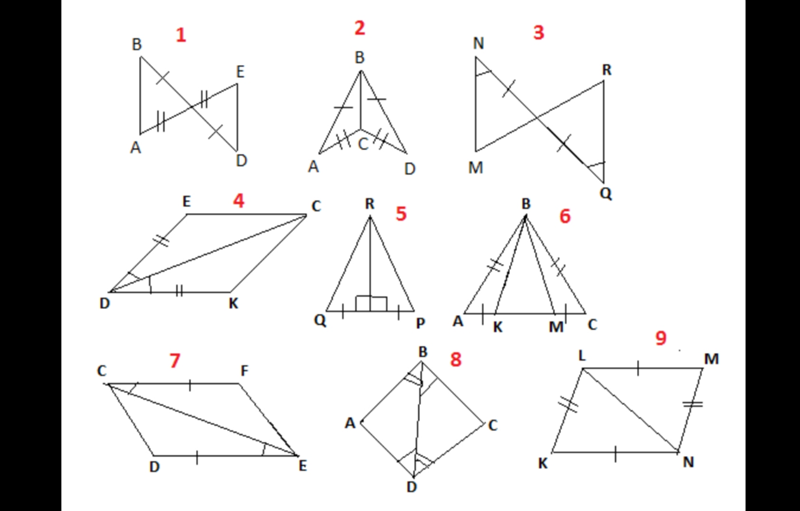 (i), мы имеем
3x + 10 = 5y + 15
⇒ 3 × 25 + 10 = 5y + 15
⇒ 75 + 10 = 5y + 15
⇒ 85 = 5 лет + 15
⇒ 85 – 15 = 5 лет
⇒ 70 = 5 лет
⇒ y = 14
Следовательно, искомые значения x и y равны 25 и 14 соответственно.

Вопрос 16.
Рассмотрите рисунок и назовите три пары равных частей в треугольниках ABC и DCB.
(i) Является ли ΔABC = ΔDCB? Почему?
(ii) Является ли AB = DC? Почему?
(iii) AC = DB? Почему? (Пример NCERT)

Решение:
(i) В ΔABC и ΔDCB
∠ABC = ∠DCB = 70° (40° + 30° = 70°) (Дано)
∠ACB = ∠DCB = 30° (Дано)
BC = CB (общий)
ΔABC = ΔDCB (по правилу ASA)
(ii) Да,
AB = DC (конгруэнтные части конгруэнтных треугольников)
(iii) Да,
AC = DB (конгруэнтные части конгруэнтных треугольников)

Вопрос 17.
На данном рисунке ΔQPS = ΔSRQ. Найдите каждое значение.
(a) x
(b) ∠PQS
(c) ∠PSR

Решение:
(a) ∆QPS = ∆SRQ
∠QPS = ∠SRQ (Конгруэнтные части конгруэнтных треугольников)
⇒ 106 = 9×0 + 12 – 12 = 2x
⇒ 94 = 2x
⇒ x = 47
∠QRS = 2 × 47 + 12 = 94 + 12 = 106°
Итак, PQRS — параллелограмм.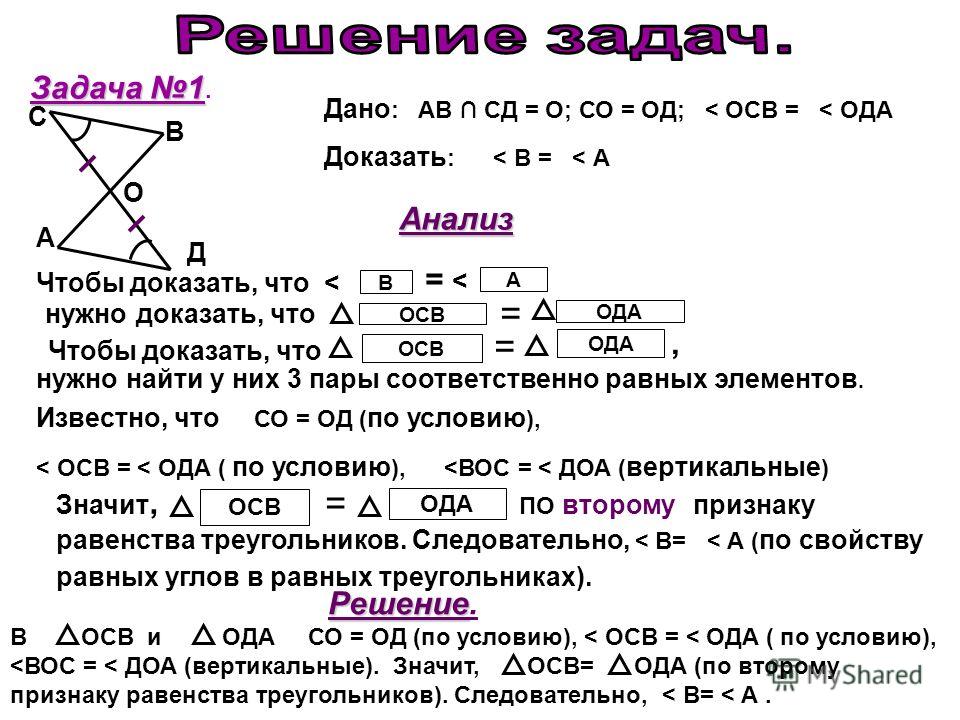
∠QSR = 180° – (42° + 106°) = 180° – 148° = 32°
(b) ∠PQS = 32° (чередующиеся внутренние углы)
(c) ∠PSQ = 180° – (∠QPS + ∠PQS) = 180° – (106° + 32°) = 180° – 138° = 42°
∠PSR = 32° + 42° = 74°

Конгруэнтность треугольников Класс 7 Дополнительные вопросы Навыки мышления высшего порядка ( HOTS) Тип

Вопрос 18.
В треугольнике ΔABC медианы BD и CE равны и пересекаются в точке O. Докажите, что треугольник ΔABC равнобедренный.

Решение:
Мы знаем, что медианы треугольника пересекаются в отношении 2 : 1.
BD = CE (Дано)
\(\frac { 2 }{ 3 }\) BD = \(\frac { 2 }{ 3 }\) CE
⇒ OB = OC
\(\frac { 1 }{ 3 }\) BD = \(\frac { 1 }{ 3 }\) CE
⇒ OE = OD
В ΔBOE и ΔCOD,
OB = OC
OE = OD
∠BOE = ∠COD (вертикально противоположные углы)
ΔBOE = ΔCOD (согласно правилу SAS)
BE = CD (конгруэнтные части конгруэнтных треугольников)
2BE = 2CD AB
⇒ ⇒ ⇒ ⇒ ⇒
Следовательно, треугольник ΔABC равнобедренный.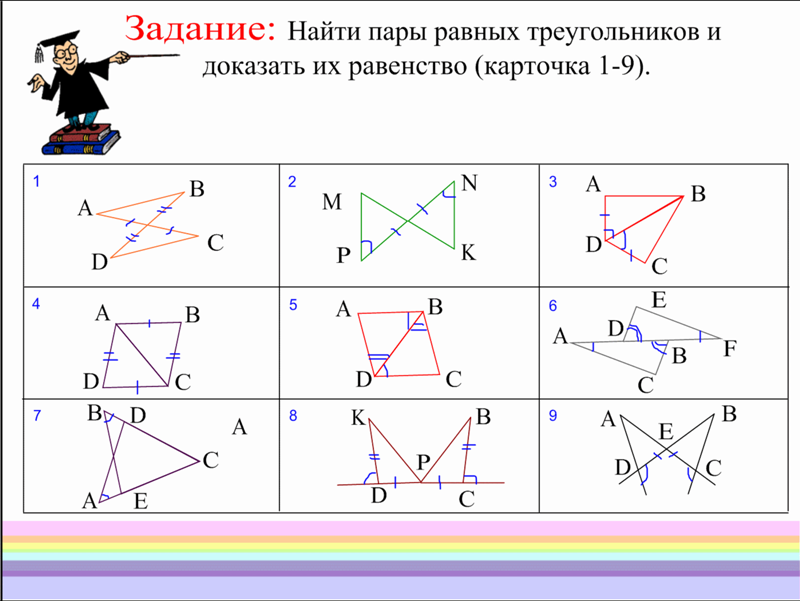

Вопрос 19.
Докажите, что длины высот, проведенные к равным сторонам равнобедренного треугольника, также равны.
(i) ∠TRQ = ∠SQR?
(ii) Если ∠TRQ = 30°, найдите углы при основании ΔPQR.
(iii) Является ли треугольник ΔPQR равносторонним?

Решение:
В ΔQTR и ΔRSQ
∠QTR = ∠RSQ = 90° (Дано)
∠TQR = ∠SRQ (Угол при основании равнобедренного треугольника)
∠QRT = = ∠RQS (Остальные третьи углы) QR9 9000 (общий)
ΔQTR = ΔRSQ (по правилу ASA)
QS = RT (конгруэнтные части конгруэнтных треугольников)
Значит доказано.
(i) ∠TRQ = ∠SQR (конгруэнтные части конгруэнтных треугольников)
(ii) В ΔQTR,
∠TRQ = 30° (дано)
∠QTR + ∠TQR + ∠QRT = 180° (свойство суммы углов)
⇒ 90° + ∠TQR + 30° = 180°
⇒ 120° + ∠TQR = 180°
⇒ ∠TQR = 180° – 120° = 60°
⇒ ∠TQR = ∠SRQ = 60°
Каждый угол при основании 60°
(iii) В ΔPQR,
∠P + ∠Q + ∠R = 180° (Свойство суммы углов)
⇒ ∠P + 60° + 60° = 180° (Из ii)
⇒ ∠P + 120° = 180°
⇒ ∠P = 180° – 120° = 60°
Следовательно, ΔPQR равносторонний треугольник.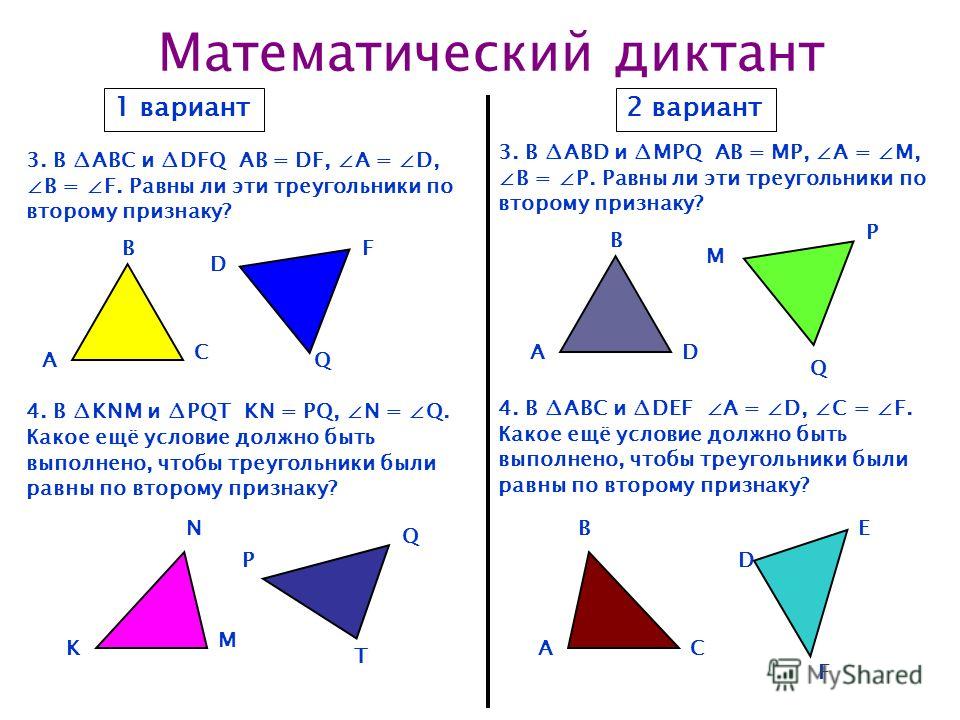

Дополнительные вопросы по математике для 7-го класса

Решения NCERT по математике для 7-го класса

Решения NCERT по математике для 7-го класса, глава 7

• Решения НЦЭРТ
• Класс 7
• Математика
• конгруэнтность треугольников

Математика NCERT 7 класс, Глава 7: Конгруэнтность треугольников — Глава посвящена конгруэнтности плоских фигур , отрезков , углов, и 4 треугольников 4.

• Конгруэнтные объекты являются точными копиями друг друга.  

Первый раздел главы посвящен конгруэнтность плоских фигур, конгруэнтность отрезков и конгруэнтность углов .

• Если два отрезка имеют одинаковую (т. е. одинаковую) длину, они конгруэнтны . Кроме того, если два отрезка конгруэнтны , они имеют одинаковую длину.
• Если два угла имеют одинаковую меру, они конгруэнтны. Кроме того, если два угла равны , их меры равны.

После этого обсуждается конгруэнтность треугольников . Упражнение 7.1 основано на концепции приведенных выше тем. Другая половина главы посвящена критериям конгруэнтности треугольников . Объяснение критерия дано интересно, они упоминаются в игровой форме. Учащиеся будут ознакомлены со следующим критерием:
1.   Критерии конгруэнтности SSS: Треугольники конгруэнтны , если три стороны одного равны трем соответствующим сторонам другого.
2.  Критерии конгруэнтности SAS: Треугольники конгруэнтны , если две стороны и угол , заключенный между ними в одном из треугольников, равны соответствующим сторонам и углу , заключенному между ними треугольника другой треугольник.
3.  Критерии конгруэнтности ASA: Два треугольника конгруэнтны , если два углов и сторона , заключенные между ними в одном из треугольников , равны соответствующим углам и стороне , заключенным между ними другого треугольника.
Особое внимание будет уделено теме  Сравнение прямоугольных треугольников.
RHS-критерий конгруэнтности: Если при соответствии, гипотенуза и одна сторона прямоугольного треугольника соответственно равны гипотенузе и одной стороне o f другой прямоугольный треугольник, тогда треугольники конгруэнтны.
Позже глава Конгруэнтность треугольников завершается кратким изложением.

Страница № 137:

Вопрос 1:

Дополните следующие утверждения:

(a) Два отрезка равны, если __________.

(b) Среди двух равных углов один имеет градусную меру 70°; градусная мера другого угла __________.

(c) Когда мы пишем ∠A = ∠B, мы на самом деле имеем в виду __________.

Ответ:

(a) Они имеют одинаковую длину

(b) 70°

(c) m ∠A = m ∠B
 

Номер страницы 137:

Два вопроса 2: 9033 реальные примеры конгруэнтных форм.

Ответ:

(i) Листы одного блокнота

(ii) Печенье в одной пачке

Страница № 137:

Вопрос 3:

Соответствующие конгруэнтные части треугольников.

Ответ:

Если эти треугольники равны, то соответствующие углы и стороны будут равны друг другу.

Ϫa ↔ Ϫf

♂ ↔ Ϫe

♂ ↔ Ϫd

Страница № 137:

Вопрос 4:

, если Δdef ΔBCA, написать часть (S). соответствуют

(i) ∠E (ii) (iii) ∠F (iv)

Ответ:

(i) ∠C

(ii)

(iii) ∠A

(iv)

9

Видео Решение для сравнения треугольников (Страница: 137 , Q.No.: 4)

NCERT Решение по математике для 7 класса — сравнение треугольников 137 , Вопрос 4

Номер страницы 149:

Вопрос 1:

Какой Критерий конгруэнтности вы используете в следующем?

(а) Дано: АС = ДФ

АВ = Германия

БК = ЭФ

Итак, ΔАВС ≅ ΔDEF

(б) Дано: ZX = РП

РК = ZY

∠PRQ = ∠XZY

Итак, ΔPQR ≅ ΔXYZ

(в) Дано: ∠МЛН = ∠ФГХ

∠NML = ∠GFH

МЛ = ФГ

Итак, ΔLMN ≅ ΔGFH

(г) Дано: ЭБ = БД

АЕ = БК

∠А = ∠С = 90°

Итак, ΔABE ≅ ΔCDB

Ответ:

(а) SSS, как стороны ΔABC равны сторонам ΔDEF.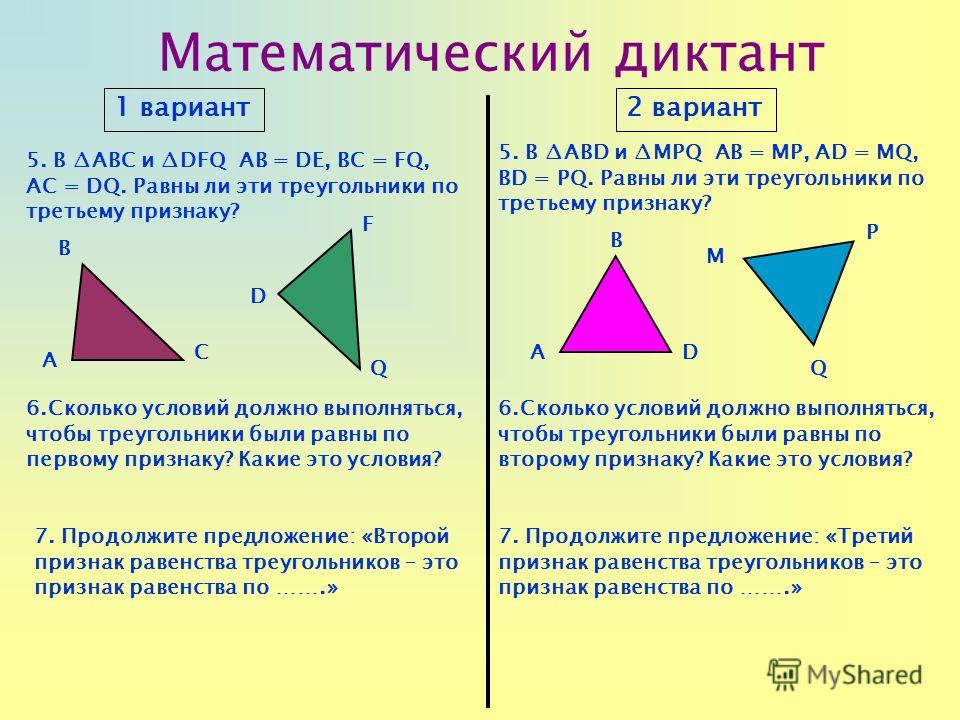

(b) SAS, как две стороны и угол между этими сторонами ΔPQR равны двум сторонам и угол между этими сторонами ΔXYZ.

(c) ASA, как два угла и сторона, заключенная между этими углами ΔLMN равны двум углам и сторона, заключенная между этими углами ΔGFH.

(d) RHS, как в данных двух прямоугольных треугольниках, одна сторона и гипотенузы соответственно равны.

Страница № 149:

Вопрос 2:

Вы хотите показать, что ΔART ≅ ΔPEN,

(a) Если вам нужно использовать критерий SSS, то вам нужно показать

(i) AR = (ii) RT = (iii) AT =

(b) Если дано, что ∠T = ∠N, и вы должны использовать критерий SAS, вам необходимо иметь

(i) RT = и (ii) PN =

(c) Если дано, что AT = PN и вы должны использовать критерий ASA, вам нужно иметь

(i) ? (ii) ?

Ответ:

(a)

(i) AR = PE

(ii) RT = EN

(iii) AT = PN

(b)

(i) RT = EN

(ii) PN = AT

(c)

(i) ∠ATR = ∠PNE

(ii) ∠RAT = ∠05 Решение Video

903 на конгруэнтность треугольников (Страница: 149 , Q.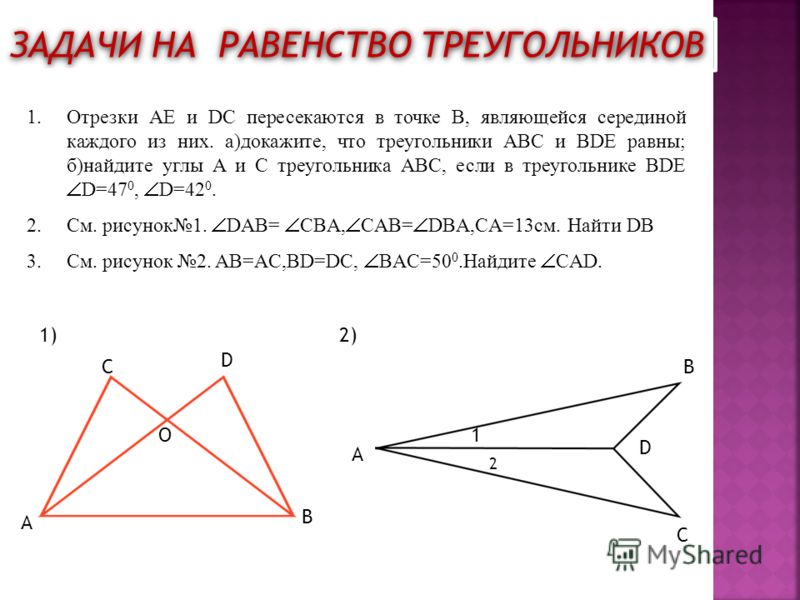 No.: 2)

NCERT Решение по математике для 7 класса — конгруэнтность треугольников 149 , Вопрос 2

Страница № 150:

Вопрос 3:

Вы должны показать, что ΔAMP ≅ AMQ.

В следующем доказательстве укажите недостающие причины.

—	Шаги	—	Причины
(и)	PM = QM	(и)	…
(ii)	∠PMA = ∠QMA	(ii)	…
(iii)	утра = утра	(iii)	…
(iv)	ΔAMP ≅ ΔAMQ	(iv)	…

Ответ:

(i) Дано

(ii) Дано

(iii) Обычный

(iv) SAS, как две стороны и угол между ними стороны ΔAMP равны двум сторонам и прилежащему углу между этими сторонами ΔAMQ.

Страница № 150:

Вопрос 4:

В ΔABC, ∠А = 30°, ∠В = 40° и ∠C = 110°

В ΔPQR, ∠Р = 30°, ∠Q = 40° и ∠R = 110°

Студент говорит, что ΔABC ≅ ΔPQR по конгруэнтности AAA критерий. Он оправдан? Почему или почему нет?

Ответ:

Нет. Это свойство означает, что эти треугольники имеют соответствующие углы равной меры. Однако это не дает никакой информации об их стороны. Соотношение сторон этих треугольников несколько иное чем 1:1. Следовательно, свойство AAA не доказывает, что два треугольника конгруэнтный.

Страница № 150:

Вопрос 5:

На рисунке два треугольника равны.

Соответствующие части промаркированы. Мы можем написать ΔRAT ≅ ?

Ответ:

Можно заметить, что

∠RAT = ∠WON

∠ART = ∠OWN

AR = OW

Следовательно, по критерию ∆WON, ARAT,

Видео Решение для сравнения треугольников (Страница: 150 , Q.No.: 5)

NCERT Решение для 7 класса по математике — сравнение треугольников 150 , вопрос 5

Страница № 150:

Вопрос 6:

Заполнено конгруэнтность:

ΔBCA ≅?

ΔQRS ≅?

Ответ:

Дано что BC = BT

TA = CA

BA общий.

Следовательно, ΔBCA ΔBTA

Аналогично, PQ = RS

TQ = QS
PT = RQ

Следовательно, ΔQRS ΔTPQ

Страница № 150:

Вопрос 7:

На квадратном листе начертите два равновеликих треугольника так, чтобы

(i) Треугольники равны.

(ii) Треугольники не равны.

Что вы можете сказать об их периметрах?

Ответ:

(i)

Здесь ΔABC и ΔPQR имеют одинаковую площадь и также конгруэнтны друг другу. Кроме того, периметр обоих треугольников будет одинаковым.

(ii)

Здесь два треугольника имеют одинаковую высоту и основание. Значит, их площади равны. Однако эти треугольники не конгруэнтны друг другу. Кроме того, периметр обоих треугольников не будет одинаковым.

Видео Решение для сравнения треугольников (Страница: 150 , Q.No.: 7)

NCERT Решение для 7 класса по математике — сравнение треугольников 150 , Вопрос 7

Страница № 150:

Вопрос 8:

7
7
7 Нарисуйте грубый набросок двух треугольников так, чтобы у них было пять пар конгруэнтных частей, но все же треугольники не конгруэнтны.

No related posts.