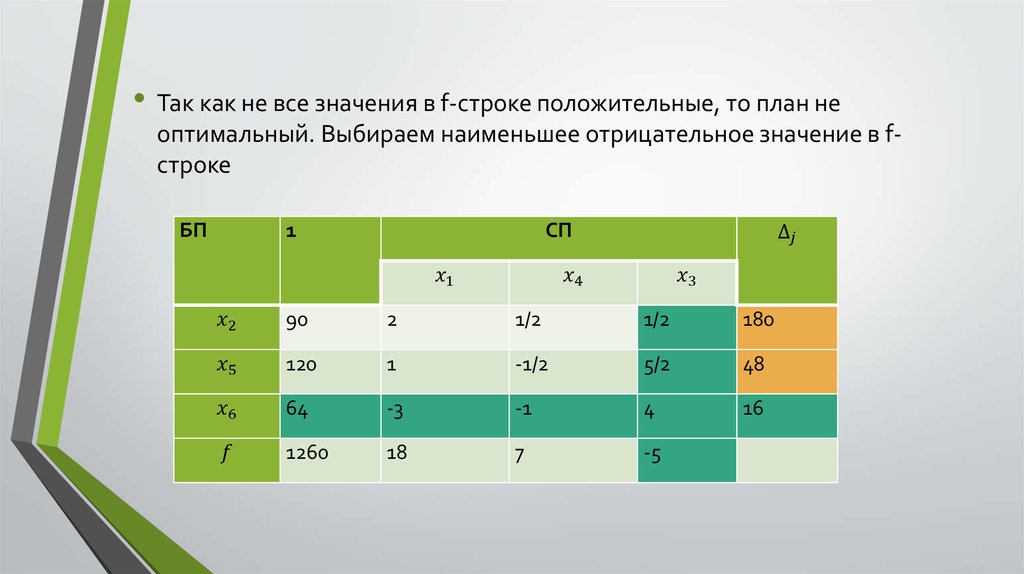
Симплекс-метод решения задачи линейного программирования
- формат doc
- размер 14.46 КБ
- добавлен 01 марта 2005 г.
Автор неизвестен.
Симплекс-метод решения задачи линейного программирования.
Описание симплекс-алгоритма. Применение симплекс-алгоритма при
решении задачи линейного программирования. Поиск допустимого
базисного решения. Примеры использования симплекс-метода.
Смотрите также
- формат djvu
- размер 3.29 МБ
- добавлен 06 сентября 2007 г.
М.: Наука. Главная редакция физико-математической литературы, 1981.
— 340 с. В книге излагаются основные разделы теории и численные методы решения задач линейного программирования. Значительное место уделяется качественному исследованию свойств содержательных моделей методами линейного программирования. Основной материал сопровождается упражнениями теоретического характера. Линейные модели, выпуклые многогранники и линейные неравенства, теория…
- формат djvu
- размер 7.38 МБ
- добавлен 09 декабря 2009 г.
Пер. с англ. — М.: Радио и связь, 1989. — 176 с: ил. ISBN 5-256-00186-8. В книге английского автора освещены основные положения и методы линейного программирования. Рассмотрены симплекс-метод и его реализация на ЭВМ, проблема вырожденности, анализ чувствительности и двойственный симплекс-метод, транспортная задача, задача о назначении, двойственность в линейном программировании и др. Алгоритмы решения различных задач линейного программирования ре.
- формат pdf
- размер 1.16 МБ
- добавлен 15 декабря 2011 г.
Учебно-методическое пособие к контрольной работе. Математический, графический и симплекс-метод решения задач линейного программирования. Решение транспортных задач. Специальные задачи линейного программирования.
- формат doc
- размер 1.28 МБ
- добавлен 29 июня 2009 г.
По каждой теме приведены все типовые примеры с подробным описанием решения задач. Содержание. Общая задача линейного программирования. Преобразование исходной модели. Графическое решение. Симплекс-метод. Двойственный симплекс-метод. Составление двойственных задач. Транспортная задача линейного программирования. а) Нахождение опорного плана.
- формат doc
- размер 734 КБ
- добавлен 13 декабря 2009 г.
Учебно-методическое пособие, Ульяновск, 2006 г. Глава 1. Основные понятия 1.1. Примеры моделей, приводящих к задачам линейного программирования 1.2. Различные формы задачи линейного программирования 1.3. Геометрическая интерпретация задач линейного программирования 1.4. Выпуклые множества и выпуклые функции 1.5. Базисные, допустимые и оптимальные решения Глава 2. Симплекс-метод 2.1. Построение допустимого базисного решения 2.2. Критерий оптимал…
Практикум
- формат pdf
- размер 271.19 КБ
- добавлен
31 октября 2010 г.
Работа посвящена наиболее распространенному методу решения задачи линейного программирования (симплекс-методу). Сформулирован алгоритм решения задачи, который проиллюстрирован на примере, предложены варианты заданий. Методические указания предназначены для студентов, изучающих дисциплину «Системный анализ». Подготовлены на кафедре САПР ИжГТУ. Год издания: 1999. Страниц: 14.
- формат doc
- размер 299.45 КБ
- добавлен 24 сентября 2010 г.
Лекции по теории линейного программирования. Содержание. Основная задача линейного программирования – в трех формах. Эквивалентность различных форм постановки основной задачи. Преобразование Лежандра. Определение двойственной задачи с помощью преобразования Лежандра. Теорема двойственности и теорема существования решения. Критерии крайней точки невырожденной канонической задачи.
Алгоритм симплекс-метода решения задачи линейного программирования….
- формат doc, html, gif, htm, rtf, txt, odt, ppt, pdf, xls
- размер 6.77 МБ
- добавлен 12 января 2010 г.
Вопросы к экзамену: Обыкновенные Жордановы исключения. Определение. Обыкновенные Жордановы исключения. Геометрический смысл. Модифицированные Жордановы исключения. Определение. Применение Жордановых исключений в линейной алгебре. Обращение матриц на примере матрицы Применение Жордановых исключений в линейной алгебре. Вычисление ранга матрицы на примере матрицы (определить ранг матрицы): Применение Жордановых исключений в линейной алгебре. Система…
- формат pdf
- размер 213.62 КБ
- добавлен 23 апреля 2011 г.
ООО «Резольвента», 2009.
— 20 с. Содержание: Постановка основной задачи линейного программирования. Графический метод решения общей задачи линейного программирования. Симплекс-метод решения общей задачи линейного программирования. Вопросы для самоконтроля. Задания для самостоятельной работы. Литература.
Статья
- формат pdf
- размер 1.3 МБ
- добавлен 13 января 2011 г.
Воткинский филиал Ижевского государственного технического университета. . Тематика лекций: Постановка задачи линейного программирования. Основная задача линейного программирования. Геометрическая интерпретация задачи линейного программирования. Симплекс-метод. Теория двойственности. Двойственный симплекс-метод. Транспортная задача. Примеры задач: симплекс-метод, двойственный симплекс-метод, транспортная задача.
Новейшие вопросы «симплекс-метод» Задавать вопрос
Вопросы, относящиеся к «симплексному алгоритму», из области математической оптимизации
- Узнать больше…
- Лучшие пользователи
- Синонимы
125 вопросы
Новейший
Активный
Баунти
Без ответа
Сортировать поНет ответов
Имеет награду
Отсортировано поНовейший
Последние действия
Наивысший балл
Самый частый
Щедрость скоро закончится
ОтмеченМои просматриваемые теги
Следующие теги:
2 голоса
1 отвечать
30 Просмотры
Уменьшение искусственной переменной, необходимой для LPP
Учитывая, что у меня есть вопрос о целевой функции для минимизации или максимизации, и у меня есть ограничение для того же самого, так что при преобразовании в форму уравнения для использования симплексного метода потребуется .
- оптимизация
- линейное программирование
- симплекс
- симплекс-метод
0 голоса
0 ответы
19 Просмотры
Как решить минимизацию с помощью двойного и симплексного метода
Как мне минимизировать $2y_1 + y_2$, используя симплекс-метод? при условии: $ 10y1 + y2 \ge 10 $ $ 2y1 + y2 \ge 8 $ $ у1 + у2 \ge 6 $ $ y1 + 2y_2 \ge 10 $ $ y1 + 12y_2 \ge 12 $ $ y1,y2 \ge 0 $ У меня есть …
- линейная алгебра
- симплекс-метод
0 голоса
0 ответы
34 Просмотры
Нахождение второй наиболее оптимальной точки с помощью модификации симплекс-метода
Итак, я играл с симплекс-методом, и в основном меня интересовало решение проблемы «найти вторую наиболее оптимальную вершину» для максимизации заданной целевой функции, чтобы быть.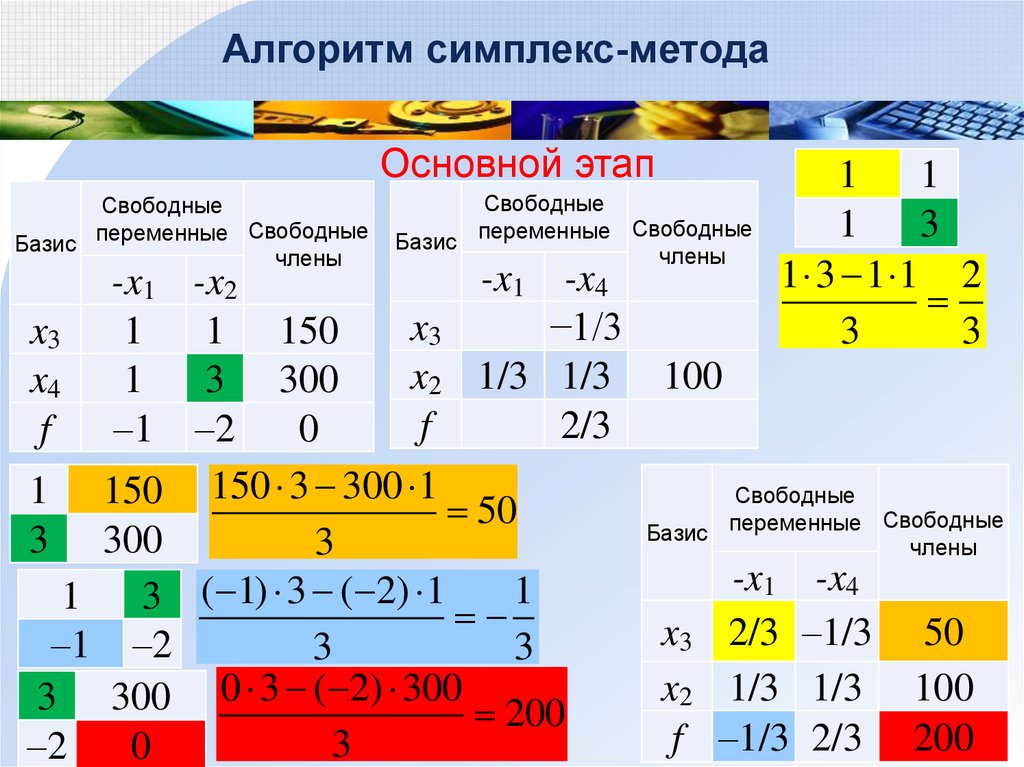
..
- оптимизация
- выпуклая оптимизация
- линейное программирование
- симплекс-метод
- двухфазный симплекс
0 голоса
0 ответы
24 Просмотры
Почему избыточные переменные не могут быть отрицательными в линейном программировании?
В качестве предыстории я исследовал симплекс-метод нестандартной формы, в котором у вас есть ограничения, содержащие символы $\ge$, например, $2x+3y \ge 14$. Я понимаю, что при переписывании такого…
- линейное программирование
- симплекс-метод
0 голоса
0 ответы
46 Просмотры
Альтернативные оптимумы в линейном программировании
Указывает ли наличие альтернативных оптимумов на то, что целевая функция параллельна неизбыточному связывающему ограничению в оптимуме?
Предположим, у меня есть следующая линейная программа
$$ \begin{массив}.
..
- линейное программирование
- симплекс-метод
0 голоса
0 ответы
38 Просмотры
Поиск смежных вершин на выпуклом многограннике, поиск среди обменов базисов?
Мой вопрос о том, как вообще перейти из одной вершины выпуклого многогранника в соседнюю. Но также у меня есть более концептуальные вопросы о том, как работает симплекс-метод. Скажем, у меня есть линейный…
- линейное программирование
- выпуклая геометрия
- многогранники
- дискретная геометрия
- симплекс-метод
-1 голоса
1 отвечать
35 Просмотры
Есть ли способ найти оптимальное решение задачи LPP с оптимальным решением для двойственного, найденным графическим методом?
Для следующей задачи LPP
$$
\text{Свернуть} \quad 12x+8y+8z \\
\text{s.
t} \quad
2x+2y+2z ≥ 1 \\
3x+y-z ≥ 1\\
\text{Где} \quad x, y, z ≥ 0
$$
Я преобразовал его в двойной с переменными $r$ &…
- линейное программирование
- симплекс-метод
0 голоса
1 отвечать
41 Просмотры
Как подойти к проблеме LP с верхними границами
Мне нужно решить следующую задачу: $$\макс: x_1+12x_2+65x_3; $$ $$x_2+4x_3 \leq 200;$$ $$x_1+10x_2+60x_3 \leq 750; $$ $$x_1,x_2,x_3 \leq 50 $$ Чтобы эффективно решить ее вручную, я попытался сделать …
- линейное программирование
- замена переменной
- операции-исследование
- симплекс-метод
1 голосование
0 ответы
26 Просмотры
Связь между вершинами в стандартной форме и базисными допустимыми решениями в канонической форме LP
Пожалуйста, проверьте правильность моих мыслей.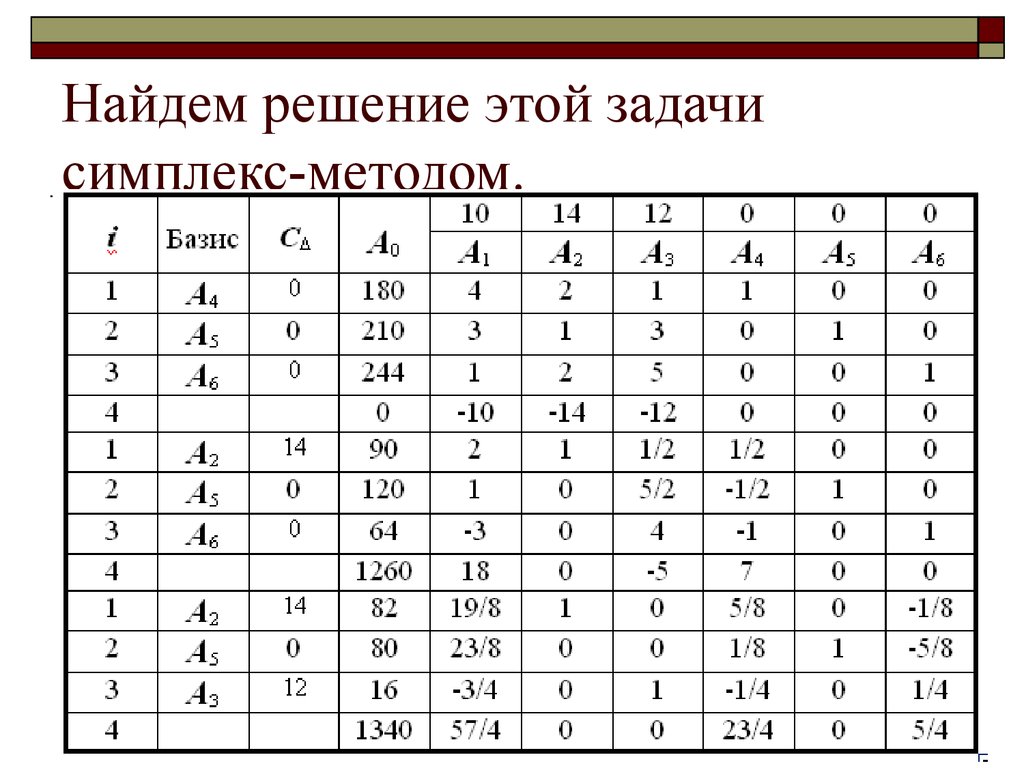
Tx$$
$$Ax\leq b,$$
$$x\geq 0,$$
где $A$ — матрица из $m$ строк и $n$ столбцов, $x\in\mathbb{…
- линейная алгебра
- неравенство
- линейное программирование
- многогранники
- симплекс-метод
0 голоса
0 ответы
39 Просмотры
Симплексные алгоритмы: определение симплексного метода для вопроса.
Я только начинаю знакомиться с основами симплексных алгоритмов, поэтому я мало что о них знаю, кроме вычислений (и это все, на чем я сейчас сосредоточен). Я изучал Big M, 2 Phase, Dual …
- линейная алгебра
- линейное программирование
- симплекс-метод
- двухфазный симплекс
0 голоса
0 ответы
33 Просмотры
Нужно ли добавлять вспомогательную переменную при добавлении нового ограничения равенства в LP?
Например, у меня есть следующая проблема:
\начать{выравнивать}
&\textrm{мин z} = -2x_1 -x_2 +x_3 \\
&\textrm{s.
t.} \\
& \qquad x_1 +2x_2 +x_3 \leq 8 \\
& \\
&\quad -x_1 +x_2 -2x_3 \leq 4 …
- линейное программирование
- решение задач
- ограничения
- симплекс-метод
0 голоса
0 ответы
50 Просмотры
Как на самом деле работает симплекс-метод?
Я узнал о симплекс-методе, о том, как поворачивать вручную, до того, как появились коммерческие решатели. И я все еще немного не понимаю, что на самом деле делают слабые переменные и цели. Мой …
- линейное программирование
- симплекс-метод
3 голоса
2 ответы
140 Просмотры
Почему мы не можем решить задачу ЛП, просто найдя все вершины допустимой области и проверив целевую функцию в каждой вершине?
Почему нельзя решить задачу, просто найдя все вершины выпуклого многогранника допустимых решений и проверив целевую функцию в каждой вершине?
Я предполагаю, что базовое решение LP может не быть .
..
- линейная алгебра
- линейное программирование
- симплекс-метод
0 голоса
0 ответы
49 Просмотры
Оптимальная стратегия первого игрока в матричной игре с одним параметром
У меня проблема со следующей проблемой: Нам дано семейство матричных игр, которое задается следующей матрицей: $$\begin{bmatrix} 2 и -1 и 0 и 4\\ -1 и а и 2 и …
- матрицы
- оптимизация
- теория игр
- симплекс-метод
2 голоса
1 отвечать
74 Просмотры
Как вы решаете задачу минимизации LP с помощью двойного метода?
Так что я только начал с темы линейного программирования в моем университете. И пока я тренировался, я нашел следующий вопрос:
$$\мин Z=3x_1+4x_2-x_3$$
$$\text{При условии: }x_1+3x_2-x_3\ge1$$
$$2x_1+x_2+…
- линейное программирование
- симплекс
- симплекс-метод
на страницу
Симплексный метод для нестандартных задач
Симплексный метод для нестандартных задач
|
| ИНДЕКС ИЗ УСЛОВИЯ |
|
| ||||||
| СТАНДАРТНАЯ ЗАДАЧА МАКСИМИЗАЦИИ — это задача линейного программирования.
задача , которая удовлетворяет всем следующим 4 УСЛОВИЯМ (Рольф, стр. 263) : | ||||||
| ||||||
|
Ссылка : Пример применения следующей процедуры к нестандартной задаче имеется, с обильными комментариями и перекрестными ссылками.
Ссылка : Для каждого шага этого раздела доступно множество УПРАЖНЕНИЙ. метод.
|
|
|
| Преобразуйте все ограничения в уравнения с резервными переменными, а затем напишите
проблема в виде таблицы с некоторым отрицательным
правые стороны, с или без Z-КОЛОНКИ. |
|
|
ПОИСК ОСНОВЫ (шаги от NS-3 до NS-6)
| Найдите строку, содержащую самое отрицательное правое число. Этот ряд будет называется РЯД ИНДИКАТОРА. Если ни одно правое число не является отрицательным, то ваша таблица СТАНДАРТ. |
| ИНДИКАТОРЫ будут состоять из всех чисел в строке, найденной в NS-3, кроме
самый правый номер; ОСНОВНАЯ КОЛОННА будет содержать самые отрицательные из этих
индикаторы. Если ни один индикатор не является отрицательным, то нет сводного столбца, и
проблема неразрешима . |
| Форма RATIOS или QUOTIENTS для всех (необъективных) строк : для каждой строки, разделите самое правое число на число в сводном столбце. |
| PIVOT будет в ROW с наименьшим неотрицательным отношением. Обратите внимание, что 0(+1) и 0(-1) оба численно равны нулю, но при расчете КОЭФФИЦИЕНТОВ учитывайте 0(+1) как положительный (ОК) и 0(-1) как отрицательное (не в порядке). |
| Выполните поворотное преобразование на приведенном выше шарнир (Рольф, стр. 98). Проверьте PIVOT ENGINE, чтобы ускориться практика. |
| Если все самые правые (необъективные строки) записи неотрицательны,
затем фаза I заканчивается. |