Квадратные уравнения. Повторение теории. Задачи повышенной сложности 8 класс онлайн-подготовка на Ростелеком Лицей |
Тема: Квадратные уравнения
Урок: Повторение теории. Задачи повышенной сложности
1. Повторение теории
Как мы с вами помним, основой теории данной темы являются формулы для вычисления корней квадратного уравнения, формула разложения квадратного трёхчлена на множители и теорема Виета.
Довольно много задач в математике сводится к решению квадратных уравнений. Некоторые примеры подобных задач мы с вами сейчас рассмотрим.
2. Решение задач
Задача №1
Решите уравнение .
Перед нами обычное квадратное уравнение, которое, однако, имеет некоторое осложнение в виде модуля.
Для начала давайте вспомним, что такое модуль: .
Из определения модуля следует правило решения квадратных уравнений, которые содержат модуль: при решении квадратных уравнений, в которых содержится модуль, необходимо раскрыть этот модуль на основе стандартного определения модуля.
Решение
Мы имеем уравнение . По определению модуля, он раскрывается на 2 случая, так что теперь рассмотрим эти случаи отдельно:
|
Если мод модулем у нас стоит число, больше или равное 0, то значок модуля мы можем просто выбросить, при этом не забывая про знак числа. (а) |
Если мод модулем у нас стоит число отрицательное, то мы убираем значок модуля, но при этом меняем знак числа, находящегося под знаком модуля. (б) |
После раскрытия модуля мы можем сказать, что исходное уравнение равносильно совокупности систем, полученных после раскрытия модуля, т. е.
ó .
Теперь решим каждую из систем отдельно:
(а)
Мы помним, что произведение равно 0 тогда и только тогда, когда хотя бы один из множителей равен 0, т. е. => .
Теперь давайте вспомним, что у нас было условие, что , поэтому после нахождения корней в данном случае мы должны проверить, удовлетворяют ли они нашему условию:
. Таким образом, мы видим, что оба корня удовлетворяют условию, поэтому мы можем сказать, что – корни заданного уравнения.
Таким образом, мы видим, что оба корня удовлетворяют условию, поэтому мы можем сказать, что – корни заданного уравнения.
Но теперь давайте вспомним, что корней может быть и больше, т. к. есть второй вариант раскрытия модуля. Давайте решим его:
(б)
Как и в случае (а), решаем данное уравнение, получая следующие корни: =>.
Далее вспоминаем об условии решения данной части исходного уравнения () и проверяем, удовлетворяют ли этому условию корни, которые мы получили:
– это неправильное равенство, поэтому корень не является корнем исходного квадратного уравнения при условии, что . Проверим второй корень: – этот корень удовлетворяет условиям, поэтому можем записать следующую систему: .
Итак, первая система (а) дала нам два корня, вторая система (б) дала один корень, поэтому теперь в ответ мы можем выписать все найденные нами корни исходного квадратного уравнения.
Ответ: .
Итак, в этом примере мы решили квадратное уравнение, которое было осложнено модулем, где вместо простого решения квадратного уравнения нам пришлось решать две системы уравнений.
Задача №2
Решите уравнение .
Если в данном случае мы просто «в лоб» возведём в квадрат первую скобку, то получим уравнение четвёртой степени, которое решать будет уже сложнее. Помимо этого, мы такого раньше не делали, т. е. это является для нас подсказкой к следующим действиям. Вместо этого мы воспользуемся методом «замены переменных», т. е. вместо какого-то выражения мы подставим на время другую переменную и решим исходное уравнение относительно неё.
Решение
Итак, сделаем следующую замену: , тогда мы получим следующую систему:
А теперь решим новое квадратное уравнение относительно y с помощью теоремы Виета:
=> .
Теперь необходимо вернуться к исходной системе и сделать обратную замену:
Таким образом мы получили корни исходного квадратного уравнения, используя метод замены.
Ответ: .
Задача №3
Решите уравнение .
Мы говорили, что в предыдущем примере метод замены был довольно явно виден невооружённым глазом, в данном же случае, на первый взгляд, абсолютно не понятно, как же решать данное уравнение. Однако мы понимаем, что раскрывать скобки и приводить это уравнение к уравнению четвёртой степени – это неправильно и сложно, поэтому будем искать замену переменных.
Однако мы понимаем, что раскрывать скобки и приводить это уравнение к уравнению четвёртой степени – это неправильно и сложно, поэтому будем искать замену переменных.
Решение
Поскольку на первый взгляд нам не понятно, какую же делать замену, можно сделать это наугад, а можно чуть помочь себе, записав исходное уравнение следующим образом:
, теперь нам видно, что , поэтому попробуем объединить первую с четвёртой скобки и вторую с третьей.
Теперь мы видим, какую же замену переменных стоит сделать:
Решим новое квадратное уравнение
Решим полученное уравнение с помощью обратной теоремы Виета:
Не забываем, что необходимо проверить, существуют ли корни данного уравнения в принципе, для этого посчитаем дискриминант получившегося квадратного уравнения: , т. е. у данного выражения корни есть.
=>
Теперь делаем обратную замену.
И подставляем полученные значения вместо в уравнения:
(б)
Вычислим дискриминант:
, поэтому в данном случае не существует ни одного корня.
Т. е. в данном случае нет корней (это также можно записать символами , где .
(а)
Вычислим дискриминант:
> 0, поэтому существует два различных вещественных корня. Найдём их.
.
Ответ: .
Мы рассмотрели несколько примеров, где решение уравнений осуществляется с помощью приведения их к виду обычного квадратного уравнения путём замены переменных.
Задача №4
Решите уравнение .Мы видим, что первая и вторая скобки похожи, но в первой возведён в квадрат.
Предположительно сделаем следующую замену:
Что же нам теперь делать с первой скобкой? Необходимо тоже выразить её через y. Для этого возведём обе части в квадрат:
Вернёмся к исходному уравнению и запишем его использовав замену:
А теперь решим данную систему:
По теореме Виета находим корни:
=>
Теперь делаем обратную замену:
Поскольку такие уравнения решать мы умеем, то только наметим их ход решения: сведём их к квадратному, учитывая, что знаменатель не равен 0, и решим каждое в отдельности.
Решением всей задачи будет следующий ответ: .
Ответ: .
3. Выводы
Итак, мы повторили теорию, связанную с квадратными уравнениями (основные формулы, теорему Виета и формулы разложения на множители). Затем рассмотрели более сложные задачи, а именно решение квадратных уравнений или тех, которые сводятся к квадратным, методом замены переменных.
Список литературы
- Башмаков М.И. Алгебра 8 класс. – М.: Просвещение, 2004.
- Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 8. – 5-е изд. – М.: Просвещение, 2010.
- Никольский С.М., Потапов М.А., Решетников Н.Н., Шевкин А.В. Алгебра 8 класс. Учебник для общеобразовательных учреждений. – М.: Просвещение, 2006.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Фестиваль педагогический идей «Открытый урок» (Источник).
- Интернет-портал Egesdam.
 ru (Источник).
ru (Источник).
Домашнее задание
- Решите уравнения: а) ; б) ;
- Найдите сумму квадратов корней уравнения: а) ; б) ;
- Тест к главе 3 Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 8. – 5-е изд. – М.: Просвещение, 2010.
Презентация «Уравнения с модулем»
Уравнения с модулем
Способы решения
Определения
- Модуль числа а – расстояние от точки с координатой а до ноля
- следствия
- 1. модуль числа неотрицателен (|a| ≥0)
а
-а
0
a, если а0
-a, если а
0, если а = 0
|a|=
2
Способы решения уравнений с модулями:
- 1. По определению модуля
- 2. Возведение обоих частей уравнения в квадрат
- 3.

- 4. Раскрытие модуля на промежутке знакопостоянства
- 5. Замена совокупностью систем
- 6. Важный частный случай
2
1. По определению модуля
|ƒ(x)| = a (а ≥0)
f(x) = a или f(x) = — a
Пример : |3x — 8| = 5
Решение:
3x — 8 = 5 или 3x — 8 = -5;
3x = 13, 3x = 3;
x = 13/3, x = 1.
Ответ: 13/3; 1.
2
Решить по определению модуля
1) |2x — 3| = 5
решение
решение
4) |11 – 2x 2 | = 3
2) |x 2 — 4x| = 5
решение
решение
2
По определению модуля № 1
|2x — 3| = 5
Решение
2x — 3 = 5 или 2x — 3 = -5
2x = 8 2x = -2
x = 4 x = -1
Ответ: -1;4
2
|x 2 + 4x| = 5
Решение
x 2 + 4x = 5 или x 2 + 4x = -5
x 2 + 4x — 5 = 0
Ответ: -5;1
x 2 + 4x + 5 = 0
D = 16 — 20= -4
D
x = -5
x = 1
2
По определению модуля № 3
Решение
|5x — 1| = 4
5x — 1 = 4 или 5x — 1 = -4
5x = 5 или 5x = -3
x =1 x =-3/5 = -0,6
Ответ: -0,6; 1
2
По определению модуля
По определению модуля № 4
решение
|11 — 2x 2 | = 3
11 — 2x 2 = 3 или 11 — 2x 2 = -3
2x 2 = 8 2x 2 = 14
x = 2 или x = -2 x = 7 x = — 7
Ответ: ; -2; 2;
2
2. Возведение обеих частей в квадрат
Возведение обеих частей в квадрат
Пример |x — 3| = |x + 2|
Решение (x — 3) 2 = (x + 2) 2 *
(x — 3) 2 — (x + 2) 2 = 0
(x — 3 + x + 2)(x — 3 — x — 2) = 0
-5∙(2x – 1) = 0, то (2x – 1) = 0
x = 1/2
Ответ:0,5
*
При возведении обоих частей в квадрат данного уравнения равносильность не нарушается, т.к. модуль всегда неотрицательный, и |а| 2 = a 2
2
Решить возведением обеих частей в квадрат
|x — 4| = |x — 1|
|x + 5| = |2x — 5|
решение
решение
|x 2 – 5x| = |x 2 – x + 4|
|x 2 + 5x +11| = |2x + 1|
решение
решение
2
Решить возведением обеих частей в квадрат
|x — 4| = |x — 1|
(x — 4) 2 – (x — 1) 2 = 0
(x — 4 + x — 1)(x — 4 — x + 1) = 0
-3(2x — 5) = 0
2x — 5 = 0
x = 2,5
Ответ: 2,5
2
Вернуться назад
Решить возведением обеих частей в квадрат
|x + 5| = |2x — 5|
(x + 5) 2 — (2x — 5) 2 = 0
(x + 5 — 2x + 5)(x + 5 + 2x — 5) = 0
(-x + 10) · 3x = 0
-3x(x — 10) = 0
Ответ: 0;10
Вернутся назад
2
Решить возведением обеих частей в квадрат
|x 2 – 5x| = |x 2 – x + 4|
(x 2 — 5x) 2 = (x 2 — x + 4) 2
(x 2 — 5x) 2 — (x 2 — x + 4) 2 = 0
(2x 2 — 6x + 4)(-4x — 4) = 0
-8(x 2 — 3x + 2)(x + 1) = 0
(x — 2)(x — 1)(x + 1) = 0
Ответ: -1; 1; 2
Вернуться назад
2
Решить возведением обеих частей в квадрат
|x 2 + 5x + 11| = |2x + 1|
(x 2 + 5x + 11) 2 = (2x + 1) 2
(x 2 + 5x +11) 2 — (2x + 1) 2 = 0
(x 2 + 7x + 12)(x 2 + 3x +10) = 0
x 2 + 7x + 12 = 0 или x 2 + 3x +10 = 0
Ответ: -4; -3.
2
3.Замена переменной
Пример: x 2 — 7|x| — 8 = 0
Решение: t = |x| условие t ≥ 0
t 2 — 7t — 8 = 0
t 1 + t 2 = 7
t 1 · t 2 = -8
t 1 = -1 не удовлетворяет условию
t 2 = 8
|x| = 8
x = 8 x = -8
Ответ: 8; -8.
2
Решить заменой переменной
x 2 – 3|x| + 2 = 0
x 2 + 3|x| = 10
решение
решение
2
Решить заменой переменной
x 2 — 3|x| + 2 = 0
Решение
Пусть t = |x| , то t ≥ 0
t 2 — 3t + 2 = 0
t = 2 или t = 1.
Тогда:
1) |x| = 2 2) |x| = 1
x = 2 или x = -2; x = 1 или x = -1.
Ответ: -2;-1;1;2
2
Решить заменой переменной
x 2 + 3|x| = 10
Решение
x 2 + 3|x| — 10 = 0
Пусть t = |x| , t ≥ 0
t 2 + 3t – 10 = 0
t = 2 или t = -5 -5
Значит ,
|x|= 2
x = 2 или x = -2
Ответ: -2; 2.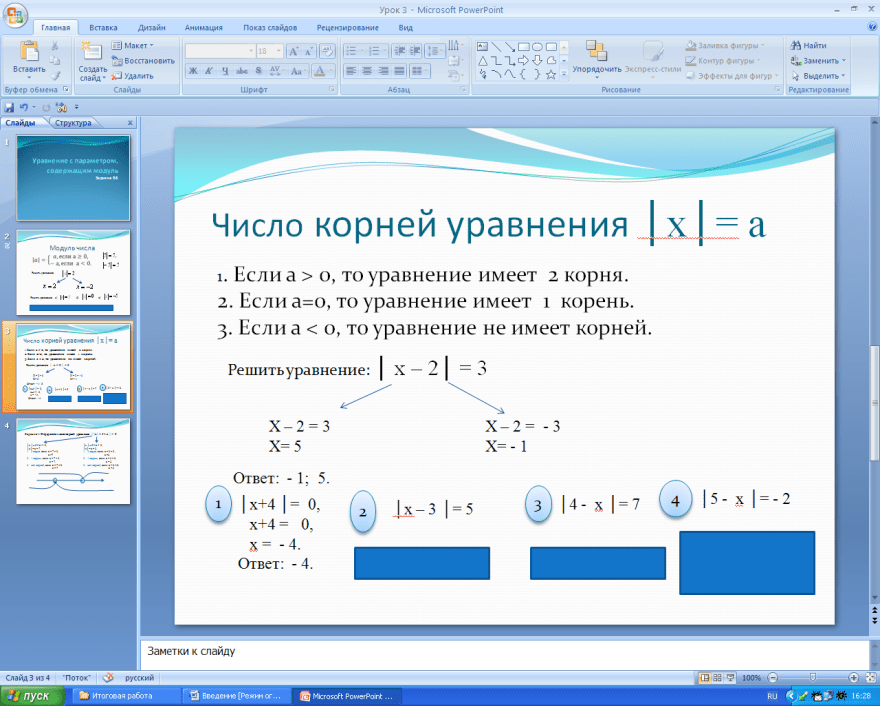
2
4.Раскрытие модуля на промежутке знакопостоянства
- Универсальный способ
Пример: |x| + |x+1|=1
Найдем нули подмодульных выражений: 0; -1
Решение:
— — +
X
X+1
-1 0
— + +
Ответ: [-1;0].
2
Решить, используя раскрытие модуля на промежутках знакопостоянства
Раскрытие модуля на промежутке знакопостоянства
2) |x — 3| + 2|x + 1| = 4
1) |5 — x| + |x — 1| = 10
решение
3) |x — 1| + |2x — 3| = 2
решение
2
Раскрытие модуля на промежутках знакопостоянства № 1
Раскрытие модуля на промежутке знакопостоянства
|5 — x| + |x — 1| = 10
— + +
x — 1
5 — x
+ 1 + 5 —
Если x ≤ 1, то
5 — x –x + 1 = 10
— 2x + 6 = 10
— 2x = 10 – 6
-2x= 4
x = -2
Если 1
5 — x + x — 1 = 10
0x + 4 = 10
0x = 10 – 4
0x= 6
нет решений
Если x ≥ 5, то
-5 + x +x — 1 = 10
2x — 6 = 10
2x = 10 + 6
2x= 16
x = 8
Ответ: — 2 ; 8
2
Раскрытие модуля на промежутках знакопостоянства № 2
|x — 3| + 2|x + 1| = 4
— + +
x + 1
x — 3
— -1 — 3 +
Если x ≤ -1, то
3 — x — 2x -2 = 4
— 3x + 1 = 4
— 3x = 4 – 1
-3x= 3
x = — 1
Если -1
3 – x + 2x + 2 = 4
x + 5 = 4
x = 4 – 5
x= -1
нет решений
Если x3, то
x — 3 +2x + 2 = 4
3x — 1 = 4
3x = 4+1
3x= 5
x = 5/3
нет решений
Ответ: — 1
2
Раскрытие модуля на промежутках знакопостоянства № 3
|x — 1| + |2x — 3| = 2
— + +
x — 1
2x — 3
— 1 — 1,5 +
1.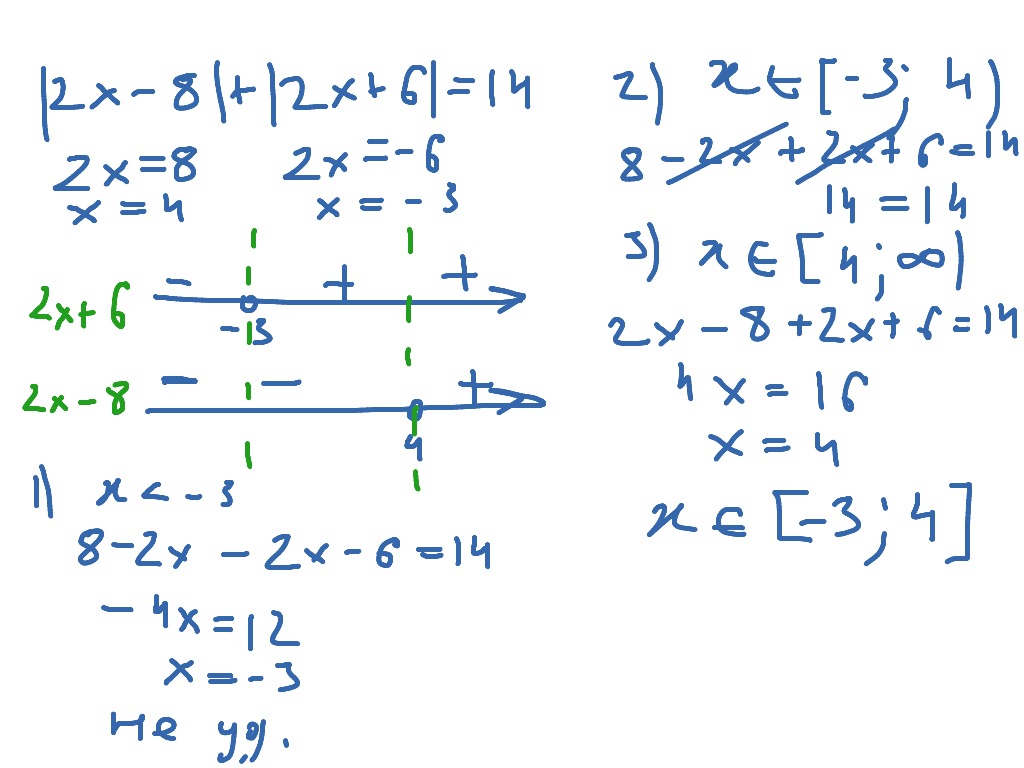 Если x ≤ 1, то
Если x ≤ 1, то
1 — x — 2x + 3 = 2
— 3x + 4 = 2
— 3x = 2 – 4
-3x= — 2
x = 2/3
2 . Если 1
x — 1 + 3 – 2x = 2
— x + 2 = 2
— x = 2 – 2
x= 0
нет решений
3 . Если x 1,5, то
x — 1 + 2x — 3 = 2
3x — 4 = 2
3x = 2 + 4
3x= 6
x = 2
Ответ: 2/3; 2
2
5.Замена совокупностью систем
|ƒ(x)| = g(х)
2
Замена совокупностью систем
Пример: |2x + 7| = 3x + 4
I способ
II способ
2
2
6. Важный частный случай
| f ( x ) | = — f ( x ), тогда f ( x ) ≤ 0
Пример: 7-4 x = |4 x -7|
Решение: т.к. |f ( x )| = -f( x ), то f( x )≤0
4 x — 7 ≤ 0
x ≤ 7/4 , 7/4 = 1,75
2
Удачи!
2
2-x+6 \equiv 0 \pmod{9}$$ Я хочу найти x с помощью модульной арифметики. Как я мог это сделать?
Как я мог это сделать?
Мое решение:
$$\begin{выравнивание*} х(х-1) &\эквив-6 \pmod{9}\\ х(х-1) &\эквив 3 \pmod{9} \end{выравнивание*}$$
Таким образом, $x$ равно: $$ х \экв 3\pmod{9}$$
или
$$x — 1 \экв 3 \pmod{9}$$
Что равно $x \equiv 4 \pmod{9}$
Я знаю, что сделал очень глупо. Так какое же правильное решение? Дайте мне инструкцию, пожалуйста.
- модульная арифметика
- делимость
- квадратика
$\endgroup$
11
$\begingroup$
Позвольте мне рассказать о том, что вы сделали, а не о том, как это сделать правильно, поскольку другие ответили различными способами найти правильный ответ.
очень неправильное то, что вы сделали, это уйти от
$ $ х (х-1) \ эквив 3 \ pmod {9} $ $
к
$$x\экв 3 \pmod{9}\quad\text{or}\quad x-1\equiv 3\pmod{9}.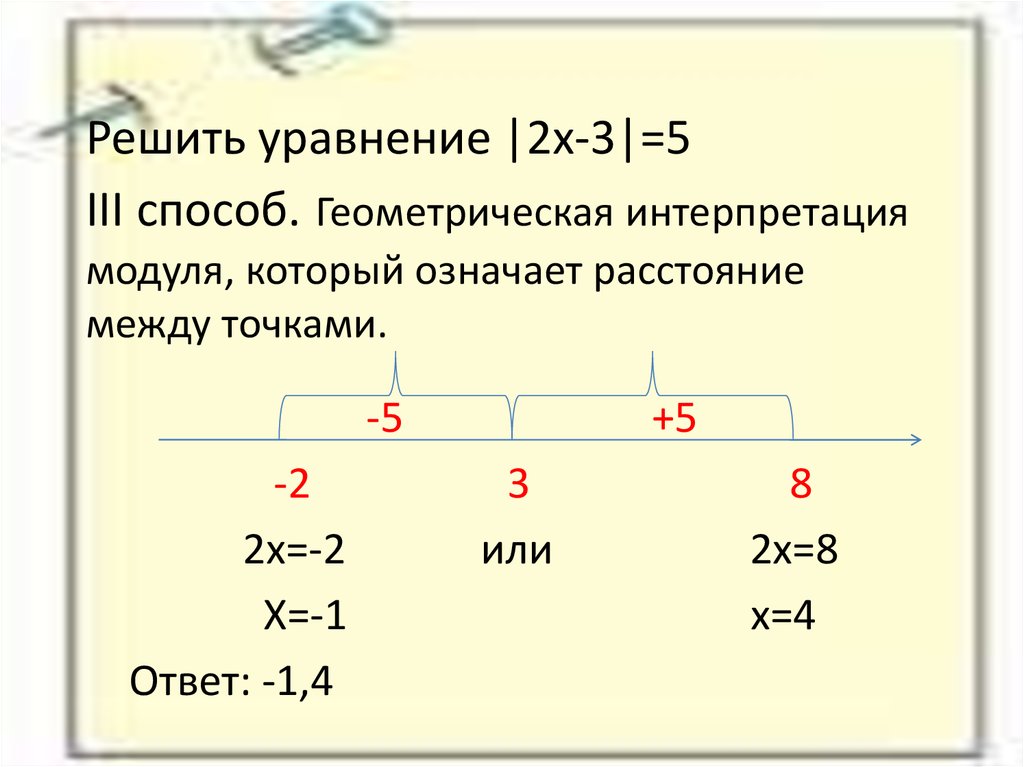 2-5x+6=0$, сказав: 92-5x &= 6\\
х(х-5)&=6
\end{выравнивание*}$$
и, следовательно, $x=6$ или $x-5=6$; поэтому $x=6$ или $x=11$.
2-5x+6=0$, сказав: 92-5x &= 6\\
х(х-5)&=6
\end{выравнивание*}$$
и, следовательно, $x=6$ или $x-5=6$; поэтому $x=6$ или $x=11$.
Это неправильно. Вы не можете этого сделать, потому что единственный способ получить $0$ при умножении двух действительных чисел, если один из них равен $0$; получение $6$ в результате продукта не означает, что один из факторов должен быть $6$.
Ваш аргумент был бы неверным в реалах; еще одна проблема здесь в том, что это было бы неправильно по модулю $9$ , даже если вы получили сравнение $x(x-1)\equiv 0\pmod{9}$. Причина в том, что когда вы работаете по модулю $9$, возможно для произведения, равного $0$, но ни один из множителей не равен $0$: действительно, $(3)(3)\equiv 0\pmod{ 9}$, например. Поэтому, когда вы работаете по модулю $9$, вы даже не можете использовать этот тип аргумента, когда произведение равно $0$, не говоря уже о том, когда оно не равно $0$.
Таким образом, вы берете неверный аргумент из другой ситуации, которая уже является проблемой, и усугубляете эту проблему, пытаясь использовать ее в ситуации, где 92},\,$ для $\, x = 3j,\,$, т. 2=(92 + 9 q + 8 \экв 0 \pmod9 \; \text{ подразумевает } \; 8 \equiv 0 \pmod9$
2=(92 + 9 q + 8 \экв 0 \pmod9 \; \text{ подразумевает } \; 8 \equiv 0 \pmod9$
Мы заключаем, что $[4]$ и $[6]$ являются решениями $\text{(1)}$.
$\endgroup$
алгоритм — решение системы связанных уравнений с разными модулями
спросил
Изменено 5 лет, 11 месяцев назад
Просмотрено 1к раз
Существует ли какой-нибудь алгоритм решения системы уравнений, выраженной в разных пространствах по модулю? Например, рассмотрим эту систему уравнений:
(x1 + x2) % 2 = 0 ( х2 + х3) % 2 = 0 (х1 + х2 + х3) % 3 = 2
Одно из решений этой системы:
x1 = 0 х2 = 2 х3 = 0
Как я мог арифметически найти это решение (без использования алгоритма грубой силы)?
Спасибо
- алгоритм
- математика
- модуль
- решение уравнений
- линейное уравнение
1
Вы можете переписать эти уравнения как
x1 + x2 = 2*n1 х2 + х3 = 2*n2 х1 + х2 + х3 = 3*n3 + 2
Итак, это задача о линейном диофантовом уравнении, для которой в литературе есть решения.
Пример: http://www.wikihow.com/Solve-a-Linear-Diophantine-Equation
См. также: https://www.math.uwaterloo.ca/~wgilbert/Research/GilbertPathria.pdf
Алгоритм:
Запишите xi как функцию nks
В этом случае:
x3 = 3* п3 + 2 - 2*п1 х2 = 2*n2 - (3*n3 + 2 - 2*n1) x1 = 2*n1 - (2*n2 - (3*n3 + 2 - 2*n1))
Поскольку деления в правой части нет, выберите любое (n1, n2, n3), и вы должны получить решение.
4
Первая строка аналогична формуле x1, x2 — все четные или все нечетные числа. Вторая строка аналогична выражению x2, x3 — все четные или все нечетные числа. Следовательно, x1,x2,x3 — все четные или все нечетные числа. С третьей строки мы можем заменить вопрос на «3 нечетных или 3 четных числа, которые в сумме составляют 3k+2».
Вы можете преобразовать свою систему в модуль LCM (наименьшее общее кратное). Просто найдите LCM всех уравнений по модулю и умножьте каждое уравнение соответствующим образом.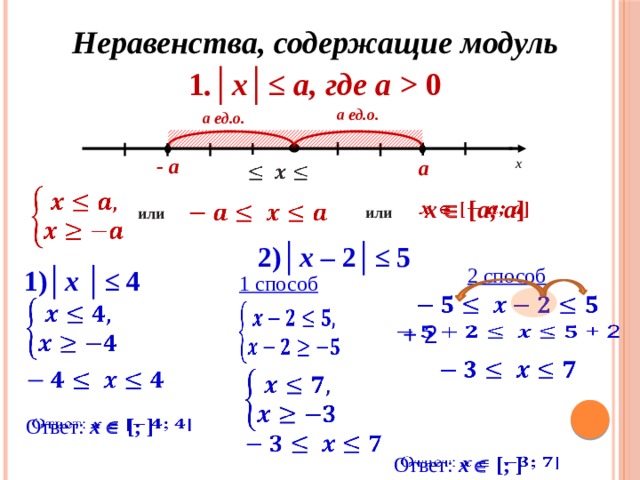

 ru (Источник).
ru (Источник).