Задачи на теорему фалеса 8 класс: Задачи на теорему Фалеса — задачи с решениями

Трапеция. Теорема Фалеса. Задачи. 8 класс

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

Урок № 4
Трапеция
Ввести понятие трапеции и ее элементов.
Познакомить с равнобедренной и прямоугольной
трапецией.
Рассмотреть свойства равнобедренной трапеции.
04.12.2012
www.konspekturoka.ru
1
В
А
Основание
С
Основание
D
АВСD – трапеция, если ВС∥AD,
АВ и СD – боковые стороны,
ВС и AD – основания.

04.12.2012
www.konspekturoka.ru
2
В
С
А
D
АВСD – равнобедренная трапеция, если ВС∥ AD,
АВ = СD – боковые стороны.
04.12.2012
www.konspekturoka.ru
3
В
С
А
D
АВСD – прямоугольная трапеция, если
ВС∥ AD,
∠А = 90° или ∠В= 90°.
04.12.2012
www.konspekturoka.ru
4
В
С
М
N
А
D
М – середина АВ
N – середина CD
MN – средняя линия трапеции
BC + AD
MN =
2
04.12.2012
www.konspekturoka.ru
5
В
С
А
D
1. В равнобедренной трапеции диагонали равны.
2. В равнобедренной трапеции углы при каждом основании
равны.
ВD = AC – диагонали трапеции
∠А = ∠D, ∠В = ∠С – углы при основаниях
04.12.2012
www.konspekturoka.ru
6
В
С
А
D
1. Если диагонали трапеции равны, то она равнобедренная.
2. Если углы при основании трапеции равны, то она
равнобедренная.
ВD = AC – диагонали трапеции
∠А = ∠D, ∠В = ∠С – углы при основаниях
04. 12.2012
www.konspekturoka.ru
7
Если на одной из двух прямых отложить последовательно
равных несколько отрезков и через их концы провести
параллельные прямые, пересекающие вторую прямую,
то они отсекут на второй прямой равные между собой
отрезки.
б) l₁ ∥ l₂
а) l₁ ∥ l₂
А₁
А₂
А₃
В₃
А₄
В₄
А₅
l₂
В₅
А₁А₂ В₂ В₁ — параллелограмм
А₁А₂ = В₁В₂
04.12.2012
А₂
В₂
А₃
l₁
А₁
В₁
В₁
С
D
А₄
В₂
В₃
В₄
А₅
В₅
l₁
l
l₁ ∥ l
l₂
А₂ А₃DC — параллелограмм
А₂A₃ = CD
www.konspekturoka.ru
А₂A₃ = В₂B₃
8
1
Задача
Докажите, что отрезок, соединяющий середины боковых
сторон трапеции, параллелен основаниям трапеции.
В
E
.
А
С
Доказательство
Пусть Е – середина АВ.
Проведем ЕF ∥ BC ∥ AD.
.F
Точка F – середина CD
(по теореме Фалеса).
D
Докажем, что ЕF — единственный
Через точки Е и F можно провести только одну прямую
(аксиома) т. е. отрезок, соединяющий середины боковых
сторон трапеции ABCD параллелен основаниям, ч. т. д.
04.12.2012
www.konspekturoka.ru
9
А
2
Задача
Дано:
Найти:
В
АВСD – трапеция, ∠A = 36°, ∠C = 117°
∠В = ?, ∠D = ?
С
117°
Решение
АВСD – трапеция, то ВС∥ AD.
∠А + ∠В = 180°
36° + ∠В = 180°
36°
D
∠С + ∠D = 180°
∠В = 180° — 36°
∠В = 144°
∠117° + ∠D = 180° ∠D = 180° — ∠117°
∠D = 63°
Ответ:
04.12.2012
∠В = 144°, ∠D = 63°
www.konspekturoka.ru
10
А
Задача
3
Дано:
АВСD – равнобокая трапеция, ∠A = 68°,
Найти:
В
∠В = ?, ∠С -?, ∠D = ?
Решение
С
Если АВСD – равнобокая трапеция,
то ∠A = ∠D = 68°,
∠ 68°+ ∠В = 180°
68°
68°
D
∠В = 180° — ∠ 68°
∠В = 112°
∠В = ∠С = 112°,
Ответ:
04.12.2012
∠С = 112°.
∠D = 68°∠, В =
112°www.konspekturoka.ru
,
11
Задача
4
АВСD – прямоугольная трапеция,
∠D = 90°, BC = 4 см, AD = 7 см, ∠A = 60°
Дано:
Найти:
АВ — ?
В
4 см
Решение
С
Проведем ВВ₁ ⊥ AD
AВ₁ = AD — B₁D
AВ₁ = 7 — 4 = 3 (см)
60°
∟
А
В₁
7 см
D
Рассмотрим ∆ АBВ₁:
∠A = 60° — по условию,
∠В₁ = 90° так как ВВ₁ ⊥ AD, то ∠В = 30°
AВ₁ = ½АВ – по свойству прямоугольного треугольника,
АВ = 3· 2 = 6 (см).
Ответ: 6 (см).
04.12.2012
www.konspekturoka.ru
12
Какой четырехугольник называется трапецией?
Как называются стороны трапеции?
Какая трапеция называется прямоугольной? Равнобедренной?
Сформулируйте свойства равнобедренной трапеции.
Сформулируйте признаки равнобедренной трапеции.
Что такое средняя линия трапеции? Свойство средней
линии трапеции.
04.12.2012
www.konspekturoka.ru
13

English     Русский Правила

в каком классе проходят, как звучит, доказательство, кратко и понятно, следствие

Формулировка Теоремы Фалеса

Определение 1

Теорема Фалеса — теорема в разделе евклидовой геометрии (планиметрии), которая доказывает существование набора параллельно секущих к паре прямых отрезков.

Исторически данная теорема приписывается греку — философу и математику Фалесу Милетскому. По одной из легенд Фалес Милетский высчитывал высоту пирамиды Хеопса, посредством измерения длины тени пирамиды на земле, а также длину тени палки измеряемой высоты. Одно из самых старых известных науке доказательств данной теории было представлено в книге «Элементы Евклида».

Рассмотрим саму теорему Фалеса:

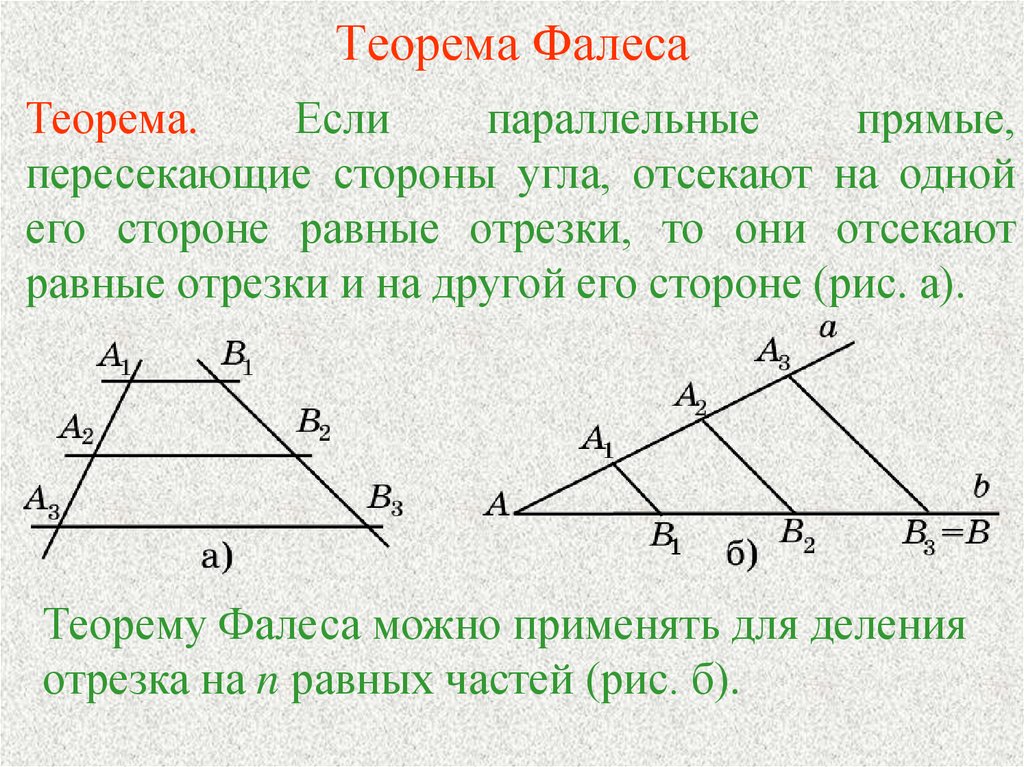
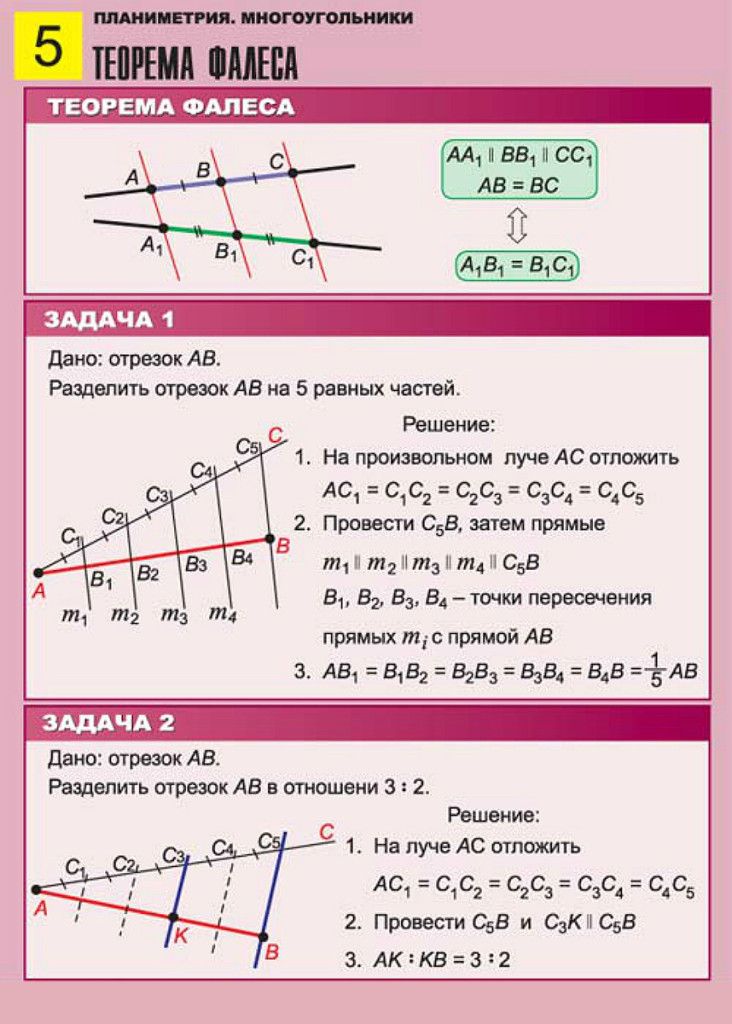
Теорема 1

Если на одной прямой из двух отделить равные отрезки, а через концы данных отрезков провести параллельные прямые, то они, пересекая вторую прямую, отделят на ней равные отрезки.

Обобщение утверждения можно представить в виде следующей формулы: 

A1A2 = A2A3

B1B2 = B2B3

Взгляните на рисунок:

Источник: microexcel.ru

Примечание 1

Совершенно не важно, пересекают ли две исходные прямые друг друга взаимно. То есть, теорема Фалеса будет верна и в случае пересекающихся прямых, и в случае параллельных прямых.

Теорема Фалеса — частный случай теоремы о пропорциональных отрезках.

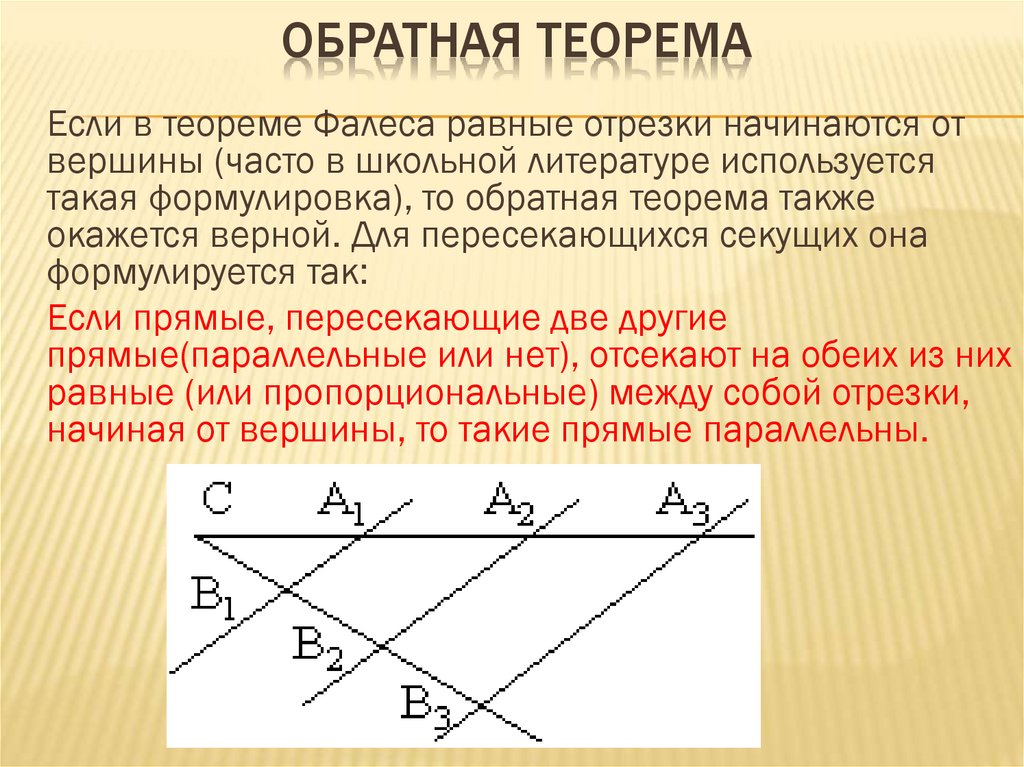
Существует также обратная теорема Фалеса. Она применяется тогда, когда равные отрезки начинаются с вершины угла, образованного пересекающимися прямыми. Рассмотрим формулировку обратной теоремы Фалеса для этого случая.

Теорема 2

В случае, если прямые, которые пересекают две другие пересекающиеся прямые, отсекают на этих двух пересекающихся прямых равные (пропорциональные) отрезки, начиная от вершины, то такие секущие прямые являются параллельными.

То есть:

CB1 = B1B2 = B2B3

CA1 = A1A2 = A2A3

Взгляните на рисунок:

 

Источник: ru.wikipedia.org

Примечание 2

Для обратной теоремы Фалеса крайне важно, чтобы равные отрезки начинались именно от вершины.

Доказательство Теоремы Фалеса

Представим доказательство теоремы Фалеса на примере задачи.

Задача 1

Дано: угол COD

A1B1 параллельна A2B2, A2B2 параллельна A3B3.

A1, A2, A3 принадлежит прямой OC.

B1, B2, B3 принадлежит прямой OD.

A1A2 равна A2A3.

Требуется доказать, что B1B2 равна B2B3.

Доказательство:

1. Для начала нам нужно провести прямую EF через точку B3. Таким образом прямая EF будет равна A1A3.
2. Теперь требуется рассмотреть получившийся четырехугольник A1FB2A2. Получается, что прямая A1F равна A2B2, согласно условиям задачи. A1A2 равна FB2, согласно нашему построению. Таким образом, A1FB2A2 представляет собой параллелограмм.
3. Согласно свойству сторон параллелограмма (противолежащим) A1A2 равна FB2.
4. По этой же схеме можно доказать, что A2B2EA3 также является параллелограммом, а его стороны A2A3 будут равны B2E.
5. Согласно условию A1A2 равна A2A3, это значит, что FB2 будет равна B2E.
6. Рассмотрим внимательно получившиеся треугольники B2B1F, B2B3E. Получается, что FB2 будет равна B2E (ранее доказали), угол B1B2F будет равен углу B3B2E (вертикальные углы), угол B2FB1 будет равен B2EB3 (внутренне накрест лежащие углы).
7. Таким образом получается, что треугольники B2B1F, B2B3E являются равными (по признаку стороны и двух прилежащих углов).
8. Согласно равенству треугольников выводится и равенство сторон. То есть, B1B2 равна B2B3.
9. Что и требовалось доказать.

Примечание 3

Параллелограмм — такой четырехугольник, у которого все стороны параллельны, то есть лежат на нескольких параллельных прямых.

Следствие из Теоремы Фалеса

Следствием данной теоремы является теорема о средней линии треугольника.

Теорема 3

Средняя линия треугольника является параллельной для одной из сторон треугольника, а также равна половине данной стороны.

Еще одним следствием теоремы Фалеса можно считать теорему о пропорциональных отрезках.

Теорема 4

Прямые, которые параллельны друг другу и пересекают стороны угла, отсекают от сторон угла равные отрезки.

Следствиями теоремы Фалеса также являются следующие правила:

1. Медиана, которая проводится к гипотенузе, будет равна половине этой гипотенузы.
2. Центр окружности, которая описывает треугольник, является серединой гипотенузы, в то же время радиус окружности равен половине длины гипотенузы треугольника, вписанного в окружность.

Примеры решения задач

Задача 2

Даны две прямые AD и AN с вершиной A. Проведем параллельные прямые BK, CM, DN. Известно, что AB = BC = CD = 6 см, BK параллельна CM, CM параллельна DN, а AK = 8 см.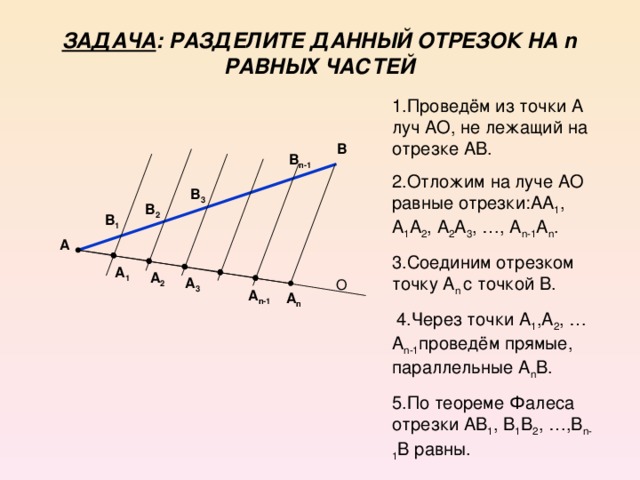 Нужно найти длину MN.   

Решение: согласно теореме Фалеса BK параллельна CM, CM параллельна DN, а также AB = BC = CD следует, что отрезок AK = KM = MN.  Таким образом, MN = AK = 8 см.

Ответ: MN = 8 см.

Задача 3

Представим, что прямая KM будет параллельная DC и пересекать угол COD таким образом, что O, C, M будут лежать на одной прямой, а O, D, K также будут лежать на одной прямой. Дано, что DC = 4, OD = 2, OK = 14. Нужно найти длину KM.

Решение: 

DC параллельна KM. Согласно теореме о пересечении двух параллельных прямых третьей прямой, получается, что OKOD=KMDC . KM=OKOD×DC=142×4=28

Ответ: KM = 28.

Объяснение урока: Параллельные прямые и поперечные: пропорциональные части

В этом объяснении мы узнаем, как использовать параллелизм прямых, чтобы найти недостающую длину отрезка поперечной прямой, разрезанной параллельными прямыми.

Определение: секущая

Секущая – это линия, которая пересекает две или более прямых в одной плоскости в различных точках.

Прямые, которые пересекает секущая, не обязательно должны быть параллельны, но в каждой из задач, которые мы рассмотрим, они параллельны.

Два примера трансверсалей: ⃖⃗𝐴𝐶 и ⃖⃗𝐷𝐹 в следующем рисунке, потому что они обе пересекают каждую из трех параллельных прямых в отчетливые точки. Мы видим, что трансверсаль ⃖⃗𝐴𝐶 пересекает прямые в точках 𝐴, 𝐵 и 𝐶, а трансверсаль ⃖⃗𝐷𝐹 пересекает их в точках 𝐷, 𝐸 и 𝐹.

Обратите внимание, что пересечения трех параллельных прямых и двух поперечных создайте четыре различных сегмента линии. Отрезок с концами в 𝐴 и 𝐵𝐴𝐵 и еще один отрезок с концами в точках 𝐵 и 𝐶𝐵𝐶 оба лежат на поперечной ⃖⃗𝐴𝐶. Аналогично, отрезок с концами в точках 𝐷 и 𝐸𝐷𝐸 и еще один сегмент с концами в 𝐸 и 𝐹𝐸𝐹 оба лежат на трансверсали ⃖⃗𝐷𝐹.

При пересечении секущей параллельными прямыми соответствующие углы равны. Таким образом, мы знаем, что четырехугольники 𝐴𝐵𝐸𝐷 ​​и 𝐵𝐶𝐹𝐸 на рисунке подобны.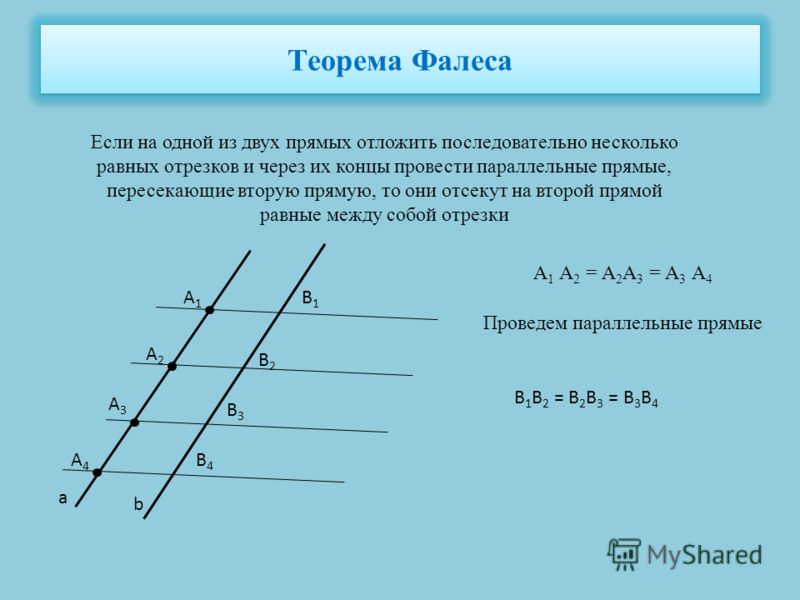 Каждый из наших четырех отрезков является стороной одного из этих четырехугольников, где 𝐴𝐵 соответствует 𝐵𝐶 и 𝐷𝐸 соответствует 𝐸𝐹. Тот факт, что соответствующие стороны подобных фигур пропорциональны, приводит нас к теореме о параллельных прямых и секущих.

Теорема: основная теорема о пропорциональности (теорема Фалеса)

Если три или более параллельных прямых пересекают две секущей, то они пропорционально отсекают секущие.

На основании этой теоремы мы знаем, что на нашем рисунке отношение длин 𝐴𝐵 к 𝐵𝐶 равно отношению длины 𝐷𝐸 к 𝐸𝐹. Мы можем записать это как пропорцию 𝐴𝐵𝐵𝐶=𝐷𝐸𝐸𝐹.

Обратите внимание, что в этой пропорции отношение каждой части уравнения содержит длины отрезков одной и той же секущей. Стоит отметить, что мы могли бы также написать пропорция, в которой отношение каждой части уравнения содержит длины соответствующие отрезки на двух различных трансверсалях. Это, 𝐴𝐵𝐷𝐸=𝐵𝐶𝐸𝐹.

Решение каждой из этих пропорций для неизвестной длины сегмента даст то же самое результат, потому что перекрестное умножение приведет либо к уравнению (𝐸𝐹)(𝐴𝐵)=(𝐵𝐶)(𝐷𝐸) или эквивалент уравнение, независимо от того, какая из двух пропорций используется.

Предположим теперь, что наша фигура выглядела следующим образом, указывая на то, что 𝐷𝐸 и 𝐸𝐹 конгруэнтны.

Это говорит нам о том, что 𝐷𝐸=𝐸𝐹, что позволяет нам заменить 𝐷𝐸 в пропорцию 𝐴𝐵𝐵𝐶=𝐷𝐸𝐸𝐹 для 𝐸𝐹, давая нам 𝐴𝐵𝐵𝐶=𝐷𝐸𝐷𝐸.

Тогда мы сможем упростить правую часть уравнения до 1, чтобы мы знали, что 𝐴𝐵=𝐵𝐶. Это приводит нас к еще одной теореме параллельные прямые и секущие.

Теорема: Специальная теорема Фалеса

Если три или более параллельных прямых отсекают конгруэнтные отрезки на одной поперечной, затем они отрезают конгруэнтные отрезки на каждой секущей.

Теперь воспользуемся этими теоремами в следующих задачах, чтобы найти недостающие длины отрезков на трансверсалях, когда две трансверсали пересекаются тремя или более прямыми.

Пример 1. Использование свойств параллельных прямых и секущих для поиска Длина недостающей стороны

Используя информацию на рисунке, определите длину 𝐸𝐹.

Ответ

На рисунке видно, что у нас есть три параллельные линии: ⃖⃗𝐴𝐷⫽⃖⃗𝐵𝐸⫽⃖⃗𝐶𝐹.

Мы также можем видеть, что эти параллельные прямые пересекаются двумя секущими ⃖⃗𝐷𝐹 и ⃖⃗𝐴𝐶. Помните что секущей называется прямая, пересекающая две или более прямых одной и той же плоскости в различных точках. Основная теорема пропорциональности (теорема Фалеса) говорит нам, что если три или более параллельных прямых пересекают две секущей, то они пропорционально отсекают их. По этой причине мы известно, что отношение длины 𝐷𝐸 к значение 𝐸𝐹 должно быть эквивалентно отношению длина 𝐴𝐵 к длине 𝐵𝐶. Таким образом, мы можем написать пропорцию 𝐷𝐸𝐸𝐹=𝐴𝐵𝐵𝐶.

Из рисунка видно, что 𝐷𝐸=48см, 𝐴𝐵=47см, и 𝐵𝐶=141см, поэтому мы можем заменить эти значения в пропорции, чтобы получить 48𝐸𝐹=47141.

Перемножение дает нам уравнение (141)(48)=(𝐸𝐹)(47), что мы можем упростить до 6768=47𝐸𝐹.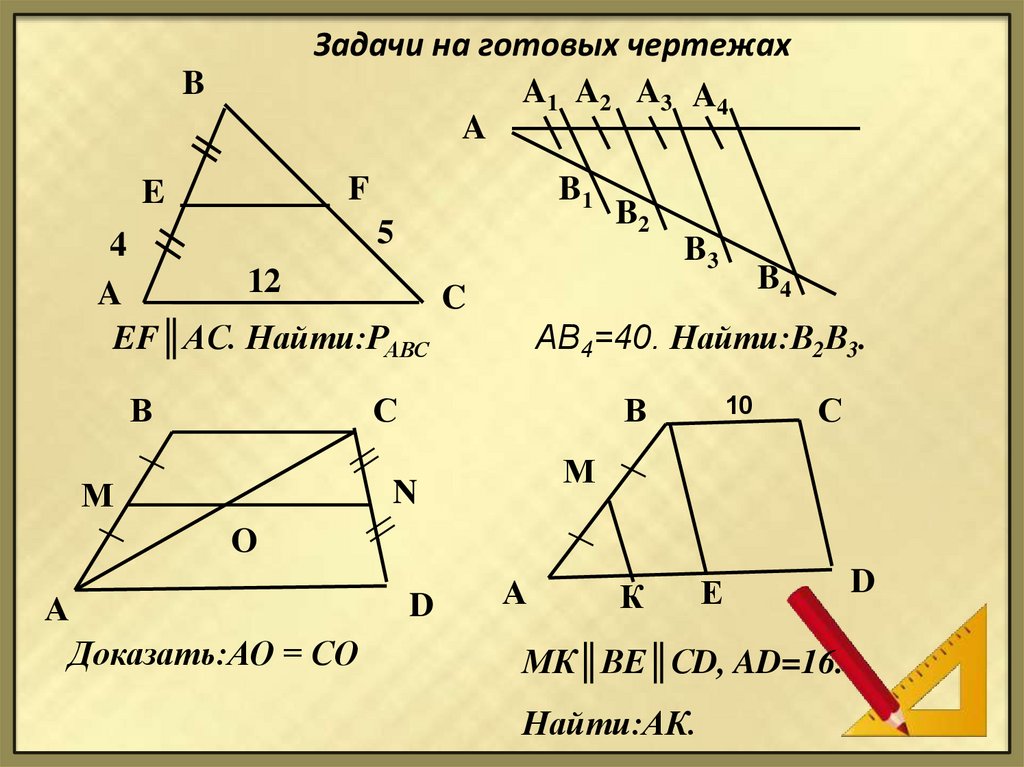

Наконец, разделив обе части уравнения на 47, получим 144=𝐸𝐹.

Итак, мы знаем, что длина 𝐸𝐹 на рисунке равна 144 см.

Примечание

Еще одна пропорция, которую мы могли бы написать, чтобы решить задачу: 𝐷𝐸𝐴𝐵=𝐸𝐹𝐵𝐶.

Мы видим, что в этой пропорции отношение каждой части уравнения содержит длины соответствующие отрезки на двух разных трансверсалях, а не длины отрезков на такая же поперечная. Подстановка в эту пропорцию дает нам 4847=𝐸𝐹141, и, умножая обе части уравнения на 141, получаем 144=𝐸𝐹.

Таким образом, мы получаем одинаковую длину для 𝐸𝐹 независимо от того, какой из двух пропорции, которые мы используем. Мы снова найдите, что длина 𝐸𝐹 на рисунке равна 144 см.

В следующем примере мы также будем использовать основную теорему пропорциональности (теорему Фалеса) найти длина отрезка линии. На этот раз, однако, нам также нужно будет использовать тот факт, что длина линии отрезок равен сумме длин более коротких непересекающихся отрезков, из которых он состоит, чтобы решить задачу проблема.

Пример 2. Использование свойств параллельных линий и нескольких пересечений для Найдите недостающую длину стороны

На рисунке линии 𝐿, 𝐿, 𝐿, и 𝐿 все параллельны. Учитывая, что 𝑋𝑍=12, 𝑍𝑁=8, 𝐴𝐵=10 и 𝐵𝐶=5, какова длина 𝐶𝐷?

Ответ

В этой задаче нам говорят, что 𝐿⫽𝐿⫽𝐿⫽𝐿.

Длины 𝑋𝑍, 𝑍𝑁, 𝐴𝐵 и 𝐵𝐶 также даны нам, поэтому мы можем пометить фигуру, как показано:

Мы видим, что каждая из прямых 𝐿, 𝐿, 𝐿 и 𝐿 пересекается двумя секущими 𝑀 и 𝑀’. Отзывать что основная теорема пропорциональности (теорема Фалеса) утверждает, что если три или более параллельный прямые пересекают две секущей, то они пропорционально отсекают секущую. Это говорит нам, что отношение длины 𝑋𝑍 к длине 𝑍𝑁 должно быть равно отношению длина 𝐴𝐶 к этому из 𝐶𝐷. Это позволяет нам записать пропорцию 𝑋𝑍𝑍𝑁=𝐴𝐶𝐶𝐷.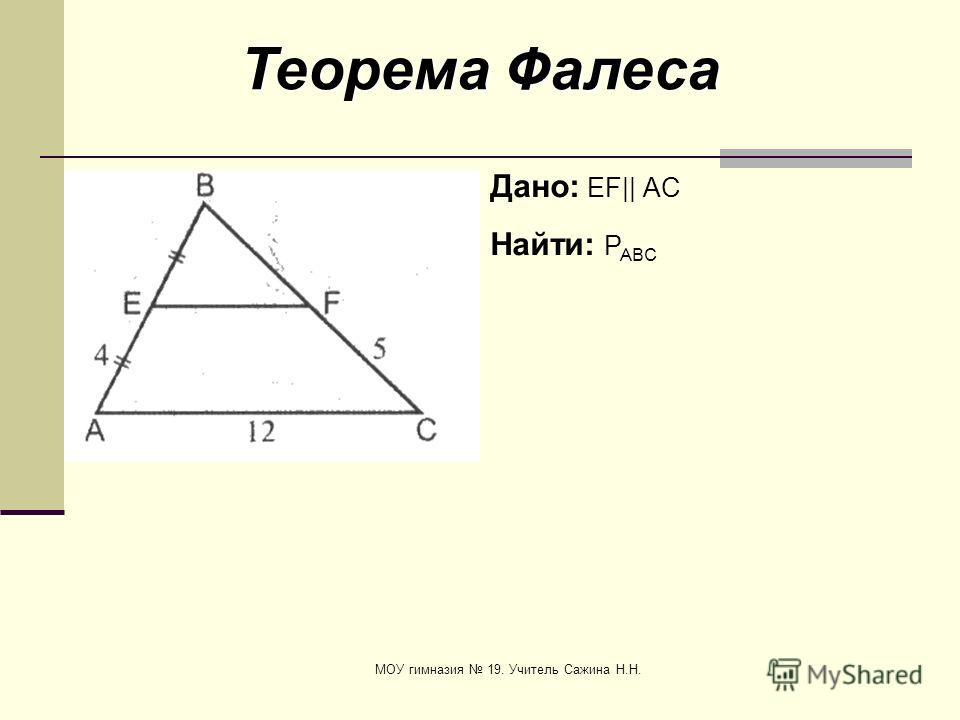

Обратите внимание, однако, что нам не задана длина ни 𝐴𝐶, ни 𝐶𝐷. Нам даны длины как 𝐴𝐵, так и 𝐵𝐶, поэтому мы можем использовать тот факт, что длина отрезка равна сумма длин более коротких непересекающихся отрезков, образующих ее, чтобы переписать пропорцию в виде способ, который позволит нам решить проблему. Поскольку 𝐴𝐶=𝐴𝐵+𝐵𝐶, мы получаем 𝑋𝑍𝑍𝑁=𝐴𝐵+𝐵𝐶𝐶𝐷.

После подстановки заданных значений 𝑋𝑍, 𝑍𝑁, 𝐴𝐵 и 𝐵𝐶 в эту пропорцию, тогда мы приходим к 128=10+5𝐶𝐷. который мы можем переписать как 128=15𝐶𝐷.

Далее перекрестное умножение дает нам уравнение (𝐶𝐷)(12)=(8)(15). который мы можем упростить до 12𝐶𝐷=120.

Наконец, чтобы найти 𝐶𝐷, мы можем разделить обе части уравнения на 12, чтобы получить 𝐶𝐷=10.

Таким образом, мы можем заключить, что длина 𝐶𝐷 на рисунке равна 10.

Далее, давайте рассмотрим задачу, в которой мы можем использовать Специальную теорему Фалеса для определения длины отрезка. длина.

Пример 3. Определение длин пропорциональных отрезков с помощью Свойства параллельных линий и многократных обходов

Учитывая, что 𝑋𝐿=9 см, найдите длину 𝑋𝑍.

Ответ

Мы видим, что в этой задаче есть четыре параллельные линии: ⃖⃗𝐴𝑋⫽⃖⃗𝐵𝑌⫽⃖⃗𝐶𝑍⫽⃖⃗𝐷𝐿

Мы также видим, что эти параллельные линии отсекают 𝐴𝐵, 𝐵𝐶 и 𝐶𝐷 на трансверсали ⃖⃗𝐴𝐷, с 𝐴𝐵≅𝐵𝐶≅𝐶𝐷, а также 𝑋𝑌, 𝑌𝑍, и 𝑍𝐿 на трансверсали ⃖⃗𝑋𝐿, с длиной 𝑋𝐿 равной 9 см. На основании этой информации, нас просят найти длину 𝑋𝑍.

Помните, что Специальная теорема Фалеса говорит нам, что если три или более параллельных прямых отрезать конгруэнтные отрезки на одной поперечной, то отсекают конгруэнтные сегменты на каждом поперечный. Таким образом, поскольку мы знаем, что 𝐴𝐵≅𝐵𝐶≅𝐶𝐷, мы также знаем, что 𝑋𝑌≅𝑌𝑍≅𝑍𝐿.

Для начала мы можем использовать тот факт, что длина отрезка равна сумме длин из более коротких непересекающихся сегментов, которые образуют его, чтобы написать уравнение 𝑋𝐿=𝑋𝑌+𝑌𝑍+𝑍𝐿.

С 𝑋𝑌≅𝑌𝑍≅𝑍𝐿, мы знаем, что 𝑋𝑌=𝑌𝑍=𝑍𝐿. Это позволяет нам подставить 𝑋𝑌 в уравнение 𝑋𝐿=𝑋𝑌+𝑌𝑍+𝑍𝐿 для обоих 𝑌𝑍 и 𝑍𝐿 чтобы получить 𝑋𝐿=𝑋𝑌+𝑋𝑌+𝑋𝑌, который мы можем затем переписать как 𝑋𝐿=3𝑋𝑌.

Напомним, что нам сказали, что длина 𝑋𝐿 равна 9 см, так что теперь мы можем подставить 9 в уравнение 𝑋𝐿=3𝑋𝑌 чтобы получить 𝑋𝐿 9=3𝑋𝑌 и делим обе части на 3, что дает нам 𝑋𝑌=3.

Помните, что 𝑋𝑌 и 𝑌𝑍 имеют одинаковую длину, поэтому мы также знаем, что 𝑌𝑍=3.

Далее, поскольку длина отрезка равна сумме длин отрезков из которых она состоит, мы можем написать уравнение 𝑋𝑍=𝑋𝑌+𝑌𝑍, и после замены 3 на 𝑋𝑌 и 𝑌𝑍 мы приходим к 𝑋𝑍=3+3,𝑋𝑍=6.или

Таким образом, длина 𝑋𝑍 на рисунке равна 6 см.

Примечание

Альтернативным методом решения является использование основная теорема пропорциональности (теорема Фалеса) .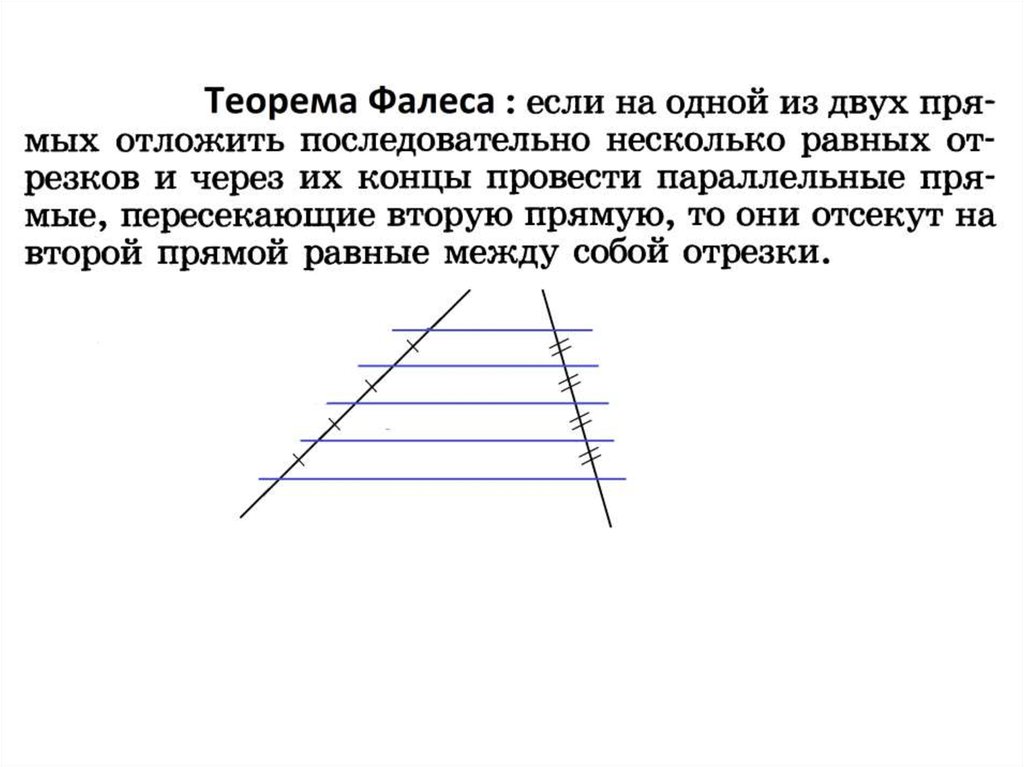 Согласно этой теореме, если три или более параллельных прямых пересекают две секущие, затем они пропорционально отсекают трансверсали. Для того, чтобы найти длину 𝑋𝑍 с помощью этого Теорема, мы должны составить и решить пропорцию, используя полученную информацию.

Предположим, что длина 𝐴𝐷 равна 𝑛. Это, 𝐴𝐷=𝑛.

Поскольку длина отрезка равна сумме длин более коротких непересекающихся отрезки, образующие его, можно написать уравнение 𝐴𝐷=𝐴𝐵+𝐵𝐶+𝐶𝐷.

Подстановка 𝐴𝐵+𝐵𝐶+𝐶𝐷 в уравнение 𝐴𝐷=𝑛 для 𝐴𝐷 тогда дает нам 𝐴𝐵+𝐵𝐶+𝐶𝐷=𝑛.

С 𝐴𝐵≅𝐵𝐶≅𝐶𝐷, мы знаем, что 𝐴𝐵=𝐵𝐶=𝐶𝐷. Поэтому теперь мы можем заменить 𝐴𝐵 в уравнение 𝐴𝐵+𝐵𝐶+𝐶𝐷=𝑛 как для 𝐵𝐶, так и 𝐶𝐷 получить 𝐴𝐵+𝐴𝐵+𝐴𝐵=𝑛, который мы можем переписать как 3𝐴𝐵=𝑛.

Далее, разделив обе части на 3, получим 𝐴𝐵=13𝑛.

Поскольку нам сказали, что 𝐴𝐵 конгруэнтно 𝐵𝐶, мы также знаем, что 𝐵𝐶=13𝑛.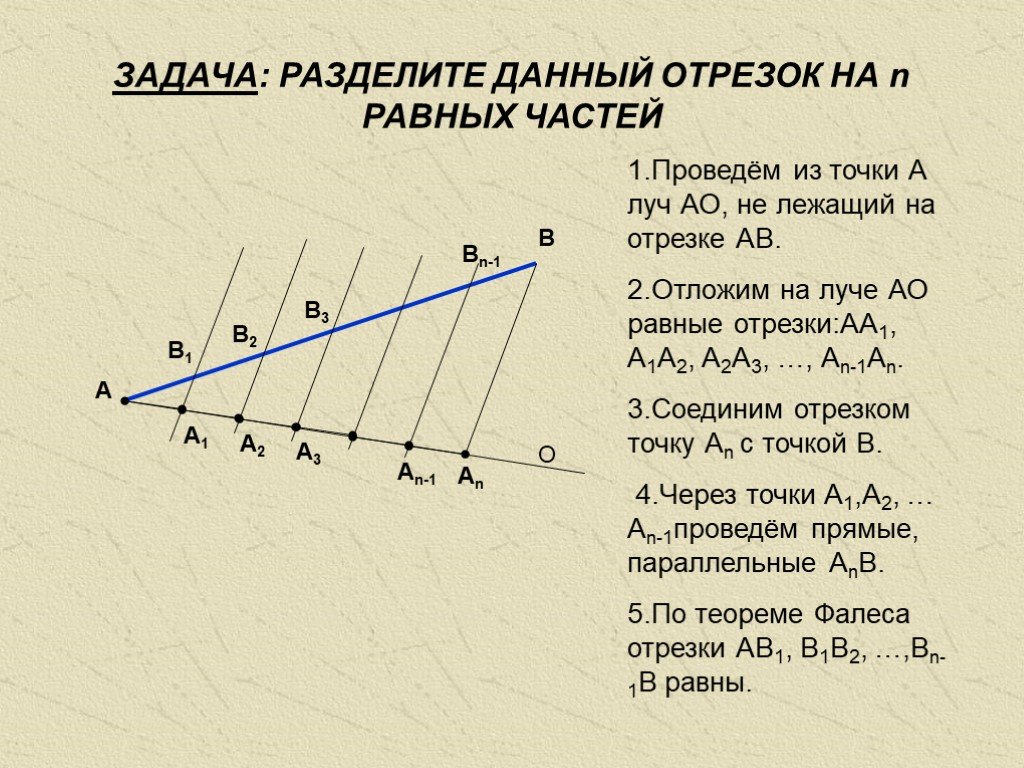 Таким образом, снова используя тот факт, что длина отрезка равна сумме длин отрезков из которых он состоит, мы можем определить длину 𝐴𝐶 через 𝑛: 𝐴𝐶=𝐴𝐵+𝐵𝐶=13𝑛+13𝑛=23𝑛.

Теперь, когда мы знаем, что длина 𝐴𝐷 равна 𝑛 и что длина 𝐴𝐶 составляет 23𝑛, мы можем организовать пропорцию, которую мы затем можем решить, чтобы найти длину 𝑋𝑍. На рисунке мы видим, что 𝐴𝐶 соответствует 𝑋𝑍, а 𝐴𝐷 соответствует 𝑋𝐿, поэтому мы можем написать 𝐴𝐶𝐴𝐷=𝑋𝑍𝑋𝐿.

Затем, заменив 23𝑛 на 𝐴𝐶, 𝑛 вместо 𝐴𝐷 и 9 вместо 𝑋𝐿, мы получаем 𝑛𝑛=𝑋𝑍9.

Это уравнение можно упростить до 23=𝑋𝑍9, и после умножения обеих частей на 9 получаем 6=𝑋𝑍.

Таким образом, мы снова определили, что длина 𝑋𝑍 на рисунке равна 6 см.

Длины отрезков не всегда являются целыми числами. Они также могут быть выражены через переменные. В следующую задачу, мы рассмотрим пример этого и решим для переменной, используя основная теорема пропорциональности (теорема Фалеса) как мы это делаем.

Пример 4. Использование свойств параллельных линий и решение линейных уравнений для определения значения неизвестного и длины отрезка

На приведенной ниже диаграмме 𝐴𝐵=10, 𝐵𝐶=(𝑥+1), 𝐶𝐷=20, 𝐸𝐹=10 и 𝐹𝐺=10. Найдите значение 𝑥 и длина 𝐺𝐻.

Ответ

Начнем с длины 𝐴𝐵, 𝐵𝐶, 𝐶𝐷, 𝐸𝐹, и 𝐹𝐺 которые были даны нам для обозначения схема как показано:

Мы видим, что на диаграмме у нас есть четыре параллельные линии: ⠀

Мы также видим, что каждая из этих прямых пересекается двумя секущими ⃖⃗𝐴𝐷 и ⃖⃗𝐸𝐻. Основная теорема пропорциональности (теорема Фалеса) говорит нам, что если три или более параллельных прямых пересекаются две трансверсали, то пропорционально отсекают трансверсали. Таким образом, мы знаем, что отношение длины 𝐴𝐵 к длине 𝐵𝐶 должно быть равно отношению длины 𝐸𝐹 к тому из 𝐹𝐺.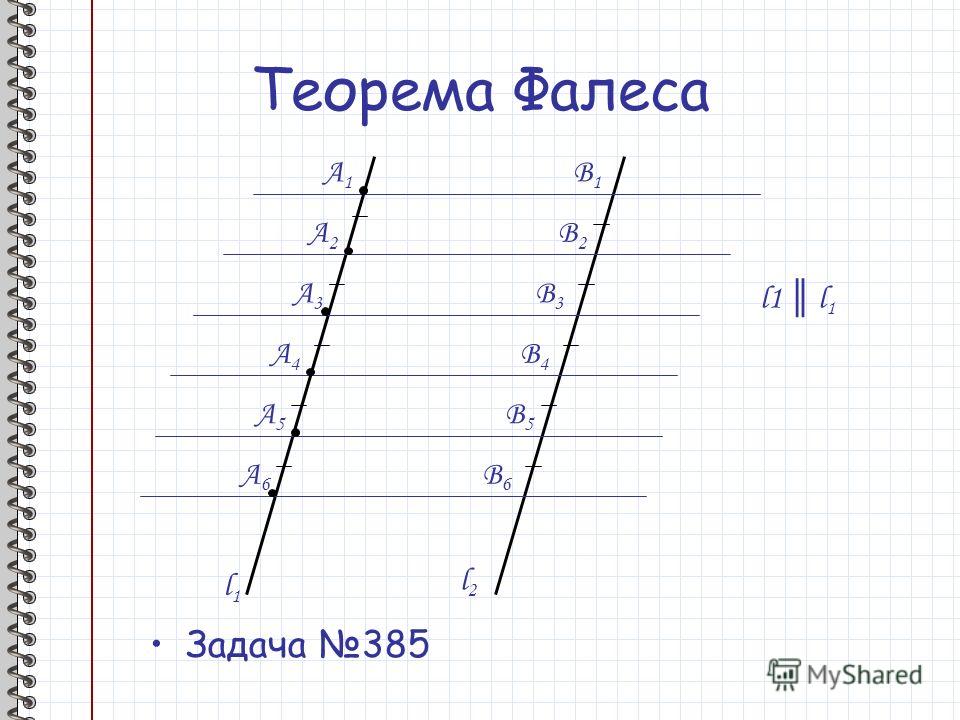 Это позволяет нам записать пропорцию 𝐴𝐵𝐵𝐶=𝐸𝐹𝐹𝐺.

Замена данных длин на 𝐴𝐵, 𝐵𝐶, 𝐸𝐹 и 𝐹𝐺 в этой пропорции дает нам 10𝑥+1=1010, и после упрощения правой части получим 10𝑥+1=1.

Теперь, чтобы исключить знаменатель в левой части, мы можем умножить обе части на 𝑥+1, чтобы получить 10=𝑥+1, и чтобы решить полученное уравнение для 𝑥, мы можем вычесть 1 из обеих частей, чтобы получить 𝑥=9.

Далее, чтобы найти длину 𝐺𝐻, мы снова можем использовать основная теорема пропорциональности (теорема Фалеса) написать пропорцию 𝐴𝐵𝐶𝐷=𝐸𝐹𝐺𝐻.

Подстановка данных значений 𝐴𝐵, 𝐶𝐷, и 𝐸𝐹 в этой пропорции дает нам 1020=10𝐺𝐻.

Обратите внимание, что числители дробей в обеих частях пропорции одинаковы. Мы, поэтому знайте, что знаменатели дробей также должны быть одинаковыми, поэтому 𝐺𝐻=20.

Таким образом, на диаграмме мы можем сделать вывод, что 𝑥=9и 𝐺𝐻=20.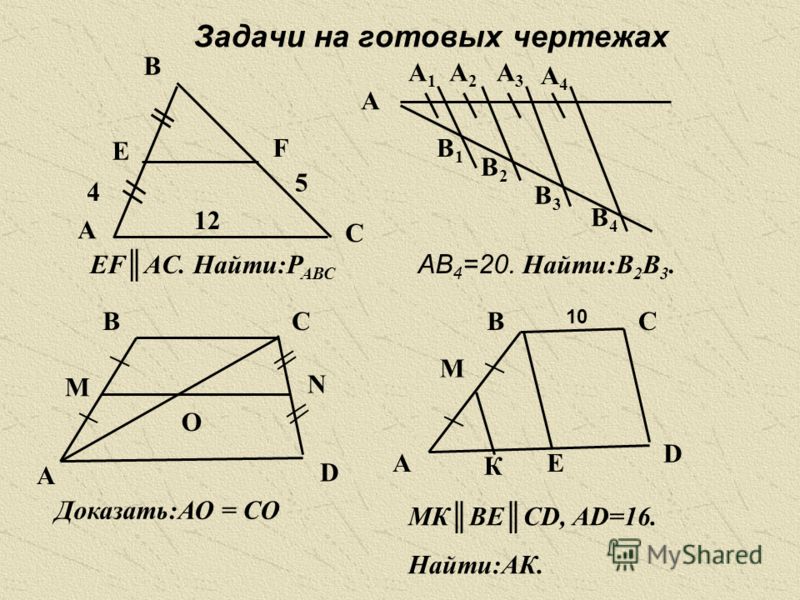

В качестве последнего примера мы будем решать две переменные вместо одной, на этот раз используя Специальная теорема Фалеса , которая поможет нам найти ответ.

Пример 5. Определение длин сторон по свойствам параллельных прямых для построения линейных уравнений

На данном рисунке найдите значения 𝑥 и 𝑦.

Ответ

Изучив рисунок, мы видим, что у нас есть три параллельные линии: ⃖⃗𝐽𝑀⫽⃖⃗𝐾𝑃⫽⃖⃗𝐿𝑄.

Мы также видим, что эти параллельные линии обрезают 𝐽𝐾 и 𝐾𝐿 на трансверсали ⃖⃗𝐽𝐿, а также 𝑀𝑃 и 𝑃𝑄 на трансверсали ⃖⃗𝑀𝑄, с 𝑀𝑃≅𝑃𝑄.

Помните, что Специальная теорема Фалеса говорит нам, что если три или более параллельных прямых отрезать конгруэнтные отрезки на одной трансверсали, то отсекают конгруэнтные отрезки на каждой поперечный. Таким образом, поскольку мы знаем, что 𝑀𝑃≅𝑃𝑄, мы также знаем, что 𝐽𝐾≅𝐾𝐿.

Конгруэнтные отрезки имеют равные длины, отсюда следует, что 𝑀𝑃=𝑃𝑄𝐽𝐾=𝐾𝐿. andthat

Из рисунка видно, что 𝐽𝐾=6𝑥–20, 𝐾𝐿=4𝑥–8, 𝑀𝑃=5𝑦–25 и 𝑃𝑄=3𝑦–7, поэтому мы можем подставляем соответствующее выражение из рисунка для каждой длины сегмента, что дает нам уравнения 5𝑦−25=3𝑦−76𝑥−20=4𝑥−8.и

Решим каждое из этих уравнений по очереди. Во-первых, решить уравнение 6𝑥−20=4𝑥−8, мы можем вычтите 4𝑥 с обеих сторон, чтобы получить 2𝑥−20=−8, а затем добавьте 20 к обеим частям, чтобы наше уравнение стало 2𝑥=12.

Наконец, мы можем разделить обе части на 2, чтобы получить 𝑥=6.

Далее, чтобы решить уравнение 5𝑦−25=3𝑦−7, мы можем вычесть 3𝑦 с обеих сторон, чтобы получить 2𝑦−25=−7, а затем добавьте 25 к обеим частям, чтобы наше уравнение стало 2𝑦=18.

Наконец, мы можем разделить обе части на 2, чтобы получить 𝑦=9.

Таким образом, на рисунке мы можем сделать вывод, что 𝑥=6 и 𝑦=9.

Примечание

Альтернативным методом решения является использование основная теорема пропорциональности (теорема Фалеса) . Напомним, что эта теорема говорит нам, что если три или более параллельных прямых пересекают две трансверсали, то они пропорционально отсекают трансверсали. По этой причине мы знаем, что отношение длины 𝐽𝐾 к длине 𝐾𝐿 должно быть эквивалентно отношению длины 𝑀𝑃 к этому из 𝑃𝑄. Следовательно, мы можем написать пропорцию 𝐽𝐾𝐾𝐿=𝑀𝑃𝑃𝑄.

Затем мы можем подставить соответствующее выражение в пропорцию для длины каждого сегмента получить 6 𝑥-204 𝑥-8 = 5 𝑦-253 𝑦-7.

Поскольку мы знаем, что 𝑀𝑃=𝑃𝑄, мы также знаем, что 𝑀𝑃𝑃𝑄=1. Следует, что 6 𝑥−204 𝑥−8=5 𝑦−253 𝑦−7=1, которые мы можем переписать в виде отдельных уравнений 6𝑥−204𝑥−8=15𝑦−253𝑦−7=1.и

Чтобы решить уравнение 6𝑥−204𝑥−8=1, мы можем начать с умножения обеих частей на 4𝑥–8, чтобы исключить знаменатель в левой части. Это дает нам 6𝑥−20=4𝑥−8, это то же самое уравнение, которое мы решили с помощью нашего предыдущего метода, чтобы найти значение 𝑥.

Чтобы решить уравнение 5𝑦−253𝑦−7=1, мы снова можем начать с исключения знаменателя, на этот раз умножив обе части уравнения на 3𝑦–7. После этого мы получаем 5𝑦−25=3𝑦−7, это то же самое уравнение, которое мы решили с помощью нашего предыдущего метода, чтобы найти значение 𝑦. Следовательно, мы получим те же 𝑥- и 𝑦-значения, используя этот метод. Опять же, мы обнаружим, что 𝑥=6 и 𝑦=9.

Теперь давайте закончим, повторив некоторые ключевые моменты.

Ключевые моменты

• Секущая — это прямая, которая пересекает две или более прямых в одной плоскости в разных точках.
• Основная теорема пропорциональности (теорема Фалеса) утверждает, что если три или более параллельных прямых пересекают две секущие, то они отсекают поперечины пропорционально.
• Специальная теорема Фалеса утверждает, что если три или более параллельных прямых отсекают конгруэнтные отрезки на одной поперечной, то они отсекают конгруэнтные отрезки отрезки на каждой секущей.
• Длина отрезка равна сумме длин образующих его более коротких непересекающихся отрезков.

Математические лаборатории для 10-го класса CBSE

Содержит разнообразные задания, относящиеся к различным областям математики, таким как арифметика, алгебра, геометрия, измерения и т. д.

Отличительные особенности математических лабораторий для 10-го класса CBSE:

• Лабораторное руководство по математике представляет собой набор из:
  (a) Лабораторных занятий по математике с Viva voce и Mental Maths.
  (b) Практическое руководство.
• Viva voce фокусируется на вопросах, основанных на действиях, чтобы сделать концепции более ясными.
• Раздел «Умственная математика» этой математической лаборатории для CBSE Class 10 предназначен для применения деятельности в различных типах задач.
• Действия говорят сами за себя. Они всесторонне объяснены и проиллюстрированы.
• Необходимые материалы легко доступны и удобны в обращении.
• Процедура описывает пошаговый метод выполнения действий.

Лаборатория математики с заданиями для 10 класса CBSE

• Задание 1. Решение системы линейных уравнений
• Занятие 2. Последовательность чисел является арифметической прогрессией (AP)
• Задание 3. Сумма первых n Условия AP
• Задание 4. Сумма первых n натуральных чисел
• Занятие 5. Сумма первых n нечетных натуральных чисел
• Задание 6. Теорема о пропорциональности, или теорема Фалеса
• Задание 7. Теорема о средней точке
• Занятие 8. Отношение площадей двух подобных треугольников
• Занятие 9. Теорема Пифагора (метод 1)
• Задание 10. Теорема Пифагора (метод 2)
• Задание 11. Теорема Пифагора (метод 3)
• Задание 12. Теорема Пифагора (метод 4)
• Задание 13. Теорема Пифагора (метод 5)
• Задание 14. Теорема Пифагора (метод 6) – Углы, опирающиеся на две хорды
• Занятие 17. Две дуги окружности конгруэнтны
• Занятие 18. Перпендикуляр, проведенный из центра окружности и делящий хорду пополам
• Задание 19. Линия, проведенная через центр окружности и делящая хорду пополам
• Задание 20. Бумага Метод разрезания и складывания
• Задание 21. Центр окружности
• Задание 22. Заполните окружность, если дана дуга окружности
• Задание 23. Равные хорды окружности равноудалены Круги равноудалены
• Занятие 25. Хорды ​​окружности, равноудаленные от центра окружности
• Занятие 26. Из двух хорд большая ближе к центру окружности
• Задание 27. Угол, опирающийся на дугу в центре окружности является двойным
• Задание 28. Углы, опирающиеся на дугу окружности в одном и том же сегменте
• Задание 29. Вписанный четырехугольник
• Задание 30. Длины касательных, проведенных из внешней точки к окружности
• Задание 31. Теорема об альтернативных сегментах
• Задание 32.

  No related posts.