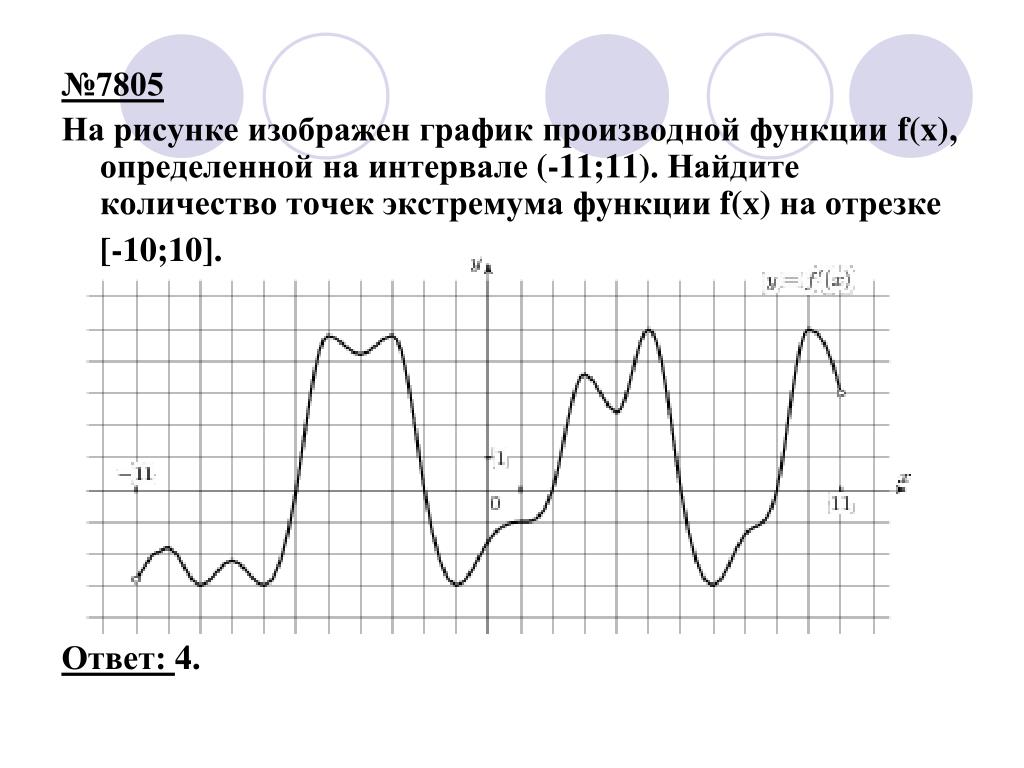
наименьшее значение на левом конце отрезка, то есть при x=-\frac{\pi}{4}. Наименьшее значение равно y\left(-\frac{\pi}{4}\right)= 32tg\left(-\frac{\pi}{4}\right)-32\cdot\left(-\frac{\pi}{4}\right)-8\pi+103= -32+103= 71.
Ответ
71
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Тип задания: 12
Тема:
Тригонометрические функции
Условие
Найдите точку минимума функции y=(0,7-x)\cos x+\sin x+2, принадлежащую промежутку \left(0; \frac{\pi}{2}\right).
Показать решение
Решение
Найдём производную исходной функции: y’= (0,7-x)’ \cos x\,+ (0,7-x)(\cos x)’+(\sin x)’+(2)’ = -\cos x+(0,7-x)\cdot (- \sin x)+ \cos x= (x-0,7) \sin x. Найдём нули производной на интервале \left(0; \frac{\pi}{2}\right), учитывая, что на этом множестве \sin x>0.
Имеем (x-0,7) \sin x=0;
x-0,7=0;
x=0,7.
Значение x=0,7 принадлежит интервалу \left(0; \frac{\pi}{2}\right). При x \in (0; 0,7) выполняется неравенство y'(x)<0. При x \in \left(0,7; \frac{\pi}{2}\right) выполняется неравенство y'(x)>0.
Отсюда x=0,7 является единственной точкой минимума на рассматриваемом интервале.
Ответ
0,7
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Тип задания: 12
Тема:
Тригонометрические функции
Условие
Найдите наименьшее значение функции y=24+\frac{9\pi}{4}-9x-9\sqrt2\cos x на отрезке \left[0; \frac{\pi}{2}\right].
Показать решение
Решение
Найдём производную исходной функции: y’=-9+9\sqrt 2 \sin x. Вычислим нули производной: y’=0;
-9+9\sqrt 2\sin x=0;
\sin x=\frac{\sqrt2}{2}.
На отрезке \left[0; \frac{\pi}{2}\right] этому уравнению удовлетворяет только x=\frac{\pi}{4}.
Из рисунка видно, что при x<\frac{\pi}{4} выполняется y'(x)<0 и исходная функция убывает. Аналогично, при x>\frac{\pi}{4} выполняется y'(x)>0 и исходная функция возрастает. Значит, наименьшее значение достигается при x=\frac{\pi}{4} и равно y\left(\frac{\pi}{4}\right)= 24+\frac{9\pi}{4}-9\cdot\frac{\pi}{4}-9\sqrt2\cos \frac{\pi}{4}= 24-9=15.
Ответ
15
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Тип задания: 12
Тема:
Тригонометрические функции
Условие
Найдите точку максимума функции y=(4x-5)\cos x-4\sin x+12, принадлежащую промежутку \left ( 0; \frac{\pi}{2} \right ).
Решение
Найдём производную исходной функции: y’= (4x-5)’\cos x+(4x-5)(\cos x)’-4(\sin x)’+(12)’= 4\cos x+(4x-5)\cdot(-\sin x)-4\cos x= -(4x-5)\sin x.
Найдём нули производной на интервале \left ( 0; \frac{\pi}{2} \right ), учитывая, что на этом множестве \sin x>0.
Имеем -(4x-5)\sin x=0,
4x-5=0,
x=\frac54.
Значение x=\frac54 принадлежит интервалу \left ( 0; \frac{\pi}{2} \right ). При x\in\left ( 0; \frac54 \right ) выполняется неравенство y'(x)>0. При x\in\left ( \frac54; \frac{\pi}{2} \right ) выполняется неравенство y'(x)<0. Отсюда x=\frac54=1,25 является единственной точкой максимума на рассматриваемом интервале.
Ответ
1,25
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Тип задания: 12
Тема:
Тригонометрические функции
Условие
Найдите наибольшее значение функции y=18\cos x+9\sqrt3 x-3\sqrt3 \pi+16 на отрезке \left [ 0; \frac{\pi}{2} \right ].
Показать решение
Решение
Найдём производную исходной функции: y’=-18\sin x+9\sqrt3.
Вычислим нули производной: y’=0.
-18\sin x+9\sqrt3=0,
\sin x=\frac{\sqrt3}{2}.
На отрезке \left [ 0; \frac{\pi}{2} \right ] этому уравнению удовлетворяет только x=\frac{\pi}{3}. Расставим знаки производной и определим промежутки монотонности исходной функции на рассматриваемом отрезке.
Из рисунка видно, что при x<\frac{\pi}{3} выполняется y'(x)>0 и исходная функция возрастает. Аналогично при x>\frac{\pi}{3} выполняется y'(x)<0 и исходная функция убывает. Значит, наибольшее значение достигается при x=\frac{\pi}{3} и равно y\left ( \frac{\pi}{3} \right )= 18\cos\frac{\pi}{3}+9\sqrt3\cdot\frac{\pi}{3}-3\sqrt3 \pi+16= 9+16=25.
Ответ
25
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Тип задания: 12
Тема:
Тригонометрические функции
Условие
Найдите наибольшее значение функции y=13tgx-13x+5 на отрезке \left [ -\frac{\pi}{4}; 0 \right ].
2x
Производная функции на всем промежутке возрастает, значит наибольшее значение функции она достигает на правом конце отрезка. Вычислим значение функции в этой точке.
y(0)=13tg0-13\cdot0+5=5
Точка 5 – наибольшее значение функции.
Ответ
5
Тип задания: 12
Тема:
Тригонометрические функции
Условие
Найдите наименьшее значение функции y=8\cos x-17x+6 на отрезке \left [ -\frac{3\pi}{2}; 0 \right ].
Показать решениеРешение
Вычислим производную функции.
y’=-8\sin x-17
Так как выражение -8\sin x при любых значениях x всегда не больше чем 8, то полученная разность меньше нуля, а это говорит о том, что функция убывает. Следовательно наименьшее значение функция достигает на правом конце отрезка. Вычислим это значение.
y(0)=8\cos0-17\cdot0+6 = 8+6=14
Точка 14 – наименьшее значение функции.
Ответ
14
Тип задания: 12
Тема:
Тригонометрические функции
Условие
Найдите точку максимума функции y=(2x-3)\cos x-2\sin x+2 на промежутке \left ( 0; \frac{\pi}{2} \right ).
Показать решение
Решение
Вычислим производную функции.
y’=2\cos x-(2x-3)\sin x-2\cos x
y’=-(2x-3)\sin x
y’=(3-2x)\sin x
Найдем точки экстремума, в которых производная функции обращается в нуль.
(3-2x)\sin x=0
\left [\begin{array}{l} 3-2x=0 \\ \sin x=0 \end{array} \right .
\left [\begin{array}{l} x=1,5 \\ x=\pi n, n \in \mathbb{Z} \notin \left ( 0; \frac{\pi}{2} \right) \end{array} \right .
На числовой оси отложим граничные точки промежутка и точку экстремума и посмотрим как ведет себя функция.
При переходе через точку x = 1,5 производная меняет знак с плюса на минус. Значит x = 1,5 – точка максимума функции.
Ответ
1,5
Лучшие репетиторы для сдачи ЕГЭ
МатематикаРусский язык
История
Сложно со сдачей ЕГЭ?
Звоните, и подберем для вас репетитора: 78007750928 © 2016—2022
Все права защищены.
Служба поддержки портала
10 класс.
Алгебра. Производная. Применение производной в задачах на экстремум и при исследовании тригонометрических функций. — Типовые задачи на производную с тригонометрическими функциями. Функция f(x)=cos²x-cosx.Комментарии преподавателяФункция f(x)=cos2x-cosx
Тригонометрические функции имеют важную особенность – наличие периода. Всю методику, которую знаем для исследования функций без тригонометрических включений, используем, но надо учесть наличие периода.
Наличие периода дает возможность провести исследование функции и построение графика на отрезке длиной, равной периоду. Затем график функции периодически распространяется для всех значений аргумента из области определения функции.
Задача.
Построить график функции .
Преобразуем формулу: .
Найдем период данной функции. У функции наименьший период .
У функции , если понизить степень и выразить через — период . Итак,
функция имеет наименьший период . Это означает, что график функции сначала можно построить на промежутке длиной , а потом продолжить по периодичности.
Функция четная, так как для всех из . График симметричный относительно оси .
Учитывая периодичность функции, можно построить график этой функции на любом промежутке, длиной . Свойство четности функции дает возможность задачу упростить, а именно, построить график на участке , а на участке — построить по симметрии.
Найдем интервалы знакопостоянства функции.
: .
, когда , отсюда или .
Знак функции на каждом интервале удобно определить с помощью единичной окружности (см. рис.1). Точки , , — точки, которые формируют интервалы знакопостоянства функции.
Рис. 1. Интервалы знакопостоянства функции на единичной окружности
Выясним знак функции на интервале .
Для этого возьмем значение функции в какой-нибудь точке из этого интервала. Например,
, значит, на этом интервале функция отрицательна. Дальше, на интервале функция меняет знак. В силу симметрии, на интервале — функция отрицательна, а на интервале — функция положительна (см. рис.2).
Рис. 2 Интервалы знакопостоянства функции
Построим график функции в окрестности каждого корня.
Точка — является точкой максимума, так как на промежутках и — функция отрицательна, кривая находится под осью , и только в точке она равна нулю. Значит, функция в окрестности корней ведет себя следующим образом (см. рис.3):
Рис. 3. График функции в окрестности каждого корня
Понятно, что на интервалах и – функция будет иметь точки экстремума.
Исследуем функцию с помощью производной:
Приравняем ее к нулю:
, отсюда .
Найдем критические точки:
— это все критические точки, которые имеет функция.
Но нам нужны те, которые попадают в выбранный промежуток: , , . Вычислим значение функции в точках , и определим – это точки максимума или минимума.
Найдем интервалы знакопостоянства производной на единичной окружности (см. рис.4).
Рис. 4. Интервалы знакопостоянства производной
Найдем знак производной, в какой- либо точке из интервала :
. Таким образом, точка — точка минимума, а — точка максимума. Вычислим:
; .
Построим график функции (см. рис.5-6).
Рис. 5. График функции на
Рис. 6. График функции
Одна из типовых задач – нахождение множества значений функции.
Ответ: .
На уроке рассмотрены особенности исследования и построения графика тригонометрической функции. Все типовые задачи решаются аналогично задачам из предыдущих уроков.
ИСТОЧНИК
http://interneturok.
ru/ru/school/algebra/10-klass/proizvodnaya/issledovanie-trigonometricheskih-funktsiy-funktsiya-f-x-cos-sup-2-sup-x-cosx
http://www.youtube.com/watch?v=sX-A2wpY5NE
https://downloader.disk.yandex.ru/disk/779ef72b0b73617de61c4dc2c21838459e86176ed8f801b37481d34346768467/56a16f54/KmTYbqVG3TgKGL9iUHPR0em0RlLtpxhP_BVgRtkosSgfwonkMOj8PI__aMfad3WZY71hHToni_M3mTC7aMwq3A%3D%3D?uid=0&filename=666.PDF&disposition=attachment&hash=RaLDsjqwggBTdSmademPwU40mOjt%2BFWdduHVDt9R80E%3D&limit=0&content_type=application%2Fpdf&fsize=8352787&hid=021760e85b03ef221c6c4091fc10c607&media_type=document&tknv=v2
http://matematikalegko.ru/issledovanie-funkcii-ege/trigonometricheskaya-funkciya-tochki-maksimuma-minimuma.html
http://www.berdov.com/ege/extremum/trigonometry/
исчисление — Проблема с нахождением критической точки триггерной функции
Задавать вопрос
спросил
Изменено 7 лет, 5 месяцев назад
Просмотрено 415 раз
$\begingroup$ 92(x/2)}=0,\стрелка вправо\sin(x/2)=\pm\frac1{\sqrt2}$$
Имеет только одно решение $x=\frac\pi2$ в $\left[\frac\pi3,\frac{2\pi}3\right]$.
2 (х / 2)}
$$ 92(х/2).
$$
$\endgroup$
1
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
исчисление — Нахождение критических точек тригонометрической функции
Задавать вопрос
спросил
Изменено 6 лет, 1 месяц назад
Просмотрено 12 тысяч раз
$\begingroup$
Итак, мне нужны критические точки (и обратите внимание на интервалы возрастания и убывания функции) для:
$2cos\left(3x\right)$ на интервале $\left[-\pi ,\pi \right] $.
Честно говоря, самой сложной частью Calc I для меня пока является ВСЕ, связанное с тригонометрией. Я чувствую, что precalc был эоны лет назад, и я искренне задаюсь вопросом, изучал ли я его когда-либо должным образом.
Взяв производную от f(x), я получаю:
$-6sin\left(3x\right)$, которое я должен установить равным $0$.
Я знаю тригонометрические функции и единичный круг, но мне кажется, что все, что связано с тригонометрией, ведет себя совершенно иначе, чем все остальное в математике. Даже обозначения меня смущают. Как найти:
$-6sin\left(3x\right) = 0$? И когда у меня есть критические точки, как мне учесть $\left[-\pi ,\pi \right]$, отмечая, где эта функция увеличивается и уменьшается?
- исчисление
- тригонометрия
$\endgroup$
1
$\begingroup$
Если $\sin(3x)=0$, то $3x=k\pi$ для некоторого целого числа $k$. Следовательно, $x=k\pi/3$, и вам просто нужно определить все целые числа $k$ такие, что $k\pi/3\in[-\pi,\pi]$. В настоящее время
$$
-\pi\le \frac{k\pi}{3}\le \pi
$$
эквивалентно
$$
-3\ле к\ле 3
$$
Итак, у нас есть семь критических точек.
Чтобы отличить точки максимума и минимума, проще всего посмотреть на вторую производную:
$$
f»(x)=-18\cos(3x)
$$
Обратите внимание, что на самом деле нет проблем с точками $-\pi$ и $\pi$, находящимися на границах, потому что функция, которую вы имеете, является ограничением функции $x\maps на 2\cos(3x)$, определенное над реалами, которая везде явно гладкая.
Вот график функции:
Обратите внимание, что это функция косинуса, но растянутая по вертикали на коэффициент $2$ и «сжатая» по горизонтали на коэффициент $3$.
$\endgroup$
$\begingroup$
Помните:
$$\sin x=0\iff x=k\pi\;,\;\;k\in\Bbb Z=\{…-2,-1,0,1,2 ,…\}\;$$ и в вашем случае
$$\sin3x=0\iff 3x=k\pi\in(-\pi,\,\pi)\iff k=0\импульс x= 0$$
Теперь у вас также есть две крайние точки $\;\pm\pi\;$, которые не могут быть проверены описанным выше методом, так как функция там не дифференцируема (так как нам нужна полная окрестность точки где функция определена так, что даже есть шанс взять предел, определяющий производную.