Подбор заданий для самостоятельной работы в 9 классе по теме «Решение задач по теории вероятностей» (из Открытого банка заданий ОГЭ-9)
Вариант 1
1.В магазине канцтоваров продаётся 120 ручек: 32 красных, 32 зелёных, 46 фиолетовых, остальные синие и чёрные, их поровну. Найдите вероятность того, что случайно выбранная в этом магазине ручка будет красной или фиолетовой.
2. В лыжных гонках участвуют 11 спортсменов из России, 6 спортсменов из Норвегии и 3 спортсмена из Швеции. Порядок, в котором спортсмены стартуют, определяется жребием. Найдите вероятность того, что первым будет стартовать спортсмен из России.
3. В среднем из 100 карманных фонариков, поступивших в продажу,
четыре неисправных. Найдите вероятность того, что выбранный наудачу в магазине фонарик окажется исправен.
4. Родительский комитет закупил 10 пазлов для подарков детям в связи с окончанием учебного года, из них 4 с машинами и 6 с видами городов. Подарки распределяются случайным образом между 10 детьми, среди которых есть Володя. Найдите вероятность того, что Володе достанется пазл с машиной.
5. На экзамене 50 билетов, Сеня не выучил 5 из них. Найдите вероятность того, что ему попадётся выученный билет.
6. У бабушки 25 чашек: 2 с красными цветами, остальные с синими. Бабушка наливает чай в случайно выбранную чашку. Найдите вероятность того, что это будет чашка с синими цветами.
7. В фирме такси в данный момент свободно 20 машин: 2 чёрных, 2 жёлтых и 16 зелёных. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчику. Найдите вероятность того, что к нему приедет жёлтое такси.
8. На тарелке лежат одинаковые на вид пирожки: 5 с мясом, 2 с капустой и 3 с вишней. Андрей наугад берёт один пирожок. Найдите вероятность того, что пирожок окажется с вишней.
9. Вероятность того, что новая шариковая ручка пишет плохо (или не пишет), равна 0,2. Покупатель в магазине выбирает одну шариковую ручку. Найдите вероятность того, что эта ручка пишет хорошо.
Вариант 2
1.В магазине канцтоваров продаётся 170 ручек: 47 красных, 33 зелёных, 14 фиолетовых, остальные синие и чёрные, их поровну. Найдите вероятность того, что случайно выбранная в этом магазине ручка будет красной или чёрной.
2. В лыжных гонках участвуют 7 спортсменов из России, 1 спортсмен
из Норвегии и 2 спортсмена из Швеции. Порядок, в котором спортсмены стартуют, определяется жребием. Найдите вероятность того, что первым будет стартовать спортсмен из Норвегии.
3. В среднем из 150 карманных фонариков, поступивших в продажу,
шесть неисправных. Найдите вероятность того, что выбранный наудачу в магазине фонарик окажется исправен.
4. Родительский комитет закупил 25 пазлов для подарков детям в связи с окончанием учебного года, из них 21 с машинами и 4 с видами городов. Подарки распределяются случайным образом между 25 детьми, среди которых есть Саша. Найдите вероятность того, что Саше достанется пазл с машиной.
5. На экзамене 35 билетов, Стас не выучил 7 из них. Найдите вероятность того, что ему попадётся выученный билет.
6. У бабушки 20 чашек: 15 с красными цветами, остальные с синими. Бабушка наливает чай в случайно выбранную чашку. Найдите вероятность того, что это будет чашка с синими цветами.
7. В фирме такси в данный момент свободно 12 машин: 3 чёрных, 6 жёлтых и 3 зелёных. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчику. Найдите вероятность того, что к нему приедет жёлтое такси.
8. На тарелке лежат одинаковые на вид пирожки: 3 с мясом, 24 с капустой и 3 с вишней. Лёша наугад берёт один пирожок. Найдите вероятность того, что пирожок окажется с вишней.
9. Вероятность того, что новая шариковая ручка пишет плохо (или не пишет), равна 0,26. Покупатель в магазине выбирает одну шариковую ручку. Найдите вероятность того, что эта ручка пишет хорошо.
infourok.ru
Разработка урока по теме «Вероятность в задачах ОГЭ» 9 класс
Урок «Решение задач по теории вероятностей» в 9 классе
Цели урока:
повторить материал по теории вероятностей, изучаемый в школьном курсе математики и вынесенный на итоговую аттестацию в 9 классе;
обобщить знания учащихся о способах и методах решения вероятностных задач;
находить вероятности случайных событий в простейших случаях.
Задачи:
создать условия для овладения учащимися системы знаний, умений и навыков с понятиями вероятности события;
способствовать запоминанию основной терминологии, умению устанавливать события вероятности;
формировать умение упорядочить полученные знания для рационального применения;
развитие навыков учащихся в вычислении классической вероятности;
способствовать развитию интереса к математике, умений применять новый материал на практике и в жизни.
Вид и форма урока:
урок – обобщение, урок – практикум.
Методы организации учебно-познавательной деятельности:
наглядные,
практические,
по усвоению материала: частично-поисковый, репродуктивный,
по степени самостоятельности: самостоятельная работа,
стимулирующие: поощрения,
виды контроля: проверка самостоятельно решенных задач.
План урока:
Организационный момент.
Проверка домашней работы.
Устная работа.
Презентация, решение задач.
Самостоятельная работа.
Подведение итогов
Комментирование домашнего задания.
Оборудование: мультимедийный проектор, карточки для самостоятельной работы.
Ход урока:
Организационный момент.
Тема нашего урока «Теория вероятностей в задачах ОГЭ 2018». Мы сегодня обобщим наши знания и умения при решении задач на нахождение вероятности случайного события и обратим внимание на ошибки, которые вы допускаете при решении задач.
Задачи по теории вероятностей это 9 задание в ОГЭ.
Все задачи на сегодняшний урок взяты с сайта ФИПИ.
Проверка домашнего задания: Решение задач с монетами.
В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орёл выпадет хотя бы один раз.
В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орёл выпадет ровно один раз.
В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орёл выпадет ровно два раза.
В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что во второй раз выпадет то же, что и в первый.
В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орёл не выпадет ни разу.
Возможные исходы:
ОО
ОР
РО
РР
Количество всех исходов: 4
Количество благоприятных исходов 3, ответ ¾ = 0, 75.
Количество благоприятных исходов 2, ответ 2/4 = 0, 5.
Количество благоприятных исходов 1, ответ ¼ = 0, 25.
Количество благоприятных исходов 2, ответ 2/4 = 0, 5.
Количество благоприятных исходов 1, ответ ¼ = 0, 25.
Устная работа.
Выполните деление: 1:25, 22:25, 47:50, 9:20, 11/20
Презентация.
1 слайд: Теория вероятностей в задачах ЕГЭ
2 слайд:
Если опыт, в котором появляется событие А, имеет конечное число n равновозможных исходов, то вероятность события А равна
m–число благоприятных исходов,
n — число всех возможных исходов.
3 слайд:
Свойство 1. Вероятность достоверного события равна единице: Р(А) = 1.
Свойство 2. Вероятность невозможного события равна нулю: Р(А) = 0.
Свойство 3. Вероятность случайного события есть положительное число, заключенное между нулем и единицей: 0 ≤ Р(А) ≤ 1.
4 – 12 слайд: Задачи
Самостоятельная работа
Самостоятельная работа
Вариант 1
На тарелке лежат одинаковые на вид пирожки: 4 с мясом, 8 с капустой
и 3 с вишней. Петя наугад берёт один пирожок. Найдите вероятность того, что пирожок окажется с вишней.В фирме такси в данный момент свободно 15 машин: 3 чёрных, 6 жёлтых и 6 зелёных. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчику. Найдите вероятность того, что к нему приедет жёлтое такси.
У бабушки 10 чашек: 7 с красными цветами, остальные с синими. Бабушка наливает чай в случайно выбранную чашку. Найдите вероятность того, что это будет чашка с синими цветами.
На экзамене 60 билетов, Олег не выучил 12 из них. Найдите вероятность того, что ему попадётся выученный билет.
Родительский комитет закупил 20 пазлов для подарков детям в связи
с окончанием учебного года, из них 10 с машинами и 10 с видами городов. Подарки распределяются случайным образом между 20 детьми, среди которых есть Коля. Найдите вероятность того, что Коле достанется пазл с машиной.В среднем из 100 карманных фонариков, поступивших в продажу,
четыре неисправных. Найдите вероятность того, что выбранный наудачу
в магазине фонарик окажется исправен.В лыжных гонках участвуют 13 спортсменов из России, 2 спортсмена
из Норвегии и 5 спортсменов из Швеции. Порядок, в котором спортсмены стартуют, определяется жребием. Найдите вероятность того, что первым будет стартовать спортсмен из России.Вероятность того, что новая шариковая ручка пишет плохо (или не пишет), равна 0,19. Покупатель в магазине выбирает одну шариковую ручку. Найдите вероятность того, что эта ручка пишет хорошо.
В магазине канцтоваров продаётся 100 ручек: 37 красных, 8 зелёных,
17 фиолетовых, остальные синие и чёрные, их поровну. Найдите вероятность того, что случайно выбранная в этом магазине ручка будет красной
или чёрной.
Вариант 2
На тарелке лежат одинаковые на вид пирожки: 3 с капустой, 8 с рисом
и 1 с луком и яйцом. Игорь наугад берёт один пирожок. Найдите вероятность того, что пирожок окажется с капустой.В фирме такси в данный момент свободно 10 машин: 5 чёрных, 1 жёлтая и 4 зелёных. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчику. Найдите вероятность того, что к нему приедет жёлтое такси.
У бабушки 10 чашек: 1 с красными цветами, остальные с синими. Бабушка наливает чай в случайно выбранную чашку. Найдите вероятность того, что это будет чашка с синими цветами.
На экзамене 40 билетов, Сеня не выучил 8 из них. Найдите вероятность того, что ему попадётся выученный билет.
Родительский комитет закупил 25 пазлов для подарков детям в связи
с окончанием учебного года, из них 18 с машинами и 7 с видами городов. Подарки распределяются случайным образом между 25 детьми, среди которых есть Володя. Найдите вероятность того, что Володе достанется пазл с машиной.В среднем из 150 карманных фонариков, поступивших в продажу,
шесть неисправных. Найдите вероятность того, что выбранный наудачу
в магазине фонарик окажется исправен.В лыжных гонках участвуют 11 спортсменов из России, 6 спортсменов
из Норвегии и 3 спортсмена из Швеции. Порядок, в котором спортсмены стартуют, определяется жребием. Найдите вероятность того, что первым будет стартовать спортсмен из России.Вероятность того, что новая шариковая ручка пишет плохо (или не пишет), равна 0,09. Покупатель в магазине выбирает одну шариковую ручку. Найдите вероятность того, что эта ручка пишет хорошо.
В магазине канцтоваров продаётся 112 ручек: 17 красных, 44 зелёных,
29 фиолетовых, остальные синие и чёрные, их поровну. Найдите вероятность того, что случайно выбранная в этом магазине ручка будет красной
или чёрной.
Вариант 3
На тарелке лежат одинаковые на вид пирожки: 1 с творогом, 12 с мясом
и 3 с яблоками. Ваня наугад берёт один пирожок. Найдите вероятность того, что пирожок окажется с мясом.В фирме такси в данный момент свободно 15 машин: 4 чёрных, 3 жёлтых и 8 зелёных. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчику. Найдите вероятность того, что к нему приедет жёлтое такси.
У бабушки 25 чашек: 5 с красными цветами, остальные с синими. Бабушка наливает чай в случайно выбранную чашку. Найдите вероятность того, что это будет чашка с синими цветами.
На экзамене 40 билетов, Оскар не выучил 12 из них. Найдите вероятность того, что ему попадётся выученный билет.
Родительский комитет закупил 20 пазлов для подарков детям в связи
с окончанием учебного года, из них 8 с машинами и 12 с видами городов. Подарки распределяются случайным образом между 20 детьми, среди которых есть Вася. Найдите вероятность того, что Васе достанется пазл
с машиной.В среднем из 100 карманных фонариков, поступивших в продажу,
пять неисправных. Найдите вероятность того, что выбранный наудачу
в магазине фонарик окажется исправен.В лыжных гонках участвуют 7 спортсменов из России, 1 спортсмен
из Норвегии и 2 спортсмена из Швеции. Порядок, в котором спортсмены стартуют, определяется жребием. Найдите вероятность того, что первым будет стартовать спортсмен из Норвегии.Вероятность того, что новая шариковая ручка пишет плохо (или не пишет), равна 0,21. Покупатель в магазине выбирает одну шариковую ручку. Найдите вероятность того, что эта ручка пишет хорошо.
В магазине канцтоваров продаётся 84 ручки, из них 22 красных, 9 зелёных, 41 фиолетовая, остальные синие и чёрные, их поровну. Найдите вероятность того, что случайно выбранная в этом магазине ручка будет красной или фиолетовой.
Вариант 4
На тарелке лежат одинаковые на вид пирожки: 4 с мясом, 5 с рисом
и 21 с повидлом. Андрей наугад берёт один пирожок. Найдите вероятность того, что пирожок окажется с повидлом.В фирме такси в данный момент свободно 10 машин: 5 чёрных, 3 жёлтых и 2 зелёных. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчику. Найдите вероятность того, что к нему приедет жёлтое такси.
У бабушки 15 чашек: 6 с красными цветами, остальные с синими. Бабушка наливает чай в случайно выбранную чашку. Найдите вероятность того, что это будет чашка с синими цветами.
На экзамене 20 билетов, Андрей не выучил 1 из них. Найдите вероятность того, что ему попадётся выученный билет.
Родительский комитет закупил 20 пазлов для подарков детям в связи
с окончанием учебного года, из них 15 с машинами и 5 с видами городов. Подарки распределяются случайным образом между 20 детьми, среди которых есть Витя. Найдите вероятность того, что Вите достанется пазл с машиной.В среднем из 50 карманных фонариков, поступивших в продажу,
шесть неисправных. Найдите вероятность того, что выбранный наудачу
в магазине фонарик окажется исправен.В лыжных гонках участвуют 7 спортсменов из России, 1 спортсмен
из Швеции и 2 спортсмена из Норвегии. Порядок, в котором спортсмены стартуют, определяется жребием. Найдите вероятность того, что первым будет стартовать спортсмен из Швеции.Вероятность того, что новая шариковая ручка пишет плохо (или не пишет), равна 0,06. Покупатель в магазине выбирает одну шариковую ручку. Найдите вероятность того, что эта ручка пишет хорошо.
В магазине канцтоваров продаётся 206 ручек: 20 красных, 8 зелёных,
12 фиолетовых, остальные синие и чёрные, их поровну. Найдите вероятность того, что случайно выбранная в этом магазине ручка будет красной
или синей.
Вариант 5
На тарелке лежат одинаковые на вид пирожки: 3 с мясом, 3 с капустой
и 4 с вишней. Саша наугад берёт один пирожок. Найдите вероятность того, что пирожок окажется с вишней.В фирме такси в данный момент свободно 30 машин: 3 чёрных, 9 жёлтых и 18 зелёных. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчику. Найдите вероятность того, что к нему приедет жёлтое такси.
У бабушки 20 чашек: 14 с красными цветами, остальные с синими. Бабушка наливает чай в случайно выбранную чашку. Найдите вероятность того, что это будет чашка с синими цветами.
На экзамене 50 билетов, Оскар не выучил 7 из них. Найдите вероятность того, что ему попадётся выученный билет.
Родительский комитет закупил 10 пазлов для подарков детям в связи
с окончанием учебного года, из них 3 с машинами и 7 с видами городов. Подарки распределяются случайным образом между 10 детьми, среди которых есть Миша. Найдите вероятность того, что Мише достанется пазл с машиной.В среднем из 150 карманных фонариков, поступивших в продажу, восемнадцать неисправных. Найдите вероятность того, что выбранный наудачу в магазине фонарик окажется исправен.
В лыжных гонках участвуют 13 спортсменов из России, 2 спортсмена
из Норвегии и 5 спортсменов из Швеции. Порядок, в котором спортсмены стартуют, определяется жребием. Найдите вероятность того, что первым будет стартовать спортсмен не из России.Вероятность того, что новая шариковая ручка пишет плохо (или не пишет), равна 0,14. Покупатель в магазине выбирает одну шариковую ручку. Найдите вероятность того, что эта ручка пишет хорошо.
В магазине канцтоваров продаётся 200 ручек: 31 красная, 25 зелёных,
38 фиолетовых, остальные синие и чёрные, их поровну. Найдите вероятность того, что случайно выбранная в этом магазине ручка будет красной
или чёрной.
Вариант 6
На тарелке лежат одинаковые на вид пирожки: 4 с мясом, 5 с капустой
и 6 с вишней. Дима наугад берёт один пирожок. Найдите вероятность того, что пирожок окажется с вишней.В фирме такси в данный момент свободно 10 машин: 1 чёрная, 1 жёлтая и 8 зелёных. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчику. Найдите вероятность того, что к нему приедет жёлтое такси.
У бабушки 10 чашек: 3 с красными цветами, остальные с синими. Бабушка наливает чай в случайно выбранную чашку. Найдите вероятность того, что это будет чашка с синими цветами.
На экзамене 20 билетов, Саша не выучил 2 из них. Найдите вероятность того, что ему попадётся выученный билет.
Родительский комитет закупил 10 пазлов для подарков детям в связи
с окончанием учебного года, из них 2 с машинами и 8 с видами городов. Подарки распределяются случайным образом между 10 детьми, среди которых есть Андрюша. Найдите вероятность того, что Андрюше достанется пазл с машиной.В среднем из 200 карманных фонариков, поступивших в продажу,
четыре неисправных. Найдите вероятность того, что выбранный наудачу
в магазине фонарик окажется исправен.В лыжных гонках участвуют 11 спортсменов из России, 6 спортсменов
из Норвегии и 3 спортсмена из Швеции. Порядок, в котором спортсмены стартуют, определяется жребием. Найдите вероятность того, что первым будет стартовать спортсмен не из России.Вероятность того, что новая шариковая ручка пишет плохо (или не пишет), равна 0,22. Покупатель в магазине выбирает одну шариковую ручку. Найдите вероятность того, что эта ручка пишет хорошо.
В магазине канцтоваров продаётся 165 ручек: 37 красных, 16 зелёных,
46 фиолетовых, остальные синие и чёрные, их поровну. Найдите вероятность того, что случайно выбранная в этом магазине ручка будет синей или чёрной.
Вариант 7
На тарелке лежат одинаковые на вид пирожки: 2 с мясом, 16 с капустой
и 2 с вишней. Рома наугад берёт один пирожок. Найдите вероятность того, что пирожок окажется с вишней.В фирме такси в данный момент свободно 20 машин: 3 чёрных, 3 жёлтых и 14 зелёных. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчику. Найдите вероятность того, что к нему приедет жёлтое такси.
У бабушки 15 чашек: 9 с красными цветами, остальные с синими. Бабушка наливает чай в случайно выбранную чашку. Найдите вероятность того, что это будет чашка с синими цветами.
На экзамене 25 билетов, Костя не выучил 4 из них. Найдите вероятность того, что ему попадётся выученный билет.
Родительский комитет закупил 20 пазлов для подарков детям в связи
с окончанием учебного года, из них 11 с машинами и 9 с видами городов. Подарки распределяются случайным образом между 20 детьми, среди которых есть Илюша. Найдите вероятность того, что Илюше достанется пазл с машиной.В среднем из 75 карманных фонариков, поступивших в продажу,
пятнадцать неисправных. Найдите вероятность того, что выбранный наудачу в магазине фонарик окажется исправен.В лыжных гонках участвуют 13 спортсменов из России, 2 спортсмена
из Норвегии и 5 спортсменов из Швеции. Порядок, в котором спортсмены стартуют, определяется жребием. Найдите вероятность того, что первым будет стартовать спортсмен из Норвегии или Швеции.Вероятность того, что новая шариковая ручка пишет плохо (или не пишет), равна 0,07. Покупатель в магазине выбирает одну шариковую ручку. Найдите вероятность того, что эта ручка пишет хорошо.
В магазине канцтоваров продаётся 264 ручки: 38 красных, 30 зелёных,
8 фиолетовых, остальные синие и чёрные, их поровну. Найдите вероятность того, что случайно выбранная в этом магазине ручка будет красной или чёрной.
Вариант 8
На тарелке лежат одинаковые на вид пирожки: 5 с мясом, 2 с капустой
и 3 с вишней. Андрей наугад берёт один пирожок. Найдите вероятность того, что пирожок окажется с вишней.В фирме такси в данный момент свободно 30 машин: 6 чёрных, 3 жёлтых и 21 зелёная. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчику. Найдите вероятность того, что к нему приедет жёлтое такси.
У бабушки 25 чашек: 2 с красными цветами, остальные с синими. Бабушка наливает чай в случайно выбранную чашку. Найдите вероятность того, что это будет чашка с синими цветами.
На экзамене 30 билетов, Серёжа не выучил 9 из них. Найдите вероятность того, что ему попадётся выученный билет.
Родительский комитет закупил 20 пазлов для подарков детям в связи
с окончанием учебного года, из них 6 с машинами и 14 с видами городов. Подарки распределяются случайным образом между 20 детьми, среди которых есть Володя. Найдите вероятность того, что Володе достанется пазл с машиной.В среднем из 150 карманных фонариков, поступивших в продажу, пятнадцать неисправных. Найдите вероятность того, что выбранный наудачу в магазине фонарик окажется исправен.
В лыжных гонках участвуют 11 спортсменов из России, 6 спортсменов
из Норвегии и 3 спортсмена из Швеции. Порядок, в котором спортсмены стартуют, определяется жребием. Найдите вероятность того, что первым будет стартовать спортсмен из Норвегии или Швеции.Вероятность того, что новая шариковая ручка пишет плохо (или не пишет), равна 0,11. Покупатель в магазине выбирает одну шариковую ручку. Найдите вероятность того, что эта ручка пишет хорошо.
В магазине канцтоваров продаётся 272 ручки: 11 красных, 37 зелёных,
26 фиолетовых, остальные синие и чёрные, их поровну. Найдите вероятность того, что случайно выбранная в этом магазине ручка будет зелёной
или синей.
Вариант 9
На тарелке лежат одинаковые на вид пирожки: 3 с мясом, 24 с капустой
и 3 с вишней. Лёша наугад берёт один пирожок. Найдите вероятность того, что пирожок окажется с вишней.В фирме такси в данный момент свободно 10 машин: 2 чёрных, 2 жёлтых и 6 зелёных. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчику. Найдите вероятность того, что к нему приедет жёлтое такси.
У бабушки 20 чашек: 15 с красными цветами, остальные с синими. Бабушка наливает чай в случайно выбранную чашку. Найдите вероятность того, что это будет чашка с синими цветами.
На экзамене 20 билетов, Оскар не выучил 7 из них. Найдите вероятность того, что ему попадётся выученный билет.
Родительский комитет закупил 25 пазлов для подарков детям в связи
с окончанием учебного года, из них 24 с машинами и 1 с видом города. Подарки распределяются случайным образом между 25 детьми, среди которых есть Андрюша. Найдите вероятность того, что Андрюше достанется пазл с машиной.В среднем из 80 карманных фонариков, поступивших в продажу,
десять неисправных. Найдите вероятность того, что выбранный наудачу
в магазине фонарик окажется исправен.В лыжных гонках участвуют 13 спортсменов из России, 2 спортсмена
из Норвегии и 5 спортсменов из Швеции. Порядок, в котором спортсмены стартуют, определяется жребием. Найдите вероятность того, что первым будет стартовать спортсмен из России.Вероятность того, что новая шариковая ручка пишет плохо (или не пишет), равна 0,13. Покупатель в магазине выбирает одну шариковую ручку. Найдите вероятность того, что эта ручка пишет хорошо.
В магазине канцтоваров продаётся 144 ручки: 30 красных, 24 зелёных,
18 фиолетовых, остальные синие и чёрные, их поровну. Найдите вероятность того, что случайно выбранная в этом магазине ручка будет синей или чёрной.
Вариант 10
На тарелке лежат одинаковые на вид пирожки: 7 с мясом, 17 с капустой
и 6 с вишней. Женя наугад берёт один пирожок. Найдите вероятность того, что пирожок окажется с вишней.В фирме такси в данный момент свободно 30 машин: 1 чёрная, 9 жёлтых и 20 зелёных. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчику. Найдите вероятность того, что к нему приедет жёлтое такси.
У бабушки 20 чашек: 10 с красными цветами, остальные с синими. Бабушка наливает чай в случайно выбранную чашку. Найдите вероятность того, что это будет чашка с синими цветами.
На экзамене 50 билетов, Сеня не выучил 5 из них. Найдите вероятность того, что ему попадётся выученный билет.
Родительский комитет закупил 20 пазлов для подарков детям в связи
с окончанием учебного года, из них 14 с машинами и 6 с видами городов. Подарки распределяются случайным образом между 20 детьми, среди которых есть Володя. Найдите вероятность того, что Володе достанется пазл с машиной.В среднем из 75 карманных фонариков, поступивших в продажу,
пятнадцать неисправных. Найдите вероятность того, что выбранный наудачу в магазине фонарик окажется исправен.В лыжных гонках участвуют 11 спортсменов из России, 6 спортсменов
из Норвегии и 3 спортсмена из Швеции. Порядок, в котором спортсмены стартуют, определяется жребием. Найдите вероятность того, что первым будет стартовать спортсмен из России.Вероятность того, что новая шариковая ручка пишет плохо (или не пишет), равна 0,29. Покупатель в магазине выбирает одну шариковую ручку. Найдите вероятность того, что эта ручка пишет хорошо.
В магазине канцтоваров продаётся 138 ручек: 34 красных, 23 зелёных,
11 фиолетовых, остальные синие и чёрные, их поровну. Найдите вероятность того, что случайно выбранная в этом магазине ручка будет красной или чёрной.
Ответы к самостоятельной работе
6. Подведение итогов
7. Комментирование домашнего задания.
infourok.ru
Разбор и решение задания №9 ОГЭ по математике
Статистика и вероятности
Рассмотрим типовые задания 9 ОГЭ по математике. Тематика 9 задания — статистика и вероятности. Задание не является трудным даже для человека, не знакомого с теорией вероятностей или статистикой.
Обычно нам предлагается набор вещей — яблок, конфет, чашек или чего угодно различающихся цветом или другим качеством. Нам необходимо оценить вероятность попадания одного из класса вещей одному человеку. Задача сводится к вычислению общего количества вещей, а затем делению числа вещей необходимого класса на общее количество.
Итак, перейдем к рассмотрению типовых вариантов.
Разбор типовых вариантов задания №9 ОГЭ по математике
Первый вариант задания
У бабушки 20 чашек: 6 с красными цветами, остальные с синими. Бабушка наливает чай в случайно выбранную чашку. Найдите вероятность того, что это будет чашка с синими цветами.
Решение:
Как было сказано выше, найдем общее число чашек — в данном случае это известно по условию — 20 чашек. Нам необходимо найти число синих чашек:
20 — 6 = 14
Теперь мы можем найти вероятность:
14 / 20 = 7 / 10 = 0,7
Ответ: 0,7
Второй вариант задания
В магазине канцтоваров продаётся 138 ручек, из них 34 красные, 23 зелёные, 11 фиолетовые, ещё есть синие и чёрные, их поровну. Найдите вероятность того, что при случайном выборе одной ручки будет выбрана красная или чёрная ручка.
Решение:
Найдем вначале число черных ручек, для этого из общего числа вычитаем все известные цвета и делим на два, так как синих и чёрных ручек поровну:
(138 — 34 — 23 — 11) / 2 = 35
После этого можем найти вероятность, сложив количество чёрных и красных, разделив на общее количество:
(35 + 34) / 138 = 0,5
Ответ: 0,5
Третий вариант задания
В фирме такси в данный момент свободно 12 машин: 1 чёрная, 3 жёлтых и 8,зелёных. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчику. Найдите вероятность того, что к нему приедет жёлтое такси.
Решение:
Найдем общее число машин:
1 + 3 + 8 = 12
Теперь оценим вероятность, разделив количество желтых на общее число:
3 / 12 = 0,25
Ответ: 0,25
Демонстрационный вариант ОГЭ 2019
На тарелке лежат пирожки, одинаковые на вид: 4 с мясом, 8 с капустой и 3 с яблоками. Петя наугад выбирает один пирожок. Найдите вероятность того, что пирожок окажется с яблоками.
Решение:
Классическая задача по теории вероятностей. В нашем случае удачный исход — это пирожок с яблоком. Пирожков с яблоками 3, а всего пирожков:
4 + 8 + 3 = 15
Вероятность того, что попадется пирожок с яблоками — это количество пирожков с яблоками, деленное на общее количество:
3 / 15 = 0,2 или 20%
Ответ: 0,2
Четвертый вариант задания
Вероятность того, что новый принтер прослужит больше года, равна 0,95. Вероятность того, что он прослужит два года или больше, равна 0,88. Найдите вероятность того, что он прослужит меньше двух лет, но не меньше года.
Решение:
Введем обозначения событий:
X – принтер прослужит «больше 1 года»;
Y – принтер прослужит «2 года или больше»;
Z – принтер прослужит «не менее 1 года, но меньше 2-х лет».
Анализируем. События Y и Z независимы, т.к. исключают друг друга. Событие X произойдет в любом случае, т.е. и при наступлении события Y, и наступлении события Z. Действительно, «больше 1 года» означает и «2 года», и «больше 2-х лет», и «меньше 2-х лет, но не менее 1 года».
Если так, то событие X можно считать суммой событий, и тогда на основании теоремы о сложении вероятностей запишем:
Р(X)=Р(Y)+Р(Z).
По условию вероятность события Х (т.е. «больше года») равно 0,95, события Y (т.е. «2 года и больше») – 0,88.
Подставим в формулу числовые данные:
0,95=0,88+Р(Z)
Получаем:
Р(Z)=0,95–0,88=0,07
Р(Z) – искомое событие.
Ответ: 0,07
Пятый вариант задания
За круглый стол на 9 стульев в случайном порядке рассаживаются 7 мальчиков и 2 девочки. Найдите вероятность того, что девочки окажутся на соседних местах.
Решение:
Для расчета вероятности используем классическую ее формулу:
где m – кол-во благоприятных исходов для искомого события, n – общее кол-во всех возможных исходов.
Одна из девочек (которая села первой) занимает стул произвольно. Значит, для другой имеется 9-1=8 стульев, чтобы сесть. Т.е. кол-во всех возможных вариантов событий равно n=8.
Другая девочка должна занять один из 2-х стульев, соседствующих со стулом первой. Только такая ситуация может считаться благоприятным исходом события. Значит, кол-во благоприятных исходов составляет m=2.
Подставляем данные в формулу для расчета вероятности:
Ответ: 0,25
spadilo.ru
Презентация по математике 9 класс ОГЭ «Теория вероятности»

ГИА « * Теория вероятностей »
Магометова Х. Н. учитель математики
МБОУ СОШ №1 с.Кизляр
2017г.

№ 1 Стас выбирает случайное трёхзначное число. Найдите вероятность того, что оно делится на 48.
- РЕШЕНИЕ: Трехзначных чисел от 100 до 999 999 — 99 = 900 999 / 48 ≈ 20 чисел, которые делятся на 48 р(А) = 20 / 900 = 0,02 Ответ: 0,02

№ 2 Игральную кость бросают дважды. Найдите вероятность того, что сумма двух выпавших чисел равна 4 или 7.
- РЕШЕНИЕ: Всего исходов 6 * 6 = 36 Сумма 4 : 1+3, 2+2, 3+1 3 исхода Сумма 7: 6+1, 5+2 , 4+3, 3+4 , 2+5, 1+5 6 исходов Благоприятных исходов 3+6=9 р(А) = 9 / 36 = 0,25 Ответ: 0,25

№ 3 На экзамене 20 билетов, Сергей не выучил 3 из них. Найдите вероятность того, что ему попадётся выученный билет.
- РЕШЕНИЕ: Билетов 20 Выучил 20 — 3 = 17 билетов р(А) = 17 / 20 = 0,85 Ответ: 0,85

№ 4 В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что орёл выпадет ровно 2 раза.
- РЕШЕНИЕ: Количество исходов 2 3 = 8 Благоприятных исходов 3 ( 1 и 2 раз выпадет орел, 2 и 3 раз выпадет орел, 1 и 3 раз выпадет орел) р(А) = 3 / 8 = 0,375 Ответ: 0,375

№ 5 Игральную кость бросают дважды. Найдите вероятность того, что хотя бы раз выпало число, меньшее 4.
- РЕШЕНИЕ: Всего исходов 6*6 = 36. Благоприятные исходы 1 +1, 1 +2, 1 +3, 1+ 4, 1+ 5, 1 +6, 2+ 1, 2 +2, 2+ 3, 2 +4 , 2+ 5, 2+ 6, 3+ 1, 3 +2, 3 +3 , 3+ 4, 3+ 5, 3+ 6, 4 +1, 4 +2, 4 +3, 5 +1, 5+ 2, 5+ 3, 6+ 1, 6+ 2, 6+ 3. Благоприятных исходов 27 р(А) = 27/36 = 0,75 Ответ: 0,75

№ 6 Коля выбирает случайное трёхзначное число. Найдите вероятность того, что оно делится на 34.
- РЕШЕНИЕ: Трехзначных чисел от 100 до 999 999 — 99 = 900 999 / 34 ≈ 29 чисел, которые делятся на 34 р(А) = 29 / 900 = 0,03 Ответ: 0,03

№ 7 Игральную кость бросают дважды. Найдите вероятность того, что наибольшее из двух выпавших чисел равно 5.
- РЕШЕНИЕ: Всего исходов 6 * 6 = 36. Благоприятные исходы: 1+ 5, 2+ 5, 3 +5, 4 +5, 5+ 5, 5+ 1, 5 +2, 5+ 3, 5+ 4. Благоприятных исходов — 9 р(А) = 9 / 36 = 0,25. Ответ: 0,25

№ 8 На экзамене 40 билетов, Валера не выучил 10 из них. Найдите вероятность того, что ему попадётся выученный билет
- РЕШЕНИЕ: Всего 40 билетов Выучил 40 — 10 = 30 билетов р(А) = 30 / 40 = 0,75 Ответ: 0,75

№ 9 Определите вероятность того, что при бросании игрального кубика (правильной кости) выпадет нечётное число очков.
- РЕШЕНИЕ: Всего исходов 6 Благоприятных исходов 3 (1,3,5 очков) р(А) = 3 / 6 = 1 / 2 = 0,5 Ответ: 0,5

№ 10 Девятиклассники Петя, Катя, Ваня, Даша и Наташа бросили жребий, кому начинать игру. Найдите вероятность того, что жребий начинать игру Пете не выпадет
- РЕШЕНИЕ: всего 5 человек без Пети 4 р(А) = 4 / 5 = 0,8 Ответ: 0,8

№ 11 Во время вероятностного эксперимента монету бросили 1000 раз, 532 раза выпал орёл. На сколько частота выпадения решки в этом эксперименте отличается от вероятности этого события?
- РЕШЕНИЕ: р(А) = 532 / 1000 = 0,532 р(В) = 1 — 0,532 = 0,468 0,532 — 0,468 = 0,064 Ответ: 0,064

№ 12 Игральную кость бросают дважды. Найдите вероятность того, что сумма двух выпавших чисел чётна.
- РЕШЕНИЕ: Всего исходов 6 * 6 = 36. Благоприятные исходы: 1+ 5, 1+3, 1+1, 2+ 2, 2+4, 2+6, 3+1, 3+3, 3+5, 4+2, 4+4, 4+6, 5+1, 5+3, 5+5, 6+2, 6+4, 6+6 Благоприятных исходов 18 р(А) = 18 / 36 = 0,5 Ответ: 0,5

№ 13 На экзамене 20 билетов, Сергей не выучил 2 из них. Найдите вероятность того, что ему попадётся выученный билет.
- РЕШЕНИЕ: Всего 20 билетов Выучил 20 — 2 = 18 билетов р(А) = 18 / 20 = 0,9 Ответ: 0,9

№ 14 Вова выбирает случайное трёхзначное число. Найдите вероятность того, что оно делится на 95.
- РЕШЕНИЕ: Трехзначных чисел от 100 до 999 999 — 99 = 900 999 / 95 ≈ 10 чисел, которые делятся на 95 р(А) = 10 / 900 = 0,01 Ответ: 0,01

№ 15 На экзамене 25 билетов, Сергей не выучил 6 из них. Найдите вероятность того, что ему попадётся выученный билет.
- РЕШЕНИЕ: Всего 25 билетов Выучил 25 — 6 = 19 билетов р(А) = 19 / 25 = 0,76 Ответ: 0,76

№ 16 Андрей выбирает случайное трёхзначное число. Найдите вероятность того, что оно делится на 10.
- РЕШЕНИЕ: Трехзначных чисел от 100 до 999 999 — 99 = 900 999 / 10 ≈ 99 чисел, которые делятся на 10 р(А) = 99 / 900 = 0,11 Ответ: 0,11

№ 17 Андрей выбирает случайное трёхзначное число. Найдите вероятность того, что оно делится на 33.
- РЕШЕНИЕ: Трехзначных чисел от 100 до 999 999 — 99 = 900 999 / 33 ≈ 30 чисел, которые делятся на 33 р(А) = 30 / 900 = 0,03 Ответ: 0,03

№ 18 На экзамене 20 билетов, Сергей не выучил 4 из них. Найдите вероятность того, что ему попадётся выученный билет.
- РЕШЕНИЕ: Всего 20 билетов Выучил 20 — 4 = 16 билетов р(А) = 16 / 20 = 0,8 Ответ: 0,8

№19 Игральную кость бросают дважды. Найдите вероятность того, что хотя бы раз выпало число, большее 3.
- РЕШЕНИЕ: Всего исходов 6*6 = 36. Благоприятные: 1+ 1, 1 +2, 1+ 3, 1 +4, 1+ 5, 1+ 6, 2+ 1, 2 +2, 2+3, 2 +4 , 2+ 5, 2+ 6, 3+ 1, 3+ 2, 3+ 3 , 3+ 4, 3+ 5, 3+ 6, 4 +1, 4 +2, 4+ 3, 5+ 1, 5 +2, 5+3, 6+ 1, 6+ 2, 6+ 3. Благоприятных исходов 27. р(А) = 27 / 36 = 0,75. Ответ: 0,75

№ 20 На тарелке лежат одинаковые на вид пирожки: 4 с мясом, 5 с рисом и 21 с повидлом. Андрей наугад берёт один пирожок. Найдите вероятность того, что пирожок окажется с повидлом.
Всего пирожков 4 + 5 + 21 = 30 С повидлом 21
р(А) = 21 / 30 = 0,7 Ответ: 0,7

№ 21 В каждой десятой банке кофе согласно условиям акции есть приз. Призы распределены по банкам случайно. Валя покупает банку кофе в надежде выиграть приз. Найдите вероятность того, что Валя не найдёт приз в своей банке.
- РЕШЕНИЕ: Банок 10 Без приза 9 банок р(А) = 9 / 10 = 0,9 Ответ: 0,9

№ 22 Определите вероятность того, что при бросании кубика выпало чётное число очков.
- РЕШЕНИЕ: Всего исходов 6 Благоприятных исходов 3 (2,4,6) р(А) = 3 / 6 = 1 / 2 = 0,5 Ответ: 0,5
multiurok.ru
Презентация к уроку по алгебре (9 класс) на тему: решение задач по теории вероятности. Гиа-2014
По теме: методические разработки, презентации и конспекты
Урок Решение задач по теории вероятностей. Модель «игральная кость»Материал данного урока содержит задачи типа В10 ЕГЭ 2012 года и может быть использоваться учителем как на уроках математики в 9-11 классах, так и на факультативных занятиях….
Урок Решение задач по теории вероятностей. Модель «игральная кость»Материал данного урока содержит задачи В10 ЕГЭ 2012 и безусловно может использоваться учителем как на уроках математики в 9-11 классах, так и на факультативных занятиях….
Подготовка к ЕГЭ. Решение задач по теории вероятностей.Презентация содержит решение задач по теории вероятностей. Можно использовать в 11 классе при подготовке к ЕГЭ….
Решение задач по теории вероятностей. Подготовка к ГИА.В данной презентации содержится подборка задач по теории вероятностей для подготовки к ГИА и ЕГЭ. Материал взят из открытого банка заданий ГИА и ЕГЭ….
Презентация к уроку «Решение задач по теории вероятностей»Этот материал поможет в подготовке к итоговой аттестации за курс основной школы, а также будет полезным при подготовке к ЕГЭ по математике….
Подготовка к ГИА «Решение задач по теории вероятностей»В презентация «Решение задач по теории вероятностей» представлены различные типы задач, встречающихся в вариантах ГИА, а также задачи в двух вариантах для самостоятельного решения с ответа…
Разработка урока – практикума по алгебре в 9 классе по теме: «Применение комбинаторики при решении задач по теории вероятностей»Разработка урока повторения изученного материала по комбинаторике и теории вероятностей….
nsportal.ru
«Решение задач по теории вероятностей. ОГЭ — 2015.»

Решение задач по теории вероятности
ГИА-2014
Крицкая Елена Николаевна
ГБОУ СОШ №426 горда Москвы

№ 132821
- Андрей выбирает трехзначное число. Найдите вероятность того, что оно делится на 33.
Решение.
Чтобы ответить на этот вопрос, нужно количество трёхзначных чисел, делящихся на 33, разделить на количество всех трёхзначных чисел.
Как вычислить количество всех трёхзначных чисел?
Первое трёхзначное число 100, последнее — 999.
Всего 900.
Все числа, которые делятся на 33, можно задать формулой 33 N , где N – целое число. Найдем, сколько таких чисел. Для этого решим неравенство:
Итак, всего таких чисел 27.
Вероятность равна 27:900=0,03 .
Ответ: 0,03

Андрей выбирает трехзначное число. Найдите вероятность того, что оно делится на 10.
№ 13282 5
Решение.
Чтобы ответить на этот вопрос, нужно количество трёхзначных чисел, делящихся на 10 разделить, на количество всех трёхзначных чисел.
Как вычислить количество всех трёхзначных чисел?
Первое трёхзначное число 100, последнее — 999.
Всего 900.
Все числа, которые делятся на 10 , можно задать формулой 10N , где N – целое число. Найдем, сколько таких чисел. Для этого решим неравенство:
Итак, всего таких чисел 90 .
Вероятность равна 90 :900=0, 1 .
Ответ: 0, 1 .

№ 132823
- Коля выбирает трехзначное число. Найдите вероятность того, что оно делится на 4.
Решение.
Как вычислить количество всех трёхзначных чисел?
Первое трёхзначное число 100, последнее — 999.
Всего 900.
Все числа, которые делятся на 4 можно, задать формулой 4 N , где N – целое число. Найдем, сколько таких чисел. Для этого решим неравенство:
Итак, всего таких чисел 249:24=225.
Вероятность равна 225:900=0,25 .
Ответ: 0,25.

№ 132827
Коля выбирает трехзначное число.
Найдите вероятность того, что оно делится на 93.
Решение.
Чтобы ответить на этот вопрос, нужно количество трёхзначных чисел, делящихся на 93, разделить на количество всех трёхзначных чисел.
Как вычислить количество всех трёхзначных чисел?
Первое трёхзначное число 100, последнее — 999.
Всего 900.
Все числа, которые делятся на 93, можно задать формулой 93 N , где N – целое число. Найдем, сколько таких чисел. Для этого решим неравенство:
Итак, всего таких чисел 9.
Вероятность равна 9:900=0,01 .
Ответ: 0,01.

№ 132873
Телевизор у Марины сломался и показывает только один случайный канал. Марина включает телевизор. В это время по восьми каналам из сорока показывают кинокомедии. Найдите вероятность того, что Марина попадет на канал, где комедия не идет.
Решение.
Чтобы ответить на вопрос задачи, нужно количество каналов, по которым комедия не идёт, разделить на общее количество каналов.
40-8=32 канала, по которым комедия не идёт.
Всего 40 каналов.
Вероятность равна 32:40=0,8 .
Ответ: 0,8.

№ 132877
Телевизор у Любы сломался и показывает только один случайный канал. Люба включает телевизор. В это время по двадцати пяти каналам из пятидесяти показывают кинокомедии. Найдите вероятность того, что Люба попадет на канал, где комедия не идет.
Решение.
Чтобы ответить на вопрос задачи, нужно количество каналов, по которым комедия не идёт, разделить на общее количество каналов.
50-25=25 канала, по которым комедия не идёт.
Всего 50 каналов.
Вероятность равна 25:50=0,5 .
Ответ: 0,5.
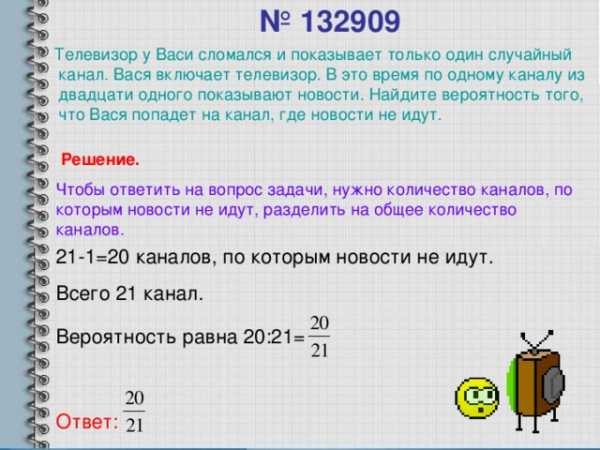
№ 132909
Телевизор у Васи сломался и показывает только один случайный канал. Вася включает телевизор. В это время по одному каналу из двадцати одного показывают новости. Найдите вероятность того, что Вася попадет на канал, где новости не идут.
Решение.
Чтобы ответить на вопрос задачи, нужно количество каналов, по которым новости не идут, разделить на общее количество каналов.
21-1=20 каналов, по которым новости не идут.
Всего 21 канал.
Вероятность равна 20:21=
Ответ:
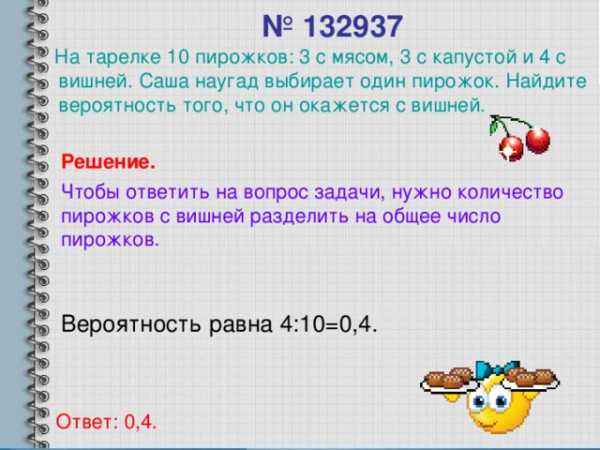
№ 132937
На тарелке 10 пирожков: 3 с мясом, 3 с капустой и 4 с вишней. Саша наугад выбирает один пирожок. Найдите вероятность того, что он окажется с вишней.
Решение.
Чтобы ответить на вопрос задачи, нужно количество пирожков с вишней разделить на общее число пирожков.
Вероятность равна 4:10=0,4.
Ответ: 0,4.
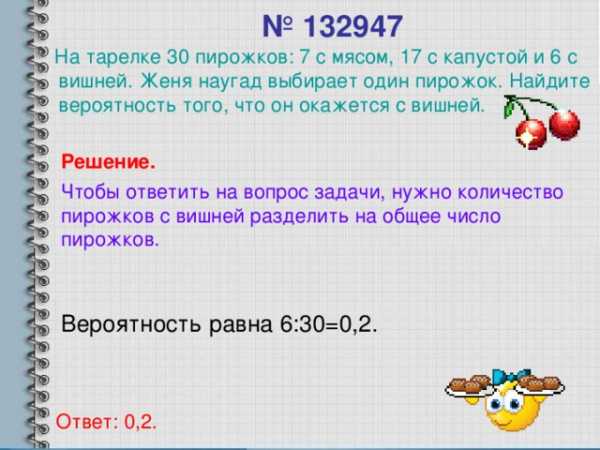
№ 132947
На тарелке 30 пирожков: 7 с мясом, 17 с капустой и 6 с вишней. Женя наугад выбирает один пирожок. Найдите вероятность того, что он окажется с вишней.
Решение.
Чтобы ответить на вопрос задачи, нужно количество пирожков с вишней разделить на общее число пирожков.
Вероятность равна 6:30=0,2.
Ответ: 0,2.

№ 132975
На тарелке семнадцать пирожков: 2 с мясом, 4 с капустой и 11 с вишней. Юра наугад выбирает один пирожок. Найдите вероятность того, что он окажется с мясом.
Решение.
Чтобы ответить на вопрос задачи, нужно количество пирожков с мясом разделить на общее число пирожков.
Вероятность равна 2:17=
Ответ:

№ 133001
В фирме такси в данный момент свободно 15 машин: 3 черных, 6 желтых и 6 зеленых. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчику. Найдите вероятность того, что к нему приедет желтое такси.
Решение.
Чтобы ответить на вопрос задачи, нужно число желтых такси разделить на общее число машин.
Вероятность равна 6:15=0,4.
Ответ: 0,4.
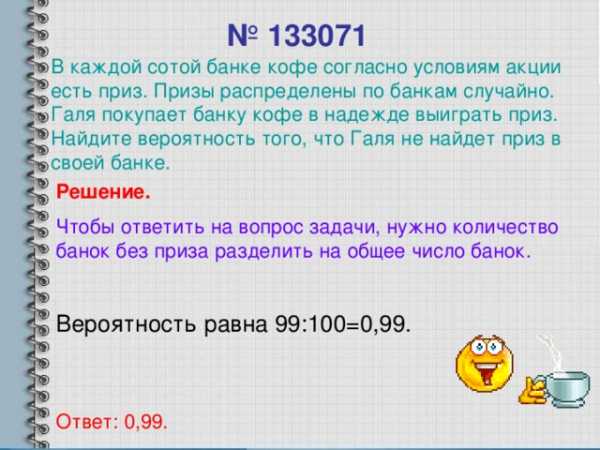
№ 133071
В каждой сотой банке кофе согласно условиям акции есть приз. Призы распределены по банкам случайно. Галя покупает банку кофе в надежде выиграть приз. Найдите вероятность того, что Галя не найдет приз в своей банке.
Решение.
Чтобы ответить на вопрос задачи, нужно количество банок без приза разделить на общее число банок.
Вероятность равна 99:100=0,99.
Ответ: 0,99.

№ 133039
В фирме такси в данный момент свободно 18 машин: 6 черных, 4 желтых и 8 зеленых. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчице. Найдите вероятность того, что к ней приедет зеленое такси.
Решение.
Чтобы ответить на вопрос задачи, нужно число зелёных такси разделить на общее число машин.
Вероятность равна 8:18=
Ответ:

№ 1330 63
В фирме такси в данный момент свободно 30 машин: 3 черных, 5 желтых и 22 зеленых. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчице. Найдите вероятность того, что к ней приедет зеленое такси.
Решение.
Чтобы ответить на вопрос задачи, нужно число зелёных такси разделить на общее число машин.
Вероятность равна 22 : 30 =
Ответ:

№ 1330 81
В каждой шестой банке кофе согласно условиям акции есть приз. Призы распределены по банкам случайно. Валя покупает банку кофе в надежде выиграть приз. Найдите вероятность того, что Валя не найдет приз в своей банке?
Решение.
Чтобы ответить на вопрос задачи, нужно количество банок без приза разделить на общее число банок.
Вероятность равна 5 : 6 =
Ответ:

№ 1330 89
Ваня с папой решили покататься на колесе обозрения. Всего на колесе тридцать кабинок, из них 3 — синие, 24 — зеленые, остальные — красные. Кабинки по очереди подходят к платформе для посадки. Найдите вероятность того, что Ваня прокатится в красной кабинке.
Решение.
Чтобы ответить на вопрос задачи, нужно количество красных кабинок разделить на общее число кабинок.
Вероятность равна
(30-(24+3)):30=0,1.
Ответ: 0,1.

№ 133129
Тема с папой решили покататься на колесе обозрения. Всего на колесе девятнадцать кабинок, из них 6 — синие, 10 — зеленые, остальные — оранжевые. Кабинки по очереди подходят к платформе для посадки. Найдите вероятность того, что Тема прокатится в оранжевой кабинке
Решение.
Чтобы ответить на вопрос задачи, нужно количество оранжевых кабинок разделить на общее число кабинок.
Вероятность равна
(19-(6+10)):19=
Ответ:

№ 1331 61
У бабушки 25 чашек: 3 с красными цветами, остальные с синими. Бабушка наливает чай в случайно выбранную чашку. Найдите вероятность того, что это будет чашка с синими цветами.
Решение.
Чтобы ответить на вопрос задачи, нужно количество чашек с синими цветами разделить на общее число чашек.
Вероятность равна
(25-3):25=22:25=0,88
Ответ: 0,88.

№ 13319 1
У дедушки 17 чашек: 5 с красными звездами, остальные с золотыми. Дедушка наливает чай в случайно выбранную чашку. Найдите вероятность того, что это будет чашка с золотыми звездами.
Решение.
Чтобы ответить на вопрос задачи, нужно количество чашек с золотыми звёздами разделить на общее число чашек.
Вероятность равна
(17-5):17=12:17=
Ответ:

№ 133221
На экзамене 40 билетов, Сеня не выучил 8 из них. Найдите вероятность того, что ему попадется выученный билет.
Решение.
Чтобы ответить на вопрос задачи, нужно количество выученных билетов разделить на общее число билетов.
Вероятность равна
(40-8):40=32:40=0,8.
Ответ: 0,8.

№ 133257
На экзамене 60 билетов, Стас не выучил 6 из них. Найдите вероятность того, что ему попадется выученный билет.
Решение.
Чтобы ответить на вопрос задачи, нужно количество выученных билетов разделить на общее число билетов.
Вероятность равна
(60-6):60=54:60=0,9.
Ответ: 0,9.
№ 133311
Родительский комитет закупил 20 пазлов для подарков детям на окончание года, из них 11 с машинами и 9 с видами городов. Подарки распределяются случайным образом. Найдите вероятность того, что Илюше достанется пазл с машиной.
Решение.
Чтобы ответить на вопрос задачи, нужно количество пазлов с машинами разделить на общее число пазлов.
Вероятность равна
9:20=0,45.
Ответ: 0,45.

№ 133319
Родительский комитет закупил 25 пазлов для подарков детям на окончание года, из них 21 с машинами и 4 с видами городов. Подарки распределяются случайным образом. Найдите вероятность того, что Саше достанется пазл с машиной.
Решение.
Чтобы ответить на вопрос задачи, нужно количество пазлов с машинами разделить на общее число пазлов.
Вероятность равна
21:25=0,84.
Ответ: 0,84.

№ 133387
В среднем на 75 карманных фонариков приходится девять неисправных. Найдите вероятность купить работающий фонарик.
Решение.
Чтобы ответить на вопрос задачи, нужно количество работающих фонариков разделить на общее число фонариков.
Вероятность равна
(75-9):75=0,88.
Ответ: 0,88.

№ 133481
В среднем из каждых 150 поступивших в продажу аккумуляторов 120 аккумуляторов заряжены. Найдите вероятность того, что купленный аккумулятор не заряжен.
Решение.
Чтобы ответить на вопрос задачи, нужно количество аккумуляторов, которые не работают разделить на общее число аккумуляторов.
Вероятность равна
(150-120):150=30:150=0,2.
Ответ: 0,2.

№ 132561
Андрей наудачу выбирает двузначное число. Найдите вероятность того, что оно оканчивается на 5.
Решение.
Чтобы ответить на этот вопрос, нужно количество двузначных чисел, оканчивающихся на 5, разделить на количество всех двузначных чисел.
Как вычислить количество всех двузначных чисел?
Первое двузначное число 10, последнее — 99.
Всего 99-9=90.
Все числа, которые оканчиваются на 5, можно задать формулой 10 N+5 , где N – целое число. Найдем, сколько таких чисел. Для этого решим неравенство:
Итак, всего таких чисел 9 .
Вероятность равна 9 :90=0, 1 .
Ответ: 0, 1 .

№ 133565
Витя наудачу выбирает двузначное число. Найдите вероятность того, что оно начинается на 9.
Решение.
Чтобы ответить на этот вопрос, нужно количество двузначных чисел, которые начинаются на 9, разделить на количество всех двузначных чисел.
Как вычислить количество всех двузначных чисел?
Первое двузначное число 10, последнее — 99.
Всего 99-9=90.
Существует 10 чисел, которые начинаются на 9 (90, 91, 92,…,99).
Вероятность равна 10:90=
Ответ:

№ 132565
Леша наудачу выбирает двузначное число. Найдите вероятность того, что оно оканчивается на 0.
Решение.
Чтобы ответить на этот вопрос, нужно количество двузначных чисел, оканчивающихся на 0, разделить на количество всех двузначных чисел.
Как вычислить количество всех двузначных чисел?
Первое двузначное число 10, последнее — 99.
Всего 99-9=90.
Все числа, которые оканчиваются на 0, можно задать формулой 10 N , где N – целое число. Найдем, сколько таких чисел. Для этого решим неравенство:
Итак, всего таких чисел 9.
Вероятность равна 9:90=0,1
Ответ: 0,1.

kopilkaurokov.ru
Материал для подготовки к ЕГЭ (ГИА) по алгебре (9 класс) на тему: Теория вероятности в задачах ОГЭ
Слайд 1
Теория вероятности в задачах ОГЭ (задание 9) по материалам открытого банка задач ОГЭ по математике 2017 года Кильдеева Ирина Владимировна – учитель математики МБОУ «Средняя общеобразовательная школа № 37» г. КемеровоСлайд 2
Классическое определение вероятности Вероятностью события А называется отношение числа благоприятных исходов, в результате которых наступает событие А, к общему числу всех (равновозможных между собой) исходов этого испытания. Вероятность некоторого события А обозначается Р(А) и определяется формулой: где N ( A ) – число элементарных исходов, благоприятствующих событию A ; N – число всех возможных элементарных исходов испытания.
Слайд 3
Вероятность случайного события есть положительное число, заключенное между нулем и единицей : В математике вероятность каждого события оценивают неотрицательным числом, но не процентами !
Слайд 4
Для нахождения вероятности случайного события при проведении некоторого испытания следует найти: 1) число всех возможных исходов данного испытания; 2) количество N ( A ) тех исходов, в которых наступает событие А; 3) частное N ( A )/ N будет равно вероятности события А. Вероятность события А обозначают Р(А). Алгоритм нахождения вероятности случайного события:
Слайд 5
События А и В называются противоположными , если они несовместны и одно из них обязательно происходит. Событие, противоположное событию А, обозначают символом Ᾱ . Сумма вероятностей противоположных событий равна 1. P(A ) + P( Ᾱ ) = 1 Вероятность противоположного события равна P( Ᾱ ) = 1 – P(A ) Противоположные события
Слайд 6
На экзамене 25 билетов, Сергей не выучил 3 из них. Найдите вероятность того, что ему попадётся выученный билет. Решение: Вероятность благоприятного случая — отношение количества благоприятных случаев к общему количеству всех исходов. В данной задаче благоприятным случаем является взятие на экзамене выученного билета. Всего благоприятных случаев 25 − 3 =22 , а количество всех случаев 25. Отношение соответственно равно Ответ: 0,88.
Слайд 7
Телевизор у Маши сломался и показывает только один случайный канал. Маша включает телевизор. В это время по трем каналам из двадцати показывают кинокомедии. Найдите вероятность того, что Маша попадет на канал, где комедия не идет. Решение: Количество каналов, по которым не идет кинокомедий: 20 – 3 = 17 Вероятность того, что Маша не попадет на канал, по которому идут кинокомедии равна отношению количества каналов, по которым не идут кинокомедии к общему числу каналов: . Ответ: 0, 85 .
Слайд 8
На тарелке 12 пирожков: 5 с мясом, 4 с капустой и 3 с вишней. Наташа наугад выбирает один пирожок. Найдите вероятность того, что он окажется с вишней. Решение: Вероятность того, что будет выбран пирожок с вишней равна отношению количества пирожков с вишней к общему количеству пирожков: Ответ: 0,2 5 .
Слайд 9
Решение: Машин желтого цвета 4, всего машин 20 . Поэтому вероятность того, что на случайный вызов приедет машина желтого цвета равна: 2 В фирме такси в данный момент свободно 20 машин: 9 черных, 4 желтых и 7 зеленых. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчику. Найдите вероятность того, что к нему приедет желтое такси. Ответ: 0,2.
Слайд 10
Решение: Вероятность того, что подойдет красная кабинка равна отношению количества красных кабинок к общему количеству кабинок на колесе обозрения. Всего красных кабинок: Поэтому искомая вероятность Миша с папой решили покататься на колесе обозрения. Всего на колесе двадцать четыре кабинки, из них 5 — синие, 7 — зеленые, остальные — красные. Кабинки по очереди подходят к платформе для посадки. Найдите вероятность того, что Миша прокатится в красной кабинке. Ответ: 0,5.
Слайд 11
Решение: Вероятность того, что чай нальют в чашку с синими цветами равна отношению количества чашек с синими цветами к общему количеству чашек. Всего чашек с синими цветами: Поэтому искомая вероятность У бабушки 20 чашек: 5 с красными цветами, остальные с синими. Бабушка наливает чай в случайно выбранную чашку. Найдите вероятность того, что это будет чашка с синими цветами. Ответ: 0,75.
Слайд 12
Решение: Вероятность получить пазл с машиной равна отношению числа пазлов с машиной к общему числу закупленных пазлов , то есть Родительский комитет закупил 25 пазлов для подарков детям на окончание года, из них 15 с машинами и 10 с видами городов. Подарки распределяются случайным образом . Найдите вероятность того, что Толе достанется пазл с машиной. Ответ: 0,6.
Слайд 13
Решение: Из каждых 80 аккумуляторов в среднем будет 80 − 76 = 4 незаряженных. Таким образом, вероятность купить незаряженный аккумулятор равна отношению числа незаряженных аккумуляторов к 80 заряженным, то есть В среднем из каждых 80 поступивших в продажу аккумуляторов 76 аккумуляторов заряжены. Найдите вероятность того, что купленный аккумулятор не заряжен. Ответ: 0,05.
Слайд 14
Решение: Вероятность получить вещевой выигрыш равна отношению количества вещевых выйгрышей к общему количеству выйгрышей В денежно-вещевой лотерее на 100 000 билетов разыгрывается 1300 вещевых и 850 денежных выигрышей. Какова вероятность получить вещевой выигрыш? Ответ: 0,013.
Слайд 15
Решение: Из 900 карт исправны 900 − 54 = 846 шт. Поэтому вероятность того, что случайно выбранная флеш -карта пригодна для записи равна: Из 900 новых флеш -карт в среднем 54 не пригодны для записи. Какова вероятность того, что случайно выбранная флеш -карта пригодна для записи? Ответ: 0,94.
Слайд 16
Решение: Всего в коробке 14+6=20 пакетиков. Вероятность того, что Павел вытащит пакетик с зелёным чаем равна 0,3. В коробке 14 пакетиков с чёрным чаем и 6 пакетиков с зелёным чаем. Павел наугад вынимает один пакетик. Какова вероятность того, что это пакетик с зелёным чаем? Ответ: 0,3.
Слайд 17
Решение: Всего спортсменов 11 + 6 + 3 = 20 человек. 11 спортсменов из России. Поэтому вероятность того, что первым будет стартовать спортсмен из России равна 0,55. В лыжных гонках участвуют 11 спортсменов из России, 6 спортсменов из Норвегии и 3 спортсмена из Швеции. Порядок, в котором спортсмены стартуют, определяется жребием. Найдите вероятность того, что первым будет стартовать спортсмен из России. Ответ: 0,55.
Слайд 18
Решение: Всего спортсменов 11 + 6 + 3 = 20 человек. Спортсменов не из России 6+3=9. Поэтому вероятность того, что первым будет стартовать спортсмен из России равна 0,45. В лыжных гонках участвуют 11 спортсменов из России, 6 спортсменов из Норвегии и 3 спортсмена из Швеции. Порядок, в котором спортсмены стартуют, определяется жребием. Найдите вероятность того, что первым будет стартовать спортсмен не из России. Ответ: 0,45.
Слайд 19
Решение: Исправных лампочек 1000 — 5 = 995. Вероятность того, что лампочка будет исправной равна отношению исправных лампочек к общему количеству лампочек 0,995. Из каждых 1000 электрических лампочек 5 бракованных. Какова вероятность купить исправную лампочку? Ответ: 0,995.
Слайд 20
Решение: Вероятность события равна отношению количества благоприятных случаев к количеству всех случаев. Среди пяти детей одна девочка. Поэтому вероятность равна 0,2. Стас, Денис, Костя, Маша, Дима бросили жребий — кому начинать игру. Найдите вероятность того, что начинать игру должна будет девочка . Ответ: 0,2.
Слайд 21
Решение: Вероятность события равна отношению количества благоприятных случаев к количеству всех случаев. Благоприятными случаями являются 3 случая, когда игру начинает Петя, Игорь или Антон, а количество всех случаев (всего детей) 6 . Поэтому искомое отношение равно 0,5. Петя, Вика, Катя, Игорь, Антон, Полина бросили жребий — кому начинать игру. Найдите вероятность того, что начинать игру должен будет мальчик. Ответ: 0,5.
Слайд 22
Решение: Вероятность того, что пакет молока протекает равна 0,5. Событие « пакет молока не течёт» является противоположным. Его вероятность равна 1 — 0,05 = 0,95 Из 1600 пакетов молока в среднем 80 протекают. Какова вероятность того, что случайно выбранный пакет молока не течёт ? Ответ: 0,95.
Слайд 23
Решение: Всего в соревнованиях участвуют 3 + 3 + 4 = 10 гимнасток. 3 гимнастки из России. Поэтому вероятность того, что первой будет выступать гимнастка из России равна 0,3. В соревнованиях по художественной гимнастике участвуют три гимнастки из России, три гимнастки из Украины и четыре гимнастки из Белоруссии. Порядок выступлений определяется жеребьёвкой. Найдите вероятность того, что первой будет выступать гимнастка из России. Ответ: 0,3.
Слайд 24
Решение: Событие « ручка пишет хорошо » противоположно событию « ручка пишет плохо (или не пишет )» вероятность которого равна 0,19. Поэтому, вероятность того, что «ручка пишет хорошо» равна 1 − 0,19 = 0,81. Вероятность того, что новая шариковая ручка пишет плохо (или не пишет), равна 0,19. Покупатель в магазине выбирает одну такую ручку. Найдите вероятность того, что эта ручка пишет хорошо. Ответ: 0,81.
Слайд 25
Решение: Найдём количество чёрных и синих ручек : (100 – 37 – 8 – 17) : 2 = 19 Вероятность того, что Алиса вытащит наугад красную или чёрную ручку равна 0,56. В магазине канцтоваров продаётся 100 ручек, из них 37 – красные, 8 – зелёные, 17 – фиолетовые, ещё есть синие и чёрные, их поровну. Найдите вероятность того, что Алиса наугад вытащит красную или чёрную ручку. Ответ: 0,56.
Слайд 26
Решение: Из 100 фонариков 100 − 8 = 92 исправны. Значит , вероятность того, что выбранный наудачу в магазине фонарик окажется исправным равна 0,92. В среднем из 100 карманных фонариков, поступивших в продажу, восемь неисправных. Найдите вероятность того, что выбранный наудачу в магазине фонарик окажется исправен . Ответ: 0,92.
Слайд 27
Используемые материалы ФИПИ Открытый банк заданий по математике 2017 года http :// 85.142.162.126/os/xmodules/qprint/index.php?theme_guid=5277E3049BBFA50A46567B64CE413F29&proj_guid=DE0E276E497AB3784C3FC4CC20248DC0
nsportal.ru
