Задачи по метрологии на погрешность: Решение типовых задач по дисциплине «Метрология, стандартизация и сертификация»

Задачи метрологии (2)

Задача 1. Вольтметр класса точности 0,5 имеет диапазон измерений от 0 до 100 В. Определить допускаемую абсолютную и относительную погрешность, если стрелка вольтметра остановилась на делении шкалы против цифры 30 В.

Решение:

Абсолютная погрешность:

где – класс точности вольтметра; – верхний предел вольтметра.

Относительная погрешность:

где – абсолютная погрешность вольтметра; – значение вольтметра.

Ответ: Допустимая абсолютная погрешность вольтметра . Допустимая относительная погрешность вольтметра .

Задача 2. Двумя амперметрами на 20 А был измерен ток на выходе трансформатора. Первый имеет погрешность 1% от верхнего предела и показал 4 А, а второй имеет погрешность 2% от верхнего предела и показал 3,98 А.

Найти относительную погрешность второго амперметра.

Решение:

Абсолютная погрешность измерения этого амперметра составляет:

Относительная погрешность второго амперметра:

Ответ: Относительная погрешность второго амперметра равна –0,5%.

Задача 3. Пользуясь правилом округления, как следует записать результаты 148935 и 575,3455, если первая из заменяемых цифр является пятой по счету (слева направо)?

Ответ: Если первая (слева направо) из заменяемых нулями и отбрасываемых цифр меньше 5, остающиеся цифры не изменяются, т. е. 148900 и 575,3.

Задача 4. 1 аршин равен 2/3 м с погрешностью 6,7%. В обиходе пользуются еще соотношением 1 м = 1,5 аршина. Зная, что 1 аршин 0,7112 м, определите погрешность последнего допущения.

Решение:

Погрешность измерения при первом допущении составляет 0,04467 единиц. При этом допущение можно написать следующим образом – 1 аршин = (2/3±0,045) м. Однако величина второго допущения может быть расписана следующим образом: 1 аршин = 0,7112 м = (2/3+0,045). Из этого делаем вывод, что погрешность последнего допущения составляет также 6,7%.

Ответ: Погрешность последнего допущения составляет 6,7%.

Задача 1. Определить вероятность внезапного отказа измерительного преобразователя за 1000 ч работы, если он состоит из 5 резисторов с интенсивностью отказов и 2 конденсаторов с .

Решение:

Интенсивность отказов измерительного преобразователя:

;

.

Вероятность безотказной работы за 1000 ч:

Вероятность отказа за 1000 ч:

Ответ: Вероятность внезапного отказа измерительного преобразования равна 0,05.

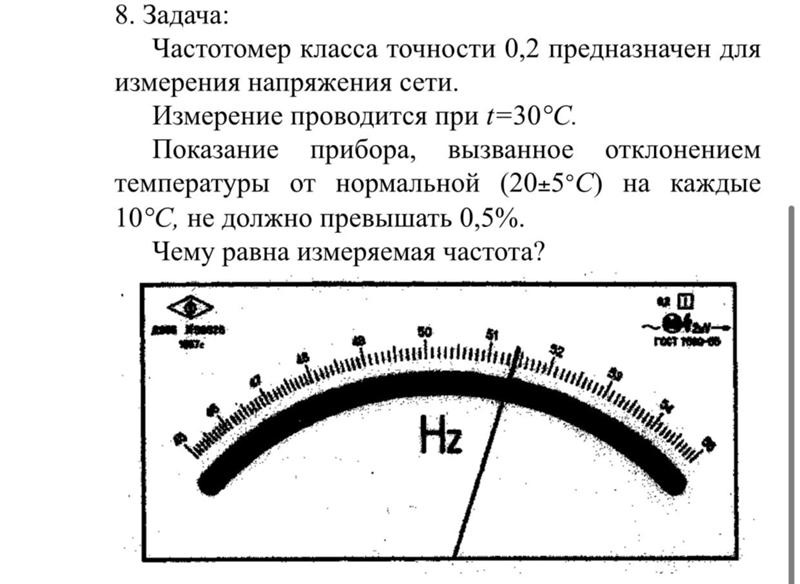
Задача 2. Определить пригодность вольтметра класса точности 1,0 с диапазоном измерений от 0 до 200 В, если при непосредственном сличении его показаний с показаниями образцового вольтметра были получены следующие данные:

Рабочий, В	25	50	75	100	150	175	200
Образцовый, В	24,9	51,5	77,9	101,5	149,9	174,5	199,9

Образцовый вольтметр имеет систематическую погрешность 0,5 В.

Решение:

По условию приведенная погрешность γ=1,0%.

77,9-75=2,9 В

Ответ: Вольтметр непригоден для использования, так как погрешность измерения превышает класс точности (погрешность измерения не может превышать допустимую, которая равна 2 В).

Задача 3. Для измерения тока от 20 А до 60 А с относительной погрешностью, не превышающей 2%, был заказан амперметр с верхним пределом измерения 100 А и классом точности 0,5. Удовлетворяет ли он поставленным условиям?

Решение:

(измеренное значение тока берем в начале шкалы, так как в начале шкалы относительная погрешность измерения больше).

что соответствует классу точности 0,5.

Ответ: Амперметр с верхним пределом измерения 100 А и классом точности 0,5 удовлетворяет поставленным условиям.

Задача 4. Электроизмерительный преобразователь состоит из 2 транзисторов с интенсивностью отказов , 3 керамических сопротивлений с и 8 резисторов с . Определить вероятность безотказной работы этого средства измерений за 1000 ч работы.

Решение:

Интенсивность отказов электроизмерительного преобразователя:

;

.

Вероятность безотказной работы за 1000 ч:

Ответ: Вероятность безотказной работы электроизмерительного преобразователя равна 0,9.

404 Cтраница не найдена

Мы используем файлы cookies для улучшения работы сайта МГТУ и большего удобства его использования. Более подробную информацию об использовании файлов cookies можно найти здесь. Продолжая пользоваться сайтом, вы подтверждаете, что были проинформированы об использовании файлов cookies сайтом ФГБОУ ВО «МГТУ» и согласны с нашими правилами обработки персональных данных.

Размер:

AAA

Изображения Вкл. Выкл.

Обычная версия сайта

К сожалению запрашиваемая страница не найдена.

Но вы можете воспользоваться поиском или картой сайта ниже

Университет Майкопский государственный технологический университет – один из ведущих вузов юга России. История университета Анонсы Объявления Медиа Представителям СМИ Газета «Технолог» О нас пишут Ректорат Структура Филиал Политехнический колледж Медицинский институт Лечебный факультет Педиатрический факультет Фармацевтический факультет Стоматологический факультет Факультет послевузовского профессионального образования Факультеты Кафедры Ученый совет Дополнительное профессиональное образование Бережливый вуз – МГТУ Новости Объявления Лист проблем Лист предложений (Кайдзен) Реализуемые проекты Архив проектов Фабрика процессов Рабочая группа «Бережливый вуз-МГТУ» Вакансии Профсоюз Противодействие терроризму и экстремизму Противодействие коррупции WorldSkills в МГТУ Научная библиотека МГТУ Реквизиты и контакты Управление имущественным комплексом Опрос в целях выявления мнения граждан о качестве условий оказания образовательных услуг Работа МГТУ в условиях предотвращения COVID-19 Документы, регламентирующие образовательную деятельность Система менеджмента качества университета Региональный центр финансовой грамотности Аккредитационно-симуляционный центр Абитуриентам Подача документов онлайн Абитуриенту 2023 Экран приёма 2022 Иностранным абитуриентам Международная деятельность Общие сведения Кафедры Новости Центр международного образования Академическая мобильность и международное сотрудничество Академическая мобильность и фонды Индивидуальная мобильность студентов и аспирантов Как стать участником программ академической мобильности Дни открытых дверей в МГТУ День открытых дверей online Университетские субботы Дни открытых дверей на факультетах Подготовительные курсы Подготовительное отделение Курсы для выпускников СПО Курсы подготовки к сдаче ОГЭ и ЕГЭ Онлайн-курсы для подготовки к экзаменам Подготовка школьников к участию в олимпиадах Малая технологическая академия Профильный класс Социально-экономический профиль Медико-фармацевтический профиль Инженерно-технологический профиль Эколого-биологический профиль Агротехнологический профиль Индивидуальный проект Кружковое движение юных технологов Олимпиады, конкурсы, фестивали Веб-консультации для абитуриентов и их родителей Веб-консультации для абитуриентов Родительский университет Олимпиады для школьников Отборочный этап Заключительный этап Итоги олимпиад Профориентационная работа Стоимость обучения Студентам Студенческая жизнь Стипендии Организация НИРС в МГТУ Студенческое научное общество Студенческие научные мероприятия Конкурсы Академическая мобильность и международное сотрудничество Образовательные программы Расписание занятий Расписание звонков Онлайн-сервисы Социальная поддержка студентов Общежития Трудоустройство обучающихся и выпускников Вакансии Обеспеченность ПО Инклюзивное образование Условия обучения лиц с ограниченными возможностями Доступная среда Ассоциация выпускников МГТУ Перевод из другого вуза Вакантные места для перевода Студенческое пространство Студенческое пространство Запись на мероприятия Отдел по социально-бытовой и воспитательной работе

Наука и инновации Научная инфраструктура Проректор по научной работе и инновационному развитию Научно-технический совет Управление научной деятельностью Управление аспирантуры и докторантуры Точка кипения МГТУ О Точке кипения МГТУ Руководитель и сотрудники Документы Контакты Центр коллективного пользования Центр народной дипломатии и межкультурных коммуникаций Студенческое научное общество Новости Научные издания Научный журнал «Новые технологии» Научный журнал «Вестник МГТУ» Научный журнал «Актуальные вопросы науки и образования» Публикационная активность Конкурсы, гранты Научные направления и результаты научно-исследовательской деятельности Основные научные направления университета Отчет о научно-исследовательской деятельности в университете Результативность научных исследований и разработок МГТУ Финансируемые научно-исследовательские работы Объекты интеллектуальной собственности МГТУ Результативность научной деятельности организаций, подведомственных Минобрнауки России (Анкеты по референтным группам) Студенческое научное общество Инновационная инфраструктура Федеральная инновационная площадка Проблемные научно-исследовательские лаборатории Научно-исследовательская лаборатория «Совершенствование системы управления региональной экономикой» Научно-исследовательская лаборатория проблем развития региональной экономики Научно-исследовательская лаборатория организации и технологии защиты информации Научно-исследовательская лаборатория функциональной диагностики (НИЛФД) лечебного факультета медицинского института ФГБОУ ВПО «МГТУ» Научно-исследовательская лаборатория «Инновационных проектов и нанотехнологий» Научно-техническая и опытно-экспериментальная база Центр коллективного пользования Научная библиотека Экспортный контроль Локальный этический комитет Конференции Международная научно-практическая конференция фундаментальные и прикладные аспекты геологии, геофизики и геоэкологии с использованием современных информационных технологий Международная научно-практическая конференция «Актуальные вопросы науки и образования» VI Международная научно-практическая онлайн-конференция Наука и университеты Международная деятельность Иностранным студентам Международные партнеры Академические обмены, иностранные преподаватели Академическая мобильность и фонды Индивидуальная мобильность студентов и аспирантов Факультет международного образования Новости факультета Информация о факультете Международная деятельность Кафедры Кафедра русского языка как иностранного Кафедра иностранных языков Центр Международного образования Центр обучения русскому языку иностранных граждан Приказы и распоряжения Курсы русского языка Расписание Академическая мобильность Контактная информация Контактная информация факультета международного образования Сведения об образовательной организации Основные сведения Структура и органы управления образовательной организацией Документы Образование Образовательные стандарты и требования Руководство. Педагогический (научно-педагогический) состав Материально-техническое обеспечение и оснащённость образовательного процесса Стипендии и меры поддержки обучающихся Платные образовательные услуги Финансово-хозяйственная деятельность Вакантные места для приёма (перевода) Международное сотрудничество Доступная среда Организация питания в образовательной организации

Errors in Measurement — GeeksforGeeks

Все экспериментальные исследования построены на измерении. Многие великие научные достижения были бы невозможны без постоянно повышающихся стандартов точности измерений. Количества измеряются с использованием международных измерений и являются абсолютно точными по сравнению с другими. Измерение производится так же, как это делают продавцы овощей: путем сравнения неизвестного количества веса с известным количеством веса. Любой расчет содержит уровень неопределенности, который называется ошибкой. Эта ошибка может возникнуть во время процедуры или даже в результате сбоя в эксперименте. В результате ни один подход не может иметь 100% точный расчет.

Целью каждого эксперимента является максимально точное определение физической величины. Однако каждое измерение состоит из некоторой ошибки, которая может возникнуть из-за наблюдателя, используемого инструмента или того и другого. Ошибки могут также закрадываться из-за небольших изменений условий эксперимента или из-за различных факторов, присущих эксперименту. Измеренное значение величины несколько отличается от ее истинного значения из-за наличия таких погрешностей.

Ошибка

Экспериментальные исследования и технологии основаны на измерениях. Любое измерение, выполненное с помощью любого измерительного прибора, дает определенную степень неопределенности. Эта неопределенность называется ошибка . Разница между реальным значением и оценочным значением величины называется ошибкой измерения. Ошибка может быть положительной или отрицательной.

Отклонение измеренной величины от фактической величины или истинного значения называется ошибкой .

E = A _м – A _t

где E – ошибка, A _м – измеренная величина, а A _t – истинное значение.

Различные типы ошибок

Ошибки в основном трех типов:

1. Систематические или постоянные ошибки:  

Тип ошибки, которая влияет на результаты эксперимента всегда в одном направлении, т. результат всегда выше или всегда ниже истинного значения, называется систематической ошибкой. На самом деле все инструментальные ошибки носят систематический характер. Если градуировка шкалы измерителя неверна или если измерения проводятся со шкалой при температуре, отличной от той, при которой она была откалибрована, будет внесена систематическая погрешность.

Итак, систематические погрешности бывают следующих видов:

(i) Инструментальные погрешности , примерами которых являются погрешность нуля винтового калибра, штангенциркуля, концевая погрешность измерительного моста и т. д.

(ii ) Личные ошибки по вине наблюдателя.

(iii) Ошибка из-за внешних причин, из-за изменений температуры, давления, скорости, высоты и т. д.

(iv) Ошибка из-за несовершенства.

Систематические ошибки обычно являются определяющими. Таким образом, они могут быть устранены путем принятия надлежащих мер предосторожности или могут быть исправлены.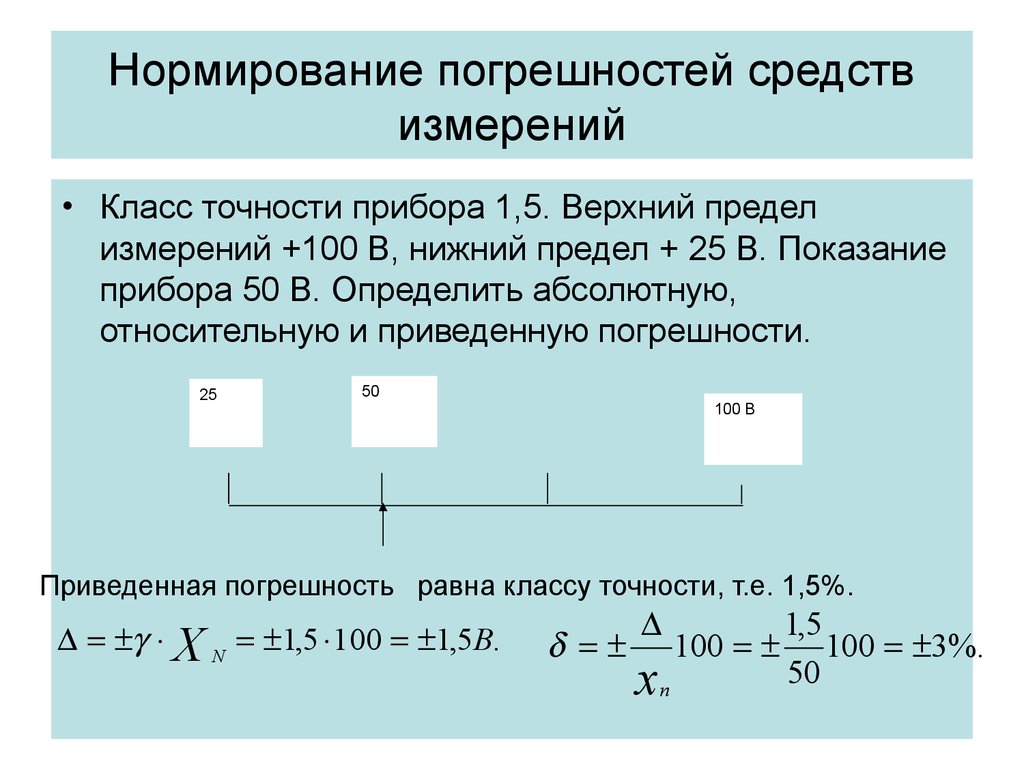 Однако, когда источник таких ошибок не может быть правильно идентифицирован, эксперимент повторяется другими методами.

2. Случайные или случайные ошибки: Результаты нескольких измерений одной и той же величины одним и тем же наблюдателем в одинаковых условиях не обнаруживают в общем точного совпадения, но отличаются друг от друга на небольшую величину. Инструмент может быть очень хорошим и чувствительным, наблюдатель может быть очень осторожным, но такие небольшие различия в результатах обычно имеют место. Невозможно проследить определенную причину таких ошибок; их источники неизвестны и неконтролируемы. Поэтому такие ошибки носят чисто случайный характер и называются случайными или случайными ошибками. Ошибка, возникающая случайно и причины которой неизвестны и неопределенны, называется 9.0009 случайная ошибка.

3. Грубые ошибки: Это крупные ошибки, возникающие из-за небрежности или излишней поспешности наблюдателя, которые также называются ошибками. В качестве примера можно привести неправильную запись некоторых данных. Так что ошибки явно не подчиняются закону и их можно избежать только при постоянной бдительности и внимательном наблюдении со стороны наблюдателя.

Погрешности наблюдений приборами и степень точности

• Во всех измерениях, даже после минимизации систематической и случайной погрешности, остаются погрешности наблюдений, присущие изготовлению используемого прибора. Шкала измерительного прибора делится изготовителем только до ее предела достоверности и не далее. Мы уже знаем, что наименьший выходной сигнал, который мы можем четко определить с помощью прибора, называется его наименьшее количество .
• Это дает наибольшую возможную ошибку, которая может возникнуть при измерениях этим прибором. Таким образом, во всех измерениях достижимая степень точности ограничена наименьшим количеством различных используемых инструментов. Например, шкала метра обычно имеет градуировку в миллиметрах. Следовательно, наибольшая погрешность, которую можно допустить при измерении длины такой шкалой, составляет 1 мм.
• Таким образом, результат измерения длины стержня должен быть выражен как длина стержня 22,4 ± 0,2 см. Это научный метод записи показаний с пределами погрешности. Это означает, что длина стержня находится между 22,6 см и 22,2 см. Ошибки известны как ошибки наблюдения или допустимые ошибки .
• Следовательно, в общем случае, если измеренное значение величины равно x, а пределы погрешности равны ∆x, то показание должно быть записано как x ± ∆x, что означает, что значение величины находится между x+ ∆x и x-∆r.

Пропорциональная ошибка и процентная ошибка

Отношение ошибки наблюдения к наблюдаемому показанию известно как пропорциональная ошибка. Если пропорциональная ошибка умножается на 100 или выражается в процентах, то она называется процентная ошибка . Пропорциональная ошибка также называется относительной ошибкой или f рациональной ошибкой .

Формула для расчета пропорциональной ошибки:

Пропорциональная ошибка = (ошибка / наблюдаемое показание)

или 

Процентная ошибка = (ошибка / наблюдаемое показание) × 100 %

0

0 6 Комбинация или распространение ошибок

Как правило, эксперимент в физике включает ряд измерений, выполненных с помощью различных инструментов. Окончательный результат затем рассчитывается путем выполнения различных математических операций. Погрешность конечного результата зависит от погрешностей отдельных измерений и от характера необходимых математических операций. Поэтому мы должны знать правила того, как ошибки комбинируются в различных математических операциях.

1. Сложение и вычитание: В этих операциях ошибки объединяются в соответствии со следующим правилом: при сложении или вычитании двух величин чистая ошибка в результате эксперимента представляет собой сумму ошибок, связанных с этими величинами.

Таким образом, если наблюдаемые значения двух величин равны x ± Δx и y ± Δy, а их сумма или разность равна z ± Δz, то ошибка Δz в значении z определяется выражением Δz = Δ.x + Δy.

например, Пусть длины двух стержней, измеренные по метровой шкале, равны 22:4 ± 0,2 см и 20,2 ± 0,2 см соответственно.

Тогда разница в их длине (22,4 – 20,2) или 2,2 см.

Но каждое показание ошибочно на 0,2 см. следовательно, наибольшая возможная ошибка в разнице составляет 0,4 см.

Так и пишем, разница в их длине 2,2±0,4см.

2. Умножение и деление: В этих операциях соответствующее правило определяется как:

Когда две величины умножаются или делятся, пропорциональная ошибка в результате равна сумме пропорциональных ошибок этих величин.

Итак, если z = xy или, z = (x/y), то согласно этому правилу

(Δz/z) = (Δx/x) + (Δy/y)

3. Полномочия количеств: Когда количество возводится в степень n, пропорциональная ошибка в конечном результате в n раз превышает пропорциональную ошибку этого количества.

Если z = x ⁿ  

Тогда по этому правилу

(Δz/z) = n(Δx/x)

г ^стр. /w ^q )

Тогда можно доказать, что:

 (Δz/z) = n (Δx/x)+p(Δy/y)+q(Δw/w)

Пропорциональная ошибка z = m × (пропорциональная ошибка x) + p × (пропорциональная ошибка y) + q × (пропорциональная ошибка w).

Примеры задач

Задача 1: Если все измерения в эксперименте выполняются до одинакового числа раз, то из-за какого измерения возникает максимальная ошибка?

Решение:

Максимальная ошибка возникает из-за измерения величины, которая появляется в формуле с максимальной степенью. Если все величины в формуле имеют одинаковые степени, то максимальная погрешность возникает из-за измерения величины, величина которой наименьшая.

Задача 2. Если длина карандаша равна (4,16 ± 0,01) см. Что это значит?

Решение:

Это означает, что истинное значение длины карандаша вряд ли будет меньше 4,15 см или больше 4,17 см.

Задача 3. Два сопротивления R ₁ =(100±5) Ом и R ₂ =(200±10) Ом соединены последовательно. Найдите эквивалентное сопротивление последовательного соединения.

Решение:

Поскольку известно, что

Эквивалентное сопротивление=R= R ₁ +R ₂

Учитывая, что сопротивление равно:

R ₁ = (100 ± 5)

R ₂ = (200 ± 10)

Следовательно,

R = (100 ± 5) + (200 ± 9 = 9 0 0 0

 900 ± 15) Ом

Задача 4: Конденсатор емкостью С = (2,0 ± 0,1) мкФ заряжается до напряжения V = (20 ± 0,2) В. Каков будет заряд Q на конденсаторе?

Решение: 

Q = CV 

   = 2,0×10 ^-6 × 20 C

   = 4,0×10 ^-5 Кулон.

Пропорциональная ошибка в C = (ΔC/C)

                                                   =5 %

Пропорциональная ошибка в V = (ΔV/V ) 

                                  = (0,2/20)

Процентная ошибка в V = (0,2/20)×100 03

Заряд конденсатора,

(ΔQ/Q) = (ΔC/C) + (ΔV /В)

Процентная ошибка в Q = 5%+1%

                                  = 6% 009 (4,0±0,24)×10 ^-5 Кулон

Задача 5: Центростремительная сила, действующая на тело массой 50 кг, движущееся по окружности радиусом 4 м с равномерной скоростью 10 м/с, рассчитывается по уравнению F = mv ² /r. Если точность измерения m, v и r составляет 0,5 кг, 0,02 м/с и 0,01 м соответственно, определите процентную погрешность силы.

Решение:

Известно, что

(ΔF/F) = (Δm/m) + 2(Δv/v) + (Δr/r) 0,5/50) 

             = 0,01

(Δv/v) = (0,02/10)

          = 0,002

(Δr/r) = (0,00003)     = 0,0025

Итак, (ΔF/F ) = 0,01 + 2(0,002) + (0,0025)

                  = 0,0165

Таким образом, процентная ошибка в силе = (0,0165) × 100%                = 1,65 %

Задача 6. Сопротивление R = V/I, где V = (200 ± 5) В, а I = (20 ± 0,2) А. Найдите процентную ошибку R.

Решение:

Пропорциональная погрешность в V = (ΔV/V)

                                                                                  = 2,5%

Пропорциональная ошибка в I = ( ΔI/I) 

                                             = (0,2/20)

Процентная ошибка в I = (0,2/20) × 100%

                                 = 1%                      = 3,5%

Задача 7. Масса измеряют длину одной стороны куба и вычисляют его плотность. Если процентные ошибки измерения массы и длины составляют соответственно 1% и 2%, то какова процентная ошибка измерения плотности?

Решение: 

Если масса куба равна m, а длина одной его стороны равна l, то его плотность

d = m/l³

Итак, (Δd/d) = (Δm /M) + 3 (ΔL/L)

Таким образом, процентная ошибка в плотности = (1 + 3 × 2)%

= 7%

Ошибки при измерении

Ошибка? Нет. .. не мерили неправильно … это примерно точность .

Измерительные приборы не точны!

Степень точности

Точность зависит от инструмента, которым вы измеряете. Но как правило:

Степень точности половина единицы каждая сторона единицы измерения

Примеры:

и 7½ измеряется как «7»
Если ваш прибор измеряет в «2» , то любое значение между 7 и 9 измеряется как «8»

Обратите внимание, что стрелка указывает на одно и то же место, но измеренные значения разные!

Плюс или Минус

Мы можем показать ошибку, используя знак «Плюс или Минус»:

±

Когда значение может быть между 6½ и 7½ : 7 ±0,5 Ошибка ±0,5
Когда значение может быть между 7 и 9 : 8 ±1 Ошибка ±1

 

Пример: забор имеет длину 12,5 метра с точностью до 0,1 метра

С точностью до 0,1 м означает, что может быть до 0,05 м в любом случае:

Длина = 12,5 ± 0,05 м

Таким образом, длина может быть где-то между 12,45 м и 12,55 м.

 

Абсолютная, относительная и процентная погрешность

Абсолютная погрешность представляет собой разницу между фактическим и измеренным значением .

Но… при измерении мы не знаем фактического значения! Поэтому используем максимально возможную ошибку.

В приведенном выше примере абсолютная ошибка составляет 0,05 м

Что случилось с ± … ? Ну, нам просто нужен размер (абсолютное значение) разницы.

Относительная ошибка — это абсолютная ошибка, деленная на фактическое измерение.

Мы не знаем фактического измерения, поэтому лучшее, что мы можем сделать, это использовать измеренное значение :

Относительная ошибка = Абсолютная ошибка Измеренное значение

Ошибка в процентах — это относительная ошибка, показанная в процентах (см. Ошибка в процентах).

Рассмотрим их на примере:

Пример: ограждение (продолжение)

Длина = 12,5 ± 0,05 м

Итак:

Абсолютная погрешность = 0,05 м

Абсолютная погрешность = 0,05 м

И:

Относительная 7 0,05 м 12,5 м   = 0,004

И:

Процентная ошибка = 0,4% 

Другие примеры:

Пример: Термометр измеряет с точностью до 2 градусов.

Температура была измерена как 38° C

Температура может быть до 1° по обе стороны от 38° (т.е. между 37° и 39°)

 

Температура = 38 ±1°

Итак:

Абсолютная погрешность = 1°

И:

И:

Относительная ошибка =   1° 38°   = 0,0263…

И:

Процентная ошибка = 2,63…%

Пример: Вы измеряете высоту растения 80 см (с точностью до сантиметра).

Это означает, что вы можете ошибиться на 0,5 см (растение может быть между 79.5 и 80,5 см высотой)

 

Высота = 80 ±0,5 см

Итак:

Абсолютная погрешность = 0,5 см

А:

Относительная погрешность =   90 9 0 8 0 0,65 см = 0,00625

А :

Процентная ошибка = 0,625% 

 

Площадь

При расчете площадей вам нужно думать как о ширине , так и о длине … они оба могут быть наименьшим размером или оба наибольшим.

Пример: Алекс измерил поле с точностью до метра и получил ширину 6 м и длину 8 м.

Измерение с точностью до метра означает, что истинное значение может быть до на полметра меньше или больше.

Ширина (w) может быть от 5,5 м до 6,5 м:

5,5 ≤ w < 6,5

Длина (l) может быть от 7,5 м до 8,5 м:

7,5 ≤ l < 8,5 9000 Площадь равна ширине × длине:

A = w × l

Наименьшая возможная площадь: 5,5 м × 7,5 м = 41,25 м ²
Измеренная площадь: 6 м × 8 м = 48 м ²
Максимально возможная площадь: 6,5 м × 8,5 м = 55,25 м 9094172 2 8

41,25 ≤ A < 55,25

 

Абсолютная, относительная и процентная погрешность

Единственная сложность здесь в том, что … какое является абсолютной погрешностью?

• От 41,25 до 48 = 6,75
• От 48 до 55,25 = 7,25

Ответ: выбери самый большой! Итак:

Абсолютная погрешность = 7,25 м ²

Относительная погрешность = 7,25 м ² 48 м ²

2.

No related posts.